Abstract
Recently, a series of urban diseases have seriously impacted the development of large and medium cities. The development of urban underground space (UUS) is widely regarded as an effective solution. Due to the irreversibility of underground space resources, it is important to formulate scientific and reasonable development planning based on evaluation of the development potential of urban underground space (DPUUS). In this work, from the perspective of society, economy, and environment, an evaluation model of the DPUUS was established, and nine indexes were selected, including population density, vehicle possessive quantity per 100 capita, policy support, GDP per capita, GDP per km2, land price, geographical position, geological conditions, and natural disasters. The comprehensive weight method (CWM) combined with subjective and objective weights was used to determine the final weight of the evaluation index. Set pair analysis (SPA) and the credible degree recognition criterion (CDRC) were applied to determine the DPUUS grade of each city, which can provide a new idea for DPUUS.
1. Introduction
With the gradual implementation of the new urbanization strategy, the number and scale of cities and towns is growing in China, and urbanization is predicted to reach 65% by 2030 [1]. At the same time, various urban diseases, such as population expansion, land shortages, traffic congestion, environmental degradation, etc., have seriously influenced the healthy, rapid, and sustainable development of large and medium cities. The development and utilization of urban underground space (UUS) is a scientific and effective solution to solving city problems and promoting sustainable urban development [2,3]. UUS is a precious non-renewable resource that can provide alternate space for urban development. First, it can save land resources and ease the tensions surrounding urban construction land. With the rapid development of most cities, it is easy to neglect the construction of UUS, resulting in the waste of UUS. Second, the development and utilization of UUS can improve urban transportation, effectively solve traffic congestion, and improve the ground environment and urban ecosystem. Lastly, UUS is covered with a certain thickness of soil or rock layers and has strong concealment, isolation, and protection. Hence, the development and utilization of UUS can strengthen the ability to prevent and reduce the extent of disasters in the city. In addition, UUS has excellent thermal characteristics and the advantages of sound insulation, being less impacted by natural disasters, and causing less environmental pollution, which can directly save energy, cut carbon emissions, and mitigate urban environmental pollution [4,5,6,7,8,9,10,11,12]. Considering these strengths, UUS mainly has four functions: underground transportation, basement car parks, underground shopping centers, and underground municipal facilities.
However, there are many problems in the development and utilization of UUSs in China, which are mainly manifested in the single-form development of aboveground and underground UUSs that lacks stratification and co-ordination while also suffering from scattered layouts. Additionally, it will have irreversible consequences once the specific use has been assigned [13]. In order to ensure the sustainable development of UUS, it is necessary to work out scientific and reasonable planning for the development and utilization of UUS, which is an important part of urban planning [14]. To achieve this, many scholars have studied UUS from different perspectives, such as research on the quantitative demand and driving factors of UUS [15,16,17,18], geological suitability affecting development and utilization of UUS [19], quality evaluation of UUS [20], sustainable development and utilization of UUS [21,22], and so on. However, the literature mentioned above focuses mainly on a single aspect of UUS, which cannot represent the development potential of one city comprehensively nor provide a reference for administrators or planners. Thus, research on the development potential of urban underground space (DPUUS) has received great interest. Wang et al. [23] investigated five key factors (geological features, land price and location conditions, economic development level, development advantages of underground space, and compatibility with urban planning) affecting DPUUS based on a case study and proposed a structural equation model. Doyle [24] presented a procedure for mapping underground resource potential, including space, groundwater, geothermal energy, and geomaterials. Zhao and Wu [25] investigated the quantitative evaluation model for UUS potential based on supply and demand. To describe the present status and development trends of UUS comprehensively, Chen et al. [26] presented a correlation analysis based on the proposed underground space development evaluation index system. All the results mentioned above have enriched research in the fields of the DPUUS. However, evaluation models of the DPUUS that consider social, economic, and environmental factors systematically have rarely been reported.
This study aims to identify the factors of the DPUUS and develop an evaluation system for the DPUUS based on set pair analysis (SPA) and the comprehensive weight method (CWM). In the system, the intuitionistic fuzzy analytic hierarchy process (IFAHP) and the entropy weight method (EWM) were employed to determine the subjective and objective weights, respectively. Subsequently, based on the minimum information entropy principle, the comprehensive weight of the evaluation indexes can be obtained, which is more reasonable and accurate. The results provide a new perspective for related research on the DPUUS.
2. Materials and Methods
2.1. Evaluation System of the DPUUS
2.1.1. Determination of the Evaluation Index
The development of UUS is driven by a series of urban problems and needs, which means the more serious the urban problems are and the more urgent the demand for UUS is, then the greater the DPUUS is. Due to high development costs, the economic level of the city is a key factor affecting the DPUUS. Additionally, the environment also plays a vital role in influencing the DPUUS, such as urban location, geological conditions, etc. Transportation hub cities often have better economic development and correspondingly have greater DPUUS. In addition, poor geological conditions not only increase the difficulty and cost of development, but also accidents or casualties, which are not conducive to the development of UUS. The framework of the DPUUS is shown in Figure 1. Recently, the DPUUS has become an important reference to assist administrators, planners, and researchers in making decisions on the development and utilization of UUS. As in the literature mentioned above, many researchers have studied this issue thoroughly, mainly in terms of influencing factors, evaluation models, and correlation analysis for the DPUUS.
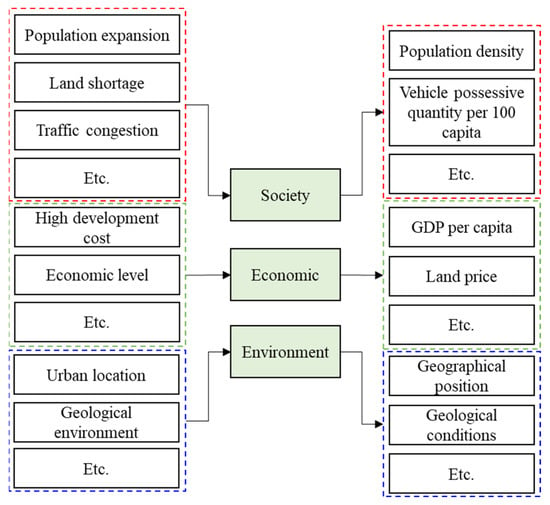
Figure 1.
Framework of the DPUUS.
- Society
Social factors, such as the urban population, residential density, population growth, urban sprawl, the shortage of space, traffic problems, etc., are the main drivers of the development and utilization of UUS [15,27,28,29]. Based on statistical data from various regions, Xu [30] discovered that population density and vehicle ownership were the main factors of UUS development. A positive correlation between urban population and developed UUS densities was found according to quantitative UUS data [29]. Considering the availability of data and the representativeness of factors, population density, vehicle possessive quantity per 100 capita, and policy support were suggested to reflect social influence.
- Economy
Compared with ground engineering in the same area, one-time investment in underground projects is about 3–4 times greater. Therefore, the size of the economy is the basic condition that ensures the development and utilization of UUS. GDP per capita, land price, and GDP per km2 have strong correlations with UUS [15,30,31]. According to Wang [32], China’s first-tier cities enter the stage of comprehensive development and utilization of UUS when their GDP per capita reaches USD 800–1000. The development of UUS reaches a rapid development period at a GDP of about USD 5000 per capita. In this period, underground buildings with multiple functions and complex technologies, such as underground complexes, begin to be widely constructed. However, second- and third-tier cities, influenced by the scale of the city, gradually enter the development stage when the GDP per capita is between USD 3000 and 5000. Considering that the development of UUS in first-tier cities is relatively mature, the GDP per capita of second- and third-tier cities was used as a reference.
- Environment
The environment is the key factor affecting the development and utilization of UUS, which can be summarized into two aspects: internal environment and external environment. The main internal environment is geological conditions, such as soil or rock properties, groundwater conditions, etc. [23], whereas the external environment includes geographical position, regional structure, and natural disasters. Geological conditions play a vital role in the use and cost of UUS [33]. Poor geological conditions not only increase construction difficulty and costs but may even cause casualties.
Based on these published research results, from the perspective of society, economy, and environment, an evaluation system of the DPUUS can be proposed. This system includes nine indexes: population density (X1), vehicles possessive quantity per 100 capita (X2), policy support (X3), GDP per capita (X4), GDP per km2 (X5), land price (X6), geographical position (X7), geological conditions (X8), and natural disasters (X9), as shown in Figure 2.
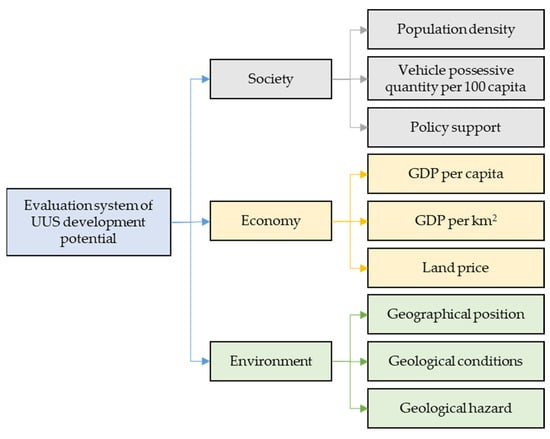
Figure 2.
Evaluation system of the DPUUS.
2.1.2. Grades of the DPUUS
Based on the above analysis and collected social, economic, and environmental data, the DPUUS is separated into five levels. The range [0, 10] is selected for the set of DPUUS values, which are combined with the “principle of equal division”; thus, the development potential level determination table can be built, as indicated in Table 1. Level I means that the development potential is very high, and the UUS can be actively developed and utilized on a large scale. Level II represents high potential within the expected range and also indicates that the UUS can be reasonably developed. Level III represents normal development potential, which means the UUS can be developed only after scientific and reasonable planning. Level IV means low potential beyond the expected range, and the UUS should be developed in a limited way. Level V represents very low potential, which may lead to a waste of funds and even cause huge losses. Correspondingly, based on the abovementioned literature and collected data [15,16,17,18], a quantitative analysis of each evaluation index is shown in Table 2.

Table 1.
Determination of the DPUUS.

Table 2.
Grade standard of indices used in this study.
2.1.3. Data Acquisition
To better guide administrators or planners in making decisions regarding the development and utilization of UUS, the DPUUS for 16 cities in China was surveyed, including Hangzhou, Wuxi, Dongguan, Foshan, Changsha, Zhengzhou, Xian, Qingdao, Tianjin, Wuhan, Chongqing, Chengdu, Jiaxing, Wenzhou, Ningbo, and Nanjing. These cities are widely distributed, and their society, economy, and environment are quite different. The index data of the model were obtained from the statistical yearbook of cities (2021).
2.2. Evaluation Method of the DPUUS
2.2.1. The CWM Based on the IFAHP and EWM
To obtain more reasonable weight, the CWM combining subjective and objective weights is used to determine the comprehensive weight of an evaluation index. The IFAHP and EWM are first employed to calculate the subjective and objective weights, respectively. The comprehensive weight can then be obtained based on the principle of information entropy [34].
- IFAHP
The IFAHP is an improved evaluation method combining an intuitionistic fuzzy set and an analytic hierarchy process, which can figure out some uncertainties effectively and reflect the expert’s judgment more truly [35]. The main steps are as follows:
(1) Establishment of the judgment matrix
The expert semi-quantitative method is employed to establish a judgment matrix, which mainly depends on the experience of the expert. To mitigate the subjectivity of evaluation, the importance value is denoted by values from 0.1 to 1.9 (Table 3). The judgment matrix, S, can be obtained by comparing the indexes with each other according to their importance and can be expressed as [36]
where n is the total number of evaluation indexes and μij and νij are the membership degree and nonmembership degree of the intuitionistic fuzzy set value, respectively.

Table 3.
Evaluation grades and values.
(2) Consistency checking
Based on judgment matrix S, the intuitionistic fuzzy set consistency judgment matrix can be established [36].
If j > i +1,
If j = i +1 or j = i, If j < i,
The distance measures d between S and can be calculated to check consistency, which can be expressed as
If d(S, ) < 0.1, S is considered to meet the requirements of consistency checking. An iteration parameter σ (σ∈[0, 1]) is always employed to change the value of the judgment matrix until consistency is met if consistency checking is not satisfied, which means experts do not need to score again [36]. The transformed matrix, S′, is
(3) Calculation of weight
The subjective weight, wsj, can be expressed as [34,36]
- EWM
The EWM is a widely used method to determine the objective weight of the evaluation index, which mainly relies on the variation degree of indexes, such as civil engineering [34,37], mechanical engineering [38], systems engineering [39], etc. The greater the information entropy, the smaller the variation degree of an index and weight and vice versa [40]. The main steps are as follows:
(1) An initial matrix is established, which is
where m represents the total number of evaluation samples and n is the total number of evaluation indexes.
(2) Normalization of indexes
To positive indexes,
To negative indexes,
(3) Determination of the proportion of the j-th index of the i-th evaluation sample, pij.
(4) Calculation of the information entropy of j-th index.
(5) Calculation of the objective weight, woj, for each index.
- Comprehensive weight
Depending on the principle of information entropy, the comprehensive weight combined with the subjective weight and objective weight can be obtained as follows [41]:
where wj represents the comprehensive weight, w1j is the subjective weight obtained using the IFAHP, and woj is the objective weight determined using the EWM.
2.2.2. Evaluation Method Based on SPA
- SPA theory
The SPA method, proposed by Zhao [42], is used to deal with uncertain problems by dividing objectives into an uncertain system and identifying the relation from the perspectives of identity, discrepancy, and contrariness. The connection degree is a main tool of the SPA method, which can be used to depict the internal relationship of a set pair. For two interrelated sets A and B, H = (A, B) can be a set pair, and the corresponding connection degree, μ, can be defined as
where p and q are the coefficients of discrepancy degree and contrary degree, respectively, with p∈[−1, 1] and q = −1. N represents the total number of attributes, N = S + F + L, in which S, F, and L are the identity, discrepancy, and contrary features of sets A and B, respectively. The parameters a, b, and c are identical degree, discrepancy degree, and contrary degree, respectively, and a + b + c = 1.
Equation (21) is a 3-element connection degree, which cannot be used to describe the problems with multiple discrepancy degrees. Hence, it is necessary to extend the 3-element connection degree to a multivariate connection degree to reflect the certain and uncertain relationship between the DPUUS and corresponding factors, which can be expressed as
where p1, p2, …, pn−2 represents the coefficient of discrepancy degree. F1, F2, …, Fn−2 represents the discrepancy features. b1, b2, …, bn−2 signifies discrepancy degrees representing different degrees of difference, and a + b1 + b2 + … + bn−2 + c = 1.
Two types of indices are introduced for the evaluation system of the DPUUS: economic indices and cost indices [43]. For economic indices, the larger the values of the indices, the greater the DPUUS, while for cost indices, the opposite is true. The graded 5-element connection degree for economic and cost indices can be expressed as Equations (23) and (24), respectively.
where n is the n-th evaluation sample, k is the k-th index, x is the value of the k-th index of the n-th sample. SI, SII, SIII, and SIV are the boundary values of the grades of the evaluation index.
- Determination of the comprehensive connection degree
Coupling comprehensive weight and connection degree, the comprehensive connection degree of multiple indices of set pair H can be obtained [42].
Given
Equation (22) can be rewritten as follows:
where f1, f2, f3, f4, and f5 indicate the probability that the DPUUS belongs to level I, II, III, IV, and V, respectively.
- Determination of DPUUS level
In order to improve the accuracy and reliability of the evaluation results, the credible degree recognition criterion (CDRC) are introduced to determine the final development potential grade of UUS [44]. Let λ be confidence, and its recognition model is
k0 is the final potential level corresponding to Equation (28), and 0.5 ≤ λ < 1.0. Generally, 0.6 or 0.7 is taken, and the larger the value is, the more conservative the evaluation result is.
3. Results and Discussion
3.1. Calculation of Subjective Weight
According to the opinions of experts with experience in the development and utilization of UUS, the judgment matrix S can be determined.
Based on Equations (2)–(5), the consistency judgment matrix and distance measure d can be obtained. d = 0.134 > 0.1, which means that the consistency of S failed to meet the requirement. Hence, Equations (7)–(9) were used to modify matrix S with δ = 0.7. Finally, matrix S satisfies consistency with d = 0.07.
Based on Equations (10)–(12), the subjective weight wsj based on the IFAHP can be obtained.
3.2. Calculation of Objective Weight
Based on the statistical yearbook of cities and advice from experts, the value of each evaluation index can be determined. In order to avoid the influence of various units of index values on evaluation results, the standardized method is adopted to deal with the original evaluation values based on Equations (14) and (15). The results are shown in Table 4.

Table 4.
Standardized result of the evaluation index.
The weight distribution and entropy of each index can then be obtained based on Equations (16) and (17). Finally, the objective weight of each index can be calculated.
3.3. Determination of Comprehensive Weight
Substituting the objective and subjective weights into Equation (20), the comprehensive weight of each index can be obtained.
3.4. Determination of Single-Index Connection Degree
Taking Hangzhou as an example, the connection degree function of the evaluation index can be plotted based on Equations (23) and (24), as shown in Figure 3. The single-index connection degrees can be seen in Table 5.
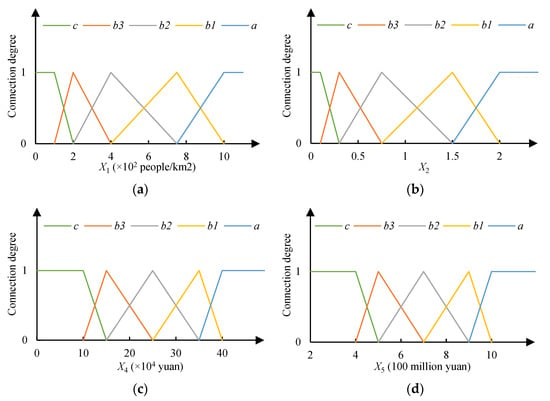
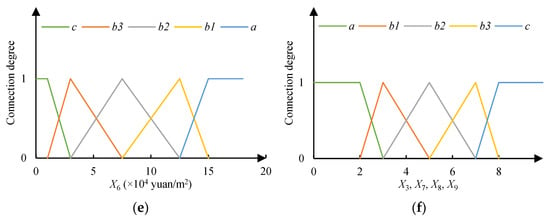
Figure 3.
Connection degree function of each index membership: (a) X1; (b) X2; (c) X4; (d) X5; (e) X6; (f) X3, X7, X8, X9.

Table 5.
Single-index connection degree of Hangzhou.
3.5. Determination of Multiple-Index Connection Degree
Coupling the comprehensive weights into the single-index connection degree, the comprehensive connection degree of the development potential of Hangzhou can be calculated based on Equation (25).
3.6. Determination of the DPUUS Level
According to Equation (28) and taking λ = 0.6, when k = 1, f1 = 0.425 < 0.6, while f1 + f2 = 0.694 > 0.6 when k = 2. Therefore, at the end of 2020, the DPUUS in Hangzhou was at level II. Similarly, the development potential grades of UUS in other cities were calculated, and the results are shown in Table 6.

Table 6.
Evaluation results of the DPUUS.
From Table 5, Nanjing has the greatest potential for UUS development, ranking first, followed by Hangzhou, Changsha, Zhengzhou, Xian, Qingdao, Tianjin, Wuhan, Chengdu, and Ningbo, all with a grade of II. Wuxi, Dongguan, Foshan, Chongqing, Jiaxing, and Wenzhou have medium development potential, with a grade of III.
In this model, population density is the most important index, which has a direct impact on the DPUUS. The larger the population density, the greater the DPUUS. The land price, natural disasters, GDP per km2, and policy support also have great influence due to their high weights in the model. According to Sun [45], the development intensity of UUS has a strong linear positive correlation with population density and GDP per km2, while the scale of per capita UUS has a certain correlation with vehicle possessive quantity per 100 capita. Hence, the abovementioned indexes can be used as important factors for administrators or planners to consider when evaluating the DPUUS.
4. Conclusions
Evaluation of the DPUUS is an important part of promoting urban sustainable development, which has great economic and social value in mitigating a series of urban problems. However, unreasonable evaluation results for the DPUUS can be unfavorable to energy conservation and sustainable urban development. Hence, it is important to scientifically estimate potential for the development of UUSs. Finally, the evaluation indicators and model were proposed. The relevant findings of this work are summarized as follows:
- (1)
- A model for the DPUUS was established based on SPA and the CWM, which analyzed the certainty and uncertainty of the DPUUS from the perspectives of identity, discrepancy, and contrariness and provided a new idea for evaluation of the DPUUS.
- (2)
- The CWM was introduced to determine the index weights and combined with the AHP and EWM to mitigate the influence of subjective factors. Meanwhile, the CDRC were employed to differentiate the DPUUS, thus avoiding the deficiency of the maximum membership principle. Both are beneficial in improving the reliability of evaluation results.
- (3)
- Due to the unavailability of data, some other critical factors are not considered in this work, such as developed underground space. Hence, it is important to conduct a comprehensive investigation of the developed UUS and take the concerned key factors of the DPUUS into account to enhance the accuracy and reliability of the evaluation model in the future.
Author Contributions
Conceptualization, Q.L. and Y.D.; methodology, Q.L.; software, B.Z.; validation, Q.L., Y.D. and B.Z.; formal analysis, Y.D.; investigation, Y.D.; resources, Q.L.; data curation, B.Z.; writing—original draft preparation, Q.L. and Y.D.; writing—review and editing, Q.L.; supervision, B.Z.; project administration, Y.D.; funding acquisition, Y.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Science and Technology Program of Zhejiang Province (2022C35026).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- China Urban Development Report Editorial Board. China Urban Development Report 2010; China City Press: Beijing, China, 2011. [Google Scholar]
- Chen, Z.L.; Wang, Y.B. The Urban Underground Space Planning; Southeast University Press: Nanjing, China, 2005. [Google Scholar]
- Shu, Y.; Peng, F.L.; Wang, X.; Zhu, H.H. Study and practice of urban underground space planning in China. China J. Undergr. Space Eng. 2006, 2, 1125–1129. [Google Scholar]
- Zhang, Q.; Phillips, R.P.; Manzoni, S.; Scott, R.L.; Oishi, A.C.; Finzi, A.; Daly, E.; Vargas, R.; Novick, K.A. Changes in photosynthesis and soil moisture drive the seasonal soil respiration-temperature hysteresis relationship. Agric. For. Meteorol. 2018, 259, 184–195. [Google Scholar] [CrossRef]
- Yu, J.; Kang, Y.; Zhai, Z. Advances in research for underground buildings: Energy, thermal comfort and indoor air quality. Energy Build. 2020, 215, 109916. [Google Scholar] [CrossRef]
- Tinti, F.; Barbaresi, A.; Benni, S.; Torreggiani, D.; Bruno, R.; Tassinari, P. Experimental analysis of shallow underground temperature for the assessment of energy efficiency potential of underground wine cellars. Energy Build. 2014, 80, 451–460. [Google Scholar] [CrossRef]
- Admiraal, H.; Cornaro, A. Underground Spaces Unveiled: Planning and Creating the Cities of the Future; Ice Publishing: London, UK, 2018. [Google Scholar]
- Bobylev, N. Strategic environmental assessment of urban underground infrastructure development policies. Tunn. Undergr. Space Technol. 2006, 21, 469. [Google Scholar] [CrossRef]
- Carmody, J.; Sterling, R. Underground Building Design: Commercial and Institutional Structures; Van Nostrand Reinhold: Washington, DC, USA, 1983. [Google Scholar]
- Sterling, R. Underground technologies for livable cities. Tunn. Undergr. Space Technol. 1997, 12, 479–490. [Google Scholar] [CrossRef]
- Wang, S.; Xia, Q.; Xu, F. Investigation of collector mixtures on the flotation dynamics of low-rank coal. Fuel 2022, 327, 125171. [Google Scholar] [CrossRef]
- Du, X.; Feng, G.; Zhang, M.; Wang, Z.; Liu, W. Influence of backfilling rate on the stability of the “backfilling body-immediate roof” cooperative bearing structure. Int. J. Min. Sci. Technol. 2022, 32, 1197–1206. [Google Scholar] [CrossRef]
- Sterling, R.; Nelson, S. Planning for Underground Space; Report. No. 375; American Planning Association, Planning Advisory Service: Chicago, IL, USA, 1983. [Google Scholar]
- Chen, Z.L.; Liu, H. The Master Planning of Urban Underground Space; Southeast University Press: Nanjing, China, 2011. [Google Scholar]
- He, L.; Song, Y.; Dai, S.Z.; Durbak, K. Quantitative research on the capacity of urban underground space—The case of Shanghai, China. Tunn. Undergr. Space Technol. 2012, 32, 168–179. [Google Scholar] [CrossRef]
- Li, X.Z.; Xu, H.; Li, C.; Sun, L.P.; Wang, R. Study on the demand and driving factors of urban underground space use. Tunn. Undergr. Space Technol. 2016, 55, 52–58. [Google Scholar] [CrossRef]
- Wu, L.M.; Xia, H.S.; Cao, X.W.; Zhang, C.; Dai, C. Research on quantitative demand of underground space development for urban rail transit station areas: A case study of metro line 1 in Xuzhou, China. Urban Rail Transit 2018, 4, 257–273. [Google Scholar] [CrossRef]
- Xia, H.S.; Lin, C.X.; Liu, X.T.; Liu, Z.S. Urban underground space capacity demand forecasting based on sustainable concept: A review. Energy Build. 2022, 255, 111656. [Google Scholar] [CrossRef]
- Dou, F.F.; Li, X.H.; Xing, H.X.; Yuan, F.; Ge, W.Y. 3D geological suitability evaluation for urban underground space development—A case study of Qianjiang Newtown in Hangzhou, Eastern China. Tunn. Undergr. Space Technol. 2021, 115, 104052. [Google Scholar] [CrossRef]
- Hou, W.S.; Yang, L.; Deng, D.C.; Ye, J.; Clarke, K.; Yang, Z.J.; Zhuang, W.M.; Liu, J.X.; Huang, J.C. Assessing quality of urban underground spaces by coupling 3D geological models: The case study of Foshan city, South China. Comput. Geosci. 2016, 89, 1–11. [Google Scholar] [CrossRef]
- Li, H.Q.; Li, X.Z.; Soh, C.K. An integrated strategy for sustainable development of the urban underground: From strategic, economic and societal aspects. Tunn. Undergr. Space Technol. 2016, 55, 67–82. [Google Scholar] [CrossRef]
- Peng, F.L.; Qiao, Y.K.; Sabri, S.; Atazadeh, B.; Rajabifard, A. A collaborative approach for urban underground space development toward sustainable development goals: Critical dimensions and future directions. Front. Struct. Civ. Eng. 2021, 15, 20–45. [Google Scholar] [CrossRef]
- Wang, X.; Zhen, F.; Huang, X.J.; Zhang, M.; Liu, Z.H. Factors influencing the development potential of urban underground space: Structural equation model approach. Tunn. Undergr. Space Technol. 2013, 38, 235–243. [Google Scholar] [CrossRef]
- Robert, D.M. From hydro/geology to the streetscape: Evaluating urban underground resource potential. Tunn. Undergr. Space Technol. 2016, 55, 83–95. [Google Scholar]
- Zhao, Y.T.; Wu, K.J. Quantitative evaluation of the potential of underground space resources in urban central areas based on multiple factors: A case study of Xicheng district, Beijing. Procedia Eng. 2016, 165, 619–621. [Google Scholar] [CrossRef]
- Chen, Z.L.; Chen, J.Y.; Liu, H.; Zhang, Z.F. Present status and development trends of underground space in Chinese cities: Evaluation and analysis. Tunn. Undergr. Space Technol. 2018, 71, 253–270. [Google Scholar] [CrossRef]
- Golany, G.S.; Ojima, T. Geo-Space Urban Design; John Wiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Bobylev, N. Mainstreaming sustainable development into a city’s master plan: A case of urban underground space use. J. Land Use Policy 2009, 26, 1128–1137. [Google Scholar] [CrossRef]
- Bobylev, N. Underground space as an urban indicator: Measuring use of subsurface. J. Tunn. Undergr. Space Technol. 2016, 55, 40–51. [Google Scholar] [CrossRef]
- Xu, H. The Study on the Impact of Urban Development Stage and Location on the Development of Urban Underground Space. Master’s Thesis, Nanjing University, Nanjing, China, 2014. [Google Scholar]
- Liu, J. An Empirical and Methodological study on Demand Forecasting for Urban Underground Space. Master’s Thesis, Tsinghua University, Beijing, China, 2009. [Google Scholar]
- Wang, B. Exploration and Practice of the Development and Utilization of Urban Underground Space. Master’s Thesis, China University of Geosciences, Beijing, China, 2013. [Google Scholar]
- Hunt, D.V.L.; Jefferson, I.; Rogers, C.D.F. Assessing the sustainability of underground space usage—A toolkit for testing possible urban futures. J. Mt. Sci. 2011, 8, 211–222. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Wang, X.; Wang, Z.; Pang, C. Evaluation on the risk of water inrush due to roof bed separation based on improved set pair analysis—Variable fuzzy sets. ACS Omega 2022, 7, 9430–9442. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z. A representable uninorm-based intuitionistic fuzzy analytic hierarchy process. IEEE Trans. Fuzzy Syst. 2020, 28, 2555–2569. [Google Scholar] [CrossRef]
- Xu, Z.; Liao, H. Intuitionistic Fuzzy Analytic Hierarchy Process. IEEE Trans. Fuzzy Syst. 2014, 22, 749–761. [Google Scholar] [CrossRef]
- Lu, H.; Sheng, X.; Du, F. Economic benefit evaluation system of green building energy saving building technology based on entropy weight method. Processes 2022, 10, 382. [Google Scholar] [CrossRef]
- Gu, H.; Zhu, H.; Cui, X. Multivariate state estimation technique combined with modified information entropy weight method for steam turbine energy efficiency monitoring study. Energies 2021, 14, 6795. [Google Scholar] [CrossRef]
- Zhu, Y.; Tian, D.; Yan, F. Effectiveness of entropy weight method in decision-making. Math. Probl. Eng. 2020, 2020, 3564835. [Google Scholar] [CrossRef]
- Bai, H.; Feng, F.; Wang, J.; Wu, T. A combination prediction model of long-term ionospheric foF2 based on entropy weight method. Entropy 2020, 22, 442. [Google Scholar] [CrossRef]
- Zhang, D.; Wei, K.; Yao, Y.; Yang, J.; Zheng, G.L.; Li, Q. Capture and prediction of rainfall-induced landslide warning signals using an attention-based temporal convolutional neural network and entropy weight methods. Sensors 2022, 22, 6240. [Google Scholar] [CrossRef] [PubMed]
- Zhao, K. Set pair and set pair analysis: A new concept and systematic analysis method. In Proceedings of the National Conference on System Theory and Regional Planning; International Institute for Applied Systems Analysis: Laxenburg, Austria, 1989; pp. 87–91. [Google Scholar]
- Deng, H.X.; Li, C.J.; Zhu, B.; Ding, J. Integrative assessment of ecocarrying capacity based on set pair. Analysis 2006, 23, 35–38. [Google Scholar]
- Li, W.; Li, Q.; Liu, Y.; Wang, S.; Pei, X. A new method of bid evaluation for renovation projects: Based on unascertained measure theory and entropy weight. PLoS ONE 2023, 17, e0271534. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.P.; Li, X.Z.; Zhou, D.K.; Wang, R.; Liu, C. Study on the correlation between underground space development and socio-economic factors. China J. Undergr. Space Eng. 2018, 14, 859–868. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).