Spatial Economic Impacts of the TEN-T Network Extension in the Adriatic and Ionian Region
Abstract
1. Introduction
- testing spatial modelling specifications, proving the statistical significance of the spatially lagged terms in predicting Gross Domestic Product per Capita (GDPC) variation intended as a proxy of the economic growth;
- forecasting the extent to which the Trans-European Transport Network (TEN-T) extension in the Adriatic–Ionian (AI) region can contribute to its regional economic growth.
2. State of the Art
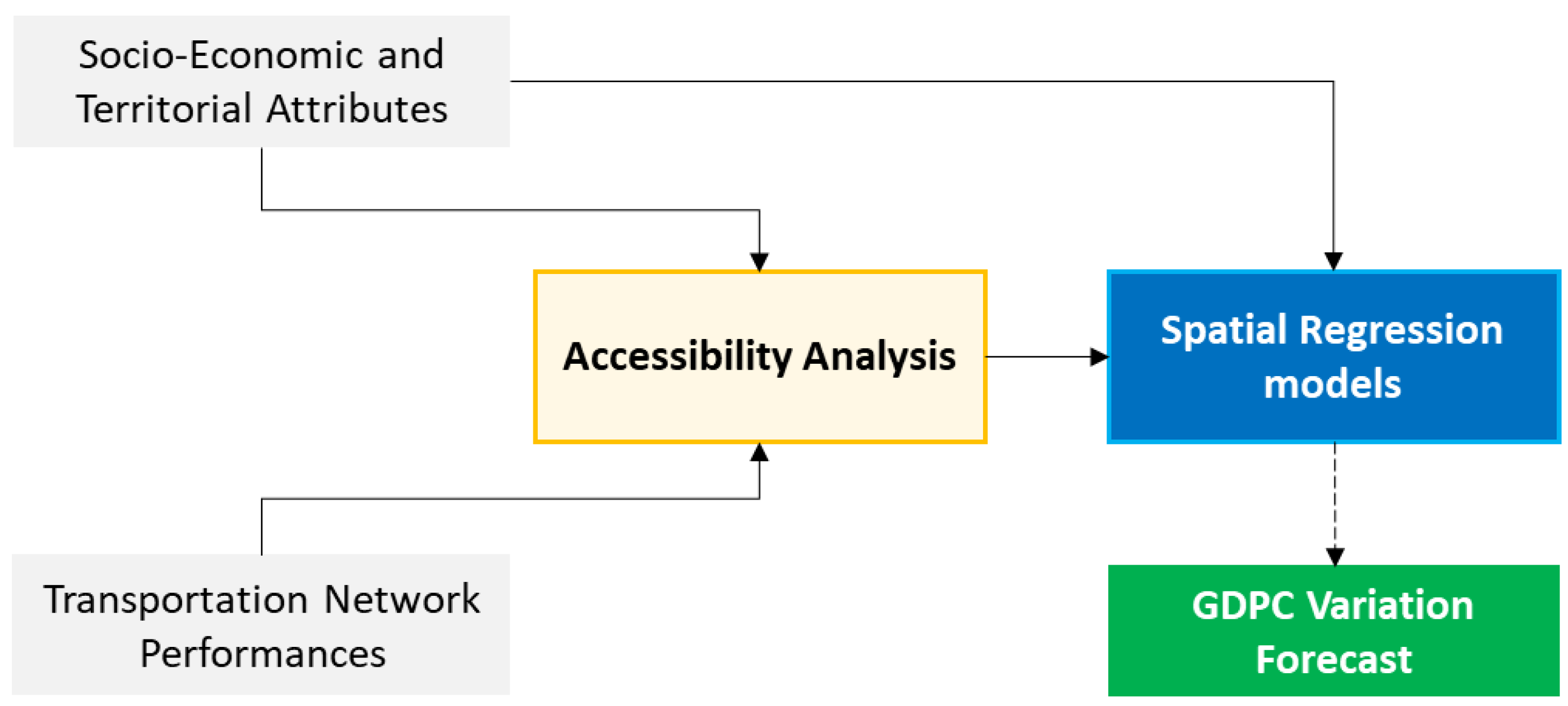
3. Methodology
3.1. Accessibility Analysis
- is the accessibility of the origin zone o to destinations d;
- is the population of the destination zone d;
- is the weighted average of the generalized travel cost on the different considered transportation modes m from the origin zone o to destinations d;
- α and β are two parameters, the output from the estimation of a descriptive trip distribu-tion model having as its denominator the same wording of the accessibility indi-cator previously introduced (see [42] for further details).
- is the travel time on the specific mode m;
- is the monetary cost on the specific mode m as expressed in Equation (3).
- in which is a constant depending on both the od pair and the mode m; is the distance through the mode m, in kilometers, between the origin zone o and destination zone d, and is the average unitary cost per kilometer referred to in the mode m;
- is an estimated coefficient.
3.2. Spatial Regression Models
- is the number of zones;
- represents the elements of the spatial weight matrix W, escribing the spatial relationship between zone i and zone j;
- is the dependent variable, i.e., GDPC, related to zone i;
- is the average of the dependent variable among all the observations.
- is the N size vector of the natural logarithm of the GDPC, in which N is the sample size; , in which i refers to the considered zone and j to the neighboring ones;
- is the N size vector of the natural logarithm of the employment rate;
- ACC is the N size vector of the potential accessibility indicator calculated through Equation (1);
- wij represents the elements of the spatial weight matrix W;
- α is the N size vector of the intercept;
- ε is the N size vector of the independent normally distributed error terms, with 0 mean and constant variance ;
- u is the N size vector of the spatially dependent error terms;
- ρ, λ, βk, θk are estimated regression coefficients; .
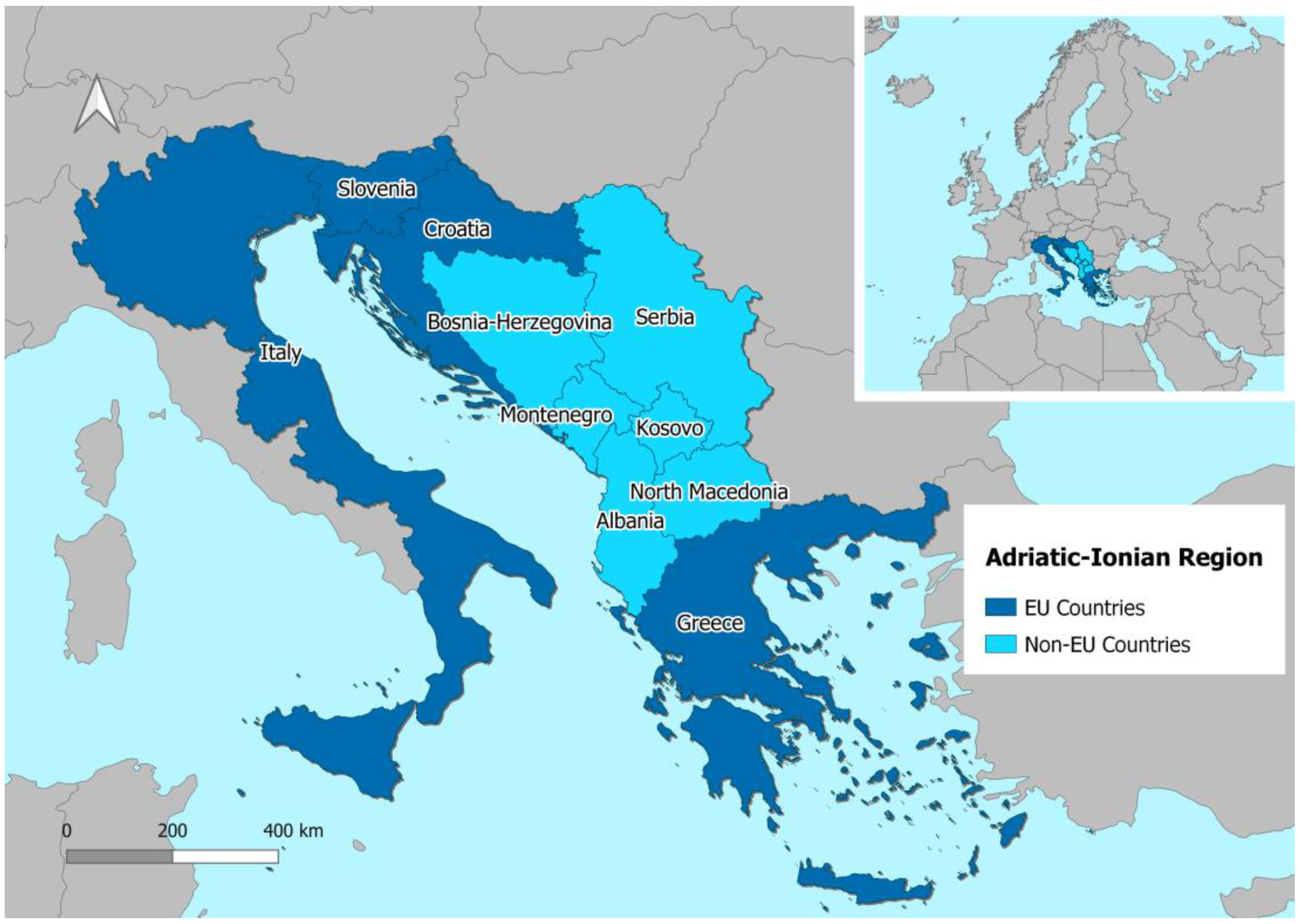
4. Application to the Adriatic and Ionian Region Case Study
4.1. Data Source
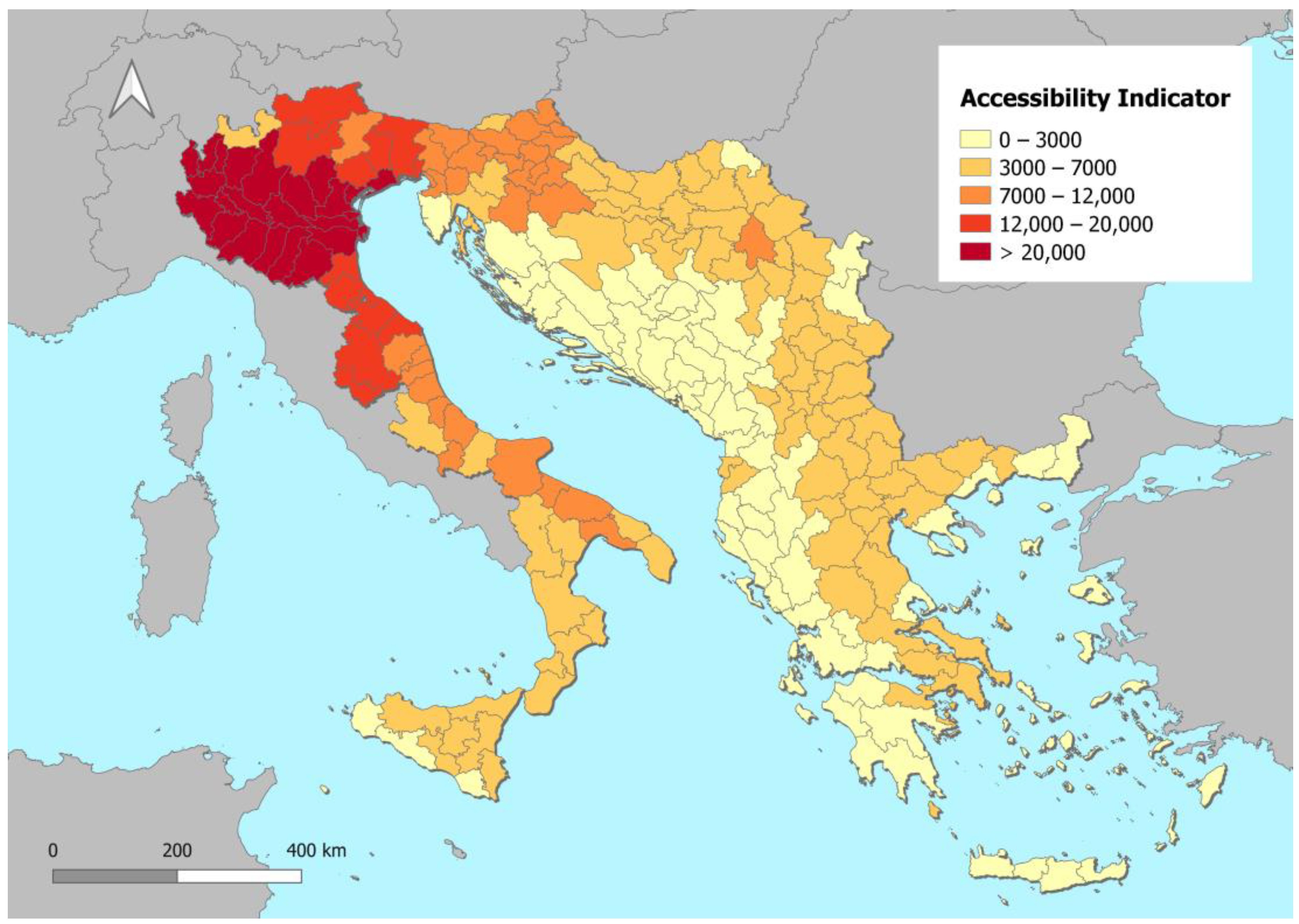
4.2. Current Scenario Accessibility Analysis
4.3. Spatial Regression Model Estimations
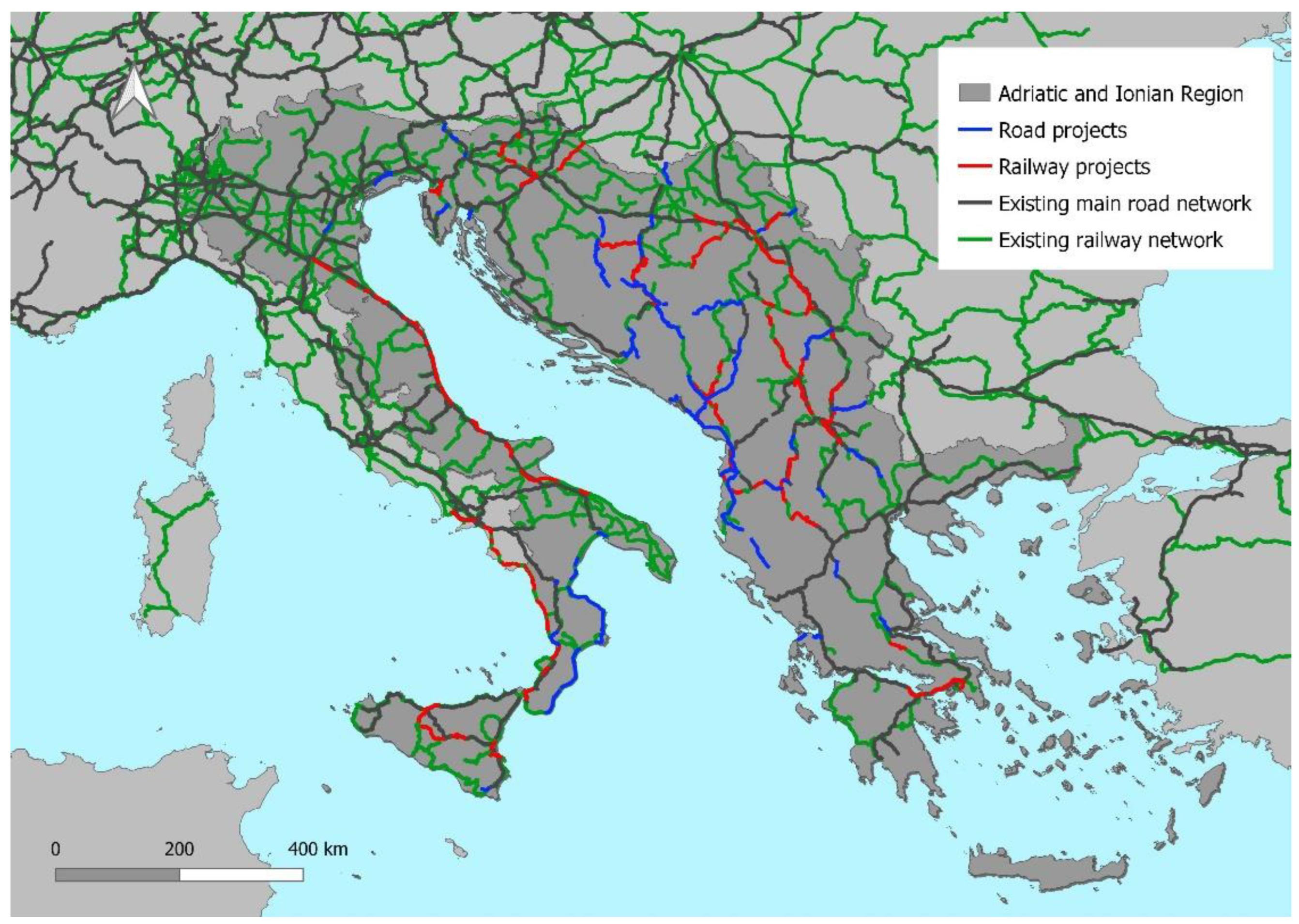
4.4. GDPC Variation Forecast Due to the TEN-T Network Extension in the AI Region
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Thomas, I. Transportation Networks and the Optimal Location of Human Activities: A Numerical Geography Approach; Edward Elgar Publishing: Cheltenham, UK, 2002. [Google Scholar]
- Cascetta, E.; Coppola, P.; Velardi, V. High-Speed Rail Demand: Before-and-After Evidence from the Italian Market. disP-Plan. Rev. 2013, 49, 51–59. [Google Scholar] [CrossRef]
- Murray, A.T.; Davis, R.; Stimson, R.J.; Ferreira, L. Public Transportation Access. Transp. Res. Part D Transp. Environ. 1998, 3, 319–328. [Google Scholar] [CrossRef]
- Spiekermann, K.; Neubauer, J. European Accessibility and Peripherality: Concepts, Models and Indicators; Report 2002; Nordregio: Stockholm, Sweden, 2002. [Google Scholar]
- Sánchez-Mateos, H.S.M.; Givoni, M. The accessibility impact of a new High-Speed Rail line in the UK—A preliminary analysis of winners and losers. J. Transp. Geogr. 2012, 25, 105–114. [Google Scholar] [CrossRef]
- Banister, D.; Berechman, Y. Transport investment and the promotion of economic growth. J. Transp. Geogr. 2001, 9, 209–218. [Google Scholar] [CrossRef]
- EC—DG REGIO. Guide to Cost-Benefit Analysis of Investment Projects for Cohesion Policy 2014–2020; EC—DG REGIO: Etterbeek, Belgium, 2015. [Google Scholar]
- Rokicki, B.; Stępniak, M. Major transport infrastructure investment and regional economic development—An accessibility-based approach. J. Transp. Geogr. 2018, 72, 36–49. [Google Scholar] [CrossRef]
- Cascetta, E.; Cartenì, A.; Henke, I.; Pagliara, F. Economic growth, transport accessibility and regional equity impacts of high-speed railways in Italy: Ten years ex post evaluation and future perspectives. Transp. Res. Part A Policy Pract. 2020, 139, 412–428. [Google Scholar] [CrossRef] [PubMed]
- Delft, C.E.; Directorate-General for Mobility and Transport (European Commission); van Essen, H.; van Wijngaarden, L.; Schroten, A.; Sutter, D.; Bieler, C.; Maffii, S.; Brambilla, M.; Fiorello, D.; et al. Handbook on the External Costs of Transport: Version 2019–1.1; Publications Office of the European Union: Luxembourg, 2020. [Google Scholar]
- Boardman, A.E.; Greenberg, D.H.; Vining, A.R.; Weimer, D.L. Cost-Benefit Analysis: Concepts and Practice; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- De Rus, G. The BCA of HSR: Should the Government Invest in High Speed Rail Infrastructure? J. Benefit-Cost Anal. 2011, 2, 1–28. [Google Scholar] [CrossRef]
- Willis, K.; Garrod, G.; Harvey, D. A review of cost–benefit analysis as applied to the evaluation of new road proposals in the U.K. Transp. Res. Part D Transp. Environ. 1998, 3, 141–156. [Google Scholar] [CrossRef]
- Bröcker, J.; Korzhenevych, A.; Schürmann, C. Assessing spatial equity and efficiency impacts of transport infrastructure projects. Transp. Res. Part B Methodol. 2010, 44, 795–811. [Google Scholar] [CrossRef]
- Adler, M.D. Cost-Benefit Analysis and Distributional Weights: An Overview; Duke University: Durham, NC, USA, 2013. [Google Scholar]
- Robson, E.N.; Wijayaratna, K.P.; Dixit, V.V. A review of computable general equilibrium models for transport and their applications in appraisal. Transp. Res. Part A Policy Pract. 2018, 116, 31–53. [Google Scholar] [CrossRef]
- Chen, Z. Measuring the regional economic impacts of high-speed rail using a dynamic SCGE model: The case of China. Eur. Plan. Stud. 2019, 27, 483–512. [Google Scholar] [CrossRef]
- Haddad, E.A.; Hewings, G.; Perobelli, F.S.; Dos Santos, R.A.C. Regional Effects of Port Infrastructure: A Spatial CGE Application to Brazil. Int. Reg. Sci. Rev. 2010, 33, 239–263. [Google Scholar] [CrossRef]
- Goldmann, K.; Wessel, J. TEN-T corridors–Stairway to heaven or highway to hell? Transp. Res. Part A Policy Pract. 2020, 137, 240–258. [Google Scholar] [CrossRef]
- Crescenzi, R.; Di Cataldo, M.; Rodríguez-Pose, A. Government quality and the economic returns of transport infrastructure investment in european regions. J. Reg. Sci. 2016, 56, 555–582. [Google Scholar] [CrossRef]
- Maucorps, A.; Jestl, S.; Römisch, R. The Effects of the EU Cohesion Policy on Regional Economic Growth: Using Structural Equation Modelling for Impact Assessment; Vienna Institute for International Economic Studies: Wien, Austria, 2020. [Google Scholar]
- Jiang, X.; He, X.; Zhang, L.; Qin, H.; Shao, F. Multimodal transportation infrastructure investment and regional economic development: A structural equation modeling empirical analysis in China from 1986 to 2011. Transp. Policy 2017, 54, 43–52. [Google Scholar] [CrossRef]
- Chen, Z.; Haynes, K. Spatial Impact of Transportation Infrastructure: A Spatial Econometric CGE Approach; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; pp. 163–186. [Google Scholar]
- LeSage, J.; Pace, R.K. Introduction to Spatial Econometrics; Chapman and Hall/CRC: New York, NY, USA, 2009. [Google Scholar]
- Bolduc, D.; Laferrière, R.; Santarossa, G. Spatial Autoregressive Error Components in Travel Flow Models: An Application to Aggregate Mode Choice. In New Directions in Spatial Econometrics; Anselin, L., Florax, R.J.G.M., Eds.; Springer: Berlin/Heidelberg, Germany, 1995; pp. 96–108. [Google Scholar]
- Haider, M.; Miller, E.J. Effects of Transportation Infrastructure and Location on Residential Real Estate Values: Application of Spatial Autoregressive Techniques. Transp. Res. Rec. J. Transp. Res. Board 2000, 1722, 1–8. [Google Scholar] [CrossRef]
- Hackney, J.K.; Bernard, M.; Bindra, S.; Axhausen, K.W. Predicting road system speeds using spatial structure variables and network characteristics. J. Geogr. Syst. 2007, 9, 397–417. [Google Scholar] [CrossRef]
- Ibeas, Á.; Cordera, R.; Dell’Olio, L.; Coppola, P.; Dominguez, A. Modelling transport and real-estate values interactions in urban systems. J. Transp. Geogr. 2012, 24, 370–382. [Google Scholar] [CrossRef]
- Cordera, R.; Coppola, P.; Dell’Olio, L.; Ibeas, Á. Is accessibility relevant in trip generation? Modelling the interaction between trip generation and accessibility taking into account spatial effects. Transportation 2017, 44, 1577–1603. [Google Scholar] [CrossRef]
- Cordera, R.; Coppola, P.; Dell’Olio, L.; Ibeas, Á. The impact of accessibility by public transport on real estate values: A comparison between the cities of Rome and Santander. Transp. Res. Part A Policy Pract. 2018, 125, 308–319. [Google Scholar] [CrossRef]
- Lopes, S.; Brondino, N.C.M.; Da Silva, A.N.R.; Da Silva, A.R. GIS-Based Analytical Tools for Transport Planning: Spatial Regression Models for Transportation Demand Forecast. ISPRS Int. J. Geo-Inf. 2014, 3, 565–583. [Google Scholar] [CrossRef]
- Zeng, C.; Song, Y.; Cai, D.; Hu, P.; Cui, H.; Yang, J.; Zhang, H. Exploration on the spatial spillover effect of infrastructure network on urbanization: A case study in Wuhan urban agglomeration. Sustain. Cities Soc. 2019, 47, 101476. [Google Scholar] [CrossRef]
- Yu, N.; de Jong, M.; Storm, S.; Mi, J. Spatial spillover effects of transport infrastructure: Evidence from Chinese regions. J. Transp. Geogr. 2013, 28, 56–66. [Google Scholar] [CrossRef]
- Gutiérrez, J.; Condeço-Melhorado, A.; Martín, J.C. Using accessibility indicators and GIS to assess spatial spillovers of transport infrastructure investment. J. Transp. Geogr. 2009, 18, 141–152. [Google Scholar] [CrossRef]
- Lopez, E.; Monzón, A.; Ortega, E.; Quintana, S.M. Assessment of Cross-Border Spillover Effects of National Transport Infrastructure Plans: An Accessibility Approach. Transp. Rev. 2009, 29, 515–536. [Google Scholar] [CrossRef]
- Moreno, R.; López-Bazo, E. Returns to Local and Transport Infrastructure under Regional Spillovers. Int. Reg. Sci. Rev. 2007, 30, 47–71. [Google Scholar] [CrossRef]
- Geurs, K.T.; van Wee, B. Accessibility evaluation of land-use and transport strategies: Review and research directions. J. Transp. Geogr. 2004, 12, 127–140. [Google Scholar] [CrossRef]
- Reggiani, A. Accessibility, Trade and Locational Behaviour; Routledge: London, UK, 2019. [Google Scholar]
- Coppola, P.; Nuzzolo, A. Changing accessibility, dwelling price and the spatial distribution of socio-economic activities. Res. Transp. Econ. 2011, 31, 63–71. [Google Scholar] [CrossRef]
- Ortega, E.; Lopez, E.; Monzón, A. Territorial cohesion impacts of high-speed rail at different planning levels. J. Transp. Geogr. 2012, 24, 130–141. [Google Scholar] [CrossRef]
- Monzón, A.; Ortega, E.; López, E. Efficiency and spatial equity impacts of high-speed rail extensions in urban areas. Cities 2013, 30, 18–30. [Google Scholar] [CrossRef]
- Cascetta, E. Transportation Systems Analysis: Models and Applications; Springer: Boston, MA, USA, 2009. [Google Scholar]
- Moran, P.A.P. The Interpretation of Statistical Maps. J. R. Stat. Soc. Ser. B Methodol. 1948, 10, 243–251. [Google Scholar] [CrossRef]
- Charron, N.; Lapuente, V.; Annoni, P. Measuring quality of government in EU regions across space and time. Pap. Reg. Sci. 2019, 98, 1925–1953. [Google Scholar] [CrossRef]
- World Bank National Accounts Data, and OECD National Accounts Data Files. GDP (Constant 2015 US$). Available online: https://data.worldbank.org/indicator/NY.GDP.MKTP.KD (accessed on 7 August 2022).
- European Commission-ARDECO Online-Knowledge for Policy. Available online: https://knowledge4policy.ec.europa.eu/territorial/ardeco-online_en (accessed on 7 August 2022).
- Eurostat-Statistics. Available online: https://ec.europa.eu/eurostat/databrowser/view/NAMA_10R_3GDP/default/table?lang=en (accessed on 7 August 2022).
- Agency for Statistics of Bosnia and Herzegovina-Statistics. Available online: https://bhas.gov.ba/?lang=en (accessed on 13 August 2022).
- Kosovo Agency of Statistics-Statistics. Available online: https://askdata.rks-gov.net/pxweb/en/ASKdata/ (accessed on 13 August 2022).
- INSTAT-Albanian Institute of Statistics-Statistics. Available online: https://www.instat.gov.al/en/ (accessed on 13 August 2022).
- World Bank—Worldwide Governance Indicators (WGI) Database. Available online: http://info.worldbank.org/governance/wgi/ (accessed on 24 August 2022).
- European Commission (2021) Proposal for a Regulation of the European Parliament and of the Council on Union Guidelines for the Development of the Trans-European Transport Network, Amending Regulation (EU) 2021/1153 and Regulation (EU) No 913/2010 and Repealing Regulation (EU) 1315/2013. Available online: https://eur-lex.europa.eu/legal-content/EN/ALL/?uri=COM%3A2021%3A812%3AFIN (accessed on 11 July 2022).
- Del Bo, C.F.; Florio, M. Infrastructure and Growth in a Spatial Framework: Evidence from the EU regions. Eur. Plan. Stud. 2012, 20, 1393–1414. [Google Scholar] [CrossRef]
- Elburz, Z.; Nijkamp, P.; Pels, E. Public infrastructure and regional growth: Lessons from meta-analysis. J. Transp. Geogr. 2017, 58, 1–8. [Google Scholar] [CrossRef]
- Crescenzi, R.; Rodríguez-Pose, A. Infrastructure and regional growth in the European Union. Pap. Reg. Sci. 2012, 91, 487–513. [Google Scholar] [CrossRef]
| SDM | SAR | SLX | SEM | |
|---|---|---|---|---|
| () | 0.161 *** | 0.126 ** | 0.115 | 0.150 ** |
| () | 0.402 *** | 0.226 *** | 0.414 *** | 0.468 *** |
| () | 0.262 *** | 0.044 | 0.263 * | 0.292 *** |
| () | −0.131 | 0.139 | ||
| () | −0.241 *** | 0.244 * | ||
| () | −0.231 *** | −0.009 | ||
| 2.040 *** | 2.497 *** | 9.102 *** | 9.206 *** | |
| 𝜌 | 0.800 *** | 0.711 *** | ||
| 0.808 *** | ||||
| Observations | 225 | 225 | 225 | 225 |
| Pseudo-R2 | 0.904 | 0.891 | 0.901 | |
| Multiple R2 | 0.730 | |||
| Log Likelihood | −0.45 | −13.93 | −116.1 | −3.84 |
| Akaike Inf. Crit. | 18.91 | 39.86 | 248.1 | 19.69 |
| LR Test | 231.2 *** | 211.4 *** | 231.6 *** |
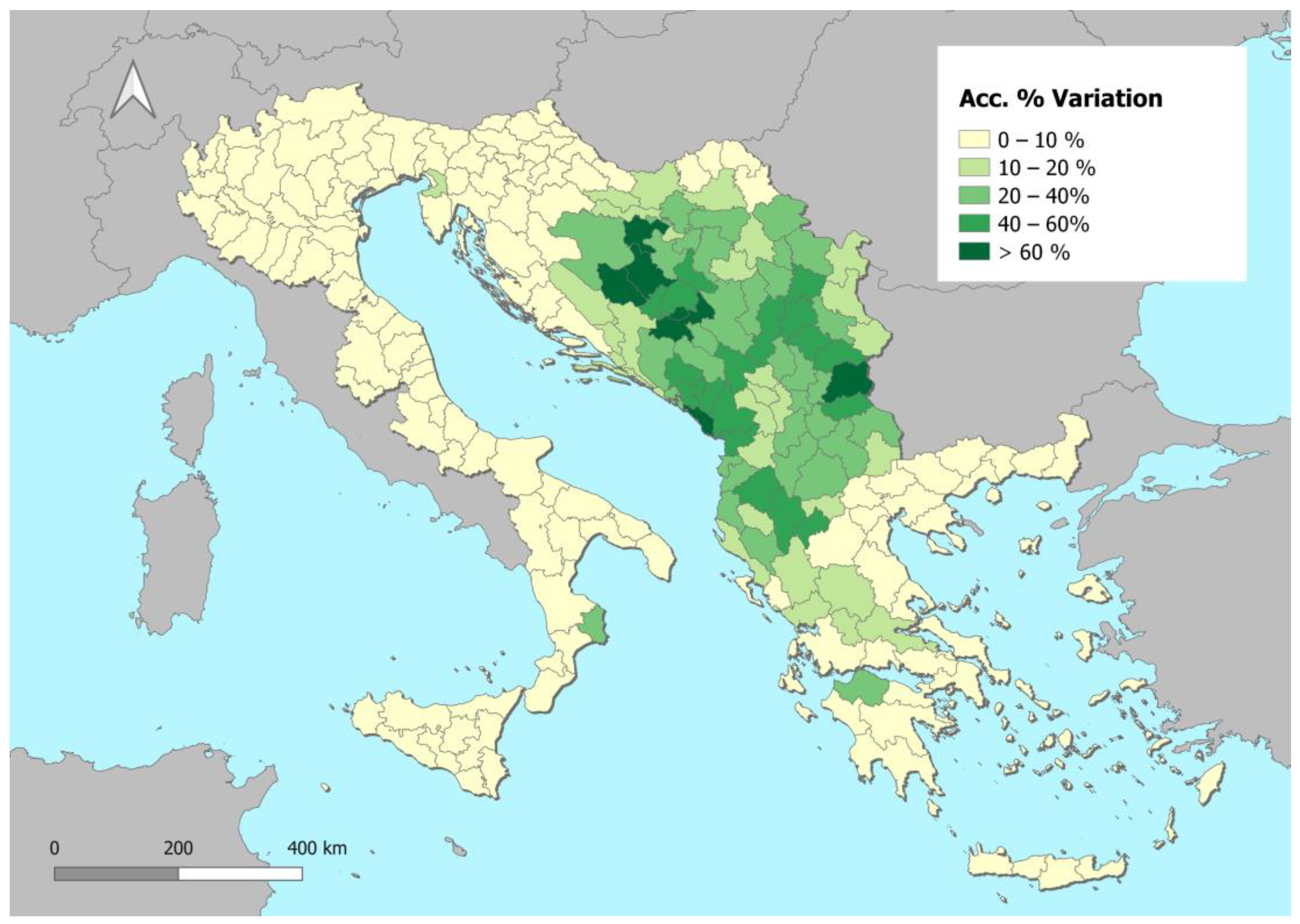
| Country | Accessibility Values (*10,000) | Accessibility Changes | |||
|---|---|---|---|---|---|
| Current Scenario | Project Scenario | Absolute | Relative | Relative NUTS 3 Range [Min–Max] | |
| Albania | 2138 | 2771 | 634 | 29.6% | [12.4–54.7%] |
| Bosnia-Herzegovina | 2428 | 3344 | 916 | 37.8% | [4.5–93.0%] |
| Croatia | 5333 | 5709 | 376 | 7.1% | [1.0–20.9%] |
| Greece | 2460 | 2634 | 175 | 7.1% | [0.0–42.0%] |
| Italy | 13,671 | 13,865 | 194 | 1.4% | [0.1–30.2%] |
| Kosovo | 3920 | 4972 | 1052 | 26.8% | [13.7–39.8%] |
| Montenegro | 1580 | 2321 | 741 | 46.9% | [21.5–93.1%] |
| North Macedonia | 4255 | 5540 | 1285 | 30.2% | [15.6–45.6%] |
| Serbia | 4180 | 5264 | 1084 | 25.9% | [2.6–62.1%] |
| Slovenia | 9391 | 9748 | 356 | 3.8% | [0.8–15.7%] |
| Adriatic–Ionian Average | 6735 | 7216 | 481 | 14.0% | [0.0–93.1%] |
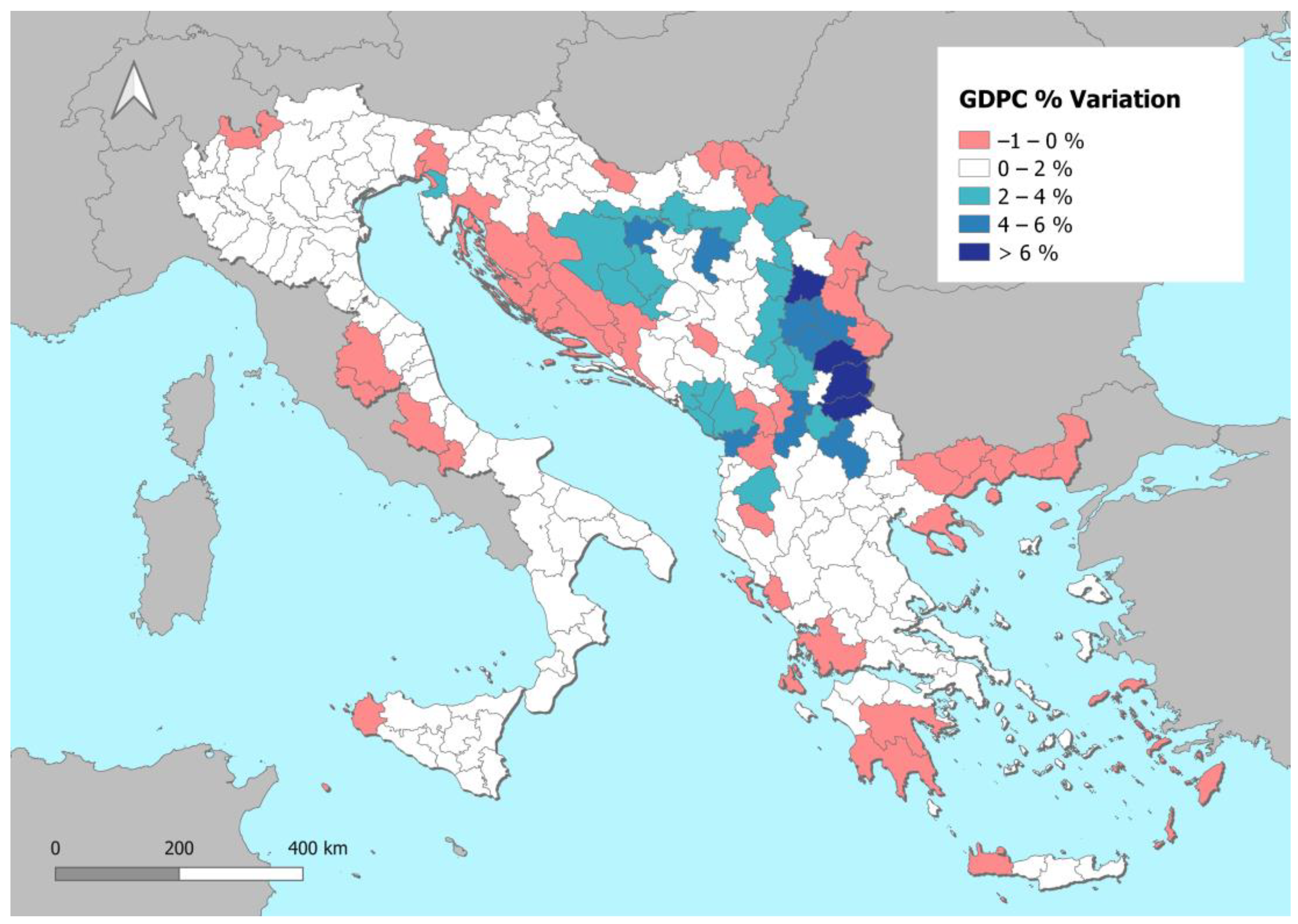
| Country | GDPC Values (€) | GDPC Changes | |||
|---|---|---|---|---|---|
| Current Scenario | Project Scenario | Absolute | Relative | Relative NUTS 3 Range [Min–Max] | |
| Albania | 3495 | 3540 | 45 | 1.3% | [−0.5–4.1%] |
| Bosnia-Herzegovina | 4574 | 4635 | 61 | 1.3% | [−0.3–4.5%] |
| Croatia | 9940 | 9993 | 53 | 0.5% | [−0.4–3.0%] |
| Greece | 13,516 | 13,539 | 23 | 0.2% | [−0.3–2.0%] |
| Italy | 26,338 | 26,378 | 40 | 0.2% | [−0.1–0.8%] |
| Kosovo | 3482 | 3543 | 60 | 1.7% | [−0.1–4.2%] |
| Montenegro | 6908 | 6998 | 90 | 1.3% | [−0.4–3.2%] |
| North Macedonia | 4497 | 4645 | 149 | 3.3% | [0.9–10.1%] |
| Serbia | 4390 | 4479 | 90 | 2.0% | [−0.8–10.2%] |
| Slovenia | 18,229 | 18,386 | 157 | 0.9% | [−0.2–3.2%] |
| Adriatic–Ionian Average | 14,177 | 14,235 | 58 | 0.9% | [−0.8–10.2%] |
| EU Countries inside the AI Region average | 19,321 | 19,367 | 46 | 0.2% | [−0.4–3.2%] |
| non-EU Countries inside the AI Region average | 4482 | 4562 | 80 | 1.8% | [−0.8–10.2%] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Fabiis, F.; Mancuso, A.C.; Silvestri, F.; Coppola, P. Spatial Economic Impacts of the TEN-T Network Extension in the Adriatic and Ionian Region. Sustainability 2023, 15, 5126. https://doi.org/10.3390/su15065126
De Fabiis F, Mancuso AC, Silvestri F, Coppola P. Spatial Economic Impacts of the TEN-T Network Extension in the Adriatic and Ionian Region. Sustainability. 2023; 15(6):5126. https://doi.org/10.3390/su15065126
Chicago/Turabian StyleDe Fabiis, Francesco, Alessandro Carmelo Mancuso, Fulvio Silvestri, and Pierluigi Coppola. 2023. "Spatial Economic Impacts of the TEN-T Network Extension in the Adriatic and Ionian Region" Sustainability 15, no. 6: 5126. https://doi.org/10.3390/su15065126
APA StyleDe Fabiis, F., Mancuso, A. C., Silvestri, F., & Coppola, P. (2023). Spatial Economic Impacts of the TEN-T Network Extension in the Adriatic and Ionian Region. Sustainability, 15(6), 5126. https://doi.org/10.3390/su15065126







