Abstract
The heavy metal pollution of cultivated land in China is severe, requiring remediation. Introducing third-party governance subjects representing market resources is inevitable to realize the specialization and socialization of cultivated land remediation. However, due to the public nature of cultivated land, the confusion about participating parties’ responsibilities and difficulty coordinating interests restrict the expected effect of cultivated land remediation. To this end, a three-party evolutionary game model among the grassroots government, governance enterprises, and supervisory enterprises is constructed and virtually simulated, taking into account the influence of random checks by the higher-level government. We found that the reward and punishment mechanism of the grassroots government, the frequency of random inspection by the higher-level government, and the amount of deduction will influence the strategy selection of the participating parties. Strengthening the awareness of the responsibility of the grassroots government, optimizing the incentive system, establishing a regular spot-check system, and improving the cost of non-compliance by enterprises can effectively resolve conflicts of interest among the participants. The study results have practical significance for further enhancing the remediation efficiency of heavy metal-contaminated cultivated land.
1. Introduction
Since the State Council approved the implementation of the National Land Remediation Plan (2016–2020), land remediation has been used nationwide to help implement ecological civilization, rural revitalization, and poverty eradication strategies. The plan has played an essential role in promoting cultivated land protection and land conservation, promoting the integrated development of urban and rural areas, and improving the ecological environment. Data from the Rural Land Remediation Monitoring and Supervision System shows that China has built 232 million mu of high-standard farmland during the 13th Five-Year Plan period (1 mu equals 0.165 acres). Of this land, 110 million mu was built by the former Ministry of Land and Resources and 122 million mu by other departments; about 87,000 land remediation projects have been completed nationwide, replenishing 18,279,800 mu of cultivated land [1]. The average quality grade of cultivated land nationwide changed from 5.09 in 2017 to 4.76 in 2021, but only 31.24% of the total cultivated land area is in Grades 1 to 3. The pollution situation of China’s cultivated land is still serious. The results of a detailed survey of the soil pollution status of agricultural land show that the primary pollutants affecting the soil environmental quality of agricultural land are heavy metals, among which cadmium is the primary pollutant [2,3].
Heavy metal pollution of cultivated land not only endangers the ecological safety of cultivated land, resulting in crop yield reduction [4,5], cultivated land biodiversity decline [6,7], and other consequences, but also leads to “cadmium rice”, “blood lead”, and other events, directly posing a serious threat to human life [8,9,10]. Under this pressure, implementing heavy metal contaminated cultivated land remediation cannot wait. To this end, China has promulgated the Soil Pollution Prevention and Control Action Plan and the Soil Pollution Prevention and Control Law and has carried out remediation and governance attempts in typical areas [11]. In March 2014, the Ministry of Agriculture and the Ministry of Finance jointly launched the “Pilot Project on Heavy Metal Contaminated Cultivated land and Crop Planting Structure Adjustment in Hunan Province”, which explored a comprehensive restoration and governance approach based on agricultural measures for 1.7 million mu of heavy metal contaminated cultivated land in the Changsha–Zhuzhou–Xiangtan area [12]. During the first year, the government-led pattern of cultivated land remediation was ineffective. Then, the pilot area began to explore the “government + third-party remediation enterprise” model in 2015, in which the government became the developer of remediation policies, the purchaser of remediation services, and the supervisor of remediation implementation. However, on the one hand, the contaminated cultivated land is numerous and widely distributed. On the other hand, due to a lack of supervision funds [13], technology, and manpower, it is difficult for the government to effectively implement the whole supervision process to third-party governance companies [14]. Therefore, the pilot area began to explore the joint governance model of “government + third-party governance enterprise + third-party supervision enterprise” in 2016 [15], forming a situation of “ladder multiple supervision” by the government and third-party supervision enterprise.
Although studies have shown that in general environmental governance, the third-party governance model can effectively improve environmental governance, research has found that third-party remediation of heavy metal pollution on cultivated land is not ideal [11]. Due to the imperfections of the multi-participation system, the third-party remediation of heavy metal-polluted cultivated land still suffers from the absence and weakening of the main body of remediation, especially since the central position of farmers cannot be manifested; the main body of responsibility is thus difficult to identify, the principle of responsibility allocation is invalid, and the communication of information between multiple participating bodies is poor [16,17,18]. More seriously, due to the large number of participating subjects and the difficulty of coordinating the interests of those heterogeneous subjects, cultivated land remediation is caught in a “collective action dilemma”, which seriously threatens the remediation effect [11]. Therefore, the key to ensuring the remediation effect of cultivated land is coordinating the conflicting interests of all participants.
Most of the existing studies about the conflicts of interests of third-party governance participants are based on a three-party game among the government, emission enterprises, and governance enterprises. Due to the existence of the institutional basis for conspiring [19,20], emission enterprises will have the incentive to conspire with governance companies to falsify EIA materials and falsify monitoring data. This conspiracy can lead to government regulatory risks [21]. Currently, due to the different technical levels of each enterprise, it is easy to cause adverse selection and for bad money drives out goods, so the third-party market mechanism needs to be further enhanced [22]. Moreover, the level of pollution control and monitoring efforts is private information that is difficult to access [23]. Third parties may seek illicit profits by cutting investments in pollution control in the name of profit maximization [24,25]. Studies show that the influence of local government will gradually weaken if the emission enterprises and third-party governance companies cooperate well. However, without the advice and support of the local government, emission enterprises and third-party governance companies will eventually fall into the dilemma of “remediating while pollution”. The key factors that influence the evolutionary stabilization strategy (ESS) of the three parties include the rent-seeking cost, the violation cost, and the social credibility of the emission enterprises; the compensation for non-compliance, the cost of remediation, the government incentives, and the rent-seeking revenue of the governance companies; and the fines and regulatory costs of the governments. In response to the opportunistic behavior caused by information asymmetry, the government can distinguish governance companies at different levels by setting reasonable subsidy intervals and disguised costs [26]. At the same time, the government can coordinate conflicts of interests by improving the legal and regulatory system, establishing a perfect monitoring system, designing incentive mechanisms for rewards and punishments based on the “principle of shared responsibility”, reducing participation and remediation costs, improving the reputation gains of both enterprises [27], and adopting cooperative games.
At present, studies about the third-party governance of cultivated land remediation and how to coordinate the conflict among the government, governance companies, and supervisory companies are relatively lacking. According to the practice of cultivated land remediation in the Changsha–Zhuzhou–Xiangtan area, this paper constructs a game model based on the special governance structure of “ladder multiple supervision”, as shown in Figure 1.
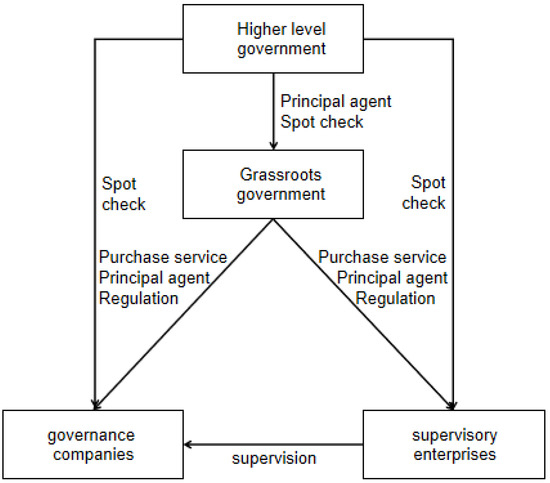
Figure 1.
“Ladder multiple supervision” relationship diagram.
The evolutionary game mainly studies the participants’ long-term game under imperfect rationality [28,29]. The strategy choices of the grassroots government, the governance enterprise, and the supervising enterprise are never achieved overnight. These choices need to be stabilized through a long period of evolution, so it is very suitable to study the behavior choices of the grassroots government, the governance enterprise, and the supervising enterprise under a third-party remediation model of heavy metal-contaminated cultivated land through the evolutionary game. Compared with previous studies, this paper proposes the following three innovations: Firstly, the evolutionary game approach is used to clarify the conflicts of interests of the three parties in the third-party remediation model of heavy metal polluted-cultivated land, and the influence of sampling by the higher-level government is considered. Third-party supervisory enterprises are also included as game subjects, which has strong practical significance. Secondly, few scholars in the existing evolutionary game literature have discussed in detail the changes and jumps in the equilibrium point under different parameter conditions, and the situation where parameter changes lead to a leap of the equilibrium point often implies profound policy insights, which is remedied in this paper. Thirdly, a simulation analysis was conducted using MATLAB 2020b to verify the validity of the model analysis under different initial conditions, and based on the analysis’s findings, countermeasures and suggestions were proposed for coordinating the conflicting interests between the three parties and to improve the efficiency of cultivated land governance.
2. Model Assumptions and Construction
The evolutionary game is an essential method to study the behavioral choice problem of multiple subjects. Based on this, this paper constructs a three-party evolutionary game model of grassroots government, a third-party governance enterprise, and a third-party supervisory enterprise to study the behavioral choices of the three subjects. Whether the grassroots government chooses “action”, whether the third-party governance enterprise chooses “active harness pollution”, or whether the third-party supervision enterprise chooses “active supervision” is the result of the game between the grassroots government, the third-party governance enterprise, and the third-party supervision enterprise.
2.1. Basic Assumptions
Hypothesis 1.
The grassroots government is participant 1. The third-party governance enterprise is participant 2. The third-party supervisory enterprise is participant 3. All three parties are finite rational participant subjects, and their strategy choices gradually evolve into and stabilize at the optimal strategy over time.
Hypothesis 2.
The strategy space of the grassroots government is A = (A1, A2) = (action, inaction) and selects A1 with probability x and A2 with probability (1 − x), x ∈ [0, 1]. The strategy space of the governing firm is B = (B1, B2) = (active harness pollution, negative harness pollution), and it chooses B1 with probability y and B2 with probability (1 − y), y ∈ [0, 1]. The strategy space of the supervisory firm is C = (C1, C2) = (active supervision, negative supervision), and it chooses C1 with probability z and C2 with probability (1 − z), z ∈ [0, 1].
Hypothesis 3.
The cost for the grassroots government to choose “action” in remediation is Cgh, the social benefit gained is Rgs, and the reward from the higher government is Jg. The cost for the grassroots government to choose “inaction” in remediation is Cgl (Cgh > Cgl). There is a probability β (β ∈ [0, 1]) that the grassroots government will be caught and punished by the higher government when it chooses “inaction”, with an administrative penalty of Fg.
Hypothesis 4.
Governance enterprises participate in heavy metal-contaminated cultivated land remediation projects through bidding, and the winning bid price is Bm. The cost of its “Active harness pollution” is Cmh, the ecological benefit for the government is Rge1, and the economic benefit is Rge2 (Rge1 + Rge2 = Rge). The cost of its “negative harness pollution” is Cml (Cmh > Cml), and when the grassroots government or the supervising enterprise practices positive behavior, the amount of its project winning bid Fm is deducted (Cmh − Cml < Fm). When the grassroots government and the supervising enterprise practice negative behavior, the probability of the governance enterprise’s “negative harness pollution” being spot-checked by the higher-level government is β; due to limitations such as technical cognition, the likelihood of being found engaging in negative behavior after spot-checking is α. Therefore, the probability of the governance enterprise being penalized is β × α.
Hypothesis 5.
Supervisory enterprises participate in heavy metal-contaminated cultivated land remediation projects through bidding, and the winning bid price is Bs. The cost of active supervision by supervisory enterprises is Csh, and the cost of negative supervision is Csl (Csh > Csl). When the grassroots government chooses “action”, the supervisory enterprise implementing “negative supervision” will be deducted from the winning bid price Fs (Csh − Csl < Fs). When the grassroots government does not act, the supervisory enterprise’s negative supervision has a β possibility of being discovered by the higher government’s random inspection.
2.2. Model Building
Based on the above assumptions, the mixed strategy game matrix of grassroots government, governance enterprises, and supervisory enterprises are constructed, as shown in Table 1.

Table 1.
Mixed strategy game matrix of grassroots government, governance enterprise, and supervisory enterprise.
3. Model Analysis
3.1. Evolutionary Stability Analysis of the Strategy of Grassroots Government
The expected and average benefits (Ux1, Ux2) of the choice of “action” or “inaction” by the grassroots government in cultivated land governance are:
Ux1 = yz(Jg + Rge + Rgs − Cgh) + y(1 − z)(Jg + Rge + Rgs − Cgh + Fs) + z(1 − y)(Jg + Rgs − Cgh + Fm) + (1 − y)(1 − z)(Jg + Rgs − Cgh + αFm + Fs)
Ux2 = yz(Rge − Cgl − βFg) + y(1 − z)(Rge − Cgl − βFg) + z(1 − y)(−Cgl − Fg + Fm) + (1 − y)(1 − z)(−Cgl − Fg)
The replication dynamic equation for the choice of strategy of the grassroots government is:
The first derivative of F(x) and the set G(y) are respectively:
Let G(y) = y(αFm + Fg − βFg) − αyzFm + z(αFm + Fs) − Jg − Rgs + Cgh − αFm − Fs − Cgl − Fg
According to the stability theorem of the differential equation, the probability of the grassroots government choosing “action” in a stable state must satisfy F(x) = 0 and . Since , G(y) is an increasing function. Therefore, when , G(y) = 0, at which time and the grassroots government cannot determine the stabilization strategy; when y < y*, G(y) < 0, at which time , x = 1 is the evolutionary stabilization strategy (ESS) of the grassroots government; conversely, x = 0 is the ESS.
The evolutionary phase diagram of the strategy of the grassroots government is shown in Figure 2.
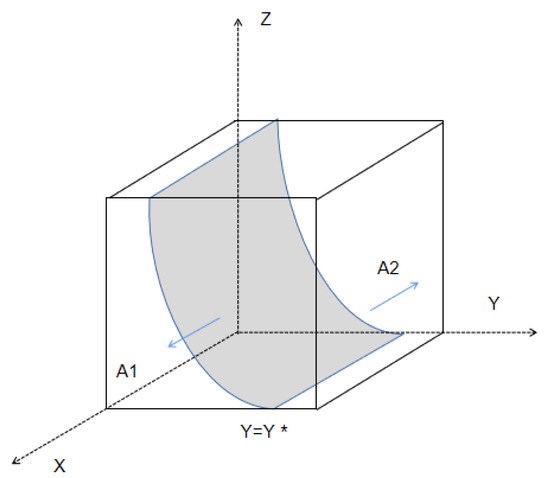
Figure 2.
Phase diagram of the evolution of grassroots government strategies.
Proposition 1.
The probability of grassroots governments choosing “action” in cultivated land remediation is positively correlated with the frequency of spot checks and the amount of incentives received by higher-levels of government and negatively correlated with the cost saved by “inaction”.
Proof.
Since , it follows that y* gradually increases when Jg, β gradually increases, or Cgh − Cgl gradually decreases. At this time, the volume of A1 in Figure 2 gradually increases, proving that the grassroots government tends to choose the probability of “action” gradually increases. □
Proposition 1 suggests that increasing the amount of incentives and the frequency of random inspections by higher-level governments can effectively motivate grassroots governments to choose the “action” strategy. It also suggests that the incremental benefits of grassroots governments choosing “action” should be greater than their incremental costs based on the cost–benefit principle. Furthermore, grassroots governments can be motivated to adopt an “action” strategy by strengthening publicity to enhance corporate awareness of compliance with the law, by strengthening the use of modern information technology, and by building and improving the mutual supervision mechanism of enterprises to reduce the cost of supervision.
Proposition 2.
In the evolutionary process, the probability of government departments choosing “action” in cultivated land remediation decreases as the probability of “active harness pollution” and “active supervision” of governance and supervisory companies increases.
Proof.
From the evolutionary stability analysis of strategy selection in the government sector, it is clear that x = 1 is the ESS when y < y*, i.e., . When y > y*, i.e., , x = 0 is the ESS; therefore, as y and z increase, the government’s stabilization strategy changes from x = 1 to x = 0. □
Proposition 2 shows that the strategy choice of governance and supervision enterprises will influence the behavior strategy of the grassroots government. The choice of “active harness pollution” and “active supervision” by governance and supervision enterprises can reduce the work intensity and difficulty of the grassroots government to a certain extent. Still, it will eventually lead to a lack of supervision by the grassroots government. In the long run, the enterprises will maximize their interests, as the principle of “Cutting corners” will affect the effect of cultivated land remediation. Therefore, the “green GDP” criterion should be included in the officials’ performance appraisal system to urge the grassroots government not to slacken the supervision of cultivated land remediation regardless of the behavioral strategies chosen by the governance and supervision enterprises [30,31].
3.2. Evolutionary Stability Analysis of the Strategy of Governing Companies
The expected and average benefits (Uy1, Uy2) of choosing “active harness pollution” or “negative harness pollution” in cultivated land remediation are
Uy1 = xz(Bm − Cmh) + x(1 − z)(Bm − Cmh) + (1 − x)Z(Bm − Cmh) + (1 − x)(1 − z)(Bm − Cmh)
Uy2 = xz(Bm − Cml − Fm) + x(1 − z)(Bm − Cml − [1 − (1 − α)(1 − αβ)]Fm) + (1 − x)Z(Bm − Cml − Fm) + (1 − x)(1 − z)(Bm − Cml − αβFm)
The replication dynamic equation for the choice of strategy of the governing companies is:
The first derivative of F(y) and the set J(z) are, respectively:
Let J(z) = (−Fmβ + Fm)xz + (Fmβ − Fm)x + (Fmβ − Fm)z − Fmβ + Cmh − Cml
According to the stability theorem of the differential equation, the probability that the governing enterprise chooses “active harness pollution” in a stable state must satisfy F(y) = 0 and . Since , J(z) is a decreasing function. Therefore, when , J(z) = 0, at which time and the governing firm cannot determine the stabilization strategy; when z < z*, J(z) > 0, at which time , y = 0 is the governing firm’s evolutionary stabilization strategy (ESS); conversely, y = 1 is the ESS.
The evolutionary phase diagram of the strategy of the governance companies is shown in Figure 3.
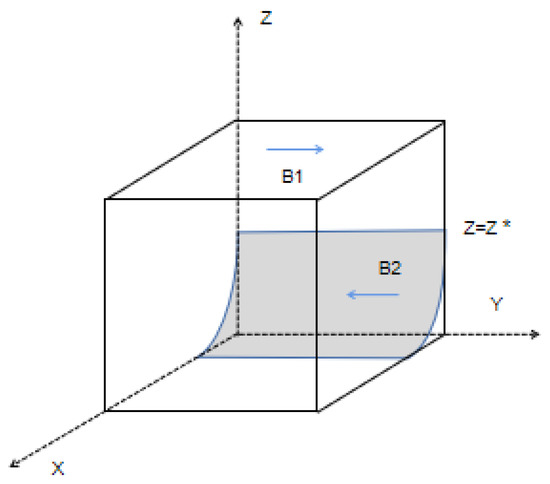
Figure 3.
Phase diagram of the evolution of third-party governance companies.
Proposition 3.
The probability of governance companies choosing “active harness pollution” in cultivated land remediation is positively correlated with the amount of deduction by the grassroots government and the probability of random inspection by the higher-level government. It is negatively correlated with the cost saved by “negative harness pollution”.
Proof.
Since , z* decreases when Fm, β gradually increases or Cmh − Cml gradually decreases, and the volume of B1 in Figure 3 gradually increases. It proves that the probability of governance companies choosing “active harness pollution” gradually improves. □
Proposition 3 shows that the choice of strategy for governing enterprises is positively correlated with the intensity of punishment and the frequency of random inspections by higher-level governments. It is negatively correlated with the cost saved by “negative harness pollution”. The government can urge governance enterprises to choose “active harness pollution” by establishing a “routine inspection” system to increase the frequency of random inspections. By setting up a third-party integrity system, such as a “blacklist”, the market access and exit mechanisms of third-party governance can be improved, in turn improving the non-compliance and trust-breaking costs of the “negative harness pollution” strategy of enterprises. Reducing the cost saved by “negative harness pollution” strategy encourages enterprises to tend toward “active harness pollution”. Currently, the environmental third-party governance market still needs to mature, and the pressure of higher fines may increase industry barriers, which is not conducive to developing the third-party market. Therefore, an incentive system such as a “tax benefit” for third-party enterprises can be appropriately introduced to increase the governance enterprise’s gain [32]. The incentive system can compensate for the “slack behavior” caused by insufficient punishment, which not only makes enterprises tend to implement positive behaviors but also contributes to the stable and healthy development of the third-party market.
Proposition 4.
In the evolutionary process, the probability of governance companies choosing “active harness pollution” in cultivated land remediation increases as the probability of government and supervisory companies choosing “action” and “active supervision” increases.
Proof.
The evolutionary stability analysis of the strategy choice of the governing firm shows that y = 0 is the ESS when z < z*, i.e., . When z > z*, i.e., , y = 1 is the ESS; therefore, the stabilization strategy of the governing firm changes from y = 0 to y = 1 with the increase in x and z. □
Proposition 4 suggests whether the governance companies choosing “active harness pollution” is influenced by the strategic choices of the government and the supervisory firm. When the government and supervisors choose “action” and to “actively supervise”, the governance companies will tend toward “active harness pollution”. Therefore not only can the effectiveness of cultivated land remediation be ensured by strengthening government supervision and information disclosure, but also by strengthening the impartiality of supervisory agencies, such as by improving the social responsibility of supervisory agencies, giving full play to the effectiveness of social forces in monitoring the efficacy of cultivated land remediation, and building a cultivated land remediation situation of shared governance by all people [33,34] to urge the governance enterprises to remediate actively.
3.3. Evolutionary Stability Analysis of the Strategy of Supervisory Enterprises
The expected and average benefits (Uz1, Uz2) of the supervisory companies choosing “active supervision” or “negative supervision” in cultivated land remediation are:
Uz1 = xy(Bs − Csh) + x(1 − Y)(Bs − Csh) + (1 − x)y(Bs − Csh) + (1 − x)(1 − y)(Bs − Csh)
Uz2 = xy(Bs − Csl − Fs) + x(1 − y)(Bs − Csl − Fs) + (1 − x)y(Bs − Csl − βFs) + (1 − x)(1 − y)(Bs − Csl − βFs)
The replication dynamic equation for the choice of strategy of the supervisory enterprises is:
The first derivative of F(z) and the set H(x) are, respectively:
Let H(x) = (βFs − Fs)x − βFs + Csh − Csl
According to the stability theorem of the differential equation, the probability that the supervisory enterprise chooses “active supervision” in a stable state must satisfy F(z) = 0 and , because H(x) is a decreasing function. Therefore, when , H(x) = 0, at which time , the supervisory enterprise cannot determine the stability strategy; when x < x*, H(x) > 0, at which time , z = 0 is the supervisory enterprises’ evolutionary stabilization strategy (ESS); conversely, z = 1 is the ESS.
The evolutionary phase diagram of the strategy of the supervisory enterprises is shown in Figure 4.
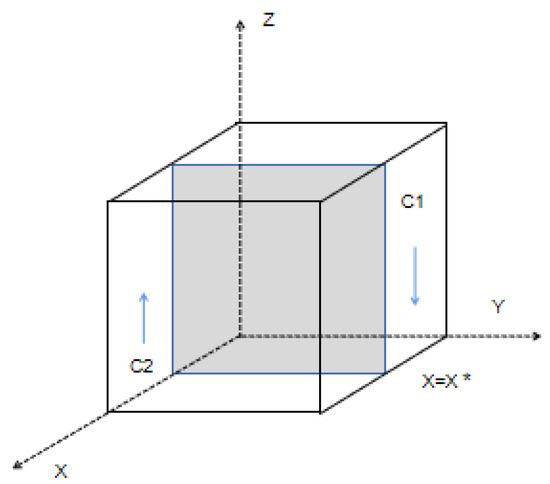
Figure 4.
Phase diagram of the evolution of third-party supervisory companies.
Proposition 5.
The probability of supervision enterprises choosing “active supervision” in cultivated land remediation is positively correlated with the amount of deduction by the grassroots government and the probability of random inspection by the higher-level government. It is negatively correlated with the cost saved by “negative supervision”.
Proof.
Since , x* gradually decreases when Fs, β gradually increases, or Csh − Csl gradually decreases. The volume of C2 in Figure 4 gradually increases, indicating that the probability of supervising enterprises tends to “actively supervise” gradually increases. □
Proposition 5 shows that the government cannot only curb the “negative supervision” of supervision enterprises by increasing the punishment and sampling probability of supervision enterprises but can also increase the cost of “negative supervision” to regulate the supervision enterprises’ behavior, for example, by establishing a credit file and credit accumulation system, strengthening information disclosure, and effectively promoting external public supervision.
Proposition 6.
In the evolutionary process, the probability of supervisory enterprise choosing “active supervision” in cultivated land remediation increases as the probability of government choosing “action” rises.
Proof.
The evolutionary stability analysis of the strategy choice of the supervisory enterprise shows that z = 0 is the ESS when x < x*. When x > x*, z = 1 is the ESS, so the stable strategy of the supervisory enterprise changes from z = 0 to z = 1 with the increase in x. □
Proposition 6 shows that the “active supervision” strategy of supervision enterprises is influenced by the government’s strategic choice, and supervision will tend to be active when the government chooses “action”. Therefore, to guarantee the effect of cultivated land remediation, it is necessary for the government supervisory department to strictly supervise and adopt a zero-tolerance attitude towards the “negative supervision” of enterprises to curb the implementation of negative behaviors by supervisory enterprises.
3.4. System Equilibrium Point Stability Analysis
According to the scholar Friedman [35], the stability of the system of differential equations can be judged based on the positive and negative Jacobi matrix. According to scholars RitzbeRger and Weibull [30], the case of a three-party game requires only the analysis of pure strategy points. The Jacobi matrix can be derived from the replicated dynamic equations of the three-party subject. From the Lyapunov method, it is known that in the stability analysis of differential systems, stability can be judged according to the positive and negative characteristics root of the equilibrium point—when all the characteristics root of the equilibrium point are negative, the point is an evolutionarily stable strategy (i.e., an asymptotically stable point). The eight pure strategy points are substituted into the Jacobi matrix in turn, and the corresponding characteristic roots of the equilibrium points are obtained. The results are shown in the following Table 2.

Table 2.
Summary of equilibrium points and their characteristic roots.
The conditions of the relative sizes of the parameters assumed in the previous section are as follows: Cmh − Cml < Fm, Csh − Csl < Fs. According to the condition that the characteristic roots are all negative, it is known that E2, E4, E5, and E6 are not evolutionarily stable points. Further analysis shows the conditions for the other four equilibrium points to become stable points and the positive and negative characteristic roots in the following Table 3.

Table 3.
Positive and negative characteristic roots and their stabilities under different conditions.
In the existing literature on three-party evolutionary games, few papers discuss the transformation and variation of equilibrium points under different parameter variations in depth. To more intuitively discover the change in the equilibrium point under the influence of various parameters and to find more managerial insights, the simulation of the equilibrium evolution under the scenario of parameter variation will be simulated next using numerical simulation techniques.
4. Computational Experimental Simulation
In this paper, we refer to the parameter settings of Lin Ze-Jian [15] to conduct numerical simulation with the help of MATLAB 2020B software under the previous assumptions. We establish arrays 1 to 4, which satisfy the equilibrium point condition, as follows:
Array 1: Rgs = 1, Cgh = 100, Cgl = 0, Fg = 15, Bm = 830, Cmh = 670, Cml = 470, Fm = 210, Bs = 21, Csh = 17, Csl = 4, Fs = 15, Jg = 15, β = 0.5, α = 0.2, Rge = 1435;
Array 2: Rgs = 1, Cgh = 100, Cgl = 0, Fg = 15, Bm = 830, Cmh = 670, Cml = 470, Fm = 410, Bs = 21, Csh = 17, Csl = 4, Fs = 15, Jg = 15, β = 0.5, α = 0.2, Rge = 1435;
Array 3: Rgs = 1, Cgh = 100, Cgl = 0, Fg = 15, Bm = 830, Cmh = 670, Cml = 470, Fm = 210, Bs = 21, Csh = 17, Csl = 4, Fs = 15, Jg = 15, β = 0.91, α = 0.2, Rge = 1435;
Array 4: Rgs = 1, Cgh = 100, Cgl = 0, Fg = 200, Bm = 830, Cmh = 670, Cml = 470, Fm = 210, Bs = 21, Csh = 17, Csl = 4, Fs = 15, Jg = 15, β = 0.5, α = 0.2, Rge = 1435.
Let the replicated dynamic equations evolve 50 times with time. The simulation results are shown in Figure 5, Figure 6, Figure 7 and Figure 8.
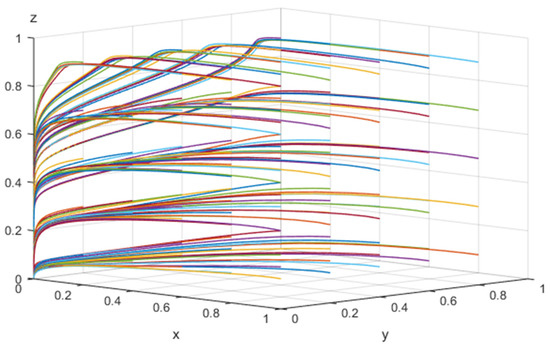
Figure 5.
The result of 50 evolutions of array 1.
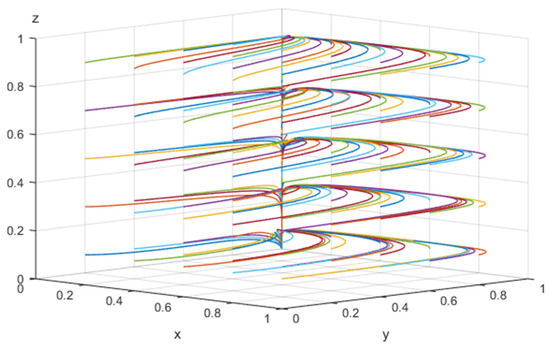
Figure 6.
The result of 50 evolutions of array 2.
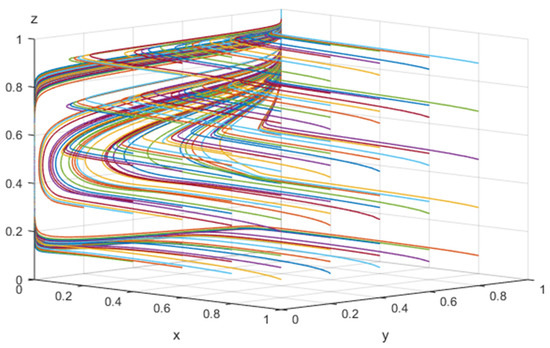
Figure 7.
The result of 50 evolutions of array 3.
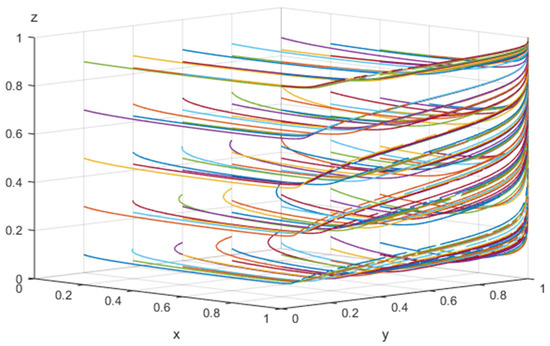
Figure 8.
The result of 50 evolutions of array 4.
The simulation results are consistent with the system evolution stability analysis’s conclusions (see Table 3 for details), which verifies the model’s validity. Considering the limited space of this paper, we only conduct further numerical simulations for E1(0, 0, 0) to verify the previous analysis of system evolutionary stability and to explore the influence of critical parameters on the evolution of the game subjects’ behavior. Meanwhile, to make later studies more rational, the parameters to be simulated in this paper are divided into two categories: the first category is reward and punishment parameters, and the second category is probability parameters. The effects of the changes in the two types of parameters on the equilibrium evolution are discussed separately in the latter part.
4.1. Effects of Changes in Reward and Punishment Class Parameters on Equilibrium Evolution
4.1.1. The Effect of Changes in the Amount of Deductions by the Grassroots Government on the Equilibrium Evolution of Governance Enterprises
From Figure 9, it can be seen that increasing the amount of deductions to governance firms and increasing the frequency of random inspections by the higher-level government can shift the equilibrium. The combination of strategies (“inaction”, “negative harness pollution”, “Negative supervision”) changes to the combination of strategies (“action”, “active harness pollution”, “Negative supervision”). However, when the amount of withholding or the frequency of spot checks by the higher-level government is too low, the behavior of the governance enterprises cannot be effectively regulated by these two methods. Therefore, while the higher-level government establishes a “regular” inspection system, setting up incentive and punishment measures compatible with the governance enterprise is the key to guaranteeing the standard behavior of governance enterprises.
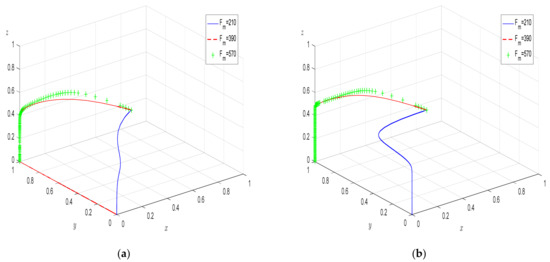
Figure 9.
The effect of parameters Fm and β on evolutionary outcome. (a) Effect of Fm when β is 0.3; (b) Effect of Fm when β is 0.8.
4.1.2. The Effect of Changes in the Amount of Deductions by the Grassroots Government on the Equilibrium Evolution of Supervisory Enterprises
From Figure 10, increasing the amount of deduction for supervisory enterprises and increasing the frequency of random inspections by the higher-level government can shift the equilibrium. The combination of strategies (“inaction”, “negative harness pollution”, “negative supervision”) changes to the combination of strategies (“inaction”, “active harness pollution”, “active supervision”). However, when the amount of deductions or the frequency of spot checks by the higher-level government is too low, it cannot effectively regulate the behavior of supervision enterprises in these two ways. Compared with Figure 9, we can find that strict supervision of supervision enterprises can be “double-pronged”. Not only can supervision enterprises actively supervise, but governance companies can also choose to actively remediate due to the pressure of “multiple supervision in a ladder”, which can improve the effect of cultivated land remediation more efficiently. Therefore, the supervisory enterprises can be based on setting a reasonable amount of deduction and a reasonable frequency of random inspection, improving the reward mechanism through a differentiated reward and punishment system, etc., to enhance their motivation and ability to implement positive behavior.
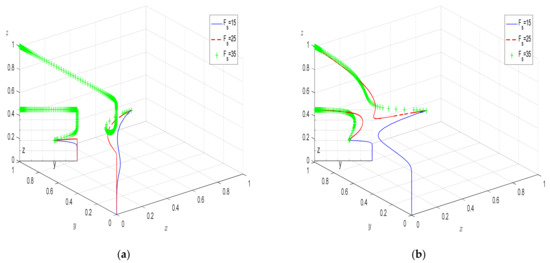
Figure 10.
The effect of parameters Fs and β on evolutionary outcome. (a) Effect of Fs when β is 0.3; (b) Effect of Fs when β is 0.8.
4.1.3. The Effect of Changes in Rewards and Punishments from Higher Levels of Government on the Equilibrium Evolution of Grassroots Government
Comparing Figure 11a and Figure 11b, it can be seen that increases in the incentives and penalties for grassroots government cause the equilibrium to shift from a combination of strategies (“inaction”, “negative harness pollution”, “negative supervision”) to a strategic combination (“action”, “active harness pollution”, “active supervision”). The reward and punishment system of the grassroots government is crucial to the third-party governance model of cultivated land. Constructing an incentive-compatible reward and punishment system for the grassroots government is an effective way to solve the third-party governance dilemma. In the real situation, the punishment for the grassroots government is shown in the form of interviews and accountability, withdrawal of project funds, transfer from the post, demotion, etc. Since this model collects the punishment in one parameter, strengthening the means mentioned above can play a certain incentive role from the perspective of the grassroots government. Comparing Figure 11a and Figure 11b, we can see that, compared with punishment, rewarding the grassroots government can transform the equilibrium point more efficiently. Therefore, we should optimize the assessment of the grassroots government, introduce the green ecological concept to establish an incentive-compatible assessment and evaluation system, and enhance the power of the grassroots government’s “action” on political performance.
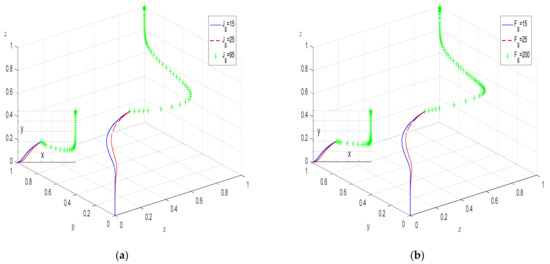
Figure 11.
The effect of parameters Fg and Jg on evolutionary outcome. (a) The impact of grassroots government incentives; (b) The impact of grassroots government punishments.
4.2. Effect of Changes in Probability Class Parameters on Equilibrium Evolution
4.2.1. The Effect of the Frequency of Spot-Checking by Higher Levels of Government on the Evolution of Equilibrium
As can be seen from Figure 12, the probability of spot checks by higher levels of government gradually increases, which causes the equilibrium to shift from a combination of strategies (“inaction”, “negative harness pollution”, “negative supervision”) to the strategy combination (“inaction”, “active harness pollution”, “active supervision”). Although the effectiveness of cultivated land remediation can be equally guaranteed in the short term when stabilized in the (“inaction”, “active harness pollution”, “active supervision”) strategy, the complex principal–agent relationship of “ladder multiple supervision” will increase the risk of “moral hazard” and “adverse selection”. Suppose the grassroots government’s long-term supervision is absent. In that case, governance enterprises and supervision enterprises will tend to negatively harness pollution and reduce supervision based on their interests. It is difficult to form a long-term guarantee mechanism for the quality of cultivated land governance. Therefore, the accountability system of the grassroots government on the governance of cultivated land should be improved [36], the expected return of “action” and the weight in the performance appraisal should be increased, the sense of responsibility of government departments should be strengthened, and adequate supervision should be ensured.
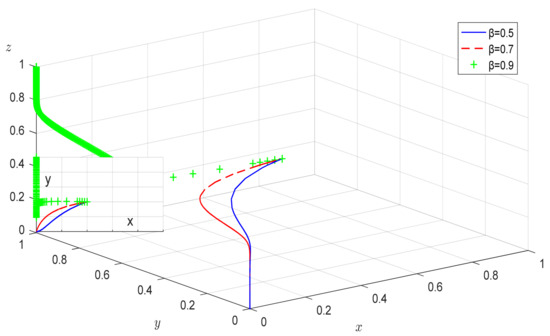
Figure 12.
Influence of Spot check frequency of higher-level government at α = 0.2.
4.2.2. A Spot Check of Governance Firms by a Higher-Level Government Can Detect the Effect of the Probability of Negative Harness Pollution on the Evolution of Equilibrium
From Figure 13, we can see that increasing α alone does not move the equilibrium point. Still, with the gradual increase in α, the arrival at the equilibrium point (“inaction”, “active harness pollution”, “active supervision”) can be gradually accelerated. Comparing Figure 12 with Figure 13, in Figure 12, where α = 0.2 and β = 0.5, the strategy tends toward (“inaction”, “negative harness pollution”, “negative supervision”). In contrast, in Figure 13, α = 0.1 and β = 0.9 tends to (“inaction”, “active harness pollution”, “active supervision”), indicating that, to a certain extent, enhancing the frequency of spot checks can compensate for the limitations of the technical cognition and workforce of the upper-level government spot checkers.
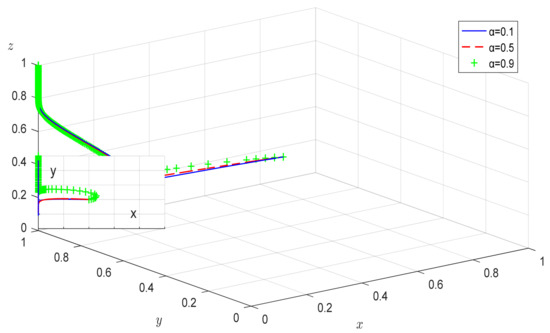
Figure 13.
The effect of α at β = 0.9.
5. Conclusions
5.1. Results and Suggestions
Based on the current practice of heavy metal-contaminated cultivated land remediation, this paper constructs a three-party evolutionary game model involving the grassroots government, governance companies, and supervision enterprises. This study analyzes the stability of each party’s strategy choice, the stability of the equilibrium strategy combination of the game system, and the influence relationship of each element; verifies the validity of the analysis’s conclusions through simulation analysis; and proposes relevant countermeasures and suggestions according to the influence relationship and stability conditions of each factor.
First, the grassroots government’s choice of “action” is a prerequisite for consistent action by the participants in cultivated land remediation. The higher probability of the government choosing “action” can increase the likelihood of the supervisory enterprises’ choice of “active supervision”. In turn, the higher probability of “action” and “active supervision” by the government and supervisory companies can increase the probability of “active harness pollution” by governance companies. However, as the probability of governance enterprises and supervisory enterprises choosing “active harness pollution” and “active supervision” increases, the probability of government departments to choose “action” will decrease. This will easily lead to the lack of supervision by the grassroots government and make it difficult to establish a long-term guarantee mechanism for the quality of cultivated land. Therefore, we can strengthen the sense of responsibility of grassroots government supervisory departments, improve the accountability system of cultivated land remediation, and establish a mutual supervision mechanism among various grassroots government departments to reduce information asymmetry and conflicts of interest between the higher-level and grassroots governments due to the commissioning agency. At the same time, the assessment of the grassroots government should be optimized. The green ecological concept was introduced to establish an incentive-compatible assessment and evaluation system to enhance the effect of the grassroots government’s “action” on political performance.
Second, the incentives of rewards and subsidies can be used to enhance the motivation and ability of governance and supervision enterprises to implement positive behaviors. The evaluation system of government-purchased services should be optimized, a relevant credit evaluation system should be built, and enterprises with high levels and a good reputation can issue proof medals and publicize them to enhance the positive incentive effect of reputation benefits. The incentive system for governance and supervision enterprises should also be improved. The enthusiasm of enterprises with differentiated reward and punishment mechanisms can be mobilized. Furthermore, enterprises can be encouraged and guided to increase research and development into vital common technologies for cultivated land pollution remediation and to support enterprises to train high-end talents in cultivated land pollution remediation, such as through scientific and technological innovation and technical services to reduce the cost of governance and supervision. By combining reputational, monetary, and tax incentives, we can save government regulation costs and enhance the endogenous motivation of enterprises to choose “active harness pollution” and “active supervision” strategies.
Third, a regular spot check system should be established, and the results of these spot checks should be published. the risk of information asymmetry of the entrusted agent should also be resolved. The public participation mechanism and information disclosure system should be improved. Enterprises with weak technical service capability, low operation and remediation levels, and poor comprehensive credit should be exposed publicly and punished. These actions would make third-party enterprises magnify the perceived value of loss through the deterrent effect of punishment to reduce their risk appetite.
Fourth, the costs of business violations and breaches of trust should be increased to prevent opportunistic behavior. The probability of implementing positive enterprise behaviors is negatively related to the cost savings from practicing a negative behavior. The government should strengthen the qualification reviews of third-party enterprises, establish third-party market access and exit mechanisms, label enterprises which have a lifetime system of severe violations, and implement a market entry ban system. These measures would increase the cost of implementing negative behaviors and regulating corporate behavior.
5.2. Limitations and Future Research
Several limitations are worth noting, which may provide ideas for the future research direction. First, one of the most common assumptions of the third-party remediation model of heavy metal-contaminated cultivated land constructed in this paper is that the participants are finite rational subjects. However, in real cases, there are inevitably non-finite rational participants due to the differences in culture and environment. Future research can further refine the model’s parameters to consider the behavior of non-finite rational participants and narrow the discrepancy between the theoretical model and the actual case. Second, this study did not consider the influence of agricultural producers, who have a strong subjective initiative in supervising the remediation of heavy metal-contaminated cultivated land. Therefore, our subsequent research direction will be constructing a dynamic game model with the participation of agricultural producers and making innovative suggestions for optimizing the remediation of heavy metal-contaminated cultivated land.
Author Contributions
Conceptualization, X.X. and J.L.; methodology, X.X. and J.L.; software, X.X.; validation, X.X., J.L. and Z.L.; formal analysis, X.X.; investigation, X.X., J.L. and Z.L.; resources, X.X., J.L. and Z.L.; data curation, X.X., J.L. and Z.L.; writing—original draft preparation, X.X. and J.L.; writing—review and editing, X.X. and J.L.; visualization, X.X.; supervision, J.L. and Z.L.; project administration, J.L.; funding acquisition, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Hunan Natural Science Fund Project (2021JJ30365).
Institutional Review Board Statement
This study has no ethical implications and therefore does not require ethical approval.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data used and processed during the current study are available from the corresponding author on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liang, M.; Kong, F.; Liang, Y. A Review and Reflection on the “13th Five-Year” Plan for Land Remediation. China Land 2021, 420, 36–38. [Google Scholar] [CrossRef]
- China Environmental Status Bulletin 2017(Excerpt 3). Environ. Prot. 2018, 46, 70–74.
- China Ecological Environment Status Bulletin 2021(Excerpt). Environ. Prot. 2022, 50, 61–74. [CrossRef]
- Bhat, J.A.; Shivaraj, S.M.; Singh, P.; Navadagi, D.B.; Tripathi, D.K.; Dash, P.K.; Solanke, A.U.; Sonah, H.; Deshmukh, R. Role of Silicon in Mitigation of Heavy Metal Stresses in Crop Plants. Plants 2019, 8, 71. [Google Scholar] [CrossRef]
- Li, Z.; Ma, Z.; van der Kuijp, T.J.; Yuan, Z.; Huang, L. A review of soil heavy metal pollution from mines in China: Pollution and health risk assessment. Sci. Total Environ. 2014, 468, 843–853. [Google Scholar] [CrossRef] [PubMed]
- Trifonova, T.A.; Alkhutova, E.Y. Phytomass change in natural phytocenosis as an indicator of technogenic pollution of soils with heavy metals. Int. J. Phytoremediat. 2016, 18, 1209–1220. [Google Scholar] [CrossRef]
- Hafez, E.E.; Elbestawy, E. Molecular characterization of soil microorganisms: Effect of industrial pollution on distribution and biodiversity. World J. Microbiol. Biotechnol. 2009, 25, 215–224. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, Y.; Wang, M.; Meng, H.; Ye, Z. Real-time detection method for heavy metal pollution in soil of mining area. Glob. Nest J. 2020, 22, 570–578. [Google Scholar] [CrossRef]
- Ikeda, M.; Watanabe, T.; Ohashi, F.; Shimbo, S. Effects of Variations in Cadmium and Lead Levels in River Sediments on Local Foods and Body Burden of Local Residents in Non-Polluted Areas in Japan. Biol. Trace Elem. Res. 2010, 133, 255–264. [Google Scholar] [CrossRef]
- Hu, H.; Jin, Q.; Kavan, P. A Study of Heavy Metal Pollution in China: Current Status, Pollution-Control Policies and Countermeasures. Sustainability 2014, 6, 5820–5838. [Google Scholar] [CrossRef]
- Huang, J.; Li, J. Problems and Countermeasures of “Third-Party Governance” of Heavy-Metal-Polluted Farmland Remediation:Take Changsha-Zhuzhou-Xiangtan Area as an Example. Econ. Geogr. 2020, 40, 179–184+211. [Google Scholar] [CrossRef]
- Huang, D.; Zhu, Q.; Zhu, H.; Xu, C.; Liu, S. Advances and prospects of safety agro-utilization of heavy metal contaminated farmland soil. Res. Agric. Mod. 2018, 39, 1030–1043. [Google Scholar] [CrossRef]
- Chapman, B.; Lindenmayer, D.B. A novel approach to the sustainable financing of the global restoration of degraded agricultural land. Environ. Res. Lett. 2019, 14, 124084. [Google Scholar] [CrossRef]
- Cheng, S. Heavy metal pollution in China: Origin, pattern and control–a state-of-the-art report with special reference to literature published in Chinese journals. Environ. Sci. Pollut. Res. 2007, 14, 489. [Google Scholar] [CrossRef]
- Lin, Z. Study on the Remidiatory Mechanism of Heavy Metal Contaminated Farmland; Hunan Science & Technology Press: Changsha, China, 2020. [Google Scholar]
- Chen, J.; Yang, Q.; Chen, J.; Zhang, C.; Wang, C.; Zhang, X.; Liu, K. Study on the Diversified Governance System of Heavy Metal Pollution Subjects in Cultivated Land in the Context of Rural Revitalization- -An Example of Dabaoshan Mining Area. Guangdong Agric. Sci. 2022, 49, 160–170. [Google Scholar] [CrossRef]
- You, G.; Xiao, J. Analysis on the Inter-governmental Responsibility-sharing Mechanism of Heavy Metal Pollution Control in Hunan Chang-Zhu-Tan Cultivated Land in Rural Revitalization. J. Southwest For. Univ. (Soc. Sci.) 2020, 4, 51–56. [Google Scholar]
- You, G.; Xiao, J. Construction of Responsibility Distribution Mechanism for Heavy Metal Pollution Governance in Cultivated Land. J. Cent. South Univ. For. Technol. (Soc. Sci.) 2020, 14, 47–52. [Google Scholar] [CrossRef]
- Wei, G.L.; Li, G.L.; Sun, X. Evolutionary Game Analysis of the Regulatory Strategy of Third-Party Environmental Pollution Management. Sustainability 2022, 14, 15449. [Google Scholar] [CrossRef]
- Copeland, B.R.; Taylor, M.S. Trade and the Environment: A Partial Synthesis. Am. J. Agric. Econ. 1995, 77, 765–771. [Google Scholar] [CrossRef]
- Liu, Q.; Li, X.; Hassall, M. Evolutionary game analysis and stability control scenarios of coal mine safety inspection system in China based on system dynamics. Saf. Sci. 2015, 80, 13–22. [Google Scholar] [CrossRef]
- Zhou, C.H.; Xie, H.L.; Zhang, X.M. Does Fiscal Policy Promote Third-Party Environmental Pollution Control in China? An Evolutionary Game Theoretical Approach. Sustainability 2019, 11, 4434. [Google Scholar] [CrossRef]
- Chen, H.; Hao, Y.; Li, J.; Song, X. The impact of environmental regulation, shadow economy, and corruption on environmental quality: Theory and empirical evidence from China. J. Clean. Prod. 2018, 195, 200–214. [Google Scholar] [CrossRef]
- Zhao, C.; Zeng, J. Can environmental management improve financial performance: An empirical study of A-shares listed companies in China. J. Clean. Prod. 2017, 141, 1051–1056. [Google Scholar]
- Liu, L. Geographic approaches to resolving environmental problems in search of the path to sustainability: The case of polluting plant relocation in China. Appl. Geogr. Sevenoaks 2013, 45, 138–146. [Google Scholar] [CrossRef]
- Kim, S.; Shin, N.; Park, S. Closed-Loop Supply Chain Coordination under a Reward-Penalty and a Manufacturer’s Subsidy Policy. Sustainability 2020, 12, 9329. [Google Scholar] [CrossRef]
- Wilson, K.R. Reputation and imperfect information. J. Econ. Theory 1982, 27, 253–279. [Google Scholar]
- Cheng, L.; Liu, G.; Huang, H.; Wang, X.; Chen, Y.; Zhang, J.; Meng, A.; Yang, R.; Yu, T. Equilibrium analysis of general N-population multi-strategy games for generation-side long-term bidding: An evolutionary game perspective. J. Clean. Prod. 2020, 276, 124123. [Google Scholar] [CrossRef]
- Cheng, L.; Chen, Y.; Liu, G. 2PnS-EG: A general two-population n-strategy evolutionary game for strategic long-term bidding in a deregulated market under different market clearing mechanisms. Int. J. Electr. Power Energy Syst. 2022, 142, 108182. [Google Scholar] [CrossRef]
- Friedman, D. A simple testable model of double auction markets. J. Econ. Behav. Organ. 1991, 15, 47–70. [Google Scholar] [CrossRef]
- Xia, J.; Li, R.Y.M.; Zhan, X.G.; Song, L.X.; Bai, W.J. A study on the impact of fiscal decentralization on carbon emissions with U-shape and regulatory effect. Front. Environ. Sci. 2022, 10, 1162. [Google Scholar] [CrossRef]
- Ouchida, Y.; Goto, D. Do emission subsidies reduce emission? In the context of environmental R&D organization. Econ. Model. 2014, 36, 511–516. [Google Scholar]
- Zhao, Z.X.; Liu, L.N.; Zhang, F.; Yang, G.Z. Does air pollution prompt corporations to implement green management? Evidence from China. Environ. Sci. Pollut. Res. 2022, 29, 8933–8946. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Qin, G.Y.; Wang, L.; Cheng, B.D.; Tian, Y. Evolutionary Game Research between the Government Environmental Regulation Intensities and the Pollution Emissions of Papermaking Enterprises. Discret. Dyn. Nat. Soc. 2021, 2021, 7337290. [Google Scholar] [CrossRef]
- Ritzberger, K.; Weibull, J.W. Evolutionary Selection in Normal Form Games. Work. Pap. Ser. 1993, 63, 1371–1399. [Google Scholar] [CrossRef]
- Zhang, T.F.; Qin, H.Y.; Xu, W.S. Environmental Regulation, Greenwashing Behaviour, and Green Governance of High-Pollution Enterprises in China. Int. J. Environ. Res. Public Health 2022, 19, 12539. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).