A New Agricultural Drought Disaster Risk Assessment Framework: Coupled a Copula Function to Select Return Periods and the Jensen Model to Calculate Yield Loss
Abstract
1. Introduction
2. Materials and Methods
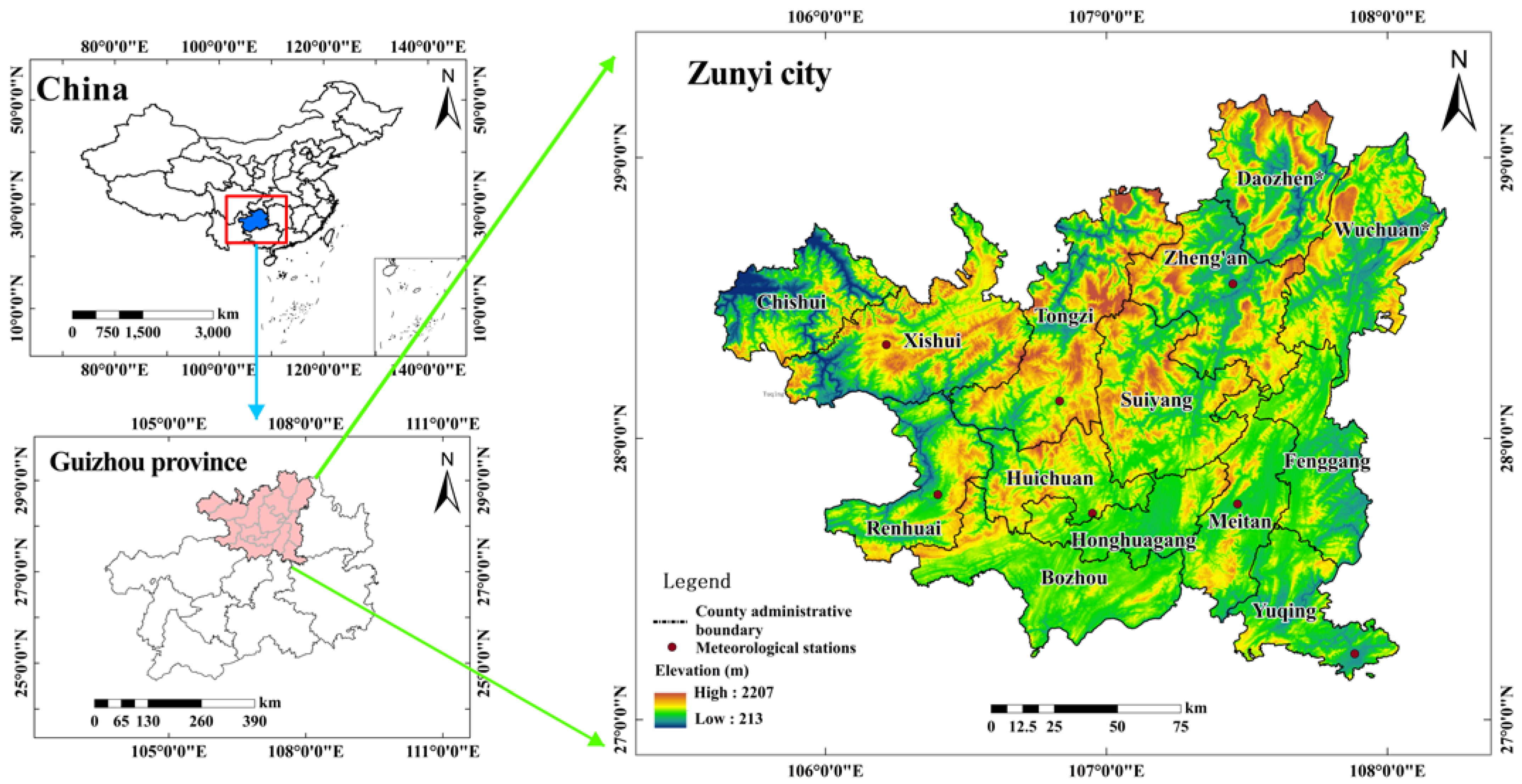
2.1. Description of the Study Area
2.2. Data Sources
2.3. Evaluation Object Selection
2.4. Methodology
2.4.1. Drought Classification
2.4.2. Analysis of Drought Feature Variables
2.4.3. Copula Function for Drought Frequency and Return Period
2.4.4. Jensen Model for Yield Loss Calculation
3. Results
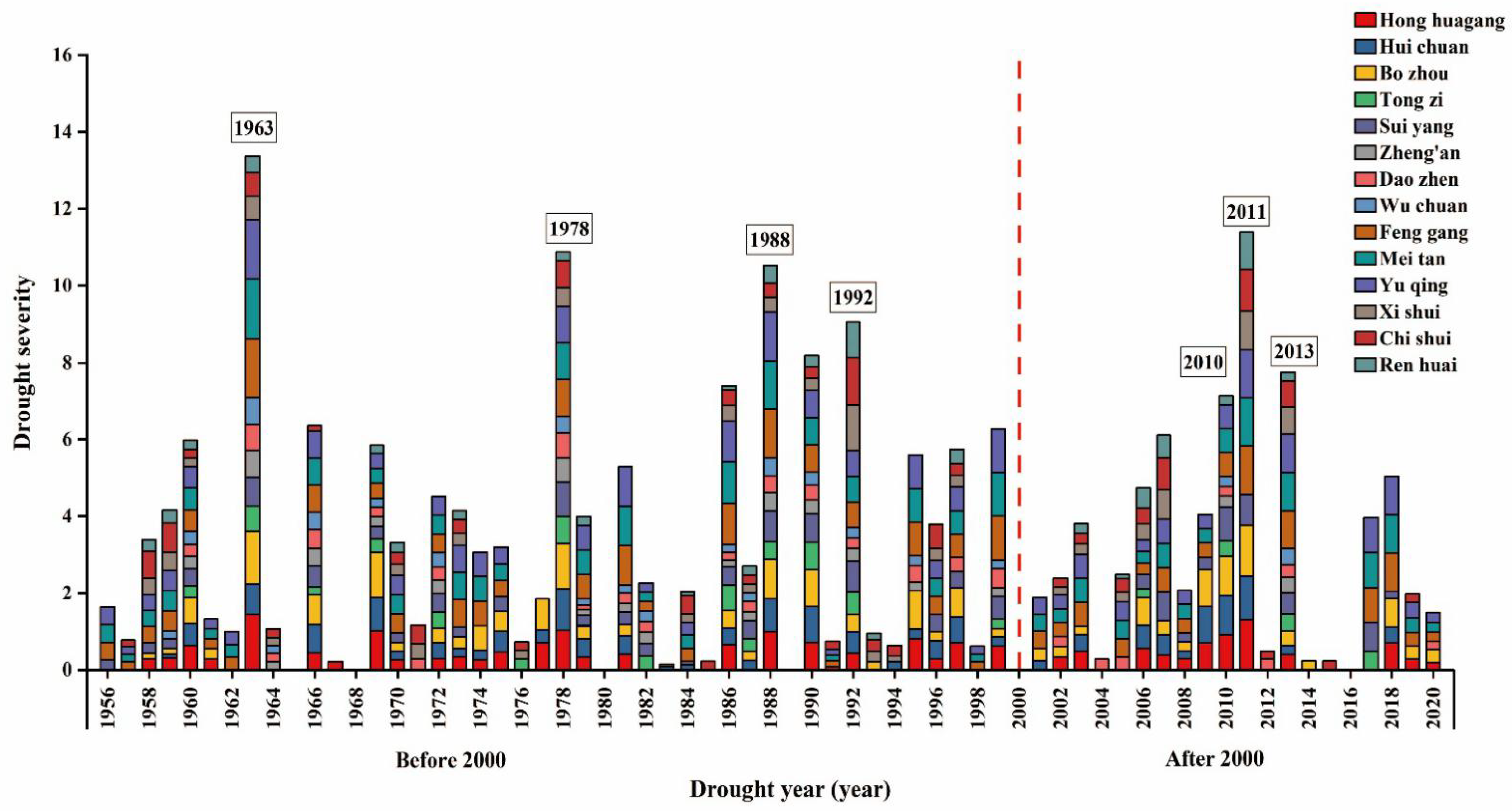
3.1. Agricultural Drought Disaster Characteristics
3.1.1. Analysis of Drought Characteristics
3.1.2. Establishment of Two-Dimensional Joint Distribution
3.1.3. Rational Analysis of Drought Characteristics Results
3.2. Agricultural Drought Risk Assessment
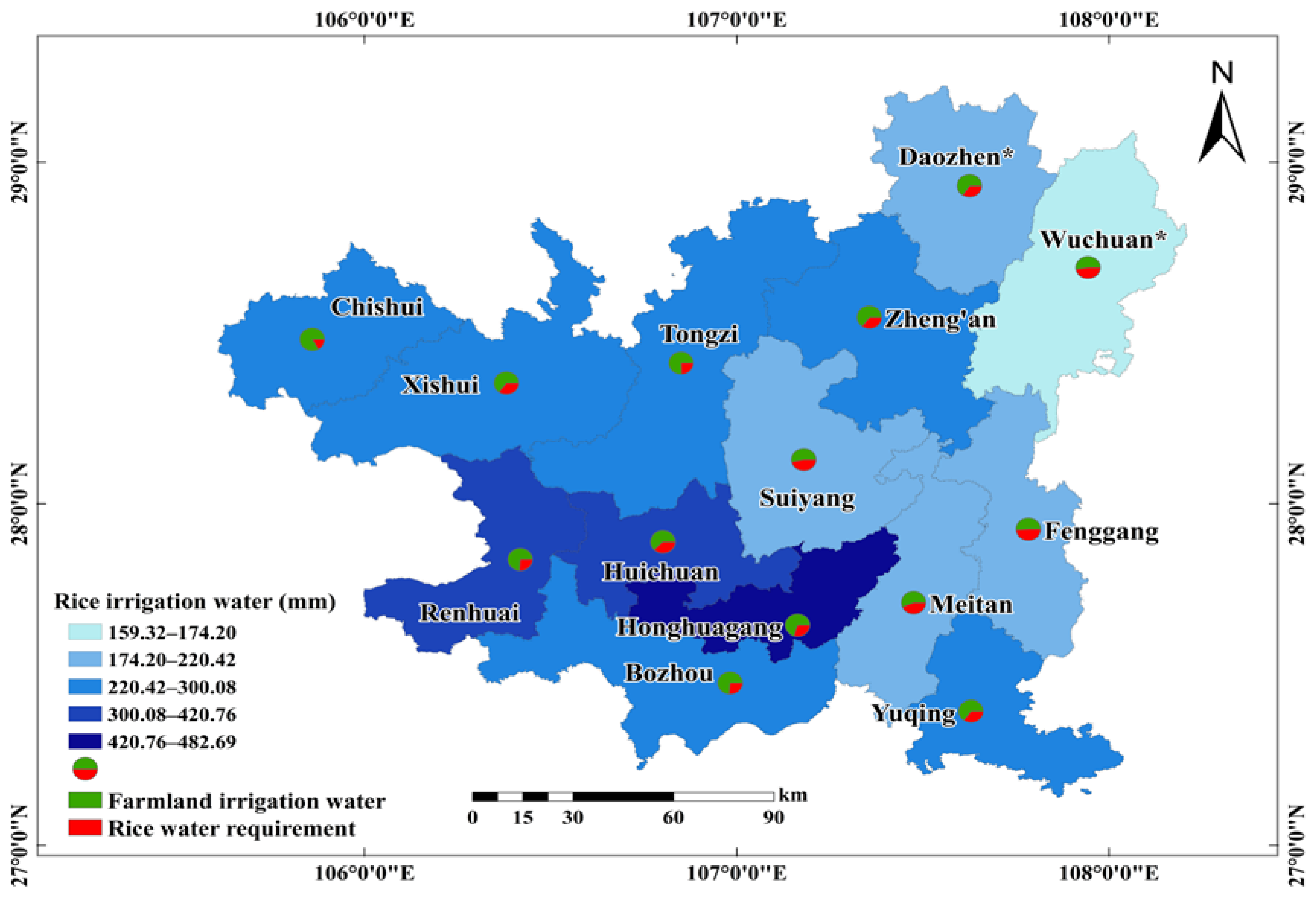
3.2.1. Distribution Characteristics of Irrigation Water
3.2.2. Drought Frequency and the Agricultural Drought Loss Rate
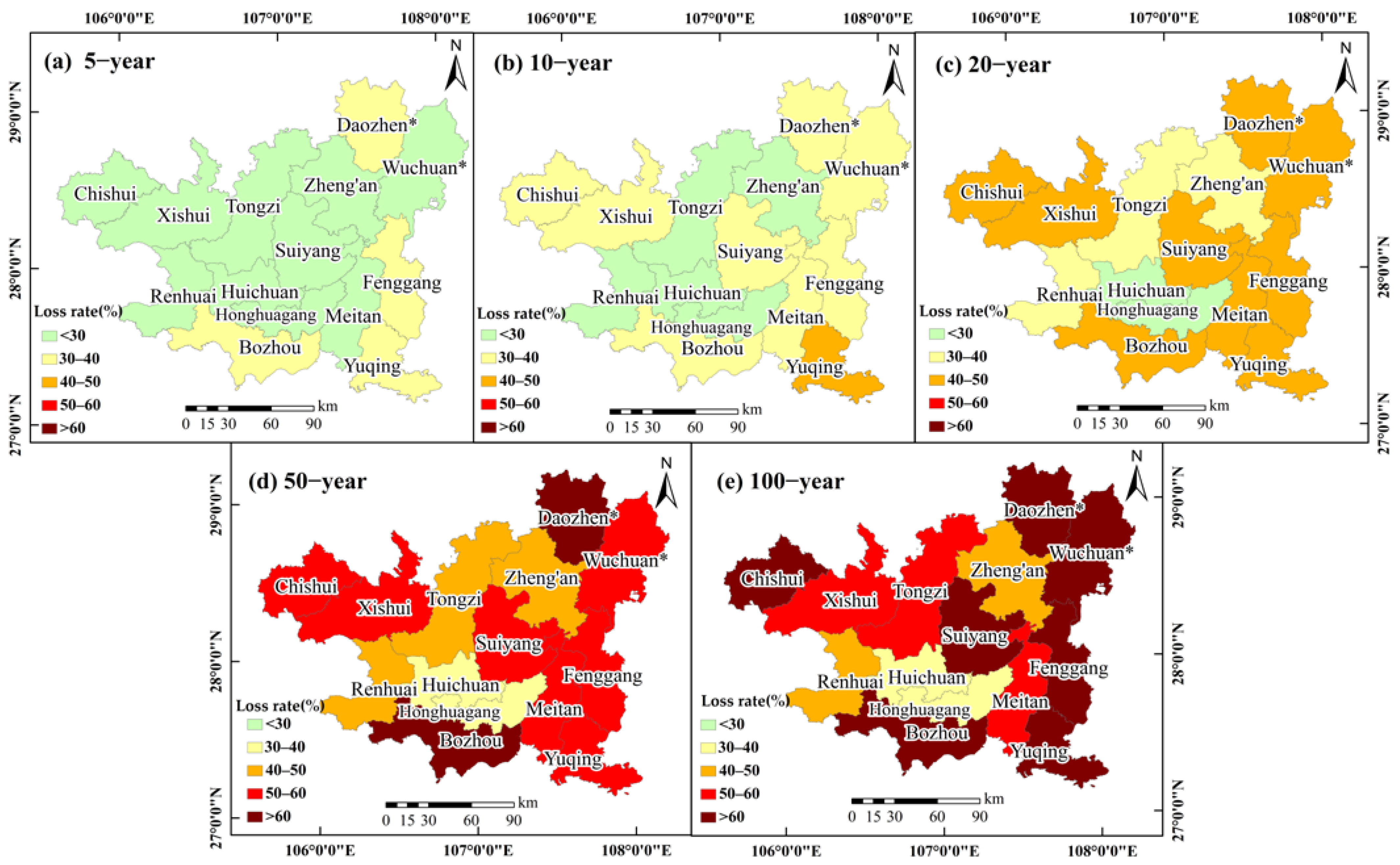
3.2.3. Spatial Distribution of Agricultural Drought Loss
4. Discussion
4.1. Frequent Drought Disaster Areas and Cause Analysis
4.2. Advantages of the Drought Risk Assessment Method Proposed in this Study
5. Conclusions
- (1)
- By using the return period calculated by a copula function and the agricultural drought loss rate calculated by the Jensen model, the possible losses caused by different frequency droughts in a certain area under a certain drought resistance condition can be quickly estimated by constructing the relationship curve of drought risk mechanism. This method is helpful for competent authorities to make scientific decisions, respond in time, and formulate appropriate and effective countermeasures.
- (2)
- Mapping the spatial distribution of drought losses under different return periods helps to compare the vulnerability between regions at the county level, so that the drought competent authorities can actively take defensive practices to mitigate drought risks. Therefore, this method broadens the technique and knowledge of risk quantification in drought risk assessment.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, Y.T.; Wei, S.C.; Li, K.W.; Zhang, J.Q.; Wang, C.Y. Drought risk assessment of millet and its dynamic evolution characteristics: A case study of Liaoning Province, China. Ecol. Indic. 2022, 143, 109407. [Google Scholar] [CrossRef]
- Jung, H.; Won, J.; Kang, S.; Kim, S. Characterization of the propagation of meteorological drought using the copula model. Water 2022, 14, 3293. [Google Scholar] [CrossRef]
- Linh, V.T.; Tram, V.N.Q.; Dung, H.M.; Phuong, D.N.D.; Liem, N.D.; Nguyen, L.D.; Yin, C.; Kortun, A.; Loi, N.K. Meteorological and hydrological drought assessment for dong nai river basin, vietnam under climate change. Mobile Netw. Appl. 2021, 26, 1788–1800. [Google Scholar] [CrossRef]
- Gidey, E.; Dikinya, O.; Sebego, R.; Segosebe, E.; Zenebe, A. Modeling the spatio-temporal meteorological drought characteristics using the standardized precipitation index (SPI) in raya and its environs, northern ethiopia. Earth Syst. Environ. 2018, 2, 281–292. [Google Scholar] [CrossRef]
- Suman, M.; Maity, R. Assessment of basin-wise future agricultural drought status across India under changing climate. J. Water Clim. Chang. 2021, 12, 2400–2421. [Google Scholar] [CrossRef]
- Guo, H.; Wen, X.L.; Wu, Y.Y.; Wang, J.A.; Liang, Q.O. Drought risk assessment of farmers considering their planting behaviors and awareness: A case study of a County from China. Ecol. Indic. 2022, 137, 108728. [Google Scholar] [CrossRef]
- Hou, M.L.; Yao, N.; Li, Y.; Liu, F.G.; Biswas, A.; Pulatov, A.; Hassan, I. Better drought index between spei and smdi and the key parameters in denoting drought impacts on spring wheat yields in Qinghai, China. Agronomy 2022, 12, 1552. [Google Scholar] [CrossRef]
- Kumar, U.; Singh, S.; Bisht, J.K.; Kant, L. Use of meteorological data for identification of agricultural drought in Kumaon region of Uttarakhand. J. Earth Syst. Sci. 2021, 130, 121. [Google Scholar] [CrossRef]
- Zhu, W.F.; Liu, X.; Li, F.H.; Zheng, W.S. Temporal and Spatial Distribution of Drought and Irrigation Water Requirement of Maize Based on Rainfall in Heilongjiang Province. Conserv. Irrig. 2018, 3, 63–67; 73. [Google Scholar]
- Tan, H.Z.; Lu, X.N.; Yang, S.Q.; Wang, Y.Q.; Li, F.; Liu, J.B.; Chen, J.; Huang, Y. Drought risk assessment in the coupled spatial–temporal dimension of the Sichuan Basin, China. Nat. Hazards 2022, 114, 3205–3233. [Google Scholar] [CrossRef]
- Luo, D.; Ye, L.L.; Sun, D. Risk evaluation of agricultural drought disaster using a grey cloud clustering model in Henan province, China. Int. J. Disaster Risk Reduct. 2020, 49, 101759. [Google Scholar] [CrossRef]
- Sahana, V.; Mondal, A.; Sreekumar, P. Drought vulnerability and risk assessment in India: Sensitivity analysis and comparison of aggregation techniques. J. Environ. Manag. 2021, 299, 113689. [Google Scholar] [CrossRef]
- Schmitt, J.; Offermann, F.; Söder, M.; Frühauf, C.; Finger, R. Extreme weather events cause significant crop yield losses at the farm level in German agriculture. Food Policy 2022, 112, 102359. [Google Scholar] [CrossRef]
- Xie, Z.T.; Xu, J.P.; Deng, Y.F. Risk analysis and evaluation of agricultural drought disaster in the major grain-producing areas, China. Geomat. Nat. Hazards Risk 2016, 7, 1691–1706. [Google Scholar] [CrossRef]
- Jehanzaib, M.; You, J.; Kwon, H.H.; Kim, T.W. Reassessing the frequency and severity of meteorological drought considering non-stationarity and copula-based bivariate probability. J. Hydrol. 2021, 603, 126948. [Google Scholar] [CrossRef]
- Wang, F.; Wang, Z.M.; Yang, H.B.; Di, D.Y.; Zhao, Y.; Liang, Q.H. A new copula-based standardized precipitation evapotranspiration streamflow index for drought monitoring. J. Hydrol. 2020, 585, 124793. [Google Scholar] [CrossRef]
- Yang, P.H.; Yu, Y.; Gu, F.; Qu, M.J.; Zhu, J.M. Prediction and risk assessment of extreme weather events based on gumbel copula function. J. Funct. Space 2022, 2022, 1–13. [Google Scholar] [CrossRef]
- Ma’rufah, U.; Hidayat, R.; Prasasti, I. Analysis of relationship between meteorological and agricultural drought using standardized precipitation index and vegetation health index. IOP Conf. Ser. Earth Environ. Sci. 2017, 54, 012008. [Google Scholar] [CrossRef]
- Huang, R.H.; Liu, Y.; Wang, Y.; Wang, L. Analyses of the causes of severe drought occurring in Southwest China from the fall of 2009 to the spring of 2010. Chin. J. Atmos. Sci. 2012, 36, 443–457. [Google Scholar]
- Han, L.Y.; Zhang, Q.; Jia, J.Y.; Wang, Y.H.; Huang, T. Drought severity, frequency, duration and regional differences in China. J. Desert Res. 2019, 39, 1–10. [Google Scholar]
- Zhang, H.; Huang, Y.; Liu, M.H.; Ding, F.; Yang, K.; Fang, C.C. Temporal and spatial variations of soil nutrientsin zunyi tobacco growing area based on spatial interpolation method. Chin. Tob. Sci. 2020, 41, 36–43. [Google Scholar] [CrossRef]
- Hu, J.M.; Gu, S.H.; Zhang, B.; Zhao, J. Rice Drought loss assessment under karst landform in Guizhou province. Guizhou Agr. Sci. 2019, 47, 138–141. [Google Scholar]
- Mao, C.Y.; Dai, L.; Yang, G.B. Dynamic analysis of spatio-temporal distribution of droughts in karst mountainous regions of Guizhou Province from 1960 to 2016. J. Water Res. Water Eng. 2021, 32, 64–72. [Google Scholar]
- Wu, Z.P.; Long, L.; Zhang, J.Y.; Zhang, D.H.; Li, Z.Y. Drought Disaster Risk Assessment and Its Climate Prediction in Guizhou Province; Meteorological Publishing House: Beijing, China, 2018; pp. 58–74. [Google Scholar]
- DB 52/T 1030; Drought Standard in Guizhou. Guizhou Bureau of Quality and Technical Supervision: Guiyang, China, 2015.
- Wu, R.; Zhang, J.Q.; Bao, Y.H.; Guo, E.L. Run theory and Copula-based drought risk analysis for Songnen grassland in northeastern China. Sustainability 2019, 11, 6032. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Gao, K.; Li, Y.; Zhang, Q.S. Maximum Likelihood Estimation Methods for Copula Models. Comput. Econ. 2022, 60, 99–124. [Google Scholar] [CrossRef]
- Kimia, N.; Mahnoosh, M.; Ashkan, S. Drought occurrence probability analysis using multivariate standardized drought index and copula function under climate change. Water Resour. Manag. 2022, 36, 2865–2888. [Google Scholar]
- Zhou, J.; Wang, Y.J.; Su, B.D.; Wang, A.Q.; Tao, H.; Zhai, J.Q.; Kundzewicz, Z.W.; Jiang, T. Choice of potential evapotranspiration formulas influences drought assessment: A case study in China. Atmos. Res. 2020, 242, 104979. [Google Scholar] [CrossRef]
- Ullah, H.; Akbar, M. Bivariate homogenous regions and projections based on copula function using RDI and SPI indices for drought risk assessment in Pakistan. Arab. J. Geosci. 2021, 14, 2338. [Google Scholar] [CrossRef]
- DB52/T 725; Water Intake Norm. Guizhou Provincial Market Supervision Administration: Guiyang, China, 2019.
- Liu, D.Y.; Liang, Z.M.; Yi, Z.Z. Dynamic evaluation model of agricultural loss of drought disaster and assessment of irrigation benefit. south-to-north water diversion wat. Sci. Technol. 2011, 9, 36–39; 62. [Google Scholar]
- Li, F.W.; Zhang, M.J.; Liu, Y.Z. Quantitative research on drought loss sensitivity of summer maize based on AquaCrop model. Nat. Hazards 2022, 112, 1065–1084. [Google Scholar] [CrossRef]
- Nakabuye, H.N.; Rudnick, D.; DeJonge, K.G.; Lo, T.H.; Heeren, D.; Qiao, X.; Franz, T.E.; Katimbo, A.; Duan, J.M. Real-time irrigation scheduling of maize using Degrees Above Non-Stressed (DANS) index in semi-arid environment. Agric. Water Manag. 2022, 274, 107957. [Google Scholar] [CrossRef]
- Xiao, J.F.; Liu, Z.D.; Duan, A.W.; Liu, Z.G. Study on Jensen Model at each growing stage for main crops in China. Wat. Saving Irrig. 2008, 7, 1–3; 8. [Google Scholar]
- Tang, Y.J.; Wei, X.M. Reasonable determination of agricultural water demand in Baojixia Irrigation district under changing environment. J. Wat. Resour. Wat. Eng. 2018, 29, 254–260. [Google Scholar]
- Luo, N. China Meteorological Disaster Dictionary; Guizhou Volume; Meteorological Publishing House: Beijing, China, 2006. [Google Scholar]
- Huang, F.; Qiu, F.; Gu, X. The Sequel to the Monograph on Early Water Disasters in Guizhou: 1990~2011; Shantou University Press: Jinan, China, 2015. [Google Scholar]
- Zheng, M.Q. Present Situation analysis and protection countermeasures of cultivated land use in Zunyi City. J. Anhui Agr. Sci. 2017, 45, 203–205; 232. [Google Scholar] [CrossRef]
- Yao, Z.L.; Zhao, D.Q.; Yao, Z.F. Meteorological drought variation trends and Cause analysis in recent 63 years in Zunyi City. Mid Low Latit. Mt. Meteorol. 2015, 39, 8–13. [Google Scholar]
- Liang, R.G.; Zhou, X.; Li, S.; Yang, D.F.; Cheng, D.R.; Pei, Y. Analysis of Temporal and Spatial Variation Characteristics of Drought in Guizhou Province and its Influencing Factors Based on CWSI. Res. Soil Wat. Conserv. 2022, 29, 284–291. [Google Scholar] [CrossRef]
- Li, B.; Wang, G.L.; Ding, H.H.; Chen, Y.L. An evaluation method of the sustainability of water resource in karst region: A case study of Zuni, China. Appl. Water Sci. 2017, 7, 1391–1397. [Google Scholar] [CrossRef]
- Qiao, S.S.; Pan, H.W.; Lei, H.J.; Xu, J.X.; Shang, C.J. Analyzing the Drought Characteristic of Zunyi Using the Accumulated Relative Humidity Index. J. Irrig. Drain. 2017, 36, 109–114. [Google Scholar]
- Pan, L.D.; Li, R.; Shu, D.C.; Zhao, L.N.; Chen, M.; Jing, J. Effects of rainfall and rocky desertification on soil erosion in karst area of Southwest China. J. Mt. Sci. 2022, 19, 3118–3130. [Google Scholar] [CrossRef]
- Song, L.; Wu, R.G.; An, L. Different sources of 10- to 30-day intraseasonal variations of autumn snow over Western and Eastern Tibetan Plateau. Geophys. Res. Lett. 2019, 46, 9118–9125. [Google Scholar] [CrossRef]
- Bal, S.K.; Sandeep, V.M.; Kumar, P.V.; Rao, A.V.M.S.; Pramod, V.P.; Manikandan, N.; Rao, C.S.; Singh, N.P.; Bhaskar, S. Assessing impact of dry spells on the principal rainfed crops in major dryland regions of India. Agric. For. Meteorol. 2022, 313, 108768. [Google Scholar] [CrossRef]
- Hu, Z.H.; Wu, Z.R.; Zhang, Y.X.; Li, Q.; Towfiqul Islam, A.R.M.; Pan, C.C. Risk assessment of drought disaster in summer maize cultivated areas of the Huang-Huai-Hai plain, eastern China. Environ. Monit. Assess. 2021, 193, 441. [Google Scholar] [CrossRef]
- Ganguli, P.; Reddy, M.J. Risk Assessment of Droughts in Gujarat Using Bivariate Copulas. Water Resour. Manag. 2012, 26, 3301–3327. [Google Scholar] [CrossRef]
- Xu, K.; Xu, X.Y.; Li, A.H.; Yang, D.W. Assessing agricultural drought disaster risk in Chengde City using stochastic method. Trans. Chin. Soc. Agric. Eng. 2013, 29, 139–146. [Google Scholar] [CrossRef]
- Liu, X.J.; Zhang, J.Q.; Ma, D.L.; Bao, Y.L.; Tong, Z.J. Dynamic risk assessment of drought disaster for maize based on integrating multisources data in the region of the northwest of Liaoning Province, China. Nat. Hazards 2013, 65, 1393–1409. [Google Scholar] [CrossRef]
- Qin, Y.; Xu, X.Y.; Xu, K.; Li, A.H.; Yang, D.W. Fuzzy evaluation system of agriculture drought disaster risk and its application. Trans. Chin. Soc. Agric. Eng. 2013, 29, 83–91. [Google Scholar]



| Drought Grade | Monthly Scale Pa Value (%) |
|---|---|
| Normal | −40 < Pa |
| Light drought | −60 < Pa ≤ −40 |
| Moderate drought | −80 < Pa ≤ −60 |
| Severe drought | −95 < Pa ≤ −80 |
| Extreme drought | Pa ≤ −95 |
| Archimedean Copula | Function Expressions | Parameter Value |
|---|---|---|
| Gumbel-Hougaard (G-H) | ||
| Clayton copula (C-C) | ||
| Frank copula (F-C) |
| Growth Stage | Rejuvenation Stage | Tillering Stage | Jointing and Booting Stage | Heading and Flowering Stage | Grain Filling Stage | Mature Stage |
|---|---|---|---|---|---|---|
| Growth period | 5.20–6.01 | 6.02–7.06 | 7.07–8.04 | 8.05–8.19 | 8.20–9.03 | 9.04–9.26 |
| −value | 1 | 1 | 1 | 1.57 | 0.9 | 0.9 |
| County Name | Utilization Coefficient of Irrigation Water | County Name | Utilization Coefficient of Irrigation Water | County Name | Utilization Coefficient of Irrigation Water |
|---|---|---|---|---|---|
| Honghuagang | 0.492 | Zheng’an | 0.485 | Yuqing | 0.487 |
| Huichuan | 0.489 | Daozhen * | 0.484 | Xishui | 0.483 |
| Bozhou | 0.492 | Wuchuan * | 0.481 | Chishui | 0.487 |
| Tongzi | 0.486 | Fenggang | 0.491 | Renhuai | 0.485 |
| Suiyang | 0.480 | Meitan | 0.491 |
| County Name | Number of Droughts (Times) | Average Drought Duration (Months) | Average Drought Severity | Maximum Drought Duration (Months) | Maximum Drought Severity |
|---|---|---|---|---|---|
| Honghuagang | 55 | 1.78 | 0.37 | 6 | 1.02 |
| Huichuan | 54 | 1.61 | 0.33 | 5 | 0.74 |
| Bozhou | 58 | 1.66 | 0.39 | 5 | 1.18 |
| Tongzi | 26 | 1.54 | 0.30 | 3 | 0.66 |
| Suiyang | 48 | 1.58 | 0.33 | 3 | 0.66 |
| Zheng’an | 21 | 1.57 | 0.30 | 3 | 0.47 |
| Daozhen * | 26 | 1.58 | 0.43 | 3 | 0.66 |
| Wuchuan * | 21 | 1.48 | 0.30 | 3 | 0.47 |
| Fenggang | 71 | 1.82 | 0.39 | 5 | 0.87 |
| Meitan | 71 | 1.80 | 0.39 | 5 | 0.87 |
| Yuqing | 71 | 1.80 | 0.39 | 5 | 0.87 |
| Xishui | 33 | 1.45 | 0.34 | 6 | 1.02 |
| Chishui | 43 | 1.58 | 0.33 | 6 | 1.24 |
| Renhuai | 27 | 1.41 | 0.30 | 3 | 0.69 |
| County Name | G-H | C-C | F-C | Optimal Copula Function | Parameters θ |
|---|---|---|---|---|---|
| Honghuagang | 0.2475 | 0.4280 | 0.3015 | G-H | 1.6618 |
| Huichuan | 0.3028 | 0.4144 | 0.3326 | G-H | 1.3159 |
| Bozhou | 0.2815 | 0.5036 | 0.3486 | G-H | 1.6814 |
| Tongzi | 0.1729 | 0.2156 | 0.1989 | G-H | 1.0844 |
| Suiyang | 0.1566 | 0.1816 | 0.1511 | F-C | 0.8570 |
| Zheng’an | 0.1380 | 0.2191 | 0.1697 | G-H | 1.2887 |
| Daozhen * | 0.1601 | 0.3152 | 0.2009 | G-H | 1.4999 |
| Wuchuan * | 0.1675 | 0.2473 | 0.2081 | G-H | 1.2723 |
| Fenggang | 0.2673 | 0.4379 | 0.3187 | G-H | 1.4925 |
| Meitan | 0.2735 | 0.4460 | 0.3238 | G-H | 1.5044 |
| Yuqing | 0.2895 | 0.4547 | 0.3386 | G-H | 1.4950 |
| Xishui | 0.2149 | 0.3170 | 0.2773 | G-H | 1.2532 |
| Chishui | 0.1909 | 0.3708 | 0.2895 | G-H | 1.3769 |
| Renhuai | 0.1453 | 0.2049 | 0.1759 | G-H | 1.0851 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, H.; Yu, J.; Pan, H.; Li, J.; Leghari, S.J.; Shang, C.; Xiao, Z.; Jin, C.; Shi, L. A New Agricultural Drought Disaster Risk Assessment Framework: Coupled a Copula Function to Select Return Periods and the Jensen Model to Calculate Yield Loss. Sustainability 2023, 15, 3786. https://doi.org/10.3390/su15043786
Lei H, Yu J, Pan H, Li J, Leghari SJ, Shang C, Xiao Z, Jin C, Shi L. A New Agricultural Drought Disaster Risk Assessment Framework: Coupled a Copula Function to Select Return Periods and the Jensen Model to Calculate Yield Loss. Sustainability. 2023; 15(4):3786. https://doi.org/10.3390/su15043786
Chicago/Turabian StyleLei, Hongjun, Jie Yu, Hongwei Pan, Jie Li, Shah Jahan Leghari, Chongju Shang, Zheyuan Xiao, Cuicui Jin, and Lili Shi. 2023. "A New Agricultural Drought Disaster Risk Assessment Framework: Coupled a Copula Function to Select Return Periods and the Jensen Model to Calculate Yield Loss" Sustainability 15, no. 4: 3786. https://doi.org/10.3390/su15043786
APA StyleLei, H., Yu, J., Pan, H., Li, J., Leghari, S. J., Shang, C., Xiao, Z., Jin, C., & Shi, L. (2023). A New Agricultural Drought Disaster Risk Assessment Framework: Coupled a Copula Function to Select Return Periods and the Jensen Model to Calculate Yield Loss. Sustainability, 15(4), 3786. https://doi.org/10.3390/su15043786






