Evaluation Method for Node Importance of Urban Rail Network Considering Traffic Characteristics
Abstract
1. Introduction
2. Literature Review
2.1. Evaluation of Node Importance of Complex Networks
2.2. Evaluation of Node Importance of Urban Rail Networks
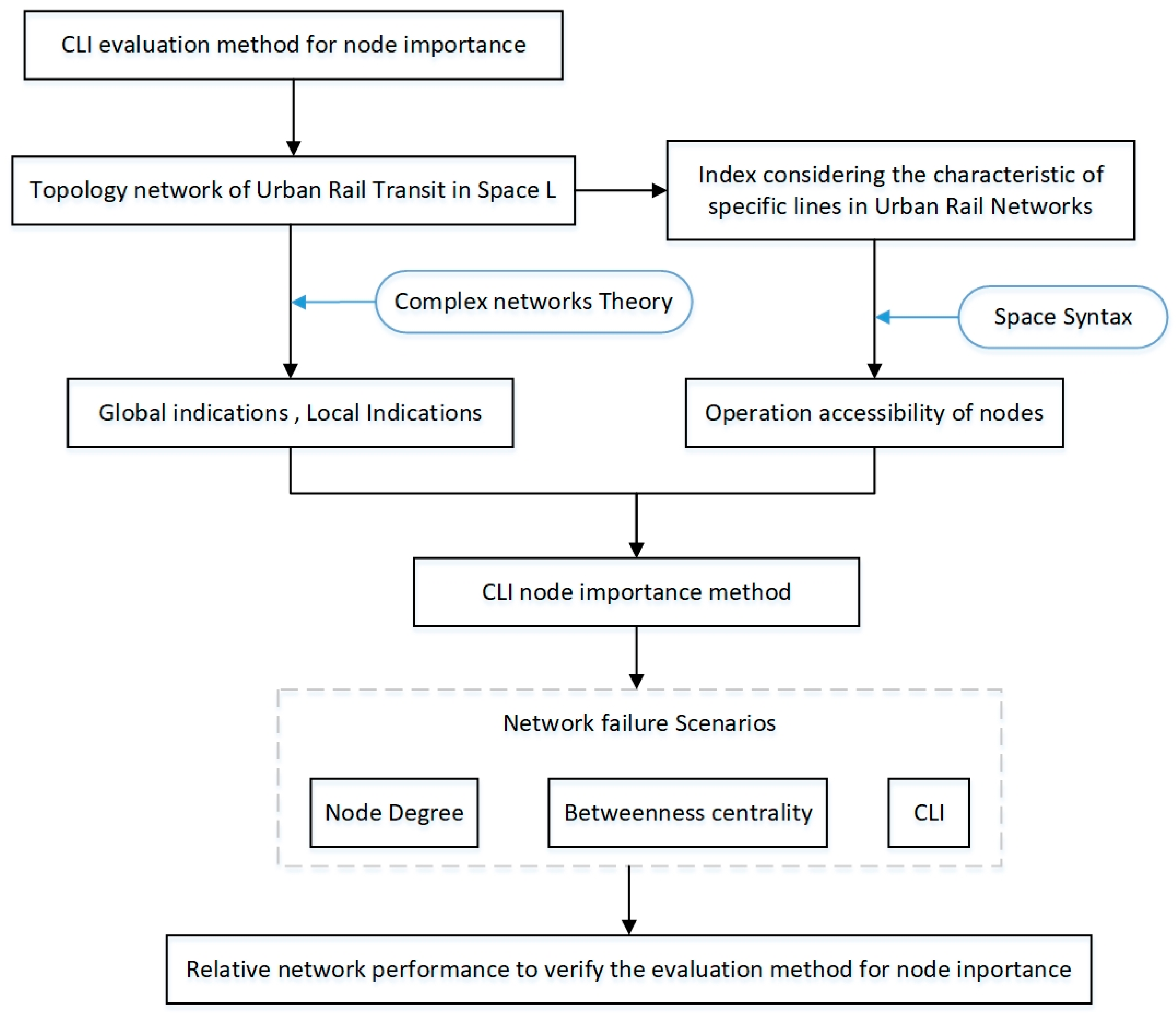
3. Methodology
- (1)
- Constructing the urban rail network with the Space L model;
- (2)
- Calculating the node degree and betweenness centrality of the nodes in the Space L network, based on complex network theory;
- (3)
- Analyzing the relationship between the lines where the stations are located with Space Syntax and obtaining the operation accessibility of the nodes;
- (4)
- Building a CLI node importance method that considers the node degree, betweenness centrality, and operation accessibility of the nodes;
- (5)
- Ranking the stations according to the calculation results of the node degree, betweenness centrality, and CLI, and comparing the stations with high importance under each method;
- (6)
- Attacking high-betweenness-centrality and high-CLI nodes in turn, comparing the network performance degradation under different node failure scenarios and giving the best method.
4. Urban Rail Complex Networks
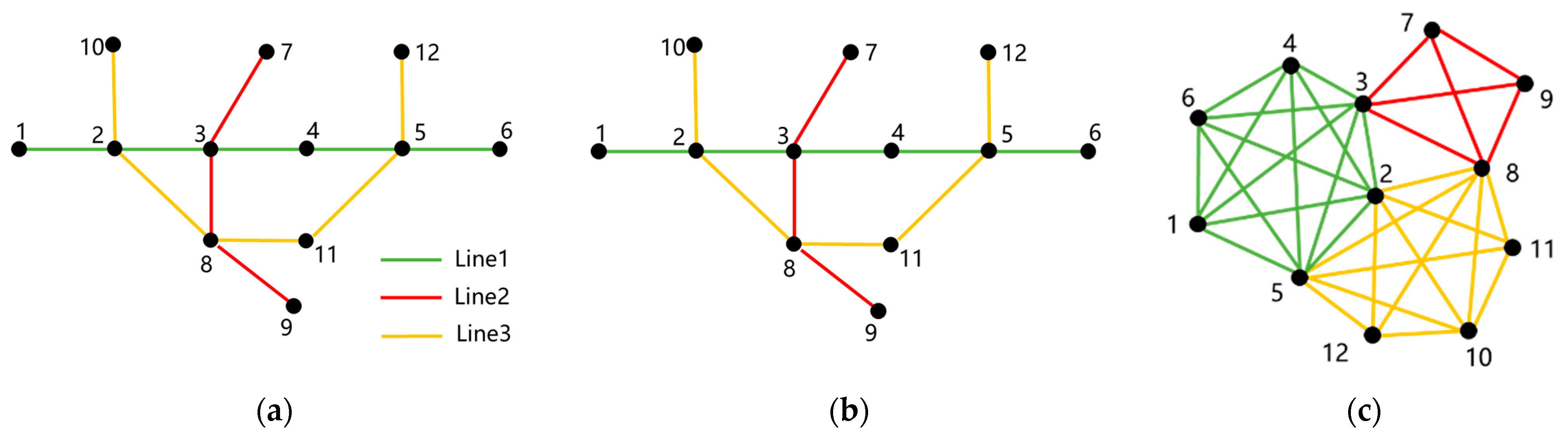
4.1. Topology Analysis of Urban Rail Networks
4.2. Typical Indicators of Complex Networks
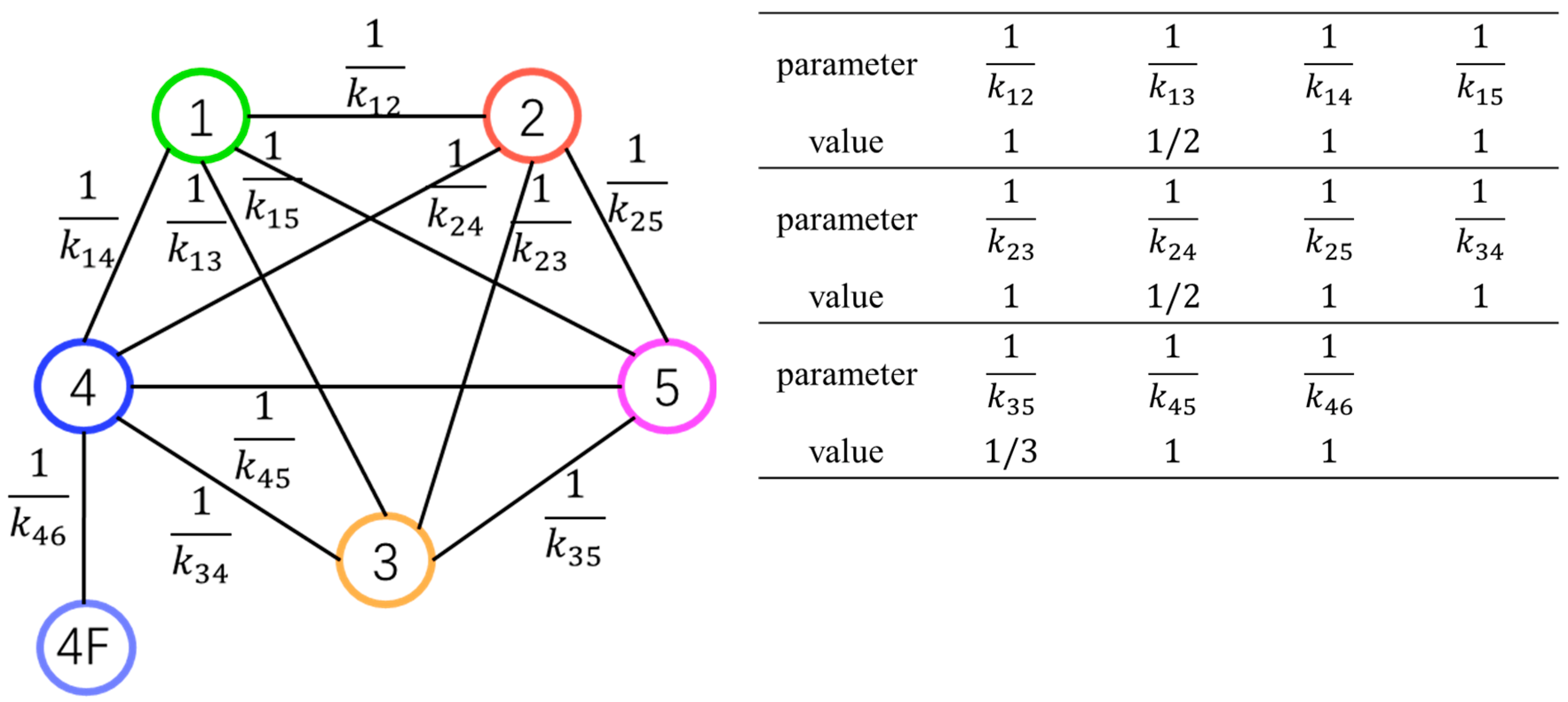
4.3. Index Considering the Characteristic of Specific Lines in Urban Rail Networks
5. Node Importance of Urban Rail Networks
5.1. Improved Evaluation Method for Node Importance
5.2. Method Validation
6. Experimental Analysis and Discussion
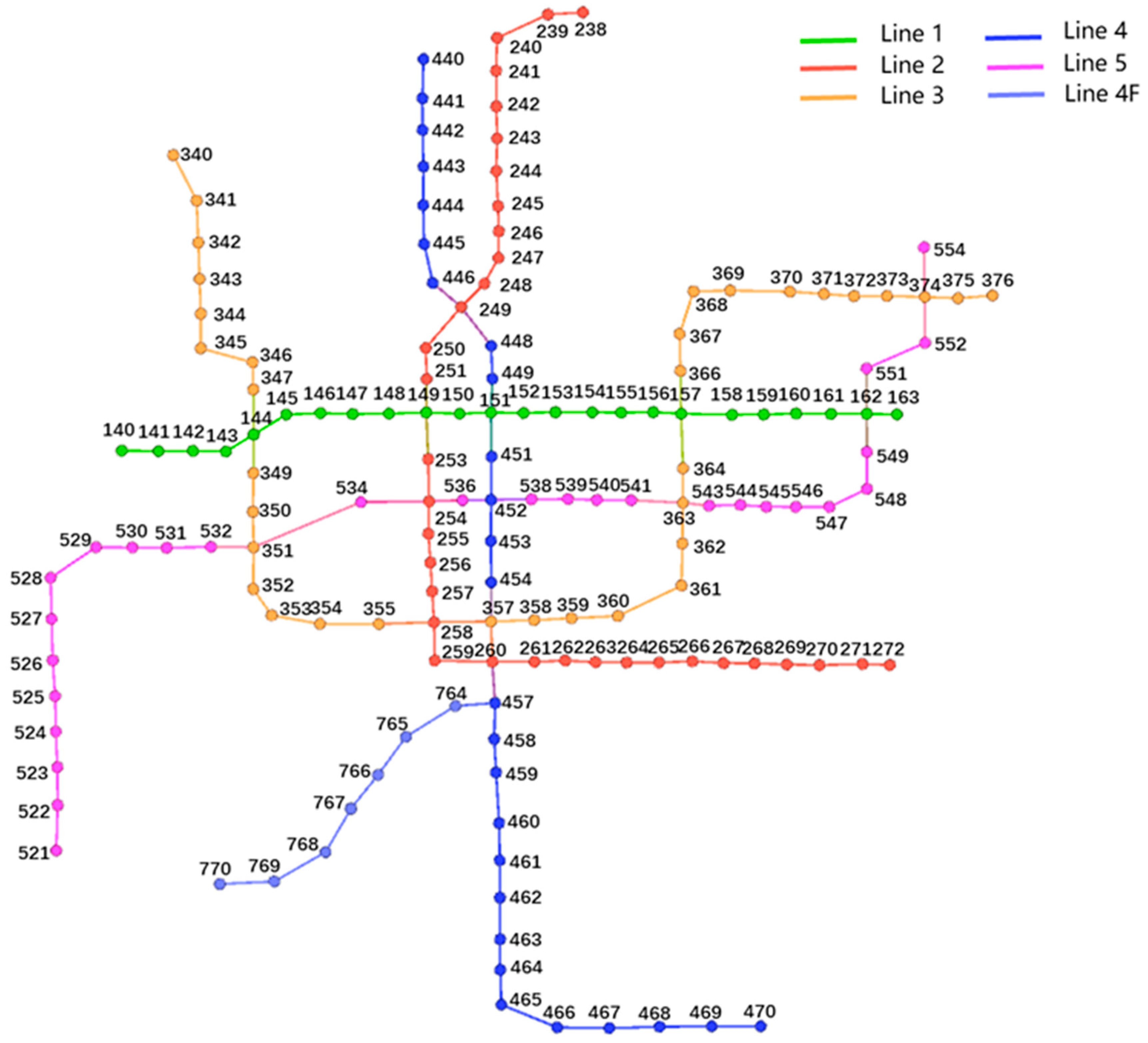
6.1. Typical Characteristic Indicators of Suzhou Railway Network
6.2. CLI Node Importance Calculation
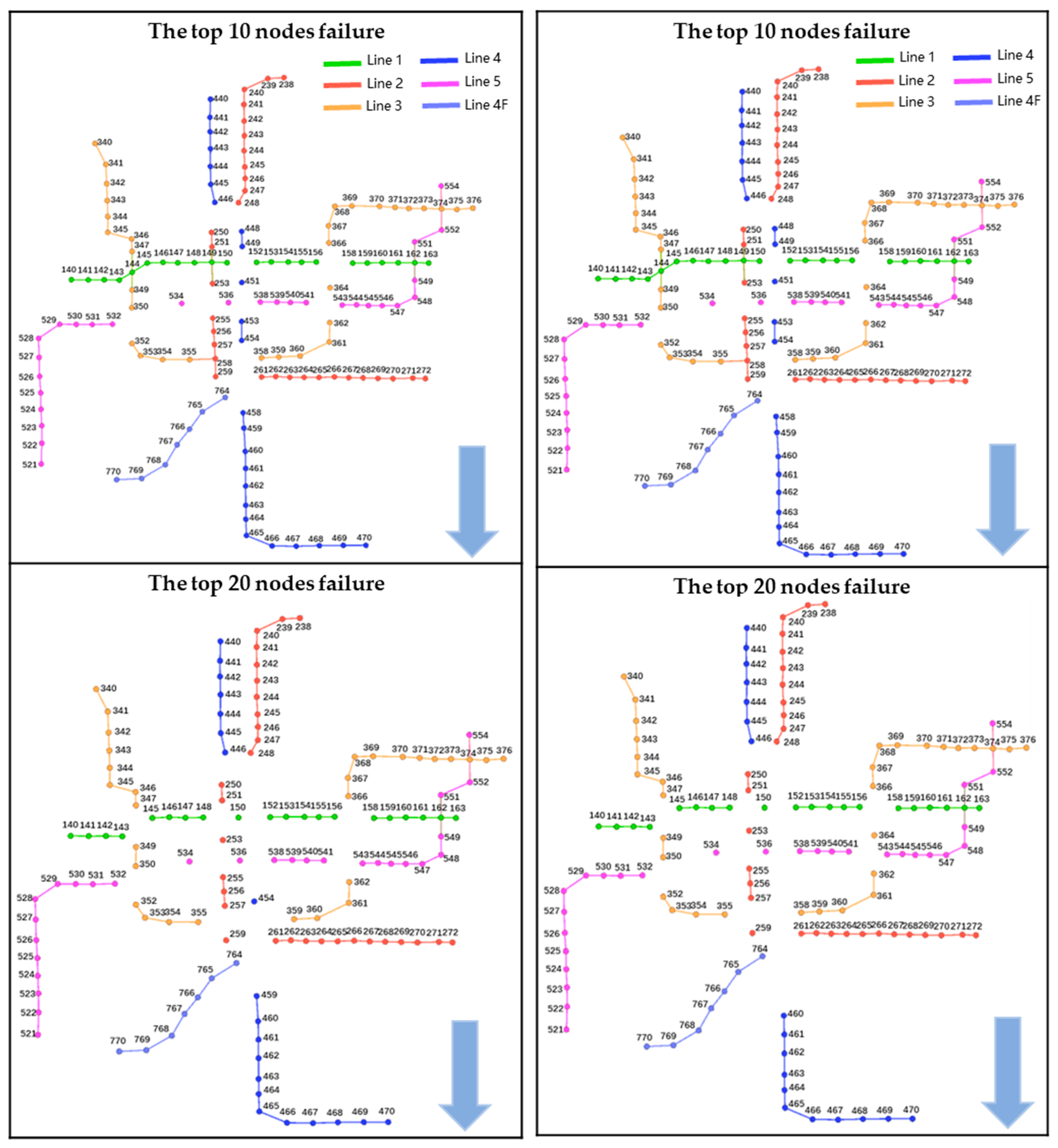
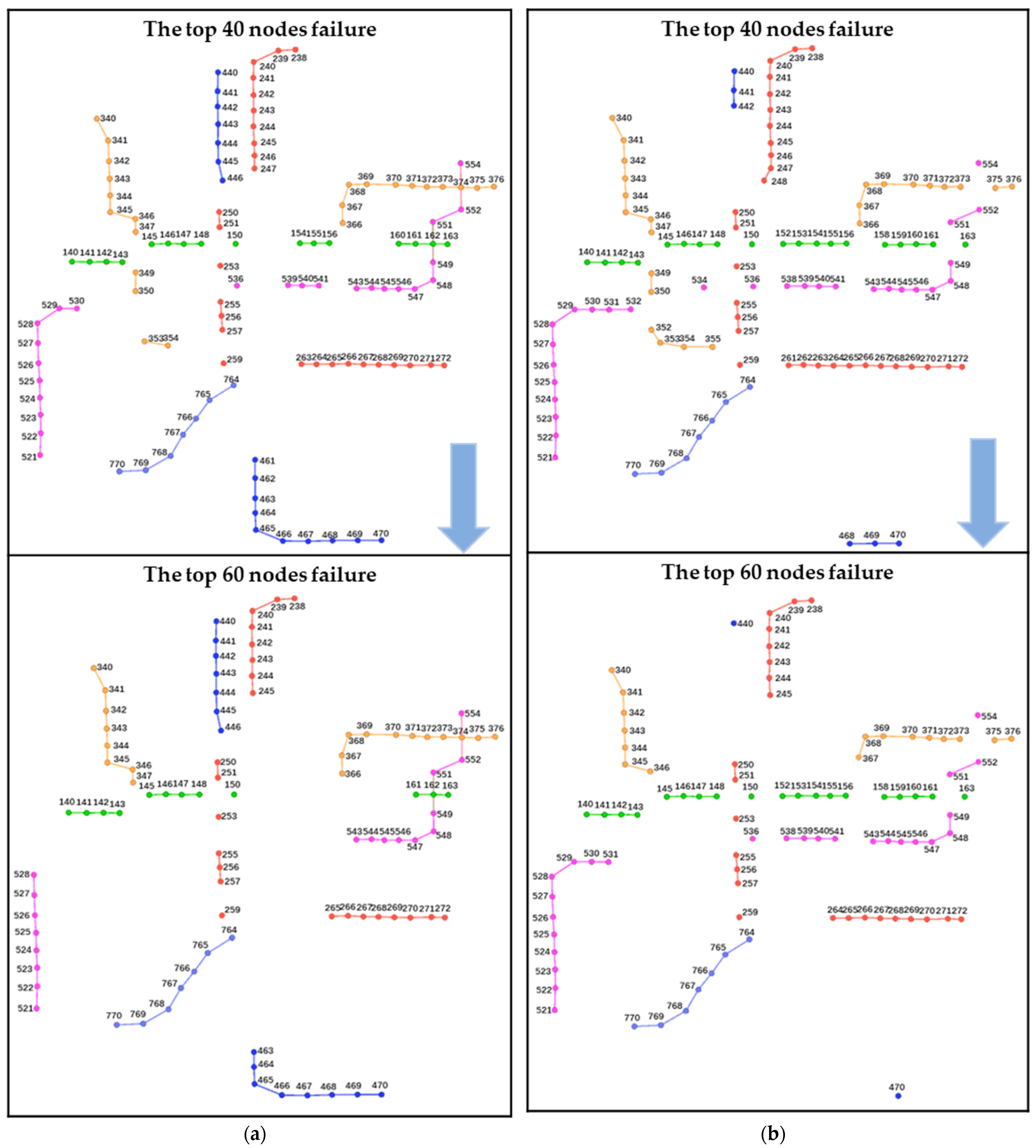
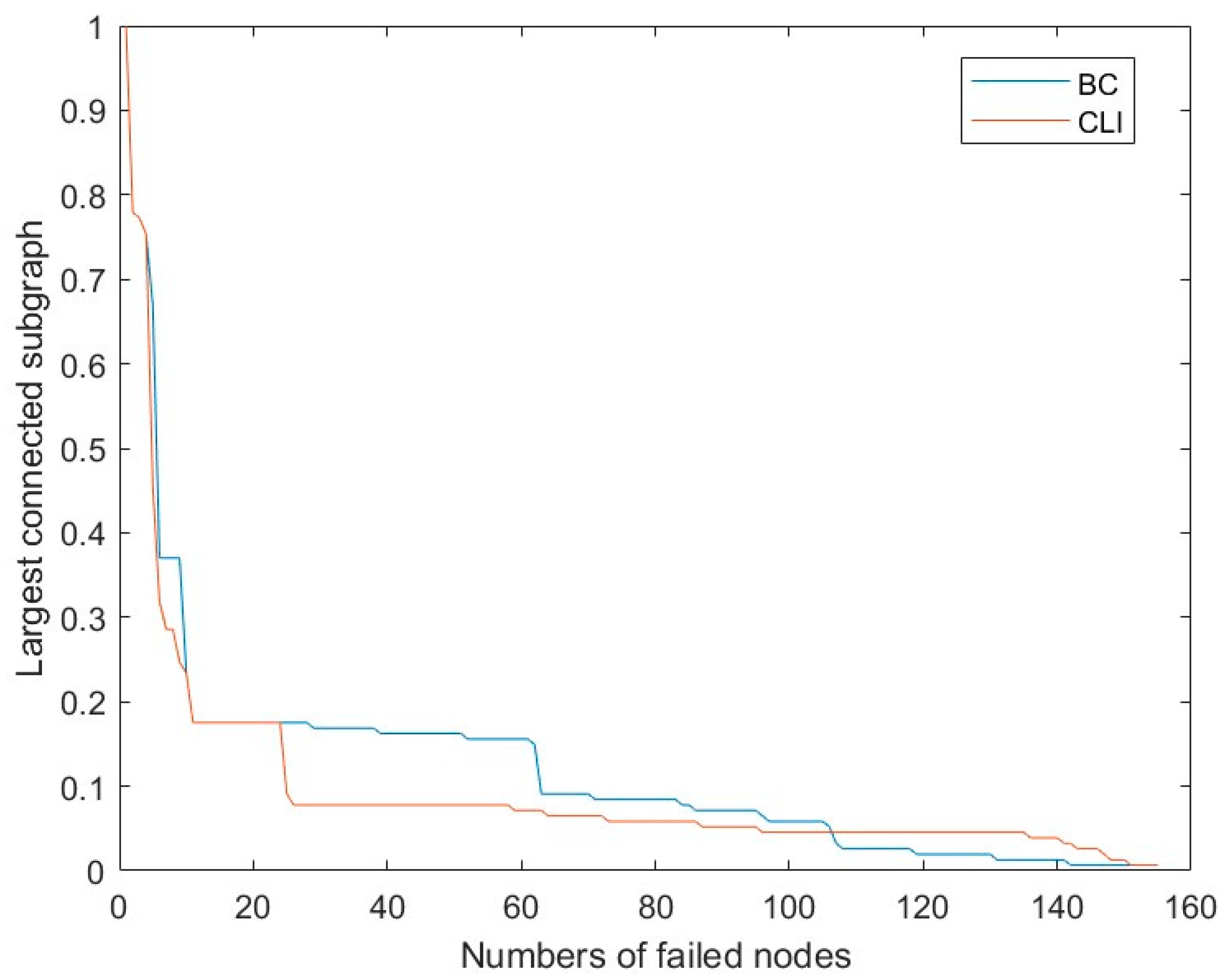
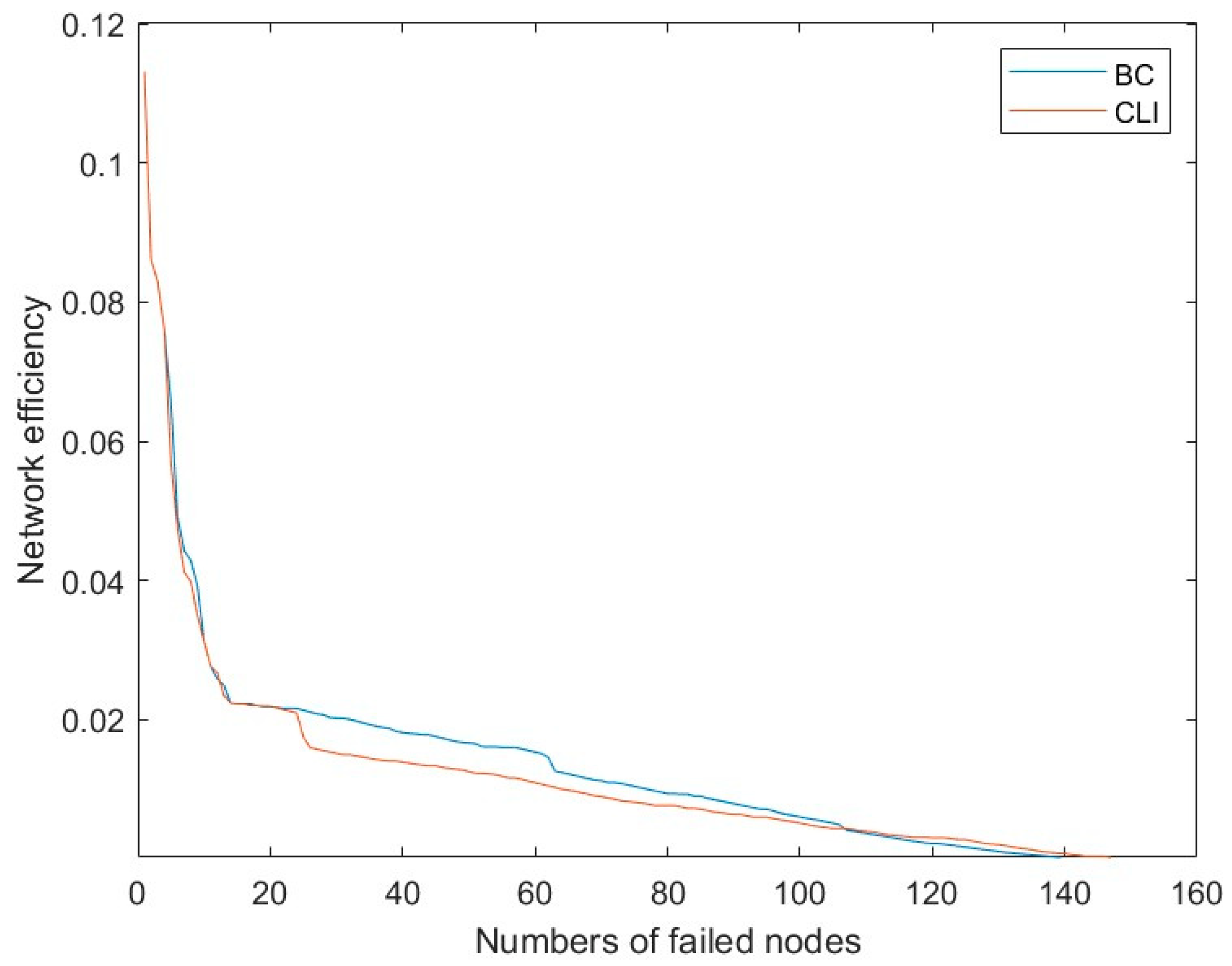
6.3. Comparative Analysis
7. Conclusions
- (1)
- Attacking the network according to the node sequence obtained by the CLI method makes the largest connected subgraph of the urban rail network decrease faster.
- (2)
- Attacking the network according to the node sequence obtained by the CLI method makes the network efficiency of the urban rail network decrease faster.
- (3)
- The node importance is related to the line accessibility, and the node importance method considering traffic characteristics can make the network performance decline faster.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ministry of Transport of the People’s Republic of China. Express Report of Urban Rail Transit Operation Data in November 2022. Available online: https://www.mot.gov.cn/ (accessed on 15 December 2022).
- China News. The Subway Station is Still Closed after a Train Overspeed Accident in Boston. Available online: https://www.chinanews.com/gj/shipin/cns-d/2021/08-04/news896940.shtml (accessed on 15 December 2022).
- Xinhua News Agency. The Investigation Report on the “July 20” Rainstorm Disaster in Zhengzhou, Henan Province Was Released. Available online: https://s.cyol.com/articles/2022-01/21/content_DgRgQOUz.html (accessed on 15 December 2022).
- Paul, S.K. Vulnerability Concepts and its Application in Various Fields A Review on Geographical Perspective. J. Life Earth Sci. 2014, 8, 63–81. [Google Scholar] [CrossRef]
- Scherb, A.; Garrè, L.; Straub, D. Reliability and Component Importance in Networks Subject to Spatially Distributed Hazards Followed by Cascading Failures. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part B Mech. Eng. 2017, 3, 021007. [Google Scholar] [CrossRef]
- Liu, Z.; Jiang, C.; Wang, J.; Yu, H. The node importance in actual complex networks based on a multi-attribute ranking method. Knowl.-Based Syst. 2015, 84, 56–66. [Google Scholar] [CrossRef]
- Ai, X. Node Importance Ranking of Complex Networks with Entropy Variation. Entropy 2017, 19, 303. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, X.; Jin, L.; Song, M.; Li, Z.J.N. A new approach for evaluating node importance in complex networks via deep learning methods. Neurocomputing 2022, 497, 13–27. [Google Scholar] [CrossRef]
- Yang, P.; Xu, G.; Chen, H. Multi-attribute ranking method for identifying key nodes in complex networks based on GRA. Int. J. Mod. Phys. B 2019, 32, 1850363. [Google Scholar] [CrossRef]
- Jiang, Z.-Y.; Zeng, Y.; Liu, Z.-H.; Ma, J.-F. Identifying critical nodes’ group in complex networks. Phys. A Stat. Mech. Its Appl. 2019, 514, 121–132. [Google Scholar] [CrossRef]
- Saito, K.; Kimura, M.; Ohara, K.; Motoda, H. Super mediator—A new centrality measure of node importance for information diffusion over social network. Inf. Sci. Comput. Sci. Intell. Syst. Appl. Int. J. 2016, 3, 34. [Google Scholar] [CrossRef]
- Zhang, C.; Lin, Z.; Wen, F.; Ledwich, G.; Xue, Y. Two-stage power network reconfiguration strategy considering node importance and restored generation capacity. IET Gener. Transm. Distrib. 2014, 8, 91–103. [Google Scholar] [CrossRef]
- Kanwar, K.; Kaushal, S.; Kumar, H. A hybrid node ranking technique for finding influential nodes in complex social networks. Libr. Hi Tech. 2019, 40, 98–114. [Google Scholar] [CrossRef]
- Khomami, M.M.D.; Rezvanian, A.; Meybodi, M.R.; Bagheri, A. CFIN: A community-based algorithm for finding influential nodes in complex social networks. J. Supercomput. 2020, 77, 2207–2236. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, K.y.; Sheng, W.; Du, S.; Jia, D. Critical node identification in active distribution network using resilience and risk theory. IET Gener. Transm. Distrib. 2020, 14, 2771–2778. [Google Scholar] [CrossRef]
- Kitsak, M.; Gallos, L.K.; Havlin, S.; Liljeros, F.; Muchnik, L.; Stanley, H.E.; Makse, H.A. Identification of influential spreaders in complex networks. Nat. Phys. 2010, 6, 888–893. [Google Scholar] [CrossRef]
- Lu, L.; Zhou, T.; Zhang, Q.M.; Stanley, H.E. The H-index of a network node and its relation to degree and coreness. Nat. Commun. 2016, 7, 10168. [Google Scholar] [CrossRef] [PubMed]
- Hébert-Dufresne, L.; Allard, A.; Young, J.G.; Dube, L.J. Global efficiency of local immunization on complex networks. Sci. Rep. 2013, 3, 2171. [Google Scholar] [CrossRef]
- Bergamini, E.; Borassi, M.; Crescenzi, P.; Marino, A.; Meyerhenke, H. Computing Top-k Closeness Centrality Faster in Unweighted Graphs. Front. Psychol. 2017, 8, 1683. [Google Scholar]
- Fei, L.; Deng, Y. A new method to identify influential nodes based on relative entropy. Chaos Solitons Fractals X 2017, 104, 257–267. [Google Scholar] [CrossRef]
- Black, W.R. Transportation: A Geographical Analysis. J. Transp. Geogr. 2004, 13, 201–203. [Google Scholar]
- Meng, Y.; Qi, Q.; Liu, J.; Zhou, W. Dynamic Evolution Analysis of Complex Topology and Node Importance in Shenzhen Metro Network from 2004 to 2021. Sustainability 2022, 14, 7234. [Google Scholar] [CrossRef]
- Lin, J.; Ban, Y. Complex Network Topology of Transportation Systems. Transp. Rev. 2013, 33, 658–685. [Google Scholar] [CrossRef]
- Latoraa, V.; Marchiorib, M. Is the Boston subway a small-world network? Phys. A Stat. Mech. Its Appl. 2002, 34, 109–113. [Google Scholar] [CrossRef]
- Li, W.; Cai, X. Empirical analysis of a scale-free railway network in China. Phys. A Stat. Mech. Its Appl. 2007, 382, 693–703. [Google Scholar] [CrossRef]
- Derrible, S.; Kennedy, C. Network Analysis of World Subway Systems Using Updated Graph Theory. Transp. Res. Rec. J. Transp. Res. Board 2009, 2112, 17–25. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, X.; Hong, L.; Wang, S.; Fei, Q. Networked analysis of the Shanghai subway network, in China. Phys. A Stat. Mech. Its Appl. 2011, 390, 4562–4570. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, M.; Liu, H.; Xu, X. Networked characteristics of the urban rail transit networks. Phys. A Stat. Mech. Its Appl. 2013, 392, 1538–1546. [Google Scholar] [CrossRef]
- Chen, S.; Zhuang, D. Evolution and Evaluation of the Guangzhou Metro Network Topology Based on an Integration of Complex Network Analysis and GIS. Sustainability 2020, 12, 538. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Y.; Zhou, M.; Li, F.; Sun, C. Robustness assessment of urban rail transit based on complex network theory: A case study of the Beijing Subway. Saf. Sci. 2015, 79, 149–162. [Google Scholar] [CrossRef]
- Zhang, D.-M.; Du, F.; Huang, H.; Zhang, F.; Ayyub, B.M.; Beer, M. Resiliency assessment of urban rail transit networks: Shanghai metro as an example. Saf. Sci. 2018, 106, 230–243. [Google Scholar] [CrossRef]
- Sun, D.; Zhao, Y.H.; Lu, Q.C. Vulnerability Analysis of Urban Rail Transit Networks: A Case Study of Shanghai, China. Sustainability 2015, 7, 6919–6936. [Google Scholar] [CrossRef]
- Xing, Y.; Lu, J.; Chen, S.; Dissanayake, S. Vulnerability analysis of urban rail transit based on complex network theory: A case study of Shanghai Metro. Public Transp. 2017, 9, 501–525. [Google Scholar] [CrossRef]
- Shen, Y.; Ren, G.; Ran, B. Cascading failure analysis and robustness optimization of metro networks based on coupled map lattices: A case study of Nanjing, China. Transportation 2019, 48, 537–553. [Google Scholar] [CrossRef]
- Li, X.L.; Zhang, P.; Zhu, G.Y. Measuring Method of Node Importance of Urban Rail Network Based on H Index. Appl. Sci. 2019, 9, 5189. [Google Scholar] [CrossRef]
- Lai, Q.; Zhang, H.H. Analysis of identification methods of key nodes in transportation network. Chin. Phys. B 2022, 31, 068905. [Google Scholar] [CrossRef]
- Liu, Y.; Tan, Y. Complexity Modeling and Stability Analysis of Urban Subway Network: Wuhan City Case Study. Procedia—Soc. Behav. Sci. 2013, 96, 1611–1621. [Google Scholar] [CrossRef]
- Sun, S.W.; Li, H.Y.; Xu, X.Y. A key station identification method for urban rail transit: A case study of beijing subway. Promet-Traffic Transp. 2017, 29, 267–273. [Google Scholar] [CrossRef]
- Xia, F.; Wang, J.; Kong, X.; Zhang, D.; Wang, Z. Ranking Station Importance With Human Mobility Patterns Using Subway Network Datasets. IEEE Trans. Intell. Transp. Syst. 2020, 21, 2840–2852. [Google Scholar] [CrossRef]
- Du, Z.; Tang, J.; Qi, Y.; Wang, Y.; Han, C.; Yang, Y. Identifying critical nodes in metro network considering topological potential: A case study in Shenzhen city—China. Phys. A Stat. Mech. Its Appl. 2020, 539, 122926. [Google Scholar] [CrossRef]
- Barucca, P.; Caldarelli, G.; Squartini, T. Tackling Information Asymmetry in Networks: A New Entropy-Based Ranking Index. J. Stat. Phys. 2018, 173, 1028–1044. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Ayyub, B.M.; Saadat, Y.; Zhang, D.M.; Huang, H.W. A double-weighted vulnerability assessment model for metrorail transit networks and its application in Shanghai metro. Int. J. Crit. Infrastruct. Prot. 2020, 29, 100358. [Google Scholar] [CrossRef]
- Xu, Z.; Chopra, S.S.; Lee, H. Resilient Urban Public Transportation Infrastructure: A Comparison of Five Flow-Weighted Metro Networks in Terms of the Resilience Cycle Framework. IEEE Trans. Intell. Transp. Syst. 2022, 23, 12688–12699. [Google Scholar] [CrossRef]
- Angeloudis, P.; Fisk, D. Large subway systems as complex networks. Phys. A Stat. Mech. Its Appl. 2006, 367, 553–558. [Google Scholar] [CrossRef]
- Ferber, C.V.; Holovatch, T.; Holovatch, Y.; Palchykov, V. Public transport networks: Empirical analysis and modeling. Eur. Phys. J. B 2009, 68, 261–275. [Google Scholar] [CrossRef]
- Hoeven, F.V.D.; Nes, A.V. Improving the design of urban underground space in metro stations using the space syntax methodology. Tunn. Undergr. Space Technol. 2014, 40, 64–74. [Google Scholar] [CrossRef]

| Index | Definition | Formula |
|---|---|---|
| D | D measures the number of other nodes directly connected to a node. | is the total number of network nodes. |
| BC | BC measures shortest number of paths through a node. | represents the number of all the shortest paths through node in the shortest path from node to node . |
| CC | CC measures the ability of a station to affect another node through the network. | represents the shortest distance between node and node . |
| EC | EC measures the shortest number of paths through a node. | is the set of neighbor nodes of node , where is a constant. |
| ID | Label | Line | ID | Label | Line | ID | Label | Line |
|---|---|---|---|---|---|---|---|---|
| 1 | 140 | 1 | 59 | 340 | 3 | 120 | 764 | 4F |
| 2 | 141 | 1 | 60 | 341 | 3 | 121 | 765 | 4F |
| 3 | 142 | 1 | 61 | 342 | 3 | 122 | 766 | 4F |
| … | … | … | … | … | … | … | … | … |
| 25 | 238 | 2 | 93 | 440 | 4 | 127 | 521 | 5 |
| 26 | 239 | 2 | 94 | 441 | 4 | 128 | 522 | 5 |
| 27 | 240 | 2 | 95 | 442 | 4 | 129 | 523 | 5 |
| … | … | … | … | … | … | … | … | … |
| Source | Target | Weight | Source | Target | Weight |
|---|---|---|---|---|---|
| 1 | 2 | 1 | … | … | … |
| 2 | 1 | 1 | 90 | 153 | 1 |
| 2 | 3 | 1 | 90 | 154 | 1 |
| … | … | … | 154 | 90 | 1 |
| Line Number | Node Number | Link Number | Average Node Degree | Network Diameter | Average Path Length | Network Cluster Coefficient |
|---|---|---|---|---|---|---|
| 6 | 154 | 163 | 2.117 | 34 | 13.718 | 0 |
| Order | Highest D Stations | D | Highest BC Stations | BC |
|---|---|---|---|---|
| 1 | Shihudong RD. | 4 | Shihudong RD. | 0.183 |
| 2 | Baodai RD. | 4 | Baodai RD. | 0.169 |
| 3 | Nanmen | 4 | Nanmen | 0.134 |
| 4 | Suoshanqiaoxi | 4 | Suoshanqiaoxi | 0.130 |
| 5 | Leqiao | 4 | Leqiao | 0.128 |
| 6 | Dongfangzhimen | 4 | Dongfangzhimen | 0.120 |
| 7 | Jinsheqiao | 4 | Hongzhuang | 0.118 |
| 8 | Suzhou railway station | 4 | Jinsheqiao | 0.115 |
| 9 | Laodong RD. | 4 | Suzhou railway station | 0.110 |
| 10 | Guangjinan RD. | 4 | Laodong RD. | 0.094 |
| Line | 1 | 2 | 3 | 4 | 4F | 5 |
|---|---|---|---|---|---|---|
| accessibility | 5.558 | 8.337 | 10.005 | 16.675 | 1.853 | 6.253 |
| Station | Line | Operational Accessibility |
|---|---|---|
| Shihudong RD. | 2/4 | 16.675 |
| Baodai RD. | 3/4 | 16.675 |
| Nanmen | 4/5 | 16.675 |
| Suoshanqiaoxi | 3/5 | 10.005 |
| Leqiao | 1/4 | 16.675 |
| Hongzhuang | 4/4F | 16.675 |
| Dongfangzhimen | 1/3 | 10.005 |
| Guangjinan RD. | 1/2 | 10.005 |
| Xingtang ST. | 1/5 | 10.005 |
| Panli RD. | 2/3 | 10.005 |
| Xiangmen | 1 | 5.558 |
| Likou | 2 | 10.005 |
| Yinchun RD. | 3 | 10.005 |
| Huolidao | 4 | 16.675 |
| Xietang | 5 | 10.005 |
| Huagang | 4F | 1.853 |
| Order | Highest CLI Stations | CLI |
|---|---|---|
| 1 | Shihudong RD. | 1.000 |
| 2 | Baodai RD. | 0.964 |
| 3 | Nanmen | 0.871 |
| 4 | Leqiao | 0.857 |
| 5 | Suzhou railway station | 0.808 |
| 6 | Suoshanqiaoxi | 0.747 |
| 7 | Hongzhuang | 0.742 |
| 8 | Dongfangzhimen | 0.721 |
| 9 | jinsheqiao | 0.708 |
| 10 | Laodong RD. | 0.623 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Ma, J.; Zhu, Z.; Guo, X. Evaluation Method for Node Importance of Urban Rail Network Considering Traffic Characteristics. Sustainability 2023, 15, 3582. https://doi.org/10.3390/su15043582
Chen T, Ma J, Zhu Z, Guo X. Evaluation Method for Node Importance of Urban Rail Network Considering Traffic Characteristics. Sustainability. 2023; 15(4):3582. https://doi.org/10.3390/su15043582
Chicago/Turabian StyleChen, Ting, Jianxiao Ma, Zhenjun Zhu, and Xiucheng Guo. 2023. "Evaluation Method for Node Importance of Urban Rail Network Considering Traffic Characteristics" Sustainability 15, no. 4: 3582. https://doi.org/10.3390/su15043582
APA StyleChen, T., Ma, J., Zhu, Z., & Guo, X. (2023). Evaluation Method for Node Importance of Urban Rail Network Considering Traffic Characteristics. Sustainability, 15(4), 3582. https://doi.org/10.3390/su15043582







