A Simulated Annealing for Optimizing Assignment of E-Scooters to Freelance Chargers

Abstract

First- and last-mile trips are becoming increasingly expensive and detrimental to the environment, especially within dense cities. Thus, new micro-mobility transportation modes such as e-scooter sharing systems have been introduced to fill the gaps in the transportation network. Furthermore, some recent studies examined e-scooters as a green option from the standpoint of environmental sustainability. Currently, e-scooter charging is conducted by competitive freelancers who do not consider the negative environmental impact resulting from not optimizing the fuel efficiency of their charging trips. Several disputes have been recorded among freelance chargers, especially when simultaneously arriving at an e-scooters location. The paper aims to find the optimal tours for all chargers to pick up e-scooters in the form of routes, such that each route contains one charger, and each e-scooter is visited only once by the set of routes, which are typically called an E-Scooter-Chargers Allocation (ESCA) solution. This study develops a mathematical model for the assignment of e-scooters to freelance chargers and adapts a simulated annealing metaheuristic to determine a near-optimal solution. We evaluated the proposed approach using real-world instances and a benchmark-simulated dataset. Moreover, we compare the proposed model benchmark dataset to the baseline (i.e., state-of-practice). The results show a reduction of approximately 61–79% in the total distance traveled, leading to shorter charging trips.

1. Introduction

Micro-mobility modes, such as dockless e-scooter systems, have recently emerged as an alternative mode of transportation, filling the gap in transportation systems. This modern transport mode gained momentum in 2018 because e-scooters are energy-efficient, environmentally friendly, easy to handle, and compact. There are many advantages to e-scooter use, including lower costs, environment friendliness, exercise and fitness, and improved accessibility to other transport systems. According to the National Association of City Transportation Officials, more than 38.5 million rides were taken with e-scooters in 2018 in the U.S. Furthermore, e-scooters are now operational in over 65 major U.S. cities [1].

Micro-mobility, such as an e-scooter, is a useful means of transportation that provides sustainability in the face of the current hazards presented by an over-growing population, traffic congestion, and greenhouse gas impacts [2]. Environmental pollution and carbon dioxide emissions can be significantly minimized by utilizing micro-mobility rather than regular motor vehicles [3,4]. Furthermore, replacing private vehicle trips with micro-mobility promotes sustainability by lowering gas emissions and traffic accidents [5]. In [6], the relation between the E-scooters and characteristics of sustainable urban development was examined, such as land use type and walkability. Recently, research has examined e-scooters as a green choice in terms of environmental sustainability [7,8].

Brisbane, Australia, recorded more than one 50,000 trips commuted by e-scooters within the first two weeks of launching the service; after four months, in mid-November 2018, the number of trips increased to one million. This highly significant rise in demand is backed by a vast, un-noticed infrastructure network designed to sustain charged and available scooters at all times. Currently, e-scooter charging primarily depends on freelancers who compete without considering the negative environmental impact resulting from not optimizing their charging-trip fuel-efficiency. Freelance chargers spend significant time searching for e-scooters because of the competitive nature of the profession and the inaccuracy of the location-finders of some e-scooters [9]. The charger’s task is to locate e-scooters that need to be charged via the app and drive them home for charging. Although simple, there are two significant problems with this approach. First, the current practice is focused on a first-come-first-serve basis and can only be verified when a charger arrives at the scooter’s location and has been unlocked with the app. This aspect of app usage results in rivalry and causes the chargers to travel long distances without first verifying the availability of the e-scooter in order to upgrade the online application. Many disputes between freelance chargers have been reported when they have simultaneously arrived at an e-scooter [10]. The rivalry between chargers can result in physical violence and threatens the safety of the operation [11]. Second, due to the nature of their tasks, freelance chargers are considered independent contractors, as defined by the “gig” economy. While this gig economy provides the chargers with flexibility and independence, it also does not guarantee a minimum wage or maximum hours [12].

We hypothesized that matching chargers with an optimal assignment of e-scooters could eliminate competition and possibly avert physical violence. It could also reduce the charging and rental costs of e-scooters that could be converted into increased income for the chargers. E-scooter assignment has been widely discussed, and potential models have been implemented in various other operations, such as e-bike and electric vehicle sharing systems. Ref. [13] proposed two approaches to solving the problem of charging shared e-bikes. Ref. [14] explored electric vehicle charging methods at the lowest possible cost for a practical vehicle sharing system. They developed a queuing network model using a nonlinear optimization system with fractional quadratic constraints. Ref. [15] suggested a model that would fit battery locations with electric taxis. Ref. [16] created a model for assigning vehicle blocks to busses in public transit, considering various temporal and spatial constraints. Ref. [17] developed a two-stage heuristic algorithm to solve the school bus routing problem. Ref. [18] investigated the optimal locations for e-scooter sharing stations and developed a mathematical model formulated as a multi-objective topic with maximum utility at minimum cost. However, they did not study the assignment of freelance chargers to e-scooter locations.

To the best of our knowledge, there have been few studies on e-scooter planning and scheduling problems in the literature, and none of these studies have addressed the problem of integrating e-scooter locations and charger-assignment. In consultation with E-Scooter-Chargers Allocation (ESCA), an e-scooter sharing company in Brisbane, Australia, we found that the allocation problem can be static or dynamic, and chargers use their private vehicles to collect e-scooters for both. The static ESCA activity assumes the e-scooter and charger positions are either the same or are slightly apart. In the dynamic ESCA activity, the positions of the e-scooters and chargers are constantly changing, significantly influencing the model and affecting the potential solution. This study formulates the static ESCA activity as a mixed-integer linear programming (MILP) model. To overcome the time computation of MILP, we adapted the simulated annealing (SA) algorithm to find an effective solution to the assignment problem.

2. Problem Statement and Formulation

In this study, a real-world assignment problem with a large number of variables was formulated as an MILP model [19], which is a combinatorial optimization problem that makes use of exact solution techniques or commercial optimization software packages (e.g., IBM ILOG-CPLEX), intractable due to unacceptably long CPU (Central Processing Unit) time and memory requirements [20]. For this reason, we developed a specific SA metaheuristic algorithm to solve the ESCA problem, where the SA approximates the optimal global solutions in the large search space of the optimization problem. The problem of assigning e-scooters to chargers was adapted as a “real-world assignment situation”, as generally known in operations research. It is a trade-off between finding an effective solution and converging in a short time. This problem is formulated using an objective function and constraints, considering both computational time and the quality of the solution, targeting a near-optimal solution while assigning jobs ($n$) to the number of individuals ($m$).

In this study, we adopt the SA algorithm to solve the assignment problem between freelance chargers and e-scooters, in which each e-scooter is assigned to only one charging freelancer at a time, considering predefined constraints.

Consider the complete graph $G=\left(V,E\right)$, where $V$ is the set of nodes with two subsets $S$ and $R$; $S\subseteq V$ and $R\subseteq V$, and E is the edge set of graph G. G is adapted to be the route network, and $V$ is the number of locations. The ESCA activity is defined on a set of e-scooters $S$ in the system and R is the set of chargers, where |S| = s, and |R| = r and assume that s ≥ 1 and r ≥ 1, unless otherwise stated, select a subset of chargers $s\subseteq S$ based on their location. The key purpose of this suggested solution is to evaluate the e-scooter location based on obtaining a successful assignment for the location to develop an efficient e-scooter assignment to a charger. The objective function consists of two types of costs, the chargers’ travel distance to collect the e-scooter and the cost of adding new freelance chargers. The cost of recruiting new chargers is included to penalize the selection of more chargers than needed to charge the e-scooters.

The ESCA aims to find the optimal tours for all chargers to pick up e-scooters in the form of routes, such that each route contains one charger, and each e-scooter is visited only once by the set of routes, which are typically called an ESCA solution. Additionally, there is only one charger located at charger location i, and each charger must return to their original location. The potential tours occur within a predetermined interval to minimize the total cost of all tours. In addition, constraints are imposed on the number of e-scooters in a tour, where the upper and lower boundaries for the number are denoted by $U$ and $L$, respectively. In this study, based on the current state-of-practice for all scenarios, we set the maximum number of e-scooters collected by each charger to six (based on the number of charging adapters received from the e-scooter operator). For each charger, $o_i$ is the number of nodes (e-scooters) visited on the charger’s path from the origin to node i; $1\le o_i\le U$ for all $i\ge 2$ and if $x_{ikk}$ = 1 then $L\le o_i\le U$ must be satisfied. For each $\left(i,j\right)$ $\in E$, we define one binary variable $x_{ijk}$ which takes the value $1$ if one charger departs from the kth node (location) and travels through the arc (edge) $ij$, and $0$ if otherwise. In the ESCA solution approach, the six charged e-scooters are returned to a single position, and hence, the solution does not achieve the redistribution of the charged e-scooters.

Figure 1 depicts an illustrative example of the ESCA, with seven chargers and twenty-four e-scooters. In this example, there is only one e-scooter at each location, and each charger collected a maximum of six e-scooters. From Figure 1, we can find four chargers have collected the twenty-four e-scooters, and the three chargers are not selected. The solution does not consider the redistribution of the charged e-scooters.

2.1. Notation

The mathematical notation of the ESCA problem formulation is presented below, including the objective function and constraints.

$s$: number of e-scooters

$r:$ number of chargers

$R$: set of charger vertices, $R=\left\{1,., r\right\}$

$S$: set of e-scooter pickup vertices, $S=\left\{ r+1,r+2,\dots , n\right\}$

$V$: set of all vertices, $V=R\cup S$; $V=\left\{1., n\right\}$

$E$: set of all arcs $ij$, $E=V\times V$

$c_{ij}:$ transportation costs traveling from $i$ to $j$; $i=1\dots V$ and $j=1\dots V$

$U$: highest number of e-scooters allocated to a charger within a sub-tour.

$L$: lowest number of e-scooters allocated to a charger within a sub-tour.

$o_i$: number of nodes (e-scooters) visited on the charger’s path from origin to node i.

$x_{ijk}$: a binary variable that equals 1 if arc $ij$ is used and belongs to the $k$th charger; 0, if otherwise.

2.2. Objective Function

Equation (1) is specified to minimize relevant e-scooter charging costs. Two expense words are used in the objective function; the expense of distances between the positions of e-scooters and freelancers, and the cost of adding a new freelancer. The first term shows the traveling costs in the two directions ($c_{kj}$, $c_{jk}$) (pick up and deliver the e-scooters), while the second term shows the costs of adding a new freelancer ($c_{ij}$).

$x_{kjk}$: a binary variable that equals 1 if arc $kj$ is used and belongs to the $k$th charger; otherwise, it equals zero.

$x_{jkk}$: a binary variable that equals 1 if arc $jk$ is used and belongs to the $k$th charger; otherwise, it equals zero.

$$f=Min\left(\left.{\displaystyle \sum }_{k=1}^r{\displaystyle \sum }_{j=r+1}^n{c}_{kj}{x}_{kjk}+c_{jk}{x}_{jkk}\right)\right.+{\displaystyle \sum }_{k=1}^r{\displaystyle \sum }_{i=r+1}^n{\displaystyle \sum }_{j=r+1}^n{c}_{ij}{x}_{ijk}$$

(1)

2.3. Constraints

Equation (2) constraints that only one charger departs from each charger location; k $\in R$.

$${\displaystyle \sum }_{j=r+1}^n{x}_{kjk}=1\forall k\in R$$

(2)

Equation (3) constraints that each e-scooter can only be visited once

$${\displaystyle \sum }_{k=1}^r{x}_{kjk}+{\displaystyle \sum }_{k=1}^r{\displaystyle \sum }_{i=r+1}^n{x}_{ijk}=1\forall j\in S$$

(3)

Equation (4) ensures that the number of chargers in the inbound direction equals the outbound direction. This means that, at each location, the number of chargers who deliver and send e-scooters must be the same at each location. In this case, using Equation (2), the number of chargers in each direction is one.

$$x_{kjk}+{\displaystyle \sum }_{i=r+1}^n{x}_{ijk}-x_{jkk}-{\displaystyle \sum }_{i=r+1}^n{x}_{jik}=0,\forall k\in R,j\in S$$

(4)

Equation (5) requires that the charger location nodes respect that the number of chargers in the outbound direction at the origin (charger start point) equals the number of chargers in the inbound direction at the same origin. In this case, based on Equation (2), the number of chargers in both directions is one.

$${\displaystyle \sum }_{j=r+1}^n{x}_{kjk}-{\displaystyle \sum }_{j=r+1}^n{x}_{jkk}=0\forall k\in R$$

(5)

Equation (6) indicates the limitations on the maximum number,$U$, of e-scooters picked up in each tour; where, if $i$ is the first node on the tour, then the initial value of nodes (e-scooters) visited on the charger’s path from the origin to node i, $O_i$ is 1.

$$O_i+\left(U-2\right){\displaystyle \sum }_{k=1}^r{x}_{kik}-{\displaystyle \sum }_{k=1}^r{x}_{ikk}\le U-1\forall i\in S$$

(6)

Equation (7) displays the limitations on the minimum number, $L$, of e-scooters picked up in each tour; where, if $i$ is the first node on the tour, then the initial value of nodes (e-scooters) visited on the charger’s path from the origin to node i, $O_i$ is 1.

$$O_i+{\displaystyle \sum }_{k=1}^r{x}_{kik}+\left(2-L\right){\displaystyle \sum }_{k=1}^r{x}_{ikk}\ge 2\forall i\in S.$$

(7)

Equation (8) prevents each charger from picking up only one e-scooter during the whole tour; therefore, tours with only one e-scooter picked up are not allowed.

$${\displaystyle \sum }_{k=1}^r{x}_{kik}+{\displaystyle \sum }_{k=1}^r{x}_{ikk}\le 1\forall i\in S.$$

(8)

Equations (9) and (10) are sub-tour elimination constraints that break all sub-tours of e-scooter nodes in which closed sub-tours are made for each charger.

$$O_i-O_j+U{\displaystyle \sum }_{k=1}^r{x}_{ijk}-\left(U-2\right){\displaystyle \sum }_{k=1}^r{x}_{jik}\le U-1;i\ne j,i,j\in S.$$

(9)

$$x_{ijk}\in \left\{0,1\right\},i,j\in Vandk\in R$$

(10)

3. The SA-Based Assignment Algorithm

Finding the optimal solution for most complex optimization problems is a highly challenging task, and, in many cases, impossible. As a problem increases in complexity, the search space for the optimal solution of the problem exponentially increases with the increase in the space of the states. Even with modern computing capabilities, large computation times are still needed to search the entire space for possible solutions. Metaheuristic techniques tend to overcome this problem by providing heuristics to guide the search process, thereby improving its efficiency in reaching near-optimal solutions within a reasonable time. Metaheuristic approaches have proven their value in solving many complex problems, such as scheduling [21,22,23]. According to [24], four aspects should be considered when comparing metaheuristic techniques:

• the solution representation
• the neighborhood structure
• the local search method within the neighborhood
• acceptance-reject criteria

These algorithms adapt the iterative improvement mechanisms, in which each iterate moves toward the solution by progressive approximation. This iterative process stops if there is no improvement in the objective function (reaching either the local minimum or maximum value). SA is among the most successful metaheuristic, and local search techniques are used to solve combinatorial optimization problems using mathematical techniques to obtain an optimal solution for complex problems by exhaustive search methods [25]. SA is a probabilistic method to obtain the approximated global optimum for a given minimum or maximum objective function, and is extensively used, with positive results. SA searches the solution space and avoids being trapped in the local optimum [26]. It starts with an annealing temperature T associated with a proposed preliminary solution as the current solution. Then, it updates the solution by searching in the neighborhood of the preliminary solution and moving toward the solution one step at a time by progressive approximation. This is accomplished by calculating the difference (∆) between the value of the objective function of the preliminary solution, f(current solution), and the value of the new solution, f(new solution), and deciding if the new step (i.e., new solution) is acceptable or not; ∆ = f(new solution) − f(current solution). If ∆ is less than zero, then the new solution is acceptable (for minimization problems); otherwise, the SA accepts the new solution with the probability of $\frac{1}{1+\exp \left(\Delta /T\right)}$ where T is the temperature to be reduced through iterations using the cooling (decreasing) factor α.

The environment of the ESCA problem is dynamic, where the number of e-scooters that need to be charged is changeable with time, especially in the peak hours. Furthermore, charger availability is changeable from time to time. Hence, we need a good and fast solution which can fit into this dynamic and does not require large computational resources. Based on these reasons, SA was selected to solve the proposed problem under these criteria. SA is one of the most common metaheuristic approaches and has been successfully used to solve the traditional capacitated vehicle routing problem (VRP) with multi-depots and its variants [27,28,29,30], where the ESCA problem is highly related to the capacitated VRP with multi-depots.

Encoding the ESCA problem in a suitable form for the SA is the most important step in the implementation process. We established two lists, one of all the chargers and another of all the e-scooters. The first charger in the chargers list was assigned the first six e-scooters in the e-scooters list. In other words, the mth charger in the chargers list was assigned the e-scooters with positions from $6\ast \left(m-1\right)+1$ to $6\ast m$ in the e-scooters list.

At the beginning of the SA, we randomly initialized two lists of e-scooters and chargers, as shown in Figure 2. Each charger was assigned a maximum of six e-scooters (based on the number of charging adapters received from the e-scooter operator). The objective was to minimize the number of freelance chargers used. The number of chargers needed was calculated as $\frac{number of e-scooters need charging}{6}$, where ⌈ ⌉ is the ceiling function. For example, for eight e-scooters and three chargers, we need $\lceil \frac{8}{6}\rceil =2$ chargers out of the three. As shown in Figure 3, the third charger was not assigned to an e-scooter.

In the implementation, the charger and e-scooter lists were set up with the proposed objective function. We searched the solution space in the proposed SA by repeatedly swapping chargers within the charger list and e-scooters within the e-scooter list, and re-evaluating the objective function. The swapping procedure is termed non-adjacent pairwise interchange (NAPI). As shown in Figure 4, NAPI was used to swap two non-adjacent elements, $i\mathrm{and}j$, within the given list.

As presented in Algorithm 1, the SA guided the above search to find a near-optimal solution.

Algorithm 1. Procedure of the proposed SA for E-Scooter-Charger Allocation

Create an initial solution 1.1 Randomly set the chargers in the charger list 1.2 Randomly set the e-scooters in the e-scooter list 1.3 Evaluate the objective function using the initial solution (initial assignment) Set the algorithm parameters 2.1 Set the initial temperature, T 2.2 Set the cooling (decreasing) parameter, α 2.3 Set the maximum number of the inner loop iterations (M_ILC) 2.4 Set the maximum number of the outer loop iterations (M_OLC) Set the outer loop counter O.L.C. = 1 While OLC < M_OLC 4.1 Set the inner loop counter I.L.C. = 1 4.2 While ILC < M_ILC 4.2.1 Swap the chargers within the charger list using non-adjacent pairwise interchange (NAPI). 4.2.2 Swap the e-scooters within the e-scooter list using NAPI 4.2.3 Evaluate the objective function using the new lists 4.2.4 Metropolis-Hastings 4.2.4.1 If the current solution is better than the previous, increment the I.L.C. and go to Step 4.2 4.2.4.2 Accepting the new solution if the prior solution is greater than the current solution with probability $\frac{1}{1+exp\left(\frac{\Delta }{T}\right)}$ increment I.L.C. and go to step 4.2. 4.2.4.3 Otherwise, reverse the charger list swap, reverse the e-scooter list swap, increment I.L.C., and go to Step 4.2. 4.3 Reduce the temperature 4.4 Increment O.L.C. and go to step 4.

As shown in the above table, the adapted SA algorithm consists of an outer and inner loop. The number of iterations in the outer loop is larger in than the inner loop. The outer loop is responsible for reducing the temperature (T) at the end of each outer iteration number (k) using Equation (11).

$$T^{k+1}=\alpha \ast T^k$$

(11)

where $T^k$ is the temperature during outer iteration number k and $T^{k+1}$ is the temperature for the next outer iteration.

Simulated annealing is a way of searching for a solution to a problem that is modeled after the physical process of annealing. Annealing is a slow process that happens when a thermal system starts melting at high temperatures, and then slowly cools down until it reaches a stable state. In this process, the system’s energy is lowered until it is at its lowest possible level [31].

The SA algorithm is able to escape local optima by using a mechanism that allows deterioration in the objective function value (OFV). This is because, in the early stages of the algorithm, when the temperature parameter T is relatively high, the search for the solution space is widely “explored”, and often “bad” solutions are accepted with high probability. As the temperature parameter T decreases, the probability of accepting solutions that lead to worse objective function values gradually decreases. This allows for controlled “uphill” movements, which eventually lead to higher quality solutions [31].

4. Computational Experiments

The validation of the developed SA algorithm was performed in two stages, first using simulation data and later using real-world data. The simulation dataset was used to evaluate the solution provided by the SA algorithm only against the state-of-practice (baseline), since this was a new application and there were no other approaches in the literature to compare. In the simulation data, we generated and randomly placed the e-scooters and chargers within a 5 km² area. This placement was based on uniform distribution and Euclidean distances. The proposed approach was evaluated using real-world instances of different sizes ([14,18]). The goal of the second dataset was to evaluate the variances of the solutions and the means and variances of the running time.

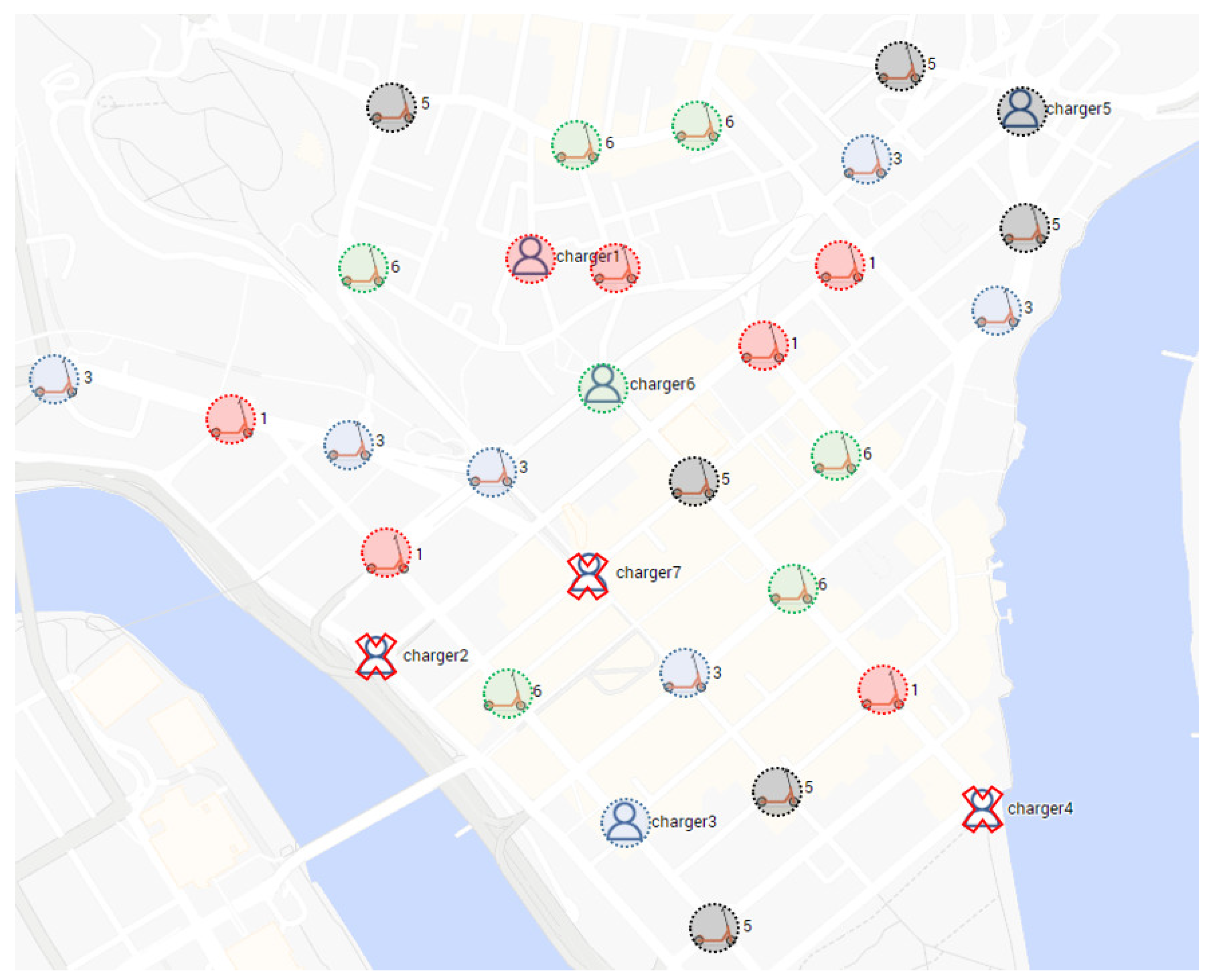
4.1. Simulated Instances

We developed an agent-based simulator in MATLAB to simulate four scenarios. In the first scenario, 120 e-scooters were to be charged by 20 chargers. In the other three scenarios, the number of chargers was increased while maintaining the number of e-scooters. The simulation assumed that each charger could collect six e-scooters during the simulation time and the chargers had a competitive approach to e-scooter collection. At the start of the simulation, each charger checked the locations of their available e-scooters, went to the nearest one, unlocked it, and picked it up. Then, the chargers referred to the app to choose their next nearest e-scooter. Each charger continued the collection process until all of their six e-scooters had been collected, and returned home to charge them. The simulation ended when all e-scooters had been collected by their respective chargers. To statistically compare the total distance traveled in the proposed approach to the baseline, 100 runs were performed for each scenario and the total distance traveled for each run was estimated. It was noted that previous studies have not considered pre-reservation of an e-scooter; thus, it could have been possible for a charger to arrive to find that another charger had already collected the e-scooter. Therefore, this proposed approach was designed to overcome this limitation and assumed the following:

(i)

Chargers can collect a maximum of six e-scooters; thereby, no competition can occur.

(ii)

This proposed algorithm heuristically minimizes the objective function, leading to a reduction in the distance traveled by the chargers.

The total distance traveled in this proposed approach and the state-of-practice was calculated for each scenario using 100 randomly generated locations for e-scooters and chargers. The distances traveled by chargers for each scenario for both the baseline and proposed algorithms are presented in Figure 5. The results indicate that assigning e-scooters to chargers saves time by reducing the total distance traveled by the chargers. Moreover, it is worth mentioning that, due to competition, the total distance traveled by the chargers in the baseline model increased as the number of chargers increased. Figure 5 shows the simulated cases that were used as a proof of concept to show the reduction in the travelled distance to collect the e-scooters. Moreover, using simulations, we were able to generate a large number of instances and statistically compare the quality of the state-of-practice and simulated annealing.

Table 1. Comparison of proposed and baseline approaches using simulated instances.

	The Baseline		SA
No. of Chargers	Mean (km)	Std (km)	Mean (km)	Std (km)	$\frac{\mathit{m}\mathit{e}\mathit{a}{\mathit{n}}_{\mathit{b}\mathit{a}\mathit{s}\mathit{e}\mathit{l}\mathit{i}\mathit{n}\mathit{e}}-\mathit{m}\mathit{e}\mathit{a}{\mathit{n}}_{\mathit{S}\mathit{A}}}{\mathit{m}\mathit{e}\mathit{a}{\mathit{n}}_{\mathit{b}\mathit{a}\mathit{s}\mathit{e}\mathit{l}\mathit{i}\mathit{n}\mathit{e}}}$	p-Value
20	213.58	66.08	82.68	4.51	0.61	$\ll 0.0001$
30	307.68	115.97	69.20	4.15	0.78	$\ll 0.0001$
40	301.04	86.06	68.03	3.85	0.77	$\ll 0.0001$
50	322.01	110.85	67.17	4.45	0.79	$\ll 0.0001$

compares the proposed approach to the state-of-practice in terms of the mean of the total distance traveled and the standard deviation for the solutions of the different simulated instances. In the state-of-practice, the increase in the number of chargers is always accompanied by an increase in the mean of the total distance traveled due to higher competition between chargers. On the other hand, the proposed SA approach uses resources more efficiently, and an increase in the number of chargers leads to a decrease in the mean total distance traveled. The Wilcoxon rank-sum test results are summarized in Table 1. This test examines the null hypothesis that the total distance traveled in the state-of-practice and the proposed approaches are samples of continuous distributions with equal medians, against the alternative that they are not.

4.2. Real-World Benchmark Instances

For validation purposes, 18 benchmark instances ranging from 13 to 410, were tested by the proposed algorithm; the data is available in [32,33].

Table A1. Evaluation of proposed approach using different sizes of benchmark instances (small and medium).

City	S	R	No. of Selected Chargers	Mean Total Dist. (km)	Std. of Total Dist.	Average Dist. per Charger (km)	Mean (s)	Std. (s)
Bari	13	3	3	17.42	0.6925	5.81	24.2825	0.6536
		4	3	16.48	0.4590	5.49	26.6802	2.8873
		5	3	16.04	0.2366	5.35	26.4121	0.9359
		6	3	15.89	0.2132	5.30	25.8882	0.2477
Denver	51	10	9	93.77	4.2992	10.43	7.6649	0.0925
		15	9	84.85	5.6836	9.43	7.6642	0.0688
		20	9	83.16	4.8102	9.24	7.7522	0.1255
		25	9	77.19	4.1236	8.57	7.7465	0.0920
Rio De Janeiro	55	10	10	156.03	4.2809	15.60	7.8684	0.1018
		15	10	130.51	4.0688	13.05	8.4486	0.5078
		20	10	126.63	5.8542	12.66	8.4389	0.1110
		25	10	118.21	6.9748	11.82	9.0633	0.1438
Boston	59	10	10	149.53	1.8104	14.95	7.9769	0.1624
		15	10	118.66	3.7801	11.87	8.1854	0.1057
		20	10	107.24	3.4410	10.72	8.7185	0.2075
		25	10	97.59	3.1160	9.76	9.0540	0.2089
Torino	75	15	13	82.49	2.6982	6.35	9.3305	0.5826
		20	13	76.46	3.6623	5.88	9.1847	0.1975
		25	13	71.20	1.7541	5.48	9.2049	0.1094
		30	13	70.67	1.7714	5.44	9.8359	0.3867
Toronto	80	15	14	85.46	1.6811	6.10	10.0570	0.3215
		20	14	80.92	3.1012	5.78	10.5567	0.5761
		25	14	77.06	3.0354	5.50	11.3008	0.6557
		30	14	74.27	4.7503	5.30	10.6710	0.4708
Miami	82	15	14	225.59	5.4343	16.11	26.4689	1.5830
		20	14	159.78	4.9159	11.41	26.2428	0.7857
		25	14	112.97	5.3943	8.07	23.9292	1.2262
		30	14	89.82	4.7962	6.41	19.5331	6.9275
Ciudad De Mexico	90	20	15	116.93	2.9714	7.80	26.1773	3.1219
		25	15	101.66	1.9904	6.78	26.5732	1.9891
		30	15	93.97	3.0322	6.26	26.9500	1.1487
		35	15	86.37	2.1399	5.76	27.5016	0.5540
Minneapolis	116	25	20	265.37	4.8507	13.27	16.0412	0.4177
		30	20	247.41	8.1364	12.37	16.1741	0.3450
		35	20	239.35	8.9119	11.97	16.2944	0.2845
		40	20	230.90	5.2024	11.54	16.2057	0.2166

and

Table A2. Evaluation of the proposed approach using large-size benchmark instances.

City	S	R	No. of Selected Chargers	Mean Total Distance (km)	Std. of Total Distance	Average Dist. per Charger (km)	Mean (s)	Std. (s)
Brisbane	150	30	25	157.26	5.5674	6.29	70.6994	0.7181
		35	25	156.90	6.5932	6.28	71.1903	0.5602
		40	25	155.55	8.3422	6.22	71.1579	0.2525
		45	25	150.21	4.5519	6.01	72.2431	0.1981
Milano	184	40	31	170.24	3.7002	5.49	78.6649	0.6661
		50	31	168.73	5.3349	5.44	78.9016	0.2877
		60	31	166.53	5.0347	5.37	79.2027	0.3343
		70	31	167.87	4.2611	5.42	79.3685	0.5798
Lille	200	40	34	404.63	12.1092	11.90	82.1638	0.3132
		50	34	397.18	19.0258	11.68	82.4724	0.4127
		60	34	334.06	19.7114	9.83	82.8899	0.2982
		70	34	280.17	20.6407	8.24	83.8384	4.2350
Toulouse	240	40	40	320.26	8.3525	8.01	66.9241	0.6171
		50	40	300.72	8.6194	7.52	69.5375	0.5668
		60	40	291.34	10.2889	7.28	78.2493	0.4577
		70	40	279.78	8.8202	6.99	70.2105	0.8201
Sevilla	258	50	43	360.48	8.5747	8.38	72.4298	2.7409
		60	43	324.76	12.1106	7.55	74.1808	1.3228
		70	43	312.89	11.3318	7.28	74.0912	1.0718
		80	43	307.98	10.4338	7.16	73.1707	0.3482
Valencia	276	50	46	485.54	10.1946	10.55	75.2697	5.1969
		60	46	439.79	9.9710	9.56	79.2874	3.0556
		70	46	402.61	7.9594	8.75	79.3139	1.5698
		80	46	396.40	8.8915	8.62	81.5518	1.4524
Bruxelles	304	60	51	486.90	16.2957	9.55	82.0023	3.2712
		70	51	448.17	16.9597	8.79	84.6469	1.9173
		80	51	439.38	14.4431	8.62	82.4134	1.1279
		90	51	428.26	9.7240	8.40	184.4216	55.3400
Lyon	336	60	56	589.37	12.5426	10.52	93.4295	4.3040
		70	56	538.87	7.5401	9.62	97.1009	6.8603
		80	56	508.91	10.7859	9.09	88.6171	2.0332
		90	56	492.42	11.8251	8.79	91.0158	1.5686
Barcelona	410	70	69	610.01	6.0656	8.84	101.2063	2.7764
		80	69	548.78	9.6474	7.95	102.5639	2.8394
		90	69	510.66	8.1314	7.40	103.1610	1.9283
		100	69	491.63	12.9522	7.13	103.7572	1.4365

show the mean and standard deviation of the travel distance and running time. The parameter tuning of the proposed algorithm was prepared using a grid search approach to find the best combination of parameters. The grid search approach is considered a straightforward approach; however, it requires high computational time. Therefore, the hyper-parameters of the algorithm were set to 1000, 20,000, 200, and 0.95 for the initial temperature, the outer loop maximum number of iterations, the inner loop number of iterations, and the cooling parameter, respectively. Table A1 and Table A2 show a similar trend in that the quality of the solution improves as the number of available chargers increases, because increasing the available e-scooters raises chances for better assignments between freelancers and e-scooters.

5. Discussion

The e-scooter/charger assignment is a dynamic problem in nature. Furthermore, operators need to monitor the status of their vehicles and run an efficient and accurate e-scooters /chargers assignment algorithm more than once a day. Hence, as shown in the paper, the SA has been proposed to provide good solutions in a reasonable time, where, from Table 1, in all cases, the SA found good solutions compared to the baseline for small and medium cases. From Table A1 and Table A2, the SA quickly found a good solution with the increasing number of rechargers, because increasing the available e-scooters raises chances for better assignments between freelancers and e-scooters. Therefore, the proposed algorithm is more suitable in the case of solving large-scale problems. The key point here is finding a good solution to the e-scooters /chargers assignment problem in a short time, considering that the SA is easy for the operator to run it.

To further discuss the proposed approach performance, we examined simulated annealing as a practical heuristic approach to solve the ESCA problem by comparing the SA to our previous work [12]. In [12], the college admission algorithm (ACA) and the black hole optimizer (BHO) algorithm were used to solve the ESCA problem, where the performance of these algorithms was compared to the results of a mixed-integer linear programming (MILP) model for small and medium cases. As ESCA is an NP-complete combinatorial optimization problem, the MILP is inapplicable to finding the exact solution for large-scale real cases.

In the current work, the SA was proposed to improve the solution of the ESCA problem compared to ACA and BHO, as shown in

Table 2. Comparison of the proposed SA, MILP, ACA, BHO, and baseline approaches using simulated instances. The SA (highlighted with colors) minimized the total distances compared to other algorithms in difference cases.

	The Baseline	MILP (Optimal)	ACA	BHO	SA
# of Chargers	Total Dis.	Total Dis.	Total Dis.	Total Distance	Total Distance
20	213.58	76.7	98.2	131.9	82.68
30	307.68	65.6	85.9	122.6	69.20
40	301.04	61.4	81.0	129.7	68.03
50	322.01	60.4	79.3	130.1	67.17

, and how far from the optimal solution using MILP.

The successful implementation of this technique can assist e-scooter firms in meeting client demand while considering rental costs and increasing the hourly fee of chargers. Further considerations should be made when developing the commercial software for the ESCA as follows:

• How to extend the model in such a way that it is generally applicable based on real data acquired from a large number of places in Australia, including Queensland.
• How to discover a decent (near optimum) solution for major e-scooter operators who may have to address this problem for thousands of e-scooters.

6. Conclusions

The public’s interest in micro-mobility modes has recently grown at a rapid rate, altering many cities’ transportation infrastructure. Micro-mobility provides an economical and quick way to commute, relieving consumers from interminable waiting and time wasted in congested locations.

Recently, the usage of dockless electric e-scooters for first- and last-mile trips has gained momentum as a micro-mobility mode. This new model has been introduced to fill the gaps in the current transportation network and mitigate traffic congestion in dense cities. The significant rise in demand for e-scooter sharing systems has been accompanied by an expanding network of freelancers to maintain the e-scooters in charged and accessible conditions. The current scenario is that freelancers compete for the charging of the e-scooters to maximize their income at the cost of the environment. In this study, we developed a mathematical model for the ESCA. Specifically, we adapted an SA algorithm that solves the ESCA problem while overcoming the common shortcomings of the existing state-of-practice approach. The performance of the SA algorithm was evaluated in two stages, using both simulation and real-world data. First, the simulated dataset was used to compare the SA algorithm approach’s solution to the state-of-practice (baseline), and the results indicated a 61% to 79% reduction in the total distance traveled. Then, the SA algorithm was evaluated using 18 instances of real-world data, and, in most cases, the results showed a near-optimal solution in less than three minutes.

Overall, this pioneering study implemented an SA algorithm to solve the ESCA problem and provided significantly better and reliable solutions than the baseline (existing state-of-practice) method. It provided the model needed for assigning e-scooters to chargers to minimize the chargers’ average distance traveled and eradicated direct competition between chargers. This could eliminate the physical violence and disputes that have been reported by chargers due to simultaneously arriving at the same e-scooter. Moreover, implementing the proposed SA model solution could help guarantee a minimum wage for chargers. Because the proposed SA algorithm uses the available resources (chargers) more efficiently and eliminates duplication of effort; it provides opportunities for maximizing e-scooter rental time, leading to a higher income for e-scooter sharing system operators.

The limitations of this study are:

• We used a static ESCA approach that does not account for time-variations in the location of e-scooters or chargers.
• Our method assumes that the chargers would accept the assignment solution, which may or may not be the case

Hence, future studies should extend the model as a fuzzy dynamic ESCA problem. Fuzzy Dynamic Programming (FDP) is a mathematical tool based on fuzzy numbers or logic that can solve many complex and multivariable problems. In FDP, the best solution of the Dynamic ESCA is obtained by decomposing the sub-problem of a single variable. Furthermore, future directions should be considered, such as the battery swapping problem, constructing charging stations, and incentivizing the users to visit the charge stations and deliver the e-scooters to recharge or swap the batteries and gain credits.