Automating Microclimate Evaluation and Optimization during Urban Design: A Rhino–Grasshopper Workflow
Abstract
:1. Introduction
1.1. Background and General Context
1.2. State of the Art in Microclimate Evaluation
1.3. Research Gap
1.4. Objectives
- -
- Build a responsive evaluation workflow based on spatial indicators.
- -
- Increase computation speed.
- -
- Reduce the computation load for genetic optimization at middle- and large scale.
2. Methodology
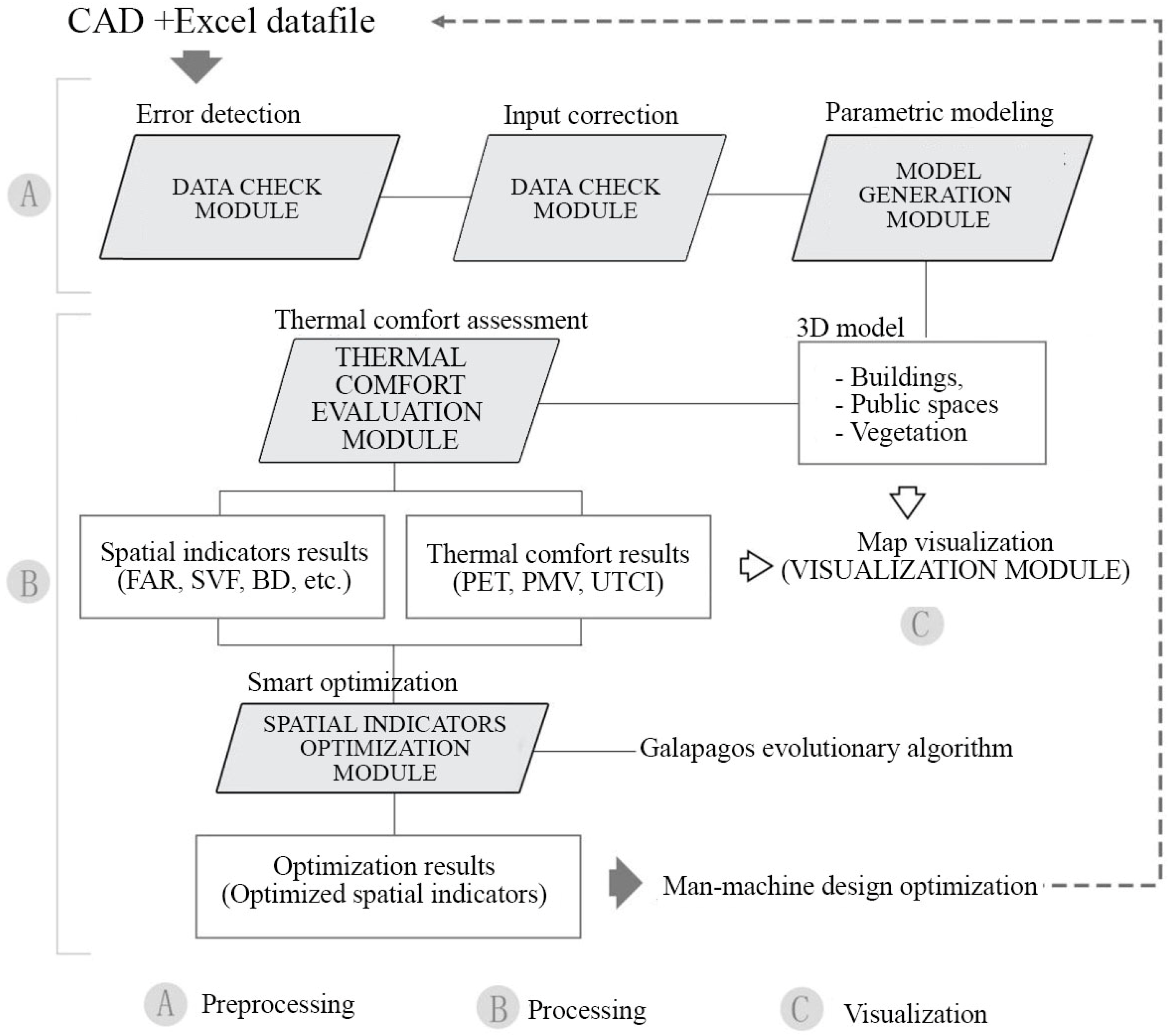
2.1. Conceptual Framework
2.2. Workflow Structure and Functions
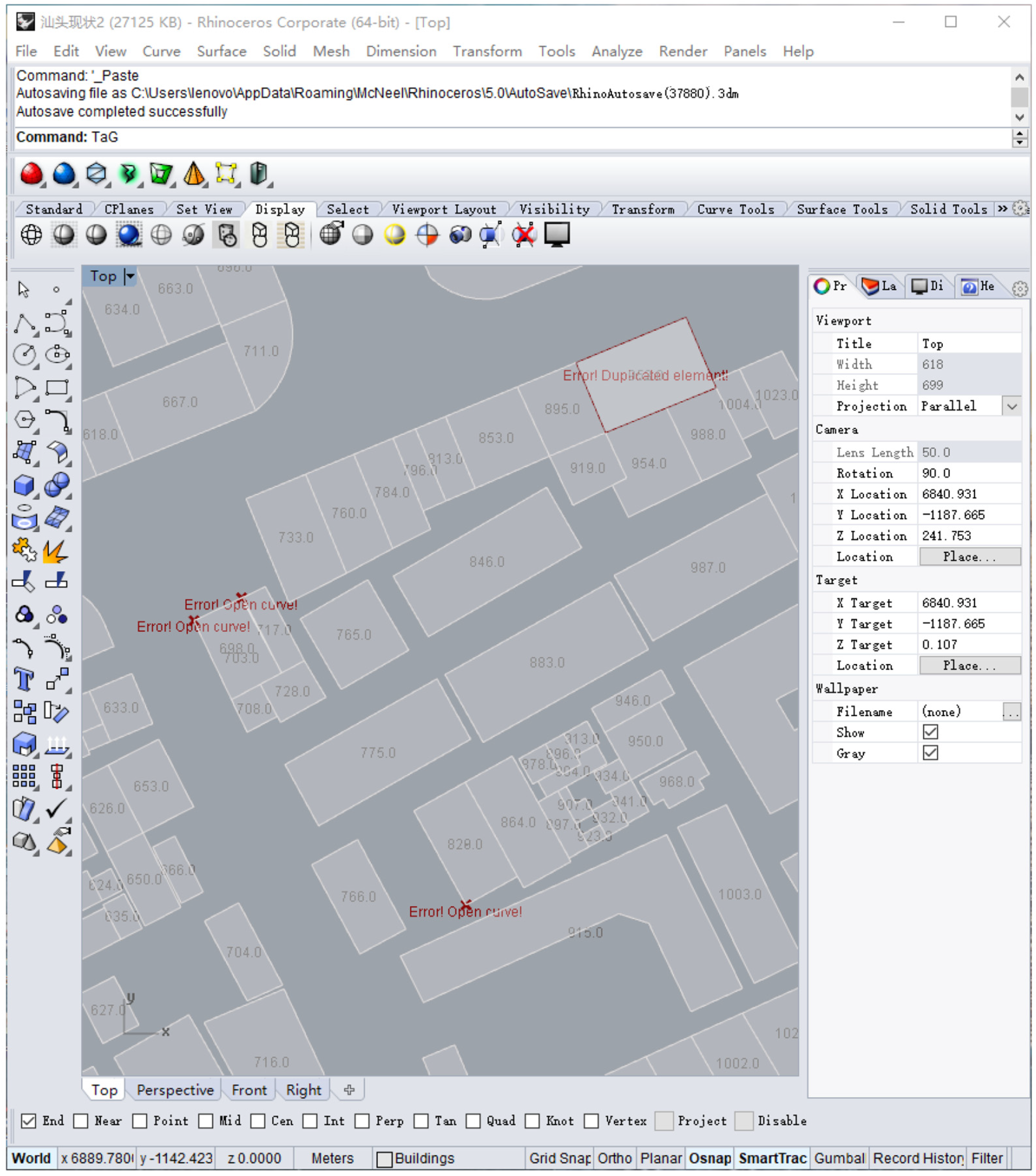
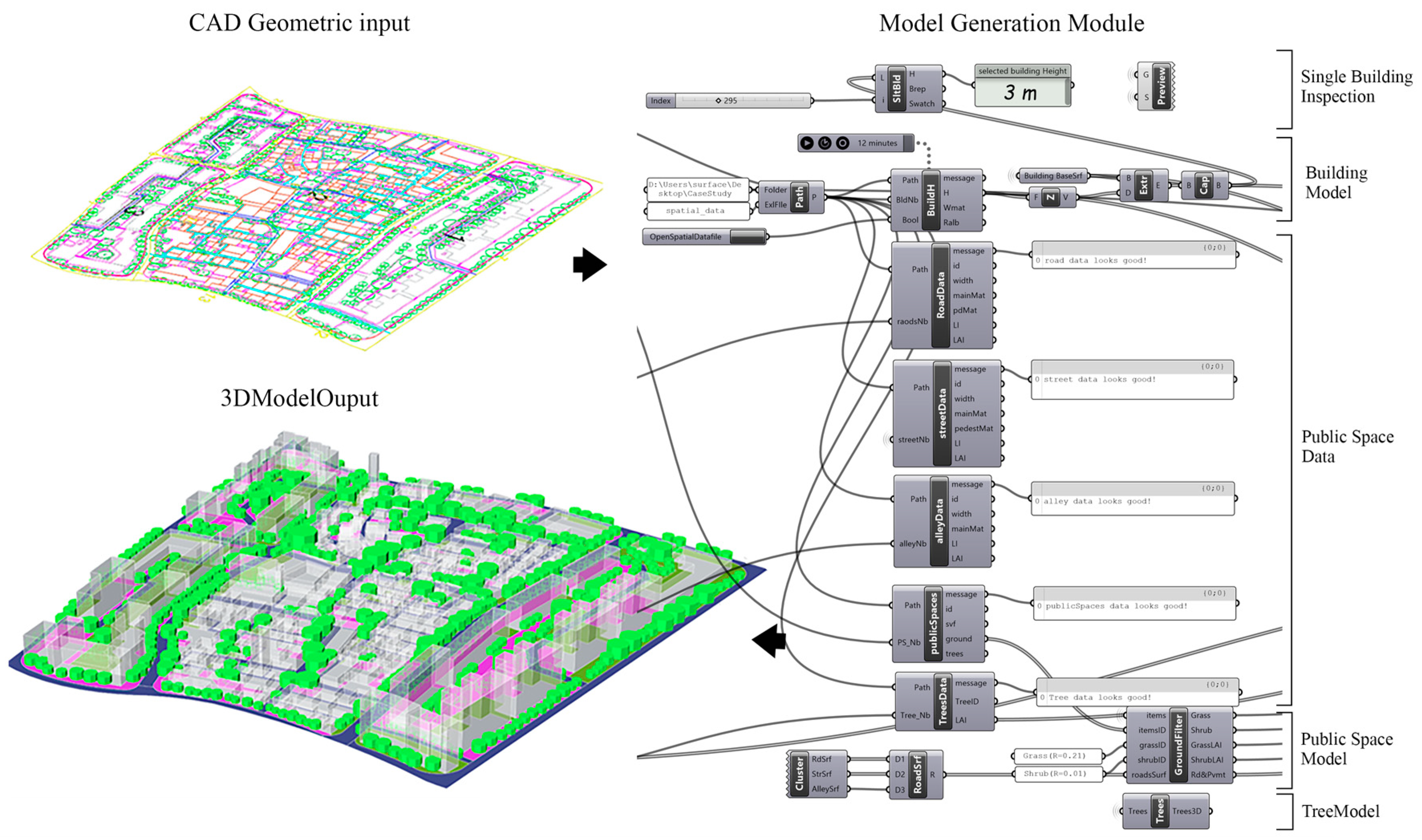
2.2.1. Model Preprocessing
- (1)
- CAD checking
- (2)
- 3D model generation:
- (3)
- Consistency verification:
- (4)
- Spatial information collection
2.2.2. Processing and Evaluation
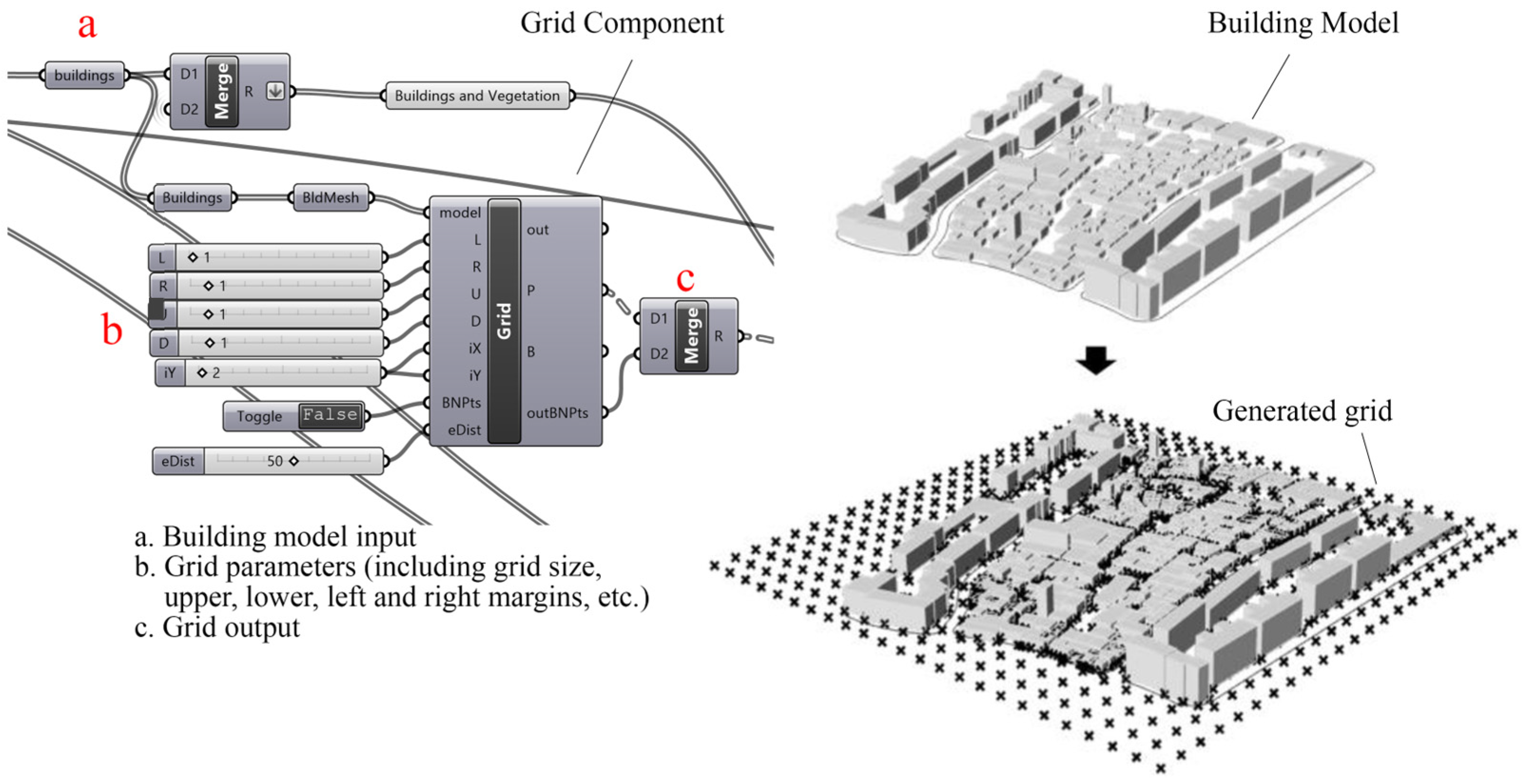
- (1)
- Calculation grid generation
- (2)
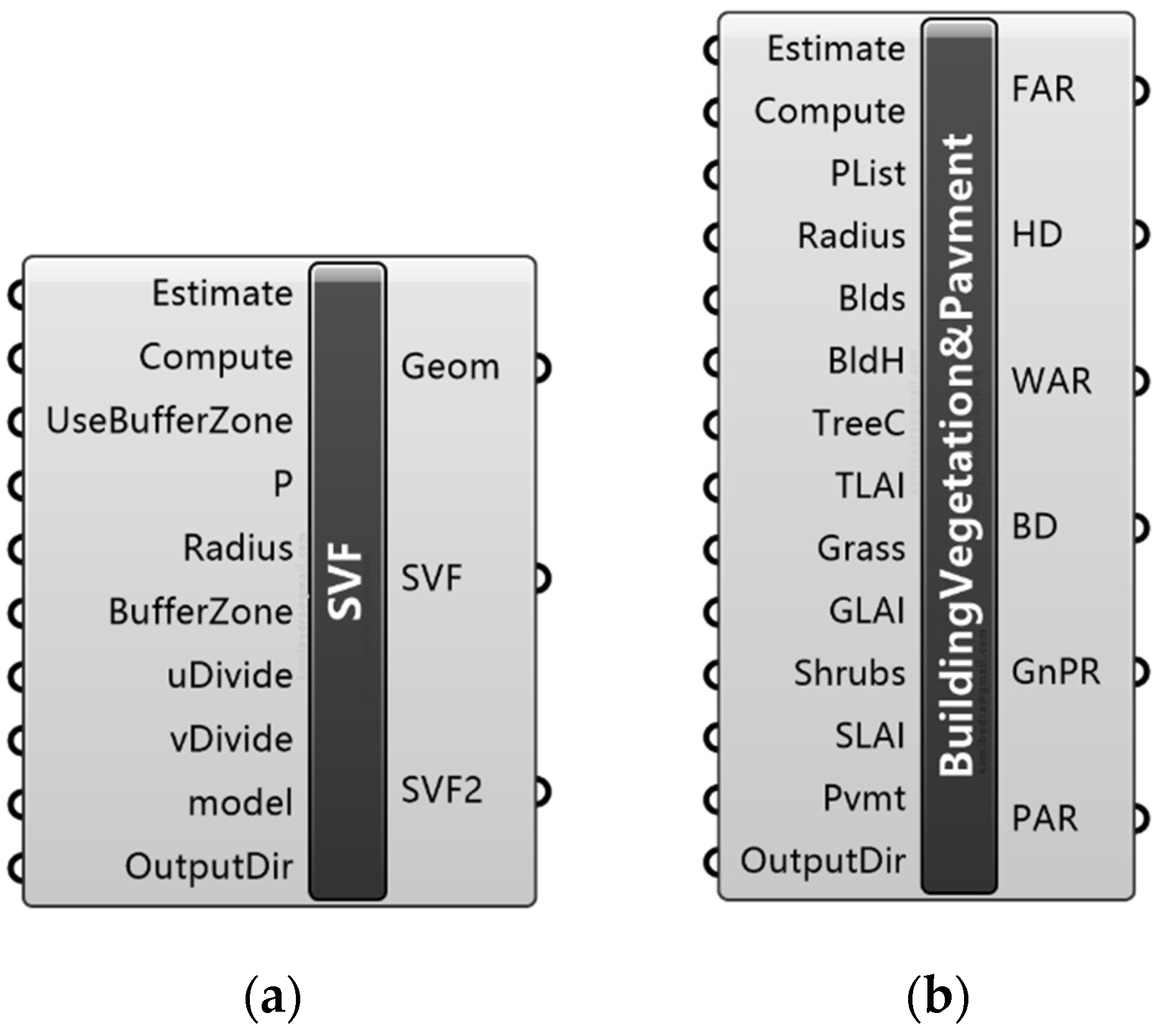
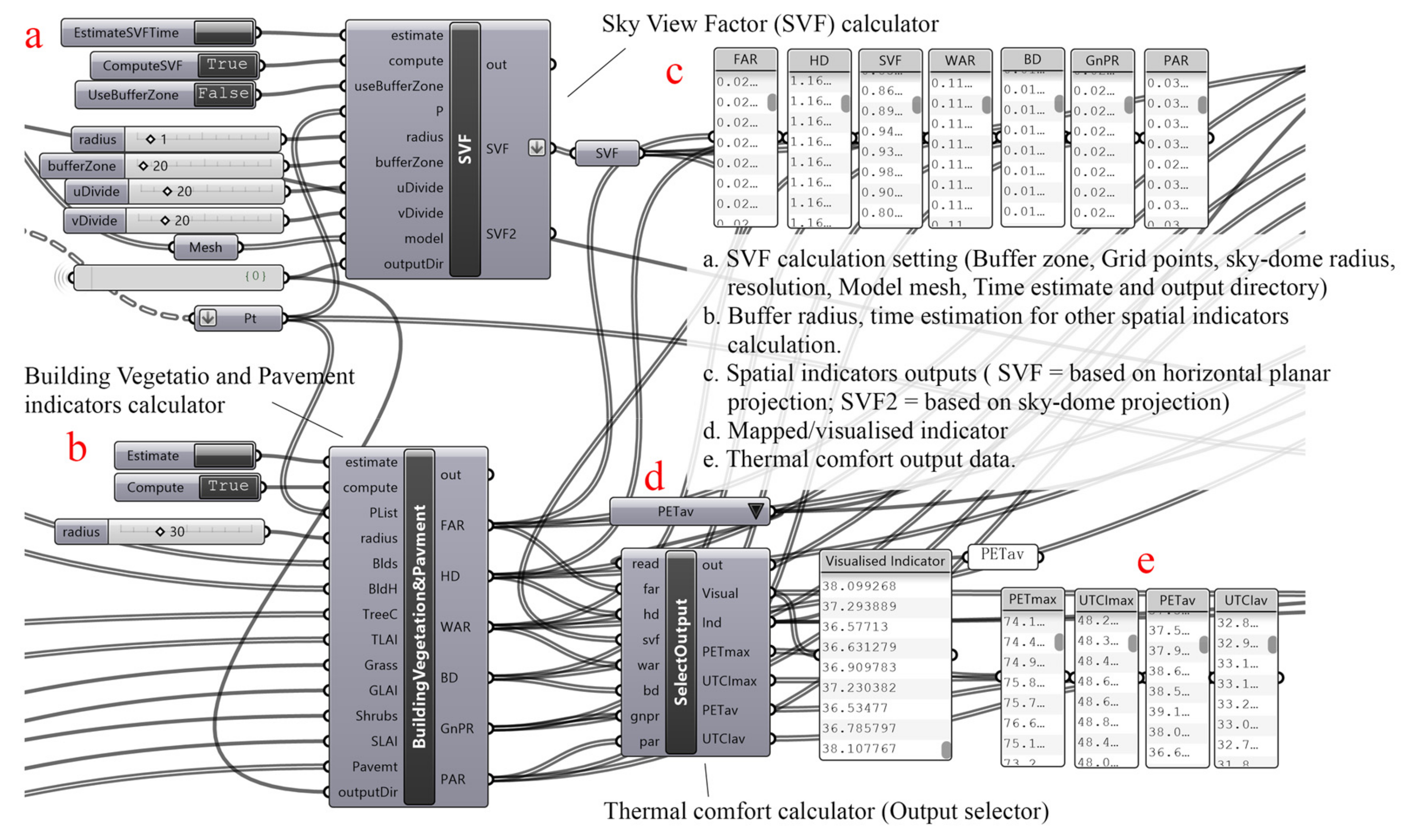
- Spatial indicators and thermal comfort evaluation
- 1.
- Spatial indicators
- 2.
- Thermal comfort evaluation
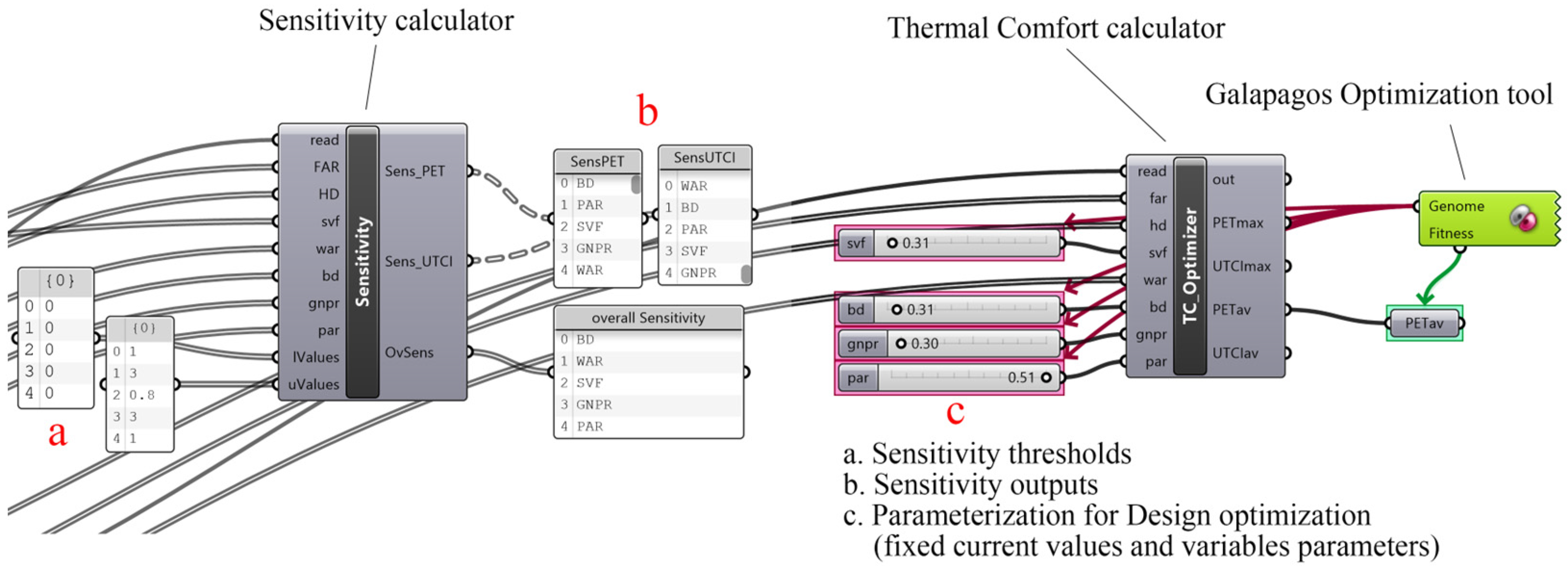
- Sensitivity analysis and thermal comfort optimization
2.2.3. Output Visualization
3. Implementation Case
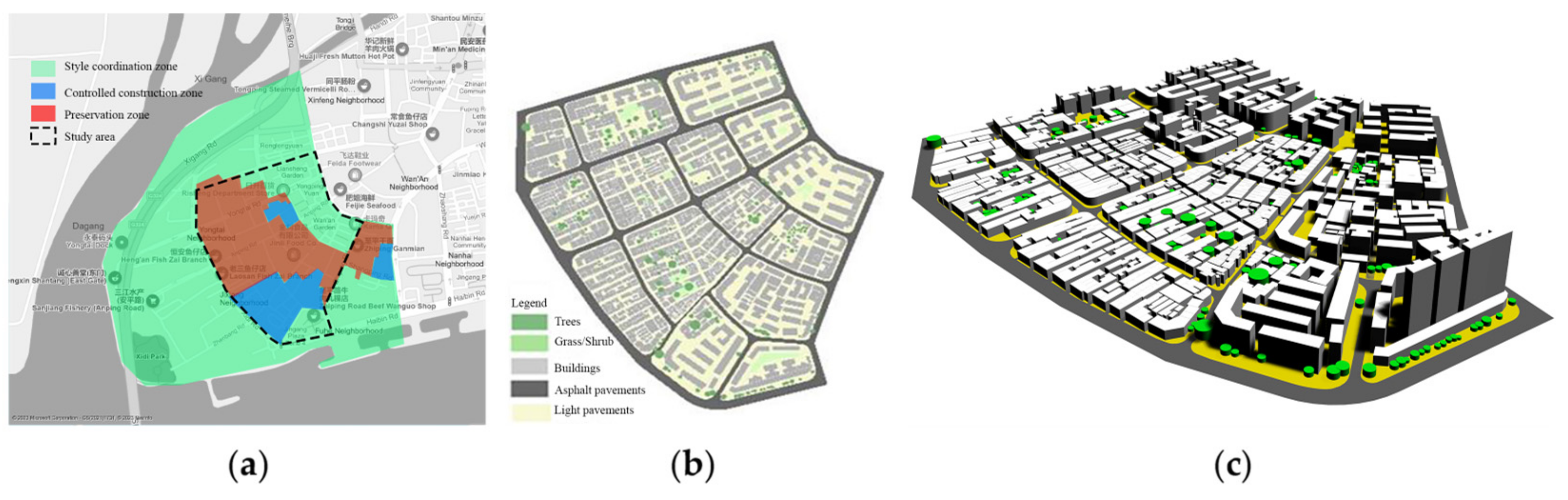
3.1. Area Location
3.2. Existing Stage
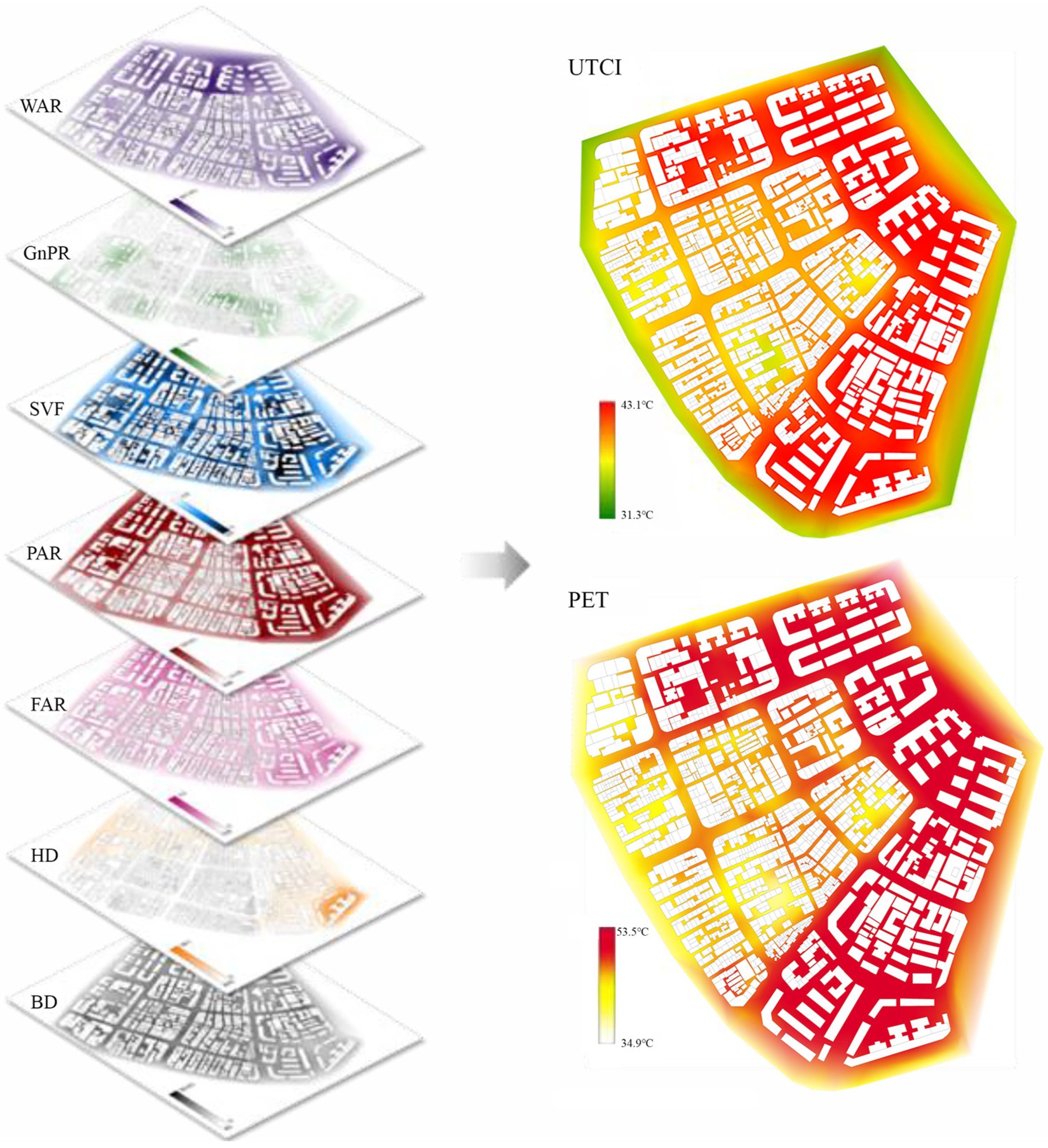
3.3. Spatial Descriptors and Thermal Comfort Outputs
3.4. Sensitivity Analysis and Optimization
3.4.1. Sensitivity Analysis
3.4.2. Optimization
3.5. Urban Model Optimization and Results
4. Discussions
4.1. Spatial Indicator Accuracy
4.2. Thermal Comfort Indicator Accuracy
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Validation of Thermal Comfort Estimation, Taking PET as an Example
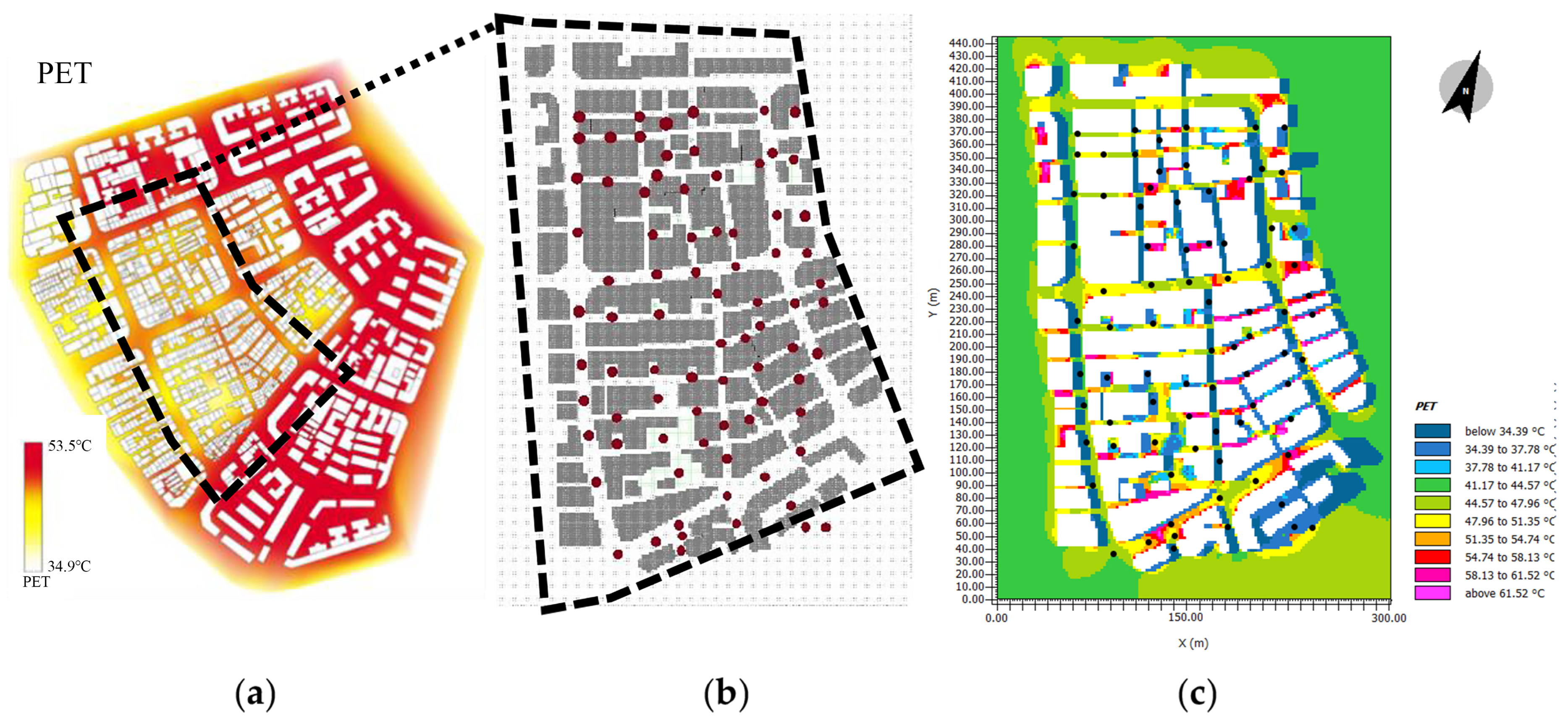
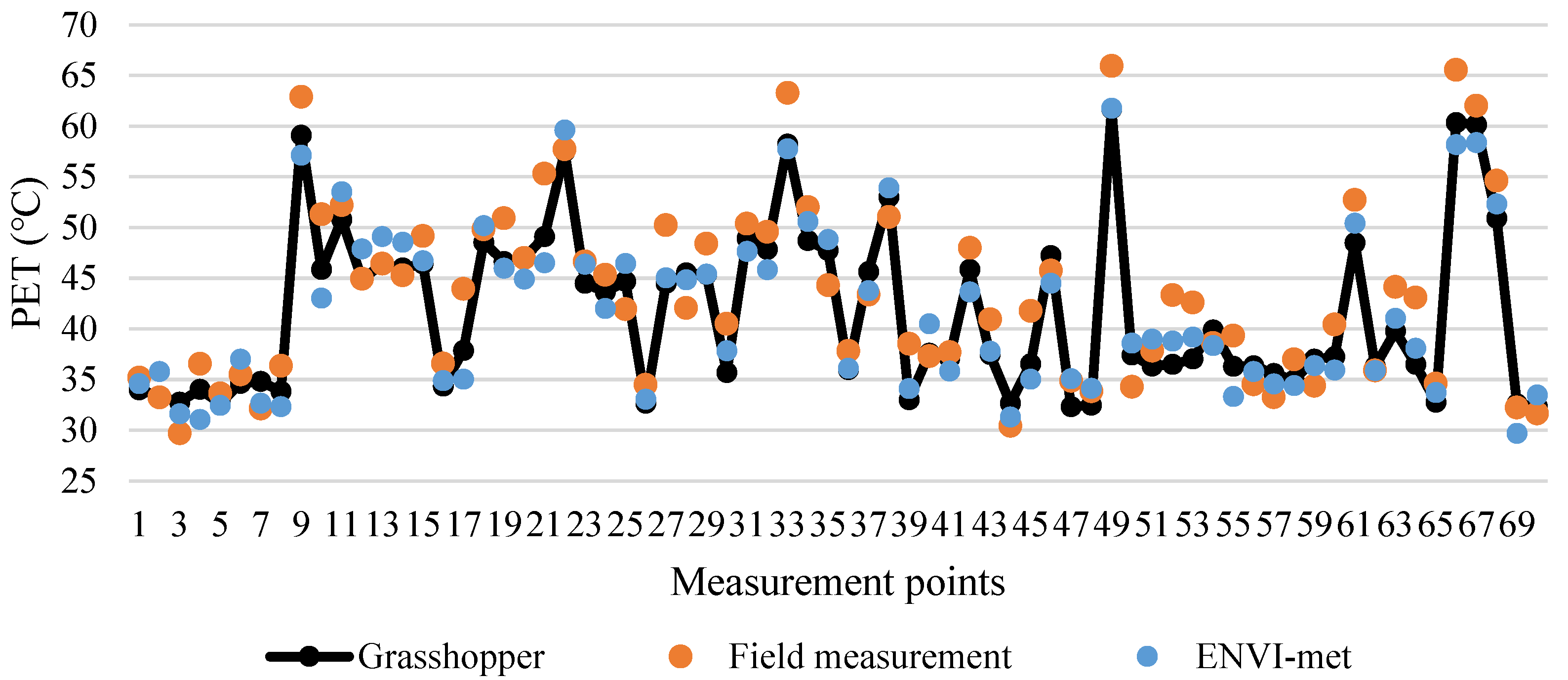
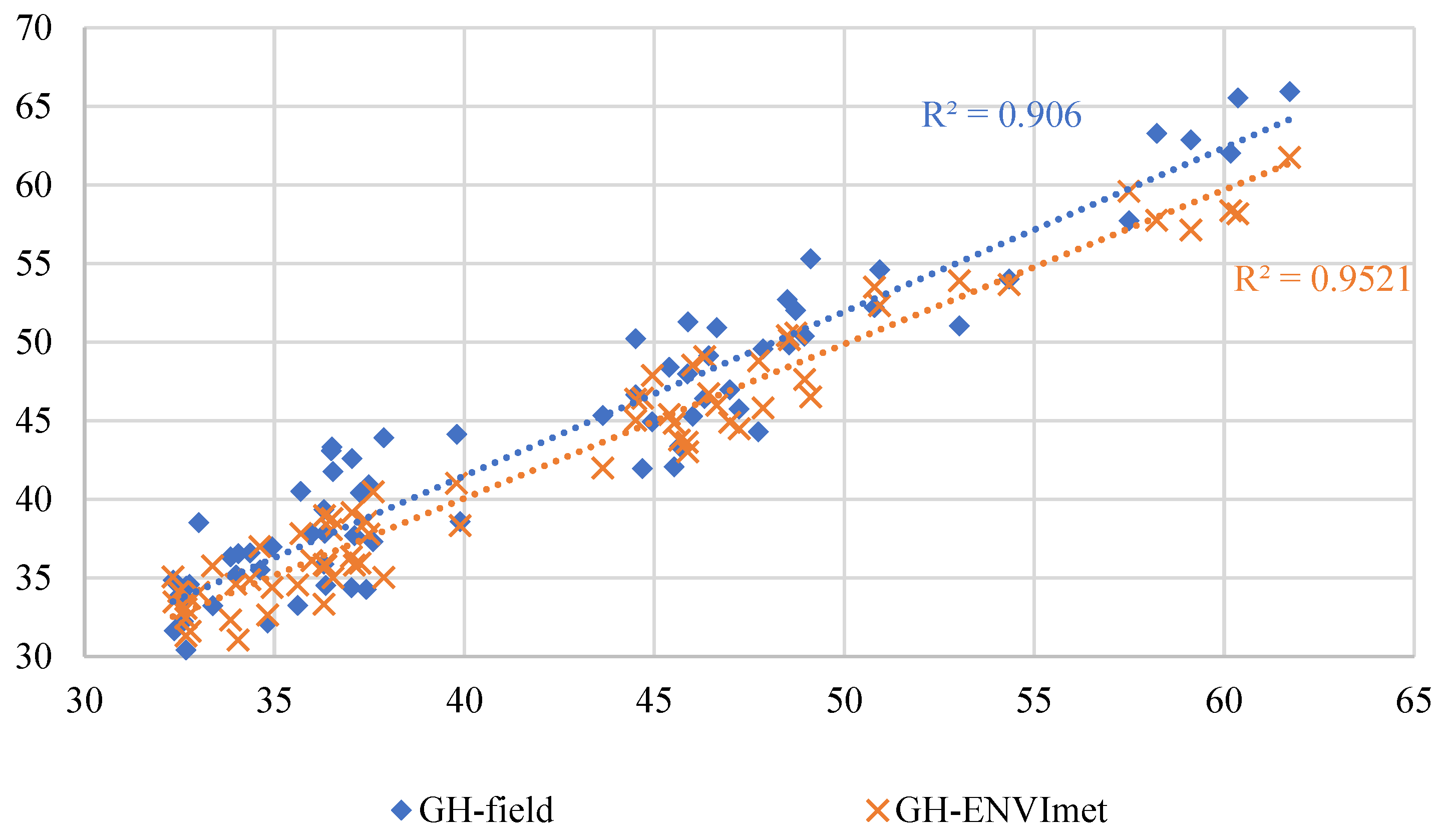
References
- Santamouris, M.; Papanikolaou, N.; Livada, I.; Koronakis, I.; Georgakis, C.; Argiriou, A.; Assimakopoulos, D. On the impact of urban climate on the energy consumption of buildings. Sol. Energy 2001, 70, 201–216. [Google Scholar] [CrossRef]
- Department of Economic and Social Affairs, Population Division, United Nations. World Urbanization Prospects: The 2018 Revision (ST/ESA/SER.A/420). New York, USA, 2019. Available online: https://population.un.org/wup/Publications/Files/WUP2018-Report.pdf (accessed on 4 December 2023).
- Natanian, J.; Aleksandrowicz, O.; Auer, T. A parametric approach to optimizing urban form, energy balance and environmental quality: The case of Mediterranean districts. Appl. Energy 2019, 254, 113637. [Google Scholar] [CrossRef]
- Allen, M.R.; Babiker, M.; Chen, Y.; de Coninck, H.; Connors, S.; van Diemen, R.; Dube, O.P.; Ebi, K.L.; Engelbrecht, F.; Ferrat, M.; et al. Summary for Policymakers. In Global Warming of 1.5 C; IPCC: Geneva, Switzerland, 2018. [Google Scholar]
- Pörtner, H.-O.; Roberts, D.C.; Tignor, M.M.B.; Poloczanska, E.; Mintenbeck, K.; Alegría, A.; Craig, M.; Langsdorf, S.; Loschke, S.; Moller, V.; et al. Climate Change 2022: Impacts, Adaptation and Vulnerability, Working Group II Contribution to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change. In Intergovernmental Panel on Climate Change 2022; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2022; p. 3056. [Google Scholar] [CrossRef]
- United Nations Framework Convention on Climate Change (UNFCCC). The Paris agreement. In Paris Climate Change Conference—November 2015; United Nations: Paris, France, 2016. [Google Scholar]
- Alonso, C.; Martín-Consuegra, F.; Oteiza, I.; Asensio, E.; Pérez, G.; Martínez, I.; Frutos, B. Effect of façade surface finish on building energy rehabilitation. Sol. Energy 2017, 146, 470–483. [Google Scholar] [CrossRef]
- Heaviside, C.; Macintyre, H.; Vardoulakis, S. The Urban Heat Island: Implications for Health in a Changing Environment. Curr. Environ. Health Rep. 2017, 4, 296–305. [Google Scholar] [CrossRef]
- McMichael, A.J.; Wilcox, B.A. Climate Change, Human Health, and Integrative Research: A Transformative Imperative. Ecohealth 2009, 6, 163–164. [Google Scholar] [CrossRef]
- Deilami, K.; Kamruzzaman, M.; Liu, Y. Urban heat island effect: A systematic review of spatio-temporal factors, data, methods, and mitigation measures. Int. J. Appl. Earth Obs. Geoinf. 2018, 67, 30–42. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y.; Yu, S.; Jia, G.; Li, H.; Li, W. Urban heat island impacts on building energy consumption: A review of approaches and findings. Energy 2019, 174, 407–419. [Google Scholar] [CrossRef]
- Williams, S.; Nitschke, M.; Weinstein, P.; Pisaniello, D.L.; Parton, K.A.; Bi, P. The impact of summer temperatures and heatwaves on mortality and morbidity in Perth, Australia 1994–2008. Environ. Int. 2012, 40, 33–38. [Google Scholar] [CrossRef]
- Lowe, S.A. An energy and mortality impact assessment of the urban heat island in the US. Environ. Impact Assess. Rev. 2016, 56, 139–144. [Google Scholar] [CrossRef]
- Jamei, E.; Ossen, D.; Seyedmahmoudian, M.; Sandanayake, M.; Stojcevski, A.; Horan, B. Urban design parameters for heat mitigation in tropics. Renew. Sustain. Energy Rev. 2020, 134, 110362. [Google Scholar] [CrossRef]
- Lin, P.; Gou, Z.; Lau, S.S.-Y.; Qin, H. The Impact of Urban Design Descriptors on Outdoor Thermal Environment: A Literature Review. Energies 2017, 10, 2151. [Google Scholar] [CrossRef]
- Adelia, A.S.; Nevat, I.; Acero, J.A.; Li, S.; Ruefenacht, L. Tool Comparison for Urban Microclimate Modelling; Technical Report. D1.2.4.1; ETH Library, ETH Zürich: Zürich, Switzerland, 2020. [Google Scholar] [CrossRef]
- Stavrakakis, G.M.; Katsaprakakis, D.A.; Damasiotis, M. Basic Principles, Most Common Computational Tools, and Capabilities for Building Energy and Urban Microclimate Simulations. Energies 2021, 14, 6707. [Google Scholar] [CrossRef]
- Toparlar, Y.; Blocken, B.; Maiheu, B.; van Heijst, G. A review on the CFD analysis of urban microclimate. Renew. Sustain. Energy Rev. 2017, 80, 1613–1640. [Google Scholar] [CrossRef]
- Wong, N.H.; Jusuf, S.K.; Tan, C.L. Integrated urban microclimate assessment method as a sustainable urban development and urban design tool. Landsc. Urban Plan. 2011, 100, 386–389. [Google Scholar] [CrossRef]
- Caetano, I.; Leitão, A. Architecture meets computation: An overview of the evolution of computational design approaches in architecture. Arch. Sci. Rev. 2019, 63, 165–174. [Google Scholar] [CrossRef]
- Nazzarri, G.; Bier, H. Towards Circular Economy in Architecture by Means of Data-driven Design-to-Robotic-Production. In Proceedings of the 37th International Symposium on Automation and Robotics in Construction, ISARC 2020: From Demonstration to Practical Use—To New Stage of Construction Robot, Kitakyushu, Japan, 27–28 October 2020; pp. 63–66. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, G.; Yao, J.; Wang, X.; Calautit, J.K.; Zhao, C.; An, N.; Peng, X. Accelerated environmental performance-driven urban design with generative adversarial network. Build. Environ. 2022, 224, 109575. [Google Scholar] [CrossRef]
- Shi, X.; Yang, W. Performance-driven architectural design and optimization technique from a perspective of architects. Autom. Constr. 2013, 32, 125–135. [Google Scholar] [CrossRef]
- Morgareidge, D.; Cai, H.; Jia, J. Performance-driven design with the support of digital tools: Applying discrete event simulation and space syntax on the design of the emergency department. Front. Arch. Res. 2014, 3, 250–264. [Google Scholar] [CrossRef]
- Lam, C.K.C.; Lee, H.; Yang, S.-R.; Park, S. A review on the significance and perspective of the numerical simulations of outdoor thermal environment. Sustain. Cities Soc. 2021, 71, 102971. [Google Scholar] [CrossRef]
- Taleghani, M.; Kleerekoper, L.; Tenpierik, M.; van den Dobbelsteen, A. Outdoor thermal comfort within five different urban forms in the Netherlands. Build. Environ. 2015, 83, 65–78. [Google Scholar] [CrossRef]
- Yang, Y.; Gatto, E.; Gao, Z.; Buccolieri, R.; Morakinyo, T.E.; Lan, H. The “plant evaluation model” for the assessment of the impact of vegetation on outdoor microclimate in the urban environment. Build. Environ. 2019, 159, 106151. [Google Scholar] [CrossRef]
- López-Cabeza, V.P.; Galán-Marín, C.; Rivera-Gómez, C.; Roa-Fernández, J. Courtyard microclimate ENVI-met outputs deviation from the experimental data. Build. Environ. 2018, 144, 129–141. [Google Scholar] [CrossRef]
- Bruse, M. ENVI-met 3.0: Updated Model Overview. 2004. Available online: www.envi-met.com (accessed on 29 September 2022).
- Elraouf, R.A.; Elmokadem, A.; Megahed, N.; Eleinen, O.A.; Eltarabily, S. Evaluating urban outdoor thermal comfort: A validation of ENVI-met simulation through field measurement. J. Build. Perform. Simul. 2022, 15, 268–286. [Google Scholar] [CrossRef]
- Caetano, I.; Santos, L.; Leitão, A. Computational design in architecture: Defining parametric, generative, and algorithmic design. Front. Arch. Res. 2020, 9, 287–300. [Google Scholar] [CrossRef]
- Michelle, B.; Gemilang, M.P. Bibliometric Analysis of Generative Design, Algorithmic Design, and Parametric Design in Architecture. J. Artif. Intell. Arch. 2022, 1, 30–40. [Google Scholar] [CrossRef]
- Frazer, J. Parametric Computation: History and Future. Arch. Des. 2016, 86, 18–23. [Google Scholar] [CrossRef]
- Schumacher, P. Parametricism: A New Global Style for Architecture and Urban Design. Arch. Des. 2009, 79, 14–23. [Google Scholar] [CrossRef]
- Delmas, A.; Donn, M.; Grosdemouge, V.; Musy, M.; Garde, F. Towards Context & Climate Sensitive Urban Design: An Integrated Simulation and Parametric Design Approach. 2018, p. 1706655. Available online: https://hal.archives-ouvertes.fr/hal-01706655 (accessed on 29 September 2022).
- Fink, T.; Koenig, R. Integrated Parametric Urban Design in Grasshopper/Rhinoceros 3D. In Demonstrated on a Master Plan in Vienna, Architecture in the Age of the 4th Industrial Revolution—Proceedings of the 37th ECAADe and 23rd SIGraDi Conference—Volume 3, University of Porto, Porto, Portugal, 11–13 September 2019; Sousa, J.P., Xavier, J.P., Castro Henriques, G., Eds.; 2019; Volume 3, pp. 313–322. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, W.; Wong, N.H.; Ignatius, M. Combining CityGML files and data-driven models for microclimate simulations in a tropical city. Build. Environ. 2020, 185, 107314. [Google Scholar] [CrossRef]
- Elwy, I.; Ibrahim, Y.; Fahmy, M.; Mahdy, M. Outdoor microclimatic validation for hybrid simulation workflow in hot arid climates against ENVI-met and field measurements. Energy Procedia 2018, 153, 29–34. [Google Scholar] [CrossRef]
- Elwy, I.; Ibrahim, Y.; Fahmy, M.; Mahdy, M. Validation of outdoor microclimate simulation for hot arid regions using a parametric workflow. In The International Conference on Civil and Architecture Engineering, Architectural Engineering Department, Military Technical College, Cairo, Egypt; Military Technical College: Cairo, Egypt, 2018; Volume 12, pp. 1–11. [Google Scholar] [CrossRef]
- Kamel, T.M. A new comprehensive workflow for modelling outdoor thermal comfort in Egypt. Sol. Energy 2021, 225, 162–172. [Google Scholar] [CrossRef]
- Gardner, N.; Haeusler, M.; Yu, D. Parametricising Sound for Early-Stage Design: An Information Design Problem? Euronoise 2021, Madrid, Portugal, 25–27 October 2021. Available online: https://documentacion.sea-acustica.es/publicaciones/Madeira21/ID212.pdf (accessed on 4 December 2023).
- Allam, S.Z. Analogous Framework for Passive Design Strategies Using Synchronized Techniques; Validation: Dual-Skin Voronoi Pattern Façade. In Proceedings of the 2019 3rd International Conference on Smart Grid and Smart Cities ICSGSC, Berkeley, CA, USA, 25–28 June 2019; pp. 158–164. [Google Scholar] [CrossRef]
- Wang, X. Using CityGML EnergyADE Data in Honeybee. 2020. Available online: https://repository.tudelft.nl/islandora/object/uuid%3Afb35db7c-9af8-488c-8d0b-263b138d8fd3 (accessed on 29 September 2022).
- Mirzabeigi, S.; Razkenari, M. Design optimization of urban typologies: A framework for evaluating building energy performance and outdoor thermal comfort. Sustain. Cities Soc. 2022, 76, 103515. [Google Scholar] [CrossRef]
- Xu, X.; Yin, C.; Wang, W.; Xu, N.; Hong, T.; Li, Q. Revealing Urban Morphology and Outdoor Comfort through Genetic Algorithm-Driven Urban Block Design in Dry and Hot Regions of China. Sustainability 2019, 11, 3683. [Google Scholar] [CrossRef]
- Amina, N.; Fatiha, B. The using of generative algorithm aided design tool (Rhinoceros/Grasshopper/Ladybug) to control solar access in urban street of hot-arid climate (Ouargla). Revue EL-Bahith En Sciences Humaines et Sociales 2021, 13, 473–486. Available online: https://www.asjp.cerist.dz/en/downArticle/119/13/1/149365 (accessed on 4 December 2023).
- Touloupaki, E.; Theodosiou, T. Performance Simulation Integrated in Parametric 3D Modeling as a Method for Early Stage Design Optimization—A Review. Energies 2017, 10, 637. [Google Scholar] [CrossRef]
- Perini, K.; Chokhachian, A.; Dong, S.; Auer, T. Modeling and simulating urban outdoor comfort: Coupling ENVI-Met and TRNSYS by grasshopper. Energy Build. 2017, 152, 373–384. [Google Scholar] [CrossRef]
- Natanian, J.; Kastner, P.; Dogan, T.; Auer, T. From energy performative to livable Mediterranean cities: An annual outdoor thermal comfort and energy balance cross-climatic typological study. Energy Build. 2020, 224, 110283. [Google Scholar] [CrossRef]
- Koenig, R.; Knecht, K.; Miao, Y. The Development of Optimization Methods in Generative Urban Design: A Review. 2020. Available online: https://www.researchgate.net/publication/344460745 (accessed on 29 September 2022).
- Shi, Z.; Fonseca, J.A.; Schlueter, A. A review of simulation-based urban form generation and optimization for energy-driven urban design. Build. Environ. 2017, 121, 119–129. [Google Scholar] [CrossRef]
- Omid, H.; Golabchi, M. Survey of parametric optimization plugins in Rhinoceros used in contemporary architectural design. In Proceedings of the Fourth International Conference on Modern Research in Civil Engineering, Architecture, Urban Management and Environment, Karaj, Iran, 21 May 2019; Volume 17. [Google Scholar]
- Ibrahim, Y.; Kershaw, T.; Shepherd, P.; Elkady, H. Multi-objective optimisation of urban courtyard blocks in hot arid zones. Sol. Energy 2022, 240, 104–120. [Google Scholar] [CrossRef]
- Abdollahzadeh, N.; Biloria, N. Outdoor thermal comfort: Analyzing the impact of urban configurations on the thermal performance of street canyons in the humid subtropical climate of Sydney. Front. Arch. Res. 2021, 10, 394–409. [Google Scholar] [CrossRef]
- El Dallal, N.; Visser, F. A climate responsive urban design tool: A platform to improve energy efficiency in a dry hot climate. Int. J. Sustain. Energy 2015, 36, 738–753. [Google Scholar] [CrossRef]
- Duering, S.; Chronis, A.; Koenig, R. Optimizing Urban Systems: Integrated Optimization of Spatial Configurations. In Proceedings of the SimAUD, Society for Modeling & Simulation International (SCS), Vienna, Austria, 25–27 May 2020; Available online: http://simaud.org/2020/proceedings/109.pdf (accessed on 29 September 2022).
- Zhai, Y.; Riederer, E. Context Specific Evolutionary Design: An Analysis on Computational Abstraction of Modern Urban Complexity. In SimAUD’20: Proceedings of the 11th Annual Symposium on Simulation for Architecture and Urban Design, May 2020; Article No. 62; pp. 1–8. Available online: https://dl.acm.org/doi/abs/10.5555/3465085.3465147 (accessed on 4 December 2023).
- Nagy, D.; Villaggi, L.; Benjamin, D. Generative Urban Design: Integrating Financial and Energy Goals for Automated Neighborhood Layout. In Proceedings of the SimAUD, Society for Modeling & Simulation International (SCS), Delft, The Netherlands, 4–7 June 2018. [Google Scholar]
- Taleb, H.; Musleh, M.A. Applying urban parametric design optimisation processes to a hot climate: Case study of the UAE. Sustain. Cities Soc. 2015, 14, 236–253. [Google Scholar] [CrossRef]
- Brook-Lawson, J.; Holz, S. CFD Comparison Project for Wind Simulation in Landscape Architecture. Full Pap. J. Digit. Landsc. Archit. 2020, 5, 318–329. [Google Scholar] [CrossRef]
- Kastner, P.; Dogan, T. Eddy3D: A toolkit for decoupled outdoor thermal comfort simulations in urban areas. Build. Environ. 2022, 212, 108639. [Google Scholar] [CrossRef]
- Hong, T.; Lee, S.H.; Piette, M.A.; Chen, Y.; Piette, M.A. CityBES: A Web-based Platform to Support City-Scale Building Energy Efficiency. Urban Comput. 2016, 14, 2016. [Google Scholar] [CrossRef]
- Behboudi, N.; Butt, F.; Abhari, A. Automatic building design with genetic algorithms and artificial neural networks (WIP). In Proceedings of the 2012 Symposium on Simulation for Architecture and Urban Design, Orlando, FL, USA, 26–30 March 2012; Article 7. pp. 1–4. Available online: https://dl.acm.org/doi/abs/10.5555/2339453.2339460 (accessed on 4 December 2023).
- Liu, W.; Lian, Z.; Zhao, B. A neural network evaluation model for individual thermal comfort. Energy Build. 2007, 39, 1115–1122. [Google Scholar] [CrossRef]
- Artificial Neural Networks Based Prediction for Thermal Comfort in An Academic Classroom|IEEE Conference Publication|IEEE Xplore, (n.d.). Available online: https://ieeexplore.ieee.org/abstract/document/6828926 (accessed on 30 September 2022).
- Li, N.; Yu, W.; Li, B. Assessing Adaptive Thermal Comfort Using Artificial Neural Networks in Naturally-Ventilated Buildings. Int. J. Vent. 2012, 11, 205–218. [Google Scholar] [CrossRef]
- Wang, B.; Yi, Y.K. Developing an adapted UTCI (Universal Thermal Climate Index) for the elderly population in China’s severe cold climate region. Sustain. Cities Soc. 2021, 69, 102813. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F.; Fung, A.S.; Raahemifar, K. Artificial neural network (ANN) based model predictive control (MPC) and optimization of HVAC systems: A state of the art review and case study of a residential HVAC system. Energy Build. 2017, 141, 96–113. [Google Scholar] [CrossRef]
- Yoon, H.-J.; Lee, D.-S.; Cho, H.; Jo, J.-H. Prediction of Thermal Environment in a Large Space Using Artificial Neural Network. Energies 2018, 11, 418. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, D.; Shi, L. Thermal-comfort optimization design method for semi-outdoor stadium using machine learning. Build. Environ. 2022, 215, 108890. [Google Scholar] [CrossRef]
- Tabadkani, A.; Aghasizadeh, S.; Banihashemi, S.; Hajirasouli, A. Courtyard design impact on indoor thermal comfort and utility costs for residential households: Comparative analysis and deep-learning predictive model. Front. Arch. Res. 2022, 11, 963–980. [Google Scholar] [CrossRef]
- Fard, Z.Q.; Zomorodian, Z.S.; Korsavi, S.S. Application of machine learning in thermal comfort studies: A review of methods, performance and challenges. Energy Build. 2022, 256, 111771. [Google Scholar] [CrossRef]
- Simon, H.; Lindén, J.; Hoffmann, D.; Braun, P.; Bruse, M.; Esper, J. Modeling transpiration and leaf temperature of urban trees—A case study evaluating the microclimate model ENVI-met against measurement data. Landsc. Urban Plan. 2018, 174, 33–40. [Google Scholar] [CrossRef]
- Adilkhanova, I.; Ngarambe, J.; Yun, G.Y. Recent advances in black box and white-box models for urban heat island prediction: Implications of fusing the two methods. Renew. Sustain. Energy Rev. 2022, 165, 112520. [Google Scholar] [CrossRef]
- Matzarakis, A.; Rutz, F.; Mayer, H. Modelling radiation fluxes in simple and complex environments: Basics of the RayMan model. Int. J. Biometeorol. 2010, 54, 131–139. [Google Scholar] [CrossRef]
- Zheng, B.; Bedra, K.B.; Zheng, J.; Wang, G. Combination of Tree Configuration with Street Configuration for Thermal Comfort Optimization under Extreme Summer Conditions in the Urban Center of Shantou City, China. Sustainability 2018, 10, 4192. [Google Scholar] [CrossRef]



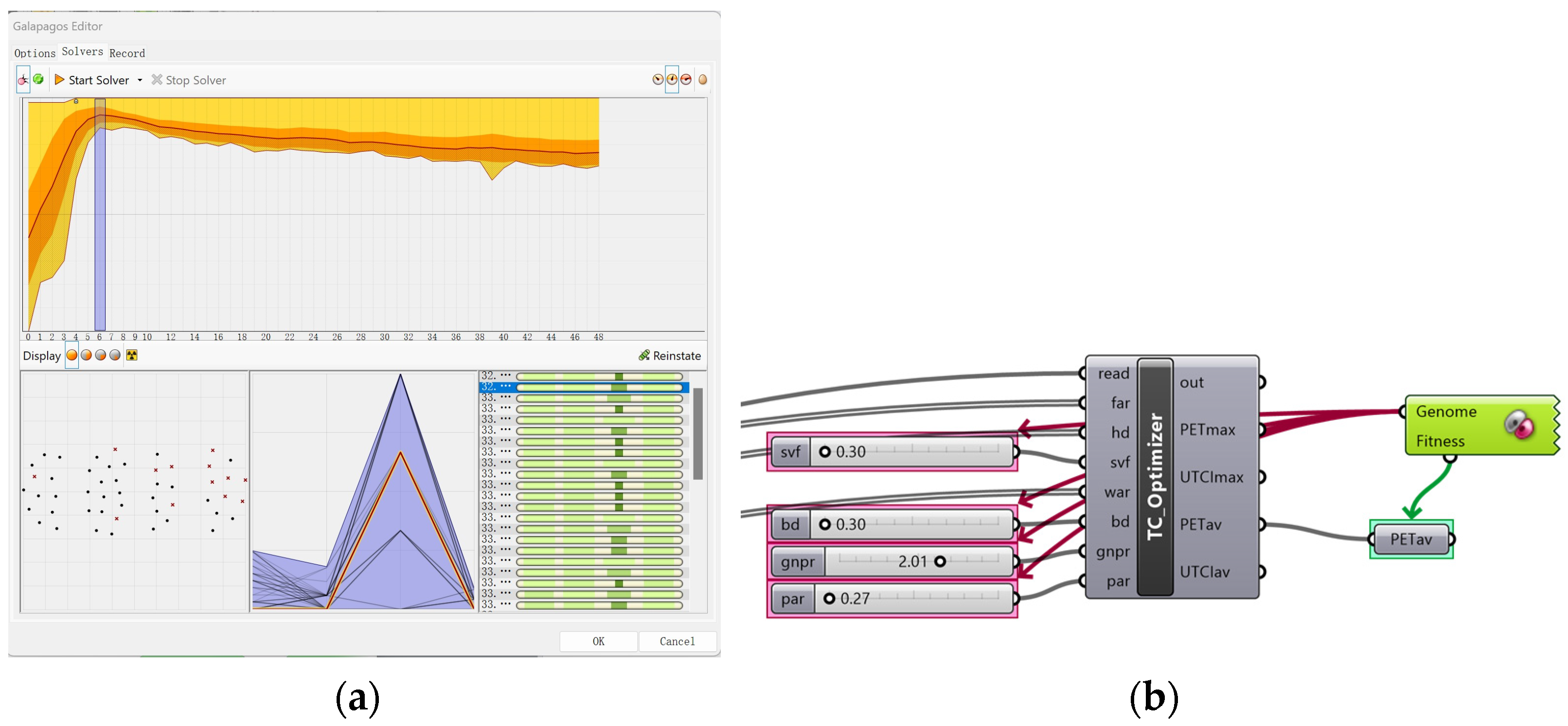


| Index | Calculation Method |
|---|---|
| Floor Area Ratio (FAR) | |
| Building Density (BD) | |
| Height Deviation of Buildings (HD) | |
| Sky View Factor (SVF) | In Rhino–Grasshopper, rays are emitted in all directions from the measurement point and the number of rays that are not blocked by buildings is counted. |
| Wall Area Ratio (WAR) | |
| Pavement Area Ratio (PAR) | |
| Green Plot Ratio (GnPR) |
| Ranking | Spatial Indicators | Sensitivity to PET | Sensitivity to UTCI |
|---|---|---|---|
| 1 | PAR | 21.3368 | 14.1912 |
| 2 | BD | 17.2726 | 11.5060 |
| 3 | GNPR | 08.4517 | 05.7009 |
| 4 | SVF | 08.3681 | 04.6764 |
| 5 | FAR | 04.4758 | 02.8764 |
| 6 | WAR | 02.6979 | 01.6986 |
| 7 | HD | 01.0103 | 00.6343 |
| Elements | Description |
|---|---|
| Hardware | Model: HP Pavilion Gaming Desktop TG01-1XXX Processor: Intel®/core (TM) i7-10700F CPU @ 2.9 GHz, 2.9 GHz, 8, 16 core System: Windows10 Family edition, x64 Memory: 16.0 GB |
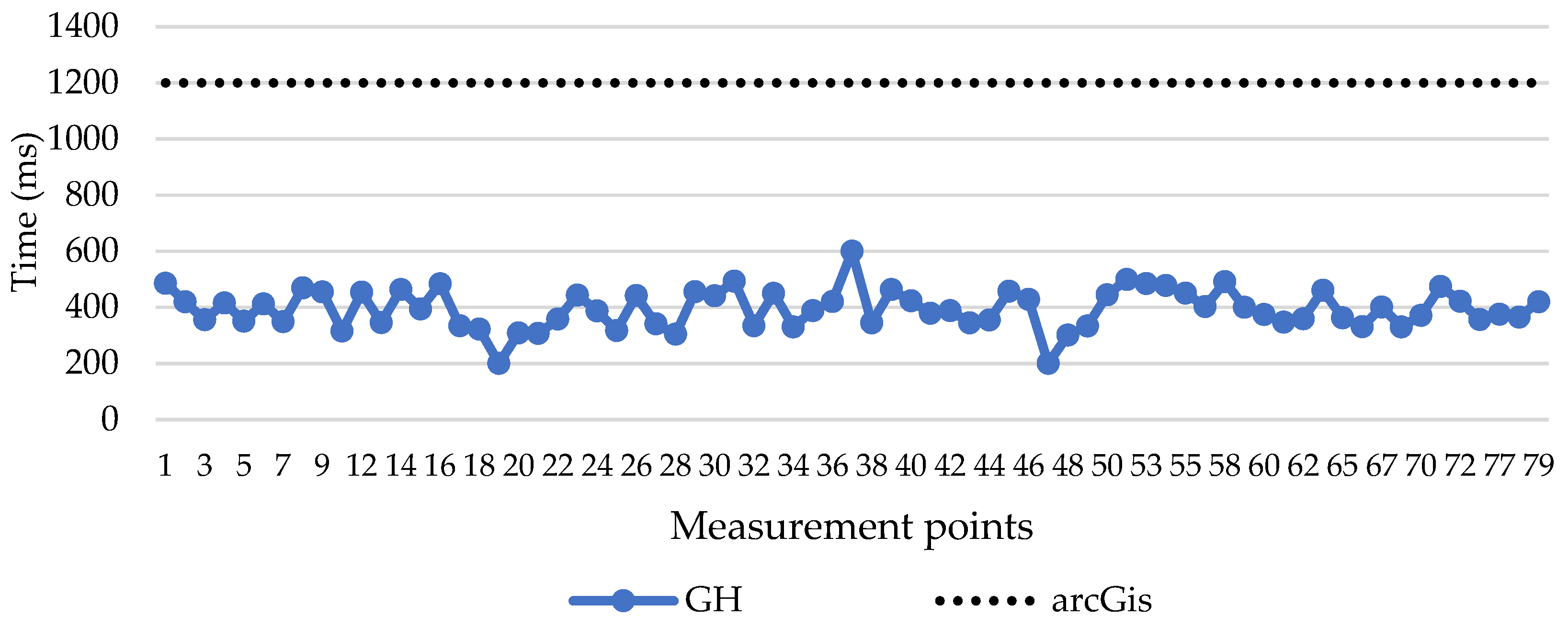
| Software | Rhino 7 vs. ArcGIS10.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bedra, K.B.; Zheng, J.; Li, J.; Sun, Z.; Zheng, B. Automating Microclimate Evaluation and Optimization during Urban Design: A Rhino–Grasshopper Workflow. Sustainability 2023, 15, 16613. https://doi.org/10.3390/su152416613
Bedra KB, Zheng J, Li J, Sun Z, Zheng B. Automating Microclimate Evaluation and Optimization during Urban Design: A Rhino–Grasshopper Workflow. Sustainability. 2023; 15(24):16613. https://doi.org/10.3390/su152416613
Chicago/Turabian StyleBedra, Komi Bernard, Jian Zheng, Jiayu Li, Zhaoqian Sun, and Bohong Zheng. 2023. "Automating Microclimate Evaluation and Optimization during Urban Design: A Rhino–Grasshopper Workflow" Sustainability 15, no. 24: 16613. https://doi.org/10.3390/su152416613
APA StyleBedra, K. B., Zheng, J., Li, J., Sun, Z., & Zheng, B. (2023). Automating Microclimate Evaluation and Optimization during Urban Design: A Rhino–Grasshopper Workflow. Sustainability, 15(24), 16613. https://doi.org/10.3390/su152416613







