Application of Wavelet Transform for Bias Correction and Predictor Screening of Climate Data
Abstract
:1. Introduction
2. Materials and Methods
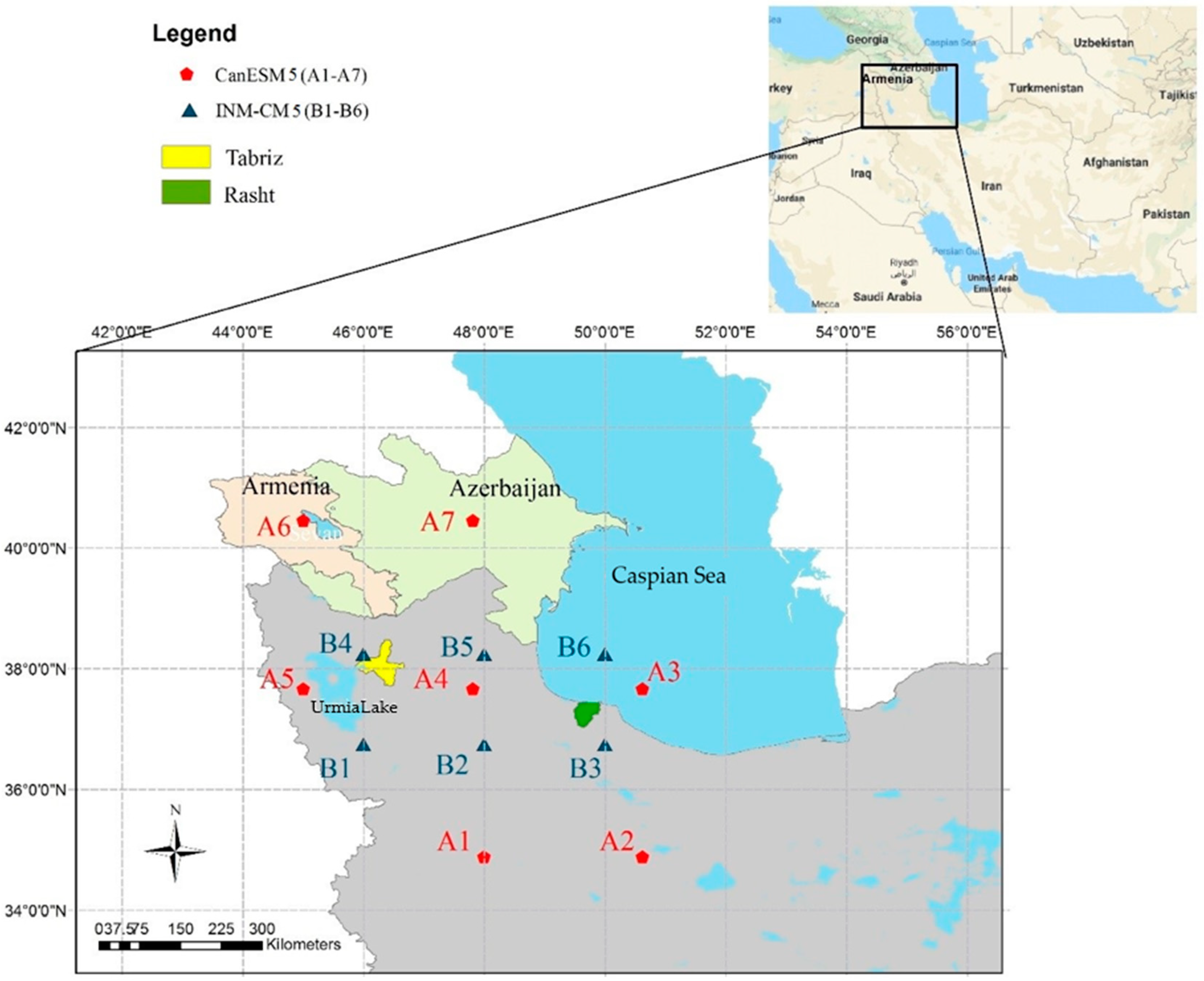
2.1. Study Area
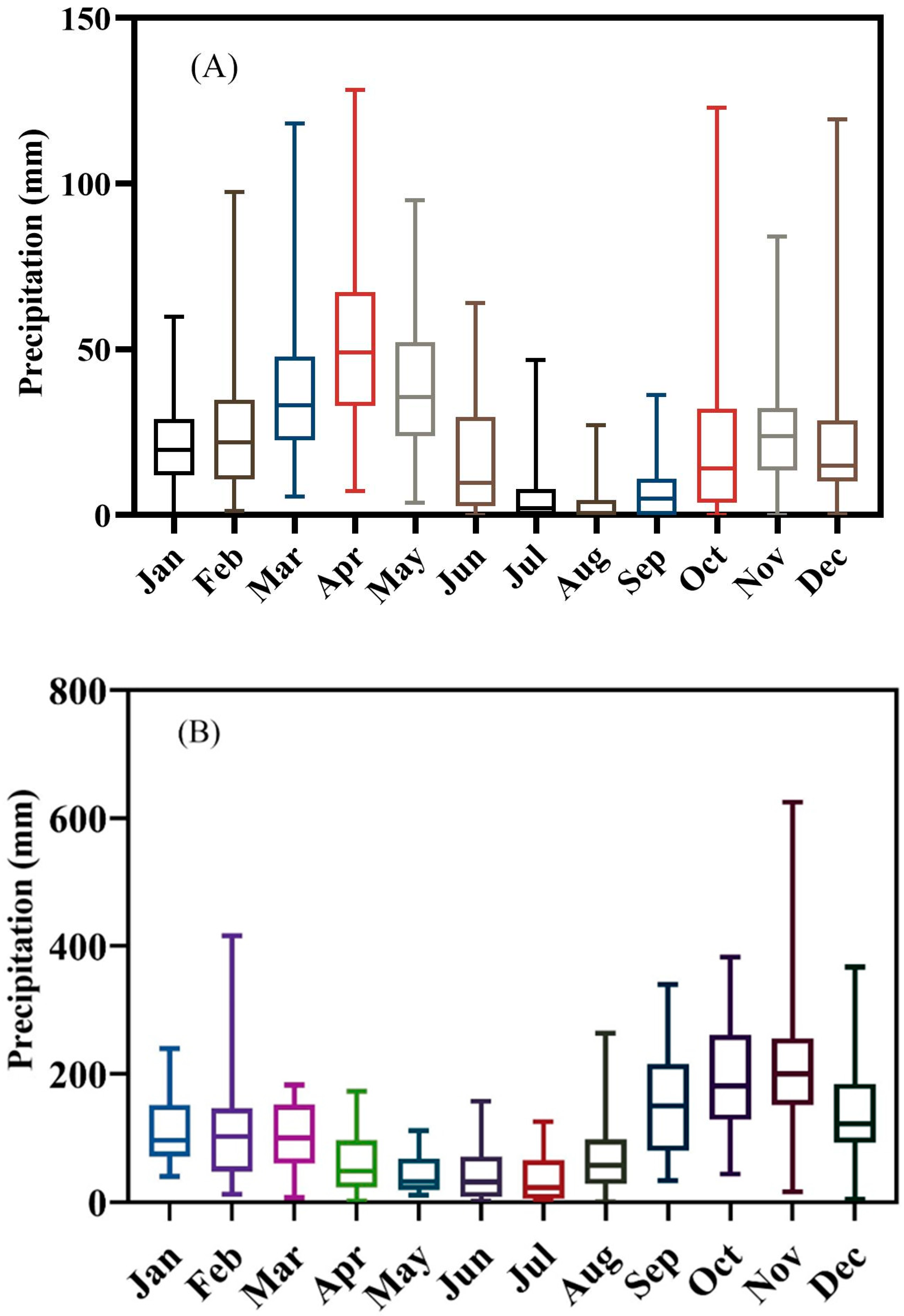
2.2. Applied Data
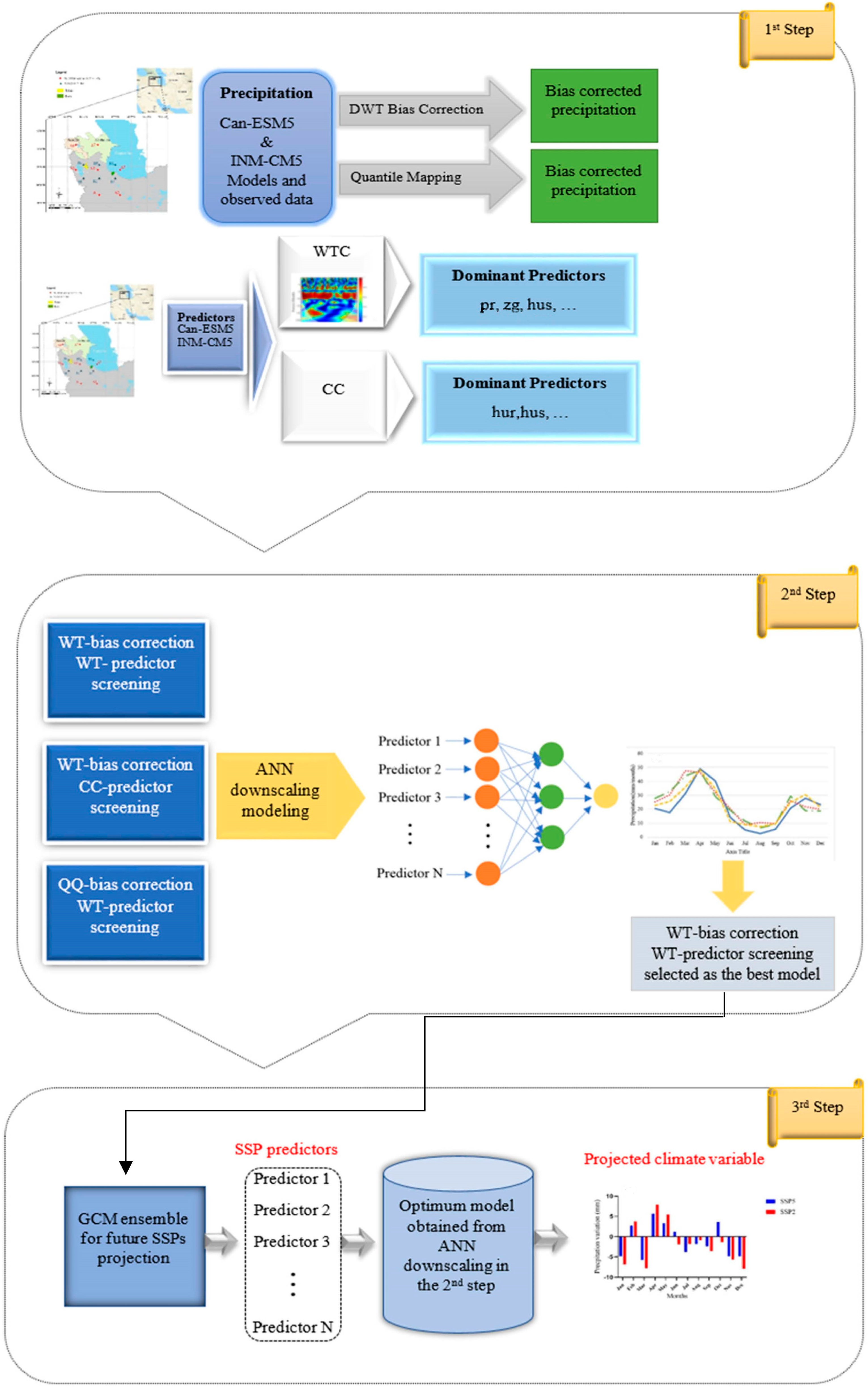
2.3. Proposed Methodology
2.3.1. First Step
2.3.2. Second Step
2.3.3. Third Step
2.4. Wavelet Analysis
2.5. Quantile Mapping (QM)
2.6. Artificial Neural Network (ANN)
3. Results and Discussion
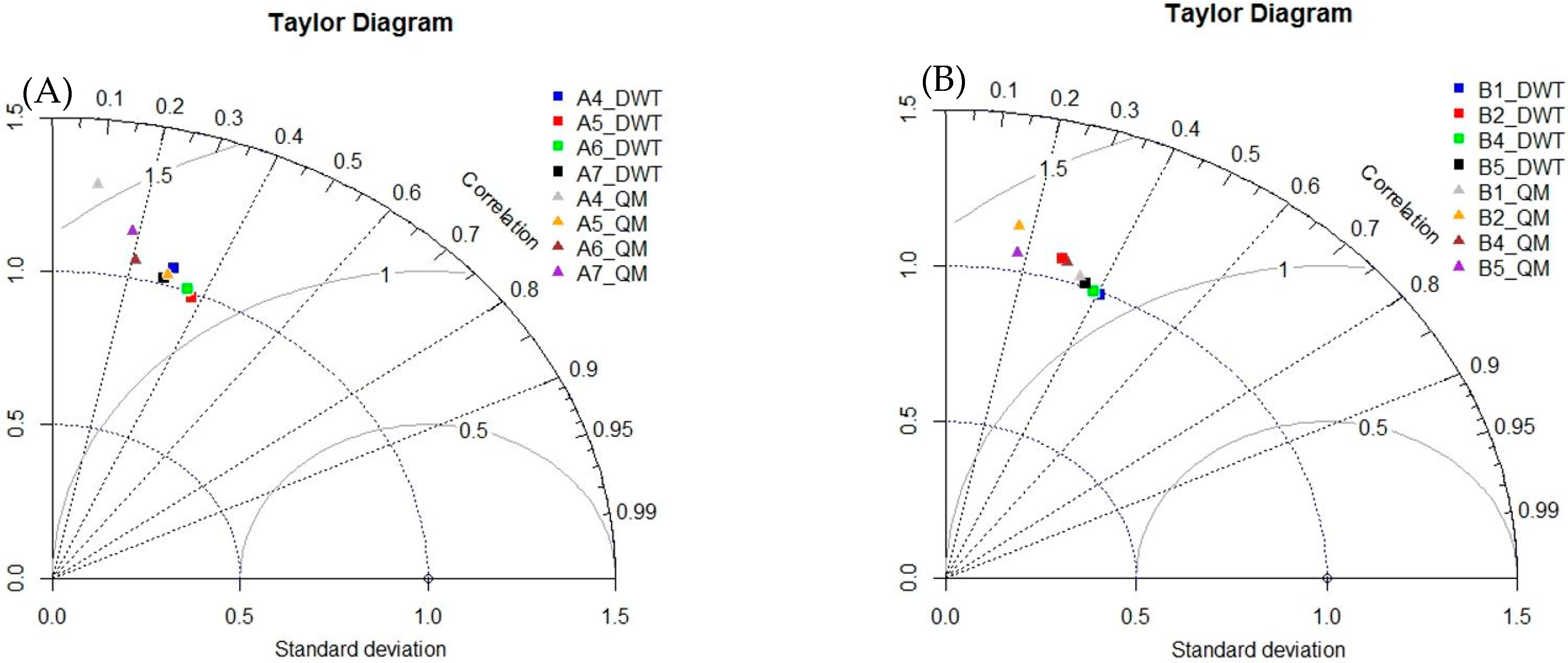
3.1. First Step—Bias Correction and Predictor Screening via WT
3.2. Second Step—ANN-Based Statistical Downscaling
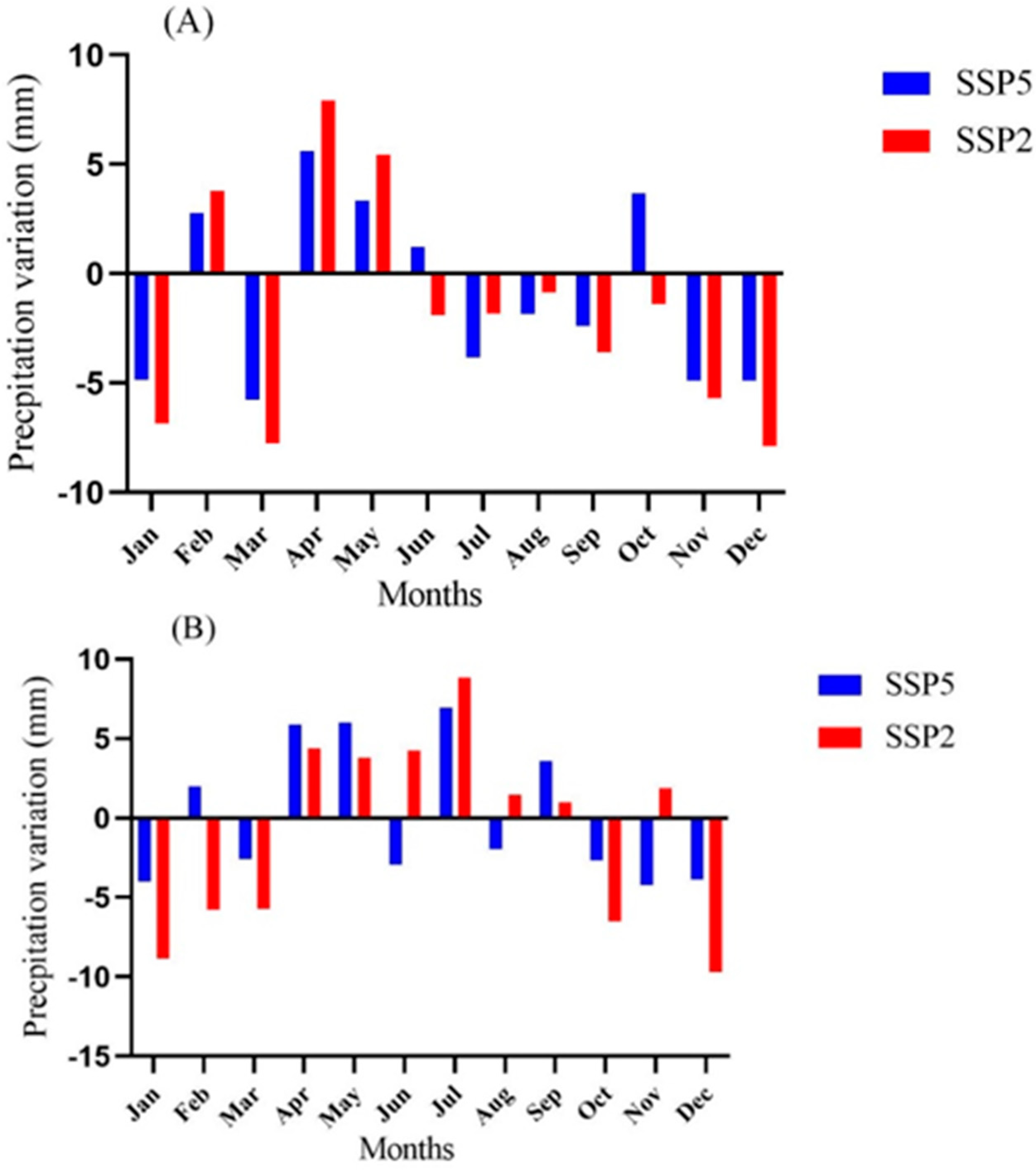
3.3. Third Step—Precipitation Projection
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wilby, R.; Wigley, T. Downscaling general circulation model output: A review of methods and limitations. Prog. Phys. Geogr. Earth Environ. 1997, 21, 530–548. [Google Scholar] [CrossRef]
- Timbal, B.; Dufour, A.; McAvaney, B. An estimate of future climate change for western France using a statistical downscaling technique. Clim. Dyn. 2003, 20, 807–823. [Google Scholar] [CrossRef]
- Pahlavan, H.A.; Zahraie, B.; Nasseri, M.; Varnousfaderani, A.M. Improvement of multiple linear regression method for statistical downscaling of monthly precipitation. Int. J. Environ. Sci. Technol. 2017, 15, 1897–1912. [Google Scholar] [CrossRef]
- Mohammad, N.; Moradkhani, H.; Susan, A.W. Statistical Downscaling of Precipitation Using Machine Learning with Optimal Predictor Selection. J. Hydrol. Eng. 2011, 16, 650–664. [Google Scholar]
- Sun, L.; Lan, Y. Statistical downscaling of daily temperature and precipitation over China using deep learning neural models: Localization and comparison with other methods. Int. J. Clim. 2020, 41, 1128–1147. [Google Scholar] [CrossRef]
- Hoai, N.D.; Udo, K.; Mano, A. Downscaling Global Weather Forecast Outputs Using ANN for Flood Prediction. J. Appl. Math. 2011, 2011, 246286. [Google Scholar]
- Harpham, C.; Wilby, R.L. Multi-site downscaling of heavy daily precipitation occurrence and amounts. J. Hydrol. 2005, 312, 235–255. [Google Scholar] [CrossRef]
- Tisseuil, C.; Vrac, M.; Lek, S.; Wade, A.J. Statistical downscaling of river flows. J. Hydrol. 2010, 385, 279–291. [Google Scholar] [CrossRef]
- Chadwick, R.; Coppola, E.; Giorgi, F. An artificial neural network technique for downscaling GCM outputs to RCM spatial scale. Nonlinear Process. Geophys. 2011, 18, 1013–1028. [Google Scholar] [CrossRef]
- Su, B.; Zeng, X.; Zhai, J.; Wang, Y.; Li, X. Projected precipitation and streamflow under SRES and RCP emission scenarios in the Songhuajiang River basin, China. Quat. Int. 2015, 380–381, 95–105. [Google Scholar] [CrossRef]
- Alotaibi, K.; Ghumman, A.R.; Haider, H.; Ghazaw, Y.M.; Shafiquzzaman, M. Future Predictions of Rainfall and Temperature Using GCM and ANN for Arid Regions: A Case Study for the Qassim Region, Saudi Arabia. Water 2018, 10, 1260. [Google Scholar] [CrossRef]
- Prathom, C.; Champrasert, P. General Circulation Model Downscaling Using Interpolation—Machine Learning Model Combination—Case Study: Thailand. Sustainability 2023, 15, 9668. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456–457, 12–29. [Google Scholar] [CrossRef]
- Feyissa, T.A.; Demissie, T.A.; Saathoff, F.; Gebissa, A. Evaluation of General Circulation Models CMIP6 Performance and Future Climate Change over the Omo River Basin, Ethiopia. Sustainability 2023, 15, 6507. [Google Scholar] [CrossRef]
- Eden, J.M.; Widmann, M.; Grawe, D.; Rast, S. Skill, Correction, and Downscaling of GCM-Simulated Precipitation. J. Clim. 2012, 25, 3970–3984. [Google Scholar] [CrossRef]
- Watanabe, S.; Kanae, S.; Seto, S.; Yeh, P.J.-F.; Hirabayashi, Y.; Oki, T. Intercomparison of bias-correction methods for monthly temperature and precipitation simulated by multiple climate models. J. Geophys. Res. Atmos. 2012, 117, 127261. [Google Scholar] [CrossRef]
- Cayan, D.R.; Maurer, E.P.; Dettinger, M.D.; Tyree, M.; Hayhoe, K. Climate change scenarios for the California region. Clim. Chang. 2008, 87, 21–42. [Google Scholar] [CrossRef]
- Rajczak, J.; Kotlarski, S.; Schär, C. Does Quantile Mapping of Simulated Precipitation Correct for Biases in Transition Probabilities and Spell Lengths? J. Clim. 2016, 29, 1605–1615. [Google Scholar] [CrossRef]
- Hassanzadeh, E.; Nazemi, A.; Adamowski, J.; Nguyen, T.-H.; Van-Nguyen, V.-T. Quantile-based downscaling of rainfall extremes: Notes on methodological functionality, associated uncertainty and application in practice. Adv. Water Resour. 2019, 131, 103371. [Google Scholar] [CrossRef]
- Gumus, B.; Oruc, S.; Yucel, I.; Yilmaz, M.T. Impacts of Climate Change on Extreme Climate Indices in Türkiye Driven by High-Resolution Downscaled CMIP6 Climate Models. Sustainability 2023, 15, 7202. [Google Scholar] [CrossRef]
- Bowden, G.J.; Dandy, G.C.; Maier, H.R. Input determination for neural network models in water resources applications. Part 1—Background and methodology. J. Hydrol. 2005, 301, 75–92. [Google Scholar] [CrossRef]
- Hertig, E.; Jacobeit, J. A novel approach to statistical downscaling considering nonstationarities: Application to daily precipitation in the Mediterranean area. J. Geophys. Res. Atmos. 2013, 118, 520–533. [Google Scholar] [CrossRef]
- Wang, W.-C.; Xu, D.-M.; Chau, K.-W.; Chen, S. Improved annual rainfall-runoff forecasting using PSO–SVM model based on EEMD. J. Hydroinform. 2013, 15, 1377–1390. [Google Scholar] [CrossRef]
- Ahmadi, A.; Han, D. Identification of dominant sources of sea level pressure for precipitation forecasting over Wales. J. Hydroinformatics 2012, 15, 1002–1021. [Google Scholar] [CrossRef]
- Sachindra, D.A.; Huang, F.; Barton, A.; Perera, B.J.C. Least square support vector and multi-linear regression for statistically downscaling general circulation model outputs to catchment streamflows. Int. J. Clim. 2013, 33, 1087–1106. [Google Scholar] [CrossRef]
- Okkan, U. Assessing the effects of climate change on monthly precipitation: Proposing of a downscaling strategy through a case study in Turkey. KSCE J. Civ. Eng. 2015, 19, 1150–1156. [Google Scholar] [CrossRef]
- Devak, M.; Dhanya, C.T. Downscaling of Precipitation in Mahanadi Basin, India Using Support Vector Machine, K-Nearest Neighbour and Hybrid of Support Vector Machine with K-Nearest Neighbour. In Geostatistical and Geospatial Approaches for the Characterization of Natural Resources in the Environment; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Baghanam, A.H.; Norouzi, E.; Nourani, V. Wavelet-based predictor screening for statistical downscaling of precipitation and temperature using the artificial neural network method. Hydrol. Res. 2022, 53, 385–406. [Google Scholar] [CrossRef]
- Rana, A.; Moradkhani, H. Spatial, temporal and frequency based climate change assessment in Columbia River Basin using multi downscaled-scenarios. Clim. Dyn. 2016, 47, 579–600. [Google Scholar] [CrossRef]
- Nguyen, H.; Mehrotra, R.; Sharma, A. Correcting for systematic biases in GCM simulations in the frequency domain. J. Hydrol. 2016, 538, 117–126. [Google Scholar] [CrossRef]
- Nourani, V.; Ghasemzade, M.; Mehr, A.D.; Sharghi, E. Investigating the effect of hydroclimatological variables on Urmia Lake water level using wavelet coherence measure. J. Water Clim. Chang. 2018, 10, 13–29. [Google Scholar] [CrossRef]
- Maraun, D.; Kurths, J. Cross wavelet analysis: Significance testing and pitfalls. Nonlinear Process. Geophys. 2004, 11, 505–514. [Google Scholar] [CrossRef]
- Jevrejeva, S.; Moore, J.C.; Grinsted, A. Influence of the Arctic Oscillation and El Niño-Southern Oscillation (ENSO) on ice conditions in the Baltic Sea: The wavelet approach. J. Geophys. Res. 2003, 108, 4677. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Ng, E.K.W.; Chan, J.C.L. Geophysical Applications of Partial Wavelet Coherence and Multiple Wavelet Coherence. J. Atmospheric Ocean. Technol. 2012, 29, 1845–1853. [Google Scholar] [CrossRef]
- Tamaddun, K.A.; Kalra, A.; Bernardez, M.; Ahmad, S. Multi-Scale Correlation between the Western U.S. Snow Water Equivalent and ENSO/PDO Using Wavelet Analyses. Water Resour. Manag. 2017, 31, 2745–2759. [Google Scholar] [CrossRef]
- Draper, N.R.; Smith, H. Applied Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1998; Volume 326. [Google Scholar]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of “goodness-of-fit” Measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Baghanam, A.H.; Vakili, A.T.; Nourani, V.; Dąbrowska, D.; Soltysiak, M. AI-based ensemble modeling of landfill leakage employing a lysimeter, climatic data and transfer learning. J. Hydrol. 2022, 612, 128243. [Google Scholar] [CrossRef]
- Nourani, V.; Ojaghi, A.; Zhang, Y. Saturated and unsaturated seepage analysis of earth-fill dams using fractal hydraulic conductivity function and its verification. J. Hydrol. 2022, 612, 128302. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing, 2nd ed.; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Labat, D. Cross wavelet analyses of annual continental freshwater discharge and selected climate indices. J. Hydrol. 2010, 385, 269–278. [Google Scholar] [CrossRef]
- Torrence, C. and G.P. Compo, A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Liu, P.C. Wavelet Spectrum Analysis and Ocean Wind Waves, in Wavelet Analysis and Its Applications; Foufoula-Georgiou, E., Kumar, P., Eds.; Academic Press: Cambridge, MA, USA, 1994; pp. 151–166. [Google Scholar]
- Torrence, C.; Webster, P.J. Interdecadal Changes in the ENSO–Monsoon System. J. Clim. 1999, 12, 2679–2690. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Bremnes, J.B.; Haugen, J.; Engen-Skaugen, T. Technical Note: Downscaling RCM precipitation to the station scale using statistical transformations—A comparison of methods. Hydrol. Earth Syst. Sci. 2012, 16, 3383–3390. [Google Scholar] [CrossRef]
- Haykin, S.; Network, N. A comprehensive foundation. Neural Netw. 2004, 2, 41. [Google Scholar]
- Maier, H.R.; Dandy, G.C. Neural networks for the prediction and forecasting of water resources variables: A review of modelling issues and applications. Environ. Model. Softw. 2000, 15, 101–124. [Google Scholar] [CrossRef]
- Yeganeh-Bakhtiary, A.; EyvazOghli, H.; Shabakhty, N.; Kamranzad, B.; Abolfathi, S. Machine Learning as a Downscaling Approach for Prediction of Wind Characteristics under Future Climate Change Scenarios. Complexity 2022, 2022, 8451812. [Google Scholar]
- Pachauri, R.K.; Allen, M.R.; Barros, V.R.; Broome, J.; Cramer, W.; Christ, R.; Church, J.A.; Clarke, L.; Dahe, Q.; Dasgupta, P.; et al. Climate Change 2014: Synthesis Report; Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Pachauri, R.K., Meyer, L., Eds.; IPCC: Geneva, Switzerland, 2014; p. 151. [Google Scholar]

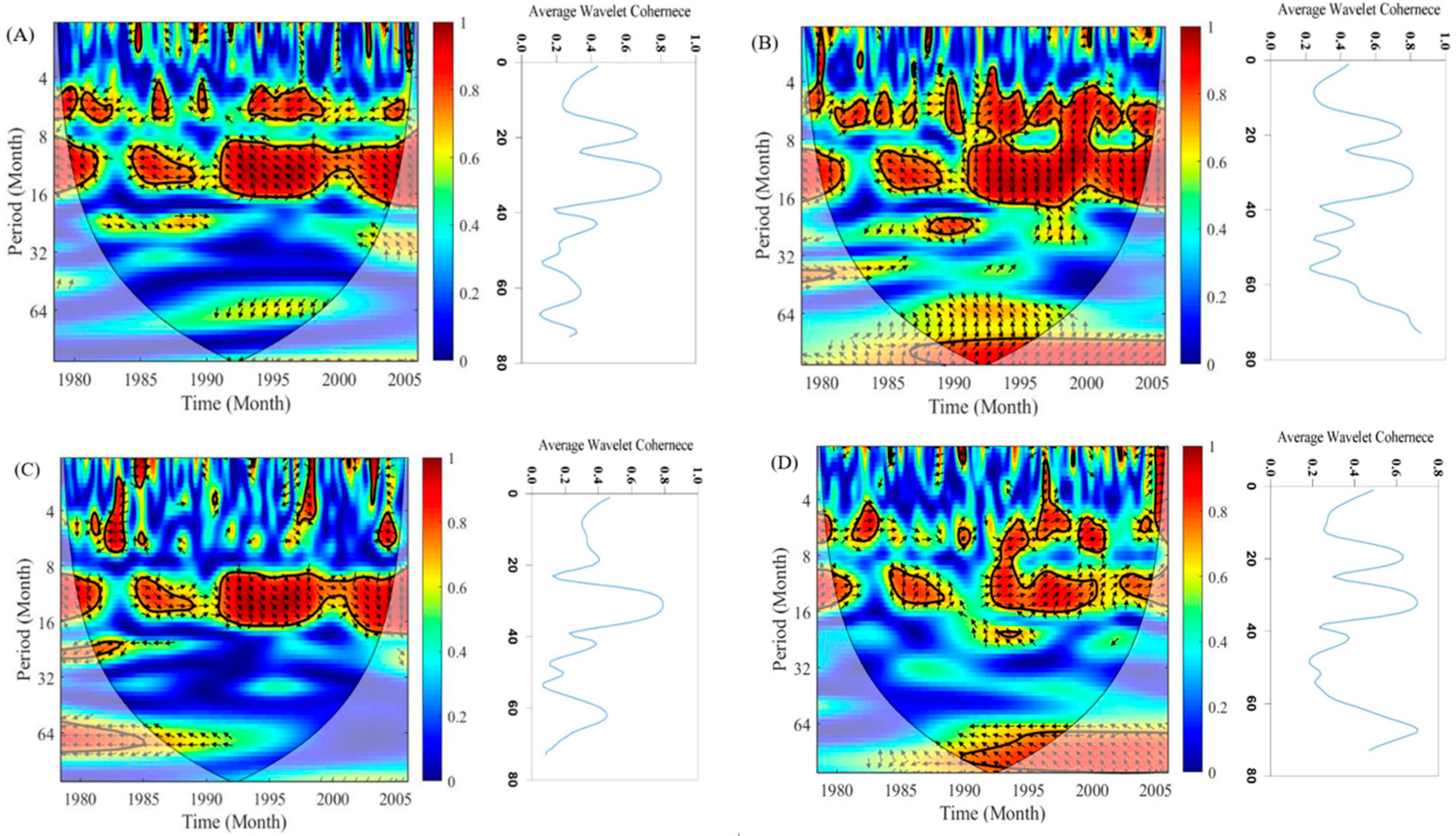
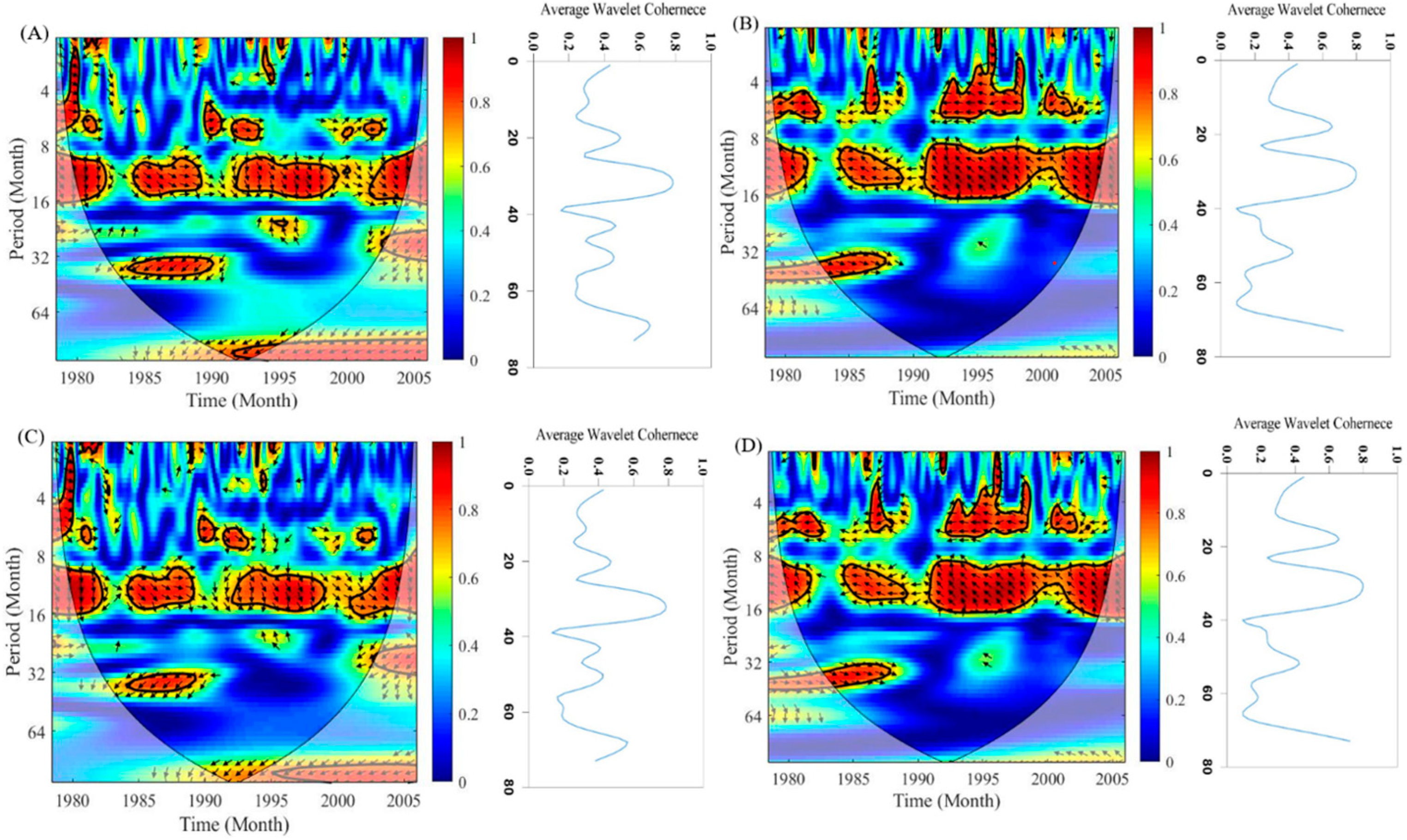
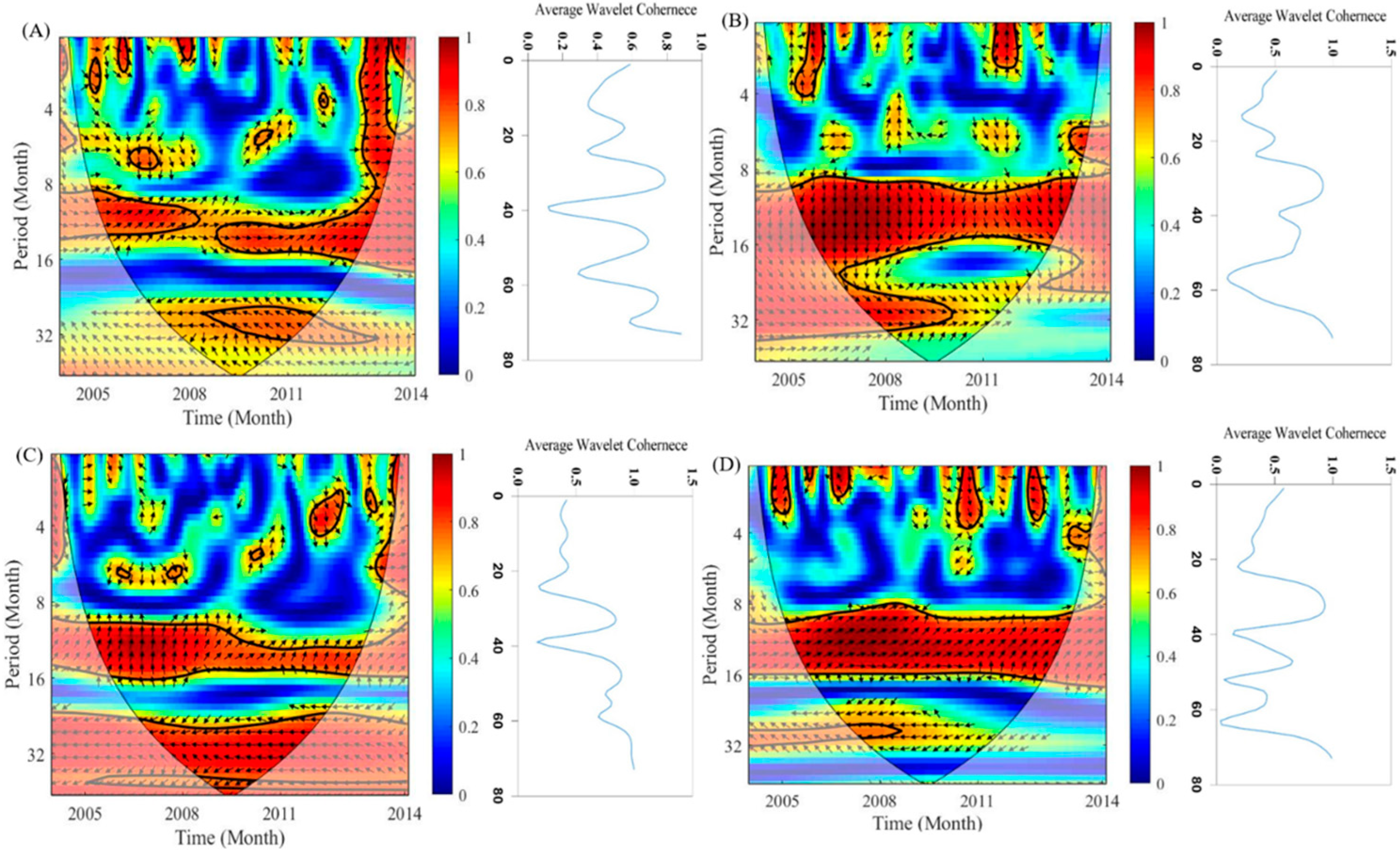
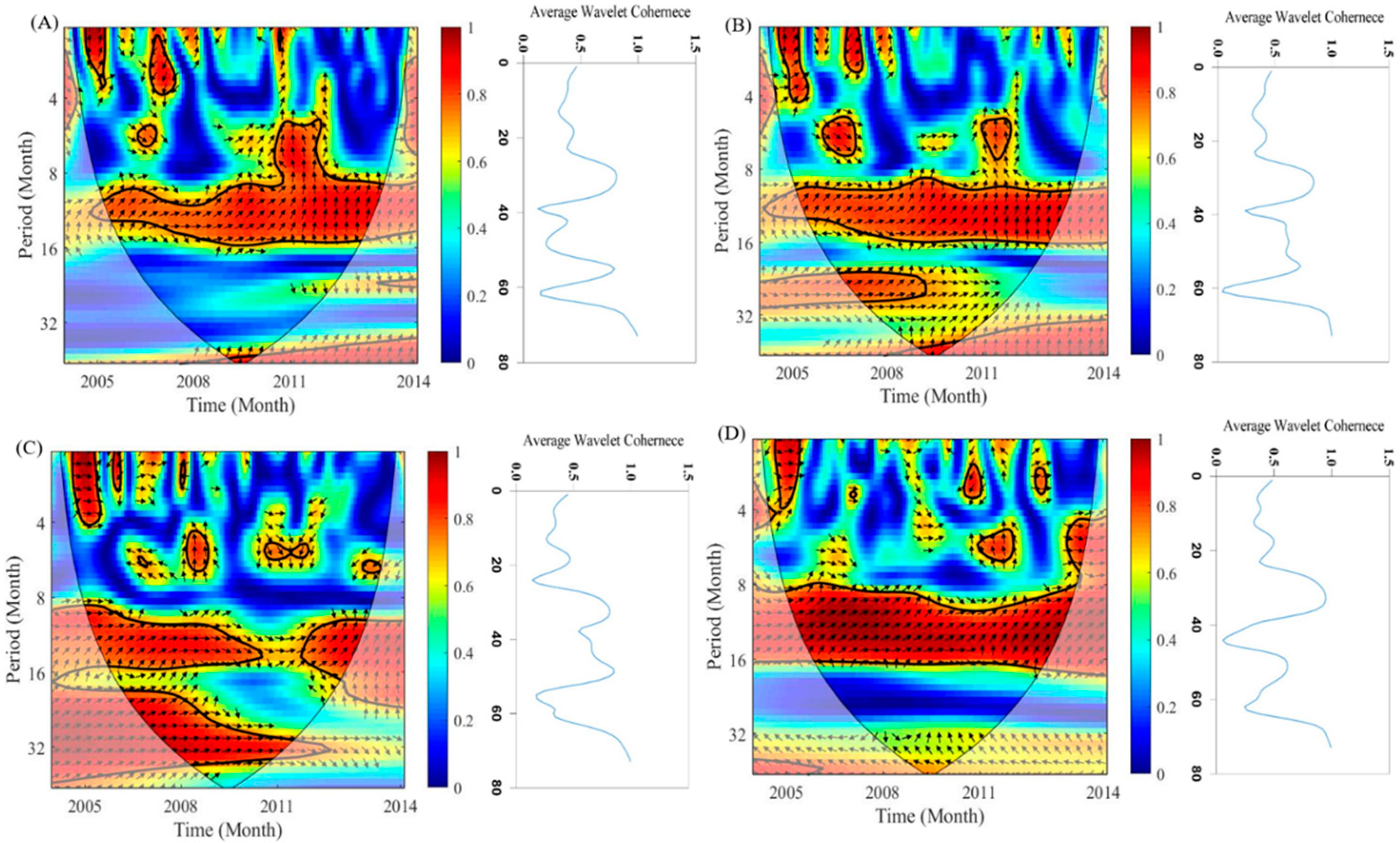

| Country | Center Acronym | Model | Grid Size | RCP (w/m2) | Applied Climate Variables in CM |
|---|---|---|---|---|---|
| Canada | CCCma 1 | Can-ESM5 | 2.81 × 2.81 | SSP2-4.5 SSP5-8.5 | P ua: eastward wind P va: northward wind P zg: geopotential height P hur: relative humidity P hus: specific humidity tas: air temperature uas: eastward near-surface wind vas: northward near-surface wind psl: air pressure at sea level hfls surface upward latent heat flux prc: convective precipitation flux pr: precipitation flux hurs: near-surface relative humidity huss: near-surface specific humidity evspsbl: water evaporation flux |
| Russia | INM 2 | INM-CM5 | 1.5 × 2 | SSP2-4.5 SSP5-8.5 |
| Selected Predictors for Tabriz (i) | Selected Predictors for Rasht (i) | |||
|---|---|---|---|---|
| CM | WTC | CC | WTC | CC |
| CAN-ESM5 | zg20000 (4) hus (5) BCP (5) BCP (6) | hur7000 (4) hur10000 (4) BCP (5) hus7000 (5) | BCP (3) hur7000 (3) BCP (4) hus100 (4) | zg85000 (1) zg85000 (2) BCP (4) zg925000 (4) |
| INM-CM5 | BCP (1) BCP (4) zg15000 (4) zg15000 (5) | BCP (1) hur15000 (2) BCP (4) hur20000 (5) | BCP (5) BCP (6) hus60000 (6) ua100 (6) | zg92500 (3) BCP (6) zg92500 (6) hfls (6) |
| Station | Bias Correction Method | Predictor Screening Method | Model | RMSE Train (mm) | RMSE Verification (mm) | DC Train | DC Verification |
|---|---|---|---|---|---|---|---|
| Tabriz | DWT | WTC | WT-ANN | 22 | 24 | 0.617 | 0.614 |
| CC | WT-CC-ANN | 29 | 30 | 0.519 | 0.444 | ||
| QM | WTC | QM-ANN | 27 | 30 | 0.411 | 0.351 | |
| CC | QM-CC-ANN | 30 | 32 | 0.476 | 0.391 | ||
| - | - | SDSM | 33 | 35 | 0.342 | 0.318 | |
| Rasht | DWT | WTC | WT-ANN | 32 | 32 | 0.589 | 0.579 |
| CC | WT-CC-ANN | 43 | 47 | 0.441 | 0.426 | ||
| QM | WTC | QM-ANN | 38 | 52 | 0.474 | 0.344 | |
| CC | QM-CC-ANN | 41 | 42 | 0.433 | 0.432 | ||
| - | - | SDSM | 43 | 46 | 0.392 | 0.371 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hosseini Baghanam, A.; Nourani, V.; Norouzi, E.; Vakili, A.T.; Gökçekuş, H. Application of Wavelet Transform for Bias Correction and Predictor Screening of Climate Data. Sustainability 2023, 15, 15209. https://doi.org/10.3390/su152115209
Hosseini Baghanam A, Nourani V, Norouzi E, Vakili AT, Gökçekuş H. Application of Wavelet Transform for Bias Correction and Predictor Screening of Climate Data. Sustainability. 2023; 15(21):15209. https://doi.org/10.3390/su152115209
Chicago/Turabian StyleHosseini Baghanam, Aida, Vahid Nourani, Ehsan Norouzi, Amirreza Tabataba Vakili, and Hüseyin Gökçekuş. 2023. "Application of Wavelet Transform for Bias Correction and Predictor Screening of Climate Data" Sustainability 15, no. 21: 15209. https://doi.org/10.3390/su152115209
APA StyleHosseini Baghanam, A., Nourani, V., Norouzi, E., Vakili, A. T., & Gökçekuş, H. (2023). Application of Wavelet Transform for Bias Correction and Predictor Screening of Climate Data. Sustainability, 15(21), 15209. https://doi.org/10.3390/su152115209








