Abstract
In response to the COVID-19 pandemic, communities utilize unmanned vehicles to minimize person-to-person contact and lower the risk of infection. This paper addresses the critical considerations of these unmanned vehicles’ maximum load capacity and service time, formulating them as constraints within a multi-traveling salesman problem (MTSP). We propose a comprehensive optimization approach that combines a genetic simulated annealing algorithm with clustering techniques and an improved Hopfield neural network (IHNN). First, the MTSP is decomposed into multiple independent TSPs using the fuzzy C-means clustering algorithm based on a genetic simulated annealing algorithm (SA-GA-FCM). Subsequently, the HNN is employed to introduce the data transformation technique and dynamic step factor to prepare more suitable inputs for the HNN training process to avoid the energy function from falling into local solutions, and the simulated annealing algorithm is introduced to solve multiple TSP separately. Finally, the effectiveness of the proposed algorithm is verified by small-scale and large-scale instances, and the results clearly demonstrate that each unmanned vehicle can meet the specified constraints and successfully complete all delivery tasks. Furthermore, to gauge the performance of our algorithm, we conducted ten simulation comparisons with other combinatorial optimization and heuristic algorithms. These comparisons indicate that IHNN outperforms the algorithms mentioned above regarding solution quality and efficiency and exhibits robustness against falling into local solutions. As presented in this paper, the solution to the unmanned vehicle traveling salesman problem facilitates contactless material distribution, reducing time and resource wastage while enhancing the efficiency of unmanned vehicle operations, which has profound implications for promoting low-carbon sustainable development, optimizing logistics efficiency, and mitigating the risk of pandemic spread.
1. Introduction
1.1. Background
As modernization advances, unmanned distribution vehicles have progressively entered the public domain, finding applications in various sectors, such as urban public transportation, airports, and recreational areas [1]. Their utility extends to enhancing logistics efficiency in freight, courier, and mail services and within industrial and manufacturing settings, where they play a vital role in material handling and assembly line automation [2,3]. The intelligent control and navigation systems of unmanned vehicles enable them to operate more efficiently. They achieve this by minimizing unnecessary accelerations and brake applications, reducing fuel consumption and exhaust emissions, and benefiting the environment significantly [4]. They support services like passenger taxis and internet-based transportation through intelligent path planning and traffic management, alleviating traffic congestion by dynamically optimizing routes and driving patterns. Additionally, these vehicles can facilitate coordinated communication, mitigating the need for frequent stops and accelerations at traffic signals and further enhancing traffic flow [5]. The future of unmanned vehicles lies in their incorporation of advanced sensors, radars, cameras, and 5G technology, equipping them with the ability to sense their surroundings and make real-time decisions. This innovation promises to significantly reduce traffic accidents stemming from human errors [6,7]. However, it is essential to acknowledge that unmanned vehicles may need help to respond effectively to complex traffic scenarios and emergencies. Ensuring their adherence to traffic regulations and ethical guidelines is a paramount concern, which, along with the establishment of robust legal frameworks and regulations, represents the focal points and avenues of exploration for researchers in the field [8]. Our study concentrates explicitly on path optimization by abstracting the unmanned vehicle delivery problem as an MTSP and employing combinatorial optimization algorithms to solve it. Particularly relevant in the context of the pandemic, this approach reduces contact among community residents and provides optimized distribution routes for unmanned vehicles. This results in decreased travel distances, streamlined traffic flow, and an overall promotion of sustainable transportation practices. The value of this application is especially pertinent in the current landscape.
1.2. Literature Review
The majority of research on unmanned vehicles has traditionally centered around the vehicles themselves, encompassing areas like sensor technology, positioning systems, communication systems, and environmental perceptions [6,7,9]. This research stream has also delved into the ramifications of unmanned vehicles on air quality and public health [10,11]. However, the current landscape sees a notable shift in focus, with increasing attention being directed towards unmanned vehicle path planning while somewhat diminishing the emphasis on the vehicles themselves [12,13]. The unmanned vehicle delivery problem is essentially a TSP or an MTSP, which is a classical NP-hard problem [14]. In practical applications, many optimization problems, such as conformal antenna surface detection [15], multi-unmanned vehicle cooperative task planning [16], autonomous underwater robotic operations [17], blockchain system technology [18], mail service shipping [19], and single- and multi-warehouse routing issues [20], can be formulated as a TSP or an MTSP. Compared with the TSP, the MTSP has acquired enormous attention. He and Hao [21] explored a neighborhood-abbreviated hybrid algorithm. Dong et al. [22] built a maximum tour distance optimization mannequin that minimized all salespeople and developed a hybrid frog-hopping algorithm. Kloster et al. [23] proposed a two-stage programming based on populating solution pools and using ensemble partitioning models. Changdar et al. [24] designed a staged algorithm to solve the MTSP with a single warehouse. The intelligent optimization algorithms to solve this problem consist of genetic algorithms [25,26], ant colony algorithms [27], particle swarm algorithms [28], Harris Eagle optimization [29], compact integer programs [30], etc. However, due to the inherent complexity of the MTSP, existing intelligent heuristic algorithms often encounter challenges like local convergence and suboptimal solution quality during the solving process. Consequently, there is a growing research interest in devising methods for efficiently and rapidly addressing the MTSP.
In recent years, artificial neural networks have gained widespread popularity and have been applied to solve a diverse range of problems, with one of the most prevalent categories being combinatorial optimization problems [31]. In 1982, Professor Hopfield, a physicist at the California Institute of Technology, introduced the Hopfield neural network model [32]. Through ongoing research and development, numerous scholars have observed that neural networks are increasingly highly efficient in tackling these intricate combinatorial optimization problems. For example, Lin and Fan [33] introduced transient chaotic neural networks in ferroelectric memristors to solve the TSP. García et al. [34] used Particle Swarm optimization to obtain an optimal solution for the population to ensure the convergence of the continuous HNN and to avoid searching for a locally optimal solution. Zhang et al. [35] applied Liapunov’s generalized characteristic to check the balance of the non-autonomous fractional-order system and proposed a new sturdy synchronization technique for neural structures and their management regulation. Saadatmand-Tarzjan proposed a constructive-optimizer neural network (CONN) for the TSP [36]. Recently, a range of options for the MTSP have been proposed primarily based on deep learning of the network. Hu et al. [37] built a modeling framework consisting of a shared plan neural community and a dispensed coverage network, which was once solved by using a two-stage strategy of deep learning and regularized optimization. Ling et al. [38] proposed a deep convolutional neural network (DCNN) based on the totally mTSP-fixing method, which can, without delay, set up the mapping relationship between parameters and best solutions, keep away from the use of iterations, and can be used to clear up mTSP beneath distinctive constraints after migration studying. Alves et al. [39] proposed a system to solve the MTSP with the help of a multi-objective evolutionary algorithm (MOEA) to generate routes. Ahsini et al. [40] combined city charts with terrain and traffic information and used ANN to optimize path travel for electric vehicles in urban areas. The similarities, differences, and representative studies of TSP and MTSP are shown in Table 1 below.

Table 1.
Similarities, differences, and representative studies of TSP and MTSP.
In summary, the TSP and MTSP belong to combinatorial optimization problems, sharing the overarching objective of discovering optimal routes. Nevertheless, they diverge concerning the number of involved salespersons and the specific optimization goals they entail. Consequently, the prevailing approach to address these complexities relies on heuristic techniques, given the inherent computational complexity. While many researchers have dedicated their efforts to optimizing unmanned vehicle routes, commonly framing the research problem as MTSP, they have crafted optimization models and intelligent algorithms tailored to different problem characteristics. Nonetheless, more research remains on unmanned vehicle emergency delivery, particularly concerning the application of Hopfield neural network-based combinatorial optimization algorithms for MTSP resolution. Based on prior research, this paper makes the following significant contributions:
- (i)
- In response to constraints such as limited delivery time due to insufficient power and the carrying capacity limitations of unmanned vehicles, we establish an MTSP model tailored for optimizing unmanned vehicle deliveries.
- (ii)
- Addressing the NP-hard nature of the model, we propose an enhanced clustering algorithm to partition the MTSP into multiple TSPs coupled with a combinatorial optimization algorithm employing the IHNN to solve TSP.
- (iii)
- Through the application of IHNN in both small-scale and large-scale instances, comparative analyses with other combinatorial optimization algorithms and heuristic methods demonstrate the robustness of IHNN, which, in turn, offers valuable insights for planning unmanned vehicle distribution routes within communities.
2. Modeling the MTSP for Cooperative Operation of Multiple Unmanned Vehicles
2.1. Problem Description
It is assumed that n unmanned vehicles depart from the community distribution center at a constant speed. They develop corresponding route plans by customer orders and actual situations. Their mission is to deliver a certain amount of material supplies to m customers and ultimately return to the distribution center. Each unmanned vehicle operates under a maximum time limit for supply distribution. Each unmanned vehicle has a specific material load limit. Each customer location must be visited only once and served exclusively by one unmanned vehicle. The model does not account for the service time at each customer location. The objective is to minimize the maximum distance traveled by any unmanned vehicle, as illustrated in Figure 1.
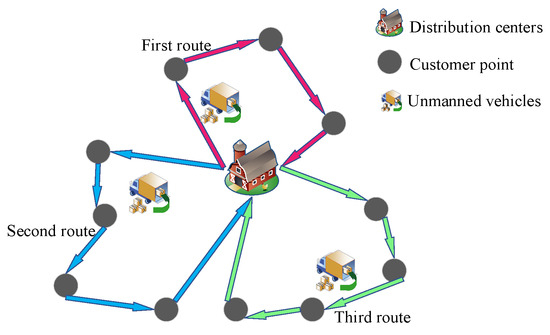
Figure 1.
Schematic diagram of unmanned vehicle delivery path.
2.2. Model Building
The MTSP is defined in a directed graph , where is the set of n vertices, and is the set of arcs, with the notation defined in Table 2.

Table 2.
Notations for the MTSP.
The mathematical model of the MTSP for unmanned vehicles with constraints such as driving time and loading capacity is as follows [19,38]:
subject to
Formula (1) represents minimizing the maximum distance traveled by all unmanned vehicles; Equation (2) represents unmanaged vehicle travel distance; Equation (3) indicates the travel time of the th unmanned vehicle; Formula (4) indicates maximum unmanned vehicle driving time not exceeding ; Formula (5) indicates that the maximum load weight of the th unmanned vehicle is Q; the constraints (6) and (7) guarantee that there are n unmanned vehicles departing from the distribution center, service all customers after the final return to the distribution center; the constraints (8) and (9) ensure that each node is accessed only once (except for the delivery center); and the constraints (10) to prevent the formation of any route that does not include a distribution center; and that Formula (11) constrains the total number of customer nodes; and Formula (12) is a 0–1 integer decision variable.
3. Combinatorial Optimization Algorithm for Solving MTSP
With the development of practice, it is difficult to find polynomial time algorithms for finding optimal solutions for many practical application problems. The use of combinatorial optimization algorithms to solve difficult problems in various fields has become a hot topic; for example, the literature [11,15,16,21,22,24,26,27,28,29], etc. all use hybrid optimization algorithms for the solution, and the results of hybrid optimization algorithms are better than those of the single algorithm solution. In this paper, a combinatorial optimization algorithm is designed to solve the MTSP with multiple unmanned vehicles to complete the order delivery, especially for the scenario where the number of customers in the community increases to hundreds, and the model structure is shown in Figure 2. In the first step, the customers were divided into two types, small scale and large scale, using standard datasets. In the second step, the fuzzy C-means clustering algorithm based on the simulated annealing genetic algorithm was utilized to decompose the MTSP into n-independent TSP. In the third step, data transformation techniques, dynamic step size factor, and the simulated annealing algorithm were introduced to the HNN for solving and obtaining the path solution for each TSP.
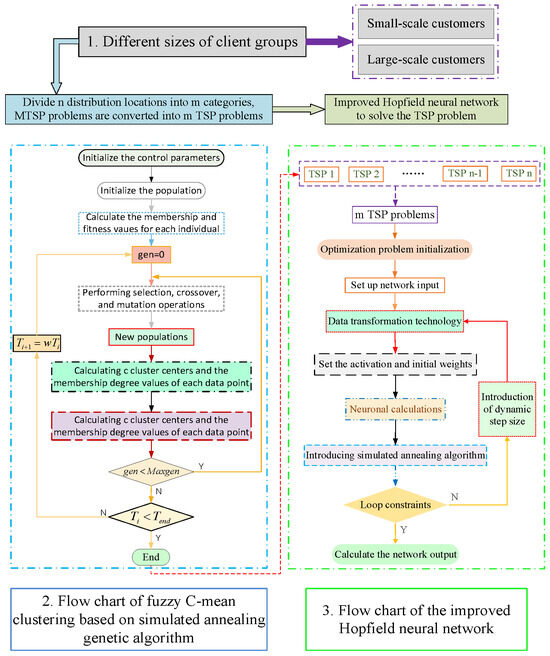
Figure 2.
Flow diagrams for combinatorial optimization models.
3.1. Fuzzy C-Means Clustering Algorithm (FCM)
Let data samples be , where represents the type of category into which all sample data are divided. denotes the corresponding categories. is defined as the similarity classification matrix. Each category is centrally positioned as . The affiliation of sample to class is , abbreviated as . The objective function is expressed as follows [41].
marks the distance between the subset and the core factor of the classification coordinates. is the wide variety of elements of the sample, and is a weighting parameter that takes a variety of values . The predominant thought of this clustering approach is to discover the most appropriate classification that yields the smallest fee of the feature . The dependency of the pattern on every cluster is comfortable by way of the sum of the values of 1, i.e., [42]
Equations (16) and (17) calculate the affiliation of the sample to the class and clustering centers , respectively [43,44].
Set , for all classes, , .
Using Equations (16) and (17) to repeatedly modify the clustering center and data affiliation and perform classification, when the algorithm is in the state of convergence, theoretically, the clustering center of each category and the affiliation degree are obtained, representing the completion of the task of fuzzy clustering classification. The algorithm has some advantages in searching speed, but it is more dependent on the value of the initial clustering center, and it may converge to the local minima if it is not correctly chosen [44].
3.2. Fuzzy C-Means Algorithm for Genetic Algorithm with Strengthening Using Simulated Annealing (SA-GA-FCM)
In the process of FCM clustering, the selection of the initial value has a great impact on the clustering effect. If it is not selected properly, it is easy to converge to the local minima. To make the FCM achieve a better sample clustering effect, the simulated annealing and genetic algorithm are introduced into the FCM, which enhances the searching ability of the FCM both locally and globally to solve the clustering problem effectively [45]. The process is shown in Figure 2, and the sequence in which the three algorithms are combined to complete the work is accomplished by the following steps [46,47].
Step 1: Setting parameters. The genetic algorithm has the number of populations sizepop, , , . The variety of annealing temperature modifications is , and the temperature cooling stage is .
Step 2: an initial random generation of c clustering centers, an initial population of a certain size chromosome, and for each clustering point, calculate the affiliation of each sample using Equation (3) and the value of individual fitness in the initial population, where .
Step 3: update the recursive iteration count attribute .
Step 4: The population is genetically manipulated, and the newly generated individuals are used in Equations (12) and (13) to calculate each clustering center, the degree of affiliation, and the individual fitness value of the evolved offspring is . If the condition of is satisfied, pre-evolutionary individuals are replaced by evolutionary offspring individuals. Otherwise, the evolved offspring is accepted with the , and pre-evolutionary individuals are discarded.
Step 5: If the number of evolutions reaches , then proceed to the next step. Otherwise, the cumulative number of evolutions.
Step 6: If is satisfied, the algorithm terminates and outputs optimization results. Otherwise, perform the operation of and go to Step 3.
3.3. Hopfield Neural Network
The challenge of path optimization typically involves addressing a nonlinear optimization problem. In this context, the Hopfield neural network, functioning as a nonlinear dynamical system, offers a more adept solution. Its distinctive strength lies in its ability to concurrently manage multiple path optimization tasks, lending it resilience against input data disturbances and noise. Compared to more intricate path planning algorithms, the Hopfield neural network employs simple neuron models and energy functions to delineate the problem. This characteristic streamlines the implementation and application, thus reducing overall complexity [35,36]. The continuous Hopfield neural network (CHNN) is realized through an assembly of straightforward electronic components. Figure 3 illustrates the schematic of a single neuron within the CHNN. This neuron features a feedback connection that spans from input to output, driving a constant state alteration in response to input.
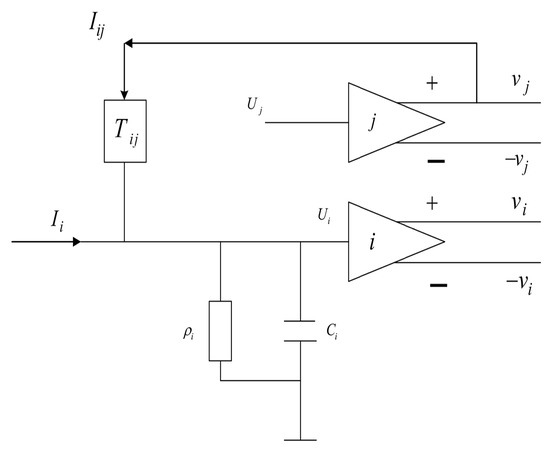
Figure 3.
A neuron of CHNN.
Each neuron has its continuously varying output value, expressed as , where and represent the input and output voltages of the neurons, respectively. For a CHNN model with an M node, the dynamic change in its neuron state [48]:
The connection weights between neurons are
The bias current is
Enter the update expression for the state:
Update the expression for the output status:
For the TSP, the energy function is expressed as
The energy functions , , , and denote the weights, while accounts for the distance between two cities. The first three of these represent the problem’s constraint terms, while the final one provides the goal of optimization. The improved energy function is given by the following equation [49].
The dynamic equation is as follows
3.4. Improved Hopfield Neural Network (IHNN)
3.4.1. Application of Data Transformation Techniques
Data transformation techniques [50] is a technique widely used in optimization problems, used to specify the degree of deviation of data values from averages, mainly through techniques (e.g., Z-score technique, logarithmic function, etc.). The method is introduced into the neural network, and the result is good for the optimization of effective solutions. When solving the TSP in the second part of Figure 2, the matrix of the output signal is processed after the initial input of the Hopfield neural network, making it easier for the energy function to tilt along the descending side of the gradient. The specific expressions are as follows [51]:
The data sample means and sizes are and , respectively.
3.4.2. Introduction of Dynamic Step Size
The step size of the HNN algorithm is a fixed constant. If the value of is too large, the algorithm will not converge with continuous jitter. Conversely, if the value of is too small, it will result in a small change in the HNN input value each time the algorithm is adjusted, leading to the algorithm easily falling into local minima [52,53].
Previously, the fixed step size is replaced by the variable step size . To speed up the convergence of the energy function, a large step size is used first, and as the convergence process proceeds, the value of the step size is gradually reduced so that the algorithm can obtain a fine convergence effect. To obtain s value, reference Formula (29), where is a constant, and and are parameters of the changing trend of the control step function.
The above-stated techniques are added to the HNN to solve the TSP; the specific process is shown in Figure 2.
3.4.3. Introducing Simulated Annealing Algorithm (SA)
The optimization concept of the HNN involves following a gradient descent path towards the nearest minimum from the initial point. As such, the entire learning process unfolds as a nonlinear optimization journey. However, this approach can lead to the emergence of local minima and undesirable oscillations, diminishing the quality of learning outcomes. In other words, it is not guaranteed to find the global minimum. To mitigate these challenges, the HNN incorporates an analog annealing algorithm [54] akin to the one detailed in Section 3.2. This annealing operation works as follows: If the energy value after a change is lower than before, the new energy value becomes the starting point for the next iteration. Conversely, if the post-change energy value is higher, the modified energy value is accepted with a certain probability, which is performed by discarding the prior energy value. The simulated annealing process is to locate an initial iteration point in the HNN closer to the global minimum than a local extreme point. Figure 2 illustrates the specific implementation details.
3.4.4. Steps to Improve Hopfield Neural Network to Solve TSP
Figure 2 gives an entire flow chart, including clustering algorithms and IHNN, where the IHNN process for resolving TSP is as follows:
- (i)
- Set initial values and weights, including , , , and ;
- (ii)
- Read in the distance between clients ();
- (iii)
- Initialization of HNN input , where and is a random value in the interval (−1,1);
- (iv)
- Calculation of using dynamic equations and calculation of in Equation (20) based on the first-order Eulerian method, where after the introduction of the dynamic step is Equation (27);
- (v)
- The sigmoid function is used to calculate in Equation (21);
- (vi)
- Introducing a data transformation technique to smooth the output signal ;
- (vii)
- Calculate the energy function , introducing the simulated annealing algorithm to make the energy more inclined to the direction of gradient descent;
- (viii)
- Check the legitimacy of the path, determine whether the iteration is over, and if not, return to step (iv);
- (ix)
- Output the energy function, the path length, and the energy change.
4. Evaluation and Design Analysis
4.1. Simulating Combinatorial Optimization Algorithms (IHNN) on Small-Scale Instances
Combined with the model and algorithm above, the programming simulation is carried out in the MATLAB environment. Taking Solomon’s [55] dataset R210 as an example, the corresponding 100 customer locations are extracted, and the coordinate unit is km. Assuming that the distribution center coordinates are (35,35), in the three scenarios, the number of unmanned vehicles is 3, 4, and 5, respectively. The clustering is divided in order, and the speed of unmanned vehicles is 60 km/h. The weight of the material at the service customer point is 2 kg. The latest service time of each customer is within 5 h. The maximum load is 80 kg, and time spent serving customers by unmanned vehicles does not count toward total delivery hours.
Specific simulation parameters are set as follows: In SA-GA-FCM, parameter settings are set as in Reference [41], according to the number of unmanned vehicles. In order of clustering, the end tolerance of the target function is 1 × 10−4, the cooling coefficient is 0.8, is 100, is 1, popsize is 40, is 100, is 0.1, and is 0.2. In the improved Hopfield neural network section, the parameters are initialized as follows [48]: is 1, is 1, the maximum number of times is 500, is 0.02, is 0.75, is −0.09, and is 0.3.
The small-scale customer data is clustered three times according to the number of unmanned vehicles, as shown in Figure 4, Figure 5 and Figure 6. The smaller the optimal target function value , the better the clustering effect.
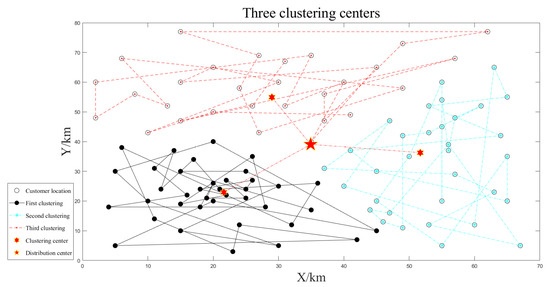
Figure 4.
Three clustering centers.
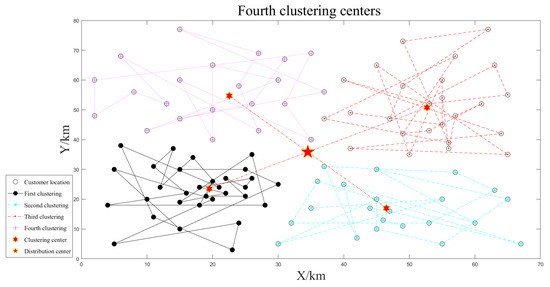
Figure 5.
Four clustering centers.
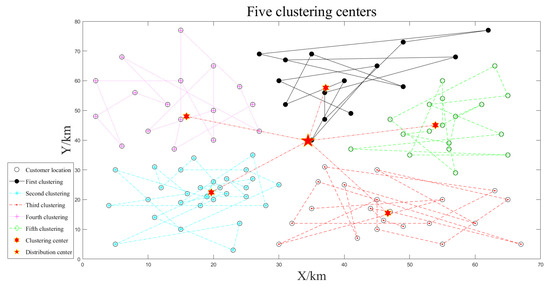
Figure 6.
Five clustering centers.
The path optimization results for unmanned vehicles are shown separately in Figure 7, Figure 8 and Figure 9. The unmanned vehicles can complete the delivery task of each customer in turn and finally return to the distribution center, and there is no situation in which the customer is not visited, or the route is intersected during each delivery. The longest driving time was 4.17 h, and the maximum loading capacity was 76 kg, which did not exceed the latest customer service time and maximum loading capacity constraints, and the task assignment was reasonable. The path planning results are shown in Table 3.
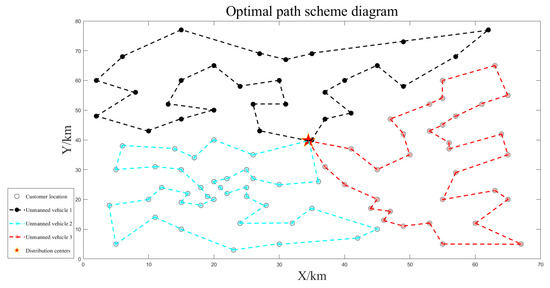
Figure 7.
Three unmanned vehicle deliveries.
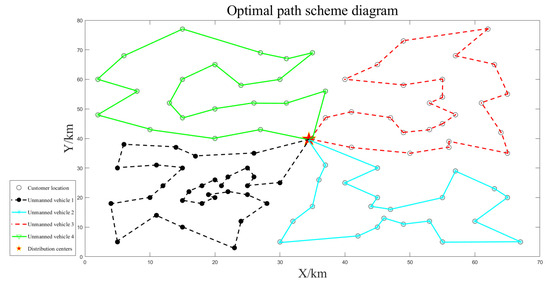
Figure 8.
Four unmanned vehicle deliveries.
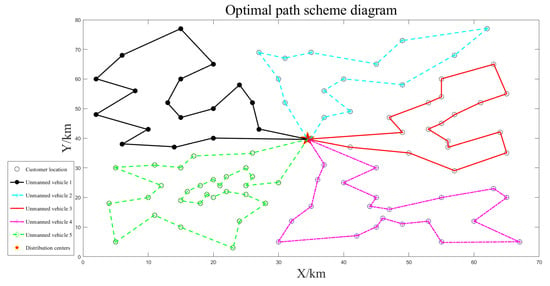
Figure 9.
Five unmanned vehicle deliveries.

Table 3.
Path planning results.
4.2. Combinatorial Optimization Algorithm Large-Scale Simulation Case
This section will use 200 customer points data from Gehring and Homberger’s [56] extended VRPTW benchmark rc1_2_1 with a large-scale example simulation with a coordinate unit of km. In the three instances where the number of unmanned vehicles is six, seven, and eight, clustering is performed in turn; the unmanned vehicle speed is 75 km/h. The material weight of the customer points is 2 kg. The minimum service time for each customer is within 6 h. The maximum load weight is 90 kg, and the algorithm parameters are the same as in Section 4.1. Similarly, for the clustering by unmanned vehicles, three clustering effects are shown in Figure 10, Figure 11 and Figure 12; each cluster can obtain a good target function value , and the clustering effect is good.
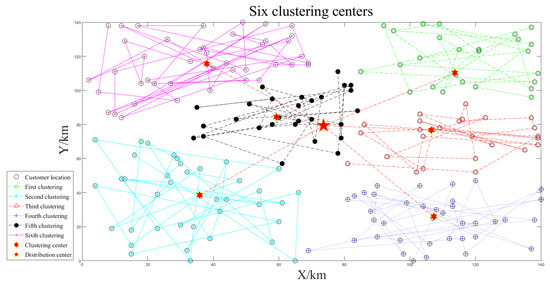
Figure 10.
Six clustering centers.
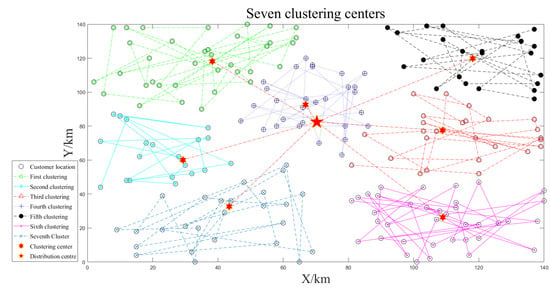
Figure 11.
Seven clustering centers.
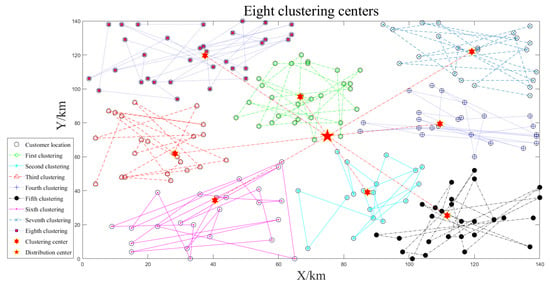
Figure 12.
Eight clustering centers.
Simulation was carried out based on the clustering results obtained from dividing the data into three clusters. The final route planning solution is illustrated in Figure 13, Figure 14 and Figure 15. In each clustering scenario, the autonomous vehicles were able to traverse all customer locations, complete the delivery tasks for each customer, and return to the distribution center. Throughout the entire task period, the maximum travel time of the autonomous vehicles was 5.67 h, which did not exceed the latest service time of 6 h for the customers. Additionally, the maximum load capacity of 86 kg did not exceed the maximum load constraint of 90 kg. Despite the increasing complexity of clustering as the number of customers grew, indicated by an increasing value of parameter , the overall clustering performance remained good. The delivery duration of the autonomous vehicles noticeably increased under each clustering scenario, and there were instances of overlapping travel routes. The specific results of the route planning are presented in Table 4.
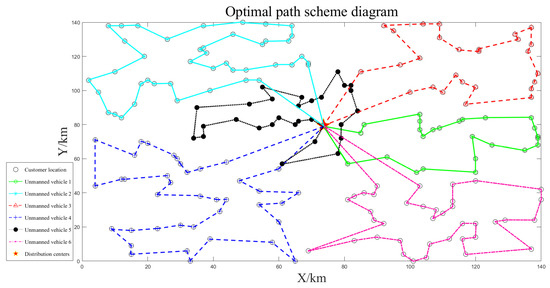
Figure 13.
Six unmanned vehicle deliveries.
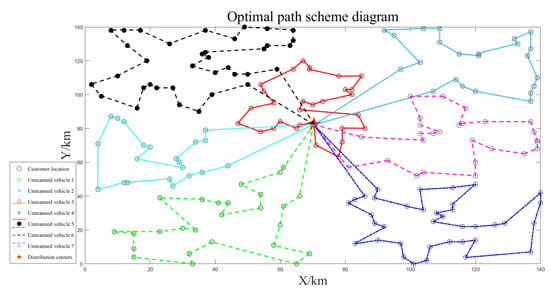
Figure 14.
Seven unmanned vehicle deliveries.
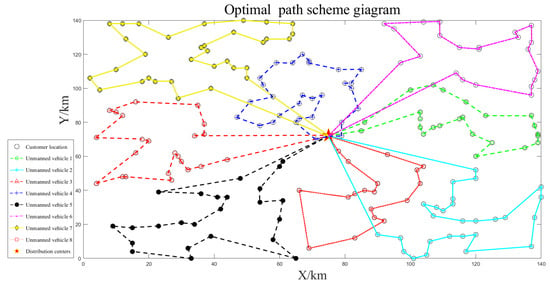
Figure 15.
Eight unmanned vehicle deliveries.

Table 4.
Path planning results.
5. Comparative Analysis of the IHNN with the Second-Order Oscillation Particle Swarm Optimization (SO-PSO) and the Hybrid Genetic Ant Colony Optimization (GA-ACA)
5.1. Second-Order Oscillation Particle Swarm Optimization (SO-PSO)
5.1.1. Proposal of Particle Swarm Optimization (PSO)
In d-dimensional space, particle i updates the speed and position through its own extreme () and the global extreme (gb) of all particles and then finds the optimal solution, i.e., [57]
where is the inertial weight, and are learning factors, and and are the random values evenly distributed between 0 and 1.
To overcome the defect of the function that the speed of flight is just the current position of the particle, Nayyef et al. [58] added the jellyfish search optimizer (JSO) to PSO to achieve good optimization results. In path planning for forest fire rescue [59], 3D unmanned aerial vehicles were employed using an improved particle swarm algorithm [60]. In addition, the optimization problem is not only studied on the selection of different meta-heuristic combinations but also the simulation of parameter adjustment [61]. Multiple optimization functions were tested by adding the Fibonacci index algorithm (FIA) to an artificial bee colony (ABC) algorithm [62]. Some scholars have provided indicators for evaluating the decision making of computational intelligence algorithms [63]. This paper takes a similar measure; to achieve global search, the SO-PSO is introduced, including the particle position and its velocity update formula in [64]
where and are random numbers, and the population evolves to half the maximum number of evolutions, take , , so that the algorithm has a strong global search capability. When population evolution exceeds the maximum number of times, take and to allow the algorithm to converge gradually.
5.1.2. SO-PSO Implementation Steps
- (i)
- Random initialization of particle position and velocity.
- (ii)
- Evaluate particulate individuals, update , and store all optimal individuals in PU.
- (iii)
- If the current number of evolutionary generations is less than 1/2 of the maximum number of generations, update as follows, where , . Similarly, if the current number of evolutionary generations is less than 1/2 of the maximum number of evolutions, then , are taken.
- (iv)
- Compare the adaptive value of the particle itself with the highest value in evolution and, if superior to the highest value, update to its own position.
- (v)
- Make a comparison with the and the gb, and update .
- (vi)
- If the evolution end condition is satisfied, the optimum result is output; otherwise, go to step (iii).
5.2. Hybrid Genetic Ant Colony Algorithm (GA-ACA)
5.2.1. Proposal of GA-ACA
In the ant colony algorithm (ACA), ants release a volatile secretion called pheromone on the paths they pass. Subsequent ants will independently choose the way to pass through based on the strength of the pheromone on the path, the path with greater pheromone strength to walk. This behavioral strategy allows ant colonies to form a positive feedback information transfer mechanism that helps them find the shortest path to their destination [65].
Let there be cities, where indicates the distance between cities, and represents the amount of information between two cities, which characterizes the actual amount of secretion of ants. Assuming that there are ants at present and using to denote the probability of an ant moving between two cities at moment , then there are
where is called the taboo table, which is used to record the current city that ant has traveled to; is some kind of heuristic information, which can be taken as in the TSP; and and indicate pheromone and heuristic, respectively. The amount of information has been updated as
where denotes the degree of pheromone decay. The pheromone increment is denoted as
where measures the amount of information ants leave between two cities in each population iteration, is a constant, and denotes the length of the path taken by ant in this round of loop iterations.
To overcome the difficulty of ant colony algorithms being prone to precocious and stagnant phenomena after evolution to a certain number of algebras, this part combines the genetic algorithm, which is characterized by high stochastic selectivity and global solid search ability. After the ACA has evolved to a certain number of generations, the genetic algorithm is dynamically introduced to effectively avoid the dilemma of local solutions, and this combined approach can better strengthen the more optimal solutions [66,67].
5.2.2. The Concrete Steps for the Implementation of the Hybrid Genetic Ant Colony Algorithm (GA-ACA)
- (i)
- Encoding. For a TSP containing cities, an array of length represents a solution, e.g., if the cities are numbered , then the encoded bit string of a particular chromosome may be , indicating that the cities are accessed in the order 4-1-8-3-7-4-2-5-6.
- (ii)
- Setup parameters. , the popsize is , and , .
- (iii)
- Calculate the fitness value of the chromosome, opt for roulette operation, and the probability value of the selection of individual is
- (iv)
- Partially matched crossover (PMX) is used to generate two random integers and in the interval . Determine the two positions to crossover the data in the middle of the two, as in Figure 16, , , exchanging segments of two paternal chromosomes with genes in the range 2–5 [68].
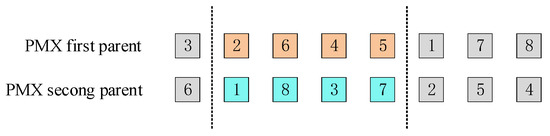 Figure 16. Parent chromosomes before partially matched crossover.
Figure 16. Parent chromosomes before partially matched crossover.
After crossing, if the same chromosome has the same city number, the city does not repeat the reservation, and the duplicate city uses partial mapping to remove; the results are as follows (Figure 17).
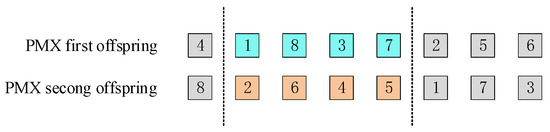
Figure 17.
Partial mapping after crossover.
- (v)
- In the mutation operation, the mutation strategy takes two random points and swaps their positions to produce two random integers in the range ; the two random points are and . The chromosome changes before the mutation are shown in Figure 18 and after the mutation in Figure 19.
 Figure 18. Chromosome sequences before mutation.
Figure 18. Chromosome sequences before mutation. Figure 19. Chromosome sequences after mutation.
Figure 19. Chromosome sequences after mutation.
- (vi)
- Start the iteration and determine whether to reach the maximum number of evolutions. If so, go to the next session; otherwise, go to (iii).
- (vii)
- After the evolution is completed, reach an optimized solution as a way to initialize the initial value of the pheromone and related parameters, including , , , , , , and .
- (viii)
- Ants start pathfinding according to the state transfer formula.
- (ix)
- Local pheromones and global pheromones are updated with the path search of ant populations.
- (x)
- Make a judgment that if the current number of evolutions is greater than the limit, the optimal result is output; otherwise, go to step (ix) to continue the iteration.
5.3. Comparative Analysis of Three Algorithm Simulations
This section selects the first clustering case (Section 4.1) in the small-scale case and the sixth clustering case (Section 4.2) in the large-scale case. IHNN performs simulation and comparison analysis with SO-PSO and GA-ACO. Before that, explanations are provided for the parameters in each algorithm. First, in SO-PSO, appropriate parameters are selected based on the referenced literature [45]. Specifically, the inertial weight is 0.9, and are both positive learning factors with a value of 2, the number of particles is 50, and the maximum number of iterations is set to 500. Secondly, in GA-ACO, parameters mentioned in the referenced literature are used. is 500, the genetic algorithm iteration count is set to 200, is 0.8, is 0.3, the pheromone constant of is 1, the pheromone factor of is 1, the expectation value inspired factor of is 5, the local pheromone volatility coefficient of is 0.9 [48]. The six algorithms are run independently 10 times, respectively; the trends in the results of the 10 runs are displayed in the bar charts of Figure 20 and Figure 21, and the convergence curves of the average shortest path length are shown in Figure 22 and Figure 23. In addition, the variation curves of the energy function of the IHNN for simulations at two different scales are plotted, as shown in Figure 24 and Figure 25.
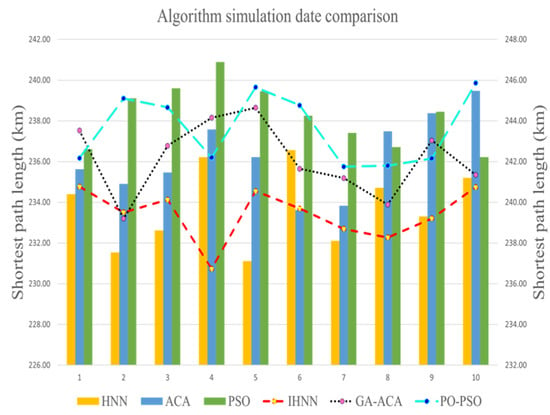
Figure 20.
Small-scale shortest path length data.
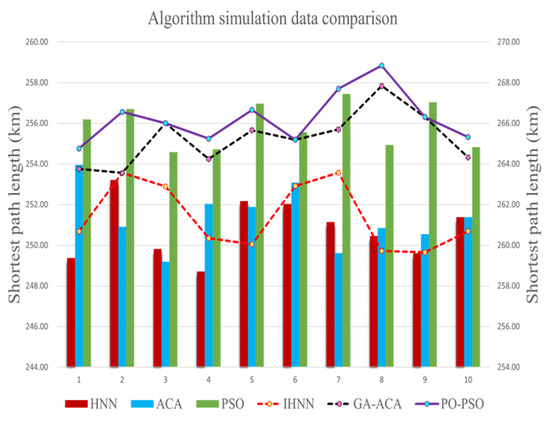
Figure 21.
Large-scale shortest path length data.
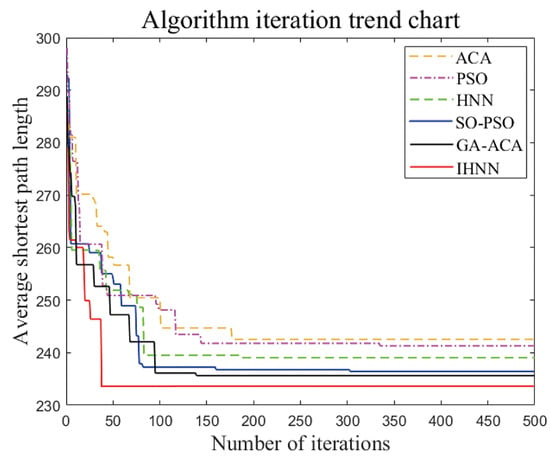
Figure 22.
Average shortest path length for small scale.
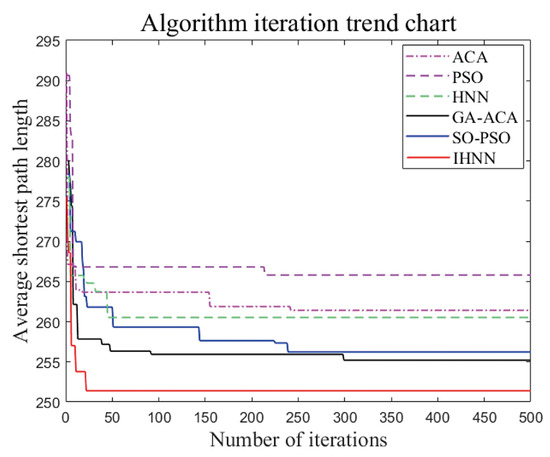
Figure 23.
Average shortest path length for large scale.
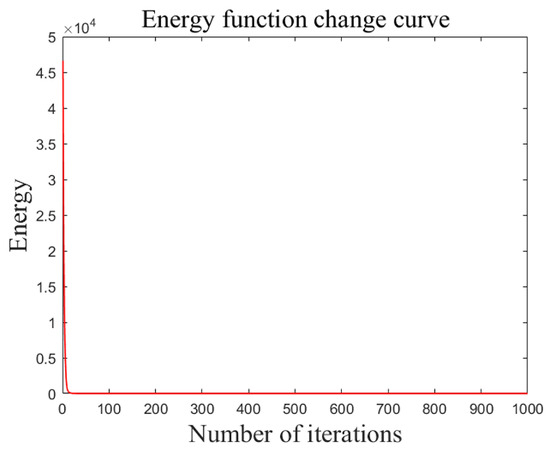
Figure 24.
Graph of small-scale energy function curve.
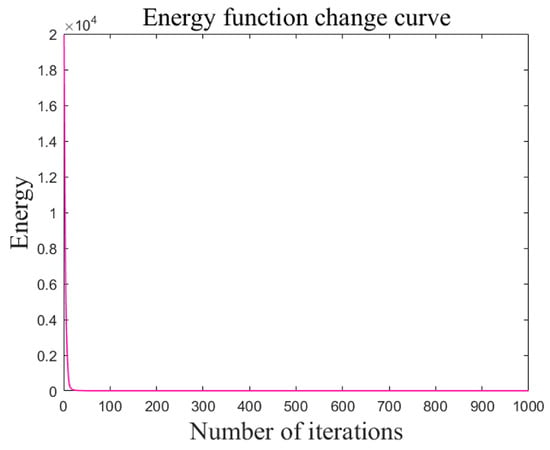
Figure 25.
Graph of large-scale energy function curve.
The IHNN consistently achieves smaller values compared to other algorithms across different scales, as is evident in Figure 20 and Figure 21. The results show a stable pattern with minimal fluctuations. In Figure 22 and Figure 23, the iterative convergence of the average shortest path length of each of the six algorithms in small-scale and large-scale instances is given, respectively. In small-scale simulations, the IHNN achieves 233.43, while the GA-ACA achieves 236.14, the SO-PSO achieves 237.61, the HNN achieves 239.78, the PSO achieves 242.26, and the ACA algorithm achieves 244.27. In large-scale simulations, IHNN achieves an average shortest path length of 251.41, while the GA-ACA achieves 255.26, the SO-PSO achieves 256.26, the HNN achieves 260.79, the PSO achieves 261.35, and the ACA achieves 265.90. From the perspective of average shortest path length, IHNN consistently outperforms the other algorithms, although the improvements in the enhanced algorithms SO-PSO and GA-ACA are also significant, with average values within the range of 1–2. In terms of convergence speed, as shown in Figure 23 and Figure 24, the energy function curve of the IHNN demonstrates good convergence behavior. In both small and large-scale simulations, IHNN achieves the lowest energy values of 5.45 and 6.69, respectively, reaching convergence within 50 generations, effectively avoiding the generation of invalid solutions. The enhanced algorithms SO-PSO and GA-ACA also exhibit good performance, as the iteration curves indicate that they do not get trapped in local optima. However, heuristic algorithms such as ACA and PSO do not perform well as they tend to get stuck in local optima and generate invalid solutions. Thus, it is illustrated from several perspectives that the combinatorial optimization algorithm developed using the Hopfield neural network not only converges better but also solves more efficiently with better results.
6. Conclusions
Addressing the challenge of community material distribution during the pandemic, we propose a combinatorial optimization algorithm that factors in critical considerations such as the maximum driving distance of unmanned vehicle distribution and the maximum allowable load. The primary objective is to minimize the maximum distance traveled by unmanned vehicles while ensuring the efficient delivery of materials to customers, which is achieved by establishing the MTSP model for unmanned vehicles.
In our approach, we employ the SA-GA-FCM methodology to cluster groups of customers, which consist of 100 and 200 individuals, corresponding to the number of unmanned vehicles at hand. The number of clusters we establish aligns with the decomposition of the MTSP into multiple TSPs. We aim to minimize the objective function values for each cluster, ensuring that these values remain consistent across multiple simulations. This approach yields a robust clustering effect, enhancing the overall efficiency of our algorithm.
Next, we apply the HNN tool, incorporating data transformation techniques and dynamic step size adjustments to enhance its capabilities. We further introduce the simulated annealing algorithm to broaden the network’s exploration of the energy function space, reducing the risk of being trapped in local optima. This integrated approach empowers HNN to identify global optimal solutions more effectively. The algorithm is then utilized to solve the TSP for unmanned vehicles across six distinct clustering scenarios.
Subsequently, simulations are conducted within the MATLAB environment, and it is observed that, across all six clustering scenarios, the objective function values improve significantly in alignment with the number of unmanned vehicles. Furthermore, multi-unmanned vehicle distributions successfully cover all customer points within the task. Regarding specific simulation results, the IHNN outperforms alternative algorithms, such as SO-PSO, GA-ACA, HNN, ACA, and PSO. In small-scale simulations, IHNN achieves average reductions of 2.71 km, 4.18 km, 6.35 km, 8.83 km, and 10.84 km in the length of the shortest paths compared to the other algorithms. In large-scale simulations, IHNN demonstrates even more significant improvements, saving 3.85 km, 4.85 km, 9.38 km, 9.94 km, and 14.49 km. Notably, the disparity between IHNN and other algorithms becomes more pronounced as the size of the client base increases when addressing the MTSP. Regarding efficiency, IHNN stands out by delivering solutions in a shorter time frame, whereas alternative algorithms require more time and are less efficient. As a result, IHNN significantly enhances both computational efficiency and solution quality, achieving superior global convergence.
This paper addresses a widely applicable combinatorial optimization problem. In real-world scenarios, multiple-traveler path planning is crucial in various domains, including logistics, flight scheduling, and city sightseeing. Examining the MTSP carries significant benefits. On the one hand, it offers effective path planning, optimizing resource allocation, and cost reduction. On the other hand, it contributes to enhanced traffic scheduling, mitigating urban traffic congestion, and elevating the efficiency and safety of autonomous driving systems. Ultimately, this fosters the sustainable development of cities. In the future, our research will expand to incorporate additional complexities, such as time window restrictions at delivery points, demand uncertainty, and variations in vehicle speeds during autonomous driving, which will enable us to better model and optimize delivery routes for unmanned vehicles in real-world, dynamic settings.
Author Contributions
Conceptualization, S.L. and X.G.; methodology, X.G.; software, L.C.; validation, X.G., L.C. and S.Z.; formal analysis, S.L.; investigation, S.Z.; resources, S.L.; data curation, X.G. and S.Z.; writing—original draft preparation, S.Z.; writing—review and editing, Y.P. and D.Z.Y.; visualization, Y.P.; supervision, D.Z.Y.; project administration, X.M. and Y.W.; funding acquisition, S.L. and X.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Chongqing Doctoral through the Train Project (Grant No. CSTB2022BSXM-JCX0099), the Science Foundation of Chongqing Jiaotong University (Grant No. 20JDKJC-B051), the Research and Innovation Program for Graduate Students in Chongqing (Grant No. 2022S0031), the Team Building Project for Graduate Tutors in Chongqing (Grant No. JDDSTD2022004).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Severino, A.; Curto, S.; Barberi, S.; Arena, F.; Pau, G. Autonomous Vehicles: An Analysis Both on Their Distinctiveness and the Potential Impact on Urban Transport Systems. Appl. Sci. 2021, 11, 3604. [Google Scholar] [CrossRef]
- Zhang, S.; Markos, C.; James, J.Q. Autonomous vehicle intelligent system: Joint ride-sharing and parcel delivery strategy. IEEE Trans. Intell. Transp. Syst. 2022, 23, 18466–18477. [Google Scholar] [CrossRef]
- Vlachos, I.P.; Pascazzi, R.M.; Zobolas, G.; Repoussis, P.; Giannakis, M. Lean manufacturing systems in the area of Industry 4.0: A lean automation plan of AGVs/IoT integration. Prod. Plan. Control 2023, 34, 345–358. [Google Scholar] [CrossRef]
- Wang, N.; Lyu, Y.; Jia, S.; Zheng, C.; Meng, Z.; Chen, J. A dynamic graph-based many-to-one ride-matching approach for shared autonomous electric vehicles. Transportation 2023, 4, 1–27. [Google Scholar] [CrossRef]
- Stoma, M.; Dudziak, A.; Caban, J.; Droździel, P. The Future of Autonomous Vehicles in the Opinion of Automotive Market Users. Energies 2021, 14, 4777. [Google Scholar] [CrossRef]
- Hakak, S.; Gadekallu, T.R.; Maddikunta, P.K.R.; Ramu, S.P.; Parimala, M.; De Alwis, C.; Liyanage, M. Autonomous Vehicles in 5G and beyond: A Survey. Veh. Commun. 2022, 39, 100551. [Google Scholar] [CrossRef]
- Ahangar, M.N.; Ahmed, Q.Z.; Khan, F.A.; Hafeez, M. A Survey of Autonomous Vehicles: Enabling Communication Technologies and Challenges. Sensors 2021, 21, 706. [Google Scholar] [CrossRef] [PubMed]
- Parekh, D.; Poddar, N.; Rajpurkar, A.; Chahal, M.; Kumar, N.; Joshi, G.P.; Cho, W. A Review on Autonomous Vehicles: Progress, Methods and Challenges. Electronics 2022, 11, 2162. [Google Scholar] [CrossRef]
- Ahmed, H.U.; Huang, Y.; Lu, P.; Bridgelall, R. Technology Developments and Impacts of Connected and Autonomous Vehicles: An Overview. Smart Cities 2022, 5, 382–404. [Google Scholar] [CrossRef]
- Gokasar, I.; Pamucar, D.; Deveci, M.; Ding, W. A novel rough numbers based extended MACBETH method for the prioritization of the connected autonomous vehicles in real-time traffic management. Expert Syst. Appl. 2023, 211, 118445. [Google Scholar] [CrossRef]
- Na, Y.; Li, Y.; Chen, D.; Yao, Y.; Li, T.; Liu, H.; Wang, K. Optimal Energy Consumption Path Planning for Unmanned Aerial Vehicles Based on Improved Particle Swarm Optimization. Sustainability 2023, 15, 12101. [Google Scholar] [CrossRef]
- Van Huynh, D.; Do-Duy, T.; Nguyen, L.D.; Le, M.T.; Vo, N.S.; Duong, T.Q. Real-time optimized path planning and energy consumption for data collection in unmanned ariel vehicles-aided intelligent wireless sensing. IEEE Trans. Ind. Inform. 2021, 18, 2753–2761. [Google Scholar] [CrossRef]
- Yu, X.; Li, C.; Yen, G.G. A knee-guided differential evolution algorithm for unmanned aerial vehicle path planning in disaster management. Appl. Soft Comput. 2021, 98, 106857. [Google Scholar] [CrossRef]
- Chapman, G.H.; Dufort, B. Using laser defect avoidance to build large-area FPGAs. IEEE Des. Test Comput. 1998, 15, 75–81. [Google Scholar] [CrossRef]
- Ding, Y.; Du, X.; Wang, C.; Tian, W.; Deng, C.; Li, K.; Wang, Z. Path Planning for Conformal Antenna Surface Detection Based on Improved Genetic Algorithm. Appl. Sci. 2023, 13, 10490. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, S.; Chen, J.; Jiang, T.; Ye, F. Multi-UAV cooperative mission assignment algorithm based on ACO method. In Proceedings of the 2020 International Conference on Computing, Networking and Communications (ICNC), Big Island, HI, USA, 17–20 February 2020; IEEE: New York, NY, USA, 2020; pp. 304–308. [Google Scholar] [CrossRef]
- Qin, H.; Shao, S.; Wang, T.; Yu, X.; Jiang, Y.; Cao, Z. Review of Autonomous Path Planning Algorithms for Mobile Robots. Drones 2023, 7, 211. [Google Scholar] [CrossRef]
- Gündüz, F.; Birogul, S.; Kose, U. Proof of Optimum (PoO): Consensus Model Based on Fairness and Efficiency in Blockchain. Appl. Sci. 2023, 13, 10149. [Google Scholar] [CrossRef]
- Gao, Z.; Yu, W.; Liu, Z. Exact Algorithms for Some Variants of the Min-Max k-Traveling Salesmen Problem on a Tree. J. East China Univ. Sci. Technol. 2021, 47, 769–778. [Google Scholar] [CrossRef]
- He, P.; Hao, J. Memetic search for the minmax multiple traveling salesman problem with single and multiple depots. Eur. J. Oper. Res. 2023, 307, 1055–1070. [Google Scholar] [CrossRef]
- He, P.; Hao, J. Hybrid search with neighborhood reduction for the multiple traveling salesman problem. Comput. Oper. Res. 2022, 142, 105726. [Google Scholar] [CrossRef]
- Dong, Y.; Wu, Q.; Wen, J. An improved shuffled frog-leaping algorithm for the minmax multiple traveling salesman problem. Neural Comput. Appl. 2021, 33, 17057–17069. Available online: https://link.springer.com/article/10.1007/s00521-021-06298-8/metrics (accessed on 20 September 2023). [CrossRef]
- Kloster, K.; Moeini, M.; Vigo, D.; Wendt, O. The multiple traveling salesman problem in presence of drone-and robot-supported packet stations. Eur. J. Oper. Res. 2023, 305, 630–643. [Google Scholar] [CrossRef]
- Changdar, C.; Mondal, M.; Giri, P.K.; Nandi, U.; Pal, R.K. A two-phase ant colony optimization based approach for single depot multiple travelling salesman problem in Type-2 fuzzy environment. Artif. Intell. Rev. 2023, 56, 965–993. Available online: https://link.springer.com/article/10.1007/s10462-022-10190-9/metrics (accessed on 20 September 2023). [CrossRef]
- Wang, Z.; Fang, X.; Li, H.; Jin, H. An improved partheno-genetic algorithm with reproduction mechanism for the multiple traveling salesperson problem. IEEE Access 2020, 8, 102607–102615. [Google Scholar] [CrossRef]
- Rinaldi, M.; Primatesta, S.; Bugaj, M.; Rostáš, J.; Guglieri, G. Development of Heuristic Approaches for Last-Mile Delivery TSP with a Truck and Multiple Drones. Drones 2023, 7, 407. [Google Scholar] [CrossRef]
- Ivković, N.; Kudelić, R.; Golub, M. Adjustable Pheromone Reinforcement Strategies for Problems with Efficient Heuristic Information. Algorithms 2023, 16, 251. [Google Scholar] [CrossRef]
- Ayari, A.; Sadok, B. PSO-based Dynamic Distributed Algorithm for Automatic Task Clustering in a Robotic Swarm. Pro. Comp. Sci. 2019, 159, 1103–1112. [Google Scholar] [CrossRef]
- Xu, L.K.; Su, S.B.; He, C. Neighborhood Greedy Harris Hawks Optimization for Solving MTSP on the Cubic Surface. Comput. Digit. Eng. 2022, 50, 1869–1875. [Google Scholar]
- Cornejo-Acosta, J.A.; García-Díaz, J.; Pérez-Sansalvador, J.C.; Segura, C. Compact Integer Programs for Depot-Free Multiple Traveling Salesperson Problems. Mathematics 2023, 11, 3014. [Google Scholar] [CrossRef]
- Schuetz, M.J.; Brubaker, J.K.; Katzgraber, H.G. Combinatorial optimization with physics-inspired graph neural networks. Nat. Mach. Intell. 2022, 4, 367–377. [Google Scholar] [CrossRef]
- Hopfield, J.; Tank, D. Neural Computation of Decisions in Optimization Problems. Biol. Cybern 1985, 52, 141–152. [Google Scholar] [CrossRef]
- Lin, Z.; Fan, Z. A Ferroelectric Memristor-Based Transient Chaotic Neural Network for Solving Combinatorial Optimization Problems. Symmetry 2023, 15, 59. [Google Scholar] [CrossRef]
- García, L.; Talaván, P.M.; Yáñez, J. The 2-opt behavior of the Hopfield Network applied to the TSP. Oper. Res. 2022, 22, 1127–1155. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, Y.; Geng, L. Stability analysis of fractional-order Hopfield neural networks with time-varying external inputs. Neural Process. Lett. 2017, 45, 223–241. [Google Scholar] [CrossRef]
- Saadatmand-Tarzjan, M. On Computational Complexity of the Constructive-Optimizer Neural Network for the Traveling Salesman Problem. Neurocomputing 2018, 321, 82–91. [Google Scholar] [CrossRef]
- Hu, Y.; Yao, Y.; Lee, W.S. A reinforcement learning approach for optimizing multiple traveling salesman problems over graphs. Knowledge-Based Syst. 2020, 204, 106244. [Google Scholar] [CrossRef]
- Ling, Z.; Zhou, Y.; Zhang, Y. Solving multiple travelling salesman problem through deep convolutional neural network. IET Cyber-Syst. Robot. 2023, 5, e12084. [Google Scholar] [CrossRef]
- Alves, R.; Silva, C.E.; Souza, J.R. Online Route Scheduling for a Team of Service Robots with MOEAs and mTSP Model. In Proceedings of the International Conference on Engineering Applications of Neural Networks, Crete, Greece, 17–20 June 2022; Springer International Publishing: Cham, Switzerland, 2022; pp. 448–460. [Google Scholar] [CrossRef]
- Ahsini, Y.; Díaz-Masa, P.; Inglés, B.; Rubio, A.; Martínez, A.; Magraner, A.; Conejero, J.A. The Electric Vehicle Traveling Salesman Problem on Digital Elevation Models for Traffic-Aware Urban Logistics. Algorithms 2023, 16, 402. [Google Scholar] [CrossRef]
- Lee, G.M.; Gao, X. A Hybrid Approach Combining Fuzzy c-Means-Based Genetic Algorithm and Machine Learning for Predicting Job Cycle Times for Semiconductor Manufacturing. Appl. Sci. 2021, 11, 7428. [Google Scholar] [CrossRef]
- Abdellahoum, H.; Mokhtari, N.; Brahimi, A.; Boukra, A. CSFCM: An improved fuzzy C-Means image segmentation algorithm using a cooperative approach. Expert Syst. Appl. 2021, 166, 114063. [Google Scholar] [CrossRef]
- Chui, K.T. Driver stress recognition for smart transportation: Applying multiobjective genetic algorithm for improving fuzzy c-means clustering with reduced time and model complexity. Sustain. Comput. Inform. Syst. 2022, 35, 100668. [Google Scholar] [CrossRef]
- Wang, M.; Wang, H.; Feng, Y.; He, Y.; Han, Z.; Zhang, B. Investigating Urban Underground Space Suitability Evaluation Using Fuzzy C-Mean Clustering Algorithm—A Case Study of Huancui District, Weihai City. Appl. Sci. 2022, 12, 12113. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, L.; Li, T. Fuzzy C-mean clustering algorithm based on genetic simulated annealing algorithm battlefield site selection. In Proceedings of the International Conference on Automation Control, Algorithm, and Intelligent Bionics (ACAIB 2023), Xiamen, China, 28–30 April 2023; SPIE: Bellingham, WA, USA, 2023; Volume 12759, pp. 425–434. [Google Scholar] [CrossRef]
- Wang, J.; Xia, J.; Tan, D.; Lin, R.; Su, Y.; Zheng, C.H. scHFC: A hybrid fuzzy clustering method for single-cell RNA-seq data optimized by natural computation. Brief. Bioinform. 2022, 23, bbab588. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhou, J.; Chen, W. Data-driven fault diagnosis for PEMFC systems of hybrid tram based on deep learning. Int. J. Hydrog. Energy 2020, 45, 13483–13495. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, B.; Li, L.; Xu, Y.; Wei, S.; Wang, Y. The Effect of Blue Noise on the Optimization Ability of Hopfield Neural Network. Appl. Sci. 2023, 13, 6028. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, W. Application of improved Hopfield Neural Network in path planning. J. Phys. Conf. Ser. 2020, 1544, 012154. [Google Scholar] [CrossRef]
- Jolai, F.; Ghanbari, A. Integrating data transformation techniques with Hopfield neural networks for solving travelling salesman problem. Expert Syst. Appl. 2010, 37, 5331–5335. [Google Scholar] [CrossRef]
- Urolagin, S.; Sharma, N.; Datta, T.K. A combined architecture of multivariate LSTM with Mahalanobis and Z-Score transformations for oil price forecasting. Energy 2021, 231, 120963. [Google Scholar] [CrossRef]
- Wu, J.; Duan, Q. An algorithm for solving travelling salesman problem based on improved particle swarm optimisation and dynamic step Hopfield network. Int. J. Veh. Des. 2023, 91, 208–231. [Google Scholar] [CrossRef]
- Zhong, C.; Chu, Z.; Luo, C.; Gan, W. A continuous hopfield neural network based on dynamic step for the traveling salesman problem. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN 2017), Anchorage, AK, USA, 14–19 May 2017; IEEE: New York, NY, USA, 2017; pp. 3318–3323. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, J.; Yin, J. Cooperative annealing Hopfield network for unconstrained binary quadratic programming problem. Expert Syst. Appl 2011, 38, 13894–13905. [Google Scholar] [CrossRef]
- Solomon, M.M. Algorithms for the vehicle routing and scheduling problems with time window constraints. Oper. Res. 1987, 35, 254–265. [Google Scholar] [CrossRef]
- Gehring, H.; Homberger, J. A parallel hybrid evolutionary metaheuristic for the vehicle routing problem with time windows. In Parallel and Distributed Processing, Proceedings of EUROGEN99, San Juan, Puerto Rico, 12–16 April 1999; Springer: Berlin/Heidelberg, Germany, 1999; Volume 2, pp. 57–64. Available online: http://citations.springer.com/item?doi=10.1007/BFb0097899 (accessed on 20 September 2023).
- Wang, F.; Zhang, H.; Zhou, A. A particle swarm optimization algorithm for mixed-variable optimization problems. Swarm Evol. Comput. 2021, 60, 100808. [Google Scholar] [CrossRef]
- Nayyef, H.M.; Ibrahim, A.A.; Mohd Zainuri, M.A.A.; Zulkifley, M.A.; Shareef, H. A Novel Hybrid Algorithm Based on Jellyfish Search and Particle Swarm Optimization. Mathematics 2023, 11, 3210. [Google Scholar] [CrossRef]
- Lin, K.; Zhang, L.; Huang, L.; Feng, Z.; Chen, T. Improved Particle Swarm Path Planning Algorithm with Multi-Factor Coupling in Forest Fire Spread Scenarios. Fire 2023, 6, 202. [Google Scholar] [CrossRef]
- Deng, L.; Chen, H.; Zhang, X.; Liu, H. Three-Dimensional Path Planning of UAV Based on Improved Particle Swarm Optimization. Mathematics 2023, 11, 1987. [Google Scholar] [CrossRef]
- Tezel, B.T.; Mert, A. A cooperative system for metaheuristic algorithms. Expert Syst. Appl. 2021, 165, 113976. [Google Scholar] [CrossRef]
- Xia, X.; Gong, M.; Wang, T.; Liu, Y.; Zhang, H.; Zhang, Z. Parameter Identification of the Yoshida-Uemori Hardening Model for Remanufacturing. Metals 2021, 11, 1859. [Google Scholar] [CrossRef]
- Martínez-Vargas, A.; Gómez-Avilés, J.A.; Cosío-León, M.A.; Andrade, Á.G. Explaining the Walking Through of a Team of Algorithms. Computer 2023, 56, 67–81. [Google Scholar] [CrossRef]
- Etminaniesfahani, A.; Gu, H.; Salehipour, A. ABFIA: A hybrid algorithm based on artificial bee colony and Fibonacci indicator algorithm. J. Comput. Sci. 2022, 61, 101651. [Google Scholar] [CrossRef]
- Di Caprio, D.; Ebrahimnejad, A.; Alrezaamiri, H.; Santos-Arteaga, F.J. A novel ant colony algorithm for solving shortest path problems with fuzzy arc weights. Alex. Eng. J. 2022, 61, 3403–3415. [Google Scholar] [CrossRef]
- Gunay-Sezer, N.S.; Cakmak, E.; Bulkan, S. A Hybrid Metaheuristic Solution Method to Traveling Salesman Problem with Drone. Systems 2023, 11, 259. [Google Scholar] [CrossRef]
- Ma, X.; Bian, W.; Wei, W.; Wei, F. Customer-Centric, Two-Product Split Delivery Vehicle Routing Problem under Consideration of Weighted Customer Waiting Time in Power Industry. Energies 2022, 15, 3546. [Google Scholar] [CrossRef]
- Sun, Z.; Gu, X. Hybrid Algorithm Based on an Estimation of Distribution Algorithm and Cuckoo Search for the No Idle Permutation Flow Shop Scheduling Problem with the Total Tardiness Criterion Minimization. Sustainability 2017, 9, 953. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).