Abstract
Air pressure monitoring is the basis of mining-intelligent ventilation. In order to optimize the coverage of monitoring nodes, the node importance in the ventilation network was taken as the optimization basis in this study. Two evaluation indexes of the extent of node coverage and the influence degree of nodes were obtained by analyzing the influence degree of node air pressure. The entropy weight method (EWM) was used to weigh the evaluation indexes to obtain the importance of all nodes in the ventilation network. A node layout method with node importance as the optimization of air pressure-monitoring nodes was proposed. The minimum distance correlation between the limited monitoring nodes and the monitored nodes was set as the constraint condition, and any air pressure monitoring node could only monitor its adjacent nodes. The nodes with high node importance were selected as air pressure-monitoring nodes in turn until the coverage of air pressure-monitoring nodes in the ventilation network was maximized. By applying the entropy weight method (EWM) and the clustering algorithm (CA) to the case mine, the research results show that the application of the entropy weight method (EWM) to optimize the air pressure-monitoring nodes was more feasible than the clustering algorithm (CA). The coverage rate was 81.6% at different constraint values, and the maximum coverage rate was 92.1%, which meets the needs of arranging the least air pressure-monitoring nodes to monitor the maximum range of air pressure changes and can carry out full coverage monitoring of mine air pressure.
1. Introduction
Air pressure monitoring is an important means to ensure the stable operation of a ventilation system, which can effectively ensure the underground air quality and the personal safety of staff. It plays an important role in the safety and sustainability of the coal mine [1,2,3]. It is unrealistic to install air pressure sensors at each node in the coal mine ventilation system, which would also lead to a serious waste of resources [4,5]. Currently, the selection of air pressure-monitoring nodes in underground ventilation networks mainly depends on the actual situation of the mine and the experience of technical personnel. It is usually concentrated in the main working places such as the branch of the fan, the mining face, and the tunneling face [6,7,8]. Nevertheless, this manual arrangement cannot meet the needs of ventilation network air pressure monitoring and lacks a corresponding theoretical basis [9,10,11]. It cannot ensure the accuracy of node selection and the maximization of coverage. Therefore, it is of great theoretical importance and practical value to scientifically and reasonably optimize the air pressure-monitoring nodes in mine ventilation systems and accurately reflect the operation status of the entire ventilation system.
In the study of mine ventilation, the monitoring method of airflow state parameters has always been a subject of extensive research by scientific and technological workers. For the monitoring of air flow state parameters, the key lies in the optimal arrangement of air speed sensors and air pressure sensors. It is the future trend of mine ventilation research to optimize the layout method of sensors, obtain the airflow information for the whole ventilation network, and then apply it as the real-time solution for intelligent ventilation networks, ventilation anomaly diagnosis, and intelligent control of air volume [12,13,14,15]. The graph theory in operational research was first introduced to study the topology of mine ventilation, which laid the foundation for the study of global mine ventilation network topology [16,17,18]. Xie Xianping et al. [19,20] simplified the ventilation network based on the network aggregation theory and proposed measurement accuracy and investment cost as two optimization objective functions. On this basis, the Fibonacci method (FM) is used to determine the number of air pressure-monitoring nodes in the multi-fan ventilation system. Zhao Dan et al. [21,22] established a ventilation system fault range library using the air volume sensitivity matrix and the air resistance–air volume correlation matrix to optimize the location of air speed sensors and monitoring nodes by artificially specifying priority. Si Junhong et al. [23,24,25] proposed an optimal layout method for multi-parameter monitoring sensors of mine airflow. Graph theory and variable fuzzy theory (VFT) were used to optimize monitoring sub-stations and multi-parameter monitoring nodes. Li Yucheng et al. [26] designed a method for optimizing the layout of air pressure sensors by using the greedy algorithm (GA), and realized the inversion of air resistance by air volume. Based on the attribute reduction algorithm of neighborhood rough set, Liu Jian et al. [27] determined the optimal position of airflow parameter monitoring according to the importance reduction branch of roadway air volume to fault location and fault quantity. Ni Jingfeng et al. [28] established a resistive fault diagnosis model based on the decision tree (DT). Combining the diagnostic rate with the optimal sensor position to determine the optimal position and a number of airspeed sensors. Liu Yujiao et al. [29] used the independent cut set method (ICSM) to determine the layout of the airspeed sensor. It is concluded that the sensor can be arranged in 30% of the roadway branches to monitor the airflow state of the whole mine. Yan Zhenguo et al. [30] proposed using the DETMAX algorithm and tabu search algorithm (TSA) to optimize the layout of sensor positions. By analyzing the impact of air resistance error and sensor error, a limited number of sensors were used to obtain information about the entire ventilation system. Through the rational planning and layout of the structure of the ventilation network, Li Bingrui et al. [31] realized the monitoring of the air volume change of all roadways with the least airspeed sensors. This ensured the full coverage monitoring of the ventilation network without blind spots.
In summary, most scholars have studied the optimal arrangement of air speed sensors, ignoring the optimal arrangement of air pressure sensors. In the few studies on the optimal layout of air pressure sensors, most of them select the most representative or complex structure nodes as air pressure-monitoring nodes. However, the mine ventilation network is a complex and connected network model. These scholars did not take into account the mutual influence between nodes in the directed connected network and failed to maximize the coverage of monitoring nodes in the ventilation network [32,33,34,35]. Graph theory is widely used in the field of mathematics [36,37,38] which can effectively evaluate the importance of directly connected network nodes. According to the importance of nodes, the most critical nodes in the ventilation network can be identified. Arranging air pressure sensors at these important nodes can ensure that the ventilation network is effectively monitored and controlled in important areas. Therefore, node importance can be used as a key indicator to evaluate the importance of all nodes in the ventilation network. It not only helps to realize the functions of real-time calculation, data acquisition, airflow control, and fault diagnosis of intelligent ventilation, but also has positive importance for the sustainable mining of coal mines.
In this paper, based on the importance of ventilation network nodes, two evaluation indexes of the extent of node coverage and the influence degree of nodes are obtained by analyzing the influence degrees between node air pressure. The entropy weight method (EWM) is used to calculate the importance of all nodes by weighting the evaluation indexes, and the corresponding air pressure monitoring node layout scheme is formulated. Through the case application, the coverage and monitoring effects of the nodes are analyzed, and the full coverage of the air pressure-monitoring nodes is analyzed.
2. Methodology and Theory
2.1. The Establishment of Monitoring Node Optimization Index
Node air pressure refers to the relative pressure of a node’s pressure in the ventilation network to the wellhead atmospheric pressure [39]. Currently, clustering algorithm (CA) or network aggregation theory are usually applied to the study of the optimization of monitoring nodes, and the most representative nodes are selected as air pressure-monitoring nodes. However, due to the large difference in node air pressure values, these methods also introduce uncertainty [40,41]. To address the problems, a viable approach involves assessing the interrelation and correlation between nodes to determine the extent of node coverage and the influence degree of a node. These determinations subsequently contribute to calculating the node importance.
For a ventilation network , the number of nodes is and the number of branches is . When the air pressure of the node changes due to the air resistance of any branch, the other nodes in the network will also change accordingly. is used to indicate the influence of the air pressure change of the node on the other nodes . Through the calculation of the ventilation network calculation program, the air pressure variation of all nodes can be obtained, thus forming the node air pressure influence matrix, denoted as , can be defined as:
where each element in the matrix is the influence degree of the air pressure change of the node on other nodes , .
However, the mine ventilation network constitutes an intricate system. Even minor alterations in air resistance within any branch can lead to substantial fluctuations in the air pressure across the entire network of nodes. In order to ensure the rationality and accuracy of the calculation results and avoid excessive differences between the values of each element in the matrix , it is necessary to standardize the values to obtain the standardized matrix, denoted as , which can be defined as:
where represents the average value of the kth column elements in the matrix , defined as: . represents the standard deviation of the kth column element in the matrix , defined as: .
After standardization, there are still large magnitude differences in the values of matrix . To ensure the accuracy of the data, the further operation is to standardize the extreme values of each column element in the matrix and to plan the values of each column element to be ‘0–1’, so as to facilitate the analysis of the correlation between the air pressure of nodes. The extreme value standardized matrix, denoted as , which can be defined as:
where represents the smallest element in the kth column of ; represents the largest element in the kth column of .
To assess the node importance under varying distance constraints, the introduction of Euclidean distance serves to dissect the spatial correlation existing between nodes. The influence similarity matrix of the influence of node air pressure is obtained by calculating the Euclidean distance between nodes in the matrix . The Euclidean distance can be calculated using:
where represents the Euclidean distance between node and node , .
To determine the extent of an individual node’s coverage, a parameter denoted as is established as a distance constraint. When the distance separating two nodes is smaller than this defined value, it signifies a robust correlation between them, facilitating mutual monitoring capabilities. Based on the constraint value , the influence similarity matrix can be transformed into a Boolean matrix according to the above constraint. The corresponding position of the nodes with an element value less than is 1, indicating that these nodes can monitor each other. The corresponding position of the node with an element value greater than is 0, indicating that these nodes cannot monitor each other. The Boolean matrix can be expressed as:
where represents the element value of the Boolean matrix, .
The Boolean matrix delineates the monitoring connections among nodes. The extent of node coverage derived from the aforementioned approach, stands as a constituent within the evaluation indices for determining node importance through the entropy weight method (EWM).
In order to effectively quantify the influence degree of the node, the node influence degree matrix can be obtained by multiplying the elements of the node air pressure extreme standard matrix and the Boolean matrix . The influence degree matrix can be calculated by:
where is the influence degree matrix of each node on other nodes.
The results of computing the influence matrix manifest the extent to which each node impacts others within the ventilation network. Furthermore, the summation of matrix rows yields the influence degree of the node. In this paper, the influence degree of a node serves as an additional evaluative metric, subsequently incorporated into the node importance calculation via the entropy weight method (EWM).
2.2. Calculation of Node Importance Based on the Entropy Weight Method
This section primarily employs the entropy weight method (EWM) to gauge the degree of variability within each index, consequently assigning suitable weights to individual indices. During the assessment of node importance, when distinct nodes exhibit substantial disparities within the same index, the information entropy of the index is minimized, indicating heightened variability and greater informational input. As a result, these indices assume increased importance in the layout of air pressure-monitoring nodes, thus warranting correspondingly larger weight values. Conversely, in scenarios where an index demonstrates limited variability and minimal differentiation among various nodes, the weight assigned to that index is diminished. Consequently, the utilization of the entropy weight method (EWM) effectively quantifies the node importance in accordance with specific indices during the arrangement of air pressure monitoring nodes.
Node importance is determined by two evaluation indexes: the extent of node coverage and the influence degree of a node. Assuming that a ventilation network has nodes, the importance of all nodes is calculated according to the two evaluation indexes. The evaluation object and evaluation index form a matrix , and the matrix elements are recorded as , where . The steps of calculating node importance using the entropy weight method (EWM) are as follows:
Step 1: Standardization of evaluation indexes. The matrix is standardized to balance the dimensional differences between the indicators, and a new matrix is obtained. The elements contained in the matrix are , as shown in Equation (7):
where represents the tth evaluation index value of the cth evaluation object in the matrix .
Step 2: Evaluation index variability. The degree of variation in the evaluation index of the evaluation object is recorded as , as shown in Equation (8):
Step 3: Information entropy calculation. According to the definition of information entropy, the information entropy of the tth evaluation index can be calculated by Equation (9):
where . If , define .
Step 4: Weight determination. The weight of evaluation index can be calculated by Equation (10):
Step 5: Comprehensive score calculation. The comprehensive score of the th evaluation object can be calculated by Equation (11):
A brief description of the calculation steps of node importance are as follows: The two evaluation indexes of the extent of node coverage and the influence degree of a node are standardized by Equation (7). The degree of variation in the two evaluation indexes under different evaluation objects is calculated using Equation (8). The information entropy of the evaluation index is calculated using Equation (9). The weight of the evaluation index is calculated using Equation (10). The comprehensive score of each evaluation object is calculated using Equation (11), that is, the node importance, which is recorded as .
2.3. Optimization Scheme of Air Pressure Monitoring Nodes
In the air pressure monitoring system, the differential air pressure sensors for airflow are typically positioned within key locations such as the main fan air chamber, enclosed roadways, air doors, and primary air roadways. However, in practical implementation, the arrangement of these monitoring nodes often hinges on human expertise. Consequently, this study integrates established research findings and practical insights to systematically identify air pressure-monitoring nodes. The overarching aim is to optimize the coverage scope of these nodes and maximize monitoring effectiveness.
Within this paper, we establish distinct classifications for various types of nodes through the following delineations: Firstly, nodes equipped with sensors are designated as “monitoring nodes”. Subsequently, nodes falling within the range of coverage provided by the air pressure monitoring nodes are denoted as “monitored nodes”. Finally, in instances where the entirety of nodes supervised by a given node attains complete coverage, said node is identified as an “uncovered node”, essentially signifying an absence of coverage.
During the process of selecting air pressure monitoring nodes, two constraints are implemented:
Constraint 1.
The distance correlation between the limited monitoring node and the monitored node is the smallest it can be.
Constraint 2.
Limit any air pressure monitoring node so it can only monitor its adjacent nodes.
The optimized strategy for establishing air pressure monitoring nodes unfolds as follows: Initially, distinct distance correlation constraint values are individually established. Building upon the previously discussed content, computations are carried out to determine the extent of node coverage and the influence degree of a node under varying constraint values. Subsequently, employing the methodology described earlier, the importance of all nodes within the ventilation network is computed. In line with this, the node with the highest importance is identified as the primary criterion. This pivotal node is designated as the initial air pressure-monitoring node. Following this, the nodes that the selected air pressure-monitoring node can effectively encompass are tabulated and subsequently excluded from consideration. Within the remaining pool of nodes, the node possessing the highest degree of importance is once again chosen as the subsequent air pressure-monitoring node. This process is repeated iteratively. Ultimately, adhering to the descending hierarchy of node importance, nodes of considerable importance are sequentially designated as air pressure-monitoring nodes. This meticulous selection continues until the ultimate objective of optimizing the coverage of air pressure-monitoring nodes throughout the ventilation network is successfully attained.
3. Example and Application
3.1. Example Ventilation Network Introduction
This study is based on a mine situated in Guizhou, where the ventilation configuration follows a central parallel mode. The ventilation setup involves auxiliary adit inlet air, main adit auxiliary inlet air, and upcast shaft return air. The ventilation network encompasses 38 nodes and 58 branches. The collective intake air capacity for the mine stands at 9414 m3/min, while the total return air capacity is 9691 m3/min. Notably, the underground mining face operates with an autonomous intake and return air system, devoid of a series ventilation arrangement. The visual representation of the mine ventilation network topology is illustrated in Figure 1.
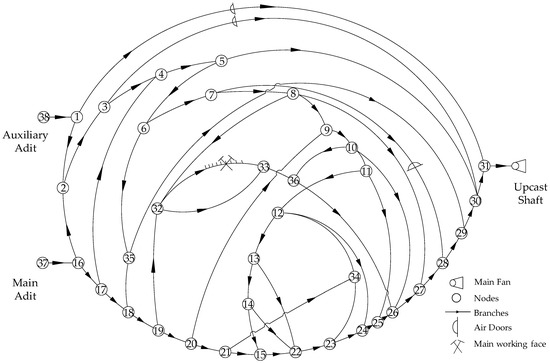
Figure 1.
Example mine ventilation network topology diagram.
Figure 1 is a complete mine ventilation network diagram. There are 38 nodes in the diagram, numbered 1~38, expressed as ‘⚪’. The line segment between any two nodes represents a branch, there is a total of 58 branches. The direction of the arrow represents the direction of the airflow. In addition, there are some ventilation facilities, such as air doors and main fans.
3.2. Optimization of Air Pressure Monitoring Node Based on the Entropy Weight Method
Firstly, according to the basic parameters of the mine ventilation network, the ventilation network solution program is written using Matlab R2020a to obtain the air pressure variation of each node in the ventilation network, and the , , , , , and other matrices are obtained. The influence similarity matrix is shown as:
Secondly, in order to realize the effective monitoring of the air pressure of the monitoring node of the pressure monitoring node, the constraint values of the correlation distance are set to be 0.10, 0.15, 0.20, 0.25 and 0.30, respectively. The values within the similarity matrix signify the degree of air pressure correlation distance between any two nodes. Smaller values indicate a stronger air pressure correlation between the respective nodes, while larger values signify a weaker air pressure correlation. The matrix is then subjected to Boolean operations based on the distance constraint values, as per Equation (5), yielding the coverage count for nodes under various constraints. By summing the matrix by rows, the influence degree of all nodes on other nodes is obtained.
Finally, the entropy weight method (EWM) is used to establish matrix and standardize it. The variation degree of the two indicators is calculated to obtain the weight, and the node importance is obtained by summing the rows. Figure 2 shows the node importance of the ventilation network under different constraint values.
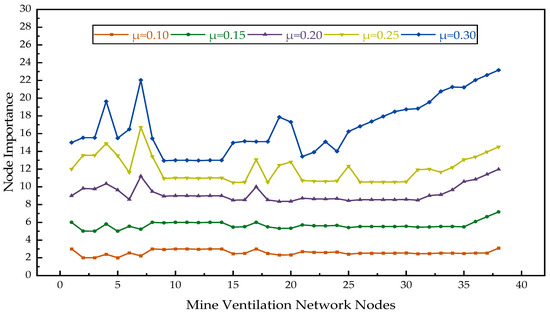
Figure 2.
Importance of all nodes in ventilation network under different constraint values.
The divergence in node importance within the ventilation network becomes evident in Figure 2, particularly when various constraint values are applied. The hierarchy of node importance within the ventilation network is organized based on distinct constraint values. The placement of air pressure-monitoring nodes, in accordance with the methodology detailed in Section 2.3, corresponds to the respective constraint values. The ensuing outcomes, encompassing monitoring nodes, monitored nodes, and uncovered nodes, across different constraint values, are comprehensively presented in Table 1.

Table 1.
Monitoring range of air pressure monitoring nodes under different constraint values.
As shown in Table 1, the distance constraint value is 0.10 and is taken as an example for analysis. Firstly, the node with the largest node importance in the whole air network node is selected as V38. According to the constraint conditions, the number of other nodes monitored by the node is one, and the monitored node is (V1). Secondly, the node V8 with the largest node importance in the uncovered node is selected. The number of nodes covered by the node is four, and the monitored nodes are (V7, V9, V32, V27). Finally, the nodes with high node importance are selected as air pressure-monitoring nodes. When = 0.10, all monitoring nodes are (V38, V8, V10, V13, V17, V21, V23, V6, V30), and uncovered nodes are (V37, V33, V28, V35, V19, V2, V5), and the range of monitoring nodes for the remaining constraint values is shown in the table above.
4. Analysis of Optimization Results
4.1. Comparative Analysis of Monitoring Range
The clustering algorithm (CA) is one of the classical algorithms in the field of clustering, which is widely used in the optimal sensor placement problem [42,43,44,45]. To verify the advantages and disadvantages of the entropy weight method (EWM) in the optimization of air pressure monitoring nodes, a comparative study was conducted with the clustering algorithm (CA).
When the clustering algorithm (CA) is used to locate the monitoring nodes, the value of the clustering number needs to be set first. Combined with the specific situation of the underground ventilation system, the minimum clustering number can be determined. Referring to the method of setting the number of clusters in [46], the maximum number of clusters in the cluster partition is . In this paper, the Davies_Bouldin Index (DB index) is used to evaluate the clustering results. The smaller the index value, the better the clustering partition effect [47].
It can be seen from Figure 3 that when the clustering number is five, the obtained DB index value is the smallest. Therefore, the optimal number of clusters is five, the location of the air pressure-monitoring node is shown in Table 2.
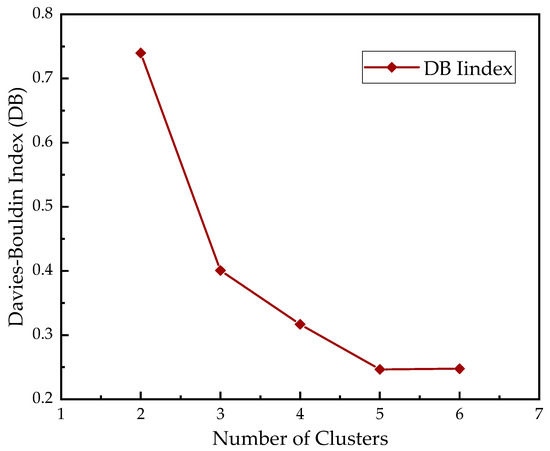
Figure 3.
The relationship curve between DB index value and cluster number c.

Table 2.
Monitoring range of optimal clustering number of air pressure monitoring nodes.
According to Table 2, when the clustering algorithm (CA) is used to divide the node partition, the number of nodes in each partition is {16, 1, 5, 1, 13}. Based on the analysis of partition 1, it is determined that the monitoring node is V17, and the monitored nodes include {V3, V5, V8, V14~V20, V22~V25, V32, V35, V36, V37}. After comparing the mine ventilation network diagram, V17 is located in the main adit, and the node farthest from the node is V29, as V29 is located in the Upcast Shaft. The two nodes are far from each other in terms of spatial distance. Obviously, this arrangement is unreasonable. Therefore, the results are optimized by the combination of Equations (4) and (5), and the optimized results are shown in the above table.
To disclose the effects of the clustering algorithm (CA) and the entropy weight method (EWM) to optimize the air pressure monitoring nodes, the probability of monitoring nodes (), the probability of monitored nodes (), the covered degree of nodes () and the uncovered degree of nodes () in the ventilation network of the two methods are calculated. The probability of monitoring nodes represents the ratio of the number of air pressure-monitoring nodes to the number of nodes in the whole air network. The probability of the monitored nodes represents the ratio of the number of nodes monitored by the air pressure monitoring nodes to the number of nodes in the whole air network. The covered degree of nodes represents the ratio of the number of all nodes in the maximum coverage area to the number of nodes in the whole air network. The uncovered degree of nodes represents the ratio of the number of nodes uncovered by the air pressure-monitoring nodes to the number of nodes in the whole air network. The calculation results of these data are helpful to evaluate the layout effect of air pressure-monitoring nodes. The results of the clustering algorithm (CA) are shown in Table 3, and the results of the entropy weight method (EWM) are shown in Table 4.

Table 3.
Node coverage rate of optimal clustering number of clustering algorithm.

Table 4.
Node coverage rate of different constraint values of entropy weight method.
It can be seen from Table 3 and Table 4 that the entropy weight method (EWM) can be used to optimize the layout of monitoring nodes. When the distance constraint values are 0.15 and 0.30 the is largest, both of which are 92.1%. When the distance constraint value is 0.15, 11 monitoring nodes are arranged, and is 28.9% lower than the constraint value which is 0.30. Considering this comprehensively, it is obvious that when the constraint value is 0.15, it meets the monitoring requirements of using the least monitoring nodes to achieve the maximum range of nodes. The clustering algorithm (CA) is used to optimize the layout of the air pressure-monitoring nodes. The optimal clustering number is five, is 13.2%, is 34.2%, is 47.4%, and is 52.6%. The monitoring effect is not as good as the application of the entropy weight method (EWM). Therefore, the entropy weight method (EWM) is superior to the clustering algorithm (CA) in the optimization of monitoring nodes, which can ensure the realization of the air pressure monitoring goal of the ventilation network in terms of efficiency and cost-effectiveness.
4.2. Analysis of Optimal Layout of Air Pressure Monitoring Nodes
In order to evaluate the effect of the clustering algorithm (CA) and the entropy weight method (EWM) on the location and layout of air pressure-monitoring nodes, their optimization results are compared. The results show that the entropy weight method (EWM) comprehensively considers the weight of each attribute, which makes the position of nodes in the layout map more scientific and reasonable, and can more accurately reflect the actual situation of the mine ventilation system. Figure 4 shows the results of the optimal arrangement of air pressure monitoring nodes in the optimal constraint value of the entropy weight method (EWM).
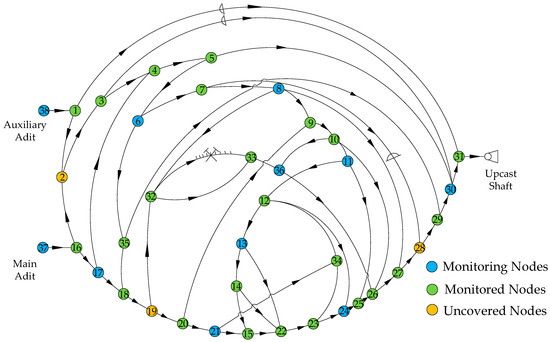
Figure 4.
Optimal layout of air pressure monitoring nodes with optimal constraint value.
From Figure 4, it can be seen that the application of the entropy weight method (EWM) to optimize air pressure-monitoring nodes not only performs well in improving monitoring efficiency and data accuracy, but also provides more reliable technical support for the safe operation of the mine ventilation system. The method can be flexibly adjusted according to the characteristics and needs of different mines, which provides a useful method and ideas for mine safety production and ventilation system optimization. Therefore, the entropy weight method (EWM) has broad application prospects in the optimization of site selection and layout of air pressure monitoring nodes and provides new ideas and references for research and practice in related fields.
4.3. Analysis of Full Coverage of Air Pressure Monitoring Nodes
By optimizing the arrangement of air pressure monitoring nodes using the entropy weight method (EWM), the coverage rate of ventilation network nodes was successfully increased to 92.1%, which means that the comprehensive monitoring of ventilation network nodes has been realized to a great extent. However, in order to achieve full coverage of the monitoring range, further attention needs to be paid to uncovered nodes.
In order to better understand the monitoring effect, a comparative analysis is made before and after the installation of the sensor for the uncovered node. The multi-node monitoring of the monitored nodes of the ventilation network is counted, and the monitored nodes are classified according to the different conditions of single monitoring node, double monitoring nodes and three monitoring nodes. Figure 5 shows the monitoring situation before and after the installation of sensors in uncovered nodes.
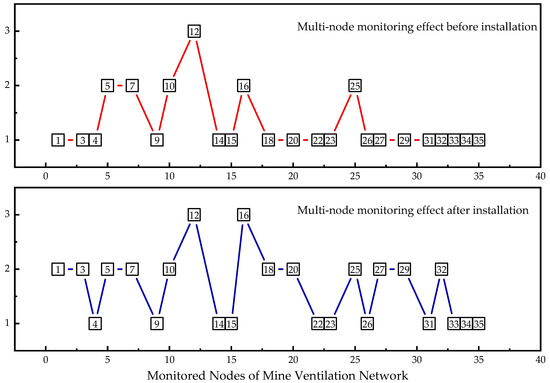
Figure 5.
Comparison chart of multi-node monitoring range.
From Figure 5, we can see the set of 24 monitored nodes. Before installing sensors in uncovered nodes, the number of monitored nodes for single-node, double-node, and three-node monitoring is eighteen, five and one, respectively. After installing sensors in uncovered nodes, the number of monitored nodes for single-node monitoring is reduced to eleven, the number of monitored nodes for double-node monitoring is increased to eleven, and the number of monitored nodes for three-node monitoring is increased to two. In order to better evaluate the monitoring effect of uncovered nodes before and after the installation of sensors, it is necessary to calculate the monitoring probability of single-node, double-node, and three-node monitoring, where and represent the ratio of the number of monitored nodes to the number of all nodes under different monitoring conditions before and after the installation of sensors by uncovered nodes, as shown in Table 5.

Table 5.
Monitoring results of uncovered nodes before and after installing sensors.
According to the data in Table 5, it can be observed that after the sensor is installed on the uncovered node, the probability of single-node monitoring decreases from 47.4% to 18.5%, while the probability of double-node monitoring increases from 13.2% to 28.9%. At the same time, the probability of three-node monitoring also increased from 2.6% to 5.7%. These calculation results show that the number of sensors can be increased, and the sensors can be targeted at uncovered nodes.
Therefore, it is an effective strategy worthy of promotion and application to increase the number of sensors and optimize the layout to achieve full coverage monitoring of the air pressure in the ventilation network nodes. Such a monitoring strategy will further improve the reliability and stability of the mine ventilation system, ensure the safety of miners, and also help to improve the safety production efficiency and sustainable development of coal mines.
5. Discussion
In this study, the entropy weight method (EWM) is used to solve the positioning problem of air pressure-monitoring nodes in mine ventilation networks, which is a new method based on a directed connected network graph. In the practical application of the case mine, it is verified that the entropy weight method (EWM) is more suitable for the positioning research of the air pressure monitoring nodes than the clustering algorithm (CA) for underground mining ventilation.
However, it is important to acknowledge that the node air pressure change data was obtained through the mine ventilation network solution program utilized in this study. It may not fully account for the various factors affecting actual roadway wind resistance, such as the roughness and cross-sectional area of the roadway section. Therefore, the data used in our analysis can be considered idealized. As mining operations progress, the structure of mine roadways tends to become increasingly complex, which presents additional challenges for mining ventilation. The method proposed in this paper can be regarded as a foundational monitoring work. However, as the ventilation network structure continues to evolve and grow in complexity, it is important to note that comprehensive monitoring can still be achieved using the approach outlined in Section 4.3 of this paper. This adaptable method allows for ongoing monitoring and adjustment, making it possible to address the emerging complexities of the ventilation network in response to the changing conditions and challenges encountered during the mining process.
In addition, the focus of this study is limited to the optimal layout of air pressure-monitoring nodes. However, the monitoring indicators involved in the actual mine ventilation system are far more than that, including temperature, humidity, harmful gas concentration, and other aspects. The future research direction can be multi-index development and explore the optimal layout method of multiple monitoring indicators to further improve the monitoring efficiency and comprehensive evaluation ability of the ventilation system. It can provide more efficient, safe and sustainable solutions for mine ventilation management.
6. Conclusions
In this study, the optimal scheme of air pressure-monitoring nodes was proposed by analyzing the influence degree of air pressure between ventilation network nodes. The entropy weight method (EWM) was used to calculate the two evaluation indexes of the extent of node coverage and the influence degree of nodes. And the node importance was taken as the optimal condition to optimize the layout of air pressure-monitoring nodes. The following conclusions were drawn:
- (1)
- The correlation between ventilation network nodes was analyzed. The process of calculating the node importance of ventilation network using the entropy weight method (EWM) was introduced. The layout scheme and specific steps of the air pressure monitoring nodes were given.
- (2)
- For the case mine ventilation network, the entropy weight method (EWM) and the cluster analysis algorithm were used to optimize the layout of air pressure-monitoring nodes. The entropy weight method (EWM) is superior to the clustering algorithm (CA) in the optimization of monitoring nodes.
- (3)
- On the basis of this study, the comparative analysis of the monitoring effect when the sensor was installed on the uncovered nodes can be further carried out, so as to improve the research on the full coverage of air pressure monitoring nodes.
Author Contributions
Conceptualization, S.Y.; methodology, S.Y. and X.Z.; validation, S.Y. and X.Z.; formal analysis, S.Y., X.Z., J.L. and N.X.; investigation, X.Z., J.L. and N.X.; writing—original draft preparation, S.Y. and X.Z.; writing—review and editing, S.Y. and X.Z.; visualization, X.Z., J.L. and N.X.; supervision, S.Y.; project administration, S.Y.; funding acquisition, S.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the Open Fund of the State Key Laboratory of Gas Disaster Detecting, Preventing and Emergency Controlling, No. 2022SKLKF05.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
First of all, we acknowledge the editors and reviewers for their valuable comments; secondly, we are grateful for the help of the fund from the State Key Laboratory of Gas Disaster Detecting, Preventing and Emergency Controlling; finally, we appreciate the authors of all references for their achievements that bring us new ideas.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Song, Y.; Yang, S.; Hu, X.; Song, W.; Sang, N.; Cai, J.; Xu, Q. Prediction of gas and coal spontaneous combustion coexisting disaster through the chaotic characteristic analysis of gas indexes in goaf gas extraction. Process Saf. Environ. Prot. 2019, 129, 8–16. [Google Scholar] [CrossRef]
- Zhang, P.; Lan, H.; Yu, M. Reliability evaluation for ventilation system of gas tunnel based on Bayesian network. Tunn. Undergr. Space Technol. 2021, 112, 103882. [Google Scholar] [CrossRef]
- Wang, J.; Jia, M.; Bin, L.; Wang, L.; Zhong, D. Regulation and optimization of air quantity in a mine ventilation network with multiple fans. Arch. Min. Sci. 2022, 67, 179–193. [Google Scholar] [CrossRef]
- Lu, X.; Yin, H. The intelligent theory and technology of mine ventilation. J. China Coal Soc. 2020, 45, 2236–2247. [Google Scholar] [CrossRef]
- Zhou, F.; Wei, L.; Xia, T. Principle, key technology and preliminary realization of mine intelligent ventilation. J. China Coal Soc. 2020, 45, 2225–2235. [Google Scholar] [CrossRef]
- Yang, S.; Tang, J.; Zhao, S.; Hua, F. Early warning on coal and gas outburst with dynamic indexes of gas emission. Disaster Adv. 2010, 3, 403–406. [Google Scholar]
- Yang, S.; Tang, J.; Wen, G.; Kang, J.; Liu, C. Coal and gas outburst disaster early warning and emergency response decision support technology. Chongqing Daxue Xuebao 2012, 35, 121–125. [Google Scholar]
- Yang, S.; Li, S.; Liu, C. Coal and gas outburst disaster early warning technology based on coal mine Internet of things. Coal Sci. Technol. Mag. 2015, 3, 109–112. [Google Scholar] [CrossRef]
- Li, Q.; Wang, F.; Wang, Y.; Forson, K.; Cao, L.; Zhang, C.; Zhou, C.; Zhao, B.; Chen, J. Experimental investigation on the high-pressure sand suspension and adsorption capacity of guar gum fracturing fluid in low-permeability shale reservoirs: Factor analysis and mechanism disclosure. Environ. Sci. Pollut. Res. 2022, 29, 53050–53062. [Google Scholar] [CrossRef]
- Li, Q.; Han, Y.; Liu, X.; Ansari, U.; Cheng, Y.; Yan, C. Hydrate as a by-product in CO2 leakage during the long-term sub-seabed sequestration and its role in preventing further leakage. Environ. Sci. Pollut. Res. 2022, 29, 77737–77754. [Google Scholar] [CrossRef]
- Wang, F.; Xiao, Z.; Liu, X.; Ren, J.; Xing, T.; Li, Z.; Li, X.; Chen, Y. Strategic design of cellulose nanofibers@ zeolitic imidazolate frameworks derived mesoporous carbon-supported nanoscale CoFe2O4/CoFe hybrid composition as trifunctional electrocatalyst for Zn-air battery and self-powered overall water-splitting. J. Power Sources 2022, 521, 230925. [Google Scholar] [CrossRef]
- Huang, X.; Liu, Y. Research and design of intelligent mine ventilation construction architecture. Int. J. Low-Carbon Technol. 2022, 17, 1232–1238. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.; Zhang, J.; Li, B.; Zhang, Z.; Dong, J.; Cui, Y. Accurate and real-time network calculation for mine ventilation without wind resistance measurement. Wind Eng. Ind. Aerodyn. 2022, 230, 105183. [Google Scholar] [CrossRef]
- Wallace, K.; Prosser, B.; Stinnette, J.D. The practice of mine ventilation engineering. Int. J. Min. Sci. Technol. 2015, 25, 165–169. [Google Scholar] [CrossRef]
- Jia, P.; Jia, J.; Song, L.; Li, Z.; Li, B. Theory of RPOD adjustment of air volume for mine intelligent ventilation. Int. J. Vent. 2022, 21, 316–329. [Google Scholar] [CrossRef]
- Moll, A.; Lowndes, I. Graph theory applied to mine ventilation analysis. Bull. Inst. Math. Its Appl. 1992, 28, 103–106. [Google Scholar]
- Foulds, L. Graph Theory: A Survey of Its Use in Operations Research; University of Canterbury: Christchurch, New Zealand, 1982; Volume 10, pp. 35–65. [Google Scholar]
- Wu, X.S.; Topuz, E. Analysis of mine ventilation systems using operations research methods. Int. Trans. Oper. Res. 1998, 5, 245–254. [Google Scholar] [CrossRef]
- Xie, X.; Duan, Z. Optimization of the Layout of Monitoring Points for Multi-Ventilator and Multi-Fan Station Ventilation System. Met. Mine 2009, 39, 147. [Google Scholar]
- Wang, T.; Xie, X.; Li, J.; Tan, X.; Yin, X.; Su, M.; Luo, W.; Cui, C. Optimization of monitoring points’ layout for the multi-fan and multi-station ventilation system. Appl. Mech. Mater. 2014, 614, 113–117. [Google Scholar] [CrossRef]
- Zhao, D.; Pan, J. Fault Source Diagnosis for Mine Ventilation Based on Improved Sensitivity Matrix and Its Wind Speed Sensor Setting. Zhongguo Anquan Kexue Xuebao 2011, 21, 78–84. [Google Scholar]
- Pan, J.; Li, Z.; Chen, Z. Fault source diagnosis for ventilation system and air velocity transducer placement in Daming Mine. J. China Coal Soc. 2013, 38, 153–158. [Google Scholar]
- Chen, K.; Si, J.; Zhou, F.; Zhang, R.; Shao, H.; Zhao, H. Optimization of air quantity regulation in mine ventilation networks using the improved differential evolution algorithm and critical path method. Int. J. Min. Sci. Technol. 2015, 25, 79–84. [Google Scholar] [CrossRef]
- Si, J.; He, S.; Cheng, G.; Chu, T. The real-time monitoring technology of air quantity based on the optimization of air velocity sensors location in mine ventilation network. Electr. Eng. Comput. Sci. 2019, 3, 164–169. [Google Scholar]
- Si, J.; Wang, X.; Wang, Y.; Li, L. Dynamic Monitoring Technology of Air Quantity in Mine Ventilation System Based on Optimum Location of Wind Speed Sensors. In Proceedings of the IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; p. 042036. [Google Scholar]
- Li, Y.; Li, J.; Deng, C.; Liu, R. Improved algorithm of air quantity calculating resistance based on diagonal subnetwork. J. China Coal Soc. 2019, 44, 1147. [Google Scholar] [CrossRef]
- Liu, J.; Jiang, Q.; Liu, L.; Wang, D.; Huang, D.; Deng, L.; Zhou, Q. Resistance variant fault diagnosis of mine ventilation system and position optimization of wind speed sensor. J. China Coal Soc. 2021, 46, 8. [Google Scholar] [CrossRef]
- Ni, J.; Le, X.; Chang, L.; Deng, L. Resistance variant fault diagnosis and optimized layout of sensors for mine ventilation based on decision tree. Saf. Sci. Technol. 2021, 17, 34–39. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Z.; Gao, K.; Huang, Y.; Zhu, C. Efficient graphical algorithm of sensor distribution and air volume reconstruction for a smart mine ventilation network. Sensors 2022, 22, 2096. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, Y.; Fan, J.; Huang, Y.; Zhong, Y. An Efficient Method for Optimizing Sensors’ Layout for Accurate Measurement of Underground Ventilation Networks. IEEE Access 2023, 11, 72630–72640. [Google Scholar] [CrossRef]
- Li, B.; Wang, W.; Chen, F.; Liu, N. Optimal arrangement of wind speed sensor based on directed path matrix method. Ind. Mine Autom. 2021, 47, 52–57. [Google Scholar] [CrossRef]
- Wang, F.; Liu, X.; Jiang, B.; Zhuo, H.; Chen, W.; Chen, Y.; Li, X. Low-loading Pt nanoparticles combined with the atomically dispersed FeN4 sites supported by FeSA-NC for improved activity and stability towards oxygen reduction reaction/hydrogen evolution reaction in acid and alkaline media. J. Colloid Interface Sci. 2023, 635, 514–523. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, C.; Yang, Y.; Ansari, U.; Han, Y.; Li, X.; Cheng, Y. Preliminary experimental investigation on long-term fracture conductivity for evaluating the feasibility and efficiency of fracturing operation in offshore hydrate-bearing sediments. Ocean Eng. 2023, 281, 114949. [Google Scholar] [CrossRef]
- Li, Q.; Zhao, D.; Yin, J.; Zhou, X.; Li, Y.; Chi, P.; Han, Y.; Ansari, U.; Cheng, Y. Sediment instability caused by gas production from hydrate-bearing sediment in Northern South China Sea by horizontal wellbore: Evolution and mechanism. Nat. Resour. Res. 2023, 32, 1595–1620. [Google Scholar] [CrossRef]
- Wei, L.; Zhou, F.; Cheng, J.; Luo, X.; Li, X. Classification of structural complexity for mine ventilation networks. Complexity 2015, 21, 21–34. [Google Scholar] [CrossRef]
- Chen, B.; Wang, Z.; Luo, C. Integrated evaluation approach for node importance of complex networks based on relative entropy. Syst. Eng. Electron. 2016, 27, 1219–1226. [Google Scholar] [CrossRef]
- Bi, Q.; Li, Y.; Shen, C. Screening of Evaluation Index and Construction of Evaluation Index System for Mine Ventilation System. Sustainability 2021, 13, 11810. [Google Scholar] [CrossRef]
- De Souza, E. Optimization of complex mine ventilation systems with computer network modelling. IFAC Proc. Vol. 2007, 40, 323–329. [Google Scholar] [CrossRef]
- Krach, A. Node method for solving the mine ventilation networks. Arch. Min. Sci. 2011, 56, 601–620. [Google Scholar]
- Li, G.; Kocsis, C.; Hardcastle, S. Sensitivity analysis on parameter changes in underground mine ventilation systems. Coal Sci. Eng. 2011, 17, 251–255. [Google Scholar] [CrossRef]
- Duhart, A.; Enrique, I. Multiple Period Mine Ventilation and Fan Selection Optimization; Laurentian University: Sudbury, ON, Canada, 2010; Volume 71. [Google Scholar]
- Yoganathan, D.; Kondepudi, S.; Kalluri, B.; Manthapuri, S. Optimal sensor placement strategy for office buildings using clustering algorithms. Energy Build. 2018, 158, 1206–1225. [Google Scholar] [CrossRef]
- Friswell, M.I.; Castro-Triguero, R. Clustering of sensor locations using the effective independence method. AIAA J. 2015, 53, 1388–1391. [Google Scholar] [CrossRef]
- Feng, Y.; Zhao, S.; Liu, H. Analysis of network coverage optimization based on feedback K-means clustering and artificial fish swarm algorithm. IEEE Access 2020, 8, 42864–42876. [Google Scholar] [CrossRef]
- An, H.; Youn, B.D.; Kim, H.S. Optimal sensor placement considering both sensor faults under uncertainty and sensor clustering for vibration-based damage detection. Struct. Multidiscip. Optim. 2022, 65, 102. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, F.; Song, W. Estimating the optimal number of clusters via internal validity index. Neural Process. Lett. 2021, 53, 1013–1034. [Google Scholar] [CrossRef]
- Xiao, J.; Lu, J.; Li, X. Davies Bouldin Index based hierarchical initialization K-means. Intell. Data Anal. 2017, 21, 1327–1338. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).