Robust Nonlinear Adaptive Control for Power Quality Enhancement of PMSG Wind Turbine: Experimental Control Validation

Abstract

Due to the intense penetration of wind energy into the power grid, grid quality and stability have become a crucial necessity in this type of power generation. It is in this context that this article has just designed an Adaptive Nonlinear Control strategy applied to the Permanent Magnet Synchronous Generator (PMSG) of 1.5 MW power, in order to generate good quality and cleanly usable energy. Interestingly, this robust control algorithm mainly uses the Lyapunov stability theory, which ensures the stability of the Wind Energy Conversion System (WECS), and therefore offers excellent results in the presence of system parametric uncertainties and changes in the elements of the external environment. To this end, the methodology followed in this in-depth study focuses on the application of the Adaptive Backstepping Control algorithm for WECS by exploiting the MATLAB/Simulink toolbox. The theoretical study and simulation of the WECS was supported by the Processor-in-the-Loop (PIL) implantation of the control in the dSPACE DS1104 embedded board to approve the effect of the control in terms of robustness against different wind profiles and parametric changes. ST-LINK communication is used to connect the embedded board and the host computer. The results obtained revealed a fast response of the different signals, a practically low ripple rate of the order of 0.1% and minor overshoots for the different electrical quantities. Operation with a unity power factor is well ensured via this control strategy. Therefore, the adaptive control applied to the WECS has verified the high performance offered and benefits from additional robustness properties.

1. Introduction

Historically, the production of electrical energy was invented by Michael Faraday in 1831 in the form of a DC generator (also called Faraday Disk). Naturally, this electric power generation faces several problems such as limited fossil fuel resources and undesirable under-productions of fuel resource utilization. Cleaner and more sustainable solutions for long-term development are emerging as promising solutions [1,2]. Wind energy production is growing more significantly than any other type and plays an important role in the energy supply of modern systems [3,4,5,6].

At this stage, the presence of power electronics and control techniques play an essential role in distributed energy generation/conversion systems. Through to power electronics and control techniques, the performance of renewable energy generation/conversion systems is constantly improving.

Active power can be routed in both directions (wind/grid) using voltage source back-to-back power converter technology. Therefore, it is possible to completely control the power (extracted/supplied) through a back-to-back power converter from voltage source to full power [7,8,9]. With more and more advanced control techniques, static power converters play a very important role, not only to reduce mechanical stress and increase energy efficiency, but also to make the whole generation system a conversion of fully controllable energy [10]. The use of power converters becomes an attractive solution for grid-connected generated energy applications, even if there are losses due to switching [11,12].

Mohammed H. Q et al. [13] present in their work the results obtained for the control of the two statics (converter on the machine side/converter on the network side) via eight proportional-integral regulators. The wind system is based on the direct drive permanent magnet synchronous generator in this study. The main objective during this work is the maximization of the power extracted via the MPPT control, and the improvement of the low voltage transmission capacity. The results obtained attest that the control algorithm can offer satisfactory results in terms of monitoring. However, the moderate quality and the ripples in the energy produced present the major disadvantages obtained by using the conventional regulation.

Several control strategies can be applied to the PMSG-based wind energy conversion system. We find, among others, the field-oriented control (FOC), the direct torque-power control (DTC-DPC) and, of course, more robust and reliable controls, such as the nonlinear Adaptive Backstepping control, which is the subject of this article.

Works [14,15,16] exploit fuzzy proportional integral (PI) controllers to control the energy flow through static power converters. In the works of Yang. B et al. [17,18], the authors used the sliding mode algorithm to improve the work promised by the standard regulators. Other authors exploit artificial intelligence technology in the form of fuzzy logic to estimate the energy yield, and to optimize the amount of wind energy extracted, such as the work of Jafarian. M et al. [19]. Siahkali et al. [20], on his side, developed a method based on fuzzy logic to properly plan wind energy production, while Calderaro. V et al. [21] exploited fuzzy logic technology to extract the maximum power coming from the wind, as well as the control of the pitch angle and the intermediate bus voltage, this for different types of wind generators.

The important remark drawn between these cited works or other works is that the regime of the wind system is previously well-known and its parameters are considered as known and controlled. However, the wind system and its uncertain nature make the control applied to extract electrical energy less efficient. It is with this in mind that this present work has just applied a control algorithm applied to nonlinear systems, known as Adaptive Backstepping Control. The application of this control algorithm is important, in order to overcome the anomalies of the parametric variations of wind system, and to have a control which adapts with the variations of the parameters of the wind system based on the PMSG, and then offers a powerful high-quality electricity to the distribution grid.

Practical verification of this control algorithm is done using the dSPACE DS1104 on-board while using the Processor-In-The-Loop test. This technique, which stands as one of the ways that companies are trying to reduce their design costs and improve the efficiency of their wind turbines, is based on the use of processor technology in the loop. A processor in the loop can provide significant benefits in many systems, including avionics and space applications and of course wind power installations. The benefits of using processor is to verify the proper functioning of the checks algorithms for these installations. Additionally, the cost savings associated with less outsourcing can also be significant. The main idea of this verification test comes to justify the originality of the work in the vision to test, in a practical way, the possibility of applying a robust adaptive control for the wind system, and this in the presence of parametric changes of the system and under a fluctuating and variable wind profile and ensure the possibility of real implantation thereafter in a practical bench. This part has just answered that the structure of modern wind turbine can be controlled by well-advanced control structures in real wind turbine installations.

For better readability of this article, this article will be structured as follows: Section 1 presents a state-of-the-art of control algorithms applied to wind energy conversion systems. Section 2 will be reserved for the modeling of the wind turbine structure, which contains both the modeling of the permanent magnet synchronous machine and the aerodynamic model of the wind turbine. Section 3 will circumspect the adaptive backstepping control algorithm applied to static converters, to extract maximum efficiency from the power produced. Section 4 reveals the verification of the control by the Processor-in-the-loop test while exploiting the DS 1104 R&D controller board and the Matlab/Simulink environment. The ControlDesk software is also used to record the various measured signals. A presentation and discussion of the various signals sampled through ControlDesk software are also disclosed in this section. Section 5 summarizes the main conclusions and the discussion of the results obtained.

2. Wind Turbine & PMSG Modeling

2.1. Wind Turbine Modeling

The modeling of the wind turbine aerodynamics is summarized according to the following mathematical equations [22]:

$$P_{aer}=\frac{1}{2}\rho .S.V_w^3$$

(1)

$$P_{Tur}=C_p\left(\lambda ,\beta \right).P_{aer}=\frac{1}{2}\rho .S.V_w^3$$

(2)

$$\lambda =\frac{R.\mathrm{\Omega }}{V_w}$$

(3)

$$\frac{1}{{\lambda }^{\prime }}=\frac{1}{\lambda +0.08\beta }-\frac{0.035}{{\beta }^3+1}$$

(4)

$$C_p\left(\lambda ,\beta \right)=0.5176\left(\frac{116}{{\lambda }^{\prime }}-0.4\beta -5\right)e^{\frac{-21}{{\lambda }^{\prime }}}+0.0068\lambda$$

(5)

$$T_{Tur}=\frac{1}{2}\frac{C_p\left(\lambda ,\beta \right).\rho .S.R^3}{{\lambda }^3}{\mathrm{\Omega }}^2$$

(6)

2.2. PMSG Modeling

In order to reduce the calculation time and study the global dynamics of the wind conversion system, a wind generator model in a two-phase reference will be used [22].

The expression of the stator voltages in Park’s frame is mentioned as follows:

$$\left\{\begin{array}{c}{V}_{sd}=-R_s.i_{sd}-{\stackrel{•}{\mathsf{\Psi }}}_{sd}-{\omega }_e.{\mathsf{\Psi }}_{sq}\\ V_{sq}=-R_s.i_{sq}-{\stackrel{•}{\mathsf{\Psi }}}_{sq}+{\omega }_e.{\mathsf{\Psi }}_{sd}\end{array}\right.$$

(7)

The expressions of stator flux components as a function of stator currents are given by:

$$\left\{\begin{array}{c}{\mathsf{\Psi }}_{sd}=L_d.i_{sd}+{\mathsf{\Psi }}_f\\ {\mathsf{\Psi }}_{sq}=L_q.i_{sq}\end{array}\right.$$

(8)

After transformation and simplification, we obtain the expressions of the stator voltages:

$$\left\{\begin{array}{c}{V}_{sd}=-R_s.i_{sd}-L_d\frac{d\left(i_{sd}\right)}{dt}-{\omega }_e.\left(L_q.i_{sq}\right)\\ V_{sq}=-R_s.i_{sq}-L_q\frac{d\left(i_{sq}\right)}{dt}+{\omega }_e.\left(L_d.i_{sd}\right)+{\omega }_e.{\mathsf{\Psi }}_f\end{array}\right.$$

(9)

Consequently, the dynamics of the stator currents are obtained as follows:

$$\left\{\begin{array}{c}\frac{d\left(i_{sd}\right)}{dt}=\frac{-1}{L_d}\left[V_{sd}+R_s.i_{sd}-{\omega }_e.\left(L_q.i_{sq}\right)\right]\\ \frac{d\left(i_{sq}\right)}{dt}=\frac{-1}{L_q}\left[V_{sq}+R_s.i_{sq}-{\omega }_e.\left(L_d.i_{sd}\right)-{\omega }_e.{\mathsf{\Psi }}_f\right]\end{array}\right.$$

(10)

The electromagnetic torque can be calculated by:

$$T_{em}=\frac{-3}{2}.p.\left[\left(L_d-L_q\right).i_{sd}.i_{sq}+{\mathsf{\Psi }}_f.i_{sq}\right]$$

(11)

The equation of the electromagnetic torque for a machine with smooth poles (L_d = L_q), which is the case in this work, results only from the flux of permanent magnet and from the component quadrature of the stator current:

$$T_{em}=\frac{-3}{2}.p.{\mathsf{\Psi }}_f.i_{sq}$$

(12)

The mechanical equation is defined by:

$$T_{Tur}-T_{em}-f_c.\mathrm{\Omega }=J.\frac{d\mathrm{\Omega }}{dt}$$

(13)

The active and reactive powers of PMSG can be expressed as follows:

$$\left\{\begin{array}{c}{P}_{gen}=T_{em}.\mathrm{\Omega }=\frac{3}{2}\left[V_{sd}.i_{sd}+V_{sq}.i_{sq}\right]\\ Q_{gen}=\frac{3}{2}\left[V_{sq}.i_{sd}-V_{sd}.i_{sq}\right]\end{array}\right.$$

(14)

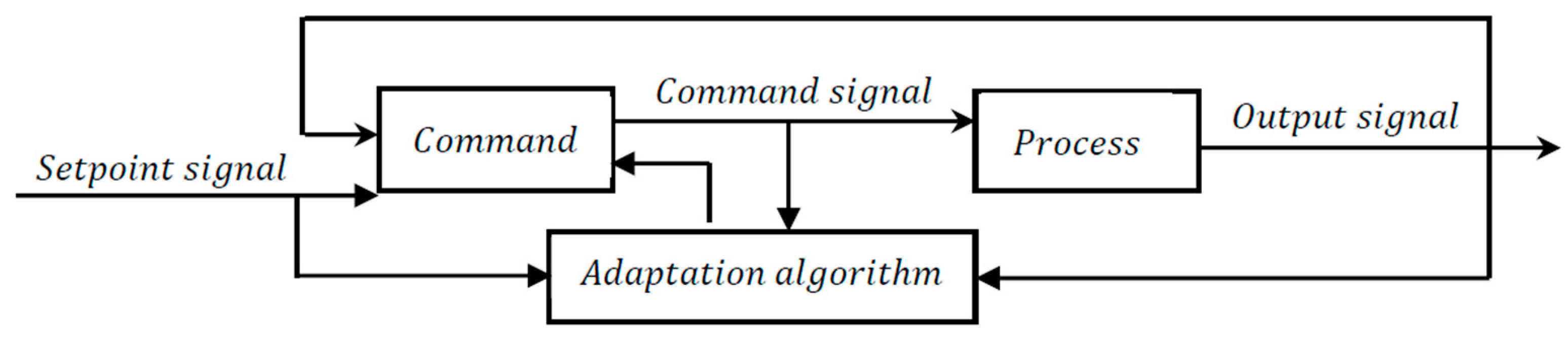
3. Adaptive Backstepping Model

3.1. Operating Principle

The origin of backstepping control is virtually unclear, due to several research works published during the 80s and early 90s. However, backstepping control has received particular attention, according to the work of Feurer in 1978 [23], and subsequently the work of Professor V. Kokotovic and Sussmann in 1989 [24], which was based on the work of Feurer and Tsinias [25]. It was from 1991 that Kanellakopoulos presented control laws using the backstepping control algorithm for a variety of nonlinear systems [26]. The technique developed by Kanellakopoulos makes it possible to offer a systematic method for nonlinear systems and is based on a representation using several subsystems of order 1 that are cascaded to dissociate the global system. The interest of mastering these different subsystems is to ensure a virtual control for the following subsystem, in order to ensure the convergence of the process towards its equilibrium state. At the end, we put a function called the Lyapunov candidate function, which ensures the overall stability of the system.

3.1.1. Adaptive Backstepping Control Synthesis

Adaptive control offers an iterative and systematic method; it uses the three essential parts of an adaptive control based on Lyapunov’s theory, namely, the control law, the adaptation law and Lyapunov’s candidate function.

The principle block diagram of the adaptive control of a closed-loop nonlinear system is shown in Figure 1 [27]:

3.1.2. Applying Adaptive Backstepping Control to PMSG

Backstepping control is based on capturing angular position. The rotor magnetic flux is produced by permanent magnets and rotates at a speed equal to that of stator synchronism. The purpose of this control is to control the electromagnetic torque of the machine by controlling the mechanical rotational speed (the torque control strategy). This control is based on the vector control of the stator voltages, which means that reference voltages must be imposed for the converter on the machine side to determine the control signals of the rectifier arms. This control strategy requires decoupling of the stator current components $i_{sd }$ and $i_{sq },$ defined in the d-q rotating frame similar to vector control. Therefore, the electromagnetic torque control is performed by controlling the current $i_{sq },$ and the flux control is performed by controlling the forward current $i_{sd }$.

According to Equations (9)–(11) and (13), the system model is defined by [22]:

$$\left\{\begin{array}{c}\frac{d\left(i_{sd}\right)}{dt}=-\frac{R_s}{L_d}..i_{sd}-\frac{L_q}{L_d}.{\omega }_e.i_{sq}-\frac{1}{L_d}.V_{sd}\\ \frac{d\left(i_{sq}\right)}{dt}=-\frac{R_s}{L_q}..i_{sq}+\frac{L_d}{L_q}.{\omega }_e.i_{sd}+\frac{1}{L_q}.{\omega }_e.{\mathsf{\Psi }}_f-\frac{1}{L_q}.V_{sq}\\ \frac{d\mathrm{\Omega }}{dt}=\frac{1}{J}.T_{Tur}-\frac{1}{J}.T_{em}-\frac{f_c}{J}.\mathrm{\Omega }=\frac{1}{J}.T_{Tur}+\frac{3}{2}.\frac{p}{J}.\left[\left(L_d-L_q\right).i_{sd}.i_{sq}+{\mathsf{\Psi }}_f.i_{sq}\right]-\frac{f_c}{J}.\mathrm{\Omega }\end{array}\right.$$

(15)

3.2. Non-Adaptive Backstepping Control Applied to PMSG

According to equations (15) and based on the assumption that all parameters of the wind system—GSAP parameters included—are known, the design of the non-adaptive backstepping control can be determined by following three essential steps [26,27]:

-

Step 1: Mechanical Rotation Speed Controller Design:

The mechanical rotational speed error is defined by the following expression:

$${\chi }_1={\mathrm{\Omega }}_{ref}-\mathrm{\Omega }$$

(16)

The dynamics of this error according to Equations (15) and (16) can be obtained by:

$${\stackrel{•}{\chi }}_1={\stackrel{•}{\mathrm{\Omega }}}_{ref}-\stackrel{•}{\mathrm{\Omega }}={\stackrel{•}{\mathrm{\Omega }}}_{ref}-\frac{1}{J}.T_{Tur}-\frac{3}{2}.\frac{p}{J}.\left[\left(L_d-L_q\right).i_{sd}.i_{sq}+{\mathsf{\Psi }}_f.i_{sq}\right]+\frac{f_c}{J}.\mathrm{\Omega }$$

(17)

If the machine has smooth poles, we will have (L_d = L_q = L_s), which offers the following simplification in the expression of the dynamics of the error of the mechanical speed:

$${\stackrel{•}{\chi }}_1={\stackrel{•}{\mathrm{\Omega }}}_{ref}-\stackrel{•}{\mathrm{\Omega }}={\stackrel{•}{\mathrm{\Omega }}}_{ref}-\frac{1}{J}.T_{Tur}-\frac{3}{2}.\frac{p}{J}.{\mathsf{\Psi }}_f.i_{sq}+\frac{f_c}{J}.\mathrm{\Omega }$$

(18)

Lyapunov’s candidate function is put in the following form [27]:

$${\gamma }_1=\frac{1}{2}{\chi }_1^2$$

(19)

Its time derivative is given by:

$${\stackrel{•}{\gamma }}_1={\chi }_1{\stackrel{•}{\chi }}_1={\chi }_1\left[{\stackrel{•}{\mathrm{\Omega }}}_{ref}-\frac{1}{J}.T_{Tur}-\frac{3}{2}.\frac{p}{J}.{\mathsf{\Psi }}_f.i_{sq}+\frac{f_c}{J}.\mathrm{\Omega }\right]$$

(20)

Based on the design of the backstepping control, the quadratic i_sq and direct i_sd stator current components are chosen as virtual inputs. These virtual inputs are known in backstepping control terminology as stabilizing functions:

$$\left\{\begin{array}{c}{i}_{sd-ref}=0\\ i_{sq-ref}=\frac{J}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}\left(-k_1{\chi }_1-{\stackrel{•}{\mathrm{\Omega }}}_{ref}+\frac{1}{J}.T_{Tur}-\frac{f_c}{J}.\mathrm{\Omega }\right)\end{array}\right.$$

(21)

In order to guarantee the stability of the system, we chose the positive constant k1 so that the virtual inputs i_sd-ref and i_sq-ref ensured the negativity of the chosen Lyapunov function [24]. In this case, the dynamics of the Lyapunov function becomes:

$${\stackrel{•}{\gamma }}_1=-k_1.{\chi }_1^2\le 0$$

(22)

-

Step 2: Design of the stator current component controller:

The errors of the magnitudes of the currents are defined by the following expressions:

$$\left\{\begin{array}{c}{\chi }_2=i_{sq-ref}-i_{sq}\\ {\chi }_3=i_{sd-ref}-i_{sd}=-i_{sd}\end{array}\right.$$

(23)

The error dynamics according to the system Equations (15), (18) and (23) are presented as follows:

$$\left\{\begin{array}{c}{\stackrel{•}{\chi }}_1=\frac{3}{2}.\frac{p}{J}.{\mathsf{\Psi }}_f.{\chi }_2-k_1.{\chi }_1\\ {\stackrel{•}{\chi }}_2={\stackrel{•}{i}}_{sq-ref}-{\stackrel{•}{i}}_{sq}=\frac{J}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}\left(-k_1.{\chi }_1-{\stackrel{••}{\mathrm{\Omega }}}_{ref}-\frac{f_c}{J}.\stackrel{•}{\mathrm{\Omega }}\right)+\frac{R_s}{L_q}.i_{sq}-\frac{L_d}{L_q}.{\omega }_e.i_{sd}-\frac{1}{L_q}.{\omega }_e.{\mathsf{\Psi }}_f+\frac{1}{L_q}.V_{sq}\\ {\stackrel{•}{\chi }}_3={\stackrel{•}{i}}_{sd-ref}-{\stackrel{•}{i}}_{sd}=-{\stackrel{•}{i}}_{sd}=\frac{R_s}{L_d}.i_{sd}+\frac{L_q}{L_d}.{\omega }_e.i_{sq}+\frac{1}{L_d}.V_{sd}\end{array}\right.$$

(24)

-

Step 3: Design of the actual control inputs and stability analysis:

The stator reference voltages are the real control inputs; to determine them, we adopt a new positive definite Lyapunov candidate function [27]:

$${\gamma }_2=\frac{1}{2}{\chi }_1^2+\frac{1}{2}{\chi }_2^2+\frac{1}{2}{\chi }_3^2$$

(25)

The time derivative of this candidate function is obtained based on the system of Equations (24):

$$\begin{array}{l}{\stackrel{•}{\gamma }}_2={\stackrel{•}{\gamma }}_1+{\chi }_2{\stackrel{•}{\chi }}_2+{\chi }_3{\stackrel{•}{\chi }}_3=-k_1.{\chi }_1^2-k_2.{\chi }_2^2-k_3.{\chi }_3^2\\ +{\chi }_2.\left[\frac{J}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}.\left(-k_1.{\chi }_1-{\stackrel{••}{\mathrm{\Omega }}}_{ref}-\frac{f_c}{J}.\stackrel{•}{\mathrm{\Omega }}\right)+\frac{R_s}{L_q}.i_{sq}-\frac{L_d}{L_q}.{\omega }_e.i_{sd}-\frac{1}{L_q}.{\omega }_e.{\mathsf{\Psi }}_f+\frac{1}{L_q}.V_{sq}+k_2.{\chi }_2\right]\\ +{\chi }_3.\left[\frac{R_s}{L_d}.i_{sd}+\frac{L_q}{L_d}.{\omega }_e.i_{sq}+\frac{1}{L_d}.V_{sd}+k_3.{\chi }_3\right]\end{array}$$

(26)

In order to guarantee the stability of the dynamics of the currents, we choose the constants k₁, k₂ and k₃ of the positive constants [24]. Moreover, the stator reference voltages make it possible to ensure the negativity of the derivative of the chosen Lyapunov function. For this, the expressions of the reference stator voltages will be established as follows:

$$\left\{\begin{array}{c}{V}_{sd-ref}=-R_s.i_{sd}-L_q.{\omega }_e.i_{sq}-L_d.k_3.{\chi }_3\\ V_{sq-ref}=\frac{J.L_q}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}\left(k_1.{\chi }_1+{\stackrel{••}{\mathrm{\Omega }}}_{ref}+\frac{f_c}{J}.\stackrel{•}{\mathrm{\Omega }}\right)-R_s.i_{sq}+L_d.{\omega }_e.i_{sd}+{\omega }_e.{\mathsf{\Psi }}_f-L_q.k_2.{\chi }_2\end{array}\right.$$

(27)

Therefore, the dynamics of the Lyapunov function will be:

$${\stackrel{•}{\gamma }}_2=-k_1.{\chi }_1^2-k_2.{\chi }_2^2-k_3.{\chi }_3^2\le 0$$

(28)

3.3. Adaptive Backstepping Control Applied to PMSG

The non-adaptive backstepping control is based on the assumption that all system parameters (PMSG parameters included) are known and invariant. This assumption is generally not true. In fact, the parameters vary with system operating conditions such as temperature change, magnetic saturation effects and load torque variation. Therefore, nonlinearities and uncertainties of unknown parameters must be taken into account in the design of the controller by using estimators (observers), which will subsequently improve the robustness of the system against parametric variations and measurement noise. In this second control algorithm, we adopt the vectors of the real parameters of the system (the PMSG parameters included) by their estimated values.

The system parameters are defined as follows:

$$\left\{\begin{array}{c}{\sigma }_1=R_S\\ {\sigma }_2=L_d=L_q=L_S\\ {\sigma }_3=J\\ {\sigma }_4=\frac{T_{Tur}}{J}\\ {\sigma }_5=\frac{f_c}{J}\end{array}\right.$$

(29)

Parameter system 29 will be replaced by:

$${\left[{\widehat{\sigma }}_1{\widehat{\sigma }}_2{\widehat{\sigma }}_3{\widehat{\sigma }}_4{\widehat{\sigma }}_5\right]}^T$$

(30)

The errors of these parameters are defined as follows:

$$\left\{\begin{array}{c}{\tilde{\sigma }}_1={\widehat{\sigma }}_1-{\sigma }_1\\ {\tilde{\sigma }}_2={\widehat{\sigma }}_2-{\sigma }_2\\ {\tilde{\sigma }}_3={\widehat{\sigma }}_3-{\sigma }_3\\ {\tilde{\sigma }}_4={\widehat{\sigma }}_4-{\sigma }_4\\ {\tilde{\sigma }}_5={\widehat{\sigma }}_5-{\sigma }_5\end{array}\right.$$

(31)

The stabilizing function defined in Equation (21) will be rewritten as follows:

$$\left\{\begin{array}{c}{i}_{sd-ref}=0\\ i_{sq-ref}=\frac{{\widehat{\sigma }}_3}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}\left(-k_1{\chi }_1-{\stackrel{•}{\mathrm{\Omega }}}_{ref}+{\widehat{\sigma }}_4-{\widehat{\sigma }}_5.\mathrm{\Omega }\right)\end{array}\right.$$

(32)

The error dynamic is redefined by:

$$\begin{array}{l}{\stackrel{•}{\chi }}_1={\stackrel{•}{\mathrm{\Omega }}}_{ref}-{\sigma }_4+\frac{3}{2}.\frac{p}{{\sigma }_3}.{\mathsf{\Psi }}_f.{\chi }_2-\frac{3}{2}.\frac{p}{J}.{\mathsf{\Psi }}_f.i_{sq-ref}+{\sigma }_5.\mathrm{\Omega }\\ =\frac{3}{2}.\frac{p}{{\sigma }_3}.{\mathsf{\Psi }}_f.{\chi }_2+\frac{{\tilde{\sigma }}_3}{{\sigma }_3}\left(-k_1.{\chi }_1-{\stackrel{•}{\mathrm{\Omega }}}_{ref}+{\widehat{\sigma }}_4-{\widehat{\sigma }}_5.\mathrm{\Omega }\right)+{\tilde{\sigma }}_4-{\tilde{\sigma }}_5.\mathrm{\Omega }-k_1.{\chi }_1\end{array}$$

(33)

$$\begin{array}{l}{\stackrel{•}{\chi }}_2=\frac{{\widehat{\sigma }}_1}{{\sigma }_2}.i_{sq}-\frac{{\tilde{\sigma }}_1}{{\sigma }_2}.i_{sq}-\frac{{\widehat{\sigma }}_2}{{\sigma }_2}.{\omega }_e.i_{sd}+\frac{{\tilde{\sigma }}_2}{{\sigma }_2}.{\omega }_e.i_{sd}-\frac{1}{{\sigma }_2}.{\omega }_e.{\mathsf{\Psi }}_f+\frac{1}{{\sigma }_2}.V_{sq}\\ +\frac{\stackrel{•}{{\widehat{\sigma }}_3}}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}\left(-k_1.{\chi }_1-{\stackrel{•}{\mathrm{\Omega }}}_{ref}+{\widehat{\sigma }}_4-{\widehat{\sigma }}_5.\mathrm{\Omega }\right)+\frac{{\widehat{\sigma }}_3}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}\left(-k_1.{\stackrel{•}{\mathrm{\Omega }}}_{ref}-{\stackrel{••}{\mathrm{\Omega }}}_{ref}+{\stackrel{•}{\widehat{\sigma }}}_4-{\stackrel{•}{\widehat{\sigma }}}_5.\mathrm{\Omega }\right)\\ -\frac{{\tilde{\sigma }}_3}{{\sigma }_3}\left(k_1-{\widehat{\sigma }}_5\right).i_{sq}-\left(k_1-{\widehat{\sigma }}_5\right).i_{sq}-\frac{{\widehat{\sigma }}_3}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}\left(k_1-{\widehat{\sigma }}_5\right)\left({\tilde{\sigma }}_4-{\tilde{\sigma }}_5\right)+\frac{{\widehat{\sigma }}_3}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}\left(k_1-{\widehat{\sigma }}_5\right)\left({\widehat{\sigma }}_4-{\widehat{\sigma }}_5.\mathrm{\Omega }\right)\end{array}$$

(34)

$${\stackrel{•}{\chi }}_3=\frac{{\widehat{\sigma }}_1}{{\sigma }_2}.i_{sd}-\frac{{\tilde{\sigma }}_1}{{\sigma }_2}.i_{sd}+\frac{{\widehat{\sigma }}_2}{{\sigma }_2}..{\omega }_e{i}_{sq}-\frac{{\tilde{\sigma }}_2}{{\sigma }_2}.{\omega }_e{i}_{sq}+\frac{1}{{\sigma }_2}.V_{sd}$$

(35)

The control laws are designed so that the dynamic current errors are stabilized as follows:

$$V_{sd-ref}=-{\widehat{\sigma }}_1.i_{sd}-{\widehat{\sigma }}_2.{\omega }_e.i_{sq}-{\widehat{\sigma }}_2.k_3.{\chi }_3$$

(36)

$$\begin{array}{l}{V}_{sq-ref}=-{\widehat{\sigma }}_1.i_{sq}+{\widehat{\sigma }}_2.{\omega }_e.i_{sd}+{\omega }_e.{\mathsf{\Psi }}_f+{\widehat{\sigma }}_2.k_2.{\chi }_2\\ -{\widehat{\sigma }}_2.\left[\begin{array}{l}\frac{{\stackrel{•}{\widehat{\sigma }}}_3}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}\left(-k_1.{\chi }_1-{\stackrel{•}{\mathrm{\Omega }}}_{ref}+{\widehat{\sigma }}_4-{\widehat{\sigma }}_5.\mathrm{\Omega }\right)+\frac{{\widehat{\sigma }}_3}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}\left(-k_1.{\stackrel{•}{\mathrm{\Omega }}}_{ref}-{\stackrel{••}{\mathrm{\Omega }}}_{ref}+{\stackrel{•}{\widehat{\sigma }}}_4-{\stackrel{•}{\widehat{\sigma }}}_5.\mathrm{\Omega }\right)\\ -\left(k_1-{\widehat{\sigma }}_5\right).i_{sq}+\frac{{\widehat{\sigma }}_3}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}.\left(k_1-{\widehat{\sigma }}_5\right)\left({\widehat{\sigma }}_4-{\widehat{\sigma }}_5.\mathrm{\Omega }\right)\end{array}\right]\end{array}$$

(37)

With: k₁, k₂ and k₃ are positive constants [24].

By replacing the values of the stator voltages expressed by Equations (36) and (37) in Equations (34) and (35).

$$\begin{array}{l}{\stackrel{•}{\chi }}_2=-k_2.{\chi }_2-\frac{{\tilde{\sigma }}_1}{{\sigma }_2}.i_{sq}+\frac{{\tilde{\sigma }}_2}{{\sigma }_2}.{\omega }_e.i_{sd}+k_2.{\chi }_2.\frac{{\tilde{\sigma }}_2}{{\sigma }_2}-\frac{{\tilde{\sigma }}_3}{{\sigma }_3}\left(k_1-{\widehat{\sigma }}_5\right).i_{sq}-\frac{{\widehat{\sigma }}_3}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}\left(k_1-{\widehat{\sigma }}_5\right)\left({\tilde{\sigma }}_4-{\tilde{\sigma }}_5\right)\\ +\frac{{\tilde{\sigma }}_2}{{\sigma }_2}\left[\begin{array}{l}\frac{\stackrel{•}{{\widehat{\sigma }}_3}}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}\left(-k_1.{\chi }_1-{\stackrel{•}{\mathrm{\Omega }}}_{ref}+{\widehat{\sigma }}_4-{\widehat{\sigma }}_5.\mathrm{\Omega }\right)+\frac{{\widehat{\sigma }}_3}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}\left(-k_1.{\stackrel{•}{\mathrm{\Omega }}}_{ref}-{\stackrel{••}{\mathrm{\Omega }}}_{ref}+{\stackrel{•}{\widehat{\sigma }}}_4-{\stackrel{•}{\widehat{\sigma }}}_5.\mathrm{\Omega }\right)\\ -\left(k_1-{\widehat{\sigma }}_5\right).i_{sq}+\frac{{\widehat{\sigma }}_3}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}\left(k_1-{\widehat{\sigma }}_5\right)\left({\widehat{\sigma }}_4-{\widehat{\sigma }}_5.\mathrm{\Omega }\right)\end{array}\right]\end{array}$$

(38)

$${\stackrel{•}{\chi }}_3=-k_3.{\chi }_3-\frac{{\tilde{\sigma }}_1}{{\sigma }_2}.i_{sd}-\frac{{\tilde{\sigma }}_2}{{\sigma }_2}.{\omega }_e{i}_{sq}-\frac{{\tilde{\sigma }}_2}{{\sigma }_2}.k_3.{\chi }_3$$

(39)

3.4. Parameter Adaptation and Stability Analysis

The last phase is the determination of the adaptation laws of the parameters. For this, a new Lyapunov function is defined with adaptation gains according to the following expression:

$${\gamma }_3=\frac{1}{2}\left({\chi }_1^2+{\chi }_2^2+{\chi }_3^2+\frac{{\widehat{\sigma }}_1^2}{{\sigma }_2.{ƛ}_1}+\frac{{\widehat{\sigma }}_2^2}{{\sigma }_2.{ƛ}_2}+\frac{{\widehat{\sigma }}_3^2}{{\sigma }_3.{ƛ}_3}+\frac{{\widehat{\sigma }}_4^2}{{ƛ}_4}+\frac{{\widehat{\sigma }}_5^2}{{ƛ}_5}\right)$$

(40)

Such that: ${ƛ}_{\mathrm{i}}$ (_i = 1, 2, 3, 4, 5) are the positive adaptation gains. The time derivative of Equation (40) gives:

$$\begin{array}{l}{\stackrel{•}{\gamma }}_3={\chi }_1.{\stackrel{•}{\chi }}_1+{\chi }_2.{\stackrel{•}{\chi }}_2+{\chi }_3.{\stackrel{•}{\chi }}_3+\frac{{\widehat{\sigma }}_1.{\stackrel{•}{\widehat{\sigma }}}_1}{{\sigma }_2.{ƛ}_1}+\frac{{\widehat{\sigma }}_2.{\stackrel{•}{\widehat{\sigma }}}_2}{{\sigma }_2.{ƛ}_2}+\frac{{\widehat{\sigma }}_3.{\stackrel{•}{\widehat{\sigma }}}_3}{{\sigma }_3.{ƛ}_3}+\frac{{\widehat{\sigma }}_4.{\stackrel{•}{\widehat{\sigma }}}_4}{{ƛ}_4}+\frac{{\widehat{\sigma }}_5.{\stackrel{•}{\widehat{\sigma }}}_5}{{ƛ}_5}\\ =-k_1.{\chi }_1^2-k_2.{\chi }_2^2-k_3.{\chi }_3^2-\frac{\frac{3}{2}.p.{\mathsf{\Psi }}_f}{{\sigma }_3}.{\chi }_1.{\chi }_2+\frac{{\tilde{\sigma }}_1}{{\sigma }_2}\left(\frac{{\stackrel{•}{\widehat{\sigma }}}_1}{{ƛ}_1}-i_{sd}.{\chi }_3-i_{sq}.{\chi }_2\right)\\ +\frac{{\tilde{\sigma }}_2}{{\sigma }_2}\left[\begin{array}{l}\frac{{\stackrel{•}{\widehat{\sigma }}}_2}{{ƛ}_2}-{\chi }_3.{\omega }_e.i_{sq}+{\chi }_2.\left({\omega }_e.i_{sd}-{\chi }_1.{\chi }_2\right)+\frac{{\stackrel{•}{\widehat{\sigma }}}_3}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}.\left(-k_1.{\chi }_1-{\stackrel{•}{\mathrm{\Omega }}}_{ref}+{\widehat{\sigma }}_4-{\widehat{\sigma }}_5.\mathrm{\Omega }\right)\\ +\frac{{\widehat{\sigma }}_3}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}.\left(-k_1.{\stackrel{•}{\mathrm{\Omega }}}_{ref}-{\stackrel{••}{\mathrm{\Omega }}}_{ref}+{\stackrel{•}{\widehat{\sigma }}}_4-{\stackrel{•}{\widehat{\sigma }}}_5.\mathrm{\Omega }\right)-\left(k_1-{\widehat{\sigma }}_5\right).i_{sq}\\ +\frac{{\widehat{\sigma }}_3}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}.\left(k_1-{\widehat{\sigma }}_5\right)\left({\widehat{\sigma }}_4-{\widehat{\sigma }}_5.\mathrm{\Omega }\right)\end{array}\right]\\ +\frac{{\tilde{\sigma }}_3}{{\sigma }_3}\left[\frac{{\stackrel{•}{\widehat{\sigma }}}_3}{{ƛ}_3}+{\chi }_1\left(-k_1.\mathrm{\Omega }-{\stackrel{•}{\mathrm{\Omega }}}_{ref}+{\widehat{\sigma }}_4-{\widehat{\sigma }}_5.\mathrm{\Omega }\right)-\left(k_1-{\widehat{\sigma }}_5\right).i_{sq}.{\chi }_2\right]\\ +{\tilde{\sigma }}_4\left[\frac{{\stackrel{•}{\widehat{\sigma }}}_4}{{ƛ}_4}+{\chi }_1-\frac{{\widehat{\sigma }}_3}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}.\left(k_1-{\widehat{\sigma }}_5\right).{\chi }_2\right]+{\tilde{\sigma }}_5\left[\frac{{\stackrel{•}{\widehat{\sigma }}}_5}{{ƛ}_5}-{\chi }_1.\mathrm{\Omega }+\frac{{\widehat{\sigma }}_3}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}.\left(k_1-{\widehat{\sigma }}_5\right).{\chi }_2.\mathrm{\Omega }\right]\end{array}$$

(41)

The adaptation laws of the parameters are determined in such a way that the derivative of the Lyapunov candidate function is defined negative as follows:

$${\stackrel{•}{\widehat{\sigma }}}_1=-{ƛ}_1\left(-i_{sd}.{\chi }_3-i_{sq}.{\chi }_2\right)$$

(42)

$${\stackrel{•}{\widehat{\sigma }}}_2=-{ƛ}_2\left[\begin{array}{l}{\chi }_3.{\omega }_e.i_{sq}+{\chi }_2\left(-{\omega }_e.i_{sd}+{\chi }_1{\chi }_2\right)+\frac{\stackrel{•}{{\widehat{\sigma }}_3}}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}\left(-k_1.{\chi }_1-{\stackrel{•}{\mathrm{\Omega }}}_{ref}+{\widehat{\sigma }}_4-{\widehat{\sigma }}_5.\mathrm{\Omega }\right)+\\ \frac{{\widehat{\sigma }}_3}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}\left(-k_1.{\stackrel{•}{\mathrm{\Omega }}}_{ref}-{\stackrel{••}{\mathrm{\Omega }}}_{ref}+{\stackrel{•}{\widehat{\sigma }}}_4-{\stackrel{•}{\widehat{\sigma }}}_5.\mathrm{\Omega }\right)-\left(k_1-{\widehat{\sigma }}_5\right).i_{sq}+\frac{{\widehat{\sigma }}_3}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}\left(k_1-{\widehat{\sigma }}_5\right)\left({\tilde{\sigma }}_4-{\tilde{\sigma }}_5.\mathrm{\Omega }\right)\end{array}\right]$$

(43)

$${\stackrel{•}{\widehat{\sigma }}}_3=-{ƛ}_3\left[{\chi }_1\left(-k_1.\mathrm{\Omega }-{\stackrel{•}{\mathrm{\Omega }}}_{ref}+{\widehat{\sigma }}_4-{\widehat{\sigma }}_5.\mathrm{\Omega }\right)-\left(k_1-{\widehat{\sigma }}_5\right).i_{sq}.{\chi }_2\right]$$

(44)

$${\stackrel{•}{\widehat{\sigma }}}_4=-{ƛ}_4\left[{\chi }_1-\frac{{\widehat{\sigma }}_3}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}\left(k_1-{\widehat{\sigma }}_5\right).{\chi }_2\right]$$

(45)

$${\stackrel{•}{\widehat{\sigma }}}_5=-{ƛ}_5\left[-{\chi }_1.\mathrm{\Omega }+\frac{{\widehat{\sigma }}_3}{\frac{3}{2}.p.{\mathsf{\Psi }}_f}\left(k_1-{\widehat{\sigma }}_5\right).{\chi }_2.\mathrm{\Omega }\right]$$

(46)

Finally, the dynamics of the Lyapunov function becomes [24]:

$${\stackrel{•}{\gamma }}_3=-k_1.{\chi }_1^2-k_2.{\chi }_2^2-k_3.{\chi }_3^2-\frac{\frac{3}{2}.p.{\mathsf{\Psi }}_f}{{\sigma }_3}.{\chi }_1.{\chi }_2\le 0$$

(47)

The structure of the adaptive nonlinear backstepping control of PMSG is shown in Figure 2, where V_sd-ref and V_sq-ref represent the reference voltages applied to the static converter on the machine side.

3.5. Grid Side Converter Control

The flow control of electrical energy transmitted to the distribution network is ensured by the grid side converter. The control serves both to keep the DC bus voltage stable, and to guarantee power transfer with unity power factor [28,29,30,31].

The representation of the electrical quantities in the rotating reference frame are represented by:

$$\left\{\begin{array}{c}\frac{d\left(i_{gd}\right)}{dt}=\frac{1}{L_f}\left[V_{fd}-V_{gd}-R_f.i_{gd}+{\omega }_g.\left(L_f.i_{gq}\right)\right]\\ \frac{d\left(i_{gq}\right)}{dt}=\frac{1}{L_f}\left[V_{fq}-V_{gq}-R_f.i_{gq}-{\omega }_g.\left(L_f.i_{gd}\right)-{\omega }_e.{\mathsf{\Psi }}_f\right]\end{array}\right.$$

(48)

$$\left\{\begin{array}{c}{P}_g=\frac{3}{2}\left[V_{gd}.i_{gd}+V_{gq}.i_{gq}\right]\\ Q_g=\frac{3}{2}\left[V_{gq}.i_{gd}-V_{gd}.i_{gq}\right]\end{array}\right.$$

(49)

According to Equations (48) and (49), it is clear that the electrical powers are directly proportional to the current components of the network. So, the backstepping control can be designed based on these steps:

The errors of the magnitudes of the grid currents are defined by the following expressions:

$$\left\{\begin{array}{c}{\xi }_{gq}=i_{gq-ref}-i_{gq}\\ {\xi }_{gd}=i_{gd-ref}-i_{gd}\end{array}\right.$$

(50)

The dynamics of these errors according to Equation (50) can be obtained by:

$$\left\{\begin{array}{c}{\stackrel{•}{\xi }}_{gq}={\stackrel{•}{i}}_{gq-ref}-{\stackrel{•}{i}}_{gq}\\ {\stackrel{•}{\xi }}_{gd}={\stackrel{•}{i}}_{gd-ref}-{\stackrel{•}{i}}_{gd}\end{array}\right.$$

(51)

Lyapunov’s candidate function is put in the following form:

$${\gamma }_g=\frac{1}{2}{\xi }_{gd}^2+\frac{1}{2}{\xi }_{gq}^2$$

(52)

Its time derivative is given by:

$${\stackrel{•}{\gamma }}_g={\xi }_{gd}.{\stackrel{•}{\xi }}_{gd}+{\xi }_{gq}.{\stackrel{•}{\xi }}_{gq}$$

(53)

Substituting the dynamics of the currents mentioned in the system of Equation (48) in the expression of Equation (53) we obtain:

$$\begin{array}{l}{\stackrel{•}{\gamma }}_g=-k_{g1}.{\xi }_{gd}^2-k_{g2}.{\xi }_{gq}^2+\frac{{\xi }_{gd}}{L_f}\left(V_{fd}-V_{gd}-R_f.i_{gd}+{\omega }_g.\left(L_f.i_{gq}\right)+k_{g1}.L_f.{\xi }_{gd}\right)\\ +\frac{{\xi }_{gq}}{L_f}\left(V_{fq}-V_{gq}-R_f.i_{gq}-{\omega }_g.\left(L_f.i_{gd}\right)-{\omega }_e.{\mathsf{\Psi }}_f+k_{g2}.L_f.{\xi }_{gq}\right)\end{array}$$

(54)

To ensure the stability of the system for injecting energy into the network, the values of $k_{g1}$ and $k_{g2}$ must be taken as positive values, and the reference voltages applied to the GSC must be chosen according to the system of Equation (55):

$$\left\{\begin{array}{c}{V}_{fd-ref}=V_{gd}+R_f.i_{gd}-L_f.{\omega }_g.i_{gq}-L_f.k_{g1}.{\xi }_{gd}\\ V_{gq-ref}=V_{gq}+R_f.i_{gq}+L_f.{\omega }_g.i_{gd}-L_f.k_{g2}.{\xi }_{gq}\end{array}\right.$$

(55)

The reference values for the direct and quadrature components of the grid currents are chosen as follows:

-

$i_{gd-ref}=0$: To guarantee the elimination of reactive power, and therefore the transfer of electrical power to the network with a unity power factor.

-

$i_{gq-ref}$: is derived through the regulation of the DC bus voltage to facilitate control of the active power transferred to the electrical network.

The design of the control is shown in Figure 2:

Figure 2. Adaptive Backstepping Control Block Diagram.

Figure 2. Adaptive Backstepping Control Block Diagram.

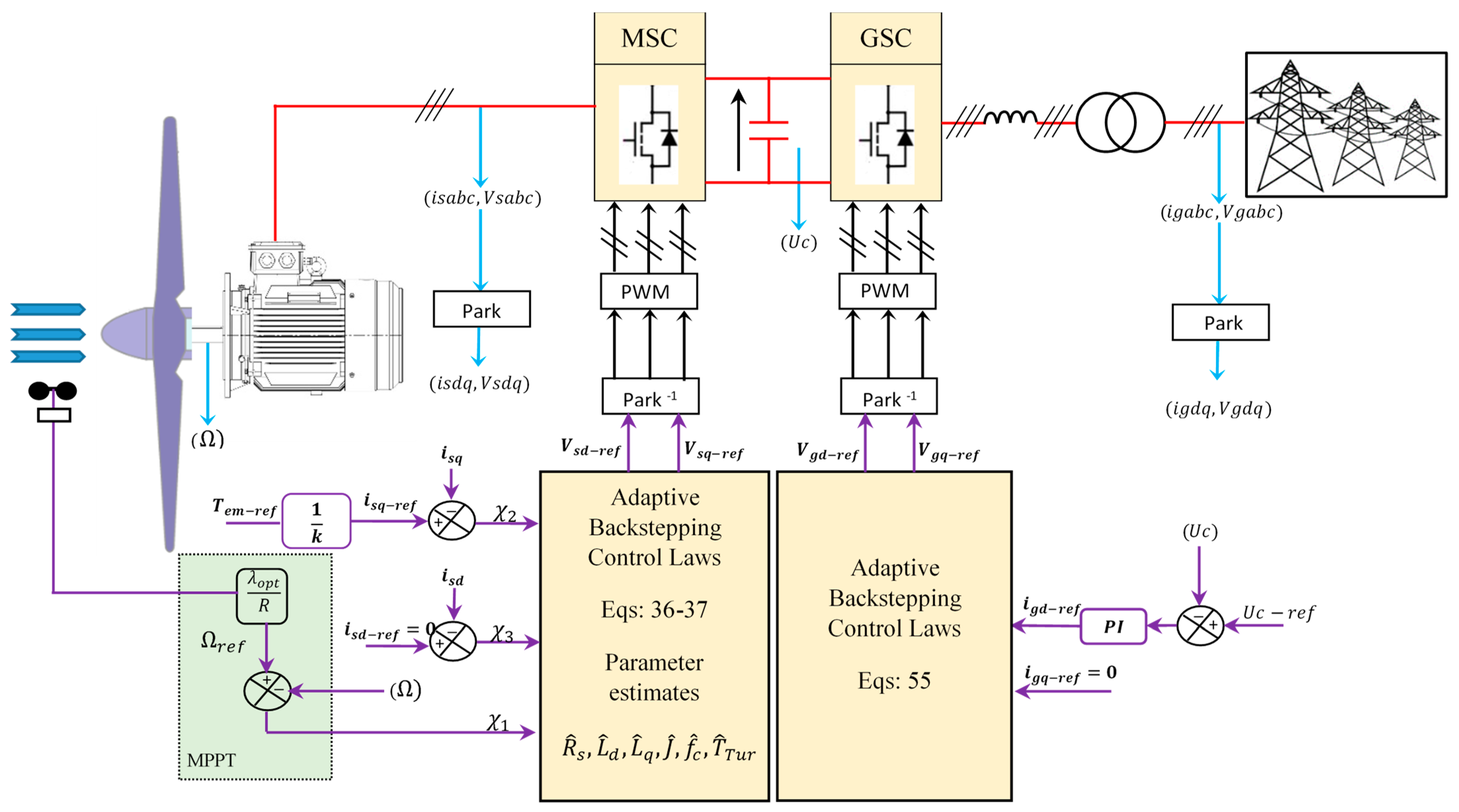
4. Experimental Verification

4.1. Description of the Experimental Platform

In order to validate the adaptive backstepping control applied to the wind conversion system based on a PMSG, a practical verification has been implemented. This is the experimental platform based on a DS1104 R&D controller board, developed by dSPACE. This controller board is essentially composed of the following elements:

▪

dSPACE 1104 embedded board enclosed in a computer. This mapping is locked in a computer which ensures the transfer of information between the software and the hardware part.

▪

Host computer containing the Matlab/Simulink environment and ControlDesk.

▪

DS1104 board connection panel.

▪

Voltage level adaptation probe.

▪

Oscilloscope to visualize the different analog signals.

The hardware part of the control board provides both application management and generates PWM control signals in TTL 0/5 V logic. The inverters need driver boards to drive the IGBTs through the TMS320F240 slave DSPs [32].

Processor-in-the-loop test is implemented to test the performance of the control applied to the wind system, based on the permanent magnet synchronous generator.

Verification of control law algorithms essentially involves the following steps:

▪

Using the Simulink modeling tool to build the control system.

▪

The simulation of the system to generate the different control results.

▪

Check the algorithm using the TargetLink tool associated with Simulink.

▪

Upload the program in C code to dSPACE embedded Board.

▪

Upload the “file.sdf” in the ControlDesk software to visualize the different signals.

4.2. dSPACE 1104 Digital Processing System

The processor board is developed by German company dSPACE. It is built with a MPC8240 main processor and 250 MHz clock frequency [32]. In addition, a second software called “ControlDesk” makes it possible to build a graphic interface, which facilitates the visualization of the different quantities in real time.

The connection of the DS 1104 R&D embedded board with the wind energy conversion chain based on the permanent magnet synchronous generator is shown schematically in Figure 3:

4.3. Results of Verification the Adaptive Backstepping Control

The general block diagram of the control is applied to the wind power conversion chain presented in Figure 3, where the control system encompasses both the control laws applied to the static converters on the machine side and on the grid side. Furthermore, Table 1 summarizes some parameters used for the study of the adaptive control of the conversion system studied.

The control algorithm applied to machine-side and grid-side static converters, was verified by the Processor-in-the-loop test while operating the DS1104 R&D controller board. On the other hand, two tests were carried out using the dSPACE board and the ControlDesk development tool. The first test is used to reveal the high performance of the system, with respect to a stepped wind profile, while the second test proves the effectiveness of the controls, with respect to the monitoring and regulation of electrical quantities, following a fluctuating wind profile.

Table 1. Parameters used in simulation.

Parameter	Value
DC bus voltage	5 × 103 V
DC Bus Capacitor	20 × 10−3 F
Filter resistance	20 × 10−5 Ω
Filter inductance	1 × 10−3 H
Sampling frequency	10 × 104 Hz
Grid frequency	50 Hz

Table 1. Parameters used in simulation.

Parameter	Value
DC bus voltage	5 × 103 V
DC Bus Capacitor	20 × 10−3 F
Filter resistance	20 × 10−5 Ω
Filter inductance	1 × 10−3 H
Sampling frequency	10 × 104 Hz
Grid frequency	50 Hz

4.3.1. Performance Test in the Presence of Step Wind

In this first test, the wind profile is taken in the form of steps, with an average speed of 7 m/s. The sampling frequency is fixed at f_e = 10 KHz. The rest of the parameters for the complete model are mentioned in

Table 2. The PMSG and wind turbine parameters.

Generator			Wind Turbine
Parameters	Symbol	Values	Parameters	Symbol	Values
Power Generator	Pnom	1.5 MW	Radius of the turbine blade	R	55 m
Pole number	p	72	Turbine and generator Moment	J	10,000 N.m
Stator Resistance	Rs	6.25 × 10−3 Ω	Specific density of air	ρ	1.22 kg/m3
d-axis inductance	Ld	4.229 × 10−3 H
q-axis inductance	Lq	4.229 × 10−3 H
Generator rotor flux	ψf	11.1464 Wb
Coefficient of friction	fc	0 N.m.s/rad

:

To show the good performances obtained via the adopted control, a comparison was made with the vector control in this test. The validation results are shown below.

According to the results obtained for this test in the presence of a wind in the form of steps, and according to the plot of the profile of the wind mentioned in Figure 4a, it is noted that the dynamics of the mechanical rotation speed presented on the Figure 4b and the active and reactive powers injected into the grid are well-coordinated, according to Figure 4g and 4h, respectively. Figure 4g clearly shows that the active power perfectly follows its mechanical reference, without forgetting the slight overshoot at the time of the sudden change in the reference power as indicated in the same figure at t = 1.8 s, t = 3.8 s and t = 5.8 s, for example. On the other hand, the reactive power injected into the distribution network remains reasonably low, compared to the total power generated, as shown in Figure 4h.

It should be noted that the nonlinear backstepping adaptive control offers better results compared to the classic vector control, both for tracking the angular velocity and for the active and reactive powers generated. The generated stator currents are shown in Figure 4c. They have a pseudo-sinusoidal shape, and they settle quickly at the transient moment. Nevertheless, they are very rich in harmonics because of the variable switching frequency.

The quality of the three-phase currents injected into the grid shown in Figure 4d also attests to the high performance of the adaptive backstepping control. Three-phase current waves are seen clearly sinusoidal on the zoom of the same figure (Figure 4d). Moreover, the requirements of the period/frequency grid are perfectly respected. Waves having a period of 20 ms, which results in a frequency of 50 Hz, are also identified in the zoom of the same figure.

The stator line-to-line voltages are shown in Figure 4e. This figure shows voltages that have alternating rectangular waveforms, rather than purely sinusoidal forms, due to the switching of the electronic switches of the machine-side converters. The maximum value of phase-to-phase voltages is of the order of 5000 V, which also represents the nominal value of the stator voltages of the synchronous machine.

Figure 4f gathers the grid voltage curves with the injected three-phase currents: we can see the good voltage/current match, which means zero phase shift, so operation with unity power factor is proposed.

The active power perfectly follows its reference with a remarkable speed and such a low static error, always following Figure 4g. On the other hand, the reactive power shown in Figure 4h is kept low for a 1.5 MW power machine, with a ripple rate that does not exceed 10 Kvar for the adaptive control, compared to almost 20 Kvar for the conventional control.

Adaptive backstepping control applied to the grid side converter provides better performance in turn. This is clearly seen in the DC bus voltage regulation shown in Figure 4i: almost perfect regulation of the intermediate circuit voltage with perfect set point tracking. Ripples of the order of +/−5 v present a ripple rate of 0.1% for a 5000 V reference voltage.

On the other hand, Figure 4j here illustrates the command signals generated to control the arms of the various electronic switches of the static converters.

4.3.2. Set Point Tracking Test in the Presence of a Fluctuating Wind

This second test is used to test the performance of the controls vis-à-vis the variation of the wind which will be fluctuating and close to reality. The sampling frequency is always maintained at f_e = 10 KHz. The validation results of this test are presented below.

According to the results obtained for this test in the presence of a variable wind, we can notice that the different instructions are well-followed. For a wind profile presented in Figure 5a, it can be seen that the mechanical rotation speed, which is a direct consequence of the mechanical drive torque, perfectly follows the variation of the wind throughout the measurement period, as mentioned in Figure 5b. The correct tracking of the set point is ensured by both control algorithms; however, the adaptive control provides tracking with less ripple in the speeds.

On the other hand, the three-phase stator currents generated are pseudo-sinusoidal with a variable period, according to Figure 5c. It is quite normal this change of period, which is a direct consequence of the wind variation which causes this change in frequency of the currents generated by the synchronous generator. However, the three-phase current injected into the grid must be maintained adequately and has a very fixed frequency, equal to the network frequency of 50 Hz, and this can be seen according to Figure 5d, which presents the shapes of the three-phase currents injected into the electrical grid.

Figure 5e presents the shapes of the three-phase stator voltages measured at the stator windings terminals. Rectangular alternating voltages of maximum value equal to 5000 V, with a zoom of a single wave of the voltages, are shown in the same figure.

To clearly show the good quality of the electrical energy supplied to the network, Figure 5f presents an extract of this energy injected into the grid in the form of 6 electrical signals: 3 waves present the current injected and the 3 others present the three-phase voltages system. Perfect sine current waves with better time matching with three-phase mains voltages are well-illustrated in this figure. In addition, a zero-phase shift between the voltage/current electrical quantities guarantees a cosφ ≃ 1.

The active power injected into the grid perfectly follows its reference value as shown in Figure 5j. The zoom of the power curves shows that the active power generated through the adaptive backstepping control offers better results, compared to the classic vector control according to Figure 5j. The same remark is raised concerning the injected reactive power: Figure 5h presents the shapes of the reactive powers injected into the grid, where it is quite clear that the regulation via the adaptive control offers better results compared to the standard control. A ripple rate around 10 Kvar for the Adaptive control, against 20 Kvar for the classic control, is also presented for this second test with a second wind profile.

The regulation of the intermediate circuit voltage generates the current $i_{DC-ref }$ necessary for the calculation of the reference active power. Figure 5i shows DC bus voltage regulation. It is clear that the regulation is of very good quality and has very low ripple, compared to the reference voltage, which is equal to 5000 V. On the other hand, Figure 5j illustrates the control signals needed to control the three-phase inverter.

4.3.3. Visualization of Analog Signals on the Oscilloscope

In order to verify analog signals and see the usefulness of the ControlDesk software, a set-up was put together consisting of the connector panel of the dSPACE 1104 kit as well as a two-input digital oscilloscope. The signals displayed in this part are the switching signals which control the static converters on the machine side and on the network side. Figure 6 illustrates a circuit diagram and shows the signals obtained.

The digital oscilloscope used is brand/reference: “EZ, Digital Oscilloscope DS 1250C” according to Figure 6, which shows the PWM control signals necessary for controlling static converters.

5. Conclusions

In this study, an adaptive nonlinear algorithm based on Lyapunov theory is proposed to control the wind power conversion system. The results obtained reveal the high performances offered in terms of robustness and tracking for the different quantities of regulation issues. The architecture of this command is first simulated in Matlab/Simulink, and then verified experimentally using the dSPACE DS1104 controller board. The improvements revealed for several tests and, according to different external variations of the wind, prove the effectiveness of the Adaptive Backstepping Control algorithm in terms of overshoots, undulations and response time for the different quantities. The main improvements made to the PMSG-based wind conversion system can be summarized in the following points:

▪

The reduced response time attests that the proposed control offers system speed in terms of monitoring electrical and mechanical quantities, even if the machine is of high power and inertia.

▪

Signal ripples are less severe by applying adaptive control, compared to conventional controls for wind conversion system.

▪

Operation with unity power factor is truly ensured through the proposed control. A zero-phase shift between the voltage/current electrical quantities is well-ensured for the electrical energy transmitted to the distribution grid.

▪

An experimental verification by Processor-in-the-loop test of the results obtained through the dSPACE DS1104 embedded board and by the ControlDesk tool are important attributes that confirm the interest and strengths that this control structure can bring to a wind conversion system.

Although this study has brought a lot of solutions to apply robust and adaptive control, such as backstepping control, future work is considered as perspective and will be developed to complete the overall study. For instance, an experimental validation of the Adaptive Backstepping Control in a complete test bench will be considered.