Spatio-Temporal Evolution of City Resilience in the Yangtze River Delta, China, from the Perspective of Statistics
Abstract
1. Introduction
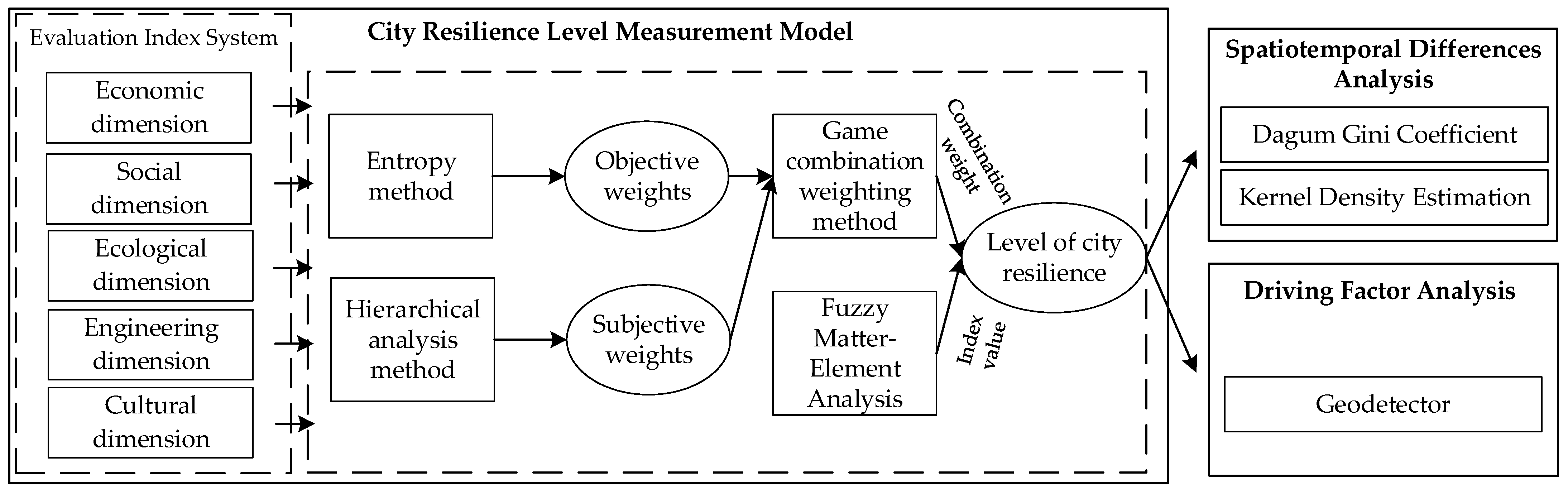
2. Methods and Data Collection
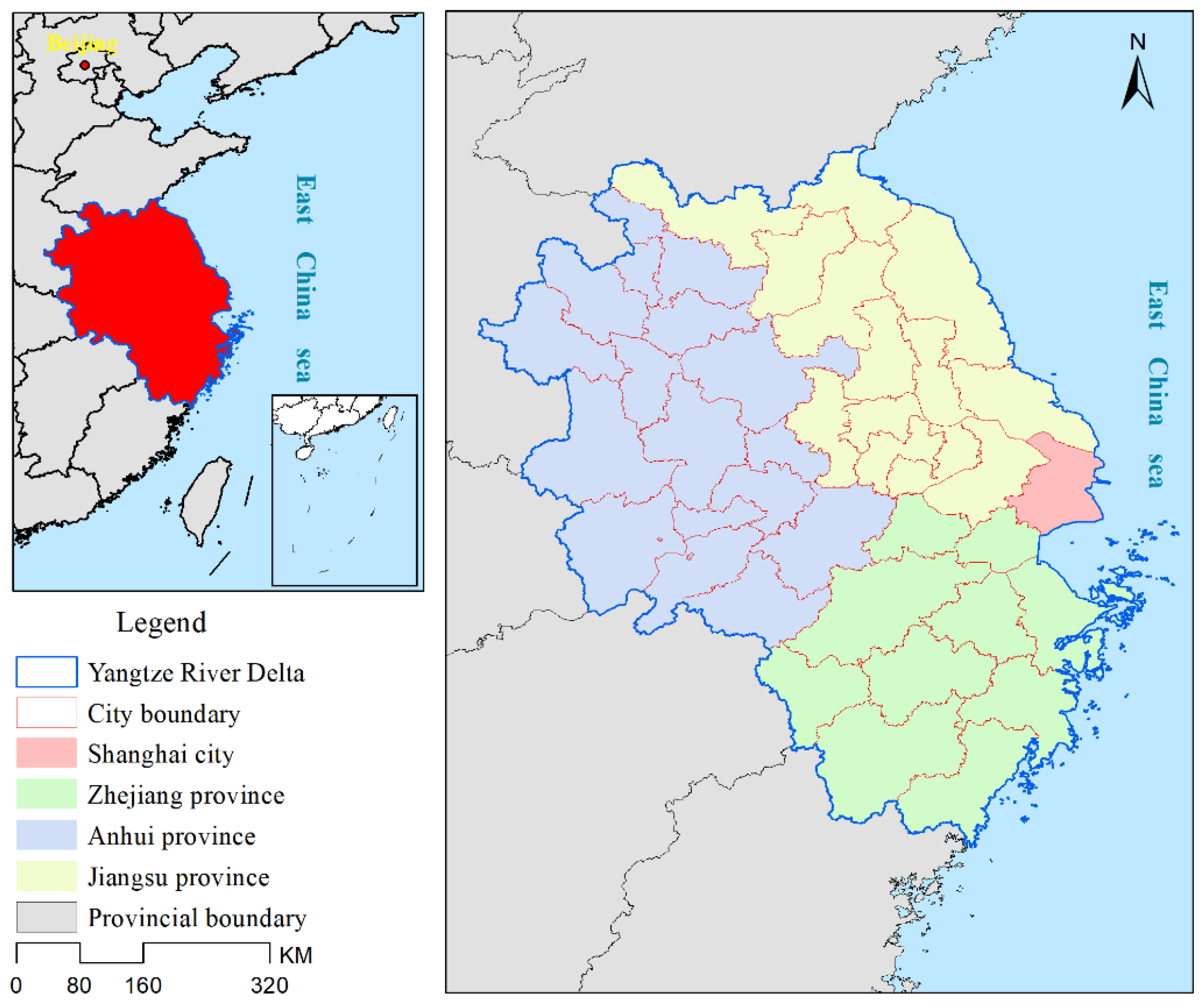
2.1. Study Area
2.2. City Resilience Assessments
2.2.1. Evaluation Index System of City Resilience
2.2.2. Comprehensive Weighting Method Based on Game Theory
2.2.3. Evaluation of City Resilience Based on Fuzzy Matter-Element Analysis
2.3. Spatiotemporal Differences Analysis
2.4. Kernel Density Estimation
2.5. Driving Factor Analysis
2.6. Data Collection
3. Results
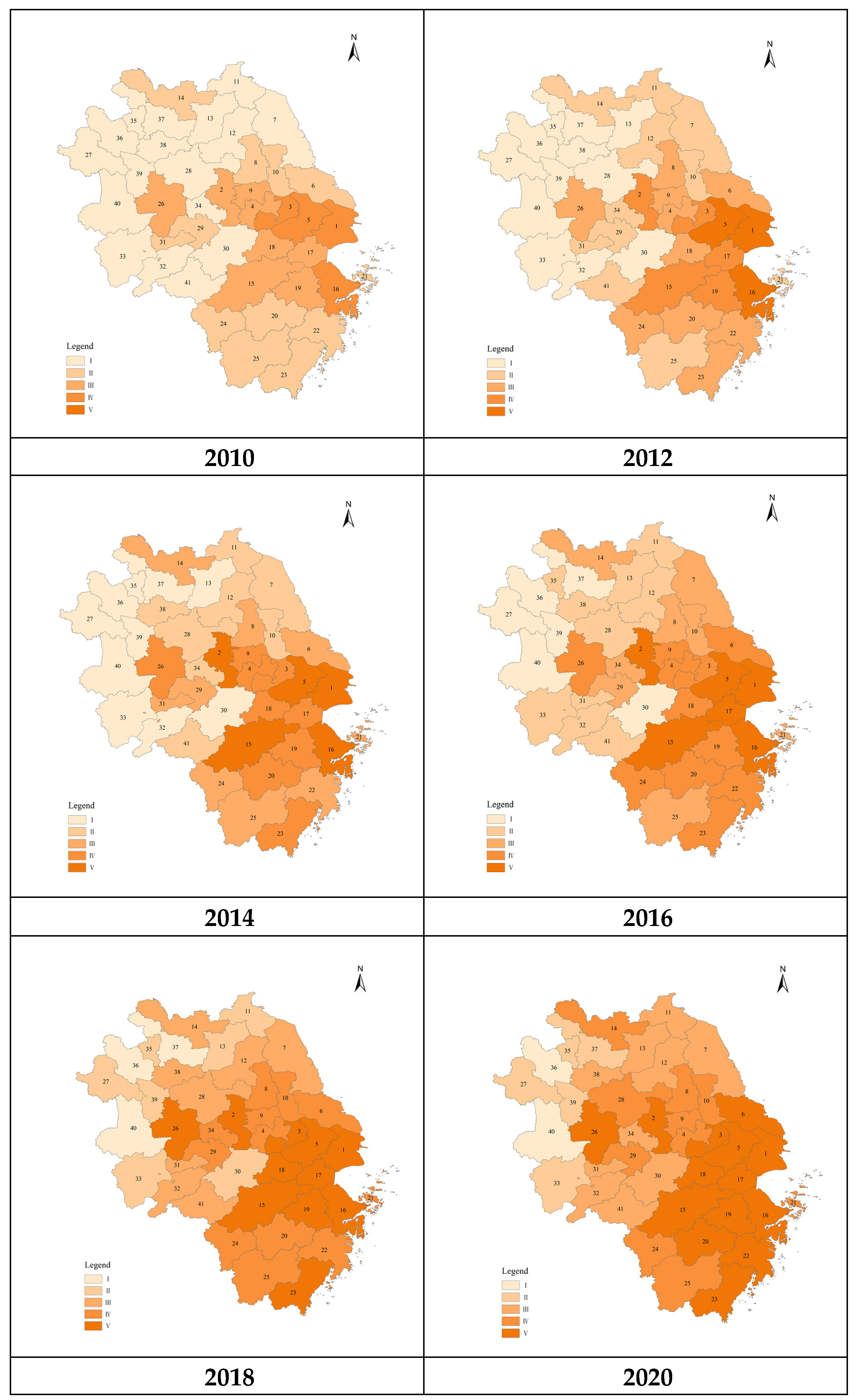
3.1. Spatiotemporal Distribution of City Resilience in the Yangtze River Delta
3.2. Spatiotemporal Difference Analysis of City Resilience in the Yangtze River Delta
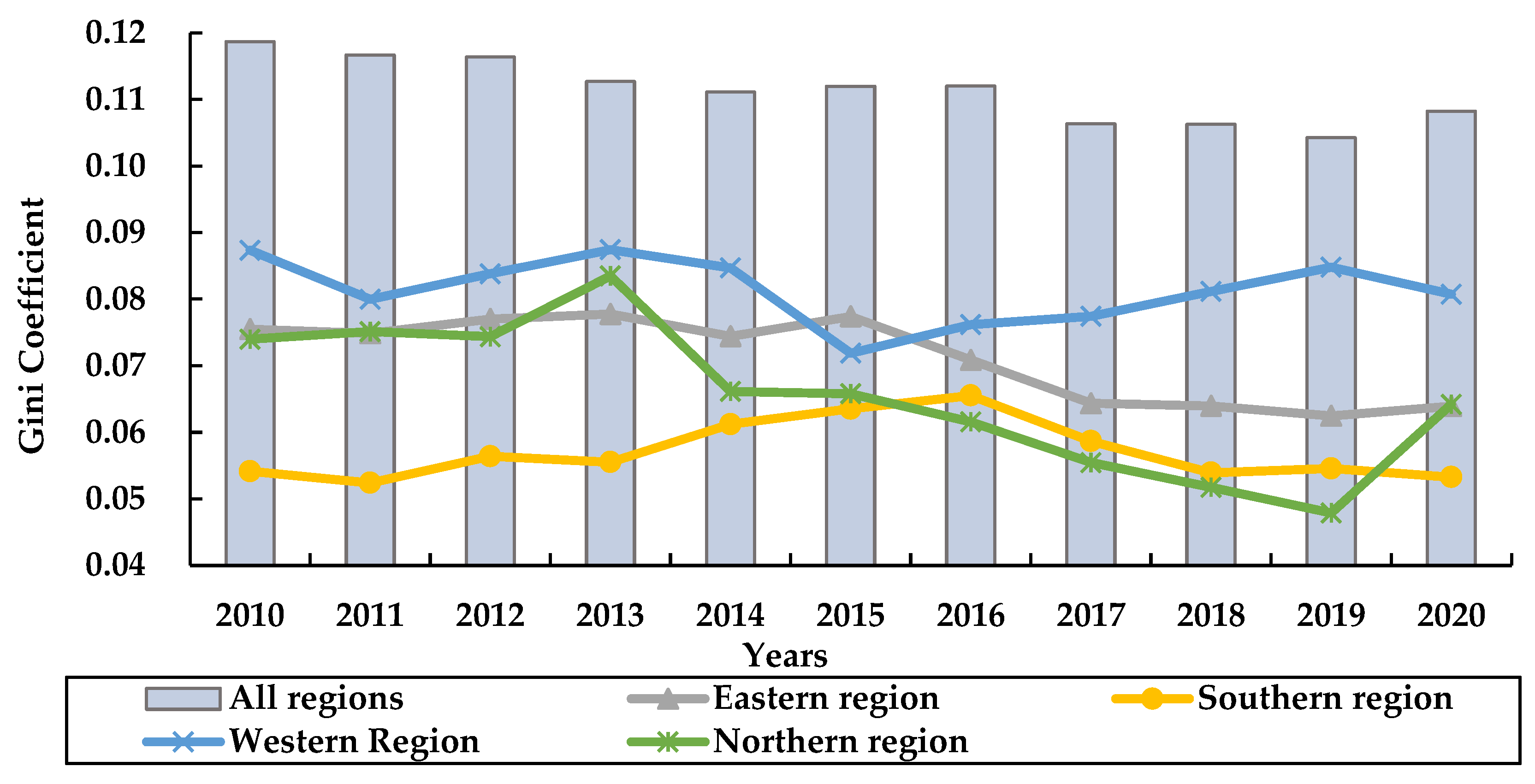
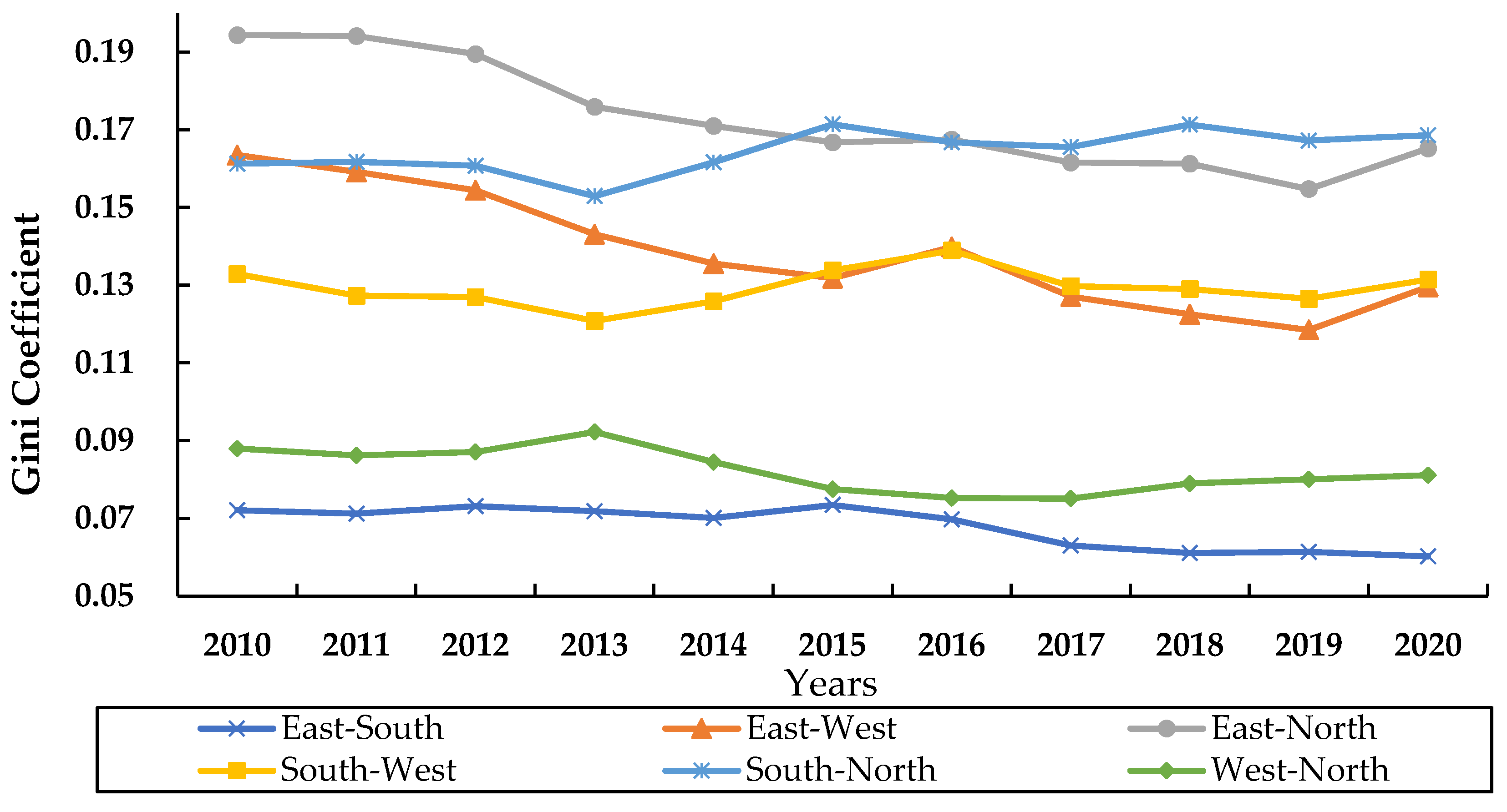
3.2.1. Dagum Gini Coefficient of City Resilience in the Yangtze River Delta
3.2.2. Decomposition
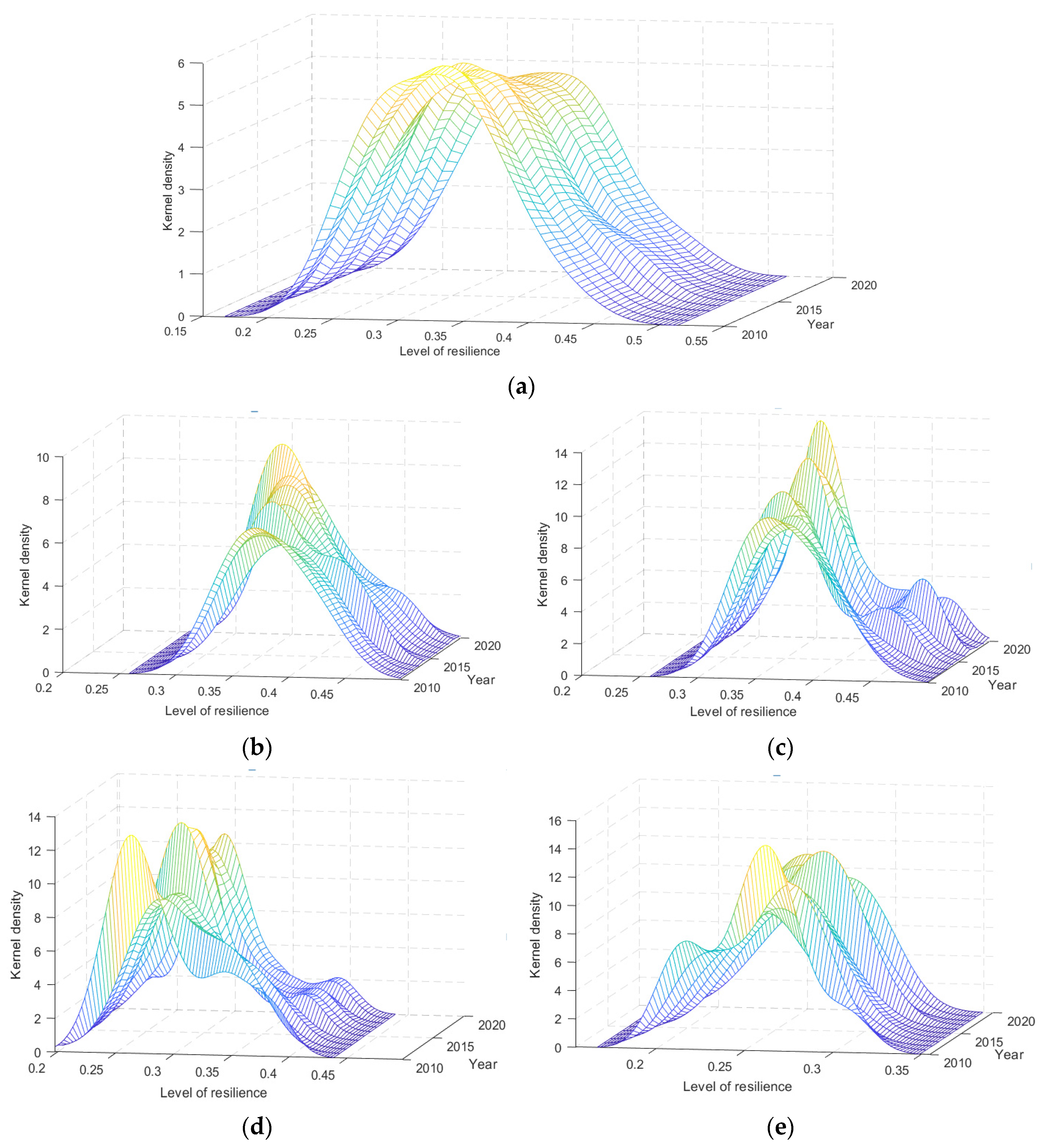
3.2.3. Kernel Density Analysis
3.3. Analysis of Driving Factors of City Resilience in the Yangtze River Delta
3.3.1. Set of Driving Factors
3.3.2. Influence of Driving Factors
4. Discussion
4.1. Mechanisms behind the Creation of City Resilience in the Yangtze River Delta
4.2. Exploration of the Construction Path of Resilient Cities in the Yangtze River Delta Based on the Characteristics of Driving Factors
4.2.1. City Resident Livelihoods
4.2.2. Adjustments to the Energy Consumption Structure
4.2.3. Optimization of Medical Resource Allocation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Korhonen, J.; Snäkin, J.P. Quantifying the relationship of resilience and eco-efficiency in complex adaptive energy systems. Ecol. Econ. 2015, 120, 83–92. [Google Scholar] [CrossRef]
- Franco, E.G. The global risks report 2020. In Proceedings of the World Economic Forum, Davos, Switzerland, 22 January 2020; pp. 6–7. [Google Scholar]
- Spaans, M.; Waterhout, B. Building up resilience in cities worldwide–Rotterdam as participant in the 100 Resilient Cities Programme. Cities 2017, 61, 109–116. [Google Scholar] [CrossRef]
- Tang, B. The Research on spatial-temporal evolution and influence factors of urban resilience: A Case Study in the Guangzhou Metropolitan Area. Front. Environ. Sci. 2022, 10, 1052930. [Google Scholar] [CrossRef]
- Ahern, J. From fail-safe to safe-to-fail: Sustainability and resilience in the new urban world. Landsc. Urban Plan. 2011, 100, 341–343. [Google Scholar] [CrossRef]
- Ma, F.; Wang, Z.; Sun, Q.; Yuen, K.F.; Zhang, Y.; Xue, H.; Zhao, S. Spatial–Temporal evolution of city resilience and Its Influencing Factors: Evidence from the Guanzhong Plain Urban Agglomeration. Sustainability 2020, 12, 2593. [Google Scholar] [CrossRef]
- Klein RJ, T.; Nicholls, R.J.; Thomalla, F. Resilience to natural hazards: How useful is this concept? Glob. Environ. Chang. Part B Environ. Hazards 2003, 5, 35–45. [Google Scholar] [CrossRef]
- Yang, Q.; Yang, D.; Li, P.; Liang, S.; Zhang, Z. Resilient city: A Bibliometric analysis and visualization. Discret. Dyn. Nat. Soc. 2021, 2021, 5558497. [Google Scholar]
- Holling, C.S. Resilience and stability of ecological systems. Annu. Rev. Ecol. Syst. 1973, 4, 1–23. [Google Scholar] [CrossRef]
- Briceño, S. Building disaster-resilient communities: The road to the second World Conference on Disaster Reduction, January 2005, Kobe, Hyogo, Japan. In Natural Resources Forum; Blackwell Publishing Ltd.: Oxford, UK, 2004; Volume 28, pp. 234–236. [Google Scholar]
- Zhang, M.; Wu, Q.; Li, W.; Sun, D.; Huang, F. Intensifier of urban economic resilience: Specialized or diversified agglomeration? PLoS ONE 2021, 16, e0260214. [Google Scholar] [CrossRef]
- Moya, J.; Goenechea, M. An approach to the unified conceptualization, definition, and characterization of Social Resilience. Int. J. Environ. Res. Public Health 2022, 19, 5746. [Google Scholar] [CrossRef]
- Sjöstedt, M. Resilience revisited: Taking institutional theory seriously. Ecol. Soc. 2015, 20, 23. [Google Scholar] [CrossRef]
- Wang, S.; Cui, Z.; Lin, J.; Xie, J.; Su, K. The coupling relationship between urbanization and ecological resilience in the Pearl River Delta. J. Geogr. Sci. 2022, 32, 44–64. [Google Scholar] [CrossRef]
- Reynolds, H.L.; Mincey, S.K.; Montoya, R.D.; Hamlin, S.; Sullivan, A.; Thapa, B.; Wilson, J.; Rosing, H.; Jarzen, J.; Grove, J.M. Green infrastructure for city resilience: A trait-based framework. Front. Ecol. Environ. 2022, 20, 231–239. [Google Scholar] [CrossRef]
- Melendez, A.; Caballero-Russi, D.; Gutierrez Soto, M.; Giraldo, L.F. Computational models of community resilience. Nat. Hazards 2021, 111, 1121–1152. [Google Scholar] [CrossRef]
- Chen, M.; Lu, Y.; Peng, Y.; Chen, T.; Zhang, Y. Key elements of attentions for enhancing city resilience: A comparison of singapore, Hong Kong and Hangzhou. Buildings 2022, 12, 340. [Google Scholar] [CrossRef]
- Tabibian, M.; Rezapour, M. Assessment of city resilience; a case study of Region 8 of Tehran city, Iran. Sci. Iran. 2016, 23, 1699–1707. [Google Scholar] [CrossRef]
- Liu, X.; Li, S.; Xu, X.; Luo, J. Integrated natural disasters city resilience evaluation: The case of China. Nat. Hazards 2021, 107, 2105–2122. [Google Scholar] [CrossRef]
- Xun, X.; Yuan, Y. Research on the city resilience evaluation with hybrid multiple attribute TOPSIS method: An example in China. Nat. Hazards 2020, 103, 55. [Google Scholar] [CrossRef]
- Palmer, R. Athens City Resilience through Culture; British Council: Hong Kong, China, 2018. [Google Scholar]
- Xiao, L.; Zhang, R.; Xiao, Q. The dynamic evolution and regional gap of ecological livability level in rural China: Based on non-parametric estimation and Dagum Gini coefficient decomposition. Chin. J. Agric. Resour. Reg. Plan. 2021, 42, 119–130. (In Chinese) [Google Scholar]
- Zhao, R.; Fang, C.; Liu, J.; Zhang, L. The evaluation and obstacle analysis of city resilience from the multidimensional perspective in Chinese cities. Sustain. Cities Soc. 2022, 86, 104160. [Google Scholar] [CrossRef]
- Liu, L.; Luo, Y.; Pei, J.; Wang, H.; Li, J.; Li, Y. Temporal and spatial differentiation in City resilience and Its influencing factors in Henan Province. Sustainability 2021, 13, 12460. [Google Scholar] [CrossRef]
- Zhang, H.; Song, Y.; Wang, D.; Pan, S. Research on the construction of environmental pollution control evaluation system in coastal areas based on WSR methodology. Manag. Rev. 2021, 33, 290–300. (In Chinese) [Google Scholar]
- Xu, W.; Zhang, X.; Cui, Y.; Tian, T.; Lin, L.; Liu, Y. Study on comprehensive evaluation of urban water resource vulnerability. Sustainability 2022, 14, 4149. [Google Scholar] [CrossRef]
- Yang, J.; Jing, P.; Gao, D.; Cao, H.B. An analysis of the development obstacle factors of water resource recycling economy in Beijing-Tianjin-Hebei urban agglomeration. China Rural Water Hydropower 2020, 10, 131–136. (In Chinese) [Google Scholar]
- Chen, J. Research on portfolio weighting evaluation method based on game theory. Fujian Comput. 2003, 9, 15–16. (In Chinese) [Google Scholar]
- Xu, S.; Zuo, Y.; Zhang, M. Evaluation of tourism ecological security in China based on Fuzzy matter-element model and diagnosis of obstacle factors. Sci. Geogr. Sin. 2021, 41, 33–43. (In Chinese) [Google Scholar]
- Wang, S.; Zhang, Y.; Wen, H. Comprehensive measurement and regional imbalance of China’s green development performance. Sustainability 2021, 13, 1409. [Google Scholar] [CrossRef]
- Ge, X.; Xu, J.; Xie, Y.; Guo, X.; Yang, D. Evaluation and dynamic evolution of eco-efficiency of resource-based cities—A case study of typical resource-based cities in China. Sustainability 2021, 13, 6802. [Google Scholar] [CrossRef]
- Wang, H.; Qin, F.; Xu, C.; Li, B.; Guo, L.; Wang, Z. Evaluating the suitability of urban development land with a Geodetector. Ecol. Indic. 2021, 123, 107339. [Google Scholar] [CrossRef]
- Zhang, P.; Yu, W.; Zhang, Y. Spatial and temporal variation of city resilience in Shandong Province and its influencing factors. Urban Issues 2018, 9, 27–34. (In Chinese) [Google Scholar]
| First-Level Indicator | Indicator’s Meaning | Secondary Indicators | Units and Properties | Entropy Method Weight | Analytic Hierarchy Process Weight | Game-Weighting Method Weight |
|---|---|---|---|---|---|---|
| Economic dimension (0.249) | Economic level | GDP per capita | CNY/person (+) | 0.037 | 0.094 | 0.054 |
| Economic structure | The proportion of GDP generated via secondary industry | % (+) | 0.011 | 0.041 | 0.020 | |
| The proportion of GDP generated via tertiary industry | % (+) | 0.016 | 0.039 | 0.023 | ||
| Economic vitality | Actual use of foreign direct investment | Billions of dollars (+) | 0.133 | 0.088 | 0.119 | |
| Economic efficiency | Unit GDP energy consumption | Ton standard coal/ CNY 10,000 (−) | 0.005 | 0.044 | 0.017 | |
| Unit GDP carbon emissions | Tons/CNY 10,000 (−) | 0.002 | 0.049 | 0.016 | ||
| Social dimension (0.260) | Population pressure | Population density | Square kilometers per person (−) | 0.006 | 0.020 | 0.010 |
| Employment pressure | Urban registration unemployment rate | % (−) | 0.022 | 0.017 | 0.020 | |
| Social management | Number of public management and social employees | Ten thousand people (+) | 0.066 | 0.010 | 0.049 | |
| Talent base | Number of college students per 10,000 people | One person (+) | 0.068 | 0.018 | 0.053 | |
| The number of sanitary technicians per 10,000 people | One person (+) | 0.018 | 0.030 | 0.021 | ||
| Social medicine | Number of hospital beds per 10,000 people | piece (+) | 0.014 | 0.032 | 0.020 | |
| Number of hospitals and health centers | a (+) | 0.028 | 0.029 | 0.028 | ||
| Social Security | Per capita social security and employment expenditure | CNY (+) | 0.037 | 0.020 | 0.032 | |
| Resident life | Per capita disposable income of urban residents | CNY (+) | 0.031 | 0.017 | 0.027 | |
| Ecological dimension (0.122) | Environmental pressure | Per capita wastewater discharge | Ton (−) | 0.006 | 0.023 | 0.011 |
| Environmental governance | Environmental investment in the proportion of fiscal expenditure | % (+) | 0.038 | 0.043 | 0.040 | |
| Governance efficiency | Comprehensive utilization of industrial solid waste | % (+) | 0.003 | 0.021 | 0.008 | |
| Harmless treatment rate of domestic waste | % (+) | 0.006 | 0.032 | 0.014 | ||
| Green level | Per capita park green space area | Square meters per person (+) | 0.018 | 0.064 | 0.032 | |
| Green coverage rate of building area | % (+) | 0.003 | 0.051 | 0.017 | ||
| Engineering dimension (0.224) | Transportation Facilities | Number of buses per 10,000 people | a (+) | 0.029 | 0.013 | 0.024 |
| Water and electricity facilities | Per capita power consumption | Kilowatt hours per person (−) | 0.049 | 0.016 | 0.039 | |
| Per capita water consumption | Cubic meters per person (−) | 0.105 | 0.020 | 0.079 | ||
| Road facilities | Per capita road area | Cubic meters per person (+) | 0.02 | 0.040 | 0.026 | |
| Communication facilities | Internet broadband penetration rate | Stong-sde (+) | 0.034 | 0.025 | 0.031 | |
| Mobile phone popularization rate | Khri-sde (+) | 0.021 | 0.032 | 0.024 | ||
| Cultural dimension (0.144) | Cultural Construction | Per capita ownership of public books | Copies/person (+) | 0.101 | 0.039 | 0.082 |
| Cultural investment | Per capita education fund investment | CNY/person (+) | 0.073 | 0.037 | 0.062 |
| Province | City (Label) |
|---|---|
| Shanghai | Shanghai (1) |
| Jiangsu | Nanjing (2), Wuxi (3), Changzhou (4), Suzhou (5), Nantong (6), Yancheng (7), Yangzhou (8), Zhejiang (9), Taizhou (10), Lianyungang (11), Huai’an (12), Suqian (13), Xuzhou (14) |
| Zhejiang | Hangzhou (15), Ningbo (16), Jiaxing (17), Huzhou (18), Shaoshing (19), Jinhua (20), Zhoushan (21), Taizhou (22), Wenzhou (23), Quzhou (24), Lishui (25) |
| Anhui | Hefei (26), Fuyang (27), Chuzhou (28), Wuhu (29), Xuancheng (30), Tongling (31), Chizhou (32), Anqing (33), Maanshan (34), Huaibei (35), Bozhou (36), Suzhou (37), Bengbu (38), Huainan (39), Lu ’an (40), Huangshan (41) |
| Years | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Within regions | 14.90 | 14.73 | 15.29 | 16.44 | 15.86 | 15.42 | 15.22 | 14.89 | 14.50 | 14.73 | 14.84 |
| Between regions | 74.46 | 75.66 | 73.93 | 69.91 | 70.63 | 71.23 | 70.68 | 72.23 | 73.84 | 73.16 | 72.50 |
| Supervariable density | 10.64 | 9.61 | 10.77 | 13.65 | 13.52 | 13.35 | 14.10 | 12.87 | 11.66 | 12.10 | 12.66 |
| Variable | Influential Factors | Index and Calculation |
|---|---|---|
| X1 | Economic development | GDP per capita |
| X2 | Industrial structure | The added value of the tertiary industry/GDP |
| X3 | Residence income | Urban per capita disposable income |
| X4 | Fiscal policy | Public fiscal expenditure/GDP |
| X5 | Scientific and technological innovation | Scientific and technological expenditure/Fiscal expenditure |
| X6 | Openness to the outside world | Total import and export/GDP |
| X7 | Ecosystem | Per capita Park green space area |
| X8 | Information dissemination | Internet popularization rate |
| X9 | Resource utilization | Total energy consumption/GDP |
| X10 | Medical conditions | The number of sanitary technicians per 10,000 people |
| Year | Factors | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | |
| 2010 | 0.801 *** | 0.406 ** | 0.831 *** | 0.265 * | 0.268 * | 0.311 | 0.453 *** | 0.817 *** | 0.248 | 0.594 *** |
| 2011 | 0.801 *** | 0.560 *** | 0.822 *** | 0.283 ** | 0.317 | 0.384 ** | 0.429 *** | 0.796 *** | 0.316 | 0.629 *** |
| 2012 | 0.811 *** | 0.614 *** | 0.748 *** | 0.220 | 0.291 | 0.321 | 0.407 ** | 0.765 *** | 0.325 | 0.652 *** |
| 2013 | 0.818 *** | 0.526 *** | 0.782 *** | 0.228 | 0.253 | 0.459 ** | 0.334 ** | 0.767 *** | 0.062 | 0.598 *** |
| 2014 | 0.765 *** | 0.433 ** | 0.826 *** | 0.171 | 0.276 ** | 0.487 *** | 0.302 ** | 0.705 *** | 0.409 ** | 0.583 *** |
| 2015 | 0.709 *** | 0.494 ** | 0.787 *** | 0.225 ** | 0.298 ** | 0.493 ** | 0.301 ** | 0.744 *** | 0.117 | 0.619 *** |
| 2016 | 0.783 *** | 0.432 * | 0.775 *** | 0.221 ** | 0.194 | 0.399 ** | 0.396 * | 0.756 *** | 0.324 * | 0.622 *** |
| 2017 | 0.746 *** | 0.270 | 0.773 *** | 0.285 ** | 0.194 | 0.357 ** | 0.325 * | 0.709 *** | 0.158 | 0.625 *** |
| 2018 | 0.777 *** | 0.351 | 0.836 *** | 0.142 | 0.209 | 0.449 ** | 0.306 * | 0.680 *** | 0.274 * | 0.691 *** |
| 2019 | 0.693 *** | 0.245 | 0.731 *** | 0.088 | 0.147 | 0.382 | 0.311 | 0.558 *** | 0.152 | 0.616 *** |
| 2020 | 0.653 *** | 0.349 | 0.815 *** | 0.226 | 0.227 | 0.371* | 0.349 ** | 0.553 *** | 0.311 | 0.694 *** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Q.; Zhong, S.; Chen, J.; Yang, C.; Zhu, Y. Spatio-Temporal Evolution of City Resilience in the Yangtze River Delta, China, from the Perspective of Statistics. Sustainability 2023, 15, 1538. https://doi.org/10.3390/su15021538
Song Q, Zhong S, Chen J, Yang C, Zhu Y. Spatio-Temporal Evolution of City Resilience in the Yangtze River Delta, China, from the Perspective of Statistics. Sustainability. 2023; 15(2):1538. https://doi.org/10.3390/su15021538
Chicago/Turabian StyleSong, Qing, Shengyuan Zhong, Junyu Chen, Chuanming Yang, and Yan Zhu. 2023. "Spatio-Temporal Evolution of City Resilience in the Yangtze River Delta, China, from the Perspective of Statistics" Sustainability 15, no. 2: 1538. https://doi.org/10.3390/su15021538
APA StyleSong, Q., Zhong, S., Chen, J., Yang, C., & Zhu, Y. (2023). Spatio-Temporal Evolution of City Resilience in the Yangtze River Delta, China, from the Perspective of Statistics. Sustainability, 15(2), 1538. https://doi.org/10.3390/su15021538






