Reversible Lane Optimization of the Urban Road Network Considering Adjustment Time Constraints
Abstract
1. Introduction
2. Bi-Level Programming Model for Reversible Lane Optimization
3. Model Solution
| Algorithm 1: Parameter initialization |
| FOR each particle i FOR each dimension randomly within permissible range randomly within permissible range END FOR END FOR DO FOR each particle i IF ELSE END IF END FOR IF j ← 0 ElSE IF END IF END IF FOR each particle i FOR each dimension Calculate velocity according to the equation END IF IF and the OD pair has path connectivity ELSE END IF END FOR END FOR WHILE maximum iterations or minimum error criteria are not attained RETUNE |
4. Calculations and Analysis of Numerical Example
5. Conclusions
- (1).
- Based on the actual situation in which the number of reversible sections that can be optimized within the adjustment time are limited, a reversible lane optimization study is conducted on the premise of ensuring normal traffic during the implementation of reversible lanes, which is conducive to the practical application of reversible lane optimization theory and will have a positive and beneficial impact on achieving sustainability goals.
- (2).
- With the goal of minimalizing the total travel time of the system, a mixed-integer bilevel programming model for reversible lane optimization constrained by adjustment time is established, a particle swarm optimization algorithm is designed to solve the model, and the effectiveness of the model and the algorithm is verified by numerical examples.
- (3).
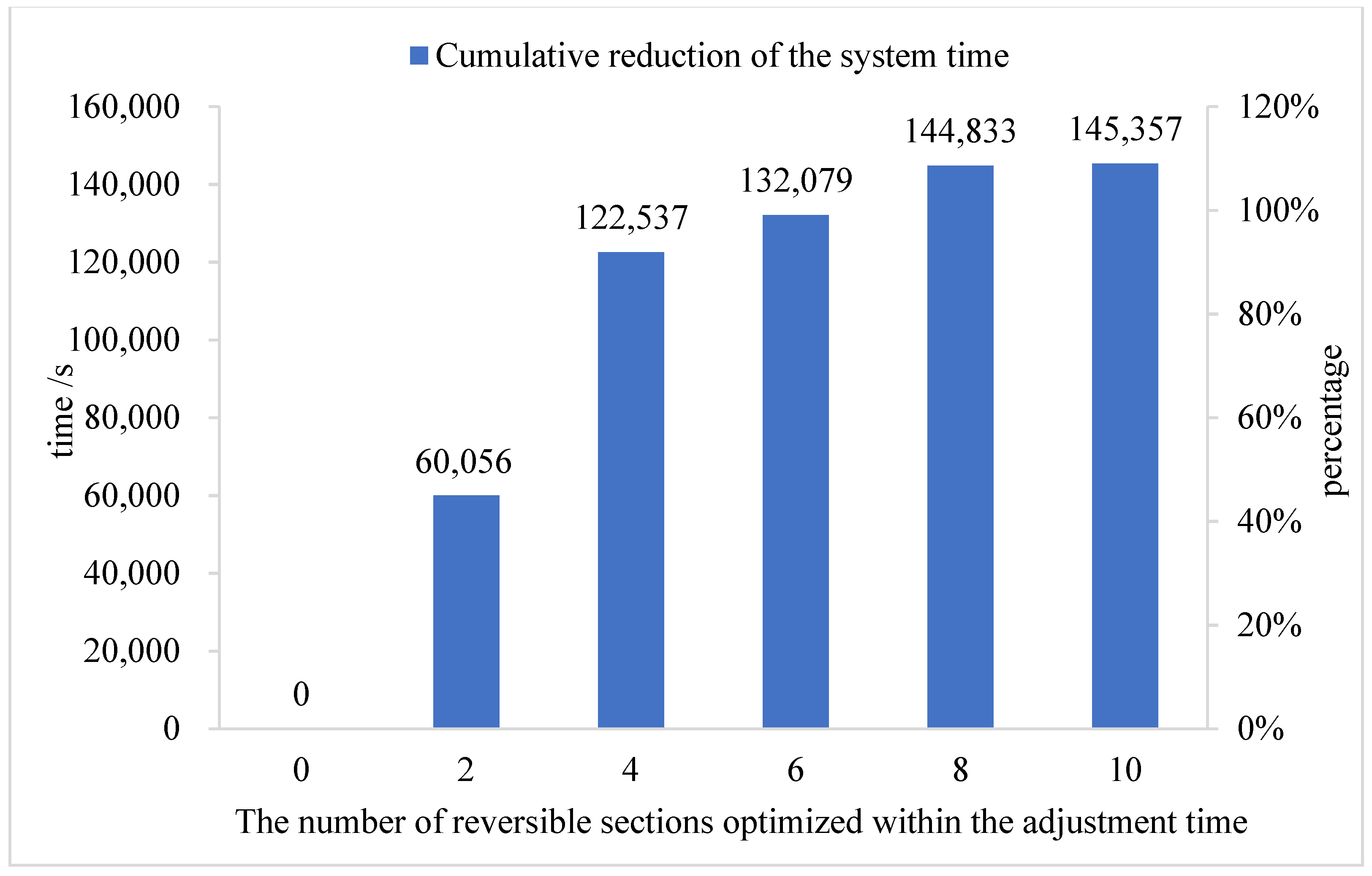
- With an increase in the number of reversible sections that can be optimized within the adjustment time, the cumulative reduction time of the system increases monotonically and the road network optimization effect improves. However, the optimization effect of the newly added reversible sections shows a decreasing trend as a whole in each stage.
- (4).
- To answer the problem of reversible lane optimization in urban road networks, we only need to optimize efficient reversible sections to achieve a good optimization effect, and it is unnecessary to pursue reversible lane optimization for all sections.
- (5).
- The question of how to control traffic at intersections with reversible lanes is an important one; in order to obtain a better reversible lane optimization system, traffic control at intersections will be fully considered in further research.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, T.; Yang, Z.; Ma, D.; Sheng, J. Bi-level programming model for dynamic reversible lane assignment. IEEE Access 2018, 6, 71592–71601. [Google Scholar] [CrossRef]
- Mao, L.N.; Li, W.Q.; Hu, P.; Zhou, G.L.; Zhang, H.T.; Zheng, G.H. Control Model Constructing on Real-Time Dynamic Reversible Lane in Condition of Connected Vehicle. In Proceedings of the 20th COTA International Conference of Transportation Professionals, Xi’an, China, 16–19 December 2020. [Google Scholar]
- Sheu, J.B.; Ritchie, S.G. Stochastic modeling and real-time prediction of vehicular lane-changing behavior. Transp. Res. Part B Meth. 2001, 35, 695–716. [Google Scholar] [CrossRef]
- Wong, C.K.; Wong, S.C. Lane-based optimization of signal timings for isolated junctions. Transp. Res. Part B Meth. 2003, 37, 63–84. [Google Scholar] [CrossRef]
- Golub, A. Perceived costs and benefifits of reversible lanes in Phoenix, Arizona. ITE J. 2012, 82, 38–42. [Google Scholar]
- Karoonsoontawong, A.; Lin, D.Y. Time-varying lane-based capacity reversibility for traffic management. Comput.-Aided. Civ. Inf. 2011, 26, 632–646. [Google Scholar] [CrossRef]
- Wojtowicz, J.; Wallace, W.A. Traffic management for planned special events using traffic microsimulation modeling and tabletop exercises. J. Transp. Saf. Secur. 2010, 2, 102–121. [Google Scholar] [CrossRef]
- Cao, Y.; Zou, Z.; Xu, H. Analysis of Traffic conflflict characteristic at temporary reversible lane. Period. Polytech. Transp. Eng. 2014, 42, 73–76. [Google Scholar] [CrossRef]
- Jiang, Y.H.; Bao, L.X. Study on setting of variable lanes near Intersection between one-way and two-way traffic. J. Shanghai Jiaotong Univ. 2011, 45, 1562–1566. [Google Scholar]
- Bede, Z.; Péter, T. Optimal control with the dynamic change of the structure of the road network. Transport 2014, 29, 36–42. [Google Scholar] [CrossRef]
- Waleczek, H.; Geistefeldt, J.; Middendorf, D.C. Traffic flow at a freeway work zone with reversible median lane. Transp. Res. Proced. 2016, 15, 257–266. [Google Scholar] [CrossRef]
- Wolshon, B.; Lambert, L. Reversible lane systems: Synthesis of practice. J. Transp. Eng. 2006, 132, 933–944. [Google Scholar] [CrossRef]
- Wu, Q.Q.; Li, D.J. Research on reversible lane optimization based on hierarchical programming model. In Proceedings of the 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference(ITNEC), Chongqing, China, 12–14 June 2020. [Google Scholar]
- Chu, K.F.; Lam, A.; Li, V. Dynamic lane reversal routing and scheduling for connected and autonomous vehicles: Formulation and distributed algorithm. IEEE. T. Intell. Transp. 2020, 21, 2557–2570. [Google Scholar] [CrossRef]
- Conceio, L.; Correia, G.; Tavares, J.P. The reversible lane network design problem (RL-NDP) for smart cities with automated traffic. Sustainability 2020, 12, 1226. [Google Scholar] [CrossRef]
- Mao, L.; Li, W.; Hu, P. Design of Real-Time Dynamic Reversible Lane in Intelligent Cooperative Vehicle Infrastructure System. J. Adv. Transp. 2020, 2020, 8896. [Google Scholar] [CrossRef]
- Di, Z.; Yang, L.X. Reversible lane network design for maximizing the coupling measure between demand structure and network structure. Transp. Res. Part E Logist. Transp. Rev. 2020, 141, 2021. [Google Scholar] [CrossRef]
- Méndez, D.P.; Gershenson, C.; Lárraga, M.E.; Mateos, J.L. Modeling adaptive reversible lanes: A cellular automata approach. PLoS ONE 2021, 16, 4326. [Google Scholar] [CrossRef]
- Dey, S.; Ma, J.; Aden, Y. Reversible lane adjustment for arterial roadways: The Washington, DC, USA experience. ITE J. 2011, 81, 26–35. [Google Scholar]
- Yue, L.; Xu, T.D.; Xia, H.P.; Du, Y.C. Reversible lane design for Shanghai world expo 2010. Urban Transp. China 2010, 8, 25–30. [Google Scholar]
- Chen, J.; Huo, Y.M. Study on setting design of variable lane on typical tide traffic road. J. Chongqing Jiaotong Univ. Nat. Sci. 2008, 27, 1127–1130. [Google Scholar]
- Ma, Y.Y.; Zeng, L.Y.; Chen, G.M. Study on dynamic traffic control for reversible lanes. Control. Theory. A. 2016, 33, 1457–1462. [Google Scholar]
- Zhang, W.H.; Han, G.F.; Yan, R. Evaluation on effect of setting variable lane in urban road section. J. Chongqing Jiaotong Univ. Nat. Sci. 2014, 33, 128–133. [Google Scholar]
- Cai, J.R.; Huang, Z.X.; Wu, L.X. Optimization of reversible lane based on autonomous vehicles. J. Highw. Transp. Res. Dev. 2018, 35, 136–150. [Google Scholar]
- Shi, F.; Su, H.Y.; Wang, X. Design of reversible lanes with tidal flow on road network. J. Transp. Sys. Eng. Inform. Technol. 2015, 15, 57–62. [Google Scholar]
- Zhang, H.Z.; Gao, Z.Y. Optimization approach for traffic road network design problem. Chin. J. Manag. Sci. 2004, 15, 86–91. [Google Scholar]
- Xu, H.Z.; Cheng, G.Z.; Pei, Y.L. Study on effect of lane-changing behavioral characteristic to capacity. Sci. Online 2010, 5, 749–753. [Google Scholar]
- Yang, X.B.; Zhang, N. Mathematical analysis of effects of lanes’s number on expressway capacity. J. Wuhan Univ. Tech. 2008, 32, 603–606. [Google Scholar]
- Wang, W.; Guo, X.C. Traffic Engineering, 1st ed.; Southeast University Press: Nanjing, China, 2009; p. 156. [Google Scholar]
- Wang, S.Y.; Wang, L. An estimation of distribution algorithmbased memetic algorithm for the distributed assembly permutation flow-shop scheduling problem. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 139–149. [Google Scholar] [CrossRef]
- Zhou, F.; Wu, J.H.; Xu, Y.; Yi, C. Optimization scheme of tradable credits and bus departure quantity for travelers’ travel mode choice guidance. J. Adv. Transp. 2020, 2020, 5161. [Google Scholar] [CrossRef]
- Shi, W.; Chen, W.; Lin, Y.; Gu, T.; Kwong, S.; Zhang, J. An adaptive estimation of distribution algorithm for multi-policy insurance investment planning. IEEE Trans. Evol. Comput. 2019, 23, 1–14. [Google Scholar] [CrossRef]


| Section | Free Travel Time (s) | Single-Lane Capacity (pcu/h) | Number of Lanes |
|---|---|---|---|
| 1-2 | 95 | 650 | 4 |
| 2-1 | 95 | 650 | 4 |
| 4-2 | 55 | 650 | 4 |
| 2-4 | 55 | 650 | 4 |
| 1-3 | 55 | 700 | 3 |
| 3-1 | 55 | 700 | 3 |
| 4-3 | 95 | 700 | 3 |
| 3-4 | 95 | 700 | 3 |
| 2-3 | 41 | 700 | 3 |
| 3-2 | 41 | 700 | 3 |
| Section | Number of Lanes | Capacity (pcu/h) | Flow (pcu/h) | Saturation | Travel Time (s) |
|---|---|---|---|---|---|
| 1-2 | 4 | 2173 | 2384 | 1.097 | 115.637 |
| 2-1 | 4 | 2173 | 473 | 0.218 | 95.032 |
| 3-1 | 3 | 1822 | 407 | 0.223 | 55.020 |
| 1-3 | 3 | 1822 | 2206 | 1.211 | 72.743 |
| 2-3 | 3 | 1822 | 761 | 0.418 | 41.188 |
| 3-2 | 3 | 1822 | 1363 | 0.748 | 42.925 |
| 4-2 | 4 | 2173 | 473 | 0.218 | 55.019 |
| 2-4 | 4 | 2173 | 2607 | 1.200 | 72.107 |
| 4-3 | 3 | 1822 | 407 | 0.223 | 95.035 |
| 3-4 | 3 | 1822 | 1983 | 1.088 | 114.968 |
| Section | Number of Lanes | Capacity (pcu/h) | Flow (pcu/h) | Saturation | Travel Time (s) |
|---|---|---|---|---|---|
| 1-2 | 7 | 3625 | 2722 | 0.751 | 99.530 |
| 2-1 | 1 | 650 | 251 | 0.386 | 95.317 |
| 3-1 | 3 | 1822 | 629 | 0.345 | 55.117 |
| 1-3 | 3 | 1822 | 1868 | 1.025 | 64.115 |
| 2-3 | 3 | 1822 | 760 | 0.417 | 41.186 |
| 3-2 | 3 | 1822 | 1140 | 0.626 | 41.943 |
| 4-2 | 4 | 2173 | 251 | 0.116 | 55.001 |
| 2-4 | 4 | 2173 | 2722 | 1.253 | 75.313 |
| 4-3 | 3 | 1822 | 629 | 0.345 | 95.202 |
| 3-4 | 3 | 1822 | 1868 | 1.025 | 110.744 |
| Section | Number of Lanes | Capacity (pcu/h) | Flow (pcu/h) | Saturation | Travel Time (s) |
|---|---|---|---|---|---|
| 1-2 | 7 | 3625 | 3015 | 0.832 | 101.828 |
| 2-1 | 1 | 650 | 231 | 0.355 | 95.226 |
| 3-1 | 3 | 1822 | 649 | 0.356 | 55.133 |
| 1-3 | 3 | 1822 | 1575 | 0.864 | 59.597 |
| 2-3 | 3 | 1822 | 759 | 0.417 | 41.186 |
| 3-2 | 3 | 1822 | 1214 | 0.666 | 42.210 |
| 4-2 | 1 | 650 | 231 | 0.355 | 55.131 |
| 2-4 | 7 | 3625 | 3089 | 0.852 | 59.347 |
| 4-3 | 3 | 1822 | 649 | 0.356 | 95.229 |
| 3-4 | 3 | 1822 | 1501 | 0.824 | 101.569 |
| Section | Number of Lanes | Capacity (pcu/h) | Flow (pcu/h) | Saturation | Travel Time (s) |
|---|---|---|---|---|---|
| 1-2 | 7 | 3625 | 2857 | 0.788 | 100.494 |
| 2-1 | 1 | 650 | 358 | 0.551 | 96.313 |
| 3-1 | 3 | 1822 | 522 | 0.286 | 55.055 |
| 1-3 | 3 | 1822 | 1733 | 0.951 | 61.748 |
| 2-3 | 3 | 1822 | 822 | 0.451 | 41.254 |
| 3-2 | 3 | 1822 | 1140 | 0.626 | 41.944 |
| 4-2 | 1 | 650 | 419 | 0.645 | 56.428 |
| 2-4 | 7 | 3625 | 2857 | 0.788 | 58.181 |
| 4-3 | 1 | 700 | 461 | 0.659 | 97.688 |
| 3-4 | 5 | 2861 | 1733 | 0.606 | 96.922 |
| Section | Number of Lanes | Capacity (pcu/h) | Flow (pcu/h) | Saturation | Travel Time (s) |
|---|---|---|---|---|---|
| 1-2 | 7 | 3625 | 2565 | 0.708 | 98.581 |
| 2-1 | 1 | 650 | 424 | 0.652 | 97.575 |
| 3-1 | 1 | 700 | 456 | 0.651 | 56.482 |
| 1-3 | 5 | 2861 | 2025 | 0.708 | 57.073 |
| 2-3 | 3 | 1822 | 761 | 0.418 | 41.188 |
| 3-2 | 3 | 1822 | 1140 | 0.626 | 41.944 |
| 4-2 | 1 | 650 | 424 | 0.652 | 56.491 |
| 2-4 | 7 | 3625 | 2565 | 0.708 | 57.073 |
| 4-3 | 1 | 700 | 456 | 0.651 | 97.559 |
| 3-4 | 5 | 2861 | 2025 | 0.708 | 98.581 |
| Section | Number of Lanes | Capacity (pcu/h) | Flow (pcu/h) | Saturation | Travel Time (s) |
|---|---|---|---|---|---|
| 1-2 | 7 | 3625 | 2552 | 0.704 | 98.500 |
| 2-1 | 1 | 650 | 424 | 0.652 | 97.575 |
| 3-1 | 1 | 700 | 456 | 0.651 | 56.482 |
| 1-3 | 5 | 2861 | 2038 | 0.712 | 57.120 |
| 2-3 | 2 | 1309 | 760 | 0.581 | 41.701 |
| 3-2 | 4 | 2341 | 1166 | 0.498 | 41.378 |
| 4-2 | 1 | 650 | 424 | 0.652 | 56.491 |
| 2-4 | 7 | 3625 | 2578 | 0.711 | 57.108 |
| 4-3 | 1 | 700 | 456 | 0.651 | 97.559 |
| 3-4 | 5 | 2861 | 2012 | 0.703 | 98.480 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, J.; Li, Z.; Xiao, Y.; Zhou, Z.; Long, Q.; Yu, J.; Zhang, J.; Zhang, L. Reversible Lane Optimization of the Urban Road Network Considering Adjustment Time Constraints. Sustainability 2023, 15, 1381. https://doi.org/10.3390/su15021381
Cai J, Li Z, Xiao Y, Zhou Z, Long Q, Yu J, Zhang J, Zhang L. Reversible Lane Optimization of the Urban Road Network Considering Adjustment Time Constraints. Sustainability. 2023; 15(2):1381. https://doi.org/10.3390/su15021381
Chicago/Turabian StyleCai, Jianrong, Zhixue Li, Yinghong Xiao, Zhaoming Zhou, Qiong Long, Jie Yu, Jinfan Zhang, and Lei Zhang. 2023. "Reversible Lane Optimization of the Urban Road Network Considering Adjustment Time Constraints" Sustainability 15, no. 2: 1381. https://doi.org/10.3390/su15021381
APA StyleCai, J., Li, Z., Xiao, Y., Zhou, Z., Long, Q., Yu, J., Zhang, J., & Zhang, L. (2023). Reversible Lane Optimization of the Urban Road Network Considering Adjustment Time Constraints. Sustainability, 15(2), 1381. https://doi.org/10.3390/su15021381






