Orthogonal Experimental Study on Remediation of Ethylbenzene Contaminated Soil by SVE
Abstract
1. Introduction
2. Materials and Methods
2.1. Contaminated Soil Collection and Determination
2.2. Specimen Preparation and Processing
2.3. Target Pollutant Detection
2.4. SVE Experimental Model
2.5. Kinetic Analysis
2.6. Orthogonal Experiments
2.7. Setting up the 3D-SVE Model
3. Results and Discussion
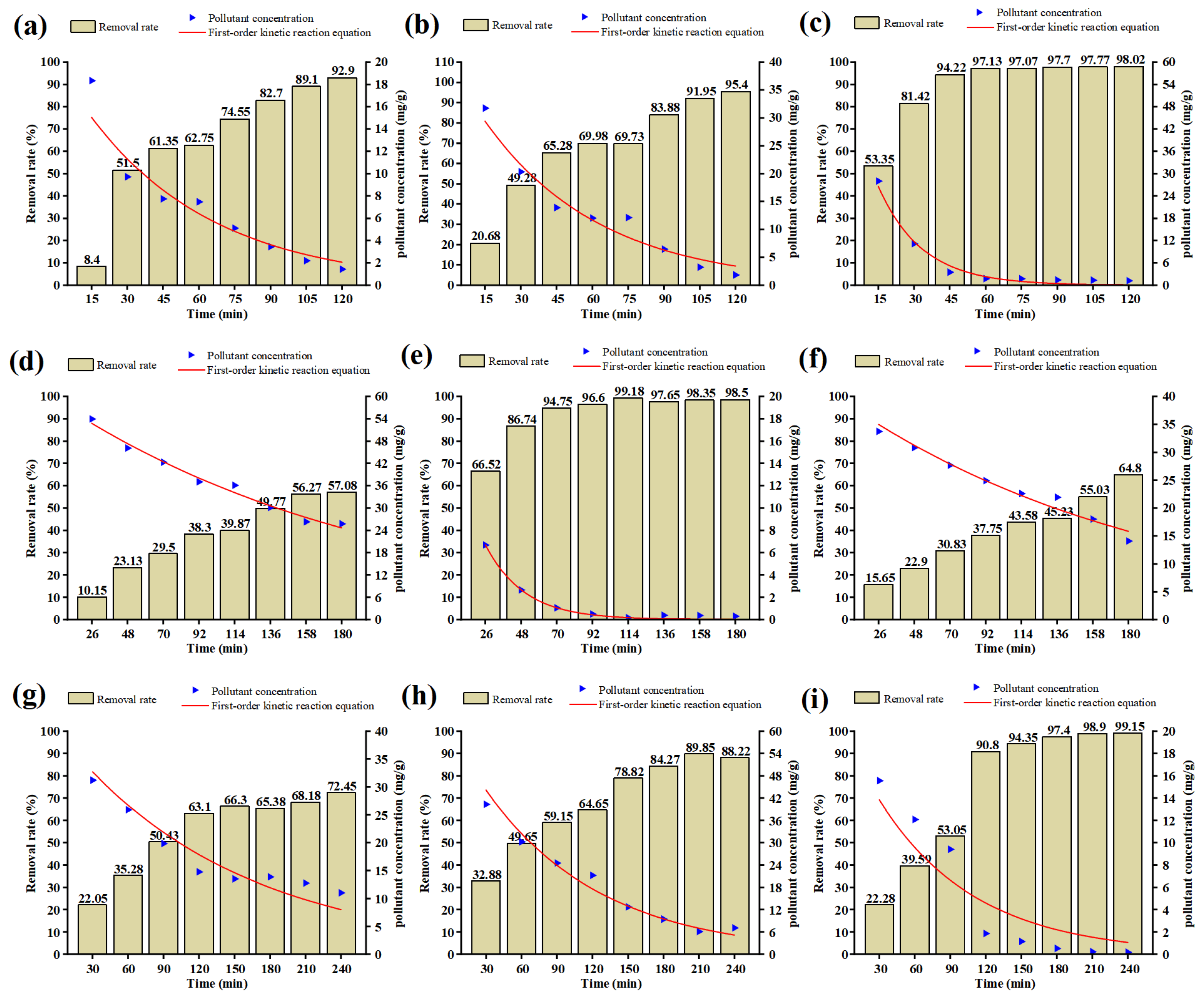
3.1. Kinetic Characteristics of Pollutant Removal in SVE
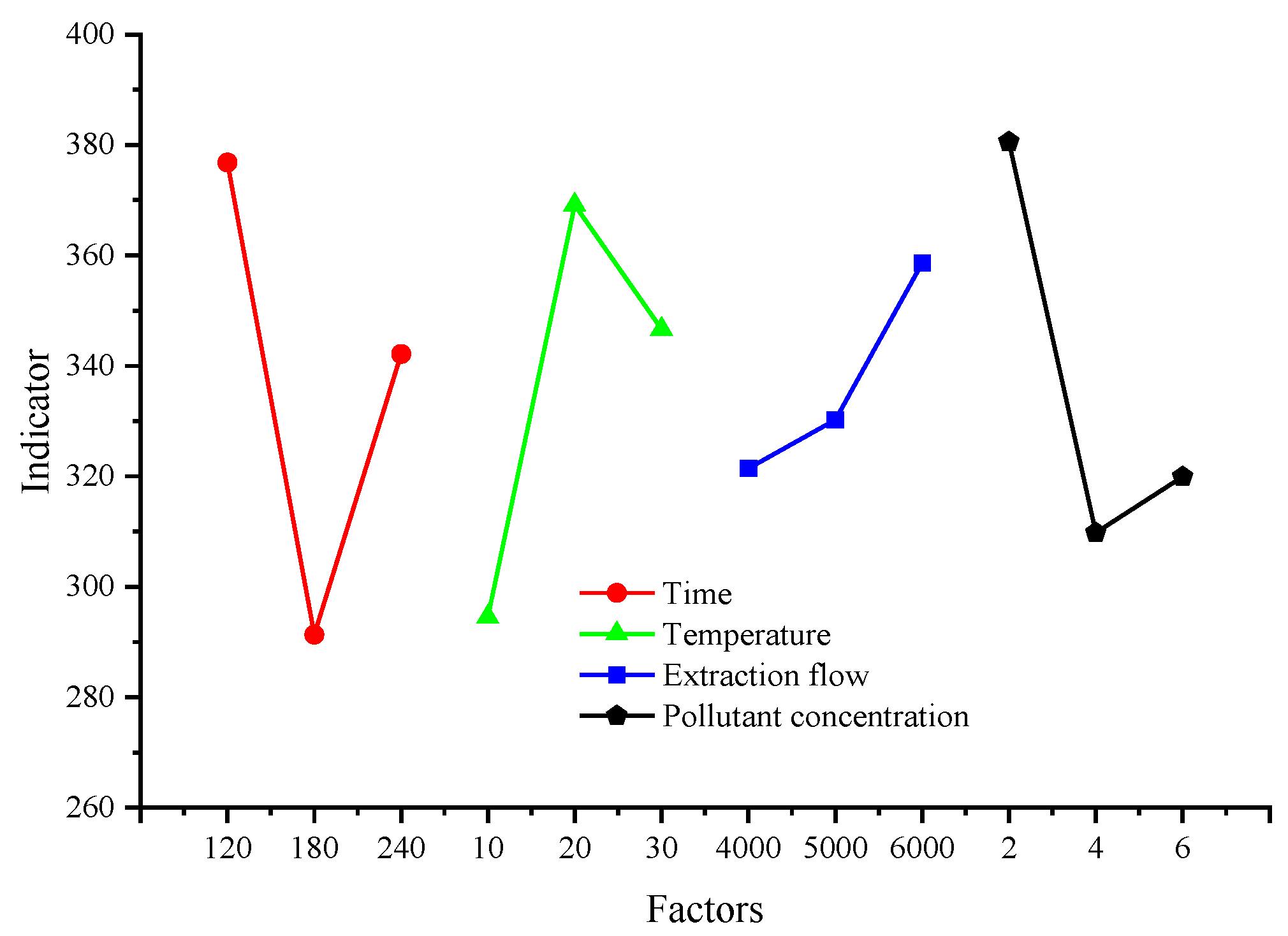
3.2. Range Analysis
3.3. Variance Analysis
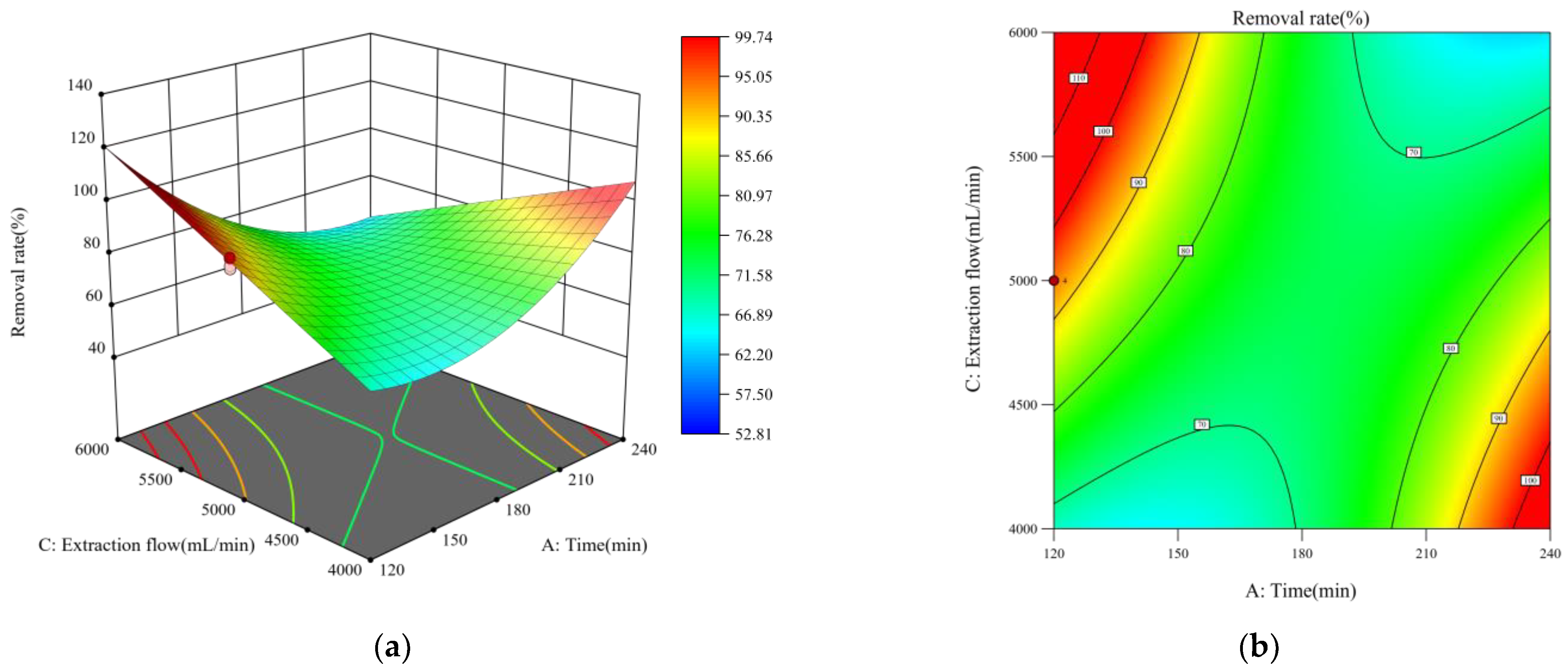
3.4. Response Surface Analysis
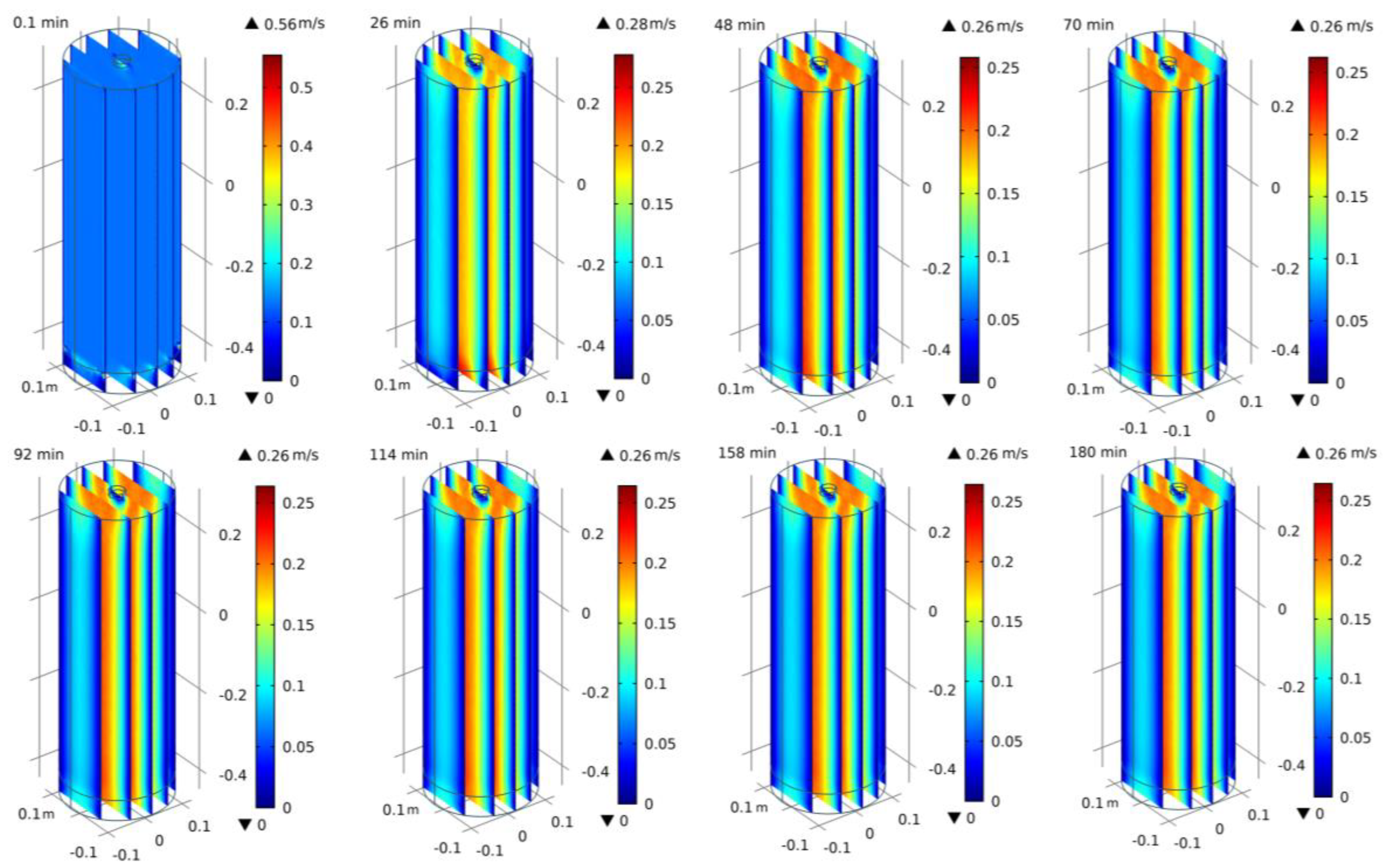
3.5. Simulation
4. Conclusions
- Based on the range analysis and the first-order kinetic reaction model, it can be concluded that test 5 (A2B2C3D1) is the optimal combination, and in addition, the half-life performance in test 3 and test 5 is better than the other groups.
- ANOVA and Duncan’s new multiple range tests showed that the effect of factors on SVE was greater than the fluctuation of data caused by errors, and four factors were significant or highly significant.
- Response surface analysis showed that time, temperature, and extraction flow rate had a positive effect on the removal rate, while the interaction of time with temperature and time with extraction flow rate had a very significant negative effect. In addition, the optimal remediation conditions were: time 180 min, temperature 20 °C, extraction flow rate 6000 mL/min, and contaminant concentration 2%.
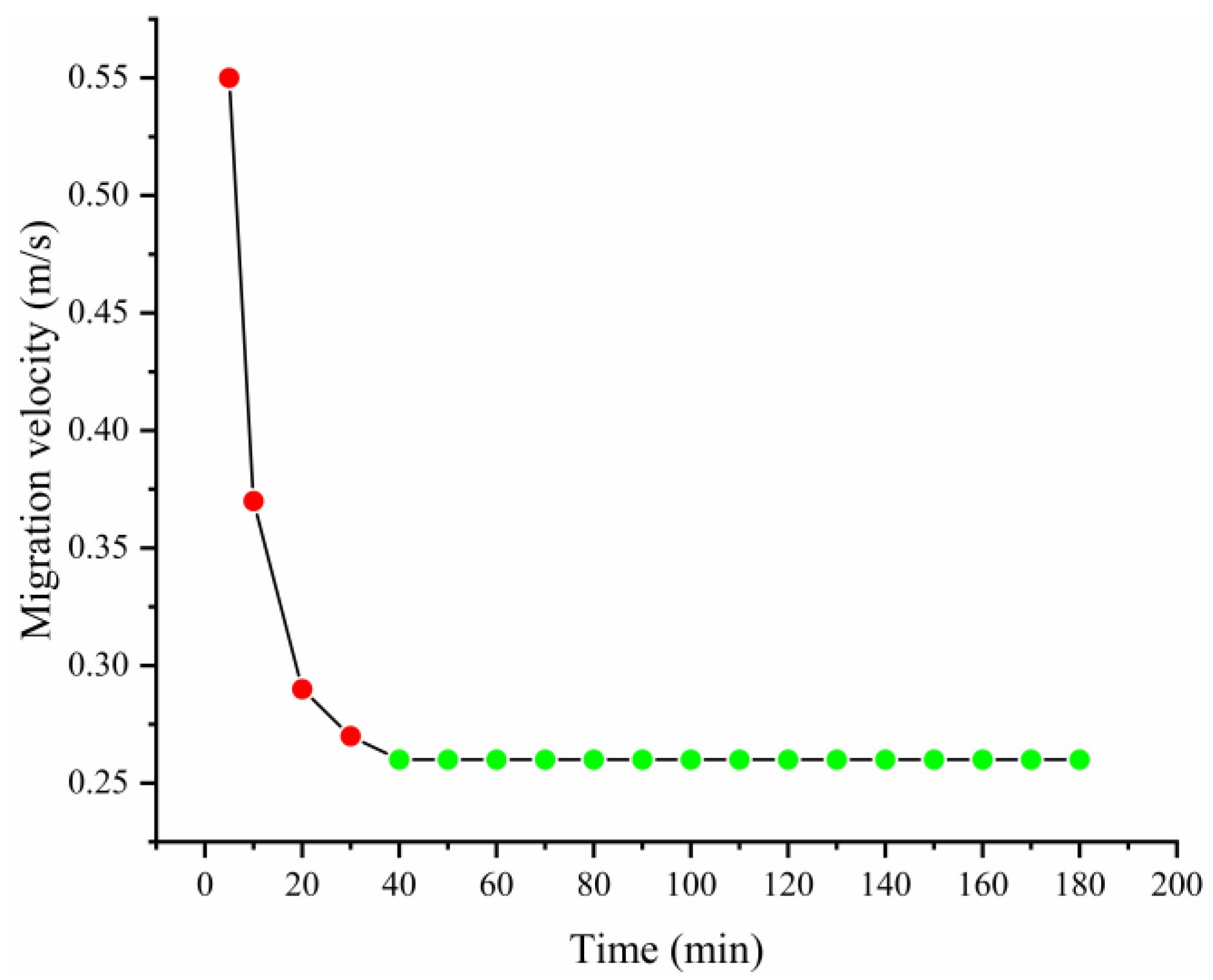
- The isometric numerical simulation showed that the maximum rate of contaminant migration remained stable after the model was heated for 40 min under the optimal combination of conditions, and a trailing effect was also observed.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Q.; Feng, Q.; Zhu, X.; Zhang, M.; Wang, Y.; Yang, L. Box Experiment Study of Thermally Enhanced SVE for Benzene. Int. J. Environ. Res. Public Health 2021, 18, 4062. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.-H.; Feng, S.-J.; Zheng, Q.-T.; Peng, C.-H.; Zhu, Z.-W.; Yang, C.-B. Transient migration behavior of VOC vapor in layered unsaturated soils subjected to multiple time-dependent point pollution sources: Analytical study. Sci. Total Environ. 2022, 806, 150370. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y. Study on Typical Influencing Factors of Non-Aqueous Pollutants in SVE Technology. Master’s Thesis, China University of Mining and Technology, Xuzhou, China, 2019. [Google Scholar]
- Yang, Y.; Wang, C.; Sha, X.; Song, M.; Sang, Y.; Zhu, L. Desorption kinetics of thermal enhanced soil vapor extraction technology used in hydrocarbon contaminated soil. Chin. J. Environ. Eng. 2019, 13, 2328–2335. [Google Scholar]
- Yang, Y.; Li, J.; Xi, B.; Wang, Y.; Tang, J.; Wang, Y.; Zhao, C. Modeling BTEX migration with soil vapor extraction remediation under low-temperature conditions. J. Environ. Manag. 2017, 203, 114–122. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Zhang, Y.; Deng, Z.; Song, H.; Wang, J.; Guo, H. An innovative method for soil vapor extraction to improve extraction and tail gas treatment efficiency. Sci. Rep.-UK 2022, 12, 6495. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.; Yang, Y.; Li, J.; Xi, B.; Wang, Y.; Wang, Y.; Tang, J. A study of layered-unlayered extraction of benzene in soil by SVE. Environ. Pollut. 2020, 263, 114219. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Shao, Z.; Liu, J.; Wen, W.; Yan, Z. Factors influencing remediation of semi-volatile petroleum hydrocarbon-contaminated soil by thermally enhanced soil vapor extraction. Chin. J. Environ. Eng. 2017, 11, 2522–2527. [Google Scholar]
- Qin, C.-Y.; Zhao, Y.-S.; Zheng, W.; Li, Y.-S. Study on influencing factors on removal of chlorobenzene from unsaturated zone by soil vapor extraction. J. Hazard. Mater. 2010, 176, 294–299. [Google Scholar] [CrossRef]
- Hinchee, R.E.; Dahlen, P.R.; Johnson, P.C.; Burris, D.R. 1,4-Dioxane Soil Remediation Using Enhanced Soil Vapor Extraction: I. Field Demonstration. Groundw. Monit. Remediat. 2018, 38, 40–48. [Google Scholar] [CrossRef]
- Poppendieck, D.G.; Loehr, R.C.; Webster, M.T. Predicting hydrocarbon removal from thermally enhanced soil vapor extraction systems: 2. Field study. J. Hazard. Mater. 1999, 69, 95–109. [Google Scholar] [CrossRef]
- Lim, M.W.; Von Lau, E.; Poh, P.E. A comprehensive guide of remediation technologies for oil contaminated soil—Present works and future directions. Mar. Pollut. Bull. 2016, 109, 14–45. [Google Scholar] [CrossRef] [PubMed]
- Hao, G.; Yong, Q.; Guangxiang, Y.; Chunxiao, W. Research progress on the soil vapor extraction. J. Groundw. Sci. Eng. 2020, 8, 57–66. [Google Scholar]
- Labianca, C.; De Gisi, S.; Picardi, F.; Todaro, F.; Notarnicola, M. Remediation of a Petroleum Hydrocarbon-Contaminated Site by Soil Vapor Extraction: A Full-Scale Case Study. Appl. Sci. 2020, 10, 4261. [Google Scholar] [CrossRef]
- Yang, X.; Yi, H.; Tang, X.; Zhao, S.; Yang, Z.; Ma, Y.; Feng, T.; Cui, X. Behaviors and kinetics of toluene adsorption-desorption on activated carbons with varying pore structure. J. Environ. Sci. 2018, 67, 104–114. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Tang, J.; Li, J.; Yang, Y.; Bai, S.; Shi, J. Numerical simulation of SVE in groundwater table fluctuation zone based on TMVOC. China Environ. Sci. 2020, 40, 350–356. [Google Scholar]
- Nguyen, V.T.; Zhao, L.; Zytner, R.G. Three-dimensional numerical model for soil vapor extraction. J. Contam. Hydrol. 2013, 147, 82–95. [Google Scholar] [CrossRef]
- Rehman, Z.U.; Khalid, U.; Ijaz, N.; Mujtaba, H.; Haider, A.; Farooq, K.; Ijaz, Z. Machine learning-based intelligent modeling of hydraulic conductivity of sandy soils considering a wide range of grain sizes. Eng. Geol. 2022, 311, 106899. [Google Scholar] [CrossRef]
- Esrael, D.; Kacem, M.; Benadda, B. Modelling mass transfer during venting/soil vapour extraction: Non-aqueous phase liquid/gas mass transfer coefficient estimation. J. Contam. Hydrol. 2017, 202, 70–79. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, Y.; Zhu, L.; Sang, Y. ERH remediation process optimization of organic contaminated soil based on COMSOL simulation. Chin. J. Environ. Eng. 2021, 15, 3642–3650. [Google Scholar]
- Yang, Y.; Zhao, C.J.; Li, J.; Bai, S.G.; Xi, B.D.; Tang, J.; Lu, N.Q. Numerical Simulation through SVE Technique based on TMVOC under Low Temperature. Res. Environ. Sci. 2017, 30, 1587–1596. [Google Scholar]
- Fen, C.-S.; Cheng, H.-C.; Ku, C.-C. An effective response surface-based optimisation approach for soil vapour extraction system design. Civ. Eng. Environ. Syst. 2008, 25, 227–243. [Google Scholar] [CrossRef]
- Fen, C.-S.; Chan, C.; Cheng, H.-C. Assessing a Response Surface-Based Optimization Approach for Soil Vapor Extraction System Design. J. Water Resour. Plan. Manag. 2009, 135, 198–207. [Google Scholar] [CrossRef]
- Sabour, M.R.; Jalali, S.H.S.; Dezvareh, G. Comprehensive Model for Remediation of Sandy Soils Contaminated with Volatile Organic Compounds Using Thermal Enhancement of Soil Vapor Extraction Method. Water Air Soil Pollut. 2017, 228, 239. [Google Scholar] [CrossRef]
- Wei, Q. Laboratory Experimental Study on Remediation of Vocs-Contaminated Site by Thermal-Enhanced Soil Vapor Extraction. Master’s Thesis, Southeast University, Nanjing, China, 2018. [Google Scholar]
- Alyüz, B.; Veli, S. Kinetics and equilibrium studies for the removal of nickel and zinc from aqueous solutions by ion exchange resins. J. Hazard. Mater. 2009, 167, 482–488. [Google Scholar] [CrossRef]
- Jin, Z.; Zhang, X.; Li, M.; Qian, C. Crack Self-healing Kinetic Model of Microbial Self-healing Concrete. Mater. Rep. 2020, 34, 1194–1200. [Google Scholar]
- Xiang, F. Discussion on Some Issues on Parameter Statistics of First-Order Chemical Kinetics Reaction Equation. J. Ecol. Rural Environ. 1998, 14, 20–25. [Google Scholar]
- Cancelli, A.M.; Gobas, F.A. Treatment of naphthenic acids in oil sands process-affected waters with a surface flow treatment wetland: Mass removal, half-life, and toxicity-reduction. Environ. Res. 2022, 213, 113755. [Google Scholar] [CrossRef]
- Yuan, L.; Ma, Y.; Zhang, J.; Men, J.; Sun, T.; Zhao, H.; Wu, H.; Wang, H.; Dai, S. Orthogonal analysis and mechanism of compressive strength and microstructure of the metakaolin-fly ash geopolymer. Case Stud. Constr. Mater. 2022, 17, e01154. [Google Scholar] [CrossRef]
- Wang, B.; Lin, R.; Liu, D.; Xu, J.; Feng, B. Investigation of the effect of humidity at both electrode on the performance of PEMFC using orthogonal test method. Int. J. Hydrogen Energy 2019, 44, 13737–13743. [Google Scholar] [CrossRef]
- Li, D.; Xu, C.; Xiong, Z. Gas flowing model of mining face and solve it using COMSOL. J. China Coal Soc. 2012, 37, 967–971. [Google Scholar]
- Shi, Y.; Rui, S.; Xu, S.; Wang, N.; Wang, Y. COMSOL Modeling of Heat Transfer in SVE Process. Environments 2022, 9, 58. [Google Scholar] [CrossRef]
- Zhao, L.; Zytner, R.G. Estimation of SVE closure time. J. Hazard. Mater. 2008, 153, 575–581. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Liu, J.; Guo, P.; Peng, J.; Zhang, L.; Li, Y. Mercury removal from spent low-level mercury catalyst by thermal treatment. Can. J. Chem. Eng. 2022, 100, S236–S245. [Google Scholar] [CrossRef]
- Meng, H.; Li, Y.-F.; Zhang, C. Modeling of discharge voltage for lithium-ion batteries through orthogonal experiments at subzero environment. J. Energy Storage 2022, 52, 105058. [Google Scholar] [CrossRef]
- Ishrat, S.I.; Khan, Z.A.; Siddiquee, A.N.; Badruddin, I.A.; Algahtani, A.; Javaid, S.; Gupta, R. Optimising Parameters for Expanded Polystyrene Based Pod Production Using Taguchi Method. Mathematics 2019, 7, 847. [Google Scholar] [CrossRef]
- Liu, P.; Xiao, X.; Chang, C.; A, D.; Li, Y.; Dong, J.; Zheng, W.; Huang, Q.; Dong, F.; Liu, X.; et al. Study on the Technology of Preparing Magnesium Oxychloride Cement Material by Calcination Extraction of Lithium By-Product Based on Orthogonal Experiment and Response Surface Method. Mater. Rep. 2020, 34, 1308–1314. [Google Scholar]
- Khalid, U.; Rehman, Z.U.; Mujtaba, H.; Farooq, K. 3D response surface modeling based in-situ assessment of physico-mechanical characteristics of alluvial soils using dynamic cone penetrometer. Transp. Geotech. 2022, 36, 100781. [Google Scholar] [CrossRef]
- Di, J.; Wang, M.; Zhu, Z. Experiment on the treatment of acid mine drainage with optimized biomedical stone particles by response surface methodology. Environ. Sci. Pollut. Res. 2018, 25, 7978–7990. [Google Scholar] [CrossRef]
- Zhu, T.; Shen, Q.; Xu, Y.; Li, C. Ionic liquid and ultrasound-assisted extraction of chestnut shell pigment with good hair dyeing capability. J. Clean. Prod. 2022, 335, 130195. [Google Scholar] [CrossRef]
- Rehman, Z.U.; Khalid, U. Optimization of COVID-19 face mask waste fibers and silica fume as a balanced mechanical ameliorator of fat clay using response surface methodology. Environ. Sci. Pollut. Res. 2022, 29, 17001–17016. [Google Scholar] [CrossRef]
- Modesto, H.R.; Lemos, S.G.; dos Santos, M.S.; Komatsu, J.S.; Goncalves, M.; Carvalho, W.A.; Carrilho, E.N.V.M.; Labuto, G. Activated carbon production from industrial yeast residue to boost up circular bioeconomy. Environ. Sci. Pollut. Res. 2021, 28, 24694–24705. [Google Scholar] [CrossRef] [PubMed]
- Pereira, L.; Maranhão, T.D.A.; Frescura, V.L.A.; Borges, D.L.G. Multivariate assessment of extraction conditions for the fractionation analysis of mercury in oily sludge samples using cold vapor atomic fluorescence spectrometry. J. Anal. At. Spectrom. 2019, 34, 1932–1941. [Google Scholar] [CrossRef]
- Roosta, M.; Ghaedi, M.; Daneshfar, A.; Sahraei, R. Experimental design based response surface methodology optimization of ultrasonic assisted adsorption of safaranin O by tin sulfide nanoparticle loaded on activated carbon. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2014, 122, 223–231. [Google Scholar] [CrossRef] [PubMed]





| Silt (%) | Clay (%) | Sand (%) | Moisture Content (%) | Organic Matter (%) | Surface Area (m2/g) | Micropore Volume (mL/g) | pH |
|---|---|---|---|---|---|---|---|
| 67.4 | 16.1 | 7.2 | 5.5 | 3.8 | 2.66 | 0.012 | 7.9 |
| Level | Factor | |||
|---|---|---|---|---|
| A (min) | B (°C) | C (mL/min) | D (%) | |
| 1 | 120 | 10 | 4000 | 2 |
| 2 | 120 | 20 | 5000 | 4 |
| 3 | 120 | 30 | 6000 | 6 |
| Test | Factor | |||
|---|---|---|---|---|
| A (min) | B (°C) | C (mL/min) | D (%) | |
| 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 2 | 2 |
| 3 | 1 | 3 | 3 | 3 |
| 4 | 2 | 1 | 2 | 3 |
| 5 | 2 | 2 | 3 | 1 |
| 6 | 2 | 3 | 1 | 2 |
| 7 | 3 | 1 | 3 | 2 |
| 8 | 3 | 2 | 1 | 3 |
| 9 | 3 | 3 | 2 | 1 |
| Material | Thermal Conductivity/ [W/(m∙K)] | Density/ (kg/m3) | Constant Pressure Heat Capacity/ [J/(kg∙K)] | Volume Fraction | Dynamic Viscosity/ (Pa·s) | Permeability/ m2 |
|---|---|---|---|---|---|---|
| Porous medium | 0.47 | 1200 | 1010 | 0.82 | - | 1.79 × 10−3 |
| Contaminant | 0.1287 | 870 | 1696.7 | - | 6.09901 × 10-4 | - |
| Test | R2 | k |
|---|---|---|
| 1 | 0.95583 | 0.01895 ± 0.00154 |
| 2 | 0.97883 | 0.02052 ± 0.00113 |
| 3 | 0.99696 | 0.05433 ± 0.00183 |
| 4 | 0.96134 | 0.00493 ± 1.11893 × 10-4 |
| 5 | 0.99875 | 0.04178 ± 9.5212 × 10-4 |
| 6 | 0.98209 | 0.00514 ± 1.6631 × 10-4 |
| 7 | 0.98394 | 0.00744 ± 2.93013 × 10-4 |
| 8 | 0.985 | 0.01023 ± 4.38981 × 10-4 |
| 9 | 0.92792 | 0.01227 ± 0.00158 |
| Test | A (min) | B (°C) | C (mL/min) | D (%) | Indicator Ⅰ (Removal Rate %) | Indicator Ⅱ (Removal Rate %) | Indicator Ⅲ (Removal Rate %) | Indicator Ⅳ (Removal Rate %) | Sum | Mean |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 120 | 10 | 4000 | 2 | 92.9 | 90.42 | 89.17 | 90.55 | 363.04 | 90.76 |
| 2 | 120 | 20 | 5000 | 4 | 95.40 | 95.90 | 92.73 | 91.64 | 375.67 | 93.92 |
| 3 | 120 | 30 | 6000 | 6 | 98.02 | 96.48 | 98.79 | 98.45 | 391.74 | 97.94 |
| 4 | 180 | 10 | 5000 | 6 | 57.08 | 52.81 | 58.95 | 56.82 | 225.66 | 56.42 |
| 5 | 180 | 20 | 6000 | 2 | 98.50 | 97.44 | 98.88 | 94.60 | 389.42 | 97.36 |
| 6 | 180 | 30 | 4000 | 4 | 64.80 | 66.83 | 64.85 | 62.41 | 258.89 | 64.72 |
| 7 | 240 | 10 | 6000 | 4 | 72.45 | 72.41 | 72.80 | 77.17 | 294.83 | 73.71 |
| 8 | 240 | 20 | 4000 | 6 | 89.85 | 85.84 | 85.32 | 81.36 | 342.37 | 85.59 |
| 9 | 240 | 30 | 5000 | 2 | 99.15 | 98.42 | 92.01 | 99.74 | 389.32 | 97.33 |
| Indicator | Factor | |||
|---|---|---|---|---|
| A (min) | B (°C) | C (mL/min) | D (%) | |
| 1130.45 | 883.53 | 964.3 | 1141.78 | |
| 873.97 | 1107.46 | 990.65 | 929.39 | |
| 1026.52 | 1039.95 | 1075.99 | 959.77 | |
| 376.82 | 294.51 | 321.43 | 380.59 | |
| 291.32 | 369.15 | 330.22 | 309.80 | |
| 342.17 | 346.65 | 358.66 | 319.92 | |
| 85.5 | 74.64 | 37.23 | 70.79 | |
| Factor | SS | df | MS | F | F0.05 | F0.01 | Significance |
|---|---|---|---|---|---|---|---|
| A (Time) | 2773.75 | 2 | 1386.87 | 241.61 | 19.46 | 99.47 | ** |
| B (Temperature) | 2199.15 | 2 | 1099.58 | 191.56 | / | / | ** |
| C (extraction flow) | 568.11 | 2 | 284.05 | 49.49 | / | / | * |
| D (Contaminant concentration) | 2198.89 | 2 | 1099.45 | 191.54 | / | / | ** |
| Error | 155.05 | 27 | 5.74 | / | / | / | / |
| Sum | 7894.95 | 35 | 3875.69 | / | / | / | / |
| Source | Sum of Squares | df | Mean Square | F-Value | Prob > F | |
|---|---|---|---|---|---|---|
| Model | 7739.41 | 7 | 1105.63 | 199.03 | <0.0001 | significant |
| A-A | 450.06 | 1 | 450.06 | 81.02 | <0.0001 | |
| B-B | 266.27 | 1 | 266.27 | 47.93 | <0.0001 | |
| C-C | 43.77 | 1 | 43.77 | 7.88 | 0.009 | |
| D-D | 1687.45 | 1 | 1687.45 | 303.76 | <0.0001 | |
| AB | 64.29 | 1 | 64.29 | 11.57 | 0.002 | |
| AC | 1811.55 | 1 | 1811.55 | 326.1 | <0.0001 | |
| A2 | 2323.69 | 1 | 2323.69 | 418.29 | <0.0001 | |
| Residual | 155.54 | 28 | 5.56 | |||
| Lack of Fit | 0.4931 | 1 | 0.4931 | 0.0859 | 0.7717 | not significant |
| Pure Error | 155.05 | 27 | 5.74 | |||
| Cor Total | 7894.95 | 35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Liu, Z.; Sun, R.; Liu, W.; Chen, Y. Orthogonal Experimental Study on Remediation of Ethylbenzene Contaminated Soil by SVE. Sustainability 2023, 15, 1168. https://doi.org/10.3390/su15021168
Zhang S, Liu Z, Sun R, Liu W, Chen Y. Orthogonal Experimental Study on Remediation of Ethylbenzene Contaminated Soil by SVE. Sustainability. 2023; 15(2):1168. https://doi.org/10.3390/su15021168
Chicago/Turabian StyleZhang, Shuangxia, Zhixiang Liu, Ruhua Sun, Weijun Liu, and Yongjun Chen. 2023. "Orthogonal Experimental Study on Remediation of Ethylbenzene Contaminated Soil by SVE" Sustainability 15, no. 2: 1168. https://doi.org/10.3390/su15021168
APA StyleZhang, S., Liu, Z., Sun, R., Liu, W., & Chen, Y. (2023). Orthogonal Experimental Study on Remediation of Ethylbenzene Contaminated Soil by SVE. Sustainability, 15(2), 1168. https://doi.org/10.3390/su15021168





