Abstract
In the past few decades, global industrial development and population growth have led to a scarcity of water resources, making sustainable management of groundwater a global challenge. The Water Quality Index (WQI) serves as a comprehensive method for assessing water quality and can provide valuable recommendations at the water quality level, optimizing policies for groundwater management. However, the subjectivity and uncertainty of the traditional WQI have negative impacts on evaluation outcomes, particularly in determining indicator weights and selecting aggregation functions. The proposed water quality index for groundwater based on the random forest (RFWQI) model in this study addresses these issues. It selects water quality indicators based on the actual pollution situation in the study area, employs an advanced random forest model to rank water quality indicators, determines indicator weights using the rank centroid method, scores the indicators using a sub-index function designed for groundwater development, and compares the results of two commonly used aggregation functions to identify the optimal one. Based on the aggregated scores, the water quality at 137 monitoring sites is classified into five levels: “Excellent”, “Good”, “Medium”, “Poor”, or “Unacceptable”. Among the 11 water quality indicators (sodium, sulfate, chloride, bicarbonate, total dissolved solids, fluoride, boron, nitrate, pH, CODMn, and hardness), chloride was given the highest weight (0.236), followed by total dissolved solids (0.156), and sodium was given the lowest weight (0.008). The random forest model exhibits a good prediction capability before hyperparameter tuning (86% accuracy, RMSE of 0.378), and after grid search and five-fold cross-validation, the optimal hyperparameter combination is determined, further improving the performance of the random forest model (94% accuracy, F1-Score of 0.967, AUC of 0.91, RMSE of 0.232). For the newly developed groundwater sub-index function, interpolation is used to score each indicator, and after comparing two aggregation functions, the NSF aggregation function is selected as the most suitable for groundwater assessment. Overall, most of the groundwater in the study area was of poor quality (52.5% of low quality) and not suitable for drinking.
1. Introduction
Groundwater quality has posed significant social, economic, environmental, and production risks in many regions worldwide [1,2]. The sustainable management of groundwater has become an important challenge. The rapid increases in population and rapid social industrialization over the past few decades have led to a severe scarcity of water resources [3,4,5]. As an essential water resource, groundwater has been heavily extracted and used, resulting in substantial degradations in both water quantity and quality [6,7]. Water quality assessments, as a crucial aspect of water resource management, play an essential role in determining the groundwater quality status, analyzing pollution sources and addressing groundwater quality restoration [8,9,10]. Surface water is used as the main water source in Karamay City, but with the development of industrial enterprises and the impact of human activities, the surface water is still polluted to varying degrees despite the cessation of development. Groundwater is the main source to supplement water shortages, so there is a certain demand for high-quality groundwater. There are 195 pollution sources in the urban area, including industrial enterprises, gas stations, and large-scale farms, which are a big threat to the improvement and maintenance of groundwater quality, so a moderate water quality evaluation is crucial to the water security of Karamay City.
Commonly used water quality assessment methods can be broadly categorized into two main types: single-factor evaluations and comprehensive evaluations [11,12]. Single-factor evaluations focus only on the most severely polluted water quality indicators, leading to a significant attenuation of the impact of other participating indicators, resulting in relatively pessimistic and one-sided evaluation results. In contrast, comprehensive evaluations take into account the status of various participating indicators, leading to reliable and comprehensive assessment results that are intuitive and easy to understand. As part of the comprehensive evaluation approach, the WQI has been widely applied and researched [13,14,15,16,17,18]. The WQI model generally includes four components: the selection of water quality indicators, assigning scores to the indicators, determining the weights of the indicators, and aggregating the results. It possesses advantages such as simplicity and flexibility [19].
In traditional WQI models, subjectivity has a significant impact on evaluation results, especially in the determination of water quality indicator weights [20]. The Delphi method is often used to establish indicator weights, but it is greatly influenced by the expertise and research scope of experts, leading to a high level of subjectivity and uncertainty in the WQI model [21]. When used as part of an objective assessment method, issues may arise, such as discrepancies between expert conclusions and actual conditions, leading to significant differences in opinions among multiple experts. Machine learning, as an emerging data processing method [22], can rank the importance of indicators by learning the relationships between data, thus mitigating the excessive subjectivity introduced by the Delphi method. The rank order centroid method is an objective weight calculation method that, based on the accurate ranking provided by random forest, assigns weight values to indicators [2]. This study obtains objective weight values by combining the random forest and rank order centroid methods.
The aggregation function, as the final step in the Water Quality Index (WQI) model, can to some extent determine the general direction of water quality assessment results [10,16]. Aggregation functions are divided into two main categories: weighted aggregation functions and unweighted aggregation functions [2]. Different weighted aggregation functions have different focuses, with different sensitivities to changes in water quality, the frequency of solar eclipse phenomena, and applicable scenarios.
The purpose of this study is to develop a water quality assessment method specifically tailored for groundwater, with the assistance of machine learning. The highlights of this research are as follows:
- (1)
- A data-driven water quality assessment method has been developed specifically for groundwater.
- (2)
- The utilization of the random forest method and formula-based calculations to determine indicator weights has significantly reduced the interference of subjectivity in water quality assessment results.
- (3)
- By comparing the effectiveness of different weighted aggregation functions in assessing groundwater, the optimal aggregation function has been identified.
- (4)
- New water quality assessment rules suitable for groundwater have been proposed.
2. Materials and Methods
2.1. Overview of the Study Area
2.1.1. Study Area
Karamay City in China has been selected as the research area for this study (Figure 1). Karamay City (longitude 84°44′ to 86°1′, latitude 44°7′ to 46°8′) is located in the western part of the Junggar Basin. It is bordered by Jia’er Mountain to the northwest, and the northern foothills of the Tianshan Mountains to the south, with the Gurbantünggüt Desert to the east. The majority of this region is covered by the Gobi Desert, with soil consisting mainly of sand and gravel and poor soil quality. Most of the soil has a high salt content. It is an area with significant petroleum and natural gas reserves, being a major mineral resource, with a long history of extraction [23].
Figure 1.
Location map of Karamay City.
2.1.2. Climate and River Characteristics
Karamay City is located in the mid-latitude inland region and belongs to a typical temperate continental climate. It is characterized by low precipitation, with predominant spring and autumn monsoons, and significant temperature differences between winter and summer. The average annual temperature is 8.6 °C. The longest sunshine duration occurs in July, reaching 302.5 h, while the lowest is in December, with only 99.8 h of sunshine. The primary source of water vapor is the westerly airflow from the Atlantic Ocean. The average annual precipitation is 108.9 mm, while the average evaporation is 2692.1 mm, making it 24.7 times the precipitation. The region is mainly fed by three inland rivers, from north to south, Baiyang River, Muhetai River, and Dalibut River, with a total length of 400 km [24]. The water supply for these rivers primarily comes from snowmelt, rainfall, and a small number of springs.
2.2. Data Collection
A total of 137 sampling points were selected for analysis, among which 60 observation wells were newly established. The initial dataset for this study was substantially improved in terms of quantity and types of water quality indicators compared to previous studies [2,25]. Sample collection was conducted during the summer months and samples were transported to nearby stations within 24 h of collection to minimize the impact of time and other factors on monitoring results. All collectors are highly trained and have relevant working experience to avoid human error affecting the samples. The collection, preservation, and transportation of the samples complied with relevant specifications to prevent any effects on the testing results due to transportation and storage. All groundwater samples were collected from observation wells with depths ranging from 50 to 300 m. The calculated and analyzed water quality dataset consisted of 42 water quality indicators (calcium, magnesium, potassium, sodium, boron, barium, vanadium, molybdenum, arsenic, bromine, nickel, manganese, iron, aluminum, copper, lead, zinc, mercury, selenium, cadmium, antimony, beryllium, silver, thallium, sulfate, chloride, bicarbonate, carbonate, total dissolved solids, anionic surfactants, ammonia, nitrate, metasilicicic acid, fluoride, petroleum hydrocarbons, volatile phenolics, nitrites, iodide, sulfides, oxygen demand, pH, and total hardness) from 137 sampling points. Conventional water quality indicators (e.g., water temperature, pH, etc.) were measured using a multi-indicator monitor (Aqua TROLL 500, Fort Collins, CO, USA), metal ions other than cesium were measured using spectrophotometry, cesium and silicon were measured using inductively coupled plasma emission spectrometry, anions (e.g., F−, Cl−, Br−, etc.) were measured using ion chromatography, petroleum hydrocarbons were measured using gas chromatography, and volatile phenolics were measured using spectrophotometry. In the dataset, sulfate, sodium, fluoride, nitrate and pH all had 12 outliers, boron had 6 outliers, carbonate had 8 outliers, TDS had 11, CODMN had 14, hardness had 16, and chloride had the most outliers with 25.
2.3. The Establishment of RFWQI Model
2.3.1. Indicator Selection
The richness of water quality indicators can enhance the comprehensiveness of water quality assessments, but it does not necessarily mean that more indicators are better [25]. Having too many water quality indicators can introduce significant uncertainty to the WQI, reducing the model’s sensitivity to pollution indicators, while also increasing the economic and time costs of assessment work [26,27]. Traditional WQI methods often refer to previous work cases or the opinions of experts and scholars to determine the participating indicators. This approach is simple and convenient, but it introduces a high level of subjectivity to water quality assessments, and differences in expertise among experts can lead to uncertainty and interference in the assessment results. In this study, based on the hydro-chemical characteristics of groundwater, indicators were selected from the pool of 44 water quality indicators, which to some extent reduced the influence of subjective indicator selection on the evaluation results.
2.3.2. The Process of Determining Weight
Weight calculation is a critical component of the WQI model and is one of the reasons for the model’s inherent uncertainty. Weight values are assigned to all selected indicators to distinguish the degree of impact that each indicator has on the water quality assessment results. This numerical value is often obtained through the Delphi method, which is convenient and efficient, but it also introduces significant subjectivity and uncertainty to the WQI. In this study, three machine learning algorithms, Support Vector Machine, random forest, and decision tree, were used to make a preliminary comparison using the Karamay City dataset. Using the AUC value as the evaluation criterion, random forest has the best learning effect with the highest AUC value of 0.995, followed by Support Vector Machine with 0.85 and decision tree with 0.79.
Random Forest Model
Machine learning is an emerging technology that efficiently processes data, aiming to enable computer systems to perform tasks by learning and improving from data, without the need for explicit programming instructions [28,29]. It empowers computers to automatically adjust and enhance their performance based on data, enabling them to complete specific tasks or predict future events. Machine learning algorithms have the capability to automatically learn patterns and rules from large-scale, high-dimensional, and complex structured data, extracting valuable information. This enables algorithms to adapt to data variations and complexities without the need for frequent code updates and modifications.
Random forest is an ensemble learning algorithm used to solve classification and regression problems. It combines predictions from multiple decision tree models to improve the overall accuracy and stability of predictions through voting or averaging. Random forest is composed of multiple decision trees. Each decision tree is trained on randomly selected samples and features. A decision tree is a basic classification and regression model that divides the dataset into different subsets, each corresponding to a class or numerical output at a leaf node. At each node of each decision tree, random forest randomly selects a subset of features as candidate features, rather than using all features. This increases the diversity between each tree, enhancing the overall model’s variety. In classification problems, random forest selects the final class through voting. Due to the use of multiple decision trees’ voting or averaging results, the problem of overfitting in individual trees can be reduced [30]. Additionally, through random feature selection and bootstrapping, random forest can reduce the overall model’s variance and improve its generalization ability. Although interpreting individual decision trees can be challenging, the overall predictions of random forest can be explained by analyzing the feature importance of each decision tree [31]. In this study, advanced random forest models were used to obtain the importance ranking of 11 models and the weight values of 11 indicators were calculated using ROC analysis.
Data Processing
Based on the filtered water quality data, the initial water quality status of the 137 monitoring points was determined. For the participating indicators, if a threshold is exceeded, the water quality at that point is considered “Unacceptable”; if all measured values of the participating indicators are below the threshold, the water quality at that point is considered “Acceptable”. The threshold values for each indicator were taken from the World Health Organization’s Drinking Water Guidelines and the China Groundwater Quality Standards, with the most stringent values selected as the thresholds in this study (Table 1). To eliminate the impact of data magnitude and different units on the calculation results, all data underwent standardization processing.

Table 1.
Indicator thresholds under different water quality standards.
Model Training
The preprocessed dataset was input into the random forest model, and the data were divided according to the preset ratio (70% for training, 30% for testing) to train the model. During the model training process, a five-fold cross-validation method was employed to augment the dataset, improving the training effectiveness and effectively reducing the likelihood of overfitting.
Hyperparameter Tuning
Random forest is a high-performance ensemble learning algorithm with up to 19 hyperparameters that can be adjusted from multiple dimensions to enhance its performance. Grid search is a common method for tuning hyperparameters, as it involves systematically exploring various combinations of hyperparameters to find the optimal set of values [33,34,35]. This approach helps to identify the best combination of hyperparameters for the random forest model.
Random Forest Model Validation
In order to evaluate the learning accuracy and ranking results of the random forest model and ensure the objectivity and reasonableness of the weight calculations, this study chose the accuracy, F1-Score, AUC value, and RMSE value as performance evaluation metrics. The five-fold cross-validation approach helps to avoid interference from overfitting and high variance during model validation. To ensure the effectiveness of the validation method, the dataset was split following the random seed pattern with a seed value of 42, where 70% of the data were allocated to the training set and 30% of the data were allocated to the test set. The establishment of a confusion matrix (Table 2) has a key role in the calculation of assessment indicators. TN, FP, FN, and TP in Equations (1) and (2) represent True Negative, False Positive, False Negative, and True Positive, respectively.

Table 2.
Confusion matrix.
Accuracy is primarily obtained by comparing the predicted values from the learning process with the actual measured values. It is used to evaluate the learning effectiveness of random forest in water quality prediction.
The F1-Score combines precision and recall into a single metric, balancing the trade-off between correctly identifying positive instances (precision) and capturing all positive instances (recall). By considering both precision and recall, the F1−Score provides a balanced evaluation of the model’s performance in correctly classifying both negative and positive samples. A higher F1-Score indicates a more reliable and accurate model for water quality prediction.
ROC (Receiver Operating Characteristic) is a graphical plot that illustrates the sensitivity (true positive rate) versus 1−specificity (false positive rate) for a binary classification model. Each point on the ROC curve represents the model’s sensitivity at a particular threshold.
AUC is the area under the ROC curve, which ranges from 0.5 to 1. It represents the degree or measure of separability. A higher AUC indicates a better ability of the model to distinguish between positive and negative instances. When the AUC value is 0.5, it means that the model’s predictions are unrelated to the dataset, indicating no discriminatory power.
The RMSE (Root Mean Square Error) is a measure of the deviation between observed values and true values. It is commonly used as a standard for evaluating the prediction accuracy of machine learning models. A smaller RMSE indicates that the observed values are closer to the true values, indicating a better predictive performance of the model. The RMSE can be calculated by Equation (3), where m represents the total number, ya represents the measured value of item a, and represents the true value of item a.
2.3.3. Sub-Index Functions
The WQI uses the fractional exponential function to convert the measured values of each index into dimensionless fractions ranging from 0 to 100. This study specifically improves the sub-index function for groundwater, with the index threshold as the upper limit. The linear interpolation method was used to assign scores to each index. A score of 100 indicates that the concentration is extremely low and the state is excellent. A score of 0 indicates that the concentration of the index significantly exceeds the standard. The improved sub-index function focuses on calculating the score and does not classify the score.
In the equation, α represents the measured value of the indicator, represents the maximum threshold for that indicator, and represents the minimum threshold for that indicator. Indicators whose thresholds exist in a range of values that are not zero at either end are calculated using Equations (5) and (6), and the remaining indicators are calculated using Equation (4).
2.3.4. Aggregation Function in WQI
The aggregation function is the final step of the WQI model. An appropriate aggregation function combines the weights with the indicator scores to ultimately obtain an objective and accurate water quality assessment result [36,37,38]. In this study, two weighted aggregation functions were computed and analyzed to select the most suitable aggregation function for groundwater assessment (Table 3). In the formula, represents the weight of the indicator and represents the score of the indicator.

Table 3.
An overview of the two different aggregation functions.
2.3.5. Evaluation Disciplines
After calculating the aggregation function, the WQI outputs a score for each monitoring site, ranging from 0 to 100, to indicate the water quality status. To provide a clear interpretation of the water quality based on different score ranges, a set of criteria is proposed in this study. Different rules for categorizing water quality may vary and have acceptable differences. In order to facilitate the understanding of water quality by water management personnel, a new classification scheme has been developed by synthesizing commonly used evaluation criteria (Table 4). The score ranges from 0 to 100, with a clear interpretation provided for different levels of scores, ranging from poor to good.

Table 4.
The evaluation disciplines adopted by different WQI models.
3. Results
3.1. Results of Indicator Selection
Based on the groundwater hydro-chemical characteristics and the pollution status of the study area, 11 evaluation indicators were selected from the initial pool of 44 water quality indicators. These selected indicators include natrium, sulfate, chloride, carbonate, total dissolved solids (TDS), fluoride, boron, nitrate, pH, CODMn, and total hardness. Figure 2 illustrates the basic status of the dataset, with water quality conditions at 137 sites influenced by 11 water quality indicators. Thicker connecting lines in the figure indicate a greater degree of influence of the indicator on water quality.
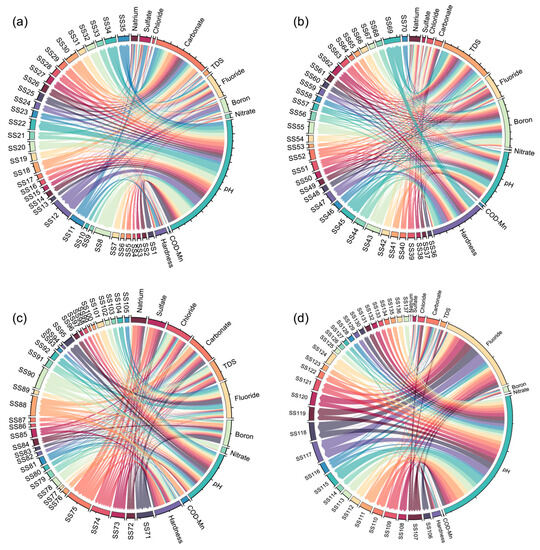
Figure 2.
An overview of 137 sampling sites with selected indicators. (a) represents the impact of water quality indicators on the water quality status of sampling sites 1~35; (b) represents the impact of water quality indicators on the water quality status of sampling sites 36~70; (c) represents the impact of water quality indicators on the water quality status of sampling sites 71~105; (d) represents the impact of water quality indicators on the water quality status of sampling sites 106~137.
3.2. Weighting Calculation
The random forest model output a ranking of the 11 water quality indicators, and based on the ROC method, the weights for each indicator were calculated (Figure 3). Chloride, TDS, CODMn, and B have higher weights in the groundwater of the study area. The random forest model assigned different weights to the 11 indicators based on decision tree information, and these weights are consistent with those calculated using the ROC method. The use of ROC as an objective weight calculation method, based on mathematical formulas, indirectly confirms the objectivity of the indicator ranking provided by the random forest model.
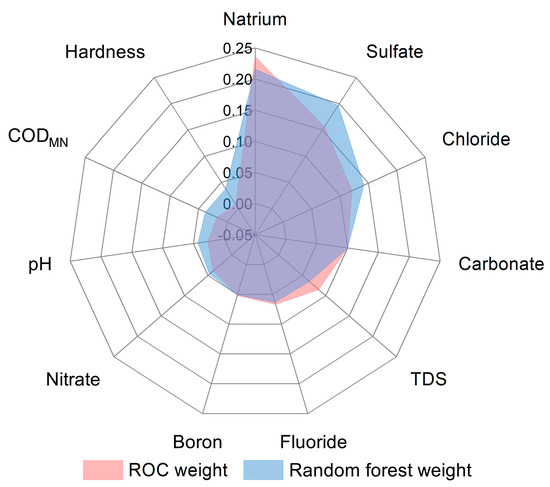
Figure 3.
Weighting results for ROC and random forest.
3.3. Indicator Scoring Results
Figure 4 displays the scores assigned to each indicator based on the formula, where a score of 100 indicates excellent water quality, while a score of 0 represents poor water quality. To reduce the ambiguity of indicator scoring, the sub-indicator functions developed with indicator thresholds require manual determination of these thresholds. When the indicator concentration exceeds the threshold, a score of 0 is assigned. The overall condition of pH is relatively good, with most data points falling within the threshold range. However, hardness, TDS, fluoride, and boron show significant instances of exceeding the thresholds, leading to localized areas with high fluoride levels. From the perspective of indicator scores, the water quality in the research area appears to be unfavorable, with a significant prevalence of indicators exceeding their respective thresholds, except for a few indicators with improved concentrations.
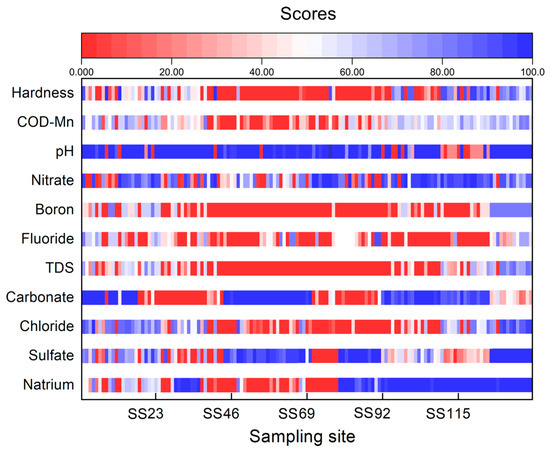
Figure 4.
Map of water quality indicator scores for each sampling site.
3.4. Aggregate Function Calculation Results
The water quality of each sampling point was evaluated comprehensively under the influence of the weighted value. Figure 5 shows the range of scores for the two weighted aggregation functions. The NSF aggregation function was calculated by aggregating 137 sets of data with the highest value being 78.682, the lowest value being 4.26, and the mean value being 44.762. The WQM aggregation function’s lowest value was 18.265, the highest value was 84.25, and the mean value was 59.127.
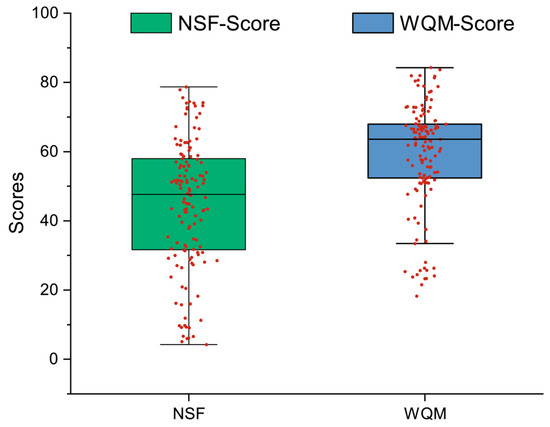
Figure 5.
The distribution map of different aggregation function calculation results. The red dots represent the water quality scores for each sampling site.
3.5. Water Quality Evaluation Results
Utilizing the weighted aggregation function, the weight values and indicator scores were aggregated to derive the final water quality assessment results (Figure 6). The NSF aggregation function, selected as the optimal choice, was applied to compute the water quality results at the 137 sampling points. The results show that 37.6% of the points fall into the “Medium” category, 9.9% have “Good” water quality, 38.3% exhibit poor water quality and are rated as “Bad” and not recommended for drinking purposes, while 14.2% are in a very poor state, unsuitable for any usage. Due to local environmental influence, the excessive fluoride, sodium ion, and chloride concentrations are likely attributed to natural background values. The causes of total hardness, TDS, sulfide, and boron values exceeding their thresholds are more complex, potentially related to natural background values, industrial wastewater discharge, and household waste disposal.
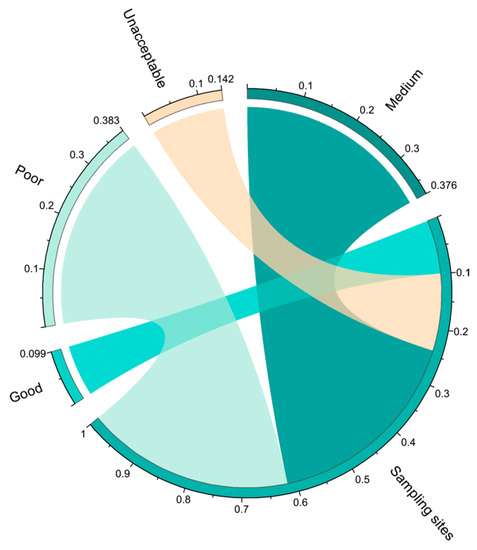
Figure 6.
Water quality level diagram of each sampling site.
4. Discussion
4.1. Objective Selection of Indicators
The traditional WQI mostly uses the Delphi method or determines indicators based on conventions, which is too subjective and susceptible to influence [39,40,41]. Reasonable selection of indicators helps to ensure the accuracy, objectivity, and comprehensiveness of water quality evaluations [25]. In this study, 11 indicators were selected from 44 indicators based on the hydro-chemical characteristics of groundwater and pollution conditions in the study area. These 11 indicators encompass commonly used parameters in groundwater quality assessments such as TDS, pH, and total hardness, as well as factors reflecting the background values and pollution conditions of the study area, such as boron, natrium, chloride, and sulfate. The indicator selection method used in this study improves the objectivity of RFWQI by selecting appropriate water quality indicators without relying on experts and conventions. The significant reduction in the number of indicators helped to control the interference of the evaluation results due to the uncertainty caused by too many dimensions and improved the accuracy of the water quality evaluation [2,42]. Through the screening of the data, all the indicators that exceeded the thresholds were included in the 11 indicators, and the remaining 33 indicators were all measured to be below the threshold value, which is not harmful to human health; thus, even though the number of indicators was greatly reduced, it still did not affect the comprehensiveness of the water quality evaluation.
4.2. Discussion of Weights Based on the Random Forest Model
4.2.1. Comparison of Different Weighting Methods
The composition of the random forest structure is more complex, the operation process involves a large number of parameters, and some parameters and patterns are determined through the learning process in the model training, which belongs to the black box model [43,44,45]. The computational process of the random forest model is not highly interpretable, but its results are in line with the characteristics of the dataset, and the assessment indicators are better, so the results still have a high degree of credibility. ROC is an objective weight calculation method [2]; the weight values obtained by mathematical methods on the basis of the random forest ordering are highly interpretable, which compensates for the lack of explanatory flaws in the black box model to a certain extent. There is a slight difference between the weight values obtained by random forest and ROC, which may be due to the unique learning method of the black box model, but the trends in the weight calculation results of the two are the same.
4.2.2. Hyperparameter Tuning for Random Forest Models
The learning performance of the random forest model under the default hyperparameter settings is already good (0.86 for accuracy and 0.377 for RMSE), but there is still room for performance improvement. In order to optimize the hyperparameters, such as the number of decision trees, the maximum depth of the decision trees, and node classification, a grid search method was employed [43]. Eventually, the best combination of hyperparameters was obtained (Table 5). Under this parameter combination, the learning effect of the random forest model was further enhanced, leading to a higher accuracy and lower RMSE (0.96 for accuracy and 0.188 for RMSE).

Table 5.
Random forest hyperparameter tuning process and optimal hyperparameter combination.
4.2.3. Random Forest Model Validation
Under the best hyperparameter combination, the random forest model was validated using six-fold cross-validation. The table shows the validation values for each fold, and to mitigate the impact of overfitting and other phenomena on the validation results, the average of the values from the five runs was taken as the final result. The table presents five validation metrics (Table 6). Figure 7 demonstrates the high AUC value of the model, indicating that the model’s learning performance is excellent, correctly identifying key water quality indicators and classifications. The low RMSE and high F1-Score also support this observation. The accuracy value of 0.94 is within an acceptable range and indicates a good performance (Table 6). The use of multiple validation metrics ensures the reliability of the random forest algorithm’s importance ranking of water quality indicators, greatly reducing subjectivity and uncertainty in the water quality evaluation results.

Table 6.
Evaluation of random forest learning effectiveness under five-fold cross-validation.
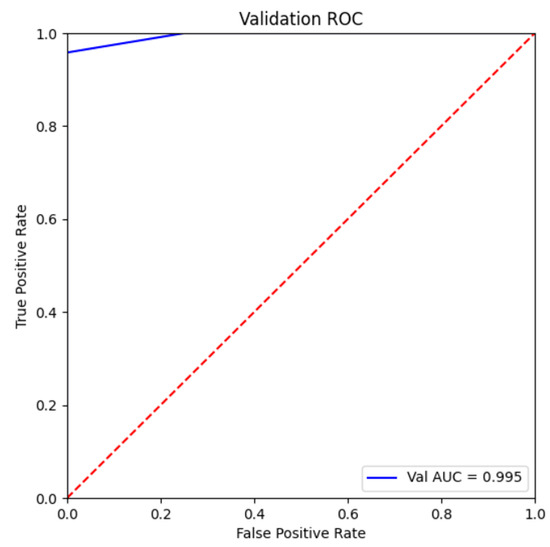
Figure 7.
Optimal AUC-ROC graph. The red dotted line represents the one–half cutoff for distinguishing between forward and reverse categorization.
During the five-fold cross-validation, although measures have been taken to control the overfitting phenomenon, there are still two calculations in which the results may be at risk of overfitting, which may be due to the structure and calculation of the algorithm itself as well as the imbalance of the dataset, among other reasons [46,47]. In this study, the parameters and results corresponding to the second highest AUC value (0.995) were used as the basis for calculations to control the impact of the overfitting phenomenon on the results of water quality assessments. All the calculated results of the five-fold cross-validation, as well as the mean values, were only used to measure the learning level of the model.
4.3. The Effect of the Application of the Improved Sub-Indicator Function
The improved indicator function better reflects the status of various water quality indicators by interpolating the threshold values. Among the data of 137 points, the pH value of 27 points exceeded the standard, and their sub-indicator scores are low or 0. The scores of the rest of the qualified points are all higher than 90. The rest of the indicators show low regional scores, which is in line with the actual situation. From the dataset, all 11 indicators except pH have a wide range of exceedance. The improved sub-indicator function fully reflects the actual situation, and there is no point where the indicator status does not match the score.
4.4. Comparison of Aggregation Effects of NSF and WQM
Compared with the WQM aggregation function, the NSF aggregation function has a wider range of scores and a higher sensitivity to the overall water quality condition, which makes it more able to observe the changes in the water quality indicators and affects the level of the evaluation scores through high sensitivity. For the weighted aggregation function, the sensitivity is mainly reflected in the way the weighted values are handled; thus, the NSF aggregation function reflects the weighted values to a greater extent and has a better representation of the highly weighted indicators. From the data distribution point of view, the NSF aggregation function has a lower maximum and average value than the WQM aggregation function, which expresses a stricter aggregation result and has a positive significance for evaluations of drinking water. For the RFWQI model, the weighted aggregation function assigns different sensitivities to the model with respect to water quality indicators. In the case of the study area, the RFWQI model has a higher sensitivity to chloride, TDS, CODMn, and boron.
When using the weighted aggregation function, eclipses are often present, as evidenced by a difference between the expected and calculated values. When the expected and calculated values are the same, the point is calculated to be free of solar eclipse. The evaluation of the solar eclipse phenomenon can verify the accuracy of the WQI model. The REWQI model sets the expected value of the number of exceeded indicators according to the water quality level and compares it with the actual number of indicators exceeding the threshold. Table 7 demonstrates the status of the occurrence of the eclipse phenomenon for the two aggregation functions. The NSF aggregation function resulted in the eclipse phenomenon in the data of 22 points in the calculation of 137 points, and all of them were concentrated in the underestimation area, i.e., the results of the water quality evaluation underestimated the actual condition of the water quality. Strict evaluation rules are conducive to drawing the attention of the government or environmental protection department to the water quality condition and further improving the water quality. The WQM aggregation function, on the other hand, has 71 points with eclipsed data, accounting for more than 50%, which is much higher than that of the NSF aggregation function. Among the 71 groups of data, 49 groups of data are overestimated, i.e., the water quality evaluation results of 49 points are better than the actual water quality condition. Loose water quality evaluation rules may lead to the inclusion of polluted water bodies in drinking water sources, which may seriously affect the health condition of water users and is not conducive to the strict management of water quality. The NSF aggregation function is better than the WQM aggregation function in terms of evaluation score distribution, sensitivity, evaluation of the eclipse phenomenon, and evaluation stringency.

Table 7.
Eclipse of different aggregation functions.
4.5. Comparison of Water Quality Evaluation Results
Figure 8 shows the spatial interpolation of the water quality evaluation results obtained by the two aggregation functions, and the water quality results obtained by the NSF aggregation function are worse than those obtained by the WQM aggregation function. The overall water quality is poor, and the water quality grades are mainly “Medium” and “Poor”, indicating that the groundwater quality in this area is low and not suitable for use as a drinking water source. On the other hand, the results of WQM indicate that the overall water quality is at an acceptable level. Combining the results of the two aggregation functions for erosion and sensitivity, the water quality evaluation results obtained from the NSF aggregation function are more suitable for the evaluation of groundwater.
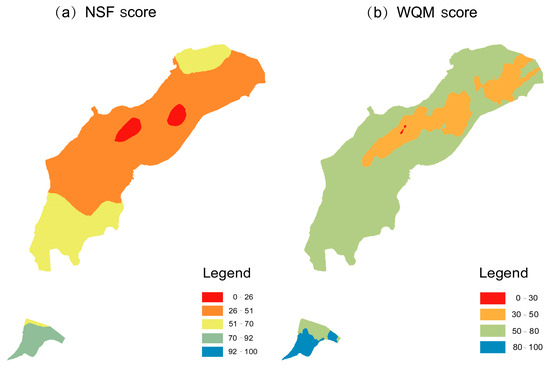
Figure 8.
Spatial distribution of the evaluation results obtained by the two aggregation functions. (a,b) show the spatial distribution of groundwater quality evaluation results in the study area determined by NSF and WQM, respectively.
Figure 8 shows the results of the RFWQI model for water quality evaluation, indicating that there are differences in the spatial distribution of groundwater quality conditions in Karamay City. This may be related to pollution sources such as gas stations and industrial enterprises that are more concentrated within the urban area. In addition to the influence of pollution sources on groundwater quality, human activities and domestic waste discharges within the urban area may also lead to regional groundwater quality deterioration. The water quality evaluation results obtained from the RFWQI model using the NSF aggregation function are more rigorous and fit well with the distribution of pollution sources and concentration of human activities in Karamay City, making the method more reliable.
4.6. Comparison of Water Quality Evaluation Results
Compared to the traditional WQI, the RFWQI has been greatly improved in four main areas (Table S2). As a commonly used water quality evaluation method, the traditional WQI is simple and effective, but there is still much room for improvement. The Delphi method and the routine-based method used in the traditional WQI make water quality evaluations highly subjective. The ambiguity and uncertainty brought by the immutable sub-index function and the aggregation function also have a negative impact on water quality evaluations. In order to improve the objectivity and accuracy of water quality evaluations, the RFWQI uses more advanced machine learning methods and other improved methods, which greatly improve the objectivity and accuracy of the WQI.
5. Conclusions
The RFWQI proposed in this study is a water quality assessment method specifically designed for groundwater. The RFWQI method takes into consideration the groundwater hydro-chemical characteristics, selects 11 water quality indicators based on the pollution conditions of the study area, ranks the indicators using a random forest model, computes the centroid weights, and investigates the impact of four different aggregation functions on the water quality assessment results. The application of random forest and centroid weighting significantly reduces the subjectivity and uncertainty inherent in traditional WQI methods, and the results are highly satisfactory. The random forest model demonstrates excellent performance even before hyperparameter tuning, making it a recommended tool for identifying key indicators in water quality assessments. The impact of the dataset on the random forest model is notable. A balanced and sufficiently large dataset can further enhance the effectiveness of the random forest model, leading to a more accurate indicator ranking and thus improving the reliability of water quality assessment results. The application of the centroid weighting method should be built upon a correct indicator ranking, and it complements the random forest approach quite well. Among the two aggregation functions compared, the NSF aggregation function exhibits a higher assessment accuracy and recognition rate, making it more suitable for groundwater quality assessments. The pessimistic evaluation criteria of water quality level are acceptable, which helps to maintain water safety, while the WQM score shows the incompatible characteristics of groundwater and its evaluation is optimistic, which poses a potential risk in the use of groundwater for drinking water. Groundwater hydro-chemical characteristics vary from one study area to another due to different factors such as human activities, groundwater recharge sources, background values, etc. The RFWQI, as a quality evaluation method for groundwater, is highly generalizable. Differences in hydro-chemical characteristics can be handled by the random forest algorithm to obtain objective indicators and weight values without relying on experts or conventions, which ensures the applicability and reliability of the RFWQI in different situations. Due to data limitations, this study only focused on summer data for computation and analysis. The RFWQI can be applied to analyze long-term time series data in the future.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/su151914477/s1, Table S1. Groundwater quality dataset of Karamay city used in the study; Table S2. Comparison and Advantages of RFWQI vs Traditional WQI.
Author Contributions
Conceptualization, Y.X.; Data curation, X.S. and W.Y.; Formal analysis, X.S. and W.Y.; Funding acquisition, Z.H.; Investigation, X.S. and M.G.; Methodology, Y.X. and T.Z.; Project administration, J.W.; Resources, W.Y. and M.G.; Software, T.Z.; Supervision, Y.X. and X.S.; Validation, Y.X. and T.Z.; Visualization, T.Z.; Writing—original draft, Y.X. and T.Z.; Writing—review and editing, J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the Hebei Province Key Research and Development Program of China (Grant No: 21374201D).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Li, N.; Lyu, H.; Xu, G.; Chi, G.; Su, X. Hydrogeochemical Changes during Artificial Groundwater Well Recharge. Sci. Total Environ. 2023, 900, 165778. [Google Scholar] [CrossRef]
- Uddin, M.G.; Nash, S.; Rahman, A.; Agnieszka, I. Olbert A Comprehensive Method for Improvement of Water Quality Index (WQI) Models for Coastal Water Quality Assessment. Water Res. 2022, 219, 118532. [Google Scholar] [CrossRef] [PubMed]
- Salehi, M. Global Water Shortage and Potable Water Safety; Today’s Concern and Tomorrow’s Crisis. Environ. Int. 2022, 158, 106936. [Google Scholar] [CrossRef] [PubMed]
- Jonsdottir, H.; Eliasson, J.; Madsen, H. Assessment of Serious Water Shortage in the Icelandic Water Resource System. Physics and Chemistry of the Earth, Parts A/B/C 2005, 30, 420–425. [Google Scholar] [CrossRef]
- Yang, P.; Zhang, S.; Xia, J.; Chen, Y.; Zhang, Y.; Cai, W.; Wang, W.; Wang, H.; Luo, X.; Chen, X. Risk Assessment of Water Resource Shortages in the Aksu River Basin of Northwest China under Climate Change. J. Environ. Manag. 2022, 305, 114394. [Google Scholar] [CrossRef] [PubMed]
- Zhao, K.; Fang, Z.; Li, J.; He, C. Spatial-Temporal Variations of Groundwater Storage in China: A Multiscale Analysis Based on GRACE Data. Resour. Conserv. Recycl. 2023, 197, 107088. [Google Scholar] [CrossRef]
- Sarami-Foroushani, T.; Balali, H.; Movahedi, R.; Kurban, A.; Värnik, R.; Stamenkovska, I.J.; Azadi, H. Importance of Good Groundwater Governance in Economic Development: The Case of Western Iran. Groundw. Sustain. Dev. 2023, 21, 100892. [Google Scholar] [CrossRef]
- Yang, T.; Zhu, Y.; Li, Y.; Zhou, B. Achieving Win-Win Policy Outcomes for Water Resource Management and Economic Development: The Experience of Chinese Cities. Sustain. Prod. Consum. 2021, 27, 873–888. [Google Scholar] [CrossRef]
- Wei, F.; Zhang, X.; Xu, J.; Bing, J.; Pan, G. Simulation of Water Resource Allocation for Sustainable Urban Development: An Integrated Optimization Approach. J. Clean. Prod. 2020, 273, 122537. [Google Scholar] [CrossRef]
- Zhao, E.; Kuo, Y.-M.; Chen, N. Assessment of Water Quality under Various Environmental Features Using a Site-Specific Weighting Water Quality Index. Sci. Total Environ. 2021, 783, 146868. [Google Scholar] [CrossRef]
- Akkoyunlu, A.; Akiner, M.E. Pollution Evaluation in Streams Using Water Quality Indices: A Case Study from Turkey’s Sapanca Lake Basin. Ecol. Indic. 2012, 18, 501–511. [Google Scholar] [CrossRef]
- Yang, X.; Chen, Z. A Hybrid Approach Based on Monte Carlo Simulation-VIKOR Method for Water Quality Assessment. Ecol. Indic. 2023, 150, 110202. [Google Scholar] [CrossRef]
- Barrie, A.; Agodzo, S.K.; Frazer-Williams, R.; Awuah, E.; Bessah, E. A Multivariate Statistical Approach and Water Quality Index for Water Quality Assessment for the Rokel River in Sierra Leone. Heliyon 2023, 9, e16196. [Google Scholar] [CrossRef] [PubMed]
- Benaissa, C.; Bouhmadi, B.; Rossi, A. An Assessment of the Physicochemical, Bacteriological Quality of Groundwater and the Water Quality Index (WQI) Used GIS in Ghis Nekor, Northern Morocco. Sci. Afr. 2023, 20, e01623. [Google Scholar] [CrossRef]
- Karangoda, R.C.; Nanayakkara, K.G.N. Use of the Water Quality Index and Multivariate Analysis to Assess Groundwater Quality for Drinking Purpose in Ratnapura District, Sri Lanka. Groundw. Sustain. Dev. 2023, 21, 100910. [Google Scholar] [CrossRef]
- Lee, H.; Park, S.; V-Minh Nguyen, H.; Shin, H.-S. Proposal for a New Customization Process for a Data-Based Water Quality Index Using a Random Forest Approach. Environ. Pollut. 2023, 323, 121222. [Google Scholar] [CrossRef] [PubMed]
- Mishra, M.; Singhal, A.; Srinivas, R. Effect of Urbanization on the Urban Lake Water Quality by Using Water Quality Index (WQI). Mater. Today Proc. 2023, in press. [Google Scholar] [CrossRef]
- Krishnamoorthy, N.; Thirumalai, R.; Lenin Sundar, M.; Anusuya, M.; Manoj Kumar, P.; Hemalatha, E.; Mohan Prasad, M.; Munjal, N. Assessment of Underground Water Quality and Water Quality Index across the Noyyal River Basin of Tirupur District in South India. Urban Clim. 2023, 49, 101436. [Google Scholar] [CrossRef]
- Uddin, M.G.; Nash, S.; Rahman, A.; Olbert, A.I. Performance Analysis of the Water Quality Index Model for Predicting Water State Using Machine Learning Techniques. Process Saf. Environ. Prot. 2023, 169, 808–828. [Google Scholar] [CrossRef]
- Uddin, M.G.; Nash, S.; Olbert, A.I. A Review of Water Quality Index Models and Their Use for Assessing Surface Water Quality. Ecol. Indic. 2021, 122, 107218. [Google Scholar] [CrossRef]
- Pesce, S.F.; Wunderlin, D.A. Use of Water Quality Indices to Verify the Impact of Córdoba City (Argentina) on Suquía River. Water Res. 2000, 34, 2915–2926. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, J.; Yang, X.; Zhang, Y.; Zhang, L.; Ren, H.; Wu, B.; Ye, L. A Review of the Application of Machine Learning in Water Quality Evaluation. Eco-Environ. Health 2022, 1, 107–116. [Google Scholar] [CrossRef]
- Changfu, X.; Hongxian, L.; Genbao, Q.; Jianhua, Q. Microcosmic Mechanisms of Water-Oil Displacement in Conglomerate Reservoirs in Karamay Oilfield, NW China. Pet. Explor. Dev. 2011, 38, 725–732. [Google Scholar] [CrossRef]
- Cao, J.; Ma, S.; Yuan, W.; Wu, Z. Characteristics of Diurnal Variations of Warm-Season Precipitation over Xinjiang Province in China. Atmos. Ocean. Sci. Lett. 2022, 15, 100113. [Google Scholar] [CrossRef]
- Jha, M.K.; Shekhar, A.; Jenifer, M.A. Assessing Groundwater Quality for Drinking Water Supply Using Hybrid Fuzzy-GIS-Based Water Quality Index. Water Res. 2020, 179, 115867. [Google Scholar] [CrossRef] [PubMed]
- Prabagar, S.; Thuraisingam, S.; Prabagar, J. Sediment Analysis and Assessment of Water Quality in Spacial Variation Using Water Quality Index (NSFWQI) in Moragoda Canal in Galle, Sri Lanka. Waste Manag. Bull. 2023, 1, 15–20. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, Y.; Wang, Z.; Geng, M.; Chen, Y.; Zhang, F. Method for Screening Water Physicochemical Parameters to Calculate Water Quality Index Based on These Parameters’ Correlation with Water Microbiota. Heliyon 2023, 9, e16697. [Google Scholar] [CrossRef]
- Karabadji, N.E.I.; Amara Korba, A.; Assi, A.; Seridi, H.; Aridhi, S.; Dhifli, W. Accuracy and Diversity-Aware Multi-Objective Approach for Random Forest Construction. Expert Syst. Appl. 2023, 225, 120138. [Google Scholar] [CrossRef]
- Hoarau, A.; Martin, A.; Dubois, J.-C.; Le Gall, Y. Evidential Random Forests. Expert Syst. Appl. 2023, 230, 120652. [Google Scholar] [CrossRef]
- Wang, S.; Qian, G.; Hopper, J. Integrated Logistic Ridge Regression and Random Forest for Phenotype-Genotype Association Analysis in Categorical Genomic Data Containing Non-Ignorable Missing Values. Appl. Math. Model. 2023, 123, 1–22. [Google Scholar] [CrossRef]
- Guo, W.; Gao, Z.; Guo, H.; Cao, W. Hydrogeochemical and Sediment Parameters Improve Predication Accuracy of Arsenic-Prone Groundwater in Random Forest Machine-Learning Models. Sci. Total Environ. 2023, 897, 165511. [Google Scholar] [CrossRef]
- GB/T14848-2017; Standard for Groundwater Quality. General Administration of Quality Supervision, Inspection and Quarantine of the PRC: Beijing, China, 2017.
- Ditton, E.; Swinbourne, A.; Myers, T. Selecting a Clustering Algorithm: A Semi-Automated Hyperparameter Tuning Framework for Effective Persona Development. Array 2022, 14, 100186. [Google Scholar] [CrossRef]
- Farhangi, F. Investigating the Role of Data Preprocessing, Hyperparameters Tuning, and Type of Machine Learning Algorithm in the Improvement of Drowsy EEG Signal Modeling. Intell. Syst. Appl. 2022, 15, 200100. [Google Scholar] [CrossRef]
- Gupta, S.C.; Goel, N. Predictive Modeling and Analytics for Diabetes Using Hyperparameter Tuned Machine Learning Techniques. Procedia Comput. Sci. 2023, 218, 1257–1269. [Google Scholar] [CrossRef]
- Kumar Ravi, N.; Kumar Jha, P.; Varma, K.; Tripathi, P.; Kumar Gautam, S.; Ram, K.; Kumar, M.; Tripathi, V. Application of Water Quality Index (WQI) and Statistical Techniques to Assess Water Quality for Drinking, Irrigation, and Industrial Purposes of the Ghaghara River, India. Total Environ. Res. Themes 2023, 6, 100049. [Google Scholar] [CrossRef]
- Ghosh, A.; Bera, B. Hydrogeochemical Assessment of Groundwater Quality for Drinking and Irrigation Applying Groundwater Quality Index (GWQI) and Irrigation Water Quality Index (IWQI). Groundw. Sustain. Dev. 2023, 22, 100958. [Google Scholar] [CrossRef]
- Rajkumar, H.; Naik, P.K.; Rishi, M.S. A Comprehensive Water Quality Index Based on Analytical Hierarchy Process. Ecol. Indic. 2022, 145, 109582. [Google Scholar] [CrossRef]
- Gupta, S.; Gupta, S.K. A Critical Review on Water Quality Index Tool: Genesis, Evolution and Future Directions. Ecol. Inform. 2021, 63, 101299. [Google Scholar] [CrossRef]
- Chandrajith, R.; Bandara, U.G.C.; Diyabalanage, S.; Senaratne, S.; Barth, J.A.C. Application of Water Quality Index as a Vulnerability Indicator to Determine Seawater Intrusion in Unconsolidated Sedimentary Aquifers in a Tropical Coastal Region of Sri Lanka. Groundw. Sustain. Dev. 2022, 19, 100831. [Google Scholar] [CrossRef]
- Haggerty, R.; Sun, J.; Yu, H.; Li, Y. Application of Machine Learning in Groundwater Quality Modeling—A Comprehensive Review. Water Res. 2023, 233, 119745. [Google Scholar] [CrossRef]
- Pan, B.; Han, X.; Chen, Y.; Wang, L.; Zheng, X. Determination of Key Parameters in Water Quality Monitoring of the Most Sediment-Laden Yellow River Based on Water Quality Index. Process Saf. Environ. Prot. 2022, 164, 249–259. [Google Scholar] [CrossRef]
- Jiang, M.; Wang, J.; Hu, L.; He, Z. Random Forest Clustering for Discrete Sequences. Pattern Recognit. Lett. 2023, 174, 145–151. [Google Scholar] [CrossRef]
- Josso, P.; Hall, A.; Williams, C.; Le Bas, T.; Lusty, P.; Murton, B. Application of Random-Forest Machine Learning Algorithm for Mineral Predictive Mapping of Fe-Mn Crusts in the World Ocean. Ore Geol. Rev. 2023, 162, 105671. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, G.; Li, P.; Wang, H.; Zhang, M.; Liang, X. An Improved Random Forest Based on the Classification Accuracy and Correlation Measurement of Decision Trees. Expert Syst. Appl. 2024, 237, 121549. [Google Scholar] [CrossRef]
- Li, L.; Spratling, M. Understanding and Combating Robust Overfitting via Input Loss Landscape Analysis and Regularization. Pattern Recognit. 2023, 136, 109229. [Google Scholar] [CrossRef]
- Kim, J.; Park, H. Limited Discriminator GAN Using Explainable AI Model for Overfitting Problem. ICT Express 2023, 9, 241–246. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).