Modeling the Hydraulic Performance of Pilot Green Roofs Using the Storm Water Management Model: How Important Is Calibration?
Abstract
:1. Introduction
1.1. Background
1.2. Hydraulic–Hydrologic Modeling: SWMM
1.3. Sensitivity Analysis
2. Materials and Methods
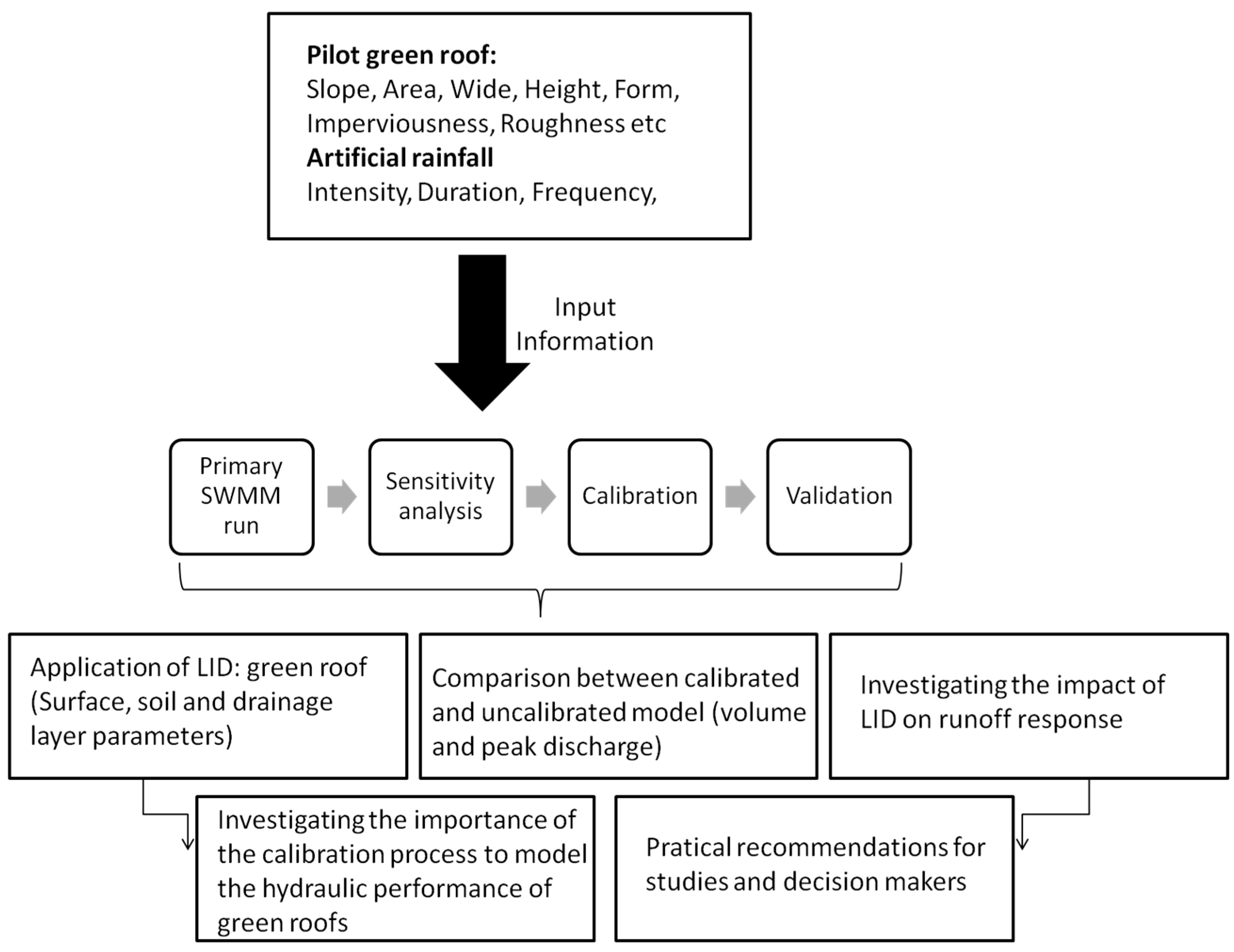
2.1. Research Steps
2.2. Pilot Green Roofs
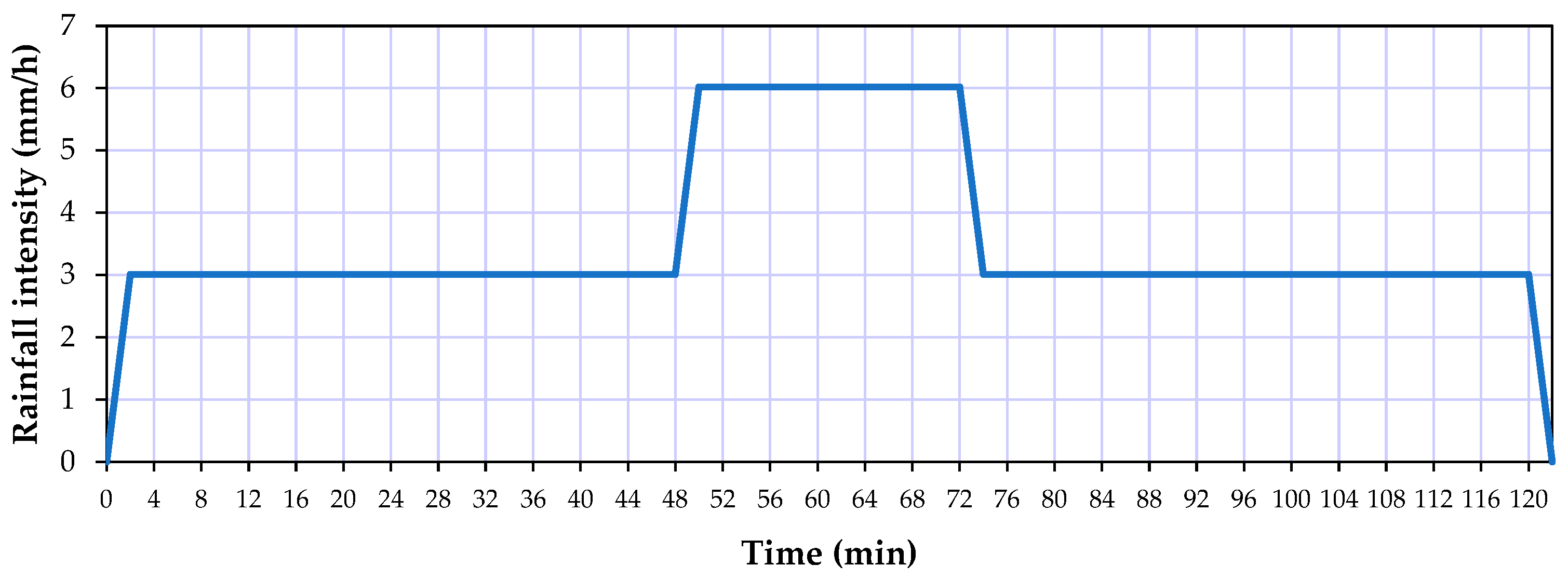
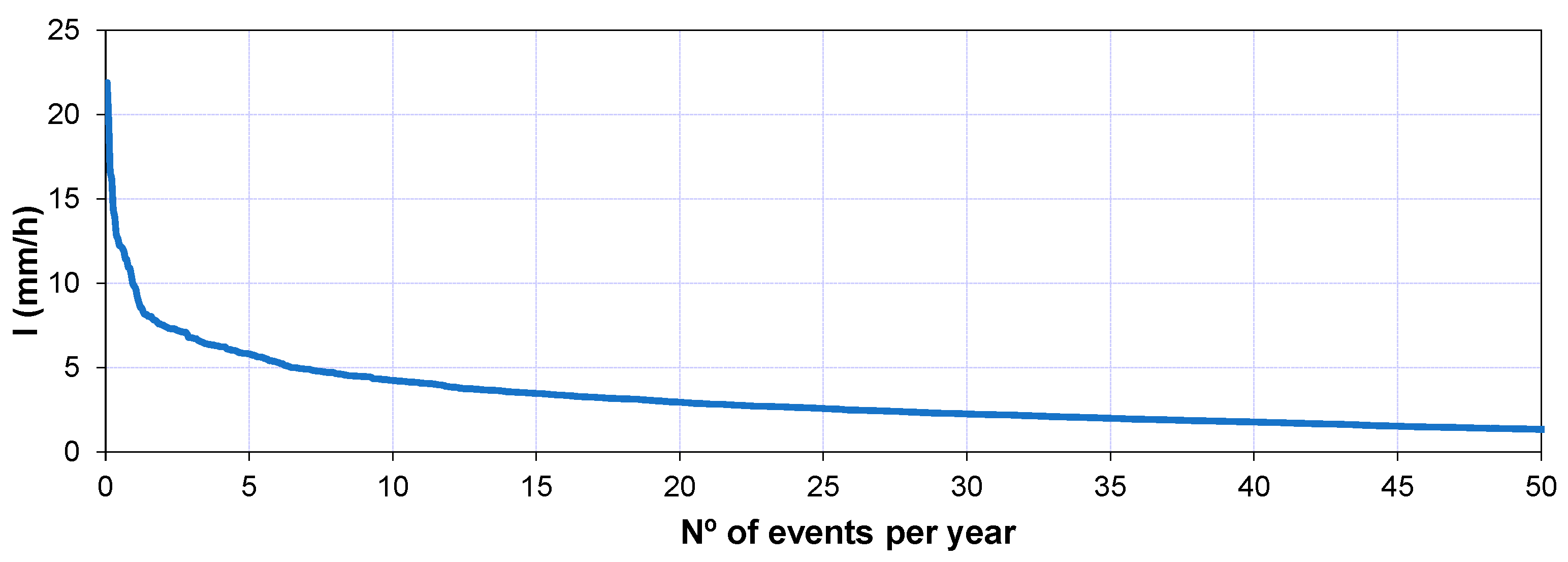
2.3. Data Collection
2.4. Applying SWMM 5.2
2.4.1. Fixed Model Settings
2.4.2. Model Calibration and Validation
2.4.3. Comparing Calibrated and Uncalibrated Simulation Approaches
- One calibrated LID control based on the geometric and physical measured characteristics of the test beds, including the measured hydraulic conductivity and porosity;
- One uncalibrated LID control based on the geometric and physical measured characteristics but with the remaining parameters, including the hydraulic conductivity and porosity, set to the default settings of SWMM 5.2.
3. Results and Discussion
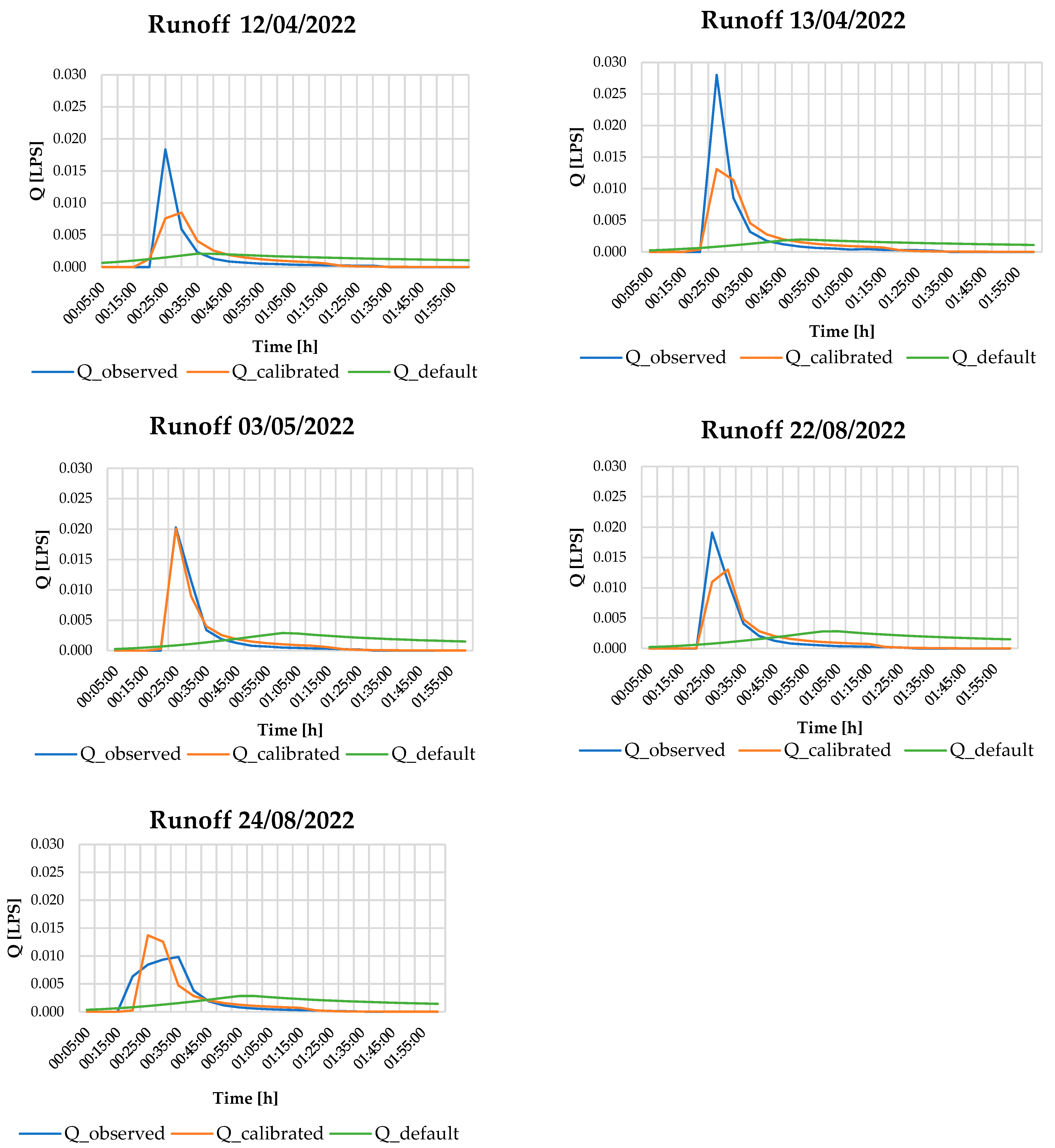
3.1. Calibration and Validation Results
3.2. Comparison of Calibrated and Uncalibrated Model Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brandão, C.; Cameira, M.d.R.; Valente, F.; Cruz de Carvalho, R.; Paço, T.A. Wet season hydrological performance of green roofs using native species under Mediterranean climate. Ecol. Eng. 2017, 102, 596–611. [Google Scholar] [CrossRef]
- Fletcher, T.D.; Shuster, W.; Hunt, W.F.; Ashley, R.; Butler, D.; Arthur, S.; Viklander, M. SUDS, LID, BMPs, WSUD and more—The evolution and application of terminology surrounding urban drainage. Urban Water J. 2015, 12, 525–542. [Google Scholar] [CrossRef]
- Orta-Ortiz, M.S.; Geneletti, D. What variables matter when designing nature-based solutions for stormwater management? A review of impacts on ecosystem services. Environ. Impact Assess. Rev. 2022, 95, 106802. [Google Scholar] [CrossRef]
- Carson, T.B.; Marasco, D.E.; Culligan, P.J.; McGillis, W.R. Hydrological performance of extensive green roofs in New York City: Observations and multi-year modeling of three full-scale systems. Environ. Res. Lett. 2013, 8, 13. [Google Scholar] [CrossRef]
- Manso, M.; Teotónio, I.; Silva, C.M.; Cruz, C.O. Green roof and green wall benefits and costs: A review of the quantitative evidence. Renew. Sustain. Energy Rev. 2021, 135, 110111. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, D.; Zhang, R.; Li, J.; Wang, W. The impact of rainfall change on rainwater source control in Beijing. Urban Clim. 2021, 37, 100841. [Google Scholar] [CrossRef]
- Qin, H.P.; Li, Z.X.; Fu, G. The effects of low impact development on urban flooding under different rainfall characteristics. J. Environ. Manag. 2013, 129, 577–585. [Google Scholar] [CrossRef]
- Eksi, M.; Rowe, D.B. Green roof substrates: Effect of recycled crushed porcelain and foamed glass on plant growth and water retention. Urban For. Urban Green. 2016, 20, 81–88. [Google Scholar] [CrossRef]
- Schultz, I.; Sailor, D.J.; Starry, O. Effects of substrate depth and precipitation characteristics on stormwater retention by two green roofs in Portland OR. J. Hydrol. Reg. Stud. 2018, 18, 110–118. [Google Scholar] [CrossRef]
- Soulis, K.X.; Ntoulas, N.; Nektarios, P.A.; Kargas, G. Runoff reduction from extensive green roofs having different substrate depth and plant cover. Ecol. Eng. 2017, 102, 80–89. [Google Scholar] [CrossRef]
- Hakimdavar, R.; Culligan, P.J.; Finazzi, M.; Barontini, S.; Ranzi, R. Scale dynamics of extensive green roofs: Quantifying the effect of drainage area and rainfall characteristics on observed and modeled green roof hydrologic performance. Ecol. Eng. 2014, 73, 494–508. [Google Scholar] [CrossRef]
- Alfredo, K.; Montalto, F.; Goldstein, A. Observed and Modeled Performances of Prototype Green Roof Test Plots Subjected to Simulated Low- and High-Intensity Precipitations in a Laboratory Experiment. J. Hydrol. Eng. 2010, 15, 444–457. [Google Scholar] [CrossRef]
- Stovin, V.; Vesuviano, G.; Kasmin, H. The hydrological performance of a green roof test bed under UK climatic conditions. J. Hydrol. 2012, 414–415, 148–161. [Google Scholar] [CrossRef]
- Johannessen, B.G.; Hamouz, V.; Gragne, A.S.; Muthanna, T.M. The transferability of SWMM model parameters between green roofs with similar build-up. J. Hydrol. 2019, 569, 816–828. [Google Scholar] [CrossRef]
- Cipolla, S.S.; Maglionico, M.; Stojkov, I. A long-term hydrological modelling of an extensive green roof by means of SWMM. Ecol. Eng. 2016, 95, 876–887. [Google Scholar] [CrossRef]
- Santos, M.L.; Silva, C.M.; Ferreira, F.; Matos, J.S. Hydrological Analysis of Green Roofs Performance under a Mediterranean Climate: A Case Study in Lisbon, Portugal. Sustainability 2023, 15, 1064. [Google Scholar] [CrossRef]
- Stovin, V.; Vesuviano, G.; De-Ville, S. Defining green roof detention performance. Water J. 2015, 14, 574–588. [Google Scholar] [CrossRef]
- Czemiel Berndtsson, J. Green roof performance towards management of runoff water quantity and quality: A review. Ecol. Eng. 2010, 36, 351–360. [Google Scholar] [CrossRef]
- Jeffers, S.; Garner, B.; Hidalgo, D.; Daoularis, D.; Warmerdam, O.; Warmerdam, O. Insights into green roof modeling using SWMM LID controls for detention-based designs. Artic. J. Water Manag. Model. 2022, 30, 484. [Google Scholar] [CrossRef]
- Burszta-Adamiak, E.; Mrowiec, M. Modelling of green roofs’ hydrologic performance using EPA’s SWMM. Water Sci. Technol. 2013, 68, 36–42. [Google Scholar] [CrossRef]
- Rosa, D.J.; Clausen, J.C.; Dietz, M.E. Calibration and Verification of SWMM for Low Impact Development. JAWRA J. Am. Water Resour. Assoc. 2015, 51, 746–757. [Google Scholar] [CrossRef]
- Iffland, R.; Förster, K.; Westerholt, D.; Pesci, M.H.; Lösken, G. Robust vegetation parameterization for green roofs in the EPA stormwater management model (SWMM). Hydrology 2021, 8, 12. [Google Scholar] [CrossRef]
- Worthen, L.L.; Davidson, C.I. Sensitivity Analysis Using the SWMM LID Control for an Extensive Green Roof in Syracuse, NY. In Proceedings of the 7th International Building Physics Conference, IBPC2018, Syracuse, NY, USA, 23–26 September 2018. [Google Scholar]
- Limos, A.G.; Mallari, K.J.B.; Baek, J.; Kim, H.; Hong, S.; Yoon, J. Assessing the significance of evapotranspiration in green roof modeling by SWMM. J. Hydroinform. 2018, 20, 588–596. [Google Scholar] [CrossRef]
- Peng, Z.; Stovin, V. Independent Validation of the SWMM Green Roof Module. J. Hydrol. Eng. 2017, 22, 04017037. [Google Scholar] [CrossRef]
- Krebs, G.; Kuoppamäki, K.; Kokkonen, T.; Koivusalo, H. Simulation of green roof test bed runoff. Hydrological processes. Hydrol. Process. 2016, 30, 250–262. [Google Scholar] [CrossRef]
- Paithankar, D.N.; Taji, S.G. Investigating the hydrological performance of green roofs using storm water management model. Mater. Today Proc. 2020, 32, 943–950. [Google Scholar] [CrossRef]
- Palermo, S.A.; Turco, M.; Principato, F.; Piro, P. Hydrological effectiveness of an extensive green roof in Mediterranean climate. Water 2019, 11, 1378. [Google Scholar] [CrossRef]
- Cristiano, E.; Urru, S.; Farris, S.; Ruggiu, D.; Deidda, R.; Viola, F. Analysis of potential benefits on flood mitigation of a CAM green roof in Mediterranean urban areas. Build. Environ. 2020, 183, 107179. [Google Scholar] [CrossRef]
- Fioretti, R.; Palla, A.; Lanza, L.G.; Principi, P. Green roof energy and water related performance in the Mediterranean climate. Build. Environ. 2010, 45, 1890–1904. [Google Scholar] [CrossRef]
- Razzaghmanesh, M.; Beecham, S. The hydrological behaviour of extensive and intensive green roofs in a dry climate. Sci. Total Environ. 2014, 499, 284–296. [Google Scholar] [CrossRef]
- Buccola, N.; Spolek, G. A pilot-scale evaluation of greenroof runoff retention, detention, and quality. Water Air Soil Pollut. 2011, 216, 83–92. [Google Scholar] [CrossRef]
- Piro, P.; Carbone, M.; De Simone, M.; Maiolo, M.; Bevilacqua, P.; Arcuri, N. Energy and Hydraulic Performance of a Vegetated Roof in Sub-Mediterranean Climate. Sustainability 2018, 10, 3473. [Google Scholar] [CrossRef]
- Doménech, I.; Perales-Momparler, S.; Morales-Torres, A.; Escuder-Bueno, I. Hydrological Performance of Green Roofs at Building and City Scales under Mediterranean Conditions. Sustainability 2018, 10, 3105. [Google Scholar] [CrossRef]
- Palla, A.; Sansalone, J.J.; Gnecco, I.; Lanza, L.G. Storm water infiltration in a monitored green roof for hydrologic restoration. Water Sci. Technol. 2011, 64, 766–773. [Google Scholar] [CrossRef] [PubMed]
- Schroll, E.; Lambrinos, J.; Righetti, T.; Sandrock, D. The role of vegetation in regulating stormwater runoff from green roofs in a winter rainfall climate. Ecol. Eng. 2011, 37, 595–600. [Google Scholar] [CrossRef]
- Rocha, B.; Paço, T.A.; Luz, A.C.; Palha, P.; Milliken, S.; Kotzen, B.; Branquinho, C.; Pinho, P.; de Carvalho, R.C. Are biocrusts and xerophytic vegetation a viable green roof typology in a mediterranean climate? A comparison between differently vegetated green roofs in water runoff and water quality. Water 2021, 13, 94. [Google Scholar] [CrossRef]
- Barnhart, B.; Pettus, P.; Halama, J.; McKane, R.; Mayer, P.; Djang, K.; Brookes, A.; Moskal, L.M. Modeling the hydrologic effects of watershed-scale green roof implementation in the Pacific Northwest, United States. J. Environ. Manag. 2021, 277, 111418. [Google Scholar] [CrossRef] [PubMed]
- Garofalo, G.; Palermo, S.; Principato, F.; Theodosiou, T.; Piro, P. The Influence of Hydrologic Parameters on the Hydraulic Efficiency of an Extensive Green Roof in Mediterranean Area. Water 2016, 8, 44. [Google Scholar] [CrossRef]
- Rossman, L.; Huber, W. Storm Water Management Model Reference Manual Volume I, Hydrology. USEPA Office of Research and Development. Washington 2015, DC. EPA/600/R-15/162A. Available online: https://nepis.epa.gov/Exe/ZyPURL.cgi?Dockey=P100NYRA.Txt (accessed on 5 June 2023).
- Rossman, L.A. Storm Water Management Model User’s Manual Version 5.0. EPA/600/R-05/040; US EPA National Risk Management Research Laboratory: Cincinnati, OH, USA, 2010. [Google Scholar]
- Chapra, S.C. Surface Water-Quality Modeling; Waveland Press: Long Grove, IL, USA, 1997; pp. 327–341. [Google Scholar]
- Rossman, L.A. Storm Water Management Model User’s Manual Version 5.2. EPA/600/R-22/030; US EPA National Risk Management Research Laboratory: Cincinnati, OH, USA, 2022. [Google Scholar]
- Leimgruber, J.; Krebs, G.; Camhy, D.; Muschalla, D. Sensitivity of model-based water balance to low impact development parameters. Water 2018, 10, 1838. [Google Scholar] [CrossRef]
- ZinCo, I. Cobertura Ecológica Extensiva “Tapete Sedum”. 2022. Available online: https://zinco.pt/sistemas/extensivas/tapete_sedum.php (accessed on 21 August 2023).
- IPMA. Boletim Anual 2022. Available online: https://www.ipma.pt/resources.www/docs/im.publicacoes/edicoes.online/20230328/RLuazVlyZulVPByQUNey/cli_20220101_20221231_pcl_aa_co_pt.pdf (accessed on 2 July 2023).
- Pordata. Available online: https://www.pordata.pt/db/portugal/ambiente+de+consulta/tabela (accessed on 5 July 2023).
- Regulatory Decree nº 23/95-Regulamento Geral dos Sistemas Públicos e Prediais de Distribuição de Água e de Drenagem de Águas Residuais, Portugal, August 1995. Available online: https://diariodarepublica.pt/dr/detalhe/decreto-regulamentar/23-1995-431873 (accessed on 21 August 2023).
- Ferreira, F. Modelação e Gestão Integrada de Sistemas de Águas Residuais. Dissertação de Doutoramento em Engenharia Civil, IST/UNL, Lisboa, Portugal, 2006. [Google Scholar]
- Hossain, S.; Hewa, G.A.; Wella-Hewage, S. A Comparison of Continuous and Event-Based Rainfall–Runoff (RR) Modelling Using EPA-SWMM. Water 2019, 11, 611. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Hamouz, V.; Muthanna, T.M. Hydrological modelling of green and grey roofs in cold climate with the SWMM model. J. Environ. Manag. 2019, 249, 109350. [Google Scholar] [CrossRef] [PubMed]
- Arjenaki, M.O.; Sanayei, H.; Heidarzadeh, H.; Mahabadi, N. Modeling and investigating the effect of the LID methods on collection network of urban runoff using the SWMM model (case study: Shahrekord City). Model. Earth Syst. Environ. 2021, 7, 1–16. [Google Scholar] [CrossRef]
- Palla, A.; Gnecco, I. Hydrologic modeling of Low Impact Development systems at the urban catchment scale. J. Hydrol. 2015, 528, 361–368. [Google Scholar] [CrossRef]
- Niazi, M.; Nietch, C.; Maghrebi, M.; Jackson, N.; Bennett, B.R.; Tryby, M.; Massoudieh, A. Storm water management model: Performance review and gap analysis. J. Sustain. Water Built Environ. 2017, 3, 04017002. [Google Scholar] [CrossRef]


| Parameter | Limos et al. [24] | Peng and Stovin [25] | Krebs et al. [26] | Jeffers, Garner et al. [19] | Leimgruber et al. [44] | ||||
|---|---|---|---|---|---|---|---|---|---|
| RV | PF | RV | PF | RV&PF | RV | PF | RV | PF | |
| Porosity | NS | - | S | S | S | S | S | S | - |
| Soil thickness | NS | - | - | - | - | S | S | S | - |
| Surface roughness | NS | - | NS | NS | NS | NS | NS | NS | - |
| Void fraction | NS | - | NS | NS | S | NS | S | NS | - |
| Surface slope | NS | - | NS | NS | - | NS | S | NS | - |
| Conductivity slope | NS | - | S | S | S | S | S | - | - |
| Hydraulic width | NS | - | - | - | - | NS | S | - | - |
| Vegetation cover | NS | - | - | - | NS | S | S | NS | - |
| Wilting point | S | - | S | S | S | S | NS | - | - |
| Soil conductivity | NS | - | - | - | S | NS | NS | - | - |
| Surface roughness | NS | - | - | - | - | NS | NS | - | - |
| Field capacity | S | - | S | S | S | S | NS | S | - |
| Suction head | NS | - | NS | NS | NS | NS | NS | NS | - |
| Thickness (mat) | NS | - | - | - | - | NS | NS | NS | - |
| Berm height | NS | - | - | - | - | NS | NS | NS | - |
| Roughness (mat) | NS | - | - | - | S | NS | S | NS | - |
| Evaporation rate | S | - | S | S | S | - | - | - | - |
| Parameters | Substrate |
|---|---|
| pH (H2O) | 7.1 |
| Nitric nitrogen (mg/L) | 3.3 |
| Extractable phosphorus (mg/L) | <1.0 |
| Extractable potassium (mg/L) | 35.9 |
| Organic matter (%) | 20.9 |
| Dry matter (%) | 54.4 |
| Density (g/cm3) | 0.53 |
| Fine fraction (%) | 26.2 |
| Coarse fraction (%) | 73.8 |
| Sand fraction (%) | 45.1 |
| Slime fraction (%) | 34.3 |
| Clay fraction (%) | 20.6 |
| Parameter | Value | Unit | Obtained through: |
|---|---|---|---|
| Area sub-catchment | 0.000103 | ha | Field measurement |
| Slope | 2 | % | Field measurement |
| Berm height | 110 | mm | Field measurement |
| Vegetation volume fraction | 0.1 | m3/m3 | SWMM Reference Manual |
| Surface roughness (Manning’s n) | 0.1 | - | SWMM Reference Manual |
| Soil thickness | 101 | mm | Field measurement |
| Porosity | 0.457 | m3/m3 | Field measurement |
| Conductivity | 5555 | mm/h | Field measurement |
| Suction head | 88.9 | mm | SWMM Reference Manual |
| Drainage mat thickness | 25 | mm | Field measurement |
| Void fraction | 0.5 | m3/m3 | Field measurement |
| Hydraulic width | 1 | m | Field measurement |
| Parameter | Value | Unit | Min–Max |
|---|---|---|---|
| Field capacity | 0.31 | m3/m3 | 0.11–0.34 |
| Wilting point | 0.004 | m3/m3 | 0–0.1 |
| Conductivity slope | 53 | - | 0.1–40 |
| Roughness (Manning’s number) | 0.4 | - | 0.001–2 |
| Date | Average Rainfall Intensity (mm/h) | Rainfall Duration (Minutes) | Test Type | NSE | VE (%) |
|---|---|---|---|---|---|
| 03-05-22 | 92.0 | 20 | Calibration | 0.98 | 2.98 |
| 27-04-22 | 55.2 | 20 | Calibration | 0.64 | 17.87 |
| 13-04-22 | 71.3 | 20 | Calibration | 0.70 | 10.71 |
| 12-04-22 | 44.8 | 20 | Calibration | 0.61 | 0.88 |
| 14-04-22 | 92.0 | 20 | Calibration | 0.58 | 6.19 |
| 05-05-22 | 55.2 | 20 | Calibration | 0.66 | 3.00 |
| 18-08-22 | 73.8 | 20 | Calibration | 0.72 | 6.45 |
| 19-08-22 | 92.0 | 20 | Calibration | 0.74 | 7.16 |
| 22-08-22 | 92.0 | 20 | Calibration | 0.83 | 2.49 |
| 24-08-22 | 77.1 | 20 | Calibration | 0.76 | 1.68 |
| 25-08-22 | 40.0 | 20 | Validation | 0.59 | 4.55 |
| 30-08-22 | 55.8 | 20 | Validation | 0.69 | 0.18 |
| 18-04-23 | 3.5 | 120 | Validation | 0.91 | −5.50 |
| 21-04-23 | 3.5 | 120 | Validation | 0.89 | 1.00 |
| 25-04-23 | 3.5 | 120 | Validation | 0.72 | −4.24 |
| Parameter (Units) | Calibrated | Default |
|---|---|---|
| Vegetation volume fraction (m3/m3) | 0.1 | 0.0 |
| Surface roughness (Mannings n) | 0.1 | 0.1 |
| Porosity (m3/m3) | 0.457 | 0.5 |
| Field capacity (m3/m3) | 0.31 | 0.2 |
| Wilting point (m3/m3) | 0.004 | 0.1 |
| Conductivity (mm/h) | 5555 | 12.7 |
| Conductivity slope (-) | 53 | 10 |
| Roughness drainage mat (Mannings n) | 0.4 | 0.1 |
| Date | Calibrated | Default | ||
|---|---|---|---|---|
| NSE | VE | NSE | VE | |
| 12-04-22 | 0.61 | 0.88% | 0.15 | 67.52% |
| 13-04-22 | 0.70 | 10.71% | 0.05 | 50.19% |
| 03-05-22 | 0.98 | 2.98% | −0.11 | 58.81% |
| 22-08-22 | 0.83 | 2.49% | −0.13 | 63.65% |
| 24-08-22 | 0.76 | 1.68% | −0.03 | 61.41% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weggemans, J.; Santos, M.L.; Ferreira, F.; Moreno, G.D.; Matos, J.S. Modeling the Hydraulic Performance of Pilot Green Roofs Using the Storm Water Management Model: How Important Is Calibration? Sustainability 2023, 15, 14421. https://doi.org/10.3390/su151914421
Weggemans J, Santos ML, Ferreira F, Moreno GD, Matos JS. Modeling the Hydraulic Performance of Pilot Green Roofs Using the Storm Water Management Model: How Important Is Calibration? Sustainability. 2023; 15(19):14421. https://doi.org/10.3390/su151914421
Chicago/Turabian StyleWeggemans, Jesse, Maria Luiza Santos, Filipa Ferreira, Gabriel Duarte Moreno, and José Saldanha Matos. 2023. "Modeling the Hydraulic Performance of Pilot Green Roofs Using the Storm Water Management Model: How Important Is Calibration?" Sustainability 15, no. 19: 14421. https://doi.org/10.3390/su151914421
APA StyleWeggemans, J., Santos, M. L., Ferreira, F., Moreno, G. D., & Matos, J. S. (2023). Modeling the Hydraulic Performance of Pilot Green Roofs Using the Storm Water Management Model: How Important Is Calibration? Sustainability, 15(19), 14421. https://doi.org/10.3390/su151914421








