Analysis of Surface Settlement Induced by Shield Tunnelling: Grey Relational Analysis and Numerical Simulation Study on Critical Construction Parameters

Abstract

Excessive surface settlement poses significant challenges to shield tunnelling construction, resulting in damage to adjacent buildings, infrastructure, and underground pipelines. This study focused on investigating the surface settlement induced by shield tunnelling during the construction of Qingdao Metro Line 6 between Haigang Road Station and Chaoyang Road Station. Firstly, the settlement data from the left line of the shield tunnel were evaluated by grey relational analysis. The relational coefficients were calculated to assess the correlation degrees of each influential parameter. Subsequently, the four critical influential parameters with the highest relational degrees were chosen to investigate their effects on surface settlement through numerical simulations under different scenarios. The results show that the four parameters with the highest relational degrees were thrust, grouting pressure, earth pressure, and strata elastic modulus. It should be noted that the strata elastic modulus significantly affects surface settlement, while the grouting pressure influences the settlement trough width in weak strata. Moreover, improper thrust magnitude can lead to an increase in surface settlement. Based on these findings, recommendations are proposed for the right-line tunnel construction and practical countermeasures for surface settlement during shield tunnelling construction are provided.

1. Introduction

Rapidly escalating urbanization calls for efficient transport systems and has made metro construction crucial to meet growing urban transportation demand. The shield tunnelling method has become the primary construction method for underground metro projects, owing to the rapid construction speed, automated operation, and minimal impact on surface traffic. However, shield tunnelling inevitably disturbs the surrounding rocks, leading to stress redistribution within the soil [1] and inducing surface settlement [2,3]. The excessive surface settlement can damage adjacent buildings and infrastructure [4,5], jeopardizing the safety of pedestrians, vehicles, and roads [6]. This in turn can lead to work stoppages and result in additional costs [7]. Moreover, it may trigger soil liquefaction and landslides, leading to severe construction accidents. Therefore, it is essential to understand and predict the behavior of surface settlement induced by shield tunnelling to ensure the safety and stability of urban areas.

An approach using Gaussian normal distribution to represent the lateral surface settlement induced by shield tunnelling was initially proposed by Peck [8]. The prediction formulas to describe surface settlement and its influential parameters were introduced and improved by subsequent researchers [9,10,11,12,13,14]. Notably, these formulas typically rely on empirical parameters and require local measurements for theoretical adjustments. In addition, some researchers have also studied surface settlement through model tests [15,16,17], but these tests have limitations in accurately imitating field conditions and actual construction scenarios. For greater authenticity and credibility, researchers utilized the measured data to analyze the correlation between the surface settlement and the influential construction parameters. For instance, Kannangara et al. [18] investigated the impact of shield tunnelling parameters on surface settlement. They identified the correlation between earth pressure and grouting pressure on the peak of surface settlement. Based on the construction data from EPB-TBM in the Moscow metro, Ter-Martirosyan et al. [19] studied the effect of metro tunnel construction parameters on surface settlement. The results indicated a close mutual relationship between earth pressure and surface settlement. Dongku Kim et al. [20] analyzed data from the construction section of the Hong Kong Metro and identified parameters such as boring speed, thrust, and cutterhead torque presented a modest correlation with the surface settlement. However, it cannot offer specific functional relationships or in-depth analysis of the complex interactions between the construction parameters and the surface settlement.

In recent years, numerical simulation methods have been widely employed to solve the interdisciplinary problems encountered in underground engineering, involving the surrounding rock deformation affected by novel metallic rock support materials [21,22] and the surface settlement issues induced by shield tunnelling [23,24,25,26,27,28,29,30]. Wang et al. [31] employed particle flow to simulate surface settlement in sandy soils, revealing its dynamic nature involving soil arch formation and destruction. Alzabeebee et al. [32] studied traffic load, microtunnel diameter, and backfill height using a finite element model. They found traffic loads significantly impact microtunnel-induced pavement settlement. Through finite element analysis, Yuan et al. [33] investigated the effect of parameters like deformation modulus, burial depth, and tunnel spacing on surface settlement during shield construction in weathered mudstone areas. Numerical simulations can theoretically model the entire shield construction process. However, existing simulations frequently suffer from inaccurate selection and validation of essential simulation parameters due to the multitude of construction variables. In addition, these simulations typically oversimplify the surface settlement process by focusing on a single and homogeneous stratum, leaving room for improvement to consider complex geological conditions and various influential parameters.

Existing data analysis methods have limitations in quantifying settlement impact patterns, and numerical simulations encounter challenges in selecting critical construction parameters. Hence, this study proposes a novel hybrid numerical approach combined with grey relational analysis to analyze the critical construction parameters influencing surface settlement comprehensively. The grey relational analysis serves to quantify the correlation degree of various parameters with surface settlement by calculating grey relational coefficients [34]. When coupled with numerical simulations, it facilitates optimized parameter selection and enhances the assessment of specific parameters’ impact on surface settlement. The engineering background was based on the shield construction section of Qingdao Metro Line 6 between Haigang Road Station and Chaoyang Road Station. This tunnel section presents complex geological conditions with diverse soil properties and various stratigraphic characteristics, where severe settlements occurred during the construction of the left line. In this study, the settlement monitoring data from the left line were evaluated by grey relational analysis to assess the relational degrees of each influential parameter. Subsequently, numerical simulations were conducted to investigate the effect of critical construction parameters on surface settlement, and recommendations are proposed for the right-line tunnelling. Finally, practical countermeasures for surface settlement during shield tunnelling construction are provided based on the research findings to ensure the safety and stability of future urban subway projects.

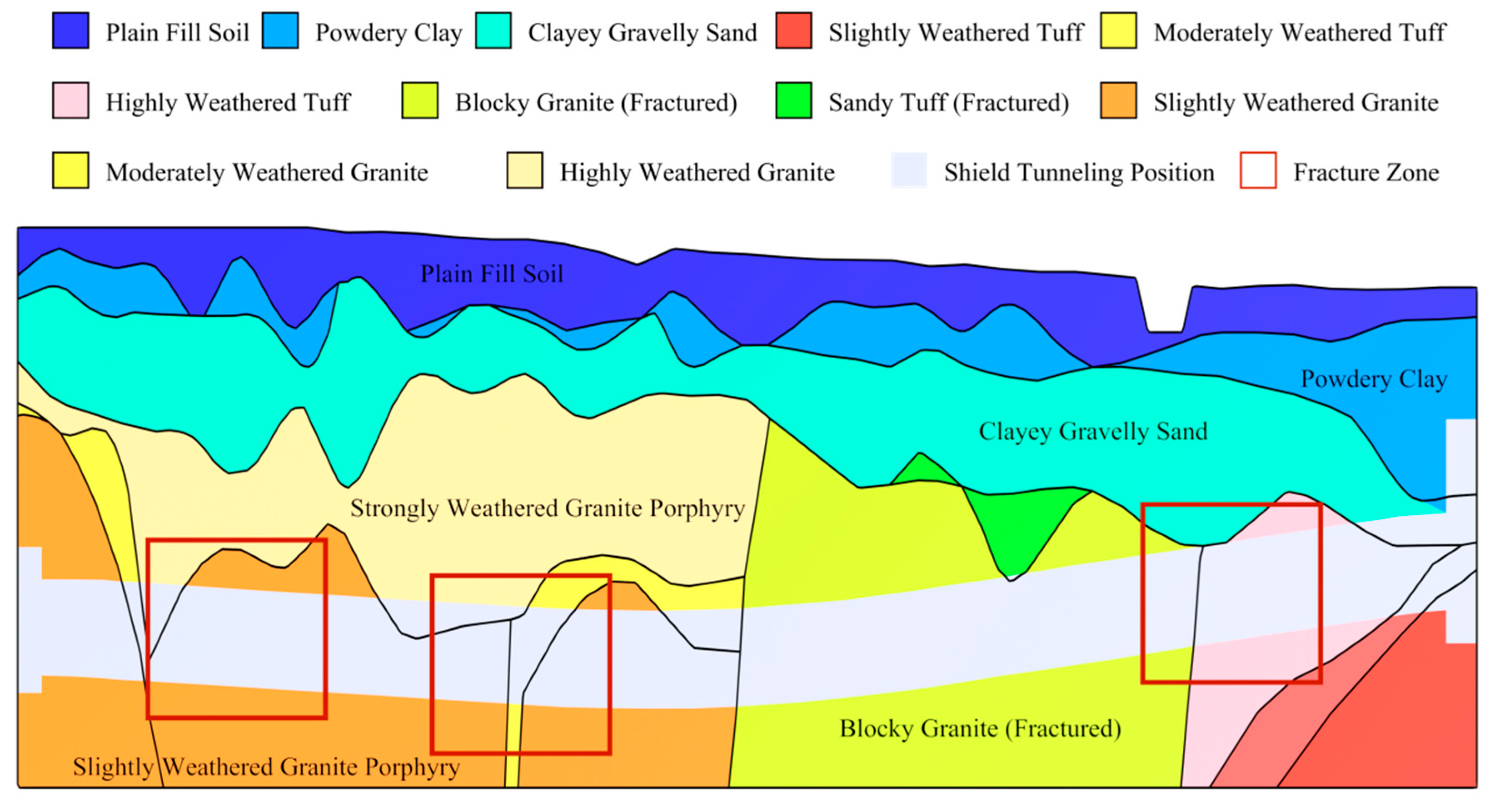
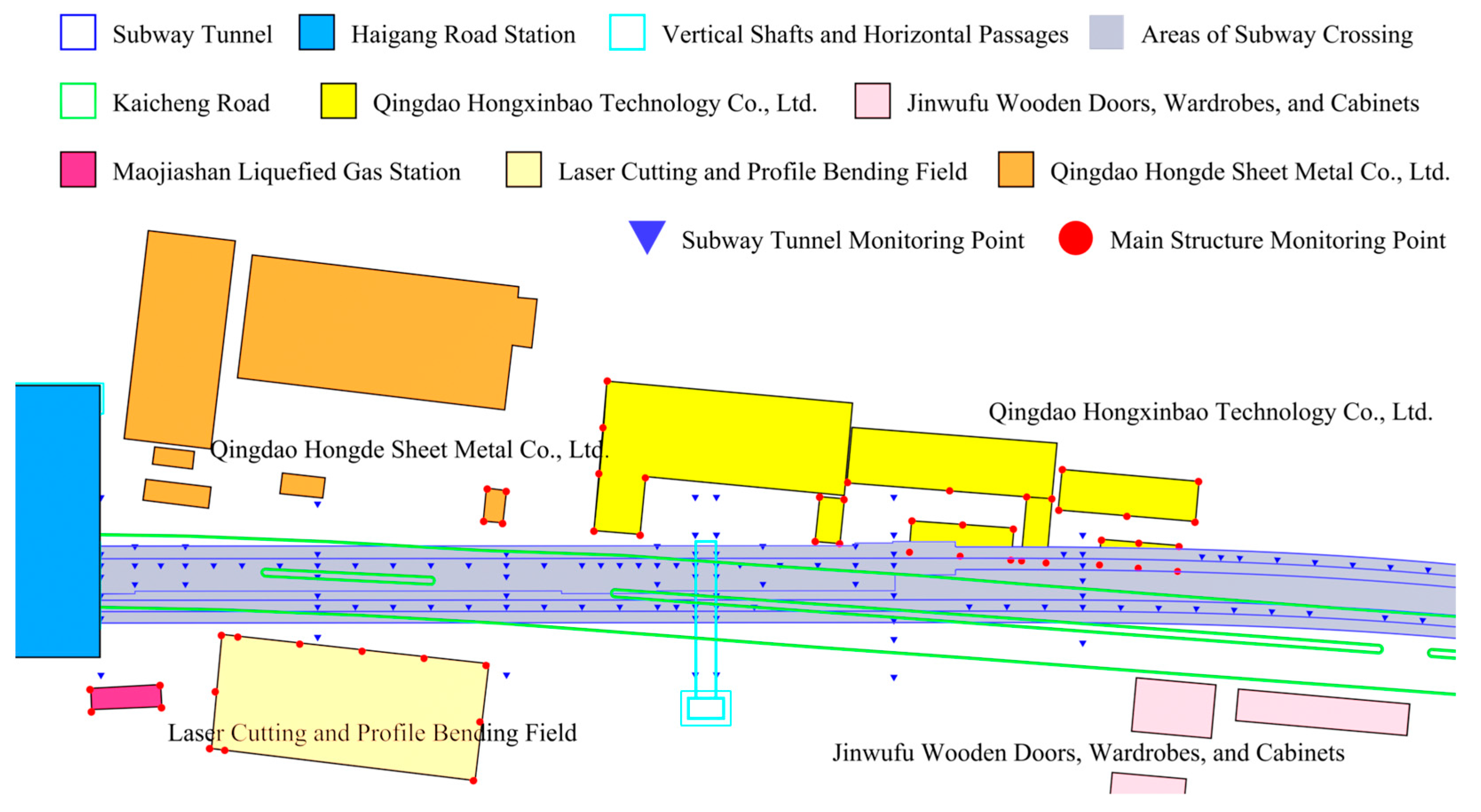
2. Project Overview

The shield construction section of Qingdao Metro Line 6, between Haigang Road Station and Chaoyang Road Station, comprises two single-line single-tunnel sections, starting and ending at Y(Z)DK 31 + 248.393~32 + 039.183. The right-line section is 790.790 m in length, while the left is 791.732 m. The depth of vault ranges from 12.9 m to 25.3 m. CR Equip. Machine 179, produced by China Railway Engineering Equipment Group Co., Ltd., headquartered in Zhengzhou, China, was employed for this tunnel section. The shield machine excavated and constructed the tunnel from Chaoyang Road Station and advanced toward Haigang Road Station, featuring an excavation diameter of ϕ = 6303 mm. The cutterhead comprised six spoke-type cutters and six face plates, totaling 34 face cutters, 12 gauge cutters, and six center cutters. The main parameters of the shield machines are detailed in

Table 1. Main parameters of the shield machine.

Parameter	CR Equip. Machine 179
Tunnel boring type	Earth pressure balance
Excavation diameter (mm)	6303
Shield diameter (mm)	6250
Cutterhead rotation speed (rpm)	0~3.7
Maximum thrust (kN)	39,000
Rated torque (kN/m)	6000
Unblocking torque (kN/m)	7200
Horizontal turning capability (m)	250
Maximum climbing capability (‰)	±50
Cutterhead opening ratio (%)	34

.

The topography of the construction section slopes from northwest to southeast. The YDK31 +248.393~+339.682 section exhibits an erosional slope landform, while the YDK31 +339.682~32 + 039.183 section displays an erosional accumulation and gently sloping landform. Within the section, there are six standard layers and 19 sublayers. The left line of the construction section traverses several main strata, including powdery clay, clayey gravelly sand, strongly weathered granite porphyry, moderately weathered granite porphyry, slightly weathered granite porphyry, blocky granite (fractured), strongly weathered tuff, moderately weathered tuff, and sandy tuff (fractured). The groundwater in the section mainly consists of quaternary pore water and bedrock fissure water. Additionally, the construction section is influenced by the Lingshanwei fracture and its secondary fracture. The fault’s exposure along the Lingshanwei area shows a northeast strike of 40° to 55°, predominantly northwest tendency, and a dip of 70° to 88°. This section reveals three fracture zones and one severely affected zone of the Lingshanwei fault.

Table 2. Stratigraphic physical and mechanical parameters of the construction section between Haigang Road Station and Chaoyang Road Station.

Stratum	Density (kg/m3)	Cohesion (kPa)	Internal Friction (°)	Elastic Modulus 1 (MPa)	Poisson’s Ratio
Plain fill soil	1650	8	14	8	0.3
Powdery clay	1980	18	16	16	0.4
Clayey gravelly sand	2050	14	28	12	0.3
Sandy tuff (fractured)	2450	25	33	40	0.3
Blocky granite (fractured)	2500	48	35	100	0.3
Slightly weathered tuff	2610	710	45	1250	0.2
Moderately weathered tuff	2600	400	40	550	0.3
Strongly weathered tuff	2300	22	30	20	0.3
Slightly weathered granite porphyry	2680	530	45	1080	0.2
Moderately weathered granite porphyry	2600	300	40	400	0.3
Strongly weathered granite porphyry	2300	15	30	18	0.3

¹ The elastic modulus in the table is the tangential modulus.

provides more detailed stratigraphic physical and mechanical parameters, sourced from the “Geotechnical Investigation Report of Qingdao Metro Line 6 Phase I Project, Haigang Road Station—Chaoyang Road Station,” supplied by Qingdao Municipal Research Institute of Surveying and Mapping. The geological profile of the left-line construction section is illustrated in Figure 1. Figure 2 and Figure 3 depict the layout of monitoring points and an aerial view in the vicinity of Haigang Road Station, respectively.

3. Grey Relational Analysis

Grey relational analysis is a quantitative method used to assess the correlation of trends among different parameters in a complex system. It is particularly suitable for systems with multiple independent variables and unclear interconnections. The method involves the following key steps.

• Determine the evaluation index sequence and the influential parameter sequence.
• Transform the obtained sequences into dimensionless form.
• Calculate the difference sequences and identify the maximum and minimum differences.
• Compute the relational coefficients and determine the grey relational degree.

The above four steps enable researchers to evaluate the influence of different factors on the evaluation index and facilitate the subsequent optimization analysis.

3.1. Model Index Determination

When calculating the relational degree in the grey relational model, it is necessary to determine the evaluation index sequence (dependent variables) and the influential parameter sequence (independent variables) that characterize the system behavior. The selection of the evaluation index sequence directly affects the rationality of the relational degree calculation results:

$$X_0=\left\{x_0\left(1\right),x_0\left(2\right),\cdots ,x_0\left(n\right)\right\}$$

(1)

$$X_i=\left\{x_i\left(1\right),x_i\left(2\right),\cdots ,x_i\left(n\right)\right\}$$

(2)

where $X_0$ is the evaluation index sequence and $X_i$ is the influential parameter sequence.

Previous studies [35,36,37,38,39] have identified several influential factors for the soil movement and surface settlement induced by shield tunnelling:

• Changes in the stress state of the excavated soil.
• Squeezing and forward movement of the soil in front of the excavation face and the surrounding soil in contact with the shield.
• Over-excavation during the tunnelling process.
• Formation of gaps around the shield due to the shield shell radius being smaller than the cutterhead radius, causing the surrounding soil to move towards the void and result in surface settlement.
• Improper grouting at the shield tail leads to soil compression and settlement.
• Interaction between the soil and the lining, as well as between the lining and the segment.
• Creep or secondary consolidation of the soft clay soil following construction disturbance around the shield tunnel, leading to continuous secondary consolidation settlement.

Among the above influential factors, factors 1, 2, and 3 affect the stability of the excavation face and can be controlled by adjusting tunnelling parameters during construction. Factors 4, 5, and 6 are related to grouting quality and can be controlled by adjusting grouting parameters. Factor 7 can be considered stratum parameters.

Based on the above correlations between the influential factors and the surface settlement, this study selected the surface settlement as the evaluation index sequence in the relational degree calculation. To ensure the measuring data’s coherence, surface settlement data were obtained from the monitoring points above the centerline of the left-line tunnel section. The influential parameter sequences selected were earth pressure, tunnelling speed, and thrust as tunnelling parameters; grouting pressure and grouting volume as grouting parameters; and the weighted average of cohesion, internal friction angle, elastic modulus, and Poisson’s ratio as stratum parameters. The impact on surface settlement was evaluated by analyzing the relational degrees of these parameters.

Table 3. Influential construction parameters and corresponding surface settlement.

Data ID	Settlement (cm)	Tunnelling Parameters			Grouting Parameters		Stratum Parameters
		Thrust (kN)	Earth Pressure (kPa)	Tunnelling Speed (mm/min)	Grouting Pressure (kPa)	Grout Volume (m3)	Cohesion (kPa)	Internal Friction (°)	Poisson’s Ratio	Elastic Modulus (MPa)
0	−3.10	10,424	83	15	272	3.4	237	39.7	0.23	471
1	−2.34	9817	94	33	244	3.1	180	37.6	0.22	477
2	−4.29	7656	69	26	207	3.1	237	38.9	0.21	518
3	−1.54	11,460	121	13	298	5.0	223	39.9	0.22	542
4	−0.61	10,138	113	15	244	4.8	164	38.2	0.22	489
5	−6.27	10,438	18	12	260	3.8	213	37.6	0.21	448
6	−2.44	9855	90	16	223	3.2	230	42.9	0.20	533
7	−3.12	9440	81	12	300	3.8	237	42.9	0.20	585
8	−5.70	6886	17	22	194	5.3	172	40.9	0.21	391
9	−7.09	7441	37	33	185	5.7	145	38.7	0.21	323
10	−9.28	7791	21	20	203	5.6	160	38.4	0.20	238
11	−9.90	7419	21	13	203	5.3	191	35.4	0.20	158
12	−8.79	7965	69	37	214	5.9	161	39.5	0.21	150
13	−8.71	9489	82	15	220	5.6	175	40.1	0.21	207
14	−7.53	7045	73	28	188	5.9	77	35.9	0.26	220
15	−7.56	7645	82	29	270	5.8	137	37.9	0.24	298
16	−4.50	8921	76	27	334	5.3	142	40.1	0.23	383
17	−3.92	7809	62	27	223	5.0	225	42.9	0.21	499
18	−3.36	9379	54	39	190	5.2	198	40.6	0.22	475
19	−1.61	9723	108	14	295	6.1	199	40.4	0.22	516
20	−0.92	10,344	118	32	277	6.1	237	42.9	0.22	524
21	−1.61	10,074	66	24	232	5.4	177	40.4	0.23	435
22	−1.34	10,217	112	27	232	4.4	155	39.3	0.24	408
23	0.03	10,678	126	26	292	4.8	147	40.1	0.24	429
24	−0.21	10,735	125	28	283	5.6	107	35.7	0.28	586
25	−2.09	9961	64	44	264	6.2	159	39.6	0.27	447
26	−1.68	9572	104	25	274	4.1	40	32.6	0.28	495
27	−2.42	9374	125	34	274	6.2	40	33.3	0.28	461
28	−1.13	11,109	105	26	247	6.2	40	31.0	0.28	520
29	−1.25	9547	109	34	237	4.4	40	29.9	0.28	510
30	−2.30	8677	142	36	233	3.6	40	27.0	0.28	454
31	−1.09	10,429	145	30	268	3.6	40	29.5	0.28	515
32	−1.11	10,260	126	41	243	3.2	40	31.2	0.28	518
33	−3.11	9504	126	38	194	3.5	40	33.5	0.27	427
34	−6.23	10,703	74	34	221	3.1	40	25.9	0.28	160
35	−7.14	7041	64	33	200	3.2	40	25.7	0.28	147
36	−7.76	7574	55	37	181	3.1	40	23.5	0.26	240
37	−10.39	7563	26	29	135	4.1	102	23.3	0.23	91
38	−10.37	7170	25	28	150	3.3	146	28.7	0.24	168
39	−3.08	9289	107	27	228	3.9	163	28.1	0.26	470
40	−2.82	9150	101	12	237	3.7	237	25.4	0.28	654

summarizes the influential construction parameters and corresponding surface settlement data collected and collated for each ring during the left-line tunnelling.

3.2. Grey Relational Degree Calculation

The grey relational degree calculation quantifies the relative influences and trends of selected influential parameter sequences compared to the evaluation index sequence. To account for the varying dimensions and magnitudes of the system’s influential parameters and minimize errors in the calculation, mean normalization is performed on the original data columns for dimensionless standardization:

$$X_0^{\ast }\left(k\right)=X_0\left(k\right)/{\overline{X}}_0\left(k=\mathrm{1,2},\cdots ,n\right)$$

(3)

$$X_i^{\ast }\left(k\right)=X_i\left(k\right)/{\overline{X}}_i\left(k=\mathrm{1,2},\cdots ,n\right)$$

(4)

where ${\overline{X}}_0$ and ${\overline{X}}_i$ represent the average values of the evaluation index sequence and influential parameter sequences, respectively.

The absolute differences between all index sequences and the influential parameter sequence are then calculated using the following formula:

$${\mathsf{\Delta }}_{0i}\left(k\right)=\left|X_0^{\ast }\left(k\right)-X_i^{\ast }\left(k\right)\right|\left(i=\mathrm{1,2},\cdots ,n\right)$$

(5)

Subsequently, the maximum and minimum absolute differences are obtained with the following formulas:

$${\mathsf{\Delta }}_{max}={Max}_i{Max}_k{\mathsf{\Delta }}_{0i}\left(k\right)$$

(6)

$${\mathsf{\Delta }}_{min}={Min}_i{Min}_k{\mathsf{\Delta }}_{0i}\left(k\right)$$

(7)

where ${\mathsf{\Delta }}_{0\mathrm{i}}\left(k\right)$ is the absolute difference between the ith influential parameter sequence and the evaluation index sequence at the kth data point, and ${\mathsf{\Delta }}_{max}$ and ${\mathsf{\Delta }}_{min}$ represent the maximum and minimum values in the set, respectively.

Next, the relational coefficient and grey relational degree are calculated using the following expressions:

$$l_{0i}=\frac{{\mathsf{\Delta }}_{min}+\rho {\mathsf{\Delta }}_{max}}{{\mathsf{\Delta }}_{0i}\left(k\right)+\rho {\mathsf{\Delta }}_{max}}$$

(8)

$$r_{0i}=\frac{1}{n}{\sum }_{k=1}^n{l}_{0i}$$

(9)

where $l_{0i}$ is the relational coefficient between the evaluation index sequence and the ith influential parameter sequence at the kth data point. The resolution coefficient $\rho$ is introduced, with smaller $\mathsf{\rho }$ values indicating greater resolution ($\rho$ ∈ (0,1), and in this paper, $\rho$ = 0.5). $r_{0i}$ stands for the relational degree between the evaluation index sequence and the kth influential parameter sequence, with a value domain of (0,1).

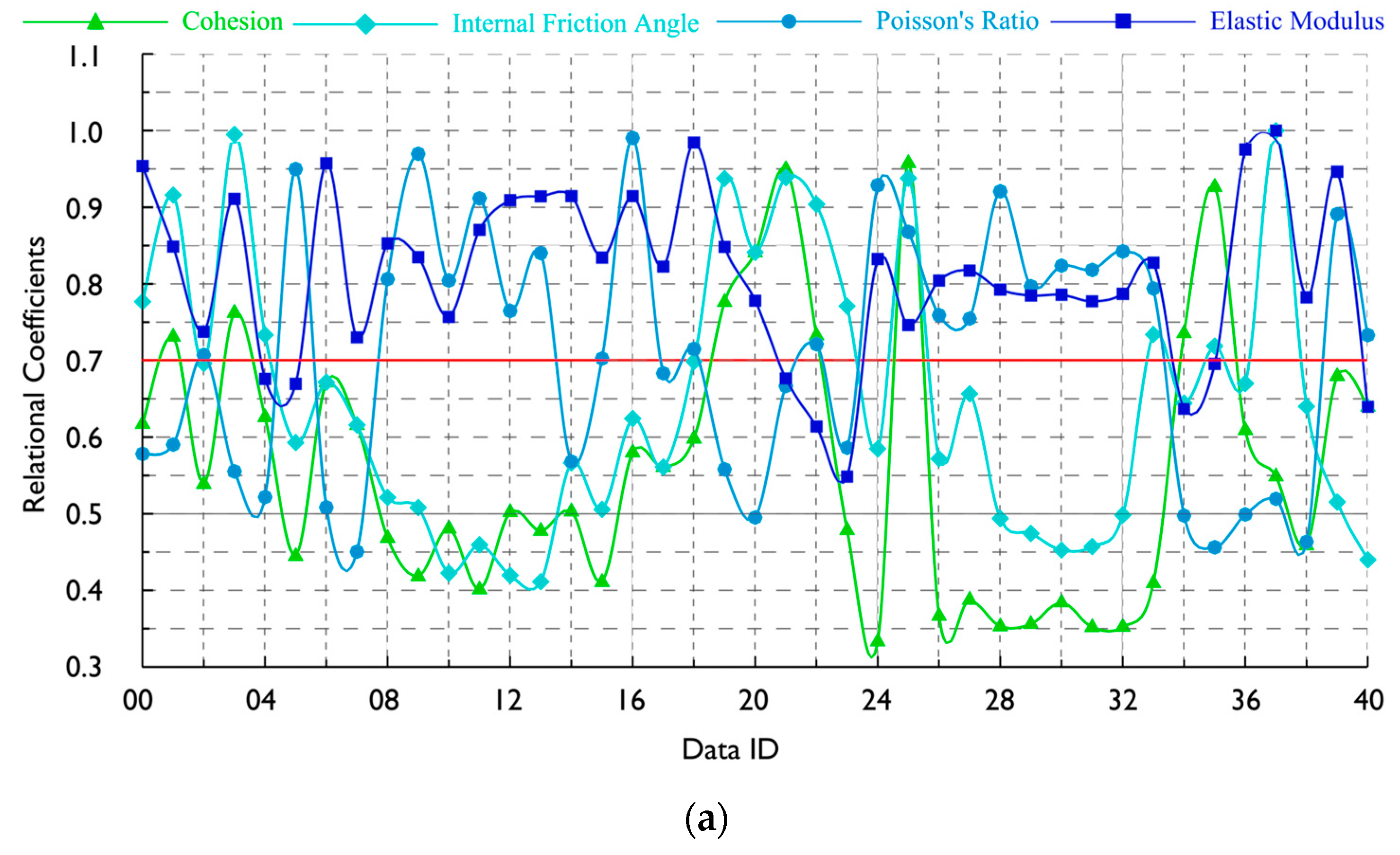
3.3. Results and Analysis

The calculation results of relational coefficients for each data point are shown in Figure 4 and

Table 4. Calculation results of grey relational coefficients.

Data ID	Relational Coefficients of Tunnelling Parameters			Relational Coefficients of Grouting Parameters		Relational Coefficients of Stratum Parameters
	Thrust	Earth Pressure	Tunnelling Speed	Grouting Pressure	Grouting Volume	Cohesion	Internal Friction	Poisson’s Ratio	Elastic Modulus
0	0.87	0.72	0.44	0.98	0.44	0.62	0.78	0.58	0.95
1	0.79	0.74	0.97	0.68	0.40	0.73	0.92	0.59	0.85
2	0.54	0.73	0.88	0.69	0.50	0.54	0.70	0.71	0.74
3	0.76	0.92	0.36	0.94	0.80	0.76	0.99	0.56	0.91
4	0.68	0.72	0.34	0.56	0.66	0.63	0.73	0.52	0.68
5	0.56	0.55	0.65	0.67	0.96	0.44	0.59	0.95	0.67
6	0.81	0.71	0.40	0.60	0.50	0.67	0.67	0.51	0.96
7	0.78	0.71	0.41	0.78	0.64	0.62	0.62	0.45	0.73
8	0.52	0.52	0.76	0.76	1.00	0.47	0.52	0.81	0.85
9	0.71	0.75	0.43	0.88	0.83	0.42	0.51	0.97	0.83
10	0.84	0.87	0.61	0.67	0.74	0.48	0.42	0.80	0.76
11	0.87	0.97	0.56	0.62	0.67	0.40	0.46	0.91	0.87
12	0.86	0.66	0.38	0.67	0.59	0.50	0.42	0.76	0.91
13	0.54	0.58	0.61	0.65	0.65	0.48	0.41	0.84	0.91
14	0.67	0.75	0.47	0.98	0.64	0.50	0.57	0.57	0.91
15	0.82	0.67	0.46	0.54	0.66	0.41	0.51	0.70	0.83
16	0.80	0.83	0.78	0.53	0.79	0.58	0.62	0.99	0.91
17	0.54	0.64	0.92	0.73	0.91	0.56	0.56	0.68	0.82
18	0.79	0.56	0.60	0.55	0.91	0.60	0.70	0.72	0.98
19	0.69	0.79	0.37	0.93	0.83	0.78	0.94	0.56	0.85
20	0.76	0.81	0.60	0.71	0.90	0.84	0.84	0.50	0.78
21	0.77	0.51	0.48	0.58	0.95	0.95	0.94	0.67	0.68
22	0.78	0.79	0.54	0.56	0.63	0.73	0.90	0.72	0.61
23	0.74	0.76	0.40	0.69	0.61	0.48	0.77	0.59	0.55
24	0.78	0.79	0.46	0.68	0.83	0.33	0.58	0.93	0.83
25	0.80	0.53	0.70	0.76	0.70	0.96	0.94	0.87	0.75
26	0.66	0.76	0.52	0.78	0.60	0.37	0.57	0.76	0.80
27	0.69	0.86	0.89	0.88	0.67	0.39	0.66	0.75	0.82
28	0.93	0.71	0.49	0.60	0.81	0.35	0.49	0.92	0.79
29	0.62	0.76	0.78	0.57	0.63	0.36	0.47	0.80	0.78
30	0.56	0.71	0.83	0.63	0.54	0.38	0.45	0.82	0.79
31	0.80	0.82	0.57	0.68	0.42	0.35	0.46	0.82	0.78
32	0.76	0.92	0.84	0.58	0.38	0.35	0.50	0.84	0.79
33	0.79	0.76	0.63	0.55	0.59	0.41	0.73	0.79	0.83
34	0.53	0.91	0.46	0.93	0.64	0.74	0.64	0.50	0.64
35	0.64	0.89	0.44	0.97	0.87	0.93	0.72	0.46	0.70
36	0.83	0.91	0.43	0.96	0.72	0.61	0.67	0.50	0.98
37	0.77	0.87	0.41	1.00	1.00	0.55	1.00	0.52	1.00
38	0.89	0.89	0.42	0.87	1.00	0.46	0.64	0.46	0.78
39	0.73	1.00	0.87	0.68	0.66	0.68	0.52	0.89	0.95
40	0.68	0.87	0.40	0.69	0.60	0.64	0.44	0.73	0.64

. The overall relational degrees of influential construction parameters are shown in

Table 5. Grey relational degrees of influential construction parameters.

	Parameter	Relational Degree	Ranking
Tunnelling Parameters	Earth Pressure (kPa)	0.762	2
	Tunnelling Speed (mm/min)	0.575	8
	Thrust (kN)	0.730	3
Grouting Parameters	Grouting Pressure (kPa)	0.726	4
	Grout Volume (m3)	0.705	6
Stratum Parameters	Cohesion (kPa)	0.562	9
	Internal Friction (°)	0.648	7
	Elastic Modulus (MPa)	0.809	1
	Poisson’s Ratio	0.708	5

.

Analysis of Figure 4, Table 4 and Table 5 yield the following observations:

• Grey relational coefficients above 0.7 indicate significant correlations between certain parameters and surface settlement. Figure 4a shows that the relation of cohesion and internal friction angle with the surface settlement is relatively low within the Data ID range of 9–15 (corresponding to tunnelling rings 280–247). Similarly, in the interval of Data ID 34–38 (corresponding to tunnelling rings 65–41), the relation between Poisson’s ratio and surface settlement is also notably low, which corresponds to fractured zone areas. This indicates a weak correlation between stratum parameters (excluding elastic modulus) and surface settlement within the fractured zone region.
• Earth pressure exhibits the highest grey relational degree among the construction parameters. Combined with Table 4 and Table 5, in Data ID 38–34, which exhibits high relational coefficients, surface settlement decreases as earth pressure gradually increases, consistent with previous studies [18]. Notably, slightly different from other findings [20], the grey correlation degree of tunnelling speed does not reach a significant level. Tunnelling speed briefly demonstrates a strong relational coefficient only when maintained near its maximum value (Data ID 25–30, corresponding to tunnelling rings 183–116). Therefore, flexibly adjusting the tunnelling speed based on the coefficients during right-line tunnelling helped mitigate surface settlement.
• While the grouting parameters did not exhibit the highest relational degrees, they still held prominent positions [40]. Notably, grouting pressure contributes slightly more to surface settlement than grouting volume. In addition, as shown in Figure 4c, the relational coefficients between the two are higher in the fractured zone than in other intervals. Therefore, ensuring the stability of grouting pressure and controlling the grouting volume are both critical for achieving the optimal grouting effect.

4. Numerical Simulation

Grey relational analysis reveals the relational degrees of different parameters with the surface settlement. However, it cannot offer specific functional relationships or in-depth analysis of the complex interactions between the construction parameters and the surface settlement. To explore the variation patterns governing the surface settlement influenced by the critical construction parameters, numerical simulations were conducted to analyze the effect of the four parameters (thrust, grouting pressure, earth pressure, and strata elastic modulus) with the highest relational degrees. In this study, we utilized Flac3D as a numerical simulation tool, which is based on the finite difference method and designed for addressing underground geotechnical problems. It employs an implicit solution algorithm, seamlessly combining the finite difference method with the analysis of two-body dynamics to accurately simulate complex underground phenomenon.

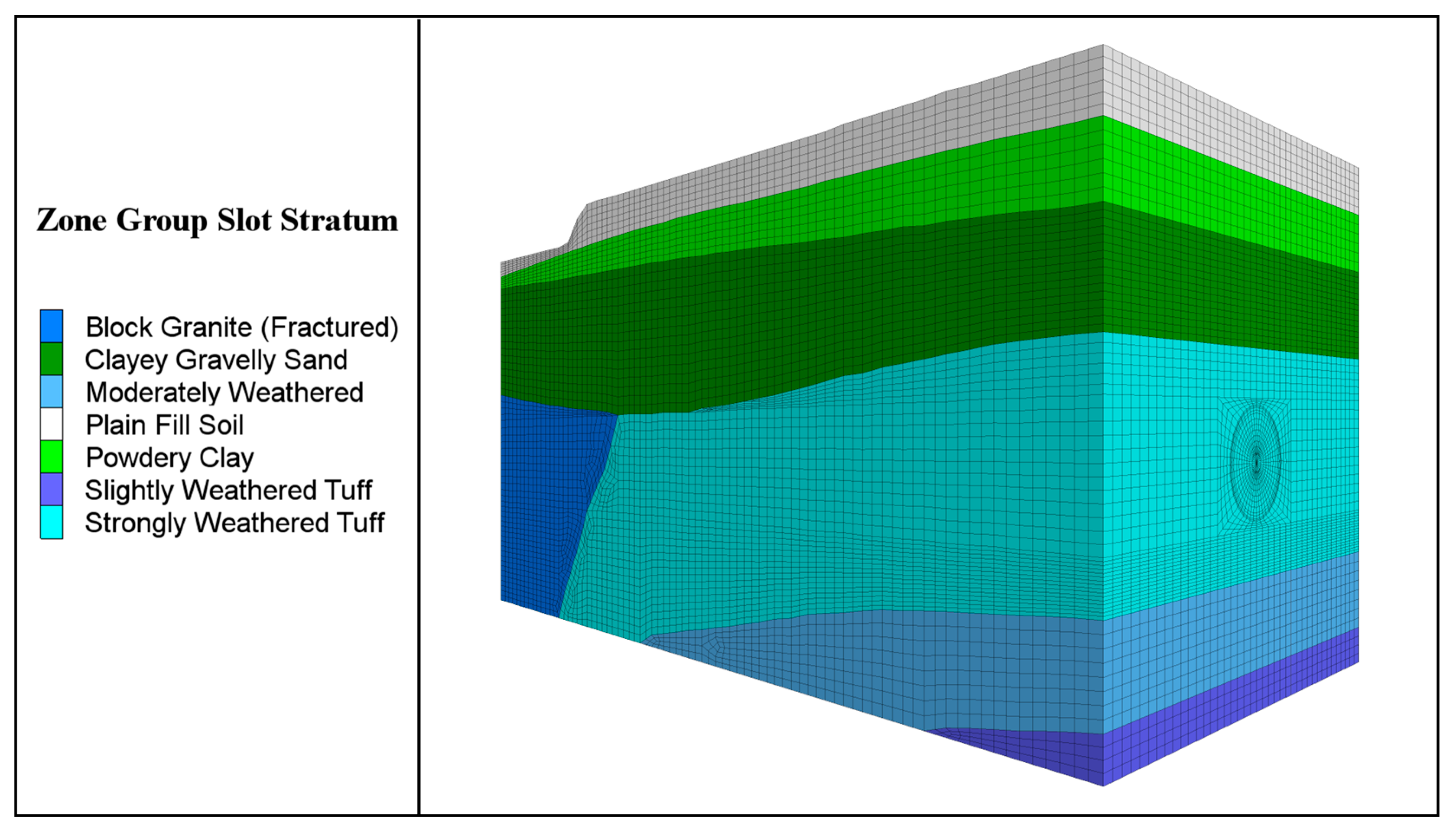
4.1. Simulation Setup

The following simplifying assumptions were made to simulate the deformation behaviors of rock and soil zones in the model.

• The tunnel structure and surrounding rock were assumed uniform and isotropic, exhibiting typical elastoplastic behavior.
• The initial stress field was induced only by the self-weight of the surrounding rock, regardless of the potential influence of groundwater on the stress distribution.
• The deformation of the rock and soil zones follows the Mohr–Coulomb strength criterion. Throughout the simulation, no progressive damage, nonlinear bending behavior, or loading–unloading cyclic loading occurred. Therefore, the lining and grouting zones were assumed as elastic material, and the shield shell zone was treated as a rigid material.

Besides the above simplifying assumptions, the following adjustments were also made to enhance the relevance to the actual conditions.

• Normal constraints were set on the surroundings and bottom of the model to simulate actual constraints on the surrounding rocks. No constraints were applied on the top.
• A fixed time-step value was implemented in the simulation, ensuring that the parameters of the grouting layer within the simulation varied in sync with the time step (time).
• The simulation considered the standard gravitational acceleration (9.8 m/s²), and the convergence threshold of the computational iterations was set at 10⁻⁵ to maintain numerical simulation accuracy.

4.2. Simulation Modelling

Based on the geological profile of Haigang Road Station to Chaoyang Road Station, the tunnelling rings from 140 to 180 (corresponding to Data ID 27–23) were selected as the representative interval to construct the numerical model. The stratum of the selected interval consists of powdery clay, clayey gravelly sand, strongly weathered tuff, moderately weathered tuff, slightly weathered tuff, and blocky granite (fractured). This interval lies within the transition zone between granite and weathered tuff, adjacent to fractured zones, encompassing both weak and stable strata. Such transitional zones frequently exhibit nonuniform physical properties like particle size distribution, porosity, and crack distribution, presenting intricate rock traits and mechanical behavior. Therefore, selecting this interval for simulation can provide comprehensive influence patterns of parameter variations under different conditions.

According to Saint-Venant’s principle, the width of the model along the X direction was set to 3–5 times the tunnel diameter to avoid boundary effects, resulting in a total width of 30 m. Similarly, the height of the model along the Z direction was 30 m, and the length of the model along the Y direction was 60 m. Additionally, to make the simulation more representative of the actual tunnelling process, grouting, lining, and segment zones were introduced to consider the influence of support processes and grouting parameters on the strata. The thickness of the shield shell zones was set to 60 mm, and the thickness of the lining zones was set to 300 mm.

To determine the optimal meshing scheme, we conducted simulations with different grid densities. The scheme that showed no significant result changes with further refinement was chosen. The final mesh scheme divided the model into grids with a 0.375 m interval, with additional refinement at the geological transitions and tunnel excavation sections. The three-dimensional numerical model is shown in Figure 5 and consists of 373,722 zones, encompassing 274,797 grid points.

4.3. Simulation Scheme

Based on the maximum and minimum values of actual construction parameters during shield tunnelling, the range for the four critical parameters were set as follows.

• The earth pressure ranges in stress from 20 to 138 kPa.
• The grouting pressure ranges in stress from 134 to 334 kPa.
• The thrust ranges in force from 6886 to 11,460 kN.
• The elastic modulus changes from 50% to 150% (compared with the exploration data).

Each parameter was set at five levels, resulting in 17 construction simulation schemes, which shown in

Table 6. Simulation scheme sets for different levels of construction parameters.

Schemes	Thrust (kN)	Earth Pressure (kPa)	Elastic Modulus (%)	Grouting Pressure (kPa)
1	6886	79	100	234
2	8030	79	100	234
3	9173	79	100	234
4	10,317	79	100	234
5	11,460	79	100	234
6	9173	20	100	234
7	9173	50	100	234
8	9173	109	100	234
9	9173	138	100	234
10	9173	79	50	234
11	9173	79	75	234
12	9173	79	125	234
13	9173	79	150	234
14	9173	79	100	134
15	9173	79	100	184
16	9173	79	100	284
17	9173	79	100	334

. Each one of critical parameters varied within the specified range, while the remaining parameters were kept at the mean values. In each simulation scheme, the entire numerical simulation process was conducted using a ring (1.5 m) as the smallest circulation unit. The procedure involved the following steps.

• Initially, the shield shell zones of the shield machine were advanced by 1.5 m to simulate the initiation of a new shield tunnelling loop.
• Subsequently, the tunnel zones, segment zones, and grouting zones were removed to mimic the excavation process of shield construction.
• After the release of surrounding rock stresses, the earth pressure, the thrust, and the grouting pressure were applied to replicate the grouting process of shield construction.
• Following the grouting process, the grouting pressure was canceled, and material parameters were assigned to grouting and the segment zones to simulate the assembly process of shield construction.
• The parameters of the grouting zones were defined as a function of time, gradually transitioning from pre-solidification parameters to post-solidification parameters with each calculation step.
• The calculation was then allowed to converge, completing one cycle of excavation.
• Subsequently, the shield shell zones of the shield machine were advanced by another 1.5 m, initiating the next tunnelling cycle.

This cyclic tunnelling process continued until the model was fully constructed. The geotechnical zone’s parameters in the model were adopted from the geological survey report (refer to Table 2), while the material parameters for the tunnel and shield shell are presented in

Table 7. Material parameters of the tunnel and shield zones.

Zone Name	Density (N/m3)	Elastic Modulus (MPa)	Poisson’s Ratio
Segment rings	3250	3000	0.2
Shield shell	9500	200,000	0.3
Grouting layer (pre-solidification)	2100	240	0.3
Grouting layer (post-solidification)	2100	720	0.3

.

4.4. Model Validation and Analysis

Simulation scheme 3, where all critical construction parameters were given the mean values, was as per the initial choice numerical simulation. Subsequently, the simulation results were compared with the actual monitoring data. The regression coefficient (R²) and root mean square error (RMSE) were used as evaluation metrics to assess the accuracy of the simulation, which is calculated as follows:

$$R^2=1-\frac{{\sum }_{i=1}^N{\left(Y_i-Y_i^{\prime }\right)}^2}{{\sum }_{i=1}^N{\left(Y_i-\bar{Y}\right)}^2}$$

(10)

$$RMSE=\sqrt{\frac{1}{N}{\sum }_{i=1}^N{\left(Y_i-Y_i^{\prime }\right)}^2}$$

(11)

where $N$ denotes the number of data samples, $Y_i$ represents the observed surface settlement values, $Y_i^{\prime }$ represents the predicted surface settlement values, and $\overline{\stackrel{‾}{Y}}$ is the mean of the observed surface settlement values.

Figure 6 displays the contour map of surface settlement, while

Table 8. Validation results of the simulation compared to the actual.

Data Name	Actual Data	Simulation Data	R2	RMSE
ZDBC65	−2.42	−2.37	0.911	0.235
(Data ID 27)
ZDBC64	−1.68	−2.04
(Data ID 26)
ZDBC63	−2.09	−2.23
(Data ID 25)
ZDBC62	−0.21	−0.56
(Data ID 24)
ZDBC61	0.03	−0.36
(Data ID 23)
ZDBC60	−1.34	−1.09
(Data ID 22)
DBC10-01	−0.79	−0.92
DBC10-01	−1.86	−2.01
DBC10-01	−1.95	−2.02
DBC10-04	−0.88	−1.01

presents the assessment results of the simulation compared to the actual. In Table 8, the R² between the simulation data and the actual monitoring data is 0.911, and the RMSE is 0.235. This high consistency between the simulation results and the monitoring settlement data not only validates the reliability of numerical simulation but also confirms the effectiveness of grey relational analysis in capturing the critical construction parameters.

Further analysis of Figure 6 yields:

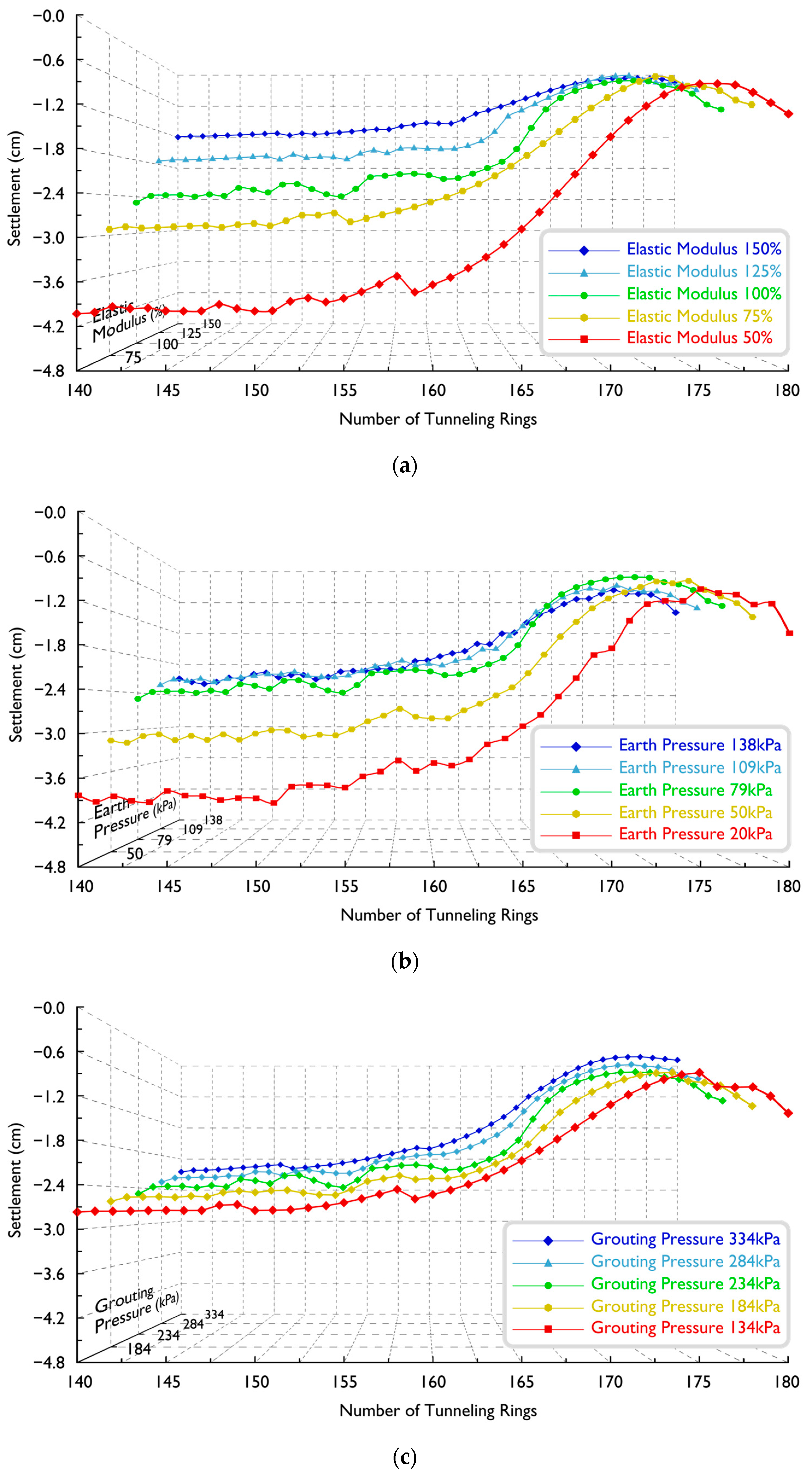
• Lateral settlement varies with strata zones, reaching up to 24.2 mm with a broad trough (approximately 20 m wide) in weak strata (140–170 rings). In more stable strata (170–180 rings), maximum surface settlement decreases to 2.1 mm with a narrower trough (about 12 m).
• Longitudinal settlement peaks at 24 mm in the 140–160 rings, with local minima at 140–145 and 152–155 rings. In stable strata, maximum surface settlement rapidly decreases from 24.2 mm to 10.3 mm.

4.5. Simulation of Influence Patterns

To further investigate the influence patterns of critical construction parameters on surface settlement, systematic numerical simulations were conducted following the simulation scheme described in Section 4.3. Figure 7 and Figure 8 present the results of maximum lateral and longitudinal settlements under different schemes of varying parameters.

From Figure 7 and Figure 8, it can be seen that:

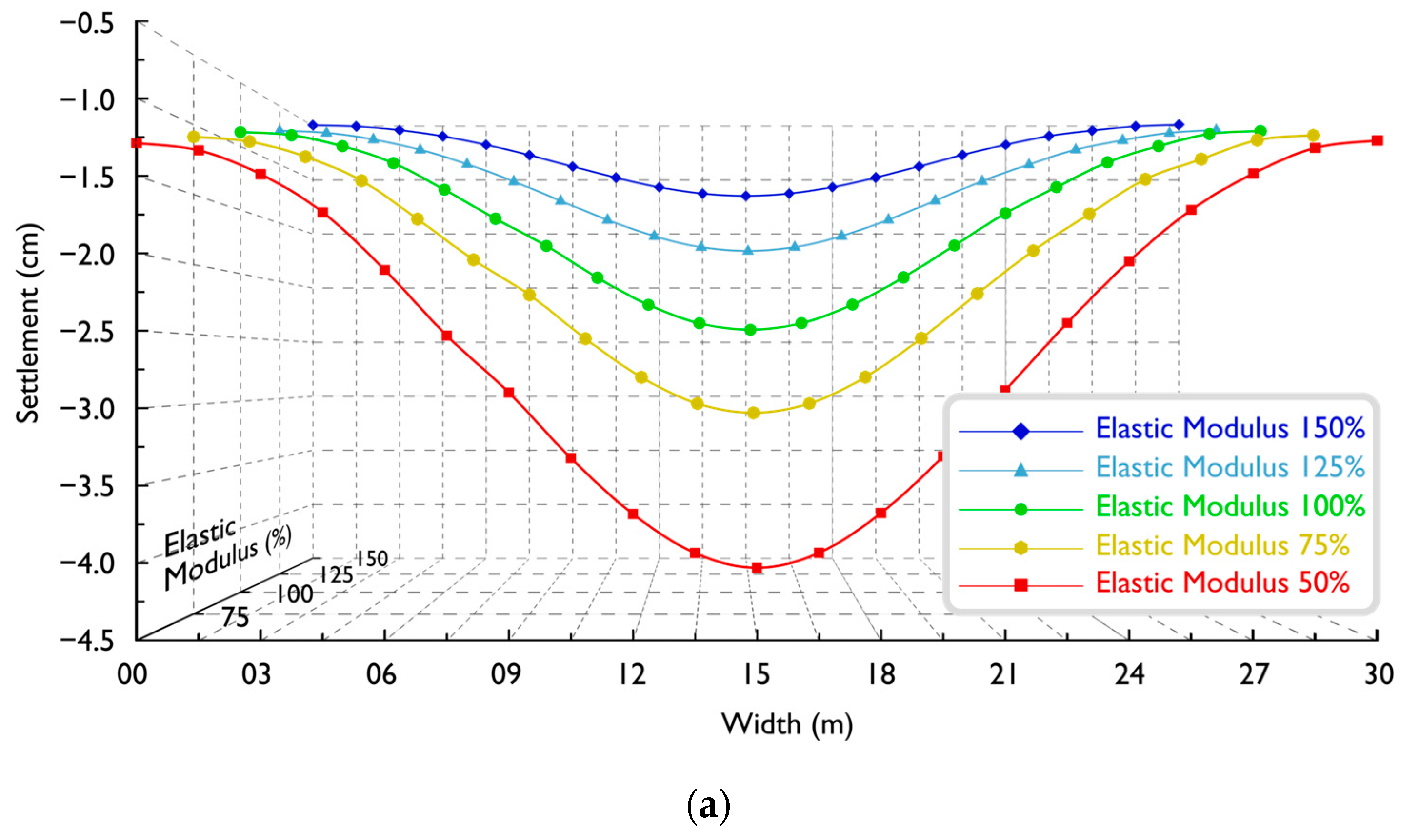
• Elastic modulus significantly impacts surface settlement, showing a nonlinear relationship (Figure 7a). Strata with smaller elastic modulus demonstrate increased sensitivity to shield tunnelling, resulting in larger settlement and wider troughs. In Figure 8a, reducing the elastic modulus from 150% to 50% leads to a 248% increase in maximum settlement (from 6.2 mm to 21.6 mm) in intervals with weak strata. Meanwhile, the impact on stable strata intervals is less than 50%. The actual settlement data across fractured zones (Table 3, Data ID 73–78) also coincide with this observation.
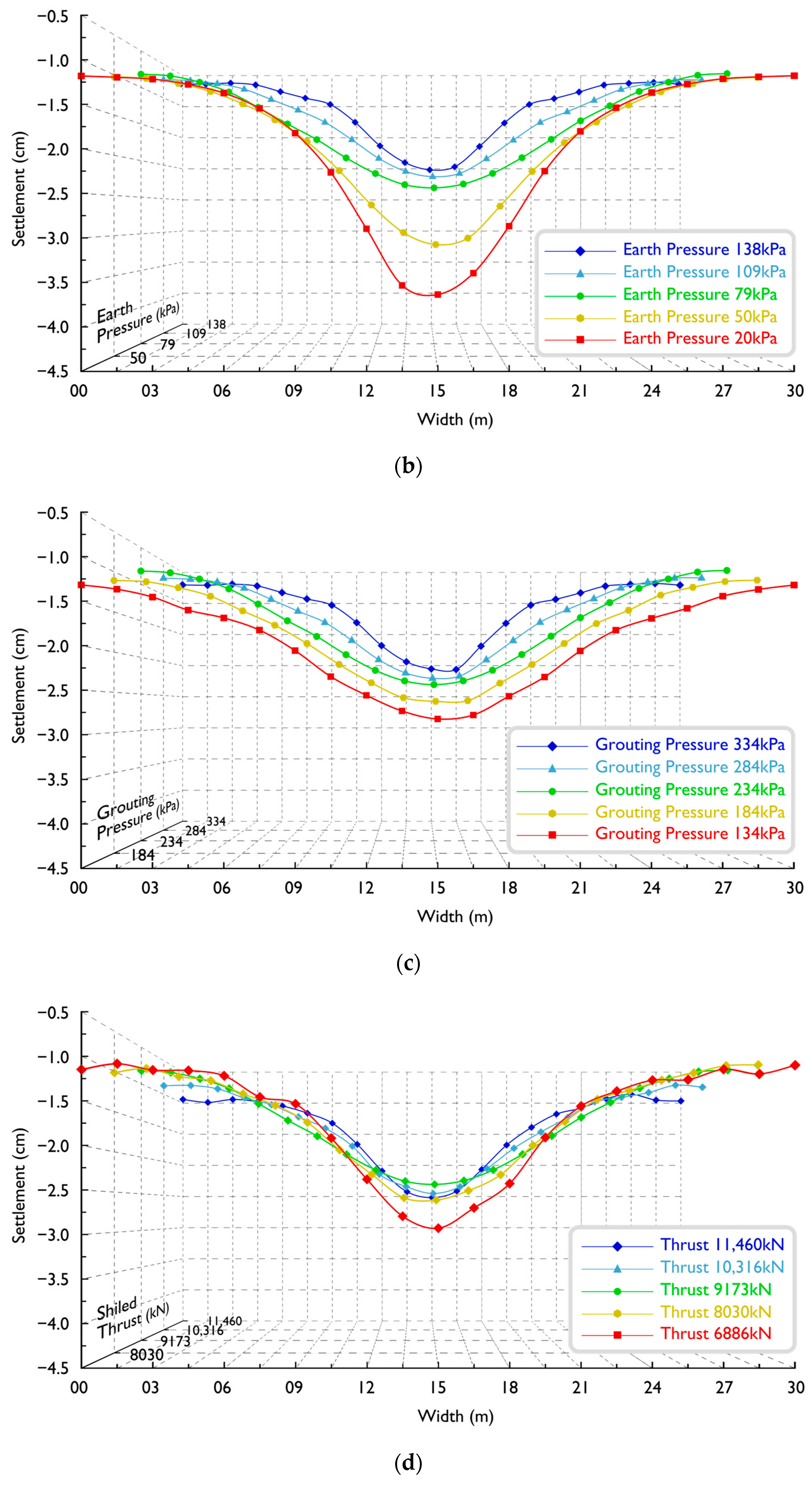
• Earth pressure’s influence on surface settlement parallels elastic modulus trends (Figure 7b and Figure 8b). In stable strata, it has a moderate impact, but in poorer geological conditions, reducing earth pressure from 138 kPa to 20 kPa increases maximum settlement from 8.6 mm to 18.3 mm, consistent with previous findings [41,42].
• As indicated in previous studies [18,36], the influence of grouting pressure on surface settlement is evident. Moreover, it greatly influences the settlement trough width in weak strata (Figure 7c). Increasing grouting pressure from 134 kPa to 334 kPa decreases the settlement trough from 10 m to 6 m. Somewhat differently from a previous study [40], no surface uplift occurs, likely due to reasonable grouting pressure within the soil’s bearing capacity.
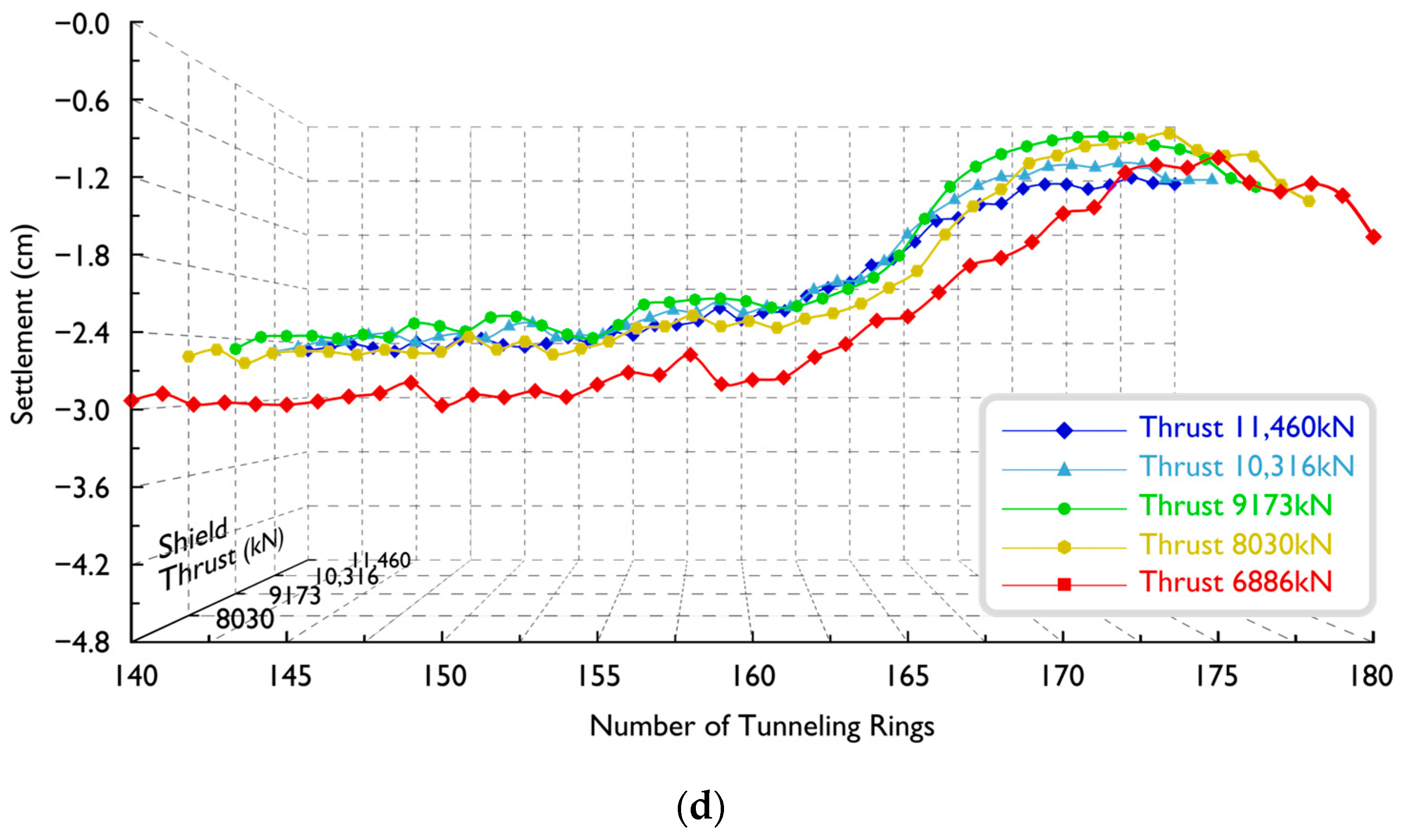
• Thrust magnitude directly affects the final surface settlement [33] (Figure 8d). Excessive thrust that is beyond the strata’s resistance during tunnelling leads to a significant surface settlement with surface uplift and subsequent sinking after shield tunnelling. Similarly, insufficient thrust results in incomplete compensation of strata displacement, leading to an increase in surface settlement.

5. Discussion

This study investigated the surface settlement in the construction section of Qingdao Metro Line 6 between Haigang Road Station and Chaoyang Road Station through a hybrid numerical approach comprised of grey relational analysis and numerical simulation. The research findings provide scientific evidence and engineering guidance for mitigating surface settlement during shield tunnel construction. Based on the results of grey relational analysis and numerical simulations, the following recommendations are proposed for the right-line tunnelling and future urban subway project.

As illustrated in Figure 7 and Figure 8, it is important to note that the elastic modulus of the stratum has a significant influence on the surface settlement. Given its inherent property as a critical stratum parameter, precise characterization of the elastic modulus can provide a direct link to the potential surface settlement and offer a scientific basis for developing effective mitigation strategies. Geotechnical investigations and predictive modelling before shield tunnelling are required. In addition, it is advisable to conduct geological predictions in advance and promptly adjust construction parameters based on real-time stratum conditions during tunnel evacuation. In regions with small elastic moduli, suitable reinforcement measures like pre-excavation grouting or enhanced ground stabilization are also recommended.

Similarly, the influence of earth pressure on the surface settlement should also be considered to mitigate the settlement fluctuations during shield tunnelling. Careful adjustments in earth pressure in sections with weak geological conditions are vital to prevent excessive surface settlement, and utilizing air pressure can enhance tunnelling efficiency in strata with stable geological conditions. In light of the notable influence of grouting pressure and thrust magnitude on surface settlement, it becomes crucial to determine suitable magnitude levels of these parameters through numerical modelling and field validation. According to the simulation results, maintaining the grouting pressure between 250 and 300 kPa and keeping the thrust force matched with the initial earth pressure can effectively mitigate surface settlement. Findings (Table 5) highlight that maintaining stable and reasonable tunnelling speed throughout the process can mitigate its impact on surface settlement. For the right-line tunnelling, maintaining a tunnelling speed similar to the left line can help control the surface settlement.

The research findings offer scientific insights and practical guidance in mitigating the surface settlement during shield tunnel construction. However, there are also some limitations and constraints in this study. One constraint lies in the assumption of the initial stress field, which considers only the self-weight of the surrounding rock and overlooked parameters like rock displacement and external influences such as tectonic shifts, geological history, and seismic activity. In addition, there are also limitations when employing the Mohr–Coulomb strength criterion for the deformation of rock and soil. It cannot fully capture the complexities of various geological conditions and mechanical phenomena, especially the deformation and fracture behavior of soft rocks. Furthermore, due to limitations in computational resources, simulation time, and data availability, consideration of influential parameters like the groundwater level shifts and soil permeability’s impact on surface settlement was omitted in this study. There are also certain insufficiencies in model dimensions created through numerical simulation.

To address these limitations, future study will concentrate on three main areas. Firstly, more accurate data of material strength will be acquired through model testing and field monitoring. Consequently, a more realistic initial in situ stress field model will be constructed based on these measuring data, thus enhancing simulation accuracy. Secondly, advanced mechanical models will be developed to comprehensively represent the variations in material strength, especially in describing the deformation and fracture behavior of soft rocks. Finally, efforts will be made to extend the numerical model size to better fit the engineering context. Additional factors will be taken into account, including groundwater levels, infiltration coefficients, fracture development, and the stratigraphic properties of other intervals. By incorporating diverse engineering scenarios and geological contexts, more precise engineering recommendations and effective control strategies for surface settlement will be provided.

6. Conclusions

This study investigated surface settlement in the urban subway construction section of Qingdao Metro Line 6 between Haigang Road Station and Chaoyang Road Station. By utilizing a hybrid numerical approach, the main conclusions are as follows.

• Earth pressure emerges as the most influential tunnelling parameter, while tunnelling speed has minimal impact. Grouting pressure has a greater effect on surface settlement than grouting volume, and strata elastic modulus significantly influences settlement.
• Numerical simulations reveal that strata with lower elastic moduli are more sensitive to shield tunnelling, resulting in larger settlement. Earth pressure and grouting pressure show similar trends, with pronounced effects in weak strata.
• For stable strata, it is feasible to consider a judicious increment in tunnelling speed and employ compressed air pressure for excavation. Keeping grouting pressure between 250 and 300 kPa and adjusting thrust with initial earth pressure can mitigate settlement.