The Biffis Canal Hydrodynamic System Performance Study of Drag-Dominant Tidal Turbine Using Moment Balancing Method
Abstract
1. Introduction
2. Methodology
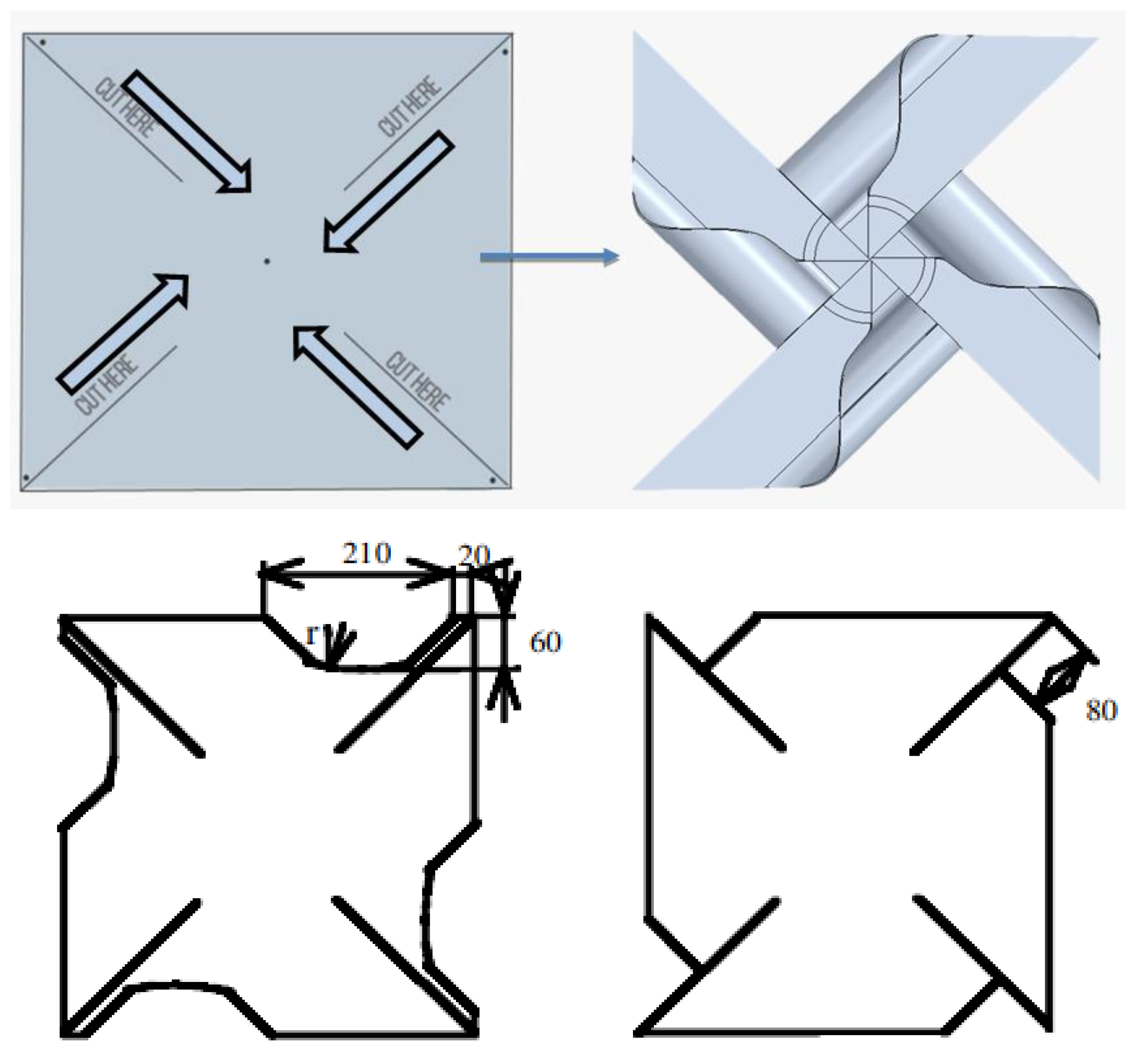
2.1. Numerical Model Development
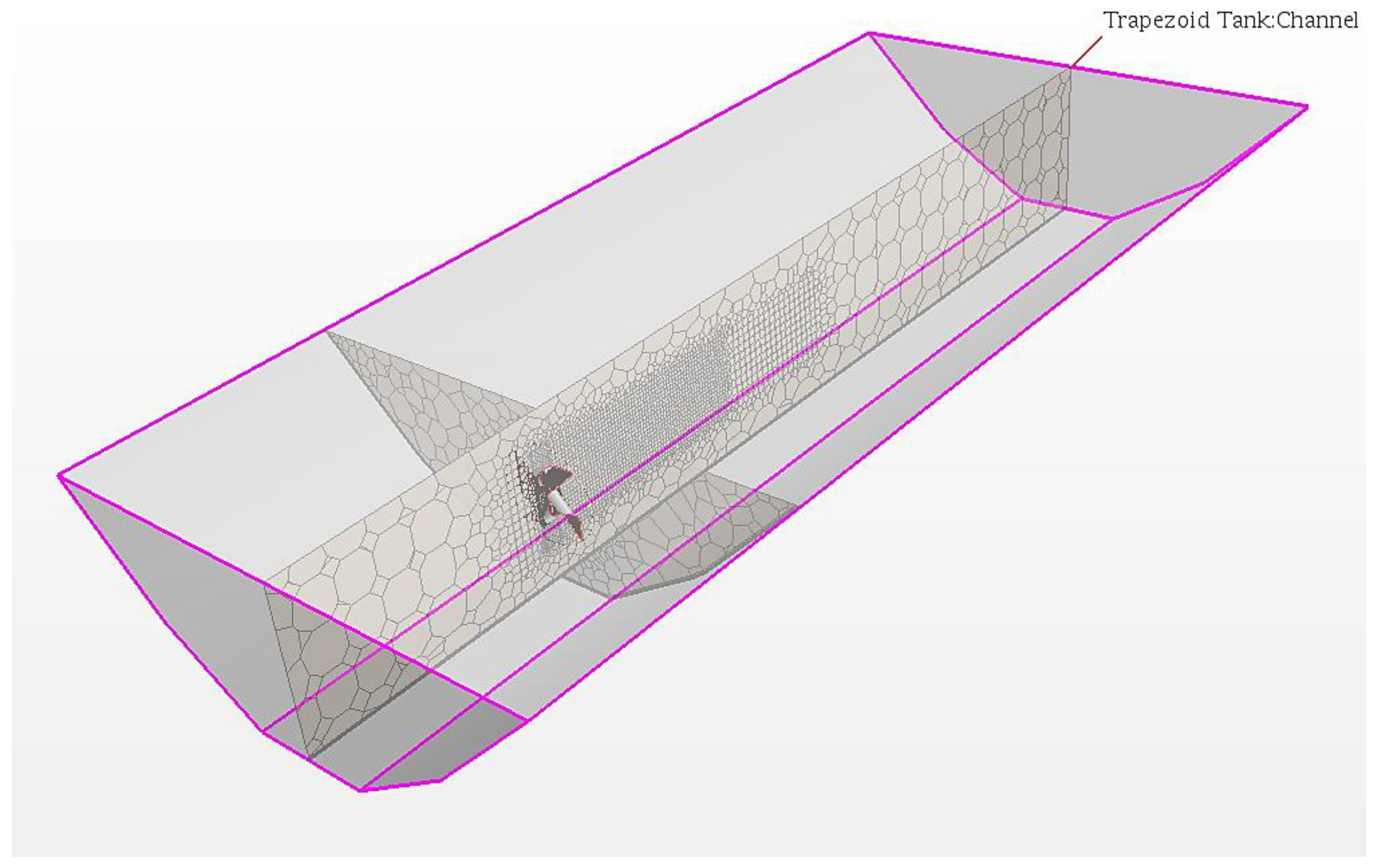
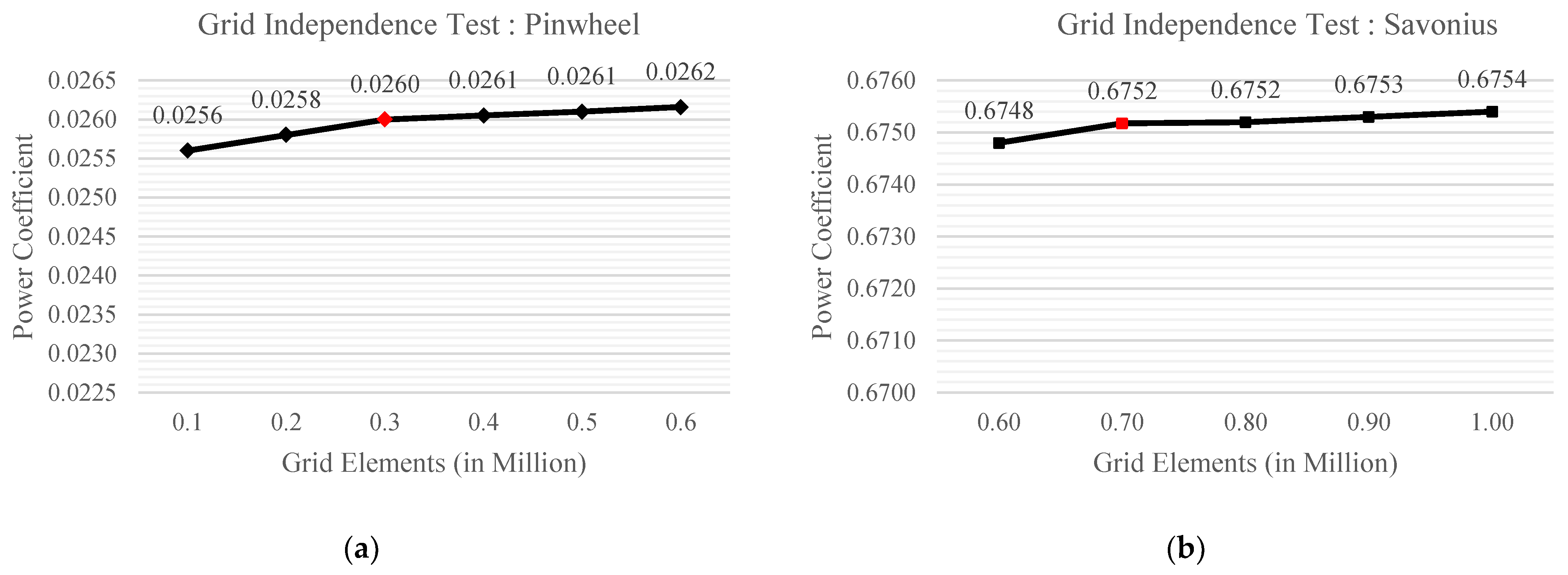
2.2. Mesh in CFD Simulation
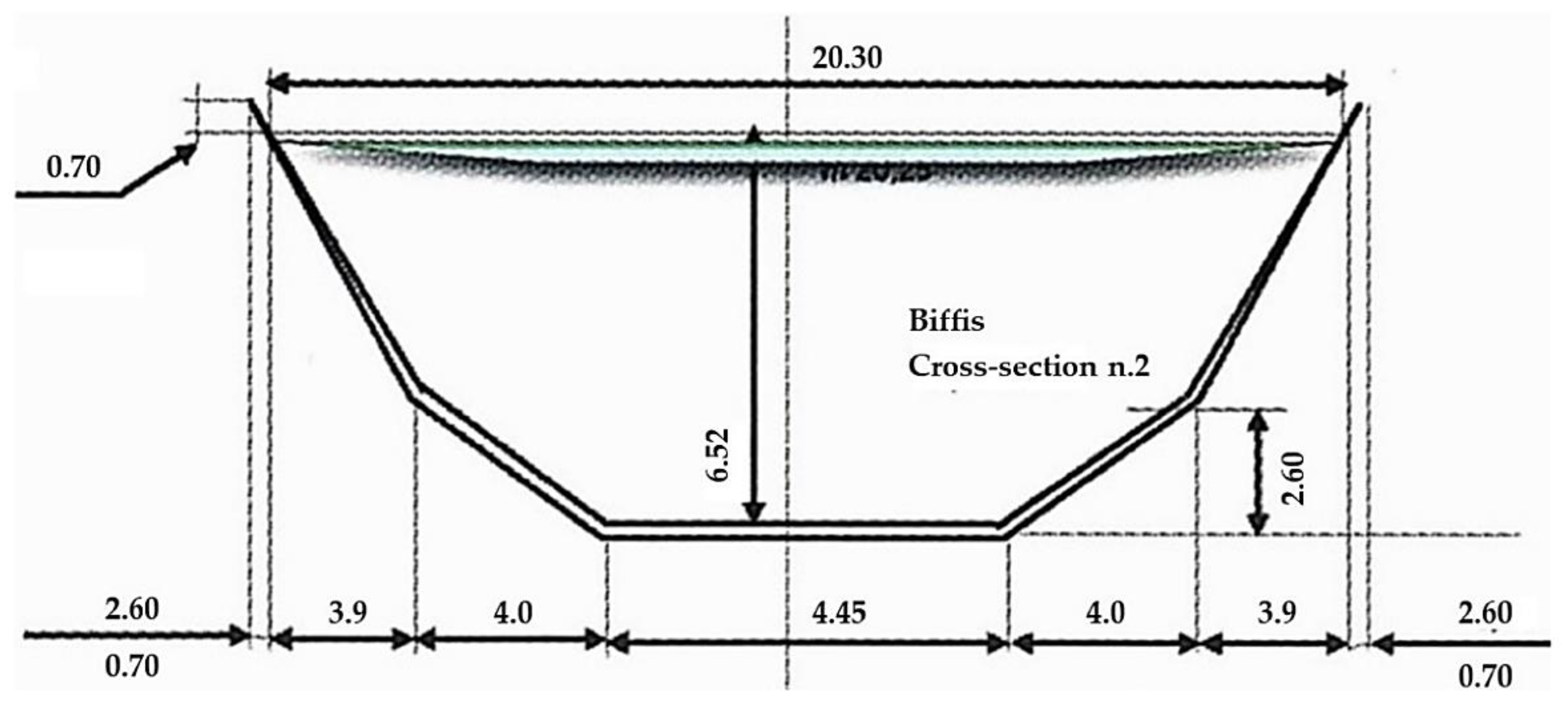
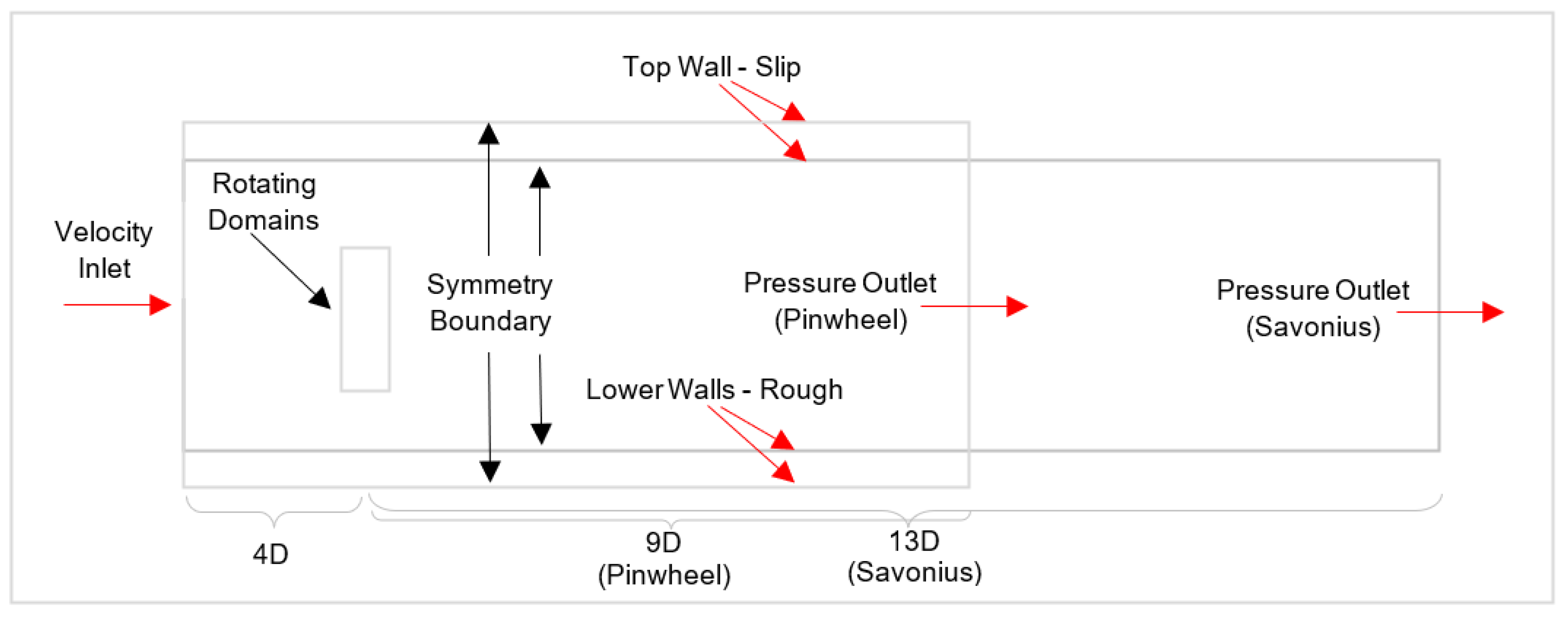
2.3. Domain and Boundary Conditions
- = Model coefficient, equal to 0.9 in RKE 2L;
- = Damping coefficient, equal to 1 in RKE 2L.
- = Turbulent kinetic energy generation coefficient;
- = Turbulence dissipation rate generation coefficient;
- = Specific dissipation rate to turbulent kinetic energy ratio;
- , , = Model constants, equal to ; 1.9 and 1.0, respectively, in RKE 2L;
- , = User-defined source terms;
- , = Turbulent Prandtl numbers, equal to 1.0 and 1.2, respectively, in RKE 2L.
2.4. Moment Analysis Method
3. Results and Discussion
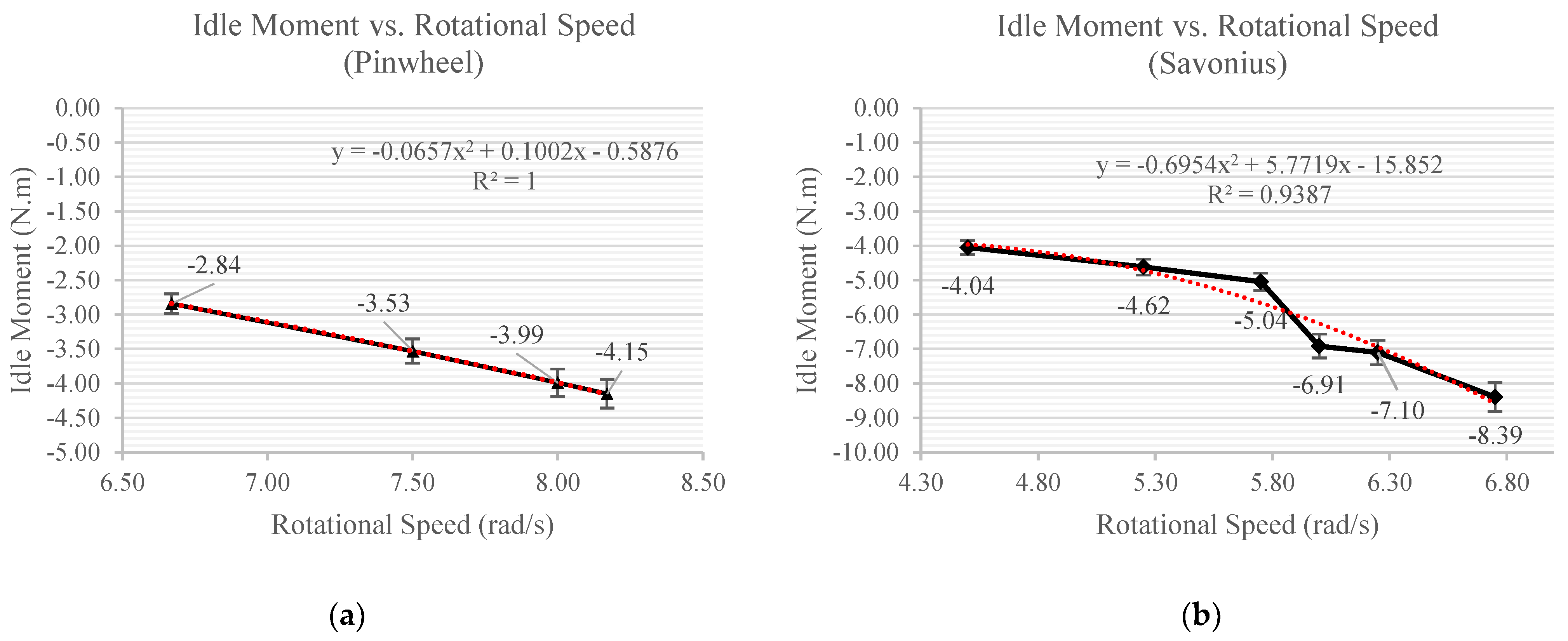
3.1. Idle and Thrust Moment Relationship Quadratic with and
3.2. Cp vs. TSR Curve
3.3. Wake Velocity Vector Plots
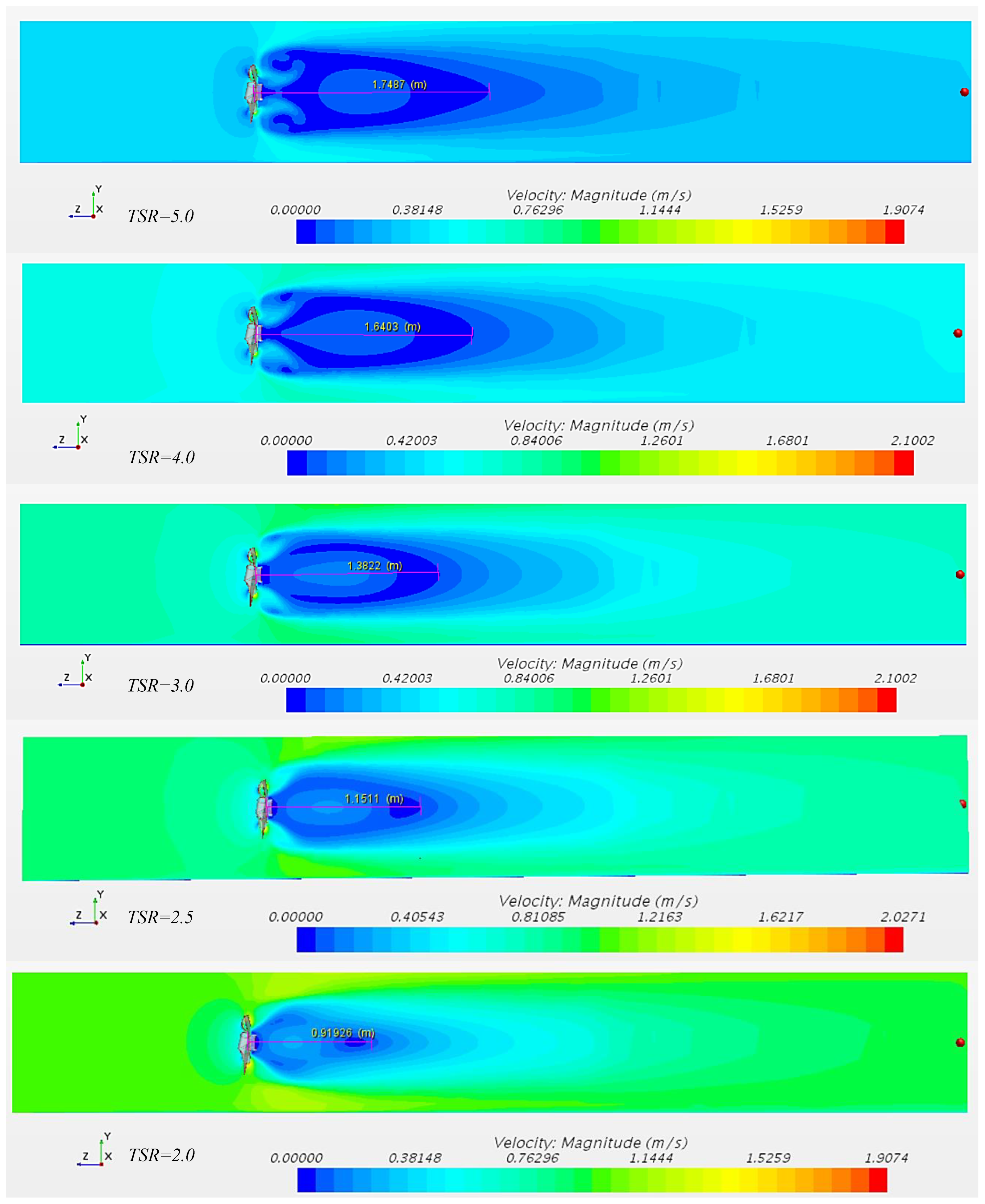
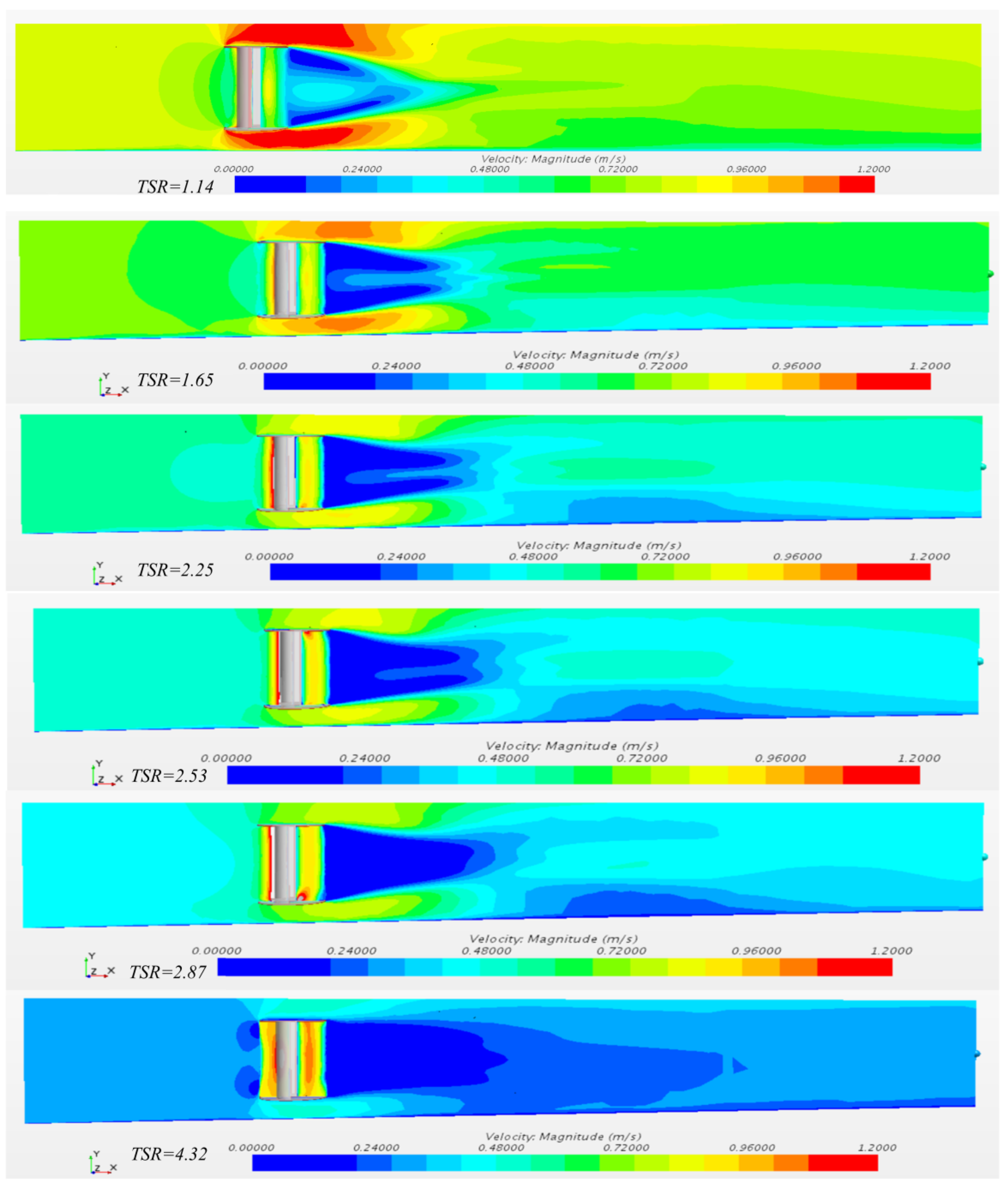
3.4. Flow Velocity and Wake Distribution
- For the wake downstream, the wake decay length (WDL) gradually shortens as the inflow velocity increases and the turbine’s working tip speed ratio (TSR) decreases. This indicates that the minimum distance required for the wake to be blended with the bypass flow reduces, leading to the gradual restoration of upstream velocity and a decrease in its impact on the downstream water potential.
- Regarding the vortex, when the inflow velocity is lower, and the TSR is higher, the downstream backflow significantly dissipates and transforms into forward flow. Two regions have small vortices between the turbine blades at the ninety-degree gap. With increasing inflow velocity and slowing down of rotation (reducing TSR), these two small vortices gradually disappear and merge into the main vortex.
- The fluid in the tail part of the Pinwheel turbine maintains static flow, creating a dead zone.
- (1)
- Due to its slender and tall shape, the turbine compresses the bypass flow in the upper and lower regions, especially at lower TSR and higher flow velocities. This feature becomes particularly pronounced at TSR = 1.14. In fact, the narrow and elongated bypass enhances the channel’s blockage efficiency.
- (2)
- Concerning the downstream wake, the presence of bypass flow and the friction with the seabed further weaken the near-bed flow velocity, making it challenging for the downstream flow to quickly return to a level close to the upstream velocity. This has long-term effects on the downstream environment, particularly on fish species with upstream migration habits. The length of the wake diffusion layer (WDL) increases with increasing TSR, consistent with the pattern observed in the Pinwheel turbine.
- (3)
- Regarding the vortex shape, two vortex streets originate from the upper and lower blades and extend downstream. At high TSR, when TSR > 2.87 (near-idle operation), the vortex streets merge to form a larger dead zone where quasi-steady flow concentrates at the ends of the blades.
3.5. Error and Uncertainty Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Angular momentum: kg∙m2/s | |
| Cross-section area of a rotor plate, m | |
| Inflow speed, m/s | |
| R | Rotor radius, m |
| Power Coefficient | |
| Thrust Coefficient | |
| R | Rotor radius, m |
| CFD | Computational Fluid Dynamics |
| EU | European Union |
| DDTTs | Drag-dominated tidal turbines |
| k-ε | Kappa-Epsilon Turbulence Model |
| k-ω | Kappa-Omega Turbulence Model |
| SST | Shear-Stress Transport Turbulence Model |
| VATs | Vertical Axis Turbines |
| DDTTs | Drag-Dominant Tidal Turbines |
| BEM | Blade Element Method |
| MRF | Moving Reference Frame |
| WDL | Wake Decay Length |
| GREEK LETTERS | |
| r | Density, kg/m3 |
| λ | Tip Speed Ratio |
| Turbine’s rotation speed, rad/s | |
| Dynamic Viscosity, Pa∙s | |
| SUBSCRIPTS | |
| opt | Optimal case |
| SUPERSCRIPTS | |
| * | Offset condition |
References
- IRENA. Innovation Outlook: Ocean Energy Technologies; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2020. [Google Scholar]
- European Commission. Tidal Flows Generate Huge Potential for Clean Electricity|Research and Innovation. Available online: https://ec.europa.eu/research-and-innovation/en/projects/success-stories/all/tidal-flows-generate-huge-potential-clean-electricity (accessed on 7 March 2023).
- Islam, M.R.; Bin Bashar, L.; Rafi, N.S. Design and Simulation of a Small Wind Turbine Blade with Qblade and Validation with MATLAB. In Proceedings of the 2019 4th International Conference on Electrical Information and Communication Technology (EICT), Khulna, Bangladesh, 20–22 December 2019. [Google Scholar] [CrossRef]
- Nemoto, Y.; Ushiyama, I. Experimental Study of a Pinwheel-Type Wind Turbine. Wind. Eng. 2003, 27, 227–236. [Google Scholar] [CrossRef]
- Islam, R.; Sultana Snikdha, Z.; Iffat, A.; Shahadat, M.M.Z. Optimum Blade Design of Pinwheel Type Horizontal Axis Wind Turbine for Low Wind Speed Areas. In Proceedings of the 2021 International Conference on Automation, Control and Mechatronics for Industry 4.0 (ACMI), Rajshahi, Bangladesh, 8–9 July 2021. [Google Scholar] [CrossRef]
- Wihadi, D.; Mardikus, S. Experimental Investigation of Blades Number of Savonius Water Turbine on Performance Characteristic. In Proceedings of the 5th International Conference on Industrial, Mechanical, Electrical, and Chemical Engineering 2019 (ICIMECE 2019), Surakarta, Indonesia, 17–18 September 2019. [Google Scholar] [CrossRef]
- Biswas, A.; Gupta, R.; Sharma, K.K. Experimental Investigation of Overlap and Blockage Effects on Three-Bucket Savonius Rotors. Wind. Eng. 2007, 31, 363–368. [Google Scholar] [CrossRef]
- Patel, V.; Patel, R. Energy Extraction Using Modified Savonius Rotor from Free-Flowing Water. Mater. Today Proc. 2021, 45, 5190–5196. [Google Scholar] [CrossRef]
- Chen, H.; Zhou, D.; Kan, K.; Xu, H.; Zheng, Y.; Binama, M.; Xu, Z.; Feng, J. Experimental investigation of a model bulb turbine under steady state and load rejection process. Renew. Energy 2021, 169, 254–265. [Google Scholar] [CrossRef]
- Kan, K.; Xu, Z.; Chen, H.; Xu, H.; Zheng, Y.; Zhou, D.; Muhirwa, A.; Maxime, B. Energy loss mechanisms of transition from pump mode to turbine mode of an axial-flow pump under bidirectional conditions. Energy 2022, 257, 124630. [Google Scholar] [CrossRef]
- Kan, K.; Binama, M.; Chen, H.; Zheng, Y.; Zhou, D.; Su, W.; Muhirwa, A. Pump as turbine cavitation performance for both conventional and reverse operating modes: A review. Renew. Sustain. Energy Rev. 2022, 168, 112786. [Google Scholar] [CrossRef]
- Yilmaz, A.E.; Meyers, J. Numerical Simulations of Flow Fields through Conventionally Controlled Wind Turbines & Wind Farms. J. Phys. Conf. Ser. 2014, 524, 012158. [Google Scholar] [CrossRef]
- Churchfield, M.J.; Schreck, S.J.; Martinez, L.A.; Meneveau, C.; Spalart, P.R. An Advanced Actuator Line Method for Wind Energy Applications and Beyond. In Proceedings of the 35th Wind Energy Symposium, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Whelan, J.I.; Graham, J.M.R.; Peiró, J. A Free-Surface and Blockage Correction for Tidal Turbines. J. Fluid Mech. 2009, 624, 281–291. [Google Scholar] [CrossRef]
- Muchala, S.; Willden, R.H.J. Impact of Tidal Turbine Support Structures on Realizable Turbine Farm Power. Renew. Energy 2017, 114, 588–599. [Google Scholar] [CrossRef]
- Koh, W.X.M.; Ng, E.Y.K. Effects of Reynolds Number and Different Tip Loss Models on the Accuracy of BEM Applied to Tidal Turbines as Compared to Experiments. Ocean. Eng. 2016, 111, 104–115. [Google Scholar] [CrossRef]
- Pucci, M.; Di Garbo, C.; Bellafiore, D.; Zanforlin, S.; Umgiesser, G. A BEM-Based Model of a Horizontal Axis Tidal Turbine in the 3D Shallow Water Code SHYFEM. J. Mar. Sci. Eng. 2022, 10, 1864. [Google Scholar] [CrossRef]
- Zhang, Y.; Mittal, S.; Ng, E.Y.-K. CFD Validation of Moment Balancing Method on Drag-Dominant Tidal Turbines (DDTTs). Processes 2023, 11, 1895. [Google Scholar] [CrossRef]
- Cacciali, L.; Battisti, L.; Dell’Anna, S. Multi-Array Design for Hydrokinetic Turbines in Hydropower Canals. Energies 2023, 16, 2279. [Google Scholar] [CrossRef]
- HE-Powergreen. HE-PowerGreen|Pure Hydro Power. Available online: https://www.he-powergreen.it/ (accessed on 28 July 2023).
- Malini, C. Il Canale Biffis. Serie Acque e Bonifiche; Sometti Editoriale: Mantova, Italy, 2017; ISBN 8874956762. [Google Scholar]
- Abu Bakar, N.A.; Mohd Shamsuddin, M.S.; Kamaruddin, N.M. Experimental Study of a Hybrid Turbine for Hydrokinetic Applications on Small Rivers in Malaysia. J. Adv. Res. Appl. Sci. Eng. Technol. 2022, 28, 318–324. [Google Scholar] [CrossRef]
- Aliferis, A.D.; Jessen, M.S.; Bracchi, T.; Hearst, R.J. Performance and Wake of a Savonius Vertical-Axis Wind Turbine under Different Incoming Conditions. Wind. Energy 2019, 22, 1260–1273. [Google Scholar] [CrossRef]
- Kang, C.; Opare, W.; Pan, C.; Zou, Z. Upstream Flow Control for the Savonius Rotor under Various Operation Conditions. Energies 2018, 11, 1482. [Google Scholar] [CrossRef]
- Yuwono, T.; Sakti, G.; Nur Aulia, F.; Chandra Wijaya, A. Improving the Performance of Savonius Wind Turbine by Installation of a Circular Cylinder Upstream of Returning Turbine Blade. Alex. Eng. J. 2020, 59, 4923–4932. [Google Scholar] [CrossRef]
- Zhang, B.; Song, B.; Mao, Z.; Tian, W. A Novel Wake Energy Reuse Method to Optimize the Layout for Savonius-Type Vertical Axis Wind Turbines. Energy 2017, 121, 341–355. [Google Scholar] [CrossRef]
- Kumar, A.; Saini, G. Flow Field and Performance Study of Savonius Water Turbine. Mater. Today Proc. 2021, 46, 5219–5222. [Google Scholar] [CrossRef]
- Salazar Marin, E.A.; Rodríguez, A.F. Design, Assembly and Experimental Tests of a Savonius Type Wind Turbine. Sci. Tech. 2019, 24, 397–407. [Google Scholar] [CrossRef]
- Crooks, J.M.; Hewlin, R.L.; Williams, W.B. Computational Design Analysis of a Hydrokinetic Horizontal Parallel Stream Direct Drive Counter-Rotating Darrieus Turbine System: A Phase One Design Analysis Study. Energies 2022, 15, 8942. [Google Scholar] [CrossRef]
- Adams, T.; Grant, C.; Watson, H. A Simple Algorithm to Relate Measured Surface Roughness to Equivalent Sand-Grain Roughness. Int. J. Mech. Eng. Mechatron. 2012, 1, 66–71. [Google Scholar] [CrossRef]
- Process Engineer’s Tools. Surface Roughness of Common Materials—Table of Reference Values. Powderprocess.net. Available online: https://www.powderprocess.net/Tools_html/Data_Diagrams/Pipe_Roughness.html (accessed on 28 July 2023).
- Hara, Y.; Hara, K.; Hayashi, T. Moment of Inertia Dependence of Vertical Axis Wind Turbines in Pulsating Winds. Int. J. Rotating Mach. 2012, 2012, 910940. [Google Scholar] [CrossRef][Green Version]
- Cebeci, T.; Bradshaw, P. Momentum Transfer in Boundary Layers; Hemisphere Publishing: London, UK; McGraw-Hill: New York, NY, USA, 1977; pp. 176–180. [Google Scholar]
- Menon, S.H.; Mathew, J.; Jayaprakash, J. Derivation of Navier—Stokes Equation in Rotational Frame for Engineering Flow Analysis. Int. J. Thermofluids 2021, 11, 100096. [Google Scholar] [CrossRef]
- Yang, B.; Lawn, C. Fluid Dynamic Performance of a Vertical Axis Turbine for Tidal Currents. Renew. Energy 2011, 36, 3355–3366. [Google Scholar] [CrossRef]



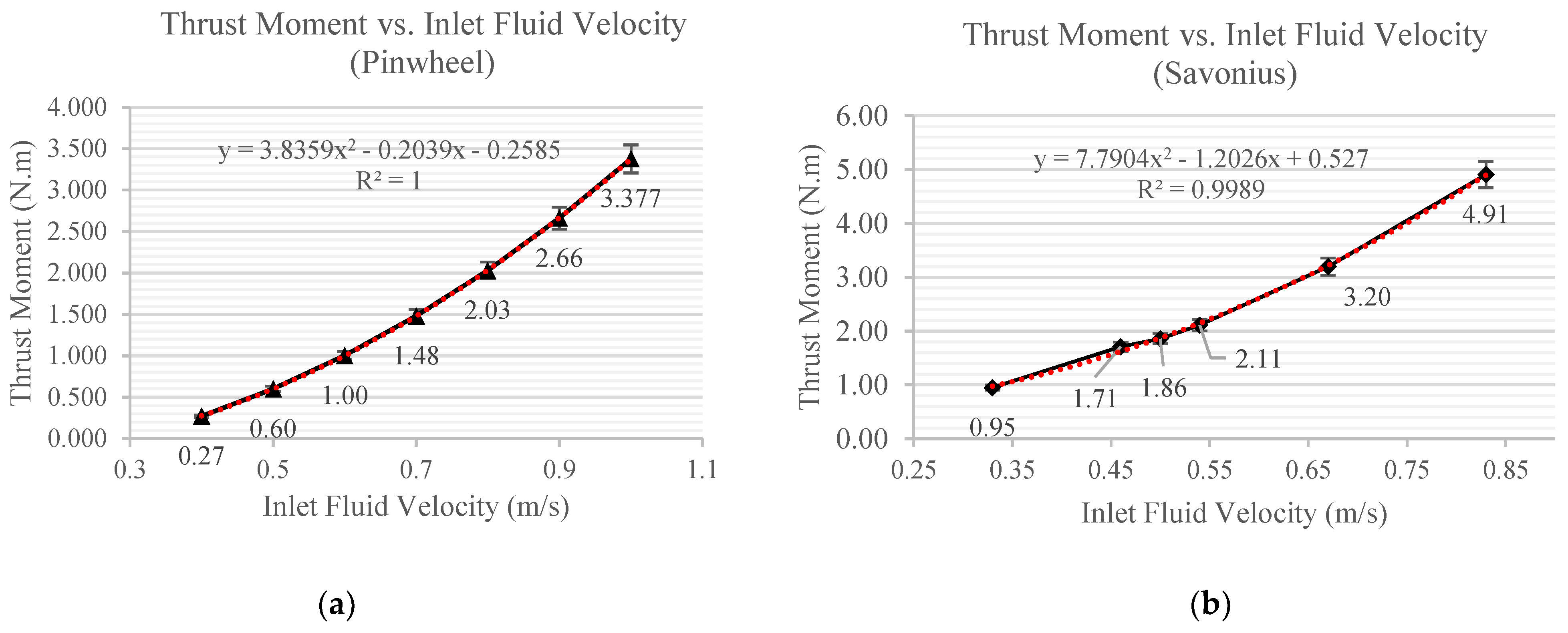

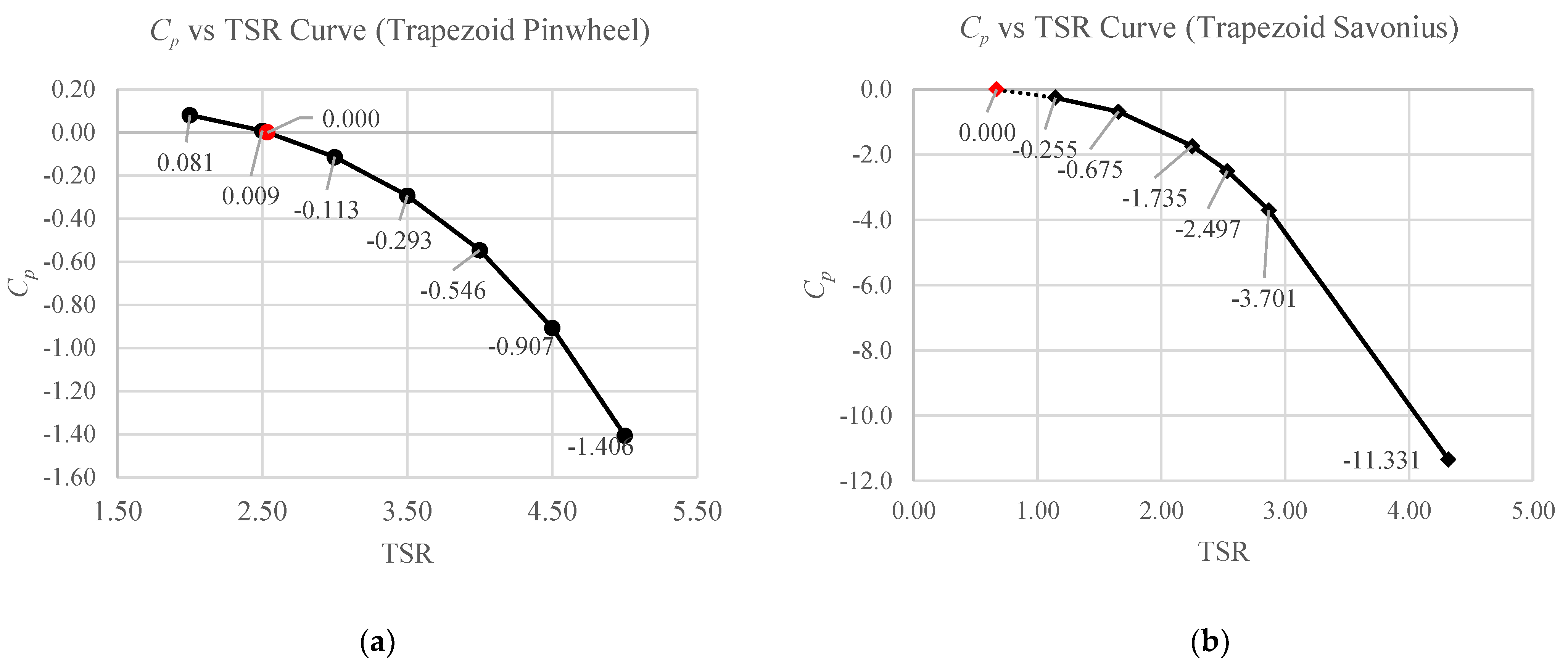
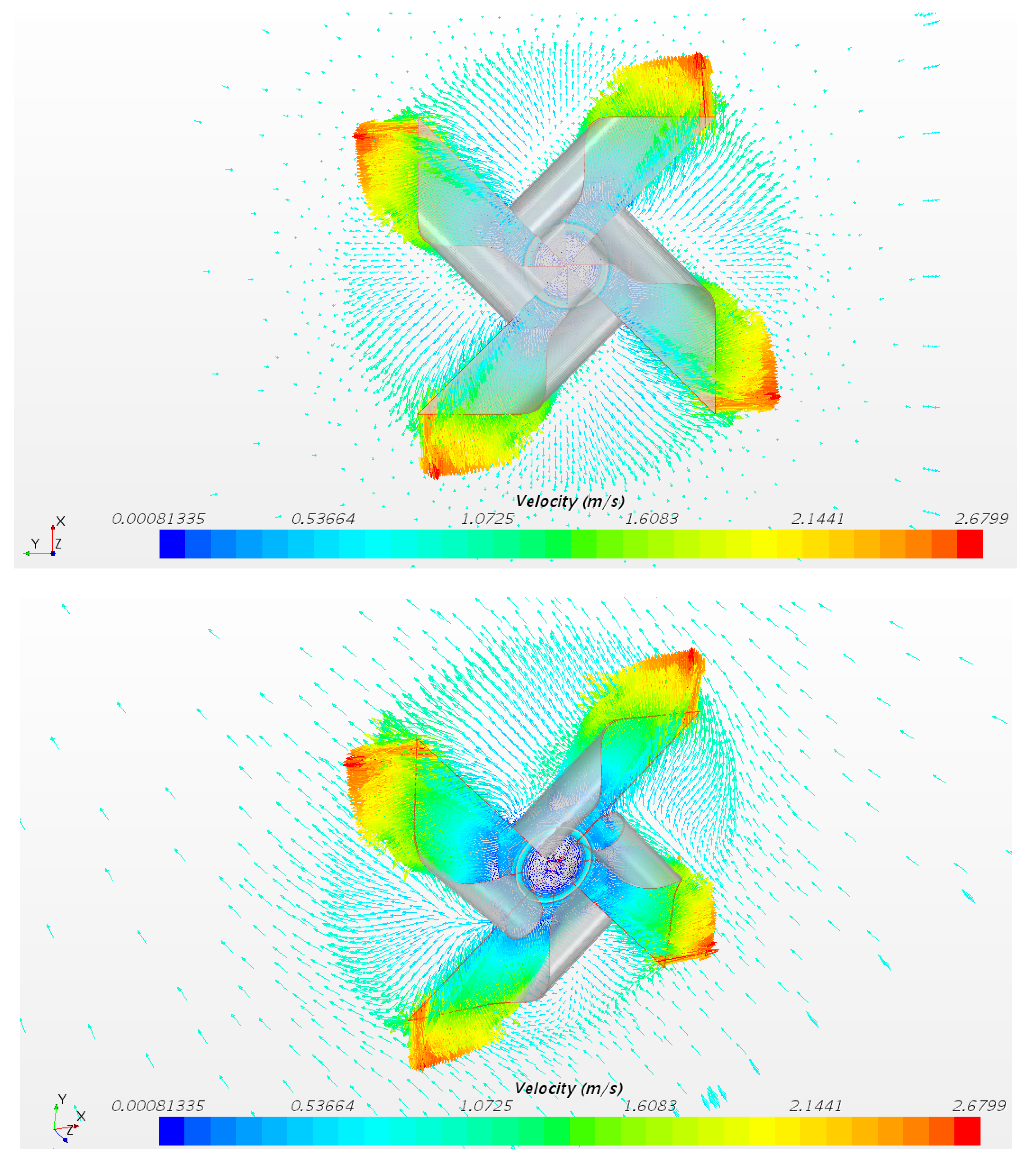

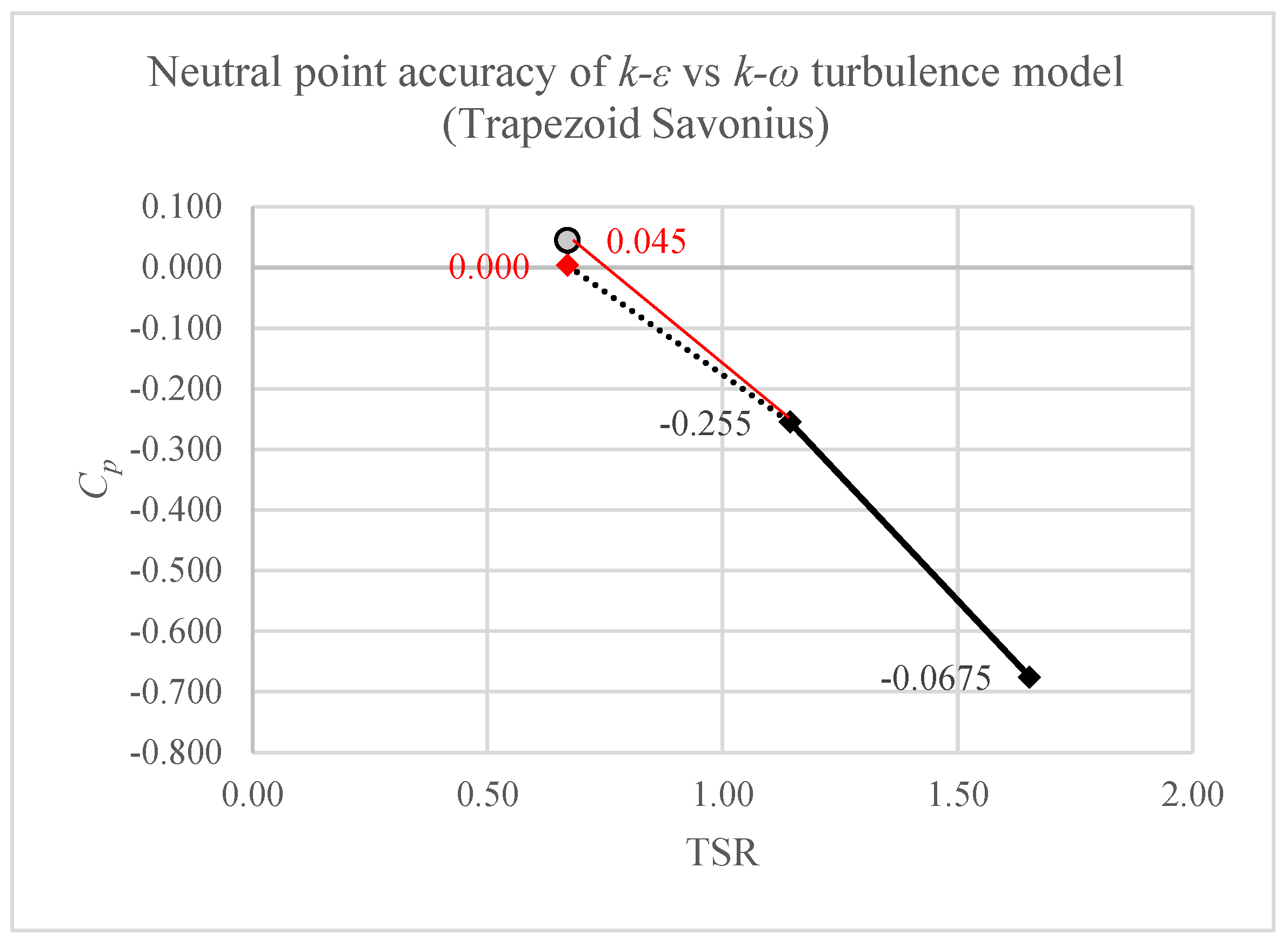
| Parameter | Pinwheel | Savonius |
|---|---|---|
| Blade Radius [m] | 0.30 | 0.211 |
| Rotor Diameter [m] | 0.60 | 0.422 |
| Rotor Height [m] | 0.60 | 0.670 |
| End-Plate Diameter [m] | - | 0.235 |
| Blade Area [m2] | 0.283 | |
| Channel Width [m] | 3.370 | |
| Channel Height [m] | 2.137 | |
| Channel Area [m2] | 2.358 (3.370 × 2.137) | |
| Aspect Ratio | 1.85 | |
| Blockage Ratio | 0.12 | |
| Target Set | Initial Set | Conditions in CFD |
|---|---|---|
| Static turbine, varying inlet flow velocity | ||
| Rotating turbine, fixed inlet flow velocity | ||
| Rotating turbine, varying inlet flow velocity |
| TSR | Rotational Speed ω (rad/s) | ||||
|---|---|---|---|---|---|
| 6.67 | 7.50 | 8.00 | 8.17 | ||
| Inlet speed U1 (m/s) | 0.4 | 5.00 | 5.63 | 6.00 | 6.13 |
| 0.5 | 4.00 | 4.50 | 4.80 | 4.90 | |
| 0.6 | 3.34 | 3.75 | 4.00 | 4.09 | |
| 0.7 | 2.86 | 3.21 | 3.43 | 3.50 | |
| 0.8 | 2.50 | 2.81 | 3.00 | 3.06 | |
| 0.9 | 2.22 | 2.50 | 2.67 | 2.72 | |
| 1.0 | 2.00 | 2.25 | 2.40 | 2.45 | |
| TSR | Rotational Speed ω (rad/s) | ||||||
|---|---|---|---|---|---|---|---|
| 4.50 | 5.25 | 5.75 | 6.00 | 6.25 | 6.75 | ||
| Inlet speed U1 (m/s) | 0.33 | 2.88 | 3.36 | 3.68 | 3.84 | 4.00 | 4.32 |
| 0.46 | 2.06 | 2.41 | 2.64 | 2.75 | 2.87 | 3.10 | |
| 0.50 | 1.90 | 2.22 | 2.43 | 2.53 | 2.64 | 2.85 | |
| 0.54 | 1.76 | 2.05 | 2.25 | 2.34 | 2.44 | 2.64 | |
| 0.67 | 1.42 | 1.65 | 1.81 | 1.89 | 1.97 | 2.13 | |
| 0.83 | 1.14 | 1.33 | 1.46 | 1.53 | 1.59 | 1.72 | |
| Model | Reference Experiment Result | Simulation Result | Error Percentage |
|---|---|---|---|
| Pinwheel (Optimal TSR) [4] | 2.0 For traditional Pinwheel | 2.537 | |
| 3.5 For optimal aerodynamic shape Pinwheel | 2.537 | ||
| Savonius (Optimal TSR) [27] | 0.7 | 0.671 |
| Pinwheel | U1 | TSR | U2 | Puseful | Premoved | η | WDL (in m) |
| 1.00 | 2.0 | 0.924 | 255.46 | 1208.48 | 21.14% | 0.92 | |
| 0.90 | 2.5 | 0.822 | 208.87 | 880.98 | 23.71% | 1.15 | |
| 0.80 | 3.0 | 0.724 | 160.46 | 618.74 | 25.93% | 1.38 | |
| 0.70 | 3.5 | 0.628 | 115.23 | 414.51 | 27.80% | 1.57 | |
| 0.60 | 4.0 | 0.535 | 75.93 | 261.03 | 29.09% | 1.64 | |
| 0.50 | 4.5 | 0.453 | 45.93 | 151.06 | 25.58% | 1.70 | |
| 0.40 | 5.0 | 0.372 | 24.67 | 77.34 | 19.62% | 1.75 | |
| Savonius | U1 | TSR | U2 | Puseful | Premoved | η | WDL (in m) |
| 0.83 | 1.14 | 0.787 | 108.86 | 698.51 | 15.59% | 0.98 | |
| 0.67 | 1.65 | 0.636 | 47.93 | 358.60 | 13.37% | 1.07 | |
| 0.54 | 2.25 | 0.506 | 35.58 | 192.41 | 18.49% | 1.26 | |
| 0.50 | 2.53 | 0.460 | 33.32 | 151.06 | 22.06% | 1.22 | |
| 0.46 | 2.87 | 0.417 | 30.19 | 117.63 | 25.67% | 1.34 | |
| 0.33 | 4.32 | 0.304 | 9.35 | 43.43 | 21.52% | 1.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Ng, E.Y.K.; Mittal, S. The Biffis Canal Hydrodynamic System Performance Study of Drag-Dominant Tidal Turbine Using Moment Balancing Method. Sustainability 2023, 15, 14187. https://doi.org/10.3390/su151914187
Zhang Y, Ng EYK, Mittal S. The Biffis Canal Hydrodynamic System Performance Study of Drag-Dominant Tidal Turbine Using Moment Balancing Method. Sustainability. 2023; 15(19):14187. https://doi.org/10.3390/su151914187
Chicago/Turabian StyleZhang, Yixiao, Eddie Yin Kwee Ng, and Shivansh Mittal. 2023. "The Biffis Canal Hydrodynamic System Performance Study of Drag-Dominant Tidal Turbine Using Moment Balancing Method" Sustainability 15, no. 19: 14187. https://doi.org/10.3390/su151914187
APA StyleZhang, Y., Ng, E. Y. K., & Mittal, S. (2023). The Biffis Canal Hydrodynamic System Performance Study of Drag-Dominant Tidal Turbine Using Moment Balancing Method. Sustainability, 15(19), 14187. https://doi.org/10.3390/su151914187









