Research on Energy Management Method of Fuel Cell/Supercapacitor Hybrid Trams Based on Optimal Hydrogen Consumption
Abstract
1. Introduction
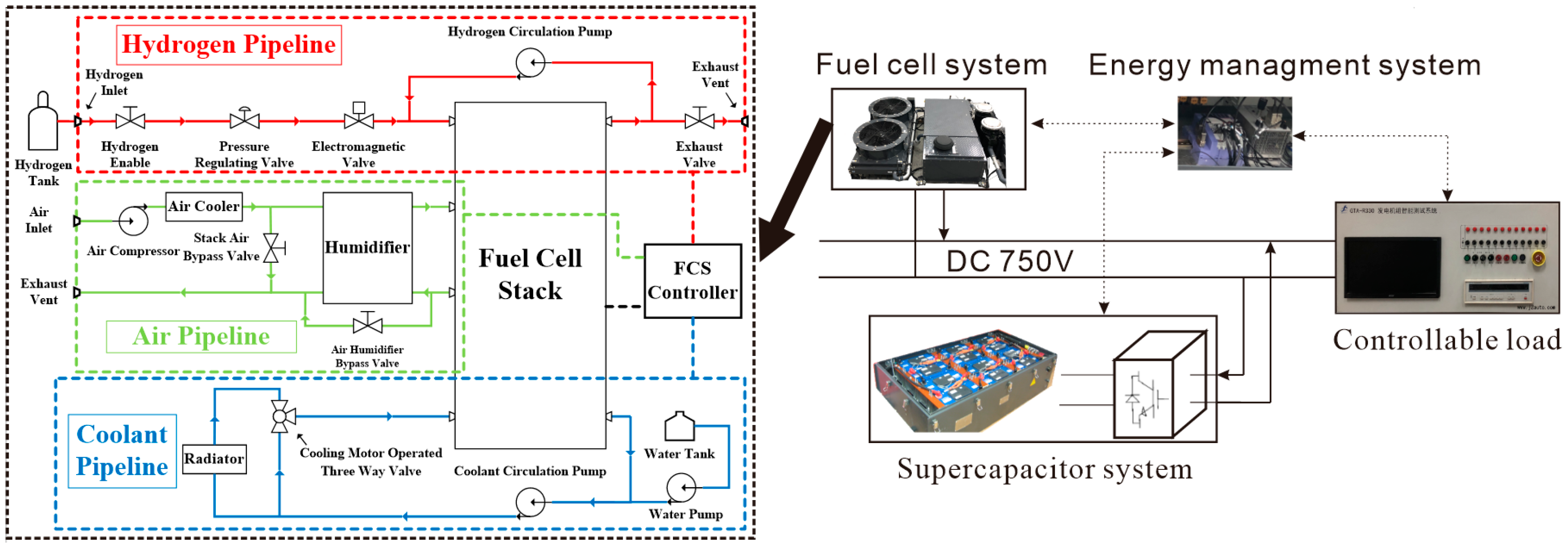
2. The Model and Topology of the Hybrid System
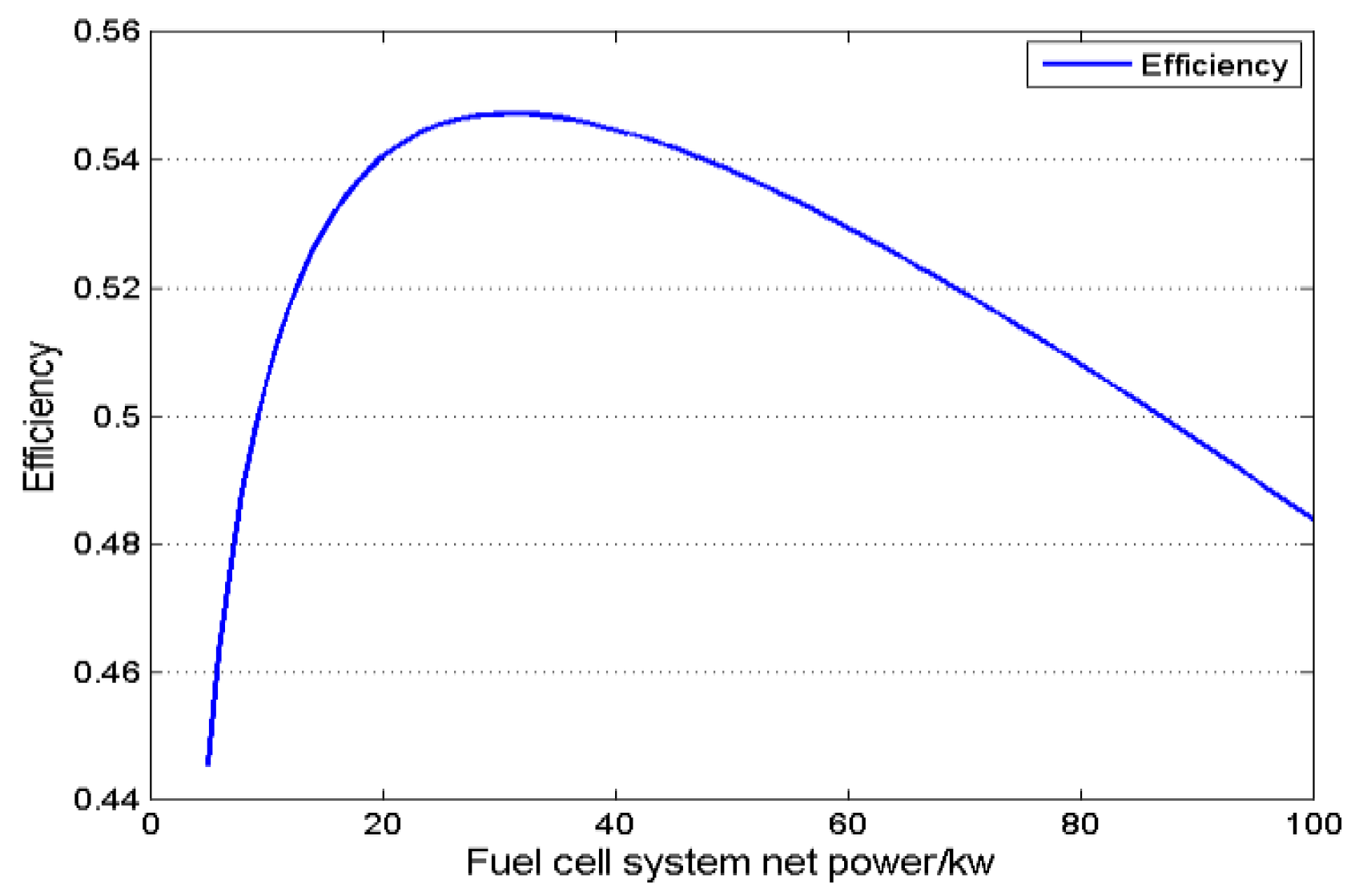
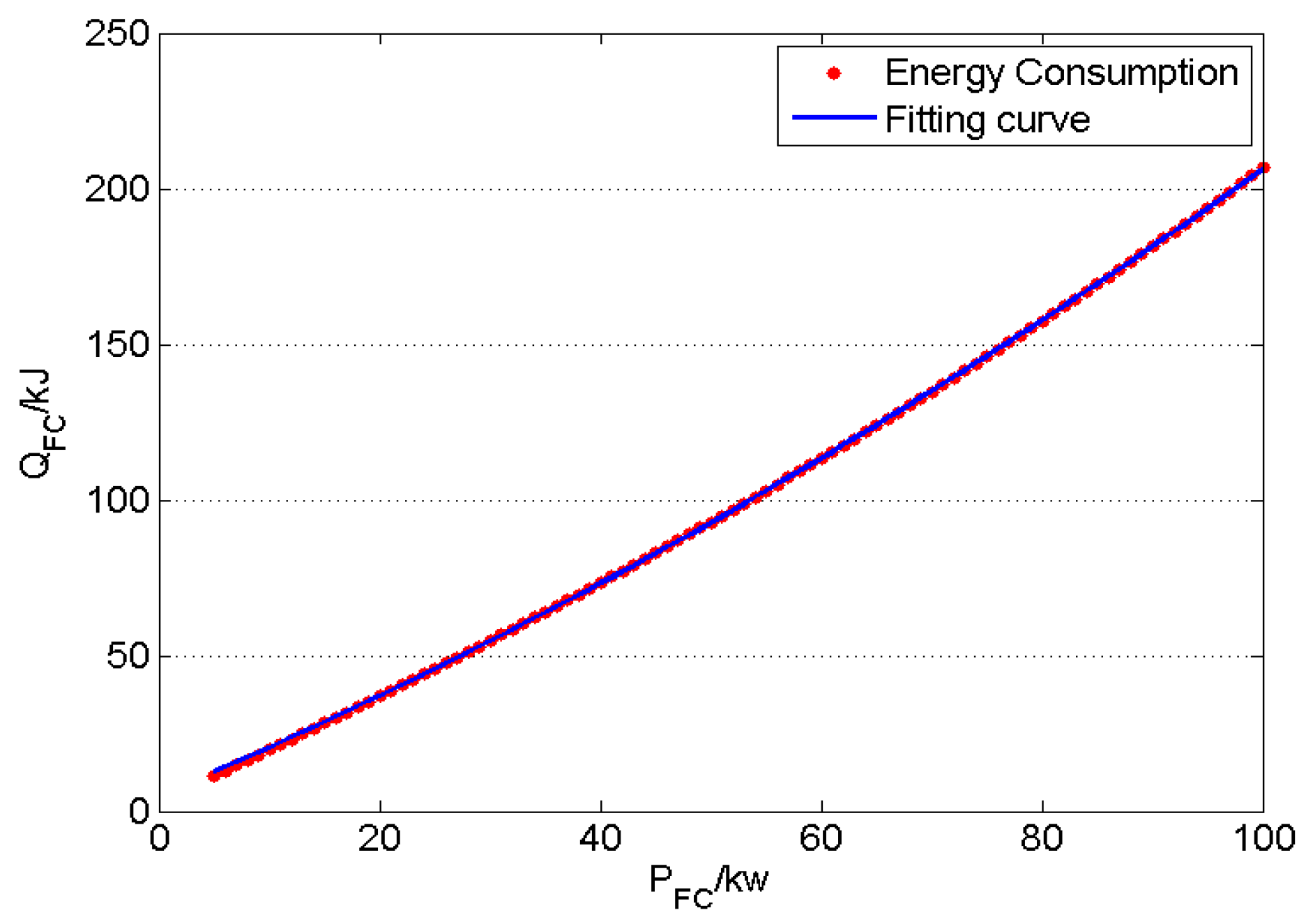
2.1. Fuel Cell System Efficiency Model
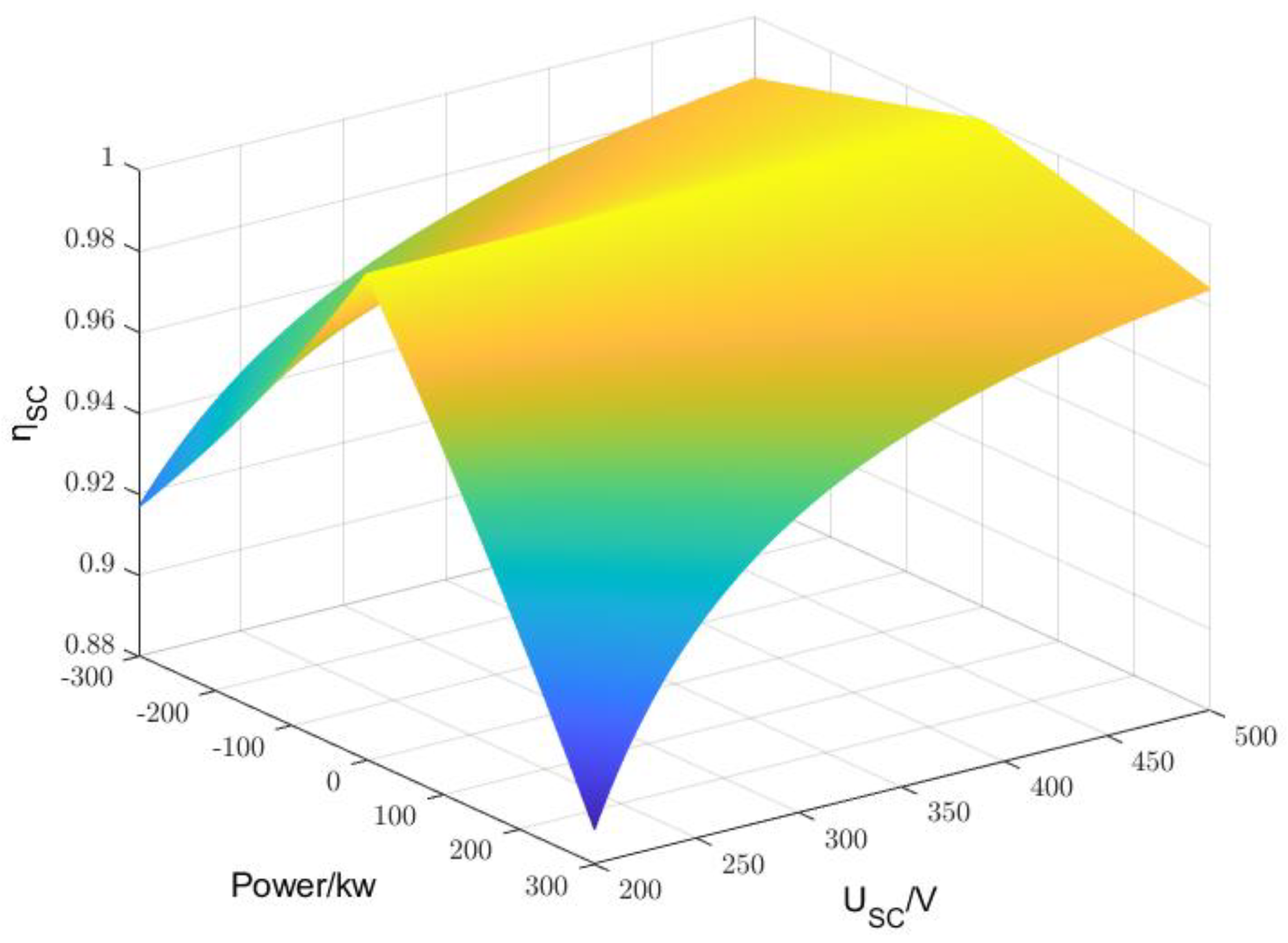
2.2. Supercapacitor System Efficiency Model
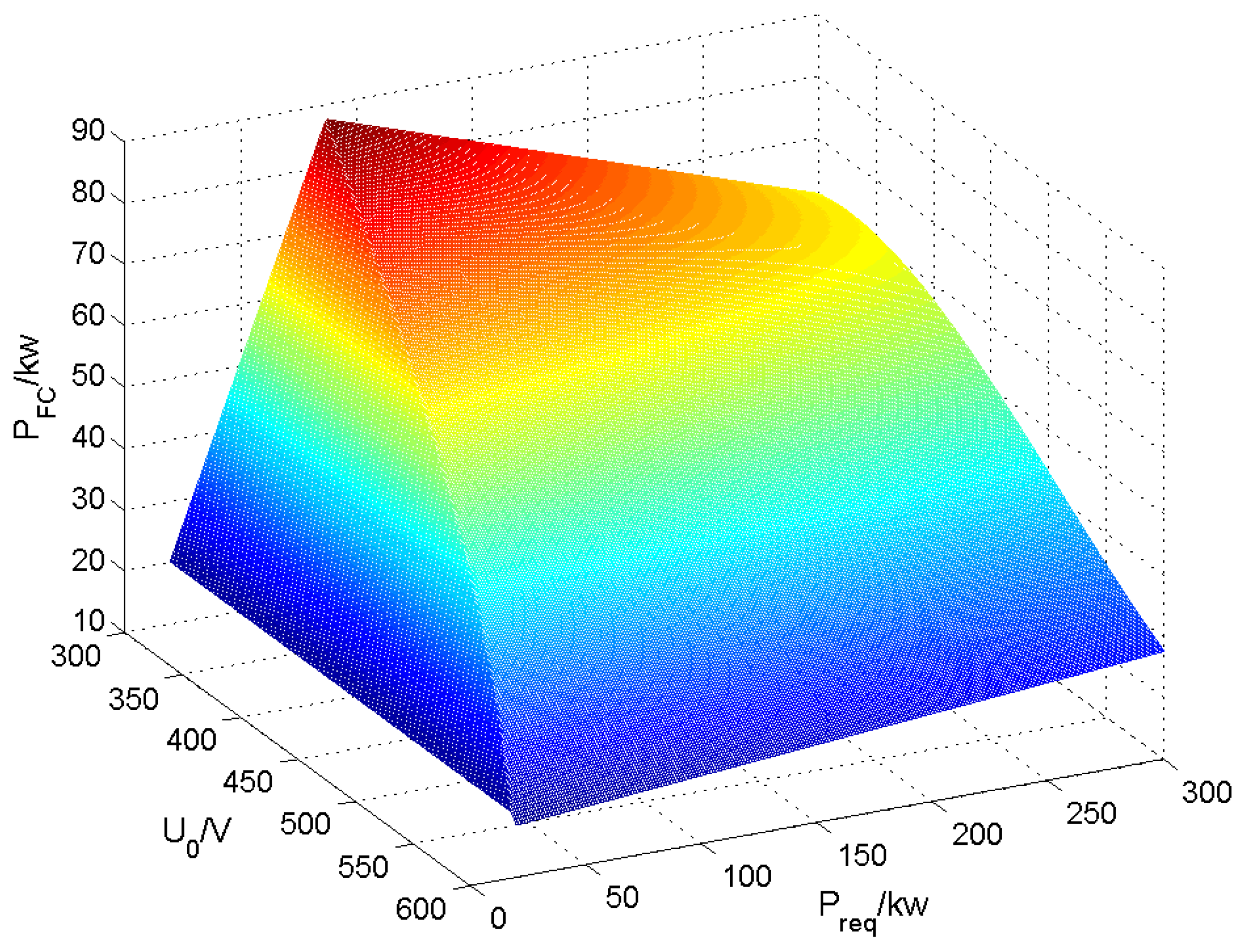
3. Optimal Hydrogen Consumption Method
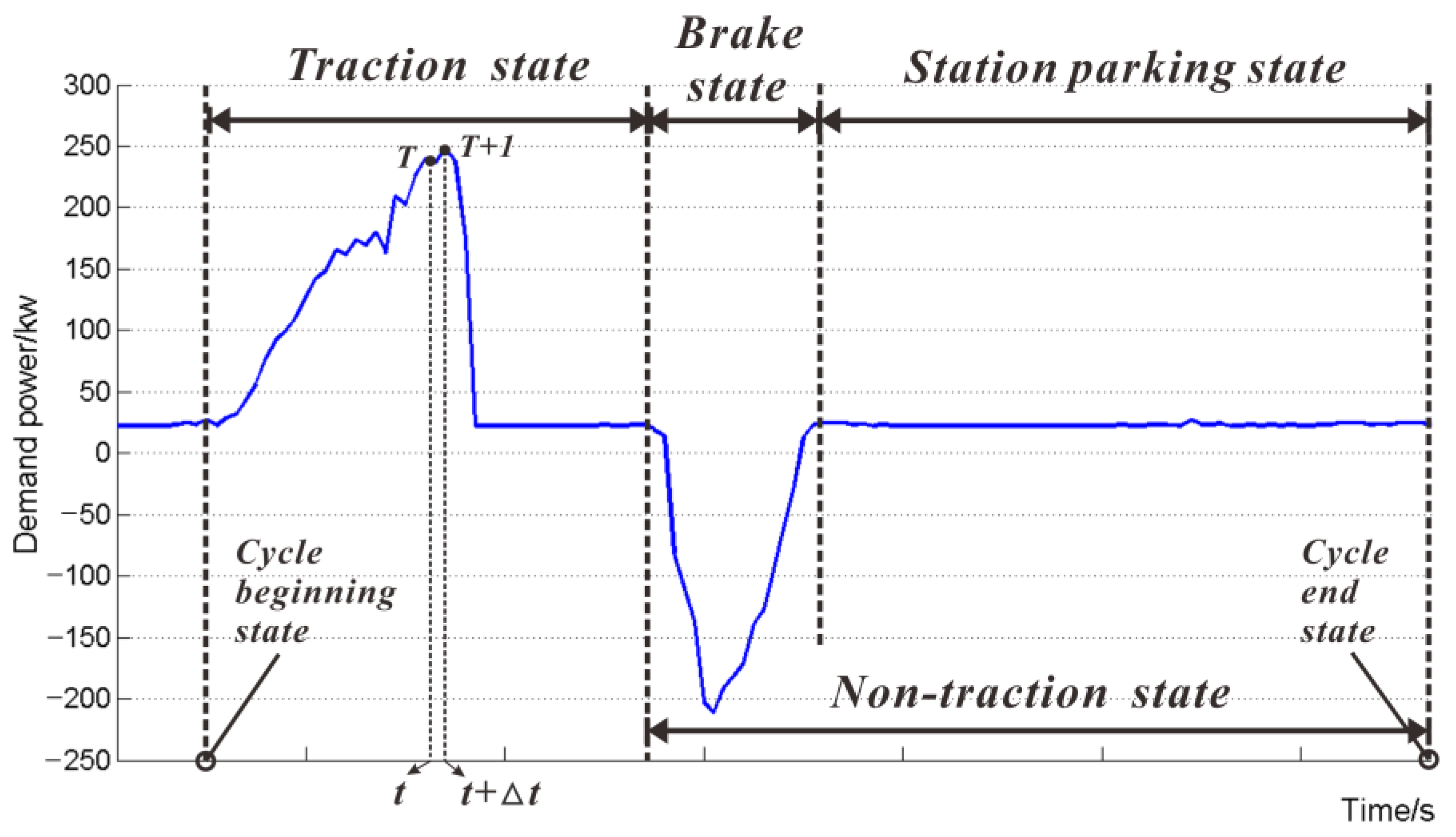
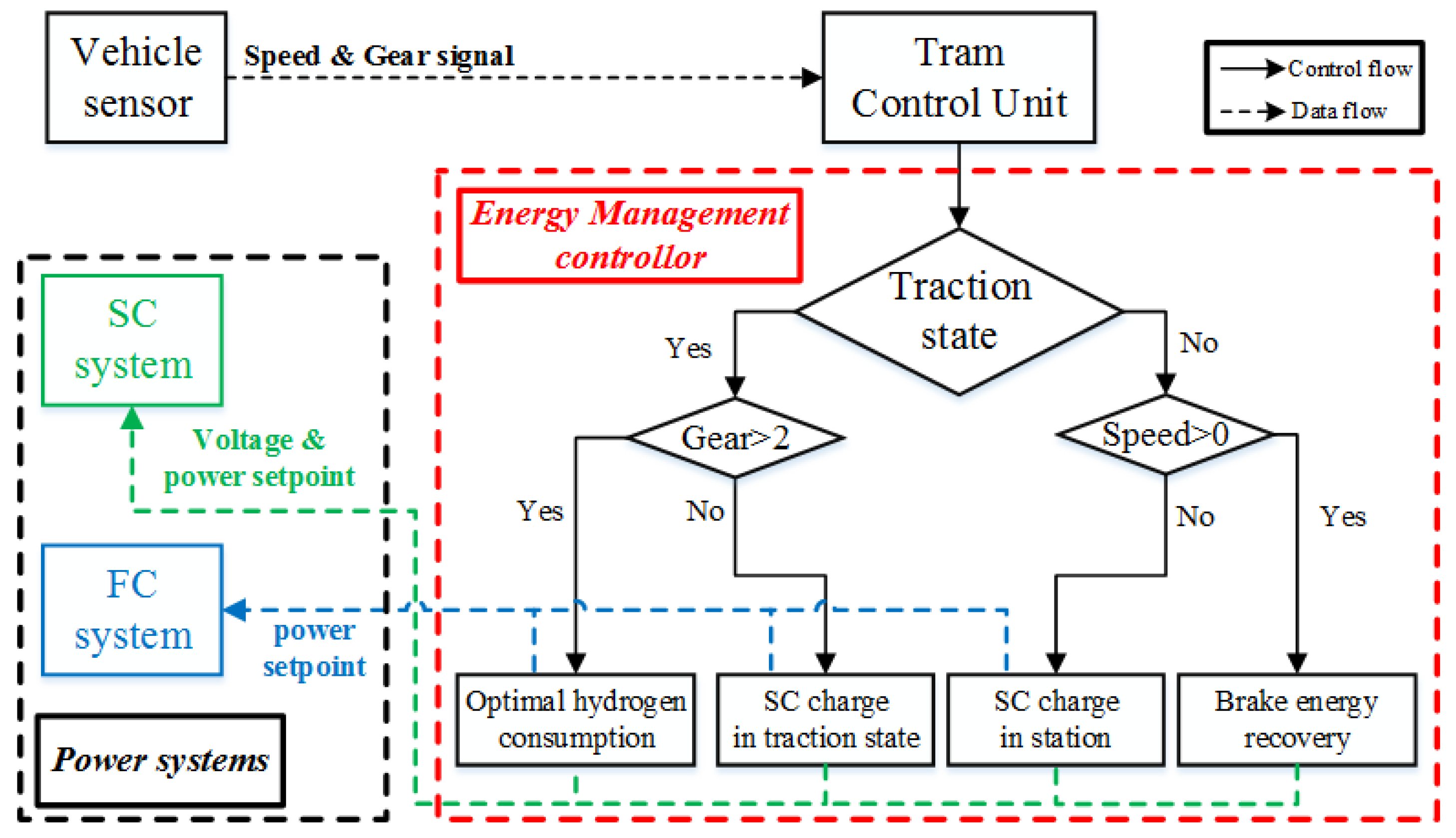
3.1. Non-Traction State
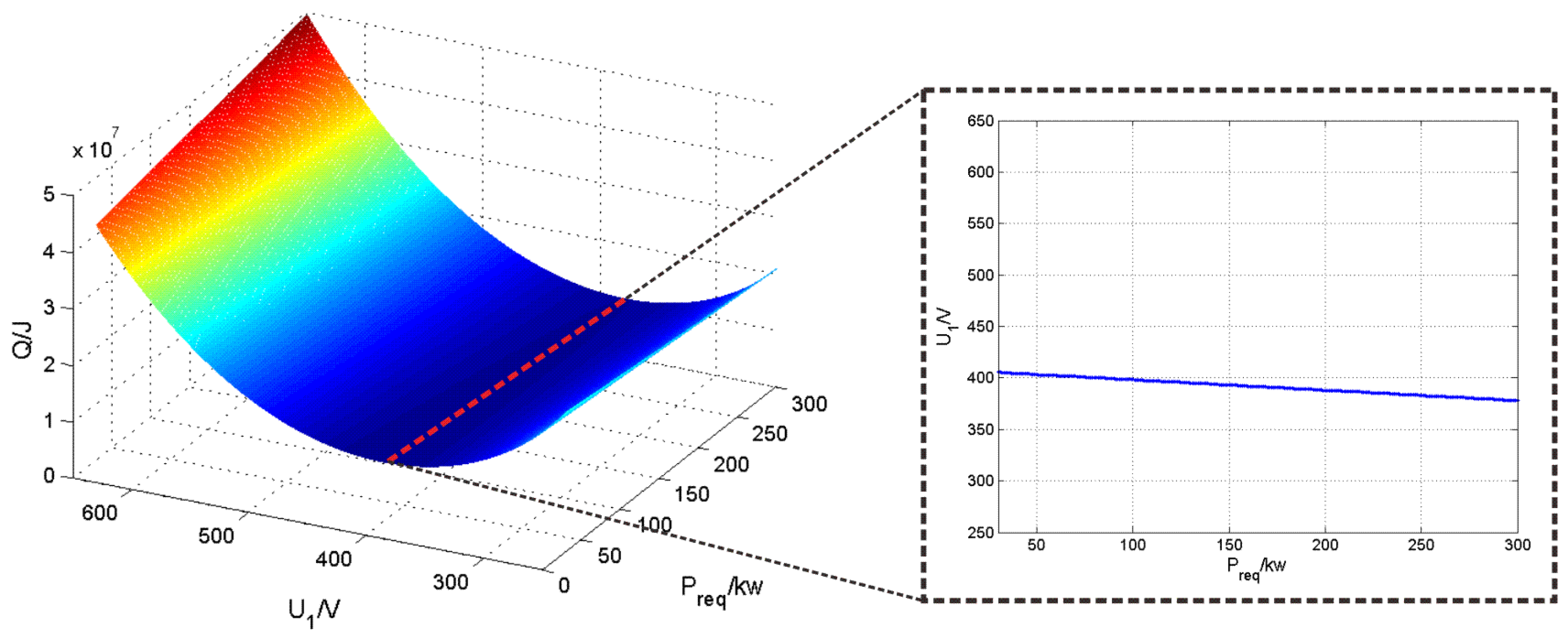
3.2. Traction State
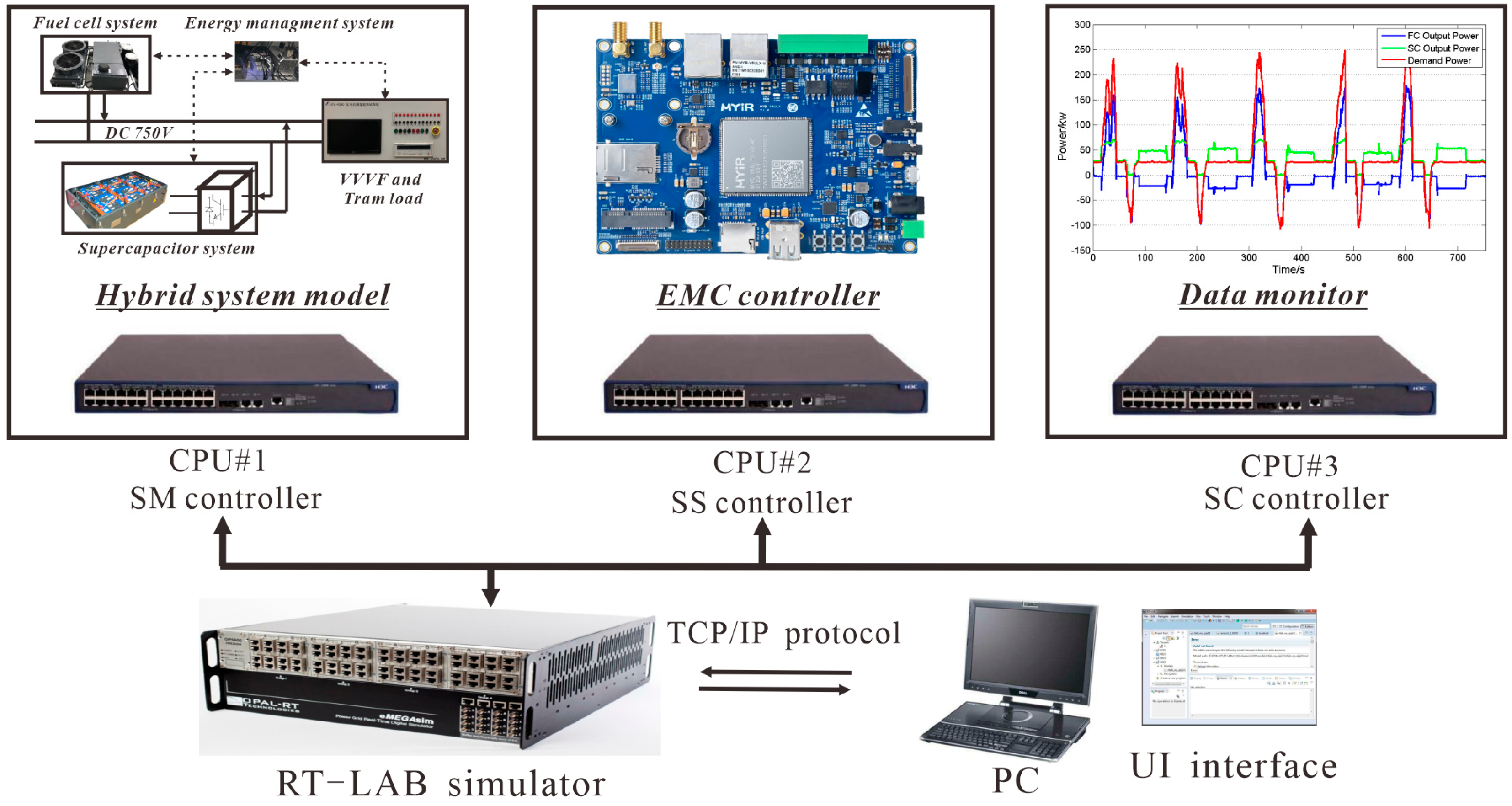
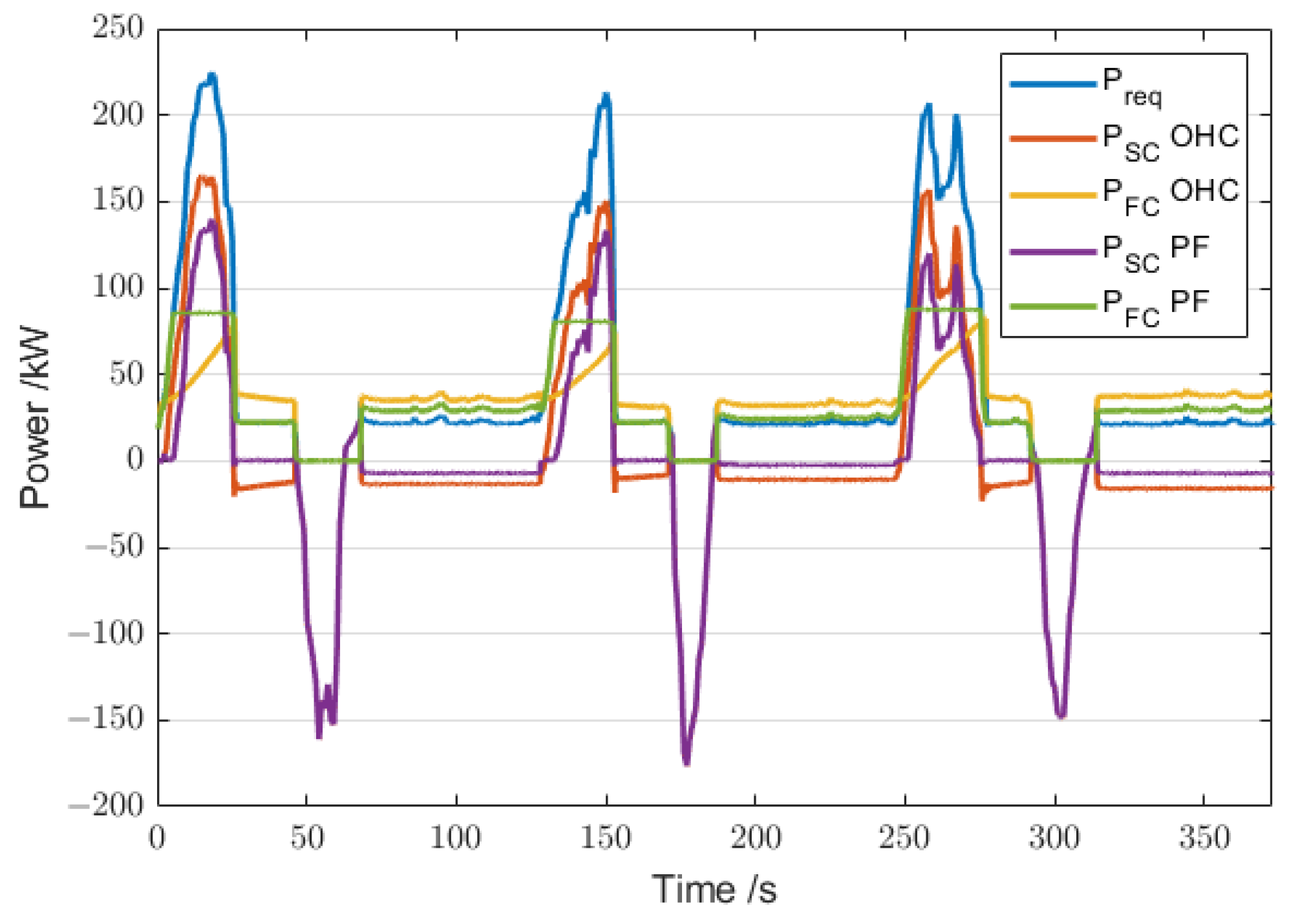
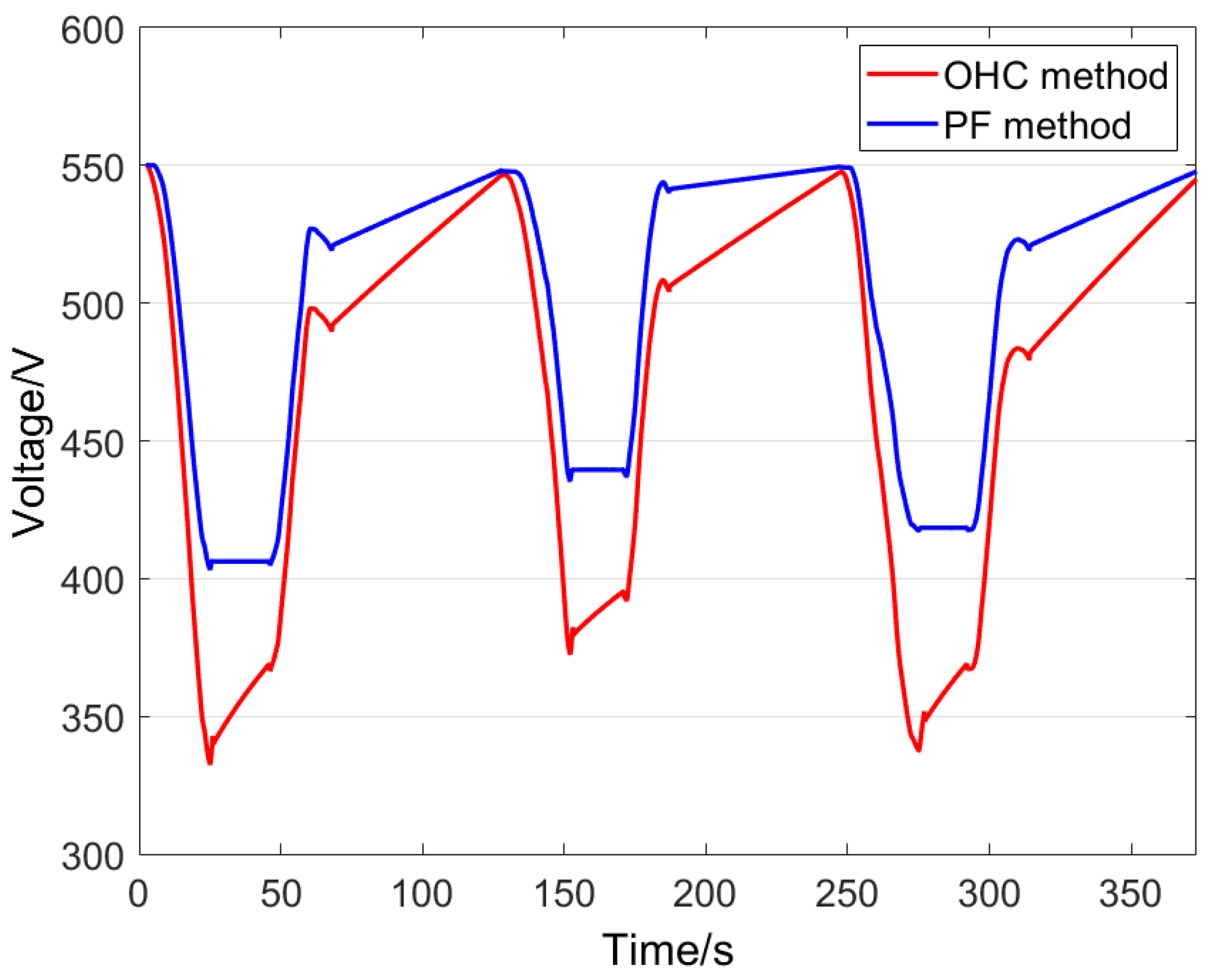
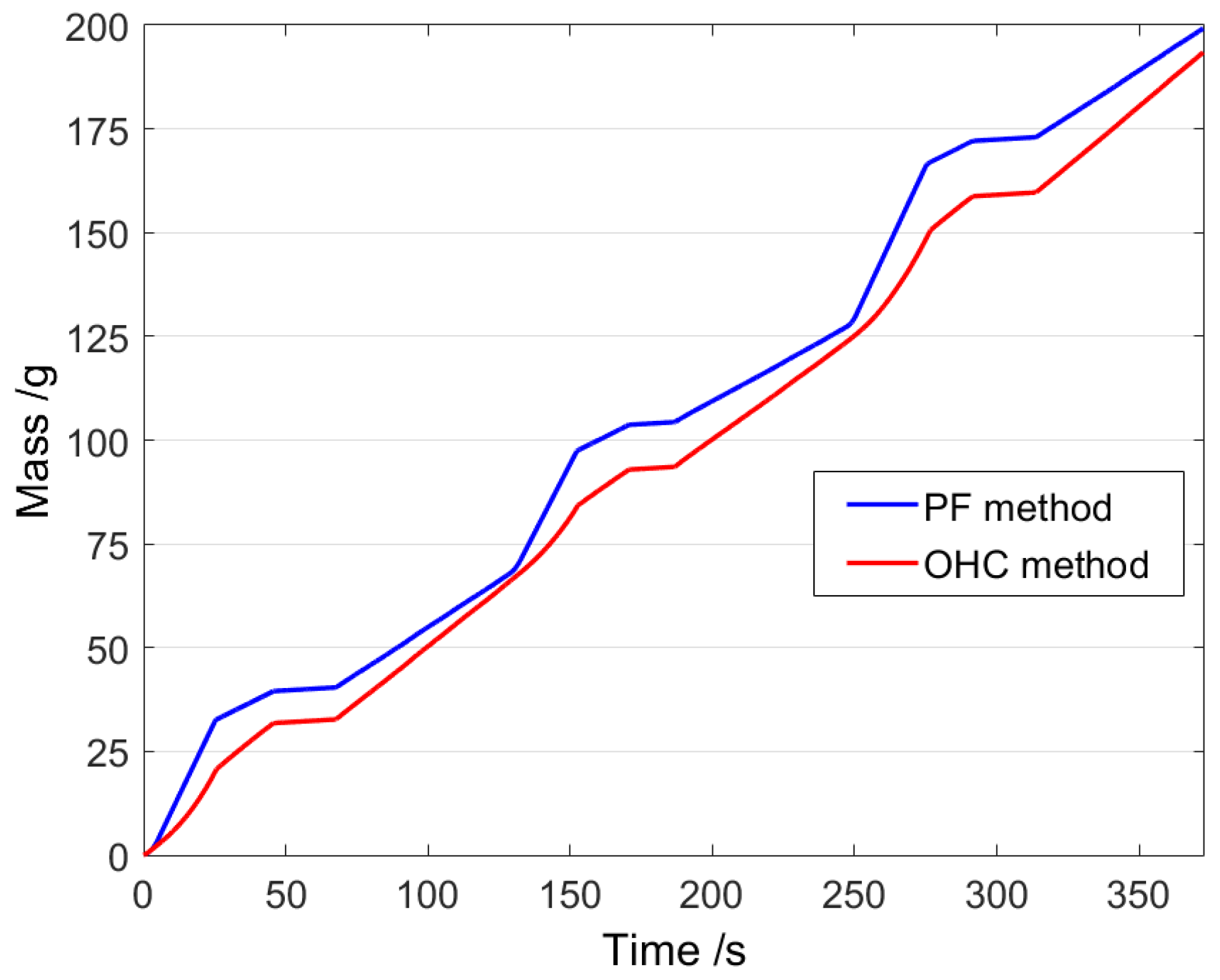
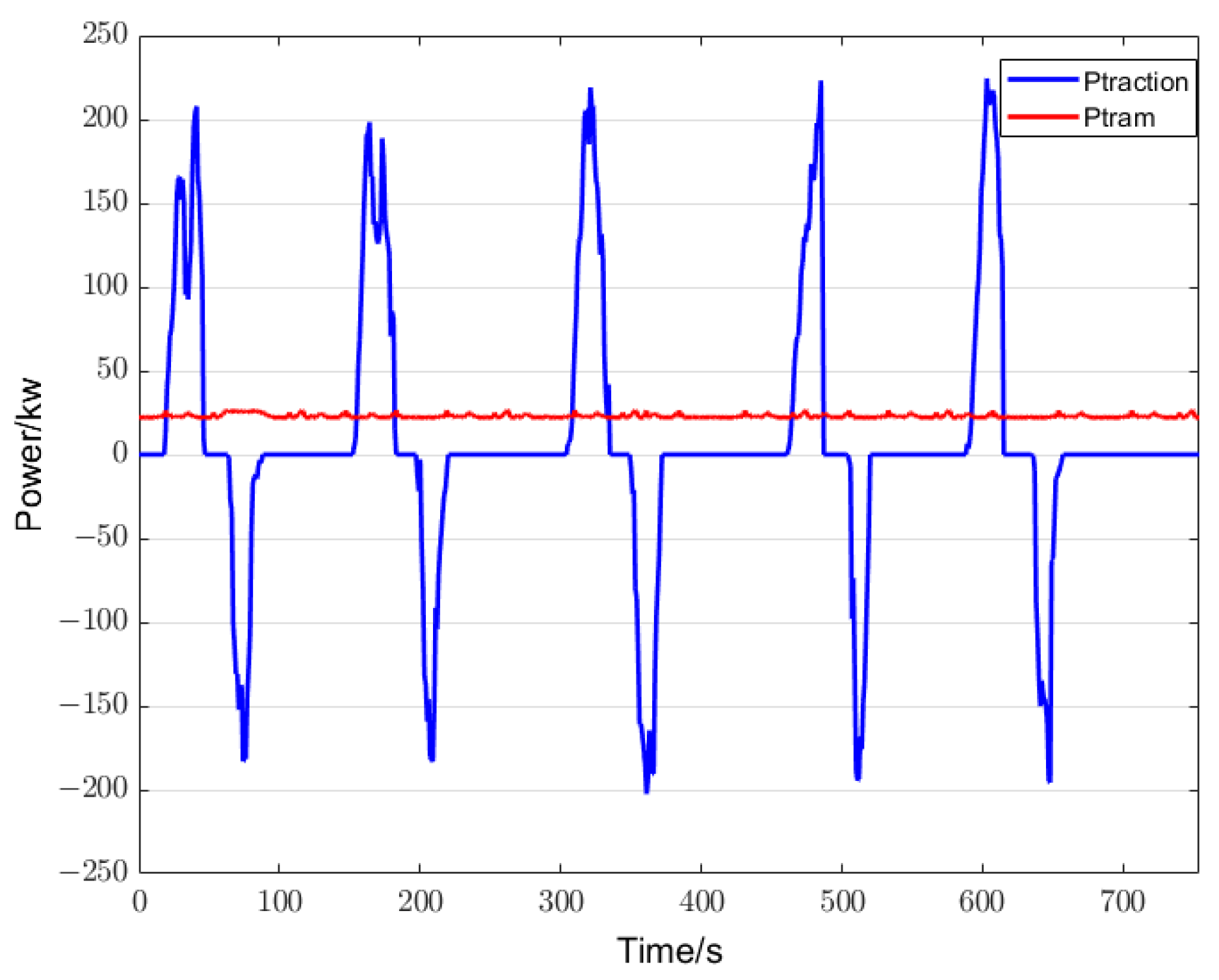
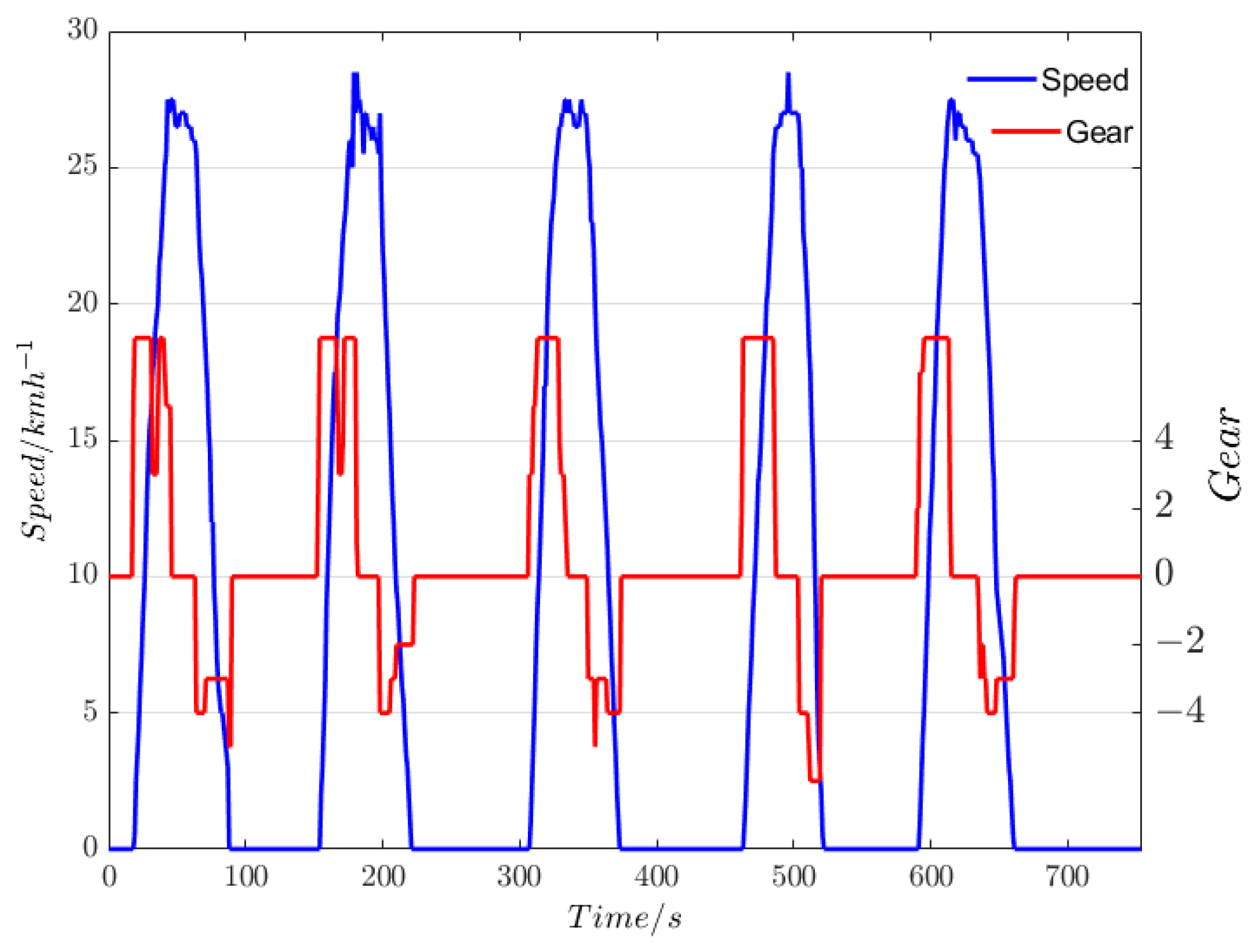
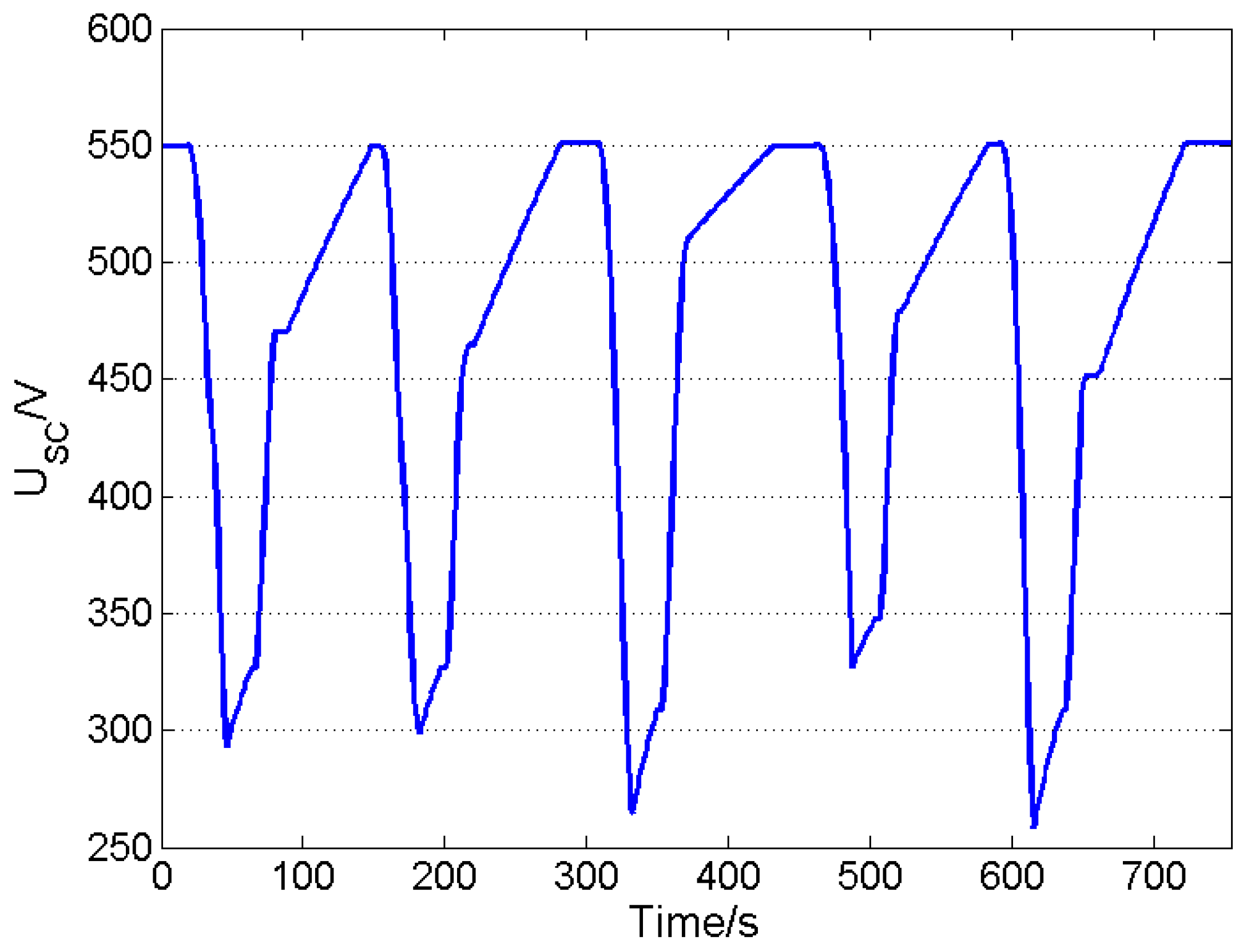
4. Experimental Verification and Results
4.1. RTLAB Hardware-in-the-Loop Simulation
4.2. Experiment for Prototype Tram
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Erdinc, O.; Uzunoglu, M. Recent trends in PEM fuel cell-powered hybrid systems: Investigation of application areas, design architectures and energy management approaches. Renew. Sustain. Energy Rev. 2010, 14, 2874–2884. [Google Scholar]
- Xie, C.; Ogden, J.M.; Quan, S.; Chen, Q. Optimal power management for fuel cell-battery full hybrid powertrain on a test station. Int. J. Electr. Power Energy Syst. 2013, 53, 307–320. [Google Scholar] [CrossRef]
- Li, Q.; Chen, W.; Liu, Z.; Li, M.; Ma, L. Development of energy management system based on a power sharing strategy for a fuel cell-battery-supercapacitor hybrid tramway. J. Power Sources 2015, 279, 267–280. [Google Scholar] [CrossRef]
- Liu, J.; Gao, Y.; Su, X.; Wack, M.; Wu, L. Disturbance-Observer-Based Control for Air Management of PEM Fuel Cell Systems via Sliding Mode Technique. IEEE Trans. Control. Syst. Technol. 2018, 27, 1129–1138. [Google Scholar] [CrossRef]
- Li, X.; Deng, Z.-H.; Wei, D.; Xu, C.-S.; Cao, G.-Y. Parameter optimization of thermal-model-oriented control law for PEM fuel cell stack via novel genetic algorithm. Energy Convers. Manag. 2011, 52, 3290–3300. [Google Scholar]
- Zhou, D.; Al-Durra, A.; Gao, F.; Ravey, A.; Matraji, I.; Simões, M.G. Online energy management strategy of fuel cell hybrid electric vehicles based on data fusion approach. J. Power Sources 2017, 366, 278–291. [Google Scholar] [CrossRef]
- Gao, F.; Blunier, B.; Miraoui, A. PEM Fuel Cell Stack Modeling for Real-Time Emulation in Hardware-in-the-Loop Applications. IEEE Trans. Energy Convers. 2011, 26, 184–194. [Google Scholar]
- Hong, L.; Chen, J.; Liu, Z.; Huang, L.; Wu, Z. A nonlinear control strategy for fuel delivery in PEM fuel cells considering nitrogen permeation. Int. J. Hydrogen Energy 2016, 42, 1565–1576. [Google Scholar] [CrossRef]
- Liu, J.; Laghrouche, S.; Ahmed, F.-S.; Wack, M. PEM fuel cell air-feed system observer design for automotive applications: An adaptive numerical differentiation approach. Int. J. Hydrogen Energy 2014, 39, 17210–17221. [Google Scholar] [CrossRef]
- Li, Q.; Wang, T.; Dai, C.; Chen, W.; Ma, L. Power Management Strategy based on Adaptive Droop Control for a Fuel Cell-Battery-Supercapacitor Hybrid Tramway. IEEE Trans. Veh. Technol. 2017, 67, 5658–5670. [Google Scholar] [CrossRef]
- Eren, Y.; Erdinc, O.; Gorgun, H.; Uzunoglu, M.; Vural, B. A fuzzy logic based supervisory controller for an FC/UC hybrid vehicular power system. Int. J. Hydrogen Energy 2009, 34, 8681–8694. [Google Scholar] [CrossRef]
- Han, Y.; Li, Q.; Wang, T.; Chen, W.; Ma, L. Multi-source Coordination Energy Management Strategy based on SOC consensus for a PEMFC-Battery-Supercapacitor Hybrid Tramway. IEEE Trans. Veh. Technol. 2018, 67, 296–305. [Google Scholar] [CrossRef]
- Cao, L.; Loo, K.H.; Lai, Y.M. Systematic Derivation of a Family of Output-Impedance Shaping Methods for Power Converters—A Case Study Using Fuel Cell-Battery-Powered Single-Phase Inverter System. IEEE Trans. Power Electron. 2015, 30, 5854–5869. [Google Scholar] [CrossRef]
- Li, Q.; Yang, H.; Han, Y.; Li, M.; Chen, W. A state machine strategy based on droop control for an energy management system of PEMFC-battery-supercapacitor hybrid tramway. Int. J. Hydrogen Energy 2016, 41, 16148–16159. [Google Scholar] [CrossRef]
- Xie, C.; Xu, X.; Bujlo, P.; Shen, D.; Zhao, H.; Quan, S. Fuel cell and lithium iron phosphate battery hybrid powertrain with an ultracapacitor bank using direct parallel structure. J. Power Sources 2015, 279, 487–494. [Google Scholar]
- Fernandez, L.M.; Garcia, P.; Garcia, C.A.; Jurado, F. Hybrid electric system based on fuel cell and battery and integrating a single dc/dc converter for a tramway. Energy Convers. Manag. 2011, 52, 2183–2192. [Google Scholar] [CrossRef]
- Russo, A.; Cavallo, A. Supercapacitor stability and control for More Electric Aircraft application. In Proceedings of the 2020 European Control Conference (ECC), St. Petersburg, Russia, 12–15 May 2020; pp. 1909–1914. [Google Scholar]
- Pour, G.B.; Ashourifar, H.; Aval, L.F.; Solaymani, S. CNTs-Supercapacitors: A Review of Electrode Nanocomposites Based on CNTs, Graphene, Metals, and Polymers. Symmetry 2023, 15, 1179. [Google Scholar]
- Andari, W.; Samir, G.; Hatem, A.; Abdelkader, M. Design, Modeling and Energy Management of a PEM Fuel Cell/Supercapacitor Hybrid Vehicle. Int. J. Adv. Comput. Sci. Appl. 2017, 8, 273–278. [Google Scholar] [CrossRef]
- Feroldi, D.; Serra, M.; Riera, J. Energy Management Strategies based on efficiency map for Fuel Cell Hybrid Vehicles. J. Power Sources 2009, 190, 387–401. [Google Scholar] [CrossRef]
- Rodatz, P.; Paganelli, G.; Sciarretta, A.; Guzzella, L. Optimal power management of an experimental fuel cell/supercapacitor-powered hybrid vehicle. Control. Eng. Pract. 2005, 13, 41–53. [Google Scholar] [CrossRef]
- García, P.; Torreglosa, J.; Fernández, L.; Jurado, F. Viability study of a FC-battery-SC tramway controlled by equivalent consumption minimization strategy. Int. J. Hydrogen Energy 2012, 37, 9368–9382. [Google Scholar] [CrossRef]
- García, P.; Torreglosa, J.P.; Fernández, L.M.; Jurado, F. Control strategies for high-power electric vehicles powered by hydrogen fuel cell, battery and supercapacitor. Expert Syst. Appl. 2013, 40, 4791–4804. [Google Scholar]
- Zhang, W.; Li, J.; Xu, L.; Ouyang, M. Optimization for a fuel cell/battery/capacity tram with equivalent consumption minimization strategy. Energy Convers. Manag. 2017, 134, 59–69. [Google Scholar]
- Zheng, J.; Zhang, X.; Xu, P.; Gu, C.; Wu, B.; Hou, Y. Standardized equation for hydrogen gas compressibility factor for fuel consumption applications. Int. J. Hydrogen Energy 2016, 41, 6610–6617. [Google Scholar] [CrossRef]
- Thounthong, P.; Pierfederici, S.; Martin, J.-P.; Hinaje, M.; Davat, B. Modeling and Control of Fuel Cell/Supercapacitor Hybrid Source Based on Differential Flatness Control. IEEE Trans. Veh. Technol. 2010, 59, 2700–2710. [Google Scholar] [CrossRef]

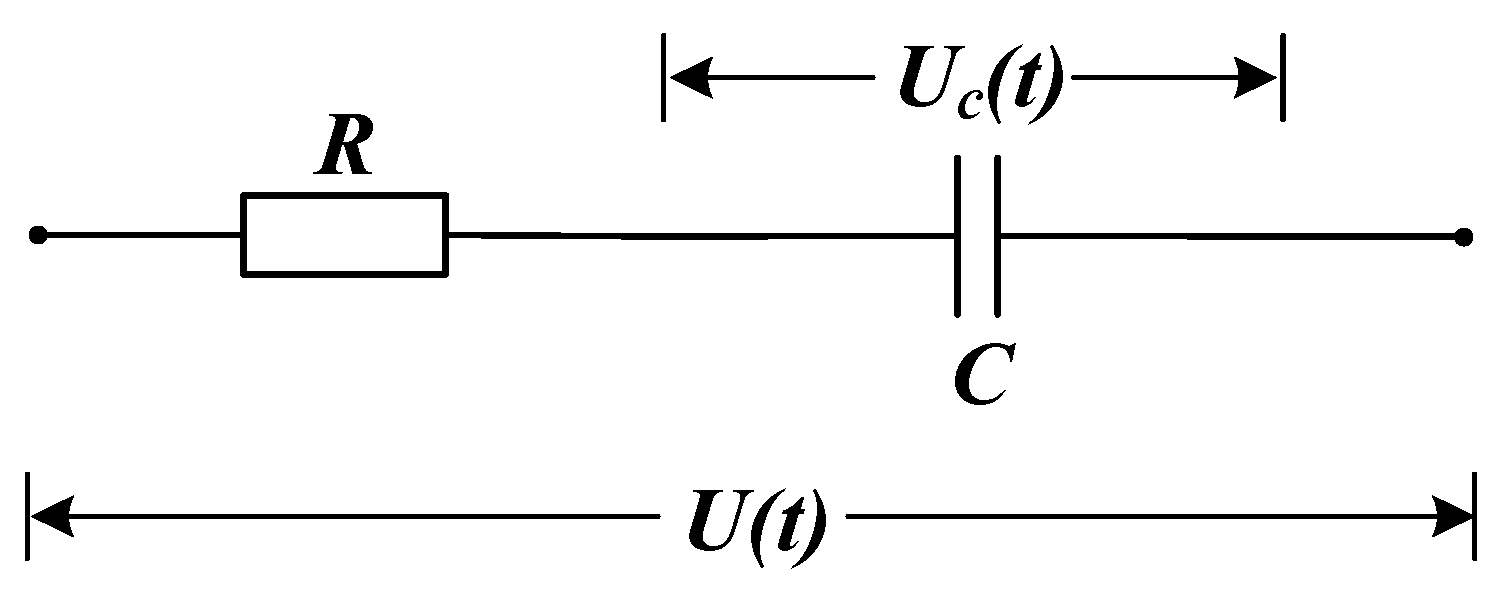


| Performance | Parameter |
|---|---|
| Tram weight | 51.06 t |
| Maximum slope | 50‰ |
| Tram size | 30.19 m × 2.65 m × 3.5 m |
| Traction system max power | 400 kw |
| Acceleration (0~30 km/h) | 1.2 m/s2 |
| System | Parameter | Value |
|---|---|---|
| Fuel cell stack | Model name | FCveloCity-HDTRC |
| Net power | 100 kw | |
| Idle power | 6 kw | |
| Current | 15 A (min.), 288 A (max.) | |
| Voltage | 400 V (min.), 588 V (max.) | |
| Reactants and Coolant | H2 supply pressure | 8 bar (nominal) |
| Oxidant | Air | |
| Coolant | 50/50 pure ethylene glycol and deionized water |
| Parameter | d1 | d2 | d3 |
|---|---|---|---|
| Value | 5.067 × 10−6 | 1.506 | 4849 |
| System | Parameter | Value |
|---|---|---|
| Supercapacitor System | Model name | Maxwell BCAP3000 (15 in series 2 in parallel) |
| No. of modules | 17 in series | |
| Capacity | 25.88 F | |
| Internal resistance | 35 mΩ | |
| Voltage | 250 V (min.), 688 V (max.), 675 V (normal) | |
| Current | −1200 A (min.), 1200 A (max.), 330 A (normal) | |
| SC DC/DC Converter | Bus Voltage | 500 V (min.), 900 V (max.) |
| SC-side current | −1100 A (min.), 1100 A (max.) | |
| Response time | At most 5 ms | |
| Switching time | At most 20 ms | |
| Efficiency | At least 98% |
| Parameter | i = 1 | i = 2 | i = 3 | i = 4 |
|---|---|---|---|---|
| pi | −1.071 × 10−8 | 1.502 × 10−5 | −0.007297 | 2.252 |
| qi | 0.001555 | −1.978 | 1069 | −2.83 × 105 |
| Method | PF | OHC |
|---|---|---|
| H2 consumption | 479.63 g | 457.98 g |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bu, Q.; Zhang, S.; Ma, N.; Luo, Q.; Sun, B. Research on Energy Management Method of Fuel Cell/Supercapacitor Hybrid Trams Based on Optimal Hydrogen Consumption. Sustainability 2023, 15, 11234. https://doi.org/10.3390/su151411234
Bu Q, Zhang S, Ma N, Luo Q, Sun B. Research on Energy Management Method of Fuel Cell/Supercapacitor Hybrid Trams Based on Optimal Hydrogen Consumption. Sustainability. 2023; 15(14):11234. https://doi.org/10.3390/su151411234
Chicago/Turabian StyleBu, Qingyuan, Shiwei Zhang, Ning Ma, Qinghe Luo, and Baigang Sun. 2023. "Research on Energy Management Method of Fuel Cell/Supercapacitor Hybrid Trams Based on Optimal Hydrogen Consumption" Sustainability 15, no. 14: 11234. https://doi.org/10.3390/su151411234
APA StyleBu, Q., Zhang, S., Ma, N., Luo, Q., & Sun, B. (2023). Research on Energy Management Method of Fuel Cell/Supercapacitor Hybrid Trams Based on Optimal Hydrogen Consumption. Sustainability, 15(14), 11234. https://doi.org/10.3390/su151411234










