Does a Cross-Correlation of Economic Policy Uncertainty with China’s Carbon Market Really Exist? A Perspective on Fractal Market Hypothesis

Abstract

Under the efficient market hypothesis (EMH), part of the literature ignores the characteristics of carbon markets. Based on the fractal market hypothesis (FMH), using the MF-DCCA method, this empirical study complements related research. We studied the non-linear multifractal correlation between carbon price fluctuations and China’s economic policy uncertainty (CNEPU) in Shenzhen, Beijing, Tianjin, and the national carbon market. The results show the following: (1) There is no linear correlation between price volatility and CNEPU in all carbon markets. (2) In the national carbon market, the correlation linkage between price fluctuation and CNEPU has not yet formed. (3) In the three regional carbon markets of Shenzhen, Beijing, and Tianjin, the long-range correlations exist with anti-persistence multifractal characteristics, which means that an increase in CNEPU will reduce price fluctuations. (4) After dividing the time scale into long-term and short-term, we found that it does not change the multifractal characteristics but it does change the fractal intensity. Finally, some suggestions are given to policymakers and carbon finance investors.

1. Introduction

Climate change poses a great threat to natural ecosystems and human society, and carbon dioxide emissions are the main driving force. Therefore, reducing carbon emissions has become a key measure to deal with climate change. At present, China is actively making carbon emission reduction commitments. President Xi delivered an important speech at the general debate of the 75th session of the United Nations General Assembly, proposing that China will scale up its intended nationally determined contributions by adopting more vigorous policies and measures. China aims for its CO₂ emissions to peak before 2030 and for carbon neutrality to be achieved before 2060. In order to implement President Xi’s commitment, relevant departments have formulated and issued a series of policies, such as the Action Plan for Carbon Dioxide Peaking before 2030, Administrative Measures for Carbon Emissions Trading (Trial), National Carbon Emissions trading market construction plan (power generation industry), etc. Pilot projects for carbon emission allowance (CEA) trading have been successively carried out in seven provinces and cities, including Beijing, Tianjin, Shanghai, Chongqing, Hubei, Guangdong, and Shenzhen, covering nearly 3000 key emission units in more than 20 industries, such as electric power, steel, and cement. China’s carbon activities in the past decade have received reasonable outcomes, which will benefit the optimization of related government policies. The improved legislation and policies will strengthen China’s regulation of emissions while promoting the quantity and quality of carbon sinks [1]. Carbon emissions trading uses the market mechanism to reduce greenhouse gas emissions, which helps to direct technology and capital towards low-carbon development and encourages emitting entities to achieve carbon emission reduction goals at a low cost. The scale of China’s carbon emission allowance trading market (carbon market) is gradually expanding. As of 30 November 2022, the cumulative transaction volume of CEA has reached 203 million tons, and the cumulative turnover has reached CNY 9.016 billion. However, the characteristics of carbon markets, inherent risks, and investment issues have also gradually become prominent with the expansion of the market scale.

The purpose of this study is to find and validate the multifractal cross-correlation between the carbon price fluctuations and economic policy uncertainties of China in Shenzhen, Beijing, and Tianjin and the national unified carbon market from the perspective of FMH. Specifically, this study explores the following issues: (1) whether a linear relationship or multifractal cross-correlation exists between price fluctuations and changes in CNEPU, (2) the characteristics of the relationship under FMH, (3) whether there are changes after dividing the time scale into long-term and short-term, and (4) the validation of the fractal market hypothesis.

To address the issues mentioned above, this study collected the daily average price of carbon emission allowance (CEA) and EPU index from the establishment date of each market to 16 June 2022. Based on the fractal market hypothesis, we conducted linear analysis and cross-correlation tests. Then, we used the MF-DCCA method to explore cross-correlation multifractal, multiscale, and sliding window analysis.

Possible contributions are as follows. Firstly, we will expand the scope of research about China’s carbon market and the EPU. We used the EPU index to measure policy factors and link the macro-level EPU with the micro-level carbon market price, revealing the long-range correlations existing with anti-persistence multifractal characteristics in the three regional carbon markets of Shenzhen, Beijing, and Tianjin, which means that the increase in CNEPU will lead to a reduction in price fluctuations. Secondly, we will broaden the theoretical perspective of carbon market price fluctuation research. We started from the perspective of the fractal market, conducting cross-correlation multifractal analysis, multiscale multifractal analysis and sliding window analysis. We validated that China’s carbon market is indeed fractal, and the cross-correlation is in line with FMH’s assumptions, providing a more realistic interpretation. Thirdly, we will increase empirical study on the national carbon market under the influence of policy factors. We found that there is no linear correlation between price volatility and CNEPU in the national markets. Furthermore, the correlation linkage between price fluctuation and CNEPU has not yet formed in the national carbon market.

This study has the following structure. Section 2 reviews the development of China’s carbon market, economic policy uncertainty, and fractal market hypothesis to put forward the hypotheses of this study; Section 3 describe the methodology of MF-DCCA; Section 4 presents a description of the data; Section 5 provides the findings and analysis of the study; Section 6 covers the explanations of the core results, policy recommendations considering the findings, limitations, and further directions.

2. Literature Review and Hypotheses

We reviewed the literature on China’s carbon market, economic policy uncertainty, and fractal market hypothesis. For China’s carbon market, we reviewed the literature from the characteristics and the correlation research into China’s carbon market. Then, we logically transitioned to reviewing the correlation between China’s carbon market and economic policy uncertainty, which was also what our paper focuses on. We summarized the hypothesis of our paper by reviewing the fractal market hypothesis. The last part of the section covers a literature summary and our work.

Some scholars have researched China’s carbon market, which can be divided into two aspects: one is about the characteristics of China’s carbon market, including trading mechanisms, influencing factors, volatility features of carbon price, etc. Based on the total amount constraint and allocation of carbon emissions, the trading mechanism allows transaction entities to adjust CEA in the form of currency within a certain range so as to achieve regional carbon emission reduction goals at the lowest cost [2]. Therefore, setting the total amount of regional carbon emission, determining the scope of industry coverage, and allocating initial carbon emission has become fundamental issues in the design of carbon trading mechanisms [3]. A reasonable carbon trading mechanism can achieve the synergistic governance effect of pollution control and carbon emission reduction [4], forming a stable allowance price [5], but the current carbon price in China presents the characteristics of long-term underestimation [6], volatility aggregation, and significant asymmetry [7]. It has something to do with the fact that carbon price formation is affected to different extents by total amount setting, allowance allocation method, offsetting mechanism, and so on [8]. In addition, energy prices [9,10], temperature changes [11], emergencies [12], and the market environment and policies [13] will also cause carbon price fluctuations.

The second is about the correlation research into China’s carbon market, including two perspectives: between different carbon markets and between the carbon market and other markets. There is a long-term equilibrium and mutual guidance relationship between Chinese and EU carbon markets [14], with an asymmetric interdependent structure [15]. The price linkage between regional pilot carbon markets is poor [16], and volatility yield and volatility spillover are time-varying, volatile, uncertain, and cyclical [17]. There is also a cross-correlation between the Chinese carbon market and the energy, stock, and electricity markets. But the cross-correlation varies among different regions and different economic periods. Moreover, the improvement in the efficiency of the power market is more conducive to carbon emission reduction, while increasing carbon cost conductance can alleviate the contradiction between “electricity price reduction” and “carbon emission reduction” [18,19,20].

Economic policy uncertainty (EPU) has a significant impact on economic development. The EPU correlation among the eight core Belt and Road countries is stronger, and the spillover effect of the core countries to the peripheral countries is statistically significant, which means that the stability of the EPU greatly promotes economic development [21]. In addition, during times of economic uncertainty, companies are more likely to engage in ESG activities, including establishing emission reduction targets [22]. EPU is also an important variable affecting the price of Chinese carbon markets because it is still a non-profit and policy-driven market [13]. However, most studies focus on the correlation between EPU and financial markets, such as the stock market [23] and the foreign exchange market [24,25]. Few kinds of literature study the correlation between China’s carbon market and the EPU. Furthermore, most research subjects are the European Union Emissions Trading System (EU ETS). For example, Ye [26] empirically concluded that there was no linear correlation between EPU and the EU carbon market and that the cross-correlation structures of different trading stages are different.

The Fractal Market Hypothesis (FMH) proposed by Edgar E.P. [27] starts from the fractal state of the market, which makes up for the defects of EMH. FMH points out that:

Hypothesis 1 (H1). 

Prices do not reflect all information in a linear way.

Hypothesis 2 (H2). 

The market is made up of many individuals with a large number of different investment horizons. Information has a different impact on different investment horizons.

Hypothesis 3 (H3). 

The investors’ choice of investment horizons is an important factor that may affect the complexity and effectiveness of information transmission.

Those assumptions are more in line with the actual situation of the Chinese carbon market. Therefore, studying the relevance of China’s carbon market from a fractal perspective has more practical significance and practical value. Among fractal methods, the MF-DCCA proposed by Zhou [28] is widely used because it can capture the multifractal characteristics between two non-stationary time series [29]. For example, Zhao [30] used MF-DCCA to analyze the long-term dynamic cross-correlation evolution between US EPU and carbon price in Guangdong.

The existing literature (a) uses the framework of efficient market hypothesis (EMH) [31] and (b) prefers traditional econometric methods to study the correlation of carbon markets. However, the non-linear shape of the carbon price yield with “peaks and thick tails” and irrational expectations of investors cannot be reflected based on EMH [32]. Our work will change the analysis framework and use the MF-DCCA method to offer a more realistic explanation for the correlation between carbon market prices and EPU from a nonlinear perspective.

3. Materials and Methods

Among fractal methods, the MF-DCCA is widely used to detect cross-correlations between two financial series. The MF-DCCA method is based on the multifractal theory and can capture the multifractal characteristics between two non-stationary time series. By eliminating the influence of local trends on the time series scale, it provides tools for studying the cross-correlation between EPU and China’s carbon market, revealing the nonlinear characteristics of carbon price fluctuations with different time scales.

Given two time series with the same length, $x\left(k\right)$, $y\left(k\right)$ where $k=1,2\cdots \cdots ,N$. The specific steps of MF-DCCA are as follows:

(1)

Construct new time series.

Compute cumulative deviation from the mean of time series $x\left(k\right)$, $y\left(k\right)$, forming two new time series:

$$X(i)={\displaystyle \sum _{k=1}^i\left[x(k)-\overline{x}\right]},Y(i)={\displaystyle \sum _{k=1}^i\left[y(k)-\overline{y}\right]},$$

(1)

where $i=1,2\cdots \cdots ,N$ and $\overline{x}$ and $\overline{y}$ are the mean values of the time series, respectively; that is:

$$\overline{x}=\frac{1}{N}{\displaystyle \sum _{k=1}^{N}x\left(k\right)},\overline{y}=\frac{1}{N}{\displaystyle \sum _{k=1}^{N}y\left(k\right)},$$

(2)

(2)

Divide sub-intervals.

Divide the new sequence $X\left(i\right)$, $Y\left(i\right)$ into non-overlapping and equal-length subintervals. Set the length of the subinterval as s, the number of subintervals as $N_s$, then:

$$N_s=\mathrm{int}\left(\frac{N}{s}\right),$$

(3)

Considering that the sequence length N is usually not an integral multiple of the subinterval length s, in order to make full use of all data, each time series needs to be segmented in reverse order again. Therefore, for a given time series, each s corresponds to $2N_s$ subintervals. Since it is necessary to fit each subinterval and ensure subintervals do not overlap, referring to Wang [33], set the value range of $N_s$ as $10\le N_s\le \frac{N}{5}$.

(3)

Fit subintervals and calculate detrended covariances.

The least squares method is used to fit each subinterval, and the fitting order is set to 1 in this paper. We can obtain local trend estimate ${\tilde{X}}_v\left(i\right)$ and ${\tilde{Y}}_v\left(i\right)$ in the interval $v\left(v=1,2\cdots \cdots ,2N_s\right)$. By detrending each subinterval, the trend covariance $F^2\left(s,v\right)$ of the vth subinterval with a time scale of s is obtained.

When $v=1,2,\cdots \cdots ,2N_s$:

$$F^2\left(s,v\right)=\frac{1}{s}{\displaystyle \sum _{i=1}^s\left|X\left(\left(v-1\right)s+i\right)-{\tilde{X}}_v\left(i\right)\right|}\cdot \left|Y\left(\left(v-1\right)s+i\right)-{\tilde{Y}}_v\left(i\right)\right|,$$

(4)

When $v=N_s+1,N_s+2,\cdots \cdots ,2N_s$

$$F^2\left(s,v\right)=\frac{1}{s}{\displaystyle \sum _{i=1}^s\left|X\left(N-\left(v-N_s\right)s+i\right)-{\tilde{X}}_v\left(i\right)\right|}\cdot \left|Y\left(N-\left(v-N_s\right)s+i\right)-{\tilde{Y}}_{\mathrm{v}}\left(i\right)\right|,$$

(5)

(4)

Construct the q-order fluctuation function.

Calculate the mean of the detrended covariance of all subintervals to obtain the $q$-order detrended volatility function.

$$F_q\left(s\right)={\left[\frac{1}{2N_s}{{\displaystyle \sum _{v=1}^{2N_s}\left[F^2\left(s,v\right)\right]}}^{\frac{q}{2}}\right]}^{\frac{1}{q}},q\ne 0$$

(6)

$$F_q\left(s\right)=\exp \left[\frac{1}{4N_s}{\displaystyle \sum _{v=1}^{2N_s}\ln \left[F^2\left(s,v\right)\right]}\right],q=0$$

(7)

(5)

Analyze the log-log graph.

For each given value of q, plot a log-log graph of $F_q\left(s\right)$ and s to analyze the scaling behavior of the detrended volatility function concerning the time scale s. If there is a long-range power-law cross-correlation relationship between time series $X\left(i\right)$ and $Y\left(i\right)$, then:

$$F_q\left(s\right)\sim s^{H_{XY}\left(q\right)},$$

(8)

Take the logarithm that is,

$$\log F_q\left(s\right)=H_{XY}\left(q\right)\log \left(s\right)+\log \left(C\right),$$

(9)

where $H_{XY}\left(q\right)$ is called the generalized Hurst index, which is the slope of the log-log graph. When $H_{XY}\left(q\right)$ changes with the value of q, the cross-correlation of two-time series has multifractal characteristics, and vice versa. When q = 2, it is the standard Hurst exponent. The value range is (0,1). If $H_{XY}\left(q\right)>0.5$, it indicates that the two-time series have long-range persistence; that is, the increase in one time series is accompanied by the increase in the other series. If $H_{XY}\left(q\right)<0.5$, it indicates that the two-time series have anti-persistence; that is, one increase in a time series is accompanied by a decrease in another series. If $H_{XY}\left(q\right)=0.5$, indicating that the two series do not have cross-correlation, the series can be considered to be a random walk.

(6)

Analyze multifractal features.

According to the research of Shadkhoo and Jafari [34], the multifractal scaling index (the Renyi exponent) ${\tau }_{XY}\left(q\right)$ is obtained, and its relationship with $H_{XY}\left(q\right)$ is:

$${\tau }_{XY}\left(q\right)=q{H}_{XY}\left(q\right)-1,$$

(10)

If ${\tau }_{XY}\left(q\right)$ is a linear function of q, the cross-correlation of two-time series is monofractal; otherwise, it has a multifractal feature. Through the Legendre transformation, the singularity strength index $\alpha$ and the multifractal spectral function $f_{XY}\left(\alpha \right)$ are obtained:

$${\alpha }_{XY}\left(q\right)={{\tau }^{\prime }}_{XY}\left(q\right)=H_{XY}\left(q\right)+q{H^{\prime }}_{XY}\left(q\right),$$

(11)

$$f_{XY}\left(\alpha \right)=q{\alpha }_{XY}\left(q\right)-{\tau }_{XY}\left(q\right)=q\left[{\alpha }_{XY}\left(q\right)-H_{XY}\left(q\right)\right]+1,$$

(12)

where ${{\tau }^{\prime }}_{XY}\left(q\right)$ and ${H^{\prime }}_{XY}\left(q\right)$ are the first derivatives of ${\tau }_{XY}\left(q\right)$ and $H_{XY}\left(q\right)$, concerning q separately. If the cross-correlation relationship between two time series has monofractal characteristics, then ${\alpha }_{XY}\left(q\right)$ is a fixed constant; if it is multifractal, then there will be a certain distribution.

(7)

Measure multifractal strength.

$$\Delta H_{XY}=H_{\max }\left(q\right)-H_{\min }\left(q\right),$$

(13)

$$\Delta {\alpha }_{XY}={\alpha }_{XY\max }-{\alpha }_{XY\min },$$

(14)

The strength of the multifractal can be measured by $\Delta H_{XY}$ and $\Delta {\alpha }_{XY}$, which is proportional to $\Delta H_{XY}$ and $\Delta {\alpha }_{XY}$, while inversely proportional to the uniformity of time series.

4. Data Description

Among all the regional CEA trading markets, the Shenzhen carbon market was the earliest to start trading. It was the first carbon market in developing countries and the first national carbon market capacity-building center that had high trading activity. The allowance turnover rate of Shenzhen has ranked first in China for six consecutive years. The Beijing carbon market has the highest average price, while its transaction activity is moderate. It focuses more on the construction of policies and systems. As for the Tianjin carbon market, it is the market with the best contract execution rate, which has reached 100% for six consecutive years. But its transaction volume is small, with low transaction prices and activity. Therefore, the selection of Shenzhen, Beijing, and Tianjin carbon markets as our research subjects could better reflect the overall characteristics of the regional carbon emission allowance trading markets. In addition, the national unified carbon emission allowance trading market was added to reflect the laws of all carbon markets in China.

We collected the daily average transaction price of CEA in the three representative regional carbon markets of Shenzhen, Beijing, and Tianjin, as well as the national carbon market. The data came from CSMAR and Wind databases. Considering data availability, the sample period was from the establishment date of each market to 16 June 2022. The measurement of economic policy uncertainty was based on the EPU index constructed by Baker [35], using the frequency of newspaper reports. Due to the need for daily data, we drew on the research of Huang and Luk [36], which built the China economic policy uncertainty (CNEPU) index with a sample of 114 newspapers. The data came from the public website created by Huang and Luk. The period of the CNEPU corresponds to the daily average price data.

$$R_t=\ln \left(\frac{P_t}{P_{t-1}}\right),$$

(15)

$$\Delta CNEPU=\ln \left(\frac{CNEP{U}_t}{CNEP{U}_{t-1}}\right),$$

(16)

where $R_t$ represents the daily return of CEA, $P_t$ represents the average price of CEA on day $t$, and $P_{t-1}$ represents the average price of CEA on day $t-1$. $\Delta CNEPU$ is the daily change in CNEPU. $CNEP{U}_t$ and $CNEP{U}_{t-1}$ represent China’s economic policy uncertainty index on the day and the previous day, respectively. According to Formulas (15) and (16), the daily logarithmic return and CNEPU daily logarithmic change in all carbon markets were calculated, respectively. Matlab (latest v.R2023a) and Stata (latest v.18) were used for data descriptive statistics and analysis.

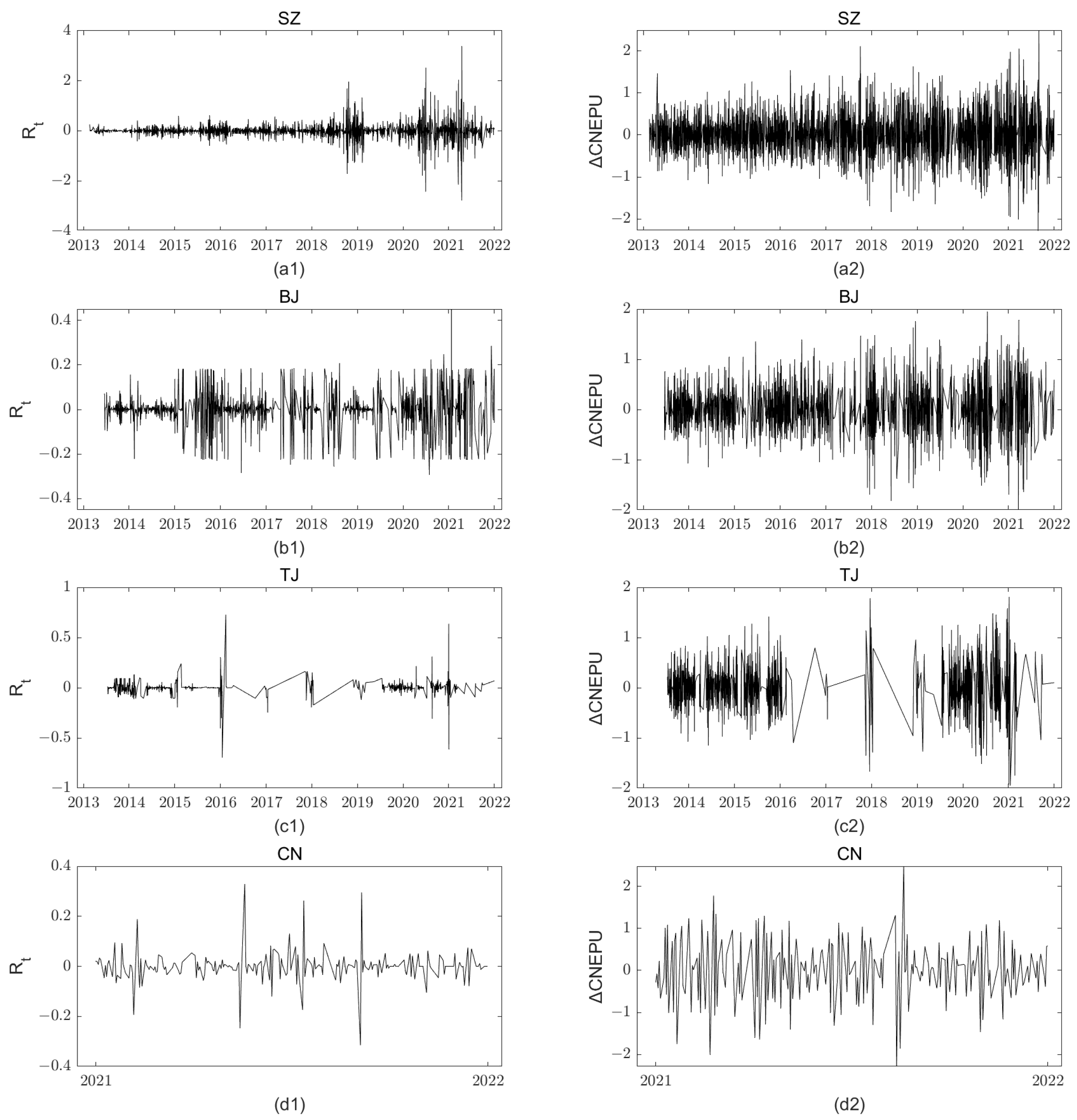
As shown in Figure 1, there are significant differences between the CEA price return and the corresponding change in CNEPU in the four carbon markets. Regarding the CEA price return, all carbon markets fluctuate around 0, but the heterogeneity is significant. For example, the Shenzhen carbon market fluctuated slightly during the initial period in 2019; then, the fluctuation range began to increase, indicating that its two-way price fluctuations gradually became more frequent and the price mechanism gradually improved. The Beijing carbon market has shown periodic characteristics, in which fluctuations were cyclical, and the large ones were concentrated, indicating that the liquidity of the Beijing market was lower than that of Shenzhen, and the trading time was more concentrated. The Tianjin carbon market presents a low degree of perfection in the price formation mechanism and trading activity in terms of both yield and volatility. Further observation found that the trading volume of the Tianjin market was extremely low from June 2016 to 2019, and the yield curve (Figure 1c1) showed sparse and poor continuity. The reason is that carbon trading in Tianjin was suspended for the next three years after the big explosion in 2015. The fluctuation in the carbon price yield in the national carbon market was significantly lower than that of the pilot carbon markets, indicating that the national carbon market was still in the initial stage of operation and the CEA price was more policy-oriented. It also shows that a well-functioning price fluctuation mechanism has not yet been formed, and the market liquidity is weak. As for the change rate in CNEPU, the three pilot markets had a high degree of matching with EPU, while the relationship between the CEA price return and EPU in the national carbon market was relatively loose.

In terms of mean and median, the daily CEA price yields and corresponding CNEPU of all four carbon markets fluctuated around 0, indicating no profitable trend in all markets in the long run. From the perspective of standard deviation, the dispersion degree of the CEA price return in Shenzhen was the highest, while that of the national market was the smallest. The dispersion degree of the regional CNEPU change rate was higher than the national level. “Non-zero” skewness indicates that the CEA price returns and CNEPU changes in all markets were asymmetrically distributed. All kurtosis values were greater than three, with a “peak” characteristic, presenting a steeper distribution. The ADF method was used to detect the stationarity of the CEA price yield and CNEPU changes.

Table 1. Descriptive statistics.

Name	Size	Mean	Median	SD	Min	Max	Skewness	Kurtosis	ADF 1
RSZ	1929	0.000	0.000	0.313	−2.773	3.370	0.362	24.754	−74.871 ***
ΔCNEPUSZ	1927	0.001	−0.015	0.549	−2.282	2.477	0.095	3.863	−70.049 ***
RBJ	1253	0.000	0.001	0.084	−0.293	0.470	−0.375	5.454	−37.565 ***
ΔCNEPUBJ	1253	0.001	−0.013	0.534	−2.000	1.943	0.082	3.686	−57.368 ***
RTJ	770	0.000	0.000	0.071	−0.693	0.728	0.068	45.496	−35.203 ***
ΔCNEPUTJ	770	0.002	−0.007	0.526	−1.945	1.811	0.012	3.836	−43.659 ***
RCN	220	0.001	0.000	0.061	−0.315	0.329	0.545	14.590	−21.118 ***
ΔCNEPUCN	220	0.003	0.010	0.724	−2.282	2.477	−0.169	3.477	−26.911 ***

¹, *** stands for p < 0.01, which is significant at the 1% level.

shows that they are all stationary time series at a 1% significance level. Based on this, the MF-DCCA method was further used to quantify the correlation between the change in CNEPU and the carbon emission allowance price return.

5. Empirical Analysis and Discussion

To investigate the relationship between CEA price fluctuations and CNEPU in Shenzhen, Beijing, Tianjin, and the national carbon emission allowance trading markets, we conducted an empirical analysis. Firstly, the Pearson coefficient and $Q_{CC}\left(m\right)$ were used to conduct a linear analysis and correlation test, respectively, to initially reveal the relationship between the CEA price fluctuation series and EPU change series. Secondly, we used the MF-DCCA method to conduct a multifractal analysis and further examine the heterogeneity of multifractal characteristics by time scale. Finally, we used a sliding window to obtain a dynamic intercorrelation index, portraying the dynamic changes in multifractal characteristics and intensity.

5.1. Linear Analysis

Before the multifractal analysis, we conducted a linear analysis of the daily CEA price return in four carbon markets and the corresponding change in the CNEPU index. We calculated the Pearson coefficient between two time series by market (

Table 2. Pearson coefficient.

${\mathit{R}}_{\mathit{t}}$ and ΔCNEPU	Pearson Coefficient
SZ	−0.0126
BJ	0.0451
TJ	−0.0066
CN	−0.0229

).

The Pearson coefficients of different markets are shown in Table 2, and they were negative in Shenzhen, Tianjin, and the national carbon markets while positive in the Beijing carbon market. But the linear correlation coefficients of all markets were close to zero, indicating that from the perspective of linear analysis, there was no linear correlation between CEA price return and the change in CNEPU.

5.2. Cross-Correlation Test

The cross-correlation test statistic $Q_{CC}\left(m\right)$ can be used to test whether there is cross-correlation between two sets of time series [37]. For any two time series of the same length $\left\{x_i\right\}$, $\left\{y_i\right\}$ (where $i$ = 1, 2∙∙∙∙∙∙, N), $Q_{CC}\left(m\right)$ is defined as follows:

$$C_i=\frac{{\displaystyle \sum _{k=i+1}^N{x}_k{y}_{k-i}}}{\sqrt{{\displaystyle \sum _{k=1}^N{x}_k^2{\displaystyle \sum _{k=1}^N{y}_k^2}}}},$$

(17)

$$Qcc\left(m\right)=N^2{\displaystyle \sum _{i=1}^m\frac{C_i^2}{N-1}},$$

(18)

If $Q_{CC}\left(m\right)$ is greater than the critical value of chi-square distribution with $m$ degrees of freedom ${\chi }^2\left(m\right)$, there is cross-correlation between two time series; otherwise, there is no cross-correlation.

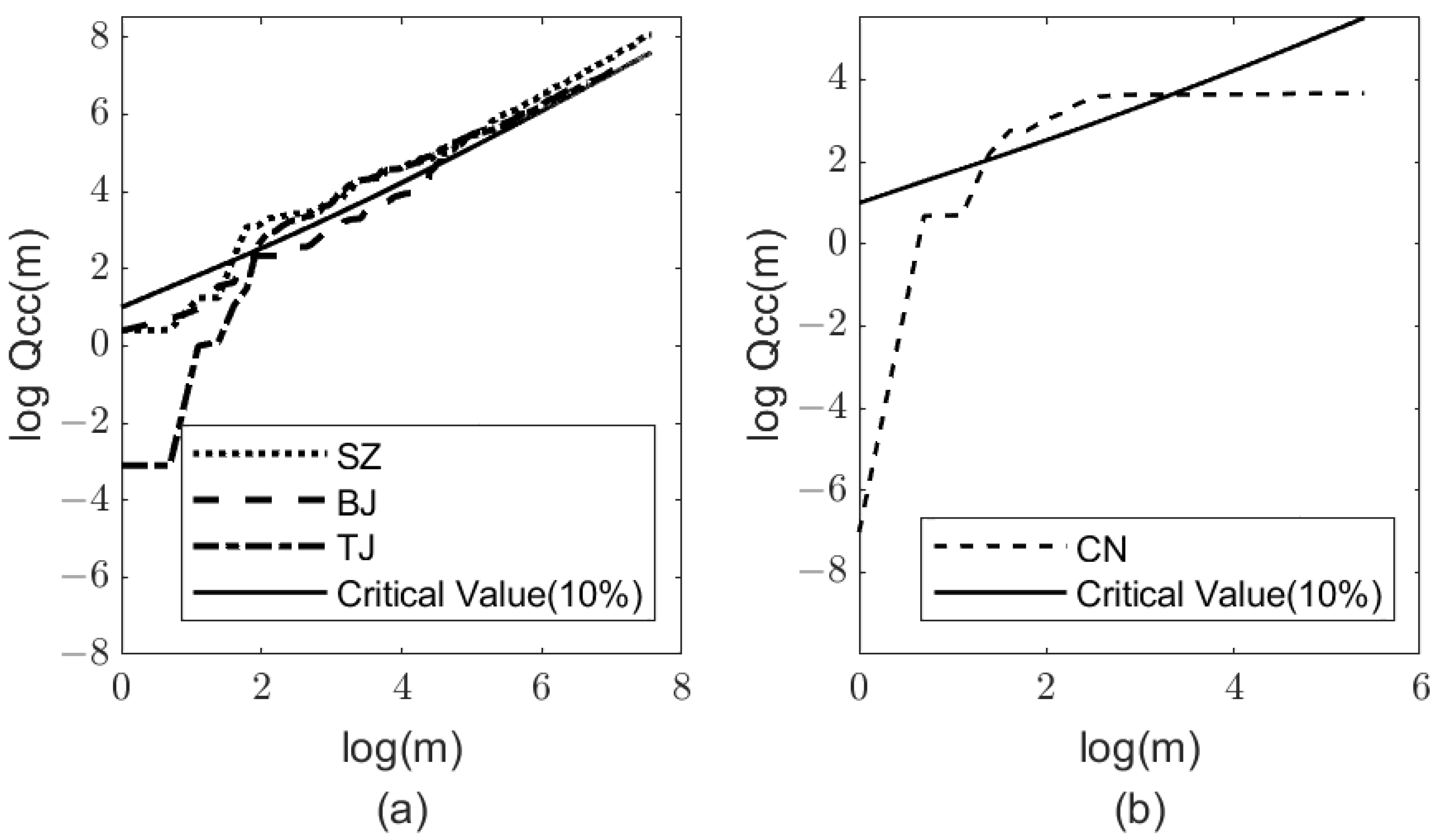
The cross-correlation test results (Figure 2) revealed that the cross-correlation statistics of three regional carbon markets deviated from the critical value, indicating that there was significant cross-correlation between their carbon price return and the change in China’s economic policy uncertainty. However, the national unified carbon market did not pass the cross-correlation test. $Qcc\left(m\right)$ was temporarily greater than the critical value in the mid-term, and the trend tended to be flat and finally fell below the critical value in the later period, indicating that the carbon price changes in the national unified carbon market did not strongly link with changes in China’s economic policy uncertainty. Although the national carbon market has been established and made great progress, its effect on the economy has not yet emerged, and long-term construction is still needed. This is consistent with the reality that the national carbon market covers few emission reduction industries and with the short run time of carbon trading and the small fluctuation in CEA prices.

5.3. Multifractal Analysis Based on MF-DCCA

5.3.1. Cross-Correlation Multifractal Analysis

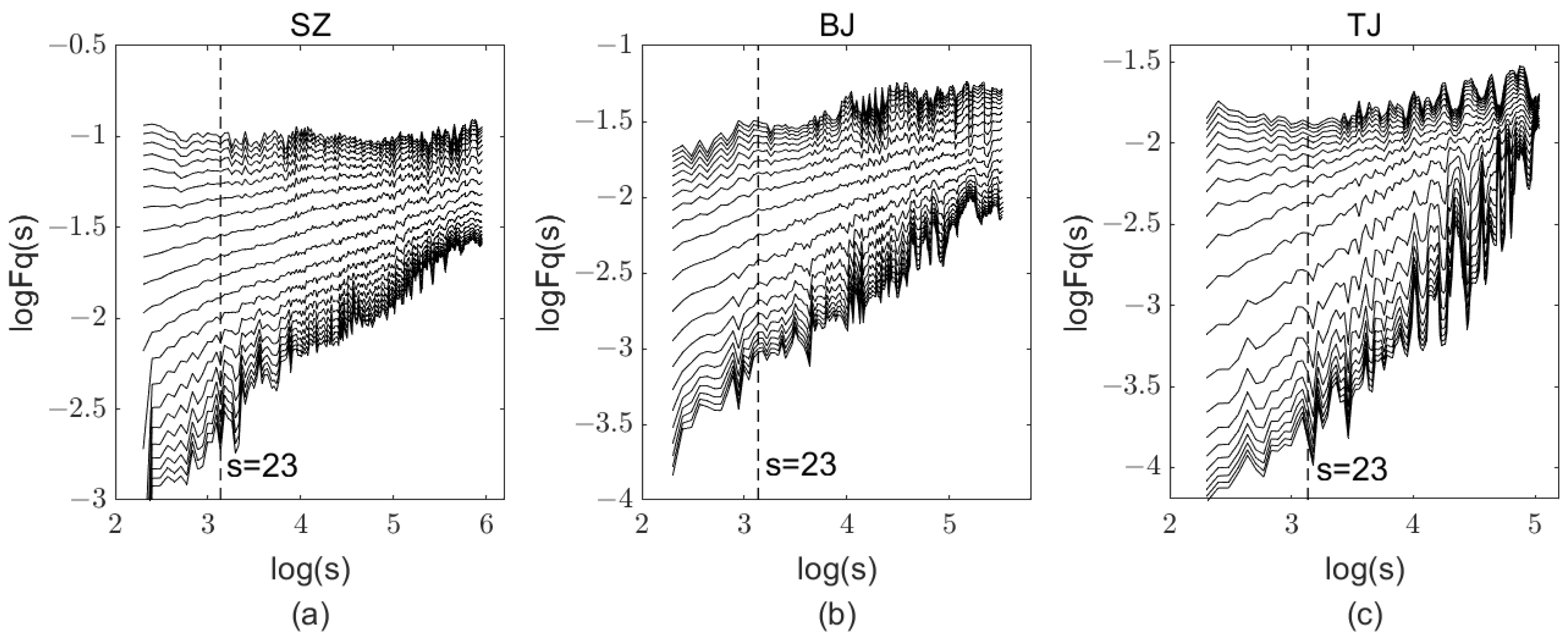
The generalized Hurst index and $F_q\left(s\right)$ in three carbon emission allowance trading markets of Shenzhen, Beijing, and Tianjin can be calculated, and then the log-log graphs of time scale s and $F_q\left(s\right)$ plotted. As shown in Figure 3, each curve corresponds to a q, and the value of q changes from −10 to 10 in order from bottom to top, with 21 curves for each subplot.

Table 3. Generalized Hurst index.

q	SZ	BJ	TJ	q	SZ	BJ	TJ
−10	0.3951	0.4859	0.8575	1	0.1500	0.2011	0.3133
−9	0.3834	0.4770	0.8498	2	0.1281	0.1741	0.2531
−8	0.3696	0.4666	0.8403	3	0.1071	0.1572	0.2117
−7	0.3533	0.4542	0.8281	4	0.0878	0.1466	0.1825
−6	0.3339	0.4392	0.8120	5	0.0710	0.1393	0.1612
−5	0.3111	0.4209	0.7894	6	0.0565	0.1339	0.1453
−4	0.2849	0.3980	0.7558	7	0.0441	0.1295	0.1330
−3	0.2555	0.3689	0.7036	8	0.0335	0.1257	0.1235
−2	0.2233	0.3319	0.6227	9	0.0243	0.1223	0.1158
−1	0.1951	0.2871	0.5132	10	0.0163	0.1192	0.1095
0	0.1721	0.2403	0.4009	ΔH	0.3787	0.3667	0.7480

reports the generalized Hurst exponent, corresponding to the slope of each curve in Figure 3.

As shown in Figure 3, for each time scale s, the fluctuation function $F_q\left(s\right)$ varied with the value of q. There was a nonlinear dependence between the fluctuation function and the time scale for all three subplots. It reveals that there was a long-range power-law cross-correlation relationship between the carbon price fluctuations and the uncertainty of China’s economic policy in all three carbon markets, further supporting the previous conclusion of cross-correlation in 4.2.

Observing the generalized Hurst index (Table 3), in general, the generalized Hurst index of all carbon markets decreased with the change in q values and did not remain constant, which suggests that there were multiple fractal features in the series of CEA price returns and the series of the change in China’s economic policy uncertainty index. By market, the generalized Hurst index in Shenzhen and Beijing carbon markets was always stable below 0.5, while the $H\left(q\right)$ of Tianjin carbon market decreased from greater than 0.5 to less than 0.5 with the q value. In terms of the standard Hurst index (q = 2), three carbon markets corresponded to 0.1281, 0.1741, and 0.2531, respectively, all less than 0.5, indicating that the cross-correlation between carbon price fluctuations and China’s economic policy uncertainty changes had an anti-persistence feature, i.e., an increase in changes in China’s economic policy uncertainty led to a decrease in carbon price volatility. We tried to determine the reason for this from both regulatory and investment perspectives. On the one hand, the increase in economic policy uncertainty tends to be a signal of regulatory changes. Emission reduction companies may choose to sit on the fence and wait until policymakers stabilize economic policy. On the other hand, in carbon markets, economic policy uncertainty usually corresponds to price or market risk. Investors may be more cautious in participating in carbon trading, resulting in fewer fluctuations in carbon prices.

From the perspective of multifractal intensity, the ΔH of the Tianjin carbon market reached 0.7480, which was much larger than that of the Shenzhen and Beijing carbon markets, indicating that there was significant intensity heterogeneity among the three carbon markets, with a specific order of Tianjin > Shenzhen > Beijing. This is in line with the small scale of transactions in the Tianjin carbon market, which is vulnerable to economic uncertainty. The early construction of the Shenzhen carbon market with high trading activity gives it a strong ability to diversify risks. The Beijing carbon market has significant periodicity. This makes the market more certain and predictable in the face of economic policy changes.

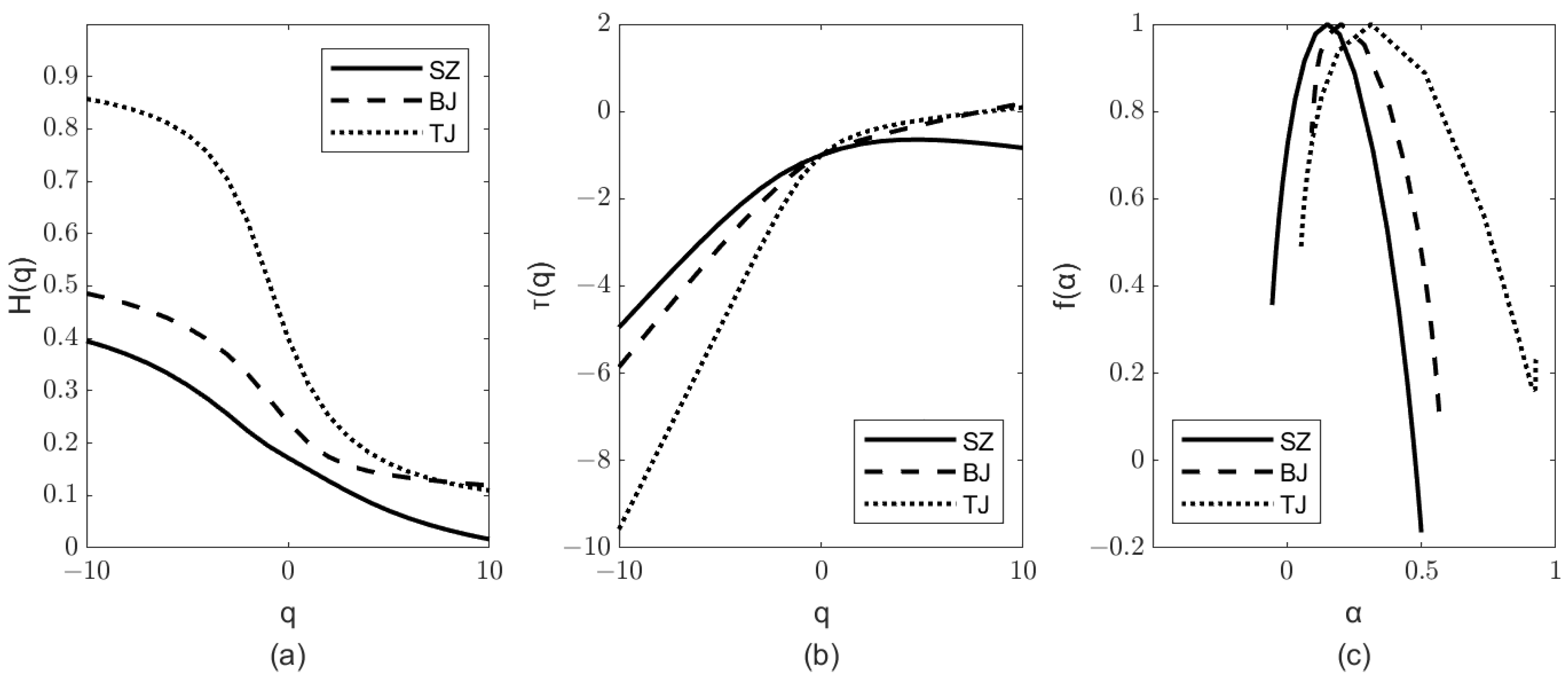
By drawing the graph with $H\left(q\right)$ and q (Figure 4a) to visually show the changes in the generalized Hurst index, it can be seen that all the curves showed a decreasing trend, and the vertical coordinates span of the curves corresponding to Shenzhen and Tianjin was larger than that of Beijing, which was consistent with the previous discussion of multifractal characteristics. To further reveal their features, the multifractal scaling index and multifractal spectrum can be calculated according to Formula (10) and the plot drawn. Figure 4b shows a non-linear relationship between $\tau \left(q\right)$ and q for all three carbon markets, exhibiting an increasing convex function with a parabolic-like shape. Figure 4c shows that the singularity intensity index is not a fixed constant, again supporting the multifractal character of the correlation between carbon price volatility and Chinese economic policy uncertainty. In addition, the corresponding spectrum widths of Shenzhen, Beijing, and Tianjin carbon markets were 0.5550, 0.4744, and 0.8737, respectively. This is also strong evidence that the multifractal intensity of the Tianjin carbon market is more significant than that of Shenzhen and Beijing.

In summary, the cross-correlation multifractal analysis of carbon price and EPU shows that the exogenous impact of policies will have a negative impact on carbon price fluctuations, i.e., an increase in economic policy uncertainty leads to a decrease in carbon price return volatility. This negative impact does not affect the three carbon markets of Shenzhen, Beijing, and Tianjin in a balanced way, but there is some heterogeneity, which is consistent with one of the assumptions of FMH, i.e., that prices do not reflect all information in a linear way (H1). Specifically, it has the greatest impact on Tianjin’s carbon market, followed by Shenzhen, and Beijing is the least affected. This conclusion suggests that the managers of China’s carbon market should, on the one hand, fully consider economic policy changes as an important influencing factor when formulating policies and strive to maintain policy consistency and stability to reduce abnormal market volatility by reducing economic policy uncertainty. On the other hand, regional market heterogeneity should be fully recognized because the same policy adjustment may have different impacts on different markets. It also provides theoretical support to firmly promote the construction of a national unified carbon emission allowance trading market. In addition, carbon finance investors should pay attention to the changes in economic policies in real-time and take advantage of the law of carbon market price changes as well as regional market heterogeneity to build a reasonable investment portfolio and enhance risk management.

5.3.2. Multiscale Multifractal Analysis

In financial markets, short-term traders frequently focus on asset prices, concentrating on analyzing daily or weekly price data and dynamically evaluating the market and then executing trades with high frequency. Long-term traders focus on long-term market conditions, paying attention to analyzing low-frequency data such as monthly or annual prices, which only execute transactions when large price changes occur over the long term. Therefore, the cross-correlation behavior on different time scales has important implications for both short-term and long-term traders.

Based on this, we referred to Wang [33] and used $s^{*}=23$ (about one trading month) as the dividing point between the short-term scale and the long-term scale to study the relationship between CEA price return and the change in CNEPU in Shenzhen, Beijing, and Tianjin markets under different time scales.

Table 4. Long-term and short-term generalized Hurst index.

q	SZ		BJ		YJ
	S < s* 1	S > s*	S < s*	S > s*	S < s*	S > s*
−10	1.3423	0.3573	0.7334	0.4812	0.5191	0.9801
−9	1.3360	0.3464	0.7083	0.4728	0.5221	0.9707
−8	1.3259	0.3336	0.6779	0.4628	0.5257	0.9588
−7	1.3091	0.3188	0.6414	0.4509	0.5302	0.9433
−6	1.2793	0.3018	0.5984	0.4363	0.5353	0.9222
−5	1.2242	0.2825	0.5498	0.4180	0.5408	0.8920
−4	1.1183	0.2614	0.4988	0.3946	0.5454	0.8467
−3	0.9109	0.2392	0.4488	0.3642	0.5454	0.7762
−2	0.5581	0.2168	0.4018	0.3255	0.5312	0.6699
−1	0.3100	0.1946	0.3590	0.2794	0.4873	0.5344
0	0.2339	0.1725	0.3244	0.2318	0.4112	0.4068
1	0.1890	0.1500	0.3029	0.1918	0.3228	0.3162
2	0.1480	0.1279	0.2927	0.1636	0.2362	0.2591
3	0.1059	0.1073	0.2887	0.1455	0.1581	0.2229
4	0.0639	0.0892	0.2871	0.1342	0.0924	0.1988
5	0.0256	0.0738	0.2860	0.1267	0.0395	0.1818
6	−0.0065	0.0609	0.2845	0.1215	−0.0024	0.1691
7	−0.0317	0.0500	0.2823	0.1175	−0.0356	0.1594
8	−0.0509	0.0407	0.2795	0.1143	−0.0622	0.1516
9	−0.0652	0.0326	0.2761	0.1115	−0.0838	0.1452
10	−0.0759	0.0257	0.2725	0.1090	−0.1016	0.1398
ΔH	1.4075	0.3247	0.4572	0.3697	0.6292	0.8349

¹, s* stands for the dividing point between the short-term scale and the long-term scale.

reports the short-term and long-term generalized Hurst indices for the three carbon markets, respectively. The results show that the cross-correlation index decreases with the change in q, indicating that under multiple time scales, the relationship between carbon price fluctuations and China’s economic policy uncertainty still presents multifractal characteristics. Regarding the standard Hurst index, all three carbon markets were below 0.5, indicating that sub-time scales have not changed the characteristics of anti-persistence. Judging from the variation range of the cross-correlation index, carbon markets show significant heterogeneity in the short and long term. Specifically, in the short term, the multifractal strength of the Shenzhen carbon market is much greater than that of Tianjin, while the Beijing carbon market is the weakest. However, in the long run, the ΔH of the three markets increased in the order of Shenzhen, Beijing, and Tianjin. It was shown that the fractional time scale changes the strength of the multifractal correlation between the series of carbon price fluctuations and the series of changes in CNEPU.

In short, considering that one of the important assumptions of FMH is the existence of investors with different investment time scales in the market, the multiscale multifractal analysis of carbon markets with nonlinear characteristics finds that a change in time scale does not change the multifractal characteristics, but does change the multifractal intensity. This coincides with another important hypothesis of fractal markets—that information has different impacts on investors with different investment time scales (H2), i.e., fluctuations in EPU create a series of information that continuously affects short-term and long-term investors differently, which in turn leads to changes in the intensity of multiple fractals in the carbon market. This conclusion shows that the investment period will make regional carbon markets respond differently to the same policy shock. It further suggests that policymakers and carbon finance investors in China’s carbon market should pay attention to the time-scale heterogeneity of the market and make rational choices in different economic environments to avoid abnormal fluctuations in the carbon market or losses in the carbon market due to policy changes.

5.3.3. Sliding Window Analysis

Sliding window analysis has been applied to the study of financial time data since Cajueiro and Tabak [38]. We used the sliding window analysis method to explore the daily dynamic changes between the carbon price fluctuations and $\Delta CNEPU$ in three CEA trading markets. Specifically, a suitable fixed number of days was chosen as the window length, and the time difference between two adjacent windows was the window sliding length. At the end of the analysis of the previous window, one sliding window length was moved to the right for analysis, and so the window kept moving right until the right end of the last window reached the end of the time series.

The length of the sliding window is the key to sliding window analysis. To capture the dynamic characteristics of the cross-correlation of the full sample, we referred to the practice of Ruan and Wang [39], set the window length to 250 days (about one trading year) and further observed the situation for 200 days and 300 days. To eliminate the instability of trading data at the early stage of the establishment of the carbon markets from adversely affecting the empirical results, the standard Hurst index ($q$ = 2) was calculated by removing the first 200, 250, and 300 days of two series, respectively. 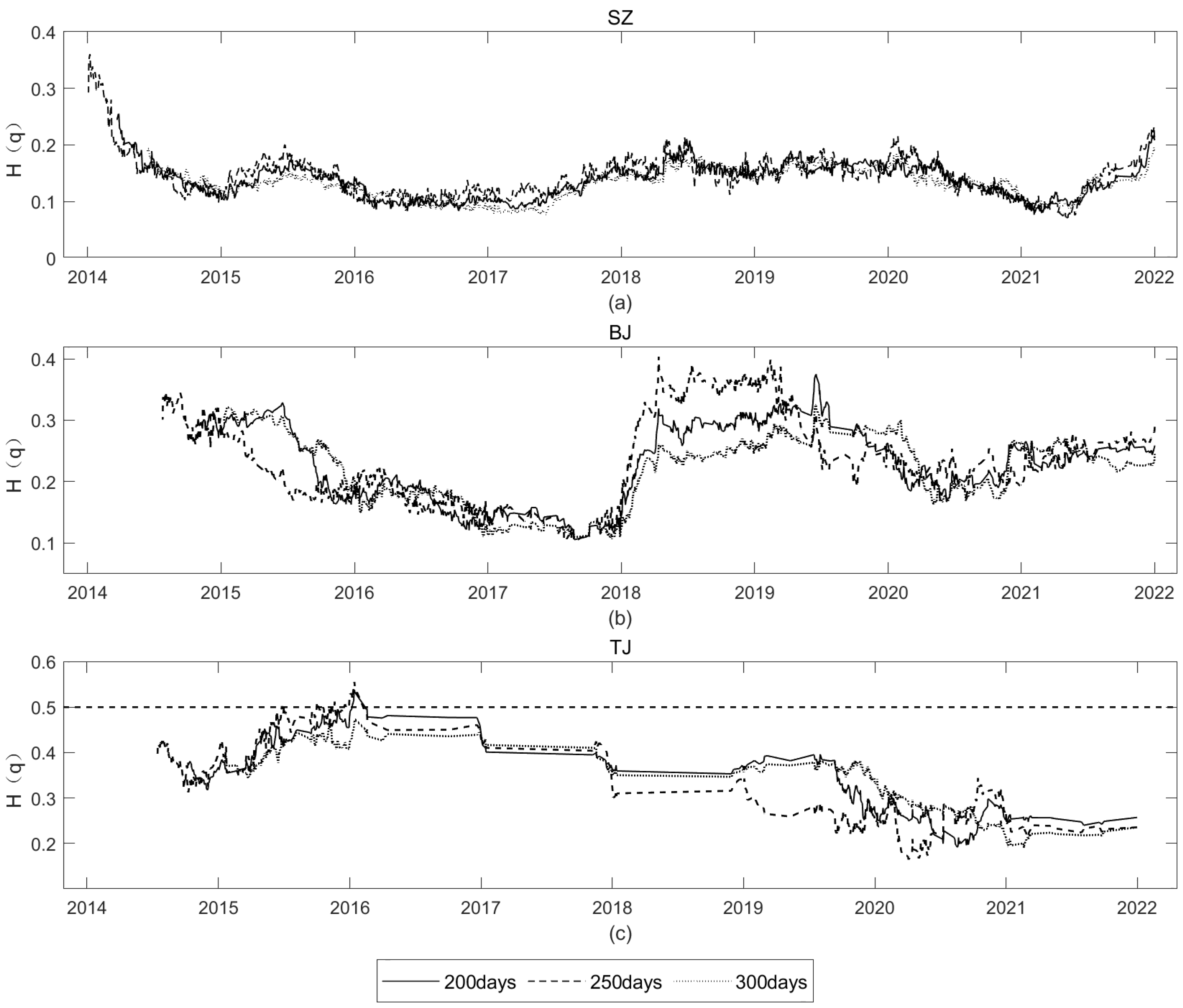The sliding length was set to 1 day, and the sample was slid forward until the end of the series to obtain the dynamic Hurst index, as shown in Figure 5, with (a), (b), and (c) plots corresponding to the Shenzhen, Beijing, and Tianjin carbon markets, respectively.

The results show that the cross-correlation indices of Shenzhen and Beijing carbon markets are all lower than 0.5. The index of the Tianjin carbon market was overwhelmingly below 0.5, and there were a few time windows with indices greater than 0.5 since 2016, mainly due to the data bias caused by the extremely small transactions of the Tianjin market from 2016 to 2019. The presence of an anti-persistence relationship between carbon price fluctuations and economic policy uncertainty can be considered; that is, the greater the economic policy uncertainty, the smaller the carbon price fluctuations, which is consistent with the previous conclusions. Further observation found that the standard Hurst index changed with the movement of the sliding window. The dynamic Hurst index of Shenzhen and Beijing carbon markets presented a “W”-shaped fluctuation. The Tianjin carbon market was not in line with Shenzhen and Beijing, according to the data, but still showed a fluctuating pattern. This shows that the anti-persistence between carbon price fluctuations and changes in China’s economic policy uncertainty are not constant and are always in a state of fluctuation. In addition, the standard Hurst index also varied with the length of the sliding window, and a shrinking of the sliding window could lead to an increase in the frequency of fluctuations and an expansion of the range of fluctuations.

In short, the sliding window divided the carbon markets into sub-markets with a fixed time scale but a greater number of sub-markets for analysis, which still supported the above conclusions and strongly supported the interaction between carbon markets and economic policy uncertainty from the perspective of FMH. In addition, the size of the time window also contributed to the volatility of the Standard Hurst Index, suggesting that in fractal markets, the investors’ choice of time scale was an important factor that may affect the complexity and effectiveness of information transmission. This conclusion suggests that carbon policymakers should choose an appropriate time window for risk monitoring and management in the carbon market. They should also use sufficient time to observe the effect of policy implementation to obtain accurate feedback and improve the accuracy and pertinence of policy implementation. For carbon finance investors, the complexity of changes in carbon finance yields will make it difficult to find the right time to invest, which may prompt investors to make long-term investments and promote production transformation and voluntary emission reduction.

6. Conclusions

We used the MF-DCCA method to conduct an empirical study on the relationship between the fluctuation in CEA prices and the uncertainty of China’s economic policy in Shenzhen, Beijing, Tianjin, and the national unified carbon emission allowance trading markets. By performing linear analysis, a mutual correlation test, multiple fractal characteristics analysis, and further analyzing its different time scale characteristics, we finally analyzed the dynamics of the correlation between carbon price volatility and economic policy uncertainty using sliding windows.

The main conclusions are as follows. First, the relationship between CEA price volatility and the change in CNEPU was examined using linear analysis. The Pearson coefficients showed that there is no linear correlation between the series of carbon price volatility and economic policy uncertainty in Shenzhen, Beijing, Tianjin, and the national carbon markets. Second, the national carbon market has not passed the Qcc cross-correlation test, indicating that there has not been a close relationship between the national carbon market and changes in China’s economic policy uncertainty. This is consistent with the fact that the national carbon market covers few emission reduction industries, the operation time of carbon trading is short, and the fluctuation in carbon price is small. Third, there is a long-range correlation between carbon price fluctuations and economic policy uncertainty in Shenzhen, Beijing, and Tianjin carbon markets, with anti-persistence multifractal characteristics; that is, the increase in CNEPU will lead to a reduction in price fluctuations. A possible explanation is that the increase in CNEPU usually corresponds to uncertainty and risk in the economic environment, and emission reduction companies will be more cautious when participating in carbon trading, resulting in less volatile carbon prices. In terms of fractal intensity, Tianjin, Shenzhen, and Beijing are in order from strong to weak. The analysis of the generalized Hurst exponent, multifractal scaling index, and multifractal spectrum further supports the above conclusion. Fourth, the fractal time scale will not change the multifractal characteristics but will change the fractal intensity. In the short term, the order of strength from strong to weak is Shenzhen, Tianjin, and Beijing, while the order of fractal strength in the long term becomes Tianjin, Beijing, and Shenzhen. Fifth, the sliding window analysis still supports the conclusion that there is an anti-persistence between carbon price fluctuations and economic policy uncertainty by characterizing the dynamic Hurst exponents of the three carbon markets. It is further pointed out that this kind of anti-persistence is not constant and will change dynamically with the movement of the time window and the change in the window length.

The research results may have some implications for carbon policymakers, regulators, and carbon finance investors. Policymakers in China’s carbon market should take into account the impact of economic policy changes and strive to maintain policy consistency and stability and reduce abnormal market fluctuations by reducing economic policy uncertainty. There are significant differences in the multifractal intensity of different time scales in different markets, implying that differentiated development levels and investment horizons can cause regional carbon markets to respond differently to the same policy shock, so regional market heterogeneity should be fully considered when formulating policies. At the same time, it also provides theoretical support for firmly promoting the construction of a unified national carbon emission allowance trading market. In addition, to choose an appropriate time window for risk monitoring and management of the carbon market, sufficient time should be used to observe the effect of policy implementation to obtain accurate feedback and promote the healthy and orderly development of China’s carbon market. Carbon investors should pay close attention to changes in economic policies in real-time and use the uncertainty of economic policies and the laws of carbon market price changes to construct a reasonable investment portfolio. Further, they should strengthen their risk management of financial assets and make rational choices in different economic environments to avoid losses in the carbon market due to economic shocks or policy changes. On the other hand, the heterogeneity and multifractal characteristics of different markets and different time scales indicate that the changes in China’s carbon market return sequence are complex. Investors may find it difficult to choose a suitable carbon market and follow up on investment at the right time. Therefore, compared to short-term speculation, they should make long-term low-carbon investment decisions, develop low-carbon technologies, and achieve production transformation and autonomous emission reduction.

This study can be further extended. We only focused on the correlation between carbon price fluctuations and China’s economic policy uncertainty. There are more policy-specific uncertainties, such as fiscal policy, monetary policy, trade policy, and exchange rate policy, which should be considered in future research.