Assessment of Variability in Hydrological Droughts Using the Improved Innovative Trend Analysis Method
Abstract
1. Introduction
2. Materials and Methods
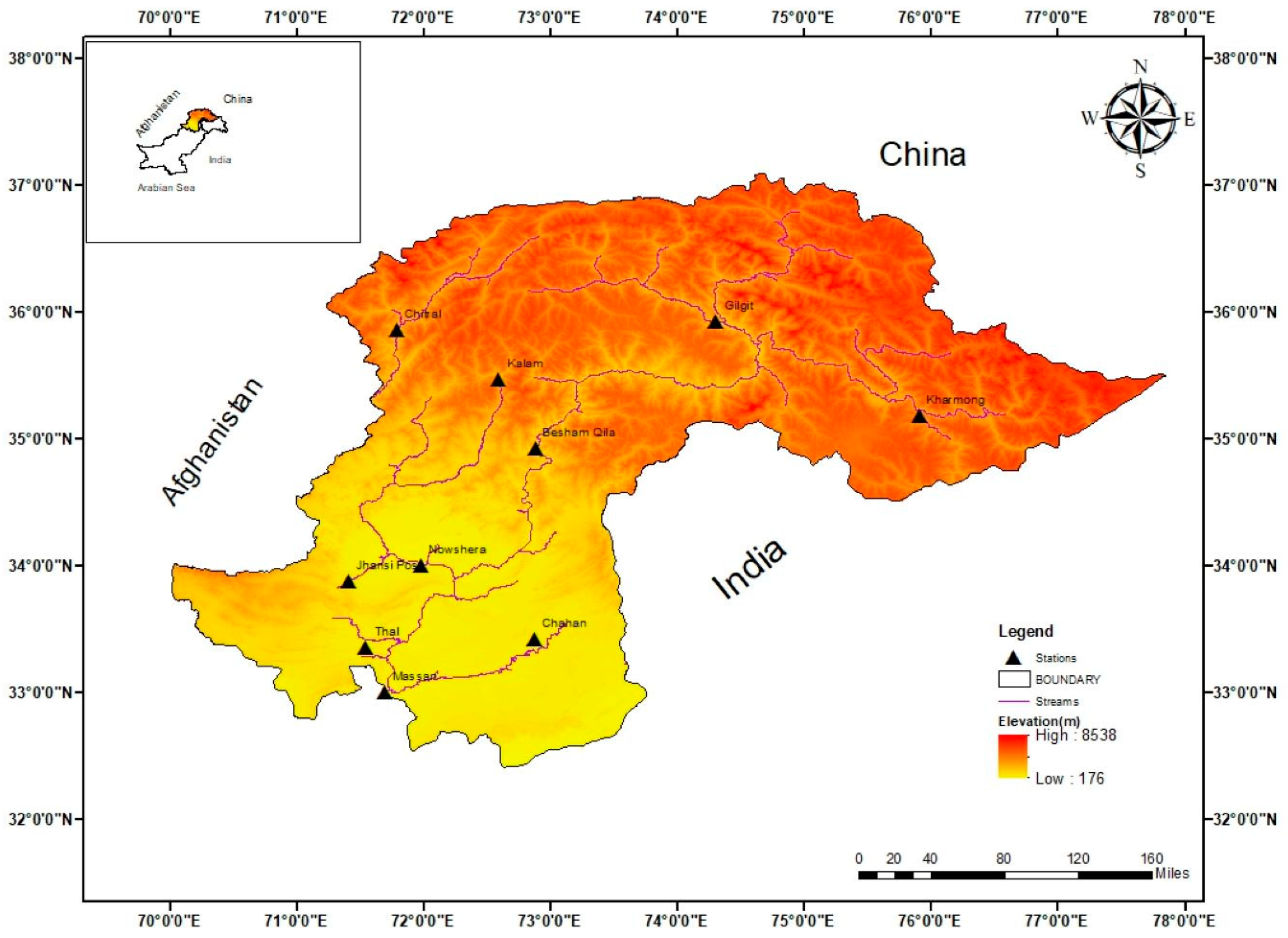
2.1. Study Area and Data Used
2.2. Assessment of Hydrological Drought
2.3. Trend Analysis Methods
2.3.1. Mann–Kendall Test
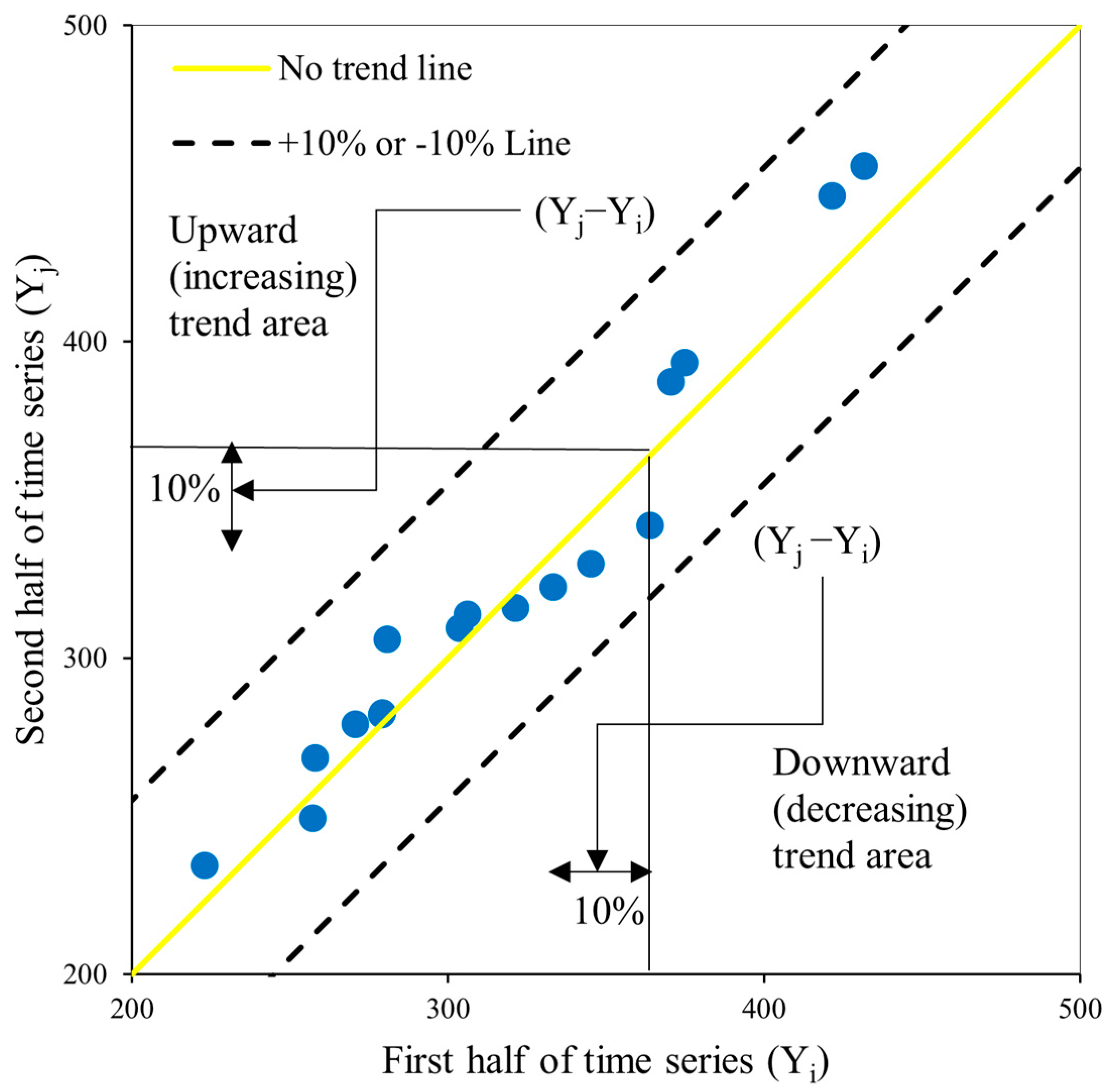
2.3.2. Innovative Trend Analysis Method
2.3.3. Şen’s Innovative Trend Analysis Method
3. Results
3.1. Statistical Analysis
3.2. Homogeneity Analysis
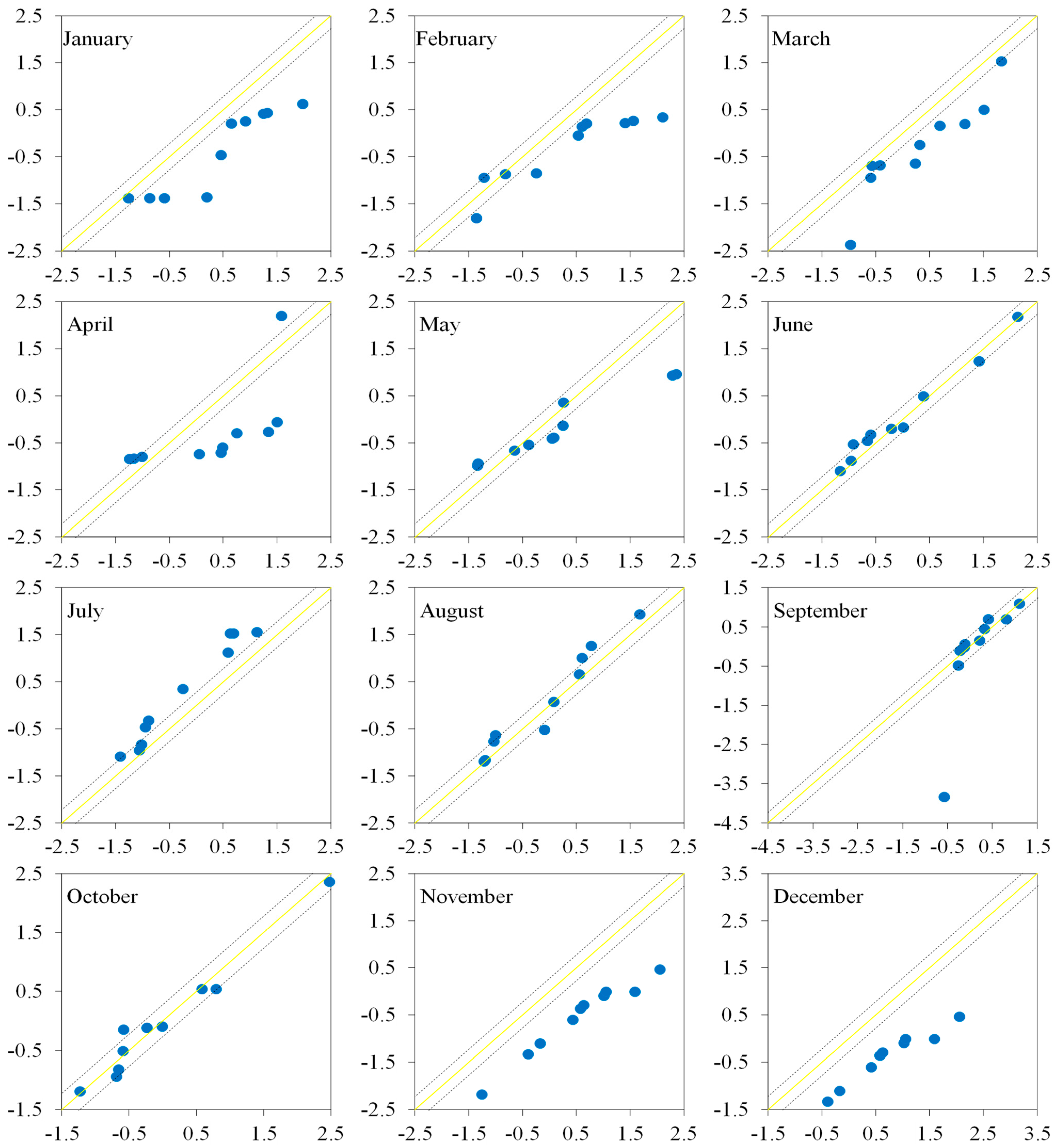
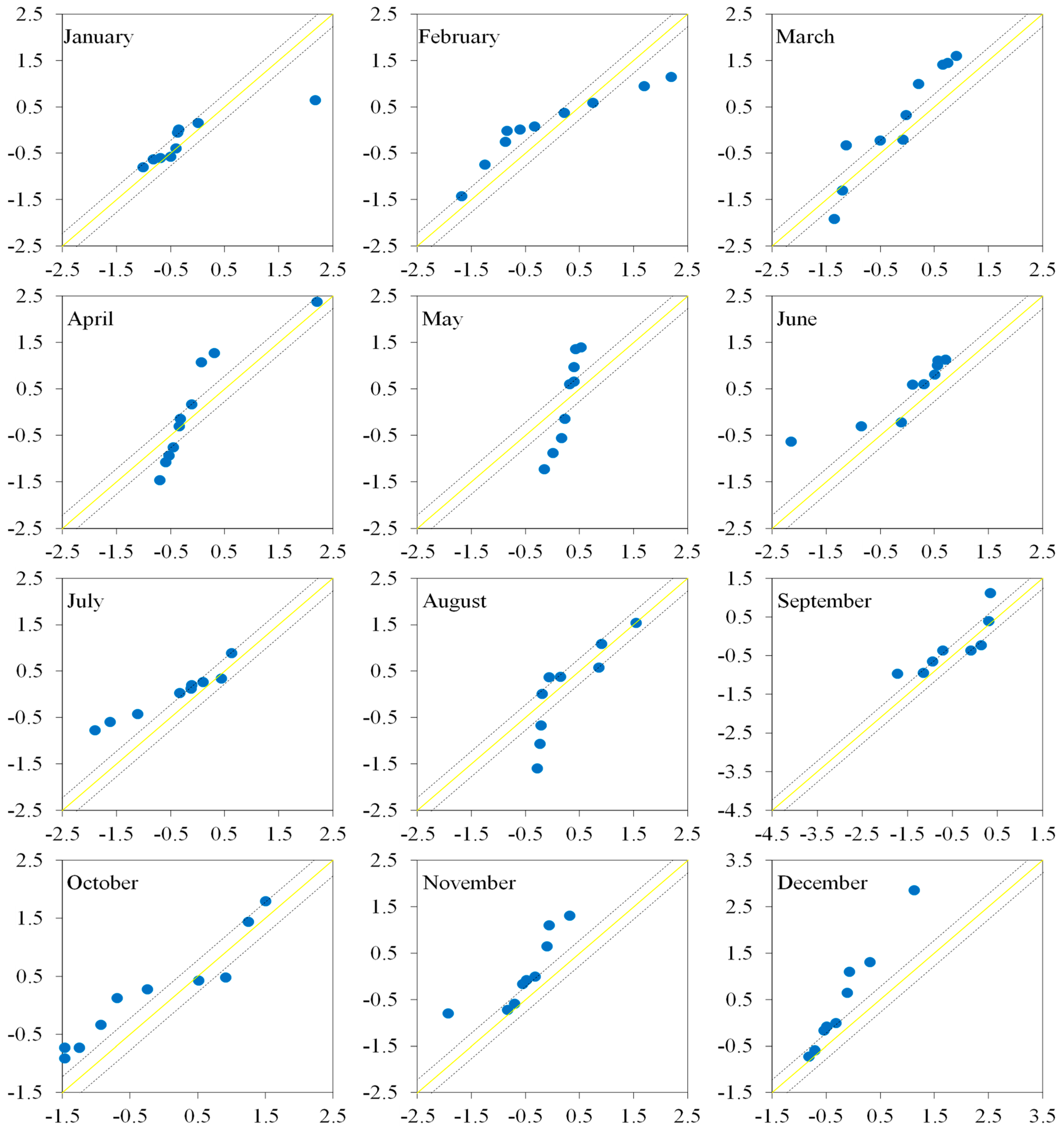
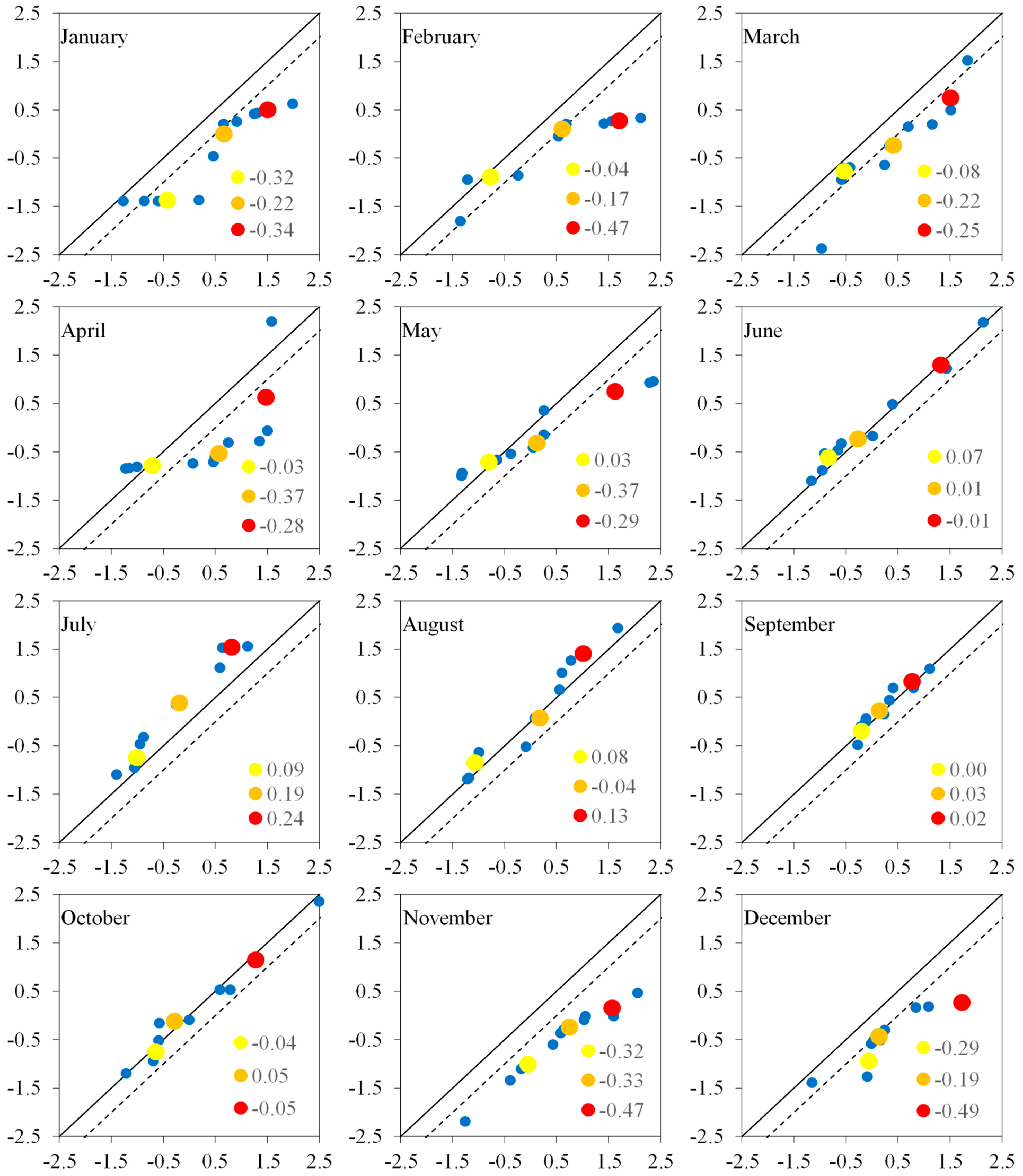
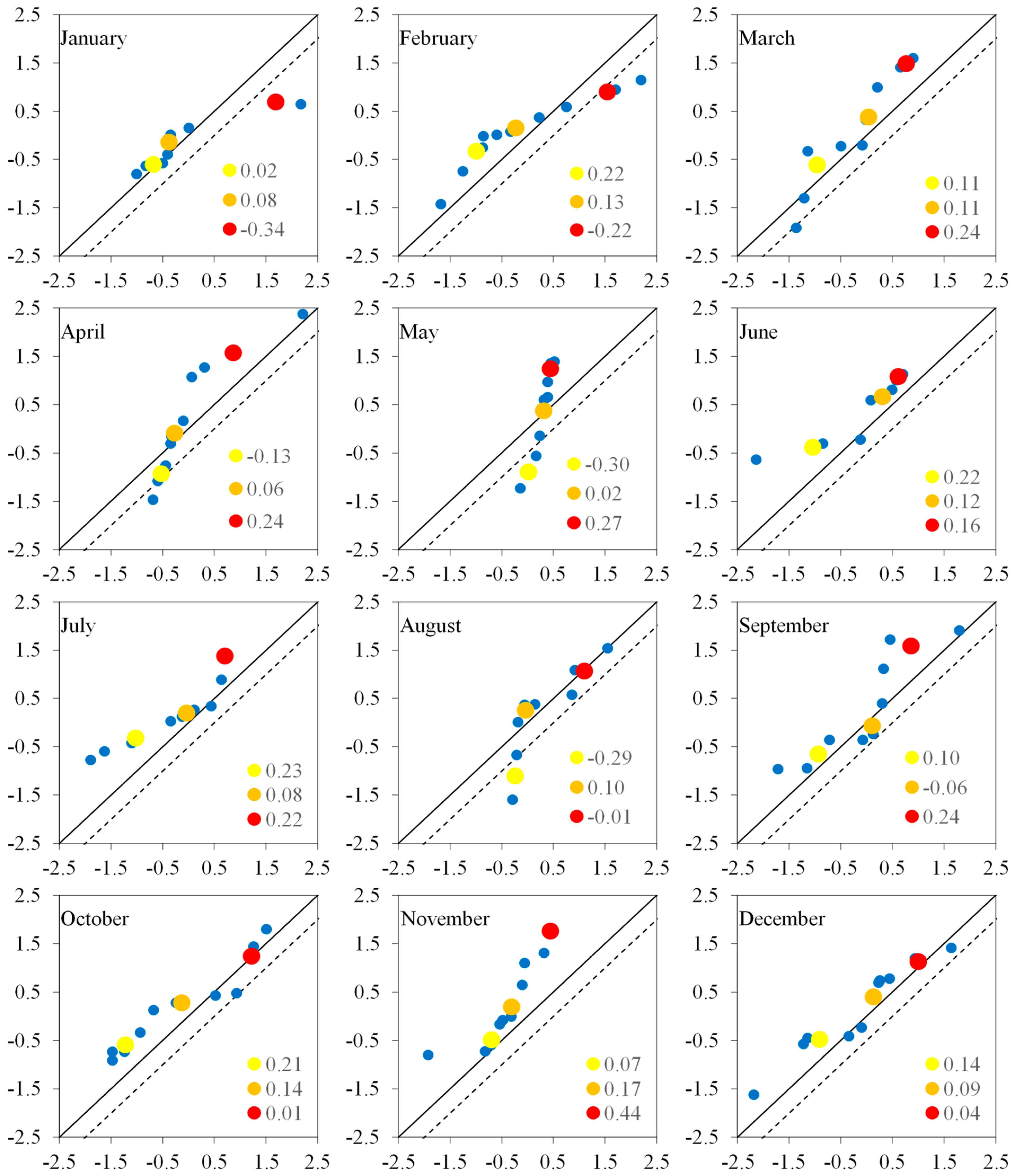
3.3. Variations in Monthly Hydrological Drought Indices
3.4. Comparison of Trend Results
4. Discussion
5. Conclusions
- From October to March, hydrological drought timeseries at the monthly scale exhibited significant downward trends;
- Hydrological drought timeseries from April to September exhibited significant increasing trends;
- The lower Indus plains’ access to water resources, where the majority of the community depends on agriculture, is consistently negatively impacted by hydrological droughts;
- IITA is a trustworthy and effective method because the results in all three methods were consistent, and it has the advantage of allowing researchers to examine patterns in the low, medium, and high values of hydrometeorological timeseries from its graphical representation over the other methods.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Crosbie, R.S.; Scanlon, B.R.; Mpelasoka, F.S.; Reedy, R.C.; Gates, J.B.; Zhang, L. Potential Climate Change Effects on Groundwater Recharge in the High Plains Aquifer, USA. Water Resour. Res. 2013, 49, 3936–3951. [Google Scholar] [CrossRef]
- Reshmidevi, T.V.; Kumar, D.N.; Mehrotra, R.; Sharma, A. Estimation of the Climate Change Impact on a Catchment Water Balance Using an Ensemble of GCMs. J. Hydrol. 2017, 556, 1192–1204. [Google Scholar] [CrossRef]
- Van Loon, A.F.; Stahl, K.; Di Baldassarre, G.; Clark, J.; Rangecroft, S.; Wanders, N.; Gleeson, T.; Van Dijk, A.I.J.M.; Tallaksen, L.M.; Hannaford, J.; et al. Drought in a Human-Modified World: Reframing Drought Definitions, Understanding, and Analysis Approaches. Hydrol. Earth Syst. Sci. 2016, 20, 3631–3650. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Nicholls, N.; Easterling, D.; Goodess, C.M.; Kanae, S.; Kossin, J.; Luo, Y.; Marengo, J.; Mc Innes, K.; Rahimi, M.; et al. Changes in Climate Extremes and Their Impacts on the Natural Physical Environment. Manag. Risks Extrem. Events Disasters Adv. Clim. Chang. Adapt. Spec. Rep. Intergov. Panel Clim. Chang. 2012, 9781107025, 109–230. [Google Scholar] [CrossRef]
- Yu, M.; Li, Q.; Hayes, M.J.; Svoboda, M.D.; Heim, R.R. Are Droughts Becoming More Frequent or Severe in China Based on the Standardized Precipitation Evapotranspiration Index: 1951–2010? Int. J. Climatol. 2014, 34, 545–558. [Google Scholar] [CrossRef]
- Stringer, L.C.; Akhtar-Schuster, M.; Marques, M.J.; Amiraslani, F.; Quatrini, S.; Abraham, E.M. Combating Land Degradation and Desertification and Enhancing Food Security: Towards Integrated Solutions. Ann. Arid Zone 2011, 50, 1–23. [Google Scholar]
- Sohrabi, M.M.; Ryu, J.H.; Abatzoglou, J.; Tracy, J. Climate Extreme and Its Linkage to Regional Drought over Idaho, USA. Nat. Hazards 2013, 65, 653–681. [Google Scholar] [CrossRef]
- Sharma, T.C.; Panu, U.S. Procédures d’analyse de Sécheresses Hydrologiques Hebdomadaires: Le Cas de Rivières Canadiennes. Hydrol. Sci. J. 2010, 55, 79–92. [Google Scholar] [CrossRef]
- Bae, H.; Ji, H.; Lim, Y.J.; Ryu, Y.; Kim, M.H.; Kim, B.J. Characteristics of Drought Propagation in South Korea: Relationship between Meteorological, Agricultural, and Hydrological Droughts. Nat. Hazards 2019, 99, 1–16. [Google Scholar] [CrossRef]
- Zhao, C.; Brissette, F.; Chen, J.; Martel, J.-L. Frequency Change of Future Extreme Summer Meteorological and Hydrological Droughts over North America. J. Hydrol. 2020, 584, 124316. [Google Scholar] [CrossRef]
- Waseem, M.; Jaffry, A.H.; Azam, M.; Ahmad, I.; Abbas, A.; Lee, J.E. Spatiotemporal Analysis of Drought and Agriculture Standardized Residual Yield Series Nexuses across Punjab, Pakistan. Water 2022, 14, 496. [Google Scholar] [CrossRef]
- Waseem, M.; Ahmad, I.; Mujtaba, A.; Tayyab, M.; Si, C.; Lü, H.; Dong, X. Spatiotemporal Dynamics of Precipitation in Southwest Arid-Agriculture Zones of Pakistan. Sustainability 2020, 12, 2305. [Google Scholar] [CrossRef]
- Muhammad, W.; Muhammad, S.; Khan, N.M.; Si, C. Hydrological Drought Indexing Approach in Response to Climate and Anthropogenic Activities. Theor. Appl. Climatol. 2020, 141, 1401–1413. [Google Scholar] [CrossRef]
- Waseem, M.; Khurshid, T.; Abbas, A.; Ahmad, I.; Javed, Z. Impact of Meteorological Drought on Agriculture Production at Different Scales in Punjab, Pakistan. J. Water Clim. Chang. 2022, 13, 113–124. [Google Scholar] [CrossRef]
- Waseem, M.; Ajmal, M.; Ahmad, I.; Khan, N.; Azam, M.; Sarwar, M. Projected Drought Pattern under Climate Change Scenario Using Multivariate Analysis. Arab. J. Geosci. 2021, 14, 544. [Google Scholar] [CrossRef]
- Sarwar, A.N.; Waseem, M.; Azam, M.; Abbas, A.; Ahmad, I.; Lee, J.E.; Haq, F.U. Shifting of Meteorological to Hydrological Drought Risk at Regional Scale. Appl. Sci. 2022, 12, 5560. [Google Scholar] [CrossRef]
- Peña-Gallardo, M.; Vicente-Serrano, S.M.; Hannaford, J.; Lorenzo-Lacruz, J.; Svoboda, M.; Domínguez-Castro, F.; Maneta, M.; Tomas-Burguera, M.; Kenawy, A. El Complex Influences of Meteorological Drought Time-Scales on Hydrological Droughts in Natural Basins of the Contiguous Unites States. J. Hydrol. 2019, 568, 611–625. [Google Scholar] [CrossRef]
- Kubiak-Wójcicka, K.; Bąk, B. Monitoring of Meteorological and Hydrological Droughts in the Vistula Basin (Poland). Environ. Monit. Assess. 2018, 190, 87–100. [Google Scholar] [CrossRef] [PubMed]
- Skakun, S.; Kussul, N.; Shelestov, A.; Kussul, O. The Use of Satellite Data for Agriculture Drought Risk Quantification in Ukraine. Geomat. Nat. Hazards Risk 2016, 7, 901–917. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, G. Analysis of Drought Hazards in North China: Distribution and Interpretation. Nat. Hazards 2013, 65, 279–294. [Google Scholar] [CrossRef]
- Ullah, I.; Ma, X.; Yin, J.; Omer, A.; Habtemicheal, B.A.; Saleem, F.; Iyakaremye, V.; Syed, S.; Arshad, M.; Liu, M. Spatiotemporal Characteristics of Meteorological Drought Variability and Trends (1981–2020) over South Asia and the Associated Large-Scale Circulation Patterns. Clim. Dyn. 2022, 60, 2261–2284. [Google Scholar] [CrossRef]
- Ullah, I.; Ma, X.; Asfaw, T.G.; Yin, J.; Iyakaremye, V.; Saleem, F.; Xing, Y.; Azam, K.; Syed, S. Projected Changes in Increased Drought Risks Over South Asia Under a Warmer Climate. Earth’s Future 2022, 10, e2022EF002830. [Google Scholar] [CrossRef]
- Bard, A.; Renard, B.; Lang, M.; Giuntoli, I.; Korck, J.; Koboltschnig, G.; Janža, M.; d’Amico, M.; Volken, D. Trends in the Hydrologic Regime of Alpine Rivers. J. Hydrol. 2015, 529, 1823–1837. [Google Scholar] [CrossRef]
- Wang, X.; Hou, X.; Wang, Y. Spatiotemporal Variations and Regional Differences of Extreme Precipitation Events in the Coastal Area of China from 1961 to 2014. Atmos. Res. 2017, 197, 94–104. [Google Scholar] [CrossRef]
- Patakamuri, S.K.; Muthiah, K.; Sridhar, V. Long-Term Homogeneity, Trend, and Change-Point Analysis of Rainfall in the Arid District of Ananthapuramu, Andhra Pradesh State, India. Water 2020, 12, 211. [Google Scholar] [CrossRef]
- Abeysingha, N.S.; Singh, M.; Sehgal, V.K.; Khanna, M.; Pathak, H. Analysis of Trends in Streamflow and Its Linkages with Rainfall and Anthropogenic Factors in Gomti River Basin of North India. Theor. Appl. Climatol. 2016, 123, 785–799. [Google Scholar] [CrossRef]
- Abghari, H.; Tabari, H.; Talaee, P.H. River Flow Trends in the West of Iran during the Past 40 years: Impact of Precipitation Variability. Glob. Planet. Chang. 2013, 101, 52–60. [Google Scholar] [CrossRef]
- Şen, Z. Innovative Trend Analysis Methodology. J. Hydrol. Eng. 2012, 17, 1042–1046. [Google Scholar] [CrossRef]
- Şen, Z. Innovative Trend Significance Test and Applications. Theor. Appl. Climatol. 2017, 127, 939–947. [Google Scholar] [CrossRef]
- Markus, M.; Demissie, M.; Short, M.B.; Verma, S.; Cooke, R.A. Sensitivity Analysis of Annual Nitrate Loads and the Corresponding Trends in the Lower Illinois River. J. Hydrol. Eng. 2014, 19, 533–543. [Google Scholar] [CrossRef]
- Onyutha, C. Identification of Sub-Trends from Hydro-Meteorological Series. Stoch. Environ. Res. Risk Assess. 2016, 30, 189–205. [Google Scholar] [CrossRef]
- Tefaruk, H.; Hatice, C. Trend, Independence, Stationarity, and Homogeneity Tests on Maximum Rainfall Series of Standard Durations Recorded in Turkey. J. Hydrol. Eng. 2014, 19, 5014009. [Google Scholar] [CrossRef]
- Elouissi, A.; Şen, Z.; Habi, M. Algerian Rainfall Innovative Trend Analysis and Its Implications to Macta Watershed. Arab. J. Geosci. 2016, 9, 303. [Google Scholar] [CrossRef]
- Ay, M.; Kisi, O. Investigation of Trend Analysis of Monthly Total Precipitation by an Innovative Method. Theor. Appl. Climatol. 2015, 120, 617–629. [Google Scholar] [CrossRef]
- Wu, H.; Qian, H. Innovative Trend Analysis of Annual and Seasonal Rainfall and Extreme Values in Shaanxi, China, since the 1950s. Int. J. Climatol. 2017, 37, 2582–2592. [Google Scholar] [CrossRef]
- Tosunoglu, F.; Kisi, O. Trend Analysis of Maximum Hydrologic Drought Variables Using Mann–Kendall and Şen’s Innovative Trend Method. River Res. Appl. 2017, 33, 597–610. [Google Scholar] [CrossRef]
- Dabanlı, İ.; Şen, Z.; Yeleğen, M.Ö.; Şişman, E.; Selek, B.; Güçlü, Y.S. Trend Assessment by the Innovative-Şen Method. Water Resour. Manag. 2016, 30, 5193–5203. [Google Scholar] [CrossRef]
- Güçlü, Y.S. Multiple Şen-Innovative Trend Analyses and Partial Mann-Kendall Test. J. Hydrol. 2018, 566, 685–704. [Google Scholar] [CrossRef]
- Birpınar, M.E.; Kızılöz, B.; Şişman, E. Classic Trend Analysis Methods’ Paradoxical Results and Innovative Trend Analysis Methodology with Percentile Ranges. Theor. Appl. Climatol. 2023, 1–18. [Google Scholar] [CrossRef]
- Şişman, E.; Kizilöz, B. The Application of Piecewise ITA Method in Oxford, 1870–2019. Theor. Appl. Climatol. 2021, 145, 1451–1465. [Google Scholar] [CrossRef]
- Bolch, T.; Kulkarni, A.; Kääb, A.; Huggel, C.; Paul, F.; Cogley, J.G.; Frey, H.; Kargel, J.S.; Fujita, K.; Scheel, M.; et al. The State and Fate of Himalayan Glaciers. Science 2012, 336, 310–314. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; van Beek, L.P.H.; Konz, M.; Shrestha, A.B.; Bierkens, M.F.P. Hydrological Response to Climate Change in a Glacierized Catchment in the Himalayas. Clim. Chang. 2012, 110, 721–736. [Google Scholar] [CrossRef] [PubMed]
- De Souza, K.; Kituyi, E.; Harvey, B.; Leone, M.; Murali, K.S.; Ford, J.D. Vulnerability to Climate Change in Three Hot Spots in Africa and Asia: Key Issues for Policy-Relevant Adaptation and Resilience-Building Research. Reg. Environ. Chang. 2015, 15, 747–753. [Google Scholar] [CrossRef]
- Hasson, S.; Böhner, J.; Lucarini, V. Prevailing Climatic Trends and Runoff Response from Hindukush-Karakoram-Himalaya, Upper Indus Basin. Earth Syst. Dyn. 2015, 6, 579–653. [Google Scholar] [CrossRef]
- Ali, S.; Wang, Q.; Liu, D.; Fu, Q.; Mafuzur Rahaman, M.; Abrar Faiz, M.; Jehanzeb Masud Cheema, M. Estimation of Spatio-Temporal Groundwater Storage Variations in the Lower Transboundary Indus Basin Using GRACE Satellite. J. Hydrol. 2022, 605, 127315. [Google Scholar] [CrossRef]
- Arshad, A.; Mirchi, A.; Samimi, M.; Ahmad, B. Combining Downscaled-GRACE Data with SWAT to Improve the Estimation of Groundwater Storage and Depletion Variations in the Irrigated Indus Basin (IIB). Sci. Total Environ. 2022, 838, 156044. [Google Scholar] [CrossRef]
- Ali, S.; Khorrami, B.; Jehanzaib, M.; Tariq, A.; Ajmal, M.; Arshad, A.; Shafeeque, M.; Dilawar, A.; Basit, I.; Zhang, L.; et al. Spatial Downscaling of GRACE Data Based on XGBoost Model for Improved Understanding of Hydrological Droughts in the Indus Basin Irrigation System (IBIS). Remote Sens. 2023, 15, 873. [Google Scholar] [CrossRef]
- Hashmi, H.N.; Siddiqui, Q.T.M.; Ghumman, A.R.; Kamal, M.A.; Mughal, H.U.R. A Critical Analysis of 2010 Floods in Pakistan. Afr. J. Agric. Res. 2012, 7, 1054–1067. [Google Scholar] [CrossRef]
- Lutz, A.F.; ter Maat, H.W.; Biemans, H.; Shrestha, A.B.; Wester, P.; Immerzeel, W.W. Selecting Representative Climate Models for Climate Change Impact Studies: An Advanced Envelope-Based Selection Approach. Int. J. Climatol. 2016, 36, 3988–4005. [Google Scholar] [CrossRef]
- Latif, Y.; Yaoming, M.; Yaseen, M. Spatial Analysis of Precipitation Time Series over the Upper Indus Basin. Theor. Appl. Climatol. 2018, 131, 761–775. [Google Scholar] [CrossRef]
- Saifullah, M.; Liu, S.; Tahir, A.A.; Zaman, M.; Ahmad, S.; Adnan, M.; Chen, D.; Ashraf, M.; Mehmood, A. Development of Threshold Levels and a Climate-Sensitivity Model of the Hydrological Regime of the High-Altitude Catchment of the Western Himalayas, Pakistan. Water 2019, 11, 1454. [Google Scholar] [CrossRef]
- Ul Hasson, S.; Böhner, J.; Lucarini, V. Prevailing Climatic Trends and Runoff Response from Hindukush-Karakoram-Himalaya, Upper Indus Basin. Earth Syst. Dyn. 2017, 8, 337–355. [Google Scholar] [CrossRef]
- Zaman, M.; Ahmad, I.; Usman, M.; Saifullah, M.; Anjum, M.N.; Khan, M.I.; Qamar, M.U. Event-Based Time Distribution Patterns, Return Levels, and Their Trends of Extreme Precipitation across Indus Basin. Water 2020, 12, 3373. [Google Scholar] [CrossRef]
- Arfan, M.; Lund, J.; Hassan, D.; Saleem, M.; Ahmad, A. Assessment of Spatial and Temporal Flow Variability of the Indus River. Resources 2019, 8, 103. [Google Scholar] [CrossRef]
- Lutz, A.F.; Immerzeel, W.W.; Kraaijenbrink, P.D.A.; Shrestha, A.B.; Bierkens, M.F.P. Climate Change Impacts on the Upper Indus Hydrology: Sources, Shifts and Extremes. PLoS ONE 2016, 11, e0165630. [Google Scholar] [CrossRef]
- Williams, M.W. The Status of Glaciers in the Hindu Kush–Himalayan Region. Mt. Res. Dev. 2013, 33, 114–115. [Google Scholar] [CrossRef]
- Bocchiola, D.; Diolaiuti, G. Recent (1980–2009) Evidence of Climate Change in the Upper Karakoram, Pakistan. Theor. Appl. Climatol. 2013, 113, 611–641. [Google Scholar] [CrossRef]
- Minora, U.; Bocchiola, D.; D’Agata, C.; Maragno, D.; Mayer, C.; Lambrecht, A.; Mosconi, B.; Vuillermoz, E.; Senese, A.; Compostella, C.; et al. 2001–2010 glacier changes in the Central Karakoram National Park: A contribution to evaluate the magnitude and rate of the “Karakoram anomaly”. Cryosph. Discuss. 2013, 7, 2891–2941. [Google Scholar] [CrossRef]
- Qureshi, A.S. Water Management in the Indus Basin in Pakistan: Challenges and Opportunities. Mt. Res. Dev. 2011, 31, 252–260. [Google Scholar] [CrossRef]
- Abbas, F.; Ahmad, A.; Khan, S.; Ali, S.; Saleem, F.; Hammad, H.; Farhad, W. Changes in Precipitation Extremes over Arid to Semiarid and Subhumid Punjab, Pakistan. Theor. Appl. Climatol. 2013, 116, 219. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1975; ISBN-10 0852641990, ISBN-13 9780852641996. [Google Scholar]
- Tabari, H.; Marofi, S.; Aeini, A.; Talaee, P.H.; Mohammadi, K. Trend Analysis of Reference Evapotranspiration in the Western Half of Iran. Agric. For. Meteorol. 2011, 151, 128–136. [Google Scholar] [CrossRef]
- Tabari, H.; Talaee, P.H.; Ezani, A.; Some’e, B.S. Shift Changes and Monotonic Trends in Autocorrelated Temperature Series over Iran. Theor. Appl. Climatol. 2012, 109, 95–108. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Ferrari, E.; Mancini, M. Trend Detection of Annual and Seasonal Rainfall in Calabria (Southern Italy). Int. J. Climatol. 2011, 31, 44–56. [Google Scholar] [CrossRef]
- del Río, S.; Penas, Á.; Fraile, R. Analysis of Recent Climatic Variations in Castile and Leon (Spain). Atmos. Res. 2005, 73, 69–85. [Google Scholar] [CrossRef]
- Bhutiyani, M.R.; Kale, V.S.; Pawar, N.J. Long-Term Trends in Maximum, Minimum and Mean Annual Air Temperatures across the Northwestern Himalaya during the Twentieth Century. Clim. Chang. 2007, 85, 159–177. [Google Scholar] [CrossRef]
- Hamed, K.H. Trend Detection in Hydrologic Data: The Mann–Kendall Trend Test under the Scaling Hypothesis. J. Hydrol. 2008, 349, 350–363. [Google Scholar] [CrossRef]
- Mavromatis, T.; Stathis, D. Response of the Water Balance in Greece to Temperature and Precipitation Trends. Theor. Appl. Climatol. 2011, 104, 13–24. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C. The Mann-Kendall Test Modified by Effective Sample Size to Detect Trend in Serially Correlated Hydrological Series. Water Resour. Manag. 2004, 18, 201–218. [Google Scholar] [CrossRef]
- Helsel, D.R.; Hirsch, R.M. Statistical Methods in Water Resources; Elsevier: Amsterdam, The Netherlands, 1992; ISBN 9780080875088. [Google Scholar]
- Ashraf, M.S.; Ahmad, I.; Khan, N.M.; Zhang, F.; Bilal, A.; Guo, J. Streamflow Variations in Monthly, Seasonal, Annual and Extreme Values Using Mann-Kendall, Spearmen’s Rho and Innovative Trend Analysis. Water Resour. Manag. 2021, 35, 243–261. [Google Scholar] [CrossRef]
- Yaseen, M.; Latif, Y.; Waseem, M.; Leta, M.K.; Abbas, S.; Bhatti, H.A. Contemporary Trends in High and Low River Flows in Upper Indus Basin, Pakistan. Water 2022, 14, 337. [Google Scholar] [CrossRef]
- Archer, D.R.D.; Fowler, H.J.H. Spatial and Temporal Variations in Precipitation in the Upper Indus Basin, Global Teleconnections and Hydrological Implications. Hydrol. Earth Syst. Sci. 2004, 8, 47–61. [Google Scholar] [CrossRef]
- Ahsan, M.; Sattarshakir, A.; Zafar, S.; Nabi, G.; Ahsan, E.M. Assessment of Climate Change and Variability in Temperature, Precipitation and Flows in Upper Indus Basin. Int. J. Sci. Eng. Res. 2016, 7, 1610–1620. [Google Scholar]

| SDI Value | ≤2.00 | 1.50–1.99 | 1.0–1.49 | 0.00–−0.99 | −1.00–−1.49 | −1.50–−1.99 | ≤−2.00 |
| Category | Extremely Wet | Severely Wet | Moderate Wet | Mild Drought | Moderate Drought | Severe Drought | Extreme Drought |
| Sr. No. | Station | Latitude (Degree) | Longitude (Degree) | Elevation (m) | Mean (m3/s) | SD | Cs | Ck | Cv |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Kharmong | 35.2 | 75.9 | 2474 | 461.1 | 482.9 | 1.487 | 1.579 | 1.047 |
| 2 | Gilgit | 35.9 | 74.3 | 2126 | 277.2 | 287.1 | 1.489 | 1.308 | 1.036 |
| 3 | Kalam | 35.5 | 72.6 | 2067 | 87.0 | 96.3 | 2.129 | 17.424 | 1.107 |
| 4 | Chitral | 35.9 | 71.8 | 1566 | 276.8 | 279.5 | 1.486 | 1.285 | 1.010 |
| 5 | Besham Qila | 34.9 | 72.9 | 753 | 2419.8 | 2672.4 | 1.466 | 1.358 | 1.104 |
| 6 | Jhansi Post | 33.9 | 71.4 | 531 | 5.8 | 10.0 | 11.559 | 312.399 | 1.714 |
| 7 | Chahan | 33.4 | 72.9 | 453 | 1.5 | 8.9 | 25.406 | 1046.472 | 5.838 |
| 8 | Thal | 33.4 | 71.5 | 427 | 24.7 | 25.6 | 7.284 | 113.445 | 1.036 |
| 9 | Nowshera | 34.0 | 72.0 | 294 | 842.9 | 766.4 | 1.587 | 3.592 | 0.909 |
| 10 | Massan | 33.0 | 71.7 | 218 | 3741.5 | 3056.2 | 1.789 | 4.286 | 0.817 |
| Station | Length of Data Years | Pettitt’s Test Xk | Cum. Deviation Test | BR Test | SNHT To | Results |
|---|---|---|---|---|---|---|
| Kharmong | 35 | 120 | 1.12 | 1.58 | 4.97 | Useful |
| Gilgit | 52 | 300 | 1.24 | 1.49 | 7.86 | Useful |
| Besham Qila | 47 | 110 | 0.59 | 0.74 | 1.58 | Useful |
| Kalam | 52 | 211 | 0.86 | 1.09 | 3.32 | Useful |
| Chitral | 52 | 292 | 1.23 | 1.23 | 7.07 | Useful |
| Jhansi Post | 52 | 308 | 1.34 | 1.34 | 15.86 ** | Useful |
| Nowshera | 52 | 186 | 0.92 | 1.26 | 7.08 | Useful |
| Thal | 47 | 304 ** | 1.39 | 1.72 | 7.68 | Useful |
| Chahan | 52 | 220 | 1.24 | 1.39 | 9.15 | Useful |
| Massan | 44 | 182 | 0.97 | 1.37 | 3.95 | Useful |
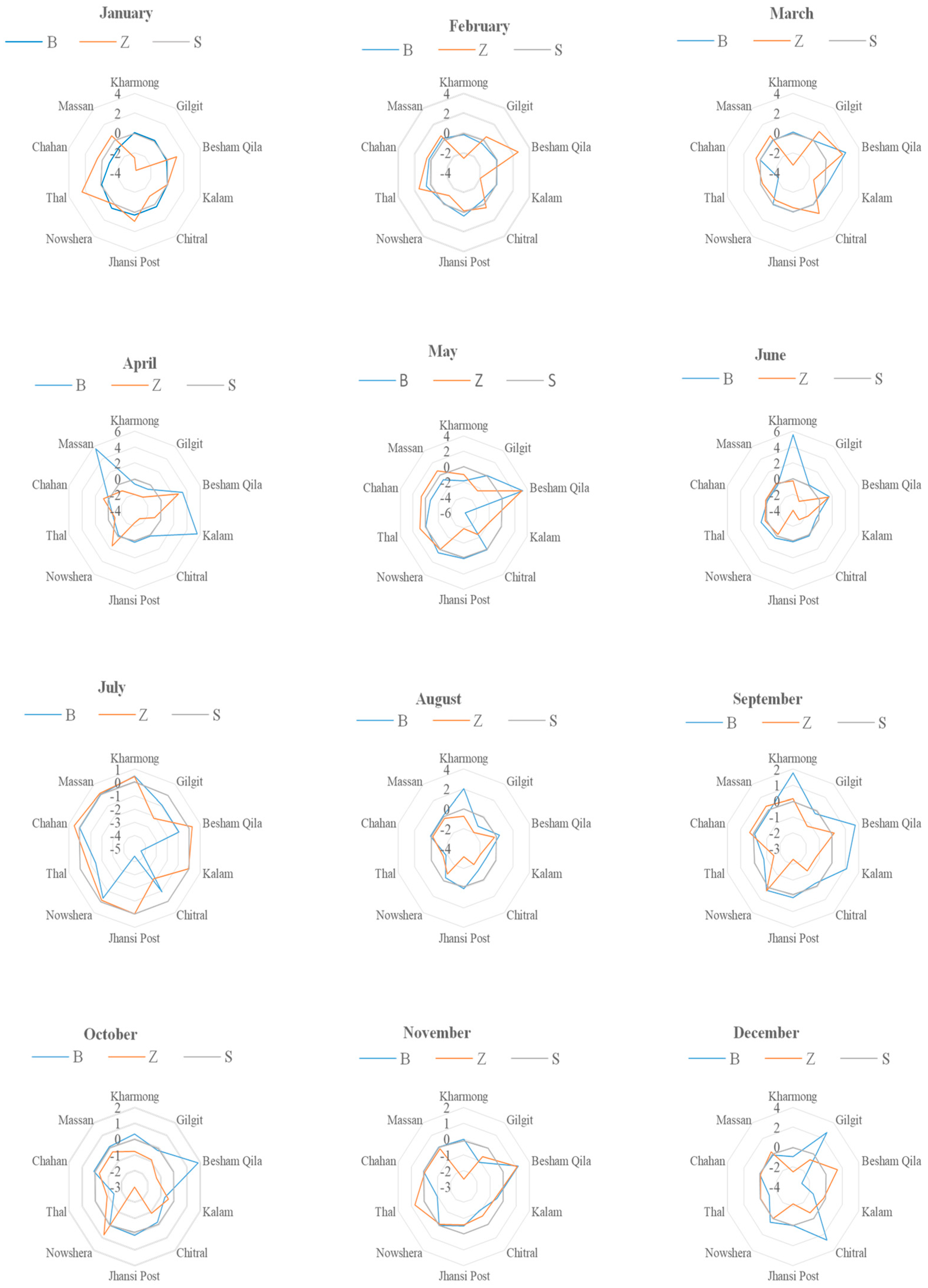
| Month | Test | Kharmong | Gilgit | Besham Qila | Kalam | Chitral | Jhansi Post | Nowshera | Thal | Chahan | Massan |
|---|---|---|---|---|---|---|---|---|---|---|---|
| January | B | 0.00 | 0.00 | −0.09 | 0.00 | 0.30 | 0.32 | 0.50 | 0.00 | −0.90 | −0.90 |
| Z | −2.54 | −3.77 | 1.14 | 0.00 | −1.01 | 0.94 | 0.00 | 2.43 | 0.55 | 0.55 | |
| S | −0.08 | −0.14 | 0.04 | 0.01 | 0.01 | 0.06 | 0.00 | 0.15 | −0.02 | −0.02 | |
| February | B | −0.18 | −0.42 | 0.02 | 0.00 | −0.42 | 0.41 | −0.09 | 0.58 | 0.27 | 0.27 |
| Z | −2.56 | 0.42 | 2.63 | −1.98 | 0.42 | −0.10 | −1.07 | 1.46 | 0.55 | 0.55 | |
| S | −0.07 | 0.00 | 0.08 | −0.05 | 0.00 | 0.05 | −0.02 | 0.07 | 0.01 | 0.01 | |
| March | B | 0.06 | 0.00 | 2.43 | 0.15 | 0.00 | 0.00 | 0.00 | −2.20 | 0.00 | 0.00 |
| Z | −3.28 | 1.14 | 2.02 | −1.46 | 1.14 | −0.42 | −0.52 | −0.26 | 0.55 | 0.55 | |
| S | −0.06 | 0.02 | 0.03 | −0.07 | 0.02 | 0.01 | −0.01 | −0.02 | 0.04 | 0.04 | |
| April | B | −0.69 | −0.69 | 3.32 | 5.60 | −0.02 | 0.07 | −0.05 | −0.75 | −0.09 | 5.60 |
| Z | −1.98 | −1.98 | 2.74 | −0.94 | −2.73 | −2.40 | 1.59 | −1.01 | 0.78 | −0.94 | |
| S | −0.06 | −0.06 | 0.05 | 0.01 | −0.12 | −0.16 | 0.08 | −0.03 | 0.07 | 0.01 | |
| May | B | −1.90 | −0.02 | 3.26 | −5.81 | −0.02 | 0.02 | 0.50 | −0.06 | −0.76 | −0.76 |
| Z | −1.04 | −2.47 | 3.15 | −1.95 | −2.47 | −3.93 | 0.00 | 0.88 | 0.71 | 0.71 | |
| S | −0.03 | −0.09 | 0.06 | −0.08 | −0.09 | −0.18 | 0.00 | 0.04 | 0.01 | 0.01 | |
| June | B | 5.56 | −0.02 | 1.52 | −0.49 | −0.02 | 0.01 | 0.36 | 0.87 | −0.10 | −0.10 |
| Z | −0.29 | −2.56 | 1.46 | −1.72 | −2.56 | −3.99 | −0.26 | 0.26 | 0.16 | 0.16 | |
| S | 0.01 | −0.10 | 0.07 | −0.09 | −0.10 | −0.15 | 0.02 | 0.03 | 0.06 | 0.06 | |
| July | B | 0.47 | −0.93 | −0.95 | −4.40 | −0.93 | −4.40 | −0.35 | −1.44 | 0.03 | 0.03 |
| Z | 0.45 | −2.17 | 0.29 | −0.03 | −2.17 | −0.03 | −0.13 | −0.78 | 0.55 | 0.16 | |
| S | 0.05 | −0.05 | 0.00 | −0.03 | −0.05 | −0.03 | 0.01 | −0.02 | 0.06 | 0.06 | |
| August | B | 2.05 | −1.22 | 0.38 | −1.22 | −1.22 | 0.05 | −0.34 | −1.83 | 0.10 | 0.10 |
| Z | −0.75 | −2.01 | −0.26 | −2.01 | −2.01 | −3.15 | −0.78 | −1.46 | −0.19 | −0.19 | |
| S | 0.02 | −0.07 | −0.03 | −0.07 | −0.07 | −0.15 | 0.02 | −0.04 | −0.04 | −0.04 | |
| September | B | 1.76 | −0.27 | 1.76 | 1.10 | −0.27 | 0.09 | 0.28 | −0.75 | −0.06 | −0.06 |
| Z | 0.13 | −1.27 | 0.13 | −1.27 | −1.27 | −2.30 | 0.29 | −1.52 | 0.32 | 0.32 | |
| S | −0.03 | −0.06 | −0.03 | −0.02 | −0.06 | −0.11 | 0.06 | −0.05 | 0.03 | 0.03 | |
| October | B | 0.33 | −0.19 | 1.85 | −0.68 | −0.19 | 0.09 | 0.04 | −1.43 | 0.11 | 0.11 |
| Z | −0.78 | −0.91 | −1.33 | −0.42 | −0.91 | −2.96 | 0.78 | −0.91 | −0.29 | −0.29 | |
| S | 0.00 | −0.05 | −0.04 | −0.01 | −0.05 | −0.12 | 0.04 | 0.00 | 0.04 | 0.04 | |
| November | B | −0.02 | −1.10 | 1.16 | −0.50 | −1.10 | −0.50 | 0.04 | −0.96 | 0.08 | 0.08 |
| Z | −2.53 | −0.68 | 1.10 | −0.58 | −0.68 | −0.58 | −0.03 | 0.75 | −0.03 | −0.03 | |
| S | −0.11 | −0.02 | 0.00 | −0.01 | −0.02 | −0.01 | 0.05 | 0.05 | 0.07 | 0.07 | |
| December | B | −0.98 | 2.73 | −2.95 | −1.56 | 2.73 | −0.06 | 0.50 | −1.07 | 0.08 | −0.06 |
| Z | −2.53 | −0.68 | 1.43 | −0.23 | −0.68 | −2.24 | 0.00 | −0.03 | −0.03 | 0.36 | |
| S | −0.09 | 0.03 | 0.01 | −0.06 | 0.03 | −0.07 | 0.00 | 0.03 | 0.07 | 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ashraf, M.S.; Shahid, M.; Waseem, M.; Azam, M.; Rahman, K.U. Assessment of Variability in Hydrological Droughts Using the Improved Innovative Trend Analysis Method. Sustainability 2023, 15, 9065. https://doi.org/10.3390/su15119065
Ashraf MS, Shahid M, Waseem M, Azam M, Rahman KU. Assessment of Variability in Hydrological Droughts Using the Improved Innovative Trend Analysis Method. Sustainability. 2023; 15(11):9065. https://doi.org/10.3390/su15119065
Chicago/Turabian StyleAshraf, Muhammad Shehzad, Muhammad Shahid, Muhammad Waseem, Muhammad Azam, and Khalil Ur Rahman. 2023. "Assessment of Variability in Hydrological Droughts Using the Improved Innovative Trend Analysis Method" Sustainability 15, no. 11: 9065. https://doi.org/10.3390/su15119065
APA StyleAshraf, M. S., Shahid, M., Waseem, M., Azam, M., & Rahman, K. U. (2023). Assessment of Variability in Hydrological Droughts Using the Improved Innovative Trend Analysis Method. Sustainability, 15(11), 9065. https://doi.org/10.3390/su15119065








