The Diffusion of Competitive Platform-Based Products with Network Effects
Abstract
1. Introduction
2. Literature Review
2.1. Research on Network Effects
2.2. Research on Two-Sided Platforms
2.3. Research on Product Diffusion
3. The Model
3.1. Consumer Decisions
3.2. Seller Decisions
- (1)
- The sellers who has not joined any platform and who will continue to do so will gain no profit; if the sellers choose to join platform , they will gain net profits , where is the learning cost incurred from preparing to produce a compatible product or service, which is assumed to be a normally distributed random variable, .
- (2)
- A seller on platform will gain when continuing to stay on; if sellers withdraws from platform k and will not join any platform, they will gain no profit; if they join the other platform, then the net profits are .
3.3. Complex User Network Construction
- (1)
- Start with order: Construct a ring-shaped network consisting of nodes, where each node is adjacent to its neighboring nodes, , with being even. Here, the nodes represent users.
- (2)
- Randomization: Add shortcuts between randomly chosen pairs of nodes with probability .
4. Computing Settings
5. Results Analysis
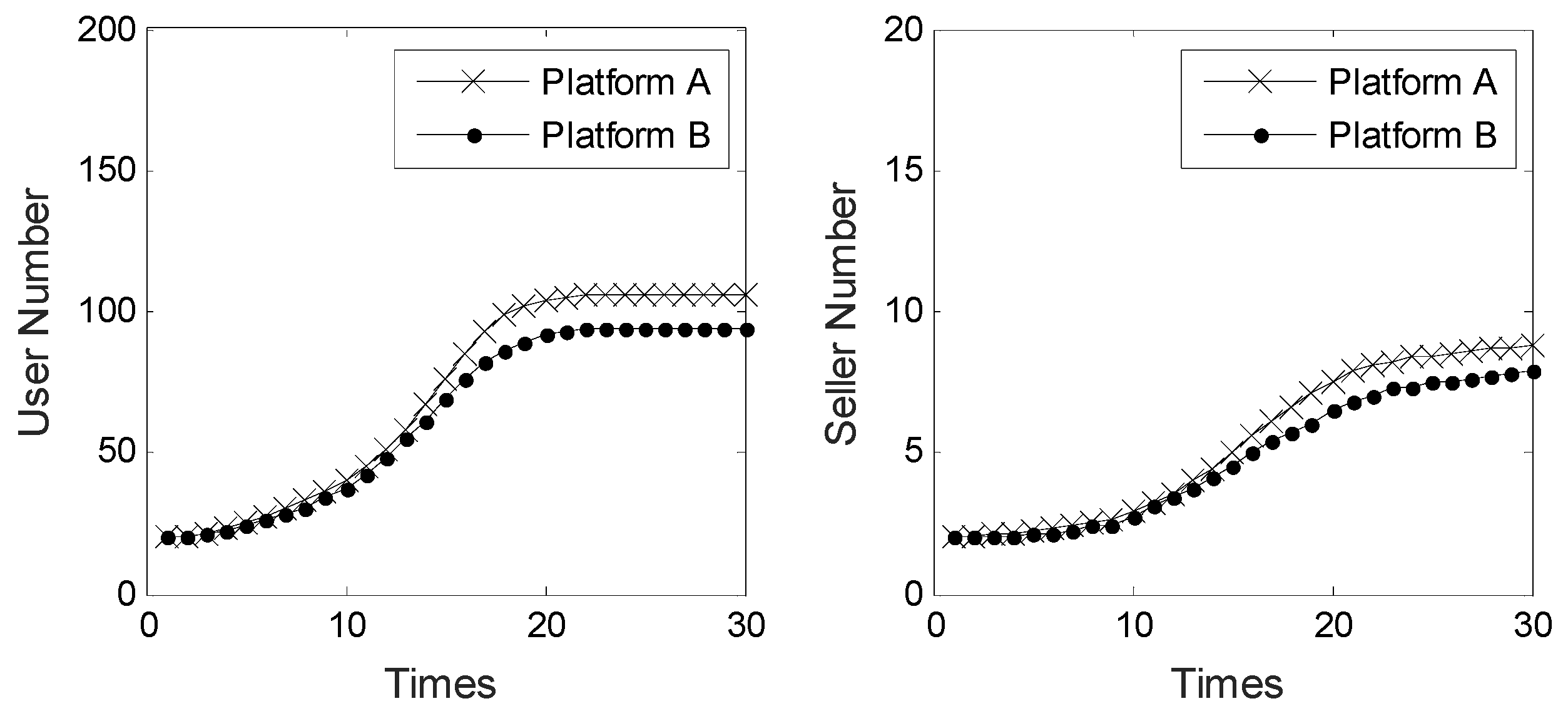
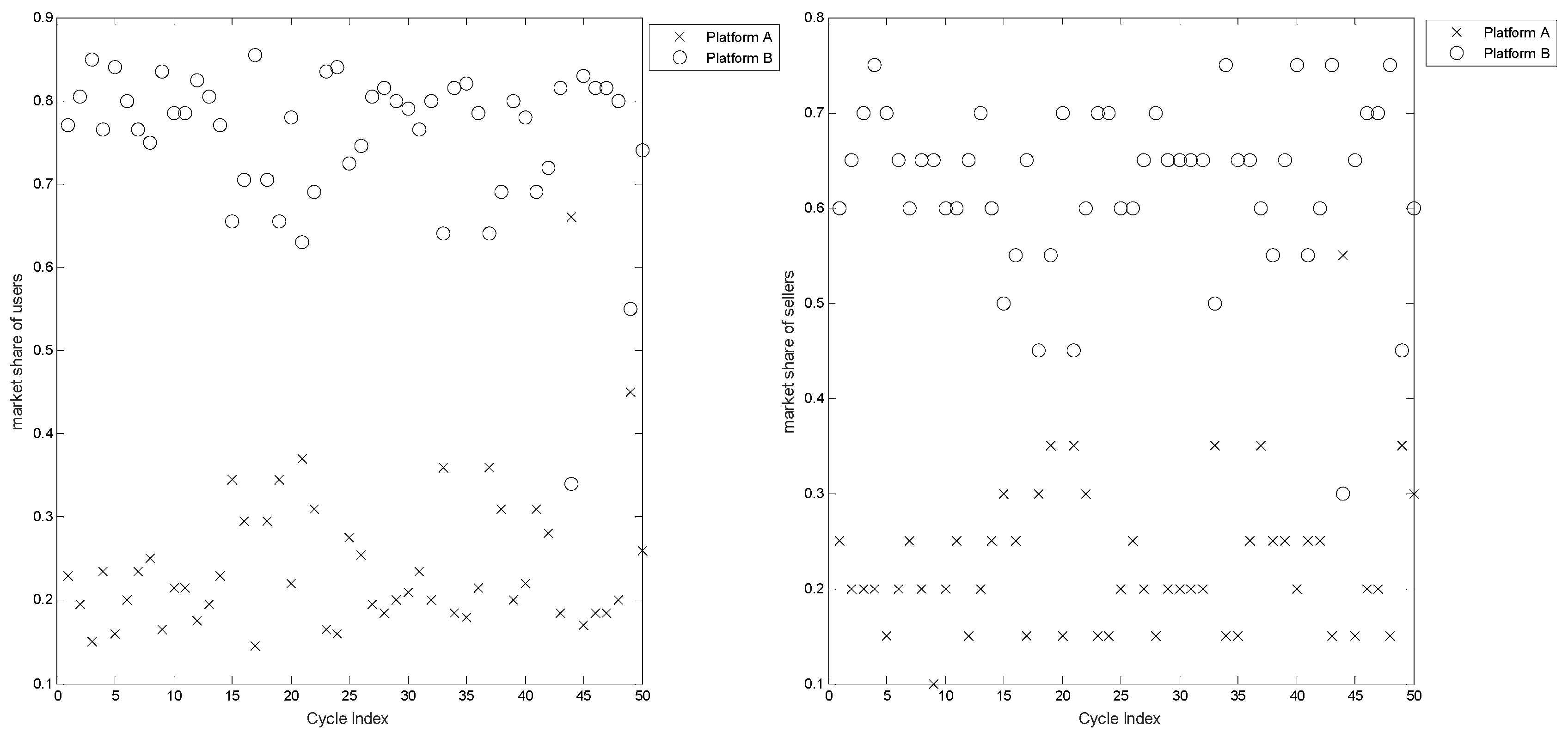
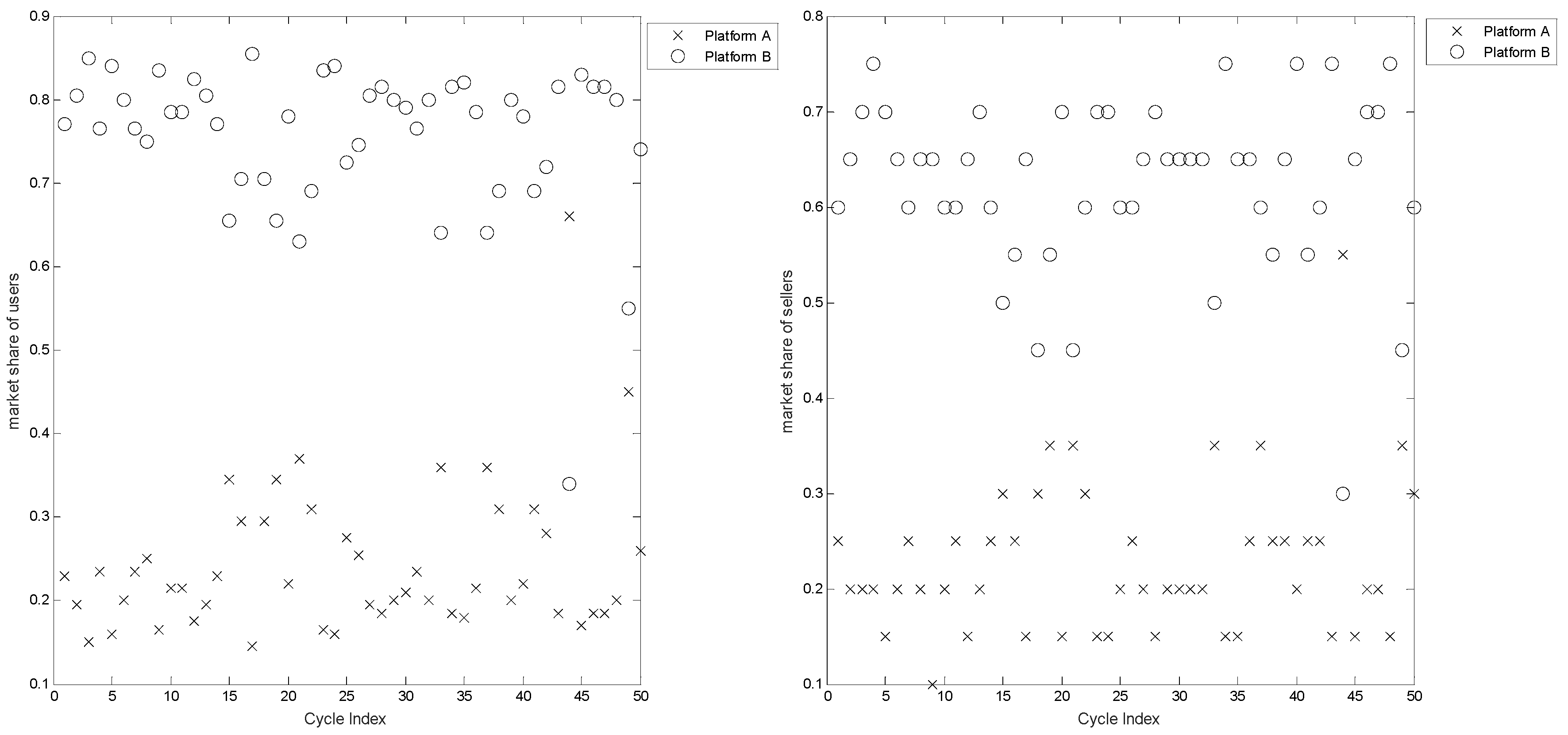
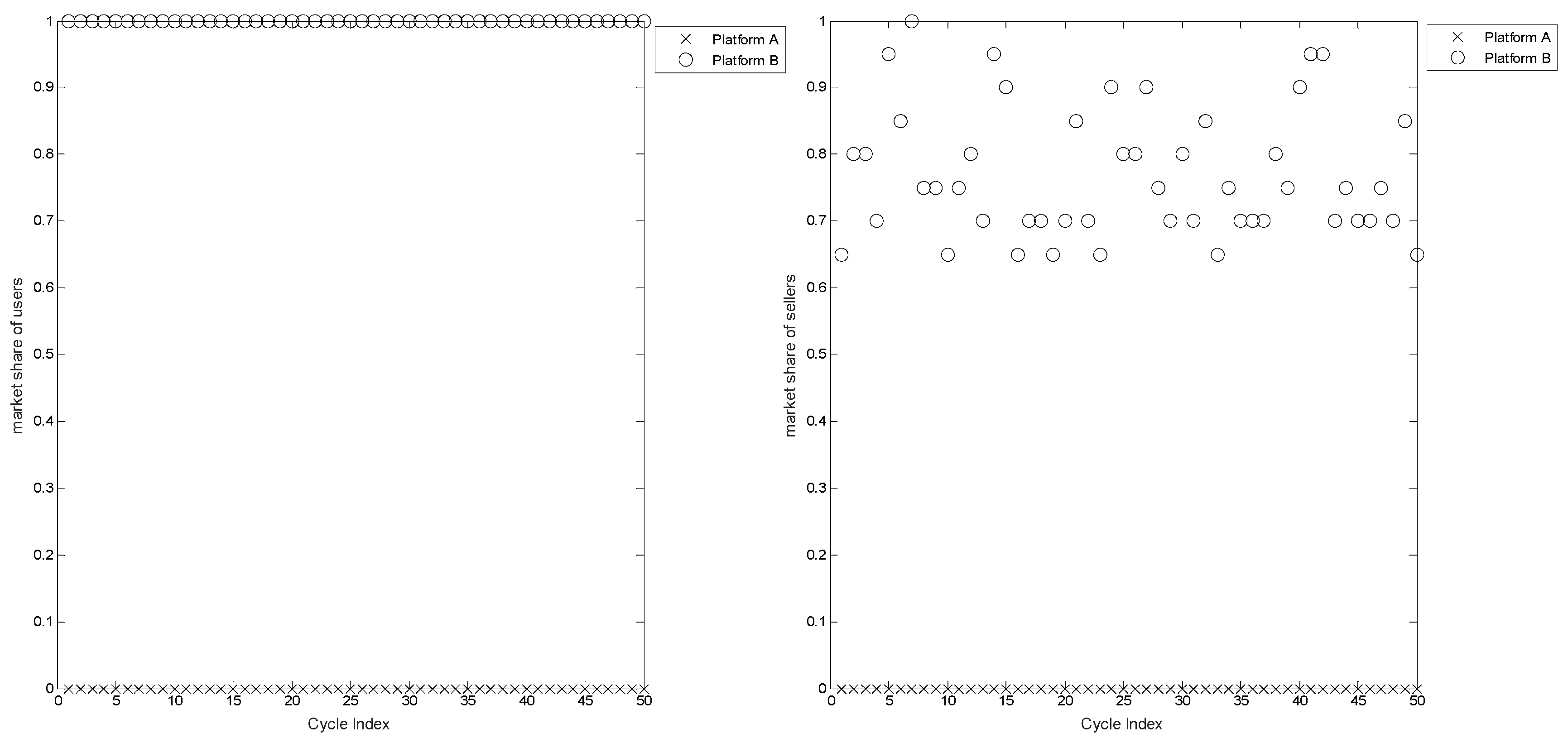
5.1. Properties of Platform Diffusion with Direct and Indirect Network Effects
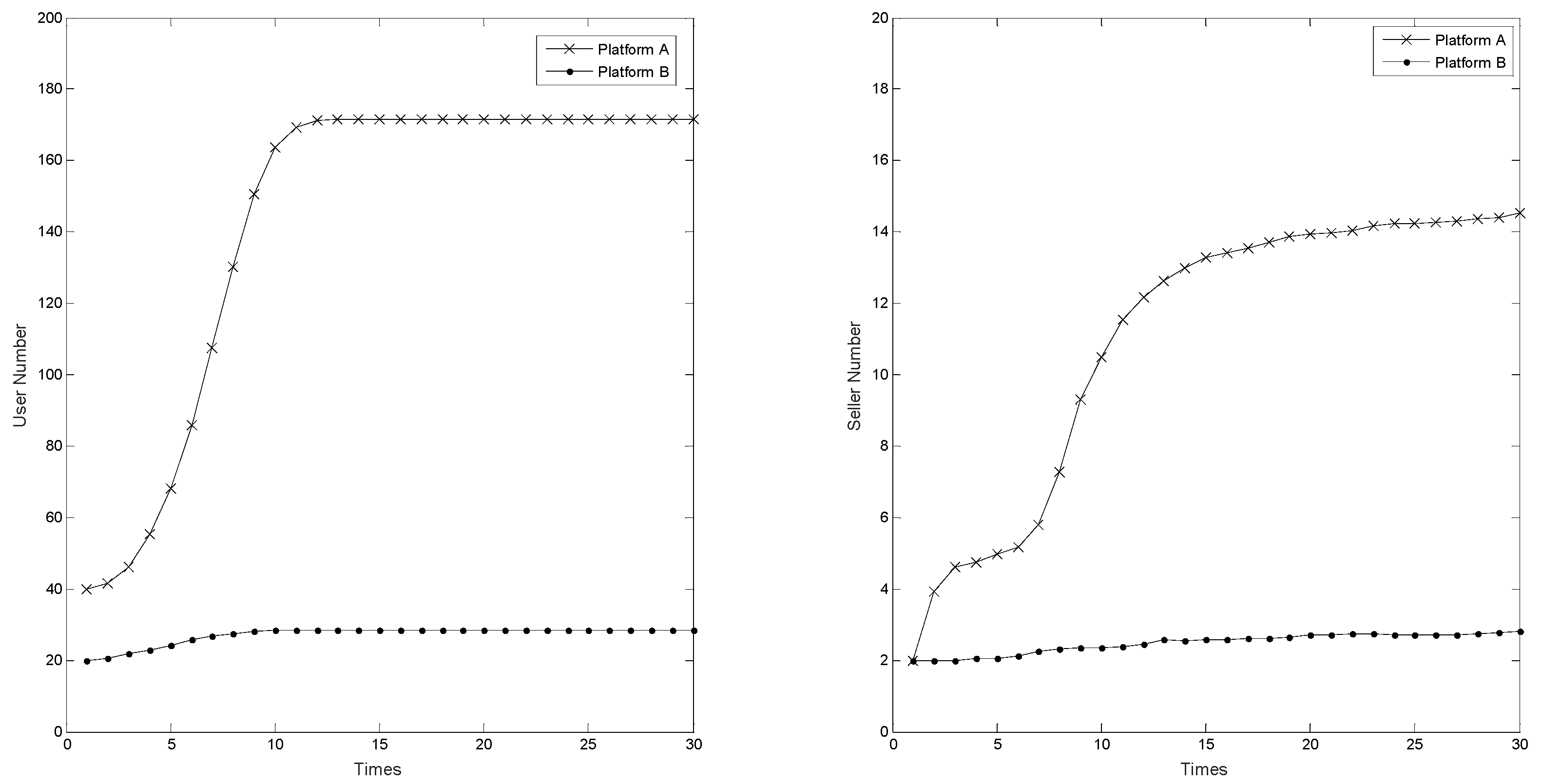
5.2. First-Mover Advantage—The Number of Users and Available Complementary Products
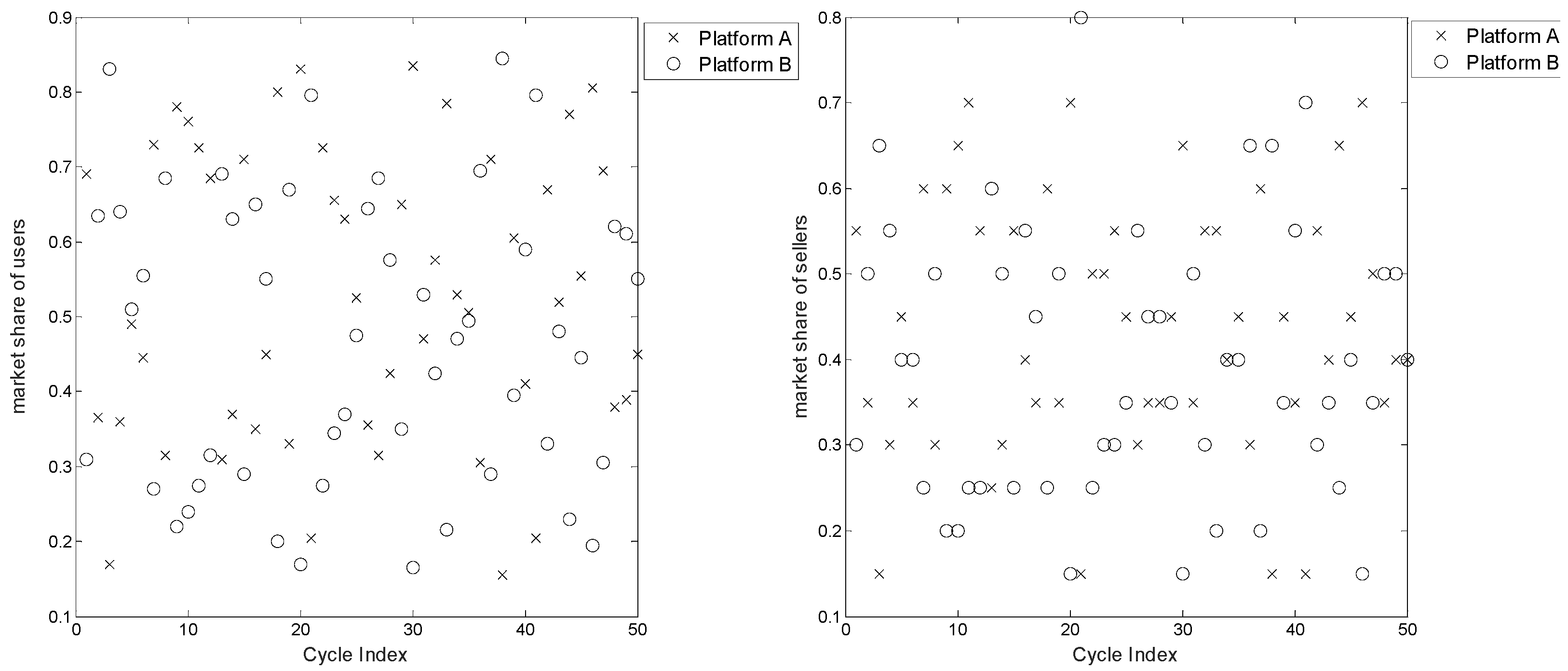
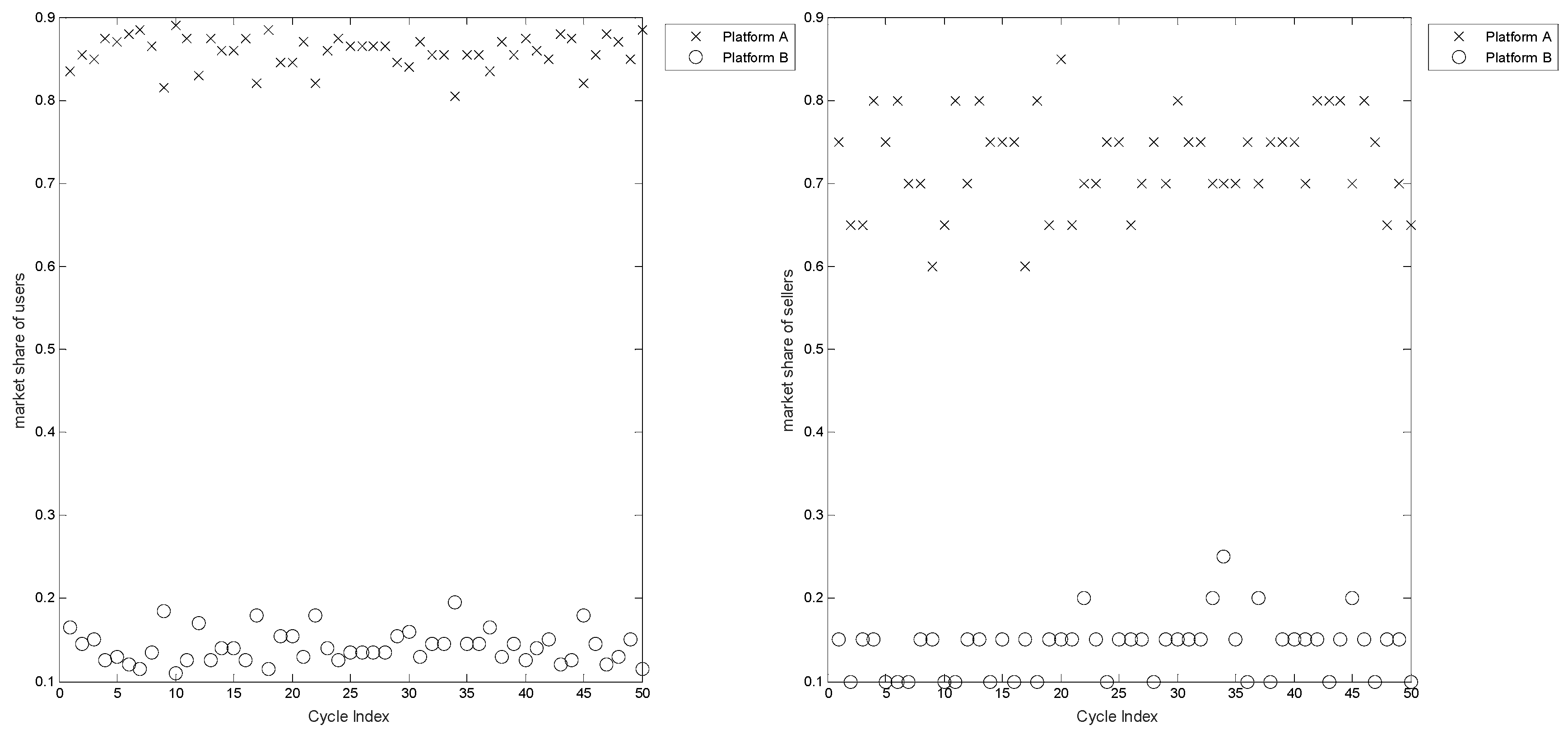
5.3. Iteration of Platforms and Consumer Heterogeneity
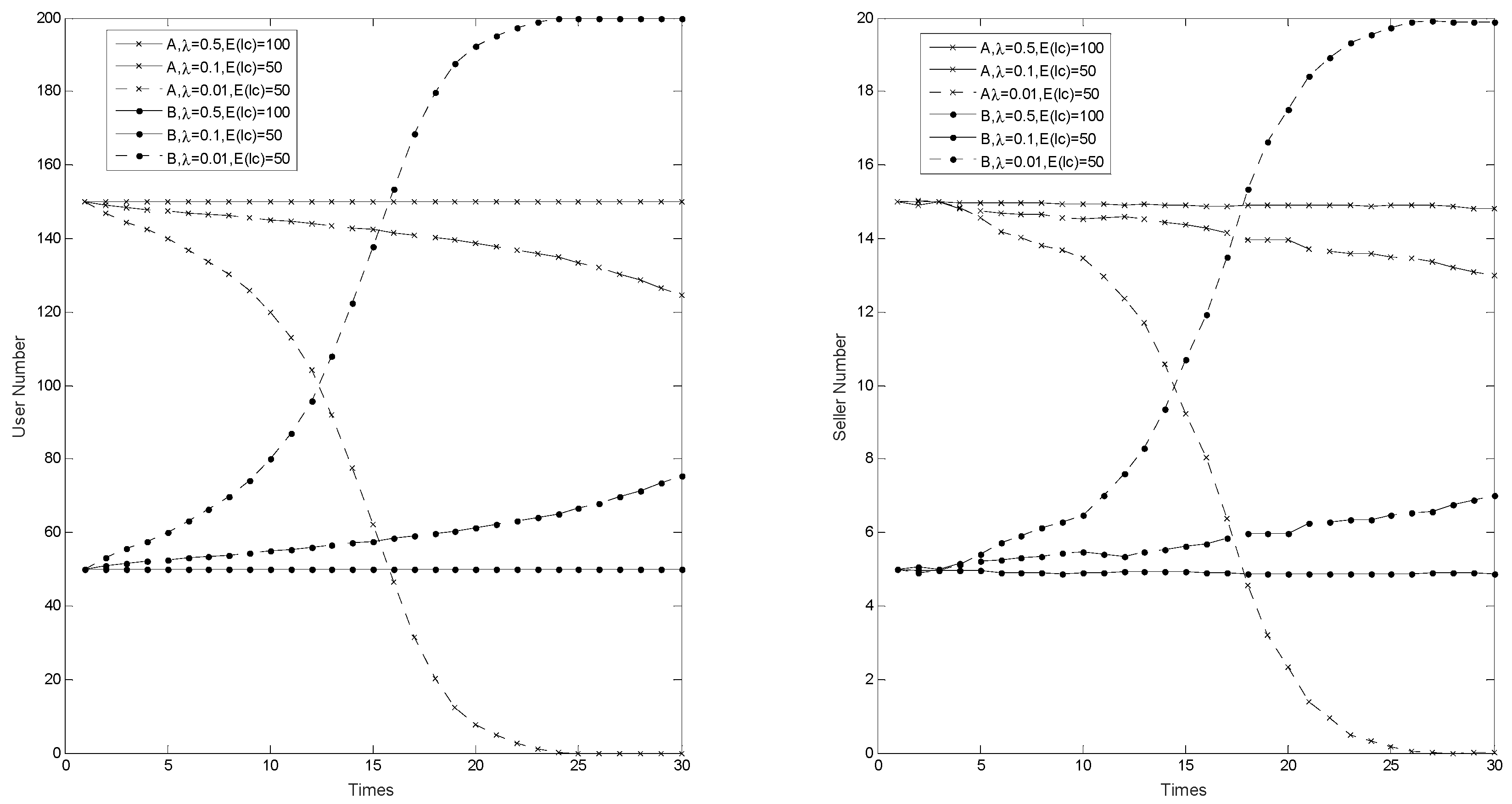
5.4. Effects of Switching and Learning Costs on Platform Competition
6. Conclusions and Discussion
6.1. Theoretical Implications
6.2. Practical Implications
6.3. Limitations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mantena, R.; Sankaranarayanan, R.; Viswanathan, S. Platform-based information goods: The economics of exclusivity. Decis. Support Syst. 2010, 50, 79–92. [Google Scholar] [CrossRef]
- Andersen, R.; Brunoe, T.D.; Nielsen, K. Platform-based product development in the process industry: A systematic literature review. Int. J. Prod. Res. 2022, 61, 1696–1719. [Google Scholar] [CrossRef]
- Rochet, J.C.; Tirole, J. Platform competition in two-sided markets. J. Eur. Econ. Assoc. 2003, 1, 990–1029. [Google Scholar] [CrossRef]
- Armstrong, M. Competition in two-sided markets. RAND J. Econ. 2006, 37, 668–691. [Google Scholar] [CrossRef]
- Carrillo, J.D.; Tan, G. Platform competition with complementary products. Int. J. Ind. Organ. 2021, 77, 102741. [Google Scholar] [CrossRef]
- Katz, M.L.; Shapiro, C. Network externalities, competition, and compatibility. Am. Econ. Rev. 1985, 75, 424–440. [Google Scholar]
- Goldenberg, J.; Libai, B.; Muller, E. Riding the Saddle: How Cross-Market Communications Can Create a Major Slump in Sales. J. Mark. 2002, 66, 1–16. [Google Scholar] [CrossRef]
- Lieven, S.D.M.; Gino, B.V. ICT-innovations today: Making traditional diffusion patterns obsolete, and preliminary insight of increased importance. Telemat. Inform. 2004, 21, 235–260. [Google Scholar] [CrossRef]
- Peres, R.; Muller, E.; Mahajan, V. Innovation diffusion and new product growth models: A critical review and research directions. Int. J. Res. Mark. 2010, 27, 91–106. [Google Scholar] [CrossRef]
- Barabási, A.-L.; Albert, R. Emergence of Scaling in Random Networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Yang, M.; Abubakar, A.H.; Jiang, P. Deep learning and complex network theory based analysis on socialized manufacturing resources utilisations and an application case study. Concurr. Eng. 2021, 29, 236–248. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Shang, Y. Sombor index and degree-related properties of simplicial networks. Appl. Math. Comput. 2021, 419, 126881. [Google Scholar] [CrossRef]
- Thompson, P. Learning by doing. Handb. Econ. Innov. 2010, 1, 429–476. [Google Scholar]
- Li, Y.; Ping, Y.; Zhong, Y.; Misra, R. Learning-by-doing in non-homogeneous tasks: An empirical study of content creator performance on a music streaming platform. Electron. Commer. Res. Appl. 2023, 58, 101241. [Google Scholar] [CrossRef]
- Chou, C.F.; Shy, O. Network effects without network externalities. Int. J. Ind. Organ. 1990, 8, 259–270. [Google Scholar] [CrossRef]
- Katz, M.L.; Shapiro, C. Systems Competition and Network Effects. J. Econ. Perspect. 1994, 8, 93–115. [Google Scholar] [CrossRef]
- Abrahamson, E.; Rosenkopf, L. Social Network Effects on the Extent of Innovation Diffusion: A Computer Simulation. Organ. Sci. 1997, 8, 289–309. [Google Scholar] [CrossRef]
- Bertrand, M.; Luttmer, E.F.P.; Mullainathan, S. Network Effects and Welfare Cultures. Q. J. Econ. 2000, 115, 1019–1055. [Google Scholar] [CrossRef]
- Farrell, J.; Klemperer, P. Coordination and lock-in: Competition with switching costs and network effects. In Handbook of Industrial Organization; Elsevier: Amsterdam, The Netherlands, 2007; Volume 3, pp. 1967–2072. [Google Scholar]
- Fainmesser, I.P.; Galeotti, A. Pricing network effects. Rev. Econ. Stud. 2015, 83, 165–198. [Google Scholar] [CrossRef]
- Belleflamme, P.; Peitz, M. Platforms and network effects. In Handbook of Game Theory and Industrial Organization; Edward Elgar Publishing: Cheltenham, UK, 2018; Volume II, pp. 286–317. [Google Scholar]
- Sui, R.; Zhang, X.; Dan, B.; Zhang, H.; Liu, Y. Bilateral value-added service investment in platform competition with cross-side network effects under multihoming. Eur. J. Oper. Res. 2023, 304, 952–963. [Google Scholar] [CrossRef]
- Kim, J.; Lee, D.-J.; Ahn, J. A dynamic competition analysis on the Korean mobile phone market using competitive diffusion model. Comput. Ind. Eng. 2006, 51, 174–182. [Google Scholar] [CrossRef]
- Tsai, B.-H.; Li, Y.; Lee, G.-H. Forecasting global adoption of crystal display televisions with modified product diffusion model. Comput. Ind. Eng. 2010, 58, 553–562. [Google Scholar] [CrossRef]
- Kimura, M. Effects for console game sales in Japan market. Asia Pac. J. Mark. Logist. 2015, 27, 61–81. [Google Scholar] [CrossRef]
- Parker, G.G.; Van Alstyne, M.W. Two-Sided Network Effects: A Theory of Information Product Design. Manag. Sci. 2005, 51, 1494–1504. [Google Scholar] [CrossRef]
- Eisenmann, T.; Parker, G.; Van Alstyne, M.W. Strategies for two-sided markets. Harv. Bus. Rev. 2006, 84, 92. [Google Scholar]
- Weyl, E.G. A Price Theory of Multi-Sided Platforms. Am. Econ. Rev. 2010, 100, 1642–1672. [Google Scholar] [CrossRef]
- Zhu, F.; Iansiti, M. Entry into platform-based markets. Strat. Manag. J. 2011, 33, 88–106. [Google Scholar] [CrossRef]
- Dou, G.; Lin, X.; Xu, X. Value-added service investment strategy of a two-sided platform with the negative intra-group network externality. Kybernetes 2018, 47, 937–956. [Google Scholar] [CrossRef]
- Rysman, M. The Economics of Two-Sided Markets. J. Econ. Perspect. 2009, 23, 125–143. [Google Scholar] [CrossRef]
- Wei, X.; Gong, H.; Song, L. Product diffusion in dynamic online social networks: A multi-agent simulation based on gravity theory. Expert Syst. Appl. 2023, 213, 119008. [Google Scholar] [CrossRef]
- Rohlfs, J.H. Bandwagon Effects in High-Technology Industries; MIT Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Tellis, G.; Yin, E.; Niraj, R. Does Quality Win? Network Effects versus Quality in High-Tech Markets. J. Mark. Res. 2009, 46, 135–149. [Google Scholar] [CrossRef]
- Himmelberg, C.; Economides, N. Critical mass and network evolution in telecommunications. In Toward a Competitive Telecommunication Industry; Routledge: New York, NY, USA, 2013; pp. 59–76. [Google Scholar]
- Goldenberg, J.; Libai, B.; Muller, E. The chilling effects of network externalities. Int. J. Res. Mark. 2010, 27, 4–15. [Google Scholar] [CrossRef]
- Iyengar, R.; Van den Bulte, C.; Valente, T.W. Rejoinder—Further reflections on studying social influence in new product diffusion. Mark. Sci. 2011, 30, 230–232. [Google Scholar] [CrossRef]
- Gupta, S.; Jain, D.C.; Sawhney, M.S. Modeling the Evolution of Markets with Indirect Network Externalities: An Application to Digital Television. Mark. Sci. 1999, 18, 396–416. [Google Scholar] [CrossRef]
- Weitzel, T.; Beimborn, D.; König, W. A Unified Economic Model of Standard Diffusion: The Impact of Standardization Cost, Network Effects, and Network Topology. MIS Q. 2006, 30, 489. [Google Scholar] [CrossRef]
- Stremersch, S.; Tellis, G.J.; Franses, P.H.; Binken, J.L. Indirect network effects in new product growth. J. Mark. 2007, 71, 52–74. [Google Scholar] [CrossRef]
- Chun, S.Y.; Hahn, M. A diffusion model for products with indirect network externalities. J. Forecast. 2008, 27, 357–370. [Google Scholar] [CrossRef]
- Gong, X.; Liu, Z.; Zheng, X.; Wu, T. Why are experienced users of WeChat likely to continue using the app? Asia Pac. J. Mark. Logist. 2018, 30, 1013–1039. [Google Scholar] [CrossRef]
- Yu, Z.; Li, S.; Tong, L. Market dynamics and indirect network effects in electric vehicle diffusion. Transp. Res. Part D Transp. Environ. 2016, 47, 336–356. [Google Scholar] [CrossRef]
- DelRe, S.A.; Jager, W.; Janssen, M.A. Diffusion dynamics in small-world networks with heterogeneous consumers. Comput. Math. Organ. Theory 2006, 13, 185–202. [Google Scholar] [CrossRef]
- Choi, H.; Kim, S.-H.; Lee, J. Role of network structure and network effects in diffusion of innovations. Ind. Mark. Manag. 2010, 39, 170–177. [Google Scholar] [CrossRef]
- Katona, Z.; Zubcsek, P.P.; Sarvary, M. Network Effects and Personal Influences: The Diffusion of an Online Social Network. J. Mark. Res. 2011, 48, 425–443. [Google Scholar] [CrossRef]
- Spulber, D. Firms and Networks in Two-Sided Markets. In The Handbook of Economics and Information Systems; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Newman, M.; Watts, D. Renormalization group analysis of the small-world network model. Phys. Lett. A 1999, 263, 341–346. [Google Scholar] [CrossRef]
- Li, Q.; Yao, H.; Mai, T.; Jiang, C.; Zhang, Y. Reinforcement-Learning- and Belief-Learning-Based Double Auction Mechanism for Edge Computing Resource Allocation. IEEE Internet Things J. 2019, 7, 5976–5985. [Google Scholar] [CrossRef]
- Kretschmer, T.; Leiponen, A.; Schilling, M.; Vasudeva, G. Platform ecosystems as meta-organizations: Implications for platform strategies. Strateg. Manag. J. 2021, 43, 405–424. [Google Scholar] [CrossRef]
- Farronato, C.; Fong, J.; Fradkin, A. Dog Eat Dog: Balancing Network Effects and Differentiation in a Digital Platform Merger. Manag. Sci. 2023. [Google Scholar] [CrossRef]
- McIntyre, D.P.; Subramaniam, M. Strategy in Network Industries: A Review and Research Agenda. J. Manag. 2009, 35, 1494–1517. [Google Scholar] [CrossRef]
- Li, H.; Zhao, N. Better earlier than longer: First-Mover Advantage in social commerce product information competition. Sustainability 2019, 11, 4630. [Google Scholar] [CrossRef]



| Parameter | Value | ||
|---|---|---|---|
| A | B | ||
| N | Size of consumer population | 200 | |
| M | Size of seller population | 20 | |
| Nk0 | Initial install bases of users | 20 | 20 |
| Mk0 | Initial install bases of users | 2 | 2 |
| α1k | Strength of direct network effect | 2 | 2 |
| α2k | Strength of indirect network effect | 2 | 2 |
| β1 | Index of direct networks | 1.5 | |
| β2 | Index of indirect network effect | 2 | |
| σ | Index of CES utility | 0.5 | |
| υ0k | Intrinsic value of platforms | 5 | 5 |
| K | Average number of neighbors of user | 8 | |
| λ | Switching costs | 0.5 | 0.5 |
| pkt | Price of platforms | 15 | 15 |
| γb | Adaptive expectation coefficient of users | 0.5 | |
| γs | Adaptive expectation coefficient of sellers | 0.5 | |
| E(Iit) | Users’ budget expectations | 10 | |
| Var(Iit) | Users’ budget variance | 4 | |
| c | Marginal cost of sellers | 10 | |
| E(lcjt) | Sellers’ expected learning costs | 100 | |
| Var(Icjt) | Variance in learning costs | 16 | |
| ρuk | Expectation factors of users | 1 | 1 |
| ρsk | Expectation factors of sellers | 0.1 | 0.1 |
| ρ | Probability of randomly added shortcuts | 0.2 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Dong, L.; Ji, T. The Diffusion of Competitive Platform-Based Products with Network Effects. Sustainability 2023, 15, 8845. https://doi.org/10.3390/su15118845
Zhang J, Dong L, Ji T. The Diffusion of Competitive Platform-Based Products with Network Effects. Sustainability. 2023; 15(11):8845. https://doi.org/10.3390/su15118845
Chicago/Turabian StyleZhang, Jie, Lingfeng Dong, and Ting Ji. 2023. "The Diffusion of Competitive Platform-Based Products with Network Effects" Sustainability 15, no. 11: 8845. https://doi.org/10.3390/su15118845
APA StyleZhang, J., Dong, L., & Ji, T. (2023). The Diffusion of Competitive Platform-Based Products with Network Effects. Sustainability, 15(11), 8845. https://doi.org/10.3390/su15118845






