Abstract
The Level of Detail (LoD), a parameter used to define the information contained in building models, is an important factor to consider in modeling building energy at the urban scale. In this research, we conducted a parametric study regarding the data requirements for the estimation of the annual residential heat demand in London. More particularly, the requirement of the observation of the actual roof type (LoD2) and the window-to-wall ratio (LoD3) was examined in two different case study areas. Meanwhile, an adaptive comfort level study was implemented using LoD5 models, and its results were assessed holistically with the heat demand to reveal the energy performance of the buildings. The results showed that there was a minor difference in the upgrade of a lower to higher LoD regarding these parameters. At an urban scale, the energy demand of buildings could be estimated using an assumption of archetypes and building ages. However, with a scalable parametric script developed in places, models with a high LoD could provide more detailed insights in the energy performance assessment without generating excessive workload.
1. Introduction
Energy is undeniably significant in developing nations in the 21st century [1]. More particularly, energy consumption has increased in recent years as a result of population needs since energy production is crucial to the prosperity and well-being of the entire world [1]. The building stock accounts for two-fifths of the total annual energy consumption worldwide [2]. The necessity for renovation, and more specifically the urgent refurbishment of existing entire city blocks or building complexes, is imperative in light of climate predictions. Climate change is impacted by carbon dioxide (CO2) emissions and other greenhouse gases that originate from human activities and the built environment [3,4]. On the other hand, the effects of greenhouse gas emissions and the climate change extend to the built environment and to the human thermal comfort [3,4]. Therefore, by creating a better built environment, not only is climate change mitigated, but the comfort and well-being of humanity also is secured. However, urban areas are primarily tied to the aforementioned issues, as more than half of the population of the world, namely 54%, is living in cities due to easy access to amenities, facilities, and career opportunities [5]. These career opportunities, however, are linked to greater industrialization and per-person energy use, both of which exacerbate climate change [6]. As a result, city-scale energy modeling is essential for slowing down climate change on a global scale, especially given the need for metropolitan areas to shift quickly.
There is no doubt that energy modeling at the urban scale is a multidimensional problem. One of the challenges that arises when modeling at city scale is the unbalance of data availability regarding construction details. Therefore, a significant parameter is the Level of Detail (LoD) applied in city models. The LoD is determined by the amount of real-world object features that are used depending on the project’s requirements and economic constraints [7]. The CityGML, which is an open model used mainly for spatial transactions, database modeling, and data storage, comprises four Levels of Details (LoDs) [8]. As shown in Figure 1, the LoD1 is the simplest representation of a building. The structure is described by a cube that is formed from the building footprint and the building height. A more detailed representation of the building is the LoD2, for which the type of the roof is added to the model. At LoD3, the windows are added to the façade of the building, and at LoD4 the indoor design of the building is added. Nonetheless, some researchers divide the LoDs in six representations by adding the LoD0, which is just the building footprint, and the LoD5, which contains the location and the orientation of the building [9].
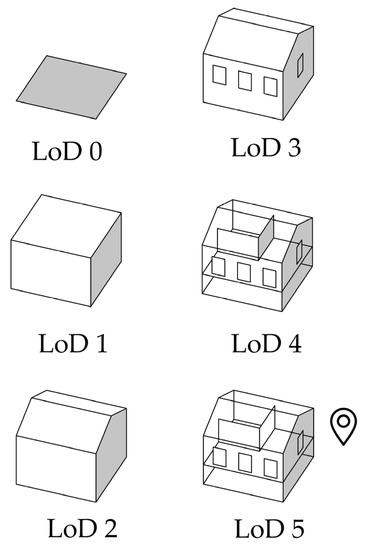
Figure 1.
Level of Detail (LoD) in building models.
Meanwhile, another key factor in urban building energy modeling is the indoor environment, which affects the thermal comfort of users, leading to human health and productivity. Thermal comfort is defined as ‘that condition of mind which expresses satisfaction with the thermal environment’. The widespread adoption of mechanical means to provide the desired indoor temperature led to a huge energy load in heating and cooling. Thus, when modeling building energy, it is crucial to consider both the level of thermal comfort users enjoy and the amount of energy consumed. By combining both, we can benchmark the energy performance within an urban building stock and rank the intervention priority.
Considering everything mentioned above, this study adopted a parametric approach to model urban building energy, including both demand and user comfort. Firstly, we created buildings with different LoDs and simulated their heat demand. Next, we used a sensitivity analysis to assess the impact of the LoDs. Lastly, the comfort level of buildings with highest and lowest heat demand identified in the previous step was obtained to gain insights on energy performance. We present a case study containing two groups of buildings in London, UK, to demonstrate our parametric approach and the result.
Therefore, the organization of the paper was constructed with an introduction of the general topic in Section 1, and then in Section 2, the background knowledge and literature review are discussed, and related past research studies are referenced that led to a research gap. In Section 3, the methodology for both the annual residential heat demand estimation and the calculation of the human thermal comfort in buildings is presented in detail. After that, the results that were obtained from the analysis are provided in Section 4, and they are analyzed and discussed in Section 5. Finally, in Section 6, the conclusions of the research paper are pointed out.
2. Background and Literature Review
2.1. Sensitivity Analysis and Building Energy Performance Rating
Sensitivity analyses have been employed by the larger construction and engineering community to examine the thermal behavior and energy performance of buildings in a range of applications [10]. For instance, a sensitivity analysis was used by Wilde et al. to examine the danger of overheating in structures under several future climatic scenarios [11]. Furthermore, Tian et al. conducted research regarding climate change, the energy performance of a building on the University of Plymouth campus and how the building might behave thermally under climatic forecasts [12]. In addition, experiments utilizing parametric analysis techniques have been carried out in order to investigate the best retrofit standard for lower heating demand and higher energy performance [13].
In addition to this, sensitivity analyses can be applied to building stock and design. More specifically, a research study by Hygh et al. investigated the effectiveness of a sensitivity analysis (particularly of the multivariate regression) for predicting building energy performance early in the design process [14]. Specifically, 27 different building design factors were tested as part of this project to determine the way they influenced buildings’ energy efficiency. One of the most important findings from this project was that the sensitivity analysis method might be used to assess the impact of each parameter on the thermal behavior of a building structure and address its heating or cooling loads [14].
Another study that combined a parametric analysis with an uncertainty analysis examined how several categories of ambiguity—more specifically, physical, design, and scenario uncertainties—affected the rating of a building’s energy efficiency [15]. According to that study by Hopfe et al., a sensitivity analysis is a suitable technique for identifying the crucial factors that affect the cooling and heating requirements of buildings [15]. Based on the aforementioned studies, it is evident that a sensitivity analysis is a useful method for determining the factors that have the greatest impact on building energy performance. This knowledge can then be applied to the design of new energy-efficient buildings as well as the calculation of the thermal behavior of the existing building stock (even if some data are lacking and assumptions need to be made).
2.2. Impactful Parameters on Energy Performance at the Building Scale
As mentioned above, numerous research projects have been carried out to identify the variables that significantly affect the energy performance of building at the individual building level. More specifically, a research study by Ioannou et al. examined both the energy efficiency and the level of comfort at the building scale while also implementing a sensitivity analysis for occupant behavior by adding it the first time in the model and subtracting it the second time [16]. More particularly, an energy analysis was conducted for a case study building located in Monte Carlo while assuming three alternative heating systems as well as Class-A and Class-F housing [16]. Given the significant contrast between the two executions of the model, the project’s results showed that occupant behavior is one of the most important factors in determining the energy performance of buildings [16]. Another research study by Olivero et al. investigated the parameters that influence a building’s energy performance by modeling and analyzing two existing public buildings: an office and a library in France and Italy, respectively [17]. The findings demonstrated that some variables such as the climate and the population are uncontrollable and unpredictable [17]. Consequently, as the occupancy of a building cannot be kept under control throughout the entirety of the building’s lifecycle and has a significant impact on its energy performance, it is clear based on the studies of Ioannou et al. (2015) and Olivero et al. (2015) that this is a challenging task [16,17].
Furthermore, other research studies have examined the impact of the building form and window-to-wall ratio on energy performance. More specifically, Zhang et al. examined the effects of geometrical factors on Chinese schools as well as the effect of the building form on thermal performance [18]. According to the research, a window-to-wall ratio (WWR) of 20–40% resulted in both an effective thermal performance and occupants’ thermal comfort. However, a large window-to-wall ratio reduced the need for illumination while simultaneously increasing the need for cooling and heating at higher and lower temperatures, respectively [18]. Another study that examined the building form established that buildings with more compact structures were characterized by higher energy losses than incompact building structures [19]. The same conclusions were drawn in Hemsath and Bandhosseini’s study, which revealed that the building form that performed best in terms of energy efficiency was the one that was closest to a square. In general, it has been found that the shape of buildings has an evident impact on energy efficiency: the more complex a shape is, the more energy it can potentially consume [20]. Finally, in order to design buildings with window geometries that result in lower energy consumption, Ghiai et al. evaluated the relationship between the window-to-wall ratio and energy consumption in Tehran [21]. The results of this study demonstrated that the window-to-wall ratio (WWR) is among the parameters that have the greatest influences on the calculation of energy demand, and more specifically that a decrease in the WWR is related to a decrease in energy consumption [21].
2.3. From Individual Building to Urban Building Energy Modeling
Nonetheless, several city energy models have been developed recently in order to estimate the energy performance at the level of cities for the reasons mentioned above as well as for climate change. The CitySim platform is an example of one of these models that has been developed to help stakeholders manage city energy issues and make better decisions [22,23]. More specifically, Frayssinet et al. estimated the energy consumption of buildings at an urban scale in 2017 with the goal of assisting decision makers in developing plans for the transformation of metropolitan regions into smart cities [23]. Particularly for this investigation, it was determined that model-simplification-related uncertainties were less likely to affect outcomes than input parameter uncertainties [24].
Moreover, Rosser et al. conducted a research project using CityGML EnergyADE to model residential buildings in two Nottingham areas for energy simulation that made use of CitySim [25]. The results implied that a comprehensive footprint geometry was not necessary for calculating energy demand at the district scale despite the fact that several assumptions had to be made due to the geometry differences between the two communities [25]. However, it should be noted that employing architectural typologies (as in the research study by Rosser et al.) yields homogeneous results, necessitating the regular updating of survey data.
On the other hand, building typologies were not only used by Rosser et al. but also in several other research publications regarding city energy simulations. More specifically, in 2013 Kaden and Kolbe estimated building energy use at the city scale using statistics and semantic 3D city models [26]. The findings of this research showed that this approach was appropriate for usage as the basis for city energy modeling. Nonetheless, a comprehensive validation of the energy demand is necessary, especially when suggestions for renovating buildings are to be provided [26]. Furthermore, a study that combined an energy simulation model with GIS 2.5D building data of Parisian structures was carried out by the French urbanism research team Atelier Parisien d’Urbanisme (APUR) [24]. In more detail, this research team used building typologies from archetypical building classes and morphological building data to predict energy usage.
In addition to the studies mentioned above, Strzalka et al. implemented research that forecasted the heating demand at the city scale [27]. The results showed that the geometrical detail was not a significant factor in influencing the results for the heating demand. Hence, a 3D city model with a simplified geometry could be used to estimate energy demand. Lastly, a research study by Dochev demonstrated that it was possible to estimate the heating demand at a city scale using building typologies, assumptions, empirical data, and census data with satisfactory results. This research presented a Python script that was validated with values taken from the TABULA project webtool [28,29].
2.4. Thermal Comfort in Buildings
The study of thermal comfort is a complex process that integrates knowledge from multiple fields including physiology, building physics, mechanical engineering, and psychology [30]. Many researchers designed methods to detect the relationship between temperature and comfort and established the recommended standards for acceptable range of indoor conditions [31]. However, for individuals, the definition of comfort is a subjective perception. A group of people in the same indoor environment may possess a wide range of satisfactory levels due to personal differences and other cultural and psychological factors that are usually not regulated by standards [32]. For building engineers, choosing the suitable comfort measurement methods in building energy modeling is crucial to acquire the accurate energy performance.
The established thermal comfort can be categorized into two types: the steady state model and the adaptive model. The main difference between these two models is the personal variables such as clothing insulation and that the metabolic rate is fixed in the steady state model, while in the adaptive model people are able to adapt to the thermal environment by adjusting clothing and expectations and acclimatizing [33]. There is a clear difference in the applicability of these two models between naturally ventilated and conditioned buildings. The adaptive model provides a more accurate range of comfort in natural ventilated buildings that is usually wider than what the steady state model suggests. For urban energy modeling (especially residentials), the adaptive model is more suitable than the steady state because they are mostly natural ventilated, and the users can respond actively according to the change in environmental temperature.
2.5. Research Gap
Numerous studies on building energy simulations have been conducted from the scale of an individual building to the level of an entire city. Examples include a research study by Yang et al. from 2020 that used geospatial and archetypal data to determine the space heating energy for a city in the Netherlands as well as a research study by Nouvel et al. that examined the accuracy of a method for calculating the heating demand in district heating systems [34,35]. In addition, a number of studies have performed parametric analyses to identify the variables that had the greatest influences on a building’s energy performance at the individual building scale, such as Coulter and Leicht’s sensitivity analysis to identify the influence of energy-modeling input parameters on the results of the energy analysis for a retrofitted building [36].
Nonetheless, limited research studies have investigated how different architectural attributes affect energy use. For instance, by analyzing the effect of morphology, typology, and other building indicators on energy consumption, Ratti et al. made recommendations for the construction of buildings. However, the majority of earlier studies either carried out parametric studies at the scale of the building or used GIS data in conjunction with other building information for city-scale energy modeling without sensitivity analyses [37,38].
This research paper focuses on the assessment of the building energy performance at the city scale for different Levels of Details (LoDs) while balancing between the heat demand and the human thermal comfort. By the term Levels of Details, it is meant that the purpose of this study was to investigate whether it is necessary to use the LoD2 or LoD3 for the estimation of the heating demand in buildings or if a simple model of LoD1 could lead to satisfactory results. In more detail, the objectives of this paper were:
- To investigate the most appropriate LoD for urban building energy modelling.
- To assess the building energy performance with human thermal comfort using parametric tools.
- To formulate recommendations regarding data for energy performance assessment.
3. Methodology
3.1. Annual Heat Demand Calculation for Different LoDs
For the calculation of the annual heat demand, a physics-based approach was implemented by using building archetypes. In the following sections, a detailed description of the method is given.
3.1.1. Data Gathering
The first step for the implementation of the constructed methodology was to download the necessary datasets. The ‘Colouring London’ dataset was downloaded in a .csv format [39]. This Volunteered Geographic Information (VGI) dataset is a part of the ‘Coloring Cities’ project from UCL University, and it provides open data regarding the building stock for free. The second dataset that was used was the OS MasterMap Topography layer for the city of London from the Ordnance Survey and Digimap in .gpkg format, which provided topographic data in detail [40]. The third dataset was the OS Building Height Attribute from the Ordnance Survey and Digimap as well in .csv format [41]. This dataset was deemed necessary due to the fact that the ‘Colouring London’ dataset is VGI and some buildings lacked height information.
3.1.2. Data Processing
In order to create the final dataset, Python programming language in Jupyter Notebook through ANACONDA was used. Firstly, the ‘Colouring London’ dataset was imported to Jupyter and data cleaning was conducted by filtering the buildings and keeping only the dwellings. After that, the OS MasterMap Topography layer was imported, and a newly joined dataset of the two aforementioned datasets was created. Following that, the OS MasterMap Building Height attribute was imported and merged with the other two datasets. After cleaning the empty values regarding the building age and the building form of the remaining residential stock, the dataset was exported in shapefile format.
The next step was importing and processing the shapefile in the QGIS platform by calculating the area and the perimeter of each building’s footprint. Then, the number of floors of each building was generated by assuming an average 3 m height of each floor. The occupancy for each building was estimated according to London’s standard minimum area per person in residential buildings, which is 32.8 m2 (areas smaller than the standard were assumed to be occupied by 1 person) [42].
The following step was importing the processed dataset back into Jupyter Notebook and inserting the thermal properties of each building based on TABULA typology according to the building age and the built form. Therefore, different U-values (thermal transmittance) were assigned for the roofs, walls, floors, and windows [43].
3.1.3. Data Imputation
In order to run the energy model, some other parameters for energy performance rating were essential to be included. In the QGIS platform, the following parameters were imported for each building:
- Internal gains: assumed to be equal to 3 W/m2 from TABULA [43].
- Window-to-wall ratio (WWR): assumed to be equal to 0.2 for LoD1 based on empirical data and Dochev’s research study [28].
- Roof type: assumed to be pitched based on the literature review and TABULA typology [43].
- Air change rate (ACR): assumed to be 0.6 [28,43].
- Heat volume coefficient: assumed to be 0.8 based on 3 m floor height [28,43].
- Inside temperature: 19.5~20 °C—according to Public Health England, a temperature range between 18 and 21 °C is the minimum range of the inside temperature in buildings in the UK for a healthy indoor environment [44].
- Percentage of façade in walls and windows: assumed to be 0 because in the UK, the ‘patch’ renovation is not applied as in Bulgaria (the model of Dochev was first applied and tested).
- Weather data: the monthly temperature and the solar radiation for the heating season were gathered from the Passive House Planning Package (PHPP) software, which provided validated weather data from NASA [45].
As the Python script for the calculation of the heat demand was validated using Dochev’s research in Bulgaria, the following step was to choose the case study area in order to impute the LoD2 and LoD3 parameters in a smaller region than the city of London. Considering that the geometry and type of buildings has a key impact on their energy performance, we selected two case study areas that each contained 49 buildings.
Case Study Area 1 was located in Lewisham, Deptford constituency, London; more specifically, in New Cross Gate Ward. It is characterized as an urban area and is mainly composed of low-rise terraced houses constructed in earlier ages. In Figure 2, Case Study Area 1 is illustrated, and its exact location compared to the city of London’s boundaries is highlighted.
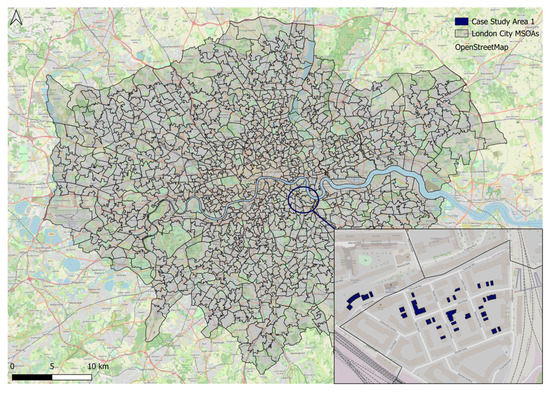
Figure 2.
Case Study Area 1—Location.
Case Study Area 2 was located in Bethnal Green and Bow constituency in London (specifically, in Spitalfields and Banglatown Ward in the local authority of Tower Hamlets). Case Study Area 2, like CSA1, is characterized as an urban area, but in contrast to CSA1, it is mostly composed of mid-rise apartment blocks completed in recent decades. In Figure 3, a similar map to the above is presented for CSA2.
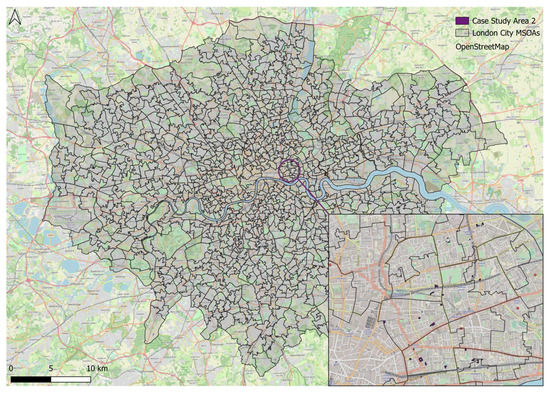
Figure 3.
Case Study Area 2—Location.
Then, for both case study areas the information on the roof type (LoD2) was imported manually for each building with the use of Google’s satellite view. Finally, for the LoD3, the Google Street View add-in in QGIS, Google Street View in a browser, and IC Measure software were used. In more detail, for each building, the street where it was located was found in QGIS, then a screenshot of the building under test was taken and the area of the windows and the walls was measured using IC Measure software in order to obtain the WWR. Therefore, for both areas, the LoD2 and LoD3 datasets were constructed.
Lastly, the completed datasets of different LoDs were exported in the shapefile format for energy and comfort level analyses.
3.1.4. Energy Model Execution
After completing the datasets for the three different LoDs, for both case study areas, the next step was to execute the energy simulations in order to calculate the annual heating demand for every Level of Detail and for both case study areas. For the calculation of the heat demand, as mentioned above, the Python script from the Github repo of Dochev’s research was used by changing the climate data [28]. To run the script successfully, QGIS v2.18.17 had to be used in combination with a Python console add-in. Finally, after the calculation of the annual heat demand, the attribute tables from the above parametric studies were exported as .csv files. Then, with the use of Excel, the percentage difference in the results from the upgrade from a lower LoD to a higher LoD were calculated, and maps of the annual heating demand percentage difference were created for both case study areas.
Figure 4 presents the complete methodological approach for annual heat demand.
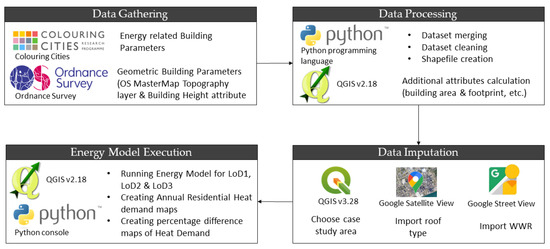
Figure 4.
Annual heat demand methodological workflow.
3.2. Adptive Comfort Level for Individual Buidlings
In this section, based on the annual heat demand acquired in the previous step, we selected buildings with low and high heat demand in each case study area to simulate and analyze their adaptive comfort level with parametric tools.
3.2.1. From Shapefile to Simulation Model
We developed a script in Grasshopper (version: 1.0.0007), a visual programming language and environment within the 3D modeling software Rhinoceros 3D (version: 7.SR25). The Grasshopper environment allowed us to utilize different developed and validated tools to complete a holistic workflow that included: (1) importing and transforming the shapefile generated in previous step; (2) reconstructing 3D building geometry with thermal attributes and a building program; (3) executing an adaptive comfort level simulation; and (4) collecting the numeric results and producing the intuitive data visualization.
The shapefiles created in the previous step were firstly imported into the Grasshopper script, and the polyline of each building’s footprint was generated using the Urbano (version: 1.4) plugin [46]. The 3D geometries were then extracted from the polyline footprint according to the building heights. In the following step, we used the Ladybug Tools (version: 1.6.0), a collection of building and environment analysis applications to create the energy modeling and simulation [47]. Firstly, the window-to-wall ratio, building program (in this case, residential), and construction materials were assigned to the 3D geometry according to the attributes of the shapefile using a series of Dragonfly components (part of the Ladybug tool; particularly used in urban building energy modeling). Secondly, it was converted into a Honeybee model (also part of the Ladybug tool) to assign different components including, floors, exterior walls, interior wall, roofs, and windows to the 3D geometries and their geographic locations. Lastly, radiance grids of each building were created and added to the Honeybee model so the comfort level could be spatially mapped.
With the roof, windows, indoor layout, building orientation, and location assigned, the created Honeybee model was at LoD5 [9].
3.2.2. Adaptive Comfort Level Execution
The Honeybee model, local climate data, simulation period, and time step were fed into the HB Adaptive Comfort Map component. We set the period as annually and the time step as hourly. The simulation obtained the surface temperature, indoor air temperature, and humidity using the EnergyPlus program [48]. The outdoor air temperature, relative humidities, and air speeds were obtained from the local climate data. By combining these, the range of thermal comfort was determined using the ASHRAE 55-2017 standard [49].
3.2.3. Visualizing and Collecting Results for Comfort Level
Based on the simulation, the conditions of each radiance grid at each hour throughout the year were generated and exported as .csv files. There were three distinct values to represent the conditions. −1 was unacceptably cold conditions; 0 was neutral (comfortable) conditions; and 1 was unacceptably hot conditions. In addition, the thermal comfort percentage (TCP) of each grid throughout the year was also generated. This was the percentage of occupied time during which the thermal conditions were comfortable. The occupied time was defined in the building program assigned to the Honeybee model. The TCPs were saved as internalized data in the Grasshopper environment.
The results were then visualized using the Ladybug Spatial Heatmap and Honeybee Visualize Thermal Map component to provide intuitive insights in 3D.
4. Results
4.1. Annual Heat Demand Calculation for Different LoDs
In this section, the results of the annual heat demand calculation are presented for the two case study areas. However, before obtaining the results, an approximate validation was implemented for the methodology that was followed.
4.1.1. Methodology Validation
As was mentioned above, the Python script at the end of the methodological approach that estimated the annual heating demand of the buildings was validated using previous research by Dochev, so for the energy balance simulation there was no need for validation [28].
However, an approximate validation was implemented specifically for the city of London in the UK. In more detail, the live tables on Energy Performance of Buildings Certificates from GOV.UK were used in order to gather information regarding the energy demand of the buildings for the period of 2008 until 2021 [50]. The average of the annual energy demand of these years was equal to 273.45 kWh/(m2·a), corresponding to 55,510 buildings. Hence, the average of the dwellings under test in this paper was calculated for every LoD in order to compare the results. The findings are presented in the following table.
Table 1 shows that the mean difference between the value taken from the live tables of GOV.UK and the calculated results was about 40 kWh/(m2·a). This difference could be characterized as acceptably small considering that it was less than 12% and that the sample size of GOV.UK is much larger than the one that was tested in this paper. In addition, the data from GOV.UK represented both heating and cooling periods, which was in contrast to this paper’s approach that took into account only the heating period. Therefore, the slight decrease in energy demand between the calculated results and the GOV.UK tables can be explained. Finally, due to a lack of data it was assumed that none of the buildings under test had been renovated, which meant that it was reasonable that the estimated heating demand was slightly higher in retrofitted buildings.

Table 1.
Validation: comparison of the average results with GOV.UK live tables on Energy Performance of Buildings Certificates mean values.
4.1.2. Annual Residential Heat Demand—Case Study Area 1
The heating demand of the case study area with the old buildings is presented in the below maps for every LoD.
The map in Figure 5 represents the heating demand of the area for LoD1, where the roof type and the WWR were assumed to be pitched and 0.2, respectively.
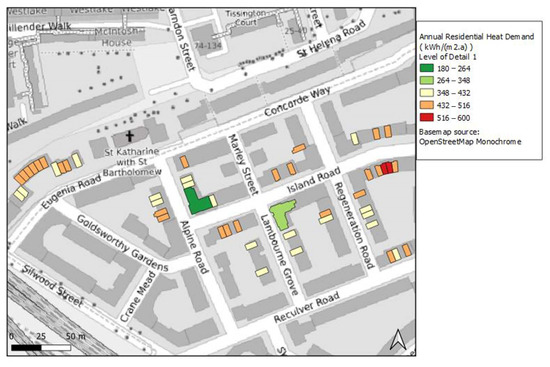
Figure 5.
Annual residential heat demand with LoD1 for Area 1.
In Figure 6 below, a map of the heating demand for Area 1 with old buildings for LoD2 is shown. At this part of energy simulations, the roof type detail was imputed from Google’s satellite view for each building, and the WWR was assumed to be equal to 0.2.
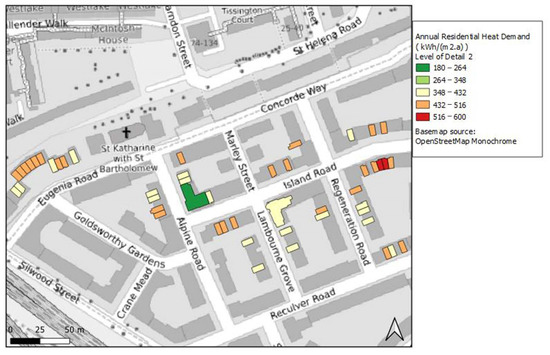
Figure 6.
Annual residential heat demand with LoD2 for Area 1.
Finally, a map of the heating demand for Area 1 with old buildings for LoD3 is presented in Figure 7. At this part of energy simulations, the WWR was imputed along with the roof type detail, from Google Street View and Google’s satellite view, respectively, for each building.
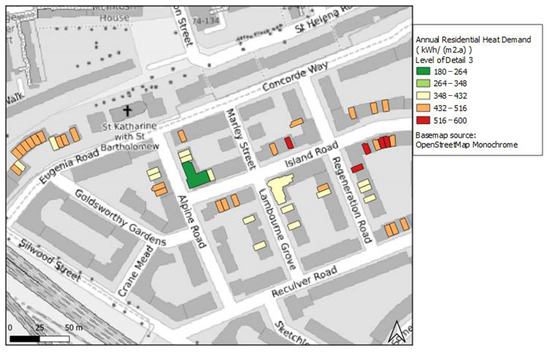
Figure 7.
Annual residential heat demand with LoD3 for Area 1.
4.1.3. Annual Residential Heat Demand—Case Study Area 2
The heating demand of the case study area with the new buildings is shown in the below maps for every LoD as for the area with old buildings.
Figure 8, Figure 9 and Figure 10 present the annual heating demand for LoD1, LoD2, and LoD3 for new buildings, respectively.
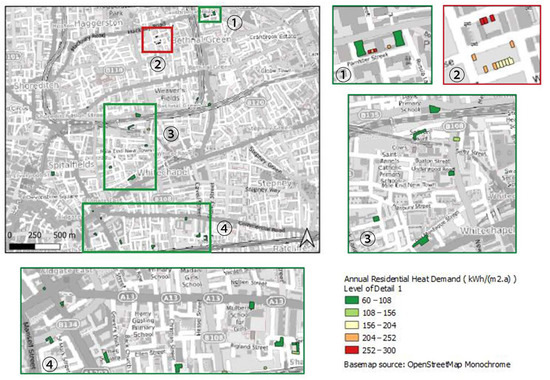
Figure 8.
Annual residential heat demand with LoD1 for Area 2.
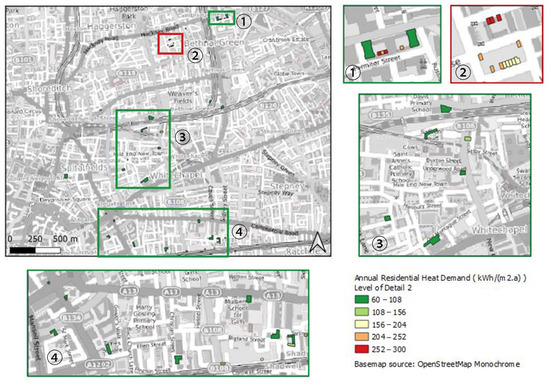
Figure 9.
Annual residential heat demand with LoD2 for Area 2.
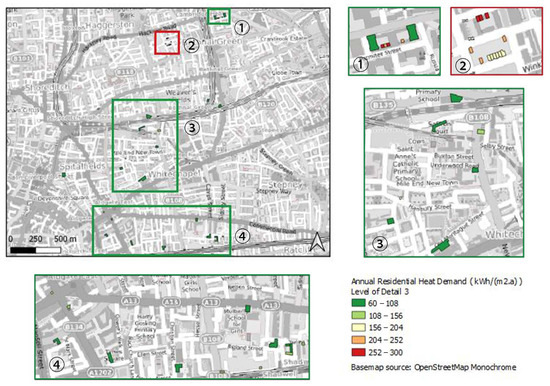
Figure 10.
Annual residential heat demand with LoD3 for Area 2.
4.1.4. Percentage Difference in Annual Residential Heat Demand—Case Study Area 1
In this section, the percentage difference of the annual residential heat demand of Area 1 is presented—it was calculated for a more convenient comparison between the results from the different LoDs.
Figure 11 demonstrates the percentage difference that occurred in the annual heating demand in the old dwellings from the upgrade of the LoD1 to LoD2. Figure 12 and Figure 13 below show the percentage difference for the LoD2 to LoD3 and for the LoD1 to LoD3, respectively.
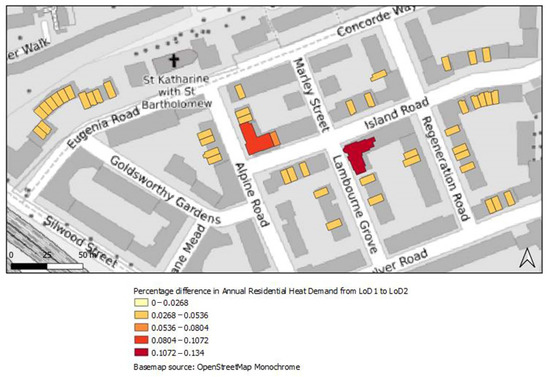
Figure 11.
Percentage difference in annual residential heat demand from LoD1 to LoD2 for Area 1.
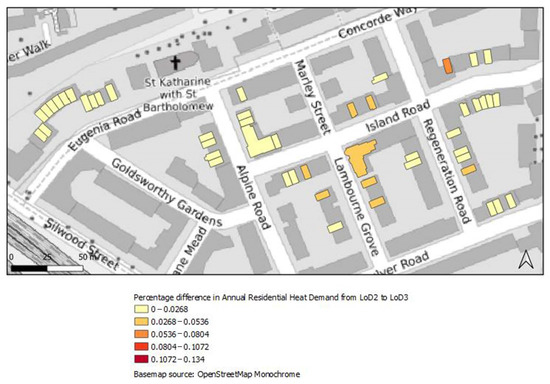
Figure 12.
Percentage difference in annual residential heat demand from LoD2 to LoD3 for Area 1.
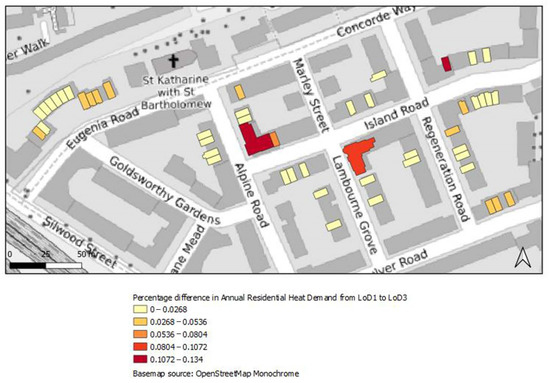
Figure 13.
Percentage difference in annual residential heat demand from LoD1 to LoD3 for Area 1.
4.1.5. Percentage Difference in Annual Residential Heat Demand—Case Study Area 2
In this subsection, the percentage difference of the annual heat demand for the upgrade of a lower to a higher LoD for Area 2 is presented. Because dwellings that have been left in this area and were analyzed were more spread across the map, areas of the main map have been zoomed in in order to make some dwellings more visible (Figure 14, Figure 15 and Figure 16).
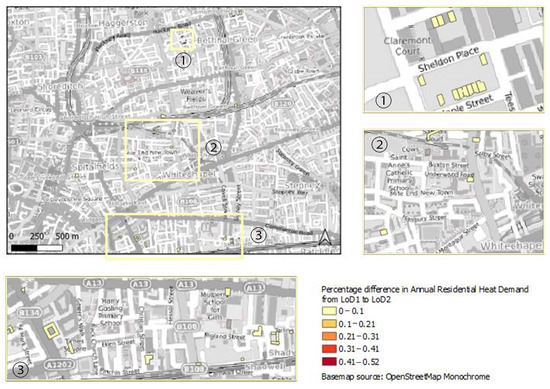
Figure 14.
Percentage difference in annual residential heat demand from LoD1 to LoD2 for Area 2.
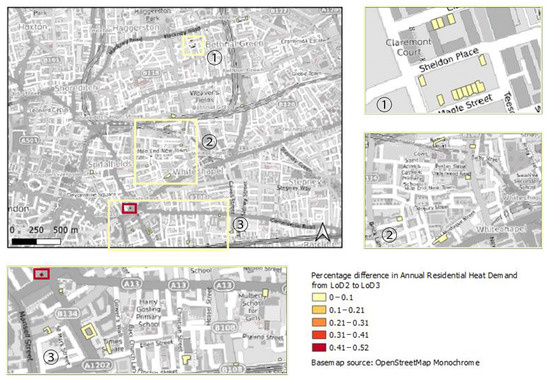
Figure 15.
Percentage difference in annual residential heat demand from LoD2 to LoD3 for Area 2.
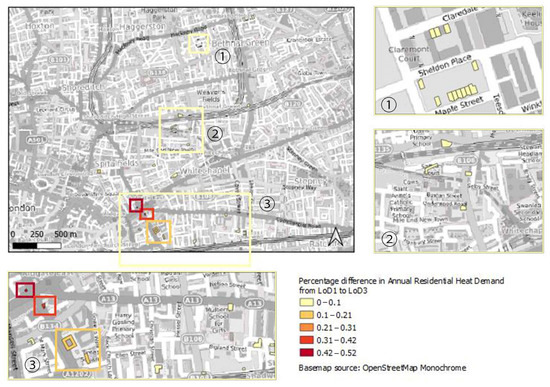
Figure 16.
Percentage difference in annual residential heat demand from LoD1 to LoD3 for Area 2.
4.2. Adaptive Comfort Level
In this section, for both areas, the top and bottom five buildings in annual heat demand ranking were selected for adaptive comfort level simulation.
4.2.1. Annual Comfort Levels—Case Study Area 1
The comfort levels of the bottom five buildings with the lowest heat demand in Area 1 are shown in Table 2 and Figure 17 and Figure 18. Among these buildings, building 2078778 and building 1983230 stood out because the condition inside was quite cold and there was only around 15% of the time during the year that the users would feel comfortable. Although they had a low heat demand, their energy performance was not satisfactory.

Table 2.
Buildings with low heat demand (Case Study Area 1).

Figure 17.
Comfort conditions mean for buildings with low heat demand in Area 1.
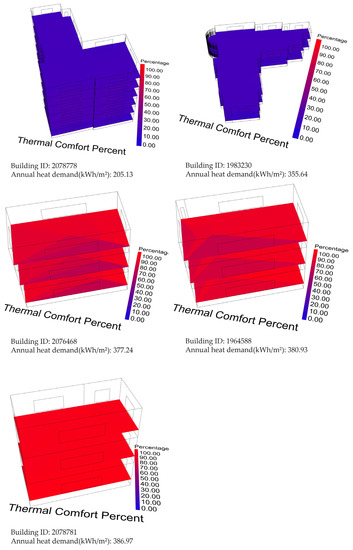
Figure 18.
Thermal comfort percentage mean (%) for buildings with low heat demand in Area 1.
The comfort levels of the top five buildings with the highest heat demand in Area 1 are shown in Table 3 and Figure 19 and Figure 20. Most of the buildings had satisfactory comfort conditions. As shown in Table 3, except for building 2078602, the remaining four buildings had a TCP over 90%. Apart from a few selected days across an annual period, users in these buildings felt comfortable most of the time. Thus, their high demands for heat load were worthwhile and justified. In comparison, building 2078602 had a low TCP of 14.23%. The users actually felt extremely cold during a majority of the year. Considering its high heat demand, its energy performance was quite unsatisfactory, and it should be prioritized for retrofitting.

Table 3.
Buildings with high heat demand (Case Study Area 1).
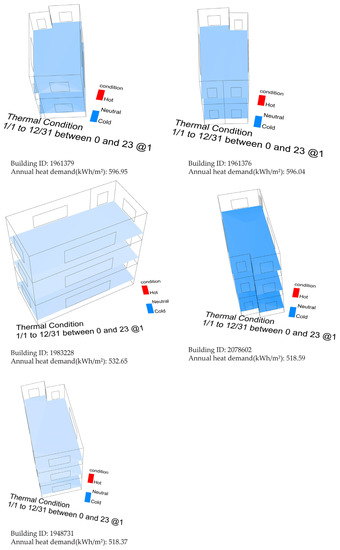
Figure 19.
Comfort conditions mean for buildings with high heat demand in Area 1.

Figure 20.
Thermal comfort percentage mean (%) for buildings with high heat demand in Area 1.
4.2.2. Annual Comfort Levels—Case Study Area 2
The comfort levels of the bottom five buildings with the lowest heat demand in Area 2 are shown in Table 4 and Figure 21 and Figure 22. Generally, compared with Area 1, buildings in Area 2 had a lower heat demand. Among those with the lowest, building 1053318 and building 1382107 were quite uncomfortable due to their coldness.

Table 4.
Buildings with low heat demand (Case Study Area 2).
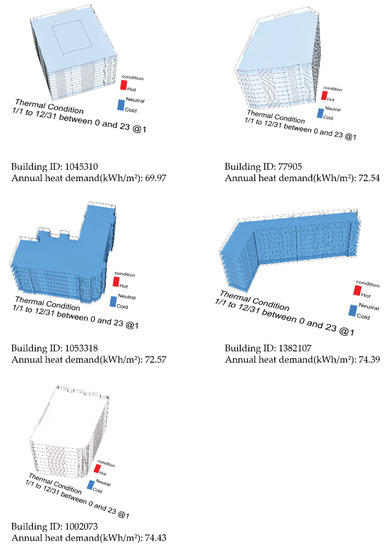
Figure 21.
Comfort conditions mean for buildings with low heat demand in Area 2.

Figure 22.
Thermal comfort percentage mean (%) for buildings with low heat demand in area 2.
The comfort levels of the top five buildings with the highest heat demand in Area 2 are shown in Table 5 and Figure 23 and Figure 24. Only building 1283218 was too cold for users, while others were generally comfortable throughout the year.

Table 5.
Buildings with high heat demand (Case Study Area 2).

Figure 23.
Comfort conditions mean for buildings with high heat demand in Area 2.
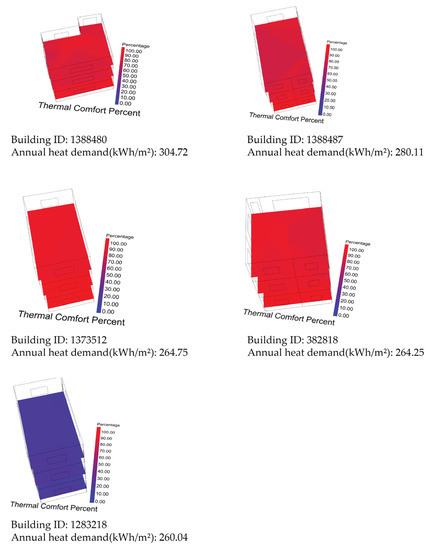
Figure 24.
Thermal comfort percentage mean (%) for buildings with high heat demand in Area 2.
5. Discussion
5.1. Annual Residential Heat Demand and LoDs
The annual residential heating demand for Area 1 was as high as expected due to the stock age of the buildings under test. This could be explained by the fact that the thermal envelope of most old dwellings does not consist of thermal insulation or consists of thermal insulation construction materials with a high thermal transmittance (U-value), which means that these properties cannot be highly energy effective. Similar results were obtained for LoD2, for which the exact roof type of each building was inserted into the dataset with the use of Google’s satellite view. As was obvious, the illustration of the map was the same as for LoD1 (except for one building that was moved to a higher heating demand class). The same occurred for LoD3, for which an estimation of the window-to-wall (WWR) ratio was inserted into the dataset by using Google Street View. Nonetheless, the illustration of the map for LoD3 (Figure 7) was insignificantly different from the above maps. Finally, only a few buildings could be seen that had changed and were classified as a higher annual residential heat demand class.
As was obvious, the illustration of the results was the same for all LoDs for Area 2 as well (Figure 8, Figure 9 and Figure 10). In particular, in the legend it can be seen that the annual heat demand in the area of London with the newest dwellings (construction year >2003) was extremely lower than the annual heat demand of older buildings. These results could be foreseen because highly energy-effective construction materials with lower thermal transmittance have been commonly chosen for buildings in recent years. Despite that, from LoD1 to LoD2 there was no difference in the results for the annual heat demand, and only for LoD3 was there a small difference. However, the difference was too small, especially when taking into consideration the time consumed for the calculation of the WWR rather than assuming a logical and average value.
For Area 1, as shown in Figure 11, most buildings had a small percentage difference from LoD1 to LoD2, with the highest for one building (represented with a dark red color; its percentage difference was between 10.72% and 13.4%). In Figure 12, for the upgrade from LoD2 to LoD3, there was a different appearance of the map for this area. As can be seen, the percentage difference was lower than in Figure 10, which meant that for old buildings at least, there was no need for the estimation of the WWR because the percentage difference could be characterized as acceptable. Finally, in Figure 13, which represents the percentage difference from LoD1 to LoD3, a quick glance shows that it is obvious that the appearance of the map changed slightly and that most buildings are represented with light yellow and light orange colors, which indicated a low-percentage difference. However, overall it could be seen that the higher proportion in differences was observed for buildings with a larger footprint and mainly for detached building forms.
For Area 2, as can be seen in Figure 14, there was not a variety of percentage differences from LoD1 to LoD2 because not all shades of colors are visible. Hence, buildings with a dark red color or orange are not visible; they represented a percentage difference up to 52% and were the minority. In contrast, some buildings on the map are represented only with light yellow, which represented a percentage difference range of 0 to 10%. Hence, even the highest percentage difference was low from the upgrade of LoD1 to LoD2 and acceptable. In Figure 15 and Figure 16, a homogeneity can be observed in the results as well as that the majority of buildings were represented by a low-percentage difference in the annual residential heat demand, which was up to 10%. Nonetheless, there were some exceptions to the rule. More particularly, one of these buildings is shown in Figure 15 inside the dark red box with a dark red color, which represented the highest percentage difference; another one is shown in Figure 16 with a dark orange color, which represented the second highest difference as mentioned previously.
In sum, it turned out that geometrical detail was not necessary for the energy demand calculation at the urban scale, as has been stated in Strzalka’s research previously [27].
5.2. Annual Residential Heat Demand and Comfort Level
Using the annual heat demand and comfort level generated from the model with a fixed LoD (LoD5 in the case study areas), the undetected energy performance patterns were revealed.
For Area 1, if only judged by the heat demand, due to low demand, building 2078778 and building 983230 will be considered as good performing, thus leading to a lower ranking in upgrading and adopting new building technologies. However, due to their low comfort level, they need to be prioritized in future retrofitting plans. The situation is similar for building 1053318 and building 1382107 in Area 2. The actionable insights are more critical for buildings with high demand since more energy was consumed inefficiently in return for a low comfort level, as in the cases of building 2078602 in Area 1 and building 1283218 in Area 2. A closer case-by-case investigation needs to be conducted by relevant stakeholders such as the local council, asset manager, and research institutions.
Between the two case study areas, due to the distinct differences in building age, the heat demand of Area 1 was generally higher. Thus, there lies a more significant impact of potential improvement in energy performance in Area 1 and other building stock with similar attributes.
6. Conclusions
In this research, we developed a data-driven approach for heat demand modeling of buildings at the urban scale. The impact of LoD on the modeling results and energy performance as assessed by comfort level were investigated for the city of London in the UK. A completed workflow including data extraction, data processing, simulation, and visualization of the results was explained. It can be scaled up and applied to building stock with a higher number and greater diversity.
This research revealed that the use of Level of Detail 1, which assumes the roof type and the WWR according to building typologies, is an effective way to evaluate annual residential heat demand at the city scale. However, the thermal comfort level investigation showed that models with a high LoD are useful for a holistic energy performance assessment. More particularly, by adding the thermal comfort metric, it was discovered that buildings with a lower energy demand that are initially interpreted as energy efficient can be characterized by low human thermal comfort. Thus, their energy performance is not satisfying because in reality a higher energy demand is needed to achieve the desired human thermal comfort level.
One of the key uses of this research can be to guide city planners and designers in acquiring actionable insights on assessing energy demand and efficiency in a simple and replicable way. The data structure and simulation algorithm can be integrated as a standard workflow with a simplified user interface to reduce the learning curve and processing time. Planners and designers can then apply the workflow in retrofitting existing buildings and design of new buildings.
There are several methodological and data improvements that could be pursued in the future. A future study would be useful to analyze larger areas with mixed-age dwellings for a comparison of the results regarding the building age and the generalization of the initial hypothesis because the current dataset included older buildings in Case Study Area 1 and newer buildings in Case Study Area 2. In addition, the refurbishment rate is a gap in this research that could be taken into consideration for future studies in order to obtain more representative results. In addition, the applicability of the insights gained could be restricted by the study area because this research was focused on the London area. Some comparative studies should be conducted across various climate zones. Lastly, simpler data processing methods interconnecting required data for the energy modeling and comfort simulation from different data sources could be developed. Policy makers may integrate such methods in their workflow and work toward a reduction in residential energy demand and the related carbon footprint.
Author Contributions
Conceptualization, A.A. and M.Z.; methodology, A.A. and M.Z.; software, A.A. and M.Z.; validation, A.A. and M.Z.; formal analysis, A.A. and M.Z.; data curation, A.A. and M.Z.; writing—original draft preparation, A.A., M.Z. and J.J.; writing—review and editing, A.A., M.Z. and J.J.; visualization, A.A., M.Z. and J.J.; project administration, A.A.; funding acquisition, A.A. and M.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by EPSRC under grant number EP/S023577/1.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. No new data were created during this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yao, S. Building Integration of Sustainable Energy Technologies on a Detached House in Shanghai; Center on Global Energy Policy at Columbia University: New York, NY, USA, 2019; p. 77. Available online: https://www.energypolicy.columbia.edu/publications/energy-and-development-changing-world-framework-21st-century/ (accessed on 20 April 2023).
- Omer, M. Energy use and environmental impacts: A general review. J. Renew. Sustain. Energy 2009, 1, 053101. [Google Scholar] [CrossRef]
- Ismail, F.H.; Shahrestani, M.; Vahdati, M.; Boyd, P.; Donyavi, S. Climate change and the energy performance of buildings in the future—A case study for prefabricated buildings in the UK. J. Build. Eng. 2021, 39, 102285. [Google Scholar] [CrossRef]
- Pachauri, R.K.; Allen, M.R.; Barros, V.R.; Broome, J.; Cramer, W.; Christ, R.; Church, J.A.; Clarke, L.; Dahe, Q.; Dasgupta, P.; et al. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014; p. 151. Available online: https://epic.awi.de/id/eprint/37530/1/IPCC_AR5_SYR_Final.pdf (accessed on 9 April 2021).
- UN. UN Survey. More Than Half of World’s Population Now Living in Urban Areas, UN Survey Finds. UN News. 2014. Available online: https://news.un.org/en/story/2014/07/472752-more-half-worlds-population-now-living-urban-areas-un-survey-finds (accessed on 9 April 2021).
- Wang, S.; Fang, C.; Guan, X.; Pang, B.; Ma, H. Urbanisation, energy consumption, and carbon dioxide emissions in China: A panel data analysis of China’s provinces. Appl. Energy 2014, 136, 738–749. [Google Scholar] [CrossRef]
- Biljecki, F. The Concept of Level of Detail in 3D City Models; GISt Report No. 62; Delft University of Technology: Delft, The Netherlands, 2013; p. 70. [Google Scholar]
- Agugiaro, G.; Hauer, S.; Nadler, F. Coupling of CityGML-based semantic city Models with energy simulation tools: Some experiences. In Proceedings of the 20th International Conference on Urban Planning, Regional Development and Information Society, Ghent, Belgium, 5–7 May 2015. [Google Scholar]
- Trace Software. The Level of Detail and the Level of Development in the BIM Environment. 2019. Available online: https://www.trace-software.com/blog/the-level-of-detail-and-the-level-of-development-in-the-bim-environment/ (accessed on 12 June 2021).
- Tian, W. A review of sensitivity analysis methods in building energy analysis. Renew. Sustain. Energy Rev. 2013, 20, 411–419. [Google Scholar] [CrossRef]
- De Wilde, P.; Tian, W. Preliminary application of a methodology for risk assessment of thermal failures in buildings subject to climate change. In Proceedings of the Eleventh International IBPSA Conference, Glasgow, Scotland, 27–30 July 2009. [Google Scholar]
- Tian, W.; de Wilde, P. Uncertainty and sensitivity analysis of building performance using probabilistic climate projections: A UK case study. Autom. Constr. 2011, 20, 1096–1109. [Google Scholar] [CrossRef]
- Gustafsson, S.-I. Sensitivity analysis of building energy retrofits. Appl. Energy 1998, 61, 11. [Google Scholar] [CrossRef]
- Hygh, J.S.; DeCarolis, J.F.; Hill, D.B.; Ranjithan, S.R. Multivariate regression as an energy assessment tool in early building design. Build. Environ. 2012, 57, 165–175. [Google Scholar] [CrossRef]
- Hopfe, J.; Hensen, J.L.M. Uncertainty analysis in building performance simulation for design support. Energy Build. 2011, 43, 2798–2805. [Google Scholar] [CrossRef]
- Ioannou, A.; Itard, L. Energy performance and comfort in residential buildings: Sensitivity for building parameters and occupancy. Energy Build. 2015, 92, 216–233. [Google Scholar] [CrossRef]
- Olivero, E.; Onillon, E.; Beguery, P.; Brunet, R.; Marat, S.; Azar, M. On key parameters influencing building energy performance. In Proceedings of the Building Simulation 2015: 14th Conference of IBPSA, Hyderabad, India, 7–9 December 2015; p. 10. [Google Scholar]
- Zhang, A.; Bokel, R.; Van den Dobbelsteen, A.; Sun, Y.; Huang, Q.; Zhang, Q. The effect of geometry parameters on energy and thermal performance of school buildings in cold climates of China. Sustainability 2017, 9, 20. [Google Scholar] [CrossRef]
- Parasonis, J.; Keizikas, A. Possibilities to reduce the energy demand for multistory residential buildings. In Proceedings of the 10th International Conference “Modern Building Materials, Structures and Techniques”, Vilnius, Lithuania, 19–21 May 2010; p. 5. [Google Scholar]
- Hemsath, T.L. Building design with energy performance as primary agent. Energy Procedia 2015, 78, 6. [Google Scholar] [CrossRef]
- Ghiai, M.M.; Mahdavinia, M.; Parvane, F.; Jafarikhah, S. Relation between energy consumption and window to wall ratio in high-rise office buildings in Tehran. Eur. Online J. Nat. Soc. Sci. 2014, 3, 10. [Google Scholar]
- Robinson, D.; Haldi, F.; Leroux, P.; Perez, D.; Rasheed, A.; Wilke, U. CitySim: Comprehensive micro-simulation of resource flows for sustainable urban planning. In Proceedings of the Eleventh International IBPSA Conference, Glasgow, Scotland, 27–30 July 2009. [Google Scholar]
- Frayssinet, L.; Merlier, L.; Kuznik, F.; Hubert, J.-L.; Milliez, M.; Roux, J.-J. Modeling the heating and cooling energy demand of urban buildings at city scale. Renew. Sustain. Energy Rev. 2018, 81, 2318–2327. [Google Scholar] [CrossRef]
- APUR. Consommations D’énergie et Émission de Gaz à Effet’. 2007. Available online: https://www.apur.org/fr/nos-travaux/consommations-energie-emissions-gaz-effet-serre-liees-chauffage-residences-principales-parisiennes (accessed on 2 February 2023).
- Rosser, J.F.; Boyd, D.S.; Long, G.; Zakhary, S.; Mao, Y.; Robinson, D. Predicting residential building age from map data. Comput. Environ. Urban Syst. 2019, 73, 56–67. [Google Scholar] [CrossRef]
- Kaden, R.; Kolbe, T.H. City-wide total energy demand estimation of buildings using semantic 3D city models and statistical data. ISPRS Ann. Photogramm. Remote Sens. Spatial Inf. Sci. 2013, II-2/W1, 163–171. [Google Scholar] [CrossRef]
- Strzalka, A.; Bogdahn, J.; Coors, V.; Eicker, U. 3D City modeling for urban scale heating energy demand forecasting. HVAC&R Res. 2011, 17, 15. [Google Scholar]
- Dochev, I. Computing Residential Heat Demand in Urban Space using QGIS. A Case Study for Shumen, Bulgaria. 2016. Available online: http://programm.corp.at/cdrom2016/files/CORP2016_proceedings.pdf (accessed on 14 April 2021).
- ‘TABULA WebTool’. Available online: https://webtool.building-typology.eu/#bm (accessed on 25 June 2021).
- Nicol, F. Thermal Comfort: A Handbook for Field Studies Towards an Adaptive Model; University of East London: London, UK, 1993. [Google Scholar]
- Taleghani, M.; Tenpierik, M.; Kurvers, S.; van den Dobbelsteen, A. A review into thermal comfort in buildings. Renew. Sustain. Energy Rev. 2013, 26, 201–215. [Google Scholar] [CrossRef]
- Frontczak, M.; Wargocki, P. Literature survey on how different factors influence human comfort in indoor environments. Build. Environ. 2011, 46, 922–937. [Google Scholar] [CrossRef]
- De Dear, R.; Brager, G.S. Developing an Adaptive Model of Thermal Comfort and Preference. 1998. Available online: https://escholarship.org/uc/item/4qq2p9c6 (accessed on 8 March 2023).
- Yang, X.; Hu, M.; Heeren, N.; Zhang, C.; Verhagen, T.; Tukker, A.; Steubing, B. A combined GIS-archetype approach to model residential space heating energy: A case study for the Netherlands including validation. Appl. Energy 2020, 280, 115953. [Google Scholar] [CrossRef]
- Nouvel, R.; Schulte, C.; Eicker, U.; Pietruschka, D.; Coors, V. CityGML-based 3D city model for energy diagnostics and urban energy policy support. IBPSA World 2013, 2013, 9. [Google Scholar]
- Coulter, T.L.S.; Leicht, R.M. A sensitivity analysis of energy modeling input parameters for energy retrofit projects. In Proceedings of the Construction Research Congress 2014, Atlanta, GE, USA, 19–21 May 2014; pp. 2244–2254. [Google Scholar] [CrossRef]
- Ratti, C.; Baker, N.; Steemers, K. Energy consumption and urban texture. Energy Build. 2005, 37, 762–776. [Google Scholar] [CrossRef]
- Baker, F.; Smith, C. A GIS and object based image analysis approach to mapping the greenspace composition of domestic gardens in Leicester, UK. Landsc. Urban Plan. 2019, 183, 133–146. [Google Scholar] [CrossRef]
- ‘Colouring London’. Available online: https://colouring.london (accessed on 26 June 2021).
- Digimap Ordnance Survey’. Available online: https://digimap.edina.ac.uk/os (accessed on 26 June 2021).
- Ordnance Survey MasterMap Building Height Attribute|OS Products’. Available online: https://www.ordnancesurvey.co.uk/business-government/products/mastermap-building (accessed on 20 June 2022).
- Centreforcities. Average Space per Resident. 2018. Available online: https://www.centreforcities.org/reader/making-room/how-much-space-do-people-in-different-cities-have/ (accessed on 2 February 2023).
- Tabula, E. Building Typology Brochure England. 2014. Available online: https://episcope.eu/fileadmin/tabula/public/docs/brochure/GB_TABULA_TypologyBrochure_BRE.pdf (accessed on 2 February 2023).
- Public Health England. Minimum Home Temperature Thresholds for Health in Winter—A Systematic Literature Review; Public Health England: London, UK, 2014. [Google Scholar]
- Passivhaus Institut Passive House Planning Package (PHPP). Available online: https://passivehouse.com/04_phpp/04_phpp.htm (accessed on 4 March 2023).
- Urbano. Food4Rhino. 2019. Available online: https://www.food4rhino.com/en/app/urbano (accessed on 13 March 2023).
- ‘Ladybug Tools|Home Page’. Available online: https://www.ladybug.tools/ (accessed on 13 March 2023).
- ‘EnergyPlus’. Available online: https://energyplus.net/ (accessed on 13 March 2023).
- ‘Standard 55—Thermal Environmental Conditions for Human Occupancy’. Available online: https://www.ashrae.org/technical-resources/bookstore/standard-55-thermal-environmental-conditions-for-human-occupancy (accessed on 13 March 2023).
- GOV.UK. Live Tables on Energy Performance of Buildings Certificates. 2021. Available online: https://www.gov.uk/government/statistical-data-sets/live-tables-on-energy-performance-of-buildings-certificates (accessed on 10 August 2021).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).