Accurate Detection of Concrete Pavement Thickness Based on Ultrasonic Array
Abstract
1. Introduction
2. Ultrasonic Array Testing Equipment and Principle
2.1. Ultrasonic Array Testing Equipment
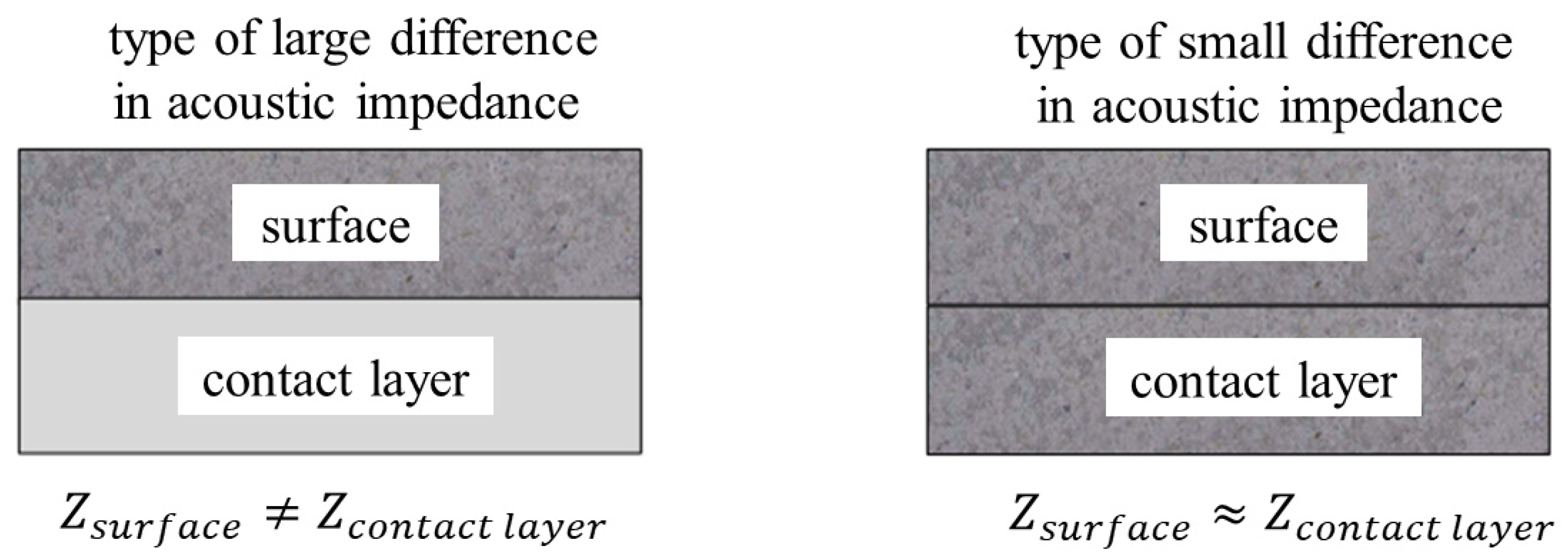
2.2. Ultrasonic Array Testing Principle for Concrete Surface Layer Thickness Detection
2.3. Classification of Concrete Pavement Structures for Ultrasonic Array Detection
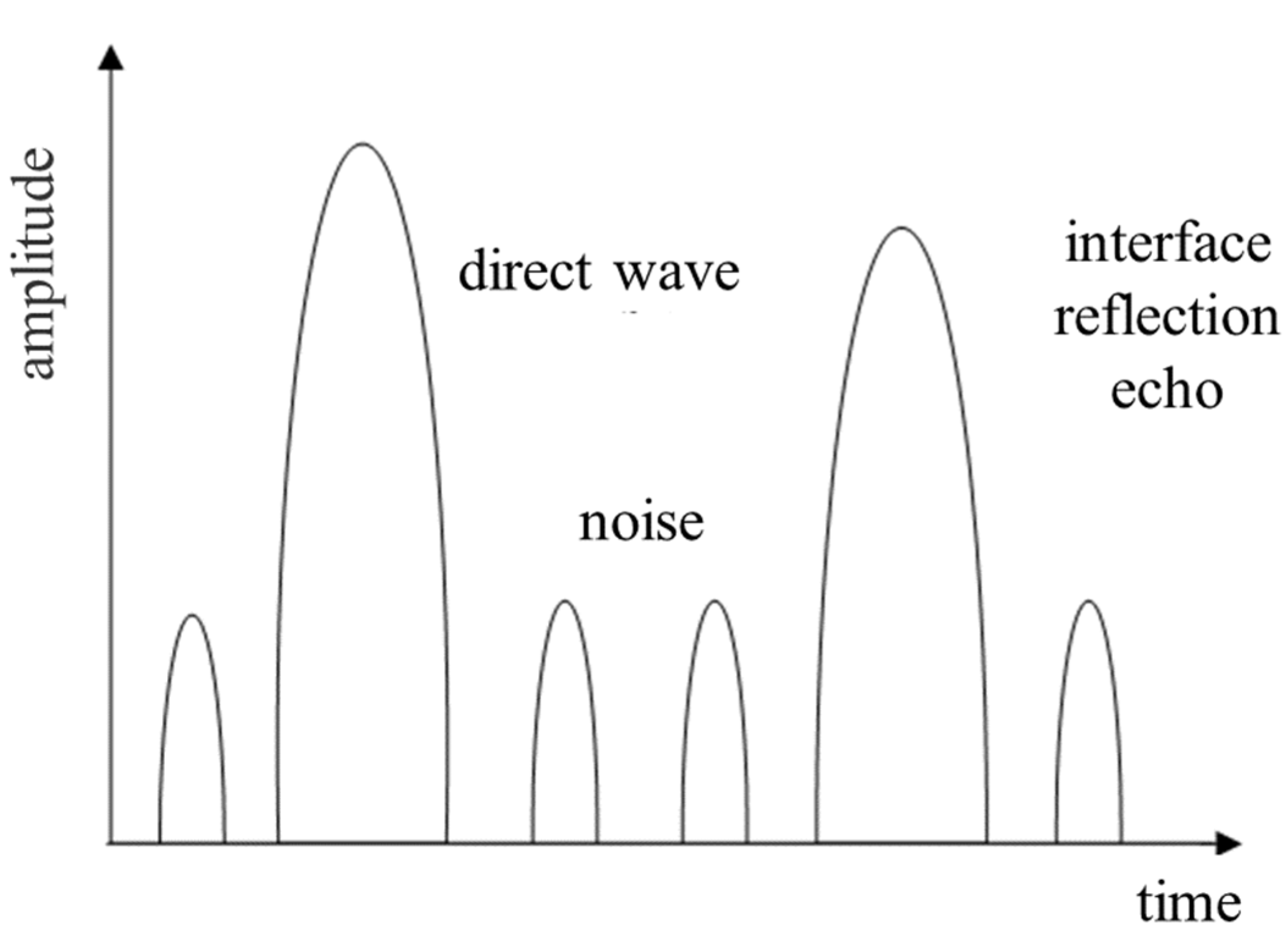
3. Signal Processing and Data Analysis
3.1. Signal Pre-Processing
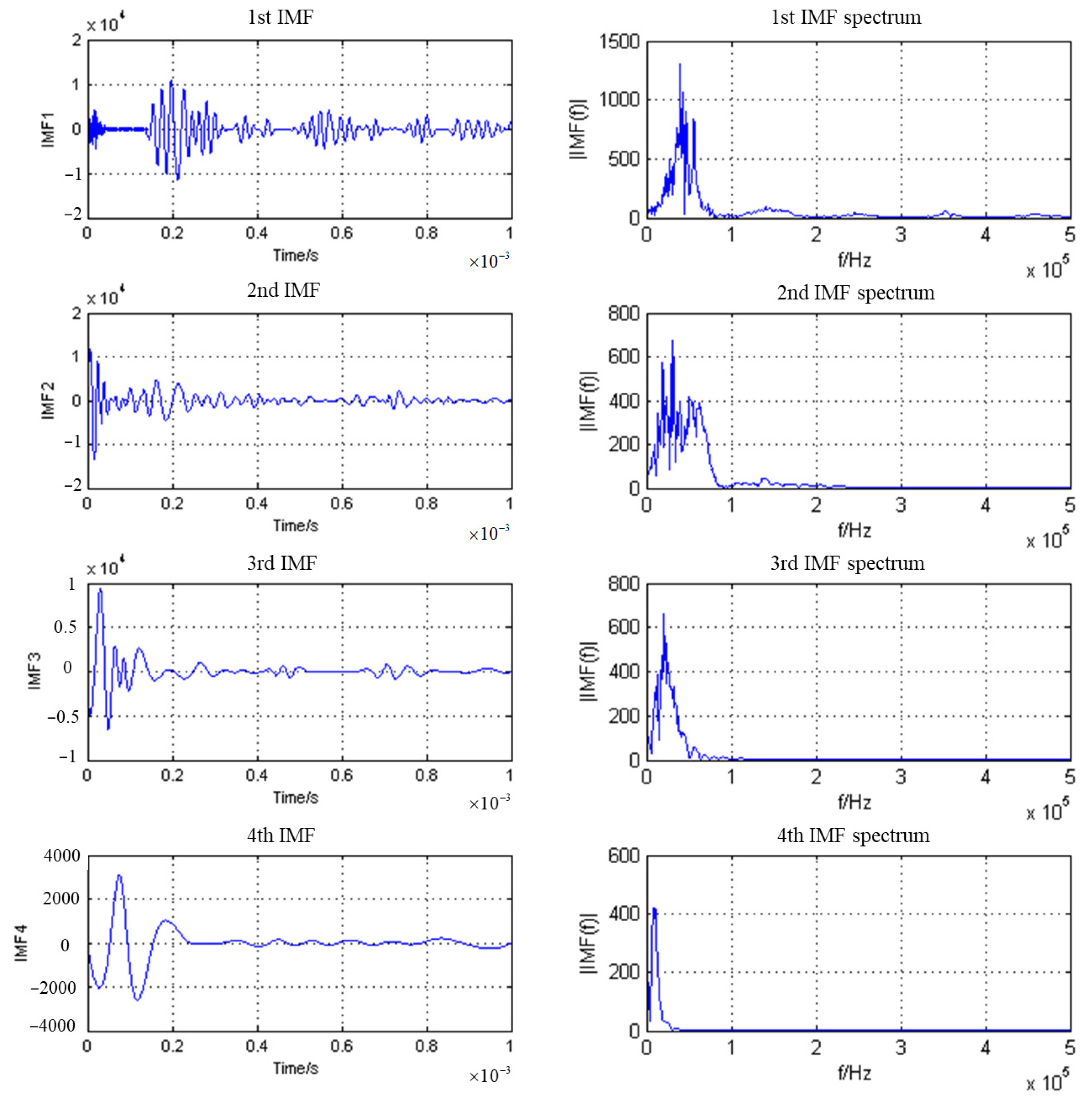
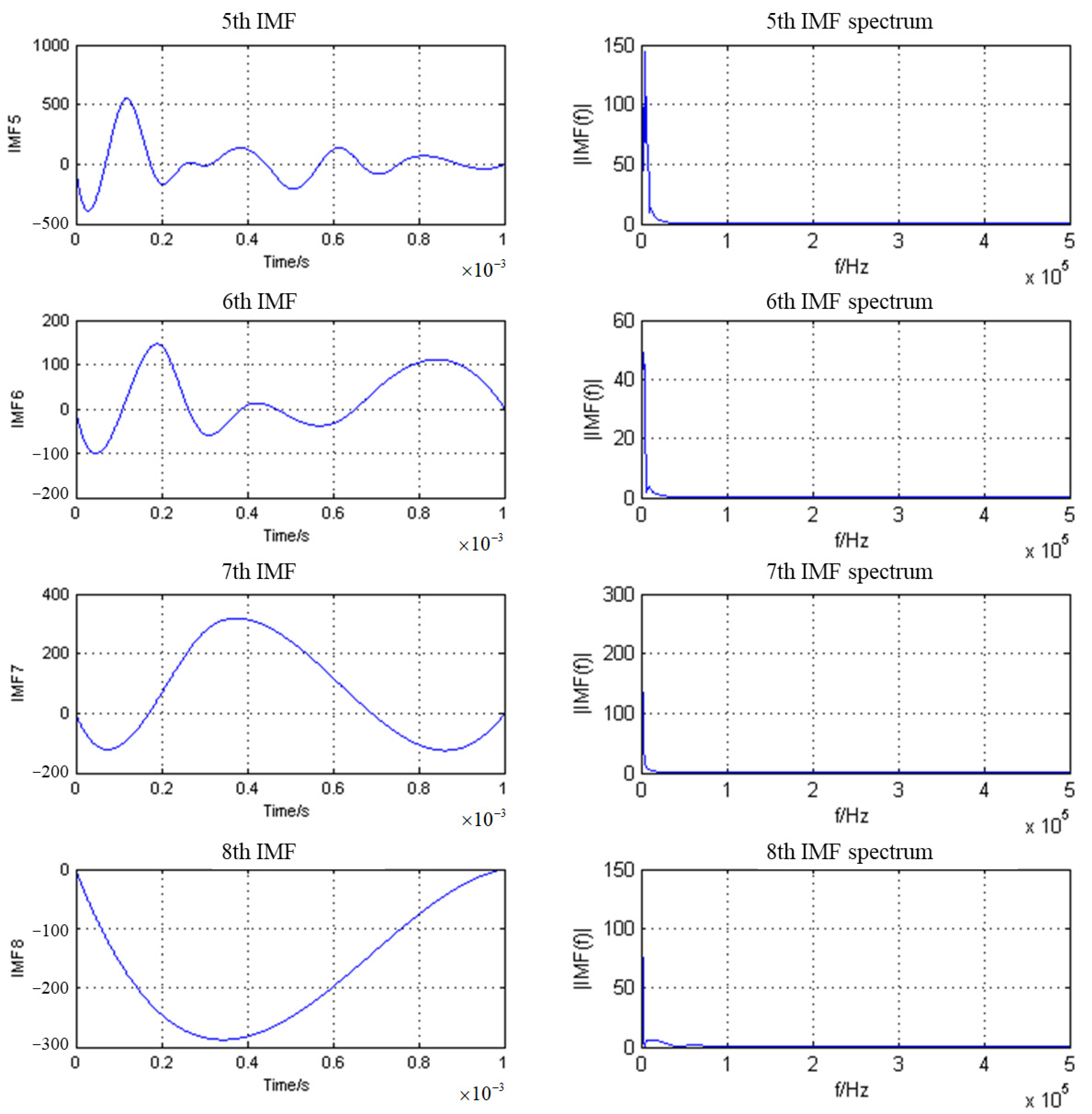
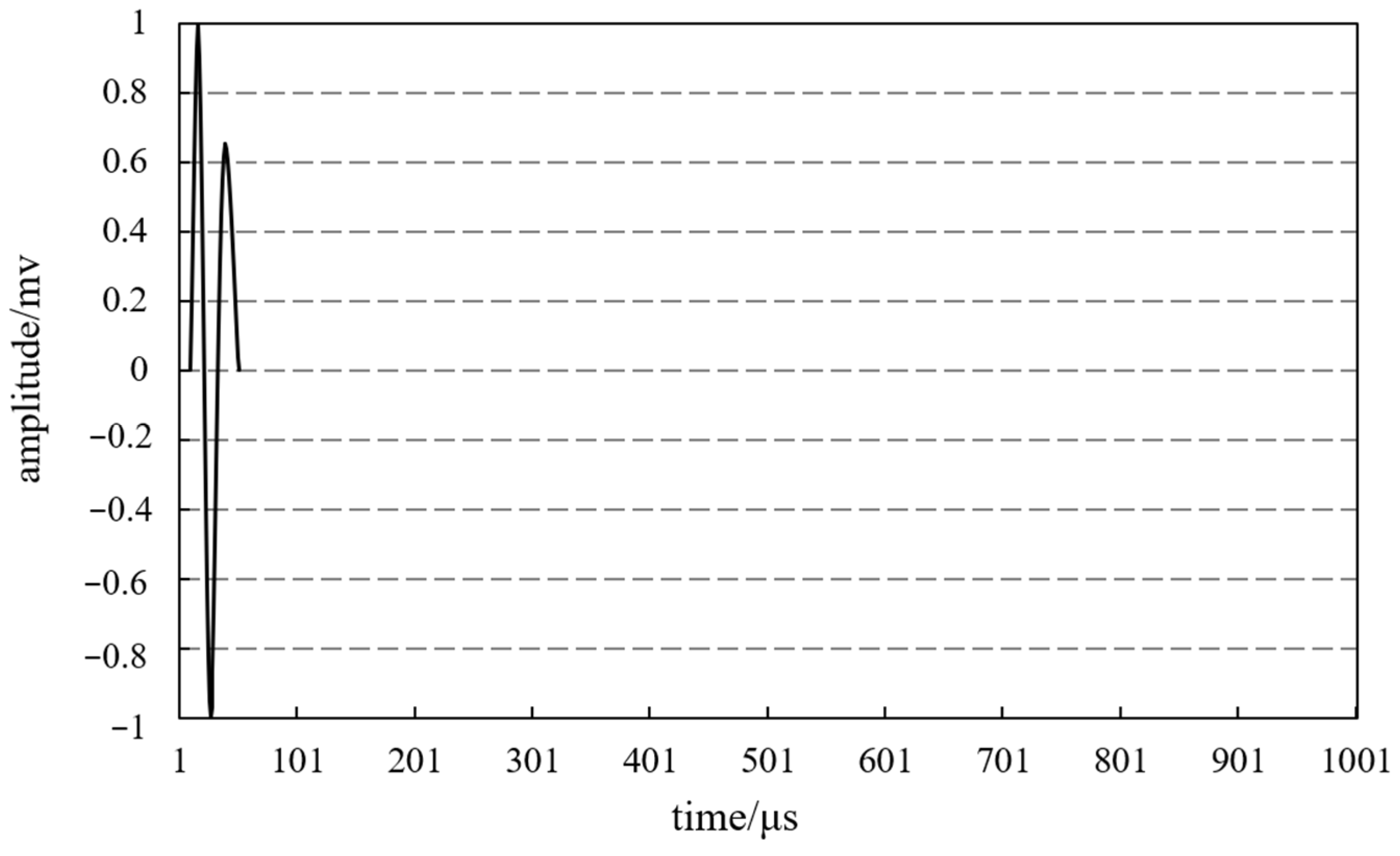
3.2. Empirical Mode Decomposition to Remove Surface Direct Waves
- (1)
- Calculate the maxima and minima values of .
- (2)
- Use the cubic spline interpolating function to calculate the maxima envelope and the minima envelope .
- (3)
- Calculate .
- (4)
- Calculate .
- (5)
- Replace with and repeat steps (1)~(4) for k times, then obtain the and . Where, is filtered data, and is filtered data.
- (6)
- Judge whether and meet the conditions of Equation (4).where, T is total number of sampling points. If the conditions are met, is the first intrinsic modal function (IMF), denoted as otherwise, repeat step (1)~(5) until the condition is met.
- (7)
- Replace with . Repeat steps (1)~(6) to obtain each intrinsic mode function in turn. Empirical modal decomposition ends when can no longer be decomposed.
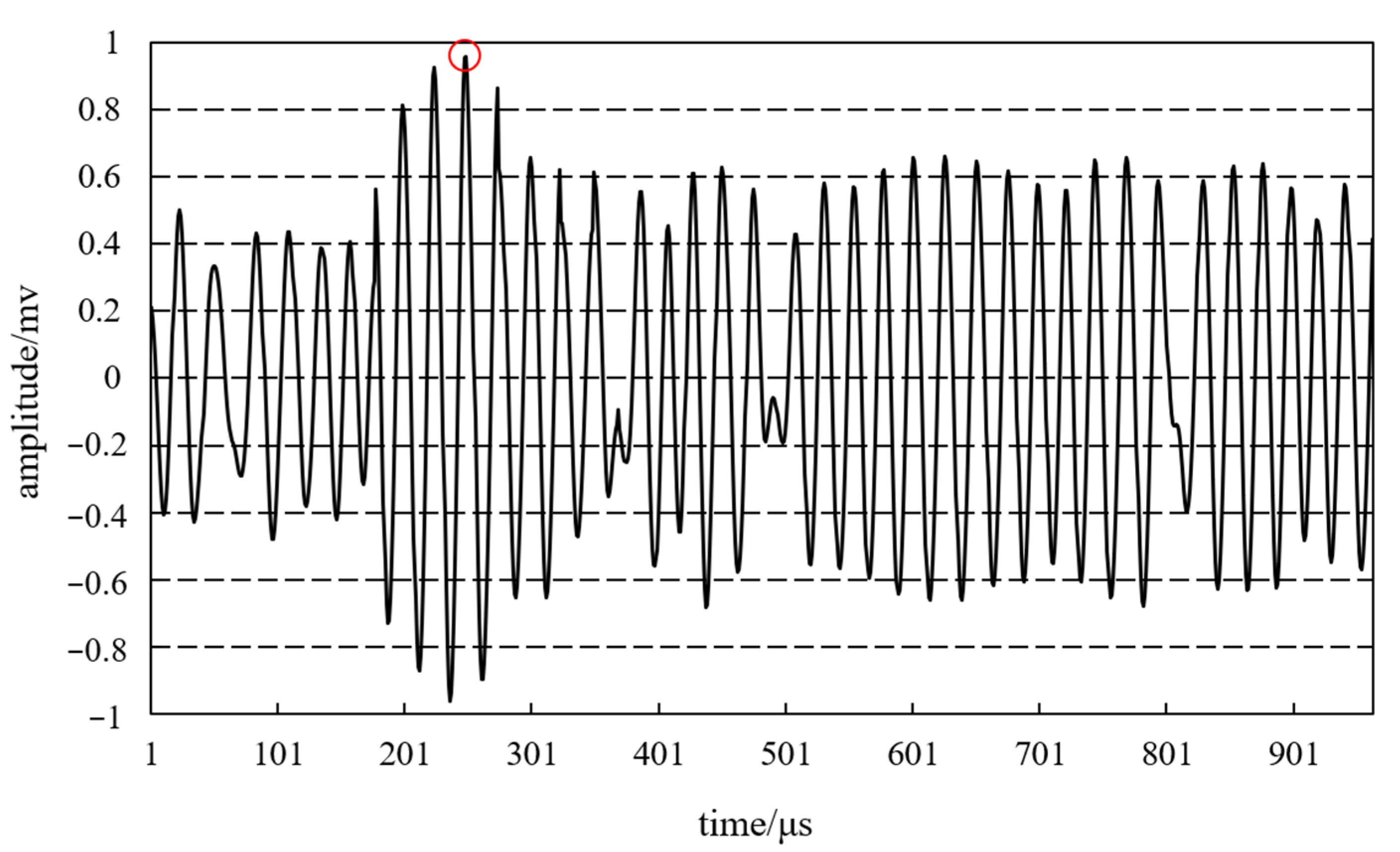
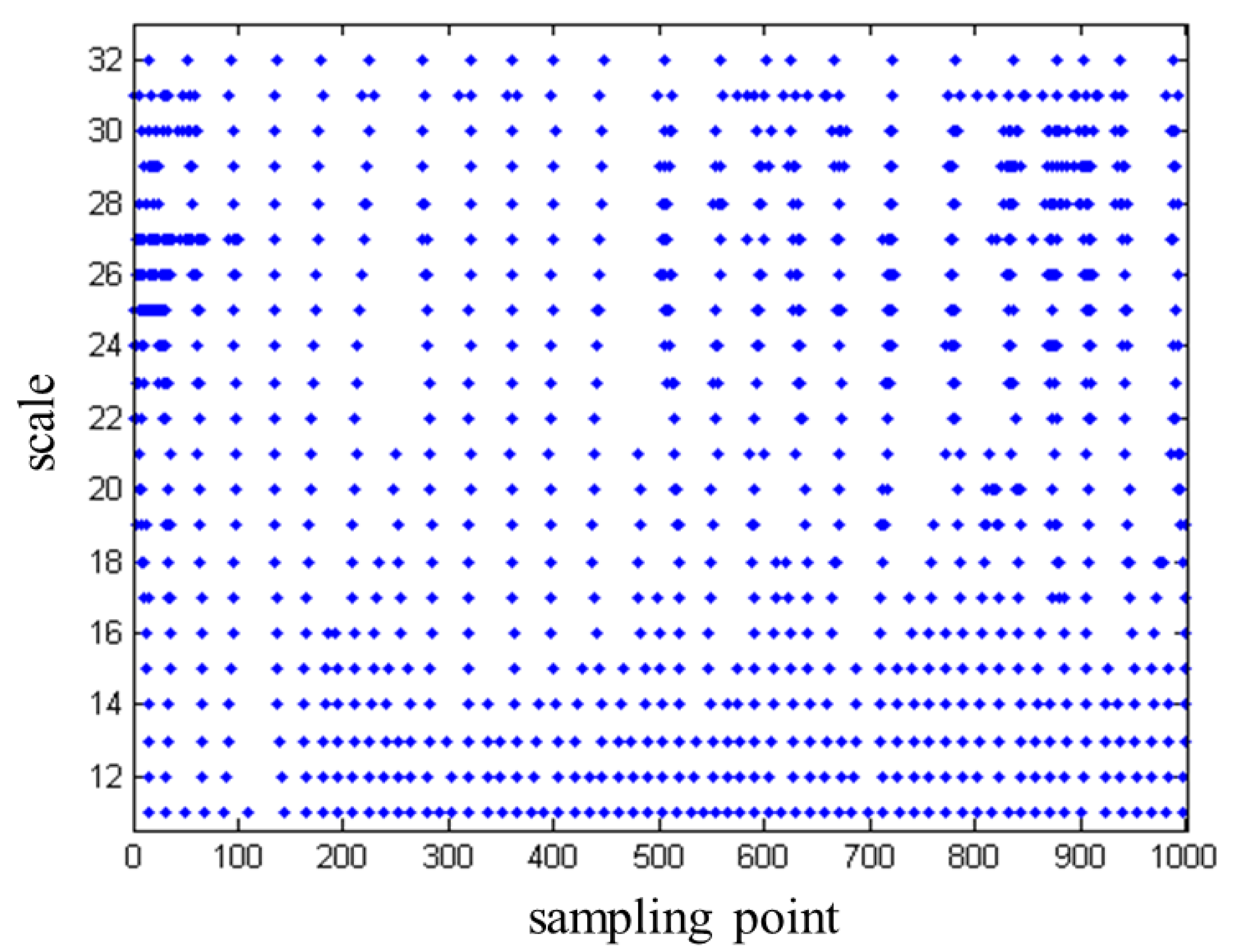
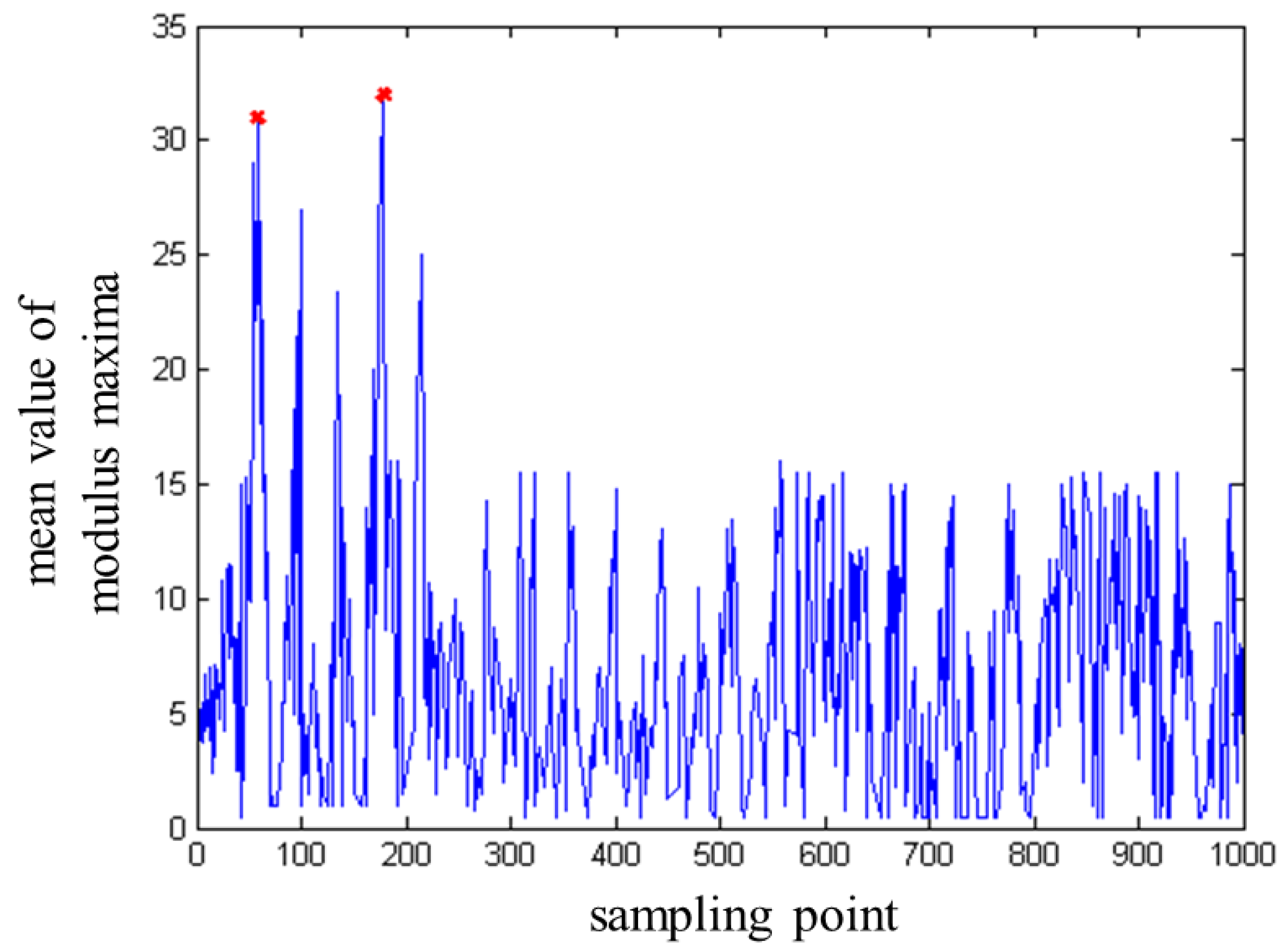
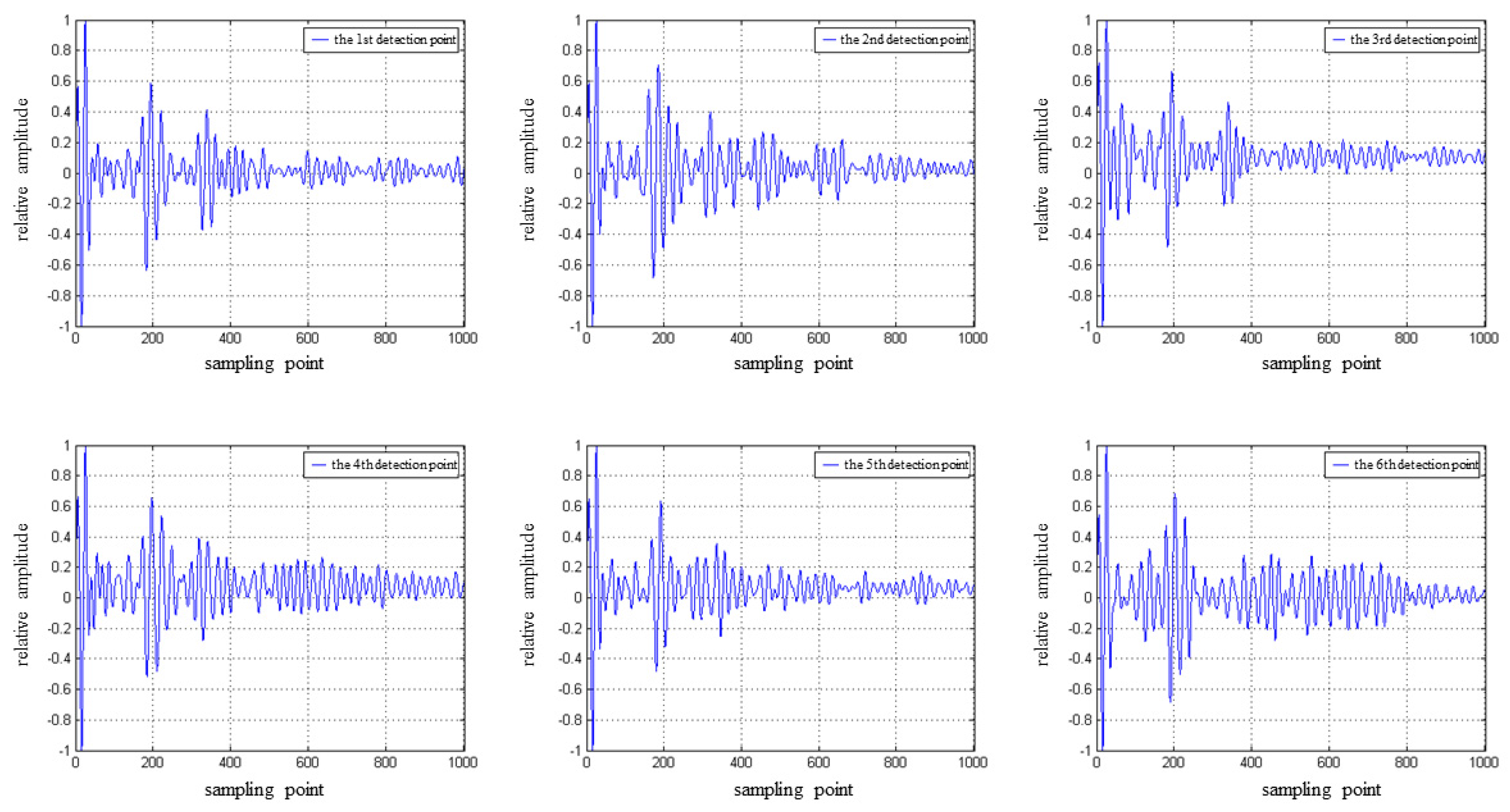
3.3. Determining the Location of the Interface Reflection Echo Starting Point
4. Field Test
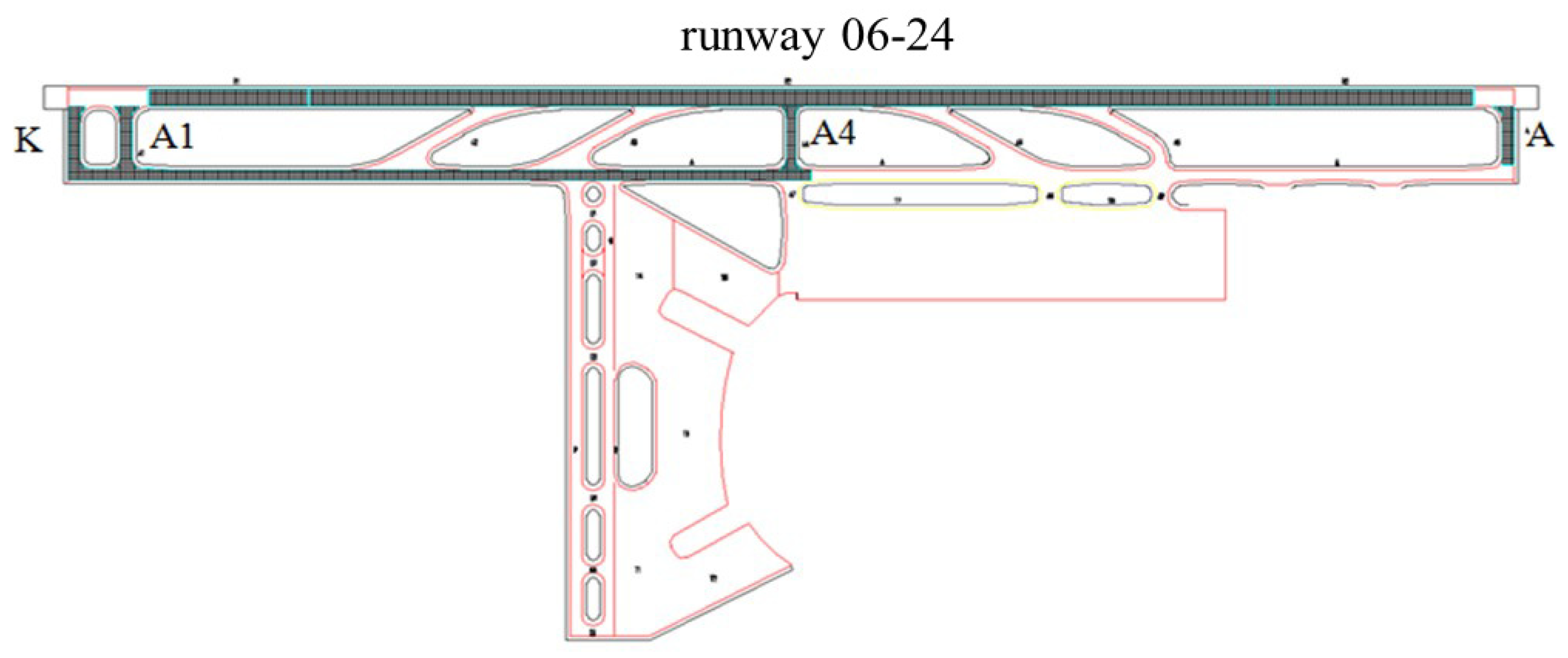
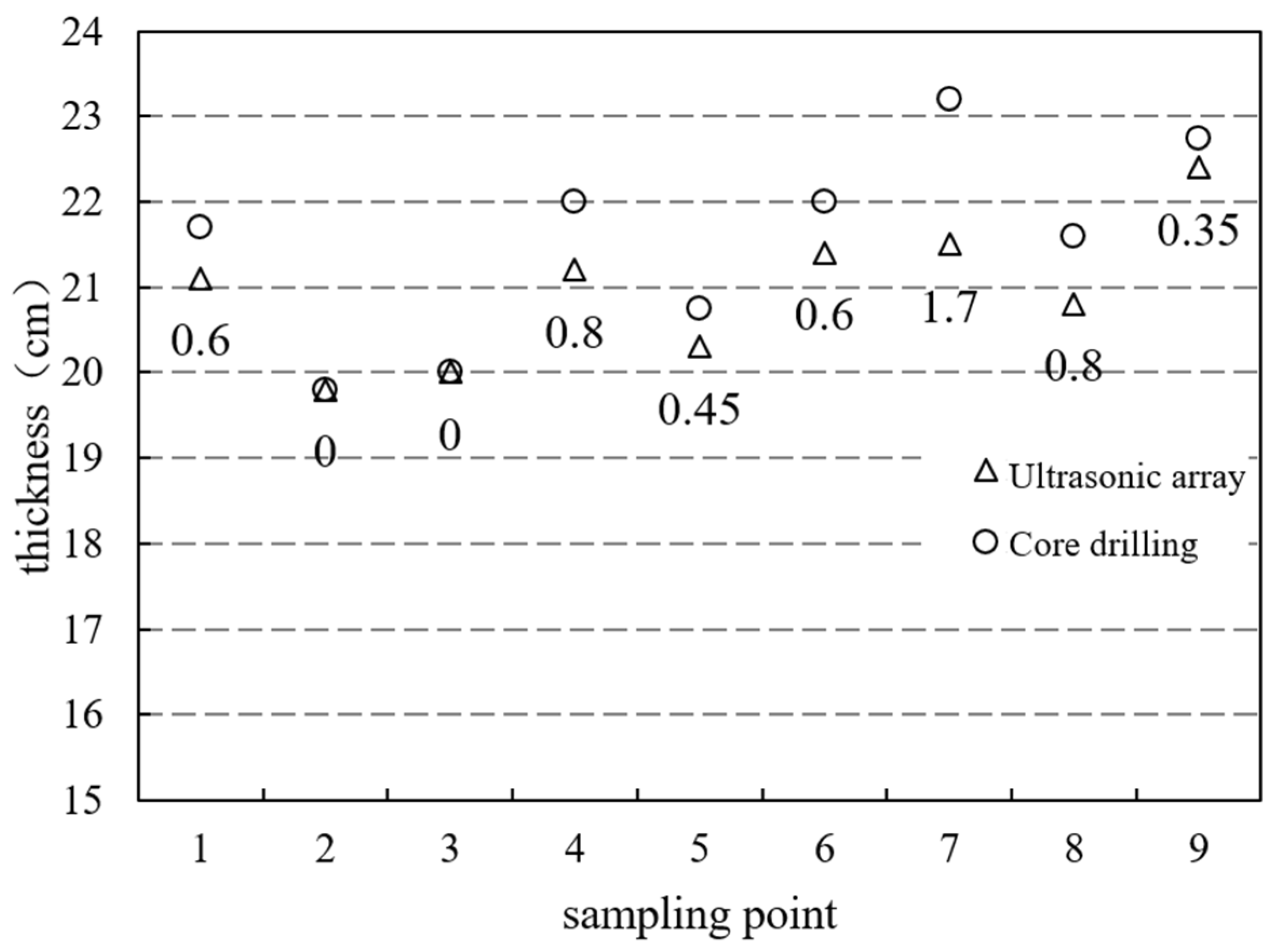
4.1. Nanjing Lukou International Airport
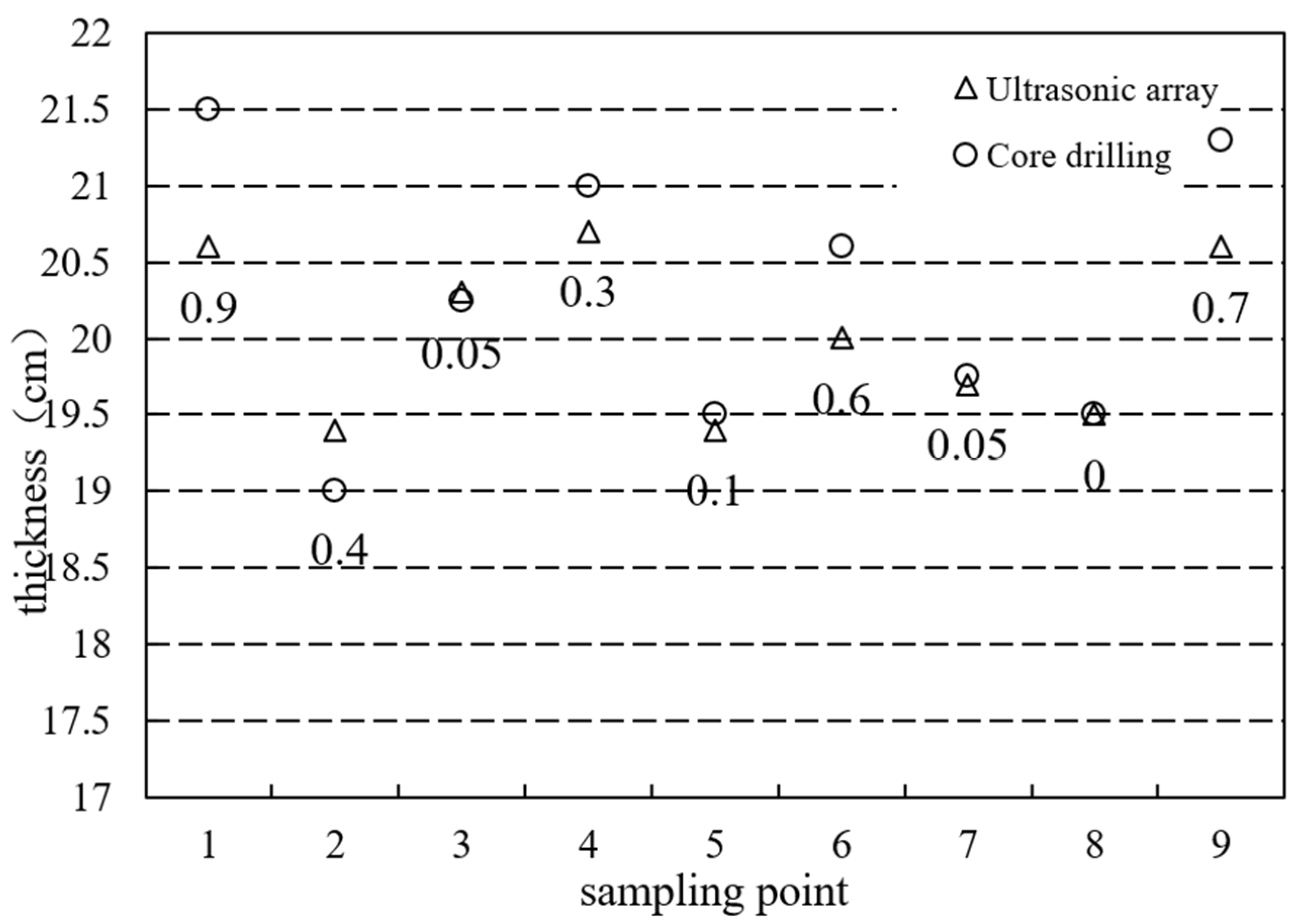
4.2. Shanghai Pudong Outer Ring Road
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ling, J.; Guan, S.; Zhao, H.; Gao, Z. Multi-hierarchy fuzzy decision-making model for PPM treatment selection of highway asphalt pavement. J. Highw. Transp. Res. Dev. 2008, 25, 25. [Google Scholar]
- Salton, M.; Terzi, S.; Terzi, O. Backcalculation of pavement layer thickness and moduli by the wavelet-neuro approach. In Proceedings of the International Conference on Transportation and Development, Houston, TX, USA, 26–29 June 2016. [Google Scholar]
- Bazi, G.; Saboundjian, S.; Ullidtz, P.; Briggs, R. Performance of an airfield flexible pavement and a novel PCN determination method. J. Transp. Eng. Part B-Pavements 2020, 146, 04020002. [Google Scholar] [CrossRef]
- Xiao, D. The development of road detection technology. In Proceedings of the 2nd International Conference on Civil, Architectural and Hydraulic Engineering (ICCAHE 2013), Zhuhai, China, 27–28 July 2013. [Google Scholar]
- Morcous, G.; Erdogmus, E. Accuracy of Ground-Penetrating Radar for Concrete Pavement Thickness Measurement. J. Perform. Constr. Facil. 2010, 24, 610–621. [Google Scholar] [CrossRef]
- Guo, Z. Application of ground penetrating radar to detect the thickness of road surface. Urban Geotech. Investig. Surv. 2017, 2–4. [Google Scholar]
- Wang, L.; Yuan, J.; Dai, N.; Wu, C.; Gao, G.; Xue, H. Analysis of interference signal of ground penetrating radar in road detection. J. Hubei Polytech. Univ. 2017, 33, 35–40. [Google Scholar]
- Williams, R.M.; Ray, L.E.; Lever, J.H.; Burzynski, A.M. Crevasse detection in ice sheets using ground penetrating radar and machine learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 7, 4836–4848. [Google Scholar] [CrossRef]
- Peters, L.; Daniels, J.J.; Young, J.D. Ground penetrating radar as a subsurface environmental sensing tool. Proc. IEEE 1994, 82, 1802–1822. [Google Scholar] [CrossRef]
- Plati, C.; Loizos, A.; Gkyrtis, K. Integration of non-destructive testing methods to assess asphalt pavement thickness. NDT E Int. 2020, 115, 102292. [Google Scholar] [CrossRef]
- Fengier, J.; Pożarycki, A.; Garbowski, T. Stiff-plate bearing test simulation based on FWD results. Procedia Eng. 2013, 57, 270–277. [Google Scholar] [CrossRef][Green Version]
- Garbowski, T.; Pożarycki, A. Multi-level backcalculation algorithm for robust determination of pavement layers parameters. Inverse Probl. Sci. Eng. 2017, 25, 674–693. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T. Semi-automatic Inspection Tool of Pavement Condition from Three-dimensional Profile Scans. Procedia Eng. 2017, 172, 310–318. [Google Scholar] [CrossRef]
- Edwards, L.; Mason, Q. Evaluation of nondestructive methods for determining pavement thickness. Concr. Pavements 2011. [Google Scholar] [CrossRef]
- Hoegh, K.E. Ultrasonic Linear Array Evaluation of Concrete Pavements. Ph.D. Thesis, University of Minnesota, Twin Cities, MN, USA, 2013. [Google Scholar]
- Vancura, M.; Khazanovich, L.; Barnes, R. Concrete Pavement Thickness Variation Assessment with Cores and Nondestructive Testing Measurements. Transp. Res. Rec. J. Transp. Res. Board 2013, 2347, 61–68. [Google Scholar] [CrossRef]
- Hoegh, K.; Khazanovich, L.; Ferraro, C.; Clayton, D. Ultrasonic linear array validation via concrete test blocks. AIP Conf. Proc. Am. Inst. Phys. 2015, 1650, 83–93. [Google Scholar]
- Wang, Z.J. Detecting Technique Research on Cement Concrete Slabs with Ultrasonic Method; Harbin Institute of Technology: Harbin, China, 2010. [Google Scholar]
- Fu, Z.W.; Hu, J.F.; Wen, Y.B.; Duan, Y.K.; Hu, Y.L.; Ge, S.Y.; Liao, X.J. Ultrasonic Modeling of Non-damaging Inspection to the Strength and Thickness of Concrete Highway Surface. J. Yunnan Univ. 2000, issue S1, 54–60. [Google Scholar]
- Wang, Z.J.; Tan, Y.Q.; Chen, F.C.; Wang, Q. Detecting compressive strength of pouring piles concrete by ultrasonic method. J. Harbin Inst. Technol. 2008, 40, 100–102. [Google Scholar]
- Zhang, G.H.; Chou, K.C. Viscosity model for fully liquid silicate melt. J. Min. Metall. Sect. B Metall. 2012, 48, 1–10. [Google Scholar] [CrossRef]
- Hoegh, K.; Khazanovich, L.; Yu, H.T. Ultrasonic tomography for evaluation of concrete pavements. Transp. Res. Rec. J. Transp. Res. Board 2011, 2232, 85–94. [Google Scholar] [CrossRef]
- Hoegh, K.; Khazanovich, L. Correlation analysis of 2D tomographic images for flaw detection in pavements. J. Test. Eval. 2012, 40, 9. [Google Scholar] [CrossRef]
- Pan, F.; Tang, D.L.; Guo, X.S.; Pan, S. Defect identification of pipeline ultrasonic inspection based on multi-feature fusion and multi-criteria feature evaluation. Int. J. Pattern Recognit. Artif. Intell. 2021, 35, 2150030. [Google Scholar] [CrossRef]
- Li, G.; Wang, X.W.; Shi, L.H. EMD denoising method and its application in lamb wave detection. Acta Metrol. Sin. 2006, 27, 149–152. [Google Scholar]
- Zhang, Q.; Chen, T.L.; Que, P.W.; Xing, Y. Compression of ultrasonic signals with the lifting scheme wavelet transform. Russ. J. Nondestruct. Test. 2008, 44, 490–495. [Google Scholar] [CrossRef]
- Trawinski, Z.; Wojcik, J. Comparison of methods used for ultrasonic examinations of IMT in the wall of the carotid artery model. Arch. Acoust. 2008, 33, 27–32. [Google Scholar]














| Detection Point Number | Ultrasonic Propagation Time (μs) | Ultrasonic Detected Thickness (mm) | Core Sample Thickness (mm) | Percentage Error (%) |
|---|---|---|---|---|
| 1 | 309 | 385 | 393 | 2.08 |
| 2 | 300 | 375 | 366 | −2.40 |
| 3 | 290 | 363 | 370 | 1.93 |
| 4 | 334 | 418 | 405 | −3.11 |
| 5 | 298 | 372 | 360 | −3.23 |
| 6 | 289 | 356 | 365 | 2.53 |
| 7 | 295 | 369 | 380 | 2.98 |
| 8 | 283 | 353 | 345 | −2.27 |
| 9 | 311 | 388 | 395 | 1.80 |
| 10 | 325 | 405 | 405 | 0.00 |
| 11 | 301 | 376 | 383 | 1.86 |
| 12 | 308 | 385 | 395 | 2.60 |
| 13 | 290 | 362 | 352 | −2.76 |
| 14 | 281 | 351 | 351 | 0.00 |
| 15 | 284 | 353 | 357 | 1.13 |
| 16 | 277 | 346 | 338 | −2.31 |
| 17 | 273 | 341 | 341 | 0.00 |
| 18 | 291 | 364 | 350 | −3.85 |
| 19 | 263 | 329 | 335 | 1.82 |
| 20 | 298 | 372 | 375 | 0.81 |
| 21 | 300 | 375 | 368 | −1.87 |
| 22 | 299 | 374 | 361 | −3.48 |
| 23 | 300 | 375 | 363 | −3.20 |
| 24 | 272 | 339 | 345 | 1.77 |
| 25 | 311 | 388 | 388 | 0.00 |
| 26 | 281 | 350 | 353 | 0.86 |
| 27 | 300 | 375 | 375 | 0.00 |
| 28 | 300 | 375 | 365 | −2.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Y.; Wu, J.; Liu, S.; Ling, J.; Zheng, Y.; Zhao, X.; Liu, L. Accurate Detection of Concrete Pavement Thickness Based on Ultrasonic Array. Sustainability 2023, 15, 8228. https://doi.org/10.3390/su15108228
Tian Y, Wu J, Liu S, Ling J, Zheng Y, Zhao X, Liu L. Accurate Detection of Concrete Pavement Thickness Based on Ultrasonic Array. Sustainability. 2023; 15(10):8228. https://doi.org/10.3390/su15108228
Chicago/Turabian StyleTian, Yu, Jinyu Wu, Shifu Liu, Jianming Ling, Yaqi Zheng, Xindong Zhao, and Le Liu. 2023. "Accurate Detection of Concrete Pavement Thickness Based on Ultrasonic Array" Sustainability 15, no. 10: 8228. https://doi.org/10.3390/su15108228
APA StyleTian, Y., Wu, J., Liu, S., Ling, J., Zheng, Y., Zhao, X., & Liu, L. (2023). Accurate Detection of Concrete Pavement Thickness Based on Ultrasonic Array. Sustainability, 15(10), 8228. https://doi.org/10.3390/su15108228






