Study on Deformation Characteristics of Retaining Structures under Coupled Effects of Deep Excavation and Groundwater Lowering in the Affected Area of Fault Zones
Abstract
:1. Introduction
2. Background
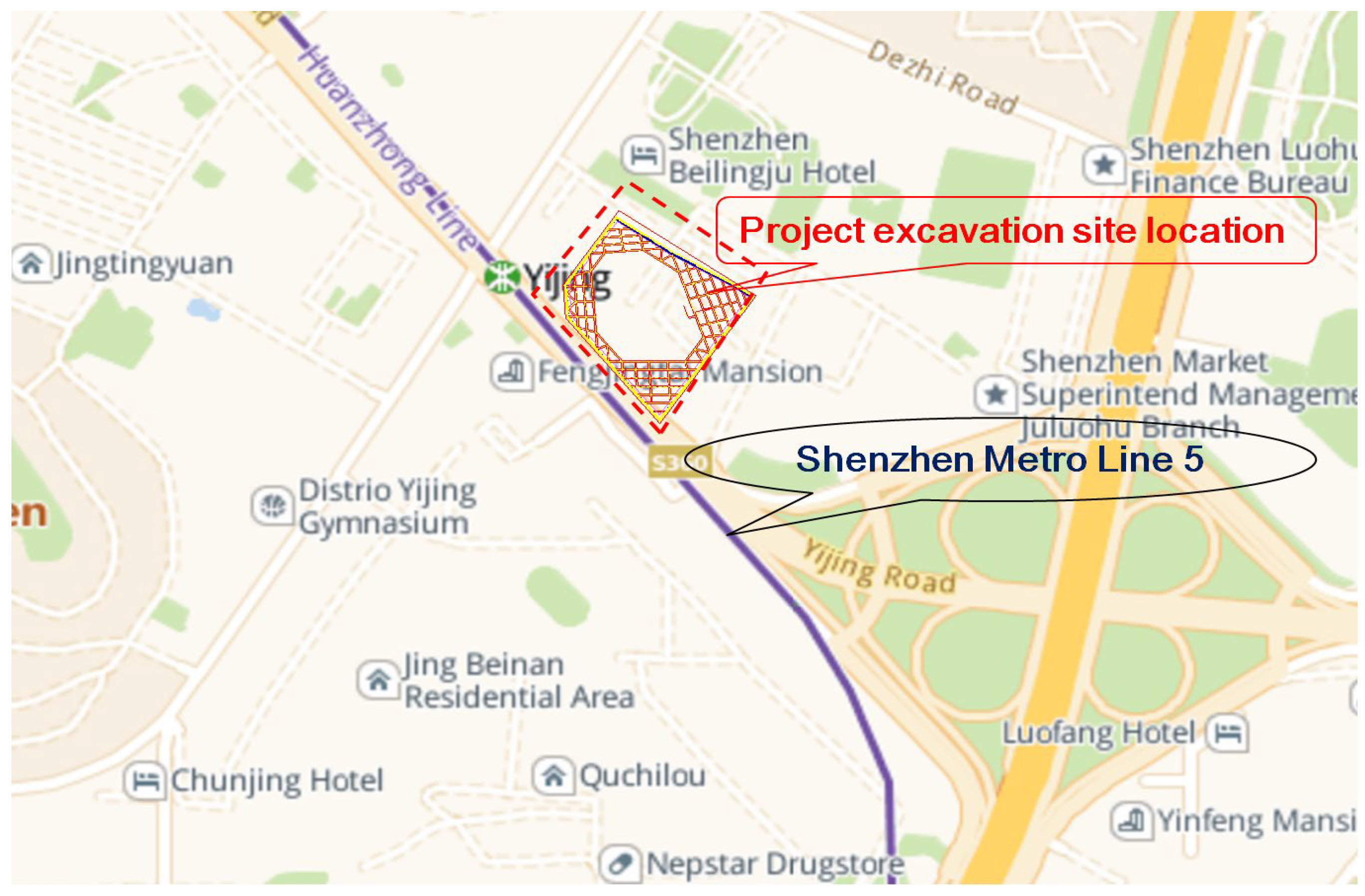
2.1. Project Overview
2.2. Geological Condition
3. Calculation of Deformation of Retaining Piles under the Coupled Effect of Excavation and Dewatering in Foundation Pit
4. Numerical Simulation Calculation
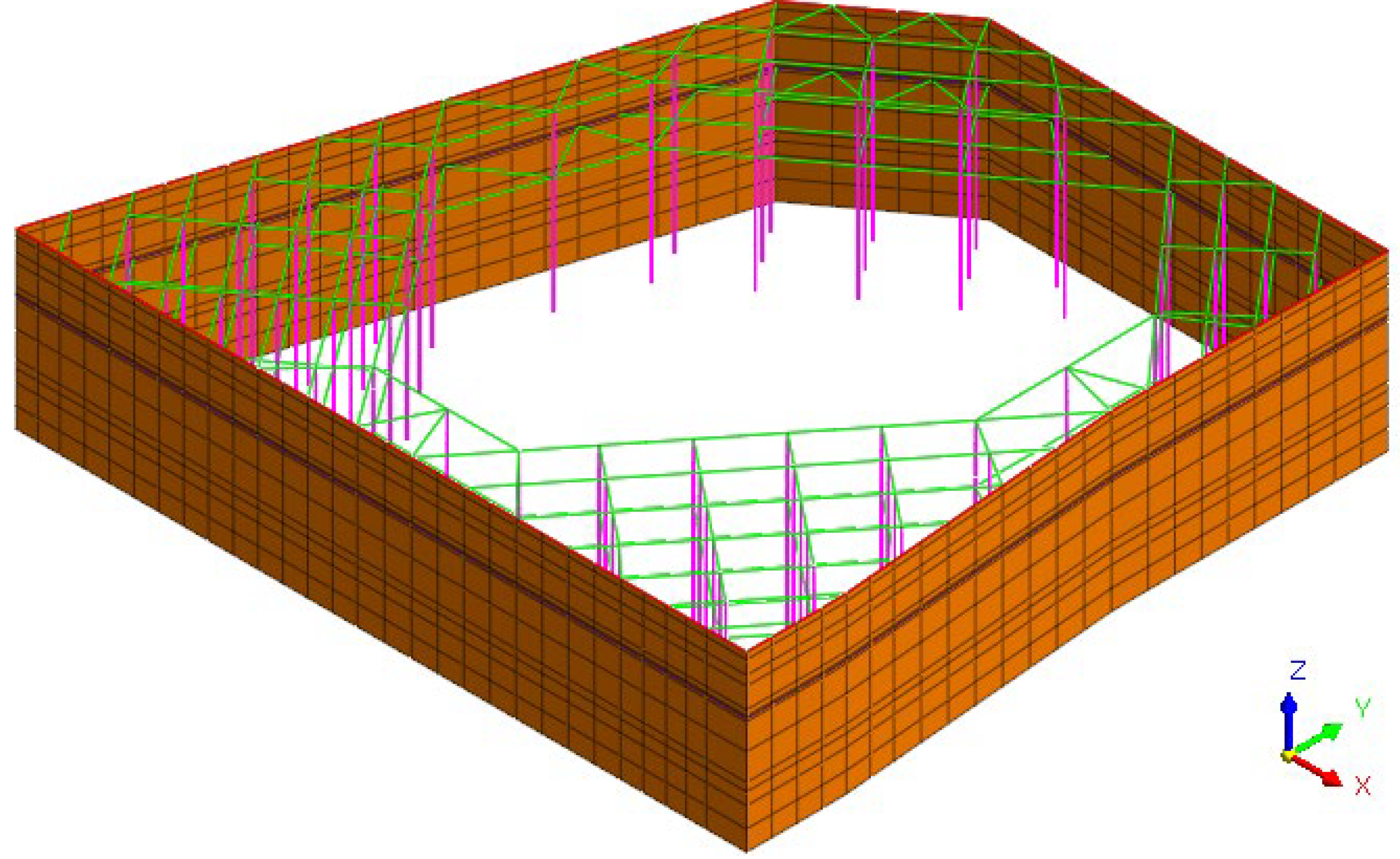
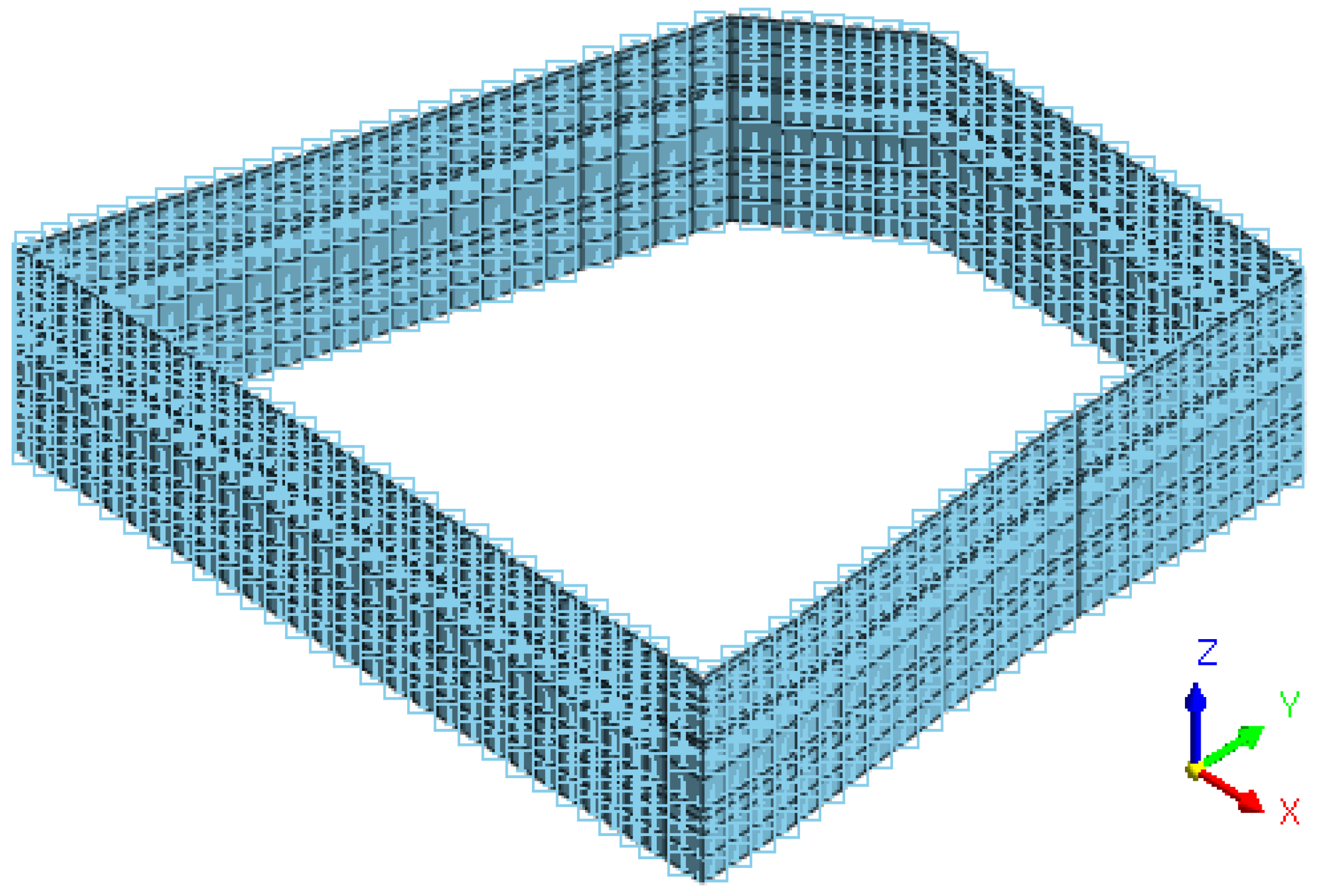
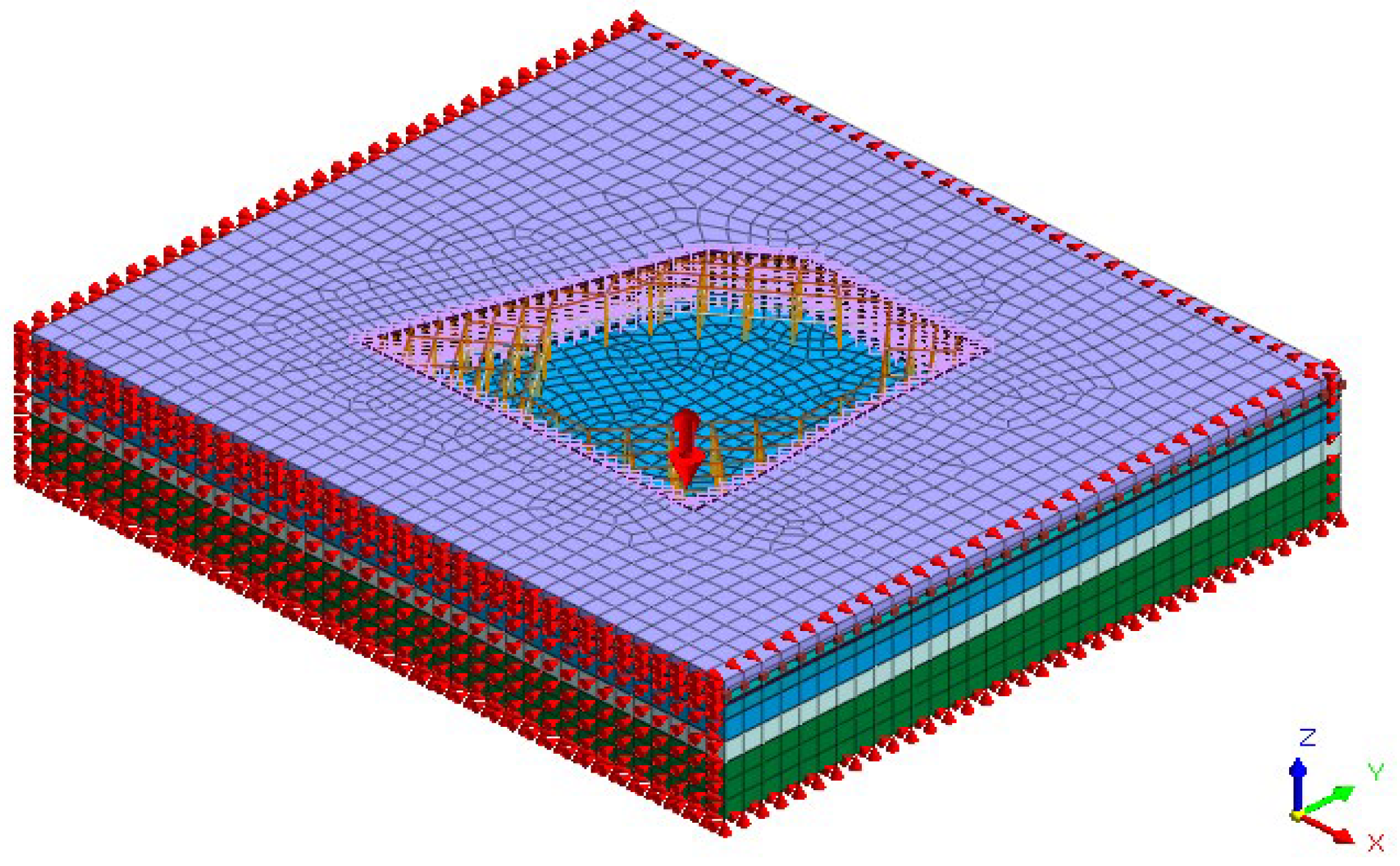
4.1. Three-Dimensional Model Establishment
4.2. Boundary Conditions and Calculation Conditions
4.3. Analysis of Numerical Simulation Results
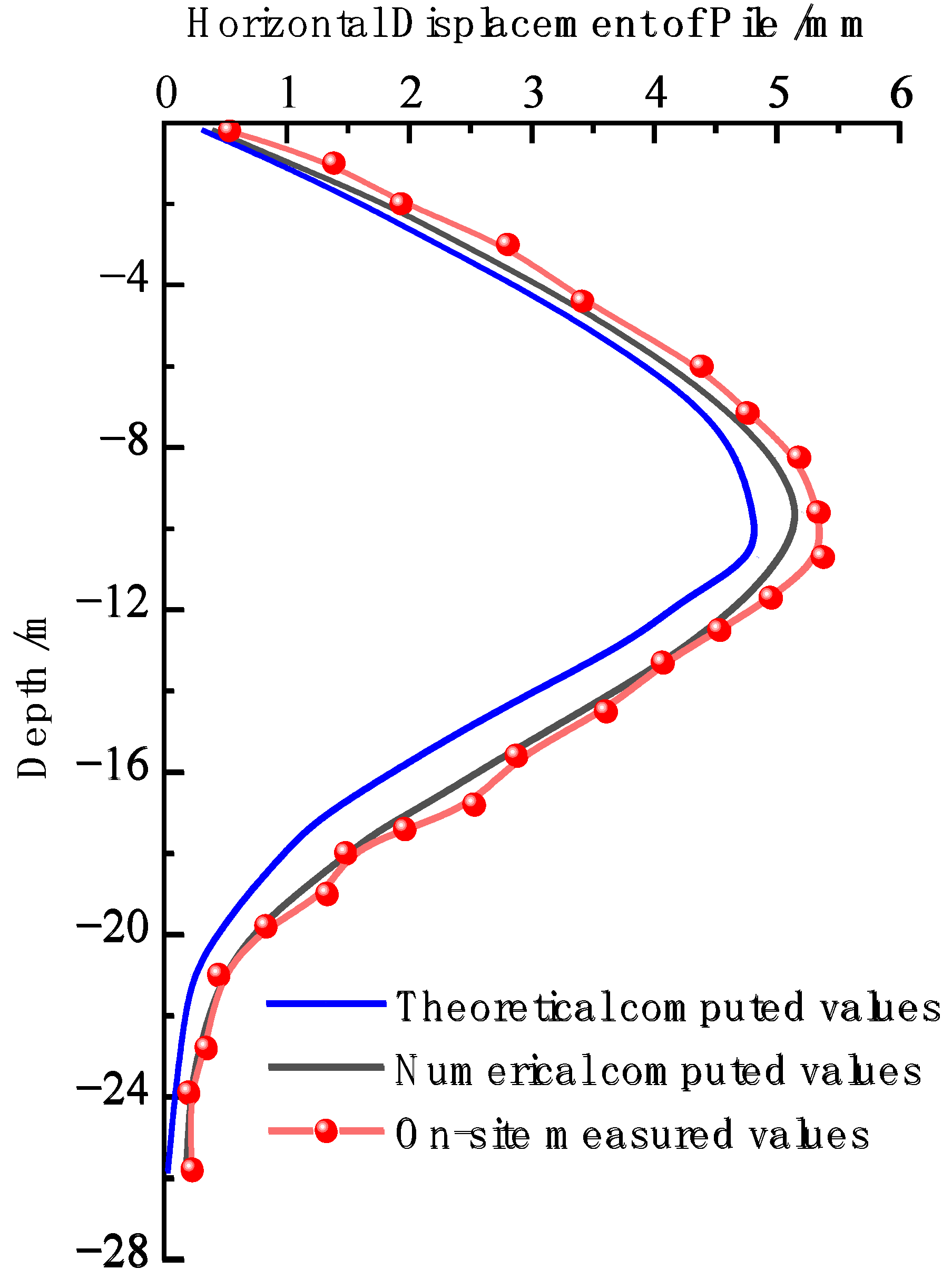
5. Comparison and Analysis of Numerical, Theoretical, and Field Measurement Results
6. Analysis of the Influence of Structural Design Parameters and Geological Parameters
6.1. Analysis of the Influence of Structural Design Parameters
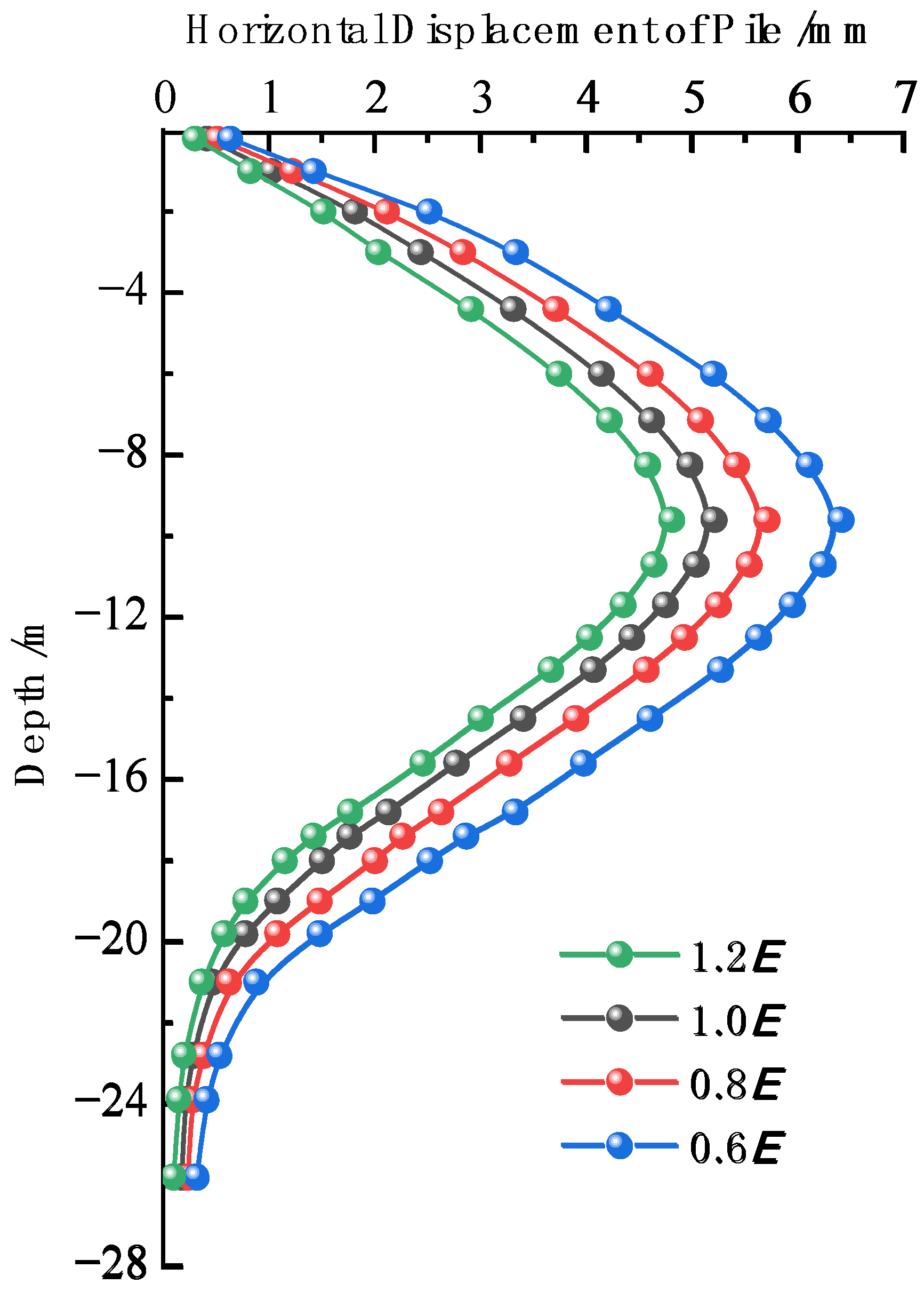
6.1.1. Analysis of the Influence of Elastic Modulus
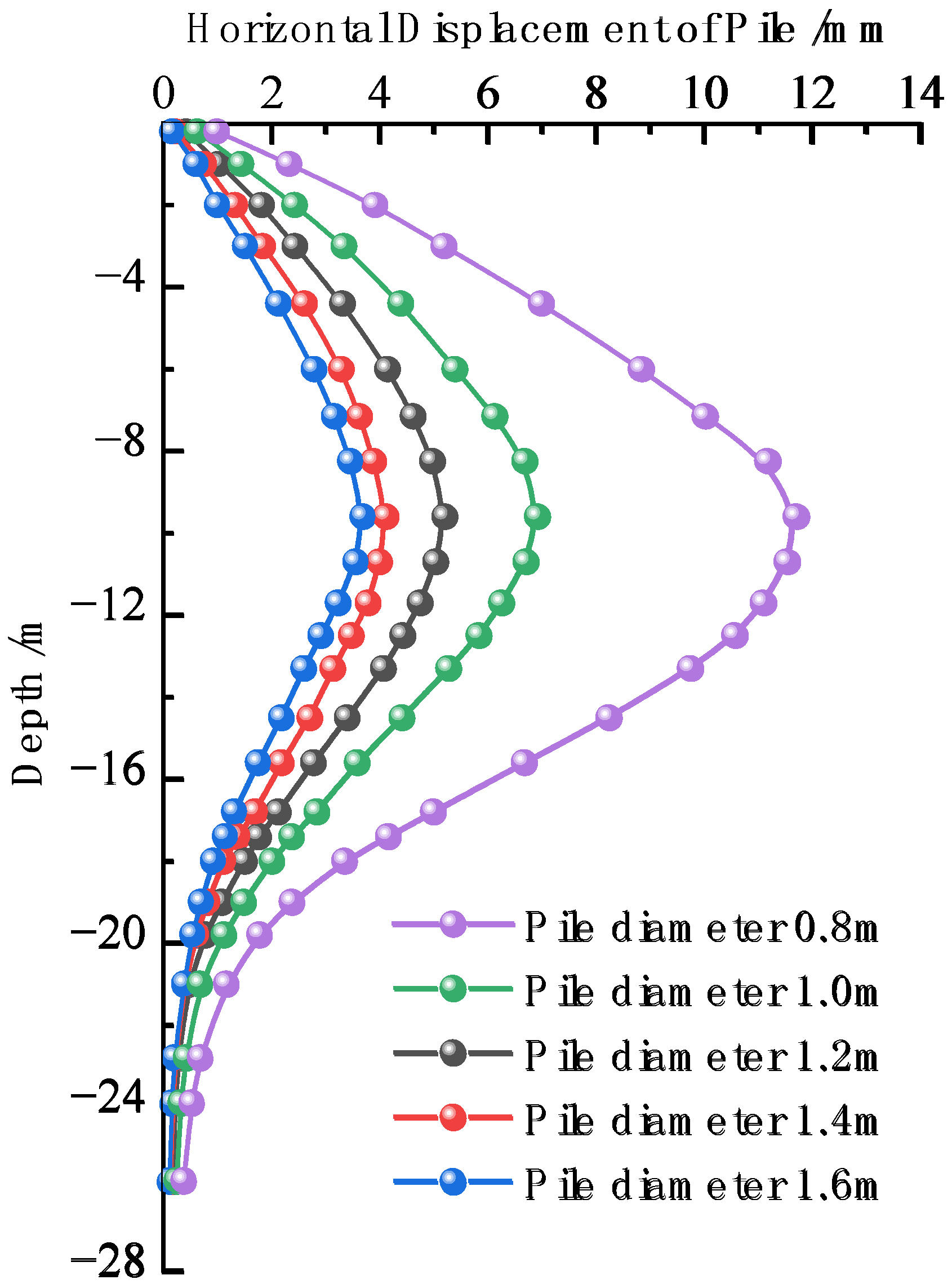
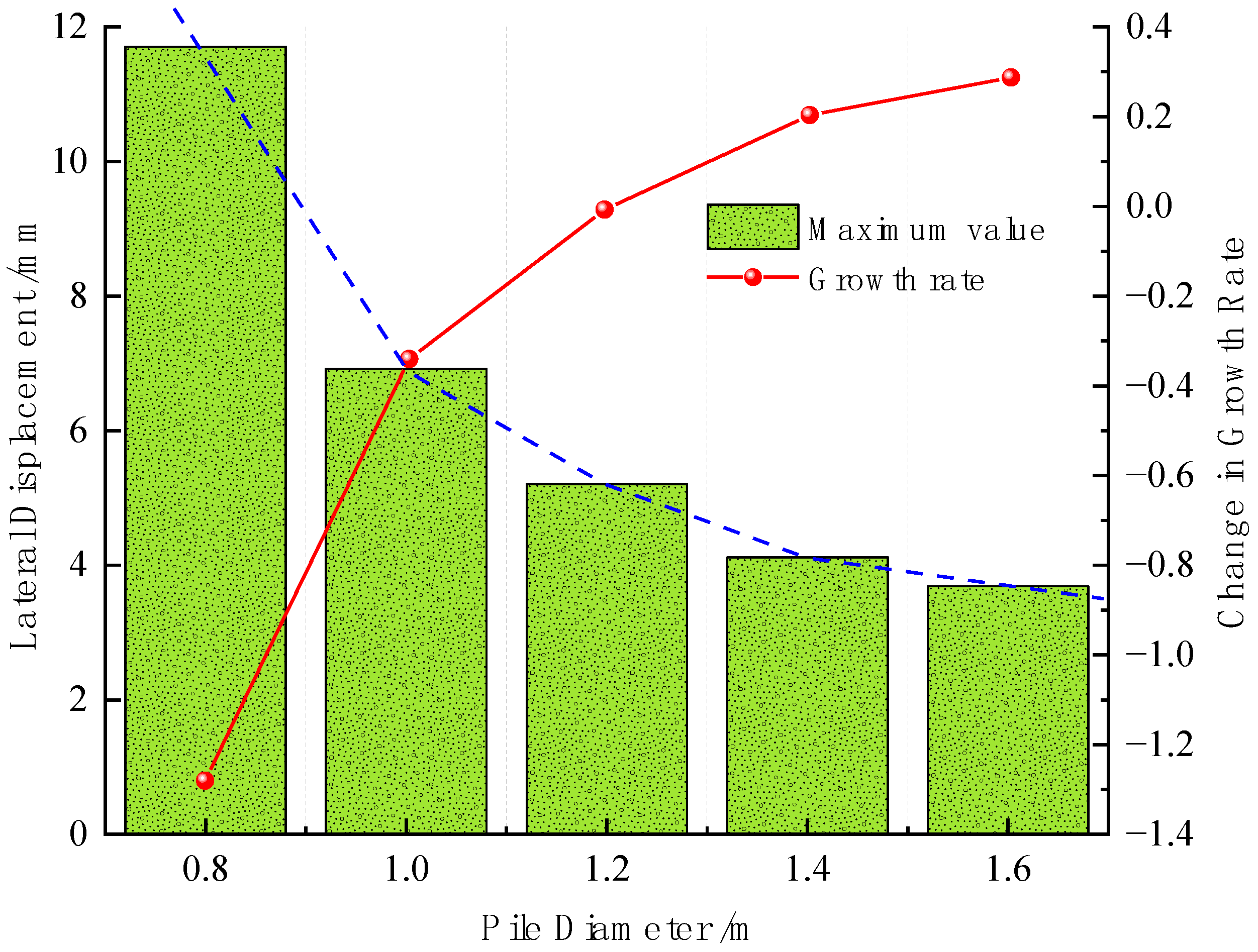
6.1.2. Analysis of the Influence of Pile Diameter
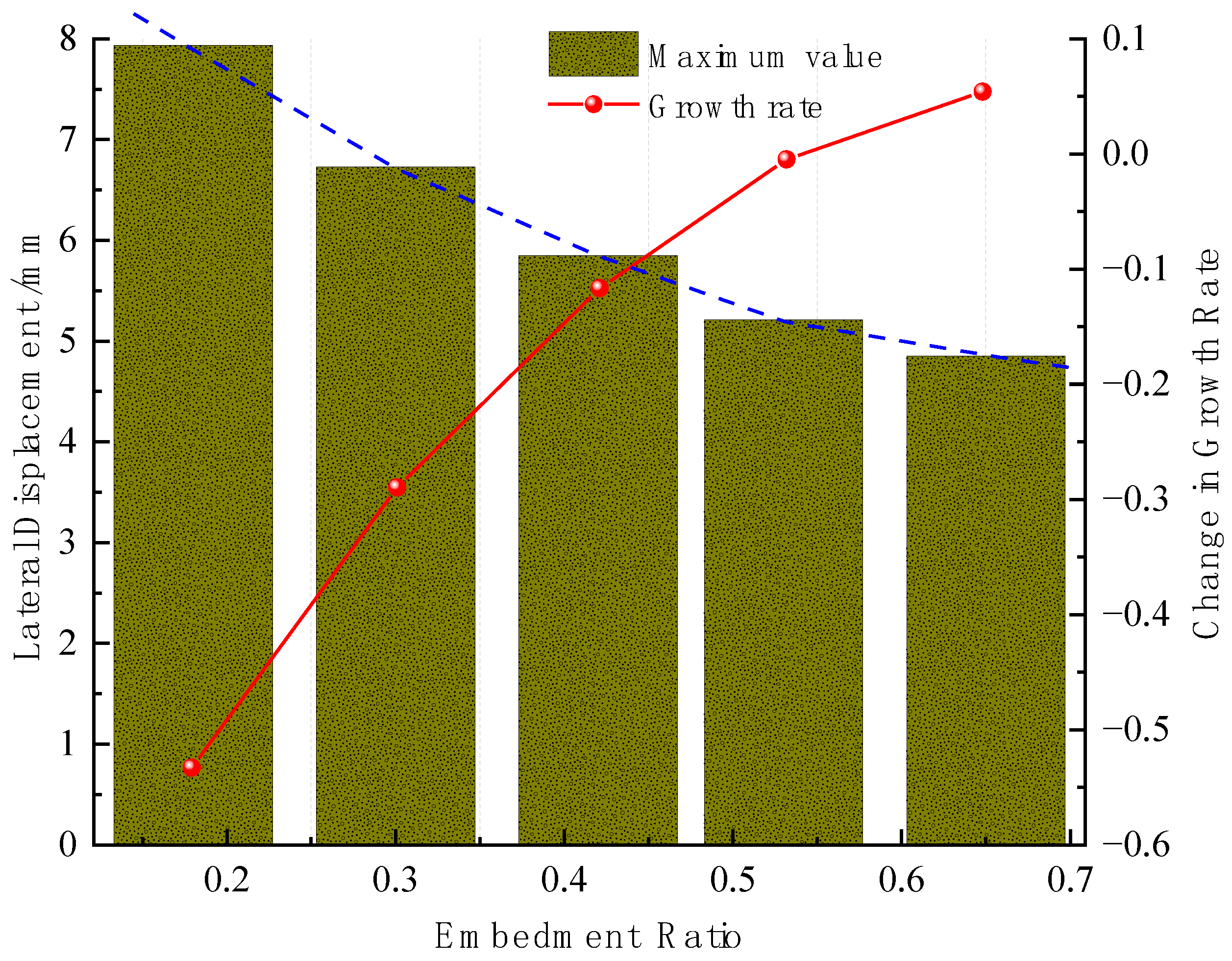
6.1.3. Analysis of the Influence of Embedment Ratio
6.2. Analysis of the Influence of Geological Parameters
6.2.1. Analysis of the Influence of Internal Friction Angle
6.2.2. Analysis of the Influence of Cohesion
6.2.3. Analysis of the Influence of Elastic Modulus
6.2.4. Sensitivity Analysis
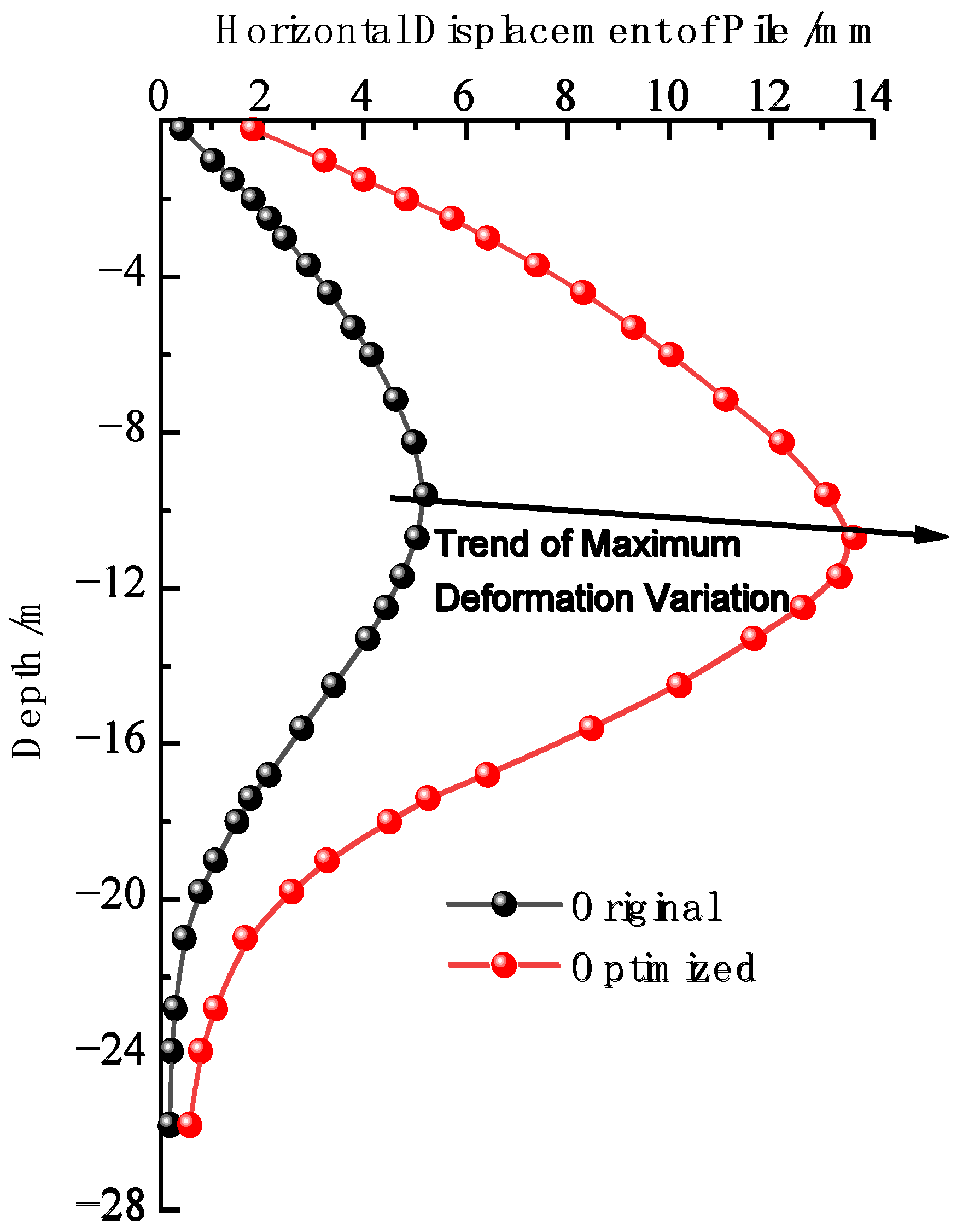
7. Structural Design Optimization
8. Conclusions
- (1)
- Based on the small deformation theory, it is proposed to consider the coupled effect of excavation and dewatering during foundation pit construction and use the energy method of elasticity theory to solve the analytical solution for the deformation of retaining piles, which yields more desirable calculation results.
- (2)
- By comparing and analyzing the results of the retaining wall deformation theory calculation, finite element calculation, and field measurement data, the numerical rules are basically consistent. Simplified calculation only considers rotational deformation and ignores the translational deformation of the wall, resulting in a large deviation between the theoretical calculation results of the wall bottom deformation and the measured values. To reduce the deviation between numerical results and measured values, strict measures such as “zone excavation, avoiding peripheral loading, and optimizing construction deployment” should be taken in pit construction, strengthen construction monitoring, and reduce the impact on retaining wall deformation.
- (3)
- The maximum deformation growth rate k (ΔSmax/Δ) of the retaining wall decreases exponentially with the increase of the structural stiffness parameters (E and I) and the embedment ratio in a certain range. To ensure the safety of retaining wall deformation, the retaining wall design must have a certain reserve of stiffness and embedment ratio.
- (4)
- With the increase of geological parameters, the lateral displacement of the retaining wall gradually decreases, and the decreasing rate gradually decreases within a certain range, that is, the maximum deformation of the retaining wall has a nonlinear relationship with the geological parameters. A quadratic function is used to fit the sensitivity function S(x) of the maximum lateral displacement of the retaining structure to the changes in various geological parameters, and the sensitivity analysis of geological parameters is carried out. It is found that the internal friction angle is the most sensitive factor, followed by cohesion, and the elastic modulus is the smallest.
- (5)
- The structural optimization plan includes replacing the original concrete struts with steel struts, adjusting the diameter of the perimeter piles from 1.2 m to 1.0 m, and increasing the maximum deformation of the perimeter piles from 5.21 mm to 13.63 mm to meet the specification’s (0.3%H) limit. The optimization of the excavation support system not only enables compliance with the standard construction procedures but also reduces investment and shortens construction time, fully aligning with the current design principles of safety, economy, and sustainable development.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dai, B.; Li, J.; Chen, Y.C.; Wu, L. Implementation design and practice of large area deep foundation pit in complex environment. Chin. J. Undergr. Space Eng. 2022, 18, 1657–1664+1695. [Google Scholar]
- Li, Z. Displacement monitoring during the excavation and support of deep foundation pit in complex environment. Adv. Civ. Eng. 2021, 2021, 5715306. [Google Scholar] [CrossRef]
- Wang, H.; Liu, S.Q.; Song, Z.; Cheng, K.; Zhou, H.; Cui, Y.Z. Design and Selection of Support for oversized deep foundation pit of adjacent subway under complex environment and weathered rock condition. Constr. Technol. 2021, 50, 135–140. [Google Scholar]
- Chen, L.L.; Wang, Y.Q.; Wang, Z.F.; Fan, F.F.; Liu, Y. Characteristics and treatment measures of tunnel collapse in fault fracture zone during rainfall: A case study. Eng. Fail. Anal. 2023, 145, 107002. [Google Scholar] [CrossRef]
- Huang, C.F.; Zhang, S.L.; Wu, S.C.; Go, Y.T. Research and application of a comprehensive forecasting system for tunnels in water-bearing fault fracture zones: A case study. Arab. J. Geosci. 2022, 15, 171. [Google Scholar] [CrossRef]
- Yan, X.D.; Gao, J.; Han, F.; Li, Z. Study on risk assessment of tunnel crossing active fault zone and its engineering application. Mod. Tunn. Technol. 2020, 57, 10–22+60. [Google Scholar]
- Xu, J.; Wang, Y. Analysis of Slip Failure Characteristics and Support Deformation Law of Structural Planes and Rock Foundation Pits with Developed Karst Caves. Appl. Sci. 2022, 12, 4076. [Google Scholar] [CrossRef]
- Zheng, G. Deformation control methods and engineering applications of excavation in soft soil areas. Chin. J. Geotech. Eng. 2022, 44, 1–36+201. [Google Scholar]
- Sun, C.; Guo, H.T. Current Situation and Prospect of New Support Technology for Deep Foundation Pit. J. Build. Sci. Eng. 2018, 35, 104–117. [Google Scholar]
- Yan, J.; Zheng, H.F.; Wang, J.J.; Chen, D. Support Technology of Deep Foundation Pit in Building Construction—Review of New Technology of Deep Foundation Pit Support Design and Construction. Ind. Archit. 2021, 51, 220. [Google Scholar]
- Yang, H.; Zhao, F.D.; Zhu, Y.P.; Ma, X.R. Analysis of deformation characteristics of deep foundation pit supporting structure in Red sandstone Formation based on fluid-solid Coupling effect. Sci. Technol. Eng. 2019, 19, 174–181. [Google Scholar]
- Ni, X.D.; Wang, C.; Tang, D.H.; Lu, J.F.; Wang, X.Y.; Chen, W.C. Early warning and inducement analysis of super-large deformation of deep foundation pit in soft soil area. J. Cent. South Univ. 2022, 53, 2245–2254. [Google Scholar]
- Shao, Y.; Chen, C.X.; Lu, Z.D.; Zhen, Y.; Zhang, Y.P. Deformation prediction analysis of herring-shaped support for deep excavation based on machine learning, J/OL. Rock Soil Mech. 2020, S2, 1–9. [Google Scholar]
- Li, E.B.; Tan, Y.H.; Zhang, S.G.; Ding, L.L. Analytical calculation of deformation of diaphragm wall in Deep foundation pit Enclosure. J. PLA Univ. Sci. Technol. 2004, 2, 57–60. [Google Scholar]
- Zeng, C.F.; Xue, X.L.; Song, W.W.; Li, M.K.; Bai, N. Rainfall triggered before the excavation deformation mechanism model test study. Rock Soil Mech. 2020, 9, 2963–2972+2983. [Google Scholar]
- Zeng, C.F.; Wang, S.; Song, W.W.; Li, M.K.; Xue, X.L.; Mei, G.X. Control effect of Inner partition Wall on Deformation of Metro deep foundation pit in soft soil area induced by pumping before excavation. Rock Mech. Eng. 2021, 40, 1277–1286. [Google Scholar]
- Hu, Z.; Zhu, D.Y. Research on Construction Risk of Subway Foundation Pit under Complex Environment. J. Hefei Univ. Technol. 2020, 43, 522–529. [Google Scholar]
- Chen, S.; Cui, J.; Liang, F. Case study on the deformation coupling effect of a deep foundation pit group in a coastal soft soil area. Appl. Sci. 2022, 12, 6205. [Google Scholar] [CrossRef]
- Cao, L.; Gao, J.; Meng, X.W.; Xia, J. Research on deformation control technology of ultra-deep foundation pit in complex environment. Build. Struct. 2020, 50, 1007–1013. [Google Scholar]
- Yu, C. Optimization Design of Large-Area Foundation Pit Support System Based on Finite Element Method. C//IOP Conference Series: Earth and Environmental Science. IOP Publ. 2019, 242, 062032. [Google Scholar]
- Tian, Z.X.; Zhao, Z.H.; Dai, C.Q.; Gang, S.X. Comparative selection of foundation pit envelope design based on complex geological environment control. Urban Rail Transit Res. 2020, 23, 152–156. [Google Scholar]
- An, P.Z.; Liu, Z.M.; Jia, B.X.; Zhou, Q.; Meng, F.L.; Wang, Z.X. Comparison and Economic Envelope Structure Schemes for Deep Foundation Pit of Subway Stations Based on Fuzzy Logic. Comput. Intell. Neurosci. 2022, 2022, 1148856. [Google Scholar] [CrossRef] [PubMed]
- Savvides, A.-A.; Papadopoulos, L. A Neural Network Model for Estimation of Failure Stresses and Strains in Cohesive Soils. Geotechnics 2022, 2, 1084–1108. [Google Scholar] [CrossRef]
- Savvides, A.A.; Papadrakakis, M. A computational study on the uncertainty quantification of failure of clays with a modified Cam-Clay yield criterion. SN Appl. Sci. 2021, 3, 659. [Google Scholar] [CrossRef]
- Liu, G.B.; Wang, W.D. Handbook of Foundation Pit Engineering, 2nd ed.; China Architecture & Building Press: Beijing, China, 2009; pp. 2–3. [Google Scholar]
- Zhang, A.Q.; Wu, A.X.; Han, B.; Wang, Y.M.; Chang, B.M.; Wang, H.; Wu, S.J. A new model for the thickness of filled retaining wall based on the theory of elastic thin plates. J. Cent. South Univ. (Sci. Technol.) 2018, 49, 696–702. [Google Scholar]
- Ciarlet, P.G.; Mardare, C. The intrinsic theory of linearly elastic plates. Math. Mech. Solids 2018, 23, 1182–1203. [Google Scholar] [CrossRef]
- Gu, W.; Zhang, L.Y.; Tan, Z.X.; Deng, K.Z. Stability analysis of open stope roof based on the model of elastic thin plates. J. Min. Saf. Eng. 2013, 30, 886–891. [Google Scholar]
- Zheng, J.H. Stiffness analysis of circular section concrete retaining piles. Fujian Archit. 2005, Z1, 232–233+221. [Google Scholar]
- Cai, Y.; Xing, Y.; Hu, D. Review of sensitivity analysis. J. Beijing Norm. Univ. 2008, 1, 9–16. [Google Scholar]
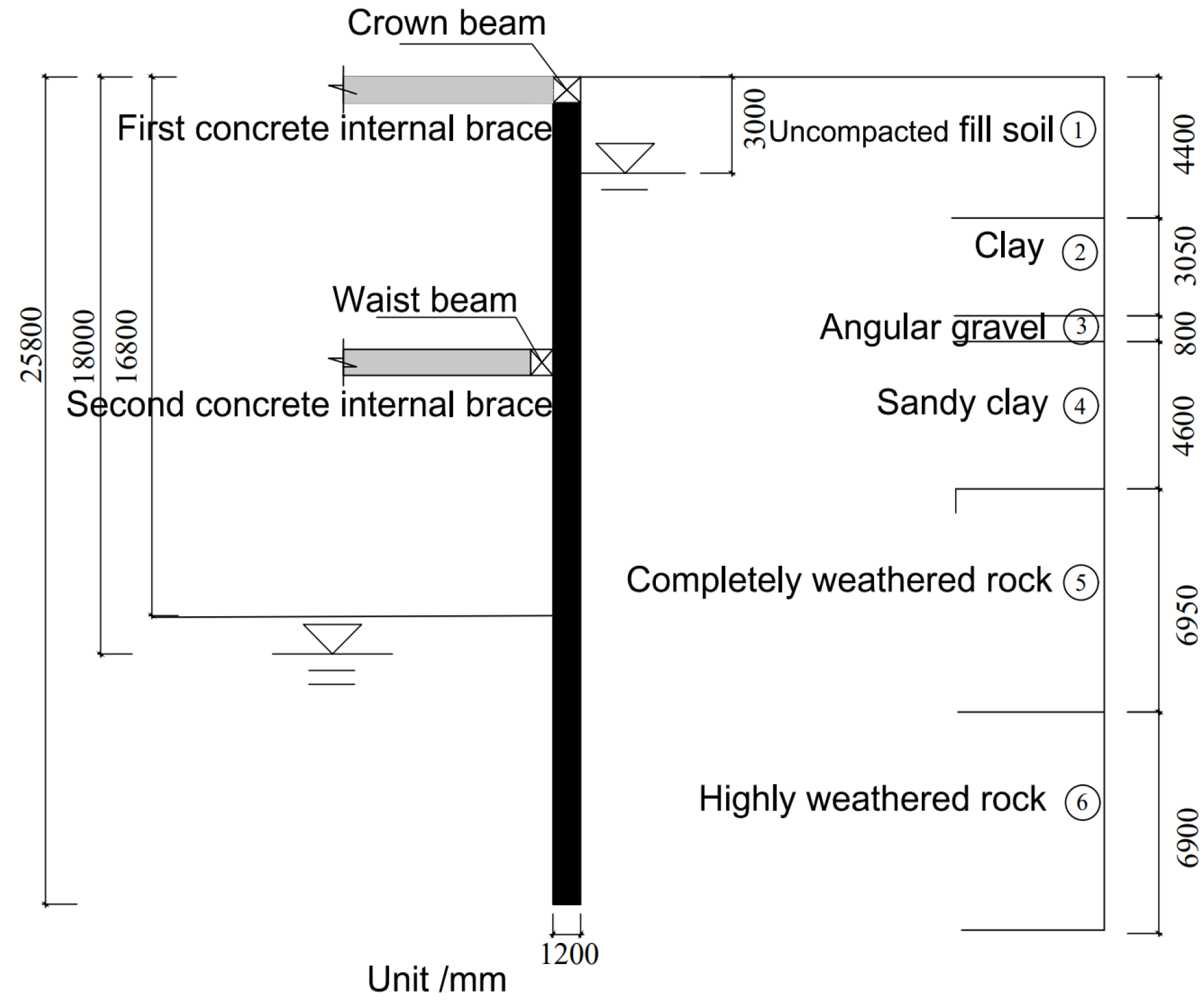










| Stratigraphic (Genetic) | Natural Weight (kN/m3) | Tri-Axial Test Secant Modulus/MPa | Secant Modulus of Elasticity/MPa | Unloading Modulus of Elasticity/MPa | Poisson’s Ratio | Cohesion (kPa) | Internal Friction Angle (°) | Permeability Coefficient (m/d) |
|---|---|---|---|---|---|---|---|---|
| ① Uncompacted fill soil | 19.0 | 2 | 2 | 6 | 0.35 | 14 | 15 | 5 |
| ② Clay | 18.5 | 2.8 | 2.8 | 8.4 | 0.33 | 25 | 18 | 0.1 |
| ③ Angular gravel | 19.5 | 6 | 6 | 18 | 0.28 | 0 | 36 | 25 |
| ④ Sandy clay | 21.0 | 8 | 8 | 24 | 0.26 | 25 | 22 | 5 |
| ⑤ Completely weathered rock | 20.0 | 16 | 16 | 48 | 0.24 | 23 | 28 | 0.1 |
| ⑥ Highly weathered rock | 20.5 | 25 | 25 | 75 | 0.23 | 20 | 32 | 0.5 |
| Name | Material | Section Dimensions/mm | Unit Weight /(kg/m³) | Elastic Modulus/GPa | Internal Friction Angle/(°) | Poisson’s Ratio |
|---|---|---|---|---|---|---|
| Retaining pile (Diaphragm wall) | C30 | Thickness 880 | 2400 | 30 | 26 | 0.2 |
| Column pile | C30 | Ø1200 | 2400 | 30 | 26 | 0.2 |
| Crown beam | C30 | 1000 × 1200 | 2400 | 30 | 26 | 0.2 |
| Support beam | C30 | 1000 × 1200 | 2400 | 30 | 26 | 0.2 |
| Waist beam | C30 | 1000 × 1200 | 2400 | 30 | 26 | 0.2 |
| Construction Stage | Construction Sequence | Working Conditions | Simulation Content |
|---|---|---|---|
| Prior to excavation of foundation pit | 1 | Initial seepage analysis | Seepage analysis before excavation of foundation pit, displacement reset. |
| 2 | Initial stress analysis | Stress analysis before excavation of foundation pit, displacement reset | |
| During excavation of foundation pit | 3 | Diaphragm wall construction | Activate foundation pit retaining piles, column piles, water cutoff curtains, and other constraints. |
| 4 | Step 1 excavation | Dewatering the foundation pit to a depth of −9 m (initial water level −3 m). | |
| 5 | First dewatering | Excavate to a depth of −8.5 m underground, activate the second inner support, and waist beam. | |
| 6 | Step 2 excavation | Excavate to a depth of −8.5 m underground, activate the second inner support, and waist beam. | |
| 7 | Second dewatering | Dewatering to a depth of −18 m underground. | |
| 8 | Step 3 excavation | Excavate to a bottom depth of −16.8 m and activate the bottom plate. |
| Indicators | Sensitive Factor Sn |
|---|---|
| Internal Friction Angle φ | 0.760 |
| Cohesion C | 0.604 |
| Elasticity Modulus E | 0.422 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, Y.; Zou, L.; Wang, Q.; Ma, F. Study on Deformation Characteristics of Retaining Structures under Coupled Effects of Deep Excavation and Groundwater Lowering in the Affected Area of Fault Zones. Sustainability 2023, 15, 8060. https://doi.org/10.3390/su15108060
Niu Y, Zou L, Wang Q, Ma F. Study on Deformation Characteristics of Retaining Structures under Coupled Effects of Deep Excavation and Groundwater Lowering in the Affected Area of Fault Zones. Sustainability. 2023; 15(10):8060. https://doi.org/10.3390/su15108060
Chicago/Turabian StyleNiu, Yungang, Liang Zou, Qiongyi Wang, and Fenghai Ma. 2023. "Study on Deformation Characteristics of Retaining Structures under Coupled Effects of Deep Excavation and Groundwater Lowering in the Affected Area of Fault Zones" Sustainability 15, no. 10: 8060. https://doi.org/10.3390/su15108060
APA StyleNiu, Y., Zou, L., Wang, Q., & Ma, F. (2023). Study on Deformation Characteristics of Retaining Structures under Coupled Effects of Deep Excavation and Groundwater Lowering in the Affected Area of Fault Zones. Sustainability, 15(10), 8060. https://doi.org/10.3390/su15108060








