Modeling and Optimization of Combined Heating, Power, and Gas Production System Based on Renewable Energies
Abstract
1. Introduction
- Presenting the effect of modeling the energy storage system, gas power system, scattered gas-burning production sources, and electric vehicles in the electricity and gas distribution network;
- Presenting an integer linear programming model for the integrated operation of electricity and gas distribution networks;
- Presenting the random model of renewable resources, energy cost, and electric cars as a scenario-based method;
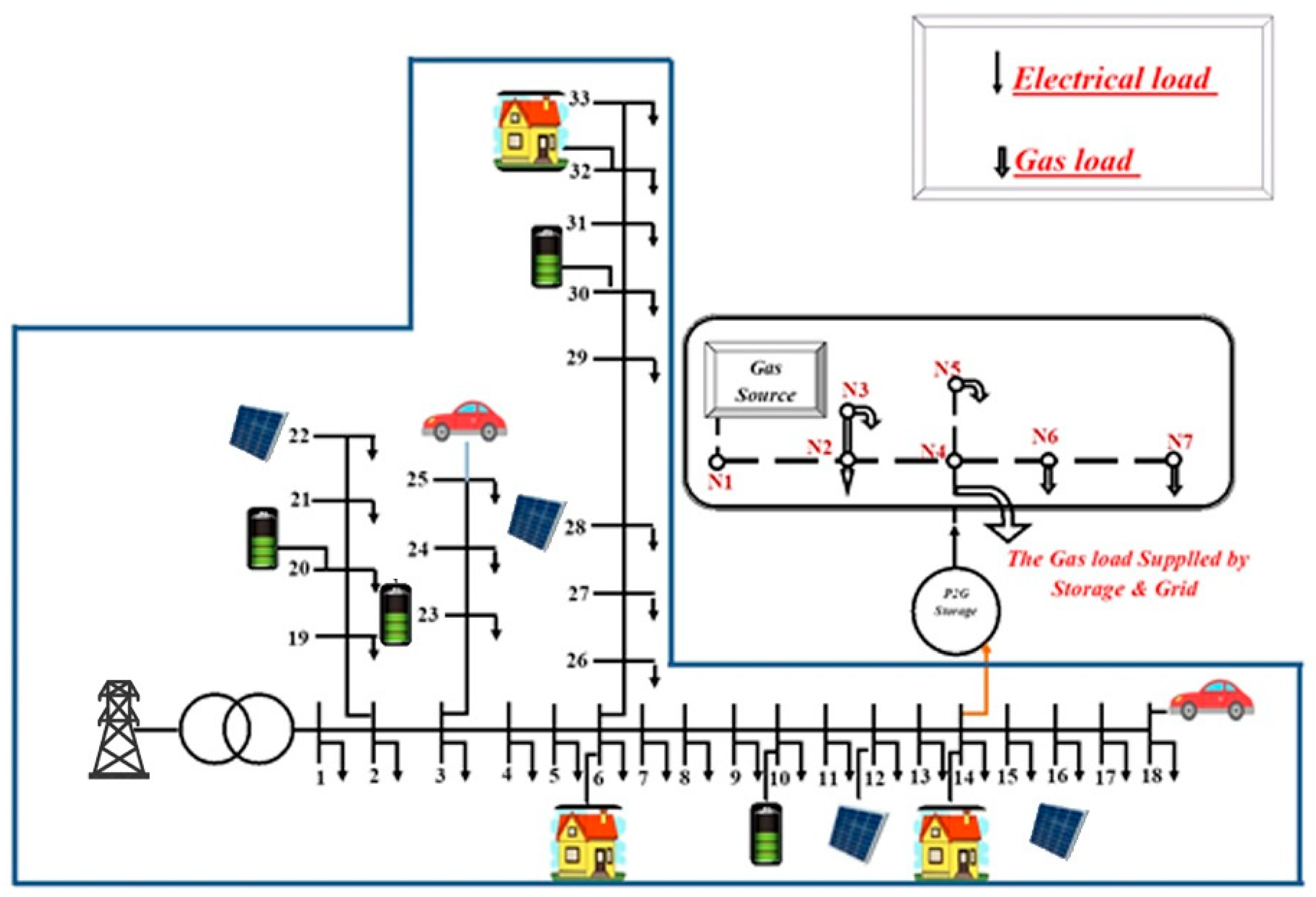
- A 24 h dynamic load modeling of IEEE standard 33 bus power distribution network and gas distribution network of 7 nodes.
2. Materials and Methods
Modeling
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Electricity price | Time series | Nt | |
| Actual power purchased | pt | A set of electrical network buses | Ne |
| Cost of natural gas | A set of gas network nodes | Ng | |
| Purchased natural gas | gt | Penalty coefficient of renewable unit | c′ |
| Discharge binary variable | Penalty factor for electric vehicles | eev | |
| Binary variable charge | The actual production of renewable resource | ||
| Minimum battery discharge power | Charging power required for electric vehicles | ||
| Maximum battery discharge power | Power used from renewable sources | ||
| Battery discharge capacity | Included charging power for electric vehicles | ||
| Minimum battery charging power | Considered probability for each scenario | ||
| Purchased natural gas | A set of scenarios | Ns | |
| Minimum and maximum amount of gas in the gas well | Number of slices in linearization | df | |
| Minimum and maximum amount of gas injected with P2G | Minimum and maximum gas pipeline flow rate | ||
| Natural gas load | Maximum battery charging capacity | ||
| A constant conversion factor of electric power to gas | Battery charging capacity | ||
| Pressure at the beginning and end of the gas pipeline | Battery power | ||
| Physical parameters of each pipeline | Minimum battery energy capacity | ||
| Minimum and maximum gas node pressure | Charging efficiency | ||
| Equal to the slope of the line | Discharge efficiency | ||
| Approximated line in linearization | Gas production by P2G | ||
| Actual power purchased from the electricity market | P2G returns | ||
| Active load and reactive load | Electric power input to P2G | ||
| Real gas DG power generation | P2G storage capacity | ||
| Active power flux in line ij | Amount of gas injection by P2G | ||
| Post reactive power | Maximum electrical power consumed by P2G | ||
| The maximum real and reactive power flux passing through line ij | Minimum and maximum storage capacity of P2G gas | ||
| Reactive power injected by gas-fired DGs | Maximum battery energy capacity | ||
| Reactive power flux in line ij | Minimum and maximum bus voltage | ||
| Square voltage of the bus | Determining the position of each piece on the same line | ||
| Impedance and reactance of line ij | Gas flow the nm pipeline and from the mn pipeline |
References
- Jahangiri, M.; Shahmarvandi, F.K.; Alayi, R. Renewable Energy-Based Systems on a Residential Scale in Southern Coastal Areas of Iran: Trigeneration of Heat Power and Hydrogen. J. Renew. Energy Environ. 2021, 8, 67–76. [Google Scholar] [CrossRef]
- Alayi, R.; Harasii, H.; Pourderogar, H. Modeling and optimization of photovoltaic cells with GA algorithm. J. Robot. Control (JRC) 2021, 2, 35–41. [Google Scholar] [CrossRef]
- Alayi, R.; Mohkam, M.; Seyednouri, S.R.; Ahmadi, M.H.; Sharifpur, M. Energy/Economic Analysis and Optimization of On-Grid Photovoltaic System Using CPSO Algorithm. Sustainability 2021, 13, 12420. [Google Scholar] [CrossRef]
- Alayi, R.; Jahangiri, M.; Najafi, A. Energy analysis of vacuum tube collector system to supply the required heat gas pressure reduction station. Int. J. Low-Carbon Technol. 2021, 16, 1391–1396. [Google Scholar] [CrossRef]
- Rehman, A.U.; Wadud, Z.; Elavarasan, R.M.; Hafeez, G.; Khan, I.; Shafiq, Z.; Alhelou, H.H. An optimal power usage scheduling in smart grid integrated with renewable energy sources for energy management. IEEE Access 2021, 9, 84619–84638. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Liang, Y.; Bi, T.; Shafie-khah, M.; Catalão, J.P.S. Data-driven chance-constrained optimal gas-power flow calculation: A bayesian nonparametric approach. IEEE Trans. Power Syst. 2021, 36, 4683–4698. [Google Scholar] [CrossRef]
- Sun, Q.; Fu, Y.; Lin, H.; Wennersten, R. A novel integrated stochastic programming-information gap decision theory (IGDT) approach for optimization of integrated energy systems (IESs) with multiple uncertainties. Appl. Energy 2022, 314, 119002. [Google Scholar] [CrossRef]
- Al-Hamed, K.H.; Dincer, I. Exergoeconomic analysis and optimization of a solar energy-based integrated system with oxy-combustion for combined power cycle and carbon capturing. Energy 2022, 250, 123814. [Google Scholar] [CrossRef]
- Huang, Y.; Kang, J.; Liu, L.; Zhong, X.; Lin, J.; Xie, S.; Meng, C.; Zeng, Y.; Shah, N.; Brandon, N.; et al. A hierarchical coupled optimization approach for dynamic simulation of building thermal environment and integrated planning of energy systems with supply and demand synergy. Energy Convers. Manag. 2022, 258, 115497. [Google Scholar] [CrossRef]
- Cao, Z.; Wang, J.; Zhao, Q.; Han, Y.; Li, Y. Decarbonization Scheduling Strategy Optimization for Electricity-Gas System Considering Electric Vehicles and Refined Operation Model of Power-to-Gas. IEEE Access 2021, 9, 5716–5733. [Google Scholar] [CrossRef]
- Hossain, M.S.; Kumar, L.; Assad, M.E.H.; Alayi, R. Advancements and Future Prospects of Electric Vehicle Technologies: A Comprehensive Review. Complexity 2022, 2022, 3304796. [Google Scholar] [CrossRef]
- Jiang, X.M.; Li, Q.F.; Yang, Y.W.; Zhang, L.T.; Liu, X.J.; Ning, N. Optimization of the operation plan taking into account the flexible resource scheduling of the integrated energy system. Energy Rep. 2022, 8, 1752–1762. [Google Scholar] [CrossRef]
- Mu, Y.; Wang, C.; Sun, M.; He, W.; Wei, W. CVaR-based operation optimization method of community integrated energy system considering the uncertainty of integrated demand response. Energy Rep. 2022, 8, 1216–1223. [Google Scholar] [CrossRef]
- Qi, F.; Shahidehpour, M.; Wen, F.; Li, Z.; He, Y.; Yan, M. Decentralized Privacy-Preserving Operation of Multi-Area Integrated Electricity and Natural Gas Systems with Renewable Energy Resources. IEEE Trans. Sustain. Energy 2019, 11, 1785–1796. [Google Scholar] [CrossRef]
- Li, Z.; Yu, Z.; Lin, D.; Wu, W.; Zhu, H.; Yu, T.; Li, H. Environmental Economic Dispatch Strategy for Power-Gas Interconnection System Considering Spatiotemporal Diffusion of Air Pollutant and P2G in Coastal Areas. IEEE Access 2020, 8, 123662–123672. [Google Scholar] [CrossRef]
- Li, B.; Chen, M.; Ma, Z.; He, G.; Dai, W.; Liu, D.; Zhang, C.; Zhong, H. Modeling Integrated Power and Transportation Systems: Impacts of Power-to-Gas on the Deep Decarbonization. IEEE Trans. Ind. Appl. 2021, 58, 2677–2693. [Google Scholar] [CrossRef]
- Chen, S.; Conejo, A.J.; Wei, Z. Gas-Power Coordination: From Day-Ahead Scheduling to Actual Operation. IEEE Trans. Power Syst. 2021, 37, 1532–1542. [Google Scholar] [CrossRef]
- Saletti, C.; Morini, M.; Gambarotta, A. Smart management of integrated energy systems through co-optimization with long and short horizons. Energy 2022, 250, 123748. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, Y.; Liu, N. A two-stage energy management for heat-electricity integrated energy system considering dynamic pricing of Stackelberg game and operation strategy optimization. Energy 2022, 244, 122576. [Google Scholar] [CrossRef]
- Niu, D.; Yu, M.; Sun, L.; Gao, T.; Wang, K. Short-term multi-energy load forecasting for integrated energy systems based on CNN-BiGRU optimized by attention mechanism. Appl. Energy 2022, 313, 118801. [Google Scholar] [CrossRef]
- Zhang, R.; Jiang, T.; Li, F.; Li, G.; Chen, H.; Li, X. Coordinated Bidding Strategy of Wind Farms and Power-to-Gas Facilities Using a Cooperative Game Approach. IEEE Trans. Sustain. Energy 2020, 11, 2545–2555. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Cai, C.; Xue, L.; Ma, L.X.Y.; Shen, H.; Chen, X.; Liu, L. Research on the optimization method of integrated energy system operation with multi-subject game. Energy 2022, 245, 123305. [Google Scholar] [CrossRef]
- Yang, W.; Guo, J.; Vartosh, A. Optimal economic-emission planning of multi-energy systems integrated electric vehicles with modified group search optimization. Appl. Energy 2022, 311, 118634. [Google Scholar] [CrossRef]
- Khani, H.; Farag, H.E.Z. Optimal day-ahead scheduling of power-to-gas energy storage and gas load management in wholesale electricity and gas markets. IEEE Trans. Sustain. Energy 2017, 9, 940–951. [Google Scholar] [CrossRef]
- Xu, D.; Zhou, B.; Wu, Q.; Chung, C.Y.; Li, C.; Huang, S.; Chen, S. Integrated Modelling and Enhanced Utilization of Power-to-Ammonia for High Renewable Penetrated Multi-Energy Systems. IEEE Trans. Power Syst. 2020, 35, 4769–4780. [Google Scholar] [CrossRef]
- Zeng, Q.; Fang, J.; Li, J.; Chen, Z. Steady-state analysis of the integrated natural gas and electric power system with bi-directional energy conversion. Appl. Energy 2016, 184, 1483–1492. [Google Scholar] [CrossRef]
- Wang, C.; Wang, S.; Liu, F.; Bi, T.; Wang, T. Risk-Loss Coordinated Admissibility Assessment of Wind Generation for Integrated Electric-Gas Systems. IEEE Trans. Smart Grid 2020, 11, 4454–4465. [Google Scholar] [CrossRef]
- Li, Y.; Liu, W.; Shahidehpour, M.; Wen, F.; Wang, K.; Huang, Y. Optimal Operation Strategy for Integrated Natural Gas Generating Unit and Power-to-Gas Conversion Facilities. IEEE Trans. Sustain. Energy 2018, 9, 1870–1879. [Google Scholar] [CrossRef]
- Clegg, S.; Mancarella, P. Integrated Modeling and Assessment of the Operational Impact of Power-to-Gas (P2G) on Electrical and Gas Transmission Networks. IEEE Trans. Sustain. Energy 2015, 6, 1234–1244. [Google Scholar] [CrossRef]
- Chen, S.; Wei, Z.; Sun, G.; Cheung, K.W.; Sun, Y. Multi-Linear Probabilistic Energy Flow Analysis of Integrated Electrical and Natural-Gas Systems. IEEE Trans. Power Syst. 2016, 32, 1970–1979. [Google Scholar] [CrossRef]
- Bayat, A.; Bagheri, A. Optimal active and reactive power allocation in distribution networks using a novel heuristic approach. Appl. Energy 2019, 233, 71–85. [Google Scholar] [CrossRef]
- Mansouri, S.A.; Ahmarinejad, A.; Nematbakhsh, E.; Javadi, M.S.; Esmaeel, A.; Catalão, J.P.S. Nezhad A sustainable framework for multi-microgrids energy management in automated distribution network by considering smart homes and high penetration of renewable energy resources. Energy 2022, 245, 123228. [Google Scholar] [CrossRef]
- Zare, M.; Saeed, S.A.; Akbari, H. Demand Response Programs Modeling in Multiple Energy and Structure Management in Microgrids Equipped by Combined Heat and Power Generation. J. Intell. Proced. Electr. Technol. 2023, 14, 99–120. [Google Scholar]
- Adetunji, K.E.; Hofsajer, I.W.; Abu-Mahfouz, A.M.; Cheng, L. Category-based multiobjective approach for optimal integration of distributed generation and energy storage systems in distribution networks. IEEE Access 2021, 9, 28237–28250. [Google Scholar] [CrossRef]
- Phommixay, S.; Doumbia, M.L.; Cui, Q. Comparative Analysis of Continuous and Hybrid Binary-Continuous Particle Swarm Optimization for Optimal Economic Operation of a Microgrid. Process Integr. Optim. Sustain. 2021, 6, 93–111. [Google Scholar] [CrossRef]
- Nahman, J.M.; Peric, D.M. Optimal planning of radial distribution networks by simulated annealing technique. IEEE Trans. Power Syst. 2008, 23, 790–795. [Google Scholar] [CrossRef]
- Bezanson, J.; Edelman, A.; Karpinski, S.; Shah, V.B. Julia: A Fresh Approach to Numerical Computing. SIAM Rev. 2017, 59, 65–98. [Google Scholar] [CrossRef]











| Components | Characteristics | Value |
|---|---|---|
| PV array [1, 2] | Size | 100 kW |
| Initial cost | USD 3882/kW | |
| Replacement fee | USD 3000/kW | |
| Maintenance cost | USD 100/year | |
| Lifetime | 25 year | |
| Inverter [1, 2] | Size | 100 kW |
| Connection mode | Three-phase | |
| Initial cost | USD 429/kW | |
| Network voltage and frequency | 415 VAC50/60 | |
| Maintenance cost | USD 0/year | |
| Lifetime | 16 year | |
| Efficiency | 95% | |
| Battery [1, 2] | Rated voltage | 6 v |
| Nominal capacity | 1156 Ah | |
| Initial cost | USD 1200 | |
| Replacement fee | USD 1000 | |
| Maintenance cost | USD 10/year |
| Scenario | Buy Gas (m3) | Power Purchase (kW) | Target Function (USD) | Execution Time (s) |
|---|---|---|---|---|
| First | 580,233 | 39,052 | 890,200 | 57 |
| Second | 567,112 | 38,121 | 890,112 | 55 |
| Third | 498,525 | 78,540 | 899,215 | 58 |
| Fourth | 523,821 | 36,998 | 881,425 | 57 |
| Type of Solver | Target Function (USD) | Execution Time (s) |
|---|---|---|
| Grooby | 879,340 | 57 |
| Muzak | 879,340 | 63 |
| Coefficient | Execution Time (s) | Target Function (USD) |
|---|---|---|
| Equal weighting factor | 57 | 890,200 |
| Unequal weighting factor | 63 | 922,021 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.-C.; Alvarez, J.R.N.; Dwijendra, N.K.A.; Kadhim, Z.J.; Alayi, R.; Kumar, R.; PraveenKumar, S.; Velkin, V.I. Modeling and Optimization of Combined Heating, Power, and Gas Production System Based on Renewable Energies. Sustainability 2023, 15, 7888. https://doi.org/10.3390/su15107888
Chen T-C, Alvarez JRN, Dwijendra NKA, Kadhim ZJ, Alayi R, Kumar R, PraveenKumar S, Velkin VI. Modeling and Optimization of Combined Heating, Power, and Gas Production System Based on Renewable Energies. Sustainability. 2023; 15(10):7888. https://doi.org/10.3390/su15107888
Chicago/Turabian StyleChen, Tzu-Chia, José Ricardo Nuñez Alvarez, Ngakan Ketut Acwin Dwijendra, Zainab Jawad Kadhim, Reza Alayi, Ravinder Kumar, Seepana PraveenKumar, and Vladimir Ivanovich Velkin. 2023. "Modeling and Optimization of Combined Heating, Power, and Gas Production System Based on Renewable Energies" Sustainability 15, no. 10: 7888. https://doi.org/10.3390/su15107888
APA StyleChen, T.-C., Alvarez, J. R. N., Dwijendra, N. K. A., Kadhim, Z. J., Alayi, R., Kumar, R., PraveenKumar, S., & Velkin, V. I. (2023). Modeling and Optimization of Combined Heating, Power, and Gas Production System Based on Renewable Energies. Sustainability, 15(10), 7888. https://doi.org/10.3390/su15107888










