Removable, Reconfigurable, and Sustainable Steel Structures: A State-of-the-Art Review of Clamp-Based Steel Connections
Abstract
1. Introduction
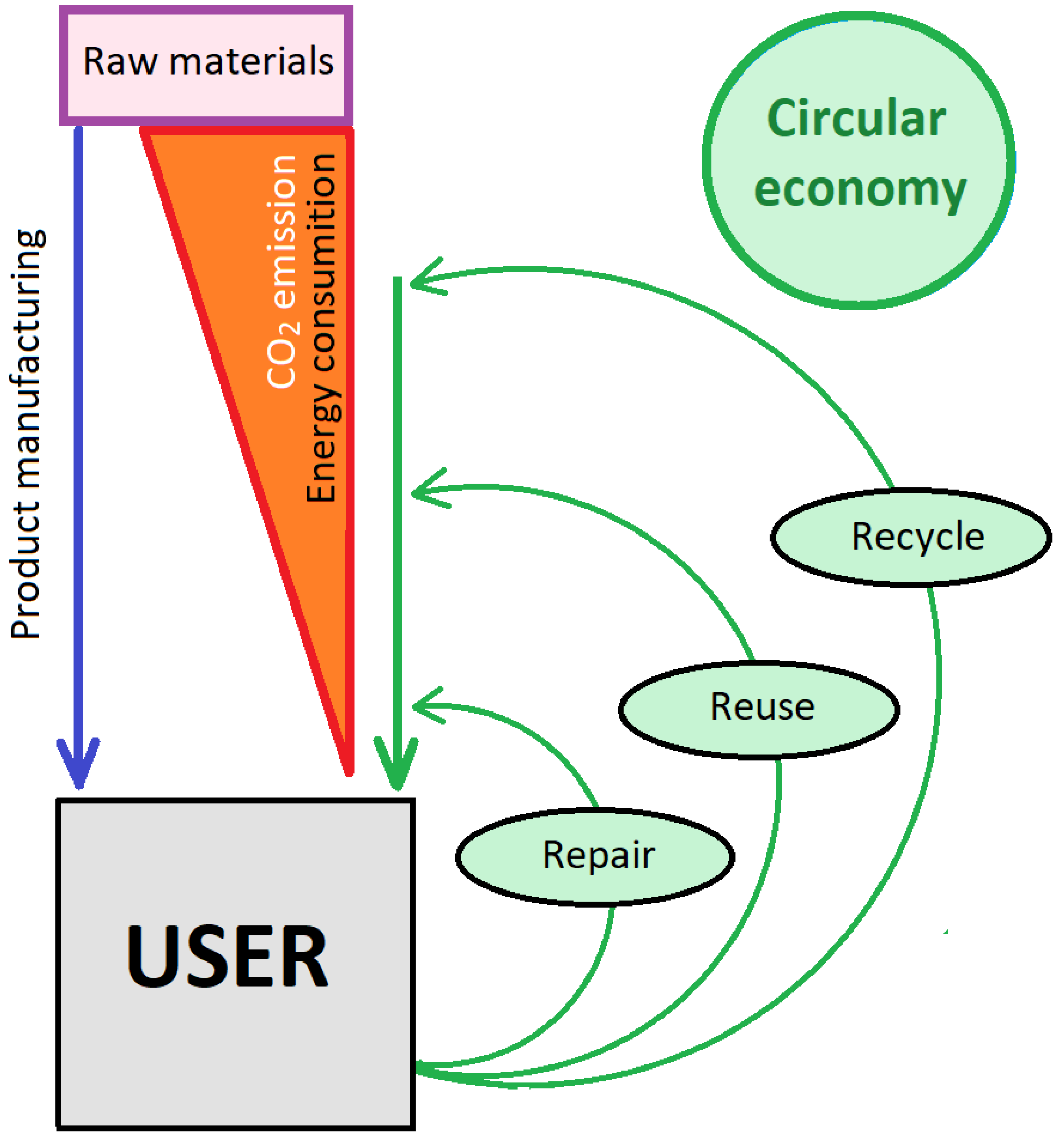
1.1. The Circular Economy According to European and World Policies
1.2. The Circular Economy Applied to Steel Structures
1.3. Design for Deconstruction (DfD)
1.4. Industrial Facilities and Associated Steel Structures
1.5. Advantages and Disadvantages of Sustainable Steel Structures
2. Non-Reconfigurable Steel Connections
2.1. Welded Connections
2.2. Bolted Connections
2.3. Connections Using Blind Bolts for Square or Rectangular Tubular Profiles
2.4. Connections Using Perforated Profiles
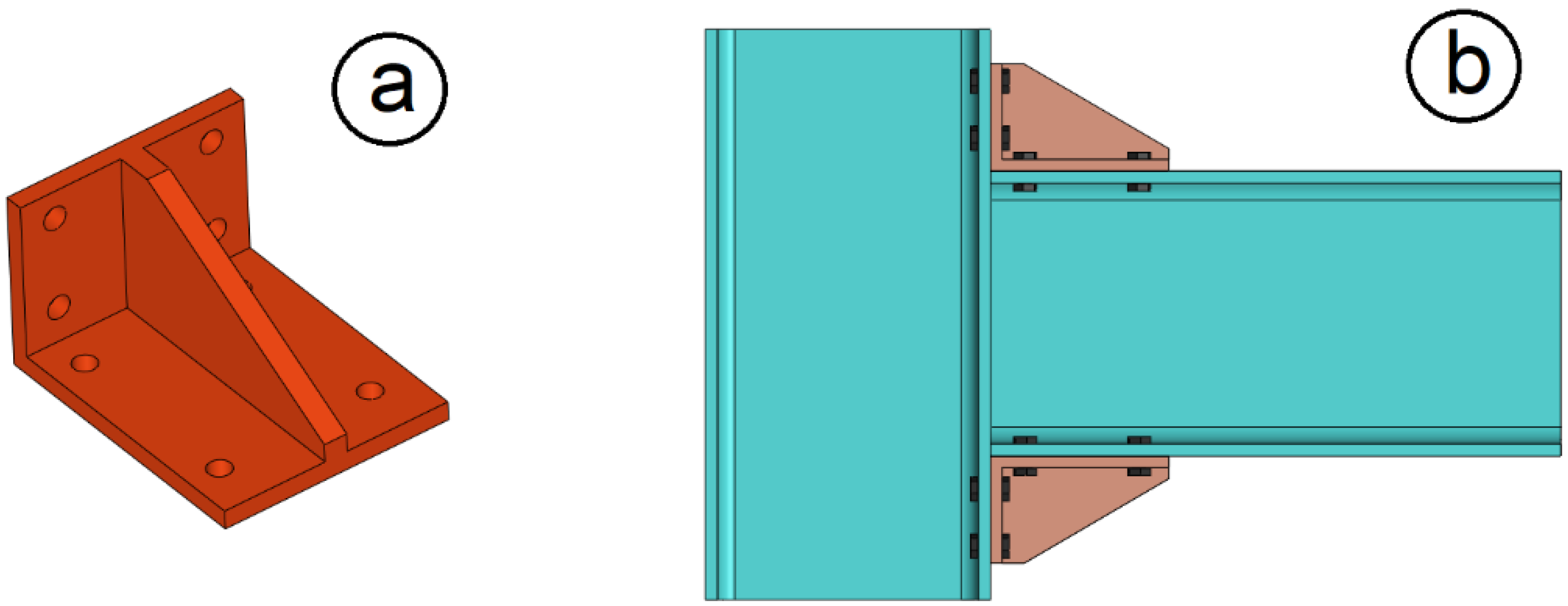
2.5. Connections Using Bolts with Removable Brackets
3. Removable and Reconfigurable Steel Connections
3.1. Quick Connections for Round Tubes
3.2. Connection of I-Type Profiles by a Collar Connection
3.3. Connection with Clamps for Square or Rectangular Tubular Profiles
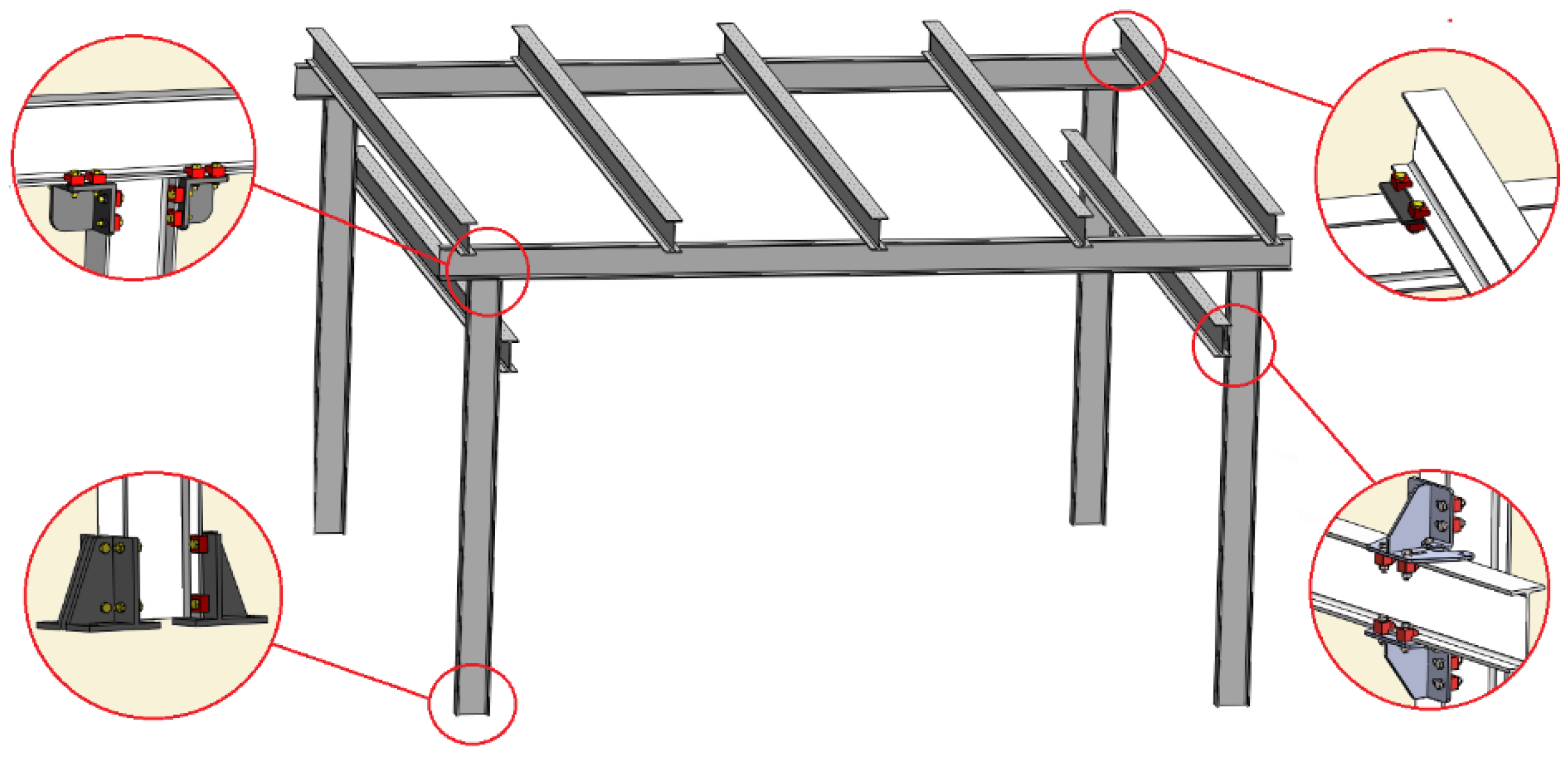
4. Clamp-Based Connections for Steel Structures from I-Type Profiles
4.1. Types of Clamps
4.2. Types of Connections
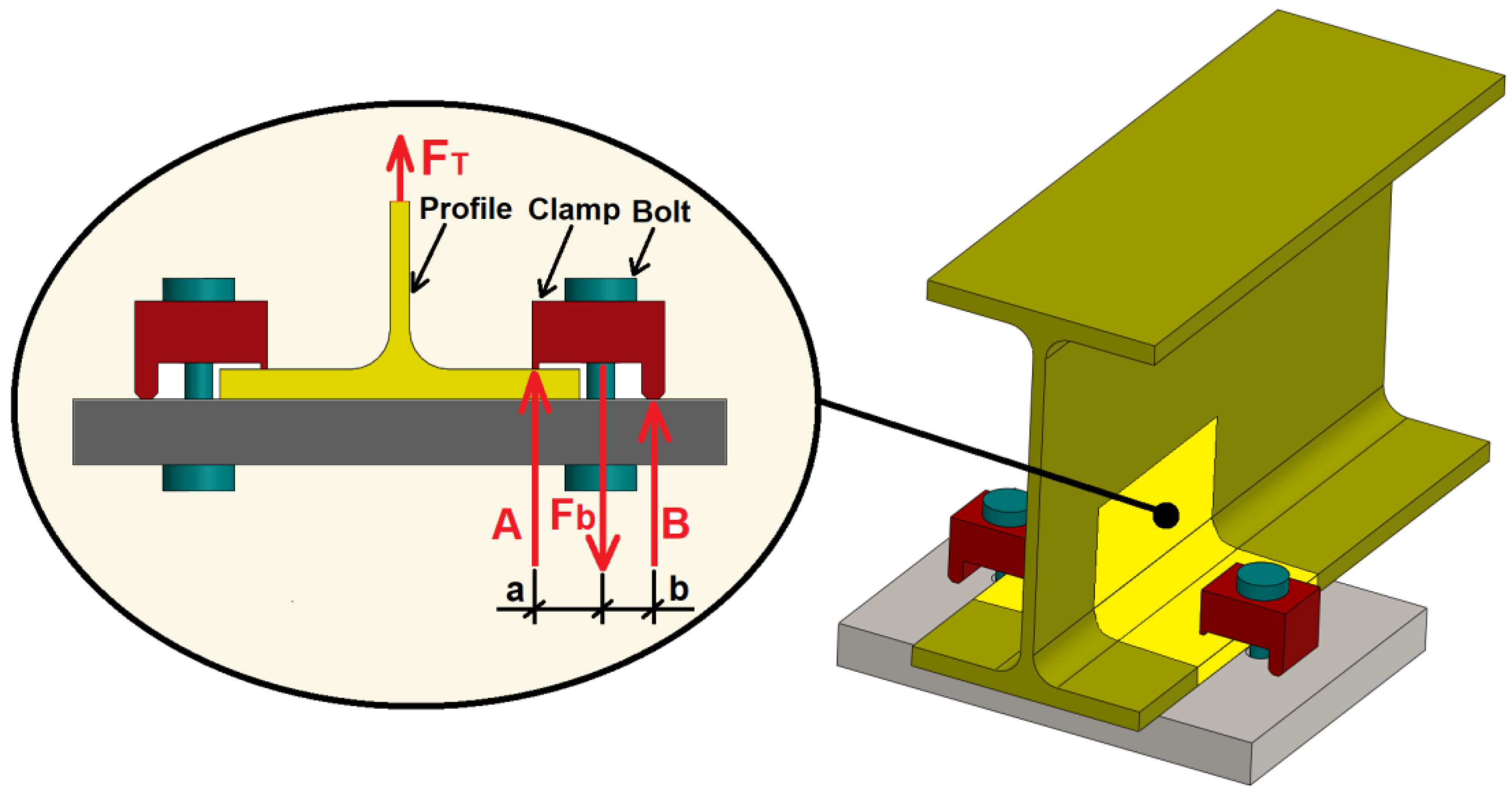
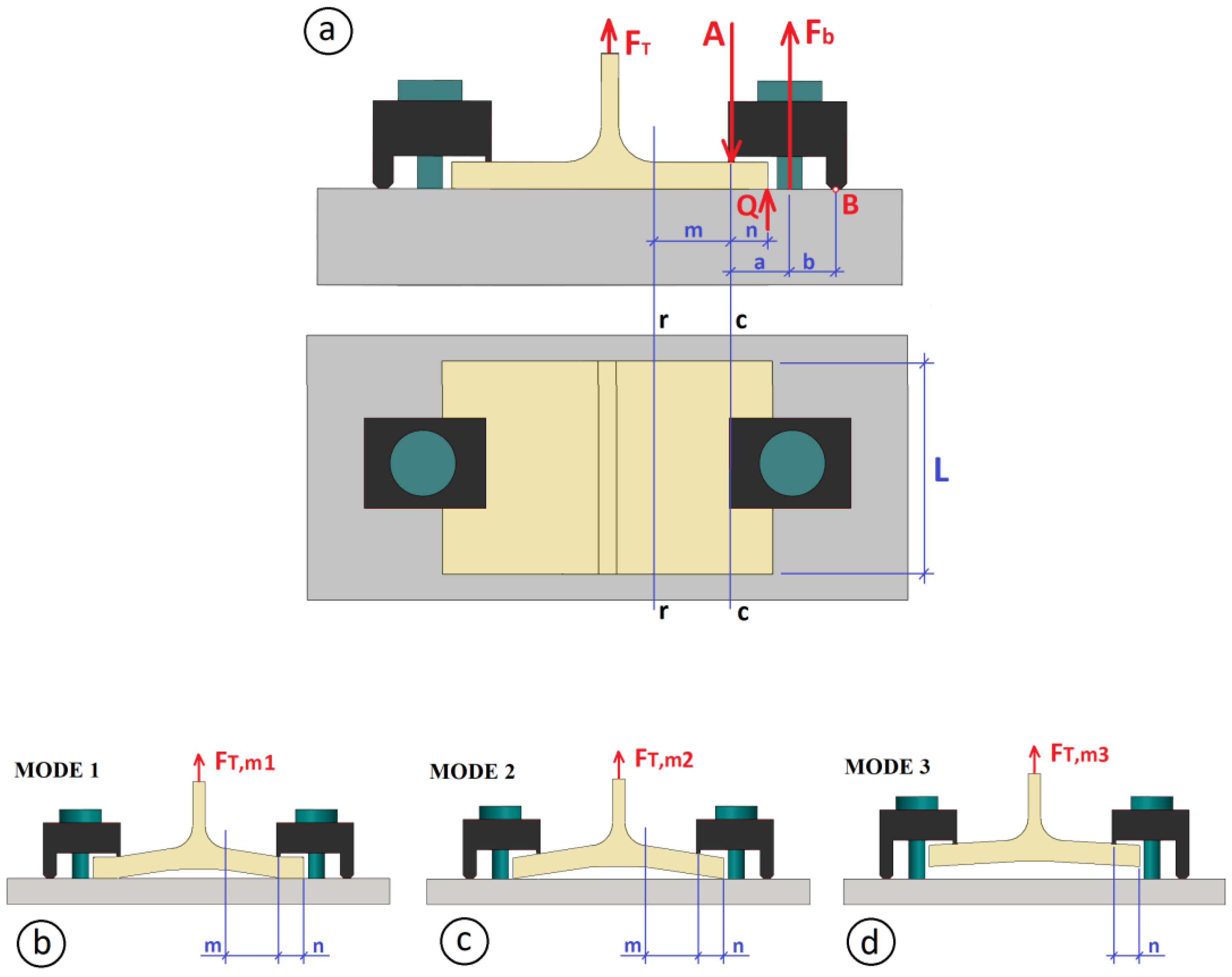
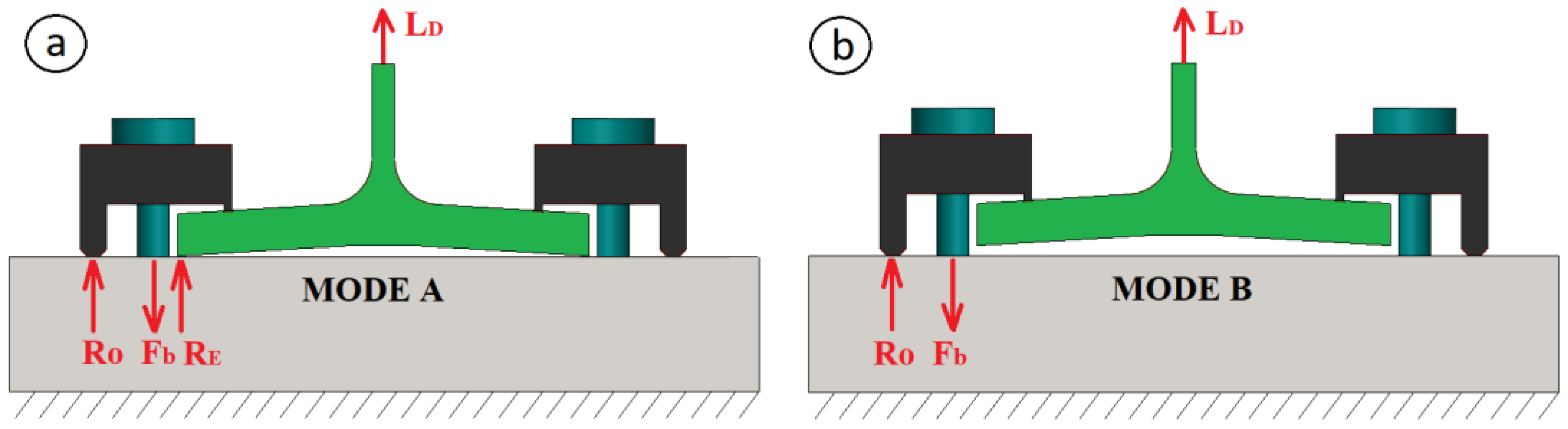
4.3. Behavior under Axial Loads
4.4. Behavior under Dynamic Loads
5. Conclusions
- ○
- They are fully dismountable.
- ○
- Fully reconfigurable structures are obtained where the only operation to be performed is to cut the profile to size.
- ○
- They allow for a great diversity of connection configurations.
- ○
- They can be defined as sustainable structures in the sense that they can be reused as many times as necessary.
- ○
- They are only valid for I-type sections.
- ○
- They are less rigid than classic bolted connections for the same number of bolts.
- ○
- There are still few studies on their mechanical behavior and methodologies for their calculation. Those that exist are focused on the behavior of the clamp, and there are still no studies on the different clamp-based connection configurations, which hinders their practical implementation on a large scale.
- ○
- This type of connection is not very industrialized, which makes it more expensive than other solutions.
- ○
- The behavior analysis under static and dynamic loads should be taken further according to the different configurations of clamp-based connections in addition to those already performed for the behavior of the clamp.
- ○
- The analysis methods should also be studied further through, e.g., analytical and numerical methods, not only for the behavior of the clamp, but also for the different configurations of clamp-based connections.
- ○
- The management of the different components after being disassembled from a structure and before being assembled in the following configuration.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- A_RES_70_1_E. Resolution Adopted by the General Assembly on 25 September 2015. 70/1. Transforming Our World: The 2030 Agenda for Sustainable Development. United Nations. Available online: https://www.un.org/en/development/desa/population/migration/generalassembly/docs/globalcompact/A_RES_70_1_E.pdf (accessed on 16 January 2023).
- Regulation (EU) 2020/852. Regulation (EU) 2020/852 of the European Parliament and of the Council of 18 June 2020 on the Establishment of a Framework to Facilitate Sustainable Investment and Amending Regulation (EU) 2019/2088. Document 32020R0852. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/HTML/?uri=CELEX:32020R0852&from=EN (accessed on 16 January 2023).
- B-1049 May 2018. Impacts of Circular Economy Policies on the Labour Market Final Report. European Commission B-1049 Brussels. May–2018. Available online: https://circulareconomy.europa.eu/platform/sites/default/files/ec_2018_-_impacts_of_circular_economy_policies_on_the_labour_market.pdf (accessed on 16 January 2023).
- CEPBD 2020. Circular Economy Principles for buildings design. European Commission. 21/02/2020 Created by GROW.DDG1. C.4. Available online: https://ec.europa.eu/docsroom/documents/39984?locale=es (accessed on 16 January 2023).
- Ellen MacArthur Foundation 2013. Towards the Circular Economy Vol. 1: An Economic and Business Rationale for an Accelerated Transition de Ellen MacArthur Foundation. Executive Summary 2013. Available online: https://ellenmacarthurfoundation.org/towards-the-circular-economy-vol-1-an-economic-and-business-rationale-for-an (accessed on 16 January 2023).
- Wang, L.; Zhu, S.; Evans, S.; Zhang, Z.; Xia, X.; Guo, Y. Automobile recycling for remanufacturing in China: A systematic review on recycling legislations, models and methods. Sustain. Prod. Consum. 2023, 36, 369–385. [Google Scholar] [CrossRef]
- Passoni, C.; Palumbo, E.; Pinho, R.; Marini, A. The LCT Challenge: Defining New Design Objectives to Increase the Sustainability of Building Retrofit Interventions. Sustainability 2022, 14, 8860. [Google Scholar] [CrossRef]
- Bertin, I.; Mesnil, R.; Jaeger, J.M.; Feraille, A.; Le Roy, R. A BIM-based framework and databank for reusing load-bearing structural elements. Sustainability 2020, 12, 3147. [Google Scholar] [CrossRef]
- O’Grady, T.M.; Minunno, R.; Chong, H.Y.; Morrison, G.M. Interconnections: An analysis of disassemblable building connection systems towards a circular economy. Buildings 2021, 11, 535. [Google Scholar] [CrossRef]
- Minunno, R.; O’Grady, T.; Morrison, G.M.; Gruner, R.L.; Colling, M. Strategies for applying the circular economy to prefabricated buildings. Buildings 2018, 8, 125. [Google Scholar] [CrossRef]
- Kibert, C.J. Deconstruction: The start of a sustainable materials strategy for the built environment. Ind. Environ. 2003, 26, 84–88. [Google Scholar]
- Waste Statistics 2018. EUROSTAT Statistics Explained—European Commission. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php/Waste_statistics#Total_waste_generation (accessed on 16 January 2023).
- Brütting, J.; Vandervaeren, C.; Senatore, G.; De Temmerman, N.; Fivet, C. Environmental impact minimization of reticular structures made of reused and new elements through Life Cycle Assessment and Mixed-Integer Linear Programming. Energy Build. 2020, 215, 109827. [Google Scholar] [CrossRef]
- Eckelman, M.J.; Brown, C.; Troup, L.N.; Wang, L.; Webster, M.D.; Hajjar, J.F. Life cycle energy and environmental benefits of novel design-for-deconstruction structural systems in steel buildings. Build. Environ. 2018, 143, 421–430. [Google Scholar] [CrossRef]
- Sansom, M.; Avery, N. Briefing: Reuse and recycling rates of UK steel demolition arisings. In Proceedings of the Institution of Civil Engineers-Engineering Sustainability; Thomas Telford Ltd.: Cham, Switzerland, 2014; Volume 167, pp. 89–94. [Google Scholar]
- Marzouk, M.; Elmaraghy, A. Design for deconstruction using integrated lean principles and bim approach. Sustainability 2021, 13, 7856. [Google Scholar] [CrossRef]
- Obi, L.; Awuzie, B.; Obi, C.; Omotayo, T.S.; Oke, A.; Osobajo, O. BIM for deconstruction: An interpretive structural model of factors influencing implementation. Buildings 2021, 11, 227. [Google Scholar] [CrossRef]
- Akbarieh, A.; Jayasinghe, L.B.; Waldmann, D.; Teferle, F.N. BIM-based end-of-lifecycle decision making and digital deconstruction: Literature review. Sustainability 2020, 12, 2670. [Google Scholar] [CrossRef]
- Kanters, J. Design for deconstruction in the design process: State-of-the-art. Buildings 2018, 8, 150. [Google Scholar] [CrossRef]
- Tingley, D.D.; Davison, B. Developing an LCA methodology to account for the environmental benefits of design for deconstruction. Build. Environ. 2012, 57, 387–395. [Google Scholar] [CrossRef]
- Akbarnezhad, A.; Ong, K.C.G.; Chandra, L.R. Economic and environmental assessment of deconstruction strategies using building information modeling. Autom. Constr. 2014, 37, 131–144. [Google Scholar] [CrossRef]
- Basta, A.; Serror, M.H.; Marzouk, M.A. BIM-based framework for quantitative assessment of steel structure deconstructability. Autom. Constr. 2020, 111, 103064. [Google Scholar] [CrossRef]
- Charef, R.; Morel, J.C.; Rakhshan, K. Barriers to Implementing the Circular Economy in the Construction Industry: A Critical Review. Sustainability 2021, 13, 12989. [Google Scholar] [CrossRef]
- Cottafava, D.; Ritzen, M. Circularity indicator for residentials buildings: Addressing the gap between embodied impacts and design aspects. Resour. Conserv. Recycl. 2021, 164, 105120. [Google Scholar] [CrossRef]
- O’Grady, T.; Minunno, R.; Chong, H.Y.; Morrison, G.M. Design for disassembly, deconstruction and resilience: A circular economy index for the built environment. Resour. Conserv. Recycl. 2021, 175, 105847. [Google Scholar] [CrossRef]
- Cabaleiro, M.; Riveiro, B.; Arias, P.; Caamaño, J.C. Algorithm for beam deformation modeling from LiDAR data. Measurement 2015, 76, 20–31. [Google Scholar] [CrossRef]
- Groover, M.P. Fundamentals of Modern Manufacturing, 4th ed.; John Wiley Sons, Inc.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Kalpakjian, S.; Schmid, S.R. Manufacturing, Engineering and Technology, 6th ed.; Prentice-Hall: New York, NY, USA, 2006. [Google Scholar]
- EN 1993-1-1:2005; Eurocode 3: Design of Steel Structures—Part 1-1: General Rules and Rules for Building. European Committee for Standardization: Brussels, Belgium, 2005.
- EN 1993-1-8: 2003; Eurocode 3: Design of Steel Structures—Part 1-8: Design of Connections. European Committee for Standardization: Brussels, Belgium, 2003.
- EN 14399-3:2005; High-Strength Structural Bolting Assemblies for Preloading. Part 3: System HR. Hexagon Bolt and Nut Assemblies. European Committee for Standardisation (CEN): Brussels, Belgium, 2005.
- Specification for Structural Steel Buildings ANSI/AISC 360-16; American National Standards Institute ANSI/American Institute of Steel Construction AISC: Chicago, IL, USA, 2016.
- Arguelles-Alvarez, R.; Arguelles-Bustillo, J.M.; Arguelles-Bustillo, R.; Arriaga-Martitegui, F.; Atienza-Reales, J.R. Estructuras de Acero: Calculo; Bellisco Ediciones: Madrid, Spain, 2005. [Google Scholar]
- Salmon, C.G.; Johnson, J.E.; Malhas, F.A. Steel Structures: Design and Behavior, 5th ed.; Pearson Prentice Hall: Hoboken, NJ, USA, 2009. [Google Scholar]
- Tamboli, A.R. Steel Connection Design and Details; McGraw-Hill Education: New York, NY, USA, 2016. [Google Scholar]
- Huang, Y.; Huang, J.; Zhang, W.; Liu, X. Experimental and numerical study of hooked-end steel fiber-reinforced concrete based on the meso-and macro-models. Compos. Struct. 2023, 309, 116750. [Google Scholar] [CrossRef]
- Tian, L.M.; Li, M.H.; Li, L.; Li, D.Y.; Bai, C. Novel joint for improving the collapse resistance of steel frame structures in column-loss scenarios. Thin-Walled Struct. 2023, 182, 110219. [Google Scholar] [CrossRef]
- Ghasemi, M.; Zhang, C.; Khorshidi, H.; Zhu, L.; Hsiao, P.C. Seismic upgrading of existing RC frames with displacement-restraint cable bracing. Eng. Struct. 2023, 282, 115764. [Google Scholar] [CrossRef]
- 3Yang, Y.; Lin, B.; Zhang, W. Experimental and numerical investigation of an arch–beam joint for an arch bridge. Arch. Civ. Mech. Eng. 2023, 23, 101. [Google Scholar]
- Zhai, S.Y.; Lyu, Y.F.; Cao, K.; Li, G.Q.; Wang, W.Y.; Chen, C. Seismic behavior of an innovative bolted connection with dual-slot hole for modular steel buildings. Eng. Struct. 2023, 279, 115619. [Google Scholar] [CrossRef]
- Liu, H.; Chen, Z.; Liu, Y.; Chen, Y.; Du, Y.; Zhou, F. Interfacial debonding detection for CFST structures using an ultrasonic phased array: Application to the Shenzhen SEG building. Mech. Syst. Signal Process. 2023, 192, 110214. [Google Scholar] [CrossRef]
- Huang, H.; Yao, Y.; Liang, C.; Ye, Y. Experimental study on cyclic performance of steel-hollow core partially encased composite spliced frame beam. Soil Dyn. Earthq. Eng. 2022, 163, 107499. [Google Scholar] [CrossRef]
- Yin, L.; Niu, Y.; Quan, G.; Gao, H.; Ye, J. A numerical investigation of new types of bolted joints for cold-formed steel moment-resisting frame buildings. J. Build. Eng. 2023, 65, 105738. [Google Scholar] [CrossRef]
- Lindaper Hollo-Bolt. Lindapter International. 2012. Available online: https://www.lindapter.com/us/product-category/hollo-boltLindapter.www.lindapter.com (accessed on 14 July 2022).
- LNA Solutions Boxbolt 2022. Available online: https://www.lnasolutions.com/products/boxbolt-type-c-icc-approved/ (accessed on 14 July 2022).
- Cabrera, M.; Tizani, W.; Ninic, J. A review and analysis of testing and modeling practice of extended Hollo-Bolt blind bolt connections. J. Constr. Steel Res. 2021, 183, 106763. [Google Scholar] [CrossRef]
- Cabrera, M.; Tizani, W.; Ninic, J.; Wang, F. Experimental and numerical analysis of preload in Extended Hollo-Bolt blind bolts. J. Constr. Steel Res. 2021, 186, 106885. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Tizani, W.; Wang, Q.Y. Strength and initial stiffness of a blind-bolt connection based on the T-stub model. Eng. Struct. 2010, 32, 2505–2517. [Google Scholar] [CrossRef]
- Lee, J.; Goldsworthy, H.M.; Gad, E.F. Blind bolted T-stub connections to unfilled hollow section columns in low-rise structures. J. Constr. Steel Res. 2010, 66, 981–992. [Google Scholar] [CrossRef]
- Yang, C.; Chen, H.; Ou, J. Experimental study on seismic performance of modular steel construction beam-to-beam combined side column joint with blind bolted connection. Thin-Walled Struct. 2023, 184, 110431. [Google Scholar] [CrossRef]
- Abdel-Jaber, M.; Beale, R.G.; Godley, M.H.R. A theoretical and experimental investigation of pallet rack structures under sway. J. Constr. Steel Res. 2006, 62, 68–80. [Google Scholar] [CrossRef]
- Galeotti, C.; Gusella, F.; Orlando, M.; Spinelli, P. On the seismic response of steel storage pallet racks with selective addition of bolted connections. Structures 2021, 4, 3806–3817. [Google Scholar] [CrossRef]
- Elias, G.C.; de Almeida Neiva, L.H.; Sarmanho, A.M.C.; Alves, V.N.; e Castro, A.F.B. Ultimate load of steel storage systems up-rights. Eng. Struct. 2018, 170, 53–62. [Google Scholar] [CrossRef]
- Ng, A.L.Y.; Beale, R.G.; Godley, M.H.R. Methods of restraining progressive collapse in rack structures. Eng. Struct. 2009, 31, 1460–1468. [Google Scholar] [CrossRef]
- Godley, M.H.R.; Beale, R.G. Investigation of the effects of looseness of bracing components in the cross-aisle direction on the ultimate load-carrying capacity of pallet rack frames. Thin-Walled Struct. 2008, 46, 848–854. [Google Scholar] [CrossRef]
- Sajja, S.R.; Beale, R.G.; Godley, M.H.R. Shear stiffness of pallet rack upright frames. J. Constr. Steel Res. 2008, 64, 867–874. [Google Scholar] [CrossRef]
- Abdel-Jaber, M.; Beale, R.G.; Godley, M.H.R. Numerical study on semi-rigid racking frames under sway. Comput. Struct. 2005, 83, 2463–2475. [Google Scholar] [CrossRef]
- Reinosa, J.M.; Loureiro, A.; Gutierrez, R.; Lopez, M. Mechanical stiffness prediction of beam-to-column stiffened angle connections. J. Constr. Steel Res. 2020, 168, 105875. [Google Scholar] [CrossRef]
- Abar, B.M.; Ghobadi, M.S. Double shear bolted bracket movement connections, part 1: Four-bolt configuration design methodology. J. Constr. Steel Res. 2020, 174, 106280. [Google Scholar] [CrossRef]
- Abar, B.M.; Ghobadi, M.S. New generation of bolted bracket connections: Safe load-carrying capacity and structural damage assessment. Eng. Struct. 2022, 252, 113662. [Google Scholar] [CrossRef]
- Pieńko, M.; Błazik-Borowa, E. Experimental studies of ringlock scaffolding connection. J. Constr. Steel Res. 2020, 173, 106265. [Google Scholar] [CrossRef]
- Zheng, Y.; Guo, Z. Investigation of connection behavior of disk-lock and cuplok steel tubular scaffold. J. Constr. Steel Res. 2021, 177, 106415. [Google Scholar] [CrossRef]
- Peng, J.L.; Wu, C.W.; Chan, S.L.; Huang, C.H. Experimental and numerical studies of practical system scaffolds. J. Constr. Steel Res. 2013, 91, 64–75. [Google Scholar] [CrossRef]
- Peng, J.L.; Ho, C.M.; Chan, S.L.; Chen, W.F. Stability study on structural systems assembled by system scaffolds. J. Constr. Steel Res. 2017, 137, 135–151. [Google Scholar] [CrossRef]
- Błazik-Borowa, E.; Jamińska-Gadomska, P.; Pieńko, M. Influence of foundation quality on the stress in the elements of steel façade scaffolding. Buildings 2020, 10, 130. [Google Scholar] [CrossRef]
- Abdel-Jaber, M.; Beale, R.G.; Shatarat, N.K.; Shehadeh, M.A. Experimental and theoretical investigations of spigot connections under cyclic loading. Adv. Steel Constr. 2019, 15, 37–46. [Google Scholar]
- Beale, R.G. Scaffold research—A review. J. Constr. Steel Res. 2014, 98, 188–200. [Google Scholar] [CrossRef]
- Abdel-Jaber, M.S.; Beale, R.G.; Allouzi, R.; Shatarat, N.K. Properties of tube and fitting scaffold connections under cyclical loads. J. Constr. Steel Res. 2020, 168, 106008. [Google Scholar] [CrossRef]
- Prabhakaran, U.; Beale, R.G.; Godley, M.H.R. Analysis of scaffolds with connections containing looseness. Comput. Struct. 2011, 89, 1944–1955. [Google Scholar] [CrossRef]
- Abdel-Jaber, M.E.; Abdel-Jaber, M.T.S.; Beale, R.G. An Experimental Study into the Behaviour of Tube and Fitting Scaffold Structures under Cyclic Side and Vertical Loads. Metals 2021, 12, 40. [Google Scholar] [CrossRef]
- Abdel-Jaber, M.; Abdel-Jaber, M.S.; Beale, R.G.; Shatarat, N.K. Cyclic Loading applied to sleeve couplers for tube and fitting scaffolds. In ACMSM25: Proceedings of the 25th Australasian Conference on Mechanics of Structures and Materials; Springer: Singapore, 2020; pp. 819–830. [Google Scholar]
- Hosseini, S.M.; Rahnavard, R. Numerical study of steel rigid collar connection affecting cyclic loading. Eng. Struct. 2020, 208, 110314. [Google Scholar] [CrossRef]
- Rezaeian, A.; Jamal-Omidi, M.; Shahidi, F. Seismic behavior of ConXL rigid connection in box-columns not filled with concrete. J. Constr. Steel Res. 2014, 97, 79–104. [Google Scholar] [CrossRef]
- Yang, C.; Yang, J.F.; Su, M.Z.; Liu, C.Z. Numerical study on seismic behaviours of ConXL biaxial moment connection. J. Constr. Steel Res. 2016, 121, 185–201. [Google Scholar] [CrossRef]
- NucleoNova. Clamping Systems Novagrip, Nucleonova S.L. 2022. Available online: www.nucleonova.es (accessed on 14 July 2022).
- LNA Solutions. LNA Solutions, Steel Connection Solutions. 2012. Available online: www.lnasolutions.com (accessed on 14 July 2022).
- Cabaleiro, M.; Riveiro, B.; Conde, B.; Caamaño, J.C. Analytical T-stub model for the analysis of clamps in structural metal connections. J. Constr. Steel Res. 2017, 130, 138–147. [Google Scholar] [CrossRef]
- Pongiglione, M.; Calderini, C.; D’Aniello, M.; Landolfo, R. Novel reversible seismic-resistant connection for sustainable and deconstructable steel structures. J. Build. Eng. 2021, 35, 101989. [Google Scholar] [CrossRef]
- Cabaleiro, M.; Conde, B.; Riveiro, B.; Caamaño, J.C. Analysis of steel connections with girder clamps according to the bolts preload. J. Constr. Steel Res. 2020, 168, 105866. [Google Scholar] [CrossRef]
- Cabaleiro, M.; Comesaña, R.; González-Gaya, C.; Caamaño, C. Analytical Model for the Fatigue Analysis of Steel Connections by Clamps According to the Lever Length. Materials 2021, 14, 7726. [Google Scholar] [CrossRef]
- Cabaleiro, M.; Moutinho, C.; González-Gaya, C.; Caetano, E.; Rosales-Prieto, V.F. Analysis of Stiffness of Clamped Connections versus Bolted Connections in Steel Structures by Means of Accelerometers and Shaking Table Tests. Sensors 2021, 21, 4778. [Google Scholar] [CrossRef] [PubMed]
- Cabaleiro, M.; Conde, B.; Caamaño, J.C.; Riveiro, B.; Gonzalez, L. Analysis of the shear behavior of structural metal joints based on the use of girder clamps. In Proceedings of the 1st Iberic Conference on Theoretical and Experimental Mechanics and Materials/11th National Congress on Experimental Mechanics, Porto, Portugal, 30 June–2 July 2021; pp. 4–7. [Google Scholar]
- Cabaleiro, M.; González, C.; Conde, B. Analyzing the effective length of I cross-section beams in connections with girder clamps for totally removable, reusable and reconfigurable structures. Procedia Manuf. 2019, 41, 90–97. [Google Scholar] [CrossRef]
- Cabaleiro, M.; González-Gaya, C.; Gonzalez, F. Experimental Analysis of the Bending Behavior of Structural Metal Connections Based on the Use of Girder Clamps to Service Life Extension of Existing Structures. In Proceedings of the 3rd RILEM Spring Convention and Conference (RSCC 2020), Guimarães, Portugal, 9–14 March 2020; Springer International Publishing: Berlin/Heidelberg, Germany; Volume 3. Service Life Extension of Existing Structures 3. [Google Scholar]








| Type | Removable | Reconfigurable | Application | Number of References at Scopus (a) | Research Level Based on Scopus References | Sustainable (b) |
|---|---|---|---|---|---|---|
| Welded | No | No | All profiles type | 10,695 | very high | very low |
| Bolted | Yes | difficult | All profiles type | 2139 | high | low |
| Blind bolts | Yes | difficult | Square/rectangular tubes | 151 | medium | low |
| Storage racks | Yes | medium | Continuously perforated columns and beams equipped with quick hooks made using tabs | 171 | medium | medium |
| Scaffolding (disk locks) | Yes | medium | Round tubes | 84 | medium | medium |
| Scaffolding (quick round tube couplers) | Yes | easy | Round tubes | 14 | low | high |
| Bolted with removable brackets | Yes | medium | I-type profiles | 18 | low | high |
| I-type profiles by a collar connection | Yes | easy | I-type profiles and square/rectangular tubes | 9 | low | high |
| Clamp-based connections for I-type profiles | Yes | easy | I-type profiles | 12 | low | very high |
| Clamp-based connections for square or rectangular profiles | Yes | easy | Square/rectangular tubes | 2 | very low | very high |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cabaleiro, M.; Conde, B.; González-Gaya, C.; Barros, B. Removable, Reconfigurable, and Sustainable Steel Structures: A State-of-the-Art Review of Clamp-Based Steel Connections. Sustainability 2023, 15, 7808. https://doi.org/10.3390/su15107808
Cabaleiro M, Conde B, González-Gaya C, Barros B. Removable, Reconfigurable, and Sustainable Steel Structures: A State-of-the-Art Review of Clamp-Based Steel Connections. Sustainability. 2023; 15(10):7808. https://doi.org/10.3390/su15107808
Chicago/Turabian StyleCabaleiro, Manuel, Borja Conde, Cristina González-Gaya, and Brais Barros. 2023. "Removable, Reconfigurable, and Sustainable Steel Structures: A State-of-the-Art Review of Clamp-Based Steel Connections" Sustainability 15, no. 10: 7808. https://doi.org/10.3390/su15107808
APA StyleCabaleiro, M., Conde, B., González-Gaya, C., & Barros, B. (2023). Removable, Reconfigurable, and Sustainable Steel Structures: A State-of-the-Art Review of Clamp-Based Steel Connections. Sustainability, 15(10), 7808. https://doi.org/10.3390/su15107808








