Ground Reaction of Lightly Overconsolidated Subsoil in Reinforced Piled Embankment under Cyclic Loads
Abstract
1. Introduction
2. Numerical Simulation
2.1. General Description
2.2. Constitutive Models
2.3. Simulation Procedure
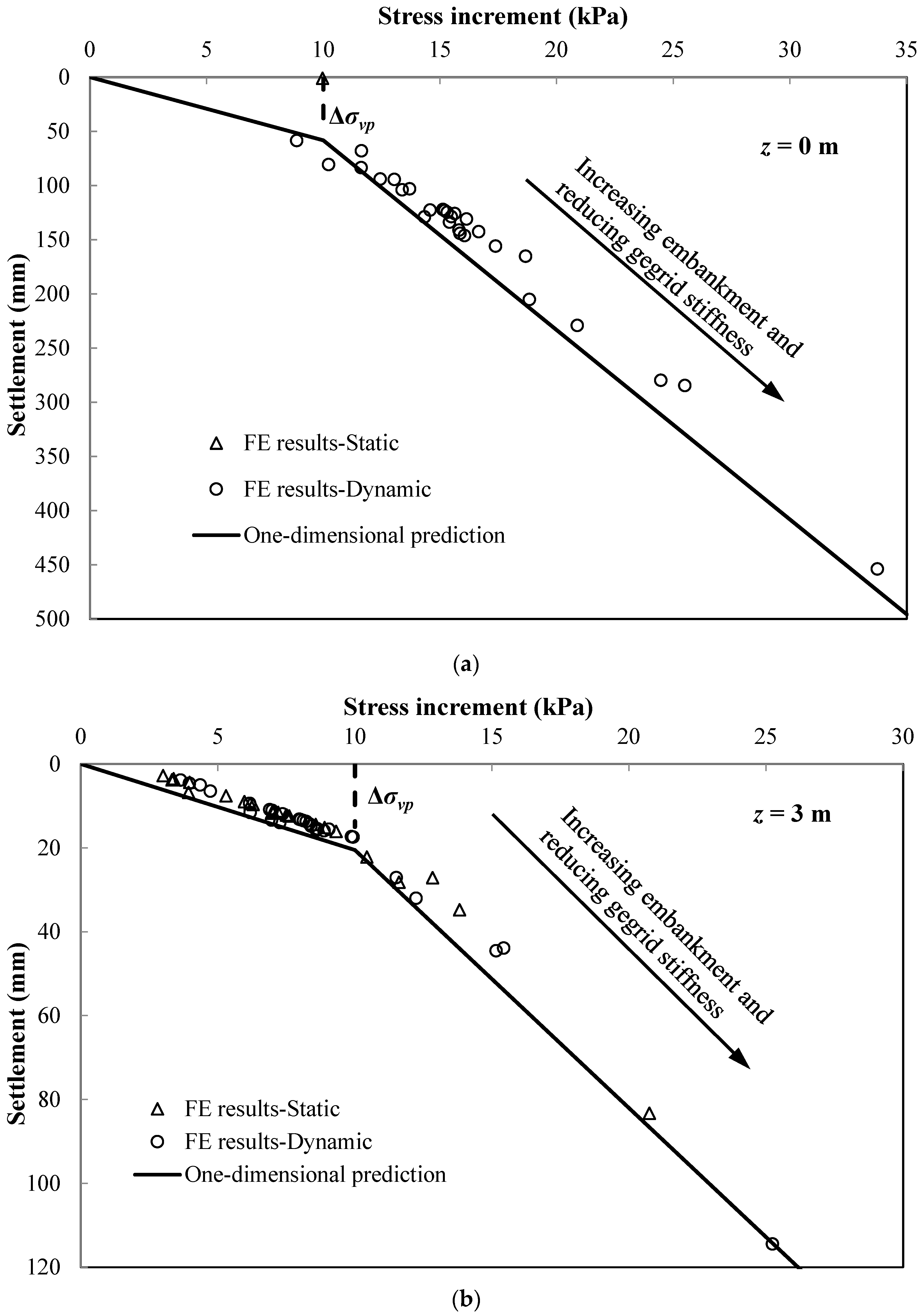
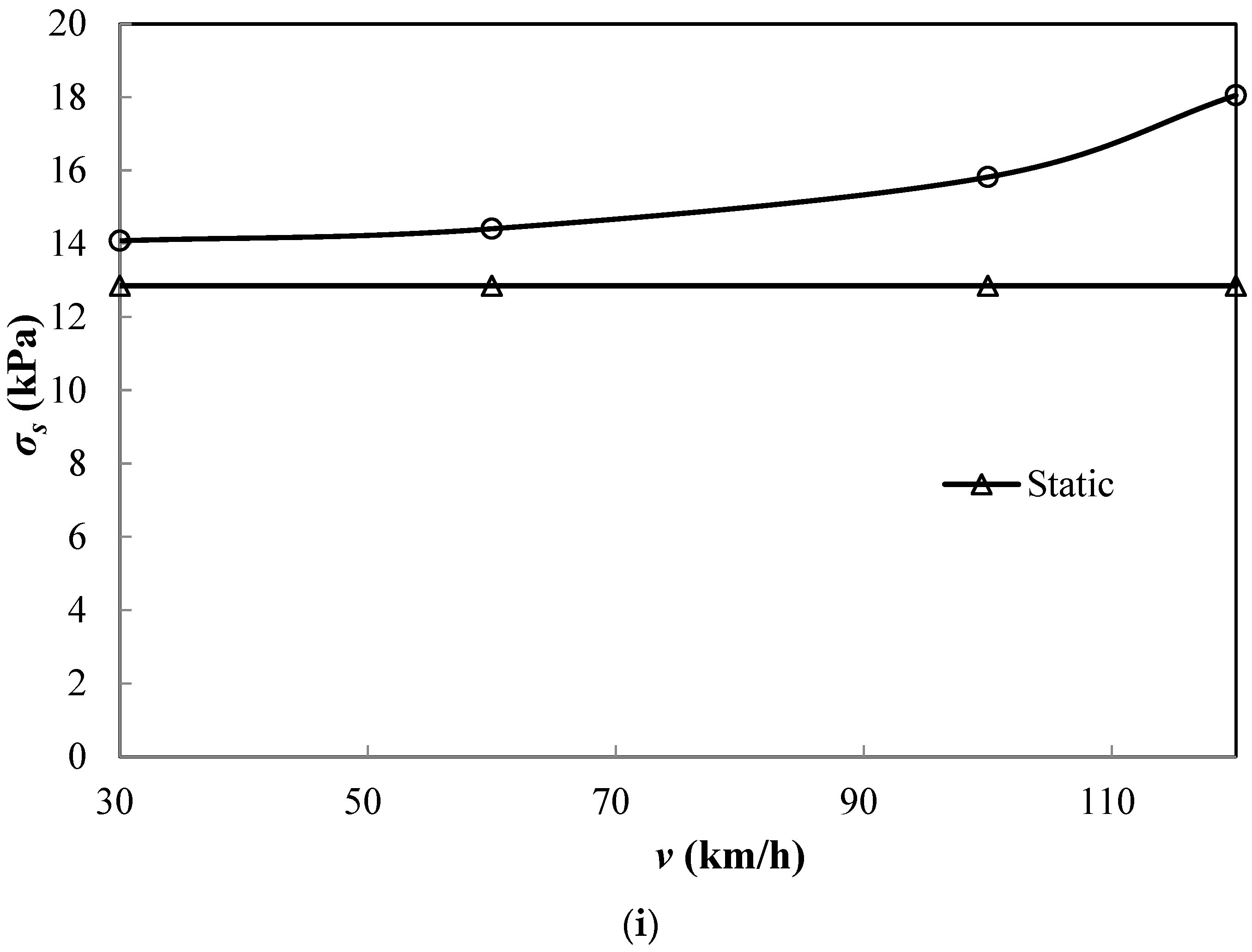
3. Ground Reaction of Lightly Overconsolidated Subsoil
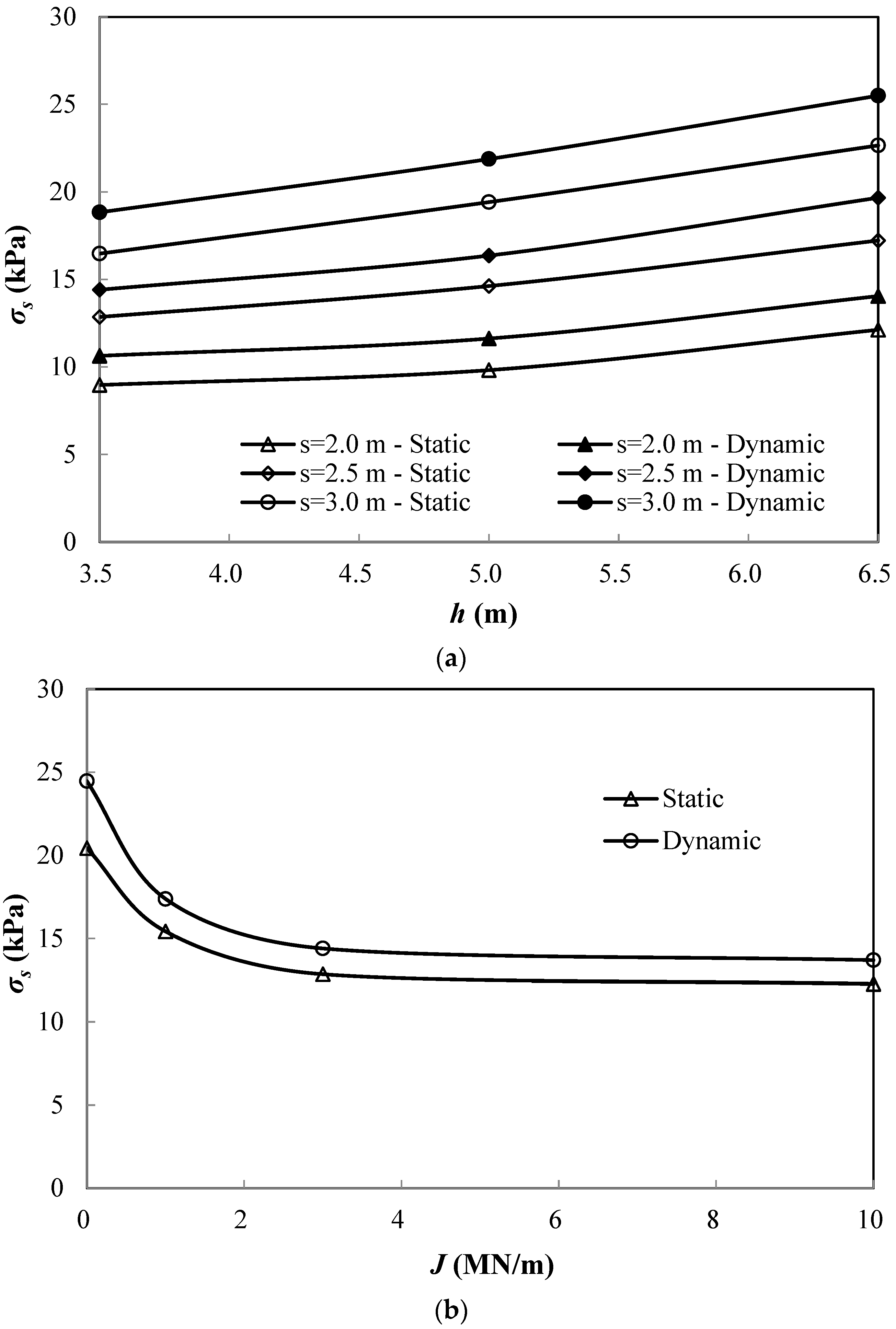
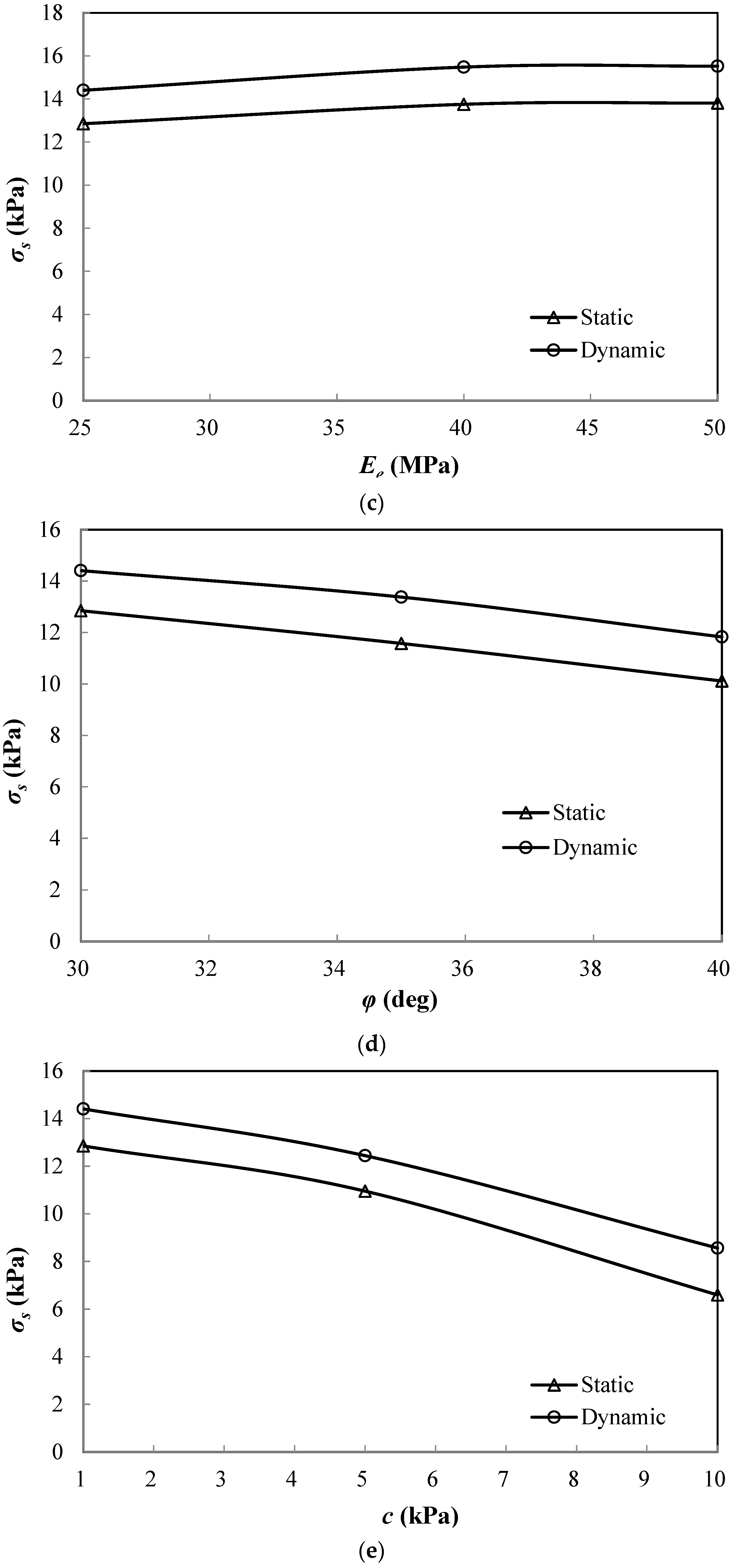
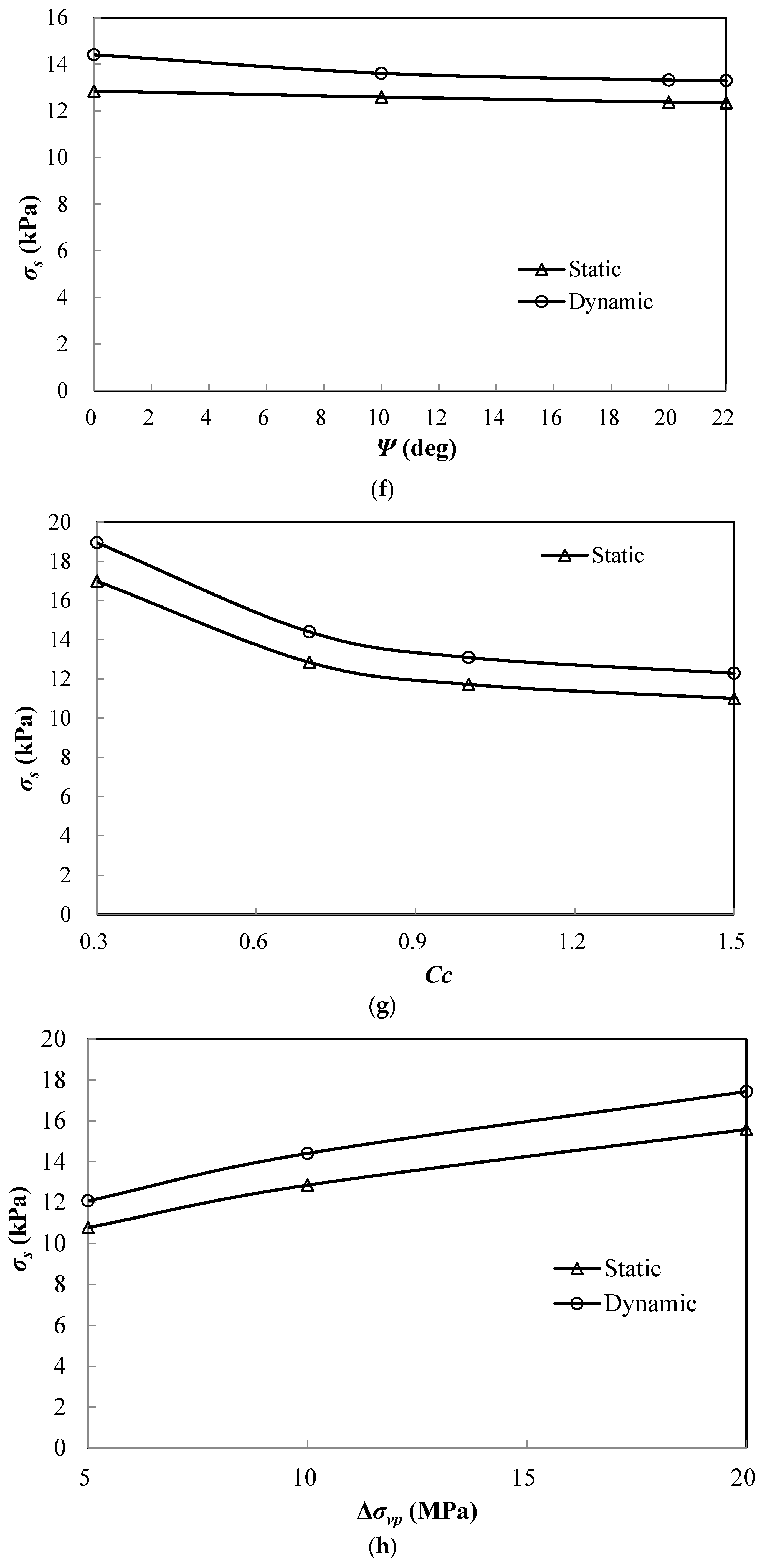
4. Parametric Study
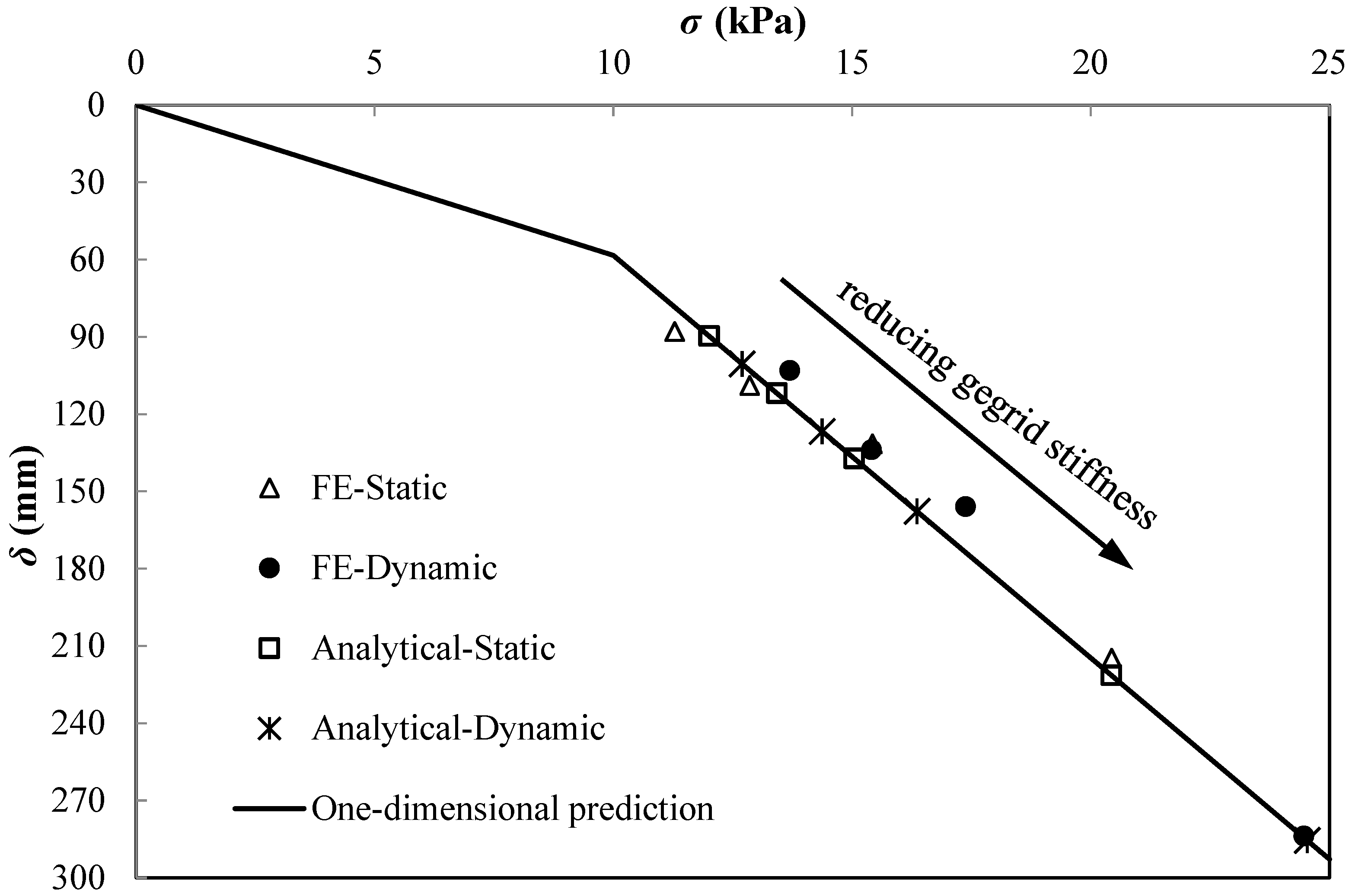
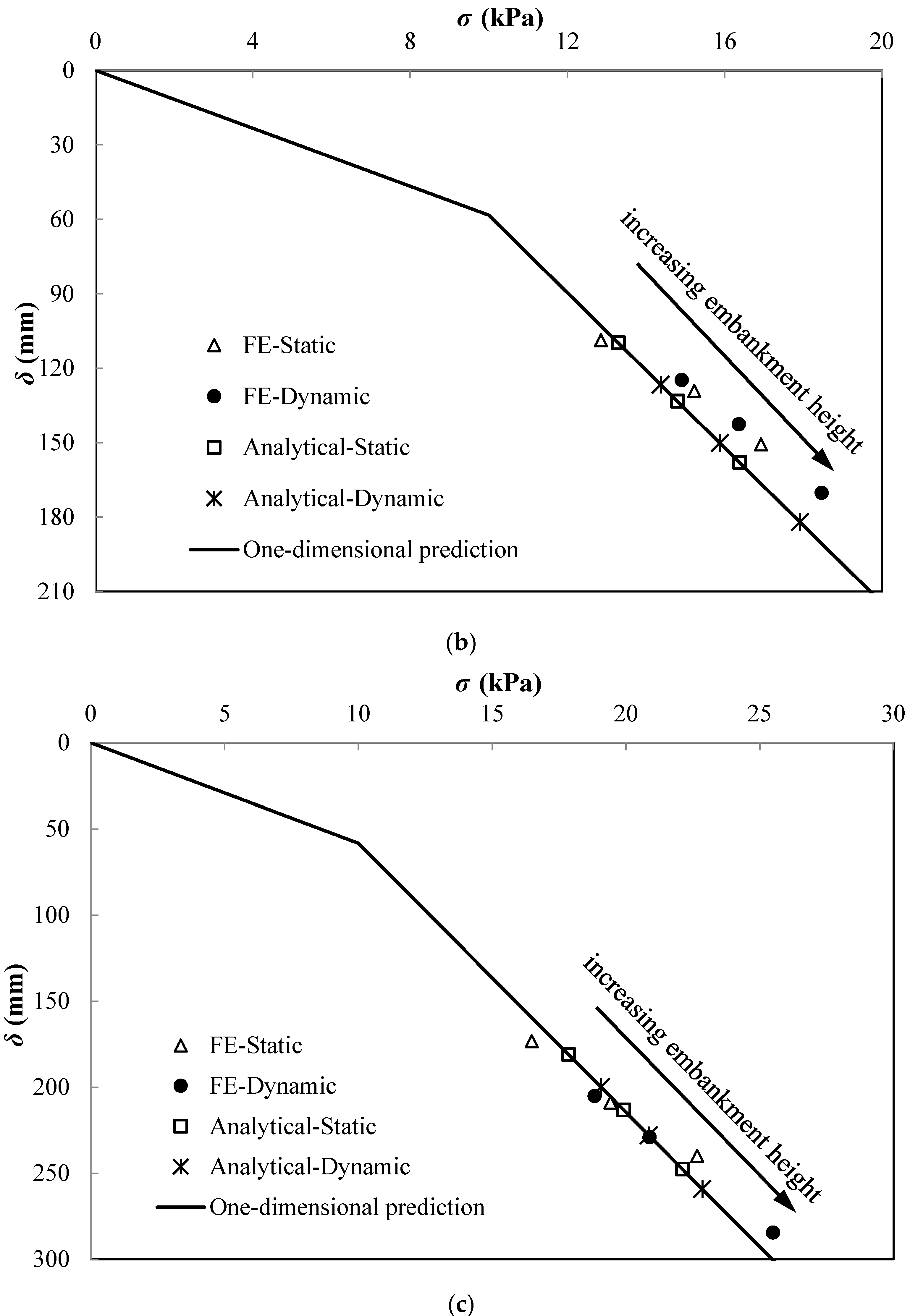
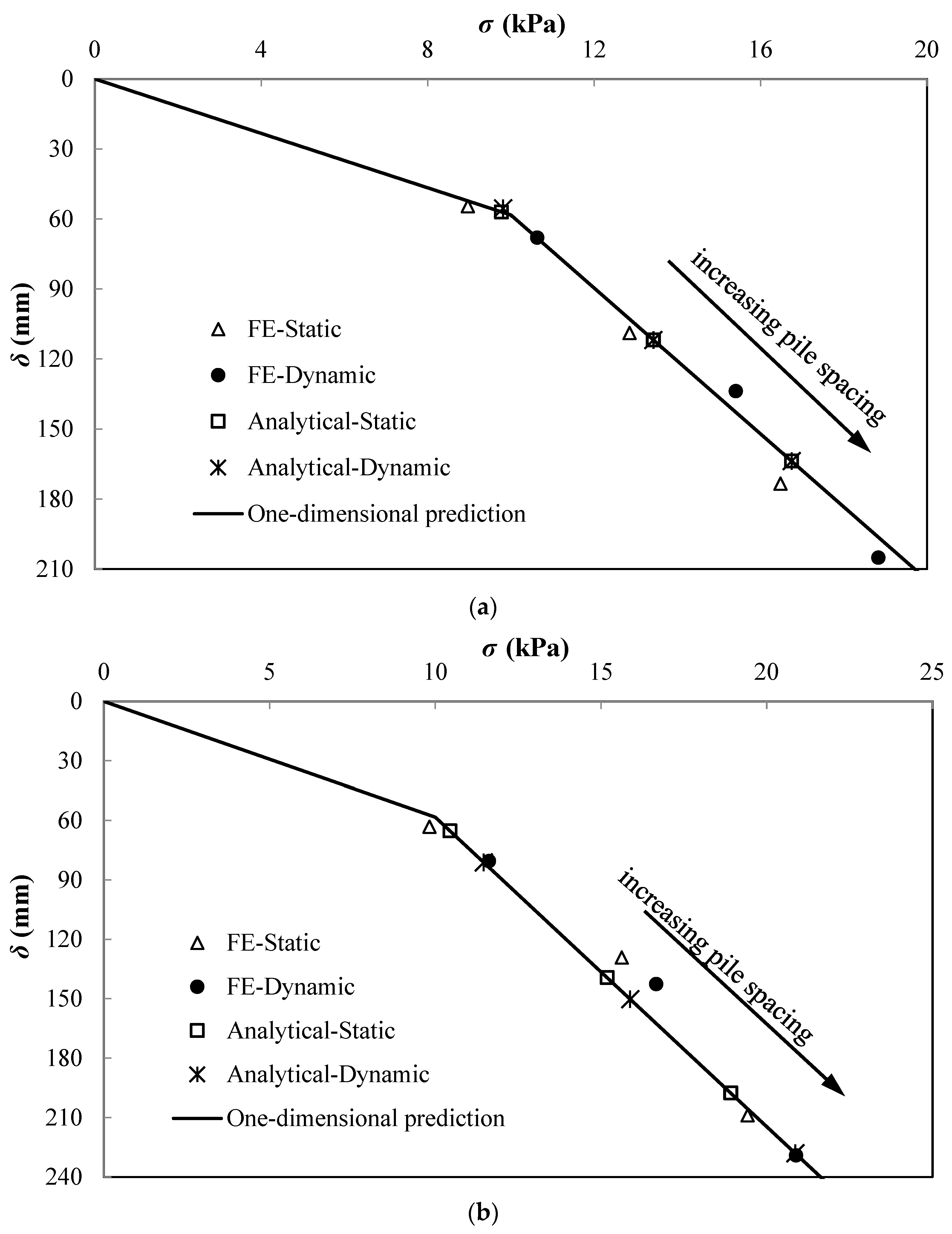
5. Comparison of the FEM with Modified Analytical Method
5.1. Modified Analytical Method
5.2. Comparison of FEM with Modified Analytical Method
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Notations
| a | (square) pile cap size (m) |
| J | long-term secant stiffness (at appropriate strain) for reinforcement (kN/m run (or MN/m)) |
| s | pile center-to-center spacing (for piles on a square grid) (m) |
| h | embankment height (m) |
| uw | excess pore water pressure (kPa) |
| Δσvp | the increment of stress to reach the preconsolidation stress in the subsoil (kN/m2) |
| φi | interface friction angle between pile and the subsoil (degrees) |
| φ’ | friction angle (degrees) |
| Cc | compression index of the subsoil |
| e0 | initial void ratio |
| M | critical stress ratio |
| λ | slope of the virgin consolidation line |
| κ | slope of the swelling line |
| P0 | static vehicle wheel load (kN) |
| M0 | unsprung weight (N∙s2/m) |
| μw/r(y) | road roughness function (mm) |
| υ | velocity of the vehicles (km/h) |
| L | geometric curve wavelength of the pavement (m) |
| t | duration time of load (s) |
| σe | vertical stress at the base of the embankment (including the effect of arching) (kN/m2) |
| σr | vertical stress carried by the reinforcement (kPa) |
| σs | vertical stress carried by the subsoil (kPa) |
| y | maximum sag in reinforcement (m) |
| ks | ‘subgrade reaction’ at the surface of the subsoil (kN/m2/m) |
| γ | unit weight (kN/m3) |
| c’ | cohesion (kPa) |
| E | Young’s modulus (MPa) |
| E0 | one-dimensional subsoil stiffness (MPa) |
| Ψ | dilation angle (degrees) |
| μ | Poisson’s ratio |
| k | permeability coefficient (m/d) |
| δ | settlement of the embankment (mm) |
References
- Han, J.; Gabr, M.A. Numerical analysis of geosynthetic-reinforced and pile-supported earth platforms over soft soil. J. Geotech. Geoenviron. Eng. 2002, 128, 44–53. [Google Scholar] [CrossRef]
- Liu, H.L.; Ng, C.W.; Fei, K. Performance of a geogrid-reinforced and pile-supported highway embankment over soft clay: Case study. J. Geotech. Geoenviron. Eng. 2007, 133, 1483–1493. [Google Scholar] [CrossRef]
- Briancon, L.; Simon, B. Performance of pile-supported embankment over soft soil: Full-scale experiment. J. Geotech. Geoenviron. Eng. 2012, 138, 551–561. [Google Scholar] [CrossRef]
- Liu, H.L.; Kong, G.Q.; Chu, J.; Ding, X.M. Grouted gravel column supported highway embankment over soft clay: Case study. Can. Geotech. J. 2015, 52, 1725–1733. [Google Scholar] [CrossRef]
- Liu, C.Y.; Shan, Y.; Wang, B.L.; Zhou, S.H.; Wang, C.D. Reinforcement load in geosynthetic-reinforced pile-supported model embankments. Geotext. Geomembr. 2022, 50, 1135–1146. [Google Scholar] [CrossRef]
- Jelušic, P.; Žlender, B. Optimal design of piled embankmentswith basal reinforcement. Geosynth. Int. 2018, 25, 150–163. [Google Scholar] [CrossRef]
- Al-Naddaf, M.; Han, J.; Xu, C.; Jawad, S.; Abdulrasool, G. Experimental investigation of soil arching mobilization and degradation under localized surface loading. J. Geotech. Geoenviron. Eng. 2019, 145, 04019114. [Google Scholar] [CrossRef]
- Van Eekelen, S.J.M.; Han, J. Geosynthetic-reinforced pile-supported embankments: State of the art. Geosynth. Int. 2020, 27, 112–141. [Google Scholar] [CrossRef]
- Ghosh, B.; Fatahi, B.; Khabbaz, H.; Nguyen, H.H.; Kelly, R. Field study and numerical modelling for a road embankment built on soft soil improved with concrete injected columns and geosynthetics reinforced platform. Geotext. Geomembr. 2021, 49, 804–824. [Google Scholar] [CrossRef]
- Pham, T.A.; Dias, D. Comparison and evaluation of analytical models for the design of geosynthetic-reinforced and pile-supported embankments. Geotext. Geomembr. 2021, 49, 528–549. [Google Scholar] [CrossRef]
- van Eekelen, S.J.M.; Bezuijen, A.; van Tol, A.F. An analytical model for arching in piledembankments. Geotext. Geomembr. 2013, 39, 78–102. [Google Scholar] [CrossRef]
- van Eekelen, S.J.M.; Bezuijen, A.; van Tol, A.F. Validation ofanalytical models for the design of basal reinforced piled embankments. Geotext. Geomembr. 2015, 43, 56–81. [Google Scholar] [CrossRef]
- Fagundes, D.F.; Almeida, M.S.S.; Thorel, L.; Blanc, M. Loadtransfer mechanism and deformation of reinforced piled embankments. Geotext. Geomembr. 2017, 45, 1–10. [Google Scholar] [CrossRef]
- King, D.J.; Bouazza, A.; Gniel, J.R.; Rowe, R.K.; Bui, H.H. Serviceability design for geosynthetic reinforced columnsupported embankments. Geotext. Geomembr. 2017, 45, 261–279. [Google Scholar] [CrossRef]
- Feng, S.J.; Ai, S.G.; Chen, H.X. Membrane effect of geosynthetic reinforcement subjected to localized sinkholes. Can. Geotech. J. 2018, 55, 1334–1348. [Google Scholar] [CrossRef]
- Chalak, C.; Briancon, L.; Villard, P. Coupled numerical and experimental analyses of load transfer mechanismsin granular-reinforced platform overlying cavities. Geotext. Geomembr. 2019, 47, 587–597. [Google Scholar] [CrossRef]
- Pham, T.A. Analysis of geosynthetic-reinforced pile-supported embankment with soil-structure interaction models. Comput. Geotech. 2020, 121, 103438. [Google Scholar] [CrossRef]
- Zhang, C.F.; Zhao, M.H.; Zhao, H.; Zhou, S. Simplified Model of Column-Supported Embankment to Account for Nonuniform Deformations of Soils. J. Eng. Mech. 2020, 146, 4020060. [Google Scholar] [CrossRef]
- Rui, R.; Ye, Y.Q.; Han, J.; Zhai, Y.X.; Wan, Y.; Chen, C.; Zhang, L. Two-dimensional soil arching evolution in geosynthetic-reinforced pile-supported embankments over voids. Geotext. Geomembr. 2022, 50, 82–98. [Google Scholar] [CrossRef]
- Terzaghi, K. Theoretical Soil Mechanics; Wiley: New York, NY, USA, 1943. [Google Scholar]
- Hewlett, W.J.; Randolph, M.F. Analysis of piled embankments. Ground Eng. 1988, 21, 12–18. [Google Scholar]
- Zhuang, Y.; Ellis, E.A. Finite-element analysis of a piledembankment with reinforcement compared with BS 8006 predictions. Géotechnique 2014, 64, 910–917. [Google Scholar] [CrossRef]
- Zhuang, Y.; Wang, K.Y. Analytical Solution for Reinforced Piled Embankments on Elastoplastic Consolidated Soil. Int. J. Geomech. 2017, 17, 04016011. [Google Scholar] [CrossRef]
- Lai, H.J.; Zheng, J.J.; Zhang, R.J.; Cui, M.J. Classification and characteristics of soil arching structures in pile-supported embankments. Comput. Geotech. 2018, 98, 153–171. [Google Scholar] [CrossRef]
- Rui, R.; Han, J.; van Eekelen, S.J.M.; Wan, Y. Experimental investigation of soil-arching development in unreinforced and geosynthetic-reinforcedpile-supported embankments. J. Geotech. Geoenviron. Eng. 2019, 145, 04018103. [Google Scholar] [CrossRef]
- Tran, Q.A.; Villard, P.; Dias, D. Discrete and continuum numerical modeling of soil arching between piles. Int. J. Geomech. 2019, 19, 04018195. [Google Scholar] [CrossRef]
- Lai, H.J.; Zheng, J.J.; Cui, M.J.; Chu, J. “soil arching” for piled embankments: Insights from stress redistribution behaviour of DEM modelling. Acta Geotech. 2020, 15, 2117–2136. [Google Scholar] [CrossRef]
- Meena, N.K.; Nimbalkar, S.; Fatahi, B.; Yang, G. Effects of soil arching on behavior of pile-supported railway embankment: 2D FEM approach. Comput. Geotech. 2020, 123, 103601. [Google Scholar] [CrossRef]
- Lv, W.H.; Wu, T.; Gu, F.; Gao, L. Evaluation of soil arching effect due to partially mobilized shear stress in piled and geosynthetic-reinforced embankment. J. Cent. South Univ. 2020, 27, 2094–2112. [Google Scholar] [CrossRef]
- Wang, K.; Cao, J.; Wang, X.; Ning, Y. Soil Arching of Piled Embankment in Equal Settlement Pattern: A Discrete Element Analysis. Symmetry 2021, 13, 1627. [Google Scholar] [CrossRef]
- BS8006; Code of Practice for Strengthened/Reinforced Soils and Other Fills, vol. 1. British Standards Institution: London, UK, 2010.
- EBGEO. Recommendations for Design and Analysis of Earth Structures Using Geosynthetic Reinforcements; EBGEO: San Ramon, CA, USA, 2011; ISBN 978-3-433-02983-1. [Google Scholar]
- Zhuang, Y.; Wang, K.Y.; Liu, H.L. A simplified model to analyse the reinforced piledembankments. Geotext. Geomembr. 2014, 42, 154–165. [Google Scholar] [CrossRef]
- Zhuang, Y.; Wang, K.Y. Three-dimensional behavior of biaxial geogrid in a piled embankment: Numerical investigation. Can. Geotech. J. 2015, 52, 1629–1635. [Google Scholar] [CrossRef]
- Zhuang, Y.; Ellis, E.A. Finite-element analysis of a piled embankment with reinforcement and subsoil. Géotechnique 2016, 66, 596–601. [Google Scholar] [CrossRef]
- Wang, H.L.; Chen, R.P.; Liu, Q.W.; Kang, X. Investigation on geogrid reinforcement and pile efficacy in geosynthetic-reinforced pile-supported track-bed. Geotext. Geomembr. 2019, 47, 755–766. [Google Scholar] [CrossRef]
- Zhao, L.S.; Zhou, W.H.; Geng, X.; Yuen, K.V.; Fatahi, B. A closed-form solution for column-supported embankments with geosynthetic reinforcement. Geotext Geomembr 2019, 47, 389–401. [Google Scholar] [CrossRef]
- Xu, C.; Liang, C.; Shen, P.P.; Chai, F. Experimental and numerical studies on the reinforcing mechanisms of geosynthetic-reinforced granular soil under a plane strain condition. Soils Found. 2020, 60, 466–477. [Google Scholar] [CrossRef]
- Zhuang, Y.; Cheng, X.T.; Wang, K.Y. Analytical solution for geogrid-reinforced piled embankments under traffic loads. Geosynth. Int. 2020, 27, 249–260. [Google Scholar] [CrossRef]
- Zhang, J.; Jia, Y.; Zheng, Y.; Miao, C. DEM Simulation of the Load Transfer Mechanism of a GRPS Embankment with a Fixed Geogrid Technique. Appl. Sci. 2021, 11, 8814. [Google Scholar] [CrossRef]
- Hu, S.; Zhuang, Y.; Zhang, X.; Dong, X. A Design Chart for the Analysis of the Maximum Strain of Reinforcement in GRPEs Considering the Arching and Stress History of the Subsoil. Appl. Sci. 2022, 12, 2536. [Google Scholar] [CrossRef]
- Heitz, C.; Lüking, J.; Kempfert, H.G. Geosynthetic reinforced and pile supported embankments under static and cyclic loading. In Proceedings of the 4th European Geosynthetics Conference, EuroGeo 4, Edinburgh, UK, 7–10 September 2008; International Geosynthetics Society (CD-ROM): Jupiter, FL, USA, 2008. [Google Scholar]
- Han, J.; Bhandari, A. Evaluation of geogrid-reinforced pile-supported embankments under cyclic loading using discrete element method. US-China Workshop Ground Improv. Technol. 2009, 188, 73–82. [Google Scholar]
- Thach, P.N.; Liu, H.L.; Kong, G.Q. Evaluation of PCC pile method in mitigating embankment vibrations from a high-speed train. J. Geotech. Geoenviron. Eng. 2013, 139, 2225–2228. [Google Scholar] [CrossRef]
- Han, G.X.; Gong, Q.M.; Zhou, S.H. Soil arching in a piled embankment under dynamic load. Int. J. Geomech. 2015, 15, 04014094. [Google Scholar] [CrossRef]
- Zhai, W.; Wei, K.; Song, X.; Shao, M. Experimental investigation into ground vibrations induced by very high speed trains on a non-ballasted track. Soil Dyn. Earthq. Eng. 2015, 72, 24–36. [Google Scholar] [CrossRef]
- Chen, R.P.; Wang, Y.W.; Ye, X.W.; Bian, X.C.; Dong, X.P. Tensile force of geogrids embedded in pile-supported reinforced embankment: A full-scale experimental study. Geotext. Geomembr. 2016, 44, 157–169. [Google Scholar] [CrossRef]
- Messioud, S.; Okyay, U.S.; Sbartai, B.; Dias, D. Dynamic response of pile reinforced soils and piled foundations. Geotech. Geol. Eng. 2016, 34, 789–805. [Google Scholar] [CrossRef]
- Pham, H.V.; Dias, D. 3D numerical modeling of a piled embankment under cyclic loading. Int. J. Geomech. 2019, 19, 04019010. [Google Scholar] [CrossRef]
- Wang, H.L.; Chen, R.P. Estimating static and dynamic stresses in geosynthetic-reinforced pile-supported track-bed under train moving loads. J. Geotech. Geoenviron. Eng. 2019, 145, 04019029. [Google Scholar] [CrossRef]
- Wang, K.Y.; Zhuang, Y.; Liu, H.L.; Miao, Y. Soil arching in highway piled embankments subjected to moving shakedown limit loads. Eur. J. Environ. Civ. Eng. 2020, 24, 1120–1134. [Google Scholar] [CrossRef]
- Zhuang, Y.; Wang, K.Y. Finite-element analysis of arching in highway piled embankments subjected to moving vehicle loads. Geotechnique 2018, 68, 857–868. [Google Scholar] [CrossRef]
- Navas, P.; Yu, R.C.; López-Querol, S.; Li, B. Dynamic consolidation problems in saturated soils solved through u–w, formulation in a LME meshfree framework. Comput. Geotech. 2016, 79, 55–72. [Google Scholar] [CrossRef]
- Potyondy, J.G. Skin friction between various soils and construction materials. Geotechnique 1961, 11, 339–353. [Google Scholar] [CrossRef]
- Huang, Y.H. Pavement Analysis and Design; Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
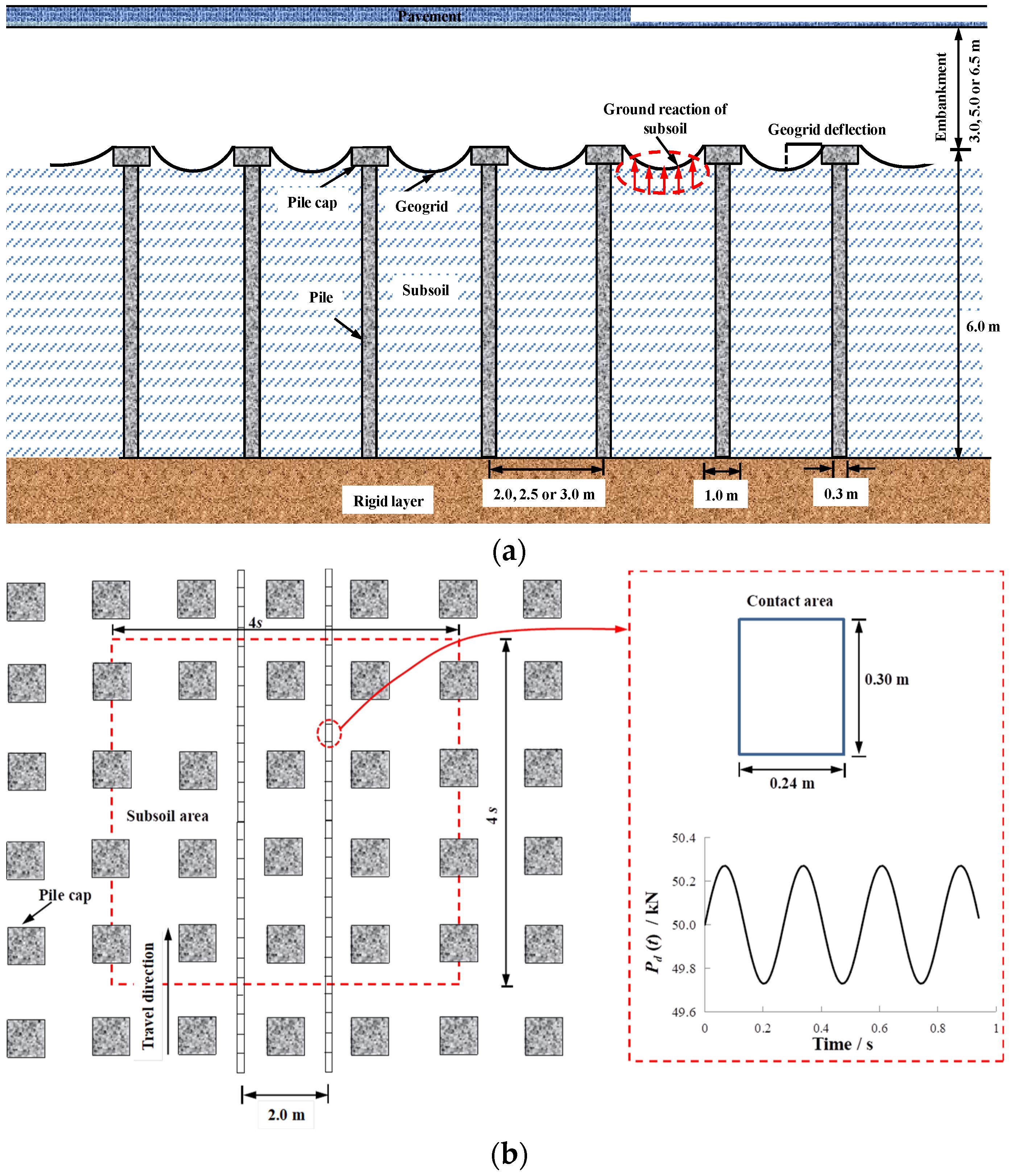
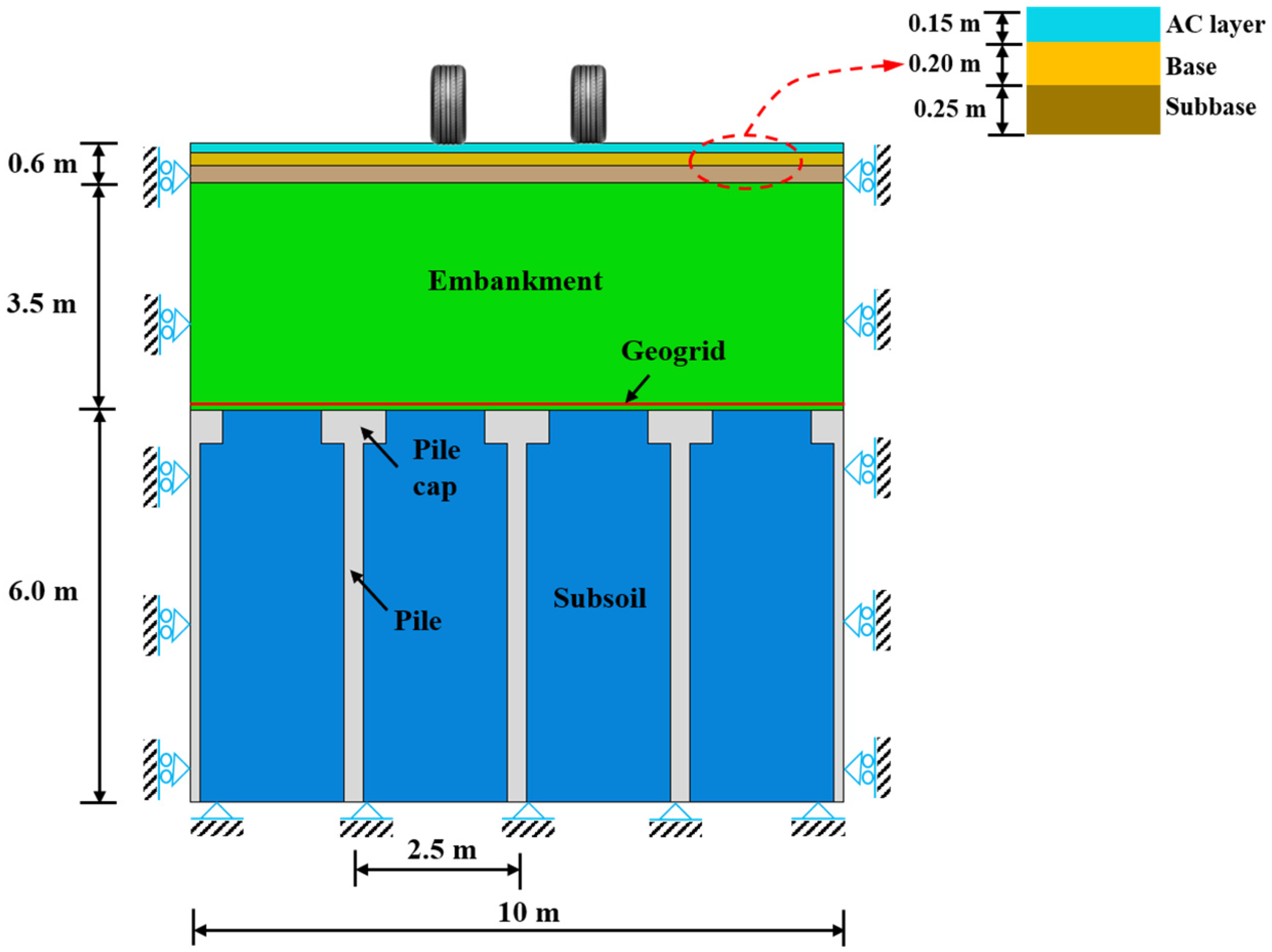
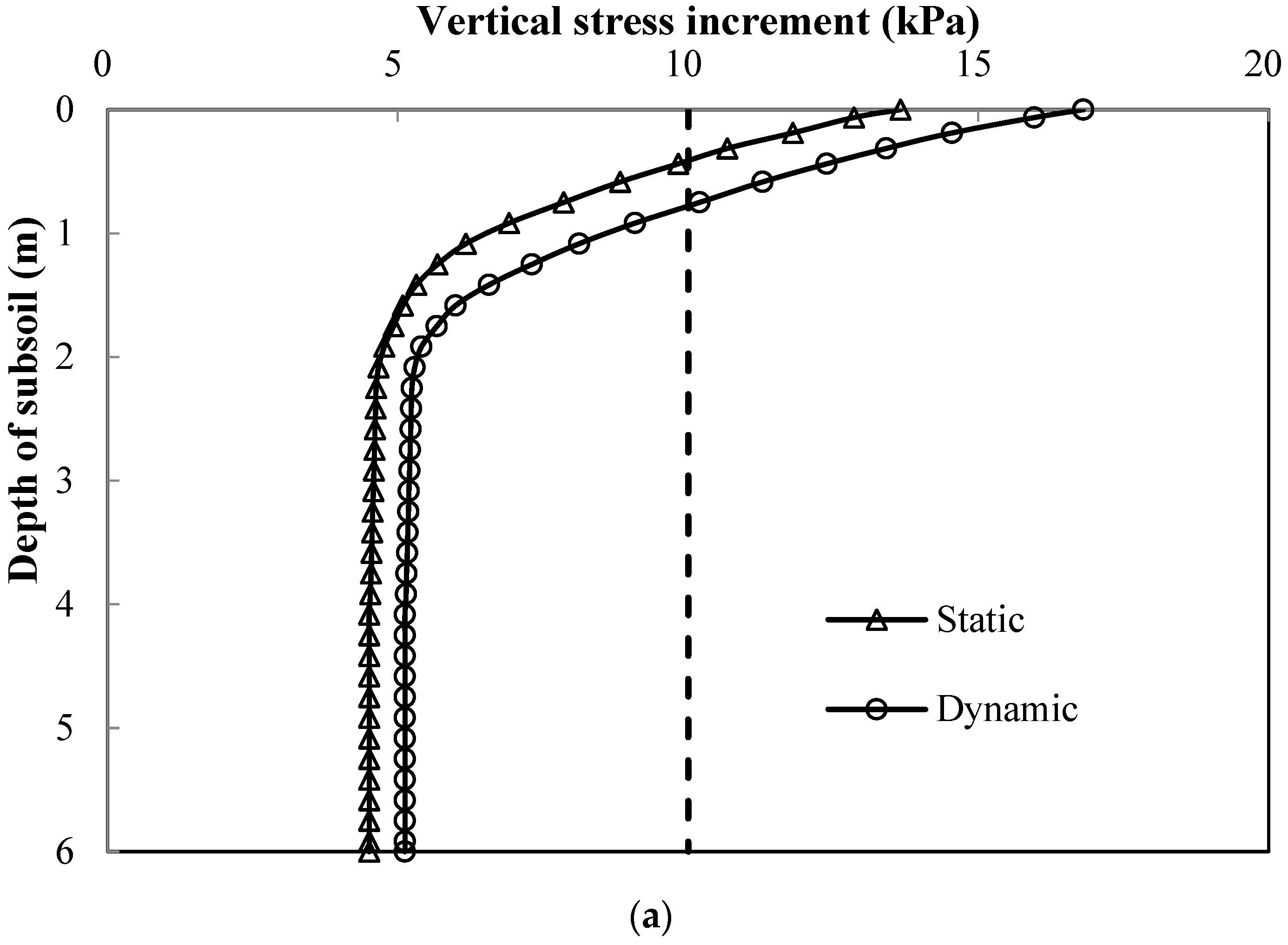
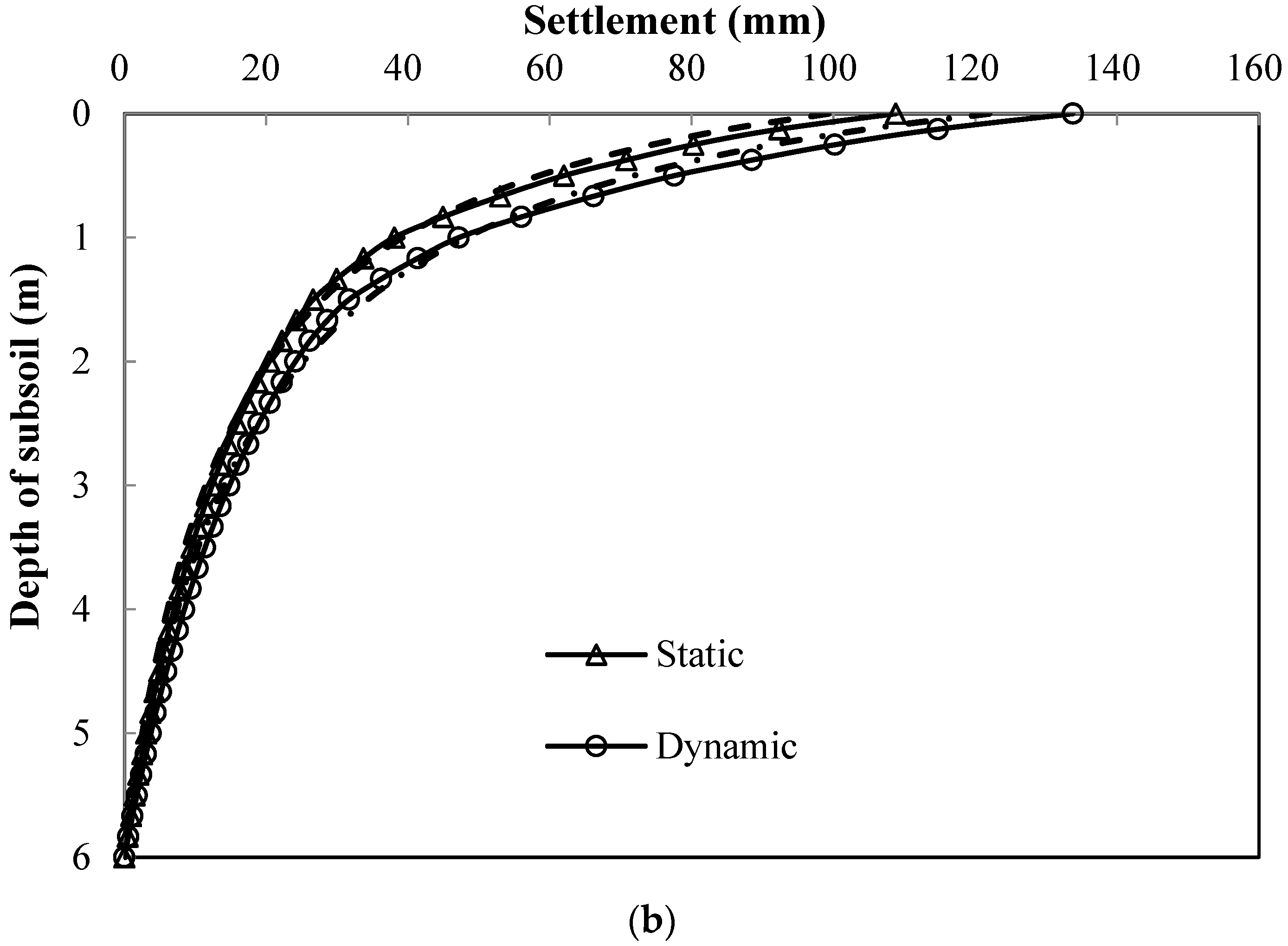


| h (m) | γ (kN/m3) | c’ (kPa) | φ’ (Degree) | E (MPa) | Ψ (Degree) | μ | Cc | M | e0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| AC layer | 0.15 | 21.0 | - | - | 4000 | - | 0.25 | - | - | - |
| Base | 0.20 | 20.0 | - | - | 1000 | - | 0.25 | - | - | - |
| Subbase | 0.25 | 18.0 | - | - | 500 | - | 0.25 | - | - | - |
| Embankment | 3.5, 5.0 or 6.5 | 17.0 | 1, 5 or 10 | 30, 35 or 40 | 25, 40 or 50 | 0, 10, 20 or 22 | 0.20 | - | - | - |
| Pile | 6.00 | 23.5 | - | - | 20,000 | - | 0.20 | - | - | - |
| Subsoil | 6.00 | 17.0 | - | 26 | - | - | 0.30 | 0.3, 0.7, 1.0 or 1.5 | 1.03 | 1.79 |
| Geogrid | Tensile stiffness J = 0, 1, 3 or 10 MN/m, v = 0 | |||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, Y.; Song, X.; Wang, K. Ground Reaction of Lightly Overconsolidated Subsoil in Reinforced Piled Embankment under Cyclic Loads. Sustainability 2023, 15, 619. https://doi.org/10.3390/su15010619
Zhuang Y, Song X, Wang K. Ground Reaction of Lightly Overconsolidated Subsoil in Reinforced Piled Embankment under Cyclic Loads. Sustainability. 2023; 15(1):619. https://doi.org/10.3390/su15010619
Chicago/Turabian StyleZhuang, Yan, Xiangwei Song, and Kangyu Wang. 2023. "Ground Reaction of Lightly Overconsolidated Subsoil in Reinforced Piled Embankment under Cyclic Loads" Sustainability 15, no. 1: 619. https://doi.org/10.3390/su15010619
APA StyleZhuang, Y., Song, X., & Wang, K. (2023). Ground Reaction of Lightly Overconsolidated Subsoil in Reinforced Piled Embankment under Cyclic Loads. Sustainability, 15(1), 619. https://doi.org/10.3390/su15010619








