Abstract
A hybrid model was developed by combining multiple-criteria decision-making (MCDM) with the analytic hierarchy process (AHP) and a fuzzy set to give decision support for choosing sustainable solutions to agricultural problems. Six steps were taken to build the suggested hybrid model: identifying and weighing criteria; normalizing data using fuzzy membership functions; calculating the weighting of the criteria using AHP; and selecting the best alternative for the agricultural problem. The objective of this case study is to demonstrate how agricultural production techniques (APTs) are becoming more complex as agricultural production becomes more complex. Organic agriculture aims to protect both the environment and consumer satisfaction by utilizing organic management practices that do not have the negative effects associated with conventional and genetic engineering production. Meanwhile, products obtained through conventional and genetic engineering techniques are more cost-effective. To present the superiority of the proposed fuzzy MCDM hybrid model, this problem is used as the causative agent’s dataset. Because the challenge involves a large number of competing quantitative and qualitative criteria, the assessment approach should improve the ratio of input data to output data. As a result, agricultural productivity should be controlled holistically. However, because the problem may contain both qualitative and quantitative facts and uncertainties, it is necessary to represent the uncertainty inherent in human thinking. To achieve superior outcomes, fuzzy set theory (FST), which enables the expression of uncertainty in human judgments, can be integrated with). The purpose of this study is to present a novel MCDM approach based on fuzzy numbers for analyzing decision-making scenarios. The proposed methodology, which is based on Buckley’s fuzzy analytic hierarchy process (B-FAHP) and the Fuzzy Technique for Order of Preference by Similarity to Ideal Solution (F-TOPSIS), uses Buckley’s fuzzy analytic hierarchy process (B-FAHP) and fuzzy TOPSIS to determine weights and rank alternatives, respectively. As a result, we attempted to include both the uncertainty and hesitancy of experts in the decision-making process through the use of fuzzy numbers. We have three main criteria in this study: Satisfaction (C1), Economy (C2), and Environment (C3). An important objective of the current research is to build a complete framework for evaluating and grading the suitability of technologies. A real-world case study is used to demonstrate the suggested paradigm’s validity.
1. Introduction
The current agricultural system, often referred to as conventional or industrial farming, has resulted in enormous gains in production and efficiency. International food production has increased over the past 50 years; the World Bank estimates that conventional agriculture, rather than increased land under cultivation, accounts for between 70% and 90% of recent increases in food output. Agriculture in the traditional sense varies by farm and country. Different farms do, however, share a number of traits, including fast technical innovation, large-scale farms, monocultures (single crops), uniform high-yield hybrid crops, reliance on agribusiness, farm mechanization, and extensive use of pesticides, fertilizers, and herbicides [1]. Despite these benefits, conventional agriculture contributes to environmental and social challenges, and the effect of conventional agricultural products on human health is debatable.
Along with conventional farms (industrial agriculture), scientists began experimenting with agricultural genetic engineering. As a result of this technological advancement, farmers began employing genetically modified seeds in agriculture. Increased crop yields, lower food costs, less reliance on pesticides, increased nutritional content and food quality, pest and disease resistance, and increased food security for the world’s growing population are just a few of the benefits of agricultural genetic engineering. Crops that mature faster and are more resistant to aluminum, boron, salt, drought, and cold have also been developed, allowing plants to survive in environments where they would not thrive ordinarily [2]. However, there are risks and disagreements involved with the use of GMOs, including potential adverse impacts on human health or the environment.
Organic farming aims to protect the environment by avoiding the negative consequences associated with conventional and genetically altered agricultural techniques, as well as to satisfy customers by providing organic products. Food safety demand has grown in lockstep with rising environmental concern, resulting in an increase in demand for organic goods. Organic agriculture has been shown to improve soil fertility and biodiversity [3]. For instance, a meta-analysis comparing conventional and organic farms discovered that organic farms had a greater soil organic matter content and had less nutrient loss [4]. As a result, it is anticipated that organic agricultural systems would be able to counteract climate change while still ensuring food security [5].
Despite the numerous benefits of organic farming, organic food is more expensive than conventional food since farmers obtain less from their land than conventional farmers do and also require more labor. Food poisoning might become increasingly prevalent. Organic food is more difficult to sell and distribute than conventional food since it is produced in lower quantities. Organic farming is incapable of providing enough food to sustain the world’s population.
MCDM is a method for choosing the best possible alternative from a large number of candidates based on a set of criteria or attributes. In recent years, interest in studies of MCDM challenges has increased, notably in the field of operations research. Due to a lack of information about the situation, the existence of a number of criteria with variable degrees of significance, and the difficulty of determining whether one criterion is important to another, these decisions are complicated in nature [6].
Everyday decision-making is important. While one-on-one comparisons seem to work well in ordinary life, they do not work well in business. Problems in company management are more complex than in personal life since most business scenarios include multiple-criteria decision-making (MCDM). To tackle these issues, multiple-criteria decision procedures should be properly chosen [7].
Many real-world decision-making problems cannot be handled using a hierarchical structure due to the interactions and dependencies between criteria. In this case, the abovementioned assumption is incorrect, and it may result in irrational action. As a result, it is necessary to define the MCDM issue in terms of a network structure. It is possible to overcome the drawbacks of the AHP approach using the TOPSIS method.
To achieve the required weighting of criteria, it is important to employ an efficient tool in combination with the TOPSIS technique. As a result, while selecting the optimal option, it is usually utilized in combination with other MCDM approaches. AHP and TOPSIS, for example, were used to rate the choices in a ranking procedure [8].
AHP is a decision science technique that was developed to address the numerous criterion problems that arise when quantitative or qualitative data are used (Saaty, 1980). MCDM has a number of applications in which issues are represented as hierarchical forms with unidirectional hierarchical relationships. The primary AHP procedures include creating a problem hierarchy, evaluating characteristics and sub-attributes relative to one another, establishing priorities, and ranking them overall [9].
As a case study, this article describes a two-step hybrid fuzzy decision-making procedure that uses fuzzy numbers to determine the best agricultural production type for a specific condition. It was believed that by implementing a two-phased and more comprehensive plan, economic, environmental, and social factors as well as technical criteria would be integrated into the decision-making environment for this problem. Furthermore, by utilizing fuzzy numbers, the authors have included the experts’ hesitation as well as the process’s ambiguity in a manner that varies from that seen in the literature. The criterion weights were determined in both hybrid approaches utilizing Buckley’s fuzzy AHP (B-FAHP) methodology and the fuzzy TOPSIS (F-TOPSIS) technique, respectively.
The rest of this paper is structured as follows: Section 2 is a review of important existing literature. Section 3 describes the specifics of the proposed combination of the B-FAHP and fuzzy TOPSIS approaches. Section 4 mathematically explains the agricultural method selection problem. Section 5 presents the experimental findings, and Section 6 contains conclusions and a discussion about possible future research.
2. Literature Review
This section conducts a comprehensive analysis of the literature about agricultural production technology selection. Additionally, we know that much of the research on agricultural production technique determination has been conducted using quantitative techniques. This section contains research that was conducted using a quantitative decision-making approach that included a hierarchy of evaluation criteria:
- (i).
- What criteria have been chosen for evaluating the agricultural production technique determination process?
- (ii).
- What method(s) is (are) being employed to resolve the issue?
- (ii).
- What data types are considered input?
- (iv).
- What uncertainties are inherent considering the problem environment?
Thus, we aim to reveal any applicability gaps between our study and past studies by evaluating the replies to the first two questions. Similarly, the responses to the other questions are analyzed to determine methodological issues. A comprehensive decision-making framework and a unique technique were developed based on the findings of the literature review. Three factors were considered throughout the review process: recent publications, journals published, and the number of citations. The first factor is based on studies published since 2010. Then, publications are ranked by their impact factors and indexing categories. Finally, the papers are ordered by their number of citations. To begin, criteria for assessing the approach to determining agricultural production technology were gathered. We gathered various parameters and created a comprehensive decision-making structure for agricultural production technology selection. Numerous articles published in the past few years have included a range of decision-making approaches based on classical and fuzzy sets. Table 1 summarizes the literature on the application of conventional and fuzzy decision-making methodologies.

Table 1.
Summary of supplier selection literature review.
MCDM techniques employ structured procedures and algorithms to determine the optimal response to a diverse set of facts, values, and stakeholder views. These tactics, in general, seek to eliminate ambiguity in decision-making. Thus, uncertainty has been considered in relation to MCDM and its numerous applications. A comprehensive examination of the multiple sources of uncertainty in environmental choices impacting MCDM outcomes is uncommon [10].
Besides the importance of raising agricultural production yields in national agricultural policies, agricultural production methods are acquiring growing value in terms of customer satisfaction, the agriproduct’s basic price ratio, and environmental effects. Similarly, Sarper Alem (2020) examined four distinct agricultural practices: “conventional farming”, “artificial intelligence-assisted farming”, “vertical farming”, and “plant-based meat”, with a particular focus on cost and “ecological” and “consumer” issues. Because no correlation between these criteria was identified, the factor weights were calculated using the interval type-2 fuzzy analytic hierarchy process. After obtaining weights, the alternatives were ranked using hesitant fuzzy TOPSIS. To account for the decision’s complexity and uncertainty, two separate multiple-criteria decision-making models were proposed [11]. Agricultural goods are analyzed from a range of angles, and a variety of methodologies are utilized to optimize agricultural output. For example, Zandi et al. (2020) used a fuzzy technique to manage agricultural risks, and their study aimed to expand the use of FMEA to agricultural risk management [12].
Ren et al. (2018) developed an enhanced multi-objective stochastic fuzzy programming technique that enables decision-makers to make logical irrigation water and land resource allocation decisions [13]. Pilevar et al. (2019) established an integrated fuzzy AHP and GIS approach for determining the suitability of land for wheat and maize growth in semi-arid regions [14]. Firdaus et al. (2020) created a strategy for organic agricultural development in Bengkulu Province. To determine the optimal strategy for developing organic agriculture, their study used a fuzzy analytical hierarchy process (fuzzy AHP).
The following techniques were ranked as a result of a previous study that used fuzzy AHP: (1) developing a competitive, export-oriented organic product; (2) assisting in the development and marketing of organic goods; and (3) establishing community-supported organic agriculture [15]. Tashayo et al. (2020) modeled agricultural land suitability for a watershed in Southern Iran using a combination of fuzzy AHP and GIS [16]. Mohammad Rezaei et al. (2014) [17] studied the efficacy of the fuzzy approach, AHP, and Simul weighting techniques for wheat cultivation in Urmia’s Southern Plain. Rahimabadi et al. (2021) used fuzzy AHP and PROMETHEE II to estimate the ecological agricultural production of Eshtehard, Iran. As a consequence, the ecological potential of the land was determined using ecological criteria in combination with the PROMETHEE II and fuzzy AHP methods. Their study’s findings demonstrated the efficacy of combining PROMETHEE II and fuzzy AHP for assessing an area’s ecological potential [18]. Demirel et al. (2012) proposed a model for creating an agricultural plan for Turkey based on linguistic notions using fuzzy AHP and an analytical network approach (ANP). The authors discussed a fuzzy AHP-based technique for addressing the numerous selection factors involved in agricultural strategy selection, such as risk considerations, ecological structure, socioeconomic structure, and technological structure [19].
3. Methodology
This section introduces the suggested approach, which is based on fuzzy numbers and was developed to aid in the selection of agricultural production techniques in Turkey. The methodology described here is based on the B-FAHP and F-TOPSIS methodologies. Following a fundamental definition of the fuzzy number idea, the steps of the B-FAHP and F-TOPSIS processes, improved with fuzzy numbers, were addressed. Following that, the proposed approach was developed in further detail. The purpose of this study was to develop a hybrid MCDM model for agricultural selection using an AHP-based fuzzy set in combination with a TOPSIS-based fuzzy set.
3.1. FST
Zadeh (1965) developed fuzzy set theory (FST) to address imprecision and uncertainty. The primary contribution of this theory is the capacity to characterize ambiguous data and to apply mathematical operations and programming to the fuzzy domain. An FS is a collection of goods with varying membership degrees. Each object is assigned a membership grade between zero and one via a membership function [20,21,22].
Tildes “∼” are placed over symbols that signify FSs. Figure 1 shows a TFN. The TFN is (l/m,m/u) or (l,m,u). The parameters l, m, and u represent the least promising, most promising, and greatest potential values for a fuzzy event. The TFN’s membership function is:
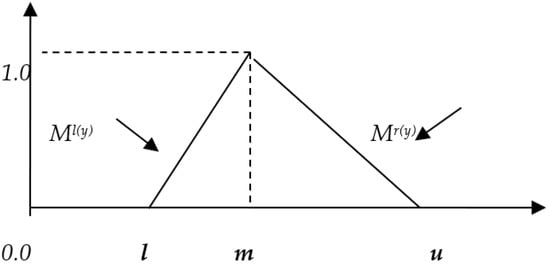
Figure 1.
The TFN .
Each TFN has a linear representation, so its membership function is:
The fuzzy number’s left and right representations of each degree of membership are as follows:
where l(y) and r(y) are the left- and right-side representations of a fuzzy number (FN). Many FN ranking systems exist in the literature. These methods yield varying rankings, and most require difficult mathematical calculations [23].
While there are several operations that can be performed on TFNs, only the most critical ones are illustrated in this study. If two positive TFNs are defined as:
(l1, m1, u1) and (l2, m2, u2), then (l1, m1, u1) + (l2, m2, u2) = (l1 + l2, m1 + m2, u1 + u2)
(l1, m1, u1) × (l2, m2, u2) = (l1 × l2, m1 × m2, u1 × u2),
(l1, m1, u1) + k = (l1 × k, m1 × k, u1 × k), where k > 0.
3.2. Fuzzy AHP
AHP is a quantifiable approach for structuring multi-person situations hierarchically in order to simplify solutions. While this approach works well with both qualitative and quantitative data, it cannot accurately reflect human thinking styles. Intermittent evaluations are typically more dependable for the decision-maker than definitive evaluations [24]. AHP is the most often used approach within MCDM. Saaty developed it to provide a consistent and simple method for analyzing complicated circumstances. It compares possible pairings in order to weight each factor and calculate a consistency ratio for a complicated circumstance. AHP employs a tree structure to decompose big issues into more manageable subproblems.
The procedure has four major steps:
- Creating a tree structure with one aim, criteria, and solutions.
- Evaluating options by each criterion.
- Pairwise comparisons with subjective weighting factor computation
- Synthesis of results from stages 2 and 3 to compute total evaluation of options based on goal achievement.
One of AHP’s key features is its multiple-criteria decision-making tool. The approach compares the relative weights of factors to define priorities and make the optimal decision [25]. AHP is a valuable logical technique for resolving a variety of MCDM issues in a wide variety of technological and scientific disciplines. AHP is especially advantageous for decision-making, including subjective judgment, because it may combine both concrete and intangible factors [6].
To deal with uncertainty, AHP was extended to fuzzy sets theory, and fuzzy AHP (FAHP) was formed. FAHP has been used to evaluate the quality of in-flight service, categorize container terminals, and perform traffic accessibility criterion prioritization. We selected Buckley’s (1985) technique due to its low level of criticism in the literature. Application procedure.
Due to AHP’s simplicity, ease of implementation, and adaptability, it has become a highly effective logical solution for MCDM problems in a wide variety of domains of technology and research. AHP has the advantage of incorporating both concrete and intangible components in decision-making procedures that require subjective judgments.
The AHP technique appears to be very beneficial in assisting with goal prioritization and overall impact assessments.
To determine the priority of the objectives, managers from various departments were examined individually. The AHP method was used to prioritize objectives and align them with various perspectives. The AHP process included the following steps:
- (1)
- examining the “criticalities” affecting the objectives in order to identify their relevance;
- (2)
- quantifying the importance of each objective in respect to the others; and
- (3)
- determining the objective weights [8].
The AHP method is generally divided into three steps as follows:
As a result, AHP is being developed using fuzzy sets to address hierarchical fuzzy difficulties.
The FAHP approach is divided into various phases. There are several methods for allocating weights to criteria based on their relative relevance. Buckley’s technique [26] was used to determine the fuzzy priority of comparison ratios with triangle membership functions.
The steps of the procedure are as follows:
Step 1: Triangular fuzzy (TF)
The fuzziness of a pairwise comparison matrix is increased. Using linguistic notions, DMs construct a pairwise comparison matrix. Anagnostopoulos et al. (2007) converted replies to fuzzy integers using a nine-point scale [27] (see Table 2).

Table 2.
Linguistic factors for assessing the relative importance of criteria (Adapted from Refs. [26,28]).
Table 2 shows how decision-makers compare the criteria in terms of linguistic terms and their TF scale.
The pairwise contribution matrices are depicted in Equation (6).
Step 2: The average calculation of choices of decision-makers (ACCDM)
If there are several decision-makers, the ACCDM () is calculated, as shown in Equation (7).
On the basis of Equation (8), the pairwise contribution matrices are updated in this context.
Step 3: Geometric mean (GM)
To paraphrase Buckley, the generalized mean is calculated for fuzzy comparison values of all criteria, as indicated in Equation (9).
Step 4: Calculation of Fuzzy Weight of Criterion (FWC)
The FWC as defined in Equation (10) should be found, as well as the steps. Vector summation is found for each .
After determining the inverse of vector summation, the FT number is modified. is multiplied by the reverse vector to obtain FWC.
Step 5: Average of the Fuzzy Weight of the Criterion (AFWC)
The AFWC is calculated.
Step 6: Normalization Mi
The normalization of Mi is calculated.
3.3. Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS)
Each plan is then compared to the ideal and worst hypothesized plans in order to decide which is the best. TOPSIS is a frequently utilized evaluation technique for multi-objective decision-making in transportation. It is increasingly utilized throughout the risk assessment process. This technique requires little more than fundamental mathematics and thinking, so it can be regarded as simple. This is referred to in this instance as the fuzzy TOPSIS technique. It performs computations identical to those of TOPSIS. It proceeds as detailed in [29].
Hwang and Yoon [30] created TOPSIS, an MCDM technique based on the positive ideal solution (PIS) and negative ideal solution (NIS). The PIS maximizes benefit while minimizing cost, whereas the NIS minimizes benefit while maximizing cost [31,32].
Assume there are m units, A = {A1, …, Am} and each unit evaluates n distinct decision criteria. In general, each choice is weighed against the n criteria.
Assume C is a collection of criteria. TOPSIS is managed in six steps as follows:
Step 1: Create a decision matrix and assign a weight to each criterion
Create a decision matrix with m possibilities and n criteria, guided by each alternative and criterion.
Step 2: Calculation of a decision matrix with a normalized decision matrix
All values can be normalized using several standardized forms. Some of the most prominent ways are the following:
where
Step 3: Determine the weighted normalized decision matrix
To obtain the weighted normalized decision matrix, multiply each column of the R matrix by the wi value.
Step 4: Determine a positive ideal solution (PIS) and negative ideal solution (NIS)
Determine the PIS and NIS. The PIS is the solution that maximizes benefit and minimizes expense, whereas the NIS maximizes cost and minimizes benefit.
PIS
NIS
where i is the benefit criteria and j is the cost criteria, respectively.
Step 5: Calculate the separation of each alternative
The separation of each alternative is applied to calculate the measures and and for each of the units is given as
Step 6: Calculate the solution’s relative proximity to the ideal solution
The alternative’s relative proximity is shown by the following:
3.4. Fuzzy TOPSIS
Step 1: Create a fuzzy decision matrix to rank options
Numerous applications of crisp and fuzzy TOPSIS have been carried out in recent years in a variety of fields, including the selection of information and communication technology projects, the evaluation of companies’ competence or financial viability, the analysis of investment projects, business communications, and other strategic decisions [33].
After selecting the ranking choices, make a matrix using linguistic terms. Equation (21) illustrates how alternatives perform. The scales and triangle membership functions used are listed in Table 2 [34].
where
Xif = (lif, mif, uif)
Step 2: The Fuzzy Decision Matrix has to be normalized
Equation (22) is used to normalize the decision matrix, and the normalized matrix is used to calculate the decision matrix represented by
Step 3: Determine the weighted normalized fuzzy decision matrix for the situation
Then, using Equation, a weighted normalized fuzzy decision matrix is generated (Equation (23) and is expressed by . In the equation, wi represents the criterion weight obtained from Section 3.2.
Step 4: Calculate both the fuzzy positive ideal and negative ideal solutions
For the specified criterion, the fuzzy PSI and fuzzy NSI reflect the maximum and minimum values obtained from the weighted normalized fuzzy decision matrix, respectively, among all the alternatives. This is determined using Equations (24) and (25).
PIS
NIS
Step 5: Determine the Euclidian distance
Using Equations (26) and (27), the Euclidian distance of each alternative is determined from FPIS and FNIS, respectively.
Step 6: Determine the closeness coefficient
Equation (28) is used to determine the closeness coefficient for each alternative option, where 0 ≤ CCf ≤ 1.
4. A Real Case Study
This section illustrates the uncertainty of the decision-making environment through the use of a real-world case study. To address the ambiguity’s drawbacks, a fuzzy set-based AHP hybrid and a fuzzy TOPSIS model were used. As illustrated in Table 2, three experts representing decision-makers (DMs) use criteria to determine the best alternative among three different alternatives (see Table 3). We have three main criteria here (see Table 4), namely, Satisfaction (C1), Economic (C2), and Environment (C3). The hierarchical function of the criteria is demonstrated in Figure 2.

Table 3.
Alternatives and explanations.

Table 4.
Criteria and explanations.
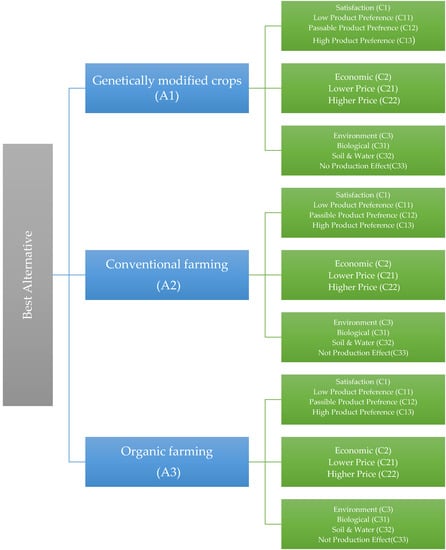
Figure 2.
The hierarchical function of the criteria and alternatives.
In the second step, three experts analyze these primary criteria. The evaluation matrix for the criteria is shown in Table 5 based on their selections.

Table 5.
Decision-maker ratings of three alternative companies.

Table 6.
Ranking alternatives.
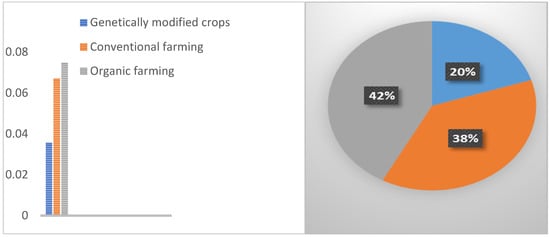
Figure 3.
Ranking alternatives.
5. Results and Discussion
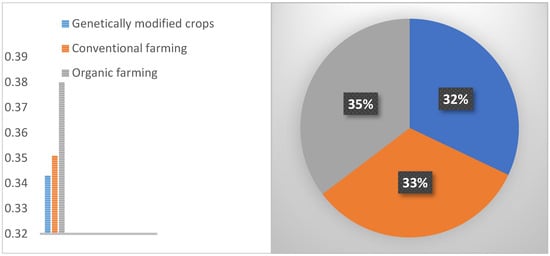
In this study, we employed B-FAHP and fuzzy TOPSIS to identify the best option among three competing farming methods. The findings are summarized in Table 7. The following choices are listed in descending order: Organic farming (A3) > Conventional farming (A2) > Genetically modified crops (A1). Overall, among the three alternatives, alternative 3, Organic farming (A3), was chosen as the most appropriate.

Table 7.
Ranking alternatives (fuzzy TOPSIS). (See Figure 4).
According to the study, crops grown using organic farming methods have a higher value in terms of consumer satisfaction and environmental impact, but a lower value in terms of price rate. Crops grown using conventional farming and genetic engineering techniques have low product prices due to their high production capacity, but they have lower value in terms of consumer satisfaction and environmental impact. In the application, the hierarchical model’s dimensions and criteria were compared pairwise. The comparison matrices’ consistency ratios are below 0.10 (CR 0.10).
Fuzzy TOPSIS and fuzzy AHP are powerful multiple-criteria decision-making methods that assist decision-makers in selecting the best alternative that will provide the best solution to address an agricultural production problem by a process of prioritizing and ranking, because it is difficult to decide which criterion is more important than the other [29].
6. Conclusions
In this research, we examined the structure of B-FAHP and fuzzy TOPSIS as a hybrid technique for solving farming selection problems. B-FAHP and fuzzy TOPSIS give DMs greater flexibility of expression while evaluating alternatives than other fuzzy sets, although there are few MCDM approaches. As a result, the B-FAHP and fuzzy TOPSIS hybrid method was adapted to a farming selection problem; three alternative solutions were ranked by DMs using 3 criteria (Satisfaction (C1), Economic (C2), and Environmental (C3)), including an environmental criterion; and the best farming type was chosen. The B-FAHP and fuzzy TOPSIS hybrid methodology outperformed the others, according to the data.
Moreover, including fuzzy MCDM methodology for other problems could result in more advantageous outcomes, as it would reveal both the priority and size of benchmarked components, which would be impossible to obtain using traditional methods alone. By combining the ideas of thinking and non-thinking assets, it was feasible to examine several aspects of agricultural production in detail, which is critical for both the current competitive environment and long-term growth. Extensive research has been conducted on agricultural production benchmarking, and previously unknown results have been discovered [39].
The most significant conclusion of this case study is the proposed farming selection approach, which crystallizes differences between alternatives and makes the best option clear in a subjective agriculture environment. Additionally, the linguistic term table that we created addresses a weakness in the calculation for the fuzzy set weighting aggregating operator. In comparison to the fuzzy AHP hybrid technique described in this research, the suggested model is parametric in terms of uncertainty and produces stable results. Further study may be conducted to expand the number of alternatives and criteria, and our FAHP technique can be compared with other MCDM methods. Other MCDM approaches such as VIKOR, PROMETHEE, and others may be extended to fuzzy sets, and q-ROF TOPSIS can be compared with these methods.
Author Contributions
Conceptualization, B.D.R. and Ş.S.; methodology, validation, investigation, resources, data curation, and writing—review and editing, Ş.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Fisher, M.R. Environmental Biology. Open Oregon Educatıonal Resources. 2021. Available online: https://openoregon.pressbooks.pub/envirobiology/chapter/9-3-conventional-agriculture/ (accessed on 1 September 2021).
- Takeda, S.; Matsuoka, M. Genetic approaches to crop improvement: Responding to environmental and population changes. Nat. Rev. Genet. 2008, 9, 444–457. [Google Scholar] [CrossRef] [PubMed]
- Mäder, P.; Fliessbach, A.; Dubois, D.; Gunst, L.; Fried, P.; Niggli, U. Soil fertility and biodiversity in organic farming. Science 2002, 296, 1694–1697. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tuomisto, H.L.; Hodge, I.D.; Riordan, P.; Macdonald, D.W. Does organic farming reduce environmental impacts—A meta-analysis of European research. J. Environ. Manag. 2012, 112, 309–320. [Google Scholar] [CrossRef] [PubMed]
- Jordan, R.; Müller, A.; Oudes, A. High Sequestration, Low Emission, Food Secure Farming. Organic Agriculture—A Guide to Climate Change and Food Security; International Federation of Organic Agriculture Movements (IFOAM)/IFOAM EUGroup: Brussels, Belgium; Bonn, Germany, 2009. [Google Scholar]
- Alossta, A.; Elmansouri, O.; Badi, I. Resolving a location selection problem by means of an integrated AHP-RAFSI approach. Rep. Mech. Eng. 2021, 2, 135–142. [Google Scholar] [CrossRef]
- Wudhikarn, R.; Chakpitak, N.; Neubert, G. Use of an analytic network process and monte carlo analysis in new product formula selection decisions. Asia-Pac. J. Oper. Res. 2015, 32, 1550007. [Google Scholar] [CrossRef]
- Shanshan, Z.; Yu, G.; Shaohua, H.; Pengzhou, T. A Hybrid MCDM Approach Based on ANP and TOPSIS for Facility Layout Selection. Trans. Nanjing Univ. Aeronaut. Astronaut. 2018, 35, 1027–1037. [Google Scholar]
- Wudhikarn, R. Improving the intellectual capital management approach using the hybrid decision method. J. Intellect. Cap. 2018, 19, 670–691. [Google Scholar] [CrossRef]
- Mosadeghia, R.; Warnkenb, J.; Tomlinsona, R.; Mirfenderesk, H. Uncertainty analysis in the application of multi-criteria decision-making methods in Australian strategic environmental decisions. J. Environ. Plan. Manag. 2013, 56, 1097–1124. [Google Scholar] [CrossRef] [Green Version]
- Sarper, A. Special Agriculture Production Selection Using Interval Type-2 Fuzzy AHP. In Intelligent and Fuzzy Techniques: Smart and Innovative Solutions, Proceedings of the INFUS 2020 Conference, Istanbul, Turkey, 21–23 July 2020; Advances in Intelligent Systems and Computing Book Series; Springer: Cham, Switzerland, 2020; Volume 1197. [Google Scholar]
- Zandi, P.; Rahmani, M.; Khanian, M.; Mosavi, A. Agricultural Risk Management Using Fuzzy TOPSIS Analytical Hierarchy Process (AHP) and Failure Mode and Effects Analysis (FMEA). Agriculture 2020, 10, 504. [Google Scholar] [CrossRef]
- Ren, C.; Li, Z.; Zhang, H. Integrated multi-objective stochastic fuzzy programming and AHP method for agricultural water and land optimization allocation under multiple uncertainties. J. Clean. Prod. 2018, 210, 12–24. [Google Scholar] [CrossRef]
- Pilevar, A.R.; Matinfara, H.R.; Sohrabia, A.; Sarmadianb, F. Integrated fuzzy, AHP and GIS techniques for land suitability assessment in semi-arid regions for wheat and maize farming. Ecol. Indic. 2020, 110, 105887. [Google Scholar] [CrossRef]
- Firdaus, A.; Adiprasetyo, T.; Suhartoyo, H. A Multicriteria Decision Making and Fuzzy-AHP Approach for Formulating Strategy to Develop Organic Agriculture in Bengkulu Province Indonesia. Adv. Biol. Sci. Res. 2021, 13, 213–218. [Google Scholar] [CrossRef]
- Tashayo, B.; Honarbakhsh, A.; Azma, A.A.; Akbari, M. Combined Fuzzy AHP–GIS for Agricultural Land Suitability Modeling for a Watershed in Southern Iran. Environ. Manag. 2020, 66, 364–376. [Google Scholar] [CrossRef] [PubMed]
- Mohammadrezaei, N.; Pazira, E.; Sokoti, R.; Ahmadi, A. Land Suitability Evaluation for Wheat Cultivation by Fuzzy-AHP, Fuzzy-Simul Theory Approach as Compared with Parametric Method in the Southern Plain of Urmia. Bull. Environ. Pharmacol. Life Sci. 2014, 3, 112–117. [Google Scholar]
- Rahimabadi, D.P.; Azarnivand, H.; Khosravi, H.; Zehtabian, G.; Nia, M.A. An ecological agricultural model using fuzzy AHP and PROMETHEE II approach. Desert 2021, 26, 71–83. [Google Scholar] [CrossRef]
- Demirel, N.Ç.; Nilay, G.; Yucenur, Y.; Demirel, T.; Musdal, H. Risk-Based Evaluation of Turkish AgriculturalStrategies using Fuzzy AHP and Fuzzy ANP. Hum. Ecol. Risk Assess. 2012, 18, 685–702. [Google Scholar] [CrossRef]
- Rouyendegh, B.D. Developing an integrated AHP and intuitionistic fuzzy TOPSIS methodology. Tech. Gaz. 2014, 21, 1313–1319. [Google Scholar]
- Qureshi, M.N.; Pradeep, K.; Dinesh, K. Framework for benchmarking logistics performance using fuzzy AHP, International Journal of Business Performance. Supply Chain. Model 2009, 1, 82–98. [Google Scholar]
- Kahraman, Ç.; Ruan, D.; Doğan, I. Fuzzy group decision-making for facility location selection. Inf. Sci. 2003, 157, 135–153. [Google Scholar] [CrossRef]
- Kahraman, Ç.; Ruan, D.; Ethem, T. Capital budgeting techniques using discounted fuzzy versus probabilistic cash flows. Inf. Sci. 2002, 42, 57–76. [Google Scholar] [CrossRef]
- Kontodimopoulos, N.; Niakas, D. A 12-year analysis of Malmquist total factor productivity in dialysis facilities. J. Med. Syst. 2006, 30, 333–342. [Google Scholar] [CrossRef] [PubMed]
- Gaudenzi, B.; Borghesi, A. Managing risks in the supply chain using the AHP method. Int. J. Logist. Manag. 2006, 17, 114–136. [Google Scholar] [CrossRef]
- Caglayan, N.; Yildizbasi, A.; Rouyendegh, B.D. Fuzzy AHP Approach to Prioritizing the Critical Success Factors of Organizational Culture. Int. J. Organ. Leadersh. 2018, 7, 454–466. Available online: https://ssrn.com/abstract=3337637 (accessed on 1 September 2021). [CrossRef]
- Bakır, M.; Atalık, Ö. Application of fuzzy AHP and fuzzy MARCOS approach for the evaluation of e-service quality in the airline industry. Decis. Mak. Appl. Manag. Eng. 2021, 4, 127–152. [Google Scholar] [CrossRef]
- Rouyendegh, B.D.; Topuz, K.; Dag, A.; Oztekin, A. An AHP-IFT Integrated Model for Performance Evaluation of E-Commerce Web Sites. Inf. Syst. Front. 2018, 21, 1345–1355. [Google Scholar] [CrossRef]
- Naseem, M.H.; Yang, J.; Xiang, Z. Prioritizing the Solutions to Reverse Logistics Barriers for the E-Commerce Industry in Pakistan Based on a Fuzzy AHP-TOPSIS Approach. Sustainability 2021, 13, 12743. [Google Scholar] [CrossRef]
- Wang, Y.M.; Elhag, T.M.S. Fuzzy TOPSIS method based on alpha level sets with an application to bridge risk assessment. Exp. Syst. App. 2006, 31, 309–319. [Google Scholar] [CrossRef]
- Rouyendegh, B.D.; Saputro, T.E. Supplier selection using integrated fuzzy TOPSIS and MCGP: A case study. Procedia—Soc. Behav. Sci. 2011, 116, 3957–3970. [Google Scholar] [CrossRef] [Green Version]
- Carlsson, C. Fuzzy multiple criteria decision making: Recent developments. Fuzzy Sets Syst. 1996, 78, 139–153. [Google Scholar] [CrossRef] [Green Version]
- Nouri, F.A.; Esbouei, S.K.; Antucheviciene, J. A hybrid mcdm approach based on fuzzy ANP and fuzzy TOPSIS for technology selection. Informatıca 2015, 26, 369–388. [Google Scholar] [CrossRef] [Green Version]
- Piya, S.; Shamsuzzoha, A.; Azizuddin, M.; Al-Hinai, N.; Erdebilli, B. Integrated Fuzzy AHP-TOPSIS Method to Analyze Green Management Practice in Hospitality Industry in the Sultanate of Oman. Sustainability 2022, 14, 1118. [Google Scholar] [CrossRef]
- ISAAA 2013 Annual Report. ISAAA Brief 46-2013. 2013. Retrieved 6 August 2014. Executive Summary, Global Status of Commercialized Biotech/GM Crops, Hurt, The Green Revolution in the Global South, p. 161. Available online: https://www.appropedia.org/Conventional_farming#cite_note-1 (accessed on 31 March 2022).
- Paull, J. Organic Agriculture in Australia: Attaining the Global Majority (51%). J. Environ. Prot. Sustain. Dev. 2019, 5, 70–74. [Google Scholar]
- USDA Blog. Organic 101: Allowed and Prohibited Substances. Retrieved 6 April 2016. Available online: Blogs.usda.gov (accessed on 1 September 2021).
- Treadwell, D.; Riddle, J.; Barbercheck, M.; Cavanaugh-Grant, D.; Zaborski, E. Cooperative Extension System, What Is Organic Farming? Archived 3 May 2016 at the Wayback Machine. Available online: https://eorganic.org/node/3498 (accessed on 1 September 2021).
- Wudhikarn, R.; Chakpitak, N.; Neub, G. Improving the Strategic Benchmarking of Intellectual Capital Management in Logistics Service Providers. Sustainability 2020, 12, 10174. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).