Next Article in Journal
A Cross-Cultural Comparison of New Implemented Sustainable Wine Tourism Strategies during the COVID-19 Crisis
Next Article in Special Issue
Harnessing Offshore Wind Energy along the Mexican Coastline in the Gulf of Mexico—An Exploratory Study including Sustainability Criteria
Previous Article in Journal
Household Migration and Intentions for Future Migration in the Climate Change Vulnerable Lower Meghna Estuary of Coastal Bangladesh
Previous Article in Special Issue
Feasibility Analysis of Promoting Wind and Solar Energy in Texas Farms
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Sustainability
Volume 14
Issue 8
10.3390/su14084687
sustainability-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Analysis of Wave Energy Behavior and Its Underlying Reasons in the Gulf of Mexico Based on Computer Animation and Energy Events Concept

by
Francisco Haces-Fernandez
1,
Hua Li
2,* and
David Ramirez
3
1
Department of Management, Marketing and Information Systems, Texas A&M University-Kingsville, Kingsville, TX 78363, USA
2
Department of Mechanical and Industrial Engineering, Texas A&M University-Kingsville, Kingsville, TX 78363, USA
3
Department of Environmental Engineering, Texas A&M University-Kingsville, Kingsville, TX 78363, USA
*
Author to whom correspondence should be addressed.
Sustainability 2022, 14(8), 4687; https://doi.org/10.3390/su14084687
Submission received: 23 February 2022 / Revised: 10 April 2022 / Accepted: 11 April 2022 / Published: 14 April 2022
(This article belongs to the Special Issue Feature Papers in Energy Sustainability)
Browse Figures
Versions Notes

Abstract

:
The complexity and variability of ocean waves make wave energy harvesting very challenging. Previous research has indicated that wave energy was mainly generated and transferred by wind, but the detailed correlation between wind and wave energy has not been discovered. Wave energy in the Gulf of Mexico (GoM) has high variability with distinct seasonal behavior. However, the underlying reasons for this unique behavior have not been discussed and discovered yet. In this paper, a computer animation-based dynamic visualization method was created to conduct exploratory and explanatory analyses of 36 years of meteorological data in the GoM from the WaveWatch III system to identify preliminary patterns and underlying reasons for the unique behavior of wave energy in the GoM. These preliminary patterns and underlying reasons were further analyzed using Energy Events and Breaks concepts. During both high and low levels wave energy periods, the detailed correlation between wave energy and the wind was analyzed and determined. High level wave power in the GoM was mainly generated by the local inland wind from northern weather patterns, while low level wave power was mainly generated by swells from the Caribbean and the Atlantic oceans, which entered the GoM through the two narrow pathways, the Straits of Yucatan and the Florida Straits. The results from this paper will also be able to help the design, placement, and operation of future wave energy converters to improve their efficiency in harvesting wave energy in the GoM.

1. Introduction

Wave energy harvesting has lagged significantly when compared to other renewable energy. Wind and solar energy, which are currently harvested with commercially mature technologies, initiated their modern development during the 1973 oil crisis as same as wave energy [1,2,3]. Even though wave energy has been studied for more than 40 years, there is no large commercial wave energy harvesting facility in operation in the world [1,2,4,5]. A large number of concepts and designs for wave energy converters (WECs) have been developed and tested, but none of them have been commercially successful. During the testing stage, many WECs have been damaged or destroyed by the ocean harsh environment at different offshore locations [4,6,7,8,9,10]. One of the fundamental problems with wave energy harvesting is the lack of in-depth understanding of wave energy behavior in each particular location. Wave energy behaves differently in diverse geographical locations, and its particular characteristics have a direct effect on the performance of wave energy harvesting equipment. Furthermore, previous studies have indicated that large temporal variability exists for wave energy at many locations, creating a complex scenario in which both high temporal and spatial variabilities must be evaluated and characterized to better understand its harvesting [1,4,8,11,12,13].
Previous studies have evaluated the interrelationship between wind and wave, but the complexity of the interaction among diverse factors impacting this phenomenon continues to require further analysis [14]. Relevant factors include the weather and physical conditions at each location [15]. Enclosed marine locations, such as the Caspian Sea or the Mediterranean are almost dependent on local wind energy transfer [1,16,17]. Large oceanic extensions allow for waves to travel long distances from their originating wind events and increase in power as they move [18]. Improving understanding of the transfer of wind to wave energy is very important to advance the development of the wave energy sector [19]. In some locations, the application of WECs may the geared to extract energy from extreme events [20], while in other sites low energy waves can be targeted [17]. Therefore, to target the placement of adequate wave harvesters in their optimal locations it is critical to understand the transfer of wind to wave energy in each geographical area [21].
The numerous factors involved in wave energy optimal harvesting require advanced analysis tools to match WECs placement and location characteristics. Chakraborty and Majumder developed a new model to assess the utilization potential of WECS on particular sites by applying multi-criteria decision-making to handle the diverse factors integrated into this assessment [22]. Deep learning methods have been applied to identify wave energy hotspots for optimal WEC placement [23] and its correct sizing and configuration [14]. Layout optimization has been studied to assess the development of commercial wave farms and collocated wind and wave farms to maximize energy harvesting [19,24]. All these approaches or their underlying assumptions apply historical meteorological data that has been recorded or modeled [14,25]. Assessing this data, related to wind and wave, is extremely complex due to its very large size and the diverse nature of its components [26,27]. The application of computer animation and the Energy Events Concept is proposed in this manuscript to aid in advancing assessment and optimization wave methods, to improve understanding of wind to wave energy transfer, and to improve validation of methods and results from these approaches.
To evaluate the proposed approach the Gulf of Mexico (GoM) was considered a promising location, considering its advantages for wave energy harvesting. Large population centers are located along its shores, with significant energy requirements for both residential and industrial consumption. Furthermore, the GoM is home to one of the largest concentrations of offshore oil platforms in the world, and great synergies would be achieved if WECs could be connected to these platforms. Previous research has indicated that there is a significant theoretical wave energy resource in the GoM to provide great benefits to the local economy if optimally extracted [28,29,30,31]. In addition, the combination of wave energy with other ocean renewable energy resources at the GoM is very interesting with very large potential and possibility for combining wind energy with wave energy [29,30,31,32,33,34].
Wave energy in the GoM is not uniformly distributed based on geographical or temporal criteria and has high variability with distinct seasonal behavior. However, the underlying reasons for this unique behavior of wave energy in the GoM haves not been discussed and discovered, which increases the challenges of harvesting wave energy in the GoM. Meanwhile, previous research has indicated that wave energy was mainly generated and transferred by wind, but the detailed correlation between wind and wave energy has not been discovered [1,11,35,36,37,38,39]. Although databases containing wave meteorological data are available, it is challenging to analyze them given the big data nature. Traditional analytics methods generate incomplete results that are unable to explain the nature of wave energy potentials and their variation in diverse geographical locations. Geographic animation has been used to analyze other geo-temporal concepts with good results, allowing to evaluate the large body of data efficiently, generating relevant analysis and accurate results.
This study has two main objectives. First, it evaluates the potential to use GIS animation to explore wave energy relevant big data and generate useful wave analysis results. Second, it explores the generation of results related to wave energy creation and behavior in particular geographical areas. It is well known that waves are generated by wind. However, each region has diverse wave energy patterns and underlying reasons are in many cases still undiscovered.
The dynamic visualization method developed in this research helps discover the time duration required for winds of particular speeds to generate quantifiable wave energy. The required duration of particular wind speeds to generate diverse wave energy categories is assessed. Furthermore, the methodology explores the time lag between wind arriving into an area and wave energy generation, potentially providing wave harvesting with a relevant forecasting tool. Energy Events concepts were applied to conduct a detailed analysis of the wave energy behavior at the GoM including the detailed correlation between wind and wave energy. A set of criteria related to the unique behavior of wave energy in the GoM were discovered. The detailed methodologies were described in the following section, while the results demonstrated that the new computer animation and correlation analysis based on Energy Events was able to provide an in-depth understanding of wave energy behavior in the GoM to improve wave energy harvesting and reduce the risk of WEC damage or destruction.

2. Methods

In this paper, data from WaveWatch III were used for calculation, visualization, and analysis.

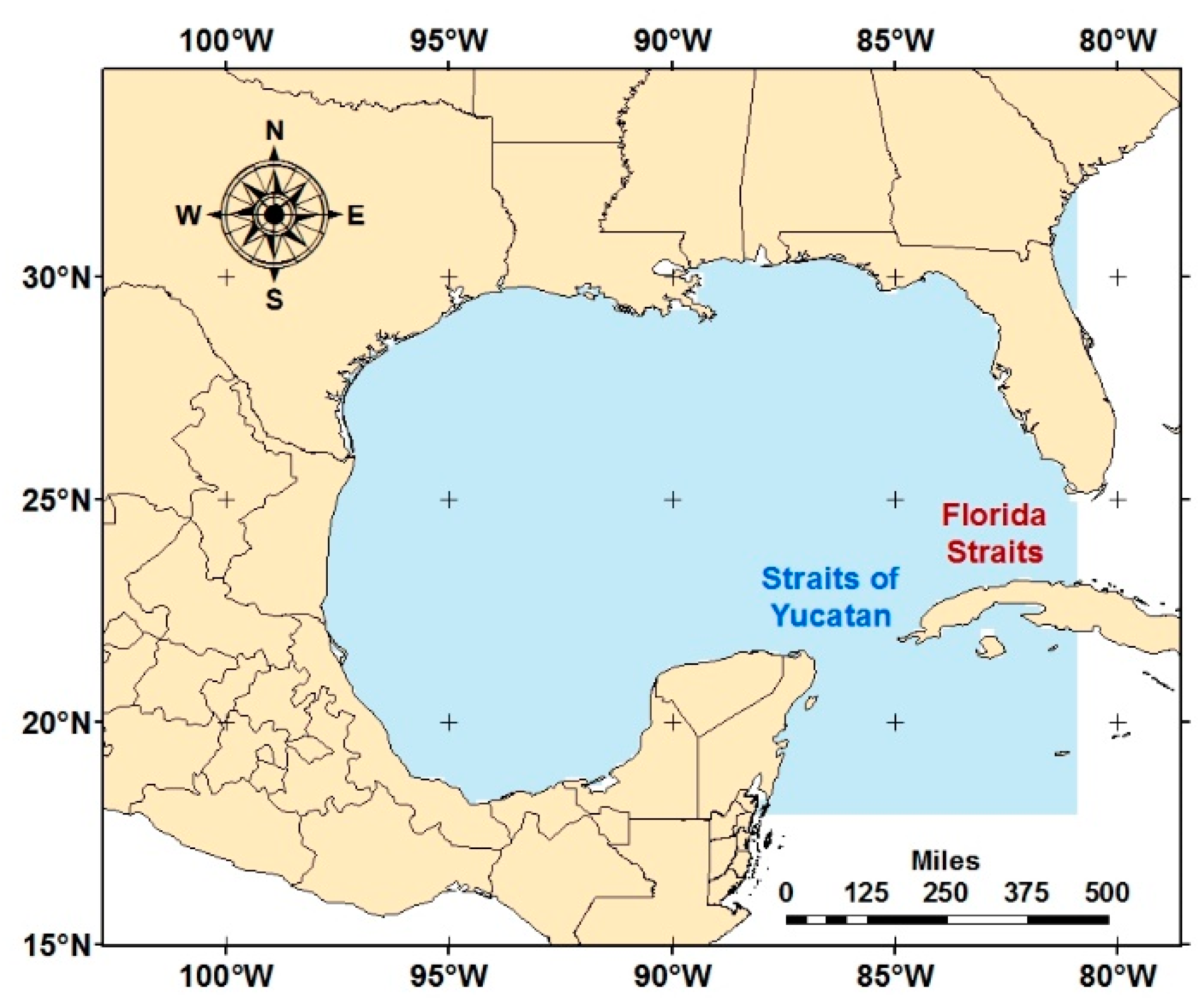
2.1. Meteorological Data and Studying Area

Hindcast meteorological data between 1979 and 2015 provided by the National Oceanic and Atmospheric Administration (NOAA) WaveWatch III system was used to perform the in-depth analysis of wave energy in the studying area [40]. Six datasets from the WaveWatch III system were used, including significant wave height (Hs), dominant wave period (Tp), wave direction, wind speed on its v and u vector formats, and wind speed resultant vector, which have a spatial resolution of 1/6 longitude by 1/6 latitude and time resolution of every 3 h. The blue rectangle in Figure 1 shows the studying area of this paper, which covers the Gulf of Mexico. The GoM has a semi-open structure with two inlets/outlets: Florida Straits and Straits of Yucatan.
Equations (1) and (2) were used in this paper to assess and characterize wave energy in the studying area. These equations evaluate Wave Power Density (P) expressed in kilowatts per meter of wave crest width (kW/m), indicating the wave power dependence on two variables: Hs as significant wave height (meters) and Te as energy wave period (seconds) [41,42,43]. Wave power density may be also denoted as wave energy flux or wave energy potential [44].
P = ρ g 2 64 π T e H s 2
When considering ρ (seawater density as the standard value in kg/m3) and g (gravity in m/s2) as constants, Equation (1) can be expressed as Equation (2).
P   ( kW / m ) = 0 . 49 T e H s 2 = 0 . 49 α T p H s 2
The wave period conversion factor (α) is applied to convert Tp (original wave period data provided by WaveWatch III) to Te. The value of α considered in this paper is 0.9, which has been used by previous studies [11,44,45,46,47,48] and is the equivalent of assuming a standard Joint North Sea Wave Observation Project (JONSWAP) spectrum. Previous research also indicated that the value of α could be 0.86 for a fully developed ocean [11,47] and approaches one as the spectral width decreases [11,47,49,50,51].
However, the nature and size of the data make the analysis and evaluation challenging. For example, one month of significant wave height (Hs) data in the GoM would be represented by a matrix of almost 2.2 million data points, while six meteorological factors over 36 years with additional calculated wave energy related results could lead to almost 7.6 × 108 data points in diverse matrices. To generate the GIS big data animation, the wave meteorological data is analyzed using implied loop computational functionalities through multidimensional matrix applications. For example, the significant wave height (Hs) and the dominant wave period (Tp) data are uploaded as 3D matrices format as indicated as Equations (3)–(6).
M H s = [ t H s 1 … t H s k ]
t H s 1 = [ H s 1 , 1 , 1 ⋯ H s i , 1 , 1 ⋮ ⋱ ⋮ H s 1 , j , 1 ⋯ H s i , j , 1 ] ,   t H s 2 = [ H s 1 , 1 , 2 ⋯ H s i , 1 , 2 ⋮ ⋱ ⋮ H s 1 , j , 2 ⋯ H s i , j , 2 ] … t H s k = [ H s 1 , 1 , k ⋯ H s i , 1 , k ⋮ ⋱ ⋮ H s 1 , j , k ⋯ H s i , j , k ]
where MHs is a 3D matrix containing all significant wave height values for selected locations and time periods. MHs consist of k layers, and each layer is a 2D matrix represented by tHsk, which contains significant wave height values for all selected locations at time period k. And Hsi,j,k is the significant wave height value at longitude i, latitude j, and time period k.
M T p = [ t T p 1 … t T p k ]
t T p 1 = [ T p 1 , 1 , 1 ⋯ T p i , 1 , 1 ⋮ ⋱ ⋮ T p 1 , j , 1 ⋯ T p i , j , 1 ] ,   t T p 2 = [ T p 1 , 1 , 2 ⋯ T p i , 1 , 2 ⋮ ⋱ ⋮ T p 1 , j , 2 ⋯ T p i , j , 2 ] … t T p z = [ T p 1 , 1 , k ⋯ T p i , 1 , k ⋮ ⋱ ⋮ T p 1 , j , k ⋯ T p i , j , k ]
where MTp is a 3D matrix containing all dominant wave period values for selected locations and time periods. MTp also has k layers, and each layer is a 2D matrix represented by tTpk, which contains dominant wave period values for all selected locations at time period k. And Tpi,j,k is the dominant wave period value at longitude i, latitude j, and time period k. Values in the MHs are squared and multiplied by their corresponding dominant wave period value applying implied loops. Finally, values are multiplied by the wave period adjustment factor α and the constant previously indicated in Equation (2). This procedure will evaluate Equation (2) by applying implied loops as expressed in Equation (7), applying Equations (3) and (6). The results will be stored in an independent 3D matrix, with the exact dimensions of both wave height and period, and the data from latitude, longitude, and time will be added to perform the animation similarly to raw data animation was performed.
P = 0.49 α ( M T p ) ( M H s ) 2

2.2. Limitation of Static Methods

Challenges exist in analyzing, visualizing, assessing, and characterizing wave energy using static and traditional data analysis methods due to the temporal and spatial nature of the big data under consideration. Temporal, spatial, and categorical attributes of wave energy data are very diverse, creating complex data that are difficult to analyze and visualize. The use of static maps combined with other representations of data and results has been performed by previous studies, generating inconclusive results, not providing the in-depth analysis required for wave energy successful harvesting [37,52,53,54]. Therefore, it becomes necessary to create new methods for the characterization of wave energy to overcome these challenges [55]. Although spatial events have been studied by geographical sciences for a long time with many tools developed to better represent, analyze, and forecast the data, there is no forecasting methodology specifically designed for wave energy harvesting yet [56,57,58]. Furthermore, since wave energy does not behave linearly in relationship with Hs, traditional statistical approaches would only present an incomplete outlook of wave energy behavior without the full spectrum of wave energy variability [59,60,61,62,63]. Performing analysis using traditional statistical methods on data with such a large size may not be feasible for researchers to observe the interactions and causality of all the involved factors [11,37,64,65].
This point is exemplified by an example of attempting to assess wave power density in January 1985 in the GoM through static maps. Figure 2 shows static maps of average and standard deviation (in kW/m) of wave power density in January 1985. The static maps show diverse behaviors for both the mean and standard deviation of wave power density, where the higher value regions of average and standard deviation were different. However, Figure 2 is not able to help identify the causes of this spatial dislocation.
Figure 3 represents the average wave power density of the entire studying area in January 1985 under 3 h temporal resolution, showing three clear peaks in wave power density during the month. However, it gives very little insight into the interpretation of the results presented in Figure 2 and no explanation of the dislocation of both characteristics (mean and standard deviation) either.
Another type of static representation of the wave power density in January 1985 is shown in Figure 4, applying 3D histograms to calculate the daily averages wave power output segmented latitude or longitude. From Figure 4a, it is observed that wave power density has incremental behavior from higher latitudes until it reaches the southern portion of the GoM. In Figure 4b, the three peaks of wave power density during the month show that most of the higher values were on higher longitudes. However, these static graphical results do not fully complement each other and are not able to provide a clear understanding of wave energy behavior in the GoM during January 1985. Furthermore, these static figures are unable to represent the wave energy variability on both temporal and spatial criteria and are unable to help discover the underlying reasons for the unique behavior of wave energy at the GoM.

2.3. GIS Big Data Animation with Energy Events

To fully understand the wave energy behavior at the GoM, a GIS-based dynamic visualization method has been created in MATLAB to visualize and analyze WaveWatch III data with its default spatial resolution. The selected meteorological data provided by WaveWatch III, as needed for each calculation, were read into computer memory using NCTOOLBOX. The data were stored on computer memory on a ncgeodataset variable that might contain four or more cell arrays, depending on the type of data being accessed. For visualizing the raw data, such as wave height and wave period, the toolbox based on the open-source Generic Mapping Tools was used for the manipulation of geographic datasets through the application of the m.map mapping package. Analyzed data were plotted on map projections with coastlines and political boundaries. Color bars in the plotted maps have adjustable ranges to allow for optimal visualization contrast of wave energy in animation. Ranges in Color Bars are visible to allow viewers correct data interpretation. Considering wave energy’s high variability, dependent on changing weather conditions, the Color Bars in the maps were designed for self-adjusting ranges and values. The adjustment allows for the minimization of average deviation for each category while maximizing deviation from the mean of each category to other categories. This provides each map with optimal contrast between the values presented in each figure, which significantly vary between the diverse animation map frames. This approach has been applied by previous research and has been demonstrated to provide good analysis for data matrix with relatively big differences in included values [20,66,67,68,69]. The contrast provided by the varying Color Bar and its ranges allows for improve geospatial analysis and gaining a better understanding of waves’ spatiotemporal behavior and variability. The main purpose of the presented frame of maps animation is to provide contrast on wave and wind behavior in particular geographical locations. Comparison and analysis between the maps and their animations should always consider that the scale and the ranges of the Color Bars in the figure legends change according to wave energy values presented in each particular fame.
In a static state, each layer of a map would only show one three-hour period at a time. The GUI was able to achieve dynamic visualization through the representation of successive sequential layers of data on the same screen through the animation function in MATLAB, which was used to better understand wave energy behavior and its underlying reasons.
Figure 5 and Figure 6 show selected frames from the animation of January 1985 data created by the GUI. Although Figure 2 shows central GoM had the highest average wave power density in January 1985, Figure 5 indicates that other regions in the GoM also had very high wave energy in the same month, which was not presented by Figure 2 or Figure 3 due to the nonlinear behavior of wave energy in the GoM. Through exploratory and explanatory analysis of the animation of January 1985, the authors also observed that wave energy in the GoM moved in a predominantly southeastern direction with some variability to the south in January 1985, causing the northern central area of the GoM to have the highest average due to the passing through of most wave energy. However, the wave energy that reached the south portion of the GoM has the highest levels, which is the major reason causing this area to have the largest variability due to less frequent but very powerful wave energy appearance. Figure 6 shows one of these observations in January 1985 as an example to explain the wave energy behavior in January 1985.
It is important to highlight that computer animation to improve scientific research has been studied for more than 30 years, but there is no computer animation application for analyzing wave energy. One of the most important characteristics of computer animation is the capability to show researchers new relationships and patterns within the body of data, which would be very difficult to reveal using traditional methodologies. By watching the animation-based dynamic visualization of these selected meteorological data and calculated results related to wave and wind energy at the same time, the authors were able to discover preliminary underlying patterns among different factors related to wave energy behavior. Without the animation, it will be extremely difficult and time-consuming to identify those preliminary patterns. Those preliminary patterns discovered were analyzed and validated through detailed exploratory data analysis later by applying the Energy Events and Breaks concept.
After identifying preliminary patterns of wave energy behavior with the computer animation, Energy Events and Breaks concepts were used to conduct further wave energy analysis [29]. Energy Event (EE) is defined as a period of time in which a type of energy in a predefined geographical region is above a certain threshold. Meanwhile, the period of time in which the given type of energy in a predefined geographical region is below a certain threshold is named Breaks. The identification of Energy Events requires the selection of a threshold, partially adapting the peak-over-threshold methodology, to mark the beginning and the end of the Energy Event over a predetermined area. Its duration is determined by the time when power is above a predetermined threshold and is reported in the results of this paper. In this paper, the wave Energy Events and Breaks were identified using kW/m as the threshold unit. Wind speed (m/s) was selected as the threshold when identifying wind Energy Events and Breaks because theoretical wind energy potential is directly related to wind speed. After defining threshold values, calendars of wave and wind Energy Events and Breaks were created indicating the date and hour when each Energy Event started and finished. Other parameters of Energy Events could be integrated into the analysis, such as average, dispersion, layer distribution, geographical distribution, velocity, direction, shape, etc. Energy Event and Break concepts identify the selected region with at least two distinctive states in the spatial and time continuum related to wave energy. Studying different factors in both Energy Events and Breaks allowed a better understanding of the characterization of the wave energy resource in the GoM and its underlying reasons for improving wave energy harvesting.
Previous research shows that the cycle of creation, transport, and disappearance of wave energy is well constrained by geographical and temporal frames at the GoM [28,29,33]. Other larger oceanic areas, such as the Pacific and Atlantic, have much more complex wave energy cycles, traveling longer distances and forming diverse swells with divergent characteristics and directions. The GoM has two very well-defined wave energy states with repetitive, similar cycles on the creation, transport, and disappearance of wave energy. Analysis based on the Energy Events and Breaks concepts could make it feasible to conduct a detailed analysis of the underlying reasons for the unique behavior of wave energy, which may be directly used to help WEC operators to increase the success of these future commercial endeavors [1,11,30,34,37].

3. Results

Wave energy patterns in the GoM were assessed and characterized by applying big data GIS animation. The exploratory and explanatory analysis of the animation for the 36 years under study allowed us to determine preliminary patterns of wave energy behavior in the GoM. This includes (1) wave energy in the GoM has well defined high and low levels, (2) high level wave energy seems to be dependent on the local wind in the GoM region, while there was no strong correlation between low level wave energy with local wind, and (3) the wind and wave energy in the GoM were not always directly correlated. There seems to be some delay in the occurrence between wind and wave energy. However, the detailed patterns and underlying reasons for these preliminary patterns were not determined by only analyzing the computer animation. Analyses based on Energy Events and Breaks concepts were conducted to examine these preliminary patterns and reveal the underlying reasons.

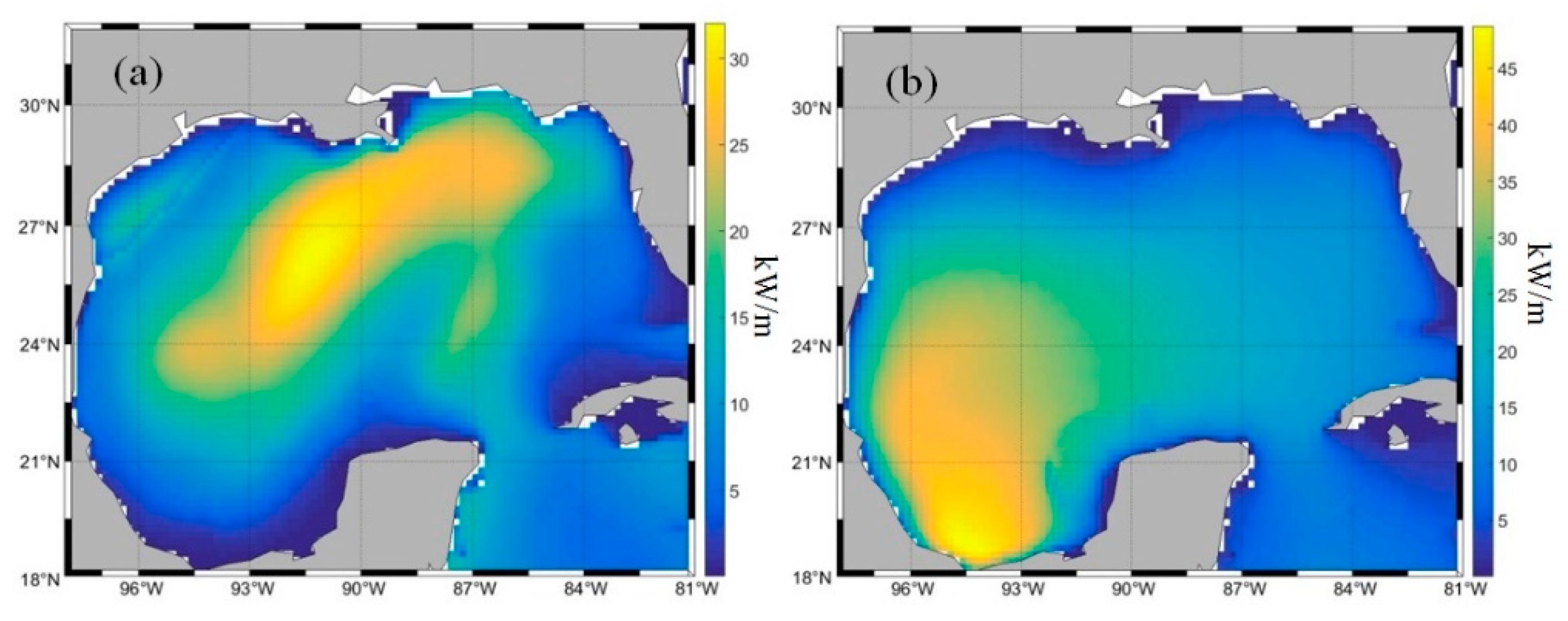
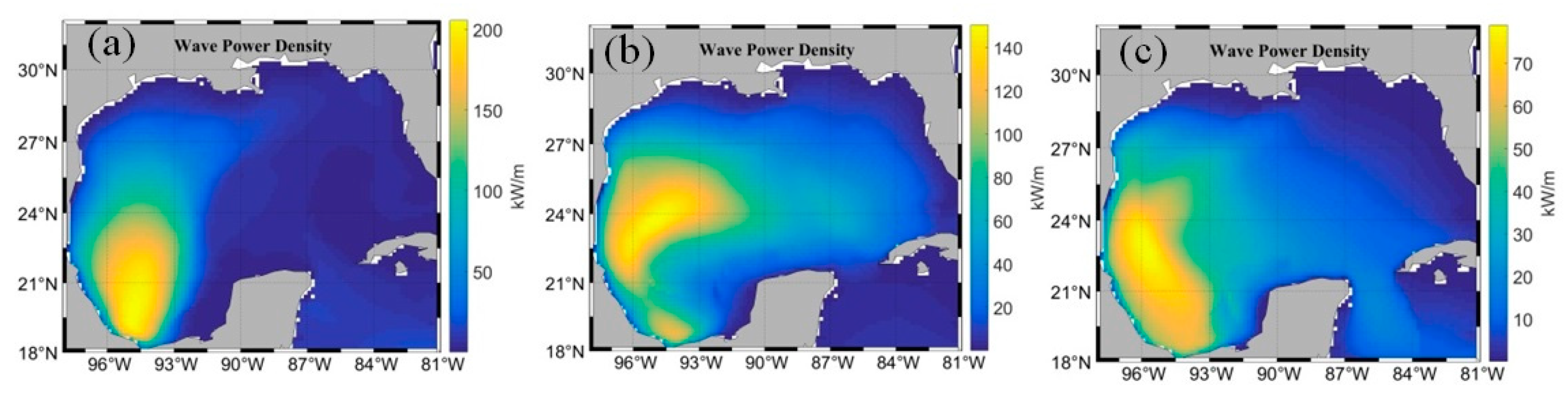
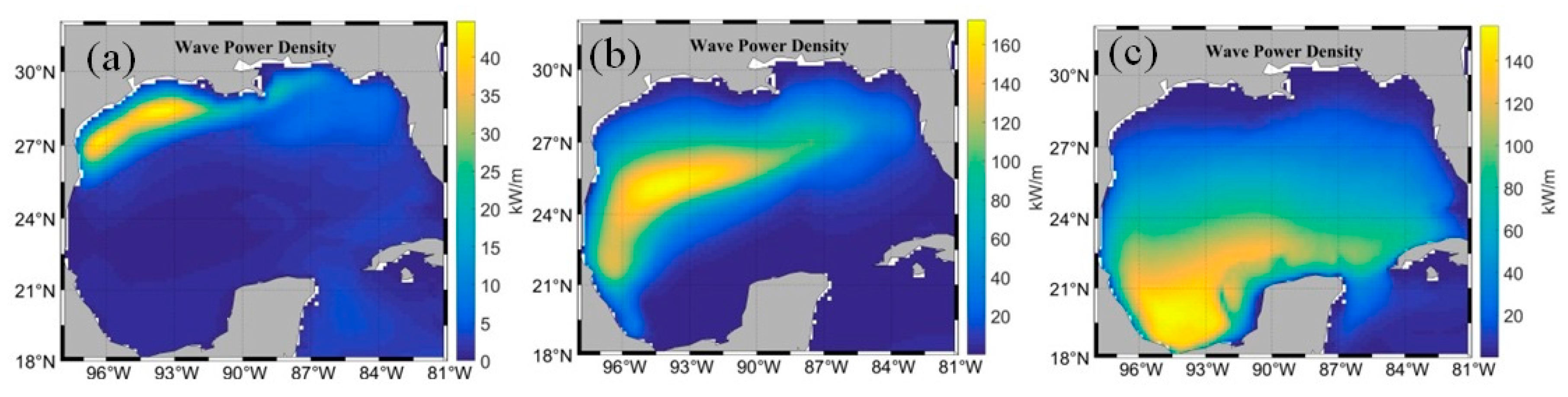
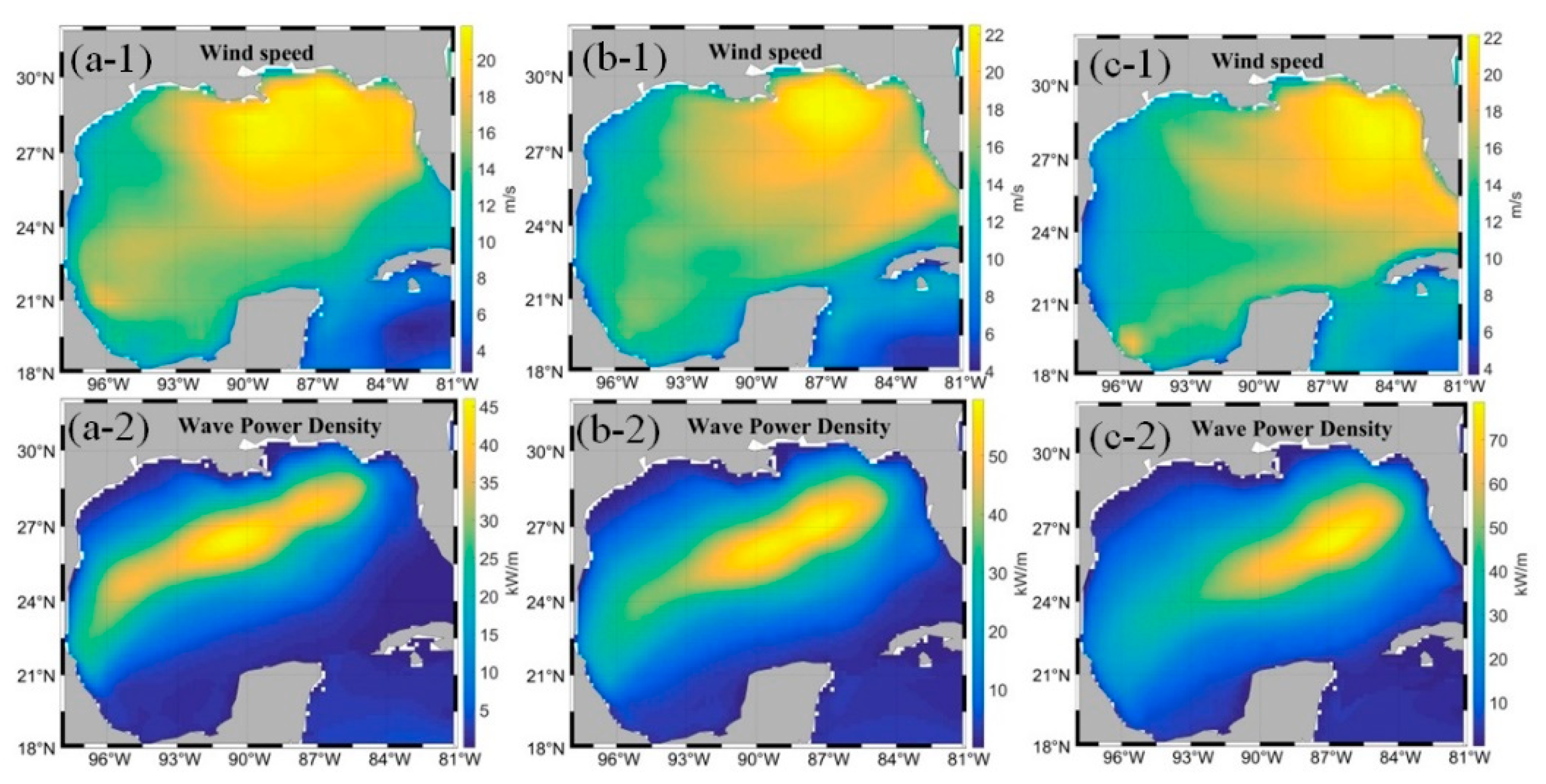
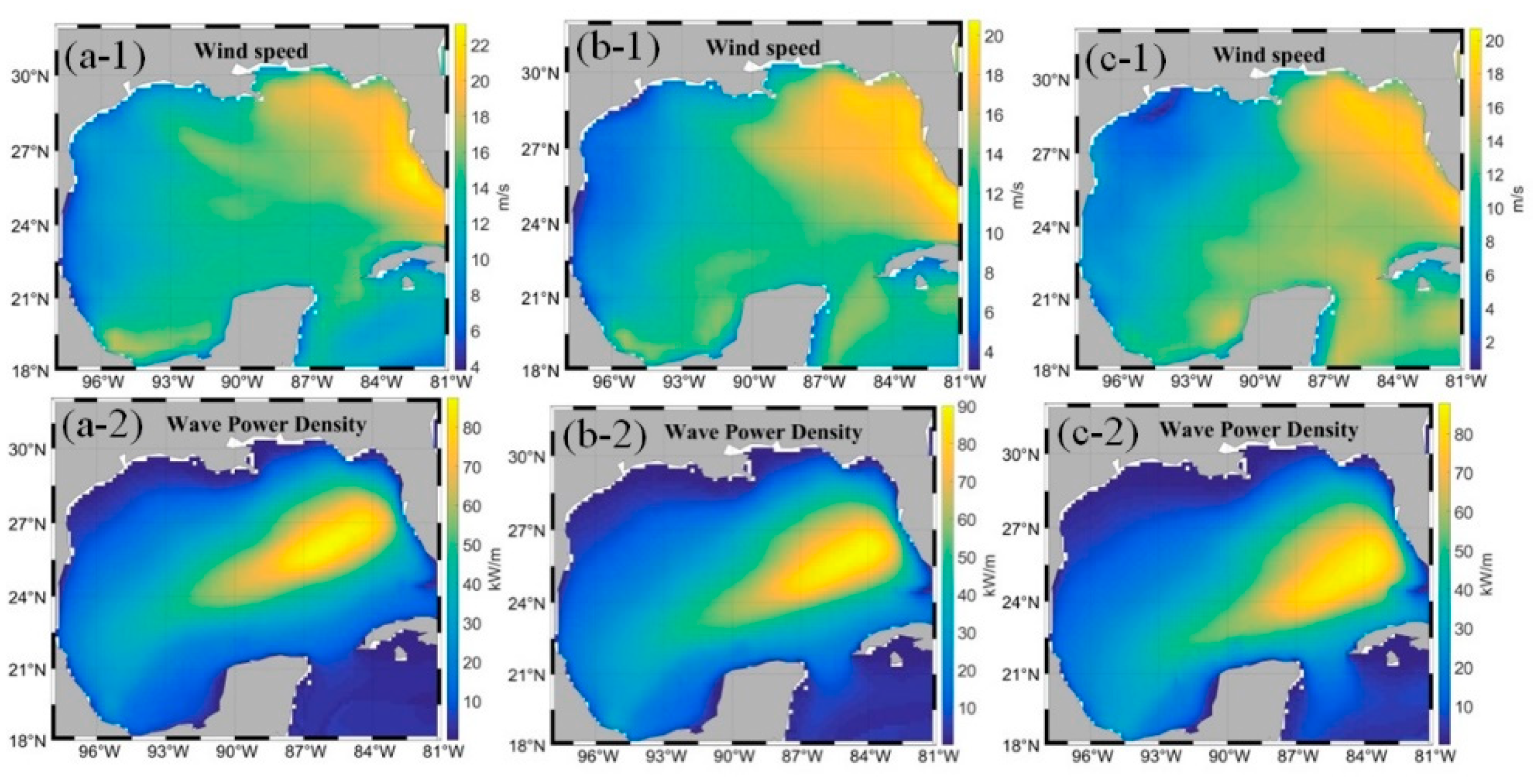
3.1. Qualitative Analysis of High Levels of Wave Energy Behavior in the GoM

Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 show sequential frames from the data animation in January 2006 to determine the changes in wind speed and wave power density. These sequential frames were used to validate the observation that high level wave energy in the GoM was mainly generated by the local winds. The wave energy patterns and characterizations described in this research were observed repeatedly during the 36 years under consideration. However, it is not possible to report all of them due to space limitations. GIS big data animation provides an effective tool to assess and evaluate big data of geo-temporal nature without requiring extensive reporting and outputs. Results shown in this research were chosen as good examples of repeated patterns observed during the study period and for the presented results. Results and discussion on wave energy behavior and its corresponding wind causality are reported for the 36 years under study.
The figures show the pattern that local wind from onshore (northwest) traveled to the southeast, and generated high wave energy in the GoM. Wave EEs were used to represent the high level wave energy. Figure 7a-1,a-2 at 18:00 h on 13 January 2006 shows that wind entered from the northwest corner of the GoM while limited wave power density (less than 8 kW/m) was available at that location. Three hours later, Figure 7b-1,b-2 shows increases in wind speed without increases in wave power density in the same region. Figure 7c-1,c-2 shows a small increment (about 4 kW/m increase than three hours ago) for wave power density six hours after observing the initial wind coming from the northwest, while the wind increased its impacted region towards the east.
Figure 8(a-1,a-2) shows a well-defined wave EE (yellow ribbon) formed with a high wave power density level (over 20 kW/m) after nine hours of the initial appearance of wind. Figure 8(b-1,b-2) indicates that wind extended to the southeast of the GoM while the wave EE continued to grow in size and intensity. Figure 8(c-1,c-2) indicates that the wave EE traveled towards the southeast with its power density increased closed to 35 kW/m while the wind was dispersing from the original northwest location.
In the following nine-hour period as shown in Figure 9, it indicates that the wave EE continued to behave as a time difference synchronous event from wind speed. However, the wave EE seemed to travel in a preset direction and keep increasing its power density (over 70 kW/m) that were a little bit different from the wind speed’s changing pattern in travel direction and intensity.
Figure 10 further supports the observation from Figure 9, which is the wave EE behaved differently with wind speed’s changing pattern. When wind dissipated from the area and started exiting through the eastern section of the GoM, the wave EE continued to strengthen (up to 90 kW/m) until reaching the Florida coast where it expanded its influence area and slightly decreased its maximum power density.
The observation from Figure 9 and Figure 10 is important. It indicates that the initial characteristics of the winds that originated a specific wave EE are the main factors affecting the characteristics and movement direction of the specific Wave EE in the GoM. This correlation between wind and wave energy behavior in the GoM, which was observed many times in the rest of the animations of the 36 years of data, can help create good predictability of the wave energy behavior in the GoM. Figure 11 shows that the wave EE started disappearing by leaving the GoM through Florida Straits and Straits of Yucatan at the end when its maximum power density dropped around 35 kW/m.
Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 show one of many wave EEs observed in the animation of January 2006 data. Similar observations were found in the animation of the entire 36 years of data. Analyzing the cycle of creation, evolution, and disappearance of wave EEs in the GoM with the new animation indicated a strong correlation between the initial characteristics of the causal northern wind systems and the wave EE behavior. The animation greatly aided in the identification of these patterns. Considering that each map represents a large volume of data, it would be difficult to use static or traditional methodologies to assess and characterize the wave EE behavior.

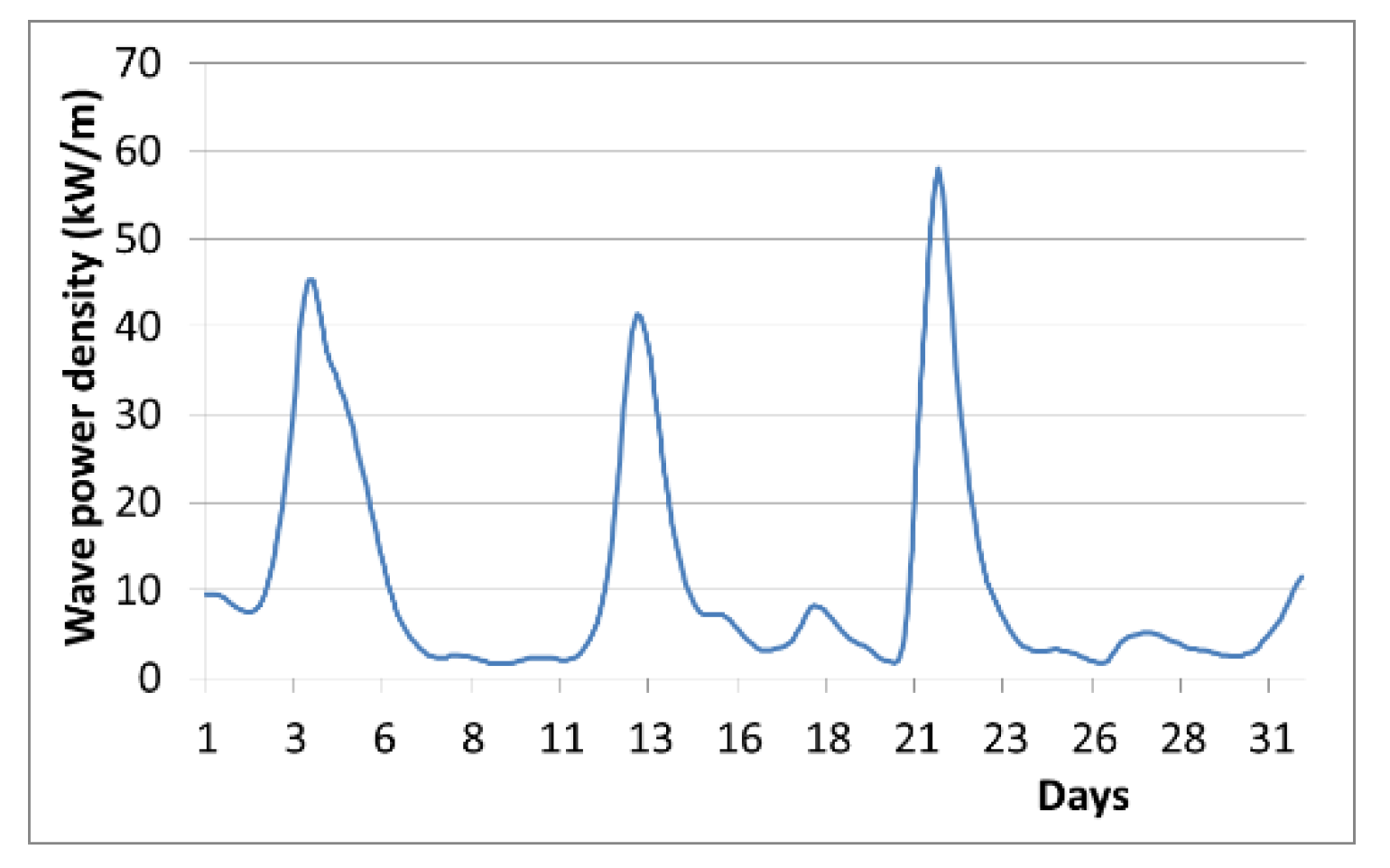
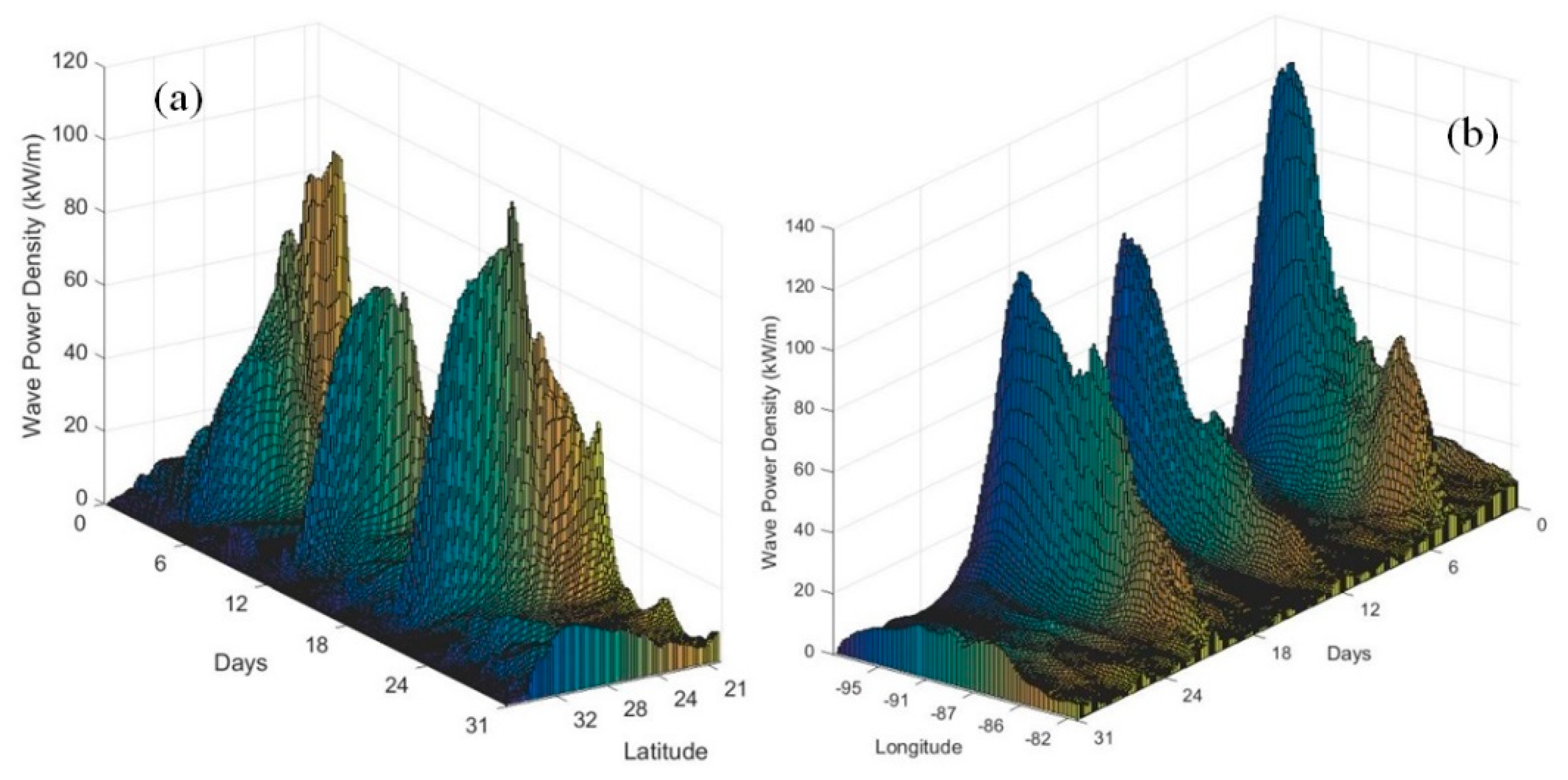
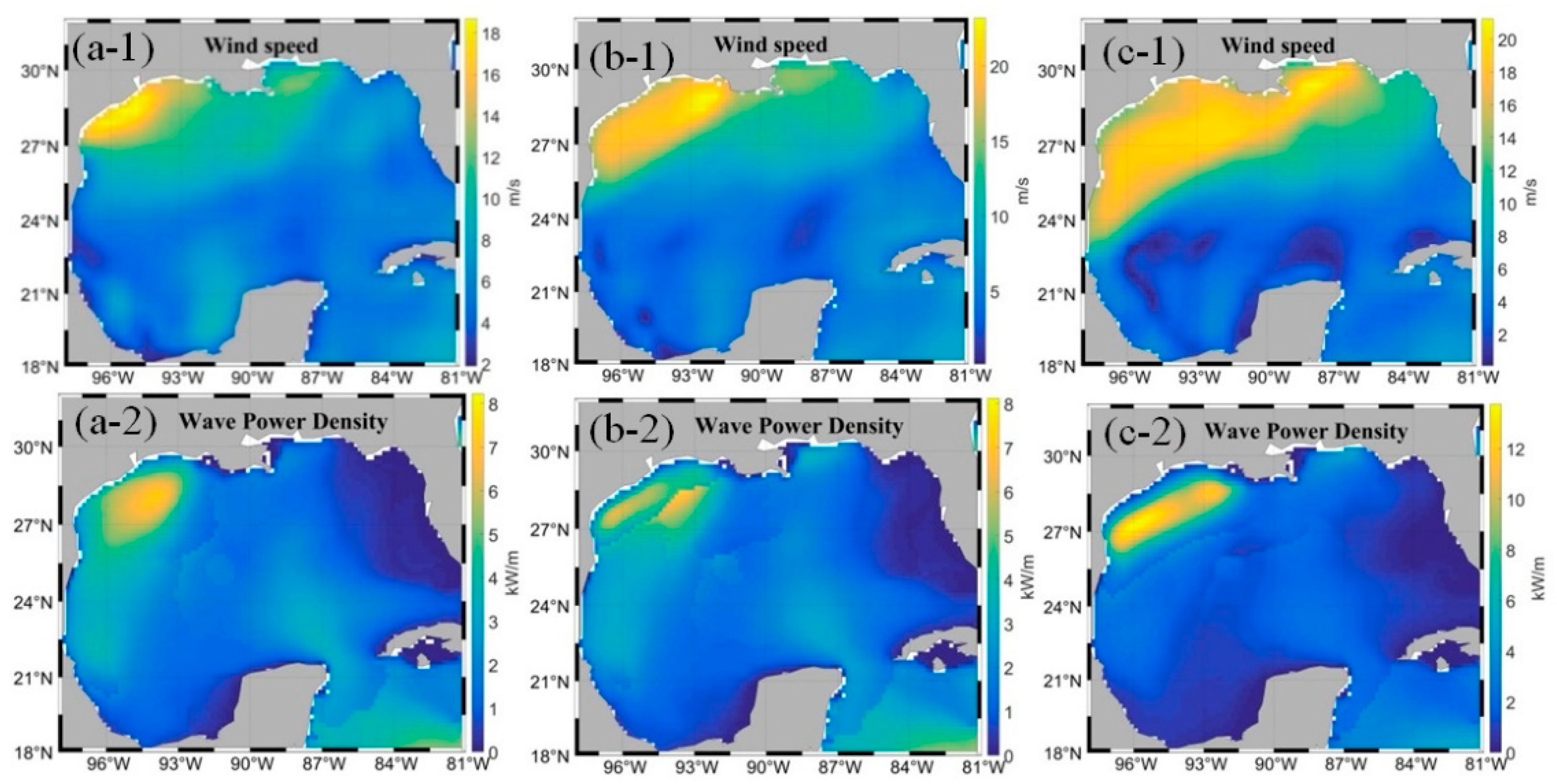
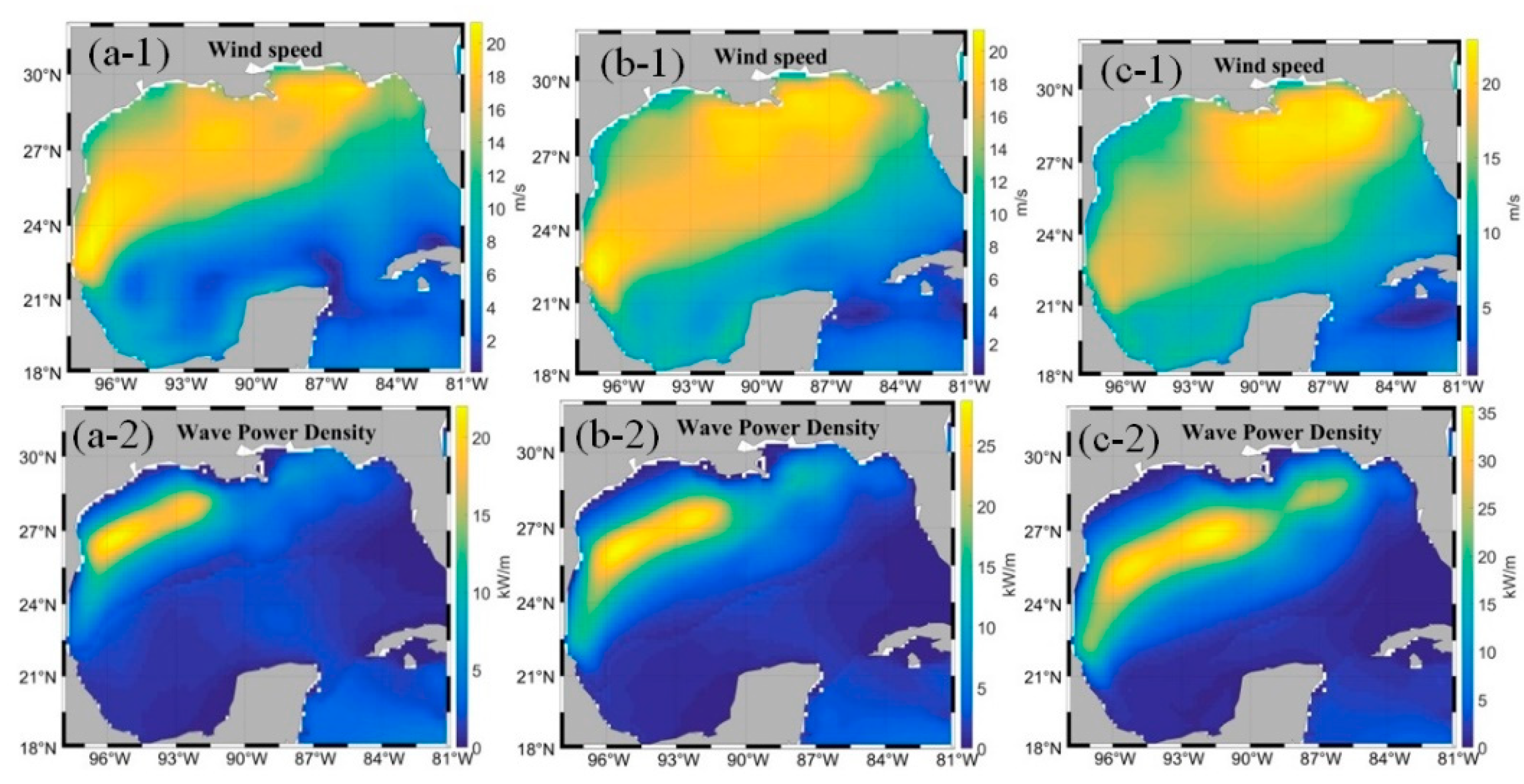
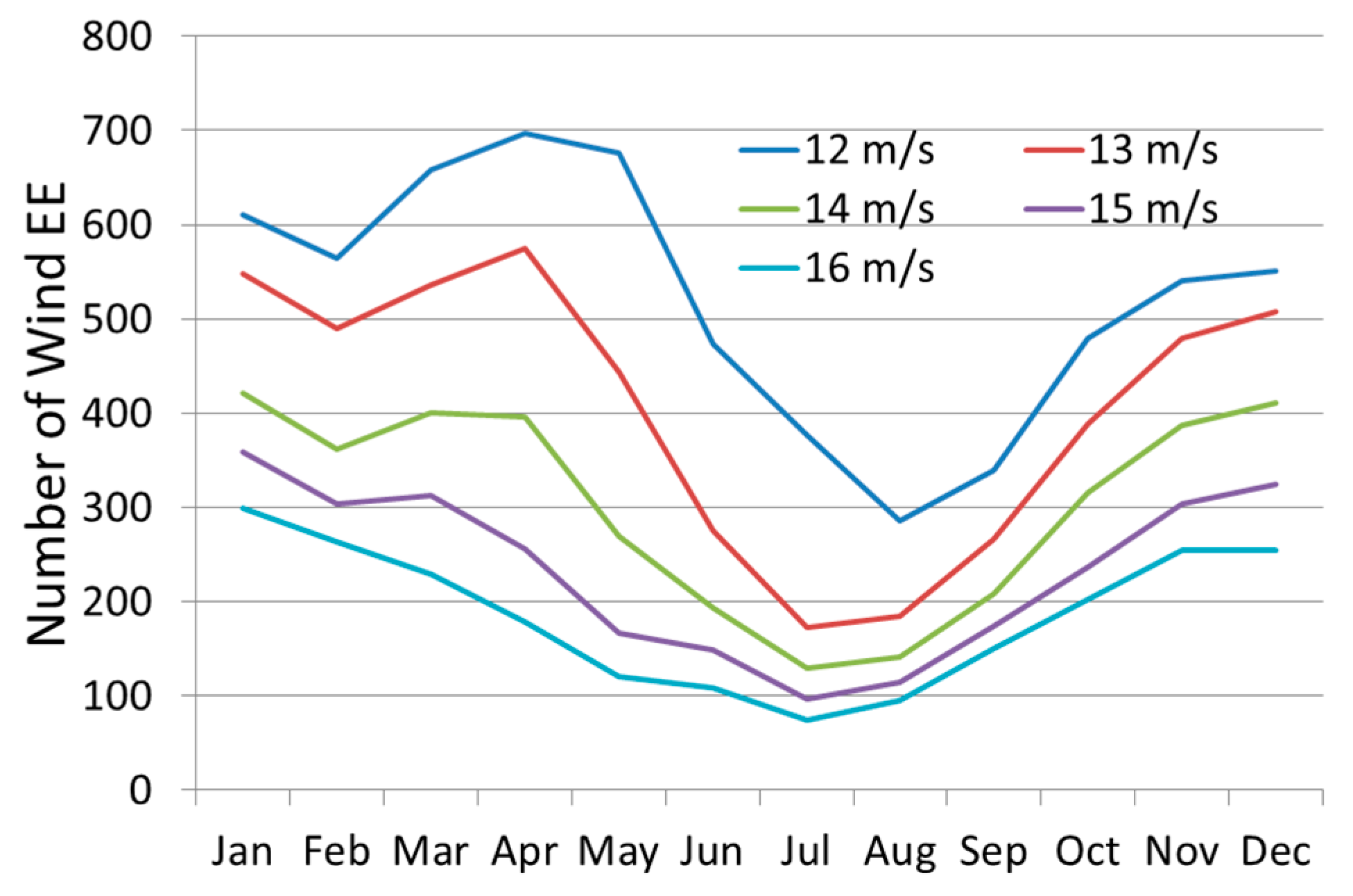
3.2. Quantitative Analysis of High Levels of Wave Energy Behavior in the GoM

As identified through the animation, most of the wave EEs in the GoM were generated by the northern wind from inland. However, the qualitative analysis of wind and wave interaction in the GoM needs to be expanded with quantitative analysis. This can reveal the exact correlation between the wind characteristics (speed and duration) and wave EEs. The time delay and other correlations between the wind and wave EEs will be characterized to develop a forecasting framework for wave energy behavior in the GoM, improving the design and operation of WECs. Categorizing wind speed to correlate with the wave EEs generated by the same wind was implemented to perform quantitative analysis. The Energy Events concept was applied to the wind in this research. A wind Energy Event was defined and identified as the wind resource in a predefined region that was over a given threshold (m/s). Five different threshold levels were applied to identify the number of wind EEs that generated wave EEs, including 12 m/s to 16 m/s in increments of 1 m/s. Lower thresholds were not considered for wind EEs because they did not generate wave EEs in the GoM area. Calendars were created for all wind EEs in the 36 years, including the starting and finishing timelines of all wind EEs under each threshold. Wind EEs’ calendar was correlated with wave EEs’ calendar under different thresholds, overlaps in locations, time periods, and direction patterns were identified and further analyzed. The analysis results are shown in Table 1 and Table 2.
Quantitative analysis of the phenomena described in Section 3.1 involves the discovery of the strength and duration of Wind Events to generate Wave Energy Events. Furthermore, the lag between the entrance of wind into the region and the initiation of wave energy is quantitatively evaluated to provide a wave energy forecasting tool. This research discovered that although wave energy is generated by wind, not all wind can produce waves. Only winds of certain strength and duration can generate wave energy. Table 1 indicates that wave EEs with low thresholds (25 and 35 kW/m) were more frequently generated by wind EEs on low thresholds (12 and 13 m/s), where 12 m/s and 13 m/s wind EEs produced more than 1000 wave EEs under 25 kW/m and 35 kW/m thresholds during 36 years. Meanwhile, the wind EEs under different thresholds (both low and high) generated similar numbers of wave EEs with high thresholds (55 to 100 kW/m). Quantitative analysis was further implemented to ascertain the reasons for low thresholds wind EEs generating more low thresholds wave EEs while high wind EEs generate similar numbers of wave EEs across all categories. Based on Figure 12, there were more low thresholds wind EEs in the GoM compared to high thresholds wind EEs, which means low thresholds wind EEs could produce more low thresholds wave EEs as highlighted by Table 1. As previously indicated, it is generally known that waves are generated from wind. However, this research indicates that not all wind generates harvestable wave energy. There was only a small portion of wind that generated harvestable wave energy, as indicated in Table 2. The wind characteristics, strength, and duration are critical in generating specific wave EEs.
A significant finding from this research is that wave EEs were not generated instantly by wind EEs, as highlighted in Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11. There is a significant time lag between wind entrance to the area and wave generation. Furthermore, Wind EE requires specific durations to generate a wave EE. Table 3 shows the mean and the standard deviation (Std) of the duration of wind EEs under different months and thresholds. It shows a high variability under different months and thresholds, which indicates that the duration of wind EEs could be a factor in determining the transfer of energy from wind to wave to generate a wave EE in the GoM.
Wind EEs need to reach a certain duration to generate wave EEs. The generation of high thresholds wave EEs may not only be related to the threshold level of wind EEs but also be related to the duration of wind EEs. Therefore, the average time needed for a certain wind EE to produce a wave EE was calculated for each threshold as shown in Table 4. A low 12 m/s wind EEs requires on average more than 38 h to generate a 100 kW/m wave EEs while it only requires 13 h to generate a 23 kW/m wave EEs. On the other hand, a high 16 m/s wind EEs can generate a 25 kW/m wave EEs on average in only 3.4 h and in only 15 h to generate a 100 kW/m wave EEs, which is less than 40% of which it took for the lowest wind level. These quantitative results provide a forecasting tool for wave energy. Having an input value the wind speeds can predict the energy profile of wave EEs that will be generated in the GoM. Table 4 forecast that as wind EEs increase their intensity they can generate more powerful wave EEs faster. On the other hand, for wind EEs longer duration is required to generate more powerful wave EEs. An increase of the wind EEs level from 12 m/s to 13 m/s decreases the time to generate a 25 kW/m wave EE by 38% compared to generating a 100 kW/m wave EE. The line chart provided in Figure 13 generates a better understanding of the relationship between the strength and duration of wind and its transfer to wave energy, identifying them as relevant factors related to the generation of wave EEs in the GoM.
Since both duration and strength of wind EEs were considered as factors of the generation of wave EEs, a frequency analysis on both factors was performed for all possible combinations to further understand the cycle of wave EEs’ creation. Figure 14a shows the number of wave EEs generated by 12 m/s wind EEs and the corresponding required duration of wind EEs. Since the profile curves of 25 kW/m and 35 kW/m wave EEs are skewed, it means that a shorter duration of 12 m/s wind EEs was able to produce 25 kW/m and 35 kW/m wave EEs. Meanwhile, the profile curves of high thresholds wave EEs in Figure 14a show high dispersion on required duration and less number of wave EEs, which indicates the duration needed for power transfer from the wind to wave on high thresholds was not uniform. Figure 14b shows the same information of 13 m/s wind EEs. The profile curves in Figure 14b increased its skewness to the right, which means reduced time and dispersion on the required duration for a 13 m/s wind EE to produce a wave EE compared to a 12 m/s wind EE.
When the thresholds of wind EEs increase to 14 m/s and 15 m/s (as shown in Figure 15), the profile curves increase their skewness to the right, which indicates the required duration and corresponding dispersion were reduced. For high thresholds wave EEs, the skewness increasing to the right indicates a better-defined behavior and a reduced average power transfer time from wind to wave. The results provided by these analyses are important to help WEC design by providing insight into the evaluation of the frequency and characteristics of wave EEs. Regions with more frequent energetic waves would require resilient WECs capable of energy extraction under those conditions. On the other hand, areas with reduced wave strength and frequency would be suitable for more sensitive and less resilient WECs, which in turn are less expensive. Therefore, the characteristics of the wave resource (wave EEs and Breaks) should drive the design characteristics and operation parameters of the WECs. Understanding how energy is transferred from wind to wave in the GoM will aid in the development of criteria required for the proper design and operation of WECs.
Figure 16 indicates that the required duration from wind to wave is significantly reduced for all wave EE categories when considering the highest wind EE threshold (16 m/s). The skewness and dispersion of the curves are similar to Figure 15, with only the 100 kW/m category showing increased dispersion. The main difference among all wave EE categories is that the number of wave EEs reduces as the threshold increases.

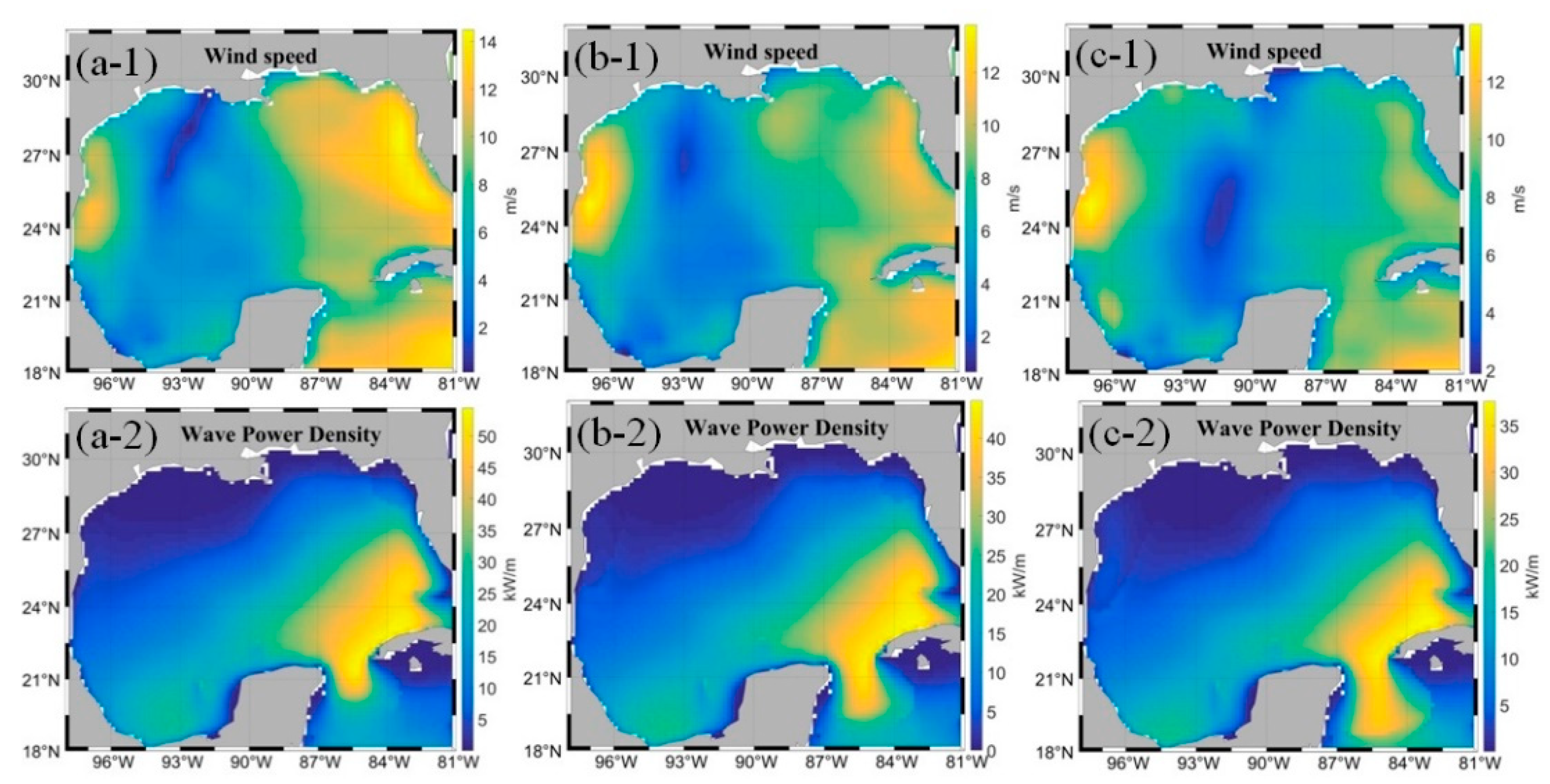
3.3. Low Levels Wave Energy in the GoM

Wave energy behavior in the GoM is unique with a distinctive two-state system with high and low levels of energy performance. During the low level periods (called Breaks), there still exists harvestable wave energy if adequately understood and forecasted. Breaks are time periods when the wave power density is less than the given threshold in a predefined region. To analyze the source of wave energy during the Breaks, the animation was used to observe its preliminary behavior patterns and underlying reasons, especially during the time periods when no wave EEs existed in the GoM. Two main sources of wave energy were discovered during the Breaks, which were related to power transferring from the Caribbean Ocean through the Straits of Yucatan and from the Atlantic Ocean through the Florida Straits (as identified in Figure 1).
A set of selected sequential frames from the animation is presented in Figure 17 and Figure 18. Figure 17 shows a swell from the Caribbean Ocean extended into the GoM through the Straits of Yucatan creating wave energy over the growing area through a combination of increasing significant wave height (Hs) and dominant wave period (Tp). This event started from hour 24:00 on 3 June 2000. The continuous temporal expansion of wave energy created by a swell entering the GoM through the Straits of Yucatan is shown in Figure 18. In both figures, the wave power density level was relatively low (less than 20 kW/m), which represents the Breaks periods.
A different scenario of wave power density changing in the GoM during the Breaks periods is presented in Figure 19 and Figure 20 through a set of selected animation frames from the January 2006 animation. This scenario started from hour 6:00 of 22 January 2006, in which the wave energy in the GoM was created by swells from the Straits of Yucatan and the Florida Straits. Both swells entered the GoM through narrow pathways and combined inside the GoM to create wave energy. The wave power density level is less than 35 kW/m, which means it happened during Breaks periods.
Figure 21 and Figure 22 show the number of months over 36 years without wind EEs and wave EEs above certain thresholds in the GoM. Figure 21 indicates that the absence of wind EEs was rare for low thresholds throughout the year while the absence of wind EEs for high thresholds increased from May to September. Weak wind EEs correlate with seasonal low summer wave power density levels in the GoM found in previous research [28,29,32]. Figure 22 shows the number of months without wave EEs above certain thresholds over 36 years. By comparing it with Figure 21, a strong correlation between wind EEs and wave EEs in the GoM was observed. From April to September, the absence of high thresholds wave EEs increased when there was fewer wind EEs. Both scenarios presented in Figure 17, Figure 18, Figure 19 and Figure 20 are part of many other similar scenarios observed in the completed animation of 36 years of data, which helped explain how wave energy was generated and presented in the GoM during the Breaks periods. Instead of local winds from inland, the wave energy in the GoM during Breaks was mainly generated by swells entering the GoM from the two narrow pathways, the Straits of Yucatan and the Florida Straits.

4. Conclusions

Using dynamic visualization based on computer animation and Energy Events concept, this paper investigated the detailed correlation between wind and wave energy and the underlying reasons for the unique behavior of wave energy in the GoM. During the wave EEs periods (high level wave energy), most of the wave energy in the GoM was generated through power transfer from the wind with increased wind speed due to local northern weather patterns in the GoM. The detailed correlation between wave energy behavior and strength and duration of wind was revealed. The wave energy behavior during wave EEs periods is mainly decided by the initial characteristics (speed, direction, duration) of the wind that originates the wave energy. During the Breaks periods, when there was no wave EE presented in the GoM, the wave energy in the GoM was mainly generated by the swells coming from the Caribbean and the Atlantic oceans, which entered the GoM through the two narrow pathways, the Straits of Yucatan and the Florida Straits. The discovery of different methods of wave energy generated in the GoM allowed a better understanding of the overall wave energy behavior in the region.
The new computer animation allowed the evaluation and discovery of new wave energy behavior patterns and their underlying reasons. Through exploratory and explanatory analysis of the animation, it enabled the authors to acquire a global perspective on wave energy behavior over large temporal and spatial criteria, and the possible interactions with other ocean resources. It was much easier and faster to identify some preliminary patterns, which were then analyzed in detail using Energy Events and Breaks concept. The combination of computer animation with other statistical and graphical rendering methods was a powerful synergetic tool for the advancement of knowledge on wave energy behavior. This synergetic tool could potentially be implemented to analyze other geographical areas with both similar and different behaviors. The study areas in this paper will be expanded to cover the Caribbean and the Atlantic oceans; so that the generation and transfer of swells entering the GoM can be tracked and analyzed together with meteorological data in the GoM to discover more detailed correlations and underlying reasons for wave energy behavior in the GoM during the Breaks periods.
The correlations and underlying reasons discovered in this paper related to wave energy behavior in the GoM will help in the design, placement, and operation of future WECs to improve their efficiency in harvesting wave energy. The discovered causality and prediction factors can be used to create a forecasting methodology specifically designed to predict wave EEs in the GoM. The forecasting method would provide new and important insights and ideas for wave energy harvesting, such as configuration-changing WECs to adapt the devices based on incoming waves to extract more wave energy. It should be noted that the meteorological data used in this paper has a spatial resolution of 1/6 longitude by 1/6 latitude (about 20 km by 20 km). Finer spatial resolution may be needed to conduct a detailed assessment and characterization of wave energy in the GoM or selected regions in the GoM for WEC design, placement, and operation purposes. The synergetic tool used in this paper will be easily used to conduct a detailed analysis if finer resolution data is available. In future research, the underlying factors of wave energy such as wave height, period, and directions will be evaluated, applying the GIS animation developed in this research. This may provide additional insights into wave energy performance in the GoM and its underlying characteristics.

Author Contributions

Data curation, F.H.-F.; Formal analysis, F.H.-F.; Funding acquisition, H.L.; Investigation, F.H.-F. and H.L.; Methodology, F.H.-F. and H.L.; Project administration, H.L.; Resources, H.L. and D.R.; Software, F.H.-F.; Supervision, H.L. and D.R.; Validation, F.H.-F.; Visualization, F.H.-F.; Writing—original draft, F.H.-F.; Writing—review & editing, H.L. and D.R. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data used in this study can be found from the databases cited in the paper. Data for the WaveWatch III can be found at the NOAA National Center for Environmental Prediction, Environmental Modeling Center online at https://polar.ncep.noaa.gov/waves/hindcasts/nopp-phase2/, accessed on 20 January 2022.

Acknowledgments

The authors are thankful to the support from CONACYT (Consejo Nacional de Ciencia y Tecnología) and COTACYT (Consejo Tamaulipeco de Ciencia y Tecnologia) through the scholarship number 218681, Texas A&M University-Kingsville, Eagle Ford Center for Research and Outreach, the Center for Research Excellence in Science and Technology-Research on Environmental Sustainability in Semi-Arid Coastal Areas (CREST-RESSACA) and National Science Foundation (award # EEC 1757812).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Cruz, J. Ocean Wave Energy: Current Status and Future Perspectives; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
  2. Holt, C. Energy from the Oceans. Phys. Educ. Lond. 2007, 42, 432. [Google Scholar] [CrossRef]
  3. Sawin, J.; Seyboth, K.; Sverrisson, F.; Adib, R.; Murdock, H. Renewables 2017 Global Status Report—REN21; REN21 Secretariat: Paris, France, 2017. [Google Scholar]
  4. Coe, R.G.; Neary, V.S. Review of methods for modeling wave energy converter survival in extreme sea states. In Proceedings of the 2nd Marine Energy Technology Symposium, METS2014, Seattle, WA, USA, 15–18 April 2014. [Google Scholar]
  5. Pelc, R.; Fujita, R.M. Renewable energy from the ocean. Mar. Policy 2002, 26, 471–479. [Google Scholar] [CrossRef]
  6. Astariz, S.; Iglesias, G. The economics of wave energy: A review. Renew. Sustain. Energy Rev. 2015, 45, 397–408. [Google Scholar] [CrossRef]
  7. Blummarch, P.A. Setback for Wave Power Technology. New York Times. 16 March 2009. Available online: https://www.nytimes.com/2009/03/16/ (accessed on 16 March 2016).
  8. Levitan, D. Why Wave Power Has Lagged Far behind as Energy Source. Yale Environment 360. Available online: https://e360.yale.edu-/feature/why_wave_power_has_lagged_far_behind_as_energy_source/2760 (accessed on 20 February 2015).
  9. Özger, M.; Şen, Z. Return period and risk calculations for ocean wave energy applications. Ocean. Eng. 2008, 35, 1700–1706. [Google Scholar] [CrossRef]
  10. Tiron, R.; Mallon, F.; Dias, F.; Reynaud, E.G. The challenging life of wave energy devices at sea: A few points to consider. Renewable and Sustainable Energy Rev. 2015, 43, 1263–1272. [Google Scholar] [CrossRef]
  11. Chawla, A.; Spindler, D.; Tolman, H. 30 Year Wave Hindcasts Using WAVEWATCH IIIR c with CFSR Winds Phase. NOAA/NWS/NCEP/MMAB, Maryland USA; National Oceanic and Atmospheric Administration. Environmental Modeling Center, Marine Modeling and Analysis Branch: Silver Spring, MA, USA, 2012.
  12. Penalba, M.; Ulazia, A.; Ibarra-Berastegui, G.; Ringwood, J.; Sáenz, J. Wave energy resource variation off the west coast of Ireland and its impact on realistic wave energy converters’ power absorption. Appl. Energy 2018, 224, 205–219. [Google Scholar] [CrossRef]
  13. Reguero, B.G.; Losada, I.J.; Méndez, F.J. A global wave power resource and its seasonal, interannual and long-term variability. Appl. Energy 2015, 148, 366–380. [Google Scholar] [CrossRef]
  14. Gu, C.; Li, H. Review on Deep Learning Research and Applications in Wind and Wave Energy. Energies 2022, 15, 1510. [Google Scholar] [CrossRef]
  15. Falnes, J. A review of wave-energy extraction. Mar. Struct. 2007, 20, 185–201. [Google Scholar] [CrossRef]
  16. Rusu, E. Evaluation of the wave energy conversion efficiency in various coastal environments. Energies 2014, 7, 4002–4018. [Google Scholar] [CrossRef] [Green Version]
  17. Bozzi, S.; Archetti, R.; Passoni, G. Wave electricity production in Italian offshore: A preliminary investigation. Renew. Energy 2014, 62, 407–416. [Google Scholar] [CrossRef]
  18. Stoutenburg, E.D.; Jenkins, N.; Jacobson, M.Z. Power output variations of co-located offshore wind turbines and wave energy converters in California. Renew. Energy 2010, 35, 2781–2791. [Google Scholar] [CrossRef]
  19. Haces-Fernandez, F.; Li, H.; Ramirez, D. A layout optimization method based on wave wake preprocessing concept for wave-wind hybrid energy farms. Energy Convers. Manag. 2021, 244, 114469. [Google Scholar] [CrossRef]
  20. Chakraborty, T.; Majumder, M. Impact of extreme events on conversion efficiency of wave energy converter. Energy Sci. Eng. 2020, 8, 3441–3456. [Google Scholar] [CrossRef] [Green Version]
  21. Chakraborty, T.; Majumder, M.; Khare, A. Application of AHP-VIKOR and GMDH framework to develop an indicator to identify utilisation potential of wave energy converter with respect to location. Int. J. Spatio Temporal Data Sci. 2019, 1, 98–113. [Google Scholar] [CrossRef]
  22. Chakraborty, T.; Majumder, M. Application of statistical charts, multi-criteria decision making and polynomial neural networks in monitoring energy utilization of wave energy converters. Environ. Dev. Sustain. 2019, 21, 199–219. [Google Scholar] [CrossRef]
  23. Gu, C.; Li, H. Wave Power Density Hotspot Distribution and Correlation Pattern Exploration in the Gulf of Mexico. Sustainability 2022, 14, 1158. [Google Scholar] [CrossRef]
  24. Neshat, M.; Mirjalili, S.; Sergiienko, N.Y.; Esmaeilzadeh, S.; Amini, E.; Heydari, A.; Garcia, D.A. Layout optimisation of offshore wave energy converters using a novel multi-swarm cooperative algorithm with backtracking strategy: A case study from coasts of Australia. Energy 2022, 239, 122463. [Google Scholar] [CrossRef]
  25. Amrutha, M.M.; Kumar, V.S. Evaluation of a few wave energy converters for the Indian shelf seas based on available wave power. Ocean. Eng. 2022, 244, 110360. [Google Scholar] [CrossRef]
  26. Naeem, M.; Jamal, T.; Diaz-Martinez, J.; Butt, S.A.; Montesano, N.; Tariq, M.I.; De-La-Hoz-Valdiris, E. Trends and future perspective challenges in big data. In Advances in Intelligent Data Analysis and Applications; Springer: Singapore, 2022; pp. 309–325. [Google Scholar]
  27. Nastasi, B.; Markovska, N.; Puksec, T.; Duić, N.; Foley, A. Renewable and sustainable energy challenges to face for the achievement of Sustainable Development Goals. Renew. Sustain. Energy Rev. 2022, 157, 112071. [Google Scholar] [CrossRef]
  28. Haces-Fernandez, F.; Martinez, A.; Ramirez, D.; Li, H. Characterization of wave energy patterns in Gulf of Mexico. In Proceedings of the IISE 2017 Annual Conference, Pittsburgh, PA, USA, 20–23 May 2017; pp. 1532–1537. [Google Scholar]
  29. Haces-Fernandez, F.; Ramirez, D.; Li, H. Wave Energy Characterization and Assessment in the U.S. Gulf of Mexico, East and West Coasts with Energy Event Concept. Renew. Energy 2018, 123, 312–322. [Google Scholar] [CrossRef]
  30. Jacobson, P.T.; Hagerman, G.; Scott, G. Mapping and Assessment of the United States Ocean Wave Energy Resource; (No. DOE/GO/18173-1); Electric Power Research Institute: Washington, DC, USA, 2011. [Google Scholar]
  31. Gadad, S.; Deka, P.C. Offshore wind power resource assessment using Oceansat-2 scatterometer data at a regional scale. Appl. Energy 2016, 176, 157–170. [Google Scholar] [CrossRef]
  32. Aderinto, T.O.; Haces-Fernandez, F.; Li, H. Design and Potential Application of Small Scale Wave Energy Converter—ASME International Mechanical Engineering Congress and Exposition. Energies 2017, 6, V006T08A084. [Google Scholar] [CrossRef]
  33. Haces-Fernandez, F. Investigation on the Possibility of Extracting Wave Energy from the Texas Coast. Master’s Thesis, Texas A&M University-Kingsville, Texas, TX, USA, 2014. [Google Scholar]
  34. Haces-Fernandez, F.; Li, H.; Ramirez, D. Assessment of the Potential of Energy Extracted from Waves and Wind to Supply Offshore Oil Platforms Operating in the Gulf of Mexico. Energies 2018, 11, 1084. [Google Scholar] [CrossRef] [Green Version]
  35. Hsu, C.T.; Wu, H.Y.; Hsu, E.Y.; Street, R.L. Momentum and energy transfer in wind generation of waves. J. Phys. Oceanogr. 1982, 12, 929–951. [Google Scholar] [CrossRef] [Green Version]
  36. Masuda, A. Nonlinear energy transfer between wind waves. J. Phys. Oceanogr. 1980, 10, 2082–2093. [Google Scholar] [CrossRef] [Green Version]
  37. Tolman, H.L. User Manual and System Documentation of WAVEWATCH III TM Version 3.14; Technical note; MMAB Contribution 276, no. 220, May 2009. Available online: https://polar.ncep.noaa.gov/mmab/papers/tn276/MMAB_276.pdf (accessed on 20 January 2022).
  38. Whitford, D.J. Teaching ocean wave forecasting using computer-generated visualization and animation-Part 1: Sea forecasting. Comput. Geosci. 2002, 28, 537–546. [Google Scholar] [CrossRef]
  39. Appendini, C.M.; Urbano-Latorre, C.P.; Figueroa, B.; Dagua-Paz, C.J.; Torres-Freyermuth, A.; Salles, P. Wave energy potential assessment in the Caribbean Low Level Jet using wave hindcast information. Appl. Energy 2015, 137, 375–384. [Google Scholar] [CrossRef]
  40. Available online: https://polar.ncep.noaa.gov/waves/wavewatch/ (accessed on 20 January 2022).
  41. Guiberteau, K.L.; Liu, Y.; Lee, J.; Kozman, T.A. Investigation of developing wave energy technology in the Gulf of Mexico. Distrib. Gener. Altern. Energy J. 2012, 27, 36–52. [Google Scholar]
  42. McArthur, S.; Brekken, T.K. Ocean wave power data generation for grid integration studies. In Proceedings of the 2010 IEEE Power and Energy Society General Meeting, Minneapolis, MN, USA, 25–29 July 2010; pp. 1–6. [Google Scholar]
  43. Thorpe, T.W. A Brief Review of Wave Energy; Harwell Laboratory, Energy Technology Support Unit: London, UK, 1999. [Google Scholar]
  44. Mirzaei, A.; Tangang, F.; Juneng, L. Wave energy potential along the east coast of Peninsular Malaysia. Energy 2014, 68, 722–734. [Google Scholar] [CrossRef]
  45. Musial, W.D. Status of Wave and Tidal Power Technologies for the United States; National Renewable Energy Laboratory: Golden, CO, USA, 2008.
  46. Kamranzad, B.; Etemad-Shahidi, A.; Chegini, V. Sustainability of wave energy resources in southern Caspian Sea. Energy 2016, 97, 549–559. [Google Scholar] [CrossRef] [Green Version]
  47. Contestabile, P.; Ferrante, V.; Vicinanza, D. Wave energy resource along the coast of Santa Catarina (Brazil). Energies 2015, 8, 14219–14243. [Google Scholar] [CrossRef] [Green Version]
  48. Hagerman, G. Southern New England wave energy resource potential. In Building Energy; Tufts University: Boston, MA, USA, 2001. [Google Scholar]
  49. Spindler, D.M.; Chawla, A.; Tolman, H.L. An Initial Look at the CFSR Reanalysis Winds for Wave Modeling; Technical Note; Environmental Modeling Center-Marine Modeling and Analysis Branch—NOAA: College Park, MA, USA, 2011.
  50. Von Landesberger, T.; Bremm, S.; Andrienko, N.; Andrienko, G.; Tekusova, M. Visual analytics methods for categoric spatio-temporal data. In Proceedings of the 2012 IEEE Conference on Visual Analytics Science and Technology (VAST), Seattle, WA, USA, 14–19 October 2012; pp. 183–192. [Google Scholar]
  51. Li, S.; Dragicevic, S.; Castro, F.A.; Sester, M.; Winter, S.; Coltekin, A.; Cheng, T. Geospatial big data handling theory and methods: A review and research challenges. ISPRS J. Photogramm. Remote Sens. 2016, 115, 119–133. [Google Scholar] [CrossRef] [Green Version]
  52. Guillou, N. Estimating wave energy flux from significant wave height and peak period. Renew. Energy 2020, 155, 1383–1393. [Google Scholar] [CrossRef]
  53. Morim, J.; Cartwright, N.; Etemad-Shahidi, A.; Strauss, D.; Hemer, M. Wave energy resource assessment along the Southeast coast of Australia on the basis of a 31-year hindcast. Appl. Energy 2016, 184, 276–297. [Google Scholar] [CrossRef]
  54. Klemeš, J.J.; Kravanja, Z.; Varbanov, P.S.; Lam, H.L. Advanced multimedia engineering education in energy, process integration and optimisation. Appl. Energy 2013, 101, 33–40. [Google Scholar] [CrossRef]
  55. Mari, R.; Bottai, L.; Busillo, C.; Calastrini, F.; Gozzini, B.; Gualtieri, G. A GIS-based interactive web decision support system for planning wind farms in Tuscany (Italy). Renew. Energy 2011, 36, 754–763. [Google Scholar] [CrossRef]
  56. Baban, S.M.; Parry, T. Developing and applying a GIS-assisted approach to locating wind farms in the UK. Renew. Energy 2001, 24, 59–71. [Google Scholar] [CrossRef]
  57. Blok, C.; Kobben, B.; Cheng, T.; Kuterema, A.A. Visualization of relationships between spatial patterns in time by cartographic animation. Cartogr. Geogr. Inf. Sci. 1999, 26, 139–151. [Google Scholar] [CrossRef]
  58. Ramírez, G.; de Dios, J.; Mejía Fuentes, O.I.; Menjívar Pino, P.J. Evaluación del Potencial Energético del Oleaje en las Costas de El Salvador. Ph.D. Thesis, Universidad de El Salvador, San Salvador, El Salvador, 2013. [Google Scholar]
  59. Sierra, J.P.; González-Marco, D.; Sospedra, J.; Gironella, X.; Mösso, C.; Sánchez-Arcilla, A. Wave energy resource assessment in Lanzarote (Spain). Renew. Energy 2013, 55, 480–489. [Google Scholar] [CrossRef]
  60. Alonso, R.; Solari, S.; Teixeira, L. Wave energy resource assessment in Uruguay. Energy 2015, 93, 683–696. [Google Scholar] [CrossRef]
  61. Neill, S.P.; Hashemi, M.R. Wave power variability over the northwest European shelf seas. Appl. Energy 2013, 106, 31–46. [Google Scholar] [CrossRef]
  62. Neill, S.P.; Lewis, M.J.; Hashemi, M.R.; Slater, E.; Lawrence, J.; Spall, S.A. Inter-annual and inter-seasonal variability of the Orkney wave power resource. Appl. Energy 2014, 132, 339–348. [Google Scholar] [CrossRef] [Green Version]
  63. Langodan, S.; Viswanadhapalli, Y.; Dasari, H.P.; Knio, O.; Hoteit, I. A high-resolution assessment of wind and wave energy potentials in the Red Sea. Appl. Energy 2016, 181, 244–255. [Google Scholar] [CrossRef]
  64. Commin, A.N.; French, A.S.; Marasco, M.; Loxton, J.; Gibb, S.W.; McClatchey, J. The influence of the North Atlantic Oscillation on diverse renewable generation in Scotland. Appl. Energy 2017, 205, 855–867. [Google Scholar] [CrossRef]
  65. Monforti, F.; Gonzalez-Aparicio, I. Comparing the impact of uncertainties on technical and meteorological parameters in wind power time series modelling in the European Union. Appl. Energy 2017, 206, 439–450. [Google Scholar] [CrossRef]
  66. Chen, J.; Yang, S.; Li, H.; Zhang, B.; Lv, J. Research on geographical environment unit division based on the method of natural breaks (Jenks). Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 3, 47–50. [Google Scholar] [CrossRef] [Green Version]
  67. Wong, M.S.; Zhu, R.; Liu, Z.; Lu, L.; Peng, J.; Tang, Z.; Chan, W.K. Estimation of Hong Kong’s solar energy potential using GIS and remote sensing technologies. Renew. Energy 2016, 99, 325–335. [Google Scholar] [CrossRef]
  68. Mellino, S.; Ulgiati, S. Mapping the evolution of impervious surfaces to investigate landscape metabolism: An Emergy–GIS monitoring application. Ecol. Inform. 2015, 26, 50–59. [Google Scholar] [CrossRef]
  69. Miller, A.; Li, R. A geospatial approach for prioritizing wind farm development in Northeast Nebraska, USA. ISPRS Int. J. Geo Inf. 2014, 3, 968–979. [Google Scholar] [CrossRef] [Green Version]
Sustainability 14 04687 g001 550
Figure 1. Studying Area in this study.
Figure 1. Studying Area in this study.
Sustainability 14 04687 g001
Sustainability 14 04687 g002 550
Figure 2. Static map of wave power density in January 1985 with a unit of kW/m: (a) average and (b) standard deviation.
Figure 2. Static map of wave power density in January 1985 with a unit of kW/m: (a) average and (b) standard deviation.
Sustainability 14 04687 g002
Sustainability 14 04687 g003 550
Figure 3. The average wave power density of the GoM area in January 1985.
Figure 3. The average wave power density of the GoM area in January 1985.
Sustainability 14 04687 g003
Sustainability 14 04687 g004 550
Figure 4. Three-dimensional histograms of daily average wave power density in January 1985 segmented by (a) latitude and (b) longitude.
Figure 4. Three-dimensional histograms of daily average wave power density in January 1985 segmented by (a) latitude and (b) longitude.
Sustainability 14 04687 g004
Sustainability 14 04687 g005 550
Figure 5. Selected frames from the animation of January 1985 indicating high wave energy in different regions at the GoM: (a) hour 18:00 of day 3, (b) hour 12:00 of day 13, and (c) hour 6:00 of day 14.
Figure 5. Selected frames from the animation of January 1985 indicating high wave energy in different regions at the GoM: (a) hour 18:00 of day 3, (b) hour 12:00 of day 13, and (c) hour 6:00 of day 14.
Sustainability 14 04687 g005
Sustainability 14 04687 g006 550
Figure 6. Selected frames from the animation of January 1985 indicating a wave Energy Event traveling from north to south: (a) hour 21:00 of day 20, (b) hour 9:00 of day 21, and (c) hour 3:00 of day 22.
Figure 6. Selected frames from the animation of January 1985 indicating a wave Energy Event traveling from north to south: (a) hour 21:00 of day 20, (b) hour 9:00 of day 21, and (c) hour 3:00 of day 22.
Sustainability 14 04687 g006
Sustainability 14 04687 g007 550
Figure 7. Sequential frames from January 2006 animation to show the changes in wind speed and wave power density on 13 January 2006: (a-1,a-2) 18:00, (b-1,b-2) 21:00, and (c-1,c-2) 24:00, where the first row shows wind speed and the second row shows row wave power density.
Figure 7. Sequential frames from January 2006 animation to show the changes in wind speed and wave power density on 13 January 2006: (a-1,a-2) 18:00, (b-1,b-2) 21:00, and (c-1,c-2) 24:00, where the first row shows wind speed and the second row shows row wave power density.
Sustainability 14 04687 g007
Sustainability 14 04687 g008 550
Figure 8. Sequential frames from January 2006 animation to show the changes in wind speed and wave power density on 14 January 2006: (a-1,a-2) 3:00, (b-1,b-2) 6:00, and (c-1,c-2) 9:00, where the first row shows wind speed and the second row shows row wave power density.
Figure 8. Sequential frames from January 2006 animation to show the changes in wind speed and wave power density on 14 January 2006: (a-1,a-2) 3:00, (b-1,b-2) 6:00, and (c-1,c-2) 9:00, where the first row shows wind speed and the second row shows row wave power density.
Sustainability 14 04687 g008
Sustainability 14 04687 g009 550
Figure 9. Sequential frames from January 2006 animation to show the changes in wind speed and wave power density on 14 January 2006: (a-1,a-2) 12:00, (b-1,b-2) 15:00, and (c-1,c-2) 18:00, where the first row shows wind speed and the second row shows row wave power density.
Figure 9. Sequential frames from January 2006 animation to show the changes in wind speed and wave power density on 14 January 2006: (a-1,a-2) 12:00, (b-1,b-2) 15:00, and (c-1,c-2) 18:00, where the first row shows wind speed and the second row shows row wave power density.
Sustainability 14 04687 g009
Sustainability 14 04687 g010 550
Figure 10. Sequential frames from January 2006 animation to show the changes in wind speed and wave power density on 14 and 15 January 2006: (a-1,a-2) 21:00, (b-1,b-2) 24:00, and (c-1,c-2) 3:00, where the first row shows wind speed and the second row shows row wave power density.
Figure 10. Sequential frames from January 2006 animation to show the changes in wind speed and wave power density on 14 and 15 January 2006: (a-1,a-2) 21:00, (b-1,b-2) 24:00, and (c-1,c-2) 3:00, where the first row shows wind speed and the second row shows row wave power density.
Sustainability 14 04687 g010
Sustainability 14 04687 g011 550
Figure 11. Sequential frames from January 2006 animation to show the changes in wind speed and wave power density on 15 January 2006: (a-1,a-2) 15:00, (b-1,b-2) 18:00, and (c-1,c-2) 21:00, where the first row shows wind speed and the second row shows row wave power density.
Figure 11. Sequential frames from January 2006 animation to show the changes in wind speed and wave power density on 15 January 2006: (a-1,a-2) 15:00, (b-1,b-2) 18:00, and (c-1,c-2) 21:00, where the first row shows wind speed and the second row shows row wave power density.
Sustainability 14 04687 g011
Sustainability 14 04687 g012 550
Figure 12. Number of wind EEs per month over 36 years.
Figure 12. Number of wind EEs per month over 36 years.
Sustainability 14 04687 g012
Sustainability 14 04687 g013 550
Figure 13. Duration required for wind EE to produce a wave EE.
Figure 13. Duration required for wind EE to produce a wave EE.
Sustainability 14 04687 g013
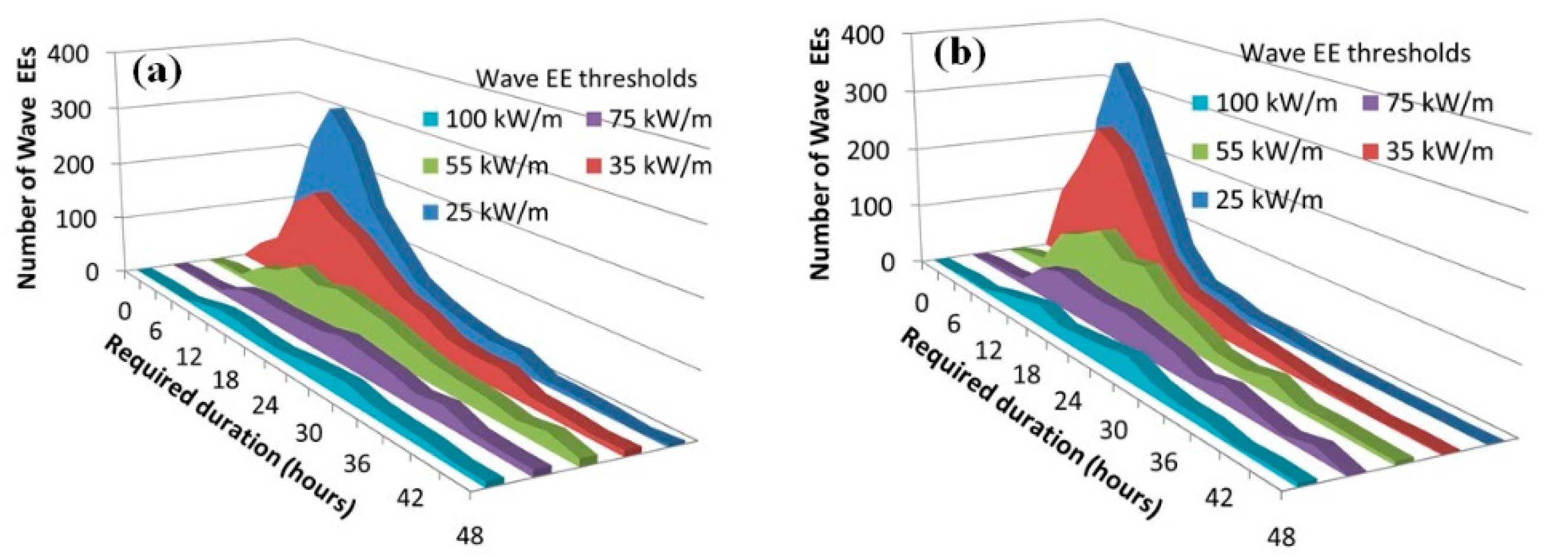
Sustainability 14 04687 g014 550
Figure 14. Three-dimensional histogram on the required number of wave EEs generated by a wind EE and its required duration over 36 years in the GoM: (a) 12 m/s wind EE, and (b) 13 m/s wind EE.
Figure 14. Three-dimensional histogram on the required number of wave EEs generated by a wind EE and its required duration over 36 years in the GoM: (a) 12 m/s wind EE, and (b) 13 m/s wind EE.
Sustainability 14 04687 g014
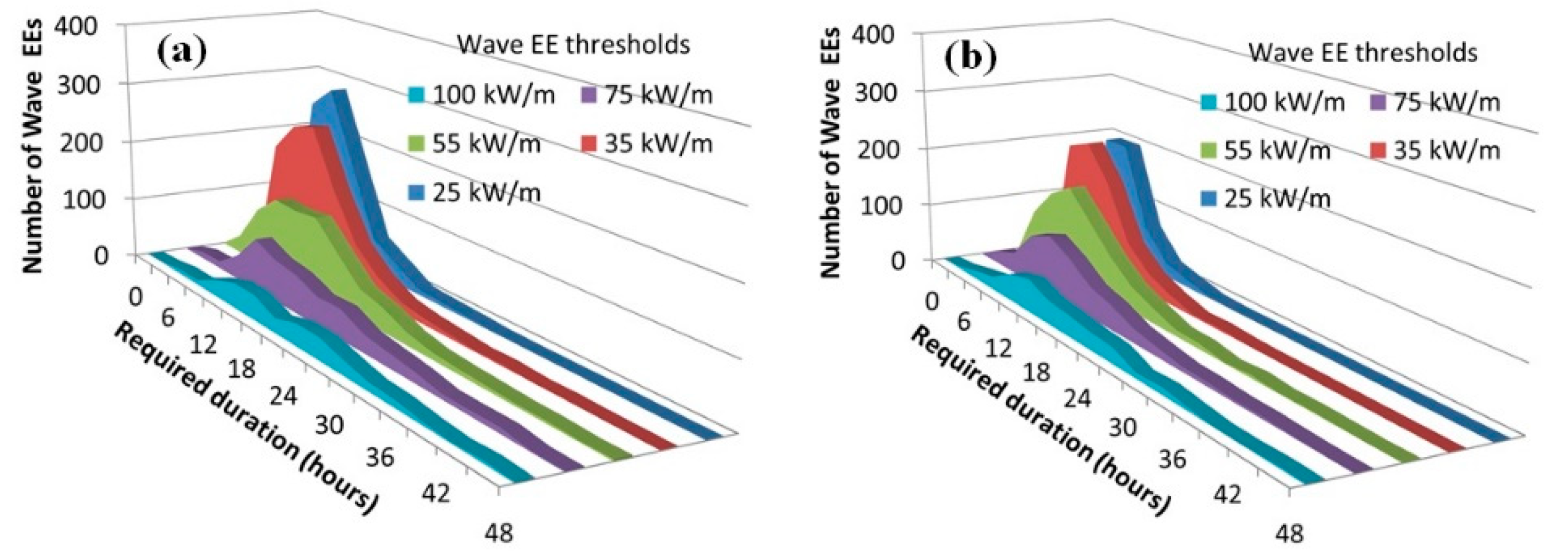
Sustainability 14 04687 g015 550
Figure 15. Three-dimensional histogram on the required number of wave EEs generated by a wind EE and its required duration over 36 years in the GoM: (a) 14 m/s wind EE and (b) 15 m/s wind EE.
Figure 15. Three-dimensional histogram on the required number of wave EEs generated by a wind EE and its required duration over 36 years in the GoM: (a) 14 m/s wind EE and (b) 15 m/s wind EE.
Sustainability 14 04687 g015
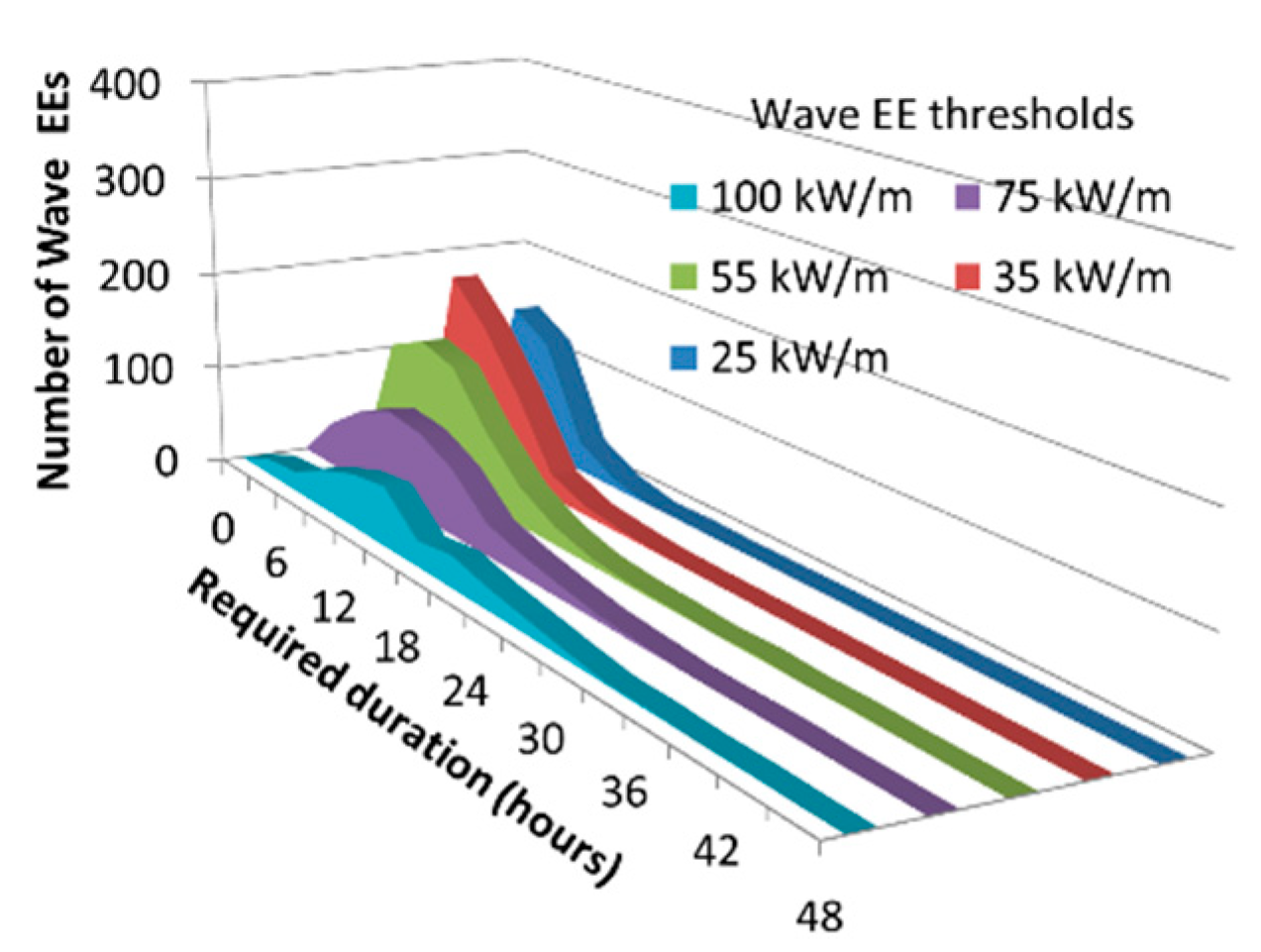
Sustainability 14 04687 g016 550
Figure 16. Three-dimensional histogram on the required number of wave EEs generated by a 16 m/s wind EE and its required duration over 36 years in the GoM.
Figure 16. Three-dimensional histogram on the required number of wave EEs generated by a 16 m/s wind EE and its required duration over 36 years in the GoM.
Sustainability 14 04687 g016
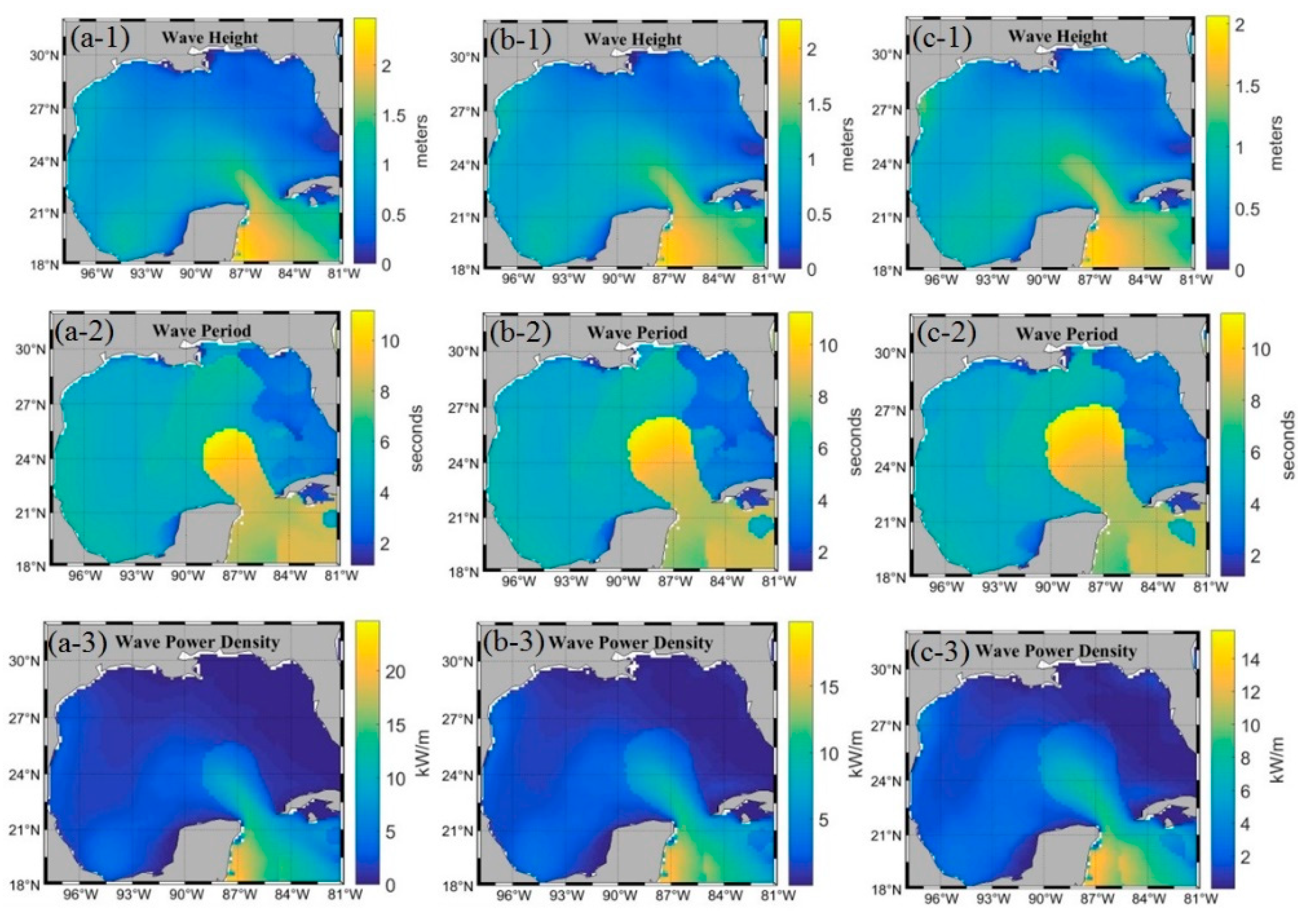
Sustainability 14 04687 g017 550
Figure 17. Sequential frames from June 2000 animation to show the changes in wave period, wave height, and wave power density on 3 and 4 June 2006: (a-1,a-2,a-3) 24:00 on June 3, (b-1,b-2,b-3) 3:00 on 4 June, and (c-1,c-2,c-3) 6:00 on 4 June, where three rows show wind height, wind period and wave power density, respectively.
Figure 17. Sequential frames from June 2000 animation to show the changes in wave period, wave height, and wave power density on 3 and 4 June 2006: (a-1,a-2,a-3) 24:00 on June 3, (b-1,b-2,b-3) 3:00 on 4 June, and (c-1,c-2,c-3) 6:00 on 4 June, where three rows show wind height, wind period and wave power density, respectively.
Sustainability 14 04687 g017
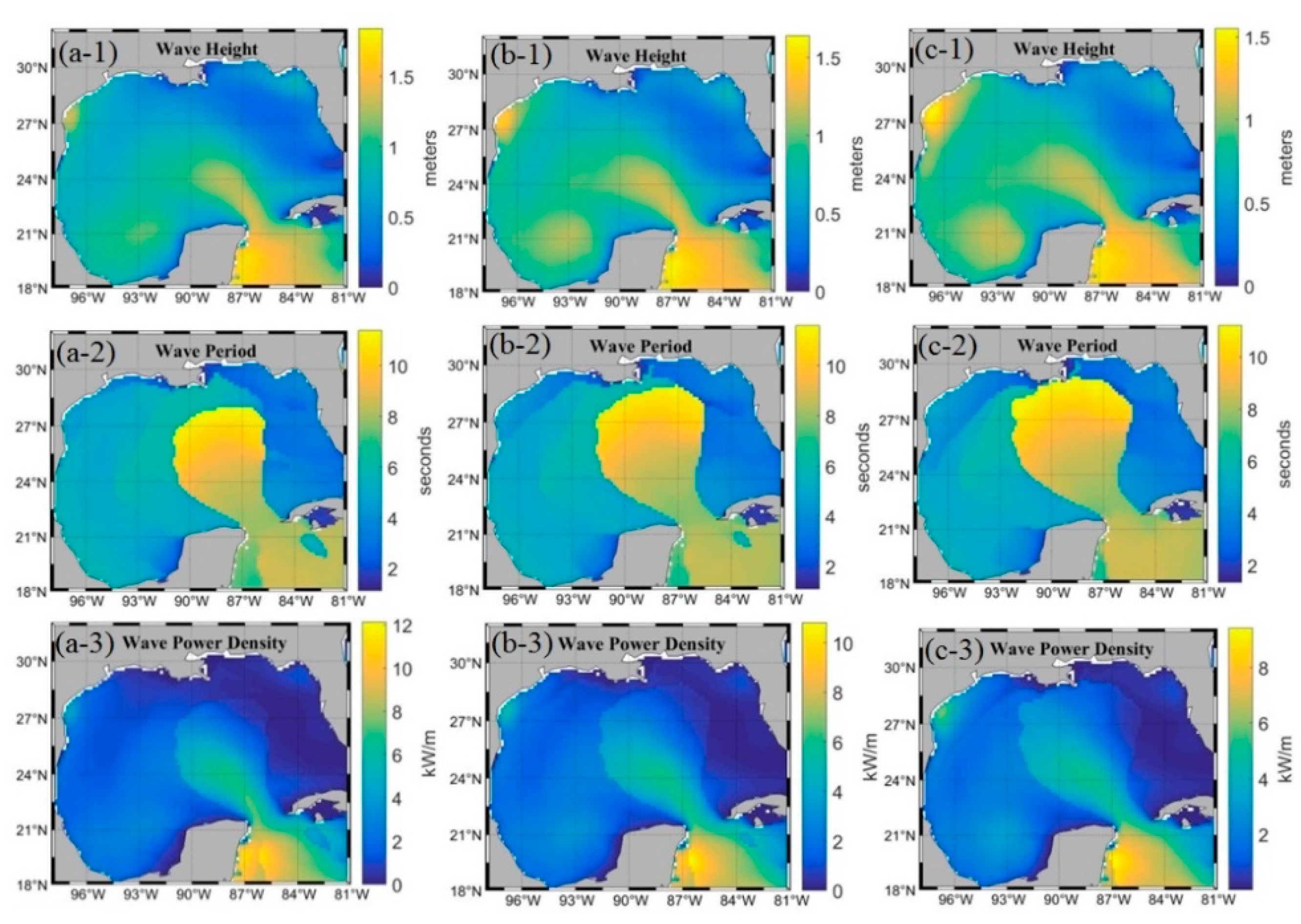
Sustainability 14 04687 g018 550
Figure 18. Sequential frames from June 2000 animation to show the changes in wave period, wave height, and wave power density on 4 June 2006: (a-1,a-2,a-3) 9:00, (b-1,b-2,b-3) 12:00, and (c-1,c-2,c-3) 15:00, where three rows show wind height, wind period and wave power density, respectively.
Figure 18. Sequential frames from June 2000 animation to show the changes in wave period, wave height, and wave power density on 4 June 2006: (a-1,a-2,a-3) 9:00, (b-1,b-2,b-3) 12:00, and (c-1,c-2,c-3) 15:00, where three rows show wind height, wind period and wave power density, respectively.
Sustainability 14 04687 g018
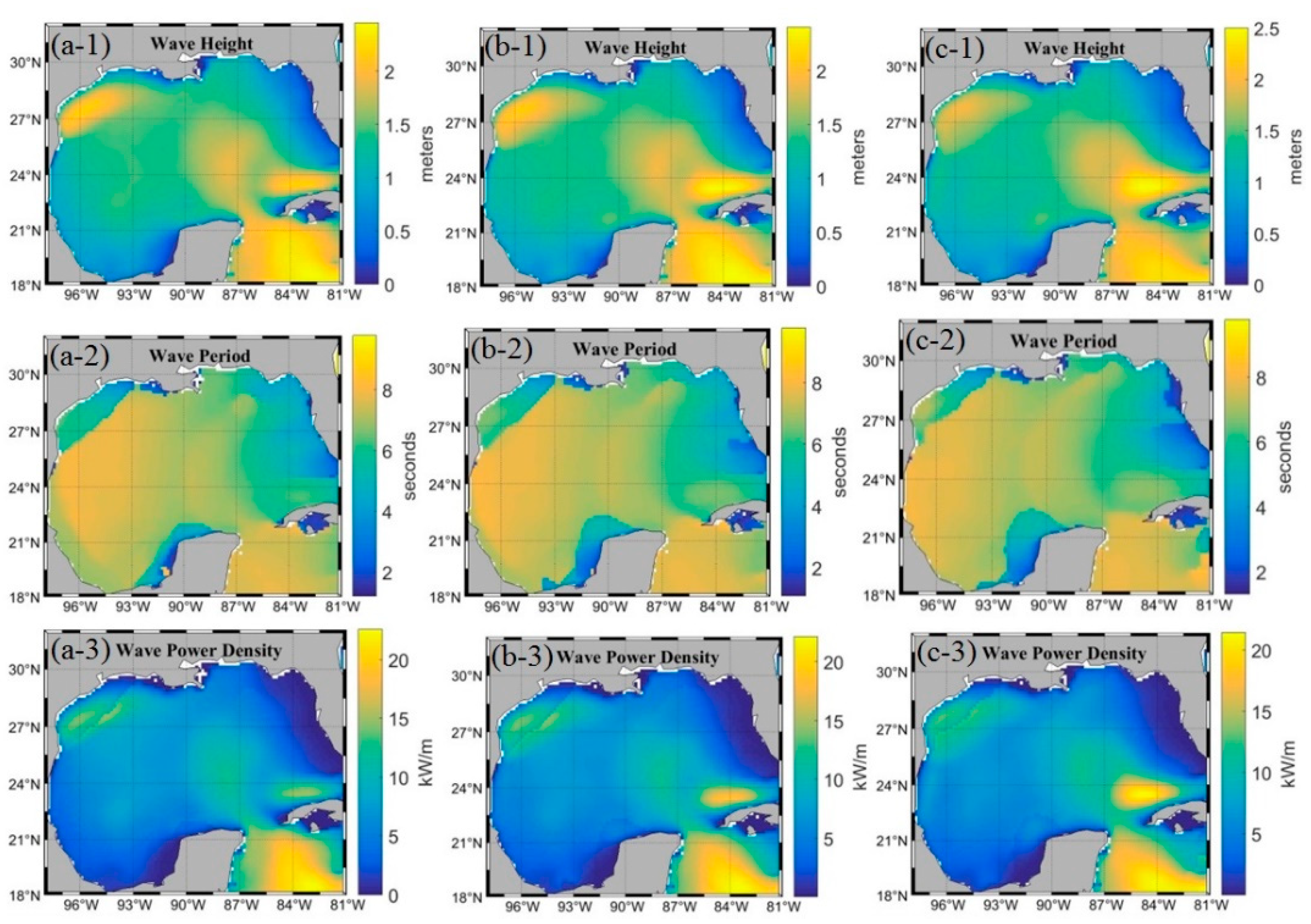
Sustainability 14 04687 g019 550
Figure 19. Sequential frames from January 2006 animation to show the changes in wave period, wave height, and wave power density on 22 January 2006: (a-1,a-2,a-3) 6:00, (b-1,b-2,b-3) 9:00, and (c-1,c-2,c-3) 12:00, where three rows show wind height, wind period and wave power density, respectively.
Figure 19. Sequential frames from January 2006 animation to show the changes in wave period, wave height, and wave power density on 22 January 2006: (a-1,a-2,a-3) 6:00, (b-1,b-2,b-3) 9:00, and (c-1,c-2,c-3) 12:00, where three rows show wind height, wind period and wave power density, respectively.
Sustainability 14 04687 g019
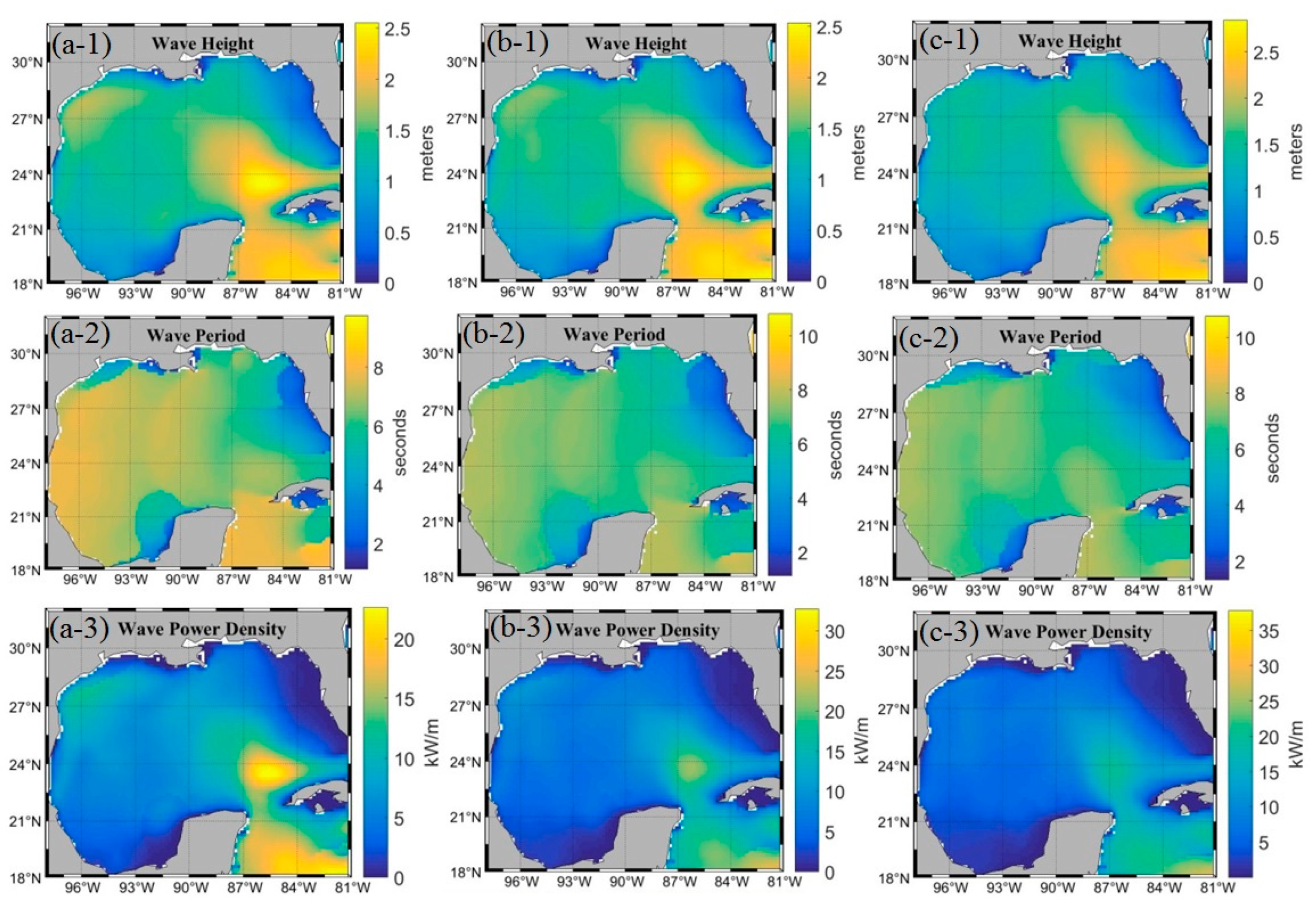
Sustainability 14 04687 g020 550
Figure 20. Sequential frames from January 2006 animation to show the changes in wave period, wave height, and wave power density on 22 January 2006: (a-1,a-2,a-3) 15:00, (b-1,b-2,b-3) 18:00, and (c-1,c-2,c-3) 21:00, where three rows show wind height, wind period and wave power density, respectively.
Figure 20. Sequential frames from January 2006 animation to show the changes in wave period, wave height, and wave power density on 22 January 2006: (a-1,a-2,a-3) 15:00, (b-1,b-2,b-3) 18:00, and (c-1,c-2,c-3) 21:00, where three rows show wind height, wind period and wave power density, respectively.
Sustainability 14 04687 g020
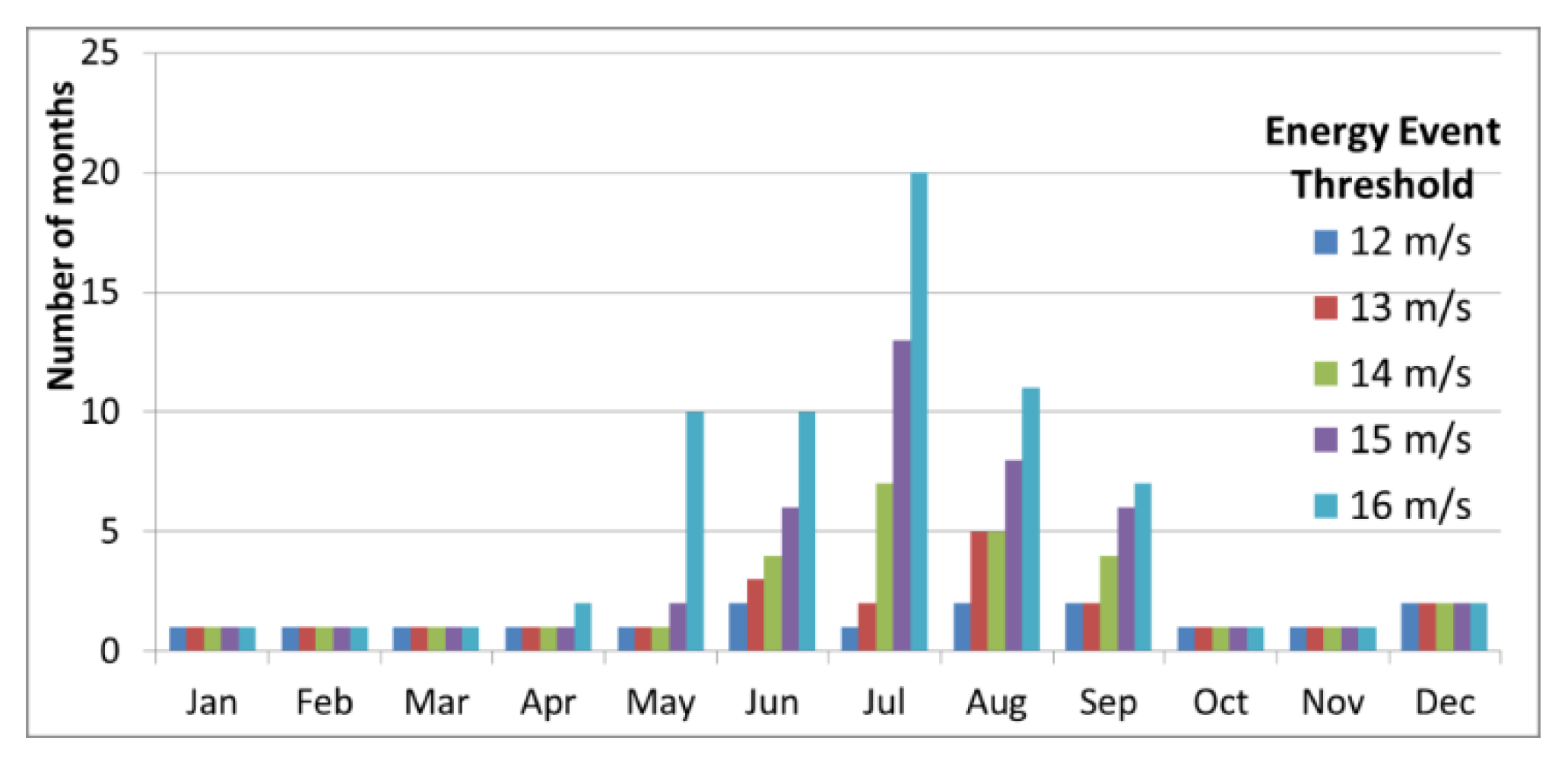
Sustainability 14 04687 g021 550
Figure 21. The number of months without wind EEs above certain thresholds in the period 1979–2014.
Figure 21. The number of months without wind EEs above certain thresholds in the period 1979–2014.
Sustainability 14 04687 g021
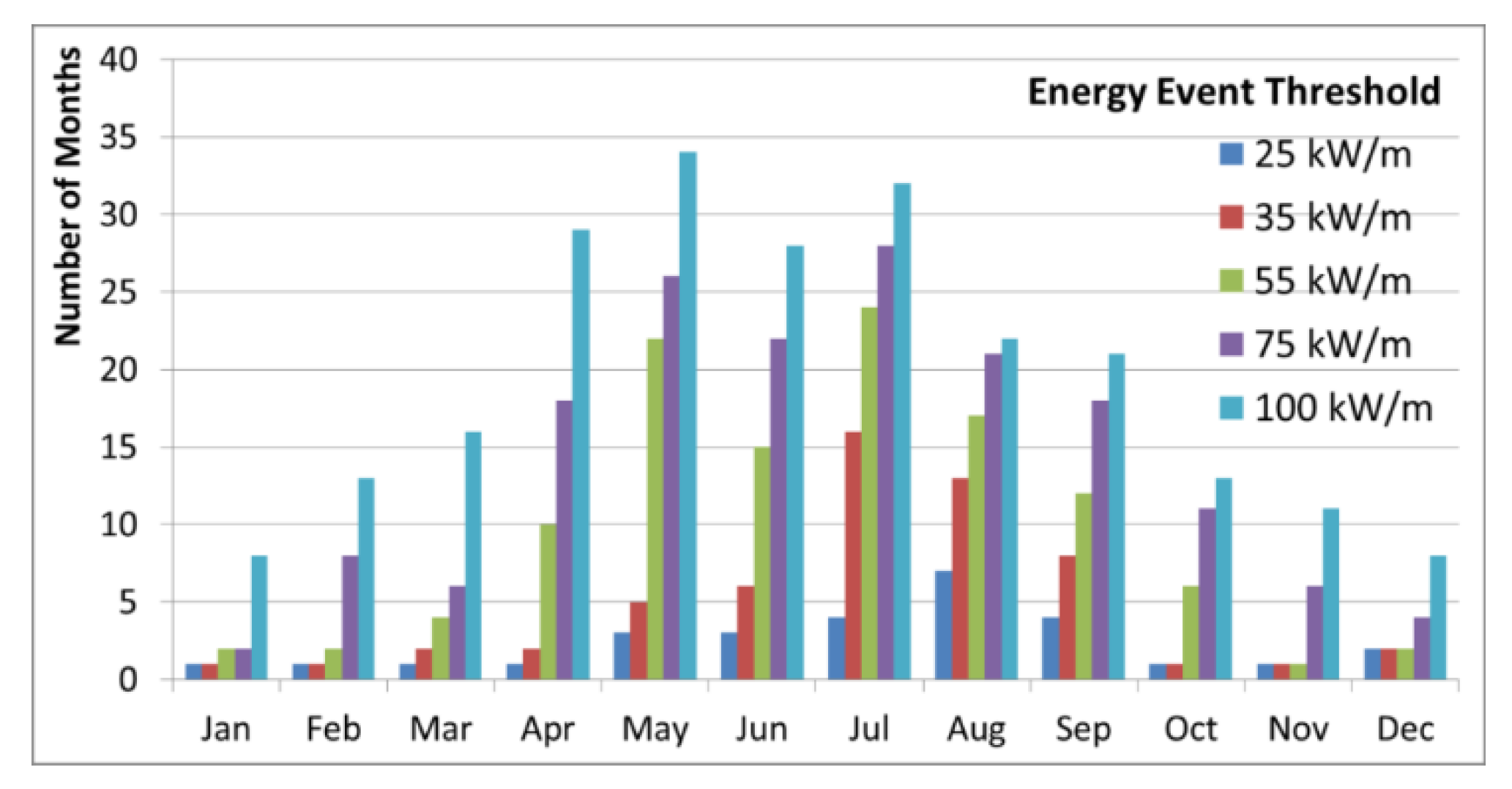
Sustainability 14 04687 g022 550
Figure 22. The number of months without Wave EEs above certain thresholds in the period 1979–2014.
Figure 22. The number of months without Wave EEs above certain thresholds in the period 1979–2014.
Sustainability 14 04687 g022
Table
Table 1. Number of wave EEs produced by wind EEs under different threshold levels in the GoM over 36 years.
Table 1. Number of wave EEs produced by wind EEs under different threshold levels in the GoM over 36 years.
Wind (m/s)Wave Energy Events (kW/m)
25355575100
1214301127690440276
1312091156733473294
14815949736483305
15503685659480308
16304461540440299
Table
Table 2. Percentage of wind EEs that generated wave EEs under different thresholds.
Table 2. Percentage of wind EEs that generated wave EEs under different thresholds.
Wind (m/s)Wave Energy Events (kW/m)
25355575100
1223%18%11%7%4%
1325%24%15%10%6%
1422%26%20%13%8%
1518%24%24%17%11%
1614%21%24%20%13%
Table
Table 3. Mean and Standard Deviation (Std) of wind EEs under different months and thresholds.
Table 3. Mean and Standard Deviation (Std) of wind EEs under different months and thresholds.
Wind (m/s)Data TypeDuration of Wind EE (h)
Jan.Feb.Mar.Apr.MayJun.Jul.Aug.Sep.Oct.Nov.Dec.
12Mean23211915111191322212423
Std272626191420182232343227
13Mean18171511911111520191918
Std221919131119202330312521
14Mean1715139710101419171616
Std19171610916182329282117
15Mean14131186991418171514
Std1515139814182430271815
16Mean11101075881416151312
Std1213118712172429261513
Table
Table 4. Average Time (hours) needed for a wind EE to produce a wave EE under different thresholds in the GoM over 36 years.
Table 4. Average Time (hours) needed for a wind EE to produce a wave EE under different thresholds in the GoM over 36 years.
Wind (m/s)Wave Energy Events (kW/m)
25355575100
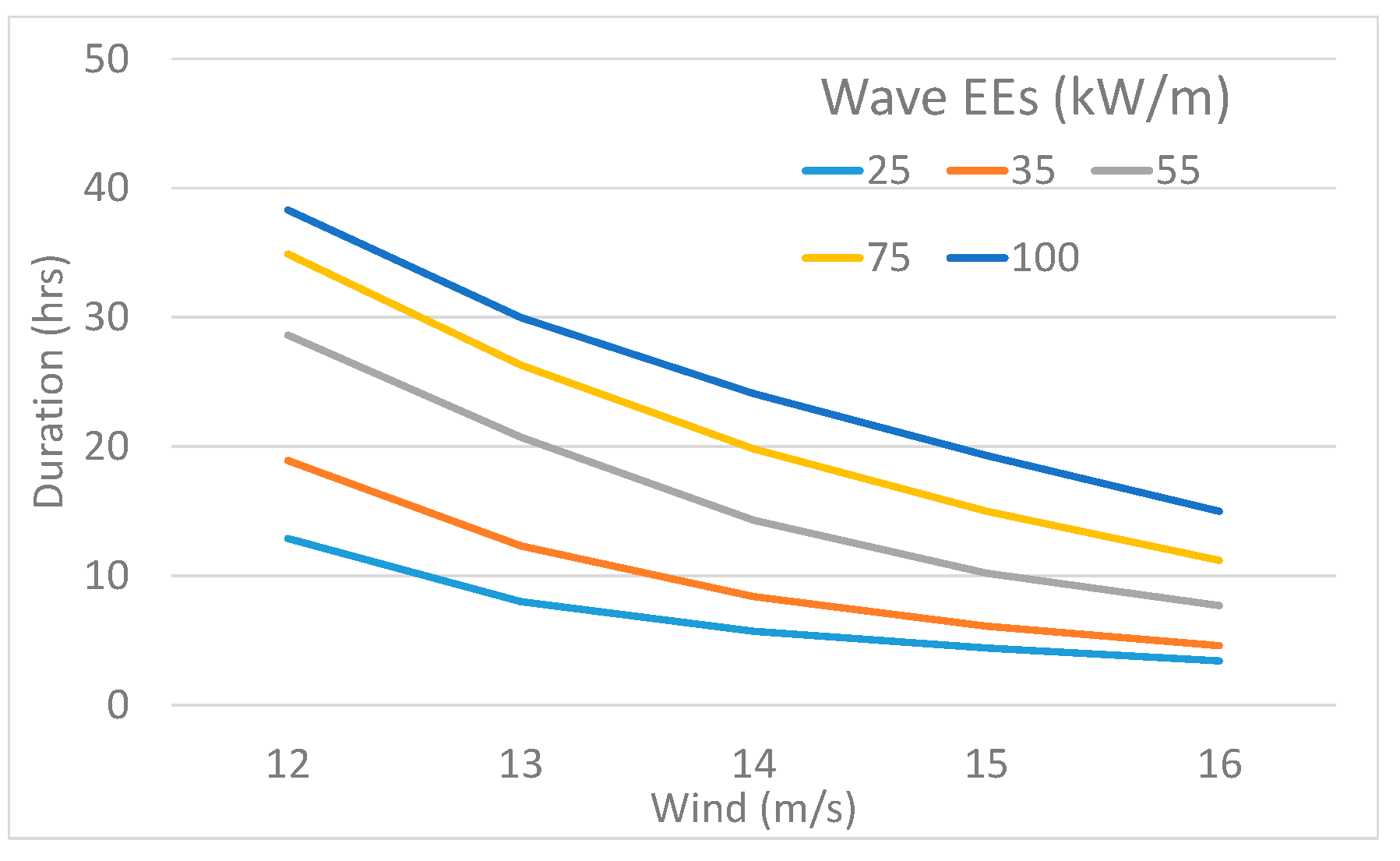
1212.918.928.634.938.3
138.012.320.726.330.0
145.78.414.319.824.1
154.46.110.215.019.3
163.44.67.711.215.0
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Haces-Fernandez, F.; Li, H.; Ramirez, D. Analysis of Wave Energy Behavior and Its Underlying Reasons in the Gulf of Mexico Based on Computer Animation and Energy Events Concept. Sustainability 2022, 14, 4687. https://doi.org/10.3390/su14084687

AMA Style

Haces-Fernandez F, Li H, Ramirez D. Analysis of Wave Energy Behavior and Its Underlying Reasons in the Gulf of Mexico Based on Computer Animation and Energy Events Concept. Sustainability. 2022; 14(8):4687. https://doi.org/10.3390/su14084687

Chicago/Turabian Style

Haces-Fernandez, Francisco, Hua Li, and David Ramirez. 2022. "Analysis of Wave Energy Behavior and Its Underlying Reasons in the Gulf of Mexico Based on Computer Animation and Energy Events Concept" Sustainability 14, no. 8: 4687. https://doi.org/10.3390/su14084687

APA Style

Haces-Fernandez, F., Li, H., & Ramirez, D. (2022). Analysis of Wave Energy Behavior and Its Underlying Reasons in the Gulf of Mexico Based on Computer Animation and Energy Events Concept. Sustainability, 14(8), 4687. https://doi.org/10.3390/su14084687

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop