A Novel Multi-Factor Three-Step Feature Selection and Deep Learning Framework for Regional GDP Prediction: Evidence from China

Abstract

Gross domestic product (GDP) is an important index reflecting the economic development of a region. Accurate GDP prediction of developing regions can provide technical support for sustainable urban development and economic policy formulation. In this paper, a novel multi-factor three-step feature selection and deep learning framework are proposed for regional GDP prediction. The core modeling process is mainly composed of the following three steps: In Step I, the feature crossing algorithm is used to deeply excavate hidden feature information of original datasets and fully extract key information. In Step II, BorutaRF and Q-learning algorithms analyze the deep correlation between extracted features and targets from two different perspectives and determine the features with the highest quality. In Step III, selected features are used as the input of TCN (Temporal convolutional network) to build a GDP prediction model and obtain final prediction results. Based on the experimental analysis of three datasets, the following conclusions can be drawn: (1) The proposed three-stage feature selection method effectively improves the prediction accuracy of TCN by more than 10%. (2) The proposed GDP prediction framework proposed in the paper has achieved better forecasting performance than 14 benchmark models. In addition, the MAPE values of the models are lower than 5% in all cases.

1. Introduction

Regional gross domestic product (GDP) can fully reflect basic economic indicators such as a region’s economic growth rate and changes in economic scale, which is equal to the sum of the added value of various industries in the region [1]. It is widely used all over the world and has become a general macroeconomic indicator to measure regional economic conditions [2]. The effective forecasting of regional GDP in economic operation and development can not only determine a certain degree of macroeconomic trend and guide the healthy development of macroeconomics but also provide a crucial basis for sustainable urban development [3]. The research on regional GDP can explore the internal driving force of local economic growth and promote the optimization and upgrading of local industrial structure [4]. Besides this, by predicting the regional GDP, local governments can make more comprehensive scientific and economic choices [4]. The government can forecast and prospect the development of the market economy so that the development plans could be formulated according to the forecast results and decisions that are beneficial to the local economy can be conducted [5]. The formulation of macro-control economic policies and the adjustment of corporate development strategies all depend on accurate forecasting of regional GDP [6].

Especially at the moment, the sudden outbreak of COVID-19 since the beginning of 2020 had such a great impact on the operation of the world economy that the major economic indicators have declined significantly [5,6,7]. However, with the continuous progress of production resumption, the major economic indicators (especially in China) have shown a rebounding momentum and continual improvement [8,9]. Given the complex world economic situation at this stage, monitoring the current state of economic operation and forecasting the future GDP trend plays a paramount role in the overall control of the macroeconomy and are of practical significance for the formulation of economic policies and macro-control in the next step [10,11,12]. GDP prediction technology can guide the direction of regional sustainable development in the future. Therefore, the research on this direction can promote regional industrial upgrading and form the direction of green development.

At present, the mainstream GDP forecasting framework mainly includes statistical models, machine learning models, and hybrid models [13]. Statistical models mainly use multiple regression and time series modeling to construct mathematical formulas for GDP changes. Machine learning models mainly include support vector machines, decision trees, and so on, which establish a nonlinear mapping of input and output. Compared with these two kinds of models, the hybrid model can effectively improve the prediction performance of the model from data analysis, feature extraction, and nonlinear modeling by effectively combining various components [14]. Considering the complexity of GDP prediction feature categories, feature engineering, and deep learning are adopted in the paper to establish an accurate multi-factor GDP prediction framework.

2. Related Works

The government forecasts the development of the market economy formulates development plans based on the forecasting results and then makes decisions that are beneficial to regional development [15,16]. Economic forecasting is based on historical statistics or survey data, using scientific methods to predict the prospects of economic phenomena [17]. The GDP forecasting is based on actual data, using scientific methods and data models to predict the future GDP value [18]. The time series forecasting methods (TSFM) are widely used in economic forecasting, which refers to a quantitative forecasting method that sorts the historical data of the prediction target according to the time series [19]. TSFM can analyze the changing trend of data and establish a mathematical model for extrapolation. Forecasting based on mathematical models and computing platforms is a commonly used time series forecasting method. Elkhan Richard et al. proposed a novel data-driven nonlinear regression model that can effectively analyze the deep correlation between national income, oil production capacity, and the environment [20].

In a recent GDP forecasting study, researchers proposed many models for forecasting analysis methods. With the development of machine learning and Nonlinear modeling technology, data-driven methods have become one of the mainstream models in GDP forecasting [21]. Abonazel and Abd-Elftah utilized the autoregressive integrated moving average (ARIMA) model to predict the Egyptian GDP data [22]. Wu and Chen studied the application of a support vector machine (SVM) in a financial time series prediction of the debt to GDP ratio index [23]. The experiment results proved the effectiveness of the evaluation indexes. Ghanem et al. proposed a functional link artificial neural network (FLANN) to predict electricity prices under the impact of COVID-19, which showed significant improvement in the forecasting accuracy [24]. Elkhan Richard et al. proposed a new nonlinear panel ARDL approach, which can effectively analyze the correlation between economic indicators and alcohol consumption and achieve better results than traditional algorithms [25]. Britta et al. proposed a new Nonlinear autoregressive distributed lag framework to analyze the core correlations between income and quality wine imports, which effectively solved the problems existing in traditional algorithms [26].

These forecasting methods have their specific characteristics. At the current stage of GDP forecast analysis, a single predictive analysis model only reflects a part of the information of the analysis object. To effectively improve the adaptability of single prediction algorithms and the comprehensive analysis ability of GDP data, scholars use an optimization algorithm to optimize the input features and parameters of the single neural network model. Yusof et al. combined artificial bee colony (ABC) with the least squares support vector machine (LSSVM) in gold prices forecasting [27]. Long et al., utilized the genetic algorithm (GA) to optimize the key information of SVM and predicted the total GDP data of Anhui province using the GDP data from 1989 to 2007 [28]. Guleryuz et al. employed particle swarm optimization (PSO) with an adaptive neuro-Fuzzy inference system (ANFIS) to predict industrial energy demand, which is affected by many economic and social parameters [29]. The above research works proved that the heuristic algorithm-based models outperformed the single predictors.

Although the above optimization algorithms have proved the availability in the forecasting application, more improvements can be added to achieve better modeling performance. The traditional time series method requires stable time series data in the forecast model, but it has poor fitting ability to complex nonlinear systems, and the forecast accuracy of GDP growth is not accurate enough [30]. To further improve the forecasting accuracy for GDP growth trends, novel deep learning models are gradually investigated and applied, which are getting better at fitting complex systems. Sa’adah and Wibowo used two learning models for the prediction of GDP in Indonesia: the long short-term memory (LSTM) and recurrent neural network (RNN), resulting in an accuracy of over 80% [31]. Liu et al. applied the gated recurrent unit (GRU) network in the prediction of Chinese energy consumption [32]. In the comparison with the multiple linear regression (MLR) and the support vector regression (SVR) models, the GRU proved the superiority of complex nonlinear sequence data processing with lower prediction errors. In the research work of Wang et al., the temporal convolutional network (TCN) is employed for the short-term prediction of power system load, the TCN displayed faster speed and less storage demand by the specific structure, which leads to the best performance compared with SVR and LSTM [33]. It is meaningful to analyze the performance of TCN in the prediction study. Therefore, the TCN is applied as the main predictor in the paper.

In economic forecasting, a reasonable forecast should be selected according to the characteristics of the data and application scenarios. In the analysis of various influencing factors of GDP, the feature cross-validation can accurately measure the effect of the proposed model used on the actual datasets, which helps to select the suitable parameters [34,35]. The multi-feature modeling can sort the importance of variables that affect GDP, then complete the steps of feature extraction and feature filtering, and select important variables for calculation [36]. Ortega-Bastida et al. used an autoencoder (AE) to simultaneously reduce the reconstruction errors and data redundancy of the impacts with the corresponding GDP values to guarantee precision in forecasting [37]. Nahil and Lyhyaoui proposed the kernel principal component analysis (KPCA) to raise generalization performance and provide effective input variables for the predictor SVR [38]. The hybrid framework performed significantly better than the single SVR. Wang and Li utilized several feature extraction methods, which contained variational mode decomposition, Kullback-Leibler divergence (KLD), energy measure (EM), and sample entropy (SE) to extract the best features of raw time-series data [39]. The experimental results showed that the feature extraction method can optimize the predictor. Kosana et al. applied Q-learning as the selection method for time series prediction, which could dynamically select the best approach to increase the total model accuracy [40]. The hybrid model was regarded as the online model selection with Q-learning (OMS-QL). Xu et al. also chose Q-learning to conduct feature selection that outperformed other feature selection algorithms in the comparative experiments [41]. Maeda-Gutiérrez et al. combined the Boruta algorithm with a random forest algorithm as a hybrid BorutaRF framework that contains the function of feature selection and classification using the cross-validation strategy [42].

Based on the above literature survey, the existing excellent feature selection and prediction framework can be summarized in Table 1.

Table 1. Basic information about these GDP forecasting models.

References	Published Year	Feature Selection
[35]	2020	AE
[38]	2018	KPCA
[39]	2018	KLD, EM, SE
[40]	2022	Q-learning
[41]	2021	Q-learning
[42]	2021	BorutaRF

Based on the above literature research, it is sinnvoll to research the application of multi-feature analysis methods with the validation process to optimize the parameters in the forecasting model. Considering the excellent feature analysis ability of feature crossing, BorutaRF, and Q-learning algorithm, this study proposed a new three-stage feature selection to optimize the input of TCN and establish a multi-data-driven GDP prediction model. The innovation and contribution of the paper are presented as follows:

(1)

To comprehensively analyze various influencing factors and improve the prediction accuracy of the traditional single-variable GDP time series prediction framework, a multi-factor data-driven GDP prediction framework is proposed to process the multivariate economic data. This multi-feature prediction and feature engineering is significantly efficient for general prediction structures.

(2)

With the excellent forecasting effect compared to the traditional shallow neural network and recursive neural network, the TCN neural network adopted in this paper is firstly applied in the field of GDP prediction, which can conduct analysis for complex nonlinear data and increase the GDP prediction accuracy.

(3)

A new three-stage feature selection framework is proposed in the paper. The feature crossing algorithm could select to explore the potential features and the deep information of the raw data. The Q-learning and BorutarRF algorithm could select features from different aspects and guarantee the quality of TCN input. The hybrid three-stage feature selection structure is applied firstly in GDP forecasting to improve the main predictor TCN.

The structure of this study is listed as follows: Section 2 introduces the technical details of deep learning and feature engineering commonly used in current mainstream GDP forecasting models. Section 3 mainly introduces in detail the applied data information, the proposed methods, and the total framework of the paper. In Section 4, comparative experiments are conducted to verify the performance improvement of the proposed model. Section 5 concludes the main contributions of this paper and prospects the research direction of GDP prediction application.

3. Methodology

3.1. Framework of the Proposed Regional GDP Forecasting Model

The influencing factors of regional GDP are complex, and the prediction accuracy of simple single series is not satisfactory enough under the circumstance. This paper proposes a regional GDP forecasting method based on the integration of economic, educational, employment, and industrial data. The accuracy of the prediction model can be improved greatly through feature analysis of the multivariate data. Moreover, a three-step feature selection method is proposed to better obtain the features that are helpful to GDP prediction. TCN network can deeply explore the nonlinear relationship between features and target prediction. In this paper, the TCN model is used to predict regional GDP in combination with selected features. The specific model framework is shown in Figure 1.

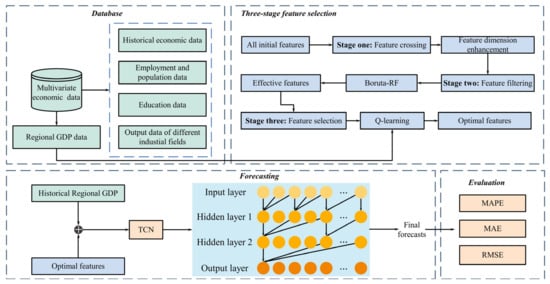
Figure 1. The core structure of the proposed GDP prediction model.

3.2. Multivariate Economic Characteristic Data

Regional economic forecasting is a typical time series forecasting problem, but it is different from traditional single time series forecasting. The regional economy is affected by education, industrial structure, transportation and logistics, geographical location, and other factors. Therefore, multivariate data analysis is indispensable to realizing accurate regional economic forecasts. In this paper, education, industry, historical economic data, population, and other factors that have a great impact on regional economic forecast are taken as the prediction features. Historical information is the first place to be considered. The historical economic information like real GDP, real consumption, and so on can reflect quite a few laws in economic development, which is instructive for GDP forecasting [43]. Employment and population decide the purchasing power of the public and further influence the market circulation and the improvement of GDP [44]. As for education and technology, positive education can promote employment, and science and technology is the basement of productivity-increasing [45]. Thus, education data is also in need to improve the accuracy of GDP prediction. Finally, industrial information is directly associated with GDP. For example, industrial output, energy consumption, the transportation efficiency are all crucial parts of the economy [46]. The stability and accuracy of the regional economic forecasting model can be greatly improved through multivariate data fusion. As shown in Figure 2, there are 20 features, which are mainly divided into four categories: historical economic indicators, employment and population, educational scale, and industrial structure.

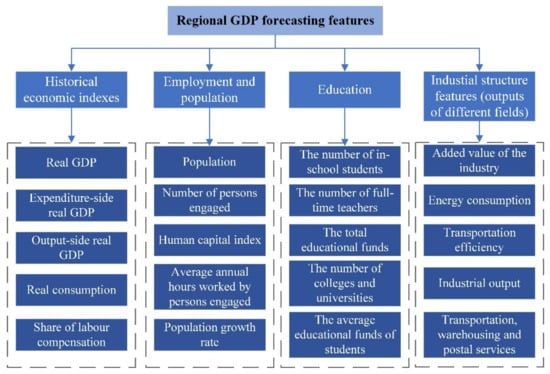
Figure 2. Initial features for regional GDP forecasting.

3.3. Three-Stage Feature Selection

3.3.1. Stage I: Feature Crossing

The 20-dimensional initial features used are divided into four groups according to different domains. The degree of correlation of features within and between groups is different, and the amount of useful information contained in the features is also different. Directly applying feature selection is easy to cause the loss of useful information, and the data cannot be exploited to the full [47]. Thus, feature crossing is utilized to solve the problems. On the one hand, the different information contained in the feature can be combined effectively by applying feature cross, which is able to improve the performance of feature selection. On the other hand, it also allows models to learn more complex nonlinear features. In this part, four feature crossing schemes are proposed. According to whether features belong to the same category, different statistical aggregation or simple calculating methods are carried out on features. Then, the new features are obtained. As shown in Figure 3, distinguishing the feature class by color and the detailed feature crossing method are illustrated below.

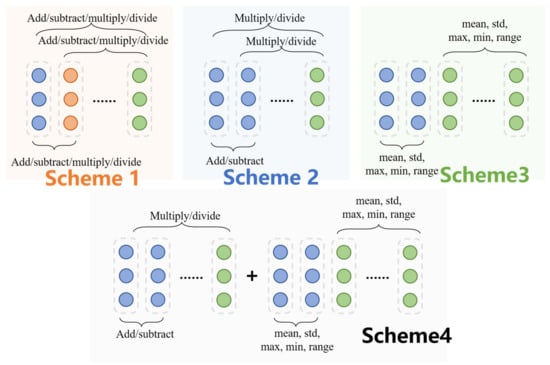
Figure 3. Feature crossing strategy.

Scheme 1: Traverse features. The 20-dimensional features are added, subtracted, multiplied, and divided.

Scheme 2: Intra-group features. If two sets of features belong to the same class, addition and subtraction are carried on each pairwise feature; otherwise, multiply and divide.

Scheme 3: Group aggregation features. For all features that belong to the same class, calculate the mean, standard deviation, maximum, minimum, and range of them to generate new features.

Scheme 4: Intra-group feature and group aggregation features. Namely, the new feature splicing obtained by Schemes 2 and 3.

3.3.2. Stage II: Feature Filtering Based on Boruta-RF

Through feature crossing, the input feature dimension is greatly increased. Among all features, some of them have no correction with the dependent variables. If all the crossed features were taken as the inputs of the feature selection part, the efficiency would be impacted. As a result, a feature filter method is adopted before feature selection. Boruta is an important feature filtering algorithm proposed by M. Kursa and R. Rudnicki [48]. The application of this method as a feature selection method belongs to filter feature selection. Different from most feature screening methods, which aim at the maximization of the evaluation function index or the optimization of the model loss function, this method aims to filter out features unrelated to dependent variables and get all feature sets related to dependent variables. Generally, it is believed that if a feature is added or deleted and the model performance does not change, then the feature is not important. However, it is not completely true. When the feature only has no or little effect on the improvement of model performance, it is not necessarily irrelevant to the dependent variable. Boruta can retain all the features related to the target value, so it is of great significance to use this algorithm as a preliminary feature filtering algorithm for feature selection.

The core idea of Boruta is to Shuffle each feature to generate its shadow feature. The shadow features are chaotic and do not correspond to the original samples. All the features and shadows are utilized to train models. Then, the shadow features with the highest importance scores are taken as the baseline, and the feature sets related to the dependent variable are selected from the crossed features according to the baseline. The specific steps are clarified as follows.

Step 1: shuffle each feature Xi in the feature matrix X and combine the shuffled features and original features [49].

$$\mathrm{X}\mathrm{s}=\mathrm{s}\mathrm{h}\mathrm{u}\mathrm{f}\mathrm{f}\mathrm{l}\mathrm{e}\left(\mathrm{X}\right)$$

(1)

$$\mathrm{X}\mathrm{n}=\left[\mathrm{X};\mathrm{X}\mathrm{s}\right]$$

(2)

where Xs and Xn are the shadow feature matrix and newly generated feature matrix respectively.

Step 2: Train the Random Forest model using the new generated features and calculate the average relative entropy of each feature. Then, calculate Zscore [50], which is given below for all features including the shadow features, and take the highest Z score value of shadow features as the baseline, named Zbase.

$$\mathrm{Z}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}=\frac{\overline{\mathrm{G}}}{{\mathrm{\sigma }}_{\mathrm{G}}}$$

(3)

where G is the related entropy of features, $\overline{\mathrm{G}}$ is the mean value of G, and ${\mathrm{\sigma }}_{\mathrm{G}}$ is the standard deviation.

Step 3: Set a percentage parameter perc, compare Zscore values of the crossed features with $\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{c}•\mathrm{Z}\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}$ and get rid of the features whose Zscore value is lower than $\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{c}•\mathrm{Z}\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}$. In the process, Benjamini Hochberg FDR and Bonferroni are adopted to guarantee the stability of the algorithm.

Step 4: Delete all shadow features and repeat the above steps until all features are marked as important or unimportant.

3.3.3. Stage III: Feature Selection Based on Reinforcement Learning

Reinforcement learning is a real-time learning method that focuses on online learning and environmental feedback [51]. It is an algorithm used to describe and solve the problem that agents maximize returns or achieve specific goals through Learning strategies during their interaction with the environment. Different from the traditional evolutionary algorithms, it can realize dynamic optimization and is inclusive of the error path optimization [52]. As a classic reinforcement learning algorithm with excellent decision-making, Q-learning is widely used in decision-making and optimization problems. In this part, a feature selection method based on Q-learning is proposed. The filtered features are further screened to avoid over-fitting the model due to excessively high feature dimensions. The specific steps are given as follows:

Step 1: Initialize the core parameters of Q-learning (the state matrix S and the action matrix a). The state matrix S represents the selection of these features. The action matrix a is the action to keep or leave these features [53].

$$\mathrm{S}=\left[{\mathrm{s}}_1,{\mathrm{s}}_2,\dots ,{\mathrm{s}}_{\mathrm{m}}\right]$$

(4)

$$\mathrm{a}=\left[\Delta {\mathrm{s}}_1,\Delta {\mathrm{s}}_2,\Delta {\mathrm{s}}_3,\dots ,\Delta s_m\right]$$

(5)

where s_m represents the selection of these features, and s_m is 0 or 1 (0 represents that the feature is not required, and 1 represents that the feature is retained). ∆s_m is the action of adding or deleting the m-th feature.

Action a: Select an action strategy according to ε-greedy.

$${\mathrm{a}}_{\mathrm{n}}=\left\{\begin{array}{c}Action based on max\mathrm{Q}\left(\mathrm{S},\mathrm{a}\right)\left(probability of 1-\mathsf{\epsilon }\right)\hfill \\ Random action\left(probability of \mathsf{\epsilon }\right)\hfill \end{array}\right.$$

(6)

$$\mathsf{\epsilon }\in \left(0,1\right)$$

(7)

where ε is the exploration probability.

Step 2: Establish the reward R, which will affect the agent’s action. In this part, the MAPE of the TCN is taken as a reward.

Step 3: The agent performs an action based on a comprehensive analysis of the current environment and the state S.

Step 4: Calculate the evaluation function Q and update the Q table. Based on the reward R received from the environment, the agent updates the state and Q table by adjusting the action of input feature changes. The calculation formula of the Q value is shown as follows [54]:

$${\mathrm{Q}}_{\mathrm{n}+1}({\mathrm{S}}_{\mathrm{n}},{\mathrm{a}}_{\mathrm{n}})={\mathrm{Q}}_{\mathrm{n}}({\mathrm{S}}_{\mathrm{n}},{\mathrm{a}}_{\mathrm{n}})+{\beta }_{\mathrm{n}}\left(\mathrm{R}({\mathrm{S}}_{\mathrm{n}},a_{\mathrm{n}})+\gamma \max {\mathrm{Q}}_{\mathrm{n}}({\mathrm{S}}_{\mathrm{n}+1},{\mathrm{a}}_{\mathrm{n}+1})-{\mathrm{Q}}_{\mathrm{n}}({\mathrm{S}}_{\mathrm{n}},{\mathrm{a}}_{\mathrm{n}})\right)$$

(8)

where a represents the agent’s behavior; S stands for the current status of an agent; R is the immediate return; γ is the discount parameter; β represents learning speed.

Step 5: When the termination condition is met, the agent stops its action. At this point, the state matrix S is the final selection result of model input features. Otherwise, repeat steps 3 to 4.

3.4. TCN for Regional GDP Forecasting

TCN is a neural network model which integrates extended causal convolution and residual connection and can be used for time series prediction [55]. TCN is composed of multiple TCN residual blocks stacked. Each TCN residual block has an important parameter pair (k, d) which represents the convolution kernel size and expansion coefficient respectively [56]. The final output of the TCN residual block is the sum of the outputs of the two paths. One path takes the input values through two levels of the same DCC and outputs them. Firstly, the input value enters the DCC after the weight initialization of layer 1. Then, the output is nonlinear transformed by the ReLU activation function. Finally, the nonlinear outputs are regularized to reduce the overfitting of the model and are input to layer 2 DCC for the same transformation again. The other path is for the input value to reach the output directly through the one-dimensional convolution layer. The path is RC, which is derived from the residual neural network. It can alleviate the problems of gradient disappearance and gradient explosion existing in the deep neural network and contribute to the construction of the deep neural network.

The core component of TCN is DCC. DCC increases the value of expansion coefficient d based on causal convolution, thus expanding the receptive field of the network, that is, accepting longer historical data [57]. The first is the application of causal convolution, which means that there is no leakage of information in the past. In the network applied in this paper, the convolution kernel is 2, the expansion coefficient is 1, and the receptive field is 3. And the ŷt GDP sequences are calculated from input sequences [xt − 2, xt − 1, xt] and have nothing to do with the input sequences [xt + 1, xt + 2, ...]. Therefore, the application of causal convolution in TCN will not give rise to information leakage. However, causal convolution has the problem of a small receptive field. Therefore, DCC expands the network receptive field by increasing the expansion coefficient. The receptive field of DCC in the same layer can be expanded to 4. The extended convolution operation can be obtained by the following equation [58]:

$$\mathrm{T}\mathrm{C}\mathrm{N}\left(\mathrm{t}\right)={\displaystyle \sum _{\mathrm{l}=0}^{\mathrm{p}-1}\mathrm{f}\left(\mathrm{l}\right){\mathrm{X}}_{\mathrm{t}-\mathrm{d}\mathrm{l}}}$$

(9)

where TCN(t) is the extended convolution operation, X represents the time series data, f is the filter function, p is the length of the data, l is the element in X.

4. Case Study

4.1. GDP Dataset

The case study is the key to evaluating the performance of different GDP prediction frameworks. In order to select valuable regional GDP data sets, based on the analysis of GDP data in the references [59], this paper adopts the data of three Provinces in China to construct the experimental analysis. The data comes from the National Statistical Yearbook, which contains GDP data and other features data for each quarter from 2005 to 2021. Table 2 gives the basic information and input features of these three data. Figure 4, Figure 5 and Figure 6 show the temporal fluctuation characteristics of three sets of GDP data. It is necessary to ensure the stability and robustness of the proposed model. To fully prove the stability and validity of the GDP prediction model, the proposed model and other benchmark models are evaluated by the ten-fold cross-validation method. In addition, ten repeated tests were used to evaluate the performance of the model. The average value of the evaluation index of the ten predicted results was used to analyze the effect of the model. This paper mainly constructs the single-step forecasting model, that is, the model predicts the GDP of the next quarter through the current moment and historical data. The key software platform used for experiments and modeling in this paper is the Python 3.8.5 platform, mainly using TensorFlow 2.3 to build the neural network. The Python was designed by Guido van Rossum, who works in Google. The version of python used in this paper is 3.8.5. The TensorFlow was created by Google open source, the version used in this paper is 2.3.

Table 2. Basic information about this GDP dataset.

GDP Data	Data 1	Data 2	Data 3
Province	Beijing	Hunan	Zhejiang
Minimum	102.3870	134.9570	274.6090
Mean	506.0497	592.2015	945.7440
Maximum	1034.3040	1200.0900	1878.7420
Standard derivation	256.8505	309.3011	441.7130

Figure 4. Raw GDP Data 1.

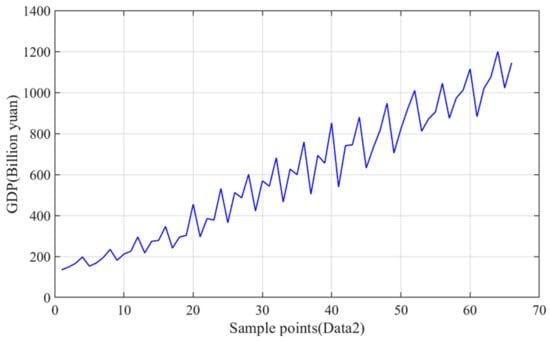
Figure 5. Raw GDP Data 2.

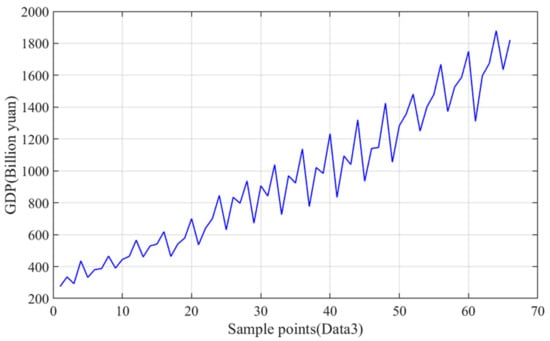
Figure 6. Raw GDP Data 3.

4.2. Performance Evaluation Indexes

The regression analysis index is the key to evaluating the performance of the model proposed in this paper. To fully analyze the modeling performance of each model, three classic indexes, which are the MAE (Mean Absolute Error), the MAPE (Mean Absolute Percentage Error), and the RMSE (Root Mean Square Error), are used in all case studies. These indexes can be obtained by the following Equation (10) [60]:

$$\left\{\begin{array}{l}\mathrm{M}\mathrm{A}\mathrm{E}=({\displaystyle \sum _{\mathrm{T}=\mathrm{1}}^{\mathrm{n}}\left|\mathrm{Y}(\mathrm{T})-\stackrel{⌢}{\mathrm{Y}}(\mathrm{T})\right|})/\mathrm{n}\\ \mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}=({\displaystyle \sum _{\mathrm{T}=1}^{\mathrm{n}}\left|(\mathrm{Y}(\mathrm{T})-\stackrel{⌢}{\mathrm{Y}}(\mathrm{T}))/\mathrm{y}(\mathrm{T})\right|})/\mathrm{n}\\ \mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{({\displaystyle \sum _{\mathrm{T}=\mathrm{1}}^{\mathrm{n}}{\left[\mathrm{Y}(\mathrm{T})-\stackrel{⌢}{\mathrm{Y}}(\mathrm{T})\right]}^2)/\mathrm{n}}}\end{array}\right.$$

(10)

where Y (T) represents true GDP data. $\stackrel{⌢}{\mathrm{Y}}(\mathrm{T})$ represents the GDP data calculated by the proposed model. N means the number of samples.

At the same time, it is necessary to select appropriate indicators to evaluate the performance differences between different models. This study utilized the Promoting percentages of the MAE (PMAE), the Promoting percentages of the MAPE (PMAPE), and the Promoting percentages of the RMSE (PRMSE) to evaluate the performance differences between different algorithms. These indexes can be obtained by the following Equation (11) [61]:

$$\left\{\begin{array}{l}{\mathrm{P}}_{\mathrm{M}\mathrm{A}\mathrm{E}}=\frac{\left(\mathrm{M}\mathrm{A}{\mathrm{E}}_{\mathrm{a}}-\mathrm{M}\mathrm{A}{\mathrm{E}}_{\mathrm{b}}\right)}{\mathrm{M}\mathrm{A}{\mathrm{E}}_{\mathrm{a}}}\\ {\mathrm{P}}_{\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}}=\frac{\left(\mathrm{M}\mathrm{A}\mathrm{P}{\mathrm{E}}_{\mathrm{a}}-\mathrm{M}\mathrm{A}\mathrm{P}{\mathrm{E}}_{\mathrm{b}}\right)}{\mathrm{M}\mathrm{A}\mathrm{P}{\mathrm{E}}_{\mathrm{a}}}\\ {\mathrm{P}}_{\mathrm{R}\mathrm{M}\mathrm{SE}}=\frac{\left(\mathrm{R}\mathrm{M}\mathrm{S}{\mathrm{E}}_{\mathrm{a}}-\mathrm{R}\mathrm{M}\mathrm{S}{\mathrm{E}}_{\mathrm{b}}\right)}{\mathrm{R}\mathrm{M}\mathrm{S}{\mathrm{E}}_{\mathrm{a}}}\end{array}\right.$$

(11)

4.3. Contrast Experiment with Benchmark Algorithms

4.3.1. Experimental Results and Analysis of Different Predictors

To fully compare and analyze the modeling effects of different predictors and prove the superiority of the TCN algorithm, this paper adopts TCN, GRU, LSTM, RNN, ELM, and RBF models to construct comparative experiments. The experiment includes a classical deep learning model and a traditional shallow neural network. Table 3 gives the regression analysis indexes of the prediction results of these algorithms. From Table 3, the following conclusions can be drawn:

Table 3. The regression analysis indexes of several predictors.

Series	Forecasting Models	MAE (Billion Yuan)	MAPE (%)	RMSE (Billion Yuan)
Data 1	TCN	25.2155	5.2263	34.0967
	GRU	26.3096	5.4412	34.9834
	LSTM	26.6932	5.4694	34.9907
	RNN	27.1426	5.5086	35.0814
	ELM	27.7391	5.6319	36.0643
	RBF	27.6943	5.6393	35.8998
Data 2	TCN	21.2653	3.9465	28.4004
	GRU	22.3954	4.0541	29.6895
	LSTM	22.5898	4.1824	29.9655
	RNN	23.2437	4.2517	30.4454
	ELM	25.7957	5.1268	33.1268
	RBF	25.3667	5.1499	32.6133
Data 3	TCN	33.9287	3.7871	50.4280
	GRU	34.7236	3.9526	50.6098
	LSTM	34.1358	3.9577	51.6374
	RNN	35.5990	3.9983	52.2030
	ELM	36.0811	4.0071	52.6383
	RBF	35.8042	4.0245	52.8738

(1)

Compared with the traditional RBF and ELM algorithms, the neural network model based on deep learning can obtain fewer error prediction results. The experimental cases fully prove that the deep learning method can achieve satisfactory modeling results in this field. The feasible reason is that the multi-layer deep network structure has certain advantages in mining the deep feature information of data.

(2)

Compared with the traditional RNN prediction model, other deep learning models can achieve more satisfactory prediction results. This proves that other deep neural networks with special structures can better resume an excellent GDP forecasting framework. The possible reason is that the RNN model has problems such as gradient descent and gradient disappearance, which to some extent limits the training effect of the model and reduces the overall accuracy.

(3)

Compared with GRU and LSTM, the TCN model adopted in this paper can achieve smaller prediction errors in all cases. This fully proves the practical value and modeling ability of the TCN algorithm in GDP forecasting. The feasible reason is that the TCN algorithm fully combines the characteristics of CNN and RNN. Therefore, TCN improves the parallel computing capability of the model while maintaining the advantages of timing modeling, which further improves the performance of the model.

4.3.2. Experimental Results and Analysis of Different Hybrid Models

In order to fully verify the application value of the GDP prediction model proposed in this paper, two parts of comparative experiments are set up in this section.

Part I: To prove that the three-stage feature selection method adopted in this paper can effectively optimize the prediction performance of the TCN algorithm, the proposed FC-BorutaRF-Q-TCN algorithm is compared with FC-BorutaRF-TCN, FC-Q-TCN, and TCN respectively.

Part II: To fully prove that the feature selection model based on reinforcement learning adopted in this paper has excellent feature selection ability, the Q-learning algorithm is compared with classical GA and PSO.

Table 4 gives the regression analysis indexes of the prediction results of these algorithms. Table 5 and Table 6 show the promoting percentages of FC-Borutarf-Q-TCN by other models. Figure 7 gives the loss of different feature selection algorithms during iteration. Table 7 shows the results of feature selection. From Table 4, Table 5, Table 6 and Table 7 and Figure 7, the following conclusions can be drawn:

Table 4. The indexes evaluation results of several forecasting models.

Series	Forecasting Models	MAE (Billion Yuan)	MAPE (%)	RMSE (Billion Yuan)
Data 1	FC-BorutaRF-Q-TCN	22.1614	4.8334	30.3021
	FC-BorutaRF-PSO-TCN	23.0066	4.9145	31.6693
	FC-BorutaRF-GA-TCN	22.9586	4.9517	30.5457
	FC-BorutaRF-TCN	23.6087	5.1034	32.1499
	FC-Q-TCN	24.1884	5.1061	33.7000
Data 2	FC-BorutaRF-Q-TCN	18.0778	3.3787	25.3888
	FC-BorutaRF-PSO-TCN	19.8081	3.5706	26.8640
	FC-BorutaRF-GA-TCN	19.8178	3.5513	26.4723
	FC-BorutaRF-TCN	20.4341	3.8091	27.5156
	FC-Q-TCN	20.8454	3.8084	27.0660
Data 3	FC-BorutaRF-Q-TCN	28.4412	3.2037	37.9007
	FC-BorutaRF-PSO-TCN	30.4008	3.5108	39.4640
	FC-BorutaRF-GA-TCN	30.6192	3.5527	40.7590
	FC-BorutaRF-TCN	33.3320	3.6871	49.9555
	FC-Q-TCN	33.3321	3.7136	49.7054

Table 5. The promoting percentages of FC-BorutaRF-Q-TCN by other models.

Methods	Indexes	Data 1	Data 2	Data 3
FC-BorutaRF-Q-TCN vs. FC-BorutaRF-TCN	PMAPE (%)	6.1304	11.5312	14.6730
	PMAE (%)	5.2906	11.2993	13.1106
	PRMSE (%)	5.7475	7.7294	24.1311
FC-BorutaRF-Q-TCN vs. FC-Q-TCN	PMAPE (%)	8.3800	13.2768	14.6732
	PMAE (%)	5.3407	11.2830	13.7306
	PRMSE (%)	10.0828	6.1967	23.7493
FC-BorutaRF-Q-TCN vs. TCN	PMAPE (%)	12.1120	14.9892	16.1736
	PMAE (%)	7.5177	14.3874	15.4049
	PRMSE (%)	11.1289	10.6041	24.8420

Table 6. The promoting percentages of the Q-learning by heuristic algorithms.

Methods	Indexes	Data 1	Data 2	Data 3
FC-BorutaRF-Q-TCN vs. FC-BorutaRF-PSO-TCN	PMAPE (%)	3.6737	8.7353	6.4459
	PMAE (%)	1.6502	5.3744	8.7473
	PRMSE (%)	4.3171	5.4914	3.9613
FC-BorutaRF-Q-TCN vs. FC-BorutaRF-GA-TCN	PMAPE (%)	3.4723	8.7800	7.1132
	PMAE (%)	2.3891	4.8602	9.8235
	PRMSE (%)	0.7975	4.0930	7.0127

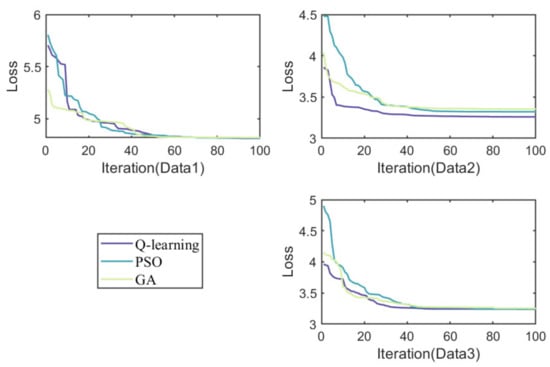
Figure 7. Loss of different feature selection algorithms during iteration.

Table 7. Feature selection results.

Series	Type of Feature	Number of Retained Features
Data 1	Historical GDP data	4
	Historical economic indexes	2
	Employment and population features	1
	Education	1
	Industrial structure features	3
Data 2	Historical GDP data	3
	Historical economic indexes	2
	Employment and population features	0
	Education	1
	Industrial structure features	3
Data 3	Historical GDP data	4
	Historical economic indexes	2
	Employment and population features	1
	Education	0
	Industrial structure features	4

(1)

Compared with the single TCN model, all the hybrid models can achieve better prediction accuracy. The experimental results fully prove the ability of the feature engineering algorithm to optimize the prediction results of the predictor. The possible reason is that the feature engineering algorithm deeply excavates the deep correlation between GDP and other feature historical data and labels from two perspectives and selects the best quality features, which effectively optimizes the modeling ability of TCN.

(2)

The prediction results of FC- BorutaRF-Q-TCN are obviously better than those of FC-Q-TCN and FC-BorutaRF-TCN. This fully proves that the three-stage feature selection algorithm adopted in this paper can deeply mine the feature information of original data and achieve better results than the single feature selection algorithm. The feasible reason is that the BorutaRF algorithm and Q-Learning algorithm fully analyze the characteristic information obtained from the original data of the FC method and optimize it from two different perspectives. Therefore, TCN can obtain the best input features and establish the optimal GDP prediction model.

(3)

Compared with PSO and GA, the feature selection algorithm based on reinforcement learning adopted in this paper can obtain the best results. This fully proves the ability of the Q-learning algorithm to analyze feature quality and make a selection. The possible reason is that, compared with other heuristic algorithms, the reinforcement learning algorithm improves the intelligence of the model by constantly training agents. Therefore, Q-learning can effectively evaluate the quality of features and select the optimal input for the TCN algorithm.

(4)

Based on feature selection results, it can be found that the largest number of retained features are historical GDP data and industrial features. In addition, the data on educational features and population features are less reserved. It proves that historical GDP data and industrial features play a paramount role in the composition of regional GDP. Based on the feature selection results, a more accurate prediction framework can be constructed in the process of establishing a GDP prediction model in the future.

4.4. Contrast Experiment with Existing Algorithms

To prove that the FC-BorutarRF-Q-TCN model proposed in this paper is an advanced GDP forecasting model with excellent research prospects, it is compared with the four existing models. The four existing models include the classical time series model (ARIMA), the traditional machine learning model (SVM), and the two most advanced models (Yan’s model [62] and Dong’s model [63]). Figure 8, Figure 9 and Figure 10 show the MAE, MAPE, and RMSE values of the proposed model and those of four existing models. Figure 11, Figure 12 and Figure 13 show the prediction results of all the comparison models. Based on Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13, the following conclusions can be drawn:

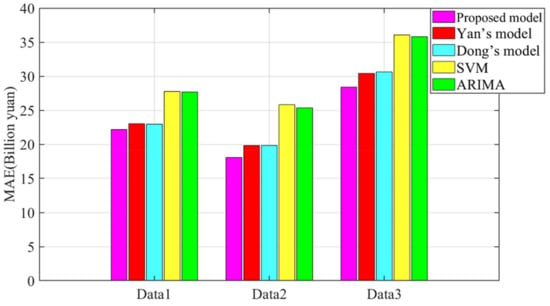
Figure 8. MAE values of the proposed model and existing models.

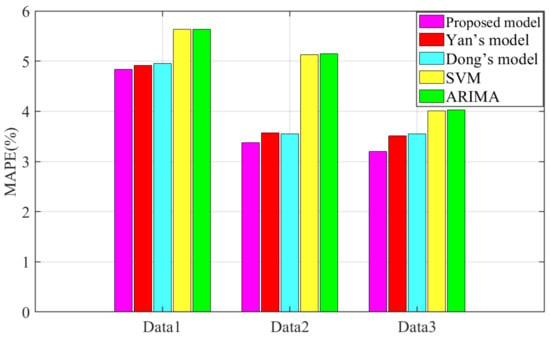
Figure 9. MAPE values of the proposed model and existing models.

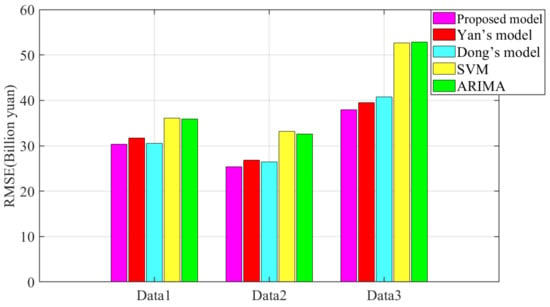
Figure 10. RMSE values of the proposed model and existing models.

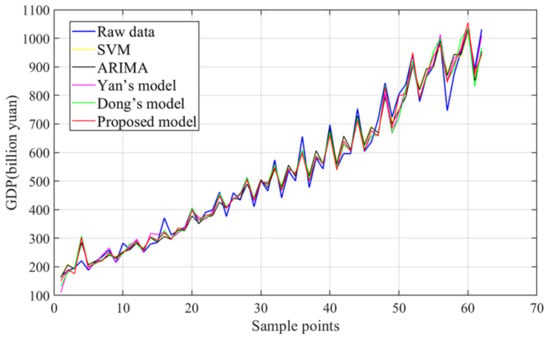
Figure 11. Predicted results of all algorithms (Data 1).

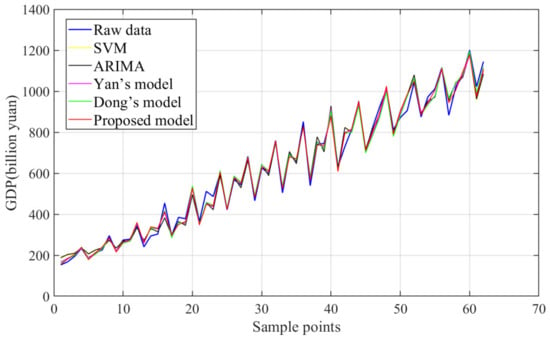
Figure 12. Predicted results of all algorithms (Data 2).

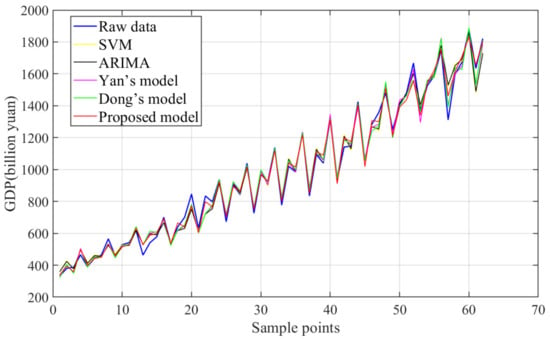
Figure 13. Predicted results of all algorithms (Data 3).

(1)

Compared with the classical ARIMA and SVM algorithms, all the mixed models can achieve more satisfactory prediction results. The experimental results fully prove the practicability and effectiveness of the hybrid model in GDP forecasting. The feasible reason is that the hybrid model effectively optimizes the input features of the GDP forecasting model from the perspective of feature analysis and data mining, which effectively improves the analysis and modeling capabilities of all predictors.

(2)

The FC-BorutarRF-Q-TCN model proposed in this paper can achieve the best prediction accuracy in all cases. This fully proves the stability and advance of the FC-BorutarRF-Q-TCN model. First of all, the model outperforms the feature crossing algorithm to mine potential feature information from the original data. Then, the BorutarRF algorithm and the Q-learning algorithm screen the features obtained by the FC algorithm from two different angles. Finally, the screened features are used as the input of TCN to build the GDP prediction model and obtain the final prediction results. Overall, the model further improves the prediction performance from multiple perspectives. Therefore, the FC-BorutarRF-Q-TCN model can achieve excellent research value in the field of GDP prediction.

4.5. Discussion

Based on the above analysis of all experimental results, the following discussion and analysis are carried out in this section:

(1)

The FC-BorutarRF-Q-TCN model proposed in this paper can achieve the best prediction accuracy in all cases. In addition, the stability and effectiveness of the model are fully proved by the results of ten-fold cross-validation and ten repeated experiments.

(2)

Table 3 fully proves the predictive performance of TCN. Compared with other neural networks, TCN effectively combines the parallel computation capability of CNN and the recursive modeling capability of RNN. Therefore, TCN has achieved excellent results in the field of GDP forecasting modeling.

(3)

Based on Table 4, Table 5, Table 6 and Table 7 and Figure 7, it can be found that the proposed three-stage feature selection framework can effectively improve the prediction performance of TCN. In addition, based on the result of feature selection, it can be seen that historical GDP data and Industrial structure features are relatively crucial indexes affecting GDP prediction. Education and population have relatively little impact on GDP prediction. Therefore, the experimental results have certain help for the future government to formulate policies and promote economic development.

(4)

Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 fully show the application prospect of the proposed model in GDP prediction. As can be seen from Figure 8, Figure 9 and Figure 10, the errors of the proposed FC-BorutarRF-Q-TCN model are significantly lower than that of other existing models. In addition, the MAPE values of the proposed model are less than 5% in all cases. In addition, based on Figure 11, Figure 12 and Figure 13, it can be found that the GDP prediction result of the proposed FC-BorutarRF-Q-TCN model is extremely close to the real GDP data, which can prove the strong practicality of the model in this field.

(5)

GDP prediction technology can provide technical support for regional economic development and policymaking. However, GDP prediction technology also has some limitations. GDP is a favorable indicator of physical production, and to some extent ignores the value of open-source products, services, free products, and other related industries. Therefore, GDP and other modern industries should be taken into consideration to comprehensively evaluate the regional economic level and formulate further development policies [64].

5. Conclusions and Future Work

As a comprehensive signal of the future economic situation, GDP forecasting technology provides technical support for national macro-economic regulation. In the paper, a new multi-data-driven GDP prediction model based on three-stage feature selection and a TCN network is proposed. The main contributions of this paper are summarized from the following perspectives:

(1)

Different from the traditional single-variable GDP time series forecasting framework, this paper proposes a multi-data-driven GDP forecasting model. The model comprehensively considers the influence of other features on GDP and further optimizes the prediction performance of the model.

(2)

Different from the traditional shallow neural network and recursive neural network, the TCN neural network adopted in the paper fully combines the training advantages of CNN and the timing sequence modeling ability of RNN. Therefore, the TCN algorithm could achieve a more excellent GDP prediction effect and is the most important predictor.

(3)

A new three-stage feature selection framework is proposed to optimize the prediction performance of TCN. On the one hand, the framework uses the FC algorithm to further mine the potential features of the original data and expand the deep information of the data. On the other hand, Q-learning and BorutarRF algorithms screen features from different angles and ensure the quality of TCN inputs. The three-stage feature Selection framework improves TCN performance by more than 10%.

(4)

The feature selection results show that historical GDP data and Industrial structure features are relatively crucial feature data for GDP prediction modeling. The feature selection results have important reference values for the government to adjust economic policy.

(5)

In order to prove the advance and practicability of the proposed FC-BorutarRF-Q-TCN prediction framework, fourteen models used by other researchers were replicated and compared with the model proposed in this paper. The experimental results show that the FC-BorutarRF-Q-TCN model is a GDP forecasting framework with excellent research prospects. The MAPE values are all less than 5%.

The proposed multi-factor data-driven GDP prediction framework provides a meaningful reference for regional economic development strategy. In the future, the model proposed can be further improved from the following perspectives to enhance its practical value:

(1)

The GDP prediction framework is mainly obtained through multi-factor data-driven training. Therefore, when the amount of data increases and updates, the model also needs to be updated and trained constantly to ensure timeliness.

(2)

The model can accurately predict the change in GDP in the next quarter. Based on the forecast results, the government makes relevant economic policies to realize the adjustment and development of the regional economic level. In the future, it is a very important step to formulate a reasonable sustainable development strategy based on the GDP prediction results.

(3)

GDP prediction technology provides effective technical guidance for the sustainable development of the regional economy. Therefore, based on the research results, it can effectively drive the upgrading of regional industries and promote green development and sustainability in the future.

(4)

GDP can effectively reflect the situation of physical production and regional economic development. However, GDP does not fully analyze related industries such as services, open-source products, and products provided by society for free. Therefore, comprehensive consideration of GDP and other industries is very indispensable for the sustainable development of the regional economy and prosperity level.