Load Deformation Effect of CBD Ground Cluster in Zhengzhou City
Abstract
1. Introduction
2. Research Methods and Data Sources
2.1. Research Method of Cluster Load Effect
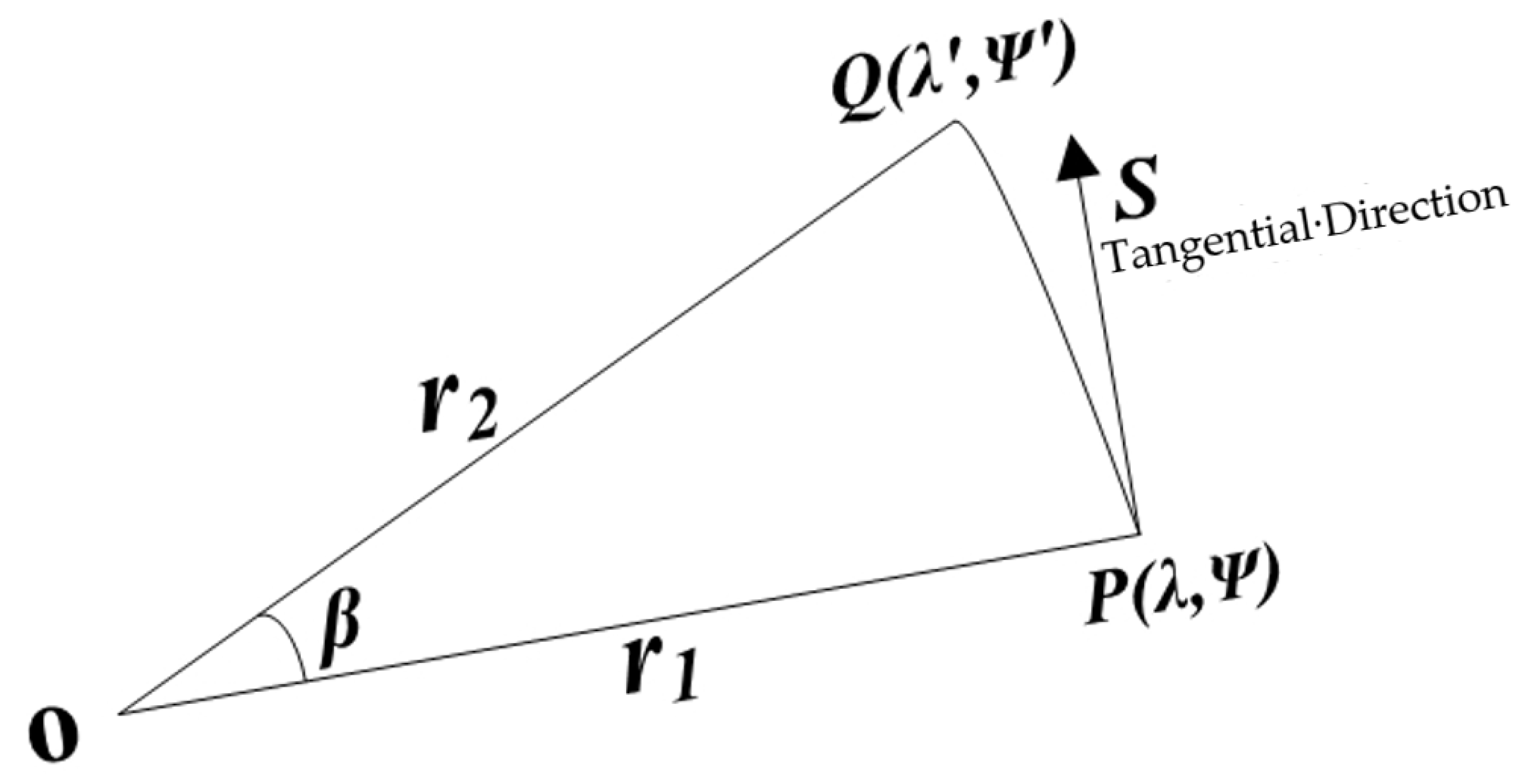
2.1.1. Ground Deformation Caused by a Single Building
2.1.2. Calculation Model of Ground Deformation and Geoid Change Caused by Cluster Load
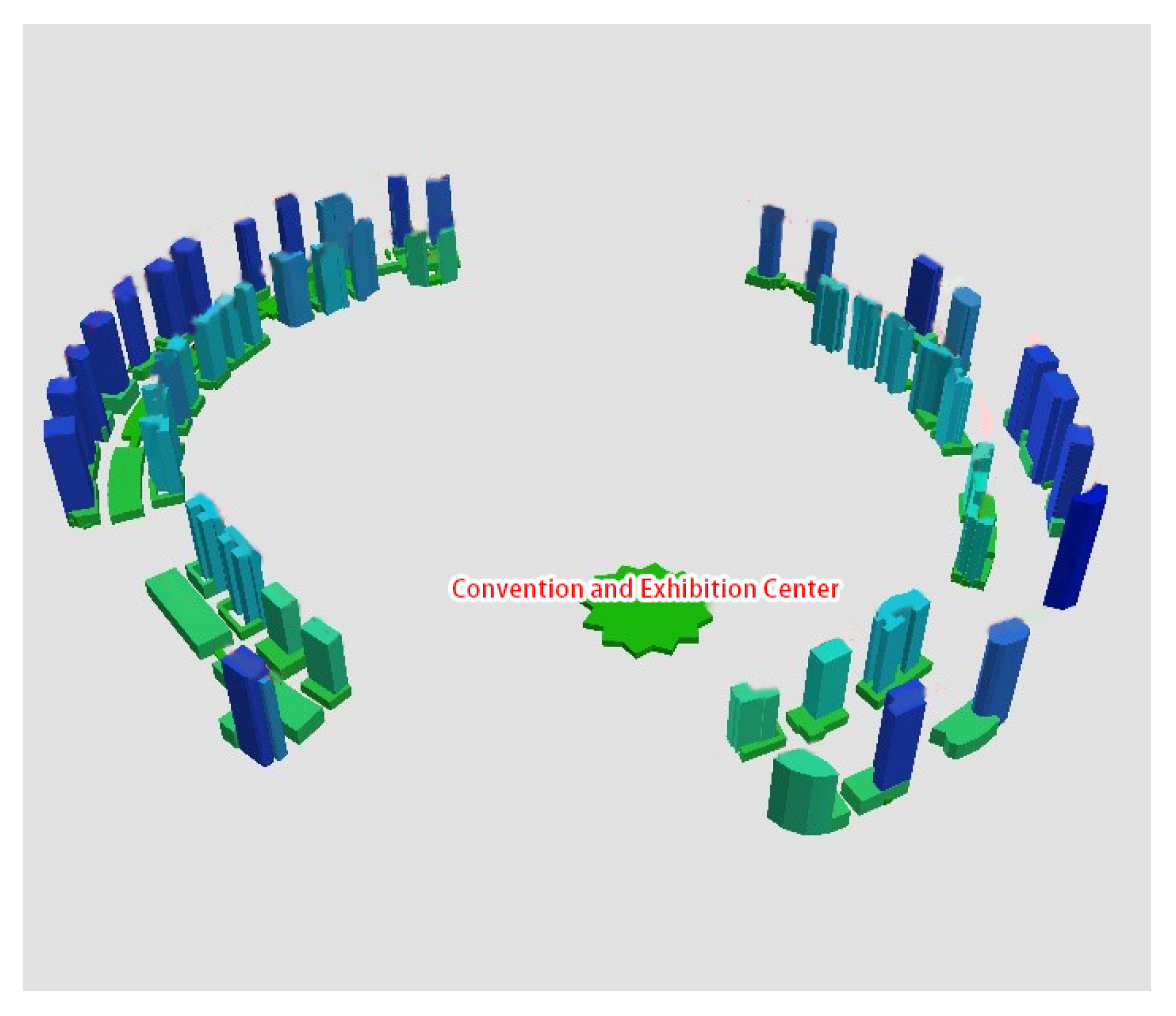
2.2. Data Source
2.3. Counting Process
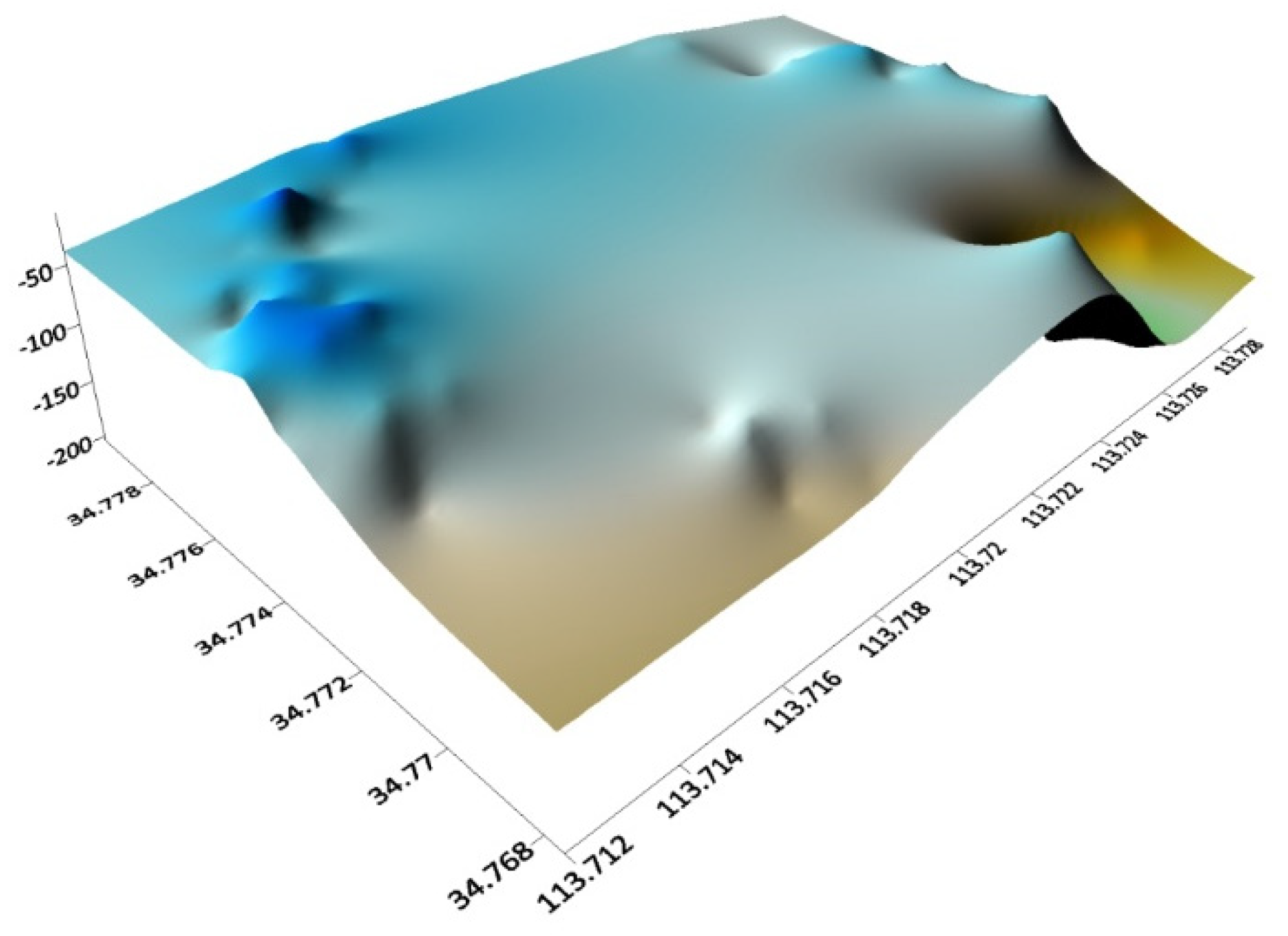
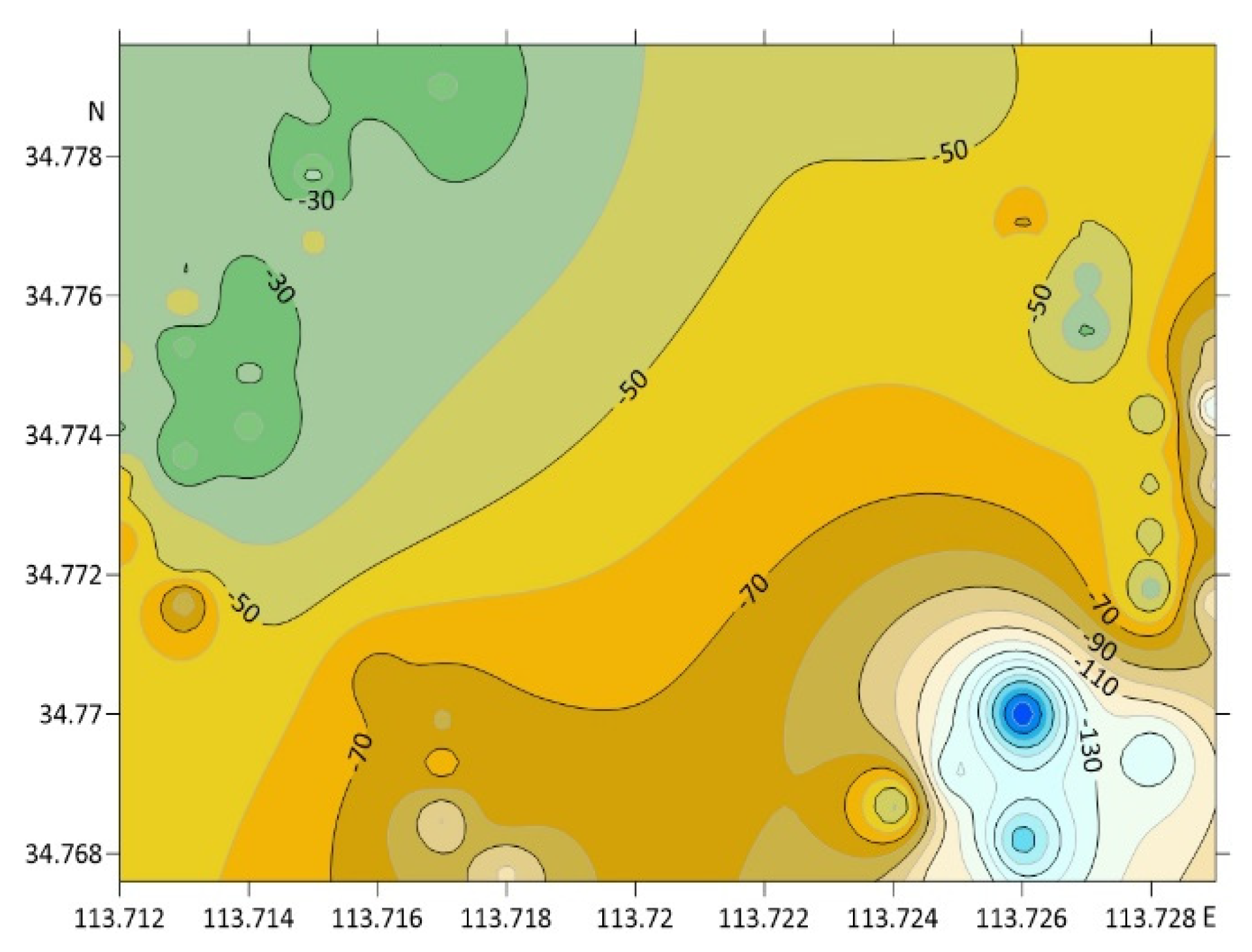
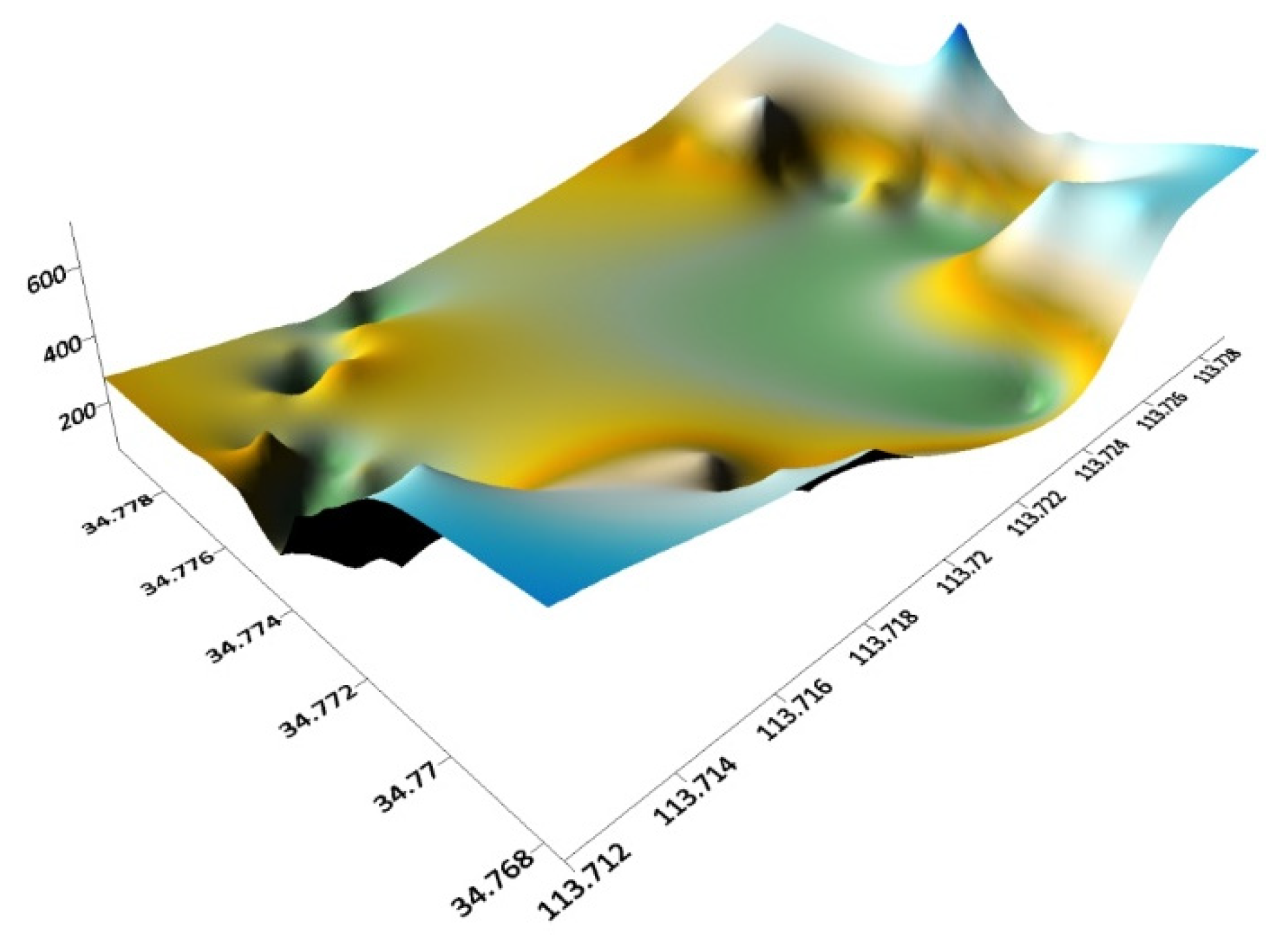
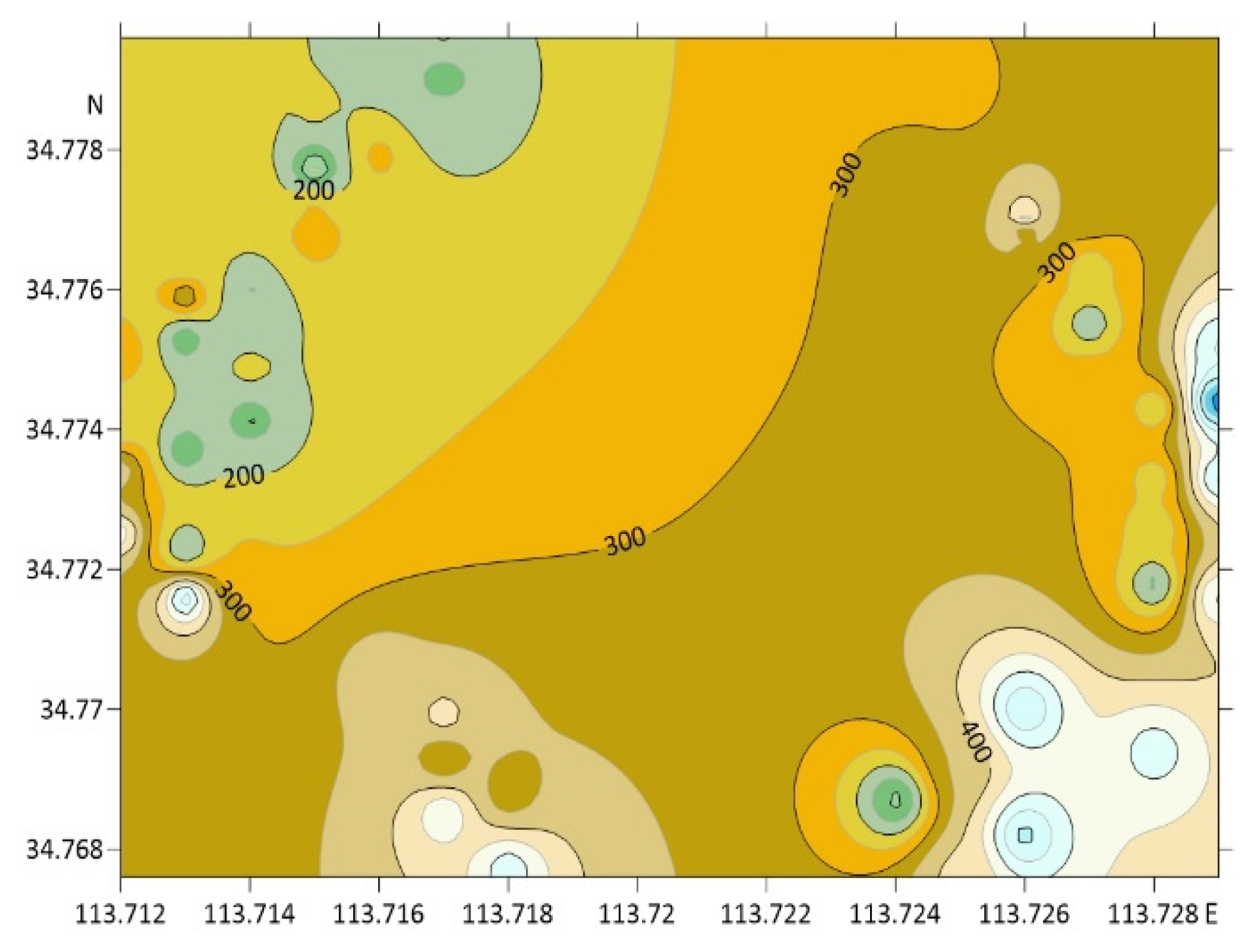
3. Result Analysis
3.1. Analysis of Ground Deformation and Stress Change Caused by Single Building
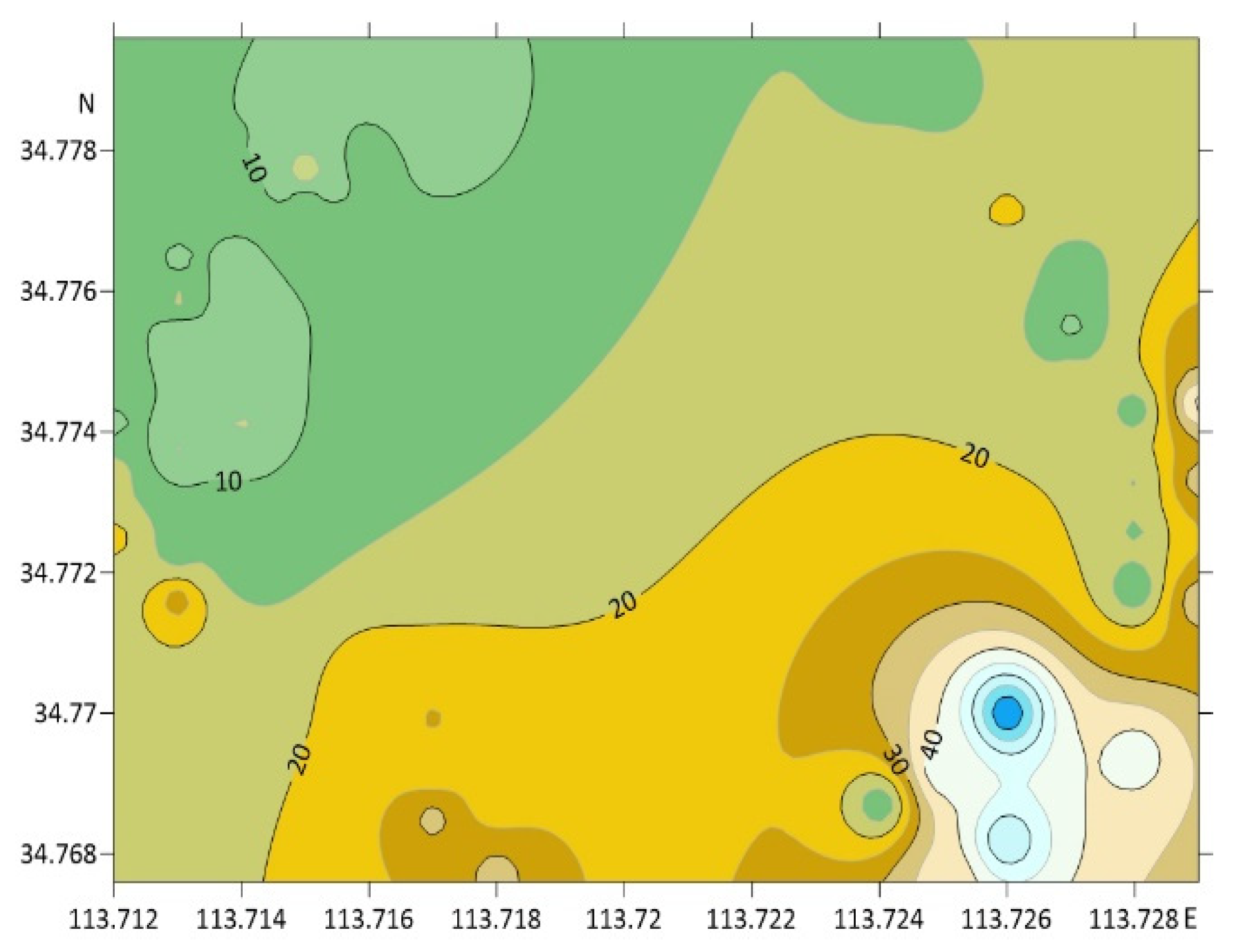
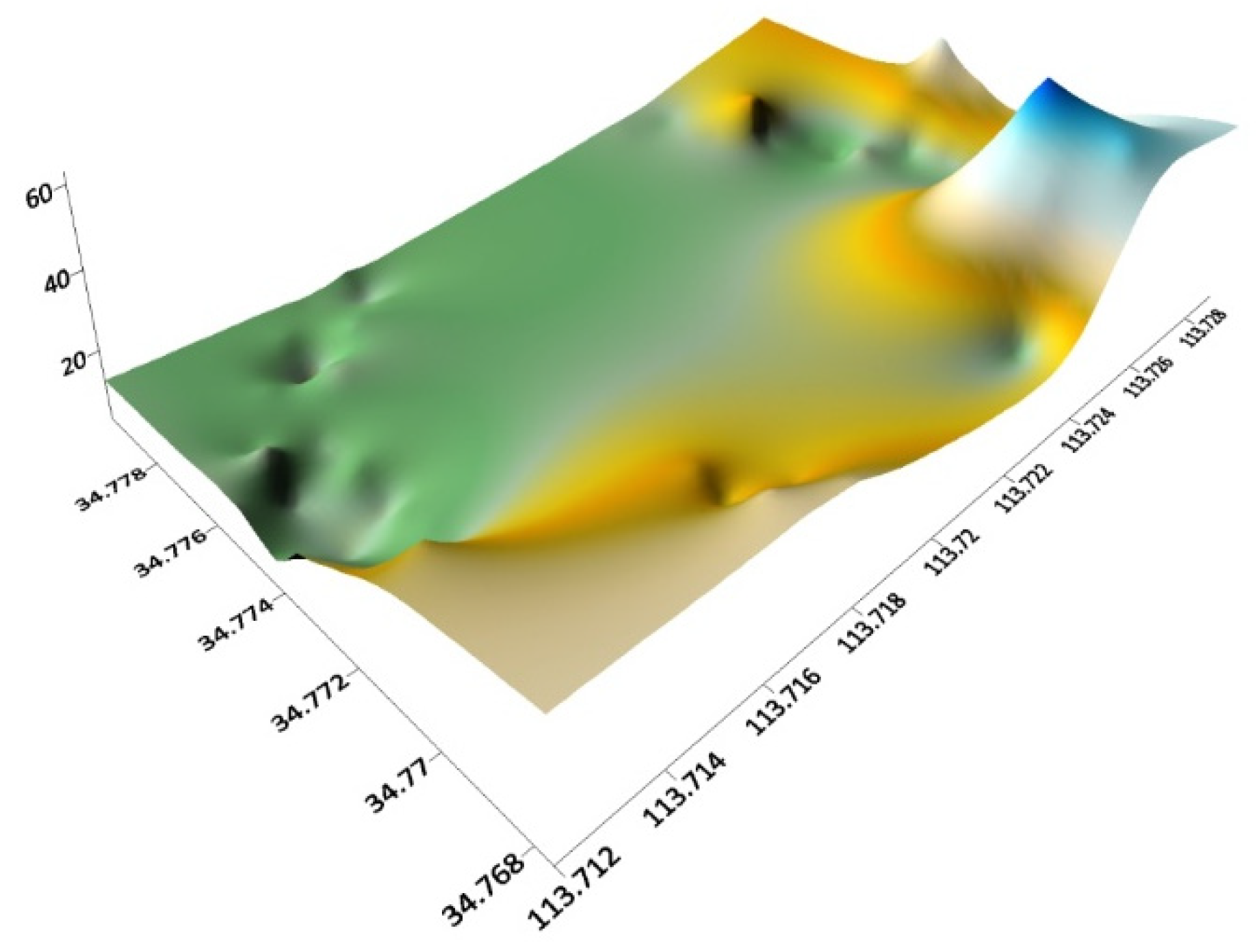
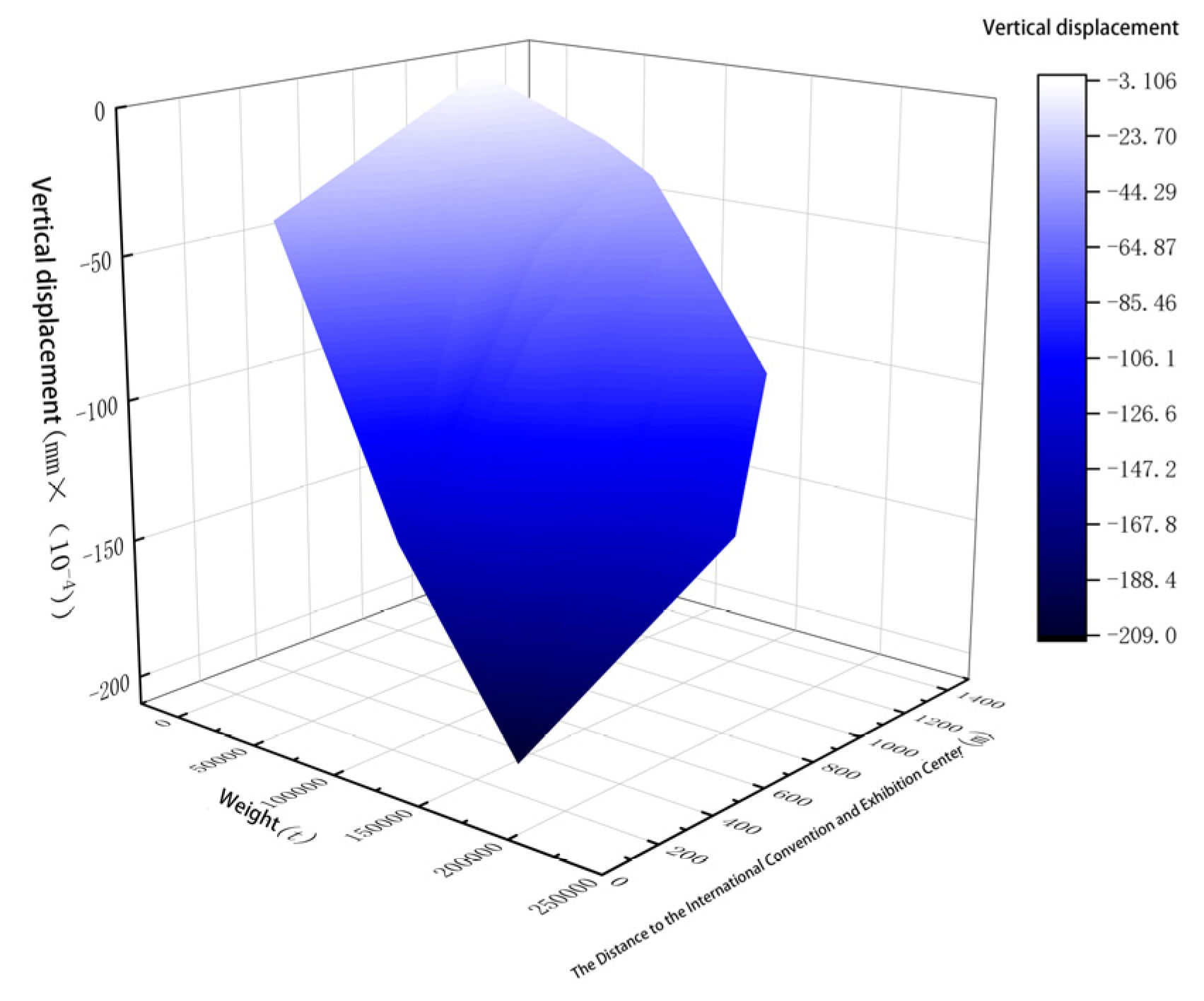
3.2. Analysis of Nearby Ground Deformation and Gravity Changes Caused by Cluster Loads
3.3. Discussion and Verification
4. Conclusions and Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dong, D.; Gross, R.S.; Dickey, J.O. Seasonal Variations of the Earth’s Gravitational Field: An Analysis of Atmospheric Pressure, Ocean Tidal, and Surface Water Excitation. Geophys. Res. Lett. 1996, 23, 725–728. [Google Scholar] [CrossRef]
- Chao, B.F.; Dehant, V.; Gross, R.S. Space Geodesy Monitors Mass Transports in Global Geophysical Fluids. Eos Trans. Am. Geophys. Union 2000, 81, 247–250. [Google Scholar] [CrossRef]
- Melchior, P. The Solid Tide of the Planet Earth; Science Press: Beijing, China, 1984. [Google Scholar]
- Dziewonski, A.M.; Anderson, D.L. Preliminary Reference Earth Model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Zhang, H.; Zheng, Y.; Liu, C. Love Number Contemporary Theory and New Technology Analysis. Prog. Geophys. 1999, 4, 50–58. [Google Scholar]
- Caputo, M. Deformation of a Layered Earth by an Axially Symmetric Surface Mass Distribution. J. Geophys. Res. Atmos. 1961, 66, 1479–1483. [Google Scholar] [CrossRef]
- Caputo, M. Tables for the Deformation of an Earth Model by Surface Mass Distributions. J. Geophys. Res. 1962, 67, 1611–1616. [Google Scholar] [CrossRef]
- Rabbel, W.; Zschau, J. Static Deformations and Gravity Changes at the Earth’s Surface Due to Atmospheric Loading. J. Geophys. 1985, 56, 81–89. [Google Scholar]
- Longman, I.M. On the Stability of a Spherical Gravitating Compressible Liquid Planet without Spin. Geophys. J. Int. 2007, 42, 621–635. [Google Scholar] [CrossRef]
- Longman, I.M. A Green’s Function for Determining the Deformation of the Earth under Surface Mass Loads: 1. Theory. J. Geophys. Res. 1962, 67, 845–850. [Google Scholar] [CrossRef]
- Farrell, W.E. Deformation of the Earth by surface loads. Rev. Geophys. Space Phys. 1972, 10, 761–797. [Google Scholar] [CrossRef]
- Guo, J.Y. Direct Proof of the Asymptotic Expression of the Loading Love Number. Chin. J. Geophys. 2000, 43, 549–555. [Google Scholar] [CrossRef]
- Xi, Q. Surface Spherical Harmonic Function and Tidal Level Expansion. Acta Seismol. Sin. 1998, 4, 441–443. [Google Scholar]
- Wu, X.; Zhang, C.; Zhao, D.; Song, M. Improvement of the Definite Integral Calculation Method of Generalized Spherical Harmonics. J. Surv. Sci. Technol. 2005, 22, 17–20. [Google Scholar]
- Mathews, P.M.; Buffett, B.A.; Shapiro, I.I. Tidal station displacements. J. Geophy. Res. 1997, 102, 20469–20477. [Google Scholar] [CrossRef]
- Sun, H. Green’s Function of Atmospheric Gravity. Sci. Bull. 1997, 42, 1640–1646. [Google Scholar]
- Le Meur, E.; Hindmarsh, R.C.A. A Comparison of Two Spectral Approaches for Computing the Earth Response to Surface Loads. Geophys. J. Int. 2000, 141, 282–298. [Google Scholar] [CrossRef][Green Version]
- Le Meur, E.; Huybrechts, P. A Model Computation of the Temporal Changes of Surface Gravity and Geoidal Signal Induced by the Evolving Greenland Ice Sheet. Geophys. J. Int. 2001, 145, 835–849. [Google Scholar] [CrossRef][Green Version]
- Zhang, Y.; Wu, X.; Wang, W.; Xu, H.; Liu, J. Research on the Tectonic Stress Field Changes before the Wenchuan m8.0 Earthquake Based on Gps Observations by Green’s Function Method. Acta Geomat. Sin. 2010, 39, 11–15. [Google Scholar]
- Shen, Y.; Yan, H.; Peng, P.; Bai, X.; Tian, D. Comparison of Green Function and Spherical Harmonic Function Methods for Surface Deformation Caused by Mass Loading. J. Wuhan Univ. 2017, 42, 1008–1014. [Google Scholar]
- Wang, X.; Chen, Y.; Liu, H. Calculating 3D Surface Deformation Based on Spherical Harmonic Transformation and Load Response. Sci. Technol. Eng. 2021, 21, 11963–11970. [Google Scholar]
- Li, W.; Wang, W.; Zhang, C.; Dong, J.; Liu, H. Effects of Regional Crustal Structure Differences on Vertical Deformation of Land Water Load in China from Grace-FO Inversion in Recent 10 Months. Geod. Geodyn. 2021, 9, 707–713. [Google Scholar]
- Wu, X.; Tian, S.; Wu, G. Research on the Relationship between Gravity Change, Crustal Deformation and Groundwater. Acta Seismol. 1992, 1, 653–660. [Google Scholar]
- Xing, C.; Zhang, Y.; Shi, S.; Du, R. The Water Storage Effect of the Three Gorges Reservoir and Its Influence on the Activity of the Fairy Mountain Fault. J. Geod. Geodyn. 2006, 26, 69–72. [Google Scholar]
- Akatsuka, M.; Miura, S.; Ohta, Y.; Sato, T.; Freymuller, J.T. Seasonal Variation of Vertical Crustal Deformation Possibly Related to Water Mass Storage in Southeast Alaska. In Proceedings of the AGU Fall Meeting 2009, San Francisco, CA, USA, 12–14 December 2009. G43A-0714. [Google Scholar]
- Gladkikh, V.; Tenzer, R.; Denys, P. Crustal Deformation due to Atmospheric Pressure Loading in New Zealand. J. Geod. Sci. 2011, 1, 271–279. [Google Scholar] [CrossRef]
- Sun, L.; Yao, Y.; Jiang, L.; Wei, G.; Wang, H.; Luo, J. The Influence of Water Load Changes in the Three Gorges Reservoir on Crustal Deformation. J. Yangtze River Sci. Res. Inst. 2015, 32, 46–50. [Google Scholar]
- Wang, L.; Chen, C.; Xian, M.A. A Water Storage Loading Model by SRTM-DEM Data and Surface Response Simulation of Gravity and Deformation in the Three Gorges Reservoir of China. Acta Geod. Cartogr. Sin. 2016, 45, 1148–1156. [Google Scholar]
- Vandam, T.M.; Herring, T.A. Detection of Atmospheric Pressure Loading Using Very Long Baseline Interferometry Measurements. J. Geophys. Res. Solid Earth 1994, 99, 4505–4517. [Google Scholar] [CrossRef]
- Vandam, T.M.; Blewitt, G.; Heflin, M.B. Atmospheric Pressure Loading Effects on Global Positioning System Coordinate Determinations. J. Geophys. Res. Solid Earth 1994, 99, 23939–23950. [Google Scholar] [CrossRef]
- Zhang, K.; Bian, S.; Tao, B. The Influence of the Establishment of the Three Gorges Reservoir on the Earth’s Gravitational Field and Crustal Deformation. Chin. J. Geophys. 2005, 37, 260–267. [Google Scholar]
- Wang, J. Geoid Undulation Caused by Building Complex Load and Its Influence on Elevation. J. Wuhan Univ. 2008, 6, 616–618. [Google Scholar]
- Zhang, H.; Xu, H.; Liu, X. The Basic Theory and Numerical Results of the Love Number of the Earth Tide. Prog. Geophys. 2004, 2, 372–378. [Google Scholar]
- Jeffreys, H. The Earth, 5th ed.; Cambridge University Press: New York, NY, USA, 1970. [Google Scholar]
- Wahr, M. Body Tides on an Elliptical, Rotating, Elastic and Oceanless Earth. Geophys. J. Int. 1981, 64, 677–703. [Google Scholar] [CrossRef]
- Dahlen, F.A. Elastic Dislocation Theory for a Self-Gravitating Elastic Configuration with an Initialstatic Stress Field. Geophys. J. Int. 1972, 28, 357–383. [Google Scholar] [CrossRef]
- Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity; Cambridge University Press: Cambridge, UK, 1927. [Google Scholar]
- Zhang, C. Ground Deformation Caused by Building Load and Its Influence on the Geoid; Tongji University: Shanghai, China, 2006. [Google Scholar]
- Zhang, S.; Zhong, M.; Tang, S. Atmospheric Load Effect on vertical Crustal Deformation of GPS Reference Stations in China. Geomat. Inf. Sci. Wuhan Univ. 2006, 31, 1090–1093. [Google Scholar]
- Zhang, Y. Earth Tide Simulation Considering the Slow Anisotropy of the Upper Ground; Chinese Institute of Scientific Surveying and Geophysics: Wuhan, China, 1997. [Google Scholar]
- Xu, H.; Mao, W.; Zhang, Y. Theoretical Model of the Earth’s Tidal Strain. Acta Seismol. Sin. 1986, 8, 275–283. [Google Scholar]
- Peltier, W.R. The LAGEOS Constraint on Deep Mantle Viscosity: Results from a New Normal Mode Method for the Inversion of Viscoelastic Relaxation Spectra. J. Geophys. Res. Solid Earth 1985, 90, 9411–9421. [Google Scholar] [CrossRef]
- Chen, J.; Li, J. Research and Implementation of High-Precision and High-Resolution Geoid in My Country’s Mainland. J. Surv. Mapp. 2001, 30, 95–100. [Google Scholar]

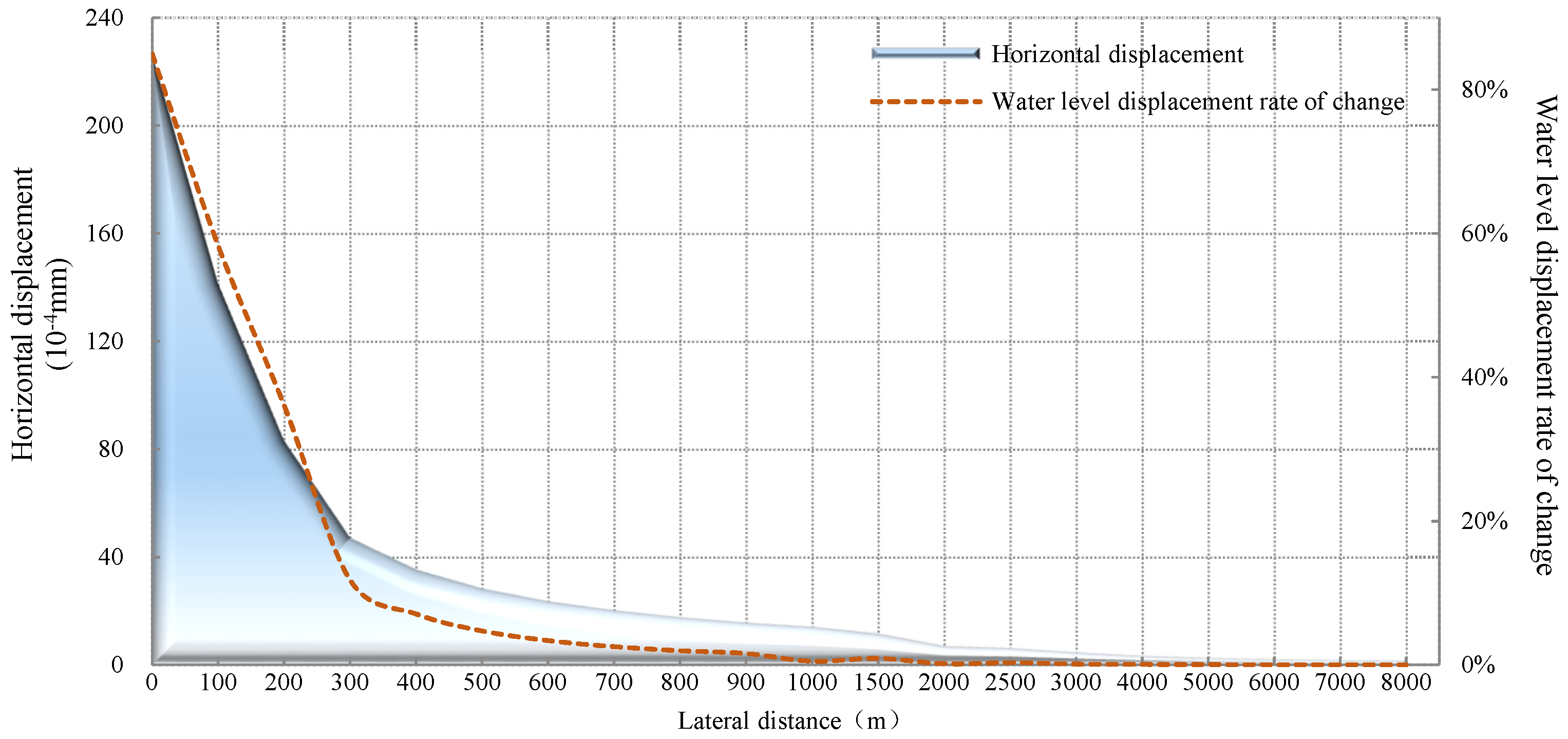
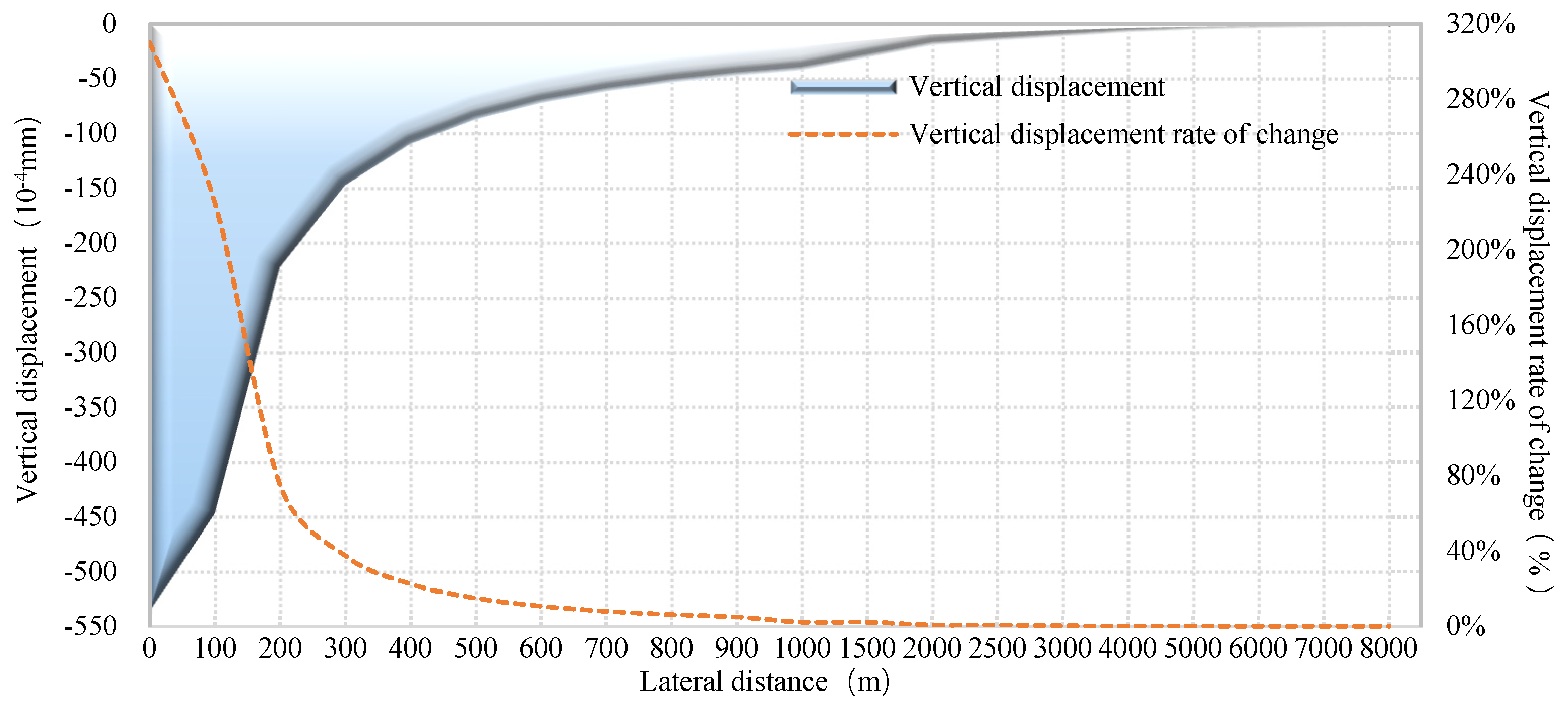
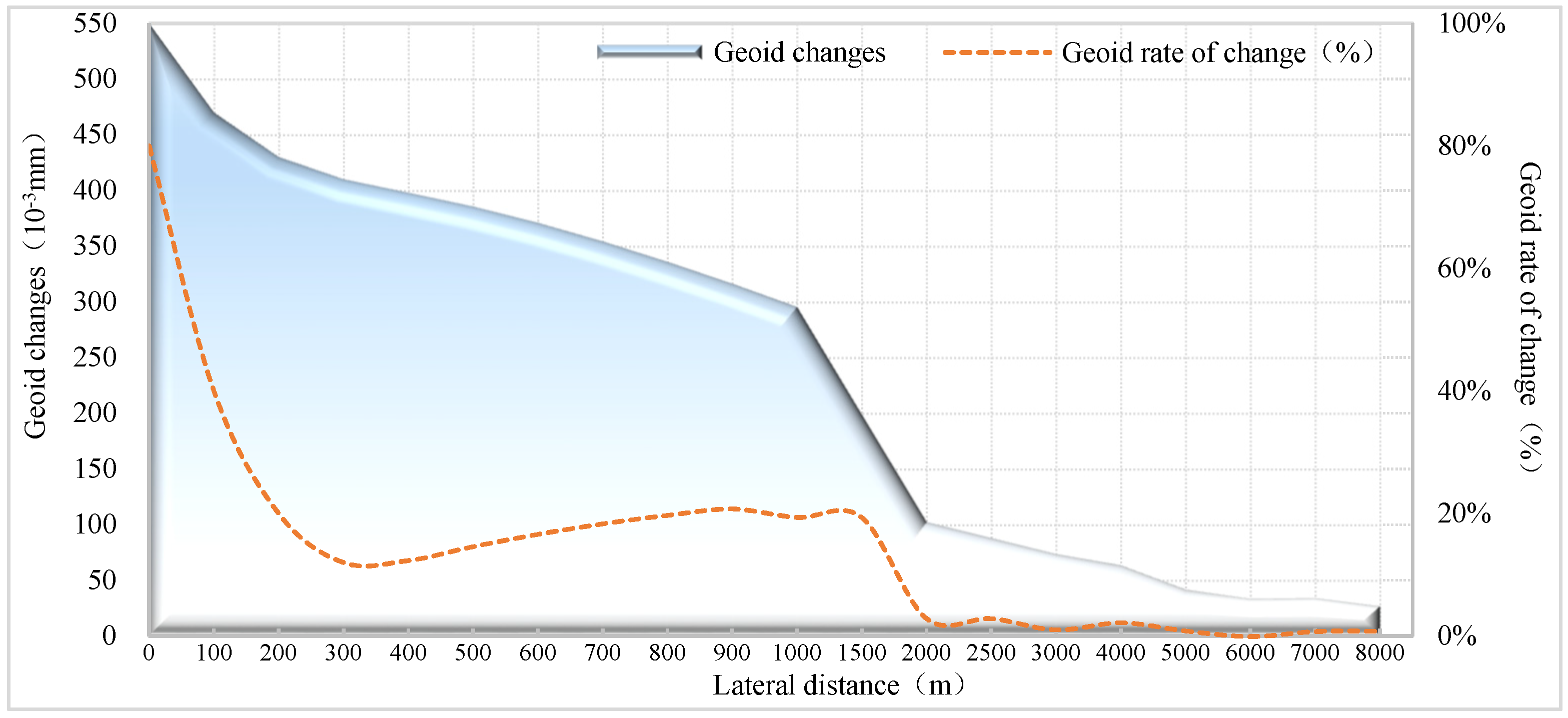




| Ground Distance to Minsheng Bank (m) | Horizontal Displacement (mm) × 10−4 | Vertical Displacement (mm) × 10−4 | Geoid Changes (mm) × 10−3 | The Geoid Is Tilted (S) × 10−4 |
|---|---|---|---|---|
| 100 | 141.6865 | −447.0230 | 419.3370 | −87.5873 |
| 200 | 70.8424 | −222.4988 | 414.9873 | −116.1458 |
| 300 | 47.2252 | −147.6574 | 407.8269 | −171.5090 |
| 400 | 35.4161 | −110.2408 | 397.9935 | −223.6964 |
| 500 | 28.3288 | −87.7892 | 385.6572 | −271.7679 |
| 600 | 23.6037 | −72.8193 | 371.0529 | −314.8861 |
| 700 | 20.2275 | −62.1289 | 354.4479 | −352.3400 |
| 800 | 17.6945 | −54.1110 | 336.1257 | −383.5529 |
| 900 | 15.7233 | −47.8757 | 316.4265 | −408.0824 |
| 1000 | 14.1457 | −42.8868 | 295.6743 | −425.6757 |
| 1500 | 11.5801 | −31.6680 | 198.8753 | −350.4609 |
| 2000 | 7.0156 | −20.4492 | 102.0762 | −275.2461 |
| 2500 | 6.2314 | −16.7157 | 87.8133 | −154.8783 |
| 3000 | 4.6164 | −12.9822 | 73.5504 | −34.5105 |
| 4000 | 3.4172 | −9.2603 | 63.4287 | −15.5991 |
| 5000 | 2.6812 | −7.0421 | 41.6534 | −14.9756 |
| 6000 | 2.1707 | −5.5758 | 33.2820 | −6.2907 |
| 7000 | 1.8103 | −4.5408 | 34.0216 | −5.6269 |
| 8000 | 1.5438 | −3.7775 | 26.5664 | −5.1875 |
| The Serial Number | Building Name | Distance to the International Convention and Exhibition Center (m) | Horizontal Displacement (×10−4 mm) | Vertical Displacement (×10−4 mm) | Geoid Changes (×10−3 mm) | The Amount of Geoid Inclination (×10−4 s) |
|---|---|---|---|---|---|---|
| 1 | Dennis 1 World | 569 | 31.45023793 | −100.7346377 | 494.4622581 | −407.0086996 |
| 2 | CITIC Tower | 500 | 22.28609813 | −71.58994436 | 318.3766515 | −230.0360243 |
| 3 | Minsheng Bank Building | 609 | 31.8830502 | −101.9255062 | 530.6703983 | −468.5733139 |
| 4 | Xin’ao Building | 532 | 20.45825586 | −65.63559866 | 305.0021309 | −234.4014766 |
| 5 | Dennis 2 World | 698 | 12.7534247 | −40.60965778 | 233.9544765 | −237.7211436 |
| 6 | Five Elements Garden Tower A | 598 | 25.4898459 | −81.52411958 | 419.1448961 | −363.4184917 |
| 7 | Five Elements Garden Tower B | 629 | 23.15702903 | −73.97067496 | 393.368437 | −358.7369287 |
| 8 | Dennis 3 Worlds | 905 | 3.796945281 | −11.98191921 | 80.32582026 | −106.7947076 |
| 9 | International Chamber of Commerce Building | 934 | 27.43757742 | −86.48290938 | 586.5287866 | −804.8882877 |
| 10 | Guolong Building | 991 | 21.80839029 | −68.56679636 | 476.5889363 | −696.4885789 |
| 11 | Five Elements Garden Block D | 861 | 11.1266982 | −35.18269975 | 229.4652653 | −289.2871798 |
| 12 | Five Elements Garden Block D | 813 | 12.88057745 | −40.81024067 | 258.5519355 | −307.35943 |
| 13 | Dennis 4 Worlds | 995 | 4.520173596 | −14.20899181 | 98.94288012 | −145.2405721 |
| 14 | Five Elements Garden Tower E | 918 | 8.456283241 | −26.67152532 | 179.7216709 | −242.3527261 |
| 15 | Weiye Caizhi Plaza | 949 | 4.152928583 | −13.08169576 | 89.27430762 | −124.5442942 |
| 16 | Expo Tower | 1100 | 9.230506099 | −28.95034766 | 199.2507399 | −303.1017238 |
| 17 | Liji Upper East International | 1000 | 17.22282853 | −54.12637633 | 377.7700455 | −557.6359029 |
| 18 | l Level I upper east international | 1100 | 4.736154894 | −14.8543676 | 102.2351707 | −155.5209105 |
| 19 | New Mango Building | 1100 | 13.75283459 | −43.13407504 | 296.8702299 | −451.6012261 |
| 20 | Zhongyuan Guangfa Financial Building | 1100 | 16.07894611 | −50.42963786 | 347.081934 | −527.983648 |
| 21 | CNPC International Huijin Building | 1200 | 9.38582782 | −29.37137886 | 198.9695094 | −312.995569 |
| 22 | Longhu Building | 977 | 9.961163531 | −31.33876793 | 216.4653261 | −311.4645876 |
| 23 | Oriental International (South) | 991 | 6.907265602 | −21.7168286 | 150.9477005 | −220.595447 |
| 24 | Oriental International (North) | 1000 | 6.596191806 | −20.72992595 | 144.6826039 | −213.5696449 |
| 25 | Dennis 6 Worlds | 1100 | 0.990395935 | −3.106255099 | 21.37879772 | −32.52158786 |
| 26 | Greenland Century Mansion | 1200 | 11.24028574 | −35.17459484 | 238.2820334 | −374.8374355 |
| 27 | Greenland Summit World | 1200 | 10.05456805 | −31.4640896 | 213.1460869 | −335.2965033 |
| 28 | Road King Building | 1200 | 9.850577681 | −30.82573584 | 208.8217093 | −328.493898 |
| 29 | Dennis International Apartment (A) | 1000 | 12.43225584 | −39.07098983 | 272.6923657 | −402.5280865 |
| 30 | Dennis International Apartment (B) | 1000 | 13.8868525 | −43.64236707 | 304.597871 | −449.6246085 |
| 31 | Dennis International Apartment (C) | 1000 | 11.9427605 | −37.53264732 | 261.9556462 | −386.6793437 |
| 32 | Dennis 7 Worlds | 1100 | 4.727362032 | −14.82678987 | 102.045367 | −155.2321797 |
| 33 | Vancouver Building | 1200 | 7.944649097 | −24.86145101 | 168.4180621 | −264.9356042 |
| 34 | Henan Agricultural Bank Building | 1200 | 9.600793554 | −30.04407818 | 203.526553 | −320.1641772 |
| 35 | World Trade Building (A) | 1000 | 7.155134041 | −22.48651998 | 156.9425898 | −231.6669196 |
| 36 | World Trade Building (B) | 1000 | 9.057557916 | −28.46528882 | 198.6708548 | −293.2630653 |
| 37 | Mobile building | 254 | 11.81174111 | −38.37932228 | 87.72484668 | −31.95131788 |
| 38 | Futures Building | 385 | 36.80129836 | −118.8447767 | 414.8423738 | −229.8514987 |
| 39 | Xin Po Building | 276 | 43.48678596 | −141.1473868 | 353.3399022 | −139.9635576 |
| 40 | Cathay Pacific Fortune Center | 383 | 54.55038978 | −176.1819911 | 611.3389495 | −336.9206096 |
| 41 | China Grain Store | 310 | 64.28028134 | −208.2647557 | 596.0240243 | −265.4599272 |
| 42 | United Center Building | 427 | 42.52385922 | −137.0691714 | 525.6722705 | −323.2217623 |
| 43 | Wanda Futures Building | 441 | 10.87449407 | −35.03222146 | 137.9250956 | −87.60130898 |
| 44 | Jingfeng International Center | 551 | 33.03784179 | −105.9075875 | 505.8941363 | −402.8799715 |
| 45 | Future International Building 26 | 495 | 14.28824269 | −45.91093369 | 201.9208415 | −144.3722277 |
| 46 | Future International Building 25 | 525 | 14.71388877 | −47.21970501 | 217.2709484 | −164.770953 |
| 47 | Wang Ding International | 645 | 32.16422201 | −102.673251 | 555.6776147 | −519.8503882 |
| 48 | Future International Building 22 | 673 | 8.522531917 | −27.1709336 | 151.8549254 | −148.4534779 |
| 49 | People’s Insurance Building | 680 | 41.25931907 | −131.4961481 | 741.0651138 | −732.3875599 |
| 50 | Future International Building 24 | 587 | 12.53806419 | −40.12353748 | 202.6188634 | −172.2813869 |
| 51 | Kunwu Building | 742 | 29.30217769 | −93.13656382 | 556.386559 | −601.2320672 |
| 52 | Future International Building 23 | 623 | 15.57058579 | −49.74938943 | 262.8634769 | −237.4217711 |
| 53 | Zhengdong Financial Building | 821 | 25.72409535 | −81.47709046 | 518.6101605 | −622.5791084 |
| 54 | Jincheng Sunshine Century (South) | 708 | 11.31098792 | −36.00178765 | 209.227494 | −215.6517103 |
| 55 | Jincheng Sunshine Century (North) | 774 | 15.85801396 | −50.33253341 | 309.0925354 | −349.0362695 |
| 56 | Jincheng Sunshine Century (Main) | 747 | 14.695301 | −46.69876694 | 280.1470389 | −304.8253995 |
| 57 | Hailian Building | 877 | 15.73914514 | −49.73139059 | 327.6976662 | −421.2945106 |
| 58 | Zhengzhou Italy International Building | 940 | 13.15189714 | −41.44422365 | 281.7707075 | −389.2237426 |
| 59 | Gram Business Building | 968 | 13.4870856 | −42.4488975 | 292.050751 | −416.0573946 |
| Total | 1040.10468 | −3315.5718 | 17,420.14634 | −18,903.85184 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Liu, W.; Qu, J.; Guo, W.; Qiu, J. Load Deformation Effect of CBD Ground Cluster in Zhengzhou City. Sustainability 2022, 14, 4047. https://doi.org/10.3390/su14074047
Yang L, Liu W, Qu J, Guo W, Qiu J. Load Deformation Effect of CBD Ground Cluster in Zhengzhou City. Sustainability. 2022; 14(7):4047. https://doi.org/10.3390/su14074047
Chicago/Turabian StyleYang, Li, Wenkai Liu, Jihong Qu, Wei Guo, and Jianhua Qiu. 2022. "Load Deformation Effect of CBD Ground Cluster in Zhengzhou City" Sustainability 14, no. 7: 4047. https://doi.org/10.3390/su14074047
APA StyleYang, L., Liu, W., Qu, J., Guo, W., & Qiu, J. (2022). Load Deformation Effect of CBD Ground Cluster in Zhengzhou City. Sustainability, 14(7), 4047. https://doi.org/10.3390/su14074047





