Progress in Developing Scale-Able Approaches to Field-Scale Water Accounting Based on Remote Sensing
Abstract
1. Introduction
- The lack of detailed fine scale observations in space and time of water cycle components, particularly for soil moisture, farm dam volumes, and vegetation transpiration;
- The need for models linking satellite data and water cycle components that are transferable in space and time, most likely using physical relationships or through fast self-calibrating data-based models; and
- The need to quantify uncertainties in the satellite and water cycle relationships beyond reporting simple root mean square errors or bias.
2. Materials and Methods
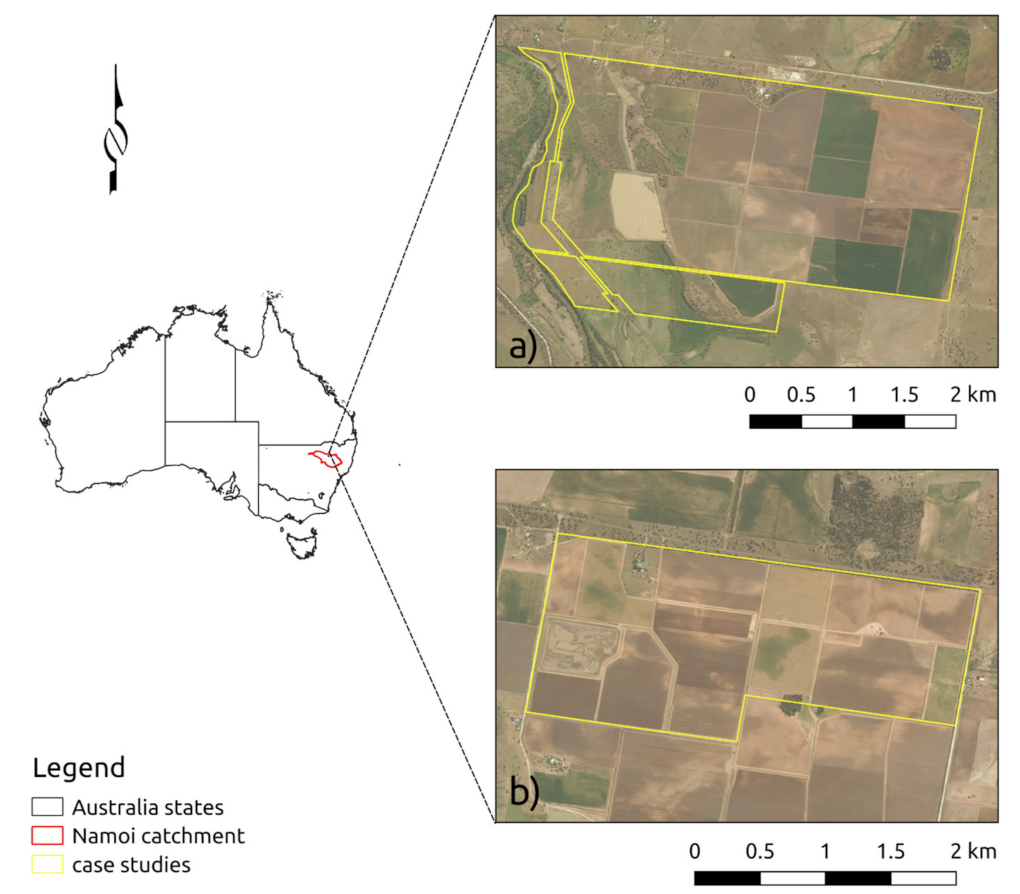
2.1. Case Studies
2.2. Data Sources
2.3. Water Demand
2.4. Water Supply
2.5. A Measure of Efficiency in Water Use
2.6. On-Farm Reservoir Volume Modeling
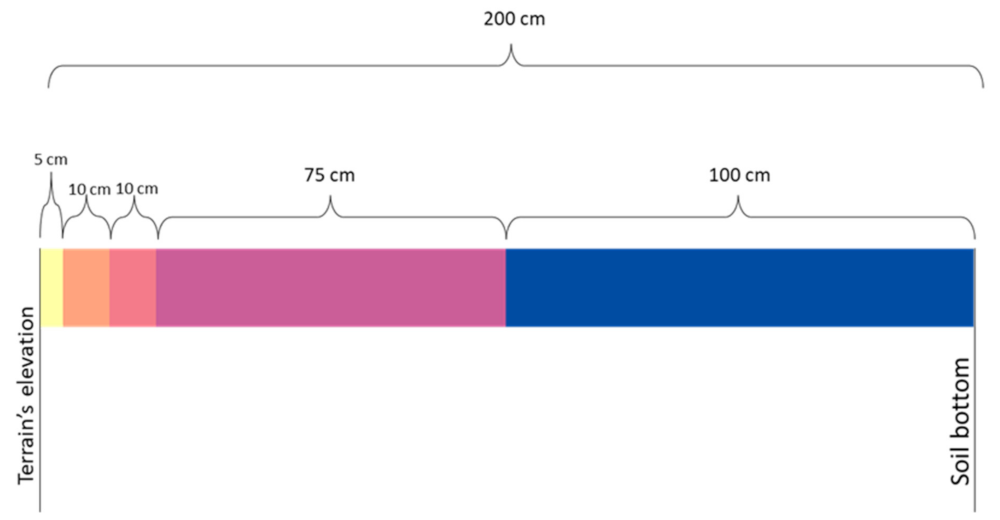
2.7. Soil Moisture Modeling
3. Results
3.1. FAO Penman-Monteith ETr
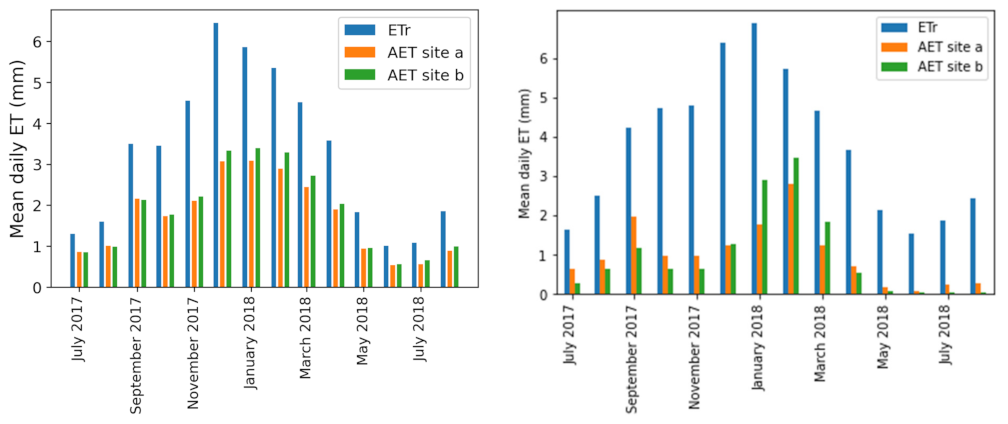
3.2. ETLook and CMRSET AET Estimates
3.3. Site Water Balance and Efficiency
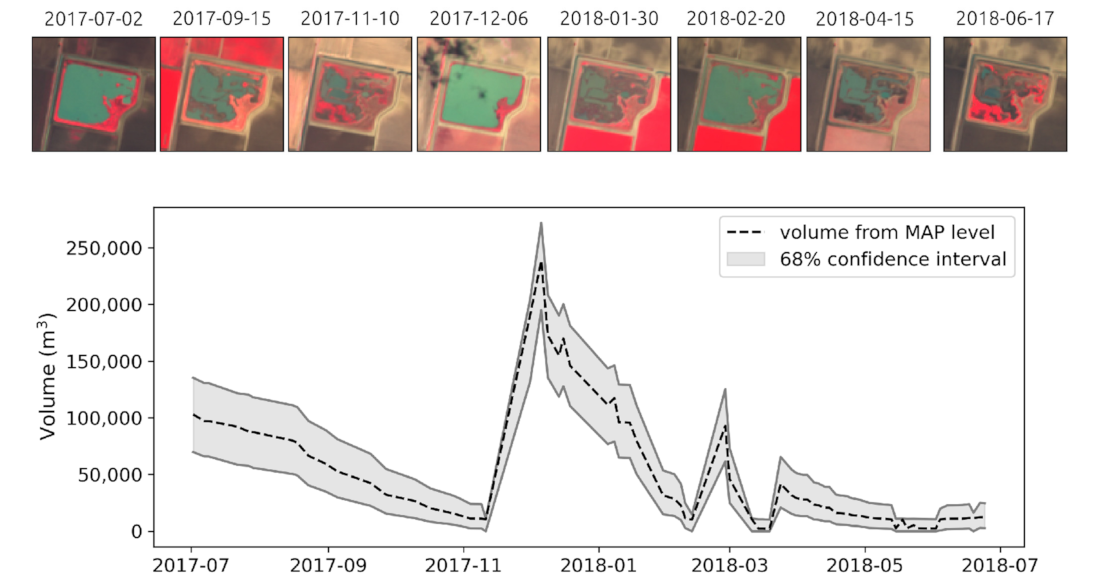
3.4. Reservoir Volume Estimates
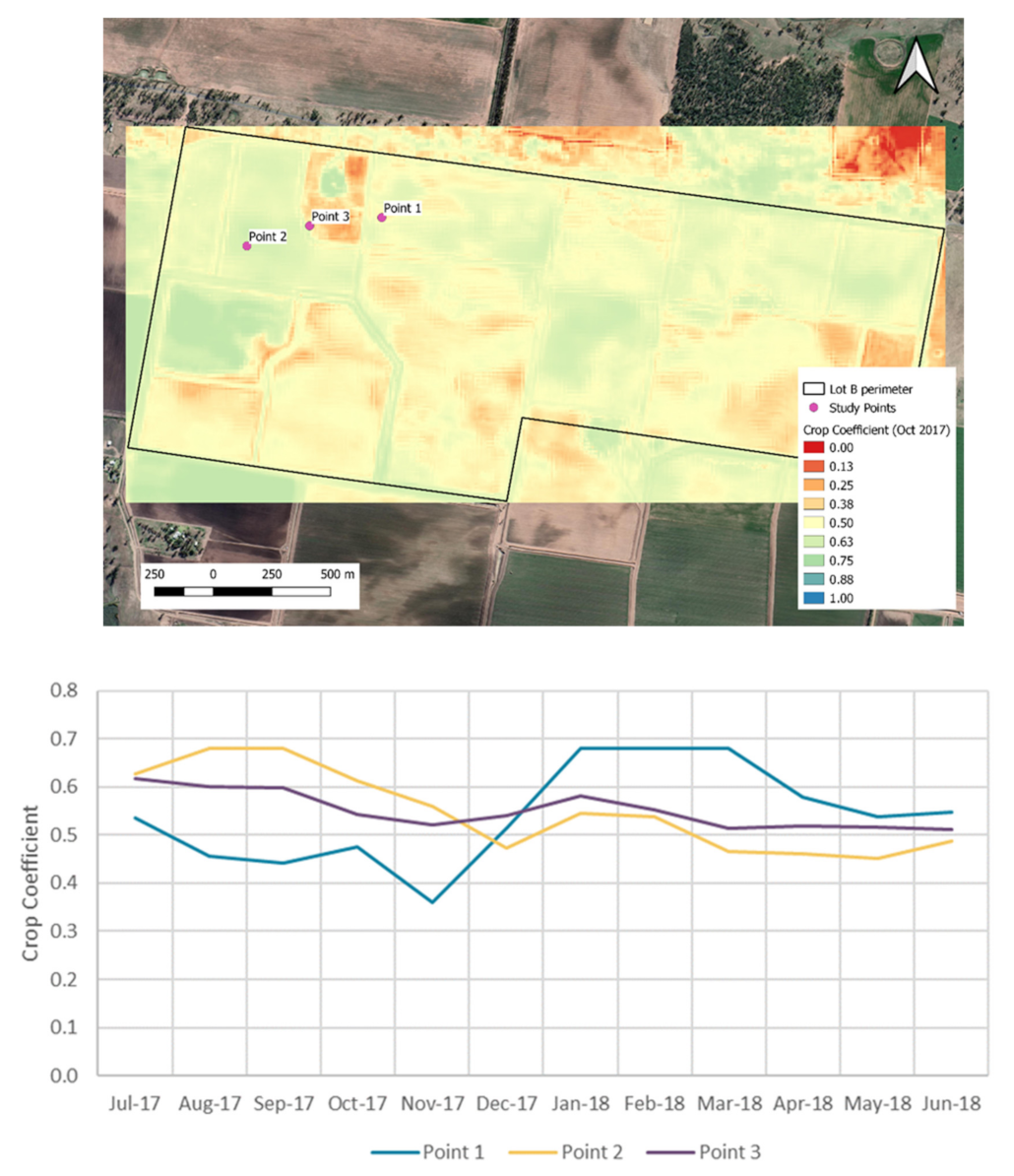
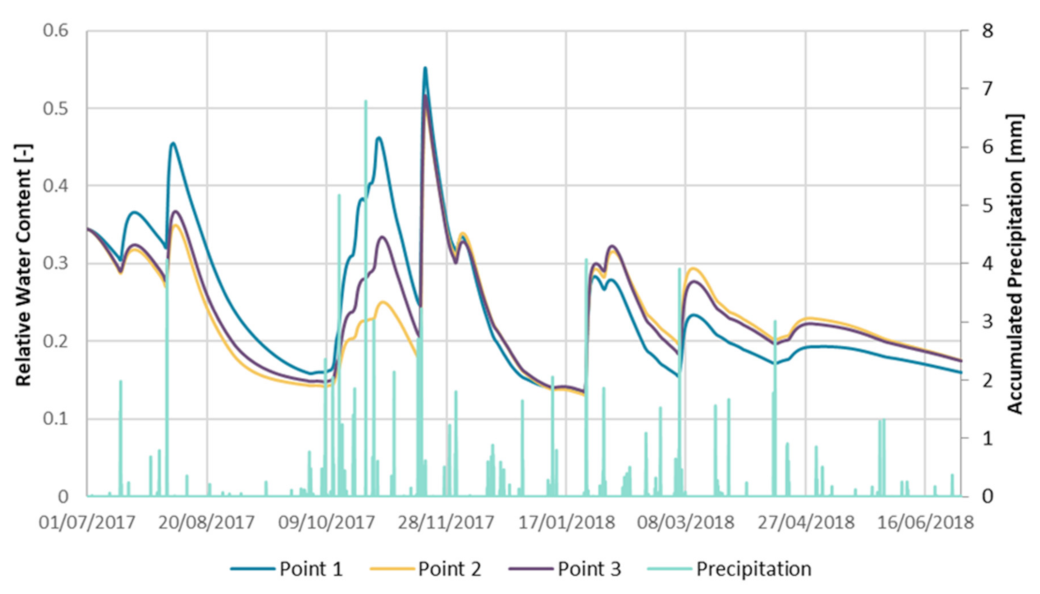
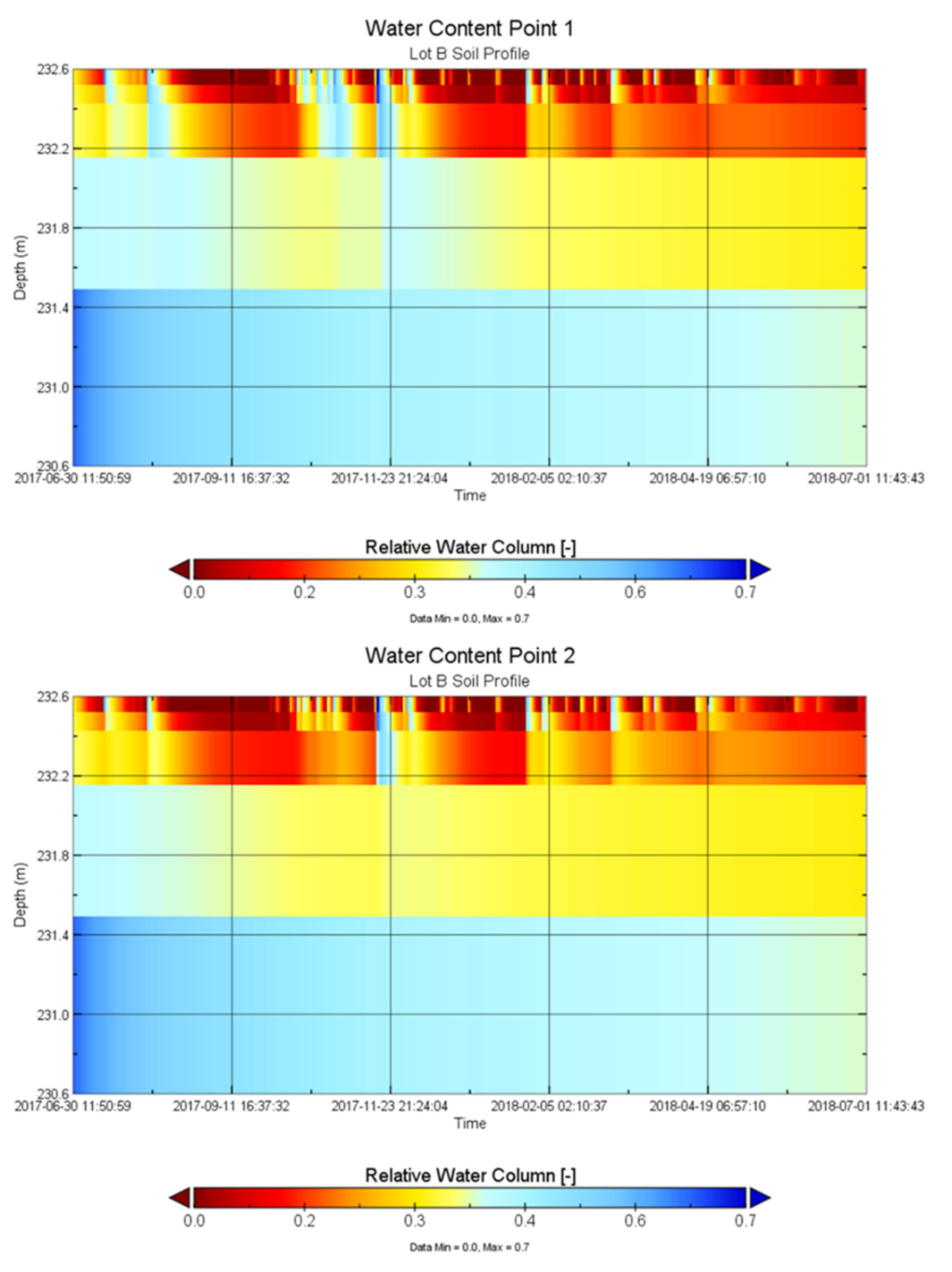
3.5. Soil Moisture Estimation
4. Discussion
4.1. General Discussion
4.2. How Do We Achieve Accurate Water Footprint and Crop Water Productivity Estimates at All Global Locations?
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Oki, T.; Kanae, S. Global Hydrological Cycles and World Water Resources. Science 2006, 313, 1068–1072. [Google Scholar] [CrossRef] [PubMed]
- D’Odorico, P.; Davis, K.F.; Rosa, L.; Carr, J.A.; Chiarelli, D.; Dell’Angelo, J.; Gephart, J.; MacDonald, G.K.; Seekell, D.A.; Suweis, S.; et al. The Global Food-Energy-Water Nexus. Rev. Geophys. 2018, 56, 456–531. [Google Scholar] [CrossRef]
- Mekonnen, M.M.; Hoekstra, A.Y. Sustainability of the blue water footprint of crops. Adv. Water Resour. 2020, 143, 103679. [Google Scholar] [CrossRef]
- Rattalino Edreira, J.I.; Guilpart, N.; Sadras, V.; Cassman, K.G.; van Ittersum, M.K.; Schils, R.L.M.; Grassini, P. Water productivity of rainfed maize and wheat: A local to global perspective. Agric. For. Meteorol. 2018, 259, 364–373. [Google Scholar] [CrossRef]
- Rosa, L.; Rulli, M.C.; Davis, K.F.; Chiarelli, D.D.; Passera, C.; D’Odorico, P. Closing the yield gap while ensuring water sustainability. Environ. Res. Lett. 2018, 13, 104002. [Google Scholar] [CrossRef]
- Davis, K.F.; Rulli, M.C.; Garrassino, F.; Chiarelli, D.; Seveso, A.; D’Odorico, P. Water limits to closing yield gaps. Adv. Water Resour. 2017, 99, 67–75. [Google Scholar] [CrossRef]
- Quinteiro, P.; Ridoutt, B.G.; Arroja, L.; Dias, A.C. Identification of methodological challenges remaining in the assessment of a water scarcity footprint: A review. Int. J. Life Cycle Assess. 2018, 23, 164–180. [Google Scholar] [CrossRef]
- Hoekstra, A.Y.; Hung, P.Q. Virtual Water Trade: A Quantification of Virtual Water Flows between Nations in Relation to International Crop Trade; UNESCO-IHE: Delft, The Netherlands, 2002. [Google Scholar]
- Escriva-Bou, A.; McCann, H.; Hanak, E.; Lund, J.; Gray, B.; Blanco, E.; Jezdimirovic, J.; Magnuson-Skeels, B.; Tweet, A. Water Accounting in Western US, Australia, and Spain: Comparative Analysis. J. Water Resour. Plan. Manag. 2020, 146, 04020004. [Google Scholar] [CrossRef]
- Chen, Y.; Colloff, M.J.; Lukasiewicz, A.; Pittock, J. A trickle, not a flood: Environmental watering in the Murray—Darling Basin, Australia. Mar. Freshw. Res. 2020, 72, 601–619. [Google Scholar] [CrossRef]
- Bretreger, D.; Yeo, I.-Y.; Quijano, J.; Awad, J.; Hancock, G.; Willgoose, G. Monitoring irrigation water use over paddock scales using climate data and landsat observations. Agric. Water Manag. 2019, 221, 175–191. [Google Scholar] [CrossRef]
- Massari, C.; Modanesi, S.; Dari, J.; Gruber, A.; de Lannoy, G.J.M.; Girotto, M.; Quintana-Seguí, P.; Le Page, M.; Jarlan, L.; Zribi, M.; et al. A Review of Irrigation Information Retrievals from Space and Their Utility for Users. Remote Sens. 2021, 13, 4112. [Google Scholar] [CrossRef]
- Dixon, H.; Sandström, S.; Cudennec, C.; Lins, H.F.; Abrate, T.; Bérod, D.; Chernov, I.; Ravalitera, N.; Sighomnou, D.; Teichert, F. Intergovernmental Cooperation for Hydrometry—What, Why and How? Hydrol. Sci. J. 2020, pp. 1–15. Available online: https://www.tandfonline.com/action/showCitFormats?doi=10.1080%2F02626667.2020.1764569&area=0000000000000001 (accessed on 20 February 2022).
- Blatchford, M.L.; Mannaerts, C.M.; Njuki, S.M.; Nouri, H.; Zeng, Y.; Pelgrum, H.; Wonink, S.; Karimi, P. Evaluation of WaPOR V2 evapotranspiration products across Africa. Hydrol. Process. 2020, 34, 3200–3221. [Google Scholar] [CrossRef]
- Mekonnen, M.M.; Hoekstra, A.Y. A global and high-resolution assessment of the green, blue and grey water footprint of wheat. Hydrol. Earth Syst. Sci. 2010, 14, 1259–1276. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, X.; Wu, S.R.; Gong, M.; Du, Y.; Wang, J.; Li, Y.; Liu, J. Spatial-temporal assessment of water footprint, water scarcity and crop water productivity in a major crop production region. J. Clean. Prod. 2019, 224, 375–383. [Google Scholar] [CrossRef]
- Kayatz, B.; Baroni, G.; Hillier, J.; Lüdtke, S.; Heathcote, R.; Malin, D.; van Tonder, C.; Kuster, B.; Freese, D.; Hüttl, R.; et al. Cool Farm Tool Water: A global on-line tool to assess water use in crop production. J. Clean. Prod. 2019, 207, 1163–1179. [Google Scholar] [CrossRef] [PubMed]
- Vanuytrecht, E.; Raes, D.; Steduto, P.; Hsiao, T.C.; Fereres, E.; Heng, L.K.; Garcia Vila, M.; Mejias Moreno, P. AquaCrop: FAO’s crop water productivity and yield response model. Environ. Model. Softw. 2014, 62, 351–360. [Google Scholar] [CrossRef]
- Bretreger, D.; Yeo, I.-Y.; Hancock, G.; Willgoose, G. Monitoring irrigation using landsat observations and climate data over regional scales in the Murray-Darling Basin. J. Hydrol. 2020, 590, 125356. [Google Scholar] [CrossRef]
- Calera, A.; Campos, I.; Osann, A.; D’Urso, G.; Menenti, M. Remote Sensing for Crop Water Management: From ET Modelling to Services for the End Users. Sensors 2017, 17, 1104. [Google Scholar] [CrossRef]
- Foster, T.; Mieno, T.; Brozović, N. Satellite-Based Monitoring of Irrigation Water Use: Assessing Measurement Errors and Their Implications for Agricultural Water Management Policy. Water Resour. Res. 2020, 56, e2020WR028378. [Google Scholar] [CrossRef]
- Safi, A.R.; Karimi, P.; Mul, M.; Chukalla, A.; de Fraiture, C. Translating open-source remote sensing data to crop water productivity improvement actions. Agric. Water Manag. 2022, 261, 107373. [Google Scholar] [CrossRef]
- Guzinski, R.; Nieto, H. Evaluating the feasibility of using Sentinel-2 and Sentinel-3 satellites for high-resolution evapotranspiration estimations. Remote Sens. Environ. 2019, 221, 157–172. [Google Scholar] [CrossRef]
- Maselli, F.; Battista, P.; Chiesi, M.; Rapi, B.; Angeli, L.; Fibbi, L.; Magno, R.; Gozzini, B. Use of Sentinel-2 MSI data to monitor crop irrigation in Mediterranean areas. Int. J. Appl. Earth Obs. Geoinf. 2020, 93, 102216. [Google Scholar] [CrossRef]
- Fuentes, I.; van Ogtrop, F.; Vervoort, R.W. Long-term surface water trends and relationship with open water evaporation losses in the Namoi catchment, Australia. J. Hydrol. 2020, 584, 124714. [Google Scholar] [CrossRef]
- Fuentes, I.; Padarian, J.; van Ogtrop, F.; Vervoort, R.W. Comparison of Surface Water Volume Estimation Methodologies that Couple Surface Reflectance Data and Digital Terrain Models. Water 2019, 11, 780. [Google Scholar] [CrossRef]
- Fuentes, I.; Scalzo, R.; Vervoort, R.W. Volume and uncertainty estimates of on-farm reservoirs using surface reflectance and LiDAR data. Environ. Model. Softw. 2021, 143, 105095. [Google Scholar] [CrossRef]
- Sandi, S.G.; Saco, P.M.; Saintilan, N.; Wen, L.; Riccardi, G.; Kuczera, G.; Willgoose, G.; Rodríguez, J.F. Detecting inundation thresholds for dryland wetland vulnerability. Adv. Water Resour. 2019, 128, 168–182. [Google Scholar] [CrossRef]
- Lettenmaier, D.P.; Alsdorf, D.; Dozier, J.; Huffman, G.J.; Pan, M.; Wood, E.F. Inroads of remote sensing into hydrologic science during the WRR era. Water Resour. Res. 2015, 51, 7309–7342. [Google Scholar] [CrossRef]
- McCabe, M.F.; Rodell, M.; Alsdorf, D.E.; Miralles, D.G.; Uijlenhoet, R.; Wagner, W.; Lucieer, A.; Houborg, R.; Verhoest, N.E.C.; Franz, T.E.; et al. The future of Earth observation in hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 3879–3914. [Google Scholar] [CrossRef]
- Karthikeyan, L.; Chawla, I.; Mishra, A.K. A review of remote sensing applications in agriculture for food security: Crop growth and yield, irrigation, and crop losses. J. Hydrol. 2020, 586, 124905. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F.; Pan, M.; Beck, H.; Coccia, G.; Serrat-Capdevila, A.; Verbist, K. Satellite Remote Sensing for Water Resources Management: Potential for Supporting Sustainable Development in Data-Poor Regions. Water Resour. Res. 2018, 54, 9724–9758. [Google Scholar] [CrossRef]
- Weiss, M.; Jacob, F.; Duveiller, G. Remote sensing for agricultural applications: A meta-review. Remote Sens. Environ. 2020, 236, 111402. [Google Scholar] [CrossRef]
- Karimi, P.; Bastiaanssen, W.G.M. Spatial evapotranspiration, rainfall and land use data in water accounting Part 1: Review of the accuracy of the remote sensing data. Hydrol. Earth Syst. Sci. 2015, 19, 507–532. [Google Scholar] [CrossRef]
- Ambrosone, M.; Matese, A.; Di Gennaro, S.F.; Gioli, B.; Tudoroiu, M.; Genesio, L.; Miglietta, F.; Baronti, S.; Maienza, A.; Ungaro, F.; et al. Retrieving soil moisture in rainfed and irrigated fields using Sentinel-2 observations and a modified OPTRAM approach. Int. J. Appl. Earth Obs. Geoinf. 2020, 89, 102113. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Cheema, M.J.M.; Immerzeel, W.W.; Miltenburg, I.J.; Pelgrum, H. Surface energy balance and actual evapotranspiration of the transboundary Indus Basin estimated from satellite measurements and the ETLook model. Water Resour. Res. 2012, 48, W11512. [Google Scholar] [CrossRef]
- Koech, R.; Langat, P. Improving Irrigation Water Use Efficiency: A Review of Advances, Challenges and Opportunities in the Australian Context. Water 2018, 10, 1771. [Google Scholar] [CrossRef]
- Feng, B.; Zhuo, L.; Xie, D.; Mao, Y.; Gao, J.; Xie, P.; Wu, P. A quantitative review of water footprint accounting and simulation for crop production based on publications during 2002–2018. Ecol. Indic. 2021, 120, 106962. [Google Scholar] [CrossRef]
- Glenn, E.P.; Doody, T.M.; Guerschman, J.P.; Huete, A.R.; King, E.A.; McVicar, T.R.; van Dijk, A.I.J.M.; van Niel, T.G.; Yebra, M.; Zhang, Y. Actual evapotranspiration estimation by ground and remote sensing methods: The Australian experience. Hydrol. Process. 2011, 25, 4103–4116. [Google Scholar] [CrossRef]
- Ray, R.L.; Fares, A.; He, Y.; Temimi, M. Evaluation and Inter-Comparison of Satellite Soil Moisture Products Using In Situ Observations over Texas, U.S. Water 2017, 9, 372. [Google Scholar] [CrossRef]
- Crow, W.T.; Berg, A.A.; Cosh, M.H.; Loew, A.; Mohanty, B.P.; Panciera, R.; de Rosnay, P.; Ryu, D.; Walker, J.P. Upscaling sparse ground-based soil moisture observations for the validation of coarse-resolution satellite soil moisture products. Rev. Geophys. 2012, 50, RG2002. [Google Scholar] [CrossRef]
- Wang, H.; Guan, H.; Gutiérrez-Jurado, H.A.; Simmons, C.T. Examination of water budget using satellite products over Australia. J. Hydrol. 2014, 511, 546–554. [Google Scholar] [CrossRef]
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [PubMed]
- Nagler, P.L.; Doody, T.M.; Glenn, E.P.; Jarchow, C.J.; Barreto-Muñoz, A.; Didan, K. Wide-area estimates of evapotranspiration by red gum (Eucalyptus camaldulensis) and associated vegetation in the Murray—Darling River Basin, Australia. Hydrol. Process. 2016, 30, 1376–1387. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Sanchez, A.H.; Picoli, M.C.A.; Camara, G.; Andrade, P.R.; Chaves, M.E.D.; Lechler, S.; Soares, A.R.; Marujo, R.F.B.; Simões, R.E.O.; Ferreira, K.R.; et al. Comparison of Cloud Cover Detection Algorithms on Sentinel—2 Images of the Amazon Tropical Forest. Remote Sens. 2020, 12, 1284. [Google Scholar] [CrossRef]
- Huffman, G.J.; Stocker, E.F.; Bolvin, D.T.; Nelkin, E.J.; Jackson, T. GPM IMERG Final Precipitation L3 1 Month 0.1 Degree x 0.1 degree V06. Available online: https://doi.org/10.5067/GPM/IMERG/3B-MONTH/06 (accessed on 21 April 2021).
- Hoffmann, L.; Günther, G.; Li, D.; Stein, O.; Wu, X.; Griessbach, S.; Heng, Y.; Konopka, P.; Müller, R.; Vogel, B.; et al. From ERA-Interim to ERA5: The considerable impact of ECMWF’s next-generation reanalysis on Lagrangian transport simulations. Atmos. Chem. Phys. 2019, 19, 3097–3124. [Google Scholar] [CrossRef]
- McNally, A.; Arsenault, K.; Kumar, S.; Shukla, S.; Peterson, P.; Wang, S.; Funk, C.; Peters-Lidard, C.D.; Verdin, J.P. A land data assimilation system for sub-Saharan Africa food and water security applications. Sci. Data 2017, 4, 170012. [Google Scholar] [CrossRef]
- Guerschman, J.P.; van Dijk, A.I.J.M.; Mattersdorf, G.; Beringer, J.; Hutley, L.B.; Leuning, R.; Pipunic, R.C.; Sherman, B.S. Scaling of potential evapotranspiration with MODIS data reproduces flux observations and catchment water balance observations across Australia. J. Hydrol. 2009, 369, 107–119. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56. Fao Rome 1998, 300, D05109. Available online: https://www.fao.org/3/x0490e/x0490e00.htm (accessed on 20 February 2022).
- Rienecker, M.M.; Suarez, M.; Todling, R.; Bacmeister, J.; Takacs, L.; Liu, H.; Gu, W.; Sienkiewicz, M.; Koster, R.; Gelaro, R. The GEOS-5 Data Assimilation System: Documentation of Versions 5.0. 1, 5.1. 0, and 5.2. 0.; NASA Goddard Space Flight Center: Greenbelt, MA, USA, 2008. [Google Scholar]
- Japan Meteorological Agency Himawari—8/9 Himawari Standard Data User’s Guide (version 1.3). Available online: http://www.data.jma.go.jp/mscweb/en/himawari89/space_segment/hsd_sample/HS_D_users_guide_en_v12.pdf (accessed on 31 December 2021).
- Fisher, A.; Flood, N.; Danaher, T. Comparing Landsat water index methods for automated water classification in eastern Australia. Remote Sens. Environ. 2016, 175, 167–182. [Google Scholar] [CrossRef]
- Neves, R. The MOHID concept. In Ocean Modelling for Coastal Management—Case Studies with MOHID; Mateus, M., Neves, R., Eds.; IST Press: Lisbon, Portugal, 2013. [Google Scholar]
- Trancoso, A.R.; Braunschweig, F.; Chambel Leitão, P.; Obermann, M.; Neves, R. An advanced modelling tool for simulating complex river systems. Sci. Total Environ. 2009, 407, 3004–3016. [Google Scholar] [CrossRef] [PubMed]
- Chambel-Leitão, P.; Ramos, T.; Domingos, T.; Neves, R. Mohid Land-Porous Media, a Tool for Modeling Soil Hydrology at Plot Scale and Watershed Scale. Open Hydrol. J. 2015, 9, 1–12. [Google Scholar] [CrossRef][Green Version]
- Simionesei, L.; Ramos, T.B.; Brito, D.; Jauch, E.; Leitão, P.C.; Almeida, C.; Neves, R. Numerical Simulation of Soil Water Dynamics under Stationary Sprinkler Irrigation with Mohid-Land. Irrig. Drain. 2016, 65, 98–111. [Google Scholar] [CrossRef]
- Galvao, P.; Chambel Leitao, P.; Neves, R.; Leitao, P.C. A different approach to the modified Picard method for water flow in variably saturated media. In Developments in Water Science; Miller, C.T., Farthing, M.W., Gray, W.G., Pinder, G.F., Eds.; Elsevier: Amsterdam, The Netherlands, 2004; Volume 55, pp. 557–567. [Google Scholar]
- Jury, W.; Gardner, W.; Gardner, W. Soil Physics; Wiley & Sons: New York, NY, USA, 1991. [Google Scholar]
- Mohanty, B.P.; Cosh, M.H.; Lakshmi, V.; Montzka, C. Soil Moisture Remote Sensing: State-of-the-Science. Vadose Zone J. 2017, 16, 1–9. [Google Scholar] [CrossRef]
- Al-Shammari, D.; Fuentes, I.; Whelan, B.M.; Filippi, P.; Bishop, T.F.A. Mapping of Cotton Fields Within-Season Using Phenology-Based Metrics Derived from a Time Series of Landsat Imagery. Remote Sens. 2020, 12, 3038. [Google Scholar] [CrossRef]
- Filippi, P.; Jones, E.J.; Wimalathunge, N.S.; Somarathna, P.D.S.N.; Pozza, L.E.; Ugbaje, S.U.; Jephcott, T.G.; Paterson, S.E.; Whelan, B.M.; Bishop, T.F.A. An approach to forecast grain crop yield using multi-layered, multi-farm data sets and machine learning. Precis. Agric. 2019, 20, 1015–1029. [Google Scholar] [CrossRef]
- Filippi, P.; Whelan, B.M.; Vervoort, R.W.; Bishop, T.F.A. Identifying crop yield gaps with site- and season-specific data-driven models of yield potential. Precis. Agric. 2021, 1–24. [Google Scholar] [CrossRef]
- Roth, G.; Harris, G.; Gillies, M.; Montgomery, J.; Wigginton, D. Water-use efficiency and productivity trends in Australian irrigated cotton: A review. Crop Pasture Sci. 2013, 64, 1033–1048. [Google Scholar] [CrossRef]




| Domain | Symbol | Unit | Description | Value |
|---|---|---|---|---|
| Porous media | θs | – | Saturated water content | 0.43 |
| θr | – | Residual water content | 0.03 | |
| N | – | Pore size distribution related term | 1.56 | |
| A | m−1 | Air entry pressure related term | 3.6 | |
| Ks | m s−1 | Saturated hydraulic conductivity | 2.8 × 10−6 | |
| Runoff | n | s m−1/3 | Surface Manning | 0.038 |
| CMRSET | ETLook | |||||
|---|---|---|---|---|---|---|
| Month | Rain | Use | Demand | Deficit | Demand | Deficit |
| July 2017 | 182 | 10 | 261 | 79 | 197 | 15 |
| August 2017 | 248 | 8 | 302 | 53 | 272 | 24 |
| September 2017 | 31 | 37 | 624 | 593 | 591 | 560 |
| October 2017 | 828 | 372 | 520 | −308 | 299 | −529 |
| November 2017 | 731 | 212 | 621 | −111 | 292 | −439 |
| December 2017 | 399 | 620 | 906 | 507 | 380 | −18 |
| January 2018 | 456 | 1278 | 942 | 486 | 554 | 98 |
| February 2018 | 435 | 721 | 771 | 336 | 785 | 350 |
| March 2018 | 457 | 71 | 725 | 268 | 385 | −72 |
| April 2018 | 210 | 18 | 562 | 353 | 215 | 5 |
| May 2018 | 128 | 75 | 293 | 164 | 58 | −70 |
| June 2018 | 34 | 22 | 162 | 128 | 22 | −12 |
| Total | 4139 | 3444 | 6687 | 2548 | 4052 | −87 |
| CMRSET | ETLook | |||||
|---|---|---|---|---|---|---|
| Month | Rain | Use | Demand | Deficit | Demand | Deficit |
| July 2017 | 189 | 24 | 258 | 68 | 87 | −103 |
| August 2017 | 246 | 20 | 285 | 39 | 199 | −47 |
| September 2017 | 34 | 87 | 606 | 572 | 357 | 323 |
| October 2017 | 839 | 873 | 532 | −307 | 195 | −644 |
| November 2017 | 745 | 497 | 655 | −89 | 198 | −547 |
| December 2017 | 426 | 1453 | 1046 | 620 | 399 | −27 |
| January 2018 | 463 | 2996 | 1065 | 602 | 895 | 433 |
| February 2018 | 429 | 1690 | 921 | 492 | 973 | 543 |
| March 2018 | 438 | 166 | 842 | 404 | 566 | 128 |
| April 2018 | 211 | 42 | 613 | 402 | 161 | −50 |
| May 2018 | 132 | 175 | 302 | 170 | 25 | −107 |
| June 2018 | 48 | 52 | 170 | 123 | 11 | −37 |
| Total | 4199 | 8074 | 7294 | 3095 | 4066 | −133 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vervoort, R.W.; Fuentes, I.; Brombacher, J.; Degen, J.; Chambel-Leitão, P.; Santos, F. Progress in Developing Scale-Able Approaches to Field-Scale Water Accounting Based on Remote Sensing. Sustainability 2022, 14, 2732. https://doi.org/10.3390/su14052732
Vervoort RW, Fuentes I, Brombacher J, Degen J, Chambel-Leitão P, Santos F. Progress in Developing Scale-Able Approaches to Field-Scale Water Accounting Based on Remote Sensing. Sustainability. 2022; 14(5):2732. https://doi.org/10.3390/su14052732
Chicago/Turabian StyleVervoort, Rutger Willem, Ignacio Fuentes, Joost Brombacher, Jelle Degen, Pedro Chambel-Leitão, and Flávio Santos. 2022. "Progress in Developing Scale-Able Approaches to Field-Scale Water Accounting Based on Remote Sensing" Sustainability 14, no. 5: 2732. https://doi.org/10.3390/su14052732
APA StyleVervoort, R. W., Fuentes, I., Brombacher, J., Degen, J., Chambel-Leitão, P., & Santos, F. (2022). Progress in Developing Scale-Able Approaches to Field-Scale Water Accounting Based on Remote Sensing. Sustainability, 14(5), 2732. https://doi.org/10.3390/su14052732







