Multiple Melting Temperatures in Glass-Forming Melts

Abstract

All materials are vitrified by fast quenching even monoatomic substances. Second melting temperatures accompanied by weak exothermic or endothermic heat are often observed at T_n+ after remelting them above the equilibrium thermodynamic melting transition at T_m. These temperatures, T_n+, are due to the breaking of bonds (configurons formation) or antibonds depending on the thermal history, which is explained by using a nonclassical nucleation equation. Their multiple existence in monoatomic elements is now demonstrated by molecular dynamics simulations and still predicted. Proposed equations show that crystallization enthalpy is reduced at the temperature T_x due to new vitrification of noncrystallized parts and their melting at T_n+. These glassy parts, being equal above T_x to singular values or to their sum, are melted at various temperatures T_n+ and attain 100% in Cu₄₆Zr₄₆Al₈ and 86.7% in bismuth. These first order transitions at T_n+ are either reversible or irreversible, depending on the formation of super atoms, either solid or liquid.

1. Introduction

Liquid–liquid phase transitions occur in glass-forming melts below and above T_m, the equilibrium thermodynamic melting transition of crystals. These transitions are driven by the density separation of two liquid states existing in all supercooled and overheated materials, including pure elements in which two liquid phases of the same composition coexist [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]. Denser glassy phases are built by vapor deposition below the glass transition temperature T_g, leading to higher glass transition temperatures and first order transitions toward liquid states [16,17,18,19]. Glacial phases with higher values of T_g result from first order transitions between T_g and T_m [20,21,22,23,24,25]. Denser phases, called G-Phases, are obtained in liquid elements by numerical simulations at very high heating rates, leading to second melting temperatures far above T_m [26,27,28,29]. Glass-forming melts undergo liquid–liquid transitions with endothermic or exothermic latent heats at nucleation temperatures T_n+ higher than T_m [30,31,32,33,34,35,36]. First order transitions are observed at temperatures T_n+ above T_m with nuclear magnetic resonance by cooling a homogeneous liquid, followed by the homogeneous nucleation of growth nuclei below T_n+, leading to melt crystallization [37,38]. Multiple liquid–liquid transitions were observed at low heating rates in bismuth [39,40] and glass-forming melts of Cu-Zr-Al [41]. It is the purpose of this publication to relate the various glass phases to melting transitions above T_m, following proposals of H. Tanaka [15,42].

Liquid−liquid structure transition plays an important role in the final microstructure and the properties of solid alloys [43]. Solidifying Bi₂Te₃ alloys after melting above T_n+ followed by various cooling rates refined the microstructure and increased the hardness with the cooling rate [44,45]. Solidifying magnetic melts after overheating below T_n+ in high magnetic fields built textured congruent and noncongruent substances [46], due to the presence of growth nuclei in melts above T_m. The classical nucleation equation cannot explain such nucleation phenomena [47,48].

A nonclassical nucleation equation involving two liquid states was built by adding an enthalpy contribution, εH_m, with ε depending on θ² = (T − T_m)²/T_m² and being a fraction of the crystal melting heat, H_m, to complete the Gibbs free energy of nuclei above and below T_m [49]. The undercooling rates of liquid elements were predicted, leading to an average minimum value of ε = 0.217 for θ = 0 due to the Lindemann coefficient at T_m [50]. The nucleation equations of liquids 1 and 2 were used to successfully predict the specific heat jump at the glass transition temperature T_g, the Vogel–Fulcher–Tammann (VFT) temperatures of fragile liquids above T_m/3 [51] and the first temperature, T_n+ [52]. The nature of surviving entities are superclusters (super atoms), or bonds and configurons, melted by liquid homogeneous nucleation instead of surface melting. This completed classical nucleation equation successfully predicts their presence above T_m [53,54] and their melting by homogeneous nucleation. The enthalpy and entropy variations of supercooled water at T_LL = 228.5 K [55] during the first cooling were predicted [56]. The formation, below T_g, of a glacial phase called Phase 3, having an enthalpy equal to the difference between those of liquids 1 and 2, explained why the transition at T_LL disappears during the first heating. The theoretical first order transitions of Phase 3, under pressure, reproduced those found by Speedy and Angell [57]. The phase diagram of water confined into carbon nanotubes was similar to that predicted by numerical simulations [58,59].

The thermodynamic properties of glass-forming melts are easy to predict when T_g and T_m are known. The singular enthalpy values of Phase 3 are zero and those calculated at T = T_m, T_g, T_om, the VFT temperature of liquid 1 and the first temperature T_n+. The nucleation equations of glacial phases used these singular enthalpies as latent heats to fix the entropy driven transition temperatures [60,61] of triphenyl phosphite [22,25], D-mannitol [24], n-butanol [23,62,63], and Zr_41.2Ti_13.8Cu_12.5Ni₁₀Be_22.5 [35,36]. The stable and ultrastable glasses formed by vapor deposition had enthalpies equal to singular values and their transition temperatures at T_g are driven by them. Other melts also had enthalpy driven transitions, such as Ti₃₄Zr₁₁Cu₄₇Ni₈ [64], and Co_81.5B_18.5 [43], in agreement with the predictions [61]. A critical supercooling and overheating rate, ΔT/T_m = 0.198 of liquid elements was predicted, in agreement with experiments on Sn droplets [65].

Phase 3 formation has, for its origin, a second order phase transition associated with critical exponents due to bonds breaking (configurons formation) when a glass is heated through T_g [66,67,68,69,70]. The Gibbs free energy of configurons disappears at T_n+ instead of T_g [58,71,72]. The debate about the absence and the presence of a phase transition at T_g is probably solved by these considerations.

The nonclassical nucleation model predicted the G-phase formation equivalent to Phase 3 formation in liquid elements via first order transitions, and the second melting temperatures observed by molecular dynamics simulations at very high heating rates [73].

The question of their observation at low heating rates was raised, considering that the crystallization enthalpy of these elements would be reduced and recovered via liquid–liquid transitions occurring above T_m [73]. The singular values of the latent heats in all glass-forming melts could correspond to percolation thresholds at various temperatures.

The coexistence of glassy phases with crystals is known and viewed as being due to phase separation after annealing near T_x, the crystallization temperature of glass-forming melts. This coexistence could result, in fact, from the presence of a glassy fraction in nanocrystallized materials having a glass transition temperature, T_g, higher than T_m, as already shown for liquid elements [73].

This paper is devoted to the second vitrification of melt fractions at first order transition temperatures, T_x, coexisting with crystals formation and predictions of multiple melting temperatures, T_n+, of this glassy fraction above T_m from singular enthalpies of glass-forming melts using a renewed completed classical nucleation equation and the configuron concept in relation with percolation thresholds. The reduction in the crystallization heat of polymers is well known and could be due to a glassy phase melted at much higher temperatures than T_m.

2. The Homogenous Nucleation of Two Glassy States

2.1. The Bulk Glassy State Below T_g

The Gibbs free energy change for a nucleus formation in a melt is given by (1) [49]:

$$∆{\mathrm{G}}_{\mathrm{ls}}=\left(\mathsf{\theta } -{\mathsf{\epsilon }}_{\mathrm{ls}}\right)∆{\mathrm{H}}_{\mathrm{m}}/{\mathrm{V}}_{\mathrm{m}}\times 4{\mathsf{\pi }\mathrm{R}}^3/3+4{\mathsf{\pi }\mathrm{R}}^2{\mathsf{\sigma }}_{\mathrm{ls}},$$

(1)

where R is the nucleus radius and, following Turnbull [47], σ_ls its surface energy, given by (2), θ the reduced temperature (T − T_m)/T_m, ΔH_m the melting enthalpy at T_m, and V_m the molar volume:

$${\mathsf{\sigma }}_{\mathrm{ls}}{\left({\mathrm{V}}_{\mathrm{m}}/{\mathrm{N}}_{\mathrm{A}}\right)}^{-1/3}={ \mathsf{\alpha }}_{\mathrm{ls}}∆{\mathrm{H}}_{\mathrm{m}}/{\mathrm{V}}_{\mathrm{m}},$$

(2)

A complementary enthalpy, ε_ls × ΔH_m/V_m, is introduced, authorizing the presence of growth nuclei above and below T_m, with ε_ls being positive or negative above T_m depending on its increase or decrease with θ. In previous works, ε_ls was only positive [49]. The discovery of positive or negative enthalpy above T_m related to the presence of antibonds or bonds sets this new rule [72]. The classical nucleation equation is obtained for ε_ls = 0 and leads to a homogeneous liquid above T_m.

The critical thermally activated energy barrier, ΔG*_ls/k_BT, is calculated in (3), assuming dε_ls/dR = 0:

$$\frac{∆{\mathrm{G}}_{\mathrm{ls}}^{*}}{{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}=\frac{16\mathsf{\pi }∆{\mathrm{S}}_{\mathrm{m} }{\mathsf{\alpha }}_{\mathrm{ls}}^3}{3{\mathrm{N}}_{\mathrm{A}}{\mathrm{k}}_{\mathrm{B}}\left(1+ \mathsf{\theta }\right){\left(\mathsf{\theta }-{\mathsf{\epsilon }}_{ls}\right)}^2},$$

(3)

where ΔS_m is the melting entropy [47,49,74]. This critical parameter is no longer infinite at the melting temperature T_m, because ε_ls is not equal to zero. This event now occurs above T_m for θ = ε_ls. The nucleation rate J = K_v exp(−ΔG*_ls/k_BT) is equal to 1 when (4) is respected:

$$∆{\mathrm{G}}_{\mathrm{ls}}^{*}/{\mathrm{k}}_{\mathrm{B}}\mathrm{T} = \ln \left({\mathrm{K}}_{\mathrm{v}}\right),$$

(4)

The surface energy coefficient α_ls in (2) is determined from (3,4) and equal to (5):

$${\mathsf{\alpha }}_{\mathrm{ls}}^3=\frac{3{\mathrm{N}}_{\mathrm{A}}{\mathrm{k}}_{\mathrm{B} }\left(1+ \mathsf{\theta }\right){\left(\mathsf{\theta }-{\mathsf{\epsilon }}_{\mathrm{ls}}\right)}^2}{16\mathsf{\pi }∆{\mathrm{S}}_{\mathrm{m}}}\ln \left({\mathrm{K}}_{\mathrm{v}}\right),$$

(5)

The nucleation temperatures θ_n− and θ_n+ obtained for d ${\mathsf{\alpha }}_{\mathrm{ls}}^3$/dθ = 0 obey (6):

$${\mathrm{d}\mathsf{\alpha }}_{\mathrm{ls}}^3/\mathrm{d}\mathsf{\theta } ({\mathsf{\theta }}_{\mathrm{n}+}-{\mathsf{\epsilon }}_{\mathrm{ls}})\left(3{\mathsf{\theta }}_{\mathrm{n}-}+2-{ \mathsf{\epsilon }}_{\mathrm{ls}}\right)=0,$$

(6)

There are two families of nucleation temperatures: θ_n− = (ε_ls − 2)/3 far below T_m and θ_n+= ε_ls above T_m. In addition to the nucleation temperatures T_n− below T_m, the existence of a homogenous nucleation temperature T_n+ above T_m is confirmed by many experiments, observing the undercooling versus the overheating rates of liquid elements, and glass-forming melts [43,65,75,76,77,78]. This nucleation temperature has confirmed the existence of a second melting temperature, T_n+, of growth nuclei above T_m, and of their homogeneous nucleation at temperatures weaker than θ_n+, as shown in several publications [30,31,32,33,34,35,36,37,38,39,79,80,81,82].

The coefficient ε_ls of the initial liquid state, called liquid 1, is a quadratic function of θ in (7) [49] for ε_ls > 0 above T_m in (1):

$${\mathsf{\epsilon }}_{\mathrm{ls}}={\mathsf{\epsilon }}_{\mathrm{ls}0}(1-{\mathsf{\theta }}^2/{\mathsf{\theta }}_{0\mathrm{m}}^2),$$

(7)

where θ_0m is the Vogel–Fulcher–Tammann (VFT) reduced temperature, leading to ε_ls = 0 for θ = θ_0m, and the VFT temperature, T_0m, of many fragile liquids being equal to ≅ 0.77 T_g. This quasi-universal value is known for numerous fragile liquids, including atactic polymers [83,84].

New liquid states are obtained for θ = θ_n+ = ε_ls and θ= θ_n−= (ε_ls − 2)/3, where ε_ls is given in (7). The reduced nucleation temperatures, θ_n−, are solutions of the quadratic equation (8):

$${\mathsf{\epsilon }}_{\mathrm{ls}0}{\mathsf{\theta }}_{\mathrm{n}-}^2/{\mathsf{\theta }}_{0\mathrm{m}}^2+3{\mathsf{\theta }}_{\mathrm{n}-}+2-{\mathsf{\epsilon }}_{\mathrm{ls}0}-∆\mathsf{\epsilon } =0, \mathrm{or} {\mathsf{\epsilon }}_{ls}\left(\mathsf{\theta }=0\right)=\left(3{\mathsf{\theta }}_{n-}+2-∆\mathsf{\epsilon }\right)/\left(1-\frac{{\mathsf{\theta }}_{n-}^2}{{\mathsf{\theta }}_{0\mathrm{m}}^2}\right)$$

(8)

where Δε is an enthalpy–coefficient change, which can induce a first order transition [52].

There is a minimum value of ε_ls0 plotted as a function of θ_0m using (8) for Δε = 0 and θ_n− = (ε_ls − 2)/3, determining the relation (9) between θ²_0m and ε_ls0, for which the two solutions of (8) are equal in fragile liquids. These values define the temperature where the surface energy is minimum and θ²_0m and ε_ls0 obey (9) and (10):

$${\mathsf{\theta }}_{0\mathrm{m}}^2=\frac{8}{9}{\mathsf{\epsilon }}_{\mathrm{ls}0}-\frac{4}{9}{\mathsf{\epsilon }}_{\mathrm{ls}0}^2,$$

(9)

$${\mathsf{\epsilon }}_{\mathrm{ls}}\left(\mathsf{\theta } =0\right)={\mathsf{\epsilon }}_{\mathrm{ls}0}=1.5{\mathsf{\theta }}_{\mathrm{n}-}+2={ \mathrm{a}\mathsf{\theta }}_{\mathrm{g}}+2,$$

(10)

Equation (9) leads to T_0m = 0.769 × T_g for a = 1, in agreement with many experimental values.

All melts and even liquid elements undergo, in addition, a bulk glass transition because another liquid state called liquid 2 exists, characterized by an enthalpy coefficient, ε_gs, given by (11), inducing an enthalpy change from that of liquid 1 at the thermodynamic transition at θ_g [50]:

$${\mathsf{\epsilon }}_{\mathrm{gs}}={\mathsf{\epsilon }}_{\mathrm{gs}0}(1-{ \mathsf{\theta }}^2/{\mathsf{\theta }}_{0\mathrm{g}}^2)-∆\mathsf{\epsilon },$$

(11)

where θ_0g² and ε_gs0 obey (12) and (13) for ε_ls > 0 and Δε is zero at the glass transition:

$${\mathsf{\theta }}_{0\mathrm{g}}^2=\frac{8}{9}{\mathsf{\epsilon }}_{\mathrm{gs}0}-\frac{4}{9}{\mathsf{\epsilon }}_{\mathrm{gs}0}^2,$$

(12)

$${\mathsf{\epsilon }}_{\mathrm{gs}}\left(\mathsf{\theta } =0\right)={ \mathsf{\epsilon }}_{\mathrm{gs}0}=1.5{\mathsf{\theta }}_{\mathrm{n}-}+2=1.5{\mathsf{\theta }}_{\mathrm{g}}+2,$$

(13)

The reduced nucleation temperatures θ_n− are solutions of the quadratic Equation (14):

$${\mathsf{\epsilon }}_{\mathrm{g}0}{\mathsf{\theta }}_{\mathrm{n}-}^2/{\mathsf{\theta }}_{0\mathrm{g}}^2+3{\mathsf{\theta }}_{\mathrm{n}-}+2-{ \mathsf{\epsilon }}_{\mathrm{gs}0}-∆\mathsf{\epsilon } =0, \mathrm{or} {\mathsf{\epsilon }}_{gs}\left(\mathsf{\theta }=0\right)=\left(3{\mathsf{\theta }}_{n-}+2-∆\mathsf{\epsilon }\right)/\left(1-\frac{{\mathsf{\theta }}_{n-}^2}{{\mathsf{\theta }}_{0g}^2}\right)$$

(14)

where Δε is the enthalpy coefficient change inducing a first order transition [52,62]. Equations (8) and (14) lead to the same nucleation temperature, T_n− = T_g, for the same coefficient, Δε, in fragile liquids.

2.2. The Glassy State of Phase 3 up to the Melting Temperature T_n+ above T_m

The difference between the coefficients ε_ls and ε_gs, Δε_lg in (15), determines the Phase 3 and the configuron enthalpies when the quenched liquid has escaped crystallization [55,71]:

$$∆{\mathsf{\epsilon }}_{\lg }\left(\mathsf{\theta }\right)=\left[{\mathsf{\epsilon }}_{\mathrm{ls}}-{\mathsf{\epsilon }}_{\mathrm{gs}}\right]=[{\mathsf{\epsilon }}_{\mathrm{ls}0}-{\mathsf{\epsilon }}_{\mathrm{gs}0}-∆\mathsf{\epsilon }-{\mathsf{\theta }}^2\left(\raisebox{1ex}{${\mathsf{\epsilon }}_{\mathrm{ls}0}$}\!\left/ \!\raisebox{-1ex}{${\mathsf{\theta }}_{0\mathrm{m}}^2$}\right.-\raisebox{1ex}{${\mathsf{\epsilon }}_{\mathrm{gs}0}$}\!\left/ \!\raisebox{-1ex}{${\mathsf{\theta }}_{0\mathrm{g}}^2$}\right.\right)],$$

(15)

The assumption of a = 1 in (10), defining the value of T_0m in (9), is the unique value for which the activation energies B₁RT/(T − T_0m) and B₂RT/(T − T_0g) of liquids 1 and 2 are equal at T_g, leading to an activation energy equal to zero for Phase 3 [71].

When the enthalpy coefficients ε_ls (θ) and ε_gs (θ) are negative in (1), the phase 3 enthalpy coefficient Δε_lg (θ) becomes equal to (16):

$$∆{\mathsf{\epsilon }}_{\lg }\left(\mathsf{\theta }\right)=-\left[{\mathsf{\epsilon }}_{\mathrm{ls}}-{\mathsf{\epsilon }}_{\mathrm{gs}}\right]=-[{\mathsf{\epsilon }}_{\mathrm{ls}0}-{\mathsf{\epsilon }}_{\mathrm{gs}0}-∆\mathsf{\epsilon }-{\mathsf{\theta }}^2\left(\raisebox{1ex}{${\mathsf{\epsilon }}_{\mathrm{ls}0}$}\!\left/ \!\raisebox{-1ex}{${\mathsf{\theta }}_{0\mathrm{m}}^2$}\right.-\raisebox{1ex}{${\mathsf{\epsilon }}_{\mathrm{gs}0}$}\!\left/ \!\raisebox{-1ex}{${\mathsf{\theta }}_{0\mathrm{g}}^2$}\right.\right)],$$

(16)

It increases with θ in (15) or decreases in (16), because of its dependence on the thermal history, and disappears at T_n+. Two reduced glass transition temperatures, θ_g and −θ_g, exist. Another analogous equation leading to Δε_lg (θ), given in (16), can be determined using the new coefficients, ε_ls0 and ε_gs0, in (10) and (13), obtained by changing θ_g in −θ_g and θ²_0m, θ²_0g deduced from (9) and (12) using these new values of ε_ls0 and ε_gs0.

These new considerations show the existence of a glassy state of a melt fraction disappearing at the virtual transition temperature, T′_g= 2T_m − T_g, governing the thermodynamics of all Phases 3, including those nucleated by first order transitions. This phenomenon of double glass state occurs because all glass-forming melts heated from their glass state are composites containing an ordered fraction of percolating bonds or antibonds (15 ± 1 % minimum) and a homogeneous liquid (85 % maximum) [58,71,72]. The first glass transition temperature, observed at T_g below T_m by heating, corresponds to the percolation of configurons in the bulk liquid, while the second transition, only due to Phase 3, disappears at T_n+, far above T_m. The partial glass state is preserved up to the nucleation temperature θ_n+= Δε_lg (θ_g) because the ordered fraction remains equal to the percolation threshold observed at θ_g below T_m. The melt transformations at θ_n+ are sharp and only observable below the virtual glass transition occurring at θ′_g = −θ_g. Note that the two VFT temperatures above T_m corresponding to this virtual glass transition are also virtual because θ²_0m and θ²_0g are negative in this case.

3. Reduction of the Crystallization Enthalpy at the Crystallization Temperature T_x

The enthalpy recovery during heating is endothermic at T_n+ for bonds and exothermic for antibonds breaking [72]. The total melting enthalpy, H, depends on the reduced temperature, θ_n+, because this homogeneous nucleation temperature, T_n+, occurs above T_m with the enthalpy change given by Equation (17) [1]:

$$∆{\mathsf{\epsilon }}_{\lg } \left({\mathsf{\theta }}_{\mathrm{n}+}\right)=\pm {\mathsf{\theta }}_{\mathrm{n}+} \mathrm{where} {\mathsf{\theta }}_{\mathrm{n}+}<-{\mathsf{\theta }}_g$$

(17)

Heating from the glass state below T_g can induce, at the same time, a first order transition at T_x, toward crystallization or not and nucleation of a new glassy state of Phase 3 with a latent heat (−ΔεH_m) and a new glass transition temperature T′_g = 2T_m − T_g. The reduced temperature θ_x is given by Equation (14), with Δε equal to singular values of the enthalpy coefficient Δε_lg of Phase 3. These singular values are zero, Δε_lg0 /2, θ_n+, Δε_lg0, −Δε_lg (θ_0m) or the sum of several singular values as observed in liquid elements and as expected from hidden thresholds of configurons [73]. The crystallization enthalpy at T_x of the liquid phase coexisting with glassy Phase 3 is given by (18):

$${\mathrm{H}}_{\mathrm{cr}}={\mathrm{H}}_{\mathrm{m}}\left(-1+∆\mathsf{\epsilon }\right),$$

(18)

The melting heat, H_3m, of each Phase 3 depends on its singular value and its contribution to Δε at T_x. This melting, depending on the heating rate, occurs at various reduced temperatures, θ_n+, defined for each singular value of Δε, or is associated with other singular values or leads to a unique melting temperature θ_n+ = Δε as shown in Equation (17):

$${\mathrm{H}}_{3\mathrm{m}}={\mathrm{H}}_{\mathrm{m}}\times {\mathsf{\theta }}_{n+},$$

(19)

The temperature T_x separates the two domains of glassy phases between T_g and T_n+. Below T_g = T_x, the bulk glassy domain takes place after the first-order transition at T_x, while the glassy fractions induced at T_x disappear at T_n+ without attaining the virtual glass transition temperature T′_g equal to (2T_m − T_g). The glass enthalpy disappears at T_n+ < T′_g by heating from −$∆\mathsf{\epsilon }{\mathrm{H}}_{\mathrm{m}}$ to $0$, giving rise to homogeneous liquid.

4. Gleaning Information in Published Works to Predict the Crystallized Fraction from the Knowledge of T_x or Melting Temperatures of Various Phases 3 above T_m

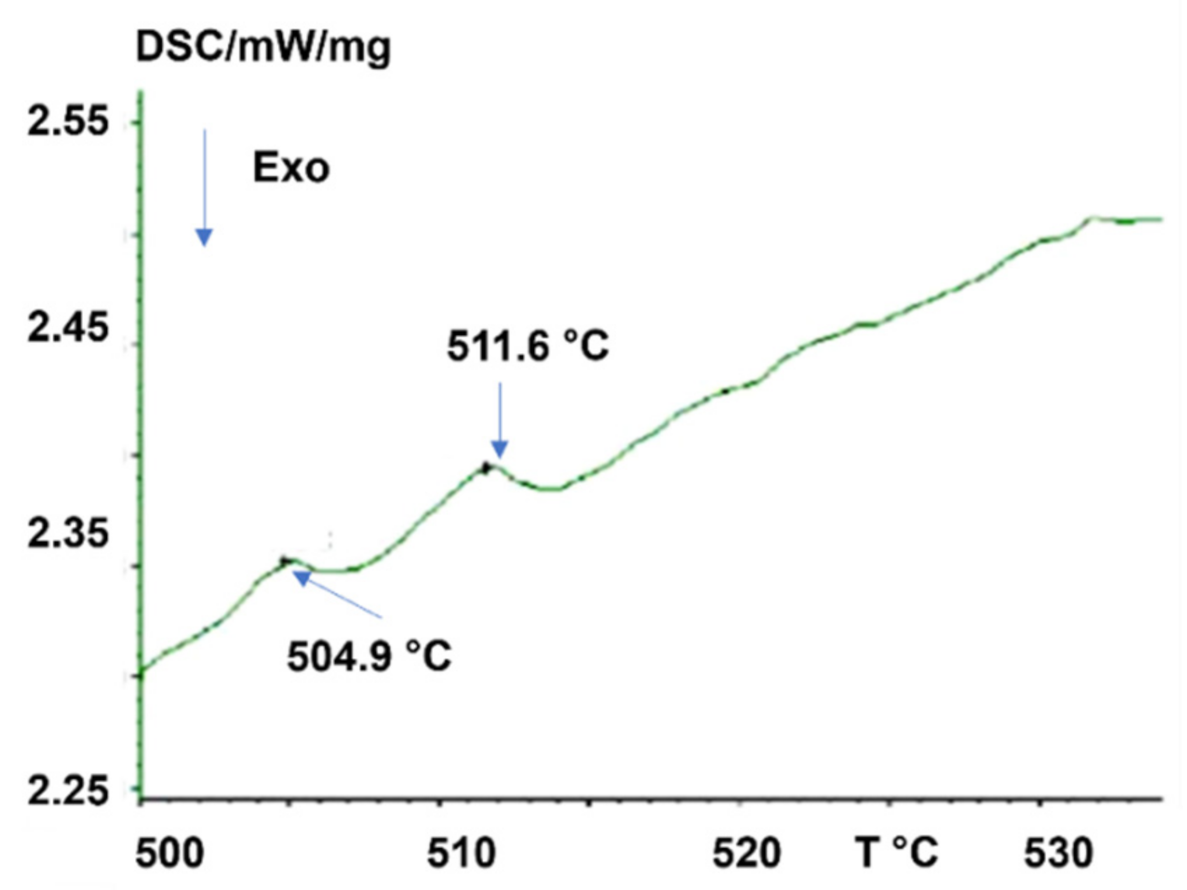
4.1. Three Melting Temperatures of Bismuth Were Observed above T_m in Two Different Experiments

DSC measurements of bismuth with a heating rate of 0.083 K/s showed two endothermic transitions, at T_1n+ = 504.9 °C (778 K) and T_2n+= 511.5 K (784.6 K), above the melting temperature T_m = 544.5 K, as shown in Figure 1 [39]. A third transition was observed with the density at T_3n+ = 1013 K in another experiment, in the absence of transformations at T_1n+ and T_2n+ [40].

With the model already developed for other liquid elements [73], these temperatures are used to calculate a Bi Lindemann coefficient equal to 0.09119, in good agreement with the value 0.095 recently found [85]. The glass transition temperature is predicted at T_g = 203.5 K and the singular enthalpy coefficients Δε are Δε_lg0 = 0.1907, −Δε_lg (θ_g) = 0.094065, −Δε_lg (θ_0m = −2/3) = 0.10594 and −Δε_lg (θ= −1) = 0.238375. The experimental coefficients, Δε, giving rise to θ_1n+= 778/544.5 −1= 0.429 and θ_2n+ = 784.6/544.5 −1= 0.44096, are equal to the theoretical ones, 0.1907 + 0.238375 = 0.429075 and 0.094065 + 0.10594 + 0.238375 = 0.43838, respectively. The total glassy fraction melted at the two temperatures, T_n+, represent 86.7%, while the crystallized fraction melted at T_m would be 13.3%. The transition at T_3n+ is expected at θ_3n+ = 0.8675 (T_3n+ = 1.8675T_m), corresponding to 1016 K in the absence of transitions at T_1n+ and T_2n+, in agreement with the second experiment. The formation of distinct glassy phases with singular enthalpies at T_x depends on the heating rate.

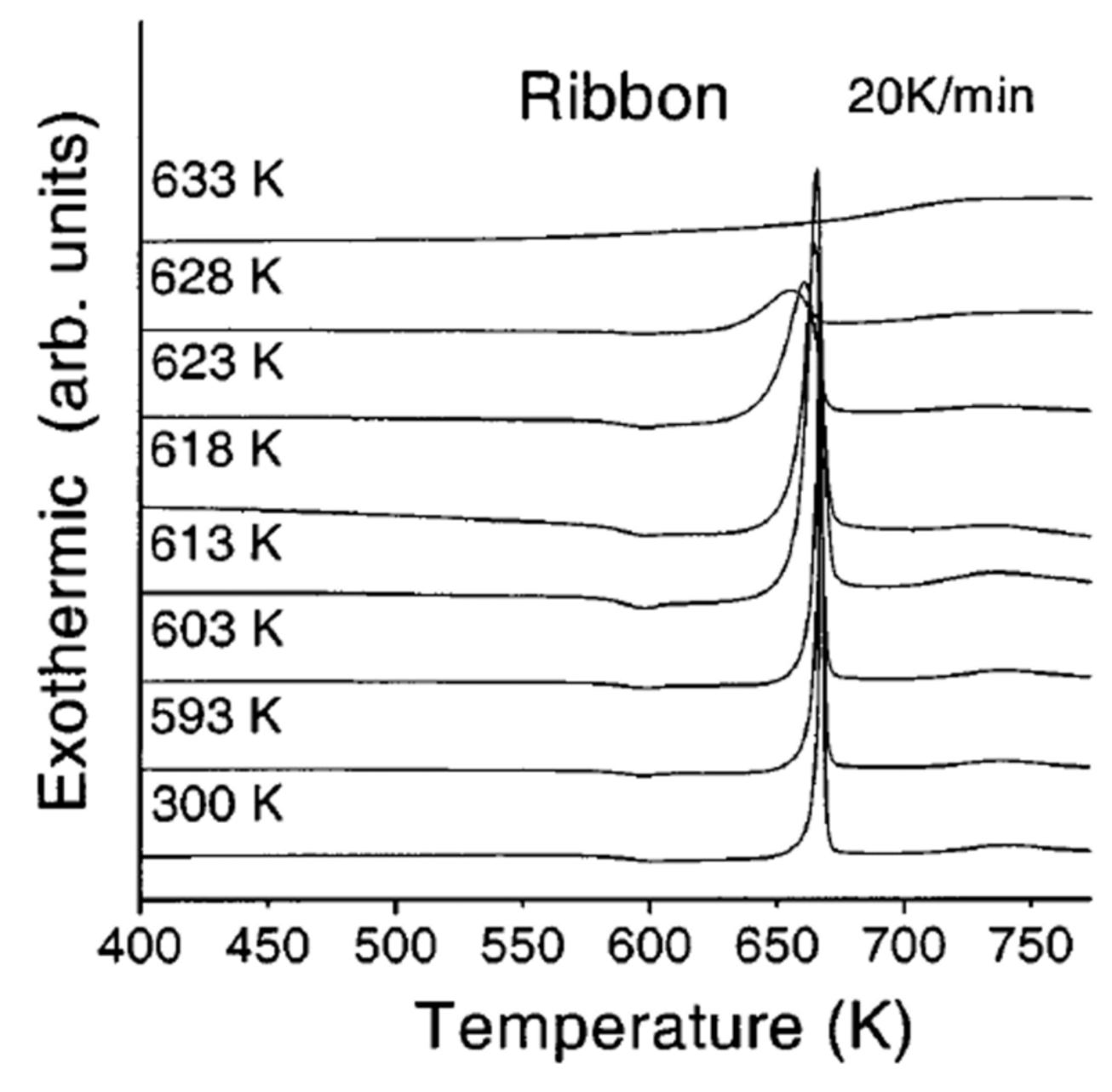
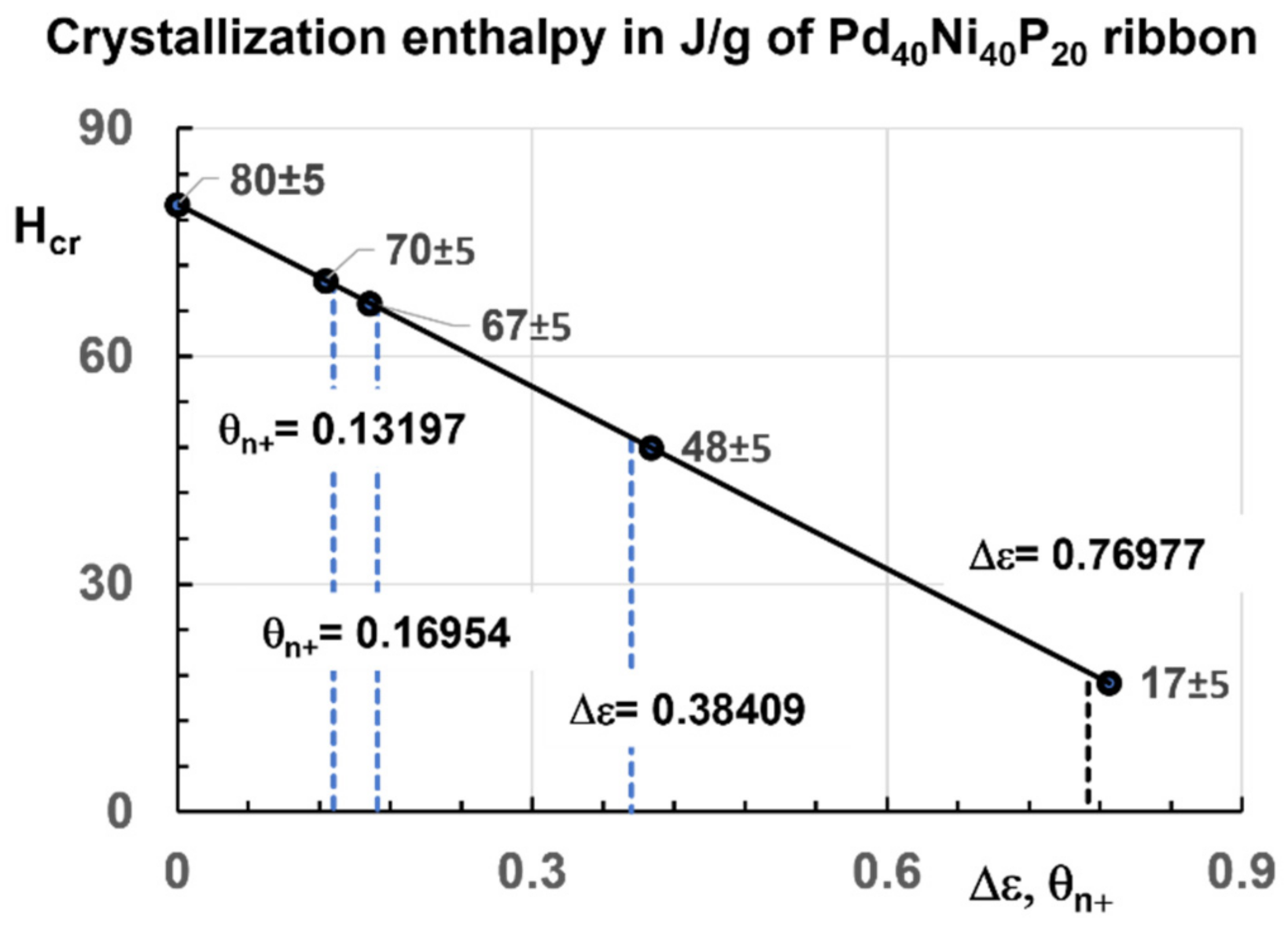
4.2. Crystallization Enthalpy Reduction of Pd₄₀Ni₄₀P₂₀ at the Temperature T_x after Quenching and Various Annealing of the Same Duration at Lower Temperatures

The bulk melting temperature is T_m = 870 K; the glass transition temperature of ribbons is T_g = 575 K (θ_g = −0.33909) and the virtual glass transition temperature T′_g = 2T_m-T_g = 1165 K (θ_n+ = 0.33909). The first order transition at T_x is unique and shown in Figure 2 [86]. An endothermic transition was observed at T_1n+ = 984 K above T_m [87]. The enthalpy coefficients are calculated using (9), (10), (12) and (13), θ_g = −0.33908 and a = 1. Liquids 1, 2, and 3 obey (20)–(22), respectively:

$${\mathsf{\epsilon }}_{\mathrm{ls}}=1.66092(1-{ \mathsf{\theta }}^2/0.250305),$$

(20)

$${\mathsf{\epsilon }}_{\mathrm{gs}}=1.49138(1-{ \mathsf{\theta }}^2/0.33713),$$

(21)

$$∆{\mathsf{\epsilon }}_{\lg }\left(\mathsf{\theta }\right)=\left[{\mathsf{\epsilon }}_{\mathrm{ls}}-{\mathsf{\epsilon }}_{\mathrm{gs}}\right]=\left[0.16954-∆\mathsf{\epsilon } -2.2118\times {\mathsf{\theta }}^2\right].$$

(22)

The singular enthalpy coefficients, Δε = θ_n+, are: 0, −Δε_lg0/2 = −0.08477, ±0.13197 at T_1n+, −Δε_lg0 = −0.16984, −Δε_lg (θ_0m) = 0.38409. The first order transition at T_x = 658.4 K, driven by the entropy of Phase 3, counted from its formation temperature at 506.7 K, being equal to (−Δε_lg − 0.25431) × H_m/T_x, leads to a singular enthalpy of Phase 3 equal to −0.25431 × H_m [60,61]. The crystallization enthalpies roughly correspond to these singular values of θ_n+, as shown in Figure 3, with (18) respected. The transition at T_x is sharp, in Figure 2, up to T_a = 618 K and broader above. The transition at θ_n+ above T_m is expected to be observable up to θ^′_g = 0.33909 = 2T_m − T_g. Too high values of Δε above θ′_g led to higher fractions of crystalline phase. The crystallization enthalpy in Figure 3 is strongly reduced after various annealing, because the melt starts with more and more crystals when the annealing temperature T_a passes 623 K before heating up to higher temperatures.

A first order transition predicted at T_x = 673.3K using Equation (14), could induce, by cooling, a maximum glassy fraction Δε = 0.33908 = 0.25431+0.08477 equal to θ′_g = 0.33908.

4.3. Melting Temperatures of Co₇₆Sn₂₄ above T_m = 1392 K

The melting temperature of Co₇₆Sn₂₄ is T_m = 1382 K. The first temperature, T_1n+, of this alloy is observed at 1583 ± 10 K, accompanied by an endothermic enthalpy [76,88]. Using (23) [52], the glass transition temperature, T_g, is predicted as being equal to 866.9 K (θ_g = −0.37275) for T_n+ = 1581.6 K (θ_n+ = 0.14441) while the virtual glass transition is (2T_m−T_g) = 1897.14 K:

$${\mathsf{\theta }}_{n+}=-0.38742\times {\mathsf{\theta }}_g.$$

(23)

The enthalpy coefficients are calculated using (9,10,12,13) and a = 1. Liquids 1, 2, and 3 obey (24)–(26), respectively:

$${\mathsf{\epsilon }}_{\mathrm{ls}}=1.62725(1-{\mathsf{\theta }}^2/0.26958),$$

(24)

$${\mathsf{\epsilon }}_{\mathrm{gs}}=1.44088(1-{\mathsf{\theta }}^2/0.35806),$$

(25)

$$∆{\mathsf{\epsilon }}_{\lg }\left(\mathsf{\theta }\right)=\left[{\mathsf{\epsilon }}_{\mathrm{ls}}-{\mathsf{\epsilon }}_{\mathrm{gs}}\right]=\left[0.18637-2.0121\times {\mathsf{\theta }}^2\right].$$

(26)

The singular values of the enthalpy coefficient Δε_lg (θ) are: Δε_lg (θ_g) = −Δε_lg0 /2 = −0.18637/2 for a stable glass, Δε_lg (θ_1n+) = −0.14441, Δε_lg0 = −0.18637 for an ultrastable glass, Δε_lg (θ_0m) = −0.35605. Two first order transition temperatures were observed at T_n− = 1129 K and 1263 K by supercooling [76,88]. They are predicted using (14) with the singular values of Δε = θ_n+ = 0.14441 and 0.33078 = 0.14441 + 0.18637. The transition for Δε_lg= −0.35605 does not exist because it would lead to a second melting temperature higher than the glass transition T′_g = 1897.14 K.

The Equations (27)–(29), used to predict Phase 3 enthalpy decreasing with temperature, are determined with θ_g = 0.37275 (T_g = 1897.14 K) and (9), (10), (12) and (13).

$${\mathsf{\epsilon }}_{\mathrm{ls}}=2.37275(1+{ \mathsf{\theta }}^2/0.34266),$$

(27)

$${\mathsf{\epsilon }}_{\mathrm{gs}}=2.49617(1-{\mathsf{\theta }}^2/0.55046),$$

(28)

$$∆{\mathsf{\epsilon }}_{\lg }\left(\mathsf{\theta }\right)=\left[{\mathsf{\epsilon }}_{\mathrm{ls}}-{\mathsf{\epsilon }}_{\mathrm{gs}}\right]=\left[-0.18637+2.0121\times {\mathsf{\theta }}^2\right].$$

(29)

Lines 1 and 2 determined by (26) and (29) in Figure 4 are obtained by heating from various glassy states depending on thermal history and heating rate and leading to exothermic or endothermic transitions at T_1n+ = 1581.6 K. An endothermic transition was observed at T_1n+ [88].

The transformation at the temperature, T_x,, of Phase 3, by heating from the glassy state, is predicted using (14) with Δε = 0.33078 = 0.14441 + 0.1837, ε_ls0 = 1.44088, and θ_0g² = 0.35806 and leads to a negative enthalpy coefficient equal to −0.33078, as shown in Figure 4. The enthalpy of Phase 3, 0.33078 × H_m, would be recovered at the second melting temperatures T_n+ = 1581.6 K (θ_n+ = 0.14441) and 1639.6 K (θ_n+ = 0.18637). The melting enthalpy of the crystallized part would be (1−0.33078) H_m = 0.66933×H_m, while the crystallization enthalpy would be −0.66933 × H_m.

The temperatures, T_x, would separate two domains of glassy states. The melt would be fully glassy below T_x after transition at T_x and partially glassy from T_x to T_n+. The glassy fractions of the melt would be 33.078% from T_x to 1581.6 K and 18.637% from 1581.6 to 1639.6 K.

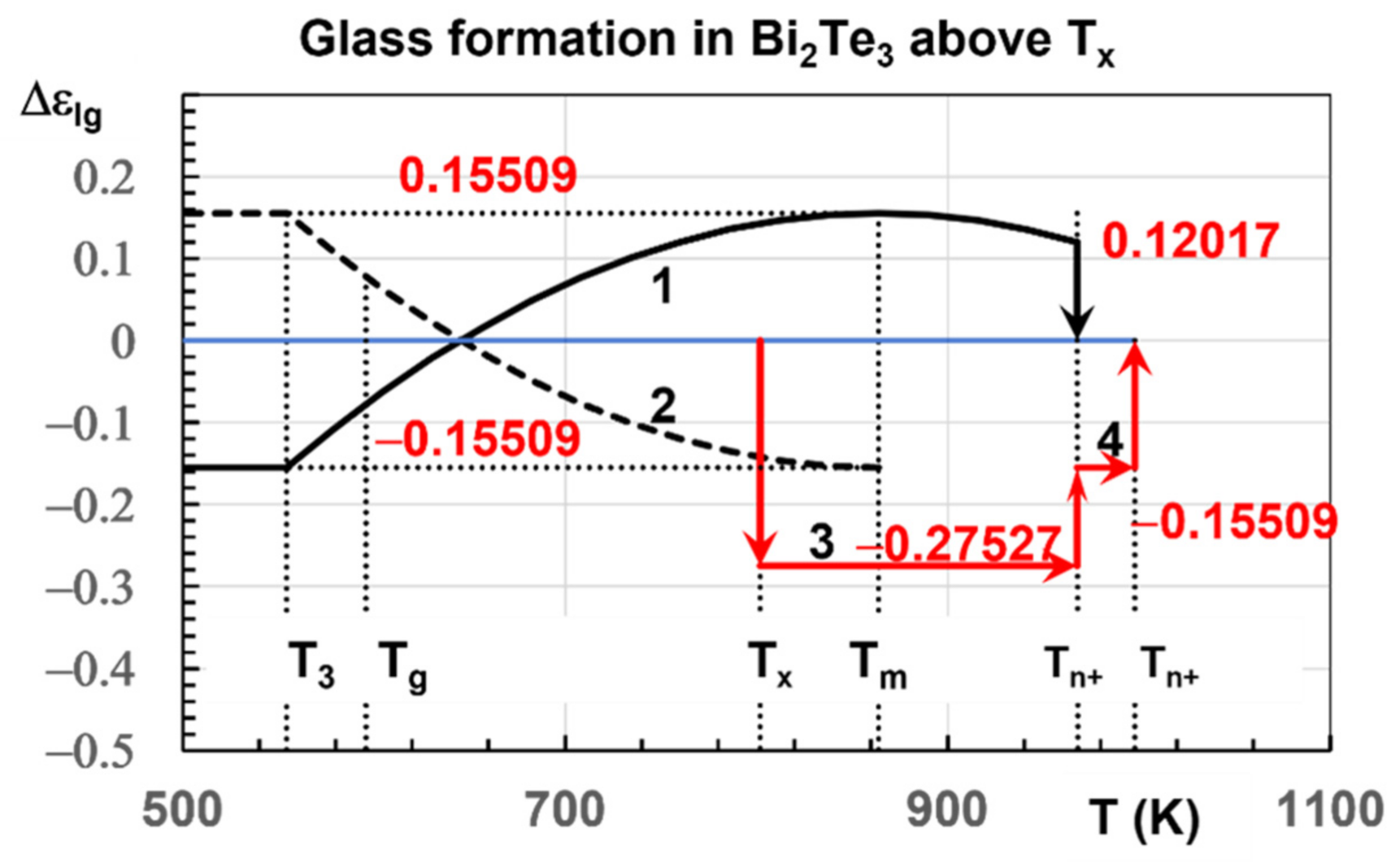
4.4. Melting Temperatures of Bi₂Te₃ and Its Alloys above T_m = 864 K

Liquid–liquid structure transitions in metallic melts have an impact on solidification [89] and play an important role in the final microstructure and the properties of the solid alloys. We note that the compound Bi₂Te₃ is used for most Peltier cooling devices and thermoelectric generators. In alloys based on this compound, during the first heating process, a temperature induced liquid–liquid structural transition existed at a temperature that we call T_1n+, which disappeared in the resistivity measurements by cooling from higher temperatures than T_n+ [44,45]. Solidifying at various cooling rates in these conditions, the microstructures were refined, and the hardness increased with the cooling rate. The glass transition temperature of Bi₂Te₃ and its alloys were unknown. Applying (23) to this compound with T_m = 864 K and T_1n+ = 967.8 K [90], the two glass transition temperatures are predicted at θ_g = −0.29576 (T_g = 586 K) and θ′_g = 0.29576 (T′_g = 1132 K). The presence of nucleation and recalescence temperatures and a temperature of recalescence below T_m upon cooling was dependent on cooling rate. The exothermic transition at T_n+ was also observed by DSC during cooling at 135 K/min.

The Equations (30)–(32) used to predict Phase 3 enthalpy increasing with temperature are determined with θ_g = −0.29576 (T_g = 586 K) and (9,10,12,13):

$${\mathsf{\epsilon }}_{\mathrm{ls}}=1.68981(1-{\mathsf{\theta }}^2/0.23296),$$

(30)

$${\mathsf{\epsilon }}_{\mathrm{gs}}=1.53472(1-{\mathsf{\theta }}^2/0.31736),$$

(31)

$$∆{\mathsf{\epsilon }}_{\lg }\left(\mathsf{\theta }\right)=\left[{\mathsf{\epsilon }}_{\mathrm{ls}}-{\mathsf{\epsilon }}_{\mathrm{gs}}\right]=\left[0.15509-2.4179\times {\mathsf{\theta }}^2\right].$$

(32)

The singular values of the enthalpy coefficient Δε_lg (θ) are: Δε_lg (θ_g) = −Δε_lg0 /2= −0.15509/2, −Δε_lg (θ_n+) = −0.12017, −Δε_lg0= −0.15509, Δε_lg (θ_0m) = −0.40818. The first order transition for Δε= 0.40818 does not exist because it would lead to a second melting temperature higher the second glass transition T′_g at 1897.1 K. It is replaced by a first order transition with Δε = 0.12017 + 0.15509 = 0.27527. Two first order transition temperatures are expected for θ_n+= Δε = 0.12017 and θ_n+ = Δε= 0.27527.

The Equations (33)–(35) used to predict Phase 3 enthalpy decreasing with temperature are determined with θ_g= 0.29576 (T_g = 1132 K) and (9), (10), (12), (13).

$${\mathsf{{\rm E}}}_{\mathrm{ls}}=2.31019(1+{ \mathsf{\theta }}^2/0.31848)$$

(33)

$${\mathsf{\epsilon }}_{\mathrm{gs}}=2.46528(1-{ \mathsf{\theta }}^2/0.5098),$$

(34)

$$∆{\mathsf{\epsilon }}_{\lg }\left(\mathsf{\theta }\right)=\left[{\mathsf{\epsilon }}_{\mathrm{ls}}-{ \mathsf{\epsilon }}_{\mathrm{gs}}\right]=\left[-0.15509+2.4179\times { \mathsf{\theta }}^2\right].$$

(35)

Lines 1 and 2, determined by (32) and (35) in Figure 5 obtained by heating from the glassy state, depend on thermal history and heating rate and lead to exothermic and endothermic transitions at T_1n+ = 967.8 K.

The crystallization of Phase 3 by heating from the glassy state is predicted at T_x = 802 K using (14), with Δε = 0.12017 + 0.15509 = 0.27527, ε_ls0 = 1.53472, and θ_0g² = 0.31736 and lead to the negative enthalpy coefficient, −0.27527, as shown in Figure 5. This transition at 802 K was observed by supercooling at 135 K/min [90] and was viewed as the nucleation temperature of nanocrystals. The glassy enthalpy −0.27527×H_m would be recovered at the second melting temperatures T_n+ = 967.9 K (θ_n+ = 0.12017) and 998 K (θ_n+ = 0.15509). The melting enthalpy of the crystallized part would be (1−0.27527) H_m = 0.72473×H_m, while the crystallization enthalpy would be −0.72473 × H_m.

4.5. The Six Melting Temperatures of Zr₄₆Cu₄₆Al₈ above 1200 K

The glass transition temperature of Zr₄₆Cu₄₆Al₈ is T_g= 715 K. There are three melting temperatures 962 K, 1034 K and 1125 K, as shown in Figure 6, inducing three unknown Phases 3 observed with heating rates between 0.1666 and 2 K/s in this noncongruent alloy and three theoretical virtual glass transition temperatures equal to 1209 K, 1353 K, and 1535 K, respectively [91]. Consequently, there are different coefficients ε_ls0, ε_gs0, θ_0g², θ_0m², Δε_lg (θ_0m), Δε = θ_n+ for every one of them, given in

Table 1. Multiple melting temperatures T_m and T_n+ of Cu₄₆Zr₄₆Al_8. T_g = 715 K; T_m, the first melting temperature; θ_g, the reduced glass transition temperature; ε_ls0, θ_0m², ε_gs0, θ_0g² calculated with (9,) (10), (12) and (13); Δε_lg (θ_0m) with (15), the enthalpy coefficient of Phase 3 at θ= θ_0m; Δε= θ_n+ the enthalpy coefficient singular values of glassy Phase 3 above T_x = 763 K; T_n+ (K), the theoretical second melting temperatures; Obs., with yes when T_n+ has been observed in Figure 7; T′_g, the virtual glass transition temperature above T_n+.

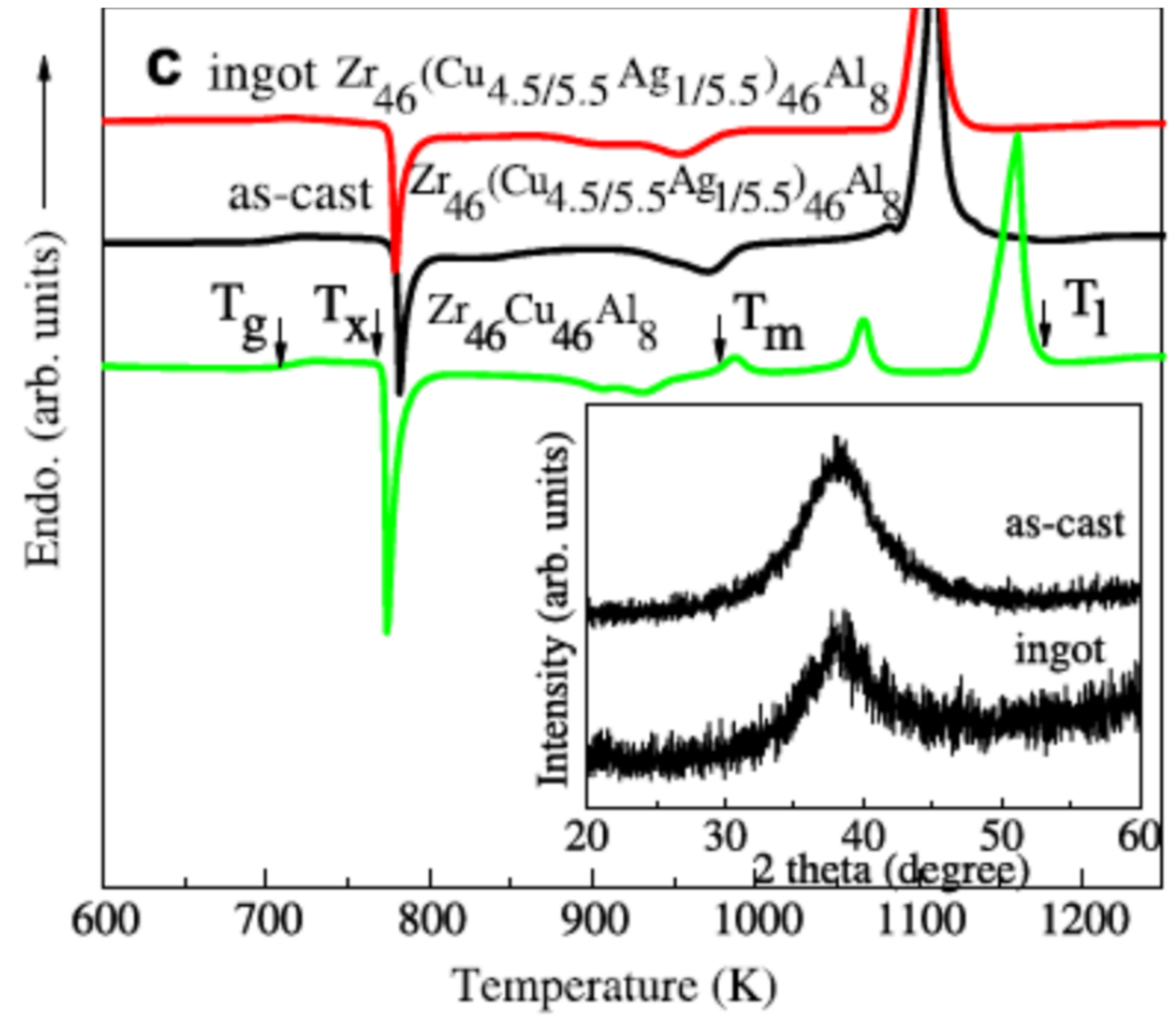
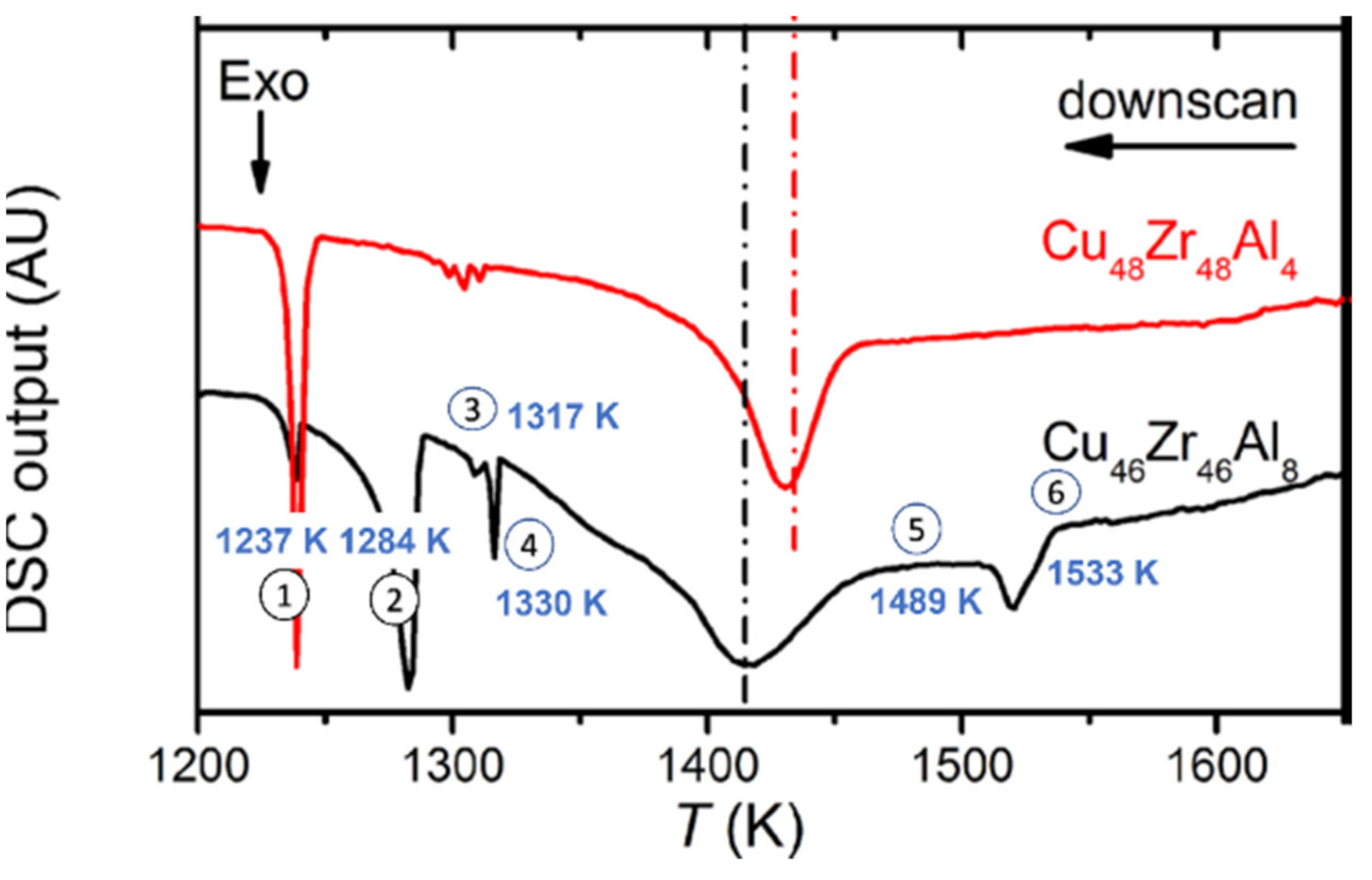
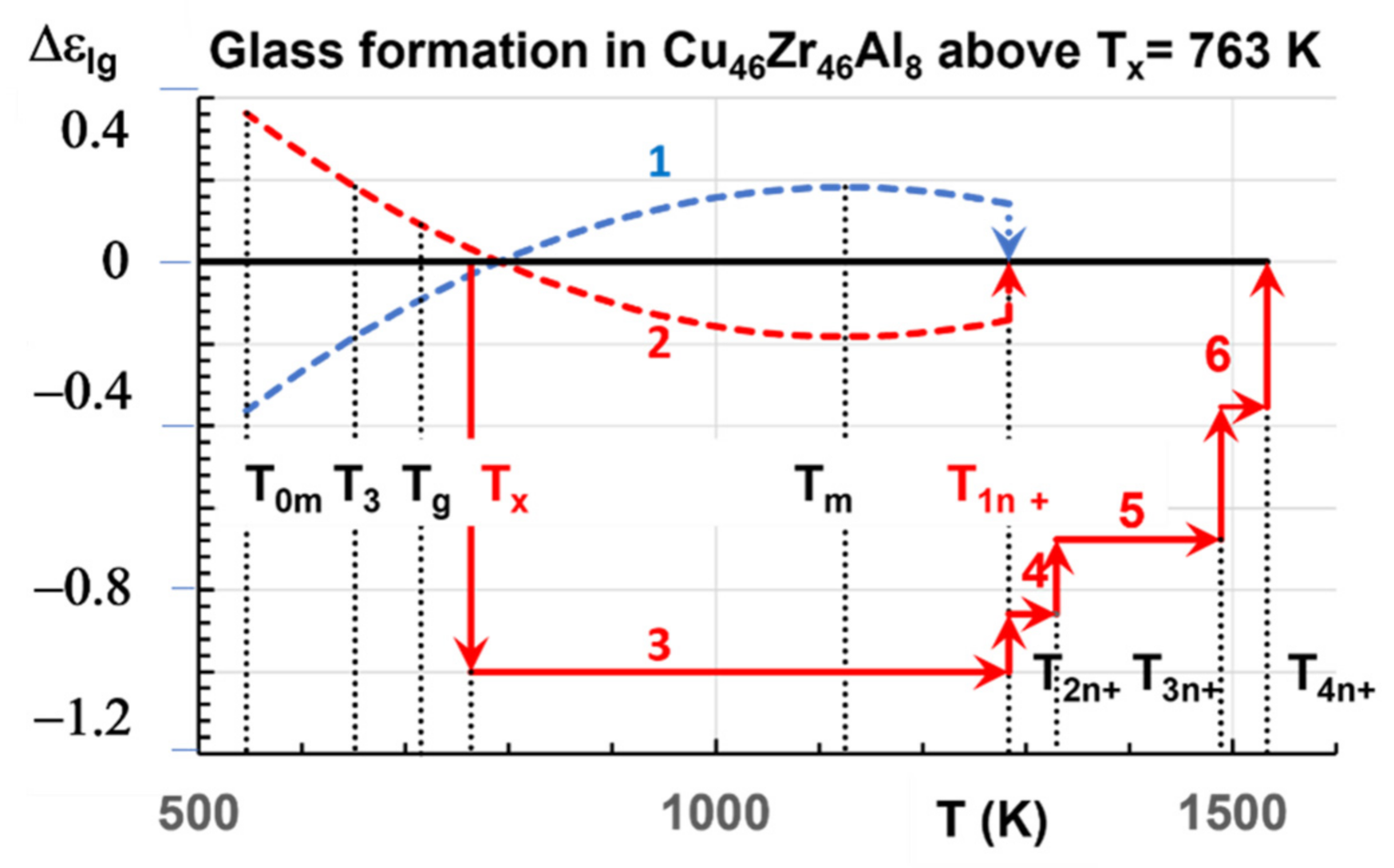
Tg	Tm	θg	εls0	θom2	εgs0	θog2	Δεlg (θ0m)	Δε= θn+	Tn+	Obs.	T′g
715	962	−025676	1.74324	0.19893	1.61486	0.27642	−0.4527	0.06419			1209
715	962	−0.25676	1.74324	0.19893	1.61486	0.27642	−0.4527	0.09947	1057		1209
715	962	−0.25676	1.74324	0.19893	1.61486	0.27642	−0.4527	0.12838	1086		1209
715	962	−0.25676	1.74324	0.19893	1.61486	0.27642	−0.4527	0.22785	1181		1209
715	1034	−0.30851	1.69149	0.23193	1.53723	0.31617	−0.40957	0.07713			1353
715	1034	−0.30851	1.69149	0.23193	1.53723	0.31617	−0.40957	0.11953	1158		1353
715	1034	−0.30851	1.69149	0.23193	1.53723	0.31617	−0.40957	0.15426	1194		1353
715	1034	−0.30851	1.69149	0.23193	1.53723	0.31617	−0.40957	0.19665	1237	Yes	1353
715	1034	−0.30851	1.69149	0.23193	1.53723	0.31617	−0.40957	0.27378	1317	Yes	1353
715	1125	−0.36444	1.63556	0.26492	1.45333	0.35311	−0.36296	0.09111			1535
715	1125	−0.36444	1.63556	0.26492	1.45333	0.35311	−0.36296	0.1412	1284	Yes	1535
715	1125	−0.36444	1.63556	0.26492	1.45333	0.35311	−0.36296	0.18222	1330	Yes	1535
715	1125	−0.36444	1.63556	0.26492	1.45333	0.35311	−0.36296	0.32342	1489	Yes	1535
715	1125	−0.36444	1.63556	0.26492	1.45333	0.35311	−0.36296	0.36296	1533	Yes	1535

and calculated with (9, 10, 12, 13, 15), a = 1 and θ_g = −0.25676 for T_m = 962 K, −0.30851 for T_m = 1034 K and −0.36444 for T_m = 1125 K. The main phase having the highest melting enthalpy corresponds to T_m = 1125 K.

Six first order transition temperatures accompanied by exothermic latent heats were observed above 1200 K by cooling the melt from 1650 K, as shown in Figure 7 [41]. These temperatures predicted in Table 1 are melting temperatures upon heating. Peaks numbered 1 to 6 correspond to predicted temperatures T_n+: for T_m = 1125 K (N°2-1284K, N°4-1330 K, N°5- 1489 K, N°6- 1533 K); for T_m = 1034 K (N°1- 1237 K, N°3- 1317 K) and for T_m = 962 K, no T_n+ above 1200 K. Peaks N°^s1 and 3 are weak compared to N°^s 2, 4, 5 and 6. The sum of the predicted enthalpy coefficients of peaks N°^s2, 4, 5 and 6 is equal to − 0.1412 − 0.18222 − 0.32342 − 0.36293 = −1.0098 ≅ −1 below T_1n+ = 1284 K instead of T_m = 1125 K, in good agreement with the melting of a glass having an enthalpy coefficient equal to −1, the enthalpy coefficient of full crystallization. A full glassy state exists below T_1n+ = 1284 K and then the glassy state fraction declines with three increases in T_n+ from T_1n+ to T_4n+ = 1533 K.

All transitions of Phases 3 with T_m = 1125 K are represented in Figure 8. Lines 1 and 2 represent Equations (15) and (16). The transition at T_x = 760.3 K occurs when Δε_lg = 0 for the phase 3 enthalpy coefficient corresponding to the lowest melting temperature T_m = 962 K. The formation, by heating, of a glass phase having an enthalpy equal to that of crystals, occurs using heating rates inducing a first order transition at T_x without crystallized fraction. The observation of glass fractions melting above T_m could be obtained by heating because all first order transitions at T_n+ were reversible and corresponded to singular enthalpies of the glassy phase and probably various percolation thresholds [41]. The first order transition at T_x = 760.3 K leading to a glassy fraction equal to 100 % corresponds to Δε= −1 at a temperature far below T_m = 1125 K, using a low heating rate. Nevertheless, a crystallization enthalpy occurs at T_m = 1125 K, as shown in Figure 6, because the melt, in this case, has not been overheated above T_4n+ = 1533 K before cooling [91]. The glassy state obtained at T_x = 760.3 K could totally escape crystallization following the red broken line N°3 using low heating rates such as 0.333 K/s, if the melt is previously overheated above T′_g = 1535 K before cooling, as shown in Figure 7.

The first order transitions are due to liquid super atom formation at T_n+. Observations of multiple temperatures, T_n+, are facilitated in this alloy because they have a first order character much stronger than those observed in La₅₀Al₃₅Ni₁₅ and Pd_42.5Ni_42.5P₁₅ studied by [37,38], due here to the spontaneous formation and percolation of solid super atoms instead of having bonds progressively built-in liquid super atoms (clusters–bound colloids) during slow cooling [72].

5. The Case of a Few Polymers

The glass transition reveals the full entropy of melting while the crystallization entropy is weaker or even disappears in atactic polymers. The incubation time of first order transitions is much higher in these polymers than in metallic and molecular glass-forming melts. The heat capacity jump at T_g is equal to 1.5 S_m without including the diverging contribution due the phase transition at T_g [52].

5.1. Polyvinyle Acetate (C₄H₆O₂)_n

The glass transition occurred at T_g ≅ 309 K with ΔC_p (T_g) = 1.02 J/g in [92]. The melting entropy S_m was equal to 29.8 J/mole/K. The melting temperature Tm was 333 K. The crystallization was not observed because T_g was close to T_m. A long annealing above T_m is necessary to crystallize this material without undercooling.

5.2. Polymer Called 1,2-Propadeniol

The glass transition temperature was T_g = 170.3 K, the solidus temperature T_s= 225 K and the partial melting heat 4900 J/mole [93]. The heat capacity jump at T_g was 77.6 J/mole due to a melting entropy of 51.74 J/mole/K and a melting enthalpy of 11642 J/mole. The recovery of the missing enthalpy (6742 J/mole) is expected at much higher temperatures than 225 K.

5.3. Poly(ethylene terephthalate)

The heat capacity jump Δε_lg (T_g) at T_g is (0.446 J/g/K) after rapid quenching, corresponds to a full melting entropy (0.2974 J/K/mole) [94,95]. The partial melting heat is 44% less giving rise after crystallization to a heat capacity jump reduction by 44%.

5.4. Bisphenol-A Polycarbonate (PC) and Poly(3-hydroxybutyrate) (PHB)

Rigid amorphous fractions, found in PC and PHB, occurred in the temperature range between the crystallization and the glass transition [96]. The authors highlight the question of when this amorphous material vitrifies. The answer could be found in this paper.

5.5. Interaction between Globular Proteins and Proteins Solutions

The interplay between crystallization and a metastable liquid–liquid phase separation (protein rich–protein poor) is of paramount importance for obtaining protein crystals of good quality [97] and this system can be modelled with a hard sphere followed by a Yukawa tail; liquid–liquid phase separation in hard sphere models of colloidal mixtures has also been studied extensively [98] but little is known at a fundamental level about thermodynamic coexistence between the crystal and glassy phases. Predictions of the interaction between globular proteins and proteins solutions (the partial glass phase discussed above) was out of the scope of current paper and could be an area of utilization of the methodological approach discussed herewith, to analyze the computer simulation data reported in the literature for basic, interaction models of statistical mechanics.

6. Conclusions

This paper is devoted to liquid–liquid transitions in glass-forming melts. A first liquid-liquid transition was often observed at a temperature T_1n+ above the equilibrium thermodynamic transition T_m after heating from the glassy state without previous first order transition at a temperature T_x weaker than T_m. This transition at T_n+ was exothermic or endothermic and associated with antibonds or bonds breaking predicted by the nonclassical nucleation model and in agreement with the configuron percolation model, as already shown in previous publications.

Separation phenomena were observed by molecular dynamics simulations of monoatomic liquid elements at very high heating rates and remain predicted. Full melting of Ag, Cu, Zr and Fe were obtained at temperatures much higher than T_m, showing that the crystal fraction can fully profit from the disappearance of any glass phase above T_m. An increase in the melting temperature of glassy phases at high heating rates is due to the finite mobility of configurons – broken chemical bonds, which at relatively low heating rates quickly condense causing the typical first order phase transformation, arrest at the temperature T_x. At higher heating rates, however, there is not enough time for condensation to occur and, thus, the melting occurs at a much higher temperature when the percolation via configurons occurs.

In this paper, some mysterious aspects of the first order transition occurring at T_x and leading to crystallization were enlightened, considering phase separation between a glassy fraction having a glass transition temperature higher than T_m and a second fraction, crystallizing at T_x, and melting at T_m. The nonclassical nucleation model predicts the existence of two glassy phases, at T_g and T′_g, in two different temperature domains separated by the temperature T_x. The transition at T_x increases T_g up to T_x and induces a new glassy phase above T_x. The temperature T′_g is virtual because the glass phase has a melting temperature higher than T_m and lower than T′_g.

These new melting temperatures are observable at T_n+ at low heating rates, as already anticipated by the reduction in the crystallization enthalpy of some monoatomic elements after supercooling and recalescence. Several new examples were found in publications. Three liquid–liquid transitions in bismuth observed in two different experiments lead to a total glassy fraction of 86.7% and a melting temperature equal to 1.867T_m in one of the two experiments and to 1.438T_m in the other. Four reversible first order liquid–liquid transitions in Cu₄₆Zr₄₆Al₈ lead to a glassy fraction of 100 %, for the phase with T_m= 1125 K and a melting temperature of 1.36T_m. Predictions of complementary liquid–liquid transitions were made for Co₇₆Sn₂₄, Pd₄₀Ni₄₀P₂₀, and Bi₂Te₃ beyond the first liquid–liquid transitions already observed. A rigid amorphous fraction, found in two polymers, did not participate in the glass fraction below T_g and appeared in the range of temperatures between T_g and T_m without knowing its vitrification temperature.

The first order transitions at T_x observed by heating were accompanied by latent heats composed of singular values of the glass enthalpy or of their sum, as already shown for monoatomic elements. They determined the first order liquid–liquid transitions at T_n+ above T_m which were reversible in Cu₄₆Zr₄₆Al₈ and observed with the same latent heats by cooling from homogeneous liquid state and heating due to the melting and formation of percolating solid superclusters (superatoms), respectively. The same transitions at T_n+ observed in La₅₀Al₃₅Ni₁₅ and Pd_42.5Ni_42.5 P₁₅ involve much weaker latent heats by cooling because percolating liquid superclusters (superatoms) formed at T_n+ from homogeneous liquid are progressively solidified by cooling from T_n+ instead of being fully solidified at T_n+.

The melts are rejuvenated above T′_g = 2T_m-T_g because all the growth nuclei of crystals are eliminated by superheating above T′_g. Many techniques of quenching, used to avoid crystallization, do not overheat melts far above T_m before quenching and are not able to reveal the various glassy states above T_x.