Research on Sustainable Development of the Regional Construction Industry Based on Entropy Theory
Abstract
1. Introduction
- The study analyzes the local primary data released by the government from 2000 to 2020 through the established statistical regression mathematical model and to determine the validity of discrete data through the Fourier sine transform, deleting the invalid data, establishing a vector matrix, and making the least-square regular fitting for valid data. The paper also aims to determine the final effective curve as a mean entropy model.
- To establish the GDP mathematical analysis model according to the overall goal set by the state (Section 4.6), to analyze the practical value of sustainability in eight provinces from 2020 to 2100 (IPCC provides that a Three Pillars study will be made) [18].
- To determine the rationality and validity of overall national targets based on data from objective 2 and to provide a scientific basis for similar government policies in the global construction industry.
- To analyze the potential of each province’s sustainable control and emission reduction and evaluate the changes in growth rate through an innovative model.
- Exploring and scientifically demonstrating the accuracy and feasibility of China’s carbon emission targets for 2030 and 2060 through a 100-year practical assessment of the sustainability of the construction industry in the top eight economic provinces.
- Searching the relevant literature with no similar literature in this field (see Section 2 for details).
- Developing a scientific algorithm and theoretical model for global construction industry development assessment through interdisciplinary fusion research, from the given data to computing future impact data and checking official statistics’ scientific accuracy and feasibility.
- Establishing an entropy weight model to improve the determination of the influence and importance of impact assessment data.
2. Literature Review
3. Methodology
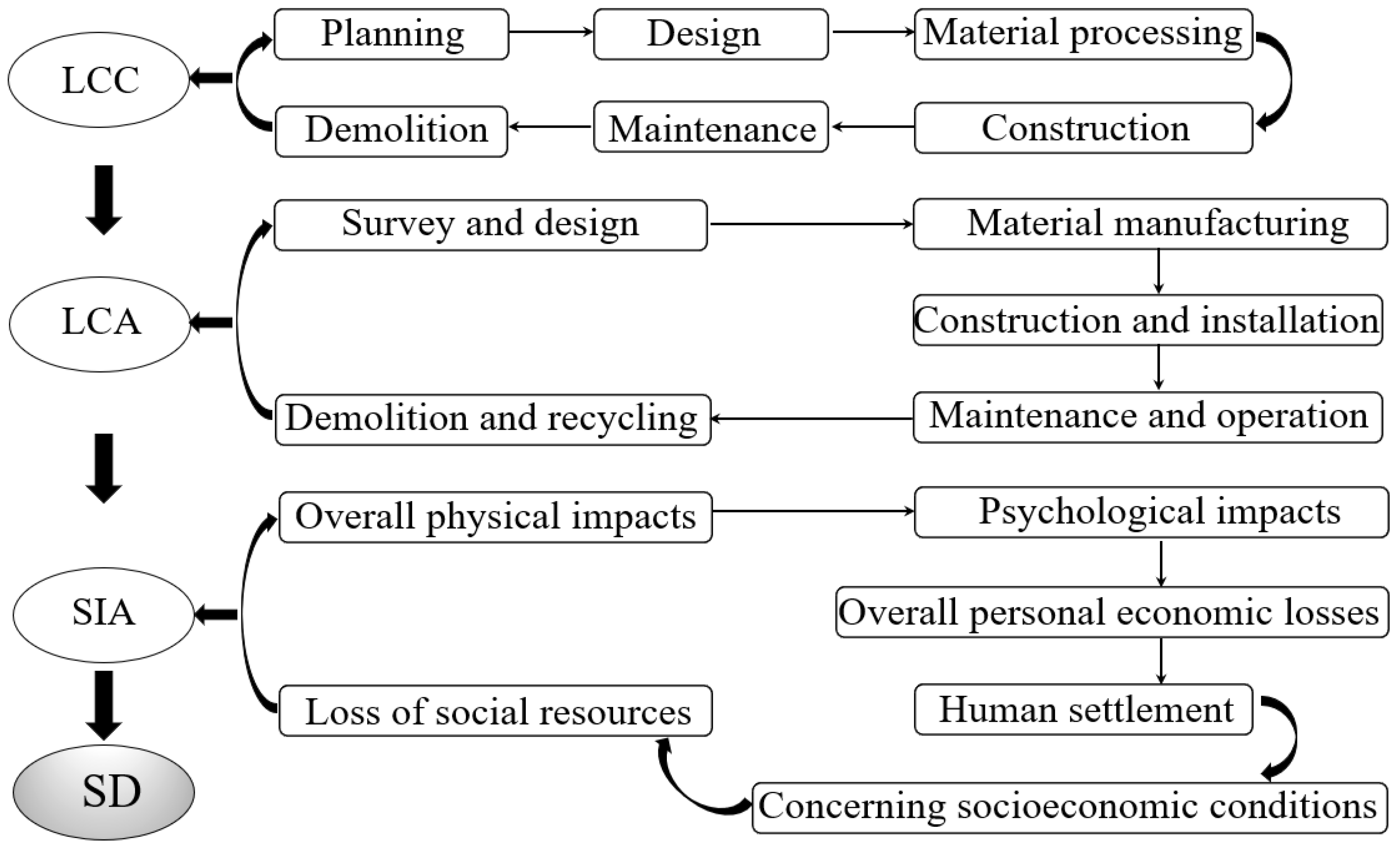
3.1. Models of LCA, LCC, and SIA
3.2. Theory Model of Scientific Algorithm
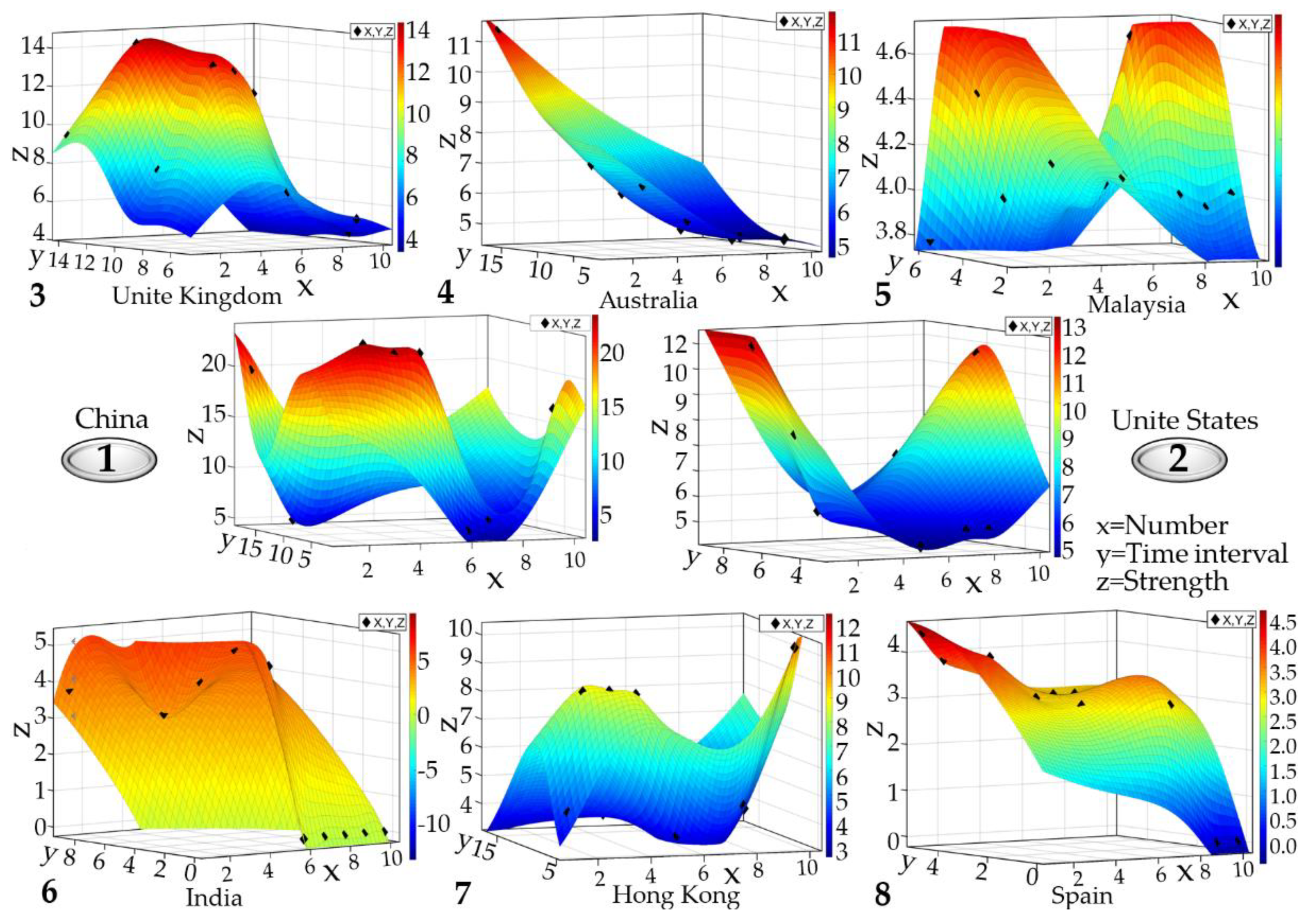
4. Results and Discussion
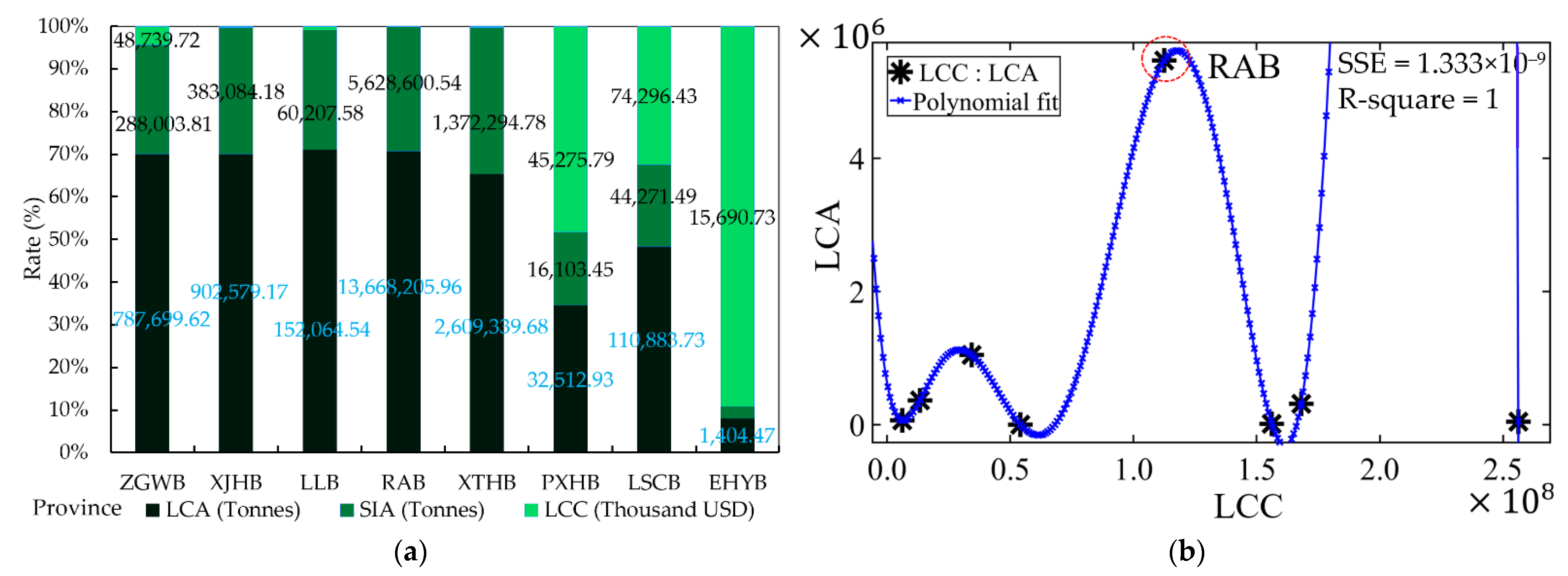
4.1. Analysis of LCC
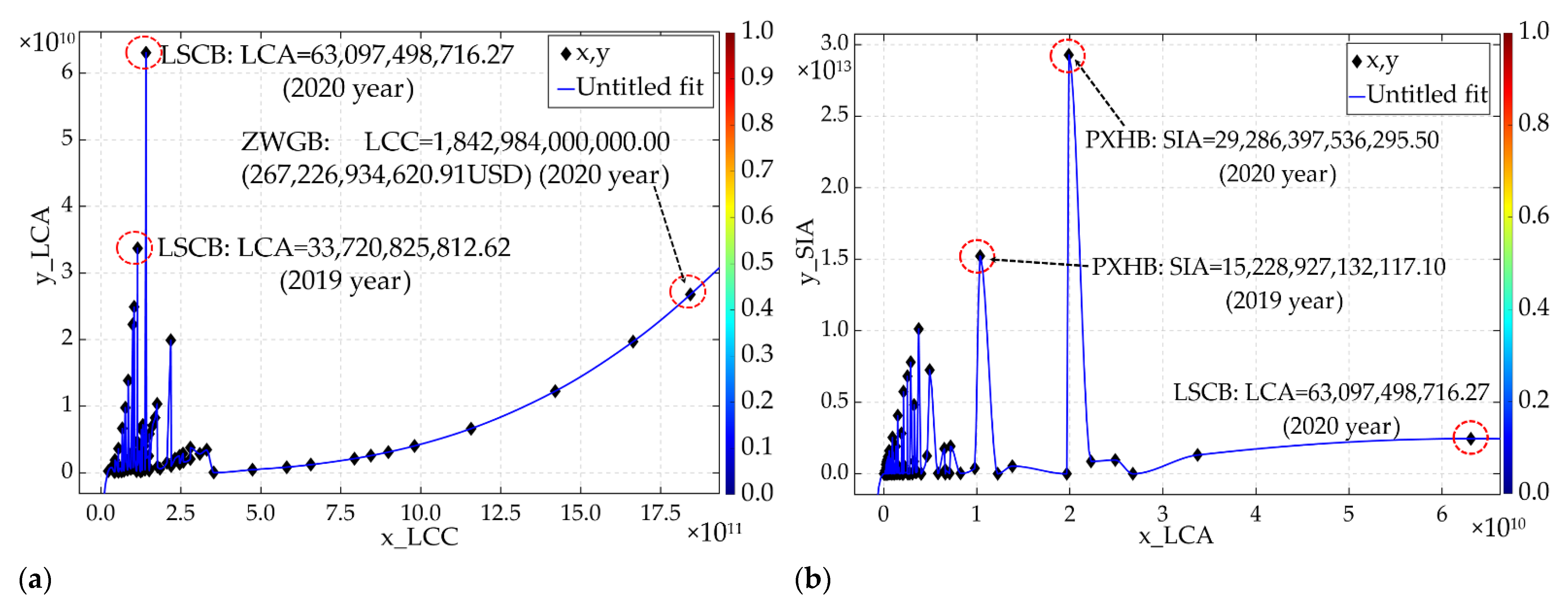
4.2. Analysis of LCA and SIA
4.3. Sustainability Analysis by Province
4.4. Establishment of the Algorithm Formula of the Provincial Model
4.4.1. The Algorithm Formula of ZWGB
4.4.2. The Algorithm Formula of XJHB, LLB, RAB, XTHB, PXHB, LSCB and EHYB
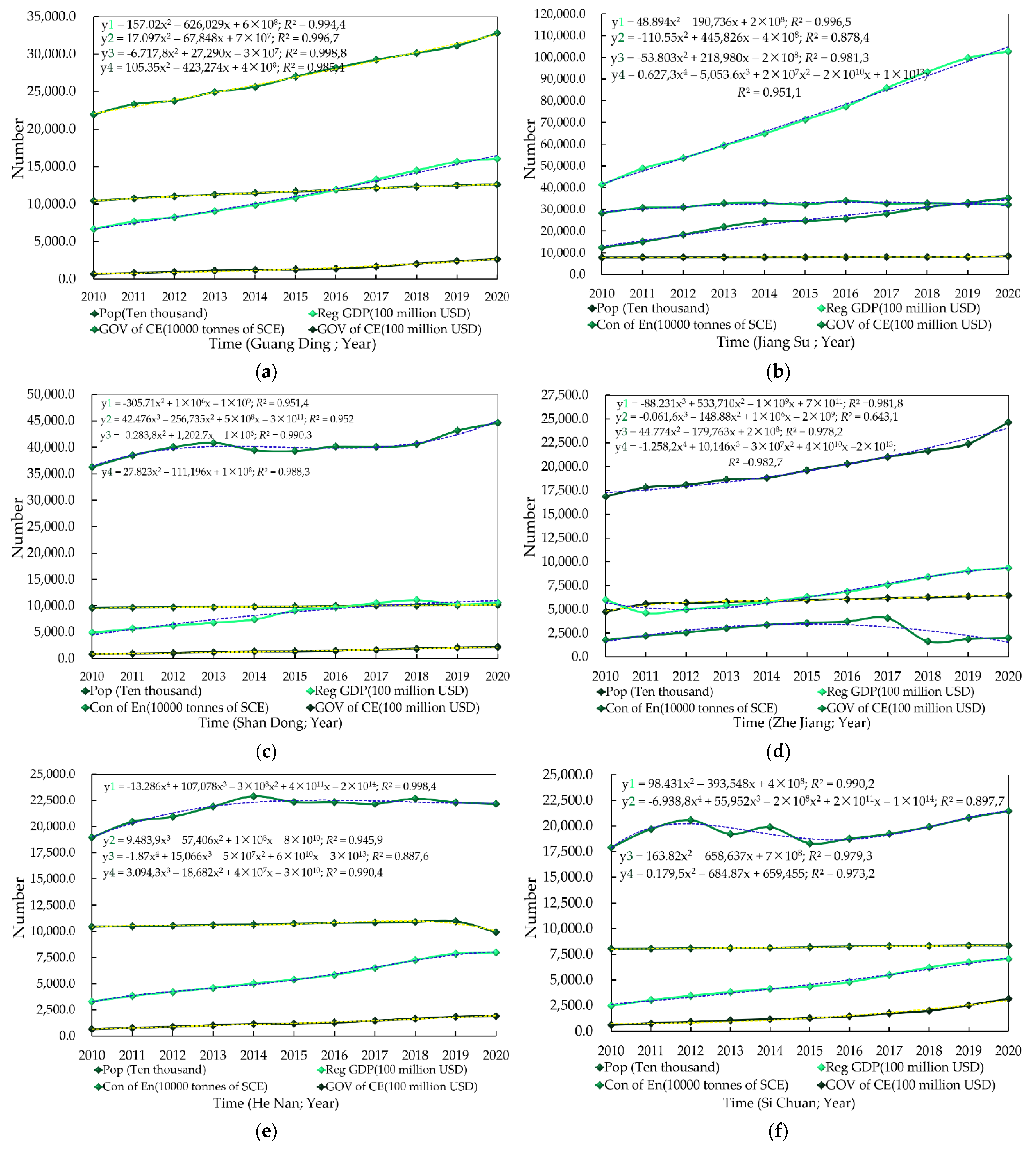
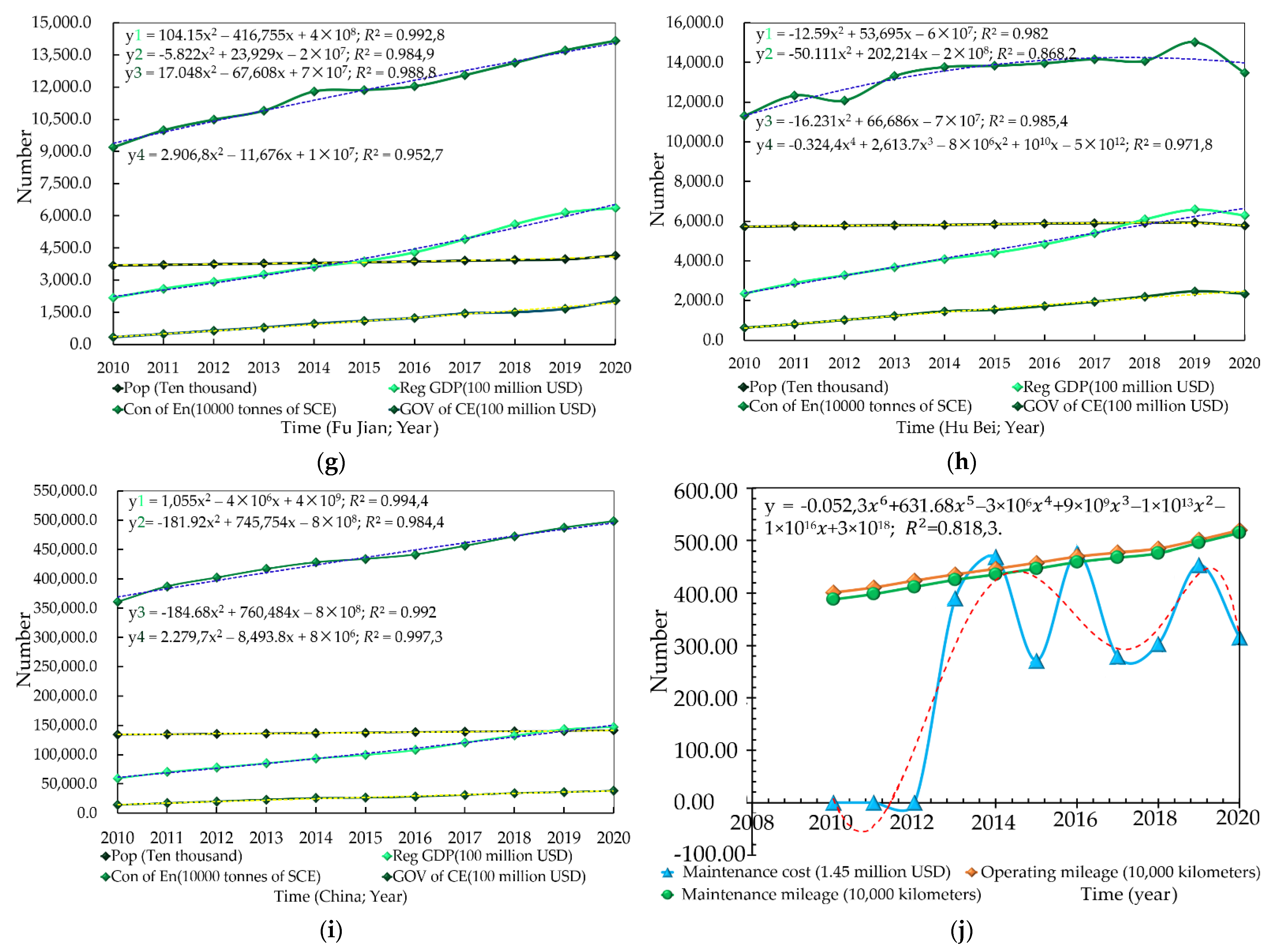
4.5. Analysis of the Construction Industry (2010~2020)
4.5.1. Scientific Algorithm Model of ZWGB
4.5.2. Scientific Algorithm Model of XJHB, LLB, RAB, XTHB, PXHB, LSCB and EHYB
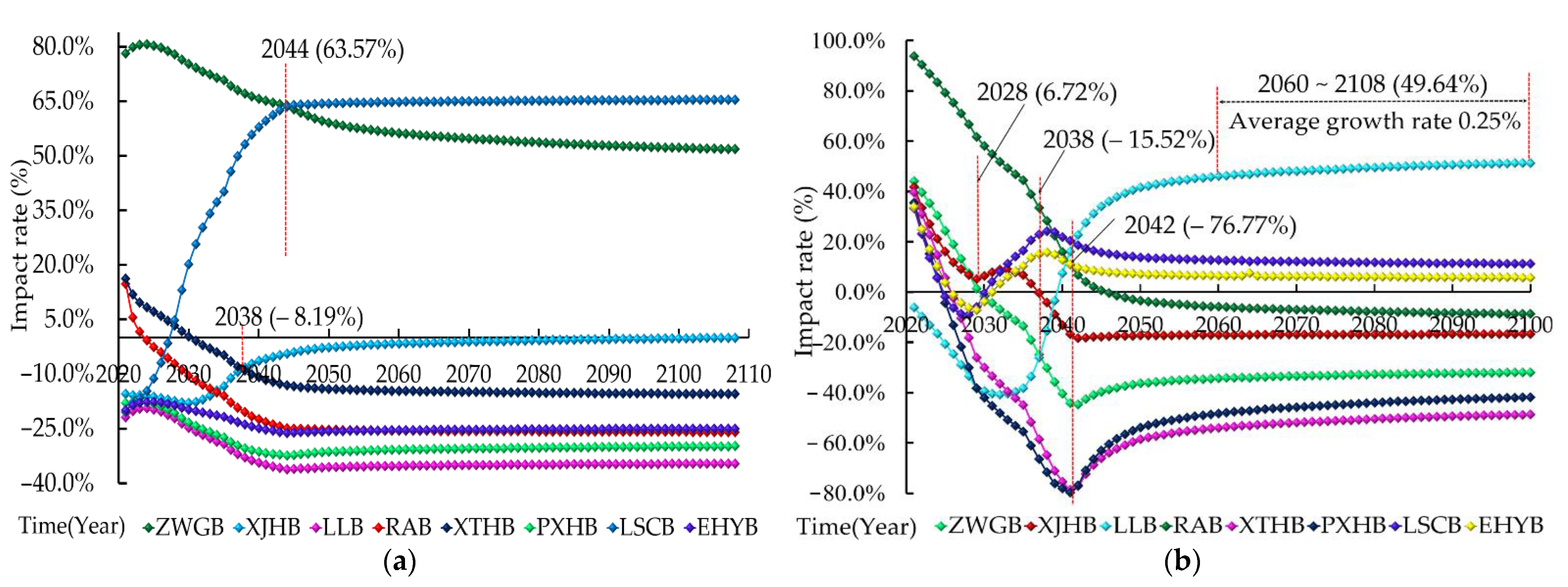
4.6. Establishing A Sustainable Forecast Model (2021~2108)
- Building a moderately prosperous society in all respects (GDP per capita of USD 10,503.2) 100 years after the founding of the Communist Party (1921–2021).
- They are building China into a great, modern, socialist country (GDP per capita of USD 52,700) 100 years after founding the People’s Republic of China (1949–2050).
- Turning China into a highly developed socialist country (GDP per capita of USD 85,000) after 100 years of reform and opening (1978–2078) [47,48], on which the GDP of China in 2021–2108 is analyzed. The eight provinces’ GDP and gross construction output value (2021–2108) are analyzed based on the Chinese GDP data obtained and Equation (3).
4.7. Analysis the Mean Entropy Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bernstein, L.; Bosch, P.; Canziani, O.; Chen, Z.; Christ, R.; Davidson, O.; Hare, W.; Huq, S.; Karoly, D.; Kattsov, V.; et al. AR4 Climate Change 2007: Synthesis Report—IPCC. 2008. Available online: https://www.ipcc.ch/report/ar4/syr/ (accessed on 22 September 2022).
- Edenhofer, O.; Pichs-Madruga, R.; Sokona, Y.; Agrawala, S.; Bashmakov, l.A.; Blanco, G.; Broome, J.; Bruckner, T.; Brunner, S.; Bustamante, M.; et al. AR5 Climate Change 2014: Mitigation of Climate Change—IPCC, 2015. 2015. Available online: https://www.ipcc.ch/report/ar5/wg3/ (accessed on 18 September 2022).
- Peters, G.P.; Geden, O. Catalysing a political shift from low to negative carbon. Nat. Clim. Chang. 2017, 7, 619–621. [Google Scholar] [CrossRef]
- Sandberg, N.H.; Brattebø, H. Analysis of energy and carbon flows in the future Norwegian dwelling stock. Build. Res. Inf. 2012, 40, 123–139. [Google Scholar] [CrossRef]
- Scott, V.; Haszeldine, R.S.; Tett, S.F.B.; Oschlies, A. Fossil fuels in a trillion tonne world. Nat. Clim. Chang. 2015, 5, 419–423. [Google Scholar] [CrossRef]
- Cui, X.; Zhao, T.; Wang, J. Allocation of carbon emission quotas in China’s provincial power sector based on entropy method and ZSG-DEA. J. Clean. Prod. 2021, 284, 124683. [Google Scholar] [CrossRef]
- Zhou, Z.W.; Alcalá, J.; Yepes, V. Research on the optimized environment of large bridges based on multi-constraint coupling. Environ. Impact Assess. Rev. 2022, 97, 106914. [Google Scholar] [CrossRef]
- People’s Daily. China’s Commitment to Reduce Emissions Inspires Global Climate Action. China Government Network 1. 2021. Available online: http://www.gov.cn/xinwen/2020-10/12/content_5550452.htm (accessed on 12 September 2022).
- Duan, H.; Zhou, S.; Jiang, K.; Bertram, C.; Harmsen, M.; Kriegler, E.; van Vuuren, D.P.; Wang, S.; Fujimori, S.; Tavoni, M.; et al. Assessing China’s efforts to pursue the 1.5 °C warming limit. Science 2021, 372, 378–385. [Google Scholar] [CrossRef] [PubMed]
- Verma, S.; Paul, A.R.; Haque, N. Selected Environmental Impact Indicators Assessment of Wind Energy in India Using a Life Cycle Assessment. Energies 2022, 15, 3944. [Google Scholar] [CrossRef]
- Langevin, J.; Harris, C.B.; Reyna, J.L. Assessing the Potential to Reduce U.S. Building CO2 Emissions 80% by 2050. Joule 2019, 3, 2403–2424. [Google Scholar] [CrossRef]
- Molina-Moreno, F.; García-Segura, T.; Martí, J.V.; Yepes, V. Optimization of buttressed earth-retaining walls using hybrid harmony search algorithms. Eng. Struct. 2017, 134, 205–216. [Google Scholar] [CrossRef]
- Zamarrón-Mieza, I.; Yepes, V.; Moreno-Jiménez, J.M. A systematic review of application of multi-criteria decision analysis for aging-dam management. J. Clean. Prod. 2017, 147, 217–230. [Google Scholar] [CrossRef]
- Golley, J.; Meng, X. Income inequality and carbon dioxide emissions: The case of Chinese urban households. Energy Econ. 2012, 34, 1864–1872. [Google Scholar] [CrossRef]
- Zhou, P.; Zhang, L.; Zhou, D.; Xia, W. Modeling economic performance of interprovincial CO2 emission reduction quota trading in China. Appl. Energy 2013, 112, 1518–1528. [Google Scholar] [CrossRef]
- Pan, X.; Teng, F.; Wang, G. Sharing emission space at an equitable basis: Allocation scheme based on the equal cumulative emission per capita principle. Appl. Energy. 2014, 113, 1810–1818. [Google Scholar] [CrossRef]
- Tong, D.; Zhang, Q.; Zheng, Y.; Caldeira, K.; Shearer, C.; Hong, C.; Qin, Y.; Davis, S.J. Committed emissions from existing energy infrastructure jeopardize 1.5 °C climate target. Nature 2019, 572, 373–377. [Google Scholar] [CrossRef]
- IPCC. Summary for Policymakers. In Climate Change 2014, Mitigation of Climate Change. Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Li, Q.; Long, R.; Chen, H.; Chen, F.; Wang, J. Visualized analysis of global green buildings: Development, barriers and future directions. J. Clean. Prod. 2019, 245, 118775. [Google Scholar] [CrossRef]
- Milani, C.J.; Yepes, V.; Kripka, M. Proposal of Sustainability Indicators for the Design of Small-Span Bridges. Int. J. Environ. Res. Public Health 2020, 17, 4488. [Google Scholar] [CrossRef] [PubMed]
- Landi, D.; Marconi, M.; Bocci, E.; Germani, M. Comparative life cycle assessment of standard, cellulose-reinforced and end of life tires fiber-reinforced hot mix asphalt mixtures. J. Clean. Prod. 2020, 248, 119295. [Google Scholar] [CrossRef]
- Zhou, Z.; Alcalá, J.; Yepes, V. Environmental, Economic and Social Impact Assessment: Study of Bridges in China’s Five Major Economic Regions. Int. J. Environ. Res. Public Health 2020, 18, 122. [Google Scholar] [CrossRef]
- Zafar, M.W.; Shahbaz, M.; Sinha, A.; Sengupta, T.; Qin, Q. How renewable energy consumption contribute to environmental quality? The role of education in OECD countries. J. Clean. Prod. 2020, 268, 122149. [Google Scholar] [CrossRef]
- Ebhota, W.S.; Tabakov, P.Y. Development of domestic technology for sustainable renewable energy in a zero-carbon emission-driven economy. Int. J. Environ. Sci. Technol. 2021, 18, 1253–1268. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, X.; Ye, A. Shake table test on transverse steel damper seismic system for long span cable-stayed bridges. Eng. Struct. 2018, 179, 106–119. [Google Scholar] [CrossRef]
- Zhou, Z.W.; Alcalá, J.; Yepes, V. Regional sustainable development impact through sustainable bridge optimization. Structures 2022, 41, 1061–1076. [Google Scholar] [CrossRef]
- Navarro, I.J.; Yepes, V.; Martí, J.V. Social life cycle assessment of concrete bridge decks exposed to aggressive environments. Environ. Impact Assess. Rev. 2018, 72, 50–63. [Google Scholar] [CrossRef]
- Navarro, I.J.; Yepes, V.; Martí, J.V.; González-Vidosa, F. Life cycle impact assessment of corrosion preventive designs applied to prestressed concrete bridge decks. J. Clean. Prod. 2018, 196, 698–713. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; García-Segura, T.; Yepes, V. Accelerated optimization method for low-embodied energy concrete box-girder bridge design. Eng. Struct. 2019, 179, 556–565. [Google Scholar] [CrossRef]
- Zhou, Z.-W.; Alcalá, J.; Kripka, M.; Yepes, V. Life Cycle Assessment of Bridges Using Bayesian Networks and Fuzzy Mathematics. Appl. Sci. 2021, 11, 4916. [Google Scholar] [CrossRef]
- Macek, D.; Snížek, V. Innovation in Bridge Life-cycle Cost Assessment. Procedia Eng. 2017, 196, 441–446. [Google Scholar] [CrossRef]
- Murphy, K. The social pillar of SD: A literature review and framework for policy analysis. Sustain. Sci. Pract. Policy 2012, 8, 15–29. [Google Scholar] [CrossRef]
- Liu, H.; Huang, J.; Zhang, W. Numerical algorithm based on extended barycentric Lagrange interpolant for two dimensional integro-differential equations. Appl. Math. Comput. 2021, 396, 125931. [Google Scholar] [CrossRef]
- Celik, E.; Olson, E.; Titi, E.S. Spectral Filtering of Interpolant Observables for a Discrete-in-Time Downscaling Data Assimilation Algorithm. SIAM J. Appl. Dyn. Syst. 2019, 18, 1118–1142. [Google Scholar] [CrossRef]
- Tari, A.; Shahmorad, S. Differential transform method for the system of two-dimensional nonlinear Volterra integro-differential equations. Comput. Math. Appl. 2011, 61, 2621–2629. [Google Scholar] [CrossRef][Green Version]
- Pons, J.J.; Penadés-Plà, V.; Yepes, V.; Martí, J.V. Life cycle assessment of earth-retaining walls: An environmental comparison. J. Clean. Prod. 2018, 192, 411–420. [Google Scholar] [CrossRef]
- Wang, Z.; Geng, L. Carbon emissions calculation from municipal solid waste and the influencing factors analysis in China. J. Clean. Prod. 2015, 104, 177–184. [Google Scholar] [CrossRef]
- Wang, R.; Feng, W.; Wang, L.; Lu, S. A comprehensive evaluation of zero energy buildings in cold regions: Actual performance and key technologies of cases from China, the US, and the European Union. Energy 2021, 215, 118992. [Google Scholar] [CrossRef]
- Yadollahi, M.; Nazari, R.; Spanos, N.J.; Minner, N. An application of fuzzy factor analysis for sustainable bridge maintenance and retrofit projects. Int. J. Manag. Sci. Eng. Manag. 2017, 12, 225–236. [Google Scholar] [CrossRef]
- China, National Development and Reform Commission. Notice on Further Liberalizing the Price of Professional Services for Construction Projects (Fagai Price [2015] No.299). National Development and Reform Commission of China 1. 2015. Available online: https://www.ndrc.gov.cn/xxgk/zcfb/tz/202009/t20200927_1239632.html (accessed on 16 September 2022).
- China, National Development and Reform Commission. Notice of the State Planning Commission of China and the Ministry of Construction on Issuing the Regulations on the Management of Engineering Survey and Design Fees.National Development and Reform Commission of China 1. 2002. Available online: https://services.ndrc.gov.cn/ecdomain/portal/portlets/bjweb/newpage/answerconsult/interactivepage.jsp?itemcode=&idseq=c244918bca3c49fa97ff044f9bd39293&code=&state=123 (accessed on 13 September 2022).
- China, Ministry of Transport of the People’s Republic. Highway Engineering Budget Estimates, Quotas, Standards, and Reforms. Ministry of Transport of the People’s Republic of China 100. 2018. Available online: https://xxgk.mot.gov.cn/2020/jigou/glj/202103/t20210331_3547339.html (accessed on 25 September 2022).
- Marti-Vargas, J.R.; Ferri, F.J.; Yepes, V. Prediction of the transfer length of prestressing strands with neural networks. Comput. Concr. 2013, 12, 187–209. [Google Scholar] [CrossRef]
- Zhou, N.; Khanna, N.; Feng, W.; Ke, J.; Levine, M. Scenarios of energy efficiency and CO2 emissions reduction potential in the buildings sector in China to year 2050. Nat. Energy. 2018, 3, 978–984. [Google Scholar] [CrossRef]
- Hao, Y.; Wang, Y.; Wu, Q.; Sun, S.; Wang, W.; Cui, M. What affects residents’ participation in the circular economy for SD? Evidence from China. Sustain. Dev. 2020, 28, 1251–1268. [Google Scholar] [CrossRef]
- Shaker, A.; Abouelatta, M.; Sayah, G.T.; Zekry, A. Comprehensive physically based modelling and simulation of power diodes with parameter extraction using MATLAB. IET Power Electron. 2014, 7, 2464–2471. [Google Scholar] [CrossRef]
- Yanbin, C.; Wei, L. China’s Economic Growth and High_Quality Development: 2020–2035. China Econ. 2021, 16, 1–17. [Google Scholar] [CrossRef]
- Hu, A.; Yan, Y.; Tang, X.; Liu, S. 2050 China: Strategic Goals and Two Stages. In 2050 China. Understanding Xi Jinping’s Governance; Springer: Singapore, 2021; pp. 45–60. [Google Scholar] [CrossRef]
- Liu, J.; Diamond, J. China’s environment in a globalizing world. Nature 2005, 435, 1179–1186. [Google Scholar] [CrossRef] [PubMed]
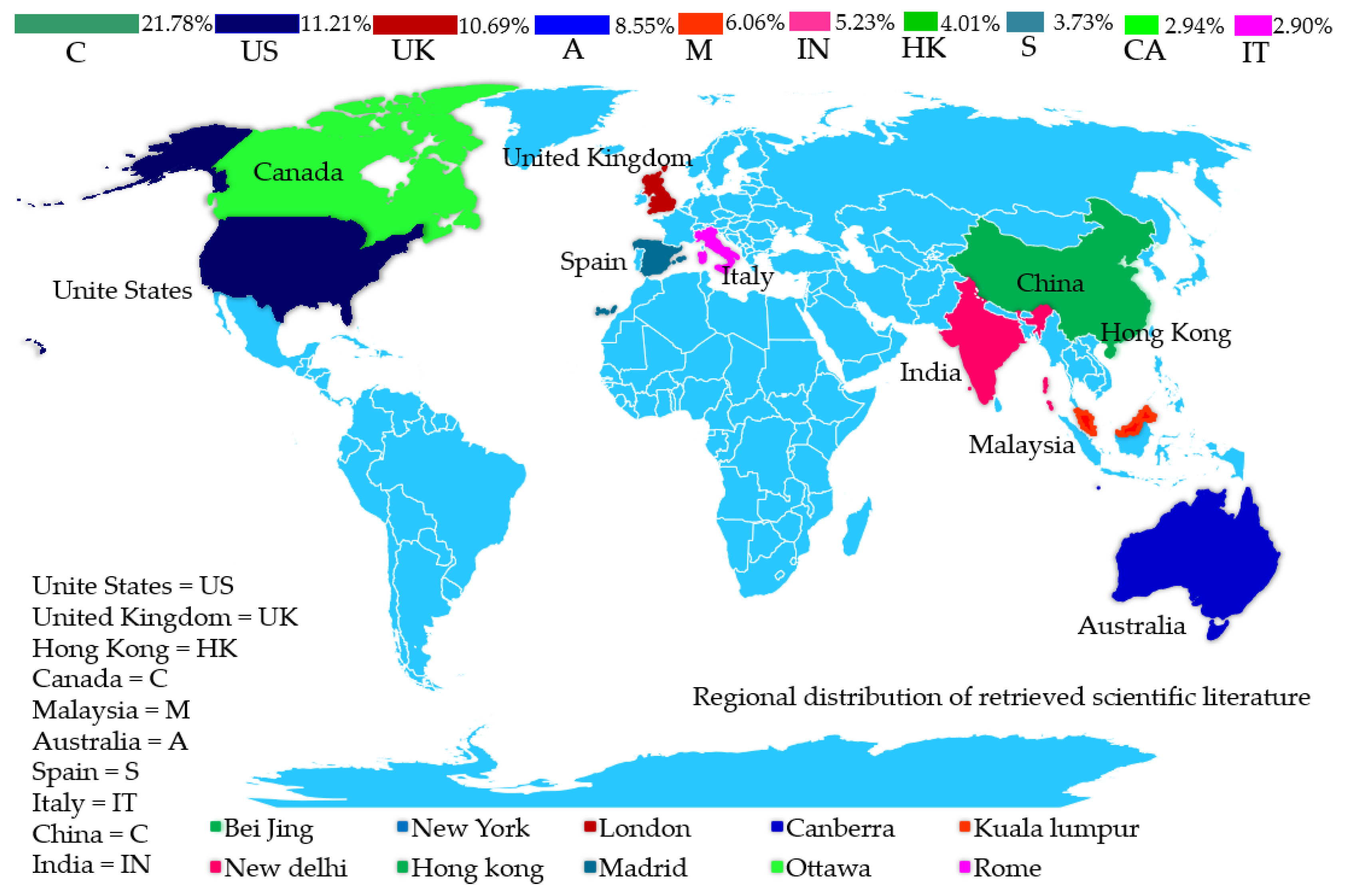



| Keyword | Negative Emissions Articles | |||||
| China | United States | United Kingdom | Australia | Malaysia | Scope | |
| Number | 2604 | 1340 | 1278 | 1023 | 725 | ⁄ |
| Time span | 1995–2022 | 1993–2022 | 1993–2022 | 1995–2022 | 1997–2021 | ⁄ |
| Number of nodes | 846 | 790 | 795 | 693 | 519 | ⁄ |
| Number of connections | 3372 | 3470 | 3445 | 2774 | 2004 | ⁄ |
| Large co-citation | 805 | 752 | 739 | 646 | 481 | ⁄ |
| Modularity: | 0.557,1 | 0.548,3 | 0.553,7 | 0.564,5 | 0.613,7 | 0.3 < |
| Silhouette: | 0.756,7 | 0.789,1 | 0.789,9 | 0.793,1 | 0.816,1 | 0.5 < < 1 |
| Harmonic mean: , | 0.641,7 | 0.647 | 0.651 | 0.659,6 | 0.700,6 | , = 0.5 |
| Keyword | Negative Emissions Articles | |||||
| India | Hong Kong | Spain | Canada | Italy | Scope | |
| Number | 626 | 480 | 446 | 352 | 347 | ⁄ |
| Time span | 1995–2021 | 2000–2022 | 2004–2021 | 1996–2021 | 1997–2021 | ⁄ |
| Number of nodes | 571 | 614 | 496 | 584 | 515 | ⁄ |
| Number of connections | 2132 | 2579 | 2042 | 2242 | 2042 | ⁄ |
| Large co-citation | 518 | 552 | 460 | 534 | 480 | ⁄ |
| Modularity: | 0.610,1 | 0.583,1 | 0.590,2 | 0.636 | 0.636,3 | |
| Silhouette: | 0.827,6 | 0.812 | 0.826,1 | 0.840,5 | 0.839,9 | < 1 |
| Harmonic mean: , | 0.702,4 | 0.678,8 | 0.688,5 | 0.724,1 | 0.724 | , = 0.5 |
| Province | Population (Ten Thousands) | GDP (100 million USD) | Consumption of Energy (10,000 t of SCE) | Gross Output Value of Construction Enterprises (100 million USD) |
|---|---|---|---|---|
| Guang Dong | 12,601.251 | 16,059.99 | 31,122.99 | 2411.79 |
| Jiang Su | 8474.802 | 14,893.93 | 32,525.97 | 4799.92 |
| Shan Dong | 10,152.745 | 10,603.48 | 40,810.54 | 2167.31 |
| Zhe Jiang | 6456.759 | 9368.68 | 22,392.77 | 1874.04 |
| He Nan | 9936.552 | 7974.40 | 22,300.00 | 1841.70 |
| Si Chuan | 8367.487 | 7046.674 | 16,382.20 | 2550.86 |
| Fu Jian | 4154.009 | 6365.93 | 13,718.31 | 1908.80 |
| Hu Bei | 5775.256 | 6058.19 | 15,019.74 | 2461.99 |
| China’s total | 141,177.872 | 147,314.80 | 487,000.00 | 36,023.86 |
| Ratio | 46.69% | 53.20% | 39.89% | 55.56% |
| Provinces | Guang Dong | Jiang Su | Shan Dong | Zhe Jiang | |
| Design name | Zhanjiang Hai Wan Bridge (ZWGB) | Xia Jia, He Bridge (XJHB) | Lou Lan Bridge (LLB) | Rui ’An Bridge (RAB) | |
| Bridge type | Main bridge | 60 + 120 + 480 + 120 + 60 m (Double pylon) | 68.358m (Single pylon) | 20 + 232 + 32 + 20 m (Single pylon) | 240 + 170 + 60 m (Single pylon) |
| Approach bridge | 9×50 + 9×50; 8×50 + 8×50m | 4×20 + 3×20m | / | 33×30 + 5×50 m; 8×30 + 20×50 m | |
| Bridge deck width | 28.5; 25.5 m | 30 m | 7 m | 36.8 m (Main beam);33 m | |
| Stay Cable | Φj 15.24 high-strength steel wires; ultimate tensile strength of 1860 Mpa. | 163Ø7 parallel steel wires, ultimate tensile strength of 1670 Mpa. | OVM200 grade steel stranded cable, the standard strength is 1860 Mpa | Adopt the diameter Ø7 polyethylene parallel steel wire rope | |
| Bridge structure | Main bridge | The main bridge is a pre-stressed concrete box girder with a beam height of 3 m. The thickness of the top plate and the inner web of the section is 0.25 m, and the thickness of the bottom plate is 0.22 m. | Pre-stressed concrete box girder: The cross-bridge of the box girder adopts a single-box double-chamber section, and the beam height is 2.0 m. The thickness of the top plate of the box girder is 25 cm; the thickness of the bottom plate is 20 cm; the thickness of the side web is 60 cm. | The main beam is 1.0 m high, the side web is 80 cm thick, the middle web is 30 cm thick, the top plate is 20 cm thick, and the bottom plate is 20 cm thick. | The main beam section is 3.2 m high; the top plate is 0.28 m thick, the bottom plate is 0.4 m thick, and the web is 0.4 m thick. |
| Approach bridge | The beam is a continuous box girder with a beam height of 2.6 m, a top plate width of 12.74 m, and a bottom plate width of 5.56 m; the top plate is 25 cm thick; the bottom plate is 25 cm thick, and the web thickness is 40 cm. | 20 m concrete simple beam; Each hole has 28 pre-stressed concrete hollow slab beams with a beam height of 0.9 m. | / | 30 m box girder is 1.8 m high; the top plate thickness is 0.25 m, the bottom plate thickness is 0.2 m; web thickness is 0.6 m; 50 m box girder is 2.8 m high, the top plate thickness is 0.25 m, the bottom plate thickness is 0.5 m, web thickness is 0.75–0.50 m. | |
| Substructure | Abutment; Pier column; Solid pier; Pier column | Abutment; Pier column; Solid pier; Pier column | Solid pier; Abutment; Pile foundation | Solid pier; Abutment; Pile foundation | |
| Construction period | 30/07/2003–30/12/2006 | 10/07/2017–29/06/2019 | 21/05/2011–11/06/2012 | 30/06/2003–13/01/2009 | |
| Estimated cost | 0.174 billion USD | 5.617 million USD | / | / | |
| Bridge function | Cross-sea highway bridge | Cross-river highway bridge | Highway bridge | Highway bridge across the Yangtze River | |
| Provinces | He Nan | Si Chuan | Fu Jian | Hu Bei | |
| Design name | Xiantao Han River Highway Bridge(XTHB) | Peng Xi, He Bridge(PXHB) | Lu Yang Sea-crossing Bridge (LSCB) | E-Huang Yangtze River Bridge (EHYB) | |
| Bridge type | Main bridge | 2 × 50 + 50 + 82 + 180 + 2 × 50 m (Single pylon) | 158 + 316 + 158 m (Double pylon) | 80 + 103 + 380 + 103 + 80 m (Double pylon) | 55 + 200 + 480 + 200 + 55 m (Double pylon) |
| Approach bridge | 14×30 m;18×30 m | 8×40 m; 40 m | 80 + 140 + 140 + 80 m; 44×80 m; 290×70 m; 88×35 m | 300 + 1380 m | |
| Bridge deck width | 23 m/1472 m | 24.5 m/1001 m | 28 m/28136 m | 24.5 m/2670 m | |
| Stay Cable | Use diameter φj15.24PE galvanized steel strand | Ø7 Galvanized high-strength steel wire, standard strength 1670 Mpa. | The stay cable is cold cast anchored parallel steel wire lashing cable, the maximum specification is 211-φ7. | The stay cable adoptsΦ7 low-relaxation high-strength parallel galvanized steel wire, the standard strength of the steel wire is 1670 Mpa | |
| Bridge structure | Main bridge | The roof thickness of the main beam is 0.30 m, and the beam height is 1.9 m | The beam height is 3.0 m, the roof thickness is 0.25m and the web thickness is 0.25–0.35 m. | The main girder is a single-box three-chamber box girder with a girder height of 3.8 m, a bridge deck width of 28.0 m, and a precast standard section length of 3.0 m. | The beam height is 2.4–4.9 m, and the bridge deck is 32 cm thick. The standard spacing of beams is 8 m. |
| Approach bridge | 30 m simply supported T-beam, 10 beams are arranged in the full width of the bridge and the beam distance is 2.30 m | Pre-stressed concrete main beam. | The main girder is a single-box single-chamber box girder; the girder height ranges from 8.0 to 4.0 m, the standard section length is 4.0~5.0 m, and the top section beam weight is 170 t. | The deputy main bridge is 300 m long, and the approach bridge is 1380 m long. | |
| Substructure | Solid pier; Abutment; Pile foundation | Solid pier; Abutment; Pile foundation | Solid pier; Abutment; Pile foundation | Solid pier; Abutment; Pile foundation | |
| Construction period | 30/06/2003–13/01/2010 | 20/03/2004–26/05/2008 | 01/07/2002–30/06/2005 | 01/07/2002–30/06/2006 | |
| Estimated cost | 0.435 billion USD | / | / | 1.032 billion USD | |
| Bridge function | Highway bridge across the Yangtze River | Cross-river highway bridge | Cross-sea highway bridge | Highway bridge across the Yangtze River | |
| Number | Name | Calculation Method | ZGWB | XJHB | LLB | RAB |
| 1 | Labor Costs | Quota × working days | 234,732.35 | 55,869.94 | 36,450.74 | 258,875.16 |
| 2 | Direct Costs | Labor + Material + Mechanical | 4,849,841.56 | 354,264.47 | 129,557.64 | 3,177,976.78 |
| 3 | Equipment Purchase Costs | 1.899%×1 | 92,098.49 | 6727.48 | 2460.30 | 60,349.78 |
| 4 | Measures Costs | 4.381%×1 | 10,283.62 | 2447.66 | 1596.91 | 11,341.32 |
| 5 | Enterprise management fees | 4.143%×2 | 200,928.94 | 14,677.18 | 5367.57 | 131,663.58 |
| 6 | Regulation fees | 30.65%×1 | 71,945.47 | 17,124.14 | 11,172.15 | 79,345.24 |
| 7 | Profits | 7.42%×5 | 14,908.93 | 1089.05 | 398.27 | 9769.44 |
| 8 | Taxes | 10%×(2+…+7) | 524,000.70 | 39,633.00 | 15,055.28 | 347,044.61 |
| 9 | Special expenses | Standard+1.5%×(2+…+7) | 217,341.42 | 39,006.96 | 58,309.40 | 188,143.67 |
| 10 | Compensation fees for land use and demolition | 0.063,81×(2+…+9) | 381,669.89 | 30,307.83 | 14,288.18 | 255,599.53 |
| 11 | Other costs of engineering construction | 3.14%×2 | 152,285.02 | 11,123.90 | 4068.11 | 99,788.47 |
| 12 | Preparation cost | 3%×2 | 145,495.25 | 10,627.93 | 3886.73 | 95,339.30 |
| 13 | Loan interest during construction period | 6.1%×(2+…+12) | 406,308.76 | 32,148.81 | 15,015.79 | 271,838.06 |
| 14 | The basic cost of the project | (1+…+13) | 7,067,108.04 | 559,178.41 | 261,176.34 | 4,728,199.78 |
| Number | Name | Calculation method | XTHB | PXHB | LSCB | EHYB |
| 1 | Labor Costs | Quota × working days | 100,472.64 | 231,917.81 | 159,123.81 | 162,438.89 |
| 2 | Direct Costs | Labor + Material + Mechanical | 970,347.71 | 4,493,336.02 | 7,453,183.18 | 1,523,020.37 |
| 3 | Equipment Purchase Costs | 1.899%×1 | 18,426.90 | 85,328.45 | 141,535.95 | 28,922.16 |
| 4 | Measures Costs | 4.381%×1 | 4401.71 | 10,160.32 | 6971.21 | 7116.45 |
| 5 | Enterprise management fees | 4.143%×2 | 40,201.51 | 186,158.91 | 308,785.38 | 63,098.73 |
| 6 | Regulation fees | 30.65%×1 | 30,794.86 | 71,082.81 | 48,771.45 | 49,787.52 |
| 7 | Profits | 7.42%×5 | 2982.95 | 13,812.99 | 22,911.88 | 4681.93 |
| 8 | Taxes | 10% × (2+…+7) | 106,715.56 | 485,987.95 | 798,215.90 | 167,662.72 |
| 9 | Special expenses | Standard+1.5%×(2+…+7) | 50,075.58 | 211,069.32 | 333,816.57 | 83,489.63 |
| 10 | Compensation fees for land use and demolition | 0.06381×(2+…+9) | 78,100.04 | 354,588.13 | 581,576.56 | 123,011.61 |
| 11 | Other costs of engineering construction | 3.14%×2 | 30,468.92 | 141,090.75 | 234,029.95 | 47,822.84 |
| 12 | Preparation cost | 3%×2 | 29,110.43 | 134,800.08 | 223,595.49 | 45,690.61 |
| 13 | Loan interest during construction period | 6.1% × (2+…+12) | 83,059.20 | 377,432.36 | 619,357.00 | 130,802.58 |
| 14 | The basic cost of the project | (1+…+13) | 1,444,685.38 | 6,564,848.10 | 10,772,750.52 | 2,275,107.14 |
| Stage | Unit | ZWGB | XJHB | LLB | RAB | XTHB | PXHB | LSCB | EHYB |
| Survey | USD | 3873.16 | 8655.88 | 8014.70 | 21,671.23 | 23,607.81 | 46,048.11 | 34,397.32 | 45,647.92 |
| Design | Million USD | 1.00 | 0.17 | 0.14 | 0.98 | 0.32 | 1.18 | 1.97 | 0.45 |
| Material and construction | Million USD | 48.74 | 3.86 | 1.80 | 32.61 | 9.96 | 45.28 | 74.30 | 15.69 |
| Maintenance | USD | 14,621.49 | 4135.31 | 11,488.10 | 65,448.69 | 106,946.80 | 95,341.25 | 138,511.17 | 21,827.83 |
| Total | Million USD | 49.80 | 4.04 | 1.96 | 33.68 | 10.41 | 46.60 | 76.44 | 16.20 |
| Name | Unit (LCC: USD) | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
| ZWGB | LCC (100 trillion) | 6875.88 | 8415.92 | 9518.13 | 11,494.09 | 12,238.16 | 13,027.77 |
| LCA (Million t) | 455.33 | 835.24 | 1208.49 | 2128.74 | 2569.68 | 3100.06 | |
| SIA (100 t) | 7759.14 | 14,232.97 | 20,593.44 | 36,275.01 | 43,788.89 | 52,826.99 | |
| XJHB | LCC (100 trillion) | 1798.82 | 2192.75 | 2671.36 | 3188.60 | 3565.90 | 3593.87 |
| LCA (Million t) | 180.95 | 327.79 | 592.75 | 1008.10 | 1410.02 | 1443.46 | |
| SIA (Million t) | 4775.69 | 8651.50 | 15,644.43 | 26,606.94 | 37,214.87 | 38,097.47 | |
| LLB | LCC (100 trillion) | 796.77 | 942.73 | 1044.51 | 1208.22 | 1350.42 | 1360.32 |
| LCA (Million t) | 125.39 | 207.71 | 282.53 | 437.32 | 610.65 | 624.18 | |
| SIA (Million t) | 4555.49 | 7546.44 | 10,264.93 | 15,888.45 | 22,186.04 | 22,677.44 | |
| RAB | LCC (100 trillion) | 1770.54 | 2199.86 | 2560.07 | 2995.46 | 3359.71 | 3558.43 |
| LCA (Million t) | 311.35 | 597.81 | 942.73 | 1510.98 | 2132.65 | 2534.29 | |
| SIA (Million t) | 837,902.23 | 1,608,830.25 | 2,537,091.09 | 4,066,355.16 | 5,739,392.57 | 6,820,289.57 | |
| XTHB | LCC (100 trillion) | 638.08 | 765.49 | 871.30 | 1015.44 | 1147.20 | 1166.88 |
| LCA (Million t) | 270.49 | 467.39 | 689.54 | 1092.02 | 1575.15 | 1657.70 | |
| SIA (Million t) | 72,538.32 | 125,342.43 | 184,916.69 | 292,849.78 | 422,412.80 | 444,551.34 | |
| PXHB | LCC (100 trillion) | 609.11 | 769.34 | 912.42 | 1055.20 | 1181.51 | 1282.87 |
| LCA (Million t) | 138.60 | 280.52 | 469.19 | 727.13 | 1022.10 | 1309.52 | |
| SIA (Million t) | 203,989.55 | 412,869.14 | 690,557.88 | 1,070,205.49 | 1,504,344.50 | 1,927,369.94 | |
| LSCB | LCC (100 trillion) | 333.16 | 487.35 | 641.55 | 791.94 | 969.92 | 1102.82 |
| LCA (Million t) | 257.64 | 823.31 | 1898.22 | 3593.38 | 6634.27 | 9778.27 | |
| SIA (Million t) | 10,026.31 | 32,040.12 | 73,872.36 | 139,843.51 | 258,186.95 | 380,543.53 | |
| EHYB | LCC (100 trillion) | 629.92 | 810.02 | 1020.87 | 1227.47 | 1458.61 | 1535.77 |
| LCA (Million t) | 137.38 | 292.57 | 586.36 | 1020.02 | 1712.56 | 1999.27 | |
| SIA (Million t) | 441.67 | 940.63 | 1885.19 | 3279.45 | 5506.06 | 6427.86 | |
| Name | Unit | 2016 | 2017 | 2018 | 2019 | 2020 | Total |
| ZWGB | LCC (100 t) | 14,216.94 | 16,778.07 | 20,588.82 | 24,117.93 | 26,722.69 | 163,846.48 |
| LCA (t) | 4029.20 | 6623.55 | 12,241.26 | 19,678.63 | 26,769.49 | 79,600.00 | |
| SIA (100 t) | 686.60 | 1128.69 | 2085.99 | 3353.36 | 4561.69 | 13,600.00 | |
| XJHB | LCC (100 trillion) | 3739.73 | 4053.64 | 4488.33 | 4799.93 | 5111.37 | 39,149.16 |
| LCA (Million t) | 1626.47 | 2071.43 | 2811.92 | 3439.20 | 14.67 | 14,900.00 | |
| SIA (Million t) | 42,927.44 | 54,671.42 | 74,215.26 | 90,771.21 | 0.025,96 | 394,000.00 | |
| LLB | LCC (100 trillion) | 1462.64 | 1664.25 | 1870.21 | 2069.00 | 2167.31 | 15,949.66 |
| LCA (Million t) | 775.91 | 1143.07 | 1622.23 | 2196.53 | 2524.78 | 10,600.00 | |
| SIA (Million t) | 28,190.39 | 41,529.98 | 58,938.78 | 79,804.17 | 91,730.08 | 383,000.00 | |
| RAB | LCC (100 trillion) | 3719.74 | 4059.79 | 1621.50 | 1874.04 | 1999.57 | 29,724.36 |
| LCA (Million t) | 2895.13 | 3764.74 | 239.04 | 369.31 | 448.74 | 15,700.00 | |
| SIA (Million t) | 7791,383.06 | 10,131,678.32 | 643,300.61 | 993,890.86 | 1,207,658.66 | 42,400,000.00 | |
| XTHB | LCC (100 trillion) | 1277.13 | 1462.52 | 1647.24 | 1841.70 | 1902.73 | 13,731.21 |
| LCA (Million t) | 2173.81 | 3265.48 | 4666.66 | 6523.41 | 7193.95 | 29,600.00 | |
| SIA (Million t) | 582,958.11 | 875,714.32 | 1,251,471.15 | 1,749,401.95 | 1,929,223.38 | 7,930,000.00 | |
| PXHB | LCC (100 trillion) | 1456.37 | 1739.42 | 1994.03 | 2550.86 | 3171.09 | 16,674.64 |
| LCA (Million t) | 1918.24 | 3272.87 | 4935.50 | 10,347.04 | 19,898.16 | 44,300.00 | |
| SIA (Million t) | 2,823,300.36 | 4,817,061.09 | 7,264,148.23 | 15,228,927.13 | 29,286,397.54 | 65,200,000.00 | |
| LSCB | LCC (100 trillion) | 1237.03 | 1449.05 | 1503.16 | 1662.53 | 2047.03 | 12,223.24 |
| LCA (Million t) | 13,829.58 | 22,284.98 | 24,888.92 | 33,720.83 | 63,097.50 | 181,000.00 | |
| SIA (Million t) | 538,211.08 | 867,275.20 | 968,614.39 | 1,312,332.01 | 2,455,606.32 | 7,040,000.00 | |
| EHYB | LCC (100 trillion) | 1720.01 | 1941.69 | 2194.36 | 2461.99 | 2339.68 | 17,399.63 |
| LCA (Million t) | 2809.50 | 4042.98 | 5837.23 | 824,597.23 | 707,633.22 | 33,800.00 | |
| SIA (Million t) | 9032.84 | 12,998.69 | 18,767.47 | 26,511.95 | 22,751.37 | 109,000.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Alcalá, J.; Yepes, V. Research on Sustainable Development of the Regional Construction Industry Based on Entropy Theory. Sustainability 2022, 14, 16645. https://doi.org/10.3390/su142416645
Zhou Z, Alcalá J, Yepes V. Research on Sustainable Development of the Regional Construction Industry Based on Entropy Theory. Sustainability. 2022; 14(24):16645. https://doi.org/10.3390/su142416645
Chicago/Turabian StyleZhou, Zhiwu, Julián Alcalá, and Víctor Yepes. 2022. "Research on Sustainable Development of the Regional Construction Industry Based on Entropy Theory" Sustainability 14, no. 24: 16645. https://doi.org/10.3390/su142416645
APA StyleZhou, Z., Alcalá, J., & Yepes, V. (2022). Research on Sustainable Development of the Regional Construction Industry Based on Entropy Theory. Sustainability, 14(24), 16645. https://doi.org/10.3390/su142416645








