A Demand Response Transaction Method for Integrated Energy Systems with a Trigonometric Membership Function-Based Uncertainty Model of Costumers’ Responsive Behaviors

Abstract

As an important regulation tool for power systems, demand response can greatly improve system flexibility and economy. However, when an integrated energy system with a large number of flexible loads is aggregated for a demand response transaction, the uncertainty in the amount of the load response should be considered. Therefore, a demand response transaction model for an integrated energy system that considers the uncertainty of customer demand responses is proposed in this paper. We first analyze the uncertainty of incentive-based demand responses. Next, we investigate the relationship between the incentive level and the fluctuation of customer response volume. The flexible loads are classified into curtailable loads, translatable loads, and replaceable loads. Fuzzy variables are then used to represent the response volume of users, and a trigonometric membership function is used to represent the degree of uncertainty in the response volume of different flexible loads. Finally, the objective functions and chance constraints containing fuzzy variables are converted into explicit equivalence classes for solving. In the case study, the impact of the uncertainty of the user response volume on the revenue of each transaction entity and the impact of the fuzzy chance constraint confidence level on the response revenue are investigated. The results show that the revenue of each transaction entity decreases to a certain extent under the consideration of the uncertainty of the user response volume; the social welfare of the whole transaction increases as the confidence level of the chance constraint changes from high to low.

1. Introduction

The development of an integrated energy system (IES) should consider safety, economy, and cleanliness. The IES integrates various energy resources such as natural gas and photovoltaic power in the region, and meets the multiple energy requirements of users [1,2]. Thus the IES is becoming a hot spot for research in the energy field [3,4].

With the development of the IES, technological advances in demand response (DR) have become a key solution to achieve this energy transition. DR can effectively increase the active participation of consumers in the IES [5]. Flexible loads in IESs have a strong DR capability. Flexible loads on the customer side can adjust their electricity consumption behavior according to the price-based DR mechanism [6,7] and the incentive-based DR mechanism [8], relieving the electricity supply tensions of the IES. Based on multiple types of low-carbon factors and price-based DR mechanisms, Ma et al. [9] constructed an energy efficiency improvement scheduling model with abandoned wind penalty costs, power purchase costs, equipment operation and maintenance costs, and carbon transaction costs as optimization targets, thus improving the comprehensive energy efficiency of the IES. Yang et al. [10] proposed the rolling optimization planning framework and model of IES considering CAES and sliding time window-based electric and heating integrated demand response (IDR), thus improving the economy and flexibility of the IES. Based on the DR potential and consumers’ consumption characteristics, as well as the coupling characteristics of the energy flows in the regionally integrated energy system (RIES), Hu et al. [11] established an RIES optimization model that considers the DR of cooling, heating and electricity consumption of flexible loads. With these researches a synergistic optimization of the supply side and the user side is achieved.

Incentive-based DR strategies are a very effective way of involving flexible loads in the grid DR process [12]. Du et al. [13] provided an in-depth analysis of an incentive-based IDR in an IES model. A customer-side IDR service architecture based on electric heating multi-energy interconnection was designed. Wang et al. [14] designed an IDR scheme that accounted for different types of consumers. By designing a price-based mechanism that implements various prices for different consumers, the total cost of user participation in an IDR can be reduced. Jiang et al. [15] incorporated consumers’ heating and cooling demands into IDR scheduling, then proposed an IDR mechanism with three effective load-shedding incentive models. The incentive methods are used to increase heating and cooling loads and increase consumers’ motivation. However, in all the above incentive-based DR studies, the response volume of the flexible load during the transaction is default certain. Yet, for IESs that aggregate a large number of flexible loads, uncertainly exists in the response volume they provide to the grid because of the specificity of the way these IESs aggregates resources. There are also inherent uncertainties such as communication delays, coupled with the fact that the response capacity provided by the user is also highly subjective [16,17]. The response volume is susceptible to a variety of factors such as unexpected next-day conditions, subjective and objective negligence, and changes in consumption behavior [18].

Traditional methods usually transform a certain optimization model into a stochastic optimization model via adding random variables with a bounded interval or a certain probability distribution [19,20]. These methods are required to form the accurate probability distribution of every random variable, while there are numerous flexible loads participating in the DR and it is unfeasible to confirm their accurate probability. Thus, a robust-based optimization model is proposed to tackle this problem [21], yet the results solved by this model could be quite conservative along with the poor economy of the system. Considering both the characteristics of flexible loads and the economy of the system, we eventually utilize the fuzzy theory with trigonometric membership function. Trigonometric membership functions of uncertain parameters can be obtained by an expert system when a fuzzy number lacks historical information, so this method has a low dependence on historical data and provides a good description of uncertainty.

Based on the above problems, this paper focuses on the uncertainty of the excitation-type flexible load response and proposes a DR transaction model for the customers to actively interact with the IES. First, the uncertainty problem of the incentive-based DR method is studied. The relationship between the uncertainty level of user responses and the incentive level is discussed. Second, fuzzy variables are used to represent user responses, and the trigonometric membership fuzzy function is then used to construct the uncertainty model of flexible load responses. Finally, the transaction model containing fuzzy variables is transformed into a deterministic model for a solution.

The contributions of this paper are threefold:

(1) We introduce the analysis of DR uncertainty. Additionally, the DR load uncertainty models of curtailable load, translated load, and replaceable load are proposed.

(2) A DR transaction model is investigated. In this model, various types of flexible load response volume uncertainty are considered.

(3) We point out the relationship between the uncertainty level of user responses and the incentive level and utilize the trigonometric membership fuzzy function to construct the uncertainty model of flexible load response. Therefore, the transaction model containing fuzzy variables is transformed into a deterministic model for a solution.

The remainder of this paper is arranged as follows. Section 1 introduces the DR load uncertainty analysis and modeling. In Section 2, a DR transaction model that considers the uncertainty of flexible loads is given. Section 3 elaborates on the process of the model uncertainty. The case study is given in Section 4 to evaluate the impact of the uncertainty of the user response volume and the fuzzy chance constraints confidence level on the transaction results of transaction stakeholders. Conclusions are presented in Section 6.

2. Demand Response Load Uncertainty Analysis and Modeling

2.1. Analysis of Demand Response Uncertainty

For incentive-based DR, the system provides more response capacity to encourage flexible users. Generally, the more flexible the load response capacity, the higher the compensation per unit of capacity. Therefore, the relationship between the response provided by the load Δ$P_i^{DR}$ and the compensation per unit of capacity $C_{unit}^{com}$ is shown in Figure 1.

From the figure, it can be seen that when 0 ≤ $C_{unit}^{com}$ ≤ $C_{unit,p}^{com}$, the users are driven by the benefits of the system because the incentive level is too low; they refuse to participate in the DR of the system. When $C_{unit,p}^{com}$ ≤ $C_{unit}^{com}$ ≤ $C_{unit,e}^{com}$, the compensation is higher, and the users participate in the DR. As the incentive level continues to increase, customers participate in a greater capacity until $C_{unit}^{com}$ = $C_{unit,e}^{com}$, when they reach the maximum response. At $C_{unit}^{com}$ > $C_{unit,e}^{com}$, flexible customers no longer increase their response capacity because they must meet their basic electricity demands.

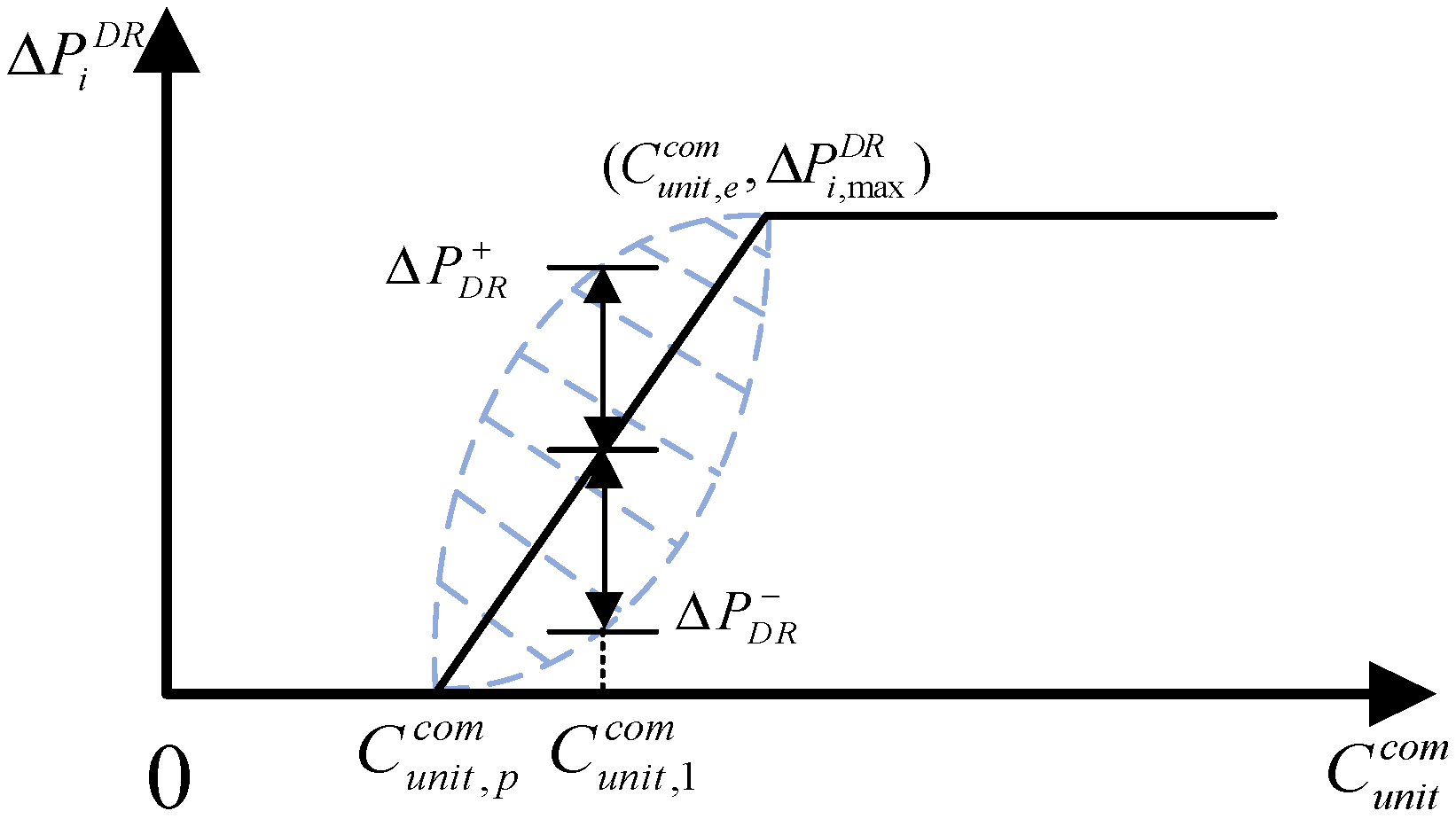
After considering the problem of user response uncertainty, the fluctuation range of the user load response volume will increase and then decrease as the excitation level increases. Thus, the DR characteristic curve considering uncertainty can be obtained, as shown in Figure 2.

As can be seen from the figure, the black diagonal line consists of the expected value of the system response to the user at each excitation level, while the two blue dashed lines indicate the upper and lower limits of the flexible user response error, respectively. The blue shaded region indicates the fluctuation range of the flexible user response volume. When $C_{unit,p}^{com}$ ≤ $C_{unit}^{com}$ ≤ $C_{unit,e}^{com}$, the fluctuation range of the user response increases and then decreases as the compensation per unit capacity increases, and the fluctuation range of the user response reaches the maximum when the compensation is $C_{unit,1}^{com}$. ${\Delta P}_{DR}^{+}$, ${\Delta P}_{DR}^{-}$ indicate the fluctuation range of the user response when the compensation per unit capacity is $C_{unit,1}^{com}$. When the excitation level is greater than $C_{unit,1}^{com}$, the error range of the response volume gradually decreases until the response volume provided by the user reaches the maximum value, and the response uncertainty is approximately negligible. Therefore, to make the response volume provided by the user meet the requirements of the system and to make the error range of the response volume as small as possible, the capacity compensation given by the system should be greater than $C_{unit,1}^{com}$.

The degree of uncertainty in user responses varies within a certain range with the level of incentive, i.e., the actual response volume from a flexible user is in error with the expected value of the system when the system provides a certain incentive cost. Thus, incentive-based DR, although bound by contract, has some uncertainty issues in practical situations.

2.2. Demand Response Load Uncertainty Modeling

The flexible resources that respond to the grid demand can be divided into two types: peak-staggered and peak-avoiding. The response characteristics of different types of flexible loads are generally different. Peak-avoiding flexible loads are mainly translatable loads, which can transfer part of the load from peak hours to low hours to reduce peak–valley differences; peak-avoiding flexible loads mainly include curtailable loads and replaceable loads, which respond to grid demand by reducing electricity consumption.

2.2.1. Curtailable Load

Due to the uncertainty of the actual response volumes of the flexible users aggregated by the virtual power plant (VPP), the response agreement between the grid and the VPP needs to specify a range of fluctuations in response volumes. The curtailable load responds to grid demand by cutting its electricity consumption, and its curtailment, as part of the system response to demand is uncertain; it is thus represented by a fuzzy parameter with trigonometric membership characteristics [22]. Using $\Delta {\tilde{P}}_i^{cu}(t)$ to denote the fuzzy form of the load response volume that can be cut, the compensation of curtailable load participation in DR is shown below:

$${\tilde{C}}_{cu}(t)={\displaystyle \sum _{i=1}^{n_{cu}}\Delta {\tilde{P}}_i^{cu}(t)C_{unit}^{cu}(t)}$$

(1)

$$\Delta {\tilde{P}}_i^{cu}(t)={\tilde{\epsilon }}_i^{cu}(t)P_{i,b}^{cu}(t)$$

(2)

where ${\tilde{C}}_{cu}(t)$ represents the fuzzy form of the curtailable load compensation cost; $C_{unit}^{cu}(t)$ represents the unit capacity compensation cost of the curtailable load; and $\Delta {\tilde{P}}_i^{cu}(t)$ denotes the fuzzy form of the load-curtailed volume.

A trigonometric membership function is used to express the degree of uncertainty of the load reduction, and the subordination parameter of the load reduction is shown in the following equation:

$$\Delta {\tilde{P}}_i^{cu}(t)=(\Delta P_{i,1}^{cu}(t),\Delta P_{i,2}^{cu}(t),\Delta P_{i,3}^{cu}(t))$$

(3)

$$\Delta P_{i,1}^{cu}(t)=r_1^{cu}\Delta P_{i,2}^{cu}(t)$$

(4)

$$\Delta P_{i,2}^{cu}(t)=\Delta P_i^{cu}(t)$$

(5)

$$\Delta P_{i,3}^{cu}(t)=r_3^{cu}\Delta P_{i,2}^{cu}(t)$$

(6)

where Δ$P_{i,1}^{cu}$(t), Δ$P_{i,2}^{cu}$(t), and Δ$P_{i,3}^{cu}$(t) represent the trigonometric membership parameters of the load reduction; $r_1^{cu}$ and $r_3^{cu}$ represent the maximum deviation coefficients of the load reduction and satisfy 0 < $r_1^{\mathit{cu}}$ < 1, $r_3^c$ > 1; and Δ$P_i^{cu}$(t) represents the planned value of the load reduction. The trigonometric membership function of the load reduction is shown in Figure 3.

2.2.2. Translatable Loads

Translatable loads include both shiftable loads and transferable loads. After considering the uncertainty of the response volumes, the fuzzy forms of the load response volumes are represented by $\Delta {\tilde{P}}_i^{trans}(t)$ and $\Delta {\tilde{P}}_i^{tran}(t)$, respectively. For shiftable loads, the compensation received for their participation in the DR is shown below:

$${\tilde{C}}_{trans}(t)={\displaystyle \sum _{i=1}^{n_{trans}}{C}_{unit,c}^{trans}(t)\Delta {\tilde{P}}_i^{trans}(t)}+{\displaystyle \sum _{i=1}^{n_{trans}}{\displaystyle \sum _{t_{af}^{st,i}\in {\vartheta }_{st}^{trans,i}}{\mu }_{t_{af}^{st,i}}^{trans,i}}{C}_{time}^{trans}\left|t_{af}^{st,i}-t_b^{st,i}\right|}$$

(7)

where ${\tilde{C}}_{trans}(t)$ represents the fuzzy form of the shiftable load compensation cost; $C_{unit,c}^{trans}(t)$ represents the unit capacity compensation cost of the shiftable load; ${\mu }_{t_{af}^{st,i}}^{trans,i}$ denotes the state of the shiftable load, and when ${\mu }_{t_{af}^{st,i}}^{trans,i}$ = 1, it means that the load is shifted to time period t; $\Delta {\tilde{P}}_i^{trans}(t)$ represents the fuzzy forms of the shiftable load response volume at t; and $C_{time}^{trans}$ represents the compensation cost in unit time.

The expression of the trigonometric membership function for the load response volume is shown in the following equation:

$$\Delta {\tilde{P}}_i^{trans}(t)=(\Delta P_{i,1}^{trans}(t),\Delta P_{i,2}^{trans}(t),\Delta P_{i,3}^{trans}(t))$$

(8)

$$\Delta P_{i,1}^{trans}(t)=r_1^{trans}\Delta P_{i,2}^{trans}(t)$$

(9)

$$\Delta P_{i,2}^{trans}(t)=\Delta P_i^{trans}(t)$$

(10)

$$\Delta P_{i,3}^{trans}(t)=r_3^{trans}\Delta P_{i,2}^{trans}(t)$$

(11)

where Δ$P_{i,1}^{trans}$(t), Δ$P_{i,2}^{trans}$(t), and Δ$P_{i,3}^{trans}$(t) represent the membership parameters of the shiftable load response volume; Δ$P_i^{trans}$(t) represents the shiftable load plan leveling load capacity; and $r_1^{trans}$ and $r_3^{trans}$ represent the maximum deviation coefficients of the load response volume.

In the case of transferable loads, the compensation received for their participation in the DR is shown below:

$${\tilde{C}}_{tran}(t)={\displaystyle \sum _{i=1}^{n_{tran}}[C_{time,n}^{tran}+C_{unit,c}^{tran}(t)\Delta {\tilde{P}}_i^{tran}(t)]}$$

(12)

where ${\tilde{C}}_{tran}(t)$ represents the fuzzy form of the transferable load compensation cost; $C_{time,n}^{tran}$ represents the rated time compensation of transferable load; $\Delta {\tilde{P}}_i^{tran}(t)$ represents the fuzzy forms of the transferable load response volume; and $C_{unit,c}^{tran}(t)$ denotes the unit capacity compensation cost of the transferable load.

The expression of the trigonometric membership for the transferable load transfer is shown in the following equation:

$$\Delta {\tilde{P}}_i^{tran}(t)=(\Delta P_{i,1}^{tran}(t),\Delta P_{i,2}^{tran}(t),\Delta P_{i,3}^{tran}(t))$$

(13)

$$\Delta P_{i,1}^{tran}(t)=r_1^{tran}\Delta P_{i,2}^{tran}(t)$$

(14)

$$\Delta P_{i,2}^{tran}(t)=\Delta P_i^{tran}(t)$$

(15)

$$\Delta P_{i,3}^{tran}(t)=r_3^{tran}\Delta P_{i,2}^{tran}(t)$$

(16)

where Δ$P_{i,1}^{tran}$(t), Δ$P_{i,2}^{tran}$(t), and Δ$P_{i,3}^{tran}$(t) represent the membership parameters of the transferable load transfer; Δ$P_i^{tran}$(t) represents the planned volume of the transferable load transfer; and $r_1^{tran}$ and $r_3^{tran}$ represent the maximum deviation coefficients of the load response.

2.2.3. Replaceable Load

The response volume of the replaceable load is the electrical energy substitution. Using $\Delta {\tilde{P}}_i^{re}(t)$ to represent the fuzzy form of the load replacement volume, the compensation of its participation in the DR is shown below:

$${\tilde{C}}_{re}(t)={\displaystyle \sum _{i=1}^{n_{re}}{C}_{unit}^{re}(t)\Delta {\tilde{P}}_i^{re}(t)}$$

(17)

where ${\tilde{C}}_{re}(t)$ denotes the fuzzy form of the replaceable load compensation cost; $C_{unit}^{re}(t)$ denotes the unit capacity compensation cost of the replaceable load; and $\Delta {\tilde{P}}_i^{re}(t)$ denotes the fuzzy form of the load replacement volume.

The expression of the trigonometric membership for $\Delta {\tilde{P}}_i^{re}(t)$ of the replaceable load is shown in the following equation:

$$\Delta {\tilde{P}}_i^{re}(t)=(\Delta P_{i,1}^{re}(t),\Delta P_{i,2}^{re}(t),\Delta P_{i,3}^{re}(t))$$

(18)

$$\Delta P_{i,1}^{re}(t)=r_1^{re}\Delta P_{i,2}^{re}(t)$$

(19)

$$\Delta P_{i,2}^{re}(t)=\Delta P_i^{re}(t)$$

(20)

$$\Delta P_{i,3}^{re}(t)=r_3^{re}\Delta P_{i,2}^{re}(t)$$

(21)

where $\Delta P_{i,1}^{re}(t)$, $\Delta P_{i,2}^{re}(t)$, and $\Delta P_{i,3}^{re}(t)$ represent the subordination parameters of the replaceable load response volume; and $r_1^{re}$ and $r_3^{re}$ represent the maximum deviation coefficients of the load response volume.

3. A Demand Response Transaction Model That Considers Uncertainty

3.1. Objective Function

This section constructs fuzzy expressions that consider various types of flexible load response volumes in a transactional model, as shown below.

The objective function of the grid operator‘s participation in a DR transaction is shown in Equation (22). This function consists mainly of the cost of the DR services purchased by the grid operator from the VPP, and the equivalent benefit to the grid of the increased stability and reliability of its own operations through DR.

$$\min {\tilde{C}}_{pg}(t)={\tilde{C}}_{vpp}^{dr}(t)-{\tilde{C}}_{eq}^{dr}(t)$$

(22)

where ${\tilde{C}}_{pg}(t)$ is a fuzzy expression for the transaction costs of the grid operator at time t; ${\tilde{C}}_{vpp}^{dr}(t)$ is a fuzzy expression for the response costs paid by the grid operator to the VPP operator at time t; and ${\tilde{C}}_{eq}^{dr}(t)$ represents a fuzzy expression for the equivalent benefits to the grid by DR at time t.

For the grid operator, the equivalence benefit is mainly expressed in the reduced investment of the grid standby capacity. A quadratic function is used to express the investment cost savings from a decrease in grid backup capacity, as shown in the following equation:

$${\tilde{C}}_{eq}^{dr}(t)=a_{pg}{\tilde{P}}_{dr}{(t)}^2+b_{pg}{\tilde{P}}_{dr}(t)$$

(23)

where a_pg and b_pg denote the economic constants associated with the grid operating state; and ${\tilde{P}}_{dr}(t)$ is the fuzzy form of the DR services volume purchased by the grid operator at t.

The response cost ${\tilde{C}}_{vpp}^{dr}(t)$ paid by the grid operator to the VPP operator is:

$${\tilde{C}}_{vpp}^{dr}(t)=\Delta {\tilde{P}}_i^{cu}(t)C_{price}^{cu}(t)+\Delta {\tilde{P}}_i^{tran}(t)C_{price}^{tran}(t)+\Delta {\tilde{P}}_i^{trans}(t)C_{price}^{trans}(t)+\Delta {\tilde{P}}_i^{re}(t)C_{price}^{re}(t)$$

(24)

where $C_{price}^{cu}(t)$, $C_{price}^{tran}(t)$, $C_{price}^{trans}(t)$ and $C_{price}^{re}(t)$ denote the unit capacity charges paid by the grid operator to the VPP for different types of flexible loads.

The objective function of the VPP’s participation in DR transaction is shown in Equation (25). This equation consists of two main terms, i.e., the cost of purchasing the DR services of the grid operator and the compensation cost provided to the flexible customers it aggregates. The compensation cost in Equation (26) represents compensation for the customers’ response capacity.

$$\min {\tilde{C}}_{vpp}(t)={\tilde{C}}_{com}^u(t)-{\tilde{C}}_{vpp}^{dr}(t)$$

(25)

$${\tilde{C}}_{com}^u(t)={\displaystyle \sum _{i=1}^{n_{cu}}{\tilde{C}}_{cu,i}(t)}+{\displaystyle \sum _{i=1}^{n_{tran}}{\tilde{C}}_{tran,i}(t)}+{\displaystyle \sum _{i=1}^{n_{trans}}{\tilde{C}}_{trans,i}(t)}+{\displaystyle \sum _{i=1}^{n_{re}}{\tilde{C}}_{re,i}(t)}$$

(26)

where ${\tilde{C}}_{vpp}(t)$ represents a fuzzy expression for the transaction cost of the VPP operator at time t; ${\tilde{C}}_{vpp}^{dr}(t)$ represents a fuzzy expression for the compensation cost provided by the VPP to the customer at time t; and ${\tilde{C}}_{com}^u(t)$ represents a fuzzy expression for the response capacity compensation provided by the VPP operator to the customer at time t.

3.2. Constraints

This section uses a fuzzy chance constraint to represent the constraint [23], allowing the established constraint to be unsatisfied to some extent. However, the confidence that the constraint holds should be no less than a predetermined confidence level.

Based on the above theory, the expressions for the load reserve constraint, the maximum customer response constraint, and the common constraint for different loads are shown below. The load reserve constraint indicates that the grid needs to allow sufficient standby capacity to solve the customers’ uncertain response problem and ensure stable system operation.

$$Cr\{{\displaystyle \sum _{i=1}^{n_{cu}}\Delta {\tilde{P}}_i^{cu}(t)+{\displaystyle \sum _{i=1}^{n_{tran}}\Delta {\tilde{P}}_i^{tran}(t)}}+{\displaystyle \sum _{i=1}^{n_{trans}}\Delta {\tilde{P}}_i^{trans}(t)}+{\displaystyle \sum _{i=1}^{n_{re}}\Delta {\tilde{P}}_i^{re}(t)}\ge (1-{\delta }_{dr})P_{\min }^{dr}(t)\}\ge {\beta }_1$$

(27)

$$Cr\{{\displaystyle \sum _{i=1}^{n_{cu}}\Delta {\tilde{P}}_i^{cu}(t)+{\displaystyle \sum _{i=1}^{n_{tran}}\Delta {\tilde{P}}_i^{tran}(t)}}+{\displaystyle \sum _{i=1}^{n_{trans}}\Delta {\tilde{P}}_i^{trans}(t)}+{\displaystyle \sum _{i=1}^{n_{re}}\Delta {\tilde{P}}_i^{re}(t)}\le P_{dr,\max }^{adlo}(t)\}\ge {\beta }_2$$

(28)

where Cr{} is the expression for the confidence level; δ_dr represents the standby capacity factor of the grid and satisfies δ_dr ∈ [0, 1], β₁ represents the confidence level that the system standby constraint holds; and β₂ represents the confidence level that the maximum user response volume constraint holds. The confidence levels that should be satisfied for multiple fuzzy chance constraints are generally considered to be the same.

For curtailable loads, the following constraints shall be met:

$${\epsilon }_{i,\min }^{cu}(t)\le {\epsilon }_i^{cu}(t)\le {\epsilon }_{i,\max }^{cu}(t)$$

(29)

$${\displaystyle \sum _{t=1}^T{\mu }_i^{cu}(t)\le }{N}_{c,i}^{\max }$$

(30)

$${\displaystyle \sum _t^{t+t_{\min }^{cu}-1}{\mu }_i^{cu}(t)\ge t_{\min }^{cu}({\mu }_i^{cu}(t)-{\mu }_i^{cu}(t-1))}$$

(31)

$${\displaystyle \sum _t^{t+t_{\max }^{cu}}(1-{\mu }_i^{cu}(t))}\ge 1$$

(32)

$$\left|\Delta P_i^{cu}(t)-\Delta P_i^{cu}(t-1)\right|\le v_{\max }^l$$

(33)

where ${\epsilon }_{i,\min }^{cu}$(t) represents the minimum cut rate of the curtailable load; $t_{\min }^{cu}$ represents the minimum continuous cut response time; $t_{\max }^{cu}$ represents the maximum continuous cut response time; $N_{c,i}^{\max }$ represents the maximum time of load cuts allowed in a dispatch cycle; $v_{\max }^l$ represents the maximum load cut rate allowed by the curtailable load; and T represents the entire response time. Equation (29) limits the response volume of the curtailable load. Equation (30) limits the maximum number of participants in the DR. Equations (31) and (32) represent continuous load response constraints, and Equation (33) is the load response speed constraint.

For translatable loads, the following constraints shall be met:

$${\lambda }_{i,\min }^{tran}(t)\le {\lambda }_i^{tran}(t)\le {\lambda }_{i,\max }^{tran}(t)$$

(34)

$${\displaystyle \sum _t^{t+T_{\min ,du}^{tran,i}}{\mu }_i^{tran}(t)\ge T_{\min ,du}^{tran,i}}({\mu }_i^{tran}(t)-{\mu }_i^{tran}(t-1)),t\in [t_r^{st},t_r^{en}-T_{\min ,du}^{tran,i}+1]$$

(35)

$${\displaystyle \sum _{t=t_b^{st}}^{t_b^{en}}\Delta P_i^{tran}(t)}={\displaystyle \sum _{t=t_{ola}^{st}}^{t_{ola}^{en}}\Delta P_{i,a}^{tran}(t)}$$

(36)

$${\displaystyle \sum _{t_{af}^{st}\in {\vartheta }_{st}^{trans,i}}{\mu }_{t_{af}^{st}}^{trans,i}}\le 1$$

(37)

where ${\lambda }_{i,\min }^{tran}$(t), and ${\lambda }_{i,\max }^{tran}$(t) represent the minimum load translate rate and maximum load translate rate, respectively; $T_{\min ,du}^{tran,i}$ represents the minimum duration of the translatable load; and Δ$P_{i,a}^{tran}$(t) represents the transferable load power after the response. Equation (34) limits the load translate rate, Equation (35) limits the duration of the translatable load, and Equation (36) ensures the balance of the response volumes.

For replaceable loads, the electrical energy substitution rates should satisfy the following constraints:

$${\mu }_{i,\min }^{re}(t)\le {\mu }_i^{re}(t)\le {\mu }_{i,\max }^{re}(t)$$

(38)

where ${\mu }_{i,\min }^{re}$(t) and ${\mu }_{i,\max }^{re}$(t) represent the minimum and maximum electrical energy substitution rates for replaceable loads, respectively.

The grid operator transaction model constraints are shown below:

$$P_{dr}(t)\ge P_{\min }^{dr}(t)$$

(39)

$$C_{price,\min }^n(t)\le C_{price}^n(t)\le C_{price,\max }^n(t),n=cu,tran,trans,re$$

(40)

where $P_{\min }^{dr}$(t) represents the minimum DR capacity required by the grid at time t; and $C_{price,\min }^n$(t) and $C_{price,\max }^n$(t) are the minimum and maximum unit response capacity offered by the grid operator to the VPP at time t, respectively. Equation (39) limits the minimum of the DR volumes, and Equation (40) limits the transaction cost of different loads.

The VPP operator transaction model constraints are shown below:

$$C_{vpp}(t)\le C_{\max }^{vpp}(t)$$

(41)

$$P_{dr}^{adlo}(t)={\displaystyle \sum _{i=1}^{n_{cu}}\Delta P_i^{cu}(t)}+{\displaystyle \sum _{i=1}^{n_{tran}}\Delta P_i^{tran}(t)+{\displaystyle \sum _{i=1}^{n_{trans}}\Delta P_i^{trans}(t)}}+{\displaystyle \sum _{i=1}^{n_{re}}\Delta P_i^{re}(t)}$$

(42)

$$P_{dr}(t)=P_{dr}^{adlo}(t)$$

(43)

$$P_{dr}^{adlo}(t)\le P_{dr,\max }^{adlo}(t)$$

(44)

$$\left|P_i^t-P_i^{t-1}\right|\le \gamma$$

(45)

where $C_{\max }^{vpp}$(t) represents the maximum transaction cost of the VPP operator; $P_{dr}^{adlo}$(t) is the DR capacity provided by the user; and $P_{dr,\max }^{adlo}$(t) represents the maximum DR capacity that can be provided by the user. Equation (41) limits the maximum transaction cost of the VPP operator. Equations (42) and (43) ensure the balance of the transaction volumes. Equation (44) limits the maximum DR volumes of the VPP operator. The parameter γ in Equation (45) represents the inclination of aggregators to alter their demand from one period to another [24].

4. Materials and Methods

4.1. Objective Function Treatment based on Pessimistic Values

From the objective function, it can be seen that each transaction model contains fuzzy variables which can be measured using optimistic and pessimistic values [22]. Taking ζ as the fuzzy variable and a confidence level β∈ [0, 1], we obtain:

$${\zeta }_{\sup }(\beta )=\sup \left\{\lambda \right|Cr\{\zeta \ge \lambda \}\ge \beta \}$$

(46)

where ζ_sup(β) represents the optimistic value of ζ with confidence β, that is, the maximum value taken by the fuzzy variable ζ with confidence β. In the equation, sup represents the upper bound value. Similarly, the expression for the pessimistic value can be obtained as shown in the following equation:

$${\zeta }_{\inf }(\beta )=\inf \left\{\lambda \right|Cr\{\zeta \le \lambda \}\ge \beta \}$$

(47)

where ζ_inf(β) represents the pessimistic value of ζ with confidence β, i.e., the minimum value taken by the fuzzy variable ζ with confidence β, and inf represents the lower bound value.

Transforming the transaction cost model into a pessimistic model for solving, the expression for the pessimistic value of each transaction model can be written as:

$$C_{\inf ,pg}(t)=(2-2{\alpha }_1)[C_{vpp,2}^{dr}(t)-C_{eq,2}^{dr}(t)]+(2{\alpha }_1-1)[C_{vpp,3}^{dr}(t)-C_{eq,1}^{dr}(t)]$$

(48)

$$C_{\inf ,vpp}(t)=(2-2{\alpha }_2)[C_{com,2}^u(t)-C_{vpp,2}^{dr}(t)]+(2{\alpha }_2-1)[C_{com,3}^u(t)-C_{vpp,1}^{dr}(t)]$$

(49)

where α₁ and α₂ represent the pessimistic confidence levels of the grid operator and the VPP operator, respectively; and C_inf,pg(t) and C_inf,vpp(t) represent the pessimistic values of the transaction costs of the grid operator and the VPP operator, respectively.

4.2. Constraint Handling Based on Clear Equivalence Classes

The chance constraints include fuzzy parameters that hold only a certain level of confidence. A review of the relevant literature reveals that these chance constraints can be transformed into the form of clear equivalence classes before solving them [23].

Suppose the function f(x, ζ) is as follows:

$$f(x,\zeta )=g_0(x)+g_1(x){\zeta }_1+g_2(x){\zeta }_2+\cdots +g_n(x){\zeta }_n$$

(50)

where ζ is a trigonometric fuzzy variable that can be expressed as (r_t1, r_t2, r_t3), t = 1, 2, ···, n; and x is a deterministic variable. The following two functions can also be defined:

$$g_t^{+}(x)=g_t(x)\vee 0$$

(51)

$$g_t^{-}(x)=-g_t(x)\wedge 0$$

(52)

When the confidence level β ≥ 0.5, the fuzzy chance constraint Cr{f(x, ζ) ≤ 0} ≥ β can be transformed into:

$$g_0(x)+(2-2\beta ){\displaystyle \sum _{t=1}^n{r}_{t2}{g}_t(x)}+(2\beta -1){\displaystyle \sum _{t=1}^n[r_{t3}{g}_t^{+}(x)-r_{t1}{g}_t^{-}(x)]}\le 0$$

(53)

When the confidence level β < 0.5, the fuzzy chance constraint Cr{f(x, ζ) ≤ 0} ≥ β can be transformed into:

$$g_0(x)+(1-2\beta ){\displaystyle \sum _{t=1}^n[r_{t1}{g}_t^{+}(x)-r_{t3}{g}_t^{-}(x)]}+2\beta {\displaystyle \sum _{t=1}^n[r_{t2}{g}_t(x)]}\le 0$$

(54)

According to the above theory, considering that the confidence value reflects the level of risk taken by the system operation, the lower the confidence level, the higher the risk of the grid operation. Therefore, considering the conservativeness of the grid operation, the confidence level of the fuzzy chance constraint is chosen to be a number greater than 0.5. For the system standby constraint in Section 3.2, when β₁ ≥ 0.5, the constraint can be transformed into a clear equivalence class form as shown in the following equation:

$$\begin{array}{l}(2-2{\beta }_1)({\displaystyle \sum _{i=1}^{n_{cu}}\Delta P_{i,2}^{cu}(t)+{\displaystyle \sum _{i=1}^{n_{tran}}\Delta P_{i,2}^{tran}(t)}}+{\displaystyle \sum _{i=1}^{n_{trans}}\Delta P_{i,2}^{trans}(t)}+{\displaystyle \sum _{i=1}^{n_{re}}\Delta P_{i,2}^{re}(t)})+\\ (2{\beta }_1-1)({\displaystyle \sum _{i=1}^{n_{cu}}\Delta P_{i,1}^{cu}(t)+{\displaystyle \sum _{i=1}^{n_{tran}}\Delta P_{i,1}^{tran}(t)}}+{\displaystyle \sum _{i=1}^{n_{trans}}\Delta P_{i,1}^{trans}(t)}+{\displaystyle \sum _{i=1}^{n_{re}}\Delta P_{i,1}^{re}(t)})\ge (1-{\delta }_{dr})P_{\min }^{dr}(t)\end{array}$$

(55)

For the maximum user response constraint, when β₂ ≥ 0.5, the constraint is transformed into the following equation:

$$\begin{array}{l}(2-2{\beta }_2)({\displaystyle \sum _{i=1}^{n_{cu}}\Delta P_{i,2}^{cu}(t)+{\displaystyle \sum _{i=1}^{n_{tran}}\Delta P_{i,2}^{tran}(t)}}+{\displaystyle \sum _{i=1}^{n_{trans}}\Delta P_{i,2}^{trans}(t)}+{\displaystyle \sum _{i=1}^{n_{re}}\Delta P_{i,2}^{re}(t)})+\\ (2{\beta }_2-1)({\displaystyle \sum _{i=1}^{n_{cu}}\Delta P_{i,3}^{cu}(t)+{\displaystyle \sum _{i=1}^{n_{tran}}\Delta P_{i,3}^{tran}(t)}}+{\displaystyle \sum _{i=1}^{n_{trans}}\Delta P_{i,3}^{trans}(t)}+{\displaystyle \sum _{i=1}^{n_{re}}\Delta P_{i,3}^{re}(t)})\le P_{dr,\max }^{adlo}(t)\end{array}$$

(56)

5. Results and Discussions

In this section, we use an international low-carbon park in eastern China as an example. This park contains a variety of load resources, mainly consisting of flexible loads as well as base loads that are not responsive. The division of peak and valley periods and electric prices are shown in

Table 1. The division of peak and valley periods.

Period		Electric Price/(￥/kW·h)
Peak period	10:00–15:00, 18:00–21:00	1.1365
Flat period	07:00–10:00, 15:00–18:00	0.7765
Valley period	00:00–07:00, 21:00–24:00	0.2702

. The flexible loads consist of shiftable loads, transferable loads, curtailable loads, and replaceable loads. The load data for flexible users are shown in

Table 2. The parameter of SL.

Type	${\mathit{t}}_{\mathit{b}}^{\mathit{s}\mathit{t}}$	${\mathit{t}}_{\mathit{t}\mathit{o}}^{\mathit{t}\mathit{r}\mathit{a}\mathit{n}\mathit{s}}$/h	[${\mathit{t}}_{\mathit{a}\mathit{c}}^{\mathit{s}\mathit{t}}$, ${\mathit{t}}_{\mathit{a}\mathit{c}}^{\mathit{e}\mathit{n}}$]	${\mathit{C}}_{\mathit{u}\mathit{n}\mathit{i}\mathit{t},\mathit{c}}^{\mathit{t}\mathit{r}\mathit{a}\mathit{n}\mathit{s}}$(￥/kW·h)	${\mathit{C}}_{\mathit{t}\mathit{i}\mathit{m}\mathit{e}}^{\mathit{t}\mathit{r}\mathit{a}\mathit{n}\mathit{s}}$(￥/kW·h)
Shiftable Load	10:00	3	[5:00, 18:00]	0.64	10

,

Table 3. The parameter of TL.

Type	${\mathit{C}}_{\mathit{t}\mathit{i}\mathit{m}\mathit{e},\mathit{n}}^{\mathit{t}\mathit{r}\mathit{a}\mathit{n}}$/￥	${\mathit{\lambda }}_{\mathbf{min}}^{\mathit{t}\mathit{r}\mathit{a}\mathit{n}}$(t)	${\mathit{\lambda }}_{\mathbf{max}}^{\mathit{t}\mathit{r}\mathit{a}\mathit{n}}$(t)	[${\mathit{t}}_{\mathit{r}}^{\mathit{s}\mathit{t}}$, ${\mathit{t}}_{\mathit{r}}^{\mathit{e}\mathit{n}}$]	[${\mathit{t}}_{\mathit{p}\mathit{g}}^{\mathit{s}\mathit{t}}$, ${\mathit{t}}_{\mathit{p}\mathit{g}}^{\mathit{e}\mathit{n}}$]	${\mathit{C}}_{\mathit{u}\mathit{n}\mathit{i}\mathit{t},\mathit{c}}^{\mathit{t}\mathit{r}\mathit{a}\mathit{n}}$(￥/kW·h)
Transferable load	30	0.2	0.8	[5:00, 9:00], [14:00, 20:00]	[4:00, 18:00]	0.44

,

Table 4. The parameter of RL.

Type	${\mathit{N}}_{\mathit{c}}^{\mathbf{max}}$	${\mathit{t}}_{\mathbf{min}}^{\mathit{c}\mathit{u}}$/h	${\mathit{t}}_{\mathbf{max}}^{\mathit{c}\mathit{u}}$/h	${\mathit{C}}_{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}^{\mathit{c}\mathit{u}}$(￥/kW·h)	${\mathit{\epsilon }}_{\mathbf{min}}^{\mathit{c}\mathit{u}}$(t)	${\mathit{\epsilon }}_{\mathbf{max}}^{\mathit{c}\mathit{u}}$(t)
Curtailable load	15	1.5	5	0.46	0.1	0.8

and

Table 5. The parameter of REL.

Type	${\mathit{C}}_{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}^{\mathit{r}\mathit{e}}$(￥/kW·h)	${\mathit{C}}_{\mathit{u}\mathit{n}\mathit{i}\mathit{t}}^{\mathit{g}\mathit{a}\mathit{s}}$(￥/m3)	${\mathit{\gamma }}_{\mathit{p}-\mathit{g}}^{\mathit{r}\mathit{e},\mathit{i}}$	${\mathit{\mu }}_{\mathbf{max}}^{\mathit{r}\mathit{e}}$(t)	${\mathit{\mu }}_{\mathbf{min}}^{\mathit{r}\mathit{e}}$(t)
Replaceable load	1.24	0.44	1.67	0.69	0.1

.

Considering that the confidence value reflects the level of risk taken by the system operation, the lower the confidence level, the higher the risk of the grid operation. The confidence of the opportunity constraint is set as β₁ = β₂ = β₃ = 0.95; the pessimistic confidence of each transaction cost is set as α₁ = α₂ = 0.9; and the reserve capacity coefficient of the power grid is set as 0.05. The allowable fluctuation range of the response rate of various flexible loads is shown in

Table 6. The characteristic curve of incentive DR considering uncertainty.

Load Type	Range of Fluctuation Ratio	Load Type	Range of Fluctuation Ratio
Curtailable load	[0.9, 1.2]	Shiftable load	[0.95, 1.05]
Transferable load	[0.8, 1.2]	Replaceable load	[0.9, 1.1]

.

It can be seen from Table 1 that for curtailable loads, $r_1^{cu}$ = 0.9 and $r_3^{cu}$ = 1.2; for transferable loads, $r_1^{tran}$ = 0.8 and $r_3^{tran}$ = 1.2; for translatable loads, $r_1^{trans}$ = 0.95 and $r_3^{trans}$ = 1.05; and for substitutable loads, $r_1^{re}$ = 0.9 and $r_3^{re}$ = 1.1.

5.1. Effect of Load Uncertainty on Response Volume and Response Revenue

5.1.1. Analysis on Load Curve Considering Users’ Response Uncertainty

When the fuzzy chance-constrained confidence level is 0.95 and the transaction costs of the pessimistic confidence level is 0.9. The results of the flexible load participation in response optimization are shown in Figure 4, including the flexible load optimization results and the load curve. It can be seen that with the response uncertainty taken into account, the participation of the flexible load can still play a role in peak shaving and valley filling.

As shown in Figure 4, under the influence of the users’ response uncertainty, the system load during the peak hours of power consumption from 10:00–15:00, and from 18:00–21:00 is reduced to a certain extent. However, from 01:00–08:00 and 22:00–24:00, the load of the whole system increases to a certain extent. It can be seen from the peak–valley difference that the peak–valley difference is 1910.88 kW before load response and 1580.55 kW after the load response. Even when considering the influence of flexible user response uncertainty, the peak–valley difference of the power grid is still reduced under the participation of a flexible load, which reduces the peak regulating the pressure of the power grid and ensures the stability of the system operation.

After participating in the DR of the power grid interaction, various flexible load responses, as shown in Figure 5, illustrate that the response increased at 16:00, mainly because of the response under the influence of an uncertain response. In this scenario, the user needs to increase the response period to reduce the impact of uncertainty factors on the power grid. The transferable load in the power consumption period of 09:00–15:00 and 19:00–20:00 is still involved in the DR. The transferable load is transferred to the flat period of power consumption such as 01:00–08:00, 16:00–18:00, and 23:00–24:00; the response volume is reduced compared with that in the deterministic response period. This is because the response volume of the transferable load fluctuates in a wide range. To reduce the influence of uncertainty, the power grid will reduce the demand for this kind of load, but the response of the load still effectively alleviates the problem of large peak–valley differences. There are some changes in the shifting periods of the shiftable load from 10:00–12:00 and from 18:00–20:00. The electrical load is shifted to 06:00–08:00 and 22:00–24:00, but the response volume does not change much because the shiftable load has high requirements for its work continuity. The production process of load equipment is complete and the electricity demand is relatively fixed, so there is rarely the problem of an uncertain response under general circumstances. Therefore, the load translation is similar to that under the deterministic response condition, which not only reduces the peak–valley difference of the system, but also ensures the continuity of the work of the shiftable load. The replaceable loads of 10:00, 14:00 and 21:00 are also involved in electrical energy substitution.

5.1.2. Analysis on Benefits of Transaction Stakeholders Considering Response Uncertainty

To fully compare the impact of users’ uncertain responses on the returns of each transaction entity, two scenarios are set up in this section:

Scenario 1: considers the incentive flexible load to participate in the transaction of the power grid, but does not consider the uncertainty of the response volume of the flexible load.

Scenario 2: when the flexible load is encouraged to participate in the grid transaction, the uncertainty of the response volume of the flexible load is considered.

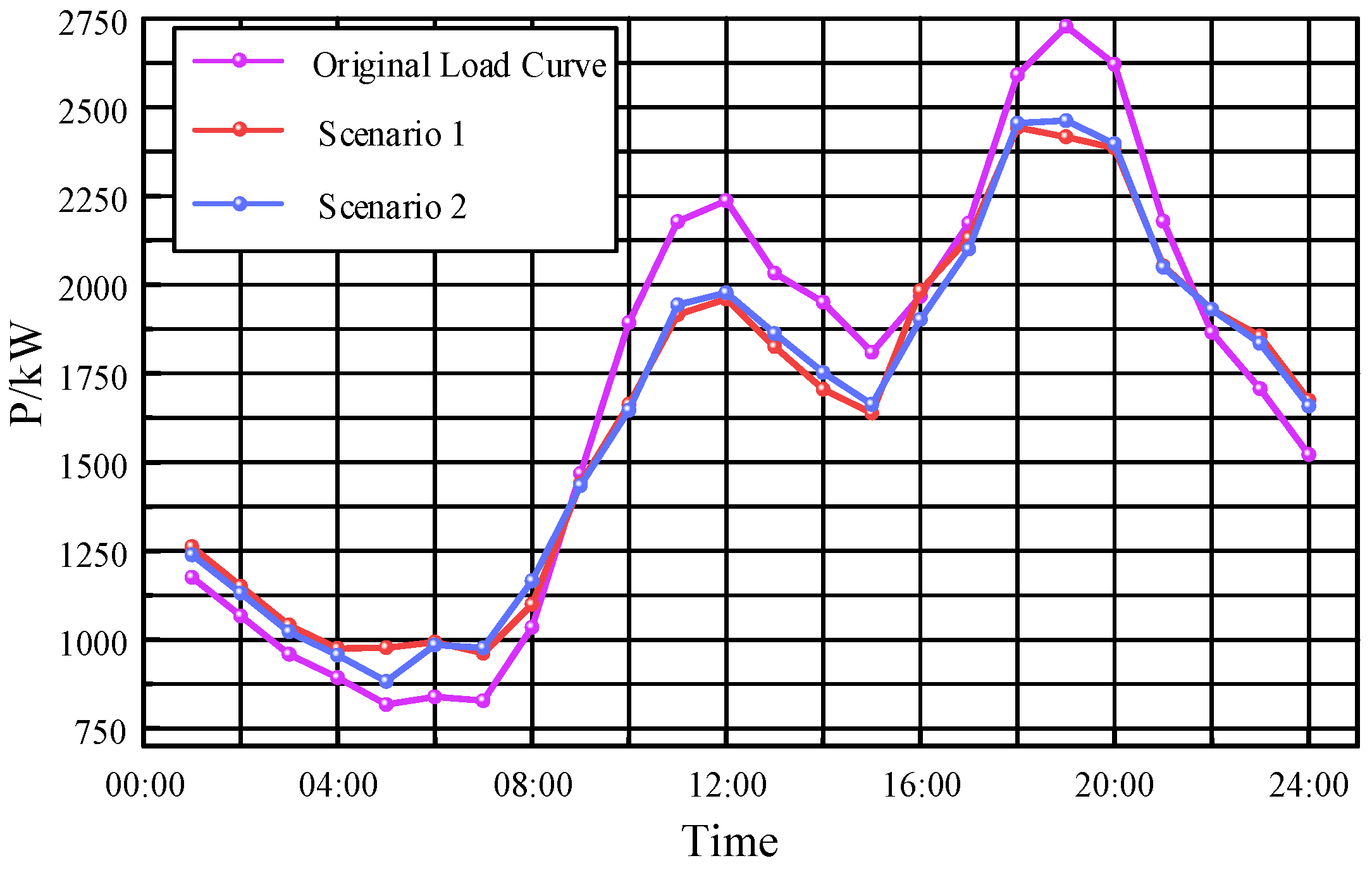
(1) After analyzing the results of the load response, the results of the combined comparison of the optimized load profiles for Scenario 1 and Scenario 2 are shown in Figure 6.

Comparing the three load curves shown above, the following conclusions can be drawn:

1. With flexible users participating in the grid DR, the peak–valley differences in their load curves are reduced to some extent both with and without accounting for uncertainty in the response volume. However, the peak–valley difference of the system load curve is higher when the uncertainty of the user response is taken into account than the peak–valley difference in the case where the uncertainty of the response is not considered.

2. The load curve accounting for response uncertainty is obtained with a confidence level of 0.95 for the opportunity constraint and a pessimistic confidence level of 0.9 for the transaction cost. When the confidence level takes different values, the load curve is a band of varying intervals. In other words, the ambiguity of the amount of customer responses introduces certain ambiguous properties into the transaction decisions of the grid operator.

(2) Accordingly, the income comparison results of each transaction entity to the two scenarios can be obtained, as shown in Figure 7.

As seen from the analysis above, during the period of the user response, the revenue of scenario 1 is higher than that of scenario 2. Thus, it can be seen that when considering the motivational flexible load response volume of uncertainty, the transaction entity yields have a certain degree of decline. Because of the uncertainty about the users’ response volume, grid operators need to increase the investment cost of the spare capacity to mitigate the user response on the impact of uncertainty. During a rise in the cost of power grid operations, income is reduced, and the decrease in the volume at the same time will lead to a decline in the benefits of VPP operators; the transaction earnings compared to not considering the response under the condition of uncertainty is reduced. At the same time, it can be seen from the figure that the income of each transaction entity reaches the maximum at 12:00 and 19:00, because the DR of the power grid is the largest at these two times, and the response volume provided by users is also the largest. Therefore, the income of each transaction entity is also the largest at these times.

To demonstrate the advantages of our proposed method, we further compare it to three other methods for solving the uncertainty as follows:

M1: our proposed method

M2: distributionally robust optimization-based method

M3: robust optimization-based method

M4: stochastic programming-based method

Accordingly, the income comparison results of each transaction entity with the above four methods can be obtained, as shown in Figure 8. It is easy to notice that the benefits of the power grid operator and VPP operator for participating in the DR transaction rank first among these methods. Thus, the fuzzy theory utilized in our model with a trigonometric membership function can effectively cope with the uncertainty brought by flexible loads.

5.2. The Effect of the Confidence Level of Fuzzy Chance Constraints on Response Returns

To verify the impact of different confidence levels of fuzzy chance constraints on the transaction based on scenario 2 in the previous subsection, the pessimism confidence of each transaction cost is unchanged at 0.9, and fuzzy chance constraint are selected at different confidence levels to analyze the income changes of each transaction entity under different confidence levels. In addition, the fuzzy parameters describing the response volume are represented by different types of membership functions for comparison. The trigonometric membership function and trapezoidal membership function are selected in this section. Accordingly, the trend of the social welfare of transactions with the confidence level of fuzzy chance constraints can be obtained, as shown in Figure 9.

It can be seen from Figure 9 that as the confidence level of opportunity constraints changes from high to low, the social welfare of the whole transaction is constantly increasing. All transaction entities participate in the transaction in response to the demand at different confidence levels, and the results reflect different attitudes towards the transaction risk. When the chance-constrained confidence level is lower, the social benefits generated by the transaction will be higher, but the lower confidence level will lead to an increase in the system risk. When the chance-constrained confidence level increases, the risk of response uncertainty to the system is reduced. Although the social benefits is reduced, the risk of the system operation is decreased greatly.

In addition, the above also compares the trapezoidal membership functions and trigonometric membership functions about social welfare under different confidence levels. As can be seen from the figure, compared to the trapezoidal membership function, the use of the trigonometric membership function to describe the uncertainty of customer response volumes is more likely to be trusted by the grid operator in its prediction of response demand volumes, and therefore has higher social welfare than the trapezoidal membership function when the chance constraint confidence level is certain.

6. Conclusions

DR is increasingly used as an essential regulation tool in power systems, however, when an IES with a large number of flexible loads is aggregated for a DR transaction, uncertainty in the amount of the load response can have an impact on the process and outcome of the transaction. In this paper, the impact of uncertainty in flexible load responses on DR transactions was considered. First, the uncertainty problem of incentive-based DR was analyzed, and the relationship between the level of incentive and the range of fluctuations in the user response volume was investigated. Subsequently, the treatment of uncertainty was introduced, and this paper used fuzzy variables to represent the user response volume. Based on this, a trigonometric membership function was used to represent the uncertainty level of the user response quantity for different types of flexible loads. Finally, for the objective function and chance constraints containing fuzzy variables, they were converted into explicit equivalence classes and then solved. The case study section examined the impact of the uncertainty of user response volumes on the revenue of each transaction entity and the impact of the fuzzy chance constraints confidence level on the response revenue. The results demonstrated that the revenue of each transaction entity decreases to a certain extent when the uncertainty of user response volume is considered, and the social welfare of the whole transaction increases as the confidence level of the chance constraint changes from high to low.

The proposed method of dealing with user response uncertainty in this paper provides some ideas and suggestions to solve the problems faced by flexible loads when participating in DR, but it can still be extended in the following two aspects. First is the study of a flexible load response strategy under multiple time scales. The research conducted in this paper did not consider the time scale and did not study the regulation of flexible loads in multiple time scales such as day-ahead, intra-day and real-time. In fact, in the case of approaching time scales, the types of flexible users that can participate in grid DR will be reduced continuously, and the uncertainty of user responses will also be reduced continuously—even in the real-time stage without considering the problem of user response uncertainty. Second is the study of user uncertainty under multiple response mechanisms. In this paper, we only consider the problem of response uncertainty of flexible loads under contract constraints, but in fact, some flexible loads can also participate in the DR of the grid under tariff guidance, and their response uncertainty cannot be ignored.