Abstract
The emergence and spread of COVID-19 has severely impacted the tourism industry worldwide. In order to limit the effect of new pandemics or any unforeseen crisis, coordinated actions need to be adopted among tourism stakeholders. In this paper, we use an evolutionary game model to analyze the conditions that promote cooperation among different stakeholders in a tourism network to control high-risk crises. A data sample of 280 EU regions is used to define the tourism network of regions with a heterogeneous dependence on tourism. The results show that cooperation is helped by the existence of a structured tourism network. Moreover, cooperation is enhanced when coordination groups include small numbers of participants and when they are formed according to the similarity of tourism dependence.
1. Introduction
The COVID-19 crisis, similar to other previous sudden international health crises, has taught us the importance of coordination and cooperation among countries and tourism stakeholders, not only to control epidemiological indicators [1], but also to enhance the recovery phase [2,3]. However, coordination has not been a real practice in the most critical moments of the current crisis. Frequently, some countries or regions adopted severe mobility restrictions at the same time as others relaxed them and allowed economic activity. The combination of opposing policies between origin and destination regions has formed a complex puzzle that commonly leads to the partial or complete cessation of tourism activity.
The case of Spain (as a destination) and Germany (as an origin) provides a good example of this situation. In 2019, more than 11 million German tourists visited Spain. During the pandemic, each of the 17 autonomous regions in Spain has had a certain degree of independence in decision-making regarding the entrance of tourists and, therefore, the policies have tended to vary to a larger or lesser extent across regions. Meanwhile, between March 2020 and March 2022, Germany passed through several pandemic-related phases. In some, traveling abroad was not advised, in others, those traveling abroad had to comply with a 10-day quarantine upon their arrival back in Germany and, in others, traveling abroad for tourism reasons was forbidden.
In this paper, we understand cooperation as the adoption of measures to control a crisis (e.g., in case of pandemic diffusion, vaccination requirements, the use of facemasks, quarantines, etc.). A cooperator agent faces an undesirable economic cost derived from the application of these commonly restrictive measures. During the COVID-19 pandemic, national and regional governments could force, by law, the rest of the tourism stakeholders (e.g., air carriers, hoteliers, and service providers) to adopt restrictions (e.g., vaccination requirements for employees and customers and compulsory mask use). Nevertheless, in many countries, individuals can freely decide whether to take the vaccine or not, avoiding the individual cost of it although assuming other costly consequences of their decision. This paper does not discuss these alternatives but assumes a tourism network where all stakeholders in it are free to cooperate or not and that the cost of cooperation is greater than the cost of non-cooperation. In this situation, some stakeholders may be tempted to follow opportunistic behavior, avoiding the cost of adopting pandemic control measures and freeriding the stable conditions achieved as the result of measures adopted by others. However, if every stakeholder behaves in this manner the crisis would inevitably worsen, provoking a general collapse and severely damaging the tourism industry and all stakeholders involved in it.
This situation can be seen as another example of the classical social dilemma known as the tragedy of the commons [4], where rational individuals looking out for their self-interest in a fragile and limited environment will inevitably lead to ruin for all. Throughout the last decades, researchers have analyzed how cooperation is possible in the absence of a central authority (e.g., a supranational authority) with enforcement capacity. The evolutionary game theory [5] has served to answer the question. Although originally applied to biological species [6], the theory has been used to represent conflicts in human societies [7]. An evolutionary game assumes rationally bounded individuals who decide strategies in an interaction situation with others according to a dynamic learning process. The existence of an indefinite number of iterations of the game allows cooperation to be achieved in social dilemma situations.
We follow the evolutionary game approach to analyze the conditions from which tourism stakeholders freely impose costly restrictions to control crises in coordination with other stakeholders. Specifically, we represent the problem by means of a collective risk dilemma model [8,9], which is a kind of social dilemma where players (stakeholders) are clustered in coordination groups and in which a threshold of cooperators is necessary to avoid the risk of an economic collapse. This model has been traditionally used to represent the dilemma of adopting costly measures to alleviate climate change in coordination with other countries [10,11], although recently it has also been applied to represent the pandemic control dilemma [12,13].
This paper deals with the role of tourism networks in the coordinated adoption of pandemic control measures. The existence of tourism networks, or a particular structure of interrelationships among stakeholders, is well recognized in the tourism literature [14,15]. When dealing with crisis control measures in tourism, stakeholders do not necessarily learn strategies from each other, but only from those who they have more connections with. In this regard, the main research question in this paper is whether the existence of a tourism network enhances or not the global levels of cooperation in the population. In this paper, we examine this issue by assuming an empirical network configuration, formed by regions in Europe as stakeholders, which is linked through the intensity of tourist flow. Regions learn and reform their cooperation strategies iteratively following strategies of other regions with which they are previously interrelated. Then, the sum of cooperation levels for the whole population in the steady state is analyzed.
Then, the objective of the paper is to analyze conditions for which tourism stakeholders freely cooperate to adopt measures to control pandemics or similar crises. Previous works along the same line ignored the existence of a structured social network of the interrelationship among agents [12,13]. In this regard, our research is closer to the real scenario than previous studies by including a tourism network in the model formulation. The simulation results show that the existence of a structured relationship among stakeholders favors cooperation. Moreover, the positive effect on global cooperation of some criteria to form coordination groups, such as the small size of groups and similarity in tourism dependence, is also enhanced by the existence of tourism networks. Therefore, our study extends previous findings and highlights the positive role of tourism networks in the adoption of coordinated control of the pandemic crisis.
2. Literature Review
2.1. Tourism Networks: Structure and Performance
Tourism can be seen as a complex system that includes a collection of interdependent stakeholders of highly differing natures (government, transportation, hospitality, tourists, etc.) which form a network of interacting nodes [15,16]. Traditionally, the empirical tourism networks that have been analyzed are formed by groups and organizations involved in a tourism destination [14,17,18], although they can be also formed by international organizations in the private or public sector [19].
In tourism networks, the actions of one stakeholder impact the rest through the links that connect them. Then, collaboration among members of the network is necessary since all of them together make up the total product or experience perceived as unique by the tourists. The suitability of the network perspective for the tourism industry has long been emphasized by scholars. For example, Jamal and Getz [20] theoretically founded the collaboration of stakeholders for tourism planning, highlighting the role of the recognition of an interdependence network as a facilitator of collaboration. Tremblay [21] focused on the point of view of economic organization, explaining the necessity of strategic alliances and coordination of dissimilar but related products, such as transportation, hospitality, and distribution services. More recently, Scott, Cooper, and Baggio [14] proposed the use of network analysis tools developed in other disciplines [22,23] to quantitatively estimate the structure and properties of the tourism networks. The latter quantitative perspective enables a more formalized theoretical founding of tourism networks and implications with significant new contributions in this area, such as the analysis of cohesiveness and information diffusion [16], resilience to climate change [24], and social capital in hotels [25].
Being part of a tourism network conveys several benefits to members, such as knowledge transfer, cooperative activities, and a sense of community [19]. In this regard, some studies have analyzed how the specific network configuration enhances or diminishes these benefits. The question about the influence of the relational structure on tourism destination development was addressed by Pavlovich [18], who analyzed the role of strong and weak ties among stakeholders and the existence of brokerage mechanisms of some agents, applying the theory of structure holes [26] to tourism networks. More recently, Zach and Hill [27] showed that the degree of agent intermediation in a tourism network (betweenness) positively influences the adoption of innovation. High levels of betweenness mean a high capacity to connect different actors, a concept also related to the bridging or brokerage mechanism. Knowledge diffusion is also dependent on the network structure, as has been recently highlighted by Valeri and Baggio [28] by means of a simulation model based on a network of interactions among tourism stakeholders in Italy. Their results show that a small increase in the number of links, following a mechanism such as the classical preferential attachment [29], enhances knowledge diffusion in the system.
Our paper is related to the previous literature by analyzing how the network structure of relationships influences tourism performance in an aspect that, to date, has not been analyzed—namely cooperation among stakeholders to control crisis.
2.2. Evolutionary Games and Applications to Tourism
An evolutionary game assumes agents are engaged in successive interactive choice situations where they can strategically decide their behavior, obtaining a payoff that depends on the decisions of others. Unlike the traditional game theory approach, evolutionary games assume agents are rationally bounded, which means that they have limited information access or suffer high deliberation costs [30]. Bounded rationality makes the agent’s choice based on limiting searches and, according to a learning behavior, copying more successful strategies in past experiences of others [31]. This suboptimal behavior is associated with dynamics, since agents correct their decision after observing the outcome derived from the collection of previous decisions in the system [7]. Then, one of the main objectives of evolutionary game theory is to analyze the conditions for a stable strategy (also called an evolutionary stable strategy) to spread in the population in the long run. These stable strategies are commonly associated with the Nash equilibrium in the game [32]. In this kind of game, cooperation is possible in the long term in certain contexts [33].
Evolutionary game models have been used to represent economic phenomena where individuals learn by interacting with others, making decisions based on limited information, comparing, or imitating more successful strategies [34]. Most of the application to tourism deals with the adoption or not of sustainable practices, involving diverse population types. For example, He, He, and Xu [35] analyzed the mechanism of adoption of green tourism in a three-population game, including local government, tourism firms, and tourists. Qingyun and Mu [36] also proposed a model to explain the interaction of strategies of three stakeholders (government, developers, and the local community) in the process of distribution of land revenue, and Antoci, Borghesi, and Galeotti [37] used evolutionary games to represent the interaction between tourists and stakeholders, where a protection mechanism (environmental bonus) is introduced by the government as an incentive to adopt sustainable practices. The adoption of green innovation strategies was also analyzed in the model proposed by He et al. [38], assuming two tour operators playing in a competitive duopoly. All the above contributions presented two or three populations playing an asymmetric evolutionary game. As expected in this kind of model [32], stable strategies are non-mixed; in other words, all members in the same population adopt pure cooperation or defection in the long term.
The above studies assume a pairwise interaction among stakeholders in the context of a well-mixed network, where any player can potentially interact and compare payoffs for strategy updating with any other belonging to the rest of the population. The question of coordination among stakeholders forming a tourism network has not been explored in tourism research yet.
2.3. Collective risk Dilemma to Control Pandemic Risk
In a multi-person game, a social dilemma occurs when players who do not cooperate receive a higher payoff than those who cooperate, taking advantage of the effort made by cooperators. However, this type of predatory strategy is only valid if developed by a small number of members. If many participants defect, cooperators obtain a lower payoff, reducing their incentive to cooperate. This is an extension of the classical two-person prisoner’s dilemma and has been traditionally studied as a public goods game or a commons game [39].
A collective risk dilemma is a kind of social dilemma where a minimum threshold must be achieved to produce or preserve the public good [8,40,41]. Instead of sharing the total contribution of cooperators among participants, as is the case of a traditional public goods game, the collective risk dilemma assumes the existence of a certain risk of losing everything if the threshold is not fulfilled. In this kind of game, agents play the game in separated groups (cooperation groups) of the same size. These models have been mostly applied to analyzing the conditions for adopting measures to prevent climate change by regions and countries [9,10,11], although some recent papers have proposed a collective risk dilemma model to represent the adoption of pandemic control measures [12,13].
2.4. Hypotheses Development
The benefits of tourism networks on tourism performance have been theoretically highlighted by several researchers. For example, Morrison et al. [19] stressed, among other aspects, that tourism networks stimulate cooperative practices for innovation, market development, and adoption of sustainable tourism. Additionally, Luthe et al. [24] show how centralization and cohesiveness of tourism networks can increase stakeholders’ resilience to climate change. More recently, Valeri and Baggio [28] also show by means of a simulation model how changes in the tourism network topology favor knowledge diffusion among stakeholders.
The effect of a social structure on cooperation has been analyzed in evolutionary games in general (Szabó and Fáth 2007 [42]). Assuming social links mean that players only interact with those agents that they have previous relationships with. In the context of a two-person game, cooperation is enhanced when social links are heterogeneous (e.g., induced by scale-free networks where most nodes have few connections and few of them are very connected) [42,43]. The existence of social ties among players also helps cooperation in public goods games [44].
The effect of social network heterogeneity on global cooperation in collective risk dilemmas has not been analyzed until now. In this context, this research includes a social network based on tourist flow among regions in Europe and analyzes the effect of this network on global cooperation among regions to control high-risk crises. The previous research in tourism networks and evolutionary games described above suggests that cooperation would be enhanced if agents coordinate strategies with those in their social network. Then, we can formulate the following hypothesis:
Hypothesis 1 (H1).
If regions in Europe coordinate strategies with other regions in their tourism network, the level of cooperation to overcome the crisis increases.
Commonly, collective risk dilemma models assume that cooperation costs are evenly distributed among participants. However, this is not necessarily the case in a real scenario. For example, in the context of measures to control climate change, wealth inequality among countries may determine different contributions to the common good. In the context of the pandemic, tourism-dependent countries are more affected by mobility restrictions than others that are less dependent on tourism, as evidence shows [45]. Theoretical studies have found that the heterogeneity of participants in a collective risk dilemma model enhances cooperation [11]. Additionally, cooperation also increases when cooperation groups are formed according to similar contribution costs [12]. In the context of tourism-dependence regions, contribution costs to avoid crises (e.g., mobility restrictions) are related to the degree of dependence on tourism. High tourism-dependence regions would suffer higher contribution costs than those with lower tourism dependence. According to previous findings, we expect that in the context of a social network based on tourist flow among regions in Europe, cooperation increases if stakeholders are grouped by similar contribution costs. Then, we posit the following hypothesis:
Hypothesis 2 (H2).
The level of cooperation among regions in Europe increases if cooperation groups are formed according to a similar tourism dependence.
3. Materials and Methods
3.1. The Model
In this section, we present a collective risk dilemma model to represent the coordination problem among tourism stakeholders with respect to crisis control. We formulate the problem adapted to a pandemic situation, such as COVID-19, but it can be translated to any other crisis where restrictive measures are necessary to avoid major economic breakdowns. It is based on previous models applied to mitigate the consequences of climate change [46,47] and pandemic control [12]. In our model, we will include different criteria to build coordination groups and a network structure of relationships among agents that influences the strategy update of every player.
Formally, the model assumes a finite set of players (Z), which represent stakeholders. Every player, i, in every time step, t, decides whether to apply pandemic control measures (vaccination requirement, capacity limitations, compulsory mask use, etc.). This is mapped into a strategy, si, which is a dichotomous variable defining two possibilities: being a cooperator (C), where si = 1, or being a defector (D), where si = 0. Cooperators adopt the pandemic control measures while defectors do not. Cooperators will suffer the income loss derived from the application of measures whereas defectors do not.
The players are organized in groups. For the sake of simplicity, we assume that group size is a constant N < Z. Groups are a collection of agents which need to cooperate to avoid pandemic spread. The agents in the group are not necessarily interrelated in the tourism network. For example, this is the case of regions belonging to the same country. Some of these regions may not be significantly interrelated in the tourism network, although they form a coordination group since they belong to the same country. If a minimum percentage of agents m, 0 ≤ m ≤ 1, in the group do not cooperate, all players in the group are subject to a probability r, 0 ≤ r ≤ 1, of an uncontrolled pandemic diffusion and a consequent economic collapse due to the high incidence of the pandemic. The economic cost will obviously be higher for stakeholders with greater economic dependence on tourism.
These conditions can be represented by the pay-off function which represents the economic benefit of every agent. Assuming CK is the number of cooperators in a certain group K, the expected pay-off of a player i belonging to group K in each time-step is:
where Θ(·) is the Heaviside function, which is one if the argument is non-negative and zero otherwise. Thus, if CK ≥ mN, the expected pay-off of a defector is the highest (normalized as 1), but if CK < mN, the expected pay-off is 1 − r < 1. In the case of being a cooperator, the pay-off decreases by ci in [0,1], which represents the percentage of income lost in the case of cooperating. This cost is not constant throughout players. By assumption, it will be larger for stakeholders that have a greater dependence on tourism.
The tourism network influences agents when renewing their strategies. The rationale of this assumption is that agents observe those players with which they have established tourism interrelationships to decide their new strategies. Then, at each time step, t, the players compare their payoff with that of a neighboring player in their tourism network and imitate the strategy followed by the other player if the latter obtained a higher pay-off in the previous time step. The probability of imitation follows the Fermi function, which assigns a larger probability of copying those strategies with a higher pay-off [40]. We call the final level of cooperation the global ratio of cooperating players in the population in the long term.
3.2. Data-Based Tourism Network
We built a tourism network that will be used to determine the possible strategy imitations in the evolutionary dynamics of the model. Nodes correspond to European regions at the NUTS2 level [48], while the edges are based on the tourist connections between each pair or region. Therefore, each player is one of the EU NUTS2 and a directed weighted edge between two regions indicates the tourist flow from one region (origin) to the other (destination). Various factors serve to justify the selection of regions and connections among them as a tourism network in a pandemic context. First, regions in Europe have a certain degree of autonomy to impose or not pandemic control restrictions, and so players (regions) satisfy the condition of being free to cooperate (impose restrictions) or not. Second, according to the study by [49], the spread of infection in regions depends on the properties of this type of international tourism network more than other factors, such as geographical proximity. Therefore, it is reasonable to assume that players preferentially follow the strategies of their linked players more than those of other regions.
Information regarding the transit of tourists between regions is available at the country level. Thus, to create a social network of connections between NUTS2 regions, we distributed the outgoing tourists of a country among its regions proportionately to the region’s number of inhabitants. Similarly, incoming tourists were distributed among the regions of the destination country based on the importance rate of each region, measured by the total night stays in the region. We considered all the 284 NUTS2 regions available in the year we analyzed (2019). Out of them, we kept the 280 for which data were available. Therefore, we obtained a directed weighted network in the group of the 280 regions, each node being one of the regions in the group of 280.
In the initial obtained weighted network, all regions are fully connected to each other. To discriminate between the relationships that are expected from a random choice and those which are not induced by a random selection, we apply a pruning Pathfinder algorithm [50]. The Pathfinder network scaling method is applied to a network to prune it by only maintaining the most significant edges. The Pathfinder algorithm has two important characteristics. First, the algorithm retains the most important edges, and second, when applied to a connected network it provides a connected pruned network (there is not a single isolated node). After applying the algorithm, the final network reduces the number of edges to 441.
3.3. Model Setup
The heterogeneity of agents and social networks makes it necessary to analyze the models by a simulation. To do this, we create an agent-based algorithm (ABM) [51,52], a computational methodology that offers numerous opportunities for practitioners and scientists. With this simulation technique, we can represent the population of heterogeneous regions as a system that evolves over time.
The parameters in the model were set according to the tourism network of the NUTS2 regions. Specifically, the income loss, ci, induced by a cooperation strategy was based on the dependence on tourism of each region. To this aim, we calculated the nights spent at tourist accommodation establishments per inhabitant in 2019 and used the value as a proxy of the economic cost for the region if there was a lockdown. The distribution of these values ranges in a wide spectrum (from 0.10 to 78.59), although the average rate is 4.11 nights per inhabitant. We use ci equal to this rate divided by 100. Then, tourism-dependent regions present a higher ci than those that are not.
Due to the model’s complexity, an analytical solution is not feasible. Then, we make use of simulations to analyze the cooperation rate achieved in the long term for each risk level r. The time horizon is 200 time steps, where stabilization of the cooperation rate was observed. The results were obtained by averaging the last 25% of the simulation time steps of 30 independent Monte Carlo runs.
To analyze the influence of group formation on the cooperation levels of the population, we present the outcome by assuming two criteria. The first is that groups are formed randomly, that is, players have the same chance to be in any group. This kind of formation has been commonly used in previous collective risk dilemma models [46,47]. The second is that groups are formed by similarity, where group members are selected according to similar values of the income loss ci. Recent research has explored the case of forming groups based on similarity [12].
In addition, to test the effect of the tourism network on the cooperation rate, we analyze two cases. First, we analyze a well-mixed population, where players are fully connected to each other. Then, the focus player can imitate the strategy of any other player in the population selected by chance. This is the common assumption in previous collective risk dilemma models. Second, we analyze a structured tourism network (social network), where players are connected according to the social network as indicated in the previous section. Then, the focus player imitates the strategy of any player with which they have a connection in the tourism network. The other parameters (m and N) were varied to check the robustness of the findings. To sum up, Table 1 shows the main parameters of the model with their values to reproduce the results.

Table 1.
Summary of the parameters of the model with their main values.
4. Results
We conducted simulations of the model to estimate the long-term cooperation levels. In general, final cooperation depends on the initial number of cooperators among players. This is illustrated in Figure 1, which shows the final level of cooperation (percentage of cooperators over total population) achieved in the long term for different initial cooperation levels and risk values, assuming the four possible combinations of social network and group formation. The group size is n = 8 and the minimum percentage of cooperating regions is m = 0.7.
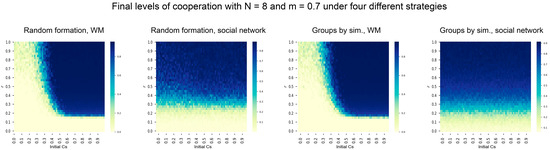
Figure 1.
The final level of cooperation in the collective risk dilemma model for different initial cooperation (initial Cs) and risk levels (r) under four scenarios.
Four scenarios are presented in Figure 1, combining the two kinds of group formation (random and by similarity) and two structures of the population (well-mixed and social network). As can be observed, there are two clear areas in the contour map of cooperation. Light-colored areas represent the combination of initial cooperation and risk levels where low final cooperation is achieved, whereas higher final cooperation is achieved in dark-colored areas.
As observed in Figure 1, the population does not achieve cooperation when the initial number of cooperators and risk levels are low. As the risk and initial cooperation increases, cooperation becomes easier. This result is expected. When the risk of an economic breakdown due to non-cooperation is low, the players do not have high incentives to cooperate and, therefore, defection is prominent. In contrast, as the risk increases, the incentive for cooperation is much higher.
There are marked differences in the cooperation levels according to the structure of the population. The cooperation area is narrower with a well-mixed population than with a structured tourism network. Higher cooperation levels are achieved in the latter case independently of the initial cooperation levels. This is not the case in a well-mixed population, where very low initial cooperation determines the outcome in the long term. The effect of group formation is not clear in Figure 1, although it seems that group formation by similarity slightly increases in the area with high cooperation levels.
The initial number of cooperators is uncertain and exogenous to the model. Then, in the next simulations, we assume it follows a uniform random variable and we calculate the final level of cooperation with respect to the complete range of risk r values for four combinations of group formation and population structure. The results are shown in Figure 2. The cases with a structured tourism network are represented by the continuous line, while the dotted lines represent the result assuming a well-mixed interlink among regions. The dark color represents the case of random formation and the light color represents the case in which the formation is created by similarity.
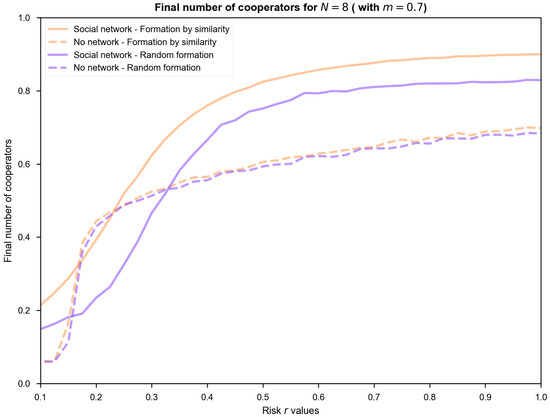
Figure 2.
The final level of cooperation for N = 8 (with m = 0.7).
According to the results, starting from high-risk values (r ˃ 0.4), the final number of cooperators increases if players are connected according to the structured tourism network. Moreover, in that case, the way of group formation is also a key factor to determine cooperation. As can be observed, assuming a structured tourism network, the cooperation levels are higher when players are assigned to groups according to similar tourism dependence. However, the effect of group formation is almost non-existent for a well-mixed population (dotted lines). In this case, the total cooperation achieved when assuming group formation at random or by similarity is almost identical for any risk value.
Then, the highest cooperation levels are achieved when groups are formed with regions with similar income loss, and the strategy update rule considers the social network among them. However, for low-risk values (r < 0.4), the final level of cooperation is higher for a well-mixed relationship among players.
Appendix A presents a robustness analysis of these results when changing the group size N and the minimum percentage of cooperating regions m. The results in Appendix A show that cooperation is easier for small-size groups but more difficult for lower m, as expected. In that case, differences among cooperation levels due to the way the group is formed and the population structure are not so marked, although the positive effect of the existence of a structured tourism network and group formation by similarity remains. The differences in cooperation level that are attained when a structured tourism network and group formation by similarity are assumed to be even higher when group size N is larger.
Summarizing, the results show that cooperation levels increase if players update strategies by observing other players, as they are connected to the structured tourism network. Then, H1 is validated. Additionally, cooperation is more enhanced when cooperating groups are formed by their similar tourism dependence than when they are formed by taking players randomly, validating H2. Moreover, the effect of these factors is augmented when group size and the required minimum number of cooperators to avoid economic collapse is large.
5. Discussion
5.1. Theoretical Implications
This paper analyzes the conditions for stakeholders belonging to tourism networks to adopt measures to control crises and avoid economic collapse. The classical tourism literature has stressed the necessity of collaboration among tourism stakeholders for tourism planning and economic organization [20,21]. Tourism network benefits stakeholders are from diverse aspects, such as enhancing innovation [27], knowledge diffusion [28], and resilience to unfavorable events, such as climate change [24]. Our findings contribute to this literature by analyzing the role of tourism networks in a high-risk crisis, such as a pandemic. Specifically, our study assumes that tourism stakeholders facing this kind of crisis are involved in a collective risk situation where participants coordinate in groups, including a certain number of stakeholders who are free to cooperate or not with other stakeholders in the group. Our main finding is that the existence of a structured social network among stakeholders favors coordination in the groups.
Technically, the positive effect of social networks in coordination games has been observed in other previous evolutionary game models, such as two-person games [43] and public goods games [44]. Our results also extend these findings to the case of collective risk models.
Then, the results show that coordination among stakeholders in the tourism network positively influences the adoption of cooperation measures to control crises in every coordination group. In the context of pandemic diffusion, and assuming the hypothetical case that groups are formed by regions in every country, the main finding means that coordination of tourism-related regions belonging to different countries to avoid pandemic diffusion helps to achieve coordination of regions in every country.
Moreover, our results indicate that coordination is also enhanced if stakeholders are grouped according to their similarity of tourism dependence. In other words, high tourism-dependent stakeholders should coordinate with other high tourism-dependent stakeholders. This finding agrees with previous results [12] and takes a step forward in this respect by showing that the combined effect of a structured social network and group formation by similarity nonlinearly increases their isolated positive effect on cooperation.
Other secondary findings can be also extracted from the analysis. First, cooperation decreases as group size increases. The reason is that the cooperator’s marginal contribution to avoid the risk of economic collapse is lower in large groups, whereas the cost is constant. Then, players have more incentive to freeride and not cooperate in larger compared to smaller groups. These observations agree with previous findings in studies that also used collective risk dilemma models in the context of climate change mitigation agreements [47].
This research engages with recent literature using evolutionary game models in tourism contexts [35,36,37,53]. These previous contributions assume asymmetric evolutionary game models including two or three types of participants, such as tourists, stakeholders, and governments, with infinite and fully connected individuals. In this kind of model, pure strategies, where all agents in every type adopt full cooperation or defection, are the common asymptotic outcome. Mixed strategies are possible when including exogenous dynamics [54] or random mutation of strategies [55]. Our paper proposes a new evolutionary game model applied to the tourism context in a multi-person game, assuming a finite population that is connected through a particular social network. These conditions make it possible to endogenously obtain mixed strategies, which is a novelty in the application of evolutionary game models in tourism research.
To determine a specific tourism network in the model, we took the case of tourist movements among 280 EU NUTS2 regions. Then, although the collective risk model in the paper is adapted to the case of regions as stakeholders, the results can be extrapolated to tourism networks in general, such as local destination networks. In this case, similar stakeholders are those whose income is dependent on tourism to a similar degree. For example, this would be the case of hotels and air carriers, which have a significant part of their income generated from tourism. On the other extreme, we can allocate local businesses or residents who do not depend on tourism to obtain income. The connection or structure of relationships among them represents the tourism network. The social dilemma would be limited to the boundaries of this specific network, but the general findings and recommendations from the analysis above would be applicable.
5.2. Practical Implications
Tourism is a complex ecosystem that involves several stakeholders. Therefore, there is a need to develop coordination mechanisms between participants to face an unforeseen crisis. In this sense, the literature has called for a government response [56] to deal with situations, such as the recent pandemic. Our research shows how to implement this call for government response and coordination in practice.
This research provides clear and direct actions to be carried out by destination management organizations (DMOs). In uncertain situations, such as the one generated by COVID-19, regions may have trouble deciding which actions to implement regarding restrictions. They may be tempted to impose the minimum possible restrictions to attract as much tourism as possible and to allow as much economic activity as possible. However, this type of behavior could lead to the previously mentioned tragedy of the commons. Instead, we provide tourism regions and the DMOs of those regions with a clear path to follow and show who they should try to cooperate with. In our case, it has been shown that the social network created by the connection between tourism-related regions significantly helps achieve enough cooperation in every group, which is not necessarily formed by tourism-related regions. For example, some regions belonging to different countries can be tourism-related (e.g., regions in UK and regions in Spain), and the coordination groups can be formed by all regions in every specific country (e.g., all regions in Spain). Therefore, regions should try to coordinate actions with the regions with which they have a strong tourism connection, namely the regions from which there is an important flow of tourists, to favor achieving enough cooperation in their own country.
5.3. Limitations
The model is not exempt from limitations, some of which open the way for future research. First, in our model, coordination must take place in groups of the same size, which departs from reality where groups can be heterogeneous in size. Second, the model only includes one source of heterogeneity (tourism-dependent income), but other kinds of heterogeneity among players can exist. In the case of regions, this could be GDP, population structure, or health system. This heterogeneity may influence pay-off and consequently update strategies. Third, regarding the tourism network used in the analysis, the data we had access to did not include the real transit of tourists between regions at the NUTS2 level, but instead the transits available were at the country level and were extrapolated to the NUTS2 level. Thus, the social network was constructed by extrapolating the importance of each region as a tourism receiver in the country and as a tourist sender in the country. It would be interesting to rerun the models based on real origin–destination data of tourists between the NUTS2 regions.
Author Contributions
Conceptualization, J.M.H. and J.B.-G.; methodology, J.M.H. and M.C.; software, M.C.; validation, M.C.; formal analysis, M.C.; investigation, J.M.H.; resources, M.C.; data curation, J.B.-G.; writing—original draft preparation, J.M.H., J.B.-G., and M.C.; writing—review and editing, J.M.H., J.B.-G., and M.C.; visualization, M.C.; supervision, J.M.H.; project administration, J.M.H.; funding acquisition, J.M.H. and M.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the University of Las Palmas de Gran Canaria, grant number COVID-19-04; and the Spanish Ministry of Science, Innovation, and Universities, the Andalusian Government, and ERDF under grants SIMARK (P18-TP-4475), CONFIA (PID2021-122916NB-I00) and RYC-2016-19800.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://ec.europa.eu/eurostat/web/tourism/data/database (accessed on 3 March 2021).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A
This Appendix includes a robustness analysis of the results according to values of the group sizes N and a minimum percentage of cooperators in any group m. Figure A1 includes the combination of two group sizes (N = 4 and 20) with the baseline case m = 0.7, showing the contour plot of the final level of cooperation for different values of the initial cooperation and risk values (upper and center panels) and the average level of cooperation assuming a random selection of the initial number of cooperators (lower panel).
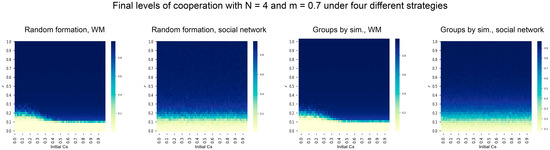
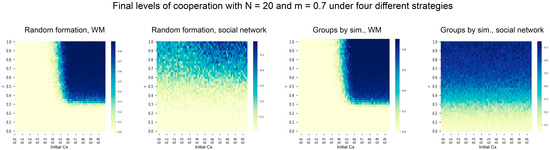
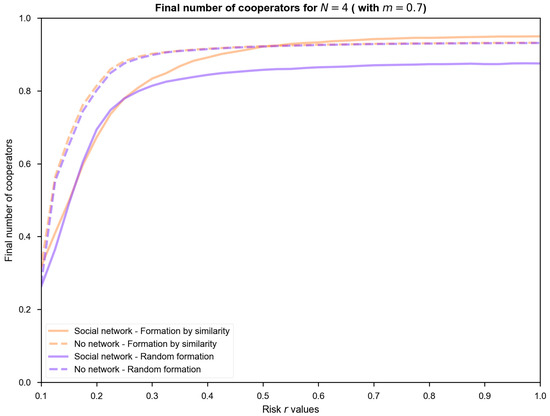
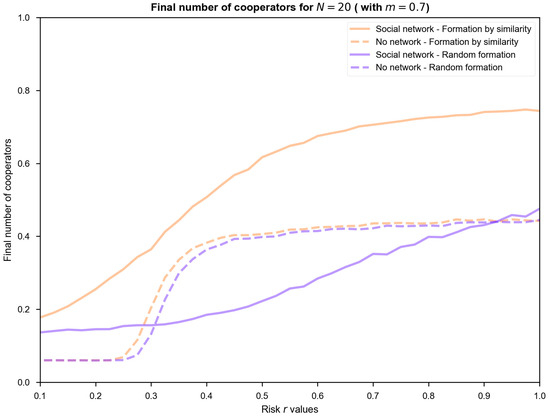
Figure A1.
Robustness analysis of cooperation levels in the collective risk dilemma model for different group sizes.
The results show that cooperation is easier for lower values of N (N = 4) than for higher values (N = 20). Moreover, differences among cooperation levels assuming a well-mixed population and structured tourism network are blurred in the case of N = 4. Nevertheless, the lower right-hand panel clearly shows that the combination of a structured tourism network with group formation according to similar income loss for cooperation obtains the highest cooperation levels in the population.
Figure A2 shows the cooperation level results obtained with a lower minimum m = 0.5 percentage of cooperation in groups than in the baseline case (m = 0.7) and two group sizes (N = 8 and 20). The results show that the optimum levels of cooperation decrease when reducing the value m. Moreover, the effect is more pronounced when combined with higher group size (lower-right panel).
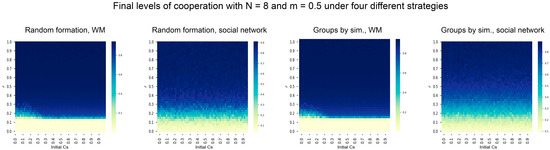
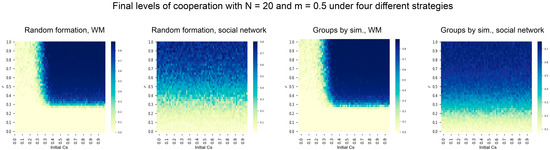
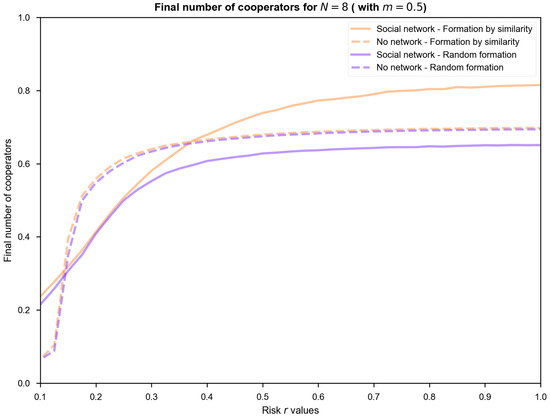
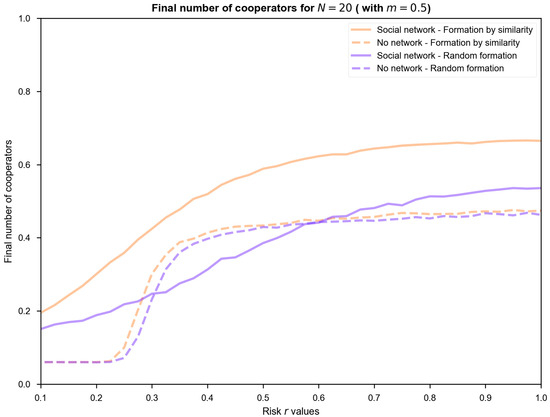
Figure A2.
Robustness analysis of cooperation levels in the collective risk dilemma model for different minimum percentages of cooperation.
References
- Svoboda, J.; Tkadlec, J.; Pavlogiannis, A.; Chatterjee, K.; Nowak, M.A. Infection Dynamics of COVID-19 Virus under Lockdown and Reopening. Sci. Rep. 2022, 12, 1526. [Google Scholar] [CrossRef]
- Jamal, T.; Budke, C. Tourism in a World with Pandemics: Local-Global Responsibility and Action. J. Tour. Futures 2020, 6, 181–188. [Google Scholar] [CrossRef]
- Stafford, G.; Yu, L.; Armoo, A.K. Crisis Management and Recovery: How Washington, DC Hotels Responded to Terrorism. Cornell Hotel. Restaur. Adm. Q. 2002, 43, 27–40. [Google Scholar] [CrossRef]
- Hardin, G. The Tragedy of the Commons Author (s): Garrett Hardin Published by: Stable URL. Am. Assoc. Adv. Sci. 1968, 162, 1243–1248. [Google Scholar]
- Sigmund, K. The Calculus of Selfishness; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Smith, J.M.; Price, G.R. The Logic of Animal Conflict. Nature 1973, 246, 15–18. [Google Scholar] [CrossRef]
- Axelrod, R. The Evolution of Cooperation; Basic Books, Inc.: New York, NY, USA, 1984. [Google Scholar]
- Milinski, M.; Sommerfeld, R.D.; Krambeck, H.J.; Reed, F.A.; Marotzke, J. The Collective-Risk Social Dilemma and the Prevention of Simulated Dangerous Climate Change. Proc. Natl. Acad. Sci. USA 2008, 105, 2291–2294. [Google Scholar] [CrossRef]
- Santos, F.C.; Pacheco, J.M. Risk of Collective Failure Provides an Escape from the Tragedy of the Commons. Proc. Natl. Acad. Sci. USA 2011, 108, 10421–10425. [Google Scholar] [CrossRef]
- Santos, F.C.; Vasconcelos, V.V.; Santos, M.D.; Neves, P.N.B.; Pacheco, J.M. Evolutionary Dynamics of Climate Change under Collective-Risk Dilemmas. Math. Model. Methods Appl. Sci. 2012, 22 (Suppl. S1), 1140004. [Google Scholar] [CrossRef]
- Vasconcelos, V.V.; Santos, F.C.; Pacheco, J.M.; Levin, S.A. Climate Policies under Wealth Inequality. Proc. Natl. Acad. Sci. USA 2014, 111, 2212–2216. [Google Scholar] [CrossRef]
- Chica, M.; Hernández, J.M.; Bulchand-Gidumal, J. A Collective Risk Dilemma for Tourism Restrictions under the COVID-19 Context. Sci. Rep. 2021, 11, 5043. [Google Scholar] [CrossRef]
- Chica, M.; Hernández, J.M.; Santos, F.C. Cooperation Dynamics under Pandemic Risks and Heterogeneous Economic Interdependence. Chaos Solitons Fractals 2022, 155, 111655. [Google Scholar] [CrossRef]
- Scott, N.; Cooper, C.; Baggio, R. Destination Networks. Four Australian Cases. Ann. Tour. Res. 2008, 35, 169–188. [Google Scholar] [CrossRef]
- Van der Zee, E.; Vanneste, D. Tourism Networks Unravelled; a Review of the Literature on Networks in Tourism Management Studies. Tour. Manag. Perspect. 2015, 15, 46–56. [Google Scholar] [CrossRef]
- Baggio, R.; Scott, N.; Cooper, C. Network Science. A Review Focused on Tourism. Ann. Tour. Res. 2010, 37, 802–827. [Google Scholar] [CrossRef]
- Novelli, M.; Schmitz, B.; Spencer, T. Networks, Clusters and Innovation in Tourism: A UK Experience. Tour. Manag. 2006, 27, 1141–1152. [Google Scholar] [CrossRef]
- Pavlovich, K. The Evolution and Transformation of a Tourism Destination Network: The Waitomo Caves, New Zealand. Tour. Manag. 2003, 24, 203–216. [Google Scholar] [CrossRef]
- Morrison, A.; Lynch, P.; Johns, N. International Tourism Networks. Int. J. Contemp. Hosp. Manag. 2004, 16, 197–202. [Google Scholar] [CrossRef]
- Jamal, T.; Getz, D. Collaboration Theory and Community Tourism Planning. Ann. Tour. Res. 1995, 22, 186–204. [Google Scholar] [CrossRef]
- Tremblay, P. The Economic Organization of Tourism. Ann. Tour. Res. 1998, 25, 837–859. [Google Scholar] [CrossRef]
- Borgatti, S.; Everett, M.; Johnson, J. Analyzing Social Networks; SAGE Publications Inc.: New York, NY, USA, 2018. [Google Scholar]
- Newman, M. The Structure and Function of Complex Networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Luthe, T.; Wyss, R.; Schuckert, M. Network Governance and Regional Resilience to Climate Change: Empirical Evidence from Mountain Tourism Communities in the Swiss Gotthard Region. Reg. Environ. Change 2012, 12, 839–854. [Google Scholar] [CrossRef]
- Sainaghi, R.; Baggio, R. Structural Social Capital and Hotel Performance: Is There a Link? Int. J. Hosp. Manag. 2014, 37, 99–110. [Google Scholar] [CrossRef]
- Burt, R.S. The Social Structure of Competition. In Networks in the Knowledge Economy; Cross, R., Parker, A., Sasson, L., Eds.; Oxford University Press: Oxford, UK, 2003; pp. 57–91. [Google Scholar]
- Zach, F.J.; Hill, T.L. Network, Knowledge and Relationship Impacts on Innovation in Tourism Destinations. Tour. Manag. 2017, 62, 196–207. [Google Scholar] [CrossRef]
- Valeri, M.; Baggio, R. Increasing the Efficiency of Knowledge Transfer in an Italian Tourism System: A Network Approach. Curr. Issues Tour. 2022, 25, 2127–2142. [Google Scholar] [CrossRef]
- Albert, R.; Barabasi, A.L. Statistical Mechanics of Complex Networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef]
- Conlisk, J. Why Bounded Rationality? J. Econ. Lit. 1996, 34, 669–700. [Google Scholar] [CrossRef]
- Börgers, T.; Sarin, R. Learning through Reinforcement and Replicator Dynamics. J. Econ. Theory 1997, 77, 1–14. [Google Scholar] [CrossRef]
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Nowak, M.A. Five Rules for the Evolution of Cooperation. Science 2006, 314, 1560–1563. [Google Scholar] [CrossRef]
- Friedman, D. On Economic Applications of Evolutionary Game Theory. J. Evol. Econ. 1998, 8, 15–43. [Google Scholar] [CrossRef]
- He, P.; He, Y.; Xu, F. Evolutionary Analysis of Sustainable Tourism. Ann. Tour. Res. 2018, 69, 76–89. [Google Scholar] [CrossRef]
- Qingyun, P.; Mu, Z. Evolutionary Game Analysis of Land Income Distribution in Tourism Development. Tour. Econ. 2021, 27, 670–687. [Google Scholar] [CrossRef]
- Antoci, A.; Borghesi, S.; Galeotti, M. Environmental Options and Technological Innovation: An Evolutionary Game Model. J. Evol. Econ. 2013, 23, 247–269. [Google Scholar] [CrossRef]
- He, Y.; He, P.; Xu, F.; Shi, C. (Victor) Sustainable Tourism Modeling: Pricing Decisions and Evolutionarily Stable Strategies for Competitive Tour Operators. Tour. Econ. 2019, 25, 779–799. [Google Scholar] [CrossRef]
- Kollock, P. Social Dilemmas: The Anatomy of Cooperation. Annu. Rev. Sociol. 1998, 24, 182–214. [Google Scholar] [CrossRef]
- Pacheco, J.M.; Santos, F.C.; Souza, M.O.; Skyrms, B. Evolutionary Dynamics of Collective Action in N-Person Stag Hunt Dilemmas. Proc. R. Soc. B Biol. Sci. 2009, 276, 315–321. [Google Scholar] [CrossRef]
- Wang, J.; Fu, F.; Wu, T.; Wang, L. Emergence of Social Cooperation in Threshold Public Goods Games with Collective Risk. Phys. Rev. E-Stat. Nonlinear Soft Matter Phys. 2009, 80, 016101. [Google Scholar] [CrossRef]
- Szabó, G.; Fáth, G. Evolutionary Games on Graphs. Phys. Rep. 2007, 446, 97–216. [Google Scholar] [CrossRef]
- Santos, F.C.; Pinheiro, F.L.; Lenaerts, T.; Pacheco, J.M. The Role of Diversity in the Evolution of Cooperation. J. Theor. Biol. 2012, 299, 88–96. [Google Scholar] [CrossRef]
- Santos, F.C.; Santos, M.D.; Pacheco, J.M. Social Diversity Promotes the Emergence of Cooperation in Public Goods Games. Nature 2008, 454, 213–216. [Google Scholar] [CrossRef]
- World Bank World Bank Open Data | Data. Available online: https://data.worldbank.org/ (accessed on 1 December 2021).
- Góis, A.R.; Santos, F.P.; Pacheco, J.M.; Santos, F.C. Reward and Punishment in Climate Change Dilemmas. Sci. Rep. 2019, 9, 16193. [Google Scholar] [CrossRef]
- Pacheco, J.M.; Vasconcelos, V.V.; Santos, F.C. Climate Change Governance, Cooperation and Self-Organization. Phys. Life Rev. 2014, 11, 573–586. [Google Scholar] [CrossRef]
- Eurostat Nuts-Nomenclature of Territorial Units for Statistic. Available online: https://ec.europa.eu/eurostat/web/nuts/background (accessed on 3 March 2021).
- Tsiotas, D.; Tselios, V. Understanding the Uneven Spread of COVID-19 in the Context of the Global Interconnected Economy. Sci. Rep. 2022, 12, 666. [Google Scholar] [CrossRef] [PubMed]
- Schvaneveldt, R.W.; Durso, F.T.; Dearholt, D.W. Network Structures in Proximity Data. Psychol. Learn. Motiv.-Adv. Res. Theory 1989, 24, 249–284. [Google Scholar] [CrossRef]
- Chica, M.; Rand, W. Building Agent-Based Decision Support Systems for Word-of-Mouth Programs: A Freemium Application. J. Mark. Res. 2017, 54, 752–767. [Google Scholar] [CrossRef]
- Macal, C.M.; North, M.J. Tutorial on Agent-Based Modeling and Simulation. In Proceedings of the Winter Simulation Conference, Orlando, FL, USA, 4–7 December 2005; Volume 2005, pp. 2–15. [Google Scholar]
- Cheung, K.S.; Li, L.H. Understanding Visitor–Resident Relations in Overtourism: Developing Resilience for Sustainable Tourism. J. Sustain. Tour. 2019, 27, 1197–1216. [Google Scholar] [CrossRef]
- Blanco, E.; Lozano, J. Ecolabels, Uncertified Abatement, and the Sustainability of Natural Resources: An Evolutionary Approach. J. Evol. Econ. 2015, 25, 623–647. [Google Scholar] [CrossRef]
- Arbara, S.; D’Autilia, R. A Population Game Model for the Expansion of Airbnb in the City of Venice. Sustainability 2021, 13, 3829. [Google Scholar] [CrossRef]
- Sharma, G.D.; Thomas, A.; Paul, J. Reviving Tourism Industry Post-COVID-19: A Resilience-Based Framework. Tour. Manag. Perspect. 2021, 37, 100786. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).