Multicriteria Decision Making and Its Application in Geothermal Power Project

Abstract

The International Energy Agency (IEA) assesses Vietnam as the second largest electricity user in Southeast Asia. The energy consumption growth rate in the region is one of the fastest in the world, with demand growing at a steady 6% per year for the past 20 years. Within the context that domestic fossil fuel production cannot keep up with demand and climate change is occurring, to avoid depending on imported energy to operate the power system, the Government of Vietnam has turned to developing renewable energy. The potential for developing geothermal energy in Vietnam is promising with more than 200 sources of water around 40 to 100 °C, which is sufficient for the development of geothermal energy projects. Today, a method to conserve natural resources and invest in renewable energy is provided by the government by controlling the importation of gas and coal while investing in building geothermal power plants. One of the hardest problems, however, is determining a suitable place to construct a geothermal power plant (GPP). For this main reason, in the hope of solving this problem, the author has proposed a decision-making model that utilizes a fuzzy set under multi-criteria conditions. It uses two methods, Fuzzy Analytic Hierarchy Process (FAHP) followed by Weighted Aggregated Sum Product Assessment (WASPAS), for a GPP site selection decision. The FAHP model is first used to determine the weights of each criterion and sub-criterion. Then, the ranking of each alternative is calculated by the WASPAS model. A final alternative is determined to be the best solution based on calculations from the methods above for identifying suitable locations for a GPP. This research has contributed a method of using a fuzzy multi-criteria decision-making model for determining a suitable location selection. This contribution also shows a development of flexibility towards decision making for other renewable energy projects worldwide.

1. Introduction

The overall demand for electricity in Vietnam is forecasted to grow up to 8–10% per year from 2021, based on the data from Vietnam Ministry of Industry and Trade. In the meantime, the current sources of energy that businesses still rely on are mainly imported fossil fuel energy sources, such as gas, coal, and petroleum. Therefore, the development of renewable energy is said to be the solution to the problem of national energy security in the future. Along with energy from wind, the sun, and ocean waves, geothermal is a clean, environmentally friendly energy source that is being used by 50 countries around the world to produce electricity [1].

The origin of geothermal energy comes from the core of the Earth where natural elements are currently decaying radioactively, such as potassium, thorium, and uranium. Due to the change of entropy generating heat, potential electrical energy of 42 million megawatts can be generated from the Earth’s average heat flow of 82 mW/m² [2]. Overall, the estimated heat coverage on Earth is around 12.6 × 10²⁴ MJ, and the crust of the Earth alone is only 0.0004% of the coverage (approximately 5.4 × 10²¹ MJ) [3]. The heat energy of the crust alone would provide more than enough energy, compared with the current overall electricity generation of 7.1 × 10¹³ MJ [4]. Such an immense source of energy exists, yet only a small portion is currently being developed. The utilization of geothermal energy is restricted to areas with a carrier that could transport sufficient equipment to trigger geothermal energy sources. The classification of the geothermal energy types is shown in

Table 1. Types of Geothermal Resources [5,6].

Resource Type	Temperature Range °C
Convective hydrothermal resources
Vapor dominated	240
Hot water dominated	20 to 350+
Other hydrothermal resources
Sedimentary basin	20 to 150
Geo-pressured	90 to 200
Radiogenic	30 to 150
Hot rock resources
Solidified	90 to 650
Part still molten	>600

; types over 150 °C are sufficient for energy generation.

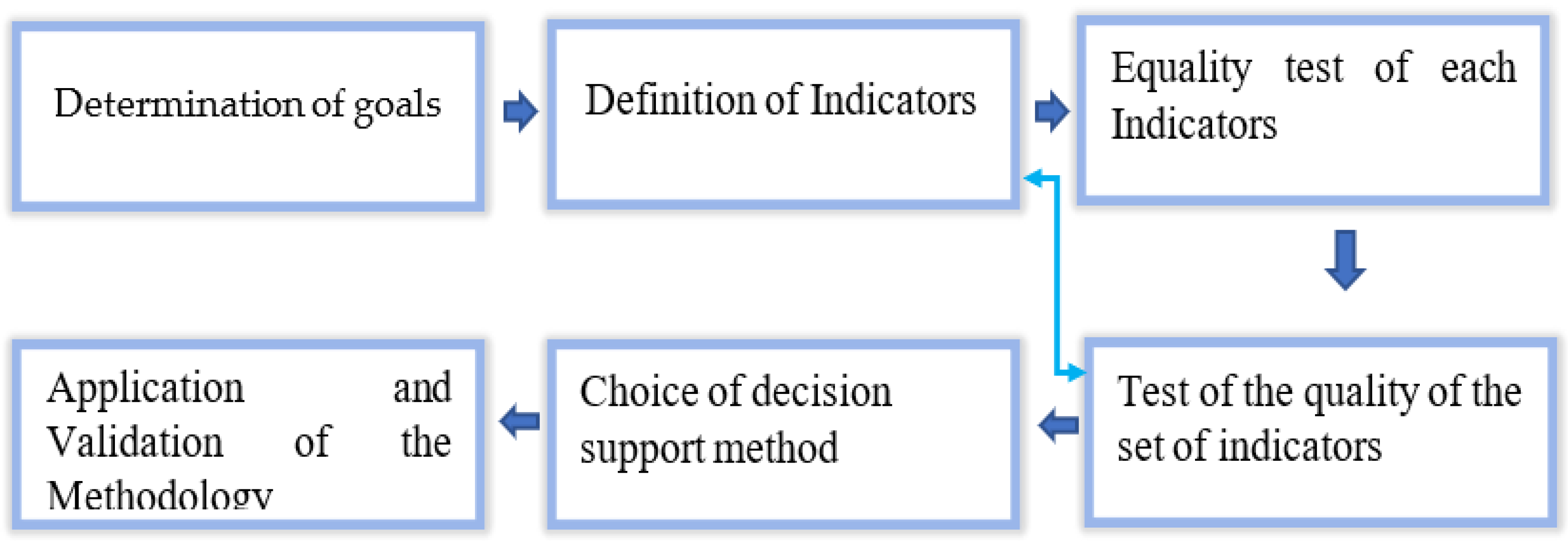
A location selection problem is modelized to determine the optimal site for a geothermal power plant. In this decision-making process, the problem considers the selection of site and ranking of alternatives. A Multicriteria Decision-Making Model (MCDM) is a section of operations research dealing with decision making that often involves unclarity, which is effectively solved using fuzzy sets with decision-making techniques. Therefore, to support researchers and decision makers, the objective of this article is to present an MCDM for determining the optimum site for a geothermal power plant. The MCDM’s process is performed through six steps, as shown in Figure 1.

A Multicriteria Decision-Making Model (MCDM), such as the Brown–Gibson model, Aggregated Indices Randomization Method (AIRM), Best Worst Method (BWM), etc., can be used to help decision-making processes. The decision maker must frequently take both qualitative and quantitative elements into account. In these situations, the MCDM technique is combined with fuzzy theory to develop a fuzzy MCDM strategy to support the decision-making processes. Although several MCDM models have been put forth to support the location evaluation and selection processes in renewable energy, very few hybrid MCDM models have been created to address the location selection for Geothermal Power Plants, particularly in a fuzzy decision-making environment. In this research work, the author has proposed a fuzzy MCDM model for the location selection of geothermal power plants. The FAHP was used to determine the weights for each criterion to rank numerous alternatives. These weights were then entered into the Weighted Aggregated Sum Product Assessment (WASPAS) model. The FAHP–WASPAS model can aid in making the best decisions since it analyzes issues using a variety of criteria and enables decision makers to examine the relationships between these criteria. It also accounts for the subjectivity, ambiguity, and diversity of the decision makers. Therefore, the model in this study can assist decision makers to select an optimal location for investing in a geothermal power plant in Vietnam.

2. Literature Review

The application of an advanced Multicriteria Decision-Making Model to analyze issues related to renewable energy plant location selection is the current trend, using methods such as the AHP model, Best worst method (BWM), TOPSIS model, Evaluation Based on Distance from Average Solution (EDAS) model, and the categorical method. Complex decision-making problems are common in many industries and business sectors, and these problems usually have multiple types of criteria. Throughout the years, Multicriteria Decision-Making Models (MCDM) were developed to support decision makers in solving such complicated problems [7,8,9,10,11]. Decision-making problems are diverse, and include supplier selection [12,13], service quality assessment [14,15], financial risk assessment tool selection [16,17], etc. Among these, MCDM models are frequently applied in facility location selection problems.

Choudhury et al. [18] developed a standardized MCDM-based approach for a water treatment plant location selection problem. The authors also developed a predictive model to automate the feasibility assessment process of potential locations. The authors’ proposed approach was applied to a peri-urban city in northeastern India and the results were consistent with the real scenario. Wang et al. [19] introduced a hybrid MCDM model based on FAHP, Data envelopment analysis (DEA), and TOPSIS methods to support the solar power plant location selection process under a vague decision-making environment. The author utilized several DEA models to identify the potential locations; then, a FAHP model was developed to calculate the weights of the selection criteria. Finally, the TOPSIS technique was applied to rank the potential locations according to their performance across the selection criteria. Kieu et al. [20] proposed an MCDM model to support a distribution center location process for agricultural supply chain. The proposed model was developed based on spherical fuzzy sets theory, AHP technique, and the combined compromise solution (CoCoSo) algorithm. A spherical FAHP model was deployed to calculate the location selection criteria weights, while a CoCoSo model was used to calculate the performance score and ranking of potential locations. The proposed model was applied to a realistic case study in the Mekong Delta Region of Vietnam to demonstrate its feasibility. Żak and Węgliński [21] developed an MCDM/A-based approach to the logistics center location selection problem. Their proposed approach utilized ELECTRE III/IV method to rank the potential regions according to their sustainability for placing the logistics center within their borders. The authors performed several computational experiments to demonstrate the approach’s calculation process. Wu et al. [22] introduced a two-stage fuzzy multiple attribute decision-making framework to support an offshore wind-PV-seawater pumped storage facility location selection process. The proposed framework was applied to a case study in China to validate the feasibility of the proposed framework. Zhang et al. [23] developed an MCDM model to support the international container intermodal hubs (ICIH) location selection process. The authors employed the GRA-TOPSIS method in combination with AHP, Entropy method, and game theory to build a decision support model. The proposed model was applied to identify an optimal location for ICIHs among 38 cities in China, and the result was compared with other popular MCDM models.

There are multiple research works about the integration of MCDM models in facility location selections in the urban planning field. Yavuz Kumlu and Tüdeş [24] proposed an MCDM model based on the combination of Geographic Information System (GIS), AHP, and TOPSIS methods to support the earthquake risk assessment process in the city of Yalova in Turkey. The result of the model can be a reference for urban planners in disaster mitigation processes. Alkaradaghi et al. [25] developed a GIS-based MCDM model for a landfill location selection problem. The studied model was built based on GIS and a combination of the weighted linear combination (WLC) method and MCDM methods. The authors applied the studied method to a case study in the Sulaimaniyah Governorate of Iraq to demonstrate its feasibility. Tahmasebi Birgani and Yazdandoost [26] introduced an MCDM-based approach to the urban drainage management plans evaluation process. The proposed framework was built based on adaptive AHP, Entropy, and TOPSIS methods. A real-world case study was tested where the studied framework was applied to evaluate four urban drainage plans for Tehran. Feyzi et al. [27] proposed a GIS-based MCDM model to calculate potential locations for a solid waste incineration power plant. The authors utilized the fuzzy analytic network process (fuzzy ANP) method to calculate the evaluation criteria weights and decision-making trial and evaluation laboratory (DEMATEL) technique to determine interrelation between the criteria. The studied model was demonstrated through a realistic case study in northern Iran. Kharat et al. [28] introduced an integrated fuzzy MCDM approach to support a landfill location selection. The proposed model was based on FAHP and fuzzy TOPSIS. An illustrative case study was performed to demonstrate the calculation process of the model. Niknam et al. [29] proposed a dynamic modelling of the reinjection process in a binary cycle geothermal power plant. In this work, the author introduces a new Antoine-based correlation for a water–CO2 mixture. Niknam et al. [30] studied the modeling of a steam-washing scrubber for solid removal in geothermal powerplants. The authors also validated industrial sizing correlations data for scrubbers in geothermal applications.

As a review of the literature shows, several MCDM models have been put forth to support location evaluation and selection processes in renewable energy, but very few hybrid MCDM models have been created to address the location selection for Geothermal Power Plants, particularly in a fuzzy decision-making environment. In this research work, the authors introduce a fuzzy Multicriteria Decision-Making Model, including the methods of fuzzy analytic hierarchy process (FAHP) and the Weighted Aggregated Sum Product Assessment (WASPAS), for a geothermal power plant site selection in Vietnam. The FAHP can be applied for ranking alternatives, but the number of alternatives selected is practically limited because of the number of pair-wise comparisons that need to be made, and a disadvantage of the FAHP approach is that the input data, expressed in linguistic terms, depend on the experience of decision makers, and thus involves subjectivity. This is the reason why we proposed the WASPAS model for ranking alternatives in the final stage. Additionally, WASPAS is presented to reaffirm it as a systematic method and solve the disadvantages of the FAHP model mentioned above.

3. Methodology

The selection process of optimal location for a geothermal power plant project is an MCDM issue involving both qualitative and quantitative considerations. In this study, the authors presented a dynamic fuzzy MCDM model for the selection of a suitable location for building a geothermal power plant by utilizing FAHP and WASPAS techniques. There are five steps in the decision-making process (Figure 2):

3.1. Triangular Fuzzy Number (TFN)

TFN is classified as (h,i,j), where h, i, and j (h ≤ i ≤ j). TFNs are shown in Figure 3 can be defined as follows [31]:

The definition below is an example of a fuzzy number.

$$\tilde{M}=(M^{o\left(y\right)},M^{i\left(y\right)})=\left[h+\left(i-h\right)y,j+\left(i-j\right)y\right],y \in \left[0,1\right]$$

(1)

$o\left(y\right) \mathrm{and} i\left(y\right)$ are the lower and upper limits of a fuzzy number, respectively. Two positive TFNs $\left(h_1, i_1, j_1\right)$ are used in the basic computations presented below$\left(h_2, i_2, j_2\right)$.

$$\left(h_1, i_1, j_1\right)+\left(h_2, i_2, j_2\right)=\left(h_1+h_2, i_1+i_2,j_1+j_2\right)$$

(2)

$$\left(h_1, i_1, j_1\right)-\left(h_2, i_2, j_2\right)=\left(h_1-h_2, i_1-i_2,j_1-j_2\right)$$

(3)

$$\left(h_1, i_1, j_1\right)\times \left(h_2, i_2, j_2\right)=\left(h_1\times h_2, i_1\times i_2,j_1\times j_2\right)$$

(4)

$$\frac{\left(h_1, i_1, j_1\right)}{\left(h_2, i_2, j_2\right)}=\left(h_1/h_2, i_1/i_2,j_1/j_2\right)$$

(5)

3.2. Fuzzy Analytical Hierarchy Process (AHP)

The FAHP model alleviates the limitations of analytical hierarchy process (AHP), allowing it to work under unclear environments. Let $X=\left\{x_1, x_2,\dots .x_n\right\}$ be the set of objects, and K$=\left\{k_1, k_2,\dots .k_n\right\}$ be the set of objectives [32].

These sets are defined as follows:

$$L_{k_i}^1,L_{k_i}^2,\dots ,L_{k_i}^m, i=1,2,\dots ,n$$

(6)

where $L_k^j\left(j=1,2,\dots . ,m\right)$ are TFNs.

The $i^{th}$ object’s fuzzy synthetic extent value as:

$$S_i={\displaystyle \sum }_{j=1}^m{L}_{k_i}^j\otimes {\left[{\displaystyle \sum }_{i=1}^n{\displaystyle \sum }_{j=1}^m{L}_{k_i}^j\right]}^{-1}$$

(7)

The possibility that $L_1\ge L_2$ is defined as:

$$V\left(L_1\ge L_2\right)=su{p}_{y\ge x}\left[min\left({\mu }_{L_1}\left(x\right),\right),\left({\mu }_{L_2}\left(y\right)\right)\right]$$

(8)

$V\left(L_1\ge L_2\right)=1$ if the couple $\left(x,y\right)$ defined with $x\ge y$ and ${\mu }_{L_1}\left(x\right)={\mu }_{L_2}\left(y\right)$.

Because $L_1$ and $L_2$ are convex TFNs, we have:

$$V\left(L_1\ge L_2\right)=1, if l_1\ge l_2$$

(9)

and

$$\left(L_2\ge L_1\right)=hgt\left(L_1◠L_2\right)={\mu }_{L_1}\left(d\right)$$

(10)

The d is denoted as the highest intersection point from ${\mu }_{L_1}$ to ${\mu }_{L_2}$ is defined by $d$.

Point d is defined with $L_1=(o_1,p_1$,$q_1)$ and $L_2=(o_2,p_2$,$q_2)$ by (9):

$$V\left(L_2\ge L_1\right)=hgt\left(L_1◠L_2\right)=\frac{l_1-q_2}{\left(p_2-q_2\right)-\left(p_1-o_1\right)}$$

(11)

The comparison between $L_1$ and $L_2$ by determining the values of $V\left(L_1\ge L_2\right)$ and $V\left(L_2\ge L_1\right)$.

$L_i\left(i=1,2,\dots k\right)$ is the probability of a convex fuzzy number being bigger than $k$ convex fuzzy numbers.

$$\left(L\ge L_1,L_2,\dots ,L_k\right)=V\left[\left(L\ge L_1\right) and \left(L\ge L_2\right) \right]$$

(12)

and $(L\ge L_k$) = min $V(L\ge L_i), i=1,2,\dots , k$

Assume that:

$$d^{\prime }\left(B_i\right)=minV\left(S_i\ge S_k\right)$$

(13)

for $k=1,2,\dots n \mathrm{and} k\#i$,

The following shows the calculation of the weight vector:

$$W^{\prime }={\left(d^{\prime }\left(B_1\right),d^{\prime }\left(B_2\right),\dots d^{\prime }\left(B_n\right)\right)}^T$$

(14)

where $B_i$ is the number of criteria, and $n$ is the number of elements.

The normalized weight vectors are now calculated as:

$$W={\left(d\left(B_1\right),d\left(B_2\right),\dots .,d\left(B_n\right)\right)}^T$$

(15)

The number $W$ is a real number.

The consistent ratio of a Saaty’s matrix is determined by evaluating it.

$$CR=\frac{CI}{RI}=\frac{\overline{\lambda }-n}{\left(n-1\right)\times RI}\le 0.1$$

(16)

3.3. Weighted Aggregated Sum Product Assessment (WASPAS)

For each potential decision-making unit (DMU), its ranking can be determined by the product between the rating of each criterion’s weight [33,34].

1.

The matrix of decision-making is normalized.

For an advantageous decision criterion, the normalization is shown in Equation (17) as follows:

$${\mathrm{q}}_{\mathrm{ij}}=\frac{{\mathrm{x}}_{\mathrm{ij}}}{\max {\mathrm{x}}_{\mathrm{ij}}}, \mathrm{i}=1,2, \dots , \mathrm{n};\mathrm{j}=1, 2, \dots , \mathrm{m}$$

(17)

For a disadvantageous decision criterion, it is shown in Equation (18):

$${\mathrm{q}}_{\mathrm{ij}}=\frac{{\mathrm{x}}_{\mathrm{ij}}}{\min {\mathrm{x}}_{\mathrm{ij}}}, \mathrm{i}=1,2, \dots , \mathrm{n};\mathrm{j}=1, 2, \dots , \mathrm{m}$$

(18)

2.

The relative significance of the i^th alternative is determined, using the Weighted Sum Model (WSM) as:

$${\mathrm{S}}_{\mathrm{i}}^1={\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{q}}_{\mathrm{ij}}\times {\mathrm{w}}_{\mathrm{j}}$$

(19)

3.

The performing evaluation index of the i^th options is determined by using the Weighted Product Model (WPM) as Equation (20):

$${\mathrm{S}}_{\mathrm{i}}^2={\displaystyle \prod }_{\mathrm{j}=1}^{\mathrm{n}}{\left({\mathrm{q}}_{\mathrm{ij}}\right)}^{{\mathrm{w}}_{\mathrm{j}}}$$

(20)

4.

The total relative importance is calculated by a combination of Equations (19) and (20).

The weighted combination of the addition and multiplication approach for WASPAS model is determined as follows:

$$\mathrm{S}={\mathsf{\lambda }\mathrm{S}}_{\mathrm{i}}^1+\left(1-\mathsf{\lambda }\right){\mathrm{S}}_{\mathrm{i}}^2=\mathsf{\lambda }{\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{q}}_{\mathrm{ij}}\times {\mathrm{w}}_{\mathrm{j}}+\left(1-\mathsf{\lambda }\right){\displaystyle \prod }_{\mathrm{j}=1}^{\mathrm{n}}{\left({\mathrm{q}}_{\mathrm{ij}}\right)}^{{\mathrm{w}}_{\mathrm{j}}}$$

(21)

with $\mathsf{\lambda }$ as the coefficient where $\mathsf{\lambda }\in$ [0,1]. Normally, its value is defaulted to $\mathsf{\lambda }$ = 0.5.

The options are then finally ordered based on the index of performance, and the best location would score the greatest.

4. Case Study

Geothermal energy has been exploited and used since the early 20th century for the purpose of heating, drying agricultural products, relaxing, bathing, etc. Since then, research and development of technology to exploit energy sources has been carried out. Geothermal energy is growing rapidly in scale and efficiency. The building of geothermal power plants (due to their low cost and ecological cleanliness) has been quite popular in many countries, such as the US, China, France, New Zealand, Japan, Philippines, Canada, Australia, etc. If direct use is included, geothermal energy is being used in 70 countries around the world. Despite facing economic and technical challenges, geothermal energy scientists still forecast optimistically that geothermal exploitation will overcome the initial difficulties and will have an important place among the energy sources of the future.

In Vietnam, according to a survey and evaluation of scientists, there are currently about 264 sources; hot springs are distributed relatively evenly across the country with an average temperature of 40–100 °C at a depth of 3 km. In addition, this energy source also has the advantage of being evenly distributed throughout the country, so it can be widely used in most localities, such as Phu Tho, Quang Binh, Hoa Binh, Quang Ngai, and Quang Tri [35].

In this research work, the author presents a fuzzy multicriteria decision-making approach to select an appropriate location for a geothermal power plant from five potential alternatives, Phu Tho (DMU1), Quang Binh (DMU2), Hoa Binh (DMU3), Quang Ngai (DMU4), and Quang Tri (DMU5)). The three main criteria are physical suitable area, socioeconomic suitable area, and technical suitable area. A list of main criteria and sub-criteria is shown in

Table 2. List of criteria.

No	Main Criteria	Sub-Criteria and Symbol	Literature Review	Experts
1	Physical suitable area	Slope (GPP01)	Lashin et al. [36]	X
		Rivers (GPP02)	Shortall et al. [37]	X
		Faults (GPP03)	Siler et al. [38]	X
2	Socioeconomic suitable area	Population Centers (GPP04)	Shortall et al. [39]	X
		Access Road (GPP05)	Yudha et al. [40]	X
3	Technical suitable area	Anomaly Zone (GPP06)	Yousefi et al. [41]	X
		Well Locations (GPP07)	Lv et al. [42]	X
		Hot Springs (GPP08)	Shi et al. [43]	X

; they are explained with proper consultation of the literature and expert opinions regarding how each criterion and sub-criterion was chosen according to its importance for determining a suitable geothermal power plant location.

Although the AHP method is widely used, AHP often has limitations because of its incapability to combine the uncertainty and vagueness that always exists in establishing the mapping of perceptions, the decision maker’s assessment, to exact numbers. To overcome these limitations, the author applied FAHP for determining the weight of criteria in the first stage of this study. A fuzzy comparison matrix based on experts’ opinions and literature consultation for all criteria is shown in

Table 3. Fuzzy comparison matrices.

Criteria	Physical Suitable Area (PSA)	Socioeconomic Suitable Area (SSA)	Technical Suitable Area (TSA)
Physical suitable area (PSA)	(1,1,1)	(1,2,3)	(3,4,5)
Socioeconomic suitable area (SSA)	(1/3,1/2,1)	(1,1,1)	(4,5,6)
Technical suitable area (TSA)	(1/5,1/4,1/3)	(1/6,1/5,1/4)	(1,1,1)

.

In this work, the author utilized the triangular fuzzy number to convert the fuzzy numbers to real numbers (α = 0.5 and β = 0.5). α = 0.5 and β = 0.5 are chosen in this case to balance the change during the conversion between the fuzzy values and real values and to equally use both the geometrical value and summation of each assessment.

$${\mathrm{Q}}_{0.5,0.5}{\left(\overline{a_{PSA,TSA}}\right)}_{ }=\left[\right(0.5 \times 3.5)+(1-0.5) \times 4.5]=4$$

(22)

f_0.5(L_PSA,TSA) = (4 −3) × 0.5 + 3 = 3.5

(23)

f_0.5(U_PSA,TSA) = 5 − (5 − 4) × 0.5 = 4.5

(24)

$${\mathrm{Q}}_{0.5,0.5}{\left(\overline{a_{TSA,PSA}}\right)}_{ }=¼$$

(25)

The real number priority when comparing the main criteria pairs is shown in

Table 4. Real number priority.

Criteria	Physical Suitable Area (PSA)	Socioeconomic Suitable Area (SSA)	Technical Suitable Area (TSA)
Physical suitable area (PSA)	1	2	4
Socioeconomic suitable area (SSA)	1/2	1	5
Technical suitable area (TSA)	1/4	1/5	1

.

The maximum individual values are calculated as follows in order to guarantee complete randomness amongst the criteria:

S1 = (1 × 2 × 4)^1/3 = 2

(26)

S2 = (1/2 × 1 × 5)^1/3 = 1.36

(27)

S3 = (1/4 × 1/5 × 1)^1/3 = 0.37

(28)

$$\sum S=S1+S2+S3=3.73$$

(29)

$${\omega }_1=\frac{2}{3.73}=0.54$$

(30)

$${\omega }_2=\frac{1.36}{3.73}=0.36$$

(31)

$${\omega }_3=\frac{0.37}{3.73}=0.1$$

(32)

$$\left[\begin{array}{ccc}1& 2& 4\\ 1/2& 1& 5\\ 1/4& 1/5& 1\end{array}\right]\times \left[\begin{array}{c}0.54\\ 0.36\\ 0.1\end{array}\right]=\left[\begin{array}{c}1.66\\ 1.13\\ 0.31\end{array}\right]$$

(33)

$$\frac{\left[\begin{array}{c}1.66\\ 1.13\\ 0.31\end{array}\right]}{\left[\begin{array}{c}0.54\\ 0.36\\ 0.1\end{array}\right]}=\left[\begin{array}{c}3.07\\ 3.14\\ 3.1\end{array}\right]$$

(34)

Based on the number of main criteria, the authors get n = 3; λ_max and CI are calculated as following:

$${\lambda }_{max}=\frac{3.07+3.14+3.1}{3}=3.1$$

(35)

$$CI=\frac{{\lambda }_{max}-n}{n-1}=\frac{3.18-3}{3-1}=0.05$$

(36)

To calculate CR value, we get RI = 0.52 with n = 3.

$$CR=\frac{CI}{RI}=\frac{0.05}{0.52}=0.0962$$

(37)

the consistency ratio, CR = 0.0962 ≤ 0.1, so there is no need to re-evaluate.

The pair-wise comparison is then shown in

Table 5. The results of pair-wise comparison matrix.

Criteria	Physical Suitable Area (PSA)	Socioeconomic Suitable Area (SSA)	Technical Suitable Area (TSA)	Weight
Physical suitable area (PSA)	1	2	4	0.5368
Socioeconomic suitable area (SSA)	1/2	1	5	0.3643
Technical suitable area (TSA)	1/4	1/5	1	0.0989
	CR = 0.0904

between the three main criteria being assessed in the case study.

The weight of criteria for each sub-criterion after applying the weighting of the three main criteria accordingly is shown in

Table 6. Weight of criteria.

Criteria	Fuzzy Sum of Each Row	Fuzzy Synthetic Extent	Degree of Possibility (Mi)	Weight of Criteria
GPP01	(7.0847, 9.9603, 14.0869)	(0.0705, 0.1385, 0.2749)	0.6768	0.1336
GPP02	(6.8694, 10.2132, 4.8605)	(0.0683, 0.1420, 0.2900)	0.7010	0.1384
GPP03	(6.7986, 9.8975, 14.1405)	(0.0676, 0.1376, 0.2759)	0.6759	0.1335
GPP04	(6.7945, 9.7136, 13.6871)	(0.0676, 0.1351, 0.2671)	0.6597	0.1303
GPP05	(5.8296, 8.3495, 12.1361)	(0.0580, 0.1161, 0.2368)	0.5762	0.1138
GPP06	(4.5197, 5.8714, 8.0751)	(0.0450, 0.0816, 0.1576)	0.3420	0.0675
GPP07	(5.3517, 6.9720, 9.3428)	(0.0532, 0.0969, 0.1823)	0.4325	0.0854
GPP08	(7.9967, 10.9484, 14.1917)	(0.0796, 0.1522, 0.2769)	1.0000	0.1975

.

The WASPAS approach is a unique combination of weighted sum model (WSM) and weighted product model (WPM). Due to simple mathematics operations and the capability to give more accurate results as compared to the individual WSM and WPM methods, the WASPAS model is now being chosen as an efficient decision-making tool in an MCDM model. In this work, a WASPAS model is applied to rank five potential locations. The results of the normalized matrix, weighted normalized matrix, and exponentially weighted matrix for the WASPAS model are displayed in

Table 7. Normalized Matrix.

Alternatives	Criteria
	GPP01	GPP02	GPP03	GPP04	GPP05	GPP06	GPP07	GPP08
DMU1	1.0000	0.7778	1.0000	0.7778	1.0000	0.8889	1.0000	0.7778
DMU2	1.0000	1.0000	0.8750	1.0000	0.7778	0.7778	0.6667	0.8889
DMU3	0.8889	0.8889	0.7500	0.6667	0.6667	1.0000	0.6667	0.6667
DMU4	0.7778	0.8889	1.0000	0.8889	1.0000	0.8889	0.7778	1.0000
DMU5	1.0000	1.0000	1.0000	1.0000	0.8889	1.0000	1.0000	1.0000

,

Table 8. Weighted Normalized Matrix.

Alternatives	Criteria
	GPP01	GPP02	GPP03	GPP04	GPP05	GPP06	GPP07	GPP08
DMU1	0.1336	0.1077	0.1335	0.1013	0.1138	0.0600	0.0854	0.1536
DMU2	0.1336	0.1384	0.1168	0.1303	0.0885	0.0525	0.0569	0.1755
DMU3	0.1188	0.1230	0.1001	0.0869	0.0759	0.0675	0.0569	0.1316
DMU4	0.1039	0.1230	0.1335	0.1158	0.1138	0.0600	0.0664	0.1975
DMU5	0.1336	0.1384	0.1335	0.1303	0.1011	0.0675	0.0854	0.1975

and

Table 9. Exponentially Weighted Matrix.

Alternatives	Criteria
	GPP01	GPP02	GPP03	GPP04	GPP05	GPP06	GPP07	GPP08
DMU1	1.0000	0.9658	1.0000	0.9678	1.0000	0.9921	1.0000	0.9516
DMU2	1.0000	1.0000	0.9823	1.0000	0.9718	0.9832	0.9660	0.9770
DMU3	0.9844	0.9838	0.9623	0.9485	0.9549	1.0000	0.9660	0.9231
DMU4	0.9670	0.9838	1.0000	0.9848	1.0000	0.9921	0.9788	1.0000
DMU5	1.0000	1.0000	1.0000	1.0000	0.9867	1.0000	1.0000	1.0000

, based on the factors of 0.5, 0.5. of the alpha and beta values of the WSM and WPM methods, accordingly.

The final ranking function value S_i was identified by using weighted sum mode S_i1 (WSM) and weighted product model Q_i2 (WSM), as can be seen in

Table 10. Coefficient value of WASPAS.

Alternatives	Si1	Si2	Si
DMU1	0.8889	0.8824	0.8857
DMU2	0.8926	0.8858	0.8892
DMU3	0.7608	0.7527	0.7567
DMU4	0.9140	0.9097	0.9118
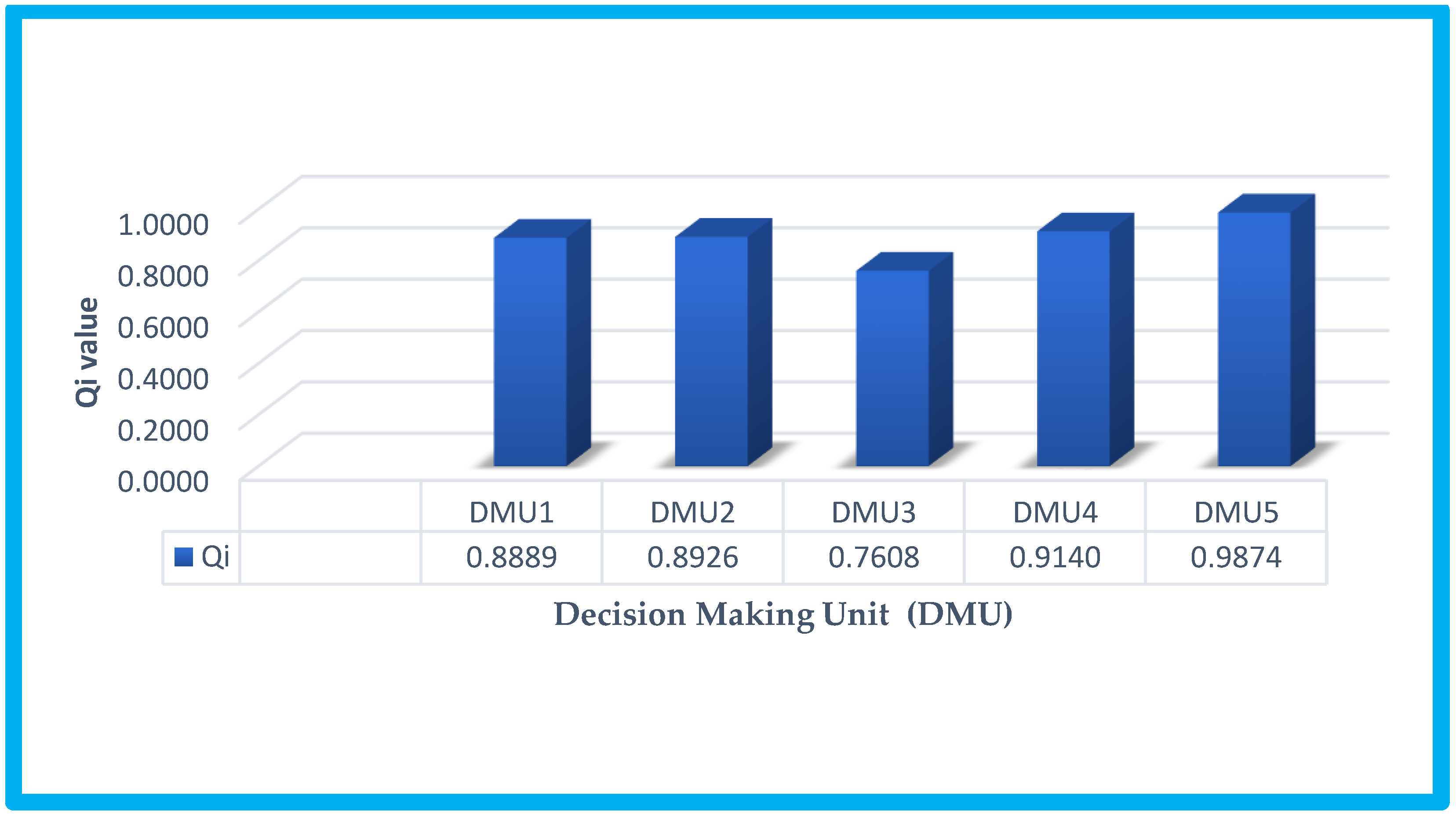
DMU5	0.9874	0.9867	0.9870

. From the results in Figure 4, the three highest suitable locations were DMU5, DMU4, and DMU2, with scores of 0.9870, 0.9118, and 0.8892, respectively. Therefore, Quang Tri (DMU5) is the optimal location, based purely on methodology calculations.

For sensitivity analysis, a modification in the coefficient λ was conducted (coefficient λ is fixed in the range of 0.1, 0.2, 0.3, …, 1). The ranking results for varying λ values are exhibited in Figure 5. The results show that the values of the coefficient λ do not affect the change in the rank of the alternative.

5. Conclusions

The selection process of determining an optimal location for a geothermal power plant project is an MCDM issue involving both qualitative and quantitative considerations. In this research work, the authors introduced a fuzzy Multicriteria Decision-Making Model, including the methods of fuzzy analytic hierarchy process (FAHP) and the Weighted Aggregated Sum Product Assessment (WASPAS), for the selection of a geothermal power plant site in Vietnam. The FAHP model is first used to determine the weights of each criterion and sub-criterion. Then, the ranking of each alternative is calculated by the WASPAS model. According to the data in Figure 4, Quang Tri (DMU5) is the optimal location.

The contribution of this research is to determine a decision support system for geothermal power in Vietnam. First, the studied approach is the first geothermal power plant site selection model in Vietnam consulting expert opinions and the literature. Second, this is the first work to introduce a case study on judging potential locations for the geothermal power plant site selection that uses a combination of FAHP and the WASPAS model. The findings also provide a useful guideline for selecting optimal locations in other types of renewable energy resources.

In the case that AHP fails to apply in methodology and does not compute a suitable answer, the decision makers can use other fuzzy integrated models such as F-TOPSIS to rank the weight of each criterion suitably.

In the future, this research can be opened to other MCDM techniques, such as Aggregated Indices Randomization Method (AIRM), Base-criterion method (BCM), the Dominance-based rough set approach (DRSA), etc.