Legs Geometry Influence on the Performance of the Thermoelectric Module
Abstract
1. Introduction
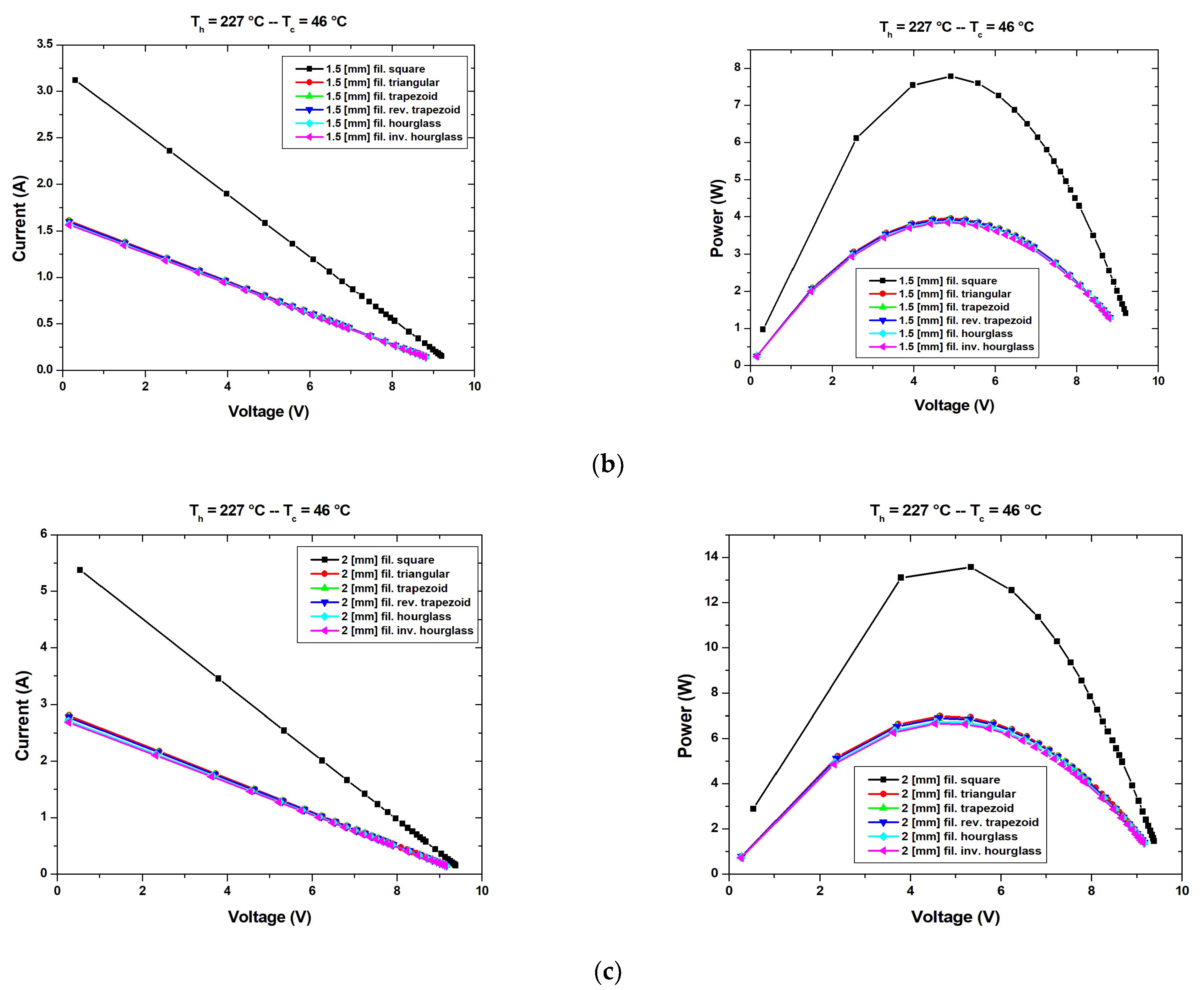
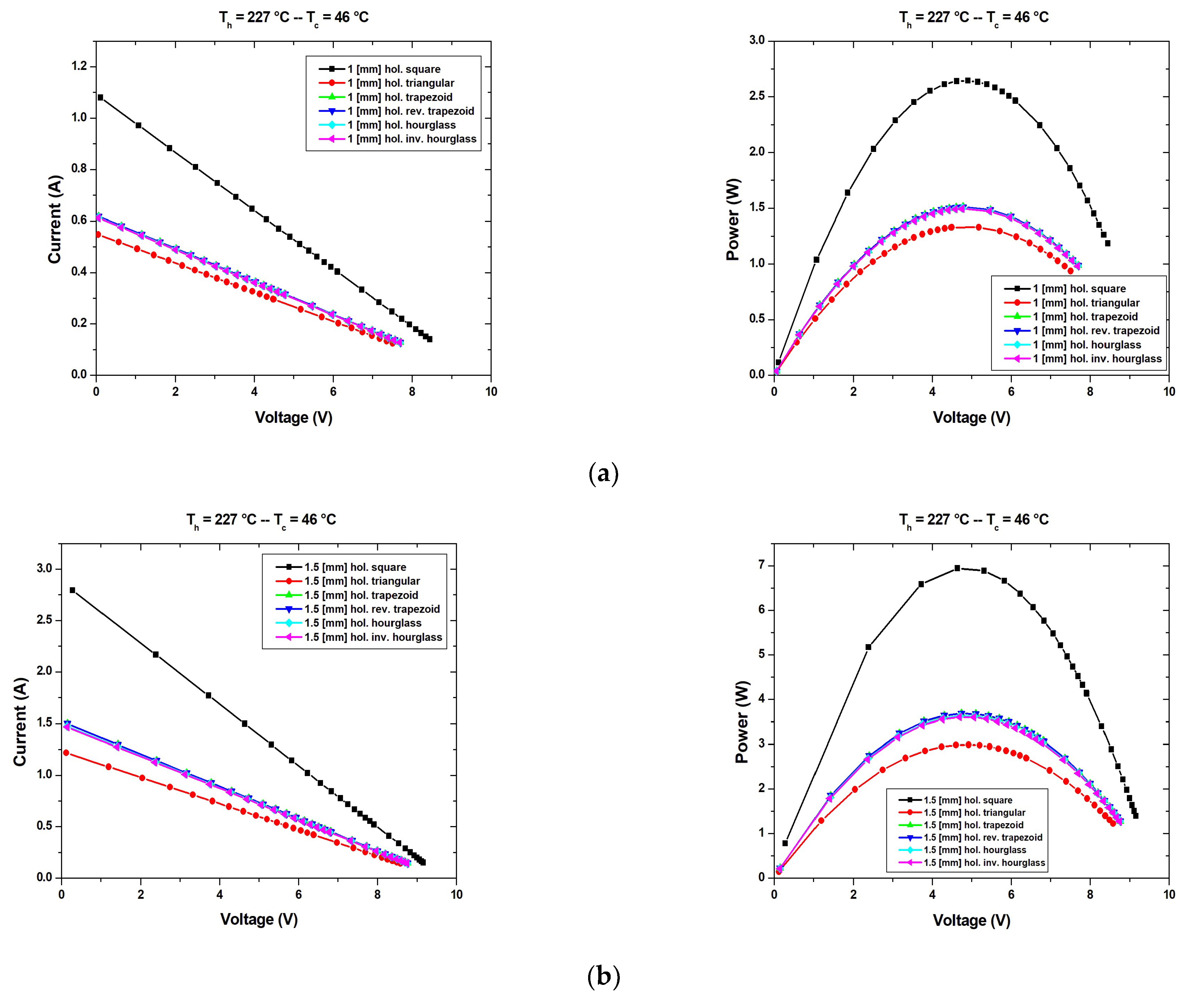
- The calculation of the maximum power, short circuit current, and open circuit voltage of the thermoelectric generator based on Bi2Te3 for different shapes of the leg using COMSOL Multiphysics [32]: square (the conventional leg shape); triangular; trapezoid; reverse trapezoid; hourglass; inverse hourglass; hollow square; hollow triangular; hollow trapezoid; hollow reverse trapezoid; hollow hourglass; hollow inverse hourglass;
- The calculation of the maximum power, short circuit current, and open circuit voltage of the thermoelectric generator based on Bi2Te3 for the first time for a square shape with internal hollow to reduce the material and thus implicitly the costs of the TEG;
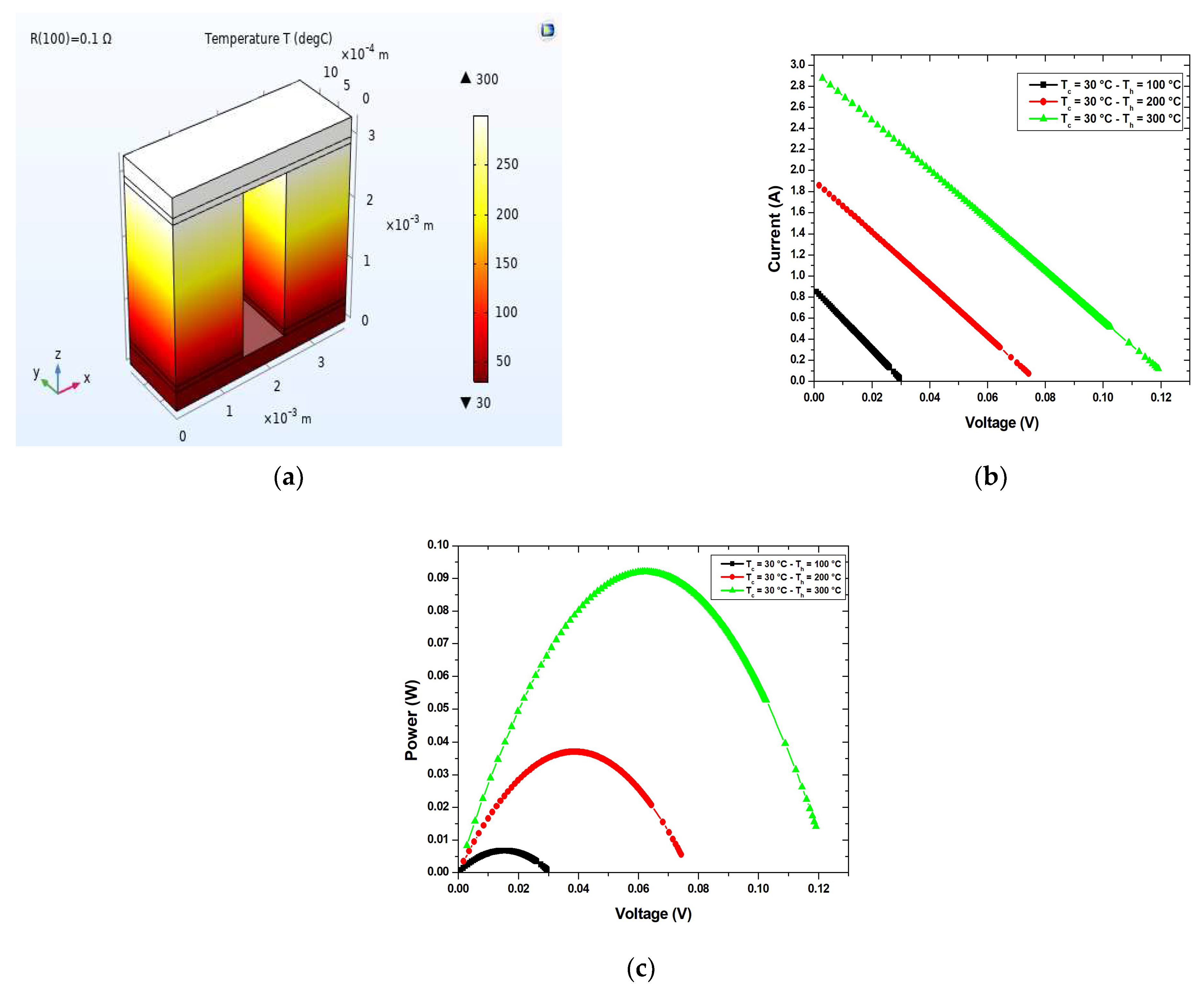
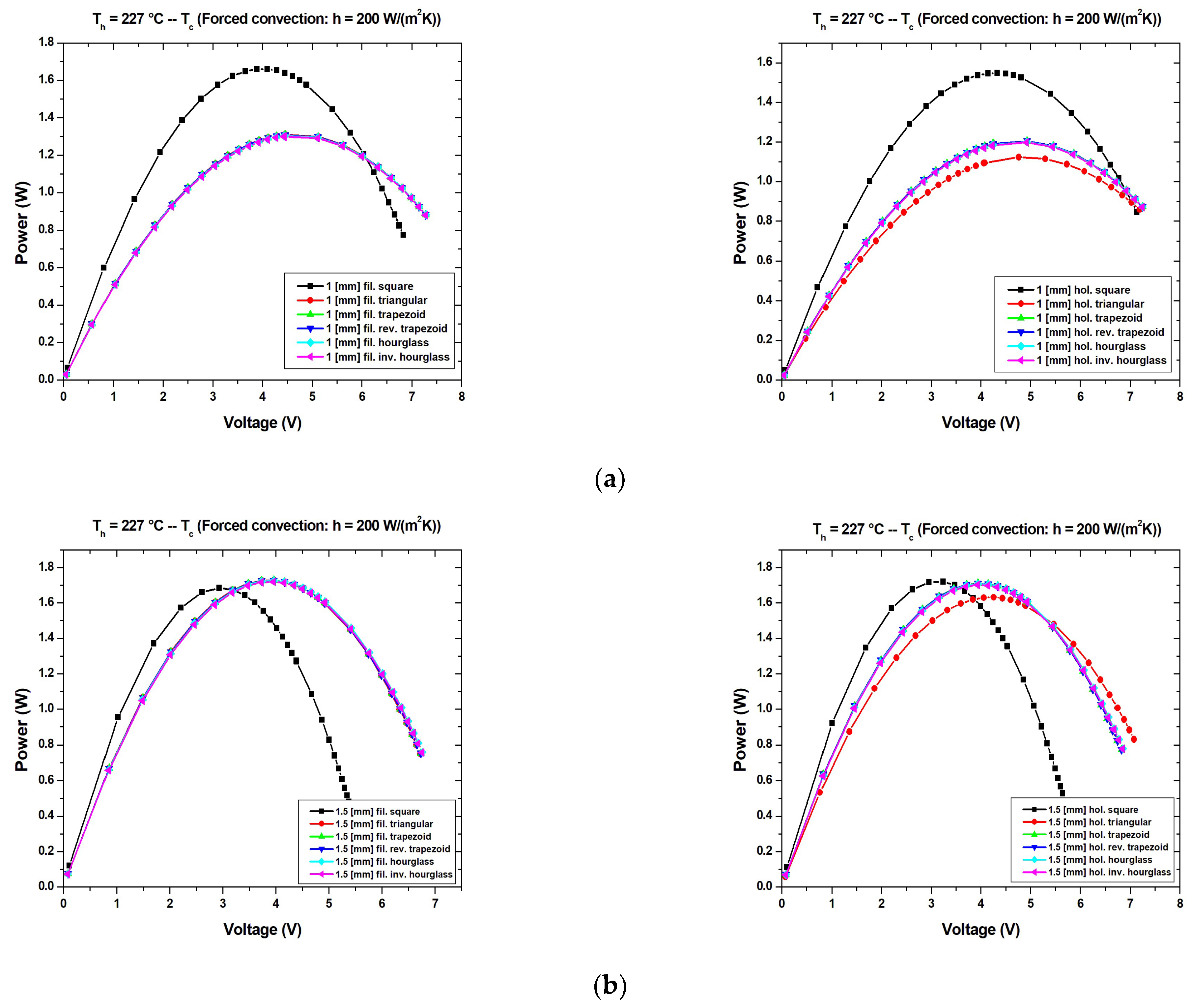
- The calculation of the maximum power and short circuit current of the thermoelectric generator based on Bi2Te3 for different difference of the temperature—the hot side is in a steady-state heating condition while the cold side is subjected to steady state, natural convection, and forced convection heating conditions;
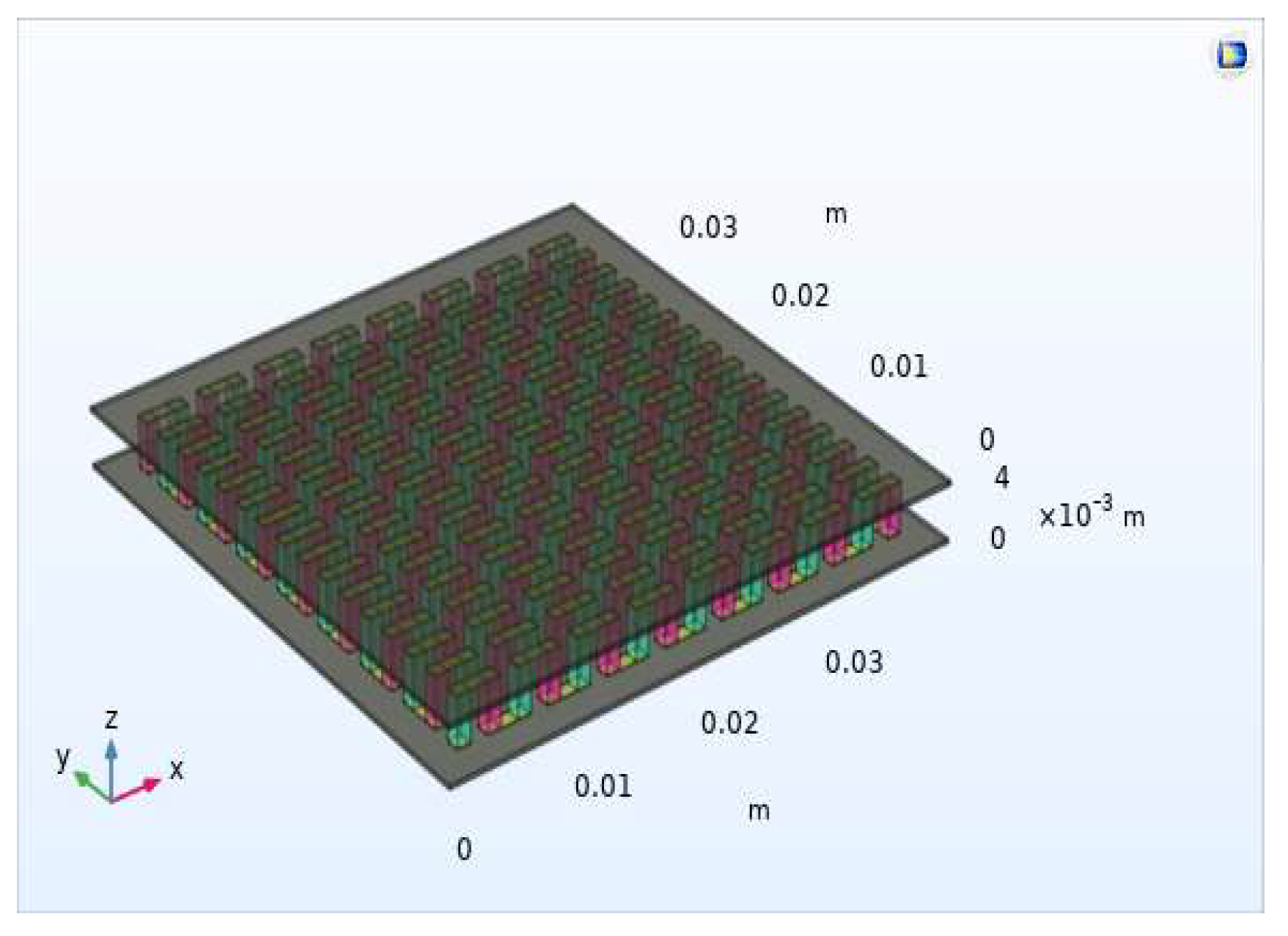
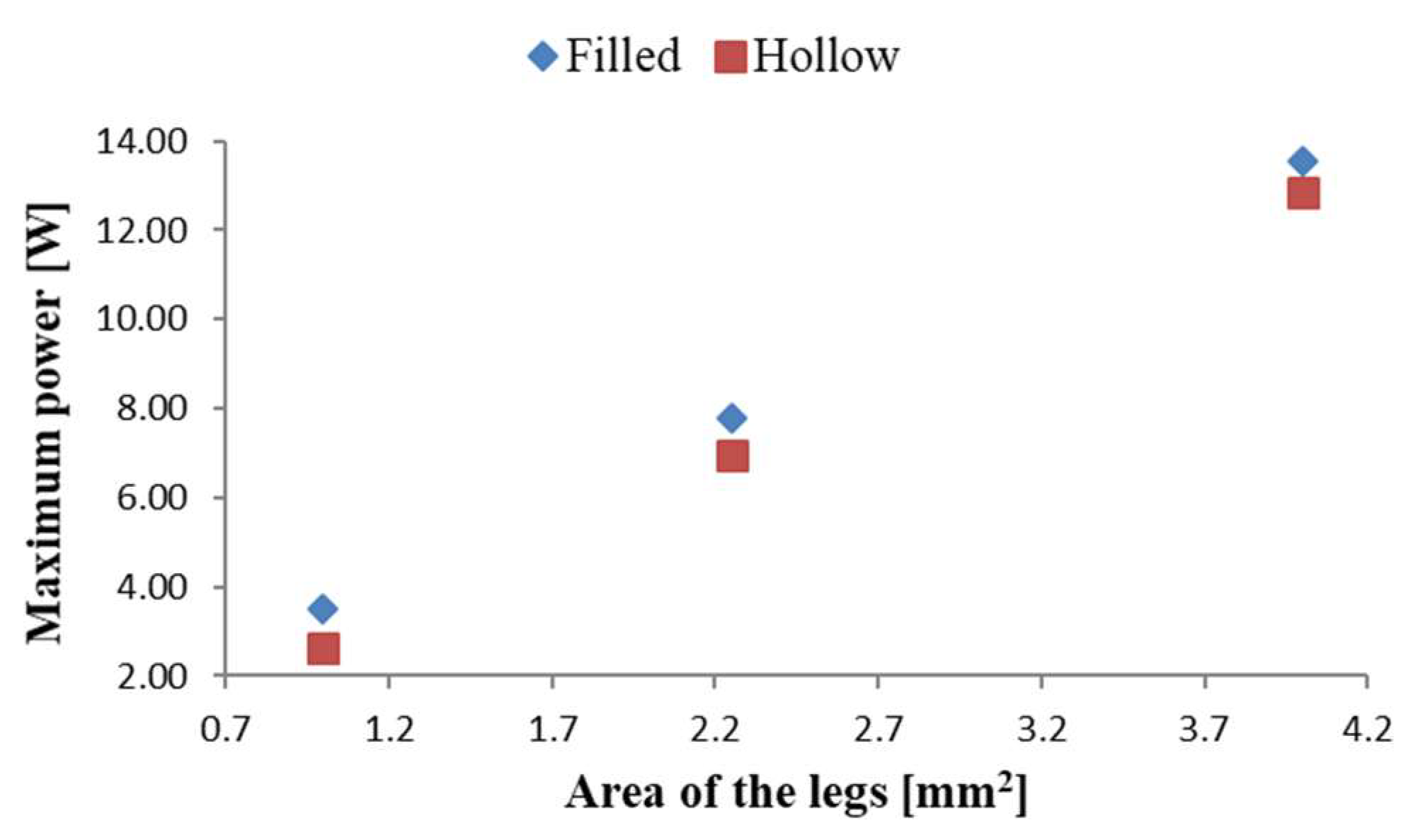
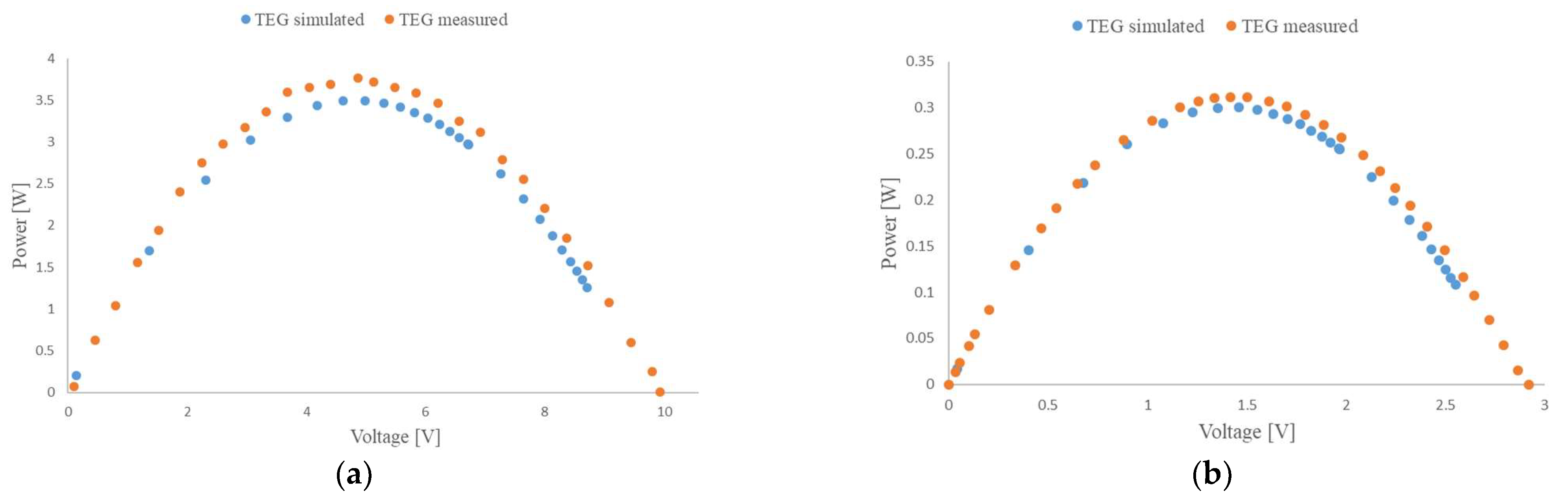
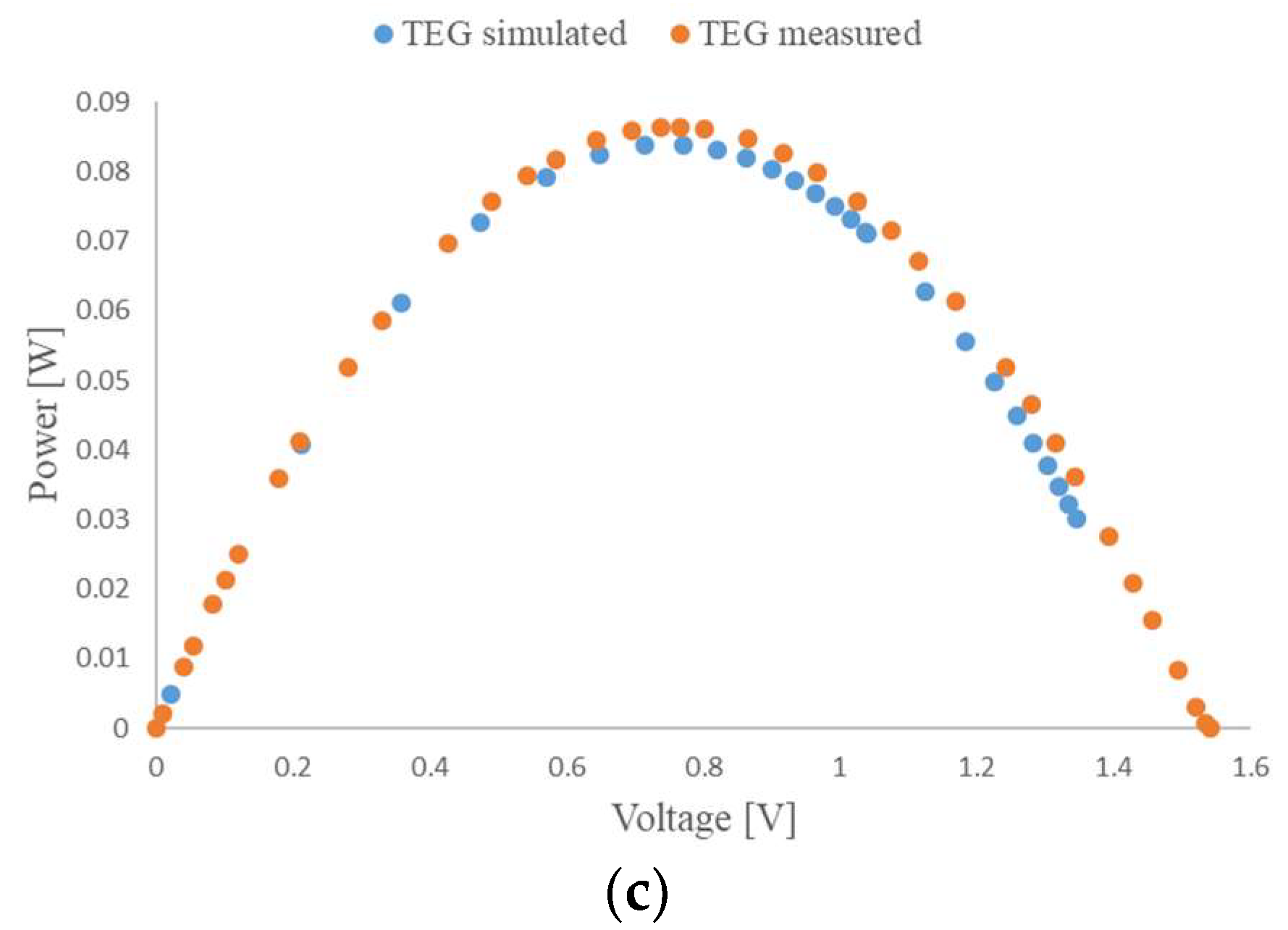
- A comparison of the generated maximum power by the thermoelectric generator, based on Bi2Te3 with sizes of 4 cm × 4 cm when the length and width of the legs varies from 1 mm × 1 mm to 1.5 mm × 1.5 mm and 2 mm × 2 mm, which leads to varying the pitch–the distance between legs;
- A comparison between the results obtained for the maximum power generated by the rectangular conventional thermoelectric generator with the COMSOL Multiphysics and one in real circumstances under illumination with sunlight.
2. Materials and Methods
- for heat transfer in solids Equations (1) and (2):
- for electric currents Equations (3)–(5):
- for thermoelectric effects Equations (6)–(8):
3. Results and Discussion
3.1. Simulation
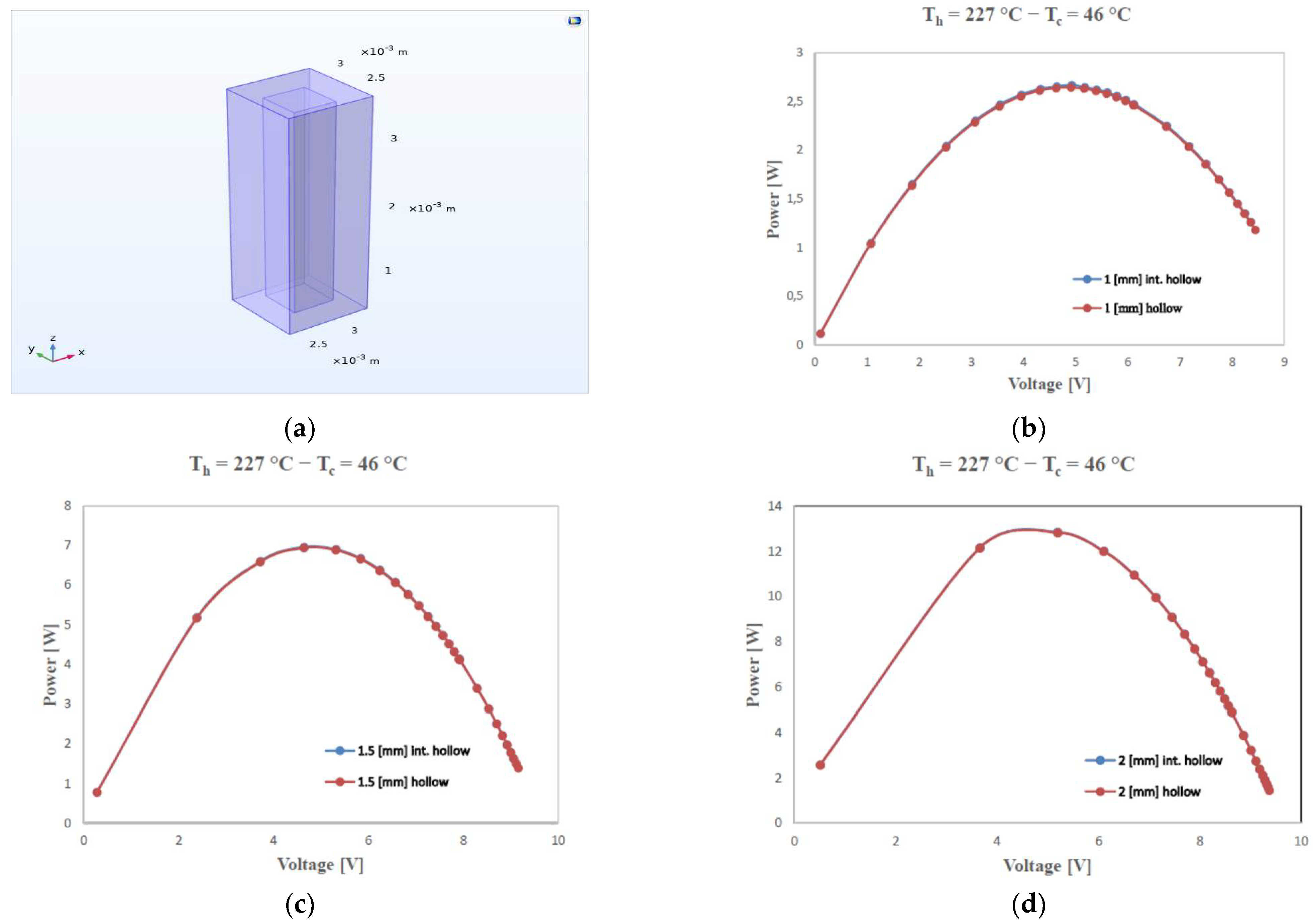
3.2. Simulation for Leg with Internal Hollow
3.3. Comparison
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mahmoudinezhad, S.; Cotfas, P.A.; Cotfas, D.T.; Rosendahl, L.A.; Rezania, A. Response of thermoelectric generators to Bi2Te3 and Zn4Sb3 energy harvester materials under variant solar radiation. Renew. Energy 2020, 146, 2488–2498. [Google Scholar] [CrossRef]
- Mahmoudinezhad, S.; Cotfas, P.A.; Cotfas, D.T.; Skjølstrup, E.J.H.; Pedersen, K.; Rosendahl, L.A.; Rezania, A. An Experimental Study on Transient Response of a Hybrid Thermoelectric–Photovoltaic System with Beam Splitter. Energies 2021, 14, 8129. [Google Scholar] [CrossRef]
- Shen, Z.G.; Tian, L.L.; Liu, X. Automotive exhaust thermoelectric generators: Current status, challenges and future prospects. Energy Convers. Manag. 2019, 195, 1138–1173. [Google Scholar] [CrossRef]
- Ambrosi, R.M.; Williams, H.; Watkinson, E.J.; Barco, A.; Mesalam, R.; Crawford, T.; Bicknell, C.; Samara-Ratna, P.; Vernon, D.; Bannister, N.; et al. European Radioisotope Thermoelectric Generators (RTGs) and Radioisotope Heater Units (RHUs) for Space Science and Exploration. Space Sci. Rev. 2019, 215, 55. [Google Scholar] [CrossRef]
- Cotfas, D.T.; Cotfas, P.A.; Ciobanu, D.; Machidon, O.M. Characterization of photovoltaic–thermoelectric–solar collector hybrid systems in natural sunlight conditions. J. Energy Eng. 2017, 143, 04017055. [Google Scholar] [CrossRef]
- Cotfas, P.A.; Cotfas, D.T. Comprehensive review of methods and instruments for photovoltaic–thermoelectric generator hybrid system characterization. Energies 2020, 13, 6045. [Google Scholar] [CrossRef]
- Cui, Y.J.; Wang, K.F.; Zheng, L.; Wang, B.L.; Zhang, C.W. Theoretical model of fatigue crack growth of a thermoelectric pn-junction bonded to an elastic substrate. Mech. Mater. 2020, 151, 103623. [Google Scholar] [CrossRef]
- Jouhara, H.; Żabnieńska-Góra, A.; Khordehgah, N.; Doraghi, Q.; Ahmad, L.; Norman, L.; Axcell, B.; Wrobel, L.; Dai, S. Thermoelectric generator (TEG) technologies and applications. Int. J. 2021, 9, 100063. [Google Scholar] [CrossRef]
- Ni, D.; Song, H.; Chen, Y.; Cai, K. Free-standing highly conducting PEDOT films for flexible thermoelectric generator. Energy 2019, 170, 53–61. [Google Scholar] [CrossRef]
- Zhu, H.; Mao, J.; Feng, Z.; Sun, J.; Zhu, Q.; Liu, Z.; Singh, D.J.; Wang, Y.; Ren, Z. Understanding the asymmetrical thermoelectric performance for discovering promising thermoelectric materials. Sci. Adv. 2019, 5, eaav5813. [Google Scholar] [CrossRef]
- Pei, J.; Cai, B.; Zhuang, H.L.; Li, J.F. Bi2Te3-based applied thermoelectric materials: Research advances and new challenges. Natl. Sci. Rev. 2020, 7, 1856–1858. [Google Scholar] [CrossRef] [PubMed]
- Olivares-Robles, M.A.; Badillo-Ruiz, C.A.; Ruiz-Ortega, P.E. A comprehensive analysis on nanostructured materials in a thermoelectric micro-system based on geometric shape, segmentation structure and load resistance. Sci. Rep. 2020, 10, 21659. [Google Scholar] [CrossRef] [PubMed]
- Soleimani, Z.; Zoras, S.; Ceranic, B.; Shahzad, S.; Cui, Y. A review on recent developments of thermoelectric materials for room temperature applications. Sustain. Energy Technol. Assess. 2020, 37, 100604. [Google Scholar] [CrossRef]
- Nozariasbmarz, A.; Krasinski, J.S.; Vashaee, D. N-Type bismuth telluride nanocomposite materials optimization for thermoelectric generators in wearable applications. Materials 2019, 12, 1529. [Google Scholar] [CrossRef] [PubMed]
- Witting, I.T.; Chasapis, T.C.; Ricci, F.; Peters, M.; Heinz, N.A.; Hautier, G.; Snyder, G.J. The Thermoelectric Properties of Bismuth Telluride. Adv. Electron. Mater. 2019, 5, 1800904. [Google Scholar] [CrossRef]
- Cui, Y.J.; Wang, B.L.; Wang, K.F. Thermally induced vibration and strength failure analysis of thermoelectric generators. Appl. Therm. Eng. 2019, 160, 113991. [Google Scholar] [CrossRef]
- Sisik, B.; LeBlanc, S. The influence of leg shape on thermoelectric performance under constant temperature and heat flux boundary conditions. Front. Mater. 2020, 7, 595955. [Google Scholar] [CrossRef]
- Fabián-Mijangos, A.; Min, G.; Alvarez-Quintana, J. Enhanced performance thermoelectric module having asymmetrical legs. Energy Convers. Manag. 2017, 148, 1372–1381. [Google Scholar] [CrossRef]
- Jovovic, V. Thermoelectric Waste Heat Recovery Program for Passenger Vehicles. Available online: http://energy.gov/sites/prod/files/2014/07/f17/ace080_barnhart_2014_o.pdf (accessed on 22 June 2022).
- Schmitz, A.; Stiewe, C.; Müller, E. Preparation of ring-shaped thermoelectric legs from PbTe powders for tubular thermoelectric modules. J. Electron. Mater. 2013, 42, 1702. [Google Scholar] [CrossRef]
- Sahin, A.Z.; Yilbas, B.S. The Thermoelement as Thermoelectric Power Generator: Effect of Leg Geometry on the Efficiency and Power Generation. Energy Convers. Manag. 2013, 65, 26–32. [Google Scholar] [CrossRef]
- Fateh, H.; Baker, C.A.; Hall, M.J.; Shi, L. High fidelity finite difference model for exploring multi-parameter thermoelectric generator design space. Appl. Energy 2014, 129, 373–383. [Google Scholar] [CrossRef]
- Thimont, Y.; LeBlanc, S. The impact of thermoelectric leg geometries on thermal resistance and power output. J. Appl. Phys. 2019, 126, 095101. [Google Scholar] [CrossRef]
- Liu, H.B.; Meng, J.H.; Wang, X.D.; Chen, W.H. A new design of solar thermoelectric generator with combination of segmented materials and asymmetrical legs. Energy Convers. Manag. 2018, 175, 11–20. [Google Scholar] [CrossRef]
- Li, M.; Dizaji, H.S.; Asaadi, S.; Jarad, F.; Anqi, A.E.; Wae-hayee, M. Thermo-economic, exergetic and mechanical analysis of thermoelectric generator with hollow leg structure; impact of leg cross-section shape and hollow-to-filled area ratio. Case Stud. Therm. Eng. 2021, 27, 101314. [Google Scholar] [CrossRef]
- Mahmoudinezhad, S.; Ahmadi Atouei, S.; Cotfas, P.A.; Cotfas, D.T.; Rosendahl, L.A.; Rezania, A. Experimental and numerical study on the transient behavior of multi-junction solar cell-thermoelectric generator hybrid system. Energy Convers. Manag. 2019, 184, 448–455. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, S.; Ge, Y.; Shan, F.; Zeng, L.; Liu, W. Geometry optimization of two-stage thermoelectric generators using simplified conjugate-gradient method. Appl. Energy 2017, 190, 540–552. [Google Scholar] [CrossRef]
- Hogblom, O.; Andersson, R. Analysis of thermoelectric generator performance by use of simulations and experiments. J. Electron. Mater. 2014, 43, 2247–2254. [Google Scholar] [CrossRef]
- Memon, S.; Tahir, K.N. Experimental and analytical simulation analyses on the electrical performance of thermoelectric generator modules for direct and concentrated quartz-halogen heat harvesting. Energies 2018, 11, 3315. [Google Scholar] [CrossRef]
- Bensafi, M.; Ameur, H.; Kaid, N.; Hoseinzadeh, S.; Memon, S.; Sohani, A. Experimental Study of Electric Power Generation with Concentrated Solar Thermoelectric Generator. Electronics 2022, 11, 1867. [Google Scholar] [CrossRef]
- Sun, D.; Shen, L.; Yao, Y.; Chen, H.; Jin, S.; He, H. The real-time study of solar thermoelectric generator. Appl. Therm. Eng. 2017, 119, 347–359. [Google Scholar] [CrossRef]
- Available online: https://www.comsol.com (accessed on 12 February 2022).
- Prasad, A.; Thiagarajan, R.C.N. Multiphysics Modelling and Multilevel Optimization of Thermoelectric Generator for Waste Heat Recovery, ATOA Scientific Technologies, Bengaluru. Available online: cn.comsol.com (accessed on 21 June 2022).
- Cui, Y.J.; Wang, K.F.; Wang, B.L.; Li, J.E.; Zhou, J.Y. A comprehensive analysis of delamination and thermoelectric performance of thermoelectric pn-junctions with temperature-dependent material properties. Compos. Struct. 2019, 229, 111484. [Google Scholar] [CrossRef]
- Shittu, S.; Li, G.; Zhao, X.; Ma, X.; Akhlaghi, Y.G.; Ayodele, E. Optimized high performance thermoelectric generator with combined segmented and asymmetrical legs under pulsed heat input power. J. Power Sources 2019, 428, 53–66. [Google Scholar] [CrossRef]
- Jaziri, N.; Boughamoura, A.; Müller, J.; Mezghani, B.; Tounsi, F.; Ismail, M. A comprehensive review of Thermoelectric Generators: Technologies and common applications. Energy Rep. 2020, 6, 264–287. [Google Scholar] [CrossRef]
- Cui, Y.J.; Wang, B.L.; Wang, K.F.; Zheng, L. Power output evaluation of a porous annular thermoelectric generator for waste heat harvesting. Int. J. Heat Mass Transf. 2019, 137, 979–989. [Google Scholar] [CrossRef]
- Available online: https://energia.imdea.org/en/instalaciones/ (accessed on 21 June 2022).
- Available online: https://www.comsol.com/material-library (accessed on 21 June 2022).
- Available online: https://www.Tecteg.com (accessed on 21 June 2022).






| Simulation | Th = 100 °C, Tc = 30 °C | Th = 200 °C, Tc = 30 °C | Th = 300 °C, Tc = 30 °C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Pmax (mW) | Isc (A) | Voc (V) | Pmax (mW) | Isc (A) | Voc (V) | Pmax (mW) | Isc (A) | Voc (V) | |
| [28] | 8.3 | 0.93 | 0.03 | 39.8 | 1.9 | 0.079 | 95 | 2.97 | 0.12 |
| This paper | 7.5 | 0.89 | 0.03 | 38.2 | 1.86 | 0.075 | 93 | 2.9 | 0.12 |
| Name | Dimensions (mm) | Description | ||
|---|---|---|---|---|
| TEG length | 40 | Total TEG length | ||
| TEG width | 40 | Total TEG width | ||
| TEG height | 4 | Total TEG height | ||
| Ceramic length | 40 | Ceramic length | ||
| Ceramic width | 40 | Ceramic width | ||
| Ceramic height | 0.3 | Ceramic thickness | ||
| Copper height | 0.1 | Copper thickness | ||
| Leg height | 3.2 | Leg height | ||
| Leg length | 1 | 1.5 | 2 | Leg length |
| Leg width | 1 | 1.5 | 2 | Leg width |
| Pitch | 1.3 | 0.9 | 0.4 | Distance between legs |
| NP | 128 | Number of thermocouples | ||
| Materials | Thermal Conductivity κ (W/(m × K)) | Electrical Conductivity σ (S/m) | Specific Heat Capacity Cp (J/(kg × K)) | Density ρ (kg/m3) | Thermal Expansion Coefficient (1/K) | Young’s Modulus E (GPa) | Poisson’s Ratio ν | Seebeck Coefficient S (V/K) |
|---|---|---|---|---|---|---|---|---|
| Ceramic | 27 | 1 × 10−12 | 900 | 3900 | 8 × 10−6 | 300 | 0.22 | 0 |
| Copper | 400 | 5.998 × 107 | 385 | 8940 | 1.7 × 10−5 | 126 | 0.34 | 6.5 × 10−6 |
| Bi2Te3 - p-type - n-type | 1.6 1.6 | 1.25 × 105 1.25 × 105 | 154 154 | 6800 6800 | --- --- | 65–59 65–59 | 0.23 0.23 | −210 × 10−6 210 × 10−6 |
| Filled | Square | Triangular | Trapezoid | Reverse Trapezoid | Hourglass | Inverse Hourglass |
|---|---|---|---|---|---|---|
| Leg Dimension | 1 (mm) × 1 (mm) × 3.2 (mm) | |||||
| Short circuit current (A) | 1.4248 | 0.7258 | 0.7234 | 0.7234 | 0.7182 | 0.7163 |
| Open circuit voltage (V) | 9.6739 | 9.6966 | 9.6972 | 9.697 | 9.7018 | 9.6941 |
| Power Output (W) | 3.4940 | 1.7726 | 1.7668 | 1.7671 | 1.7548 | 1.7486 |
| Leg Dimension | 1.5 (mm) × 1.5 (mm) × 3.2 (mm) | |||||
| Short circuit current (A) | 3.1197 | 1.6081 | 1.5966 | 1.5966 | 1.5734 | 1.5648 |
| Open circuit voltage (V) | 9.6592 | 9.6854 | 9.6862 | 9.687 | 9.6943 | 9.6809 |
| Power Output (W) | 7.7827 | 3.9585 | 3.9302 | 3.9311 | 3.8760 | 3.8492 |
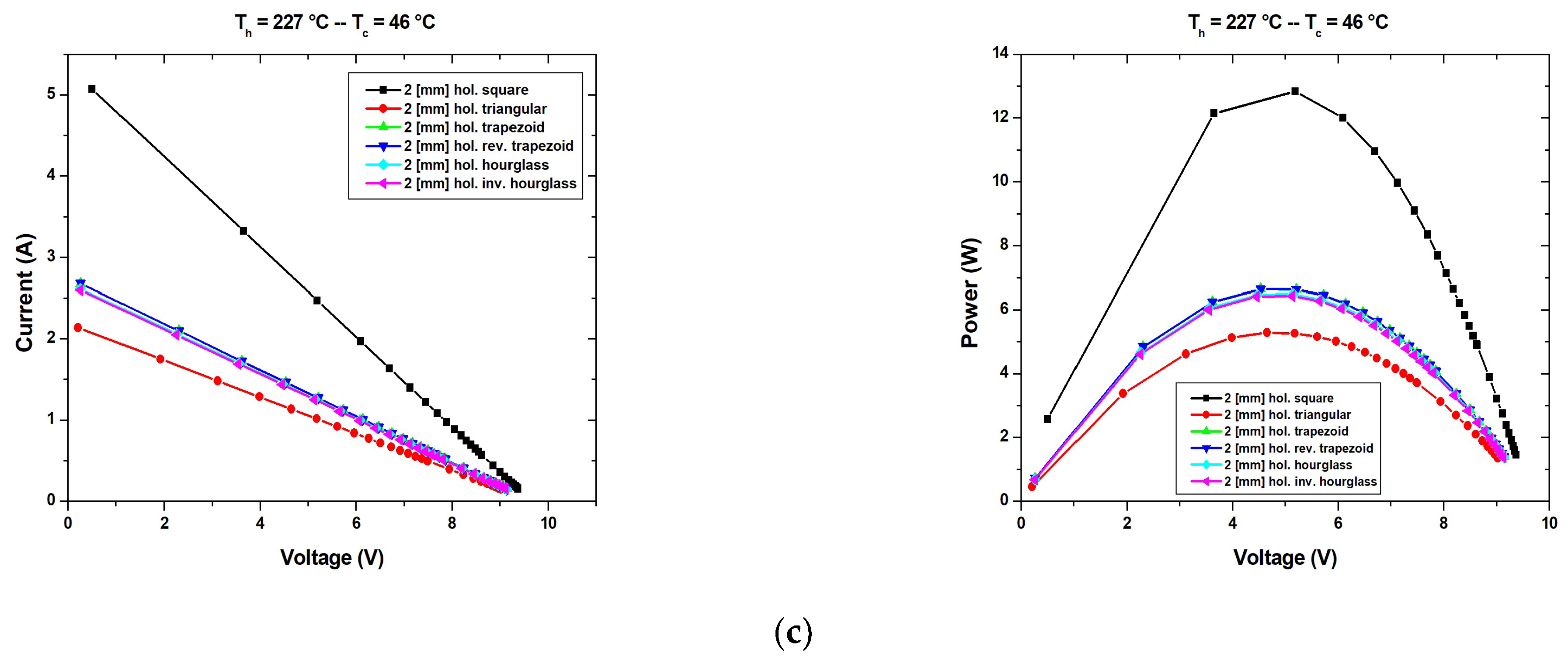
| Leg Dimension | 2 (mm) × 2 (mm) × 3.2 (mm) | |||||
| Short circuit current (A) | 5.3728 | 2.8077 | 2.7733 | 2.7734 | 2.7112 | 2.6876 |
| Open circuit voltage (V) | 9.6449 | 9.6751 | 9.6762 | 9.6769 | 9.6874 | 9.6695 |
| Power Output (W) | 13.563 | 6.9840 | 6.8923 | 6.8947 | 6.7335 | 6.6580 |
| Hollow | Square | Triangular | Trapezoid | Reverse Trapezoid | Hourglass | Inverse Hourglass |
|---|---|---|---|---|---|---|
| Leg Dimension | 1 (mm) × 1 (mm) × 3.2 (mm) | |||||
| Short circuit current (A) | 1.0798 | 0.5475 | 0.6178 | 0.6178 | 0.6135 | 0.6121 |
| Open circuit voltage (V) | 9.6884 | 9.7057 | 9.7027 | 9.7032 | 9.7061 | 9.7002 |
| Power Output (W) | 2.6443 | 1.3299 | 1.5078 | 1.5080 | 1.4979 | 1.4934 |
| Leg Dimension | 1.5 (mm) × 1.5 (mm) × 3.2 (mm) | |||||
| Short circuit current (A) | 2.7946 | 1.2181 | 1.4964 | 1.4965 | 1.4740 | 1.4668 |
| Open circuit voltage (V) | 9.6676 | 9.6978 | 9.6896 | 9.6903 | 9.6969 | 9.6848 |
| Power Output (W) | 6.9441 | 2.9899 | 3.6796 | 3.6804 | 3.6250 | 3.6022 |
| Leg Dimension | 2 (mm) × 2 (mm) × 3.2 (mm) | |||||
| Short circuit current (A) | 5.0687 | 2.1366 | 2.6786 | 2.6786 | 2.6134 | 2.5971 |
| Open circuit voltage (V) | 9.6505 | 9.6904 | 9.6786 | 9.6793 | 9.6892 | 9.6725 |
| Power Output (W) | 12.833 | 5.2843 | 6.6386 | 6.6407 | 6.4793 | 6.4287 |
| Filled | Square | Triangular | Trapezoid | Reverse Trapezoid | Hourglass | Inverse Hourglass |
|---|---|---|---|---|---|---|
| Leg Dimension | 1 (mm) × 1 (mm) × 3.2 (mm) | |||||
| Temp. Range (°C) (Difference (°C)) | 204–227 (23) | 190–227 (37) | 190–227 (37) | 190–227 (37) | 190–227 (37) | 190–227 (37) |
| Short circuit current (A) | 73.97 × 10−3 | 71.53 × 10−3 | 71.52 × 10−3 | 71.52 × 10−3 | 71.49 × 10−3 | 71.46 × 10−3 |
| Power Output (W) | 23.13 × 10−3 | 40.53 × 10−3 | 40.64 × 10−3 | 40.64 × 10−3 | 40.91 × 10−3 | 40.90 × 10−3 |
| Leg Dimension | 1.5 (mm) × 1.5 (mm) × 3.2 (mm) | |||||
| Temp. Range (°C) (Difference (°C)) | 216–227 (11) | 207–227 (20) | 207–227 (20) | 207–227 (20) | 207–227 (20) | 207–227 (20) |
| Short circuit current (A) | 75.03 × 10−3 | 74.41 × 10−3 | 74.40 × 10−3 | 74.40 × 10−3 | 74.39 × 10−3 | 74.34 × 10−3 |
| Power Output (W) | 11.15 × 10−3 | 20.99 × 10−3 | 21.14 × 10−3 | 21.14 × 10−3 | 21.48 × 10−3 | 21.48 × 10−3 |
| Leg Dimension | 2 (mm) × 2 (mm) × 3.2 (mm) | |||||
| Temp. Range (°C) (Difference (°C)) | 220–227 (07) | 215–227 (12) | 215–227 (12) | 215–227 (12) | 214–227 (13) | 214–227 (13) |
| Short circuit current (A) | 74.81 × 10−3 | 75.13 × 10−3 | 75.14 × 10−3 | 75.14E × 10−3 | 75.16 × 10−3 | 75.09 × 10−3 |
| Power Output (W) | 6.444 × 10−3 | 12.47 × 10−3 | 12.63 × 10−3 | 12.63 × 10−3 | 12.97 × 10−3 | 12.98 × 10−3 |
| Hollow | Square | Triangular | Trapezoid | Reverse Trapezoid | Hourglass | Inverse Hourglass |
|---|---|---|---|---|---|---|
| Leg Dimension | 1 (mm) × 1 (mm) × 3.2 (mm) | |||||
| Temp. Range (°C) (Difference (°C)) | 199–227 (28) | 183–227 (44) | 186–227 (41) | 186–227 (41) | 186–227 (41) | 186–227 (41) |
| Short circuit current (A) | 73.21 × 10−3 | 69.87 × 10−3 | 70.64 × 10−3 | 70.64 × 10−3 | 70.61 × 10−3 | 70.58 × 10−3 |
| Power Output (W) | 29.51 × 10−3 | 49.69 × 10−3 | 45.68 × 10−3 | 45.68 × 10−3 | 45.95 × 10−3 | 45.93 × 10−3 |
| Leg Dimension | 1.5 (mm) × 1.5 (mm) × 3.2 (mm) | |||||
| Temp. Range (°C) (Difference (°C)) | 214–227 (13) | 203–227 (24) | 206–227 (21) | 206–227 (21) | 206–227 (21) | 206–227 (21) |
| Short circuit current (A) | 75.03 × 10−3 | 73.75 × 10−3 | 74.27 × 10−3 | 74.27 × 10−3 | 74.26 × 10−3 | 74.21 × 10−3 |
| Power Output (W) | 12.45 × 10−3 | 26.87 × 10−3 | 22.42 × 10−3 | 22.42 × 10−3 | 22.77 × 10−3 | 22.76 × 10−3 |
| Leg Dimension | 2 (mm) × 2 (mm) × 3.2 (mm) | |||||
| Temp. Range (°C) (Difference (°C)) | 220–227 (07) | 211–227 (16) | 214–227 (13) | 214–227 (13) | 221–227 (06) | 214–227 (13) |
| Short circuit current (A) | 74.91 × 10−3 | 74.95 × 10−3 | 75.13 × 10−3 | 75.13 × 10−3 | 75.15 × 10−3 | 75.08 × 10−3 |
| Power Output (W) | 6.861 × 10−3 | 16.26 × 10−3 | 13.08 × 10−3 | 13.08 × 10−3 | 13.44 × 10−3 | 13.43 × 10−3 |
| Filled | Square | Triangular | Trapezoid | Reverse Trapezoid | Hourglass | Inverse Hourglass |
|---|---|---|---|---|---|---|
| Leg Dimension | 1 (mm) × 1 (mm) × 3.2 (mm) | |||||
| Temp. Range (°C) (Difference (°C)) | 185–227 (42) | 164–227 (63) | 164–227 (63) | 164–227 (63) | 163–227 (64) | 163–227 (64) |
| Short circuit current (A) | 142.0 × 10−3 | 132.6 × 10−3 | 132.5 × 10−3 | 132.5 × 10−3 | 132.4 × 10−3 | 132.3 × 10−3 |
| Power Output (W) | 80.59 × 10−3 | 126.2 × 10−3 | 126.5 × 10−3 | 126.5 × 10−3 | 127.2 × 10−3 | 127.1 × 10−3 |
| Leg Dimension | 1.5 (mm) × 1.5 (mm) × 3.2 (mm) | |||||
| Temp. Range (°C) (Difference (°C)) | 205–227 (22) | 191–227 (36) | 191–227 (36) | 191–227 (36) | 190–227 (37) | 190–227 (37) |
| Short circuit current (A) | 147.3 × 10−3 | 143.6 × 10−3 | 143.6 × 10−3 | 143.5v | 143.5 × 10−3 | 143.3 × 10−3 |
| Power Output (W) | 41.79 × 10−3 | 74.27 × 10−3 | 74.74 × 10−3 | 74.73 × 10−3 | 75.80 × 10−3 | 75.77 × 10−3 |
| Leg Dimension | 2 (mm) × 2 (mm) × 3.2 (mm) | |||||
| Temp. Range (°C) (Difference (°C)) | 214–227 (13) | 204–227 (23) | 204–227 (23) | 204–227 (23) | 203–227 (24) | 203–227 (24) |
| Short circuit current (A) | 148.0 × 10−3 | 147.2 × 10−3 | 147.2 × 10−3 | 147.2 × 10−3 | 147.1 × 10−3 | 147.0 × 10−3 |
| Power Output (W) | 24.84 × 10−3 | 46.43 × 10−3 | 46.99 × 10−3 | 46.98 × 10−3 | 48.12 × 10−3 | 48.15 × 10−3 |
| Hollow | Square | Triangular | Trapezoid | Reverse Trapezoid | Hourglass | Inverse Hourglass |
|---|---|---|---|---|---|---|
| Leg Dimension | 1 (mm) × 1 (mm) × 3.2 (mm) | |||||
| Temp. Range (°C) (Difference (°C)) | 177–227 (50) | 153–227 (74) | 158–227 (69) | 158–227 (69) | 158–227 (69) | 158–227 (69) |
| Short circuit current (A) | 138.9 × 10−3 | 126.7 × 10−3 | 129.4 × 10−3 | 129.4 × 10 3 | 129.3 × 10−3 | 129.2 × 10−3 |
| Power Output (W) | 98.85 × 10−3 | 145.5 × 10−3 | 137.5 × 10−3 | 137.5 × 10−3 | 138.1 × 10−3 | 138.0 × 10−3 |
| Leg Dimension | 1.5 (mm) × 1.5 (mm) × 3.2 (mm) | |||||
| Temp. Range (°C) (Difference (°C)) | 203–227 (24) | 183–227 (44) | 189–227 (38) | 189–227 (38) | 189–227 (38) | 189–227 (38) |
| Short circuit current (A) | 147.0 × 10−3 | 140.8 × 10−3 | 143.0 × 10−3 | 143.0 × 10−3 | 142.9 × 10−3 | 142.7 × 10−3 |
| Power Output (W) | 46.35 × 10−3 | 91.46 × 10−3 | 78.67 × 10−3 | 78.66 × 10−3 | 79.77 × 10−3 | 79.74 × 10−3 |
| Leg Dimension | 2 (mm) × 2 (mm) × 3.2 (mm) | |||||
| Temp. Range (°C) (Difference (°C)) | 213–227 (14) | 198–227 (29) | 203–227 (24) | 203–227 (24) | 215–227 (12) | 202–227 (25) |
| Short circuit current (A) | 148.1 × 10−3 | 145.9 × 10−3 | 147.0 × 10−3 | 147.0 × 10−3 | 147.0 × 10−3 | 146.8 × 10−3 |
| Power Output (W) | 26.34 × 10−3 | 59.20 × 10−3 | 48.48 × 10−3 | 48.48 × 10−3 | 49.77 × 10−3 | 49.72 × 10−3 |
| Filled | Square | Triangular | Trapezoid | Reverse Trapezoid | Hourglass | Inverse Hourglass |
|---|---|---|---|---|---|---|
| Leg Dimension | 1 (mm) × 1 (mm) × 3.2 (mm) | |||||
| Temp. Range (°C) (Difference (°C)) | 69.8–227 (157.2) | 51.1–227 (175.9) | 51.2–227 (175.8) | 51.2–227 (175.8) | 51.1–227 (175.9) | 51–227 (176) |
| Short circuit current (A) | 0.8098 | 0.5529 | 0.5518 | 0.5517 | 0.5492 | 0.5482 |
| Power Output (W) | 1.6602 | 1.3097 | 1.3077 | 1.3076 | 1.3035 | 1.2999 |
| Leg Dimension | 1.5 (mm) × 1.5 (mm) × 3.2 (mm) | |||||
| Temp. Range (°C) (Difference (°C)) | 111–227 (116) | 81.3–227 (145.7) | 81.5–227 (145.5) | 81.5–227 (145.5) | 80.9–227 (146.1) | 80.8–227 (146.2) |
| Short circuit current (A) | 1.0975 | 0.8655 | 0.8630 | 0.8627 | 0.8574 | 0.8548 |
| Power Output (W) | 1.6838 | 1.7285 | 1.7280 | 1.7273 | 1.7259 | 1.7191 |
| Leg Dimension | 2 (mm) × 2 (mm) × 3.2 (mm) | |||||
| Temp. Range (°C) (Difference (°C)) | 140–227 (87) | 107–227 (120) | 107–227 (120) | 107–227 (120) | 106–227 (121) | 106–227 (121) |
| Short circuit current (A) | 1.2373 | 1.0673 | 1.0639 | 1.0634 | 1.0567 | 1.0529 |
| Power Output (W) | 1.3938 | 1.7276 | 1.7333 | 1.7324 | 1.7443 | 1.7377 |
| Hollow | Square | Triangular | Trapezoid | Reverse Trapezoid | Hourglass | Inverse Hourglass |
|---|---|---|---|---|---|---|
| Leg Dimension | 1 (mm) × 1 (mm) × 3.2 (mm) | |||||
| Temp. Range (°C) (Difference (°C)) | 61.3–227 (165.7) | 45.5–227 (181.5) | 47.9–227 (179.1) | 47.9–227 (179.1) | 47.8–227 (179.2) | 47.7–227 (179.3) |
| Short circuit current (A) | 0.7027 | 0.4557 | 0.4962 | 0.4961 | 0.4939 | 0.4930 |
| Power Output (W) | 1.5482 | 1.1232 | 1.2043 | 1.2042 | 1.2005 | 1.1978 |
| Leg Dimension | 1.5 (mm) × 1.5 (mm) × 3.2 (mm) | |||||
| Temp. Range (°C) (Difference (°C)) | 106–227 (121) | 71.1–227 (155.9) | 79–227 (148) | 79–227 (148) | 78.4–227 (148.6) | 78.3–227 (148.7) |
| Short circuit current (A) | 1.0636 | 0.7566 | 0.8378 | 0.8375 | 0.8320 | 0.8296 |
| Power Output (W) | 1.7195 | 1.6315 | 1.7100 | 1.7094 | 1.7074 | 1.7010 |
| Leg Dimension | 2 (mm) × 2 (mm) × 3.2 (mm) | |||||
| Temp. Range (°C) (Difference (°C)) | 137–227 (90) | 94.4–227 (132.6) | 106–227 (121) | 106–227 (121) | 144–227 (83) | 104–227 (123) |
| Short circuit current (A) | 1.2257 | 0.9741 | 1.0525 | 1.0521 | 1.0446 | 1.0416 |
| Power Output (W) | 1.4319 | 1.7731 | 1.7438 | 1.7429 | 1.7537 | 1.7467 |
| TEG | Square | Hollow Square | Square with Internal Hollow |
|---|---|---|---|
| Leg Dimension | 1 (mm) × 1 (mm) × 3.2 (mm) | ||
| Short circuit current (A) | 1.4248 | 1.0798 | 1.0864 |
| Open circuit voltage (V) | 9.6739 | 9.6884 | 9.6913 |
| Power Output (W) | 3.4940 | 2.6443 | 2.6704 |
| Leg Dimension | 1.5 (mm) × 1.5 (mm) × 3.2 (mm) | ||
| Short circuit current (A) | 3.1197 | 2.7946 | 2.8028 |
| Open circuit voltage (V) | 9.6592 | 9.6676 | 9.6675 |
| Power Output (W) | 7.7827 | 6.9441 | 6.9658 |
| Leg Dimension | 2 (mm) × 2 (mm) × 3.2 (mm) | ||
| Short circuit current (A) | 5.3728 | 5.0687 | 5.0771 |
| Open circuit voltage (V) | 9.6449 | 9.6505 | 9.6504 |
| Power Output (W) | 13.563 | 12.833 | 12.853 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rjafallah, A.; Cotfas, D.T.; Cotfas, P.A. Legs Geometry Influence on the Performance of the Thermoelectric Module. Sustainability 2022, 14, 15823. https://doi.org/10.3390/su142315823
Rjafallah A, Cotfas DT, Cotfas PA. Legs Geometry Influence on the Performance of the Thermoelectric Module. Sustainability. 2022; 14(23):15823. https://doi.org/10.3390/su142315823
Chicago/Turabian StyleRjafallah, Abdelkader, Daniel Tudor Cotfas, and Petru Adrian Cotfas. 2022. "Legs Geometry Influence on the Performance of the Thermoelectric Module" Sustainability 14, no. 23: 15823. https://doi.org/10.3390/su142315823
APA StyleRjafallah, A., Cotfas, D. T., & Cotfas, P. A. (2022). Legs Geometry Influence on the Performance of the Thermoelectric Module. Sustainability, 14(23), 15823. https://doi.org/10.3390/su142315823








