On the Sustainability of Shared Mobility Since COVID-19: From Socially Structured to Social Bubble Vanpooling
Abstract
1. Introduction
2. Public Transport, Shared Mobility, and the Spread of COVID-19
- (1)
- as a vector that facilitates the spread of communicable diseases from one place to another (mobility as a vector) [27]. Communicable diseases spread over space when infectious persons move (using transportation modes) from one location to another, where they might infect other persons.
- (2)
- as an environment (transportation means and settings) where people are confined, crowded, and might become infected (mobility as an activity) [28].
3. From Socially Structured Vanpooling to Social Bubble Vanpooling
3.1. Social Bubbles of Riders
3.2. Spatio-Temporal Pooling Phase
- For each pair of clusters and , compute
- Two clusters and are merged if:where is the maximum duration required to travel from a location in cluster to a location in cluster .
3.3. Social Bubble Pooling Phase
- Commuter i is a relative of commuter j ().
- Commuter i works with commuter j ().
- Commuter i follows commuter j on social networks ().
- Commuter i has blocked j on social networks ().
- Commuter i has expressly declined a ride share with j ().
3.4. Operating Cost of Pandemic-Resilient Pooling
4. Simulation-Based Experiments
4.1. Epidemiological Model
- During any day of the simulation, commuters can be either susceptible, exposed, recovered, asymptomatic infectious, pre-symptomatic infectious, or symptomatic infectious (to reflect the case of travelers who develop mild symptoms and not tested but still commute and do not comply to self-isolation instructions).
- Commuters who are asymptomatic infectious, pre-symptomatic infectious, and symptomatic infectious spread the disease over susceptible commuters with different transmission levels.
- Isolated or quarantined commuters temporarily cannot travel until they are recovered (or test negative after the quarantine period in which case they become susceptible), which means that pools with isolated or quarantined commuters may need to be updated to find new commuters (according to the flexible re-pooling scheme presented in Section 3.4).
- Recovered commuters need to resume their travel activity and need to either join their initial pools or join a new pool.
- Deceased commuters are permanently removed and their initial pools may need to be updated.
- The same model applies for drivers who can be infectious/become infected. In the simulation we assume that isolated or quarantined drivers will be replaced by new ones, which means that buses are still available for commuting.
- In case the driver or a member of a pool tests positive, the driver and all the pool members are quarantined and the bus may be used for a different pool of commuters.
4.2. Agent-Based Model and Activity Patterns
- Initialize the population of commuters and vans;
- Identify the list of pools and assign commuters to vans according to the SBV algorithm defined in Section 3.4;
- Determine the initial number and location of initially infected commuters
- For every simulation day t:
- (a)
- If working day, then:
- -
- Make the trip of every van j from home to the main activity location (work, school, university, etc.);
- -
- Calculate the probability of infection of every individual i in every van j making the trip from home to the main activity location;
- -
- Calculate the probability of infection of every individual in the main activity context;
- -
- Make the trip of every van j from the main activity location to home;
- -
- Calculate the probability of infection of every individual i making the trip of every van j from home to the main activity location;
- (b)
- Calculate the probability of infection of every individual at home;
- (c)
- Apply the epidemiological model and change the states of commuters/drivers;
- (d)
- Apply the intervention model (quarantine after contact tracing and/or testing), if any;
- (e)
- Reconstruct or update pools and reassign commuters to vans (flexible reassignment), if needed;
- Update the infection incidence probability p using , where I is the number of reported infected cases and T is the size of the total population;
- Stop simulation at the end-of simulation period or if there are no more infected individuals.
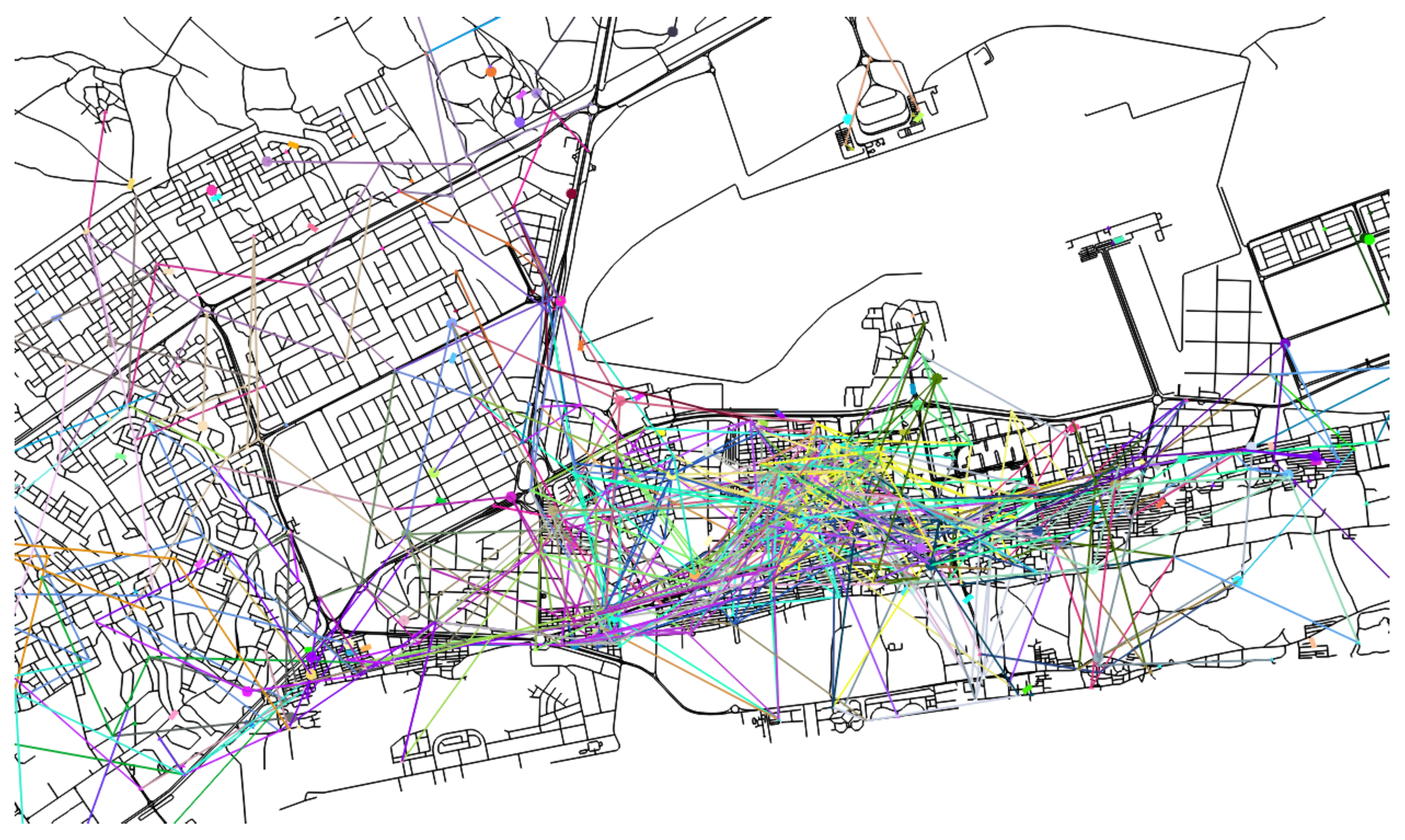
4.3. Experimental Setup
| Parameter | Meaning | Value | Reference |
|---|---|---|---|
| Probability that a susceptible individual i traveling in the trip of the van on day t be infected | Calculated in the simulation | [76] | |
| Exposure (latent) period (in days) | 2.5 | [81] | |
| Pre-symptomatic infectious period (in days) | 1 | [81] | |
| Infectious period (in days) | 6 | [81] | |
| Isolation period (in days) | 15 | National policy of Oman | |
| Quarantine period (in days) | 14 | National policy of Oman | |
| Infection rate of COVID-19 | 2.5 | Ministry of Health, Oman | |
| Death rate | 0.0107 | Ministry of Health, Oman | |
| Recovery rate | 0.9252 | Ministry of Health, Oman |
- Trip-based vanpooling, where pools of riders are formed for every trip.
- Long-term committed vanpooling (pools are formed of the same riders during the period of service) without social bubbles, i.e., pools are formed using only the spatio-temporal clustering step.
- Social bubble based vanpooling proposed in this paper.
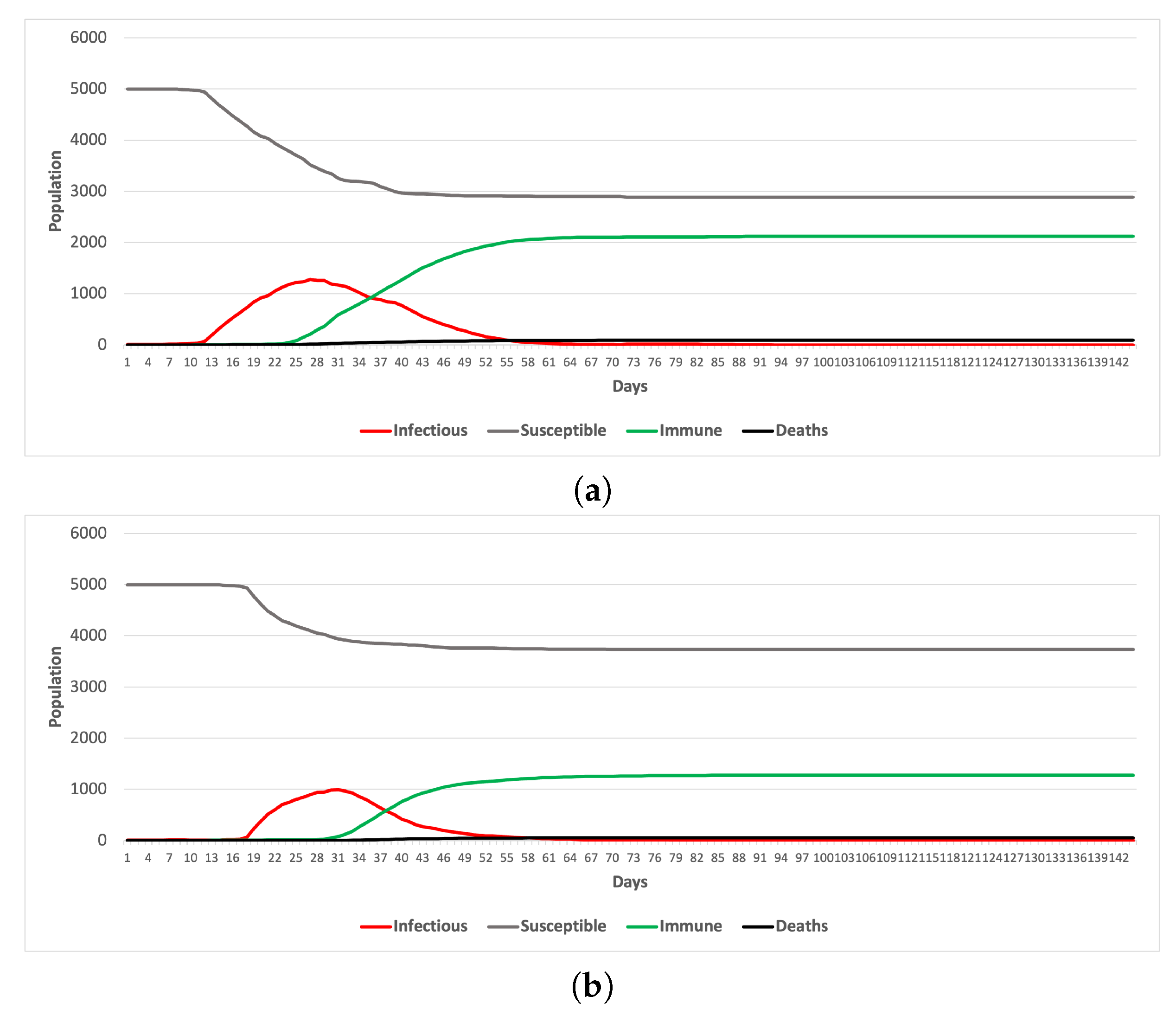
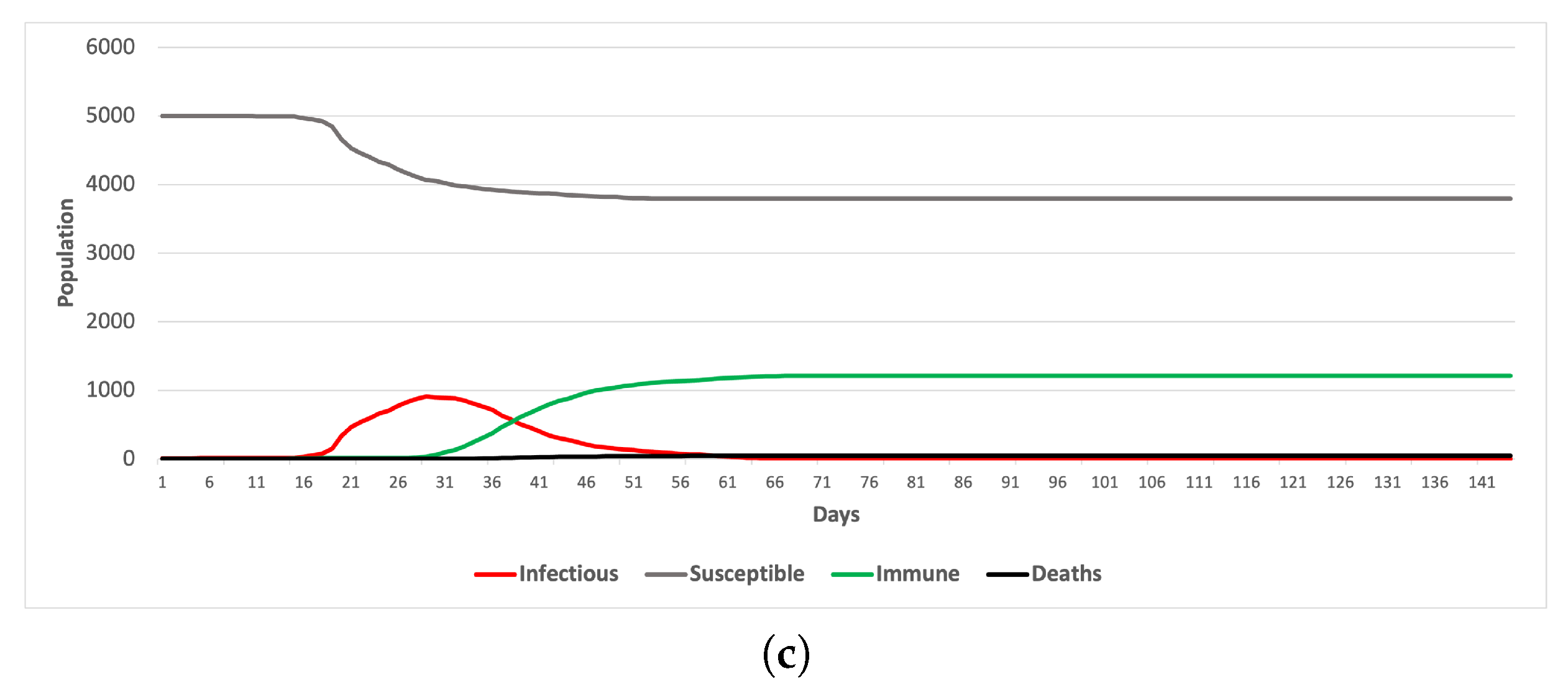
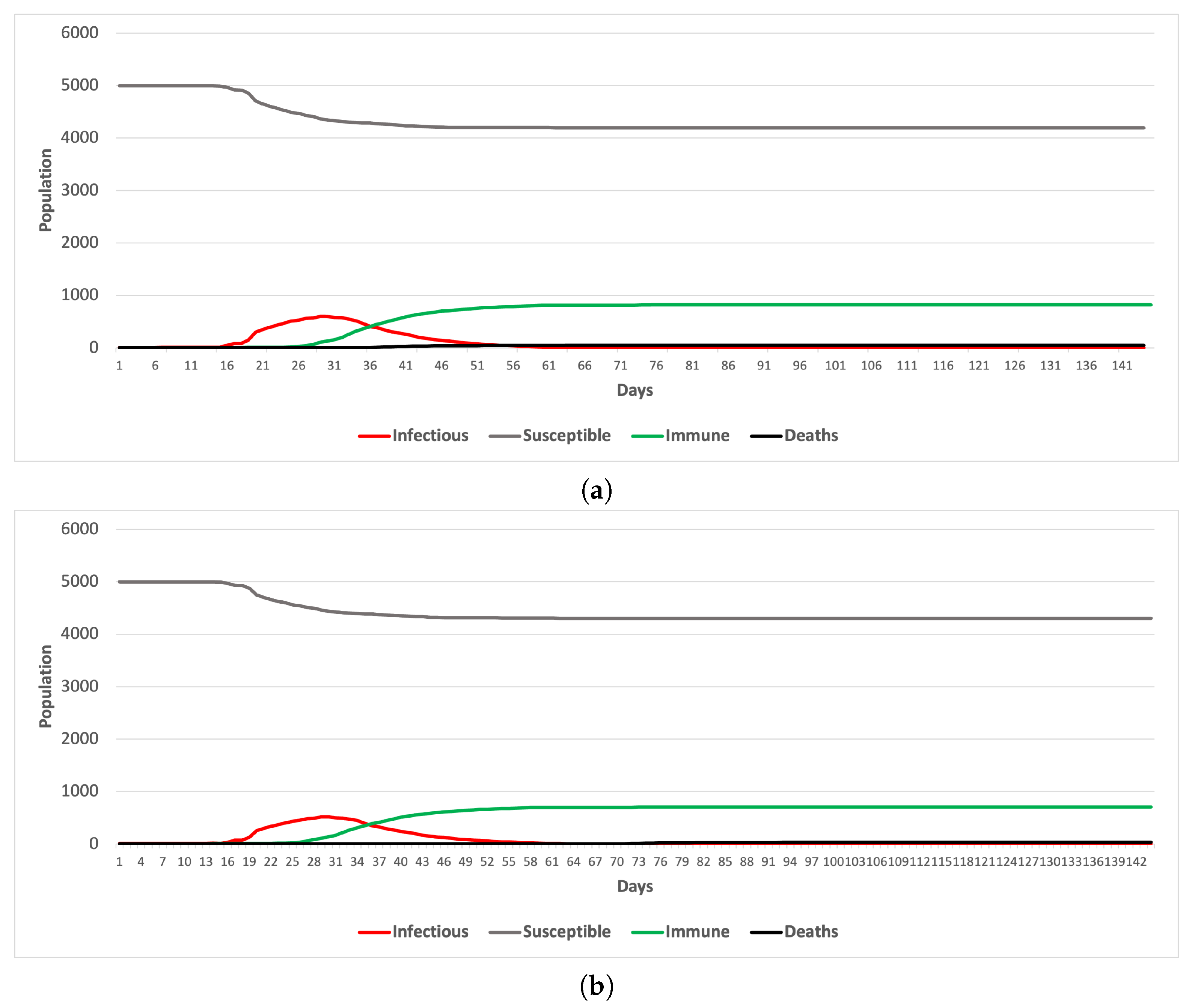
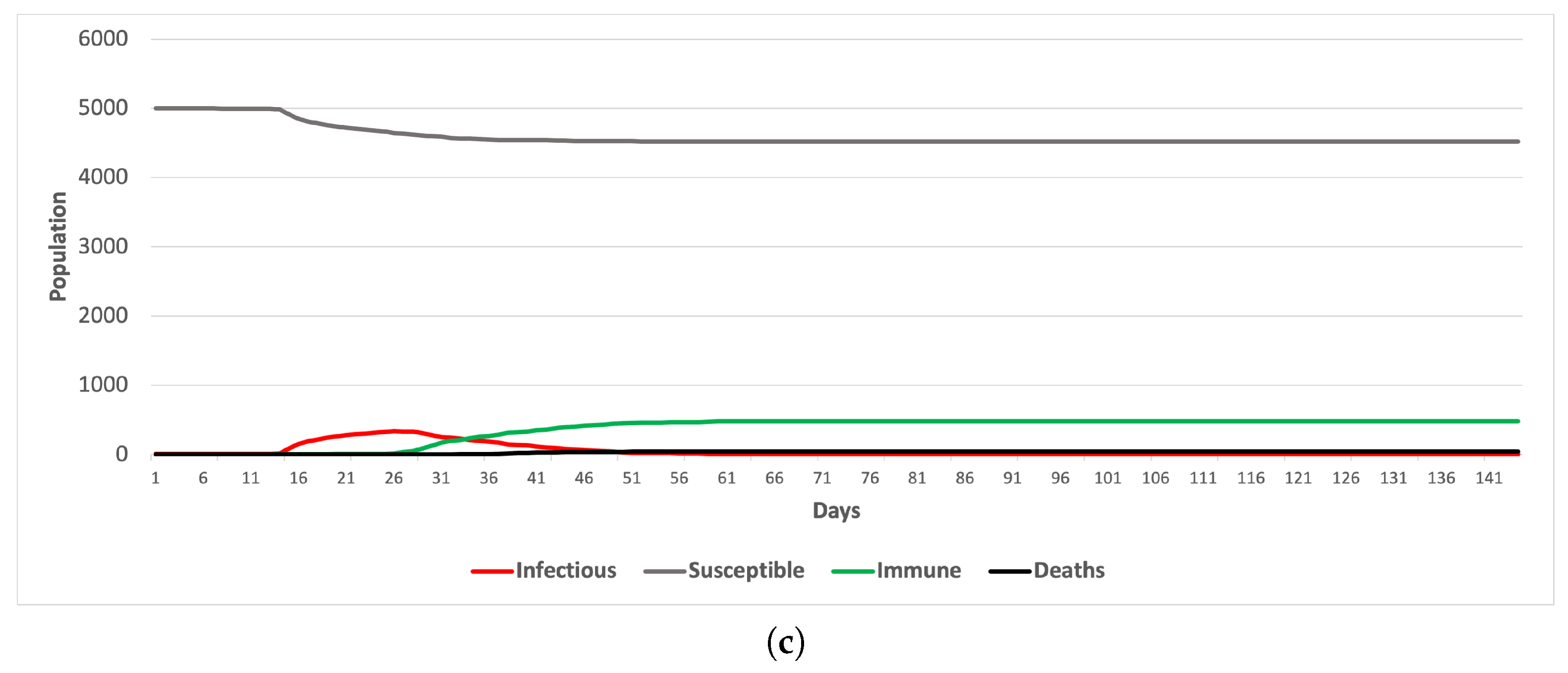
5. Results and Discussion
5.1. Scenario 1
5.2. Scenario 2
- Enforcing contact tracing and quarantine is more effective in controlling the spread of the disease when the bubble-based ridesharing scheme is adopted as a commuting mode.
- It is possible to sustain the transportation service without compromising the efforts to mitigate the spread of the pandemic.
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Hayashi, Y.; Frank, L.D. COVID-19 and transport: Findings from a world-wide expert survey. Transp. Policy 2021, 103, 68–85. [Google Scholar] [CrossRef] [PubMed]
- Aloi, A.; Alonso, B.; Benavente, J.; Cordera, R.; Echániz, E.; González, F.; Ladisa, C.; Lezama-Romanelli, R.; López-Parra, Á.; Mazzei, V.; et al. Effects of the COVID-19 Lockdown on Urban Mobility: Empirical Evidence from the City of Santander (Spain). Sustainability 2020, 12, 3870. [Google Scholar] [CrossRef]
- Honey-Rosés, J.; Anguelovski, I.; Chireh, V.K.; Daher, C.; Konijnendijk van den Bosch, C.; Litt, J.S.; Mawani, V.; McCall, M.K.; Orellana, A.; Oscilowicz, E.; et al. The impact of COVID-19 on public space: An early review of the emerging questions: Design, Perceptions and Inequities. Cities Health 2020, 5, S263–S279. [Google Scholar] [CrossRef]
- Rahimi, E.; Shabanpour, R.; Shamshiripour, A.; Mohammadian, A.K. Perceived risk of using shared mobility services during the COVID-19 pandemic. Transp. Res. Part F Traffic Psychol. Behav. 2021, 81, 271–281. [Google Scholar] [CrossRef]
- Morshed, S.A.; Khan, S.S.; Tanvir, R.B.; Nur, S. Impact of COVID-19 pandemic on ride-hailing services based on large-scale Twitter data analysis. J. Urban Manag. 2021, 10, 155–165. [Google Scholar] [CrossRef]
- Du, J.; Rakha, H.A. Covid-19 impact on ride-hailing: The chicago case study. Transp. Find. 2020, 17838. [Google Scholar] [CrossRef]
- De Palma, A.; Vosough, S. Long, medium, and short-term effects of COVID-19 on mobility and lifestyle. In THEMA (THéorie Economique, Modélisation et Applications); Technical Report; Université de Cergy-Pontoise: Cergy, France, 2021. [Google Scholar]
- Hyland, P.; Vallières, F.; Shevlin, M.; Bentall, R.P.; McKay, R.; Hartman, T.K.; McBride, O.; Murphy, J. Resistance to COVID-19 vaccination has increased in Ireland and the United Kingdom during the pandemic. Public Health 2021, 195, 54–56. [Google Scholar] [CrossRef] [PubMed]
- Edwards, B.; Biddle, N.; Gray, M.; Sollis, K. COVID-19 vaccine hesitancy and resistance: Correlates in a nationally representative longitudinal survey of the Australian population. PLoS ONE 2021, 16, e0248892. [Google Scholar] [CrossRef]
- Ball, P. Anti-vaccine movement might undermine pandemic efforts. Nature 2020, 581, 251. [Google Scholar] [CrossRef]
- Hörcher, D.; Singh, R.; Graham, D.J. Social distancing in public transport: Mobilising new technologies for demand management under the Covid-19 crisis. Transportation 2021, 49, 735–764. [Google Scholar] [CrossRef]
- Edelson, P.J.; Phypers, M. TB transmission on public transportation: A review of published studies and recommendations for contact tracing. Travel Med. Infect. Dis. 2011, 9, 27–31. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez, A.; Miravet, D.; Domènech, A. COVID-19 and urban public transport services: Emerging challenges and research agenda. Cities Health 2020, 5, S177–S180. [Google Scholar] [CrossRef]
- Budd, L.; Ison, S. Responsible Transport: A post-COVID agenda for transport policy and practice. Transp. Res. Interdiscip. Perspect. 2020, 6, 100151. [Google Scholar] [CrossRef]
- Shokouhyar, S.; Shokoohyar, S.; Sobhani, A.; Gorizi, A.J. Shared Mobility in Post-COVID Era: New Challenges and Opportunities. Sustain. Cities Soc. 2021, 67, 102714. [Google Scholar] [CrossRef]
- Koehl, A. Urban transport and COVID-19: Challenges and prospects in low-and middle-income countries. Cities Health 2020, 5, S185–S190. [Google Scholar] [CrossRef]
- Prati, G. Gender equality and women’s participation in transport cycling. J. Transp. Geogr. 2018, 66, 369–375. [Google Scholar] [CrossRef]
- Goodman, A.; Aldred, R. Inequalities in utility and leisure cycling in England, and variation by local cycling prevalence. Transp. Res. Part F Traffic Psychol. Behav. 2018, 56, 381–391. [Google Scholar] [CrossRef]
- Tirachini, A.; Cats, O. COVID-19 and Public Transportation: Current Assessment, Prospects, and Research Needs. J. Public Transp. 2020, 22. [Google Scholar] [CrossRef]
- Zhang, J. Transport policymaking that accounts for COVID-19 and future public health threats: A PASS approach. Transp. Policy 2020, 99, 405–418. [Google Scholar] [CrossRef]
- Gkiotsalitis, K.; Cats, O. Public transport planning adaption under the COVID-19 pandemic crisis: Literature review of research needs and directions. Transp. Rev. 2020, 41, 374–392. [Google Scholar] [CrossRef]
- Vlacic, L.B. A Pandemic-Resilient Transportation System Paradigm [Editor’s Column]. IEEE Intell. Transp. Syst. Mag. 2021, 13, 3–4. [Google Scholar] [CrossRef]
- Haddad, H.; Bouyahia, Z.; Jabeur, N.; Yasar, A.U.H. Socially Structured Vanpooling: A Case Study in Salalah, Oman. IEEE Intell. Transp. Syst. Mag. 2022, 14, 242–252. [Google Scholar] [CrossRef]
- Sannigrahi, S.; Pilla, F.; Basu, B.; Basu, A.S.; Molter, A. Examining the association between socio-demographic composition and COVID-19 fatalities in the European region using spatial regression approach. Sustain. Cities Soc. 2020, 62, 102418. [Google Scholar] [CrossRef]
- Almagro, M.; Orane-Hutchinson, A. JUE Insight: The determinants of the differential exposure to COVID-19 in New York city and their evolution over time. J. Urban Econ. 2020, 127, 103293. [Google Scholar] [CrossRef]
- Pijls, B.G.; Jolani, S.; Atherley, A.; Derckx, R.T.; Dijkstra, J.I.; Franssen, G.H.; Hendriks, S.; Richters, A.; Venemans-Jellema, A.; Zalpuri, S.; et al. Demographic risk factors for COVID-19 infection, severity, ICU admission and death: A meta-analysis of 59 studies. BMJ Open 2021, 11, e044640. [Google Scholar] [CrossRef]
- Merler, S.; Ajelli, M. The role of population heterogeneity and human mobility in the spread of pandemic influenza. Proc. R. Soc. B Biol. Sci. 2010, 277, 557–565. [Google Scholar] [CrossRef]
- Browne, A.; St-Onge Ahmad, S.; Beck, C.R.; Nguyen-Van-Tam, J.S. The roles of transportation and transportation hubs in the propagation of influenza and coronaviruses: A systematic review. J. Travel Med. 2016, 23, tav002. [Google Scholar] [CrossRef]
- Tizzoni, M.; Bajardi, P.; Decuyper, A.; Kon Kam King, G.; Schneider, C.M.; Blondel, V.; Smoreda, Z.; González, M.C.; Colizza, V. On the use of human mobility proxies for modeling epidemics. PLoS Comput. Biol. 2014, 10, e1003716. [Google Scholar] [CrossRef]
- Findlater, A.; Bogoch, I.I. Human mobility and the global spread of infectious diseases: A focus on air travel. Trends Parasitol. 2018, 34, 772–783. [Google Scholar] [CrossRef]
- Goscé, L.; Johansson, A. Analysing the link between public transport use and airborne transmission: Mobility and contagion in the London underground. Environ. Health 2018, 17, 84. [Google Scholar] [CrossRef]
- Nakata, Y.; Röst, G. Global analysis for spread of infectious diseases via transportation networks. J. Math. Biol. 2015, 70, 1411–1456. [Google Scholar] [CrossRef]
- Olsen, S.J.; Chang, H.L.; Cheung, T.Y.Y.; Tang, A.F.Y.; Fisk, T.L.; Ooi, S.P.L.; Kuo, H.W.; Jiang, D.D.S.; Chen, K.T.; Lando, J.; et al. Transmission of the severe acute respiratory syndrome on aircraft. N. Engl. J. Med. 2003, 349, 2416–2422. [Google Scholar] [CrossRef]
- Mangili, A.; Gendreau, M.A. Transmission of infectious diseases during commercial air travel. Lancet 2005, 365, 989–996. [Google Scholar] [CrossRef]
- Mohr, O.; Askar, M.; Schink, S.; Eckmanns, T.; Krause, G.; Poggensee, G. Evidence for airborne infectious disease transmission in public ground transport—A literature review. Eurosurveillance 2012, 17, 20255. [Google Scholar] [CrossRef]
- Lapidus, N.; De Lamballerie, X.; Salez, N.; Setbon, M.; Delabre, R.M.; Ferrari, P.; Moyen, N.; Gougeon, M.L.; Vely, F.; Leruez-Ville, M.; et al. Factors associated with post-seasonal serological titer and risk factors for infection with the pandemic A/H1N1 virus in the French general population. PLoS ONE 2013, 8, e60127. [Google Scholar] [CrossRef]
- Lim, W.Y.; Chen, C.H.; Ma, Y.; Chen, M.I.; Lee, V.J.; Cook, A.R.; Tan, L.W.; Tabo Jr, N.F.; Barr, I.; Cui, L.; et al. Risk factors for pandemic (H1N1) 2009 seroconversion among adults, Singapore, 2009. Emerg. Infect. Dis. 2011, 17, 1455. [Google Scholar] [CrossRef]
- Goh, E.H.; Jiang, L.; Hsu, J.P.; Tan, L.W.L.; Lim, W.Y.; Phoon, M.C.; Leo, Y.S.; Barr, I.G.; Chow, V.T.K.; Lee, V.J.; et al. Epidemiology and relative severity of influenza subtypes in Singapore in the post-pandemic period from 2009 to 2010. Clin. Infect. Dis. 2017, 65, 1905–1913. [Google Scholar] [CrossRef]
- Guerrisi, C.; Ecollan, M.; Souty, C.; Rossignol, L.; Turbelin, C.; Debin, M.; Goronflot, T.; Boëlle, P.Y.; Hanslik, T.; Colizza, V.; et al. Factors associated with influenza-like-illness: A crowdsourced cohort study from 2012/13 to 2017/18. BMC Public Health 2019, 19, 879. [Google Scholar] [CrossRef]
- Troko, J.; Myles, P.; Gibson, J.; Hashim, A.; Enstone, J.; Kingdon, S.; Packham, C.; Amin, S.; Hayward, A.; Van-Tam, J.N. Is public transport a risk factor for acute respiratory infection? BMC Infect. Dis. 2011, 11, 16. [Google Scholar] [CrossRef]
- Xu, F.; McCluskey, C.C.; Cressman, R. Spatial spread of an epidemic through public transportation systems with a hub. Math. Biosci. 2013, 246, 164–175. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, A.; Wang, J. Exploring the roles of high-speed train, air and coach services in the spread of COVID-19 in China. Transp. Policy 2020, 94, 34–42. [Google Scholar] [CrossRef]
- Fang, H.; Wang, L.; Yang, Y. Human mobility restrictions and the spread of the novel coronavirus (2019-ncov) in China. J. Public Econ. 2020, 191, 104272. [Google Scholar] [CrossRef]
- Zheng, R.; Xu, Y.; Wang, W.; Ning, G.; Bi, Y. Spatial transmission of COVID-19 via public and private transportation in China. Travel Med. Infect. Dis. 2020, 34, 101626. [Google Scholar] [CrossRef]
- Kraemer, M.U.; Yang, C.H.; Gutierrez, B.; Wu, C.H.; Klein, B.; Pigott, D.M.; Du Plessis, L.; Faria, N.R.; Li, R.; Hanage, W.P.; et al. The effect of human mobility and control measures on the COVID-19 epidemic in China. Science 2020, 368, 493–497. [Google Scholar] [CrossRef]
- Bilgin, N.M. Tracking COVID-19 Spread in Italy with Mobility Data. 2020. Available online: https://ssrn.com/abstract=3585921 (accessed on 22 November 2022).
- Kuo, P.F.; Chiu, C.S. Airline transportation and arrival time of international disease spread: A case study of Covid-19. PLoS ONE 2021, 16, e0256398. [Google Scholar] [CrossRef]
- Lan, F.Y.; Wei, C.F.; Hsu, Y.T.; Christiani, D.C.; Kales, S.N. Work-related COVID-19 transmission in six Asian countries/areas: A follow-up study. PLoS ONE 2020, 15, e0233588. [Google Scholar] [CrossRef]
- Harris, J.E. The Subways Seeded the Massive Coronavirus Epidemic in New York City; Technical Report; National Bureau of Economic Research: Cambridge, MA, USA, 2020. [Google Scholar]
- Toyokawa, T.; Shimada, T.; Hayamizu, T.; Sekizuka, T.; Zukeyama, Y.; Yasuda, M.; Nakamura, Y.; Okano, S.; Kudaka, J.; Kakita, T.; et al. Transmission of SARS-CoV-2 during a 2-h domestic flight to Okinawa, Japan, March 2020. Influenza Other Respir. Viruses 2021, 16, 63–71. [Google Scholar] [CrossRef]
- Musselwhite, C.; Avineri, E.; Susilo, Y. Editorial JTH 16—The Coronavirus Disease COVID-19 and implications for transport and health. J. Transp. Health 2020, 16, 100853. [Google Scholar] [CrossRef]
- Johansson, M.A.; Wolford, H.; Paul, P.; Diaz, P.S.; Chen, T.H.; Brown, C.M.; Cetron, M.S.; Alvarado-Ramy, F. Reducing travel-related SARS-CoV-2 transmission with layered mitigation measures: Symptom monitoring, quarantine, and testing. BMC Med. 2021, 19, 94. [Google Scholar] [CrossRef]
- Speaker, S.L.; Doherty, C.M.; Pfoh, E.; Dunn, A.; Hair, B.; Daboul, L.; Shaker, V.; Rothberg, M. Social behaviors associated with a positive COVID-19 test result. Cureus 2021, 13, e13064. [Google Scholar] [CrossRef]
- Ozbilen, B.; Slagle, K.M.; Akar, G. Perceived risk of infection while traveling during the COVID-19 pandemic: Insights from Columbus, OH. Transp. Res. Interdiscip. Perspect. 2021, 10, 100326. [Google Scholar] [CrossRef] [PubMed]
- Mojumder, M.N.; Ahmed, M.A.; Sadri, A.M. Identifying ridesharing risk, response, and challenges in the emergence of novel coronavirus using interactions in uber drivers forum. Front. Built Environ. 2021, 7, 619283. [Google Scholar] [CrossRef]
- Paudel, D.; Melendez, K.A.; Chacreton, D.; Das, T.K.; Reina Ortiz, M.; Kwon, C. Measuring the Impact of the Large-Scale Adoption of Ridesharing on the Spread of Infectious Diseases; Technical Report; Department of Industrial and Management Systems Engineering, University of South Florida: Tampa, FL, USA, 2021. [Google Scholar]
- Wong, H.J.Y.; Deng, Z.; Yu, H.; Huang, J.; Leung, C.; Miao, C. A Testbed for Studying COVID-19 Spreading in Ride-Sharing Systems. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence (IJCAI-20) Demonstrations Track, Yokohama, Japan, 11–17 July 2020; pp. 5294–5296. [Google Scholar]
- Kucharski, R.; Cats, O.; Sienkiewicz, J. Modelling virus spreading in ride-pooling networks. Sci. Rep. 2021, 11, 7201. [Google Scholar] [CrossRef] [PubMed]
- Safranek, C.W.; Scheinker, D. A computer modeling method to analyze rideshare data for the surveillance of novel strains of SARS-CoV-2. Ann. Epidemiol. 2022, 76, 136–142. [Google Scholar] [CrossRef]
- Danon, L.; Lacasa, L.; Brooks-Pollock, E. Household bubbles and COVID-19 transmission: Insights from percolation theory. Philos. Trans. R. Soc. B 2021, 376, 20200284. [Google Scholar] [CrossRef]
- Connor, C. Computing for Numeracy: How Safe is Your COVID-19 Social Bubble? Numer. Adv. Educ. Quant. Lit. 2021, 14, 1–14. [Google Scholar] [CrossRef]
- Leng, T.; White, C.; Hilton, J.; Kucharski, A.; Pellis, L.; Stage, H.; Davies, N.G.; Keeling, M.J.; Flasche, S. The effectiveness of social bubbles as part of a Covid-19 lockdown exit strategy, a modelling study. Wellcome Open Res. 2020, 5, 213. [Google Scholar] [CrossRef]
- Lorenc, A.; Kesten, J.M.; Kidger, J.; Langford, R.; Horwood, J. Reducing COVID-19 risk in schools: A qualitative examination of secondary school staff and family views and concerns in the South West of England. BMJ Paediatr. Open 2021, 5, e000987. [Google Scholar] [CrossRef]
- Ismail, S.A.; Saliba, V.; Bernal, J.L.; Ramsay, M.E.; Ladhani, S.N. SARS-CoV-2 infection and transmission in educational settings: A prospective, cross-sectional analysis of infection clusters and outbreaks in England. Lancet Infect. Dis. 2021, 21, 344–353. [Google Scholar] [CrossRef]
- Dix, A. Impact of a small number of large bubbles on Covid-19 transmission within universities. arXiv 2020, arXiv:2008.08147. [Google Scholar]
- Shaw, J.; Day, T.; Malik, N.; Barber, N.; Wickenheiser, H.; Fisman, D.N.; Bogoch, I.; Brownstein, J.I.; Williamson, T. Working in a bubble: How can businesses reopen while limiting the risk of COVID-19 outbreaks? CMAJ 2020, 192, E1362–E1366. [Google Scholar] [CrossRef] [PubMed]
- Bouyahia, Z.; Haddad, H.; Jabeur, N.; Nait-Sidi-Moh, A. Optimization of Chartered Buses Routes Under Uncertainties Using Probabilistic Vehicle Routing Problem Modeling. In Proceedings of the 9th International Conference on Ambient Systems, Networks and Technologies (ANT 2018), Porto, Portugal, 8–11 May 2018. [Google Scholar]
- Currie, C.S.; Fowler, J.W.; Kotiadis, K.; Monks, T.; Onggo, B.S.; Robertson, D.A.; Tako, A.A. How simulation modelling can help reduce the impact of COVID-19. J. Simul. 2020, 14, 83–97. [Google Scholar] [CrossRef]
- Cintra, P.; Citeli, M.; Fontinele, F. Mathematical Models for Describing and Predicting the COVID-19 Pandemic Crisis. arXiv 2020, arXiv:2006.02507. [Google Scholar]
- Hou, C.; Chen, J.; Zhou, Y.; Hua, L.; Yuan, J.; He, S.; Guo, Y.; Zhang, S.; Jia, Q.; Zhao, C.; et al. The effectiveness of quarantine of Wuhan city against the Corona Virus Disease 2019 (COVID-19): A well-mixed SEIR model analysis. J. Med Virol. 2020, 92, 841–848. [Google Scholar] [CrossRef] [PubMed]
- Sen, D.; Sen, D. Use of a modified SIRD model to analyze COVID-19 data. Ind. Eng. Chem. Res. 2021, 60, 4251–4260. [Google Scholar] [CrossRef]
- Danon, L.; Brooks-Pollock, E.; Bailey, M.; Keeling, M. A spatial model of COVID-19 transmission in England and Wales: Early spread, peak timing and the impact of seasonality. Philos. Trans. R. Soc. B 2021, 376, 20200272. [Google Scholar] [CrossRef]
- Tuite, A.R.; Fisman, D.N.; Greer, A.L. Mathematical modelling of COVID-19 transmission and mitigation strategies in the population of Ontario, Canada. CMAJ 2020, 192, E497–E505. [Google Scholar] [CrossRef]
- Giordano, G.; Blanchini, F.; Bruno, R.; Colaneri, P.; Di Filippo, A.; Di Matteo, A.; Colaneri, M. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat. Med. 2020, 26, 855–860. [Google Scholar] [CrossRef]
- Ogden, N.H.; Fazil, A.; Arino, J.; Berthiaume, P.; Fisman, D.N.; Greer, A.L.; Ludwig, A.; Ng, V.; Tuite, A.R.; Turgeon, P.; et al. Modelling scenarios of the epidemic of COVID-19 in Canada. Can. Commun. Dis. Rep. 2020, 46, 198. [Google Scholar] [CrossRef]
- Chang, S.L.; Harding, N.; Zachreson, C.; Cliff, O.M.; Prokopenko, M. Modelling transmission and control of the COVID-19 pandemic in Australia. Nat. Commun. 2020, 11, 5710. [Google Scholar] [CrossRef]
- Haddad, H.; Moulin, B.; Thériault, M. An Integrated Approach for Communicable Disease Geosimulation Based on Epidemiological, Human Mobility and Public Intervention Models. In Analyzing and Modeling Spatial and Temporal Dynamics of Infectious Diseases; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015; pp. 403–442. [Google Scholar]
- Perez, L.; Dragicevic, S. An agent-based approach for modeling dynamics of contagious disease spread. Int. J. Health Geogr. 2009, 8, 50. [Google Scholar] [CrossRef]
- Cliff, O.M.; Harding, N.; Piraveenan, M.; Erten, E.Y.; Gambhir, M.; Prokopenko, M. Investigating spatiotemporal dynamics and synchrony of influenza epidemics in Australia: An agent-based modelling approach. Simul. Model. Pract. Theory 2018, 87, 412–431. [Google Scholar] [CrossRef]
- Taillandier, P.; Gaudou, B.; Grignard, A.; Huynh, Q.N.; Marilleau, N.; Caillou, P.; Philippon, D.; Drogoul, A. Building, composing and experimenting complex spatial models with the GAMA platform. Geoinformatica 2019, 23, 299–322. [Google Scholar] [CrossRef]
- Bi, Q.; Wu, Y.; Mei, S.; Ye, C.; Zou, X.; Zhang, Z.; Liu, X.; Wei, L.; Truelove, S.A.; Zhang, T.; et al. Epidemiology and transmission of COVID-19 in 391 cases and 1286 of their close contacts in Shenzhen, China: A retrospective cohort study. Lancet Infect. Dis. 2020, 20, 911–919. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, Y.; Qian, X.; Li, J. A knowledge graph-based method for epidemic contact tracing in public transportation. Transp. Res. Part Emerg. Technol. 2022, 137, 103587. [Google Scholar] [CrossRef]


| Symbol | Meaning | SSV | SBV |
|---|---|---|---|
| Rider i’s origin (home) geographic location (longitude, latitude) | ✓ | ✓ | |
| Rider i’s activity destination geographic location (longitude, latitude) | ✓ | ✓ | |
| = [, ] | Start and end dates of the service period of the rider i | ✓ | ✓ |
| Rider i’s earliest time interval to start the trip | ✓ | ✓ | |
| Rider i’s latest time interval to start the trip | ✓ | ✓ | |
| Travel time window of rider i from home to the activity’s destination location | ✓ | ✓ | |
| Travel time window of rider i from the activity location to home | ✓ | ✓ | |
| = ({day}, , ) | Rider i’s slots, where every slot is defined by a set of days and travel time windows | ✓ | ✓ |
| Rider i’s budget range | ✓ | ✓ | |
| Rider i’s age | ✓ | ✓ | |
| Rider i’s health risk level with respect to communicable diseases, value , 1 = very low risk level, 2 = low risk level, 3 = medium risk level, 4 = high risk level, and 5 = very high risk level | ✗ | ✓ | |
| Rider i’s social preferences: , where j is the rider in the same spatial cluster as i, | ✓ | ✗ | |
| Rider i’s safety value , 1 = not important, 5 = extremely important | ✓ | ✗ | |
| Rider i’s comfort value , 1 = not important, 5 = extremely important | ✓ | ✗ | |
| Rider i’s value for driver experience , 1 = not important, 5 = extremely important | ✓ | ✗ | |
| Rider i’s value for van cleanness , 1 = not important, 5 = extremely important | ✓ | ✗ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haddad, H.; Bouyahia, Z.; Horchani, L. On the Sustainability of Shared Mobility Since COVID-19: From Socially Structured to Social Bubble Vanpooling. Sustainability 2022, 14, 15764. https://doi.org/10.3390/su142315764
Haddad H, Bouyahia Z, Horchani L. On the Sustainability of Shared Mobility Since COVID-19: From Socially Structured to Social Bubble Vanpooling. Sustainability. 2022; 14(23):15764. https://doi.org/10.3390/su142315764
Chicago/Turabian StyleHaddad, Hedi, Zied Bouyahia, and Leila Horchani. 2022. "On the Sustainability of Shared Mobility Since COVID-19: From Socially Structured to Social Bubble Vanpooling" Sustainability 14, no. 23: 15764. https://doi.org/10.3390/su142315764
APA StyleHaddad, H., Bouyahia, Z., & Horchani, L. (2022). On the Sustainability of Shared Mobility Since COVID-19: From Socially Structured to Social Bubble Vanpooling. Sustainability, 14(23), 15764. https://doi.org/10.3390/su142315764







