Abstract
Precision farming is the newest agricultural approach in countries with highly mechanized field operations, and the role of unmanned ground vehicles (UGVs) in smart farming is becoming increasingly prominent. This work aimed to evaluate the stability of the DEDALO UGV developed by the University of BOLOGNA for precision orchard and vineyard management. The driving part of the machine is somewhat peculiar; it moves autonomously in the field combined with a tank to store water and pesticide mixture for crop protection, with an additional structure to carry agricultural implements. The study aimed to evaluate the stability of the agricultural unladen UGV, and mulcher and sprayer mounted configurations. In the case of the sprayer, the stability behavior was evaluated with an empty and full tank. The machine, in terms of stability, was studied both laterally and longitudinally. A theoretical model was developed based on the upstream side forces measured during experimental tipping tests. The results of the experimental data were compared with the theoretical predicted results to validate the model. In the lateral test, the average value of the limit stability angle was 48 degrees, while in the longitudinal test, it was 49 degrees. The results of the model were statistically correlative (R2 > 95) and denoted that the most stable condition occurred in the case of the UGV fitted with the mulcher in the longitudinal tipping position (56 degrees), while the most unstable condition was the case of the unladen UGV in the longitudinal tipping position (40 degrees). Although the stability problem is not directly connected with the operator, as these machines do not require a driver, the lack of stability can lead to the UGV overturning with consequent risks for the surrounding environment and damage to the UGV body.
1. Introduction
Precision farming is currently the newest agricultural approach in countries with highly mechanized field operations, and the role of unmanned ground vehicles (UGVs) in smart farming is becoming increasingly prominent. The new UGVs, expensive machines designed with technologically advanced sensors and actuators, require research activities and fixed rules to assess performance safety in their normal operation in the field.
The tractor is the most popular vehicle operating in countries where farming is complemented by agricultural machines, where it is used to increase work productivity and contemporarily decrease fatigue in manual handling [1]. The main reason for the high use of tractors in conventional farming, both in arable crops and orchard and vineyard cultivation, but also in animal husbandry, is consequent to the specific design of the vehicle addressed, which propels agricultural equipment by supplying power when in motion or stationery, combined with the action of pulling trailers or carrying and pulling agricultural tools and machinery [2].
All around the world, because of its very high versatility, operators gained trust in the tractor, which they wrongly considered as a machine able to perform all tasks in many different environments. Consequently, incorrect usage of the vehicle often caused fatalities and severe injuries, mainly associated with tractor rollover events [3,4]. As an effect of this, it is well recognized that agriculture is a work environment that faces a very high number of fatal accidents every year [5,6].
Over the years, the feasible solution adopted to protect the tractor driver with respect to the consequences of rollover accidents was a passive protection, obtained by mounting a rollover protective structure (ROPS) that had met standardized strength tests to assess its ability to preserve the driver’s safety clearance zone in case of impact on the ground [7,8,9]. Research at the international level was performed to indagate the ROPS performance and the stability behavior of the tractor to identify limits and actions to improve the level of safety for drivers [10,11,12].
Contemporarily to its increased safety performance, the tractor evolved in its design and operation, following farm management change. Nowadays, precision farming is the newest agricultural approach in countries with highly mechanized field operations. The aim is to deliver agriculture with minimized financial and environmental risk thanks to optimized input quantities and more precise targets that are in line with the principle of parsimony [13]. In precision agriculture, the digital farm is the final goal, and mechatronic, telemetric, and robotic disciplines are involved in collecting and managing data from farming operations to develop algorithms that can support the farmer in addressing proper decisions based on the variability assessed in the farm [14]. Models for strategic scenario planning and risk assessments for farmers, policymakers, and scientists have been developed [15]. The progressive development and adoption of technological innovations have been recently studied in wine farm management, and the findings highlighted the issues of a sector which, although having broad investment and finance options, lacks human, territorial, and organizational resources for the successful adoption of technological innovations [16]. Equivalent considerations are of potential validity for the other sectors of agriculture.
Nonetheless, in modern agriculture, the design of the tractor has changed, and sensors and actuators combined with a controller area network (CAN) can sense the main tractor organs. Moreover, in addition to implementing a standardized communication protocol, known as the ISObus protocol [17], the tractor is digitally connected to its implements so that operators can manage the adjustment of tools in real time. Contemporary systems to assist the operator in tractor driving have also been mounted, with the most advanced applications represented by autonomous guidance [18], even if, in Europe, autonomous tractors are only allowed to run in the field under the supervision of the operator, who is seated on the driver seat and available to directly operate the vehicle if necessary, only allowing semi-autonomous guidance in practice [19]. It well recognized that there is technology currently available for designing autonomous tractors, but the rules to market these unmanned tractors are very stringent. The main issue in Europe is to define ad hoc rules for managing the artificial intelligence implemented in autonomous vehicles, including the tractor, to guarantee an acceptable level of safety performance while preserving its operation. Once the rules have been issued, autonomous vehicles could certainly contribute to reducing the fatalities associated with tractor rollovers. Researchers have worked on the design of autonomous tractors since the fifties of the last century, fitting them with technological features available at the time [20]. In recent years, an alternative approach has been proposed to design small multi-utility self-directed vehicles, not identifiable as tractors, which can perform agricultural tasks in open fields and in orchard and vineyard soils at very low forward speeds [21].
All highly automated vehicles, independent of design features, require that a defined safety performance and safety rules for their operation be issued. In 2018, the International Standardisation Organisation (ISO) published the ISO standard 18497, titled Agricultural Machinery and Tractors—Safety of Highly Automated Agricultural Machines (Principles for Design) [22]. The standard relates to the requirements for starting and moving highly automated agricultural machines. A test method for a human detection system is foreseen with a stop function, or a control transfer to the operator, if an error in the perception system is detected. The approach of a protective zone around the machine is adopted, even a dynamic zone that relies on the perception system, though it is not yet known how it could be implemented [23].
A subject not considered in the recent requirements relates to the stability performance of these highly automated machines. The issue of machinery stability and potential overturning risk has been identified, not only for the tractor but also for agricultural self-propelled machines (ASPMs) [24]. The ISO standard 16231-2 aimed to assess the static stability angle of ASPMs with respect to a reference limit angle identified for each ASPM category to define the safety measures required case by case [25].
Stability is also a very important issue for highly automated machines operating in agriculture. Although the stability of the UGV is not directly connected with operator safety, as these machines do not require a driver, the lack of stability can lead to rollover with potential multiple rolls and consequent risks with respect to the human perception system, the protective zone around the machine, and the UGV body.
Agriculture is a dynamic environment, and it is difficult to define a priori the features of the working areas. In Italy, orchards and vineyards are often developed in mountainous and hilly areas, and severe injuries or fatal accidents from tractors overturning frequently occur [26]; therefore, unmanned ground vehicles are ideal to replace the ride-on tractors in these very sloped areas where dedicated cultivations are of high interest, such as vineyards on steep sloped areas, which are not only common in Italy but also in other European countries such as Austria and Germany. Consequently, the stability issue must be considered as part of the safety performance required for these vehicles.
The UGV’s unstable condition is assessable based on the geometric parameters and the specific design of the autonomous vehicle, according to an evaluation approach in line with the ISO standard 16231-2.
The study was centered around the stability performance analysis of the DEDALO UGV, designed at the Alma mater Studiorum, University of Bologna for orchard and vineyard operation. The unladen UGV and two additional implemented and mounted vehicle configurations, a mulcher configuration and a sprayer configuration, were investigated to understand the effect on lateral and longitudinal stability with respect to the sloped ground.
A mathematical model was then developed and the results of the experimental tests with the predicted results were compared.
2. Experimental Evaluation
The tests were performed at the official OECD (Organization for Economic Co-operation and Development) Test Station, Laboratorio di Meccanica Agraria, of the Alma Mater Studiorum, University of Bologna (UNIBO). The DEDALO UGV for orchard and vineyard operations, designed at the Department of Electrical Electronic and Information Engineering (DEI), was evaluated in the experimental tests. The aim of the study was to analyze the UGV’s stability performance. Three different UGV configurations were subjected to the stability test: a UGV in unladen weight condition, a UGV mounted with a mulcher, and a UGV fitted with an air-assisted sprayer. Lateral and longitudinal tipping experimental tests were carried out to assess the critical unstable conditions.
2.1. The Agricultural UGV Dimensions
The Alma Mater Studiorum, University of Bologna, recently developed the DEDALO UGV prototype, specifically designed for precision orchard and vineyard management (Figure 1).
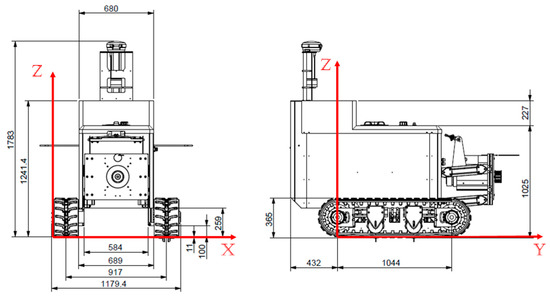
Figure 1.
Unladen agricultural UGV.
As reported in Mengoli et al. [27], this prototype is a small and lightweight structure for spraying and mowing operations. The UGV is a tracked vehicle driven by electric motors and the distance between the tracks is adjustable to match the inter-row width. The mounted implements were powered by a 16 kW petrol engine in reason of the reasonably high-energy demands (e.g., pertaining to the air-assisted sprayer).
The control logic of the UGV was divided into:
- -
- The low-level (LL) controller;
- -
- The high-level (HL) controller.
The LL component, directly connected to the vehicle actuators and motor drivers, controls the safety procedures by transmitting velocity set-points to the electrical motors for locomotion while collecting telemetry data. The HL controller is the smartest element of the system because it relates to the implementation of the navigation algorithms. The autonomous navigation is based on the information provided by the onboard sensors, both in open-field and in-row orchard scenarios. Two computers (one for the LL control and the second for the HL control) process all the input/output signals and the control algorithms.
The sensors fitted on the vehicle were:
- -
- Motor encoders to ensure vehicle odometry;
- -
- A 9-axis inertial measurement unit (IMU) with integrated 3-axis accelerometers, 3-axis gyroscopes, and 3-axis magnetometers;
- -
- A GNSS receiver for global localization, to be used mainly in the open-field scenario;
- -
- A 3D LiDAR to estimate the surrounding obstacles, to be used mainly with in-row navigation.
In orchard and vineyard navigation, the GNSS receiver was not used and the LiDAR measurement was processed to provide relative localization with respect to the tree and/or vine rows using the Hough transform algorithm.
The locomotion electrical motors to drive the rubber tracks of the platform were equipped with sinusoidal encoders to estimate the speed of the vehicle.
2.2. Actual Test Configurations
2.2.1. Unladen Agricultural UGV
The UGV in this study was a small-sized vehicle with a mass of 630 kg, fitted with sensors and operating implements. The platform was rigid and there were no free moving parts. The tracks were made of fairly thick rubber material, since the deformation was considered negligible. At the front of the machine, a special four-point lift part was fitted to connect the agricultural equipment. An internal combustion engine drove the power take-off.
The DEDALO UGV of the University of Bologna, due to its size and weight, was assimilated to an agricultural tractor belonging to category C2 (EU regulation 167/2013), which represented the narrow-track tractors that operate mainly in fruit- or vine-growing contexts. The main dimensions (Figure 1), such as the length, width, height, wheelbase, and track width, were as follows:
- -
- Total length: 1900 mm;
- -
- Overall width: 1179.4 mm;
- -
- Total height: 1783 mm;
- -
- Wheelbase: 1044 mm;
- -
- Track width: 917 mm.
The unladen UGV was the first UGV configuration considered for the experimental tests (Figure 2a).

Figure 2.
Agricultural UGV configurations: (a) unladen; (b) UGV–mulcher; (c) UGV–sprayer.
2.2.2. Agricultural UGV Fitted with Mulcher
The UGV was linked to an agricultural implement dedicated to grass mulching. The mulcher had a mass of 150 kg and was carried out on the front lift. The rotor of the mulcher was equipped with interchangeable swinging knives of different shapes and sizes. The UGV fitted with the mulcher was the second UGV configuration considered for the experimental tests (Figure 2b). The mulcher connection produced a length increase of 280 mm with respect to the unladen configuration, but the overall width was not affected; the width of the mulcher was equivalent to the unladen UGV width.
2.2.3. Agricultural UGV Fitted with the Sprayer
The UGV was equipped with an agricultural implement designed for crop protection. The air-assisted sprayer had a mass of 100 kg and was mounted on the front of the UGV. The spraying equipment was fitted with a centrifugal fan to allow the airstream to transport the liquid jet, and a volumetric pump for the liquid mixture pressure. Eight hydraulic nozzles, four on each side of spraying, were located at the air outlets according to a modern spray design intended to localize the liquid at different canopy heights. A 200-L tank was mounted on the central part of the UGV. In the test, two different configurations for the sprayer were considered: the UGV with the empty sprayer tank and the UGV with the full tank (Figure 2c). The water mass added to the tank was 190 kg. The sprayer linkage produced a length increase of 190 mm with respect to the unladen UGV length; however, in the case of the mulcher implement linkage, the overall width was not affected. Nevertheless, the total height increased to 1920 mm.
2.3. Forces and Tipping Angles during the Experimental Tests
Basing on the three UGV configurations, the experimental tests performed are schematized in Table 1. The center-of-gravity (CoG) position of the three UGV configurations was determined, and lateral and longitudinal tipping tests were executed.

Table 1.
Planning of experimental tests.
The experimental test was repeated three times for each configuration to ensure the reliability of the data.
2.3.1. Centre of Gravity Position Determination
The CoG height (Z location in Figure 1) for each tested configuration, as depicted in Figure 3, was indirectly obtained by calculating the period of oscillation, which was measured with the vehicle secured on an oscillating platform at two different pivot heights, according to the parallel axis theorem [28,29]. The longitudinal CoG position (X-Y locations in Figure 1) was obtained using electronic scales located under the tracks.

Figure 3.
Agricultural UGV on the oscillating platform: (a) unladen; (b) UGV–mulcher; (c) UGV–sprayer.
2.3.2. Lateral Tipping Test
To carry out the controlled lateral rollover tests, the vehicle was positioned on a tilting platform to bring the left track closer to the axis of rotation and initiate the lifting effect during the tipping action of the platform, while the right track was further away from the axis of rotation of the tilting platform. The longitudinal direction of the vehicle was parallel to the rotation axis of the tilting platform. To overcome the non-perfect adherence of the vehicle during the rotation of the platform, a dedicated structure was designed to prevent the vehicle from sliding downward.
A load cell was positioned under the right track to measure the upstream side force of the different UGV configurations. A digital level was used to monitor the angle of inclination of the UGV equivalent to the tilting platform angle in real time.
Once the UGV was positioned and secured to the tilting platform, it was gradually raised to obtain a progressively increasing slope. At regular time intervals, the following data were recorded: the force on the load cell for estimating the phase of unstable equilibrium and the slope angle of the platform as the digital-level data.
The lateral tipping test was repeated for all UGV configurations, and it was stopped at the maximum achievable inclination equivalent to the condition of the unstable equilibrium. The experimental test was repeated three times for each configuration (Figure 4).

Figure 4.
Agricultural UGV during the lateral tipping test: (a) initial position; (b) final position.
2.3.3. Longitudinal Tipping Test
To carry out the longitudinal stability tests, the vehicle was positioned on the tilting platform with longitudinal arrangement with respect to the direction of inclination of the base platform to simulate, and consequently to hypothesize, the limit conditions of the vehicle’s stability both uphill and downhill on a sloping field.
The longitudinal direction of the vehicle was perpendicular to the axis of rotation of the tilting platform. The non-perfect adherence of the vehicle during the rotation of the platform was overcome by means of a dedicated structure that prevented the vehicle from sliding downward.
Under each front axle of the tracks, a load cell was positioned to monitor the UGV stability status in real time. As the inclined plane was progressively raised, the force on the front axle was progressively reduced to zero, corresponding to the condition of unstable equilibrium.
Once the UGV was positioned and secured to the tilting platform, it was gradually raised to obtain a progressively increasing slope. At regular time intervals, two types of data were recorded: the force on the load cell and the sloped angle of the platform.
The longitudinal tipping test was performed on all UGV configurations until the maximum achievable inclination was achieved. The experimental test was repeated three times for each configuration (Figure 5).

Figure 5.
Agricultural UGV during the longitudinal tipping test: (a) initial position; (b) final position.
3. Theoretical Model
The UGV CoG position change and stability condition during the progressive rotation of a tiltable platform were predicted basing on the initial position of the UGV prototype. In the first stage of the evaluation, the UGV was in the horizontal position (Figure 6a), i.e., the CoG and upstream track contact point with the ground (PT) coordinates were:
where is the horizontal distance and is the height of the CoG with respect to the rotation axis. W is the distance of the upstream prototype component in contact with the ground with respect to the rotation axis. In the rotation time (Figure 6b), after the initial position, the UGV polar coordinates in the plane were:
where , α is the tilting angle, and .
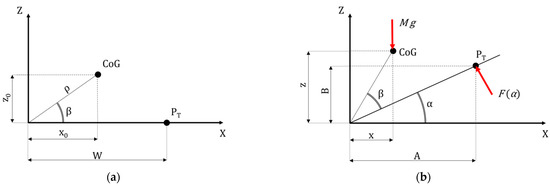
Figure 6.
Agricultural UGV model analyzing the virtual lateral tipping: (a) the UGV horizontal position; (b) the UGV tilted position.
Referring to the UGV mass, the normal force acting on the upstream track of the prototype as a function of the inclination (α) to which the UGV was subjected was calculated:
where is the UGV mass and is the gravitational acceleration.
The approach used to analyze the case study of the lateral tipping was adapted to the case study of the longitudinal tipping by considering the y coordinate instead of the x coordinate.
4. Validation
The model data were compared to the experimental results. The numerical model was developed using MATLAB (MATLAB® version R2021b). The upstream side force (F) was calculated with respect to the sloped angle () of the tilted platform. R2 and the root mean square error (RMSE) were computed for comparison purposes by operating a dedicated Matlab function to calculate the R2 value based on actual and model data. The experimental results were related to the four UGV configurations (Table 1).
4.1. Comparison between Predicted and Experimental Results
The results of the experimental tests were compared to the results of the predicted data and the upstream side forces were overlapped to demonstrate the differences. The values of the mass and the CoG position for the four UGV configurations are summarized in Table 2. Values of the upstream side force with respect to the platform tilting angle () are shown in Figure 7.

Table 2.
UGV masses and CoG positions, R2, and RMSE data for lateral and longitudinal tests.
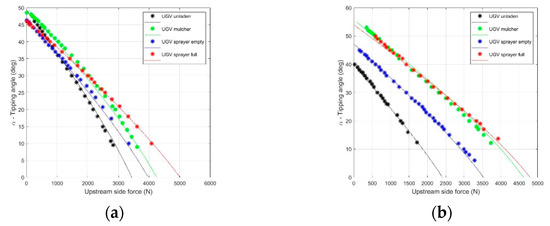
Figure 7.
Tilting angle vs. upstream force for the four different UGV configurations: (a) Lateral tipping; (b) Longitudinal tipping. The experimental data represent the average of three repeated tests.
It is worth noting that the upstream force decreased, increasing the slope angle. The assessed behaviors are attributable to the fact that increasing the angle of the slope meant that the mass distribution was affected and the load was mainly on the downstream part of the UGV. Both R2 and RMSE are reported in Table 2; the predicted results of the model show a statistically significant correlation (R2 > 95). Moreover, the RMSE was less than 1 degree. Model data obtained by combining the effects of the mounted implements are shown in Figure 8.
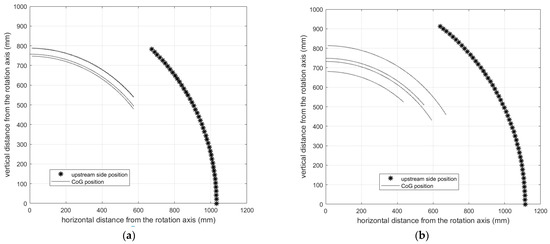
Figure 8.
Center of mass and upstream contact point trajectory during the tipping behavior: lateral tipping (a); and longitudinal tipping (b).
4.2. Stability Angle Results
The lateral stability angle () was calculated, referring to the CoG coordinates in the initial and final phases of the tipping action (see Figure 6 and Figure 8):
The approach used to analyze the lateral stability angle was adapted to the longitudinal one by considering the y coordinate instead of the x coordinate. Table 3 shows the stability angles of the four UGV configurations.

Table 3.
Stability angles: lateral tipping and longitudinal tipping.
5. Discussion
Based on the study of the stability behavior (both lateral and longitudinal) of the UGV in different implement configurations analyzed during the controlled tests, a theoretical model was developed to foresee the stability angles of the UGV–implement complex. The analysis assessed the normal force sustained by the upstream side of the UGV in the tilted position. The implement type, as well as its geometry and inertia, affected the stability angle. Due to the actual UGV conditions during the experimental test, especially when the tilt angle increased, some repeated tests failed to reach the zero-force value and the precise measurement of the angle equivalent to the unstable condition was difficult to obtain.
A theoretical model was developed to predict the variation of the UGV CoG and the stability condition during the progressive rotation of the tiltable platform. Based on the initial position of the UGV and considering the rotation about an axis, the normal force acting on the upstream track of the UGV was calculated.
The model did not consider the effect of the vehicle sliding downward or the lack of grip on the platform, therefore ignoring the ground–track interaction by simply considering a rotation without translation. A comparison of the virtual and actual results allowed the theoretical model to be calibrated and validated, showing that the model was reliable in reason of a relative error less than 5% (R2 > 95%).
The modelling approach allowed a complete mapping of the stability angle, with respect to the CoG position of the vehicle, taking into consideration lateral and longitudinal contributions.
In the lateral test, the average value of the limit stability angle was 48 degrees, while in the longitudinal test it was 49. These values are very close; however, the standard deviation changed from 1.5 degrees to 7.3 degrees, respectively. In the longitudinal test, the variability was greater, demonstrating that the stability angle was influenced by the implement more in the longitudinal stability behavior than in the lateral behavior. Indeed, the lateral test denoted that the angle of stability did not show variability with respect to the implement. On the contrary, in the case of the longitudinal test, the implement significantly affected the stability angle of the UGV.
The approach adopted in the analysis showed to be of interest in studying the stability conditions of the UGV. Although the stability of the UGV was not directly connected with the operator, the lack of stability can lead to rollover with multiple potential rolls and consequent risks with respect to the human perception system and the protective zone around the machine, which can damage the UGV body.
It is necessary to define the operation of the unmanned vehicles with respect to steep-sloped fields. The stability issue is a safety performance required for UGVs, and the results obtained clearly demonstrate that both the lateral and longitudinal assessments are necessary to define a safe limit slope for operation on hilly areas. Regarding the stability of narrow-track tractors for orchard and vineyards, if the tractor is a front-mounted ROPS, only the lateral stability need to be assessed, since the lateral rollover is considered the main cause of accidents in agriculture [8]. Nevertheless, it would also be important for the tractor to evaluate the safety performance of the tractor–implement interaction and to understand the most critical conditions to increase the safety of the tractor–implement complex and so reduce the number of potential tractor accidents.
6. Conclusions
Controlled rollover tests were performed on an agricultural UGV designed to operate in vineyard and orchard soils. The actual tests involved the evaluation of lateral and longitudinal stability, and a theoretical mathematical model was developed. The validation of the model (R2 > 95%) allowed test results to be analyzed and the limit stability angles of the UGV (with and without connected implements) to be calculated. A mulcher and an air-assisted sprayer were considered in the assessment. Assessing the condition of the UGV unstable equilibrium in the actual tests required the testing procedure to be carefully managed, since it is difficult to perfectly identify the angle of instability. A reasonably high angle was obtained in the controlled conditions. The theoretical method, however, required simplified assumptions with respect to the geometry and features of the vehicle and the carried implements. Nevertheless, a comparison of the two approaches allowed reliable limit stability values to be calculated. The averaged values were 48 and 49 degrees for the lateral and longitudinal stability evaluations, respectively. The most unstable configuration, as it reached the unstable equilibrium first, was the unladen UGV in the longitudinal evaluation (40 degrees), while the most stable one was the UGV mounted with the mulcher, even in the longitudinal evaluation (56 degrees).
Due to the variability of the stability angles, it seems advisable to analyze the stability of the autonomous vehicles with and without connected implements. The theoretical model based on geometrical dimensions represents a useful tool for calculating the lateral and longitudinal limit angles in different configurations of the unmanned agricultural vehicles. The linkage of the implement allows its effect to be post-analyzed in terms of the stability of the UGV–implement complex. An added value of the theoretical model is the possibility of evaluating the effect on the stability of the center of mass of the implements, with respect to the precise location on the vehicle body.
The safety performance of UGVs is a very important issue when it comes to properly industrializing these vehicles on the market. With respect to this subject, stability must be considered to define the behaviors of autonomous vehicles in steep-slope areas. Indeed, UGVs are frequently recognized as being of interest in agricultural areas with hazardous operating conditions for traditional tractors, such as highly sloped vineyards. Consequently, the limit slopes need to be identified by studying the stability performance of unmanned vehicles to avoid a potential misuse.
In a future step, the dynamic effect in vehicle operations could be evaluated by means of the accelerometers and the inertial unit fitted on the UGV, implementing the model with the data collected in field. Considering the active sensors, stability control in real time will be permitted, allowing the best working parameters for the UGV to be foreseen so that the vehicle can be customized according to the equipment. This would allow for the optimization of the stability behavior of complex UGV equipment.
Author Contributions
Conceptualization, methodology, and investigation: V.R., B.F. and E.C.; software and data curation: B.F.; writing—original draft preparation: V.R., B.F. and E.C.; writing—review and editing: V.R., B.F. and E.C.; funding acquisition: V.R. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Italian MIUR within the project “New technical and operative solutions for the use of drones in Agriculture 4.0” (PRIN 2017, Prot. 2017S559BB).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors appreciate the support and help of Dario Mengoli and Roberto Tazzari in the experimental tipping tests.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Binswanger, H. Agricultural Mechanization: A Comparative Historical Perspective. World Bank Res. Obs. 1986, 1, 27–56. [Google Scholar] [CrossRef]
- OECD. OECD Standard Code for the Official Testing of Agricultural and Forestry Tractors; OECD Standard Codes; OECD: Paris, France, 2022. [Google Scholar]
- Rondelli, V.; Martelli, R.; Casazza, C. Tractor Rollover Fatalities, Analyzing Accident Scenario. J. Saf. Res. 2018, 67, 99–106. [Google Scholar] [CrossRef] [PubMed]
- Veronico, L.; Brusco, A.; Boscioni, R. Andamento Degli Infortuni Sul Lavoro e Delle Malattie Professionali. 2020. Available online: https://www.inail.it/cs/internet/docs/alg-dati-inail-2020-luglio-pdf.pdf (accessed on 1 September 2022).
- Myers, J.R.; Hendricks, K.J. Agricultural Tractor Overturn Deaths: Assessment of Trends and Risk Factors. Am. J. Ind. Med. 2010, 53, 662–672. [Google Scholar] [CrossRef] [PubMed]
- Facchinetti, D.; Santoro, S.; Galli, L.E.; Pessina, D. Agricultural Tractor Roll-over Related Fatalities in Italy: Results from a 12 Years Analysis. Sustainability 2021, 13, 4536. [Google Scholar] [CrossRef]
- OECD. OECD Standard Code for the Official Testing of Protective Structures on Agricultural and Forestry Tractors (Static Test); OECD Code 4; OECD: Paris, France, 2022. [Google Scholar]
- OECD. Standard Code for the Official Testing of Front Mounted Roll-Over Protective Structures on Narrow-Track Wheeled Agricultural and Forestry Tractors; OECD Code 6; OECD: Paris, France, 2022. [Google Scholar]
- Reynolds, S.J.; Groves, W. Effectiveness of Roll-over Protective Structures in Reducing Farm Tractor Fatalities. Am. J. Prev. Med. 2000, 18, 63–69. [Google Scholar] [CrossRef]
- Capacci, E.; Franceschetti, B.; Guzzomi, A.; Rondelli, V. Energy Absorption in Actual Tractor Rollovers with Different Tire Configurations. Int. J. Environ. Res. Public Health 2021, 18, 6517. [Google Scholar] [CrossRef] [PubMed]
- Jarén, C.; Alfaro, J.R.; Arazuri, S.; De León, J.L.P.; Arana, J.I. Assessing rollover safety provided by rops tests following sae standard J1194 versus OECD code 4. Trans. ASABE 2009, 52, 1453–1459. [Google Scholar] [CrossRef]
- Moberg, H.A. Tractor Safety Cabs: Test Methods and Experiences Gained during Ordinary Farm Work in Sweden; National Swedish Testing Institute for Agricultural Machinery: Uppsala, Sweden, 1964. [Google Scholar]
- Whelan, B.; Taylor, J. Precision Agriculture for Grain Production Systems; CSIRO Publishing: Clayton, Australia, 2013; ISBN 9780643107472. [Google Scholar]
- Ayoub Shaikh, T.; Rasool, T.; Rasheed Lone, F. Towards Leveraging the Role of Machine Learning and Artificial Intelligence in Precision Agriculture and Smart Farming. Comput. Electron. Agric. 2022, 198, 107119. [Google Scholar] [CrossRef]
- Recchia, L.; Boncinelli, P.; Cini, E.; Vieri, M.; Pegna, F.G.; Sarri, D. Multicriteria Analysis and LCA Techniques: With Applications to Agro-Engineering Problems. Green Energy Technol. 2011, 91. [Google Scholar] [CrossRef]
- Sarri, D.; Lombardo, S.; Pagliai, A.; Perna, C.; Lisci, R.; De Pascale, V.; Rimediotti, M.; Cencini, G.; Vieri, M. Smart Farming Introduction in Wine Farms: A Systematic Review and a New Proposal. Sustainability 2020, 12, 7191. [Google Scholar] [CrossRef]
- ISO Standards ISO 11783-3:2018; Tractors and Machinery for Agriculture and Forestry—Serial Control and Communications Data Network. ISO: Geneva, Switzerland, 2018.
- Marshall, J.A.; Sun, W.; L’Afflitto, A. A Survey of Guidance, Navigation, and Control Systems for Autonomous Multi-Rotor Small Unmanned Aerial Systems. Annu. Rev. Control. 2021, 52, 390–427. [Google Scholar] [CrossRef]
- 2013/167/UE. Mother Regulation. 2013. Available online: https://eur-lex.europa.eu/legal-content/IT/ALL/?uri=celex:32013R0167 (accessed on 1 September 2022).
- Rondelli, V.; Franceschetti, B.; Mengoli, D. A Review of Current and Historical Research Contributions to the Development of Ground Autonomous Vehicles for Agriculture. Sustainability 2022, 14, 9221. [Google Scholar] [CrossRef]
- Quaglia, G.; Visconte, C.; Scimmi, L.S.; Melchiorre, M.; Cavallone, P.; Pastorelli, S. Design of a UGV Powered by Solar Energy for Precision Agriculture. Robotics 2020, 9, 13. [Google Scholar] [CrossRef]
- ISO Standards ISO 18497; 2018 Agricultural Machinery and Tractors—Safety of Highly Automated Agricultural Machines—Principles for Design. ISO: Geneva, Switzerland, 2018.
- Tiusanen, R.; Malm, T.; Ronkainen, A. An Overview of Current Safety Requirements for Autonomous Machines-Review of Standards. Open Eng. 2020, 10, 665–673. [Google Scholar] [CrossRef]
- Capacci, E.; Franceschetti, B.; Ciuffoli, A.; Rondelli, V. The Stability of Self-Propelled Sprayers According to the ISO 16231 Standardized Procedure. Chem. Eng. Trans. 2017, 58, 61–66. [Google Scholar] [CrossRef]
- ISO 16231-2; Self-Propelled Agricultural Machinery—Assessment of Stability. ISO: Geneva, Switzerland, 2015.
- Pessina, D.; Facchinetti, D. A Survey on Fatal Accidents for Overturning of Agricultural Tractors in Italy. Chem. Eng. Trans. 2017, 58, 79–84. [Google Scholar] [CrossRef]
- Mengoli, D.; Tazzari, R.; Marconi, L. Autonomous Robotic Platform for Precision Orchard Management: Architecture and Software Perspective. In Proceedings of the 2020 IEEE International Workshop on Metrology for Agriculture and Forestry (MetroAgriFor), Trento, Italy, 4–6 November 2020; pp. 303–308. [Google Scholar] [CrossRef]
- Casini-Ropa, G. Equipment and Methods for the Measurement of the Height from the Ground of the Centre of Gravity on Agricultural Machinery [Attrezzatura e metodo per il rilievo da terra dell’altezza del baricentro delle machine agricole]. Riv. di Ing. Agrar. 1976, 2, 81–85. [Google Scholar]
- Franceschetti, B.; Rondelli, V.; Ciuffoli, A. Comparing the Influence of Roll-Over Protective Structure Type on Tractor Lateral Stability. Saf. Sci. 2019, 115, 42–50. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).