New Insights into the Impact of Local Corruption on China’s Regional Carbon Emissions Performance Based on the Spatial Spillover Effects
Abstract
:1. Introduction
2. Literature Review
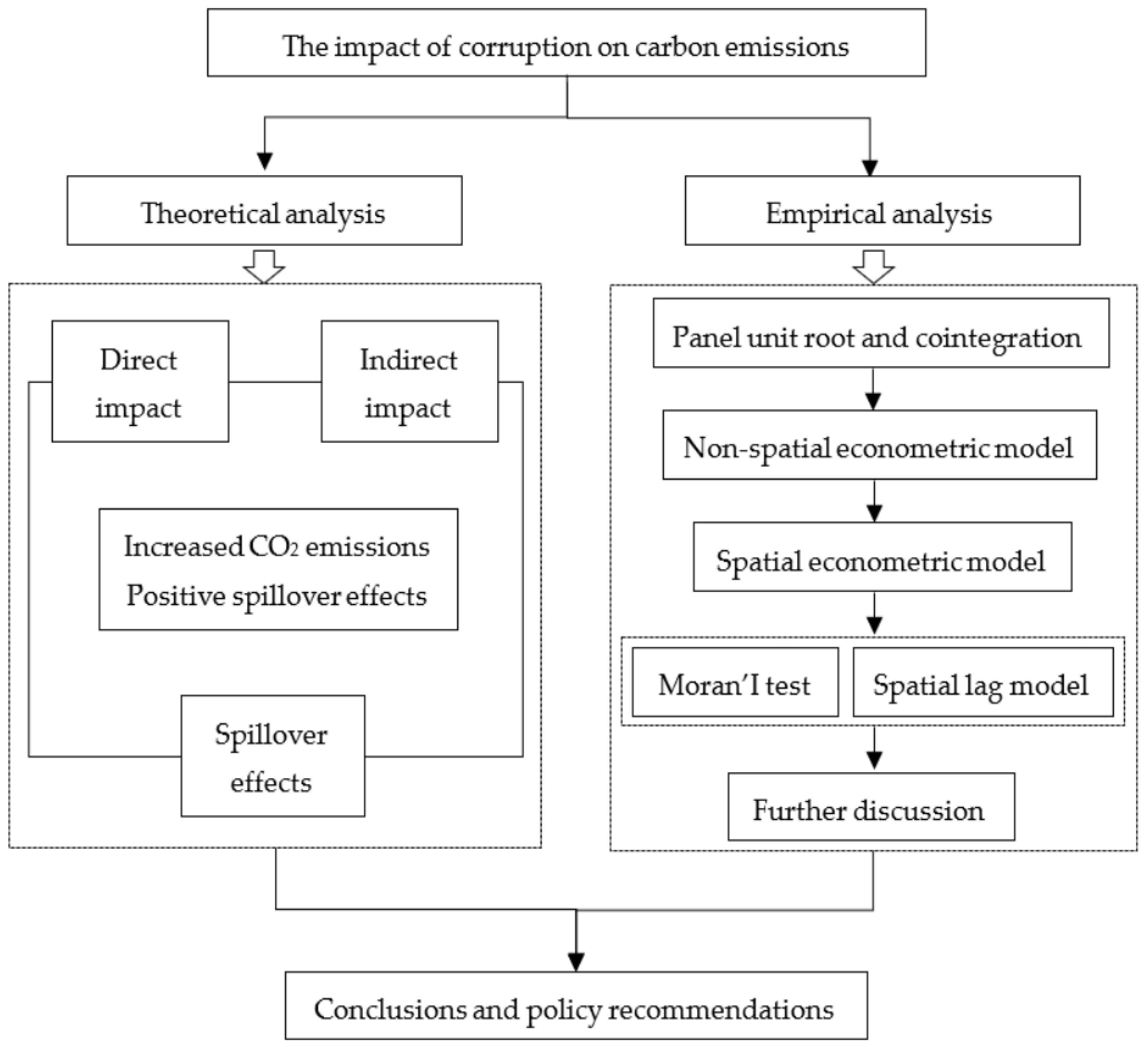
3. Theoretical Analysis and Research Hypotheses
3.1. The Direct Impact of Corruption on CO2 Emissions
3.2. The Spatial Spillover Effects of Corruption on CO2 Emissions
3.3. The Indirect Impact of Corruption on CO2 Emissions
4. Methods, Variables and Data Sources
4.1. Model Specification
4.1.1. Traditional Econometric Model
4.1.2. Spatial Econometric Model
4.1.3. Moderating Effect Model
4.2. Variables and Data Sources
4.2.1. Dependent Variable
4.2.2. Independent Variable
4.2.3. Moderating Variables
4.2.4. Control Variables
4.2.5. Data Sources
5. Results and Discussion
5.1. Panel Unit Root and Cointegration Test
5.2. Non-Spatial Econometric Analysis
5.3. Spatial Econometric Analysis
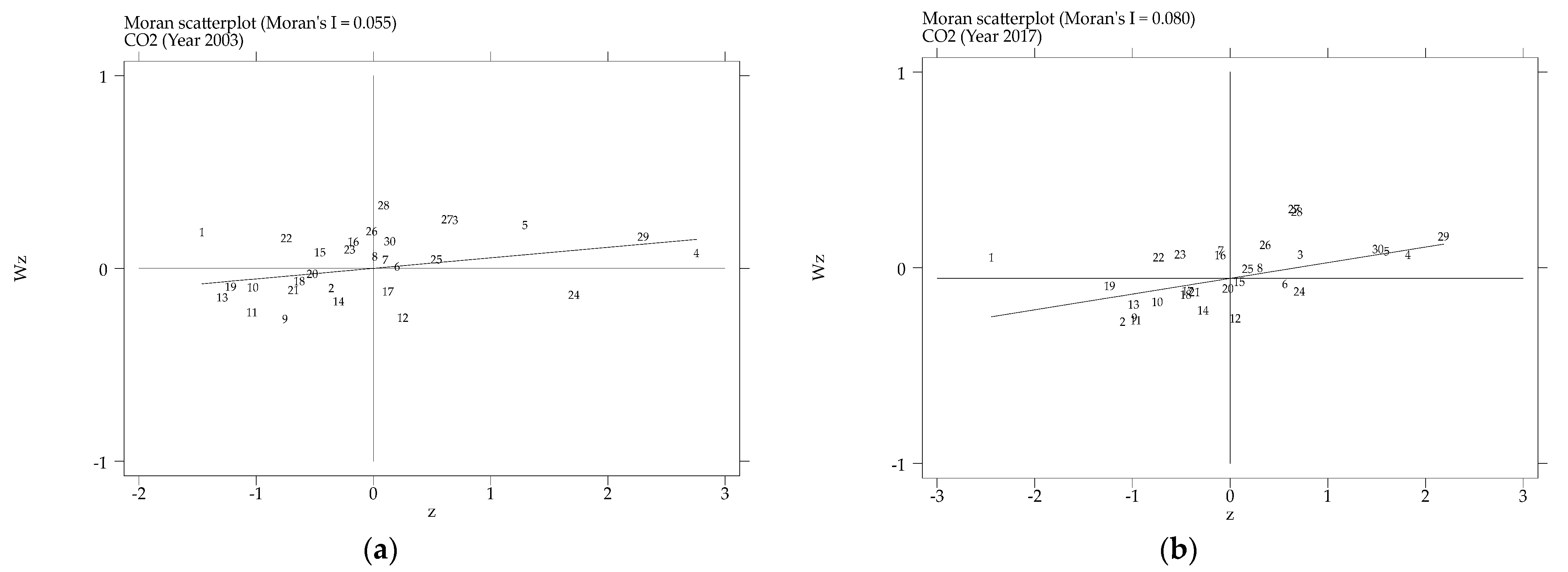
5.3.1. Spatial Autocorrelation Analysis
5.3.2. Results of Spatial Econometric Model
5.3.3. Regional Heterogeneity Analysis
5.3.4. Robustness Tests
5.4. Further Discussion
5.4.1. Moderating Effect Analysis
5.4.2. Anti-Corruption Campaign Policy Analysis
6. Conclusions and Policy Implications
7. Limitations and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Weitzel, M.; Ma, T. Emissions embodied in Chinese exports taking into account the special export structure of China. Energy Econ. 2014, 45, 45–52. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Deng, X.; Wang, J.; Zhang, F.; Liang, S. Carbon emission efficiency in China: A spatial panel data analysis. China Econ. Rev. 2019, 56, 101313. [Google Scholar] [CrossRef]
- Barrows, G.; Ollivier, H. Foreign demand, developing country exports, and CO2 emissions: Firm-level evidence from India. J. Dev. Econ. 2021, 149, 102587. [Google Scholar] [CrossRef]
- Xu, B.; Lin, B. How industrialization and urbanization process impacts on CO2 emissions in China: Evidence from nonparametric additive regression models. Energy Econ. 2015, 48, 188–202. [Google Scholar] [CrossRef]
- Xu, X.; Li, S. Neighbor-Companion or Neighbor-Beggar? Estimating the Spatial Spillover Effects of Fiscal Decentralization on China’s Carbon Emissions Based on Spatial Econometric Analysis. Sustainability 2022, 14, 9884. [Google Scholar] [CrossRef]
- Cui, L.; Li, R.; Song, M.; Zhu, L. Can China achieve its 2030 energy development targets by fulfilling carbon intensity reduction commitments? Energy Econ. 2019, 83, 61–73. [Google Scholar] [CrossRef]
- Dong, F.; Hua, Y.; Yu, B. Peak Carbon Emissions in China: Status, Key Factors and Countermeasures—A Literature Review. Sustainability 2018, 10, 2895. [Google Scholar] [CrossRef] [Green Version]
- Gong, W.; Wang, C.; Fan, Z.; Xu, Y. Drivers of the peaking and decoupling between CO2 emissions and economic growth around 2030 in China. Environ. Sci. Pollut. Res. 2022, 29, 3864–3878. [Google Scholar] [CrossRef]
- Esfahani, H.S.; Ramırez, M.T. Institutions, infrastructure, and economic growth. J. Dev. Econ. 2003, 70, 443–477. [Google Scholar] [CrossRef]
- Lee, C.C.; Chang, C.H.; Arouri, M.; Lee, C.C. Economic growth and insurance development: The role of institutional environments. Econ. Model. 2016, 59, 361–369. [Google Scholar] [CrossRef]
- Qiang, Q.; Jian, C. Natural resource endowment, institutional quality and China’s regional economic growth. Resour. Policy 2020, 66, 101644. [Google Scholar] [CrossRef]
- Seldadyo, H.; De Haan, J. Is corruption really persistent? Pac. Econ. Rev. 2011, 16, 192–206. [Google Scholar] [CrossRef]
- Deng, J. The National Supervision Commission: A new anti-corruption model in China. Int. J. Law Crime Justice 2018, 52, 58–73. [Google Scholar] [CrossRef]
- Lin, S.; Zhao, D.; Marinova, D. Analysis of the environmental impact of China based on STIRPAT model. Environ. Impact Assess. Rev. 2009, 29, 341–347. [Google Scholar] [CrossRef]
- Wang, Y.; Kang, Y.; Wang, J.; Xu, L. Panel estimation for the impacts of population-related factors on CO2 emissions: A regional analysis in China. Ecol. Indic. 2017, 78, 322–330. [Google Scholar] [CrossRef]
- Halicioglu, F. An econometric study of CO2 emissions, energy consumption, income and foreign trade in Turkey. Energy Policy 2009, 37, 1156–1164. [Google Scholar] [CrossRef] [Green Version]
- Alam, M.M.; Murad, M.W.; Noman, A.H.M.; Ozturk, I. Relationships among carbon emissions, economic growth, energy consumption and population growth: Testing Environmental Kuznets Curve hypothesis for Brazil, China, India and Indonesia. Ecol. Indic. 2016, 70, 466–479. [Google Scholar] [CrossRef]
- Shahbaz, M.; Haouas, I.; Van Hoang, T.H. Economic growth and environmental degradation in Vietnam: Is the environmental Kuznets curve a complete picture? Emerg. Mark. Rev. 2019, 38, 197–218. [Google Scholar] [CrossRef]
- Wang, G.; Chen, X.; Zhang, Z.; Niu, C. Influencing Factors of Energy-Related CO2 Emissions in China: A Decomposition Analysis. Sustainability 2015, 7, 14408–14426. [Google Scholar] [CrossRef] [Green Version]
- Wu, L.; Sun, L.; Qi, P.; Ren, X.; Sun, X. Energy endowment, industrial structure upgrading, and CO2 emissions in China: Revisiting resource curse in the context of carbon emissions. Resour. Policy 2021, 74, 102329. [Google Scholar] [CrossRef]
- Wang, Z.; Yin, F.; Zhang, Y.; Zhang, X. An empirical research on the influencing factors of regional CO2 emissions: Evidence from Beijing city, China. Appl. Energy 2012, 100, 277–284. [Google Scholar] [CrossRef]
- Chen, J.; Gao, M.; Ma, K.; Song, M. Different effects of technological progress on China’s carbon emissions based on sustainable development. Bus. Strateg. Environ. 2020, 29, 481–492. [Google Scholar] [CrossRef]
- Amri, F.; Zaied, Y.B.; Lahouel, B.B. ICT, total factor productivity, and carbon dioxide emissions in Tunisia. Technol. Forecast. Soc. Chang. 2019, 146, 212–217. [Google Scholar] [CrossRef]
- Liang, Q.M.; Fan, Y.; Wei, Y.M. Carbon taxation policy in China: How to protect energy- and trade-intensive sectors? J. Policy Model. 2007, 29, 311–333. [Google Scholar] [CrossRef]
- Mardones, C.; Baeza, N. Economic and environmental effects of a CO2 tax in Latin American countries. Energy Policy 2018, 114, 262–273. [Google Scholar] [CrossRef]
- Oates, W.E. On the evolution of fiscal federalism: Theory and institutions. Natl. Tax J. 2008, 61, 313–334. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Hao, Y.; Weng, J.H. How does energy consumption affect China’s urbanization? New evidence from dynamic threshold panel models. Energy Policy 2019, 127, 24–38. [Google Scholar] [CrossRef]
- Gray, W.B.; Shadbegian, R.J. ‘Optimal’ pollution abatement—whose benefits matter, and how much? J. Environ. Econ. Manag. 2004, 47, 510–534. [Google Scholar] [CrossRef]
- Song, M.; Zhu, S.; Wang, J.; Zhao, J. Share green growth: Regional evaluation of green output performance in China. Int. J. Prod. Econ. 2020, 219, 152–163. [Google Scholar] [CrossRef]
- Porter, M.E.; Van der Linde, C. Toward a new conception of the environment-competitiveness relationship. J. Econ. Perspect. 1995, 9, 97–118. [Google Scholar] [CrossRef]
- Sinn, H.W. Public policies against global warming: A supply side approach. Int. Tax Public Financ. 2008, 15, 360–394. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, X.; Guo, X. Environmental regulation and green productivity growth: Empirical evidence on the Porter Hypothesis from OECD industrial sectors. Energy Policy 2019, 132, 611–619. [Google Scholar] [CrossRef]
- Xu, X.; Li, X.; Zheng, L. A Blessing or a Curse? Exploring the Impact of Environmental Regulation on China’s Regional Green Development from the Perspective of Governance Transformation. Res. Public Health 2022, 19, 1312. [Google Scholar] [CrossRef]
- Krishnan, S.; Teo, T.S.; Lim, V.K. Examining the relationships among e-government maturity, corruption, economic prosperity and environmental degradation: A cross-country analysis. Inf. Manag. 2013, 50, 638–649. [Google Scholar] [CrossRef]
- Lisciandra, M.; Migliardo, C. An empirical study of the impact of corruption on environmental performance: Evidence from panel data. Environ. Resour. Econ. 2017, 68, 297–318. [Google Scholar] [CrossRef]
- Dincer, O.C.; Fredriksson, P.G. Corruption and environmental regulatory policy in the United States: Does trust matter? Resour. Energy Econ. 2018, 54, 212–225. [Google Scholar] [CrossRef]
- Ren, Y.S.; Ma, C.Q.; Apergis, N.; Sharp, B. Responses of carbon emissions to corruption across Chinese provinces. Energy Econ. 2021, 98, 105241. [Google Scholar] [CrossRef]
- Welsch, H. Corruption, growth, and the environment: A cross-country analysis. Environ. Dev. Econ. 2004, 9, 663–693. [Google Scholar] [CrossRef] [Green Version]
- Cole, M.A. Corruption, income and the environment: An empirical analysis. Ecol. Econ. 2007, 62, 637–647. [Google Scholar] [CrossRef]
- Akhbari, R.; Nejati, M. The effect of corruption on carbon emissions in developed and developing countries: Empirical investigation of a claim. Heliyon 2019, 5, e02516. [Google Scholar] [CrossRef]
- Leal, P.H.; Marques, A.C. The environmental impacts of globalisation and corruption: Evidence from a set of African countries. Environ. Sci. Policy 2021, 115, 116–124. [Google Scholar] [CrossRef]
- Maddison, D. Environmental Kuznets curves: A spatial econometric approach. J. Environ. Econ. Manag. 2006, 51, 218–230. [Google Scholar] [CrossRef]
- Burnett, J.W.; Bergstrom, J.C.; Dorfman, J.H. A spatial panel data approach to estimating U.S. state-level energy emissions. Energy Econ. 2013, 40, 396–404. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, T.; Wang, J.; Guo, F.; Kan, X.; Yuan, R. Spatial analysis on carbon emission abatement capacity at provincial level in China from 1997 to 2014: An empirical study based on SDM model. Atmos. Pollut. Res. 2019, 10, 97–104. [Google Scholar] [CrossRef]
- Rios, V.; Gianmoena, L. Convergence in CO2 emissions: A spatial economic analysis with cross-country interactions. Energy Econ. 2018, 75, 222–238. [Google Scholar] [CrossRef]
- Xu, L.; Fan, M.; Yang, L.; Shao, S. Heterogeneous green innovations and carbon emission performance: Evidence at China’s city level. Energy Econ. 2021, 99, 105269. [Google Scholar] [CrossRef]
- Li, W.; Xu, J.; Ostic, D.; Yang, J.; Guan, R.; Zhu, L. Why low-carbon technological innovation hardly promote energy efficiency of China?–Based on spatial econometric method and machine learning. Comput. Ind. Eng. 2021, 160, 107566. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, B.; Chen, Z. Has the anti-corruption campaign decreased air pollution in China? Energy Econ. 2020, 91, 104878. [Google Scholar] [CrossRef]
- Muslihudin, M.; Hendarto, E.; Rostikawati, R.; Windiasih, R.; Wulan, T.R. Relationship between environmental damage and corruption cases in Indonesia. E3S Web Conf. 2018, 73, 02011. [Google Scholar] [CrossRef] [Green Version]
- Zhou, A.; Li, J. Impact of anti-corruption and environmental regulation on the green development of China’s manufacturing industry. Sustain. Prod. Consump. 2021, 27, 1944–1960. [Google Scholar] [CrossRef]
- Hao, Y.; Gai, Z.; Yan, G.; Wu, H.; Irfan, M. The spatial spillover effect and nonlinear relationship analysis between environmental decentralization, government corruption and air pollution: Evidence from China. Sci. Total Environ. 2021, 763, 144183. [Google Scholar] [CrossRef] [PubMed]
- Yin, Z.; Li, L.; Hueng, C.J.; Yu, Y. The effects of corruption on China’s provincial eco-efficiency. J. Asia. Pac. Econ. 2022, 1–20. [Google Scholar] [CrossRef]
- Biswas, A.K.; Farzanegan, M.R.; Thum, M. Pollution, shadow economy and corruption: Theory and evidence. Ecol. Econ. 2012, 75, 114–125. [Google Scholar] [CrossRef] [Green Version]
- Cao, X.; Kostka, G.; Xu, X. Environmental political business cycles: The case of PM2.5 air pollution in Chinese prefectures. Environ. Sci. Policy 2019, 93, 92–100. [Google Scholar] [CrossRef]
- Burgess, R.; Hansen, M.; Olken, B.A.; Potapov, P.; Sieber, S. The political economy of deforestation in the tropics. Q. J. Econ. 2012, 127, 1707–1754. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Hao, X.; Zhou, M. Does institutional quality affect air pollution? Environ. Sci. Pollut. Res. 2022, 29, 28317–28338. [Google Scholar] [CrossRef]
- Esquivias, M.A.; Sugiharti, L.; Rohmawati, H.; Rojas, O.; Sethi, N. Nexus between Technological Innovation, Renewable Energy, and Human Capital on the Environmental Sustainability in Emerging Asian Economies: A Panel Quantile Regression Approach. Energies 2022, 15, 2451. [Google Scholar] [CrossRef]
- Sarkar, B.; Ganguly, B.; Sarkar, M.; Pareek, S. Effect of variable transportation and carbon emission in a three-echelon supply chain model. Transp. Res. Pt. e-Logist. Transp. Rev. 2016, 91, 112–128. [Google Scholar] [CrossRef]
- Getis, A. Reflections on spatial autocorrelation. Reg. Sci. Urban Econ. 2007, 37, 491–496. [Google Scholar] [CrossRef]
- Wu, H.; Xu, L.; Ren, S.; Hao, Y.; Yan, G. How do energy consumption and environmental regulation affect carbon emissions in China? New evidence from a dynamic threshold panel model. Resour. Policy 2020, 67, 101678. [Google Scholar] [CrossRef]
- LeSage, J.P.; Pace, R.K. The biggest myth in spatial econometrics. Econometrics 2014, 2, 217–249. [Google Scholar] [CrossRef] [Green Version]
- Du, L.; Wei, C.; Cai, S. Economic development and carbon dioxide emissions in China: Provincial panel data analysis. China Econ. Rev. 2012, 23, 371–384. [Google Scholar] [CrossRef]
- Sovacool, B.K.; Walter, G.; Van de Graaf, T.; Andrews, N. Energy governance, transnational rules, and the resource curse: Exploring the effectiveness of the Extractive Industries Transparency Initiative (EITI). World Dev. 2016, 83, 179–192. [Google Scholar] [CrossRef] [Green Version]
- López-Cazar, I.; Papyrakis, E.; Pellegrini, L. The extractive industries transparency initiative (EITI) and corruption in Latin America: Evidence from Colombia, Guatemala, Honduras, Peru, and Trinidad and Tobago. Resour. Policy 2021, 70, 101907. [Google Scholar] [CrossRef]
- Goel, R.K.; Rich, D.P. On the economic incentives for taking bribes. Public Choice 1989, 61, 269–275. [Google Scholar] [CrossRef]
- Fisman, R.; Gatti, R. Decentralization and corruption: Evidence across countries. J. Public Econ. 2002, 83, 325–345. [Google Scholar] [CrossRef] [Green Version]
- Bakhsh, S.; Yin, H.; Shabir, M. Foreign investment and CO2 emissions: Do technological innovation and institutional quality matter? Evidence from system GMM approach. Environ. Sci. Pollut. Res. 2021, 28, 19424–19438. [Google Scholar] [CrossRef]
- Zheng, H.; Gao, X.; Sun, Q.; Han, X.; Wang, Z. The impact of regional industrial structure differences on carbon emission differences in China: An evolutionary perspective. J. Clean Prod. 2020, 257, 120506. [Google Scholar] [CrossRef]
- Lee, L.F.; Yu, J. Identification of spatial Durbin panel models. J. Appl. Econom. 2016, 31, 133–162. [Google Scholar] [CrossRef]
- Geniaux, G.; Martinetti, D. A new method for dealing simultaneously with spatial autocorrelation and spatial heterogeneity in regression models. Reg. Sci. Urban Econ. 2018, 72, 74–85. [Google Scholar] [CrossRef]
- Elhorst, J.P. Matlab software for spatial panels. Int. Reg. Sci. Rev. 2014, 37, 389–405. [Google Scholar] [CrossRef] [Green Version]
- Sjöberg, E. An empirical study of federal law versus local environmental enforcement. J. Environ. Econ. Manag. 2016, 76, 14–31. [Google Scholar] [CrossRef]

| Themes | Conclusions | References | |
|---|---|---|---|
| The influencing factors of carbon emissions | Non-institutional factors | Population (+) Economic growth (Inverted U) Energy consumption structure (−) Technological progress (+/−) | Lin et al. [14]; Wang et al. [15]. Halicioglu, [16]; Alam et al. [17]; Shahbaz et al. [18]. Wang et al. [19]; Wu et al. [20]. Wang et al. [21]; Chen et al. [22]; Amri et al. [23]. |
| Institutional factors | Carbon taxation (−) Environmental decentralization (+/−) Environmental regulation (Uncertain) | Liang et al. [24]; Mardones and Baeza, [25]. Oates, [26]; Wu et al. [27]; Gray and Shadbegian, [28]; Song et al. [29]. Porter and Van der Linde, [30]; Sinn, [31]; Wang et al. [32]; Xu et al. [33]. | |
| The nexus between corruption and environmental pollution | Positive impact Non-linear relationship No significant effect | Krishnan et al. [34]; Lisciandra and Migliardo, [35]; Dincer and Fredriksson, [36]. Ren et al. [37]; Welsch, [38]; Cole, [39]. Akhbari and Nejati, [40]; Leal and Marques, [41]. | |
| The application of spatial econometrics in carbon emissions | Static spatial econometric models (Uncertain) | Maddison, [42]; Burnett et al. [43]; Wang et al. [44]. | |
| Dynamic spatial econometric models (Uncertain) | Rios and Gianmoena, [45]; Xu et al. [46]; Li et al. [47]. | ||
| Variables | Definition | Unit | Mean | S.D. | Min | Max | VIF |
|---|---|---|---|---|---|---|---|
| lnCI | Carbon emission intensity | tons/10,000 Yuan | 0.829 | 0.573 | −1.123 | 2.493 | − |
| Corr | Local corruption | pieces/10,000 persons | 3.485 | 1.322 | 0.517 | 8.121 | 2.03 |
| lnGDP | Real GDP per capita | Yuan/person | 10.024 | 0.643 | 8.216 | 11.467 | 7.92 |
| IS | Industrial structure | % | 0.999 | 0.523 | 0.497 | 4.237 | 1.26 |
| lnFDI | Foreign direct investment | Yuan/person | 5.919 | 1.385 | 1.825 | 8.737 | 2.19 |
| lnRD | R&D investment | Yuan/person | 5.715 | 1.245 | 2.705 | 8.892 | 7.59 |
| Level | First Difference | |||||||
|---|---|---|---|---|---|---|---|---|
| LLC | IPS | PP-Fisher | ADF-Fisher | LLC | IPS | PP-Fisher | ADF-Fisher | |
| lnCI | −7.0211 *** | −3.9036 *** | 170.3890 *** | 122.9100 *** | −6.4140 *** | −4.3226 *** | 188.9270 *** | 119.8340 *** |
| Corr | −3.0900 *** | −0.9918 | 93.9209 *** | 75.9034 * | −6.7158 *** | −3.8847 *** | 293.5760 *** | 111.0480 *** |
| lnGDP | −9.7458 *** | −2.7978 *** | 264.8100 *** | 87.0992 ** | −7.1940 *** | −1.5294 * | 145.2690 *** | 105.7880 *** |
| IS | 2.8913 | 8.2056 | 32.6066 | 12.4135 | −4.6349 *** | −0.7670 | 173.9180 *** | 88.2529 ** |
| lnFDI | −2.5876 *** | −0.5206 | 121.4500 *** | 82.0770 ** | −5.1103 *** | −5.0067 *** | 271.1220 *** | 129.1840 *** |
| lnRD | −11.6738 *** | −3.3505 *** | 208.1430 *** | 102.3260 *** | −3.1456 *** | −3.0231 *** | 258.5250 *** | 96.8835 *** |
| Pedroni Test | Statistic | Prob. | Weighted Statistic | Prob. |
|---|---|---|---|---|
| Alternative hypothesis: common AR coefficients (within-dimension) | ||||
| Panel v-statistic | −3.2494 | 0.9994 | −4.3982 | 1.0000 |
| Panel rho-statistic | 2.9563 | 0.9984 | 2.9695 | 0.9985 |
| Panel PP-statistic | −3.5753 | 0.0002 | −3.6254 | 0.0001 |
| Panel ADF-statistic | −3.2915 | 0.0005 | −3.5917 | 0.0002 |
| Alternative hypothesis: individual AR coefficients (between-dimension) | ||||
| Group rho-statistic | 5.5566 | 1.0000 | ||
| Group PP-statistic | −5.9392 | 0.0000 | ||
| Group ADF-statistic | −3.5332 | 0.0002 | ||
| Kao test | T-statistic | Prob. | ||
| ADF | −1.5569 | 0.0597 | ||
| Variables | Dependent Variables: lnCI | |||||
|---|---|---|---|---|---|---|
| Pooled-OLS | FE | RE | FGLS | DIF-GMM | SYS-GMM | |
| lnCIit-1 | 0.7977 *** | 0.7501 *** | ||||
| (12.5648) | (23.5345) | |||||
| Corr | 0.1241 *** | 0.0294 *** | 0.0244 *** | 0.0213 ** | 0.0295 *** | 0.0251 *** |
| (6.7129) | (3.0889) | (2.5916) | (2.2864) | (3.0297) | (3.0020) | |
| lnGDP | 0.2170 *** | −0.3461 *** | −0.4178 *** | −0.4634 *** | −0.5678 *** | −0.2753 *** |
| (2.8861) | (−4.1909) | (−6.8791) | (−7.5654) | (−5.6944) | (−4.3408) | |
| IS | −0.2309 *** | −0.2224 *** | −0.3373 *** | −0.3393 *** | −0.1044 ** | −0.1642 *** |
| (−6.2756) | (−4.8939) | (−12.0366) | (−12.0838) | (−2.3583) | (−7.2698) | |
| lnFDI | −0.1317 *** | −0.0582 *** | −0.0551 *** | −0.0491 *** | −0.0223 * | −0.0631 *** |
| (−7.1722) | (−4.4806) | (−4.2821) | (−3.8086) | (−1.8898) | (−6.1195) | |
| lnRD | −0.1807 *** | 0.1497 *** | 0.0689 ** | 0.0927 *** | 0.2787 *** | 0.0418 |
| (−4.7541) | (3.6844) | (1.9816) | (2.6389) | (3.7114) | (1.4349) | |
| _cons | 0.2645 | 4.0287 *** | 5.2016 *** | 5.4298 *** | ||
| (0.4545) | (5.3479) | (12.2005) | (13.5440) | |||
| R2 | 0.6015 | 0.4224 | 0.4956 | 0.4790 | ||
| AR (1)/p-value | −4.73 [0.000] | −5.63 [0.000] | ||||
| AR (2)/p-value | −0.75 [0.451] | −0.41 [0.683] | ||||
| Hansen | 0.3632 | 0.4140 | ||||
| Obs | 450 | 450 | 450 | 450 | 420 | 420 |
| Year | W1 | W2 | W3 | |||
|---|---|---|---|---|---|---|
| Moran’s I | Z-Value | Moran’s I | Z-Value | Moran’s I | Z-Value | |
| 2003 | 0.055 *** | 2.579 | 0.078 | 1.042 | 0.182 ** | 1.918 |
| 2004 | 0.059 *** | 2.688 | 0.096 | 1.198 | 0.210 *** | 2.141 |
| 2005 | 0.054 ** | 2.524 | 0.102 | 1.244 | 0.227 *** | 2.281 |
| 2006 | 0.058 *** | 2.634 | 0.118 | 1.386 | 0.244 *** | 2.423 |
| 2007 | 0.061 *** | 2.722 | 0.155 * | 1.718 | 0.278 *** | 2.719 |
| 2008 | 0.076 *** | 3.137 | 0.170 * | 1.853 | 0.305 *** | 2.950 |
| 2009 | 0.079 *** | 3.220 | 0.202 ** | 2.136 | 0.330 *** | 3.159 |
| 2010 | 0.082 *** | 3.317 | 0.213 ** | 2.242 | 0.347 *** | 3.309 |
| 2011 | 0.080 *** | 3.283 | 0.208 ** | 2.208 | 0.340 *** | 3.273 |
| 2012 | 0.086 *** | 3.424 | 0.204 ** | 2.165 | 0.336 *** | 3.224 |
| 2013 | 0.087 *** | 3.456 | 0.204 ** | 2.166 | 0.335 *** | 3.211 |
| 2014 | 0.088 *** | 3.498 | 0.207 ** | 2.195 | 0.339 *** | 3.249 |
| 2015 | 0.083 *** | 3.365 | 0.208 ** | 2.209 | 0.338 *** | 3.249 |
| 2016 | 0.083 *** | 3.344 | 0.191 ** | 2.049 | 0.327 *** | 3.145 |
| 2017 | 0.080 *** | 3.272 | 0.176 * | 1.915 | 0.309 *** | 2.999 |
| Pooled OLS | Spatial Fixed Effect | Time Fixed Effect | Double Fixed Effect | |
|---|---|---|---|---|
| LM-lag | 51.5270 *** | 20.5718 *** | 8.1407 *** | 2.7529 * |
| Robust LM-lag | 7.7057 *** | 16.5113 *** | 2.8036 * | 42.5913 *** |
| LM-error | 47.1213 ** | 6.3835 ** | 5.4666 ** | 0.3186 |
| Robust LM-error | 3.3001 * | 2.3230 | 0.1294 | 40.1570 *** |
| Variables | W1 | W2 | ||||
|---|---|---|---|---|---|---|
| SLM | SEM | SDM | SLM | SEM | SDM | |
| Corr | 0.0272 *** | 0.0275 *** | 0.0129 | 0.0297 *** | 0.0297 *** | 0.0210 ** |
| (2.9048) | (2.9163) | (1.4937) | (3.1490) | (3.1553) | (2.5048) | |
| lnGDP | −0.3546 *** | −0.3483 *** | −0.4762 *** | −0.3582 *** | −0.3485 *** | −0.4026 *** |
| (−4.3773) | (−4.2545) | (−6.4385) | (−4.3814) | (−4.2823) | (−5.4269) | |
| IS | −0.2187 *** | −0.2134 *** | −0.2969 *** | −0.2142 *** | −0.2118 *** | −0.0783 * |
| (−4.9066) | (−4.7882) | (−6.6012) | (−4.7650) | (−4.6862) | (−1.7883) | |
| lnFDI | −0.0566 *** | −0.0569 *** | −0.0501 *** | −0.0585 *** | −0.0591 *** | −0.0535 *** |
| (−4.4419) | (−4.4364) | (−4.4493) | (−4.5499) | (−4.5766) | (−4.6513) | |
| lnRD | 0.1546 *** | 0.1542 *** | 0.2138 *** | 0.1474 *** | 0.1477 *** | 0.1440 * |
| (3.8797) | (3.8228) | (5.9585) | (3.6670) | (3.6677) | (4.0752) | |
| W × Corr | 0.3705 *** | −0.0438 * | ||||
| (5.7684) | (−1.7540) | |||||
| W × Xcontrol | YES | YES | ||||
| ρ | 0.5656 *** | 0.0024 | 0.1622 ** | −0.0481 | ||
| (7.6390) | (0.0175) | (2.4806) | (−0.6964) | |||
| λ | 0.4210 *** | 0.1330 *** | ||||
| (4.4126) | (1.9446) | |||||
| R2 | 0.9599 | 0.9590 | 0.9675 | 0.9593 | 0.9590 | 0.9655 |
| Log-Lik | 332.8261 | 331.4109 | 383.2699 | 331.9051 | 331.3931 | 369.8930 |
| Variables | W1 | W2 | ||||
|---|---|---|---|---|---|---|
| Direct Effect | Indirect Effect | Total Effect | Direct Effect | Indirect Effect | Total Effect | |
| Corr | 0.0281 *** | 0.0363 ** | 0.0644 ** | 0.0298 *** | 0.0058 * | 0.0356 *** |
| (2.9682) | (2.0827) | (2.5650) | (3.3444) | (1.7263) | (3.2156) | |
| lnGDP | −0.3619 *** | −0.4682 ** | −0.8300 *** | −0.3588 *** | −0.0698 * | −0.4286 *** |
| (−4.2845) | (−2.4547) | (−3.2737) | (−4.3372) | (−1.8354) | (−4.0421) | |
| IS | −0.2253 *** | −0.2909 *** | −0.5163 *** | −0.2174 *** | −0.0421 * | −0.2595 *** |
| (−4.9487) | (−2.6124) | (−3.6119) | (−4.9261) | (−1.9213) | (−4.5850) | |
| lnFDI | −0.0585 *** | −0.0753 *** | −0.1338 *** | −0.0586 *** | −0.0114 * | −0.0699 *** |
| (−4.4713) | (−2.5825) | (−3.4878) | (−4.6800) | (−1.8963) | (−4.3539) | |
| lnRD | 0.1587 *** | 0.2047 ** | 0.3634 *** | 0.1469 *** | 0.0285 * | 0.1754 *** |
| (3.8159) | (2.3768) | (3.0863) | (3.5996) | (1.7853) | (3.4494) | |
| Variables | Eastern | Central | Western | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Coefficient | Direct | Indirect | Coefficient | Direct | Indirect | Coefficient | Direct | Indirect | |
| Corr | 0.0392 ** | 0.0395 ** | −0.0105 | −0.0161 | −0.0192 * | 0.0106 * | −0.0116 | −0.0130 | −0.0149 |
| (2.0275) | (2.0292) | (−1.5292) | (−1.6274) | (−1.6953) | (1.6636) | (−0.9015) | (−0.9560) | (−0.8645) | |
| lnGDP | −0.2114 * | −0.2147 * | 0.0562 | −0.2427 | −0.2813 | 0.1568 | −1.0078 *** | −1.0886 *** | −1.2406 *** |
| (−1.7467) | (−1.6980) | (1.3989) | (−1.6201) | (−1.5129) | (1.4594) | (−8.8003) | (−8.5059) | (−2.8333) | |
| IS | −0.1464 *** | −0.1502 *** | 0.0385 ** | 0.0332 | 0.0396 | −0.0214 | −0.2925 *** | −0.3165 *** | −0.3627 * |
| (−3.2001) | (−3.3197) | (2.2366) | (0.5270) | (0.5202) | (−0.5028) | (−3.0607) | (−2.9875) | (−2.0061) | |
| lnFDI | −0.1544 *** | −0.1557 *** | 0.0408 ** | 0.0371 * | 0.0450 * | −0.0250 * | −0.0321 ** | −0.0348 ** | −0.0391 * |
| (−5.8033) | (−5.8598) | (2.4955) | (1.7887) | (1.8264) | (−1.7646) | (−2.0218) | (−2.0448) | (−1.6895) | |
| lnRD | 0.4366 *** | 0.4453 *** | −0.1168 *** | −0.1105 ** | −0.1355 ** | 0.0755 ** | 0.0142 | 0.0138 | 0.0168 |
| (7.8986) | (7.5827) | (−2.5687) | (−2.1543) | (−2.2566) | (2.1211) | (0.2394) | (0.2128) | (0.2137) | |
| ρ | −0.3443 ** | −0.9090 *** | 0.5535 *** | ||||||
| (−2.4396) | (−7.0481) | (7.1945) | |||||||
| R2 | 0.9738 | 0.9877 | 0.9491 | ||||||
| Log-Lik | 179.5103 | 173.6148 | 135.1368 | ||||||
| Variables | Adjusting the Explanatory Variables | Adjusting the Sample Interval | Adjusting the Spatial Weight Matrix | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Coefficient | Direct | Indirect | Coefficient | Direct | Indirect | Coefficient | Direct | Indirect | |
| Corr | 0.0816 ** | 0.0849 ** | 0.1083 * | 0.0372 *** | 0.0389 *** | 0.0666 ** | 0.0265 *** | 0.0273 *** | 0.0152 ** |
| (2.0360) | (2.0822) | (1.6716) | (3.3281) | (3.3543) | (2.1975) | (2.9088) | (2.8735) | (2.3817) | |
| lnGDP | −0.3705 *** | −0.3809 *** | −0.4867 ** | −0.3663 *** | −0.3769 *** | −0.6442 ** | −0.3658 *** | −0.3811 *** | −0.2123 *** |
| (−4.5598) | (−4.6526) | (−2.5513) | (−3.7497) | (−3.6313) | (−2.2540) | (−4.6262) | (−4.6075) | (−3.0535) | |
| IS | −0.2156 *** | −0.2213 *** | −0.2822 *** | −0.0678 | −0.0697 | −0.1183 | −0.1865 *** | −0.1946 *** | −0.1084 *** |
| (−4.7768) | (−4.6957) | (−2.5986) | (−1.2870) | (−1.2407) | (−1.0843) | (−4.2881) | (−4.2365) | (−2.9552) | |
| lnFDI | −0.0568 *** | −0.0594 *** | −0.0758 ** | −0.0533 *** | −0.0564 *** | −0.0967 ** | −0.0563 *** | −0.0595 *** | −0.0331 *** |
| (−4.4340) | (−4.3886) | (−2.5127) | (−3.6209) | (−3.4942) | (−2.1942) | (−4.5222) | (−4.5412) | (−3.0708) | |
| lnRD | 0.1424 *** | 0.1486 *** | 0.1891 ** | 0.1847 *** | 0.1909 *** | 0.3274 ** | 0.1434 *** | 0.1498 *** | 0.0834 *** |
| (3.5817) | (3.5917) | (2.4394) | (3.6481) | (3.7736) | (2.2621) | (3.6850) | (3.7680) | (2.8010) | |
| ρ | 0.5577 *** | 0.6322 *** | 0.3738 *** | ||||||
| (7.4110) | (8.8634) | (6.7125) | |||||||
| R2 | 0.9595 | 0.9689 | 0.9619 | ||||||
| Log-Lik | 330.5606 | 308.3479 | 340.3653 | ||||||
| Variables | Local Competition Effect (FDI) | Innovation Distortion Effect (R&D) | ||||
|---|---|---|---|---|---|---|
| Coefficient | Direct | Indirect | Coefficient | Direct | Indirect | |
| Corr | 0.0337 *** | 0.0351 *** | 0.0424 ** | 0.0345 *** | 0.0355 *** | 0.0381 ** |
| (3.5063) | (3.4678) | (2.3251) | (3.7253) | (3.6152) | (2.2586) | |
| lnGDP | −0.3751 *** | −0.3850 *** | −0.4671 ** | −0.4338 *** | −0.4460 *** | −0.4785 ** |
| (−4.6445) | (−4.6470) | (−2.5663) | (−5.3678) | (−5.2466) | (−2.5334) | |
| IS | −0.2104 *** | −0.2156 *** | −0.2619 ** | −0.1763 *** | −0.1794 *** | −0.1927 ** |
| (−4.7435) | (−4.7004) | (−2.4864) | (−3.9682) | (−3.7826) | (−2.2579) | |
| lnFDI | −0.0688 *** | −0.0711 *** | −0.0861 *** | −0.0614 *** | −0.0630 *** | −0.0676 ** |
| (−5.1149) | (−4.9892) | (−2.6044) | (−4.9195) | (−4.7609) | (−2.4648) | |
| lnRD | 0.1507 *** | 0.1551 *** | 0.1881 ** | 0.1632 *** | 0.1671 *** | 0.1792 ** |
| (3.8084) | (3.8026) | (2.3903) | (4.1910) | (4.2359) | (2.3956) | |
| Corr × lnFDI | 0.0160 *** | 0.0165 *** | 0.0201 ** | |||
| (2.6352) | (2.6412) | (1.9792) | ||||
| Corr × lnRD | 0.0245 *** | 0.0252 *** | 0.0271 ** | |||
| (4.7085) | (4.9295) | (2.4543) | ||||
| ρ | 0.5484 *** | 0.5148 *** | ||||
| (7.1719) | (6.3339) | |||||
| R2 | 0.9606 | 0.9619 | ||||
| Log-Lik | 336.6735 | 344.9714 | ||||
| Variables | 2003–2012 | 2013–2017 | ||||
|---|---|---|---|---|---|---|
| Coefficient | Direct | Indirect | Coefficient | Direct | Indirect | |
| Corr | 0.0037 | 0.0035 | 0.0008 | −0.0138 | −0.0141 | −0.0038 |
| (0.4178) | (0.3986) | (0.3605) | (−1.1296) | (−1.1816) | (−0.8330) | |
| lnGDP | −0.2124 ** | −0.2144 *** | −0.0495 | −1.0146 *** | −1.0241 *** | −0.2626 |
| (−2.5642) | (−2.5969) | (−1.5369) | (−9.7129) | (−9.5175) | (−1.5874) | |
| IS | −0.2781 *** | −0.2813 *** | −0.0638 * | −0.1413 *** | −0.1438 *** | −0.0360 |
| (−5.2371) | (−5.1889) | (−1.9457) | (−2.8371) | (−2.8485) | (−1.4118) | |
| lnFDI | −0.0373 ** | −0.0378 *** | −0.0086 | 0.0089 | 0.0086 | 0.0018 |
| (−2.5726) | (−2.5811) | (−1.5760) | (0.6851) | (0.6439) | (0.4500) | |
| lnRD | 0.1185 *** | 0.1184 *** | 0.0270 * | 0.0013 | −0.0008 | 0.0009 |
| (3.1012) | (2.9880) | (1.6520) | (0.0224) | (−0.0132) | (0.0458) | |
| ρ | 0.1877 ** | 0.2047 ** | ||||
| (2.4852) | (2.0642) | |||||
| R2 | 0.9766 | 0.9961 | ||||
| Log-Lik | 335.7928 | 275.9317 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Yi, B. New Insights into the Impact of Local Corruption on China’s Regional Carbon Emissions Performance Based on the Spatial Spillover Effects. Sustainability 2022, 14, 15310. https://doi.org/10.3390/su142215310
Xu X, Yi B. New Insights into the Impact of Local Corruption on China’s Regional Carbon Emissions Performance Based on the Spatial Spillover Effects. Sustainability. 2022; 14(22):15310. https://doi.org/10.3390/su142215310
Chicago/Turabian StyleXu, Xianpu, and Bijiao Yi. 2022. "New Insights into the Impact of Local Corruption on China’s Regional Carbon Emissions Performance Based on the Spatial Spillover Effects" Sustainability 14, no. 22: 15310. https://doi.org/10.3390/su142215310
APA StyleXu, X., & Yi, B. (2022). New Insights into the Impact of Local Corruption on China’s Regional Carbon Emissions Performance Based on the Spatial Spillover Effects. Sustainability, 14(22), 15310. https://doi.org/10.3390/su142215310






