Two-Phase Stratified Random Forest for Paddy Growth Phase Classification: A Case of Imbalanced Data

Abstract

The United Nations Sustainable Development Goals (SDGs) have had a considerable impact on Indonesia’s national development policies for the period 2015 to 2030. The agricultural industry is one of the world’s most important industries, and it is critical to the achievement of the SDGs. The second major aspect of the SDGs, i.e., zero hunger, addresses food security (SDG 2). To measure the status of food security, accurate statistics on paddy production must be accessible. Paddy phenological classification is a way to determine a food plant’s growth phase. Imbalanced data are a common occurrence in agricultural data, and machine learning is frequently utilized as a technique for classification issues. The current trend in agriculture is to use remote sensing data to classify crops. This paper proposes a new approach—one that uses two phases in the bootstrap stage of the random forest method—called a two-phase stratified random forest (TPSRF). The simulation scenario shows that the proposed TPSRF outperforms CART, SVM, and RF. Furthermore, in its application to paddy growth phase data for 2019 in Lamongan Regency, East Java, Indonesia, the proposed TPSRF showed higher overall accuracy (OA) than the compared methods.

1. Introduction

The agricultural sector plays a crucial role in reaching the UN’s Sustainable Development Goals (SDGs) on a worldwide scale. Food security is one of the main indicators of the SDGs listed in the second objective, namely zero hunger (SDGs 2). A country needs access to reliable paddy production data to assess the state of food security. Observing food crops, particularly paddies, has been used to achieve the goal of SDG two. Monitoring of the paddy growth phase was carried out by Statistics Indonesia (BPS) by the conducting of an area sample frame (ASF) survey, using samples taken at random for as much as 5% of the total paddy field area (LBS). BPS data on the growth phase of paddy are crucial in predicting a harvest, but they contain limited information about individual variations in non-sampled areas.

On the other hand, the paddy growth phase can be observed using remote sensing techniques. Landsat-8 satellite imagery data can be a solution to the weakness of the ASF survey method in terms of the limited sample size of rice fields in Indonesia. Many researchers have utilized remote sensing. In agriculture, remote sensing data are used for plant species classification [1,2], harvested area estimation [3], and rice mapping [4,5]. The utilization of remote sensing data in the form of pixels for a segmented method in ASF results in the creation of “Geo Big Data” [6,7], which requires new technologies and resources, such as cloud computing [8], that can handle massive amounts of satellite imagery. Dean [9] has used machine learning to solve big data problems. Many fields and disciplines take advantage of remote sensing. Remote sensing imagery has been utilized to model the paddy growth phase in agriculture because the paddy fields have many spatio-temporal features that may be used to find vegetation indexes [10], plant species classification [11], harvested area estimation [3], or rice mapping [4]. Chang et al. [12] have stated that there are four growth phases for rice, each based on the characteristics of the reflectance spectrum. The paddy growth phases are also a challenge; Kim et al. [13] have tried to classify the rice plant phases. Zhao et al. [4] have stated that spectral bands during the growing season can be used to identify rice growth phases. Dong et al. [14] have stated that many features/variables involved in mapping agricultural areas need to be discussed comprehensively. The solution offered by Singha et al. [15] was to use phenological features or growth phases, which greatly reduced errors due to spectral similarity.

One problem that may occur in machine learning is imbalanced data classes [16]. An imbalance of data classes occurs when one class has a much larger amount of data than other classes. Under conditions of imbalanced data, most of the classifiers in machine learning will be biased toward the problem of imbalanced data, because the classifier’s likelihood of predicting the major class will be greater than the minor class [17]. Suryono et al. [18] used the random forest (RF) method to solve the imbalance problem in ASF data. The issue of imbalanced data has been addressed through the conduct of numerous studies, one of which took an algorithm-level approach. The approach at the algorithm level is made by creating or modifying an algorithm that considers the significance of the positive class. Algorithm-level methods include cost-sensitive and recognition-based approaches, such as support vector machines (SVM) and radial basis functions [19], as well as random forest classification [20]. To overcome the problem of imbalances in paddy growth phase data, this paper proposes a random forest method that uses a two-phase stratified random forest (TPSRF) to improve the performance of the random forest.

Sheykhmousa et al. [21] compared the RF method’s performance with the SVM method and RF has consistently higher performance. This machine learning algorithm is widely used for classification since it is insensitive to multicollinearity and classification decisions are taken from the majority vote among all trees [22]. Because it is an ensemble method, RF can be used to answer the problem of temporal autocorrelation in rice growth phase data [23].

Suryono et al. [18] have conveyed that have been indications of imbalanced data in paddy growth phase data in Indonesia. RF has been widely developed for imbalanced cases such as the balanced random forest (BRF) method developed by Hema et al. [24] and the weighted random forest (WRF) method developed by Chen et al. [25]. More et al. [26] have stated that BRF has several weaknesses, namely that it allows important data to be wasted as part of undersampling process carried out at the bootstrap stage, which can alter the classification results. Wu et al. [27] introduced a stratified random forest (SRF) method as a solution to the classification of genome-wide SNP data with imbalanced data.

2. Materials and Methods

2.1. Dataset

The study used Landsat-8 satellite imagery for January–December 2019, which was processed through the Google Earth engine (GEE) to produce raw data containing the image capturing date, coordinates, and vegetation index. Landsat-8 collects data every 16 days. The variables used in this study were the spectral emission band 1 (coastal aerosol), band 2 (blue), band 3 (green), band 4 (red), band 5 (NIR), band 6 (short-wave infrared—SWIR) 1, and band 7 (short-wave infrared—SWIR) 2, as well as four selected indices, namely EVI, NDVI, NDBI, and NDWI. The vegetation index was derived from the spectral band and was chosen based on research to identify the paddy growth phase [10]. The Agency for the Assessment and Application of Technology Indonesia (BPPT) aided Statistics Indonesia (BPS) in developing the area sample framework (ASF) survey, which was used to collect response data in 2019. The label data contained the response variables from the observation coordinates, which were ASF samples, and produced five classes of paddy growth phases, which are labeled as early vegetative (Class 1), late vegetative (Class 2), generative (Class 3), harvest (Class 4), land preparation/bera (Class 5), and crop failure/puso (Class 6). This study examined the paddy growth phase in Lamongan Regency, East Java, which is one of the largest rice producers in Indonesia.

2.1.1. Vegetation Index (VI) Composite Extraction

Vegetation index (VI) is a spectral modification of two or more bands designed to calculate the contribution of vegetation characteristics, comparing photosynthetic activity and canopy structural variation spatially and temporally [28]. The rice growth phase has been the subject of numerous studies using satellite image data to calculate the vegetation index [2]. These studies made use of a variety of satellite images, including Landsat-7 and Modis, which were later developed into Landsat-8. The four vegetation indexes that were derived from satellite imagery for the purpose of determining the phenology of paddy fields were Enhanced Vegetation Index (EVI), Normalized Difference Vegetation Index (NDVI), Normalized Difference Built-Up Index (NDBI), and Normalized Difference Water Index (NDWI). The surface bidirectional reflectance factors (BRF) for each band were ρ_NIR and ρ_RED [13].

2.1.2. Area Sampling Framework (ASF)

BPS and BPPT developed the area sampling framework (ASF) to calculate the monthly harvested paddy areas. An area framework is used in this sampling method [29]. In the entire research area, samples from the ASF survey were taken on a square area of 300 m × 300 m. Segments are regions with an area of 300 m by 300 m. One segment is divided into 9 subsegments with a size of 100 m × 100 m. One segment is counted as 1 sample area. The number of segment samples is 5% of the segment population in one block. The ASF survey in Lamongan Regency was conducted every month for a full year and collected data for 208 segments or 1872 subsegments. The total subsegments for a year were 22,464 subsegments. Rice phenology data from all subsegments of the field survey are used to calculate monthly estimates of the harvested area [30].

There are six phenology categories for paddy that were recorded in the ASF’s paddy growth phases.

Table 1. Paddy phenology definitions and visual displays in the ASF survey.

No	Paddy Phenology	Definition	Visual Display
1	Early vegetative	The early vegetative phase starts from the first growth phase until the tiller reaches its maximum
2	Late vegetative	This phase starts from the appearance of the first tiller until the maximum number of tillers appears
3	Generative	This phase starts when the panicles come out until they ripen and then harvest
4	Harvesting	This phase is from the beginning to the end of the harvest
5	Bera (land preparation)	The phase when the paddy fields are cultivated to get ready for the growth of the paddy
6	Puso (crop failure)	This label causes rice production to fall below 11 percent of normal due to natural disasters or pests.

provides both the visual representation and definition of the paddy phenology category.

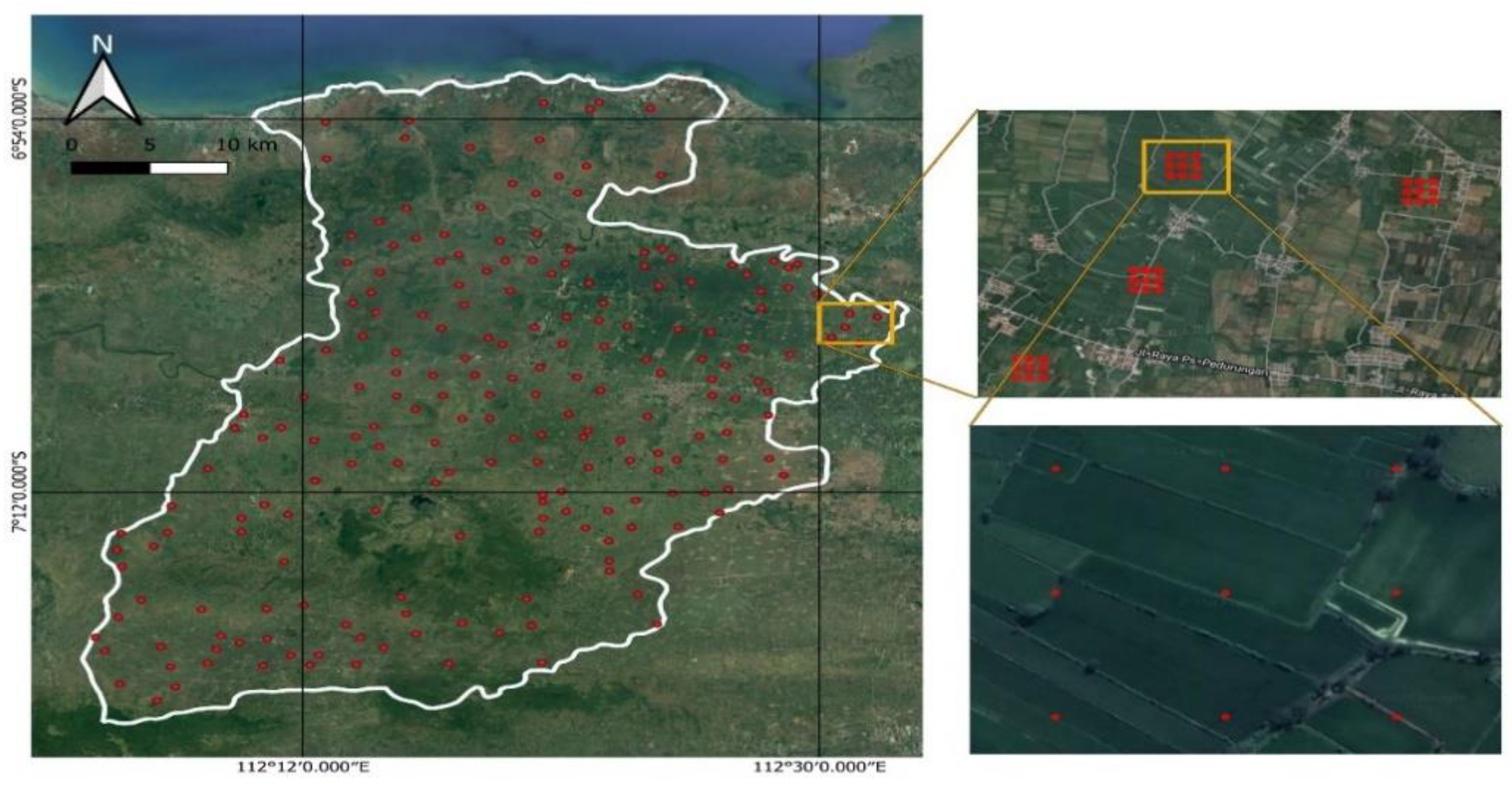
2.2. Study Area

Lamongan is a regency in East Java province. Geographically, Lamongan has a position at 6°51′5″ to 7°23′6″ south latitude and is between the east longitude lines 112°4′41″ and 112°33′12″. In Landsat-8 imagery, Lamongan can be found on path/row 119/065. Lamongan comprises 50.17% lowlands with an altitude of 0 to 25 m, 45.68% plains with an altitude of 25 to 100, and 4.15% lands with an altitude of more than 100 m above sea level. Lamongan is bounded on the north by the Java Sea, on the south by the regencies of Jombang and Mojokerto, on the west by the regencies of Tuban and Bojonegoro, and on the east by the regency of Gresik (Figure 1).

2.3. Methodology

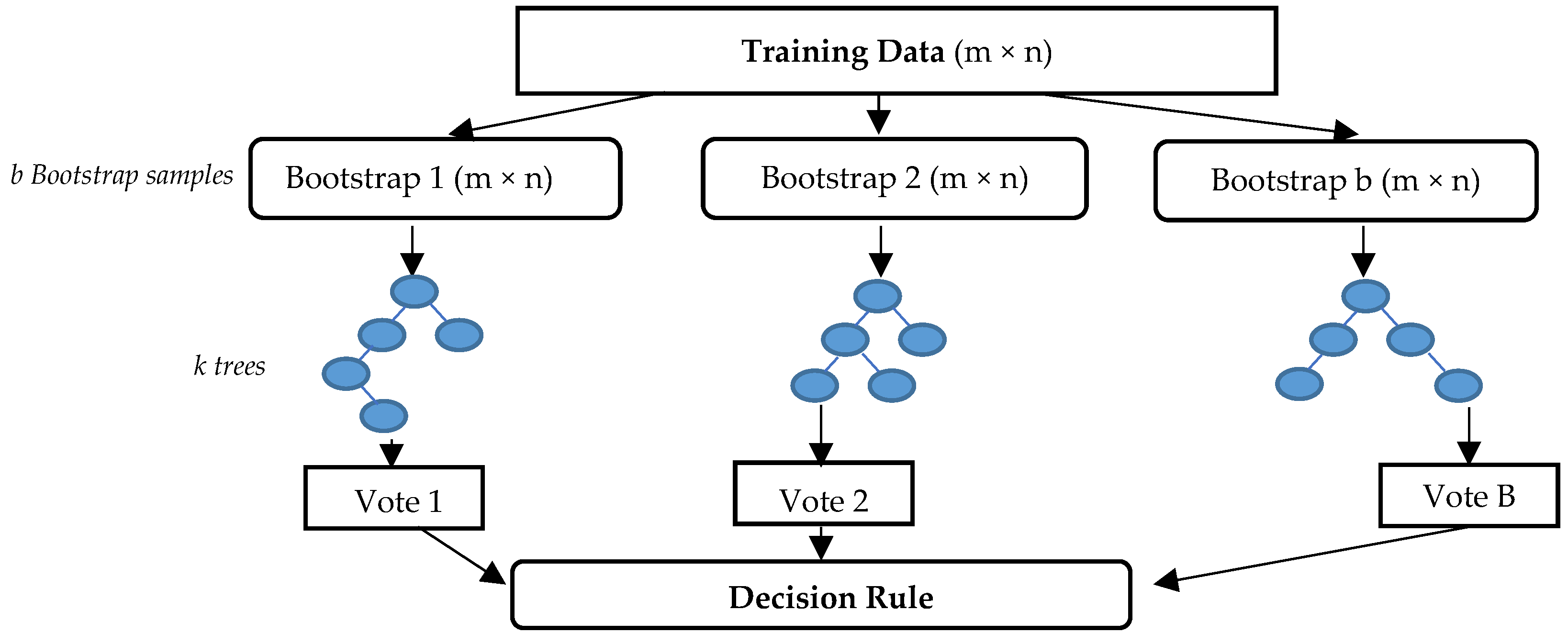
2.3.1. Random Forest

Random forest [20] is a CART development, using bagging and random feature selection in the decision tree, which selects multiple features at random in each iteration. The resulting tree contains as many iterations as possible, so it resembles a forest. Classification decisions are taken from the majority vote among all trees [22]. The problem with the DT is to the need to minimize the residual in order to choose which feature to use as a separator. The resulting tree structure is highly similar as a result, leading to a high predictor correlation. If the predictions from the sub-models are not related to one another or have a very low correlation, then the ensemble of predictions will work well when combined. In simple terms, the random forest formation algorithm can be stated as follows. Suppose we have training data of size n and consisting of p explanatory variables (predictors). The algorithm steps of this study adapted from Breiman [20] are as follows (Figure 2):

• In the bootstrap stage, we drew a random sample with size n returns from the training data;
• Using the bootstrap example, the tree was constructed until it reached its maximum size (without returns). We arranged a tree based on these data, but randomly selected m < p explanatory variable in each separation process and performed the best separation (random sub-setting stage);
• We repeated steps 1–2 b times to form a forest consisting of b trees. We then created a combined estimate based on the b trees using the most votes.

Ye et al. [31] proposed a stratified random forest (SRF), a stratified sampling technique for selecting feature subspaces for random forest. The principle was to divide the features into two categories. Strong informative features were found in one group, while weak informative features were found in the other. The features were then chosen proportionally at random from each group for the feature subset selection. The ability to ensure that each subspace contains sufficient informative features for classification in high-dimensional data is one of the advantages of stratified sampling. The number of groups is referred to as a parameter in the SRF. This method selects the same number of variables from each group randomly to form a subspace in the selection of subspaces.

2.3.2. Two-Phase Stratified Random Forest (TPSRF)

The stratified sampling method divides a set of variables into numerous groups, each with a uniform level of informativeness. The proposed algorithm (two-phase stratified random forest) developed a random forest model from data training using the stratified sampling algorithm on the random forest stage’s bootstrap section. The distinction between TPSRF and SRF is that the TPSRF method utilizes a stratified step to select samples on the bootstrap, whereas SRF uses stratified sampling for feature selection.

Some steps of the bootstrap algorithm from the two-phase stratified random forest proposed in this study are as follows:

• We determined the bootstrap sample (Z), as far as K from the training data (Z).
• We generated a tree on RF with data in the bootstrap sample, repeating the following steps recursively for each terminal node in the tree until a minimum node size of $n{s}_{\min }$ was obtained, i.e.,

  2.1.

  We determined the number of strata samples k (n_k) (1st phase);

  • We determined the major class and minor class
    • We sorted in descending order of strata based on the number of N_k
    • The minor class was the smallest cumulative number of classes where ${\theta }_1\le 20\%$
    • We calculated the number of strata in the minor class $\left({\theta }_1\right)$ and the number of strata in the major class $\left({\theta }_2\right)$
  • We determined the minor class $\left({\theta }_1\right)$ and major class $\left({\theta }_2\right)$ members
  • We determined the strata weights in the minor class $\left({\theta }_1\right)$ and major class $\left({\theta }_2\right)$

  2.2.

  We sampled the kth strata as far as n_k (2nd phase).

• We chose the best variable or split point.
• We split a node into two subnodes.

2.3.3. Assessment Matrices

The accuracy, precision, and recall were used to evaluate the prediction’s performance. The confusion matrix shows the predicted results and performance metrics for the classification issues (

Table 2. Confusion matrix.

	Actual Positive (AP)	Actual Negative (AN)
Predicted Positive (PP) Predicted Negative (PN)	True Positives (TP) False Negatives (FN)	False Positives (FP) True Negatives (TN)

). The values (AP, AN) denote positive and negative test data, respectively, and the values (PP, PN) denote predicted results for positive and negative classes. For each class, the number of true and false predictions is summarized [32].

TP is the outcome when the model correctly predicts the positive class, TN is the outcome when the model correctly predicts the negative class, FP is the outcome where the model incorrectly predicts the positive class, and FN is the outcome where the model incorrectly predicts the negative class. The evaluation metrics that are formulated to evaluate the classification results from the collected data are outlined in Equations (1)–(3).

$$\mathrm{Accuracy}=\frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TP}+\mathrm{TN}+\mathrm{FP}+\mathrm{FN}},$$

(1)

$$\mathrm{Precision}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}},$$

(2)

$$\mathrm{Recall}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}.$$

(3)

The calculation of the degree of consistency between the two measurement procedures or the degree of agreement between observers when using a nominal scale, was determined using Kappa statistics [33]. The Kappa coefficient can measure the degree of agreement that can group objects into mutually exclusive classes.

The Kappa statistic’s equation $\left(\kappa \right)$ is:

$$\kappa =\frac{{\displaystyle {\sum }_{i=1}^v{p}_{ii}-{\displaystyle {\sum }_{i=1}^v{p}_{i+}{p}_{+i}}}}{1-{\displaystyle {\sum }_{i=1}^v{p}_{i+}{p}_{+i}}},$$

(4)

where ${\displaystyle {\sum }_{i=1}^v{p}_{ii}}$ is the proportion of agreements, ${\displaystyle {\sum }_{i=1}^v{p}_{i+}{p}_{+i}}$ is the expected proportion of chance agreements. The F1 score is the average of the harmonics of precision and sensitivity. The F1 score equation is as follows:

$$\mathrm{F}1\mathrm{score}=\frac{2\times Recall\times Precision}{Recall+Precision}$$

(5)

2.3.4. Data Preprocessing

The two stages used in data preprocessing were data formation and data extraction. The data formation stage was carried out by combining the variables derived from the ASF data and the satellite image data. This study used seven variables from the Landsat-8 imagery with the names Aerosol, Blue, Green, Red, NIR, SWIR 1, and SWIR 2 (

Table 3. Types and uses of the Landsat-8 Band (used in the study).

Band Name	Landsat-8 Spectral Range (µm)	Vegetation Index (VI)	Equation
Coastal Aerosol	0.43–0.45	EVI	$EVI=\frac{2.5({\rho }_{NIR}-{\rho }_{RED})}{(1+{\rho }_{NIR}+6{\rho }_{RED}-7.5{\rho }_{RED})}$
Blue	0.45–0.51
Green	0.53–0.59	NDVI	$NDVI=\frac{({\rho }_{NIR}-{\rho }_{RED})}{({\rho }_{NIR}+{\rho }_{RED})}$
Red	0.63–0.67
NIR	0.85–0.88	NDBI	$NDBI=\frac{({\rho }_{SWIR1}-{\rho }_{NIR})}{({\rho }_{SWIR1}+{\rho }_{NIR})}$
SWIR1	1.57–1.65
SWIR2	2.11–2.29	NDWI	$NDWI=\frac{({\rho }_{NIR}-{\rho }_{SWIR1})}{({\rho }_{NIR}+{\rho }_{SWIR1})}$

), as well as four selected indices, namely EVI, NDVI, NDBI, and NDWI, and the ASF survey data as response variables.

Figure 3 shows the 2019 distribution of the ASF sample subsegments in Lamongan Regency. The ASF survey collects data on the paddy growth phase of as many as 208 segments in a month. This indicates that there were 1872 subsegments in total per month, and 22,464 per year. The monthly enumeration was carried out in the same subsegment. Figure 3 shows the observation point in one sample segment (nine subsegments).

The Landsat-8 imagery in each period produced 11 layer bands (Figure 4). In applying the random forest classification model, seven layer bands were used, namely layer bands 1 to 7. After obtaining the data from the Landsat-8 images and the data labels from the ASF surveys, we extracted the Landsat-8 image data into numbers.

The data extraction process was carried out with a scale of 40 m × 40 m according to the location of the sample subsegment in the ASF survey. The initial data frame consisted of bands one to seven, ASF label data, and several identities from other ASF surveys. The vegetation index values were calculated from band one to band seven, namely: the EVI, NDVI, NDWI, and the NDBI. The basic features were seven bands and four vegetation indices. Then, from the 11 basic features, the temporal features were derived for four Landsat-8 periods, namely period t to period t−3, so that there were 44 total temporal features. Period t is the Landsat-8 period adjacent to the ASF survey enumeration period every month. The period t−1 is the previous period.

2.3.5. Imbalanced Data

A classification data set with unbalanced class proportions is called imbalanced data; the number of data in one data class may be lower or higher than the number of data in another data class. The group of data classes with fewer data is the minor class $\left({\theta }_1\right).$ The other data class group is called the major class $\left({\theta }_2\right).$

The ASF data with 1872 subsegments showed different proportions for each class in the paddy growth phase. This indicates that the ASF data had an imbalanced class. The classification method had difficulty performing generalization functions during the machine learning process because of this condition. Almost all classification algorithms, including CART, SVM, random forest, and others perform poorly when applied to data with extreme degrees of imbalance. The classification methods mentioned above were not specifically designed to deal with class imbalance problems. Classification of data with imbalanced classes is an urgent issue in machine learning, for example, remote sensing [34]. If they are working on imbalanced data, almost all classification algorithms will produce much higher accuracy for the majority class than for the minority class [35]. This difference is an indicator of poor classification performance.

3. Results and Discussion

3.1. Models Simulation

This section evaluates the performance of the RF model and the two-phase stratified RF model. This simulation study used a remote sensing dataset from the UCI machine learning repository. The dataset used was Forest Covertype/Covtype data to predict forest cover type using cartographic variables. Observations used with a 30 × 30 m area were based on data from the Resource Information System (RIS), the United States Forest Service (USFS), and the US Geological Survey (USGS). The study area included four forest areas located in the Roosevelt National Forest in northern Colorado. The simulation data contained 581,012 records with six land cover classification classes based on the main tree species, namely: spruce/fir (Class 1), lodgepole pine (Class 2), ponderosa pine (Class 3), cottonwood/willow (Class 4), aspen (Class 5), and Douglas fir (Class 6).

To evaluate the classification of the paddy growth phase, this study simulated nine scenarios to show how the accuracy reacted under different proportions of major class $\left({\theta }_1\right)$, minor class $\left({\theta }_2\right)$, training data $\left(d_1\right)$, and testing data $\left(d_2\right)$. The complete scenario of this simulation study can be seen in

Table 4. Machine learning algorithm scenarios using the simulation data.

Scenario	${\mathit{\theta }}_1$	${\mathit{\theta }}_2$	${\mathit{d}}_1$	${\mathit{d}}_2$
1	0.05	0.95	0.70	0.30
2	0.20	0.80	0.70	0.30
3	0.40	0.60	0.70	0.30
4	0.05	0.95	0.80	0.20
5	0.20	0.80	0.80	0.20
6	0.40	0.60	0.80	0.20
7	0.05	0.95	0.90	0.10
8	0.20	0.80	0.90	0.10
9	0.40	0.60	0.90	0.10

.

The performance of the model was evaluated using four measurement criteria, namely accuracy, precision, recall, and F1 score in cases of extremely imbalanced, imbalanced, and nearly balanced data proportions. The scenarios for the extremely imbalanced cases were scenarios 1, 4, and 7, the imbalanced cases were scenarios 2, 5, and 8, and the nearly balanced cases were scenarios 3, 6, and 9.

Simulation data were used to compare the implementation of the proposed two-phase stratified random forest, random forest, SVM, and CART.

Table 5. CART, SVM, random forest, and two-phase stratified random forest statistics for the simulation data set.

Scenario	Method	Class 1			Class 2			Class 3
		Precission	Recall	F1-Score	Precission	Recall	F1-Score	Precission	Recall	F1-Score
1	RF	0.92	0.94	0.93	1.00	0.96	0.98	0.89	0.97	0.93
	TPSRF	0.95	0.98	0.97	0.98	1.00	0.99	0.82	0.98	0.90
	SVM	0.94	0.96	0.95	0.94	0.85	0.90	0.89	0.88	0.89
	CART	0.92	0.83	0.87	0.87	0.84	0.86	0.91	0.87	0.89
2	RF	0.93	0.98	0.95	1.00	0.96	0.98	0.98	0.93	0.95
	TPSRF	0.97	0.89	0.93	0.95	0.95	0.95	0.90	0.97	0.94
	SVM	0.98	0.98	0.98	1.00	0.93	0.96	0.93	0.93	0.93
	CART	0.95	0.87	0.91	0.91	0.98	0.94	0.80	0.97	0.88
3	RF	0.87	0.93	0.90	1.00	1.00	1.00	0.95	1.00	0.98
	TPSRF	1.00	1.00	1.00	0.94	0.89	0.92	0.90	0.95	0.92
	SVM	1.00	0.93	0.96	0.95	0.95	0.95	0.91	1.00	0.95
	CART	0.93	0.81	0.87	0.95	1.00	0.97	0.90	0.95	0.92
4	RF	0.83	0.98	0.90	1.00	1.00	1.00	0.83	0.84	0.83
	TPSRF	0.77	1.00	0.87	1.00	0.94	0.97	0.77	0.92	0.84
	SVM	0.88	0.98	0.93	0.91	0.90	0.91	0.81	0.67	0.73
	CART	0.89	0.63	0.74	0.94	0.96	0.95	0.73	0.79	0.76
5	RF	0.97	0.97	0.97	0.97	0.97	0.97	0.74	0.93	0.82
	TPSRF	0.00	0.00	0.00	1.00	1.00	1.00	0.73	0.76	0.74
	SVM	1.00	0.91	0.95	0.88	0.91	0.90	0.67	0.80	0.73
	CART	0.85	0.85	0.85	0.94	0.86	0.90	0.90	0.60	0.72
6	RF	0.93	1.00	0.96	1.00	1.00	1.00	0.95	0.90	0.93
	TPSRF	1.00	0.88	0.93	1.00	1.00	1.00	0.82	0.88	0.85
	SVM	0.81	1.00	0.90	0.88	0.88	0.88	0.94	0.81	0.87
	CART	1.00	0.76	0.87	0.94	0.83	0.88	0.67	0.93	0.78
7	RF	0.95	0.97	0.96	1.00	0.93	0.96	0.61	0.68	0.64
	TPSRF	0.94	0.92	0.93	0.97	0.92	0.94	0.86	0.67	0.75
	SVM	0.95	0.95	0.95	0.90	0.93	0.91	0.70	0.76	0.73
	CART	0.87	0.87	0.87	0.79	0.88	0.83	0.70	0.63	0.67
8	RF	1.00	0.96	0.98	1.00	0.90	0.95	0.82	0.78	0.80
	TPSRF	0.92	0.96	0.94	1.00	0.92	0.96	0.94	0.63	0.75
	SVM	0.93	1.00	0.96	0.90	0.95	0.93	0.80	0.70	0.74
	CART	0.92	0.96	0.94	0.90	0.82	0.86	0.61	0.61	0.61
9	RF	0.82	1.00	0.90	1.00	0.92	0.96	0.56	0.82	0.67
	TPSRF	0.92	0.92	0.92	1.00	1.00	1.00	0.77	0.83	0.80
	SVM	0.82	1.00	0.90	1.00	0.92	0.96	0.59	0.91	0.71
	CART	0.78	0.70	0.74	0.83	0.77	0.80	0.82	0.50	0.62
Scenario	Method	Class 4			Class 5			Class 6
		Precission	Recall	F1-score	Precission	Recall	F1-score	Precission	Recall	F1-score
1	RF	0.40	0.15	0.22	0.86	0.81	0.83	0.75	0.85	0.80
	TPSRF	0.75	0.20	0.32	0.94	0.86	0.90	0.85	0.88	0.86
	SVM	0.14	0.08	0.10	0.80	0.83	0.81	0.72	0.85	0.78
	CART	0.23	0.23	0.23	0.67	0.64	0.65	0.54	0.76	0.63
2	RF	0.50	0.75	0.60	0.94	0.92	0.93	0.93	0.95	0.94
	TPSRF	0.67	0.60	0.63	0.92	0.89	0.91	0.85	0.89	0.87
	SVM	0.25	0.50	0.33	0.85	0.92	0.88	0.89	0.83	0.86
	CART	0.75	0.19	0.30	0.84	0.86	0.85	0.83	0.89	0.86
3	RF	1.00	0.50	0.67	1.00	0.85	0.92	0.85	1.00	0.92
	TPSRF	1.00	0.20	0.33	0.90	1.00	0.95	0.90	1.00	0.95
	SVM	0.00	0.00	0.00	0.92	0.88	0.90	0.82	0.82	0.82
	CART	0.50	0.33	0.40	0.85	0.96	0.90	1.00	0.89	0.94
4	RF	0.71	0.78	0.74	0.93	0.79	0.85	0.92	0.81	0.86
	TPSRF	0.83	0.75	0.79	0.92	0.91	0.91	0.91	0.81	0.86
	SVM	0.59	0.76	0.67	0.82	0.77	0.79	0.86	0.75	0.80
	CART	0.72	0.63	0.67	0.66	0.72	0.69	0.61	0.88	0.72
5	RF	0.92	0.73	0.81	0.86	0.81	0.83	0.75	0.83	0.79
	TPSRF	0.65	0.67	0.66	0.94	0.79	0.86	0.76	0.74	0.75
	SVM	0.70	0.62	0.66	0.70	0.74	0.72	0.68	0.66	0.67
	CART	0.53	0.73	0.62	0.61	0.83	0.70	0.83	0.77	0.80
6	RF	0.76	0.76	0.76	0.79	0.85	0.81	0.76	0.72	0.74
	TPSRF	0.75	0.75	0.75	0.88	0.88	0.88	0.82	0.88	0.85
	SVM	0.60	0.53	0.56	0.82	0.69	0.75	0.64	0.78	0.70
	CART	0.53	0.47	0.50	0.54	1.00	0.70	0.78	0.64	0.70
7	RF	0.80	0.84	0.82	0.97	0.87	0.92	0.87	0.72	0.79
	TPSRF	0.81	0.94	0.87	0.91	0.86	0.89	0.83	0.67	0.74
	SVM	0.78	0.84	0.81	0.96	0.71	0.82	0.72	0.64	0.68
	CART	0.82	0.77	0.79	0.82	0.79	0.81	0.58	0.78	0.67
8	RF	0.86	0.89	0.87	1.00	0.86	0.93	0.63	0.79	0.70
	TPSRF	0.80	0.94	0.86	0.88	0.88	0.88	0.74	0.58	0.65
	SVM	0.85	0.89	0.87	0.94	0.55	0.70	0.52	0.74	0.61
	CART	0.83	0.81	0.82	0.66	0.83	0.73	0.68	0.57	0.62
9	RF	0.71	0.80	0.75	0.90	0.69	0.78	0.67	0.29	0.40
	TPSRF	0.86	0.93	0.89	1.00	0.92	0.96	0.89	0.67	0.76
	SVM	0.71	0.75	0.73	1.00	0.69	0.82	0.56	0.36	0.43
	CART	0.75	0.73	0.74	0.62	1.00	0.76	0.50	0.78	0.61

presents the measurement accuracy of the proposed CART, SVM, RF, and TPSRF methods with scenarios based on Table 4. When the major class was set to 60% of the total data, the minor class CART obtained a high F1-score. The SVM obtained the highest F1-score when the minor class had a proportion of testing data of 0.7. Table 5 shows that the performance of the RF and TPSRF was quite high in all the scenarios used. The RF had a lower F1-score in scenario 1, where the major class was 95 percent $\left({\theta }_2=0.95\right)$, and the minor class was 5 percent $\left({\theta }_1=0.05\right)$, with the proportion of testing data at 0.8. The F1-score in this scenario was 0.22 in class 4. Meanwhile, the TPSRF experienced a decrease in the F1-score in scenario 1, where the major class was 0.95 and the minor class was 0.05 with the proportion of testing data at 70 percent $\left(d_1=0.7\right)$. The F1-score in this scenario was 0.32. From the simulation data above, it was concluded that the RF and TPSRF methods had higher accuracy measures than CART and SVM.

3.2. Application to Real Data

The measurement data included ASF survey data for January to December 2019, as many as 22,464 observations, and feature data from Landsat-8 from November 2018 to December 2019. Bands 1 through 7 and ASF data make up the first data frame. Bands from the initial data frame were used to calculate the vegetation index values.

Table 6. Accuracy measure of the CART, SVM, RF, and TPSRF methods.

Method	Landsat-8 and ASF Dataset
	Recall (%)	Precision (%)	Accuracy (%)	Kappa
CART	60.40	60.92	66.82	0.58
SVM	64.33	60.91	70.17	0.62
RF	74.40	70.70	77.64	0.71
TPSRF	71.50	69.49	80.49	0.74

displays the results of the accuracy measures consisting of the recall, precision, accuracy, Kappa, and F1-scores. The CART and SVM had an overall accuracy of 66.82% and 70.17% (respectively). The accuracy of these models in predicting the overall class was still low. This shows that these models could not effectively predict classes in which there were imbalanced data. The RF method is used to handle imbalanced data to improve the minority classes’ prediction performance. The RF produced an overall accuracy of 77.64%. The Kappa statistic value of the RF was also higher than the CART and SVM methods, at 0.71. The proposed method, TSPRF, was used to improve the accuracy of the RF output. The TSPRF produced higher accuracy and Kappa values than the RF, namely, 80.49% and 0.74, respectively.

The overall accuracy (OA) of the TPSRF was 80.49 percent. With a Kappa statistic of 0.74, this model efficiently categorized paddy phenology, suggesting an outstanding condition in terms of agreement strength. Class 6 had the highest user accuracy (UA) of 93.24 percent as shown in

Table 7. Confusion matrix of the prediction of the TPSRF algorithm.

		Actual Class						PA (%)
		1	2	3	4	5	6
Predicted Class	1	177	9	4	7	14	5	81.94
	2	10	32	10	0	0	0	61.54
	3	6	9	139	31	1	3	73.54
	4	2	2	19	129	0	16	76.79
	5	7	0	0	4	14	5	46.67
	6	10	0	0	29	13	400	88.50
UA (%)		83.49	61.54	80.81	64.50	33.33	93.24

. This demonstrated that the TSPRF method in class 6 was accurately classifying the data in the actual class. The highest producer’s accuracy (PA) was also in class 6, 88.50 percent. This shows that in class 6, the TSPRF method succeeded in correctly classifying the data in the predicted class. In addition, TPSRF achieved a higher plant classification performance than other classification methods by studying temporal features automatically from time series satellite imagery. In this research, the main objective of the proposed TPSRF was to achieve high classification efficiency. Therefore, TPSRF optimizes the bootstrap stage by performing two phases. The first phase determines the number of samples of k (n_k) strata by sorting in order of strata based on the number of N_k, determining that the minor class is the cumulative number of the smallest class where ${\theta }_1\le 20\%$, and calculating the number of strata in the minor class $\left({\theta }_1\right)$ and the number of strata in the major class $\left({\theta }_2\right)$. The second phase takes n_k samples of the kth strata. This optimization implies that there has been a significant improvement in the value of accuracy and Kappa statistics (Table 6). The results show that the model proposed by TPSRF has the best performance in classification accuracy and is suitable to be applied to paddy growth phase classification. The results of the TPSRF classification can be used to obtain data on harvested areas to develop sustainable agriculture in Indonesia. TPSRF can be used by stakeholders in the improvement of conventional data collection methods to become more objective, scientific, and modern so that the collection of agricultural data becomes more timely, accurate, and valuable for the growth of food security and sustainability.

4. Conclusions

In conclusion, the proposed method of using a two-phase stratified random forest (TPSRF) to overcome the imbalanced data problem in the case of paddy growth phase in Lamongan Regency has been shown to be the appropriate strategy. In terms of the accuracy of the paddy growth phase classification in all classes, the TPSRF classification algorithm outperformed the CART, SVM, and RF classification algorithms based on experimental and simulation data. The TPSRF had the highest overall accuracy and Kappa statistics based on the experimental and actual data (80.49 percent and 0.74). TPSRF can be used by stakeholders to improve conventional data collection methods so that they become more objective, scientific, and modern and that collected agricultural data becomes more timely, accurate, and valuable for the growth of food security and sustainability. In order to classify imbalanced big geo data, more research employing various models is required. Other methods, such as a neural network, could help the model perform better.