Modeling of Acoustic Vibration Theory Based on a Micro Thin Plate System and Its Control Experiment Verification

Abstract

As a novel control method, acoustic manipulation technology shows extraordinary talents in culturing of tissue and cell, microchip processing and research on material chemistry, which is closely relevant to the vibration modes and the driving signals of the acoustic system. In this paper, bringing up reasonable assumptions, from the perspective of vibration force analysis of a thin plate, the response function of the forced vibration thin plate is derived combining with the Green’s function. Simultaneously, the effective vibration frequencies of micro thin plate are determined. Using the finite element simulation software Comsol 5.6 building thin plate geometry in 2D, the vibration modes of a thin plate are numerically analyzed from the top view and the side view. Additionally, an experimental platform is established, and the vibration experiments of a square micro thin plate (5 cm × 5 cm × 0.625 mm) driven by a central acoustic source is conducted. By comparison, the corresponding experimental results are in good agreement with simulations. Furthermore, single particle motion control is also realized based on the presented platform, and the underlying mechanism is the effects of nodes and anti-nodes on particle motion. The vibrating platform here will become an effective manipulation tool for many scientific fields with the advantage of micro size, good compatibility, and multipurpose.

1. Introduction

The acoustic vibration system generally includes an acoustic source, centrally fixed thin plate and controlled target. Under different acoustic source excitation, the centrally fixed thin plate will produce various vibration modes owing to the nodes and antinodes. As a result, the motion of a micro-nano target can be controlled by setting the precise excitation frequency and intervals. Nevertheless, the determination of effective vibration frequency for a vibration system is of great significance, as not all vibration frequencies can be used for target manipulation. Intriguingly, acoustic vibration of the thin plate has a wide application prospect including the manipulation based on chip [1,2,3], the culture of cells and tissues [4,5], particles forming, self-assembly, classification of particles, particle movement and other promising micro-nano manipulations [6,7,8,9,10,11]. Those are difficult to be accomplished by directly applying external mechanical force because of the micro-nano size of the manipulation object and the high-precision requirements for the hardware platform [12]. Initial research on microparticles manipulation is based on optical tweezers, and a lot of research findings have been reported [13,14]. Although the precisely manipulation and capture have been achieved by optical technique, the disadvantages are also obvious, such as biological incompatibility, destructiveness and high cost [15,16]. Analogously, using magnetic field and electric field technologies, the maneuvering targets are limited to electromagnetic performances [17,18,19,20]. Combining with thin plate vibration characteristics and acoustic excitation, the method of acoustic manipulation is a kind of effective alternative for multipurpose and well compatibility application fields.

Acoustic manipulation related to the particle forming can be traced back to 1787, the discovery of Chladni patterns [21,22,23,24]. When an external excitation driving a center-fixed metal thin plate, the uniformly distributed sand particles on it will move towards the position of the node lines, and gradually, a regular pattern will be formed known as “Chladni patterns”. The formation of a Chladni pattern is deeply dependent on the material properties and the geometry of the thin plate, more critically, the frequencies of driving signals and driving duration. Generally, Chladni patterns come down to the propagation of the acoustic standing wave, which is similar to Helmholtz theorem, a fundamental theorem describing the uniqueness of the electromagnetic field. However, on the other hand, exploring the vibration theory of a thin plate reveals the essence of the formation of Chladni patterns and is conducive to its further application. Analyzing the characteristics of nonlinear vibration of a thin plate, inevitably, structural mechanics is needed. Depending on the stress analysis and equilibrium conditions, after reasonable mathematical assumptions and deduce the response function of forced vibration in a thin plate. The vibration response function reflects the vibration modes of the thin plate and its influencing factors from the perspective of mathematical theory.

Notably, a continuum consists of an infinite number of elements making it difficult to use the numerical calculation method directly. Hence, it is necessary to discretize the continuum into finite elements connected by nodes and solved by the method of structural matrix analysis [25,26,27]. When the research circumstances involve structural mechanics [28], hydrodynamics [29], electric field, magnetic field, and multi-field coupling [30], the finite element method is often applied in simulation, which was formally proposed by famous American structural engineer and earthquake engineer Ray W. Clough in the 1960s. It uses a mathematical approximation to simulate the real physical system such as geometry, stress, and load conditions. Through simple and interconnected elements with a finite number of nodes, a finite number of unknowns can be used to approximate the real system with infinite unknowns. A set of displacement components on finite discrete nodes are obtained to approximate the whole continuum. With the advantages of versatility, powerful function including all kinds of linear and nonlinear problems, and simple description expressed in matrix form. In this work, Comsol Multiphysics version 5.6 is used to perform the thin plate vibration mode analysis. The procedure for Comsol simulation can be divided into three parts: (1) geometric construction and meshing, (2) physical field and boundary condition settings, and (3) configuration solver for the study problem.

It is traditionally believed that the motion of the micro-nano particles on the acoustic excited thin plate is disordered and is even chaotic. Nowadays, some relevant studies show that the motion has its regularity. Strategically, in terms of theoretical derivation, the acoustic vibration system of a thin plate is modeled and the vibration response function is solved, which makes full use of mathematical hypothesis, Green’s function and convolution response. Additionally, modeling the acoustic vibration system based on the Structural Mechanics module in Comsol Multiphysics, the results of finite element simulation analysis are obtained. Constructing an experimental platform reasonably and rigorously is very critical for the success of experimental results. In this study, a square micro silicon thin plate is used to explore the vibration characteristics. As the driving signal, sinusoidal signal generator is also built in computer software and transmitted through the data acquisition card and signal amplifier. Then, the piezoelectric driver receiving the signal excites the thin plate. As a consequence, thin plate vibration can be observed.

Acoustic manipulation technology is closely related to the vibration of thin plates driven by acoustic waves. So that the mechanism of a forced vibration thin plate promotes the development of acoustic technology. How to generate the vibration mode of thin plate and what kinds of factors affect them? How to transform the acoustic waves propagation on thin plate into analyze of finite elements? In this paper, the theory of forced vibration thin plates will be discussed and solved in detail. Using Comsol Multiphysics version 5.6, modeling and analysis of vibration of thin plate. Furthermore, a miniature acoustic control platform will be designed and built. Based on this, vibration mode and single particle control experiments will be executed and verified.

2. Theoretical Analysis of Thin Plate Vibration

The plate geometry studied is shown in Figure 1. Establish the coordinate system $(x,y,z)$ that the plane $(x,y)$ coincides with the neutral surface of a static metal plate with thickness h and density $\rho$. Considering ${\epsilon }_x,{\epsilon }_y$ are normal strains along x-axis and y-axis, respectively, ${\gamma }_{xy}$ is shear strain, correspondingly, ${\sigma }_x,{\sigma }_y$ are normal stresses, ${\tau }_{xy}$ is shear stress. $w(x,y,t)$ is the deflection of thin plate along z axis.

From the points of view of strain and generalized Hooke’s law, the following results of the relationship between stress and strain are obtained

$$\left\{\begin{array}{c}{\epsilon }_x=-z\frac{{\partial }^{2}w}{\partial x^2}\hfill \\ {\epsilon }_y=-z\frac{{\partial }^{2}w}{\partial y^2}\hfill \\ {\gamma }_{xy}=-2z\frac{{\partial }^{2}w}{\partial x\partial y}\hfill \end{array}\right.$$

(1)

$$\left\{\begin{array}{c}{\sigma }_x=-\frac{Ez}{1-{\upsilon }^2}(\frac{{\partial }^{2}w}{\partial x^2}+\upsilon \frac{{\partial }^{2}w}{\partial y^2})\hfill \\ {\sigma }_y=-\frac{Ez}{1-{\upsilon }^2}(\frac{{\partial }^{2}w}{\partial y^2}+\upsilon \frac{{\partial }^{2}w}{\partial x^2})\hfill \\ {\tau }_{xy}=-\frac{Ez}{1+\upsilon }\frac{{\partial }^{2}w}{\partial x\partial y}\hfill \end{array}\right.$$

(2)

where E is Young’s modulus and $\upsilon$ indicates Poisson’s ratio.

Calculate the bending moment and the torque per unit length along the x-axis and y-axis.

$$\left\{\begin{array}{c}{M}_x={\int }_{-\frac{h}{2}}^{\frac{h}{2}}{\sigma }_{x}zdz=-D(\frac{{\partial }^{2}w}{\partial x^2}+\upsilon \frac{{\partial }^{2}w}{\partial y^2})\hfill \\ M_y={\int }_{-\frac{h}{2}}^{\frac{h}{2}}{\sigma }_{y}zdz=-D(\frac{{\partial }^{2}w}{\partial y^2}+\upsilon \frac{{\partial }^{2}w}{\partial x^2})\hfill \\ M_{xy}=M_{yx}={\int }_{-\frac{h}{2}}^{\frac{h}{2}}{\tau }_{xy}zdz=-D\frac{{\partial }^{2}w}{\partial x\partial y}\hfill \end{array}\right.,$$

(3)

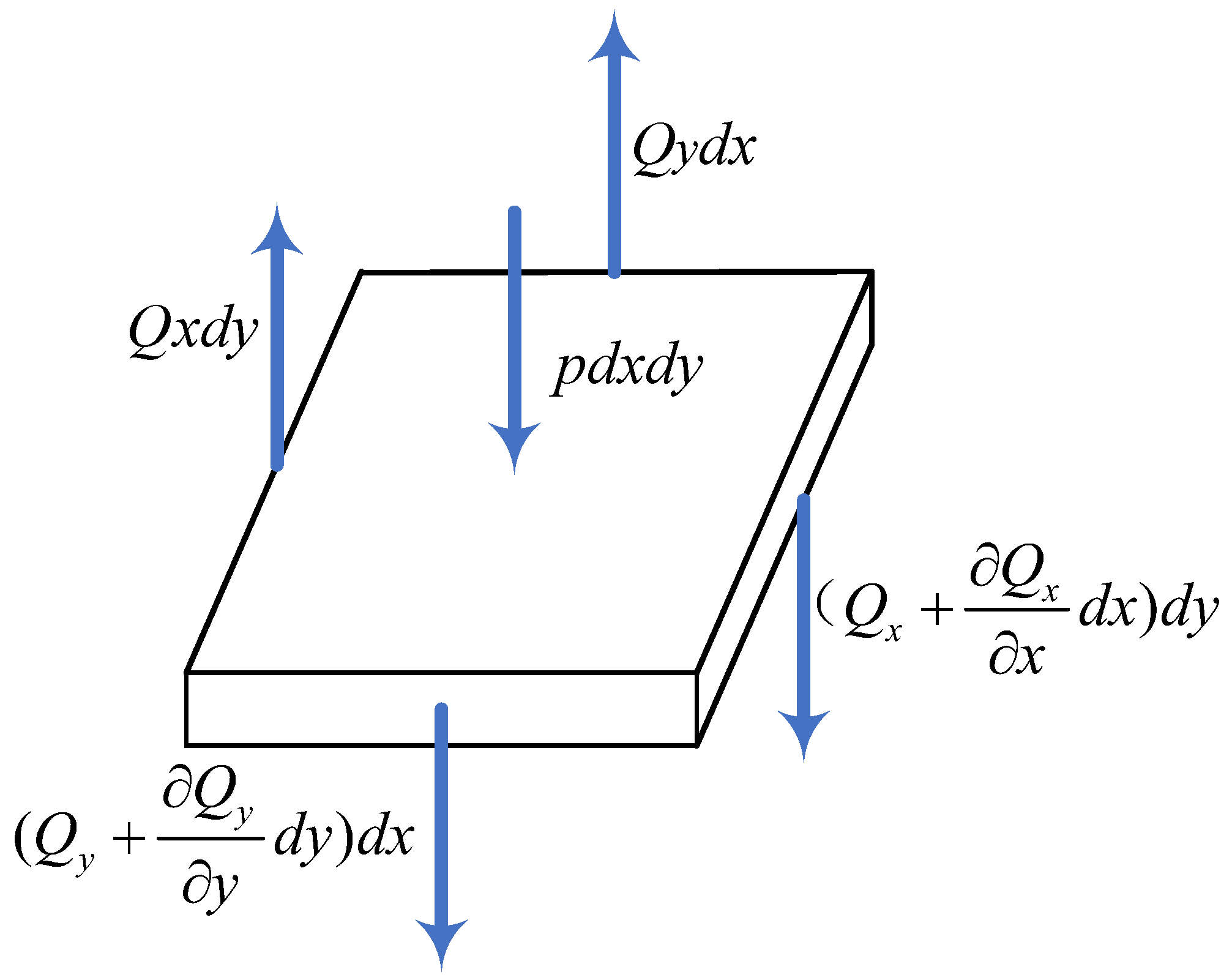
with $D=\frac{E{h}^3}{12(1-{\upsilon }^2)}$ is the Bending Stiffness, which is related to the structural and material properties of thin plates. Set the inertia force along the z axis as $-\rho h\frac{{\partial }^{2}w}{\partial t^2}$. For arbitrary micro cuboid with sizes of dx-dy, unit length shear force along z-axis that on the cross-section with x, y axes are $Q_y,Q_x$ respectively. On the basis of D’Alembert’s principle, $\sum F_z=0$, that is force balance in the z-axis direction, and the stress diagram is shown in Figure 2. Consequently,

$$\begin{array}{c}\left[(Q_x+\frac{\partial Q_x}{\partial x}dx)-Q_x\right]dy+\left[(Q_y+\frac{\partial Q_y}{\partial y}dy)-Q_y\right]dx+\left[p(x,y,t)-\rho h\frac{{\partial }^{2}w}{\partial t^2}\right]dxdy=0\hfill \end{array}$$

(4)

with p(x, y, t) the external load.

Similarly, force balance in the x-axis and y-axis direction satisfy the $\sum F_x=0$, $\sum F_y=0$. Consequently,

$$\left\{\begin{array}{c}{Q}_x=\frac{\partial M_y}{\partial x}+\frac{\partial M_{xy}}{\partial y}\hfill \\ Q_y=\frac{\partial M_x}{\partial y}+\frac{\partial M_{yx}}{\partial x}\hfill \end{array}\right.$$

(5)

Substitute Equation (5) into Equation (4), as a result

$$\frac{{\partial }^2{M}_y}{\partial x^2}+2\frac{{\partial }^2{M}_{xy}}{\partial x\partial y}+\frac{{\partial }^2{M}_x}{\partial y^2}+p(x,y,t)=\rho h\frac{{\partial }^{2}w}{\partial t^2}$$

(6)

Substituting Equation (3) into Equation (6), the vibration equation of the thin plate is

$$\rho h\frac{{\partial }^{2}w}{\partial t^2}+D{\nabla }^{4}w=p(x,y,t)$$

(7)

in which ${\nabla }^4$ is the double Laplace operator, defined as ${\nabla }^4={\nabla }^2\left({\nabla }^{2}w\right)$.

When p(x, y, t) = 0, Equation (7) is the basic equations of free vibration of thin plate. From the actual application point of view, more attention should be given to the forced vibration of the thin plate. When the external load is an ideal point source excitation located at the coordinate point $(x_0,y_0)$, a two-dimensional Dirac function is introduced to the vibration equation, which is defined as

$$\delta (x-x_0,y-y_0)=\left\{\begin{array}{c}\infty ,(x=x_0,y=y_0)\hfill \\ 0,\mathrm{other}\mathrm{domain}\hfill \end{array}\right.$$

(8)

with $\int \int (x-x_0,y-y_0)dxdy=1.$

The forced vibration equation of thin plate excited by a point source is described as

$$\rho h\frac{{\partial }^{2}w}{\partial t^2}+D{\nabla }^{4}w=p(x,y,t)\delta (x-x_0,y-y_0)$$

(9)

Substituting $p(x,y,t)=P(x,y;\omega )e^{-i\omega t}$, $w(x,y,t)=W(x,y;\omega )e^{-i\omega t}$ into Equation (9). The forced vibration equation independent of time is obtained as

$$({\nabla }^4-\frac{\rho h{\omega }^2}{D})W(x,y;\omega )=\frac{{\omega }^2}{D}P(x,y;\omega )\delta (x-x_0,y-y_0)$$

(10)

For a linear operator L, the response under the action of the point source is Green’s function, i.e., $LG=\delta$. Thus, the vibration response of Equation (10) can be solved by convolution G*P. As a result

$$W(x,y;\omega )=G(x,y;\omega )\ast \frac{{\omega }^2}{D}P(x,y;\omega )\delta (x-x_0,y-y_0)$$

(11)

in which the eigenmode expansion of the Green’s function is

$$G(x,y;\omega )=\sum _n\frac{{\Phi }_n^{*}(x_0,y_0)·{\Phi }_n^{}(x,y)}{{{\lambda }_n}^2-{\lambda }_{}^2}$$

(12)

When it comes to a square thin plate with side length $0<x=y<l$, the eigenmode is expressed as

$${\Phi }_{n_1{n}_2}^{}(x,y)=\frac{2}{l}cos(\frac{n_1\pi }{l}x)cos(\frac{n_2\pi }{l}y)$$

(13)

with the eigenvalues ${\lambda }_{n_1{n}_2}=\frac{\pi }{l}\sqrt{(n_1^2+n_{{}_2}^2)}$, $n_1,n_2=1,2,3,\dots$ Accordingly, considering the convolution-invariant property of impulse function and the scaling properties, the response of forced vibration thin plate is derived as

$$\begin{array}{c}W(x,y;\omega )=G(x,y;\omega )\ast \frac{{\omega }^2}{D}P(x,y;\omega )\delta (x-x_0,y-y_0)\hfill \\ =G(x,y;x_0,y_0,\omega )·P(x_0,y_0;\omega )\hfill \\ =P(x_0,y_0;\omega )\frac{{\omega }^2}{D}{\left(\frac{2}{l}\right)}^2{\displaystyle \sum _{n_1{n}_2}}\frac{cos\left(\frac{n_1\pi }{l}{x}_0\right)cos\left(\frac{n_2\pi }{l}{y}_0\right)cos\left(\frac{n_1\pi }{l}x\right)cos\left(\frac{n_2\pi }{l}y\right)}{{{\lambda }_n}^2-{\lambda }_{}^2}\hfill \end{array}$$

(14)

From the response function in Equation (14), the forced vibration of a thin plate is closely related to the material and geometric properties of the plate under the excitation of a specific frequency signal, in addition, the amplitude of the excitation signal. It is evidently ascertained that the deflection surface is symmetrical about the $x=\frac{l}{2}$ axis and $y=\frac{l}{2}$ axis. Concurrently, the positive, negative, and zero values of vibration response $W(x,y;\omega )$ are obtained respectively at different positions on the thin plate, which will cause the varying vibration modes. The proposed mathematical model is suitable for the square thin plate characterized by the side length l and thickness h. When it comes to various plate material, the Bending Stiffness, Young’s modulus, Poisson’s ratio and density can be adjusted accordingly.

3. Finite Element Simulation Analysis

The finite element method plays a vital role in many fields such as modern structural mechanics, thermodynamics and hydrodynamics, which is an effective numerical analysis method. Using finite element method, a continuous medium will be discretized into several simple basic geometric elements realized by meshing, which are interconnected via nodes.

Comsol Multiphysics version 5.6 simulation application is used to analyze the thin plate vibration. The geometric model of the thin plate is modeled under the 2D Structural Mechanics-Plate Module. The governing equation in Structural Mechanics is

$$M\ddot{u}+C\dot{u}+Ku=f\left(t\right)$$

(15)

where $M\ddot{u}$ represents the inertia force, $C\dot{u}$ is the viscous force, $Ku$ indicates the elastic force, and is the load. In detail, M, C, K are mass matrix, damping matrix, and stiffness matrix, u is the midplane displacement. Essentially, the equilibrium differential equation in Equation (15) has a curious coincidence with Equation (4) in Section 2, which indicates the relationship between mid-plane displacement and force balance. Moreover, the frequency domain form for Equation (15) is

$$(-{\omega }^{2}M+i\omega C+K)u=f$$

(16)

Especially when $C=0$, $f=0$, the corresponding equation expresses the undamped free vibration for a thin plate.

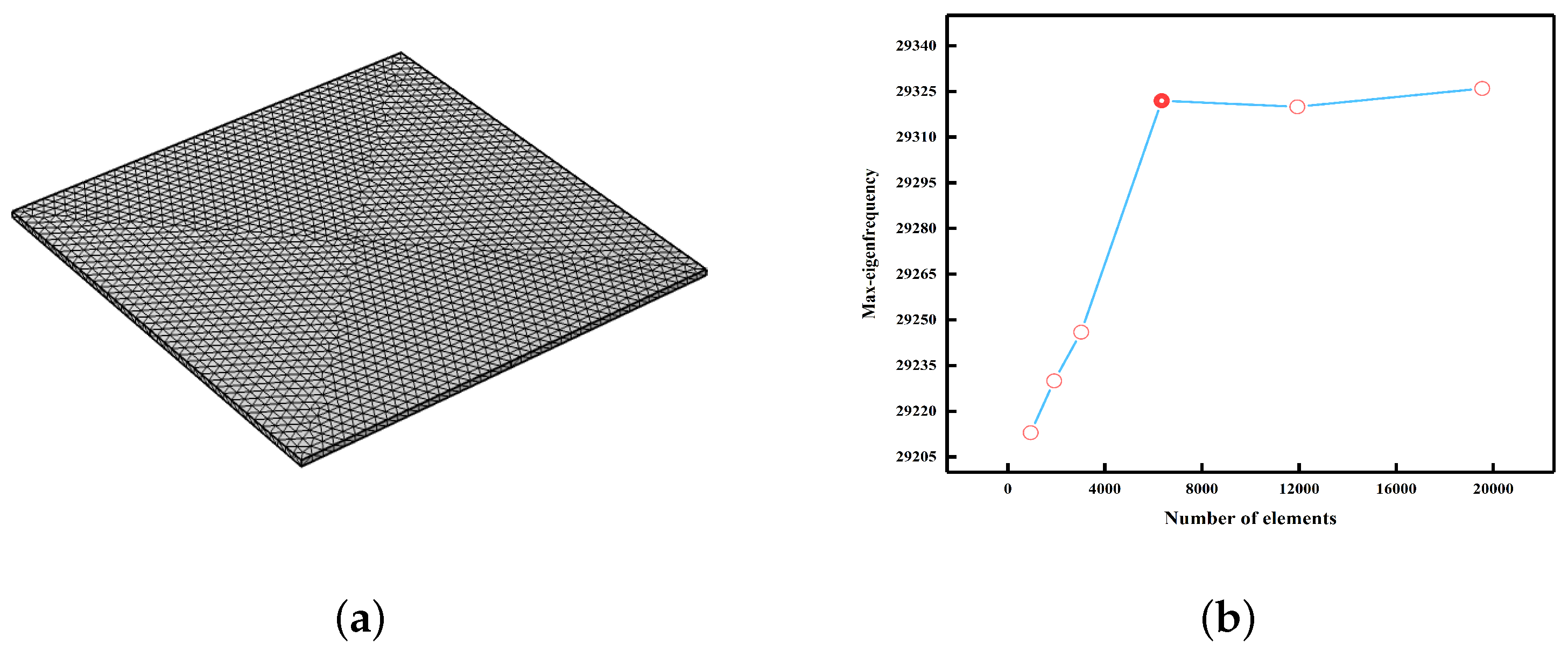
In simulation environment, the thin plate geometry is a square of length 0.05 m, thickness 0.625 mm, and the corresponding mesh is set as physics-controlled with a setting of Hyperfine, which contains 6342 elements for full plate. This geometry was modeled using Silicon, which has a density of 2329 kg/m${}^3$, Young’s modulus of $170\times {10}^9$ Pa, and a Poisson’s ratio of 0.28. Square plate with mesh is shown in Figure 3a. Mesh convergence is studied based on the maximum eigenfrequency. When the change of the solution obtained by further subdividing the grid can be ignored, it can be said that the grid has converged. Figure 3b shows the maximum eigenfrequency versus the number elements, and mesh convergence was obtained for about 6342 mesh elements [31].

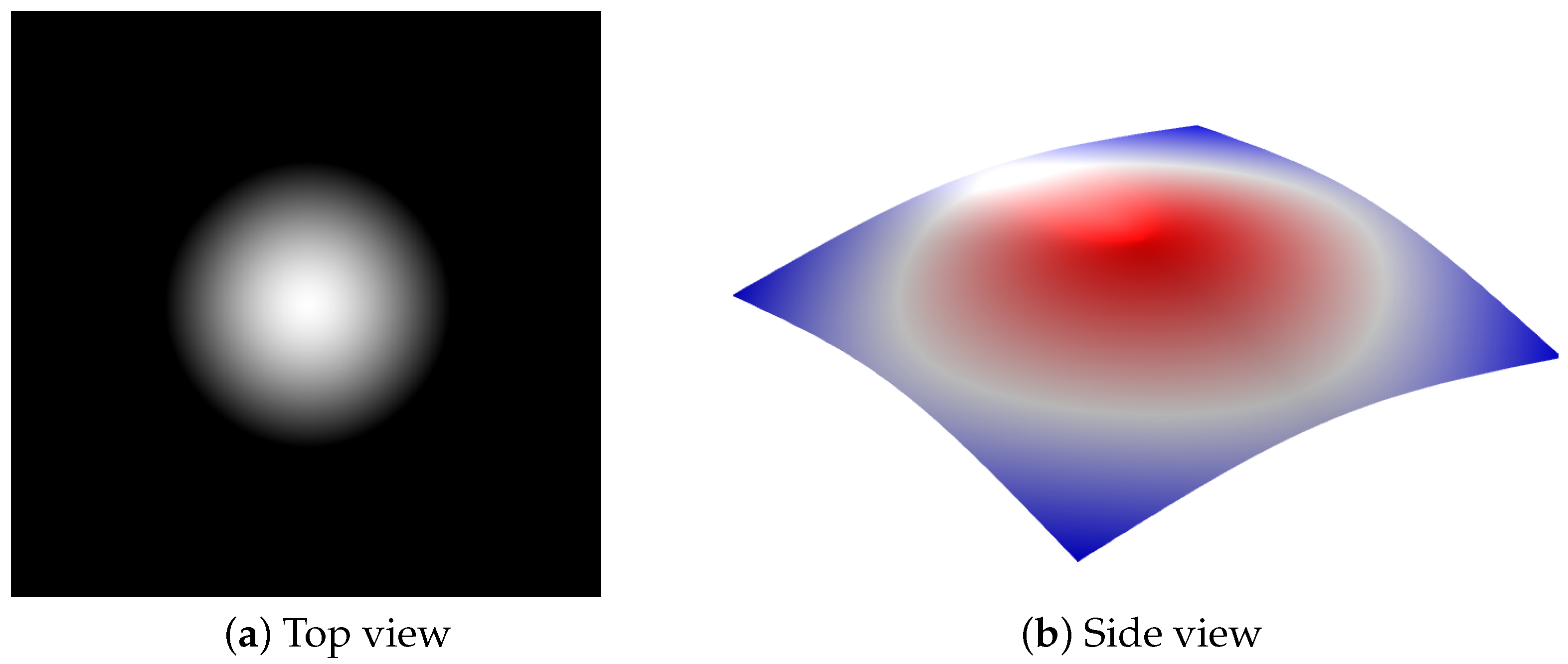
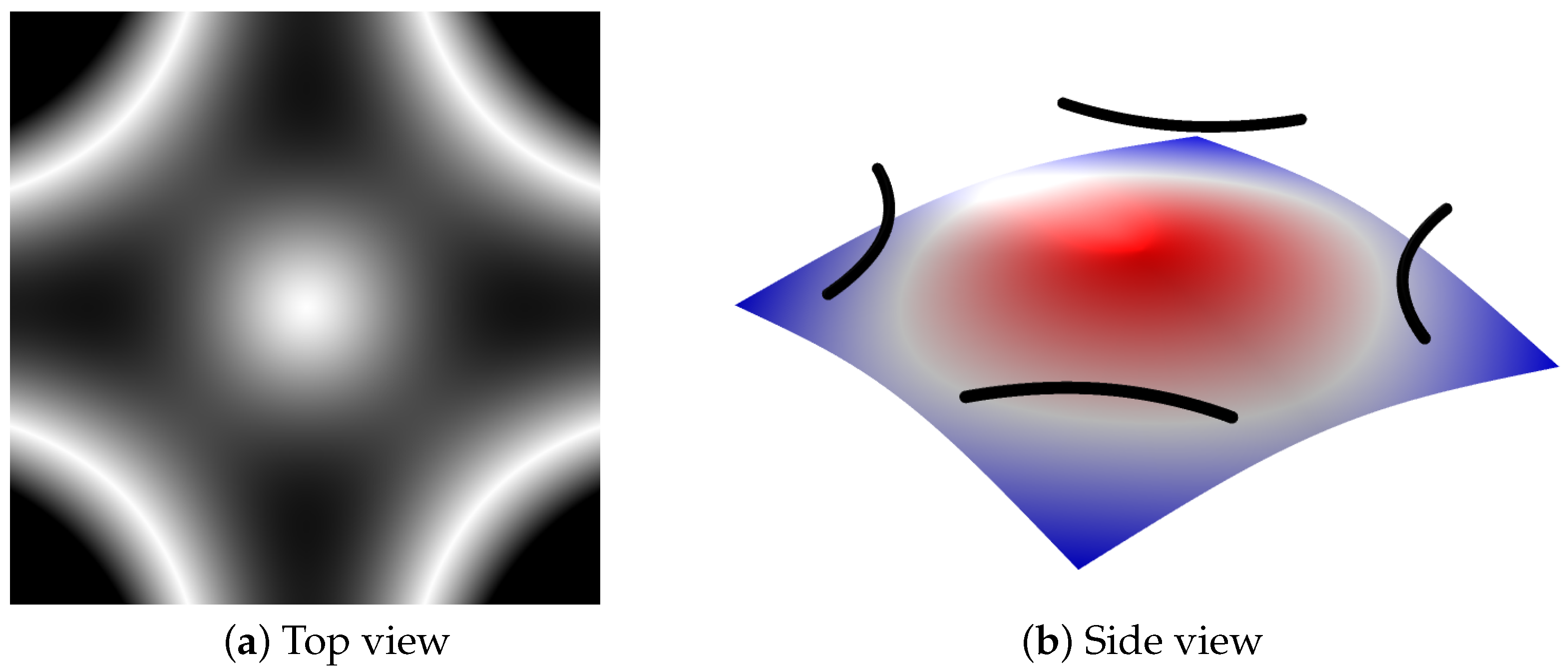
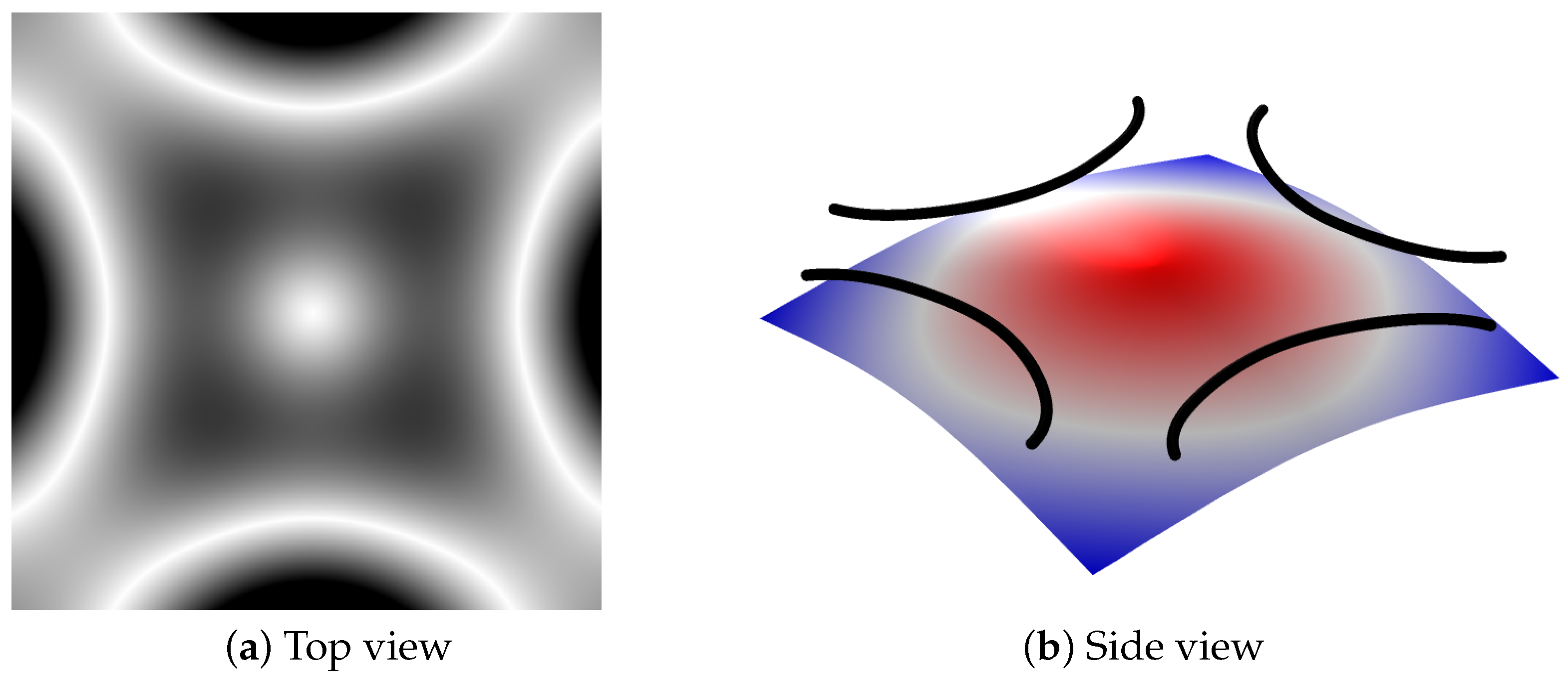
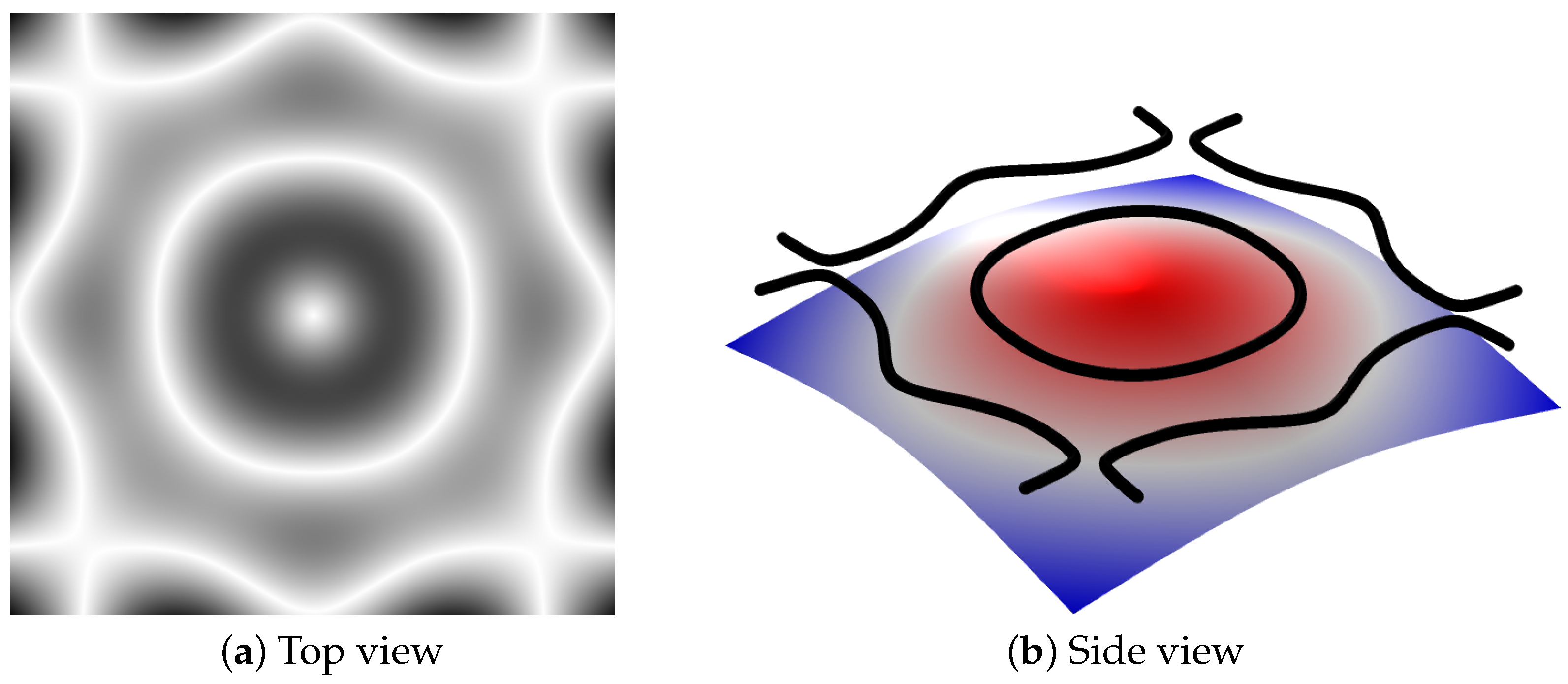
The vibration modes of the thin plate with different driving frequencies are obtained under the study of eigenfrequencies solver by Comsol Multiphysics with 39,084 iterations, and the first six vibration modes are shown in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 from the top view and the side view.

In fact, from the theory of eigenvalues in Section 2, there are infinite eigenfrequencies, which means infinite modes can be found. In the top view of vibration modes, the bright white curves and areas refer to the position with zero displacement or smaller ones where the particle matter will be located during the vibration experiment based on the hardware plate. The red and blue areas in the side view, respectively, indicate the positive and negative displacement, and the resulted vibration mode is outlined by black curve outlines that can correspond to the top view one by one. As we can see, the vibration modes are patterns that are symmetrical about the central axis, which is in line with the conclusion of theoretical analysis. On the other hand, when exciting the thin plate using an ideal point source, according to the distribution of generated sound pressure, the position with lower sound pressure will generate node lines that are consistent with the vibration mode. More intriguingly, one can observe that the vibration patterns are becoming more complex with gradually increase of driving frequencies.

4. Experimental Results

4.1. Vibration Mode Experiment

At first, we will introduce the experimental platform shown in Figure 10. In which, a piezoelectric actuator is sticked at the bottom center of the thin plate (5 cm × 5 cm × 0.625 mm). A sinusoidal acoustic signal generator is built using LABVIEW, which is accepted by the acquired card (USB-6363) and then is sent to actuator via amplifier. Directly above the thin plate, a high-definition camer (P67-C1911) is fixed to collect particle dynamics on the thin plate.

Solid sand is used for making patterns of the vibration mode of the thin plate. Three sizes of solid sand particles are prepared for reflecting the vibration mode. Smaller and larger sand particles will be motionless or bouncing falling of the sheet, separately, neither has a good display effect. After test and verification, for a better presentation effect, sand particles with an average diameter of 0.085 mm were used in the experiment. Two axis sliding table and column level measuring instrument are used to adjust and measure the levelness of the thin plate. Firstly, sprinkle the solid sand particles on the thin plate (as shown in Figure 11) and then change the frequencies of the sine wave signal generator until a stable pattern is formed. Record the vibration mode of the thin plate with a camera. Different modes resulted from sand particles on the surface of thin plate will be generated under the excitation of different frequencies.

Experiments are performed on the square thin silicon plate, and the various vibration modes are obtained on the plate with different shapes at the various frequency. During the experiment, when the thin plate is excited, some areas will vibrate while others will not. More specifically, one can see standing waves along the nodal line of the plate that generated by excitation source. Sand particles move from the antinode with the largest amplitude of standing wave to the nodal line with the lowest and zero amplitude of standing wave, forming a beautiful symmetrical pattern. Coming back to the response of forced vibration in Section 2, the symmetry of patterns and the various values of deflection at different positions of the thin plate result in different vibration modes, which can be fully verified in the experimental process. The frequency was resized according to eigenfrequencies in Section 3 (1140.6 Hz, 4685.6 Hz, 8925.9 Hz, 14,442 Hz, 22,688 Hz, 29,322 Hz) by sine wave signal generator built with LabVIEW and obtain the vibration modes of square thin plate.

From the comparison of simulation results in Section 3 and experimental results in Section 4.1, the experimental vibration modes in Figure 12 correspond well with the simulation results in Section 3, and become more and more complex as the frequency gets higher. This is because, as the excitation frequency increases, more nodal lines will be generated on the thin plate. Successful visualization of vibration mode indicates that the displacement field can be effectively established with the help of the experimental platform to manipulate micro targets.

On the other hand, the error between the results of experimental and numerical simulations can’t be ignored. The essence of a thin plate vibration simulation and experiment is to determine the node line corresponding to a certain characteristic frequency. Therefore, the node line area of plate vibration simulation and experiment can be regarded as an error index. The relative error equation is defined as

$$E=\frac{\left|S_s-S_e\right|}{S_s}\%$$

(17)

where, $S_s$(cm${}^2$) is the node-line area in simulation results, $S_e$(cm${}^2$) is the node-line area in experimental results. According to the simulation and experimental results, we reported the area change of node line in simulation and experiment in Figure 13a. Consequently, the report of error between experiment and simulation is shown as the histogram Figure 13b. Future work, efforts should be made to reduce errors.

4.2. Single Particle Control

The proposed experimental platform in this paper is expected to manipulate micro and nano particles without contact due to its its micro characteristics and good compatibility. In this sub-section, we try to control the motion of individual particles on the thin plate based on the specific acoustic excitation frequency. Combined with theoretical analysis, finite element simulation and experimental verification, the effective frequencies can be obtained. Meanwhile, the effective acoustic excitation frequency can be used to realize the control of particle motion on thin plate. The mechanism of motion behind the single particle control is that the particle placed on the any position or antinode of the excited thin plate will move towards the position of the node line of the plate and locate there.

For the purpose of demonstrating the motion control of a single particle, the single particle with diameter of 0.08 mm is placed on the thin plate as is shown in Figure 14. According to one of the vibration mode experiment, the movement trend of the particle can be preliminarily judged (f = 7602.6 Hz). Video screenshots of particle motion are presented to illustrate the results of particle motion control. Before the frequency excitation, the particle is located in the position S of the plate, as is shown in Figure 14a. From Figure 14c, after frequency excitation, the particles finally stabilize at the position T of the plate. Figure 14b records the position of particle during frequency excitation. As an example, the motion control of a single particle from position S to position T is realized in Figure 14 based on the experimental platform. For the further step, we will focus on more complex particle motion control based on the thin plate system.

5. Discussion

Acoustic technology is an novel micro-nano manipulation method. Hence, acoustic vibration theory and acoustic control platform are all eager to be studied and developped. Especially, the effectiveness and operability of the experimental platform also need to be verified by experiments.

In this paper, we present an acoustic manipulation platform (shown in Figure 9). The plate size is only 5 cm × 5 cm × 0.625 mm, whcih is suitable for the target of micro nano size. Piezoelectric actuator drvien by sinusoidal acoustic signal provides effective exciting force for the platform. At beginning, the vibration problem of thin plate driven by acoustic wave has been solved, ulteriorly, Comsol Multiphysics version 5.6 is used to design and simulation the thin plate vibration mode. The vibration mode experiments of thin plate correspond perfectly with the software simulation results. Based on the vibration modal simulation and experiment of thin plate, the control experiment of a single particle is carried out.

Acoustic manipulation technology is widely used in high tech material processing, 3D printing technology, particle trajectory tracking and particle separation. Further, thin plate systems still need to be improved and more complex and precise manipulation tasks are expected to be realized on the presented platform.

6. Conclusions

In this paper, starting from the stress analysis of thin plate, the response function of forced vibration of a thin plate is determined, combining with Green’s function and properties of convolution operation, and the basic properties of the response function are revealed. The presented mathematical model is applicable to a square thin plate with different material properties. Nextly, finite element simulation for the vibration of thin plate is performed based on the Comsol Multiphysics. The vibration modes of different eigenfrequencies are shown to illustrate the symmetry of the vibration modes and the complexity of vibration pattern with increasing frequency.

Moreover, the hardware platform for experimental manipulation is built and reported. The vibration experiments of a square thin plate driven by a central excitation source is carried out. The experimental results of the modes correspond well with the simulations by comparison, and single particle motion control is also realized using the hardware platform. Actually, the effective visualization of thin plate vibration modes using sand particles means the successful establishment of a thin plate displacement field under different frequency signals. In future work, the platform is considered to be a powerful manipulation tool in the fields of capture and manipulation for a micro-nano target.