A Reliability-Based Stochastic Traffic Assignment Model for Signalized Traffic Network with Consideration of Link Travel Time Correlations
Abstract
1. Introduction
2. Model Assumptions and Model Establishment
2.1. Model Assumptions
- (1)
- It is assumed that OD demand and link flow follow normal distribution [6].
- (2)
- (3)
- It is assumed that the variation coefficient of OD demand in the traffic network is the same as the variation coefficient of path flow.
2.2. Model Establishment
2.2.1. Probability Distribution of Traffic Flow
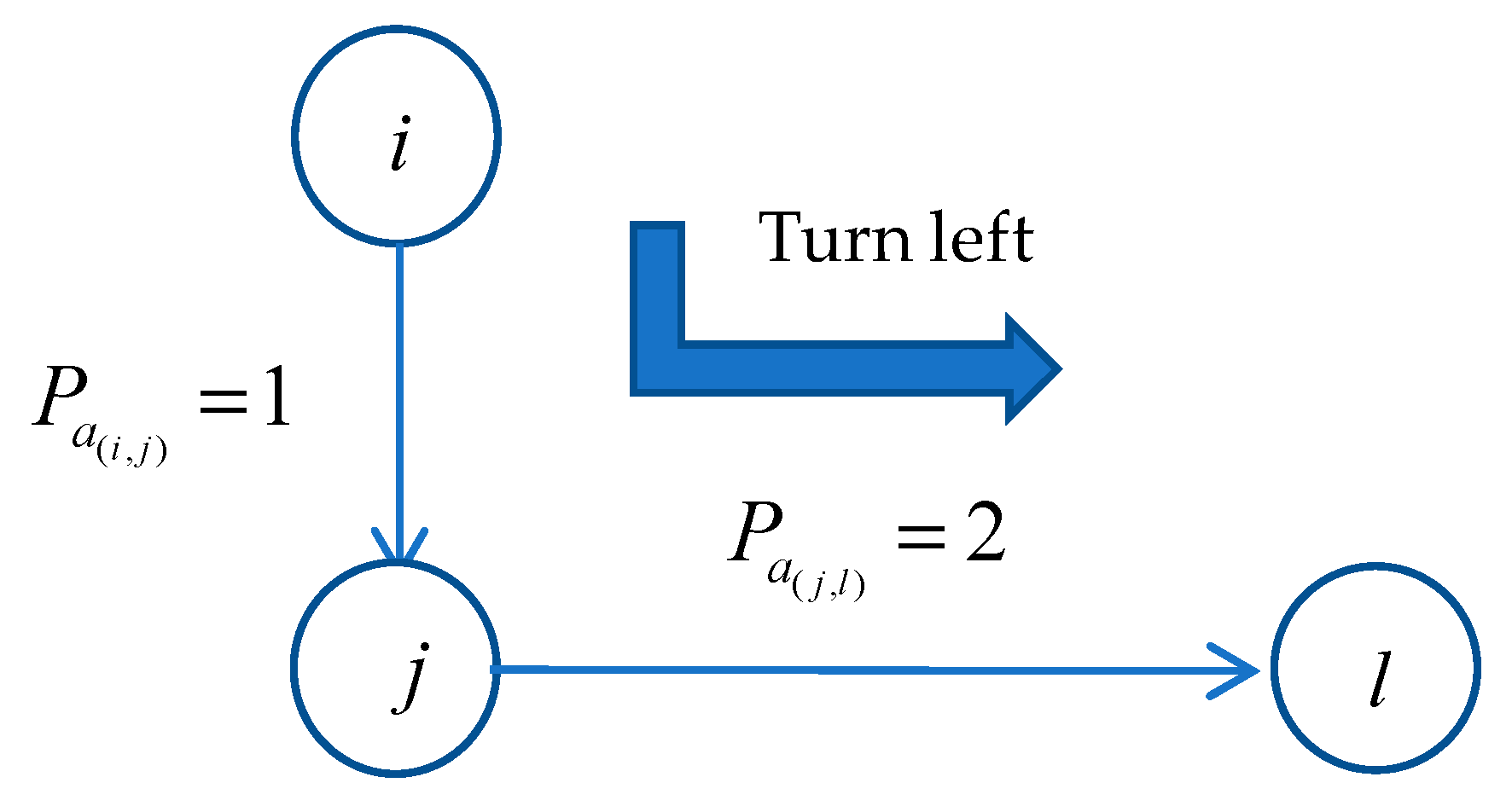
2.2.2. Probability Distributions of Link and Path Travel Time
2.2.3. Waiting Time at Signalized Intersections
2.2.4. The Path Effective Travel Time
3. Analysis of the Existence of Solutions
4. Algorithm Design
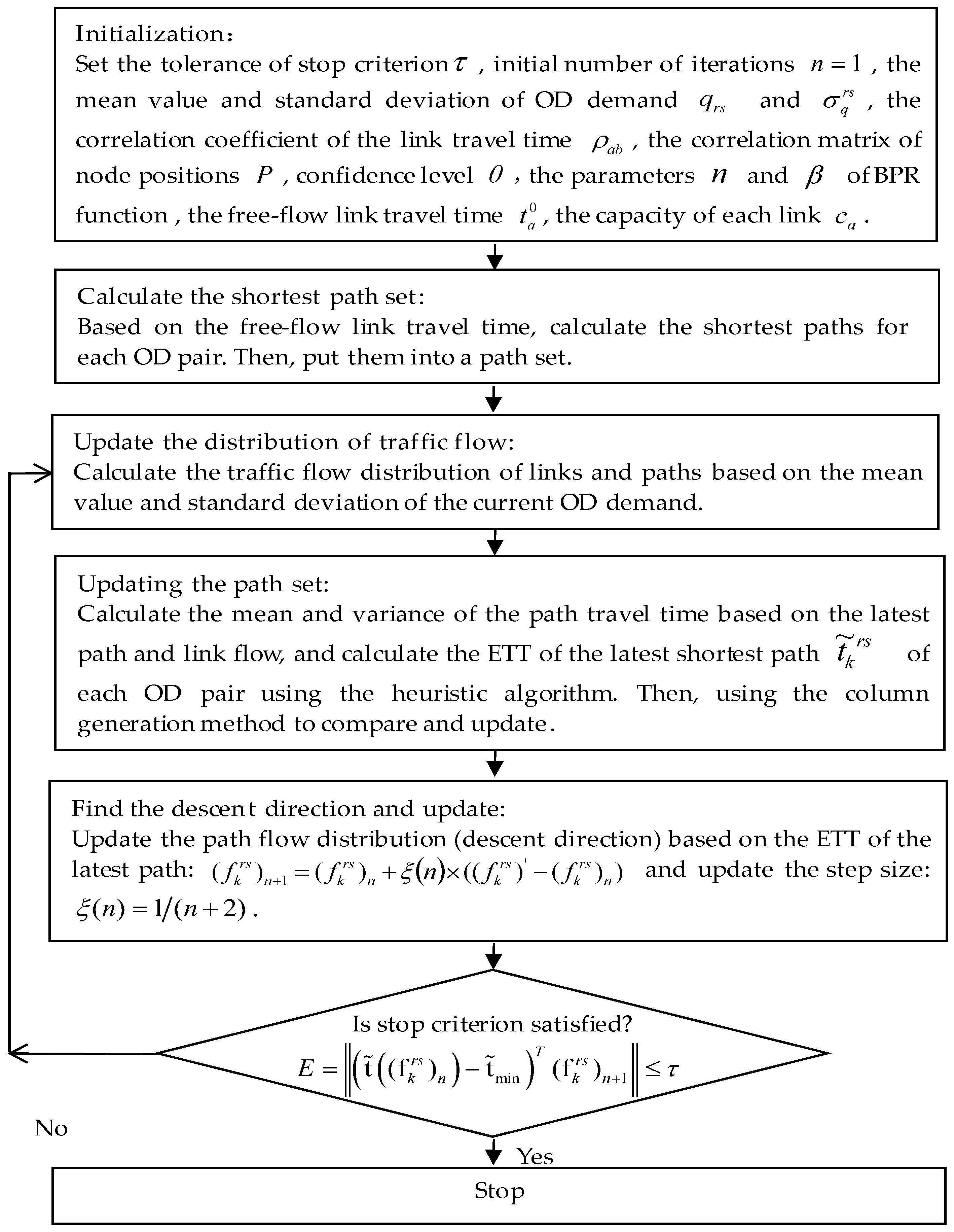
4.1. Algorithm Steps
4.2. The Flowchart of the Heuristic Algorithm
5. Numerical Examples
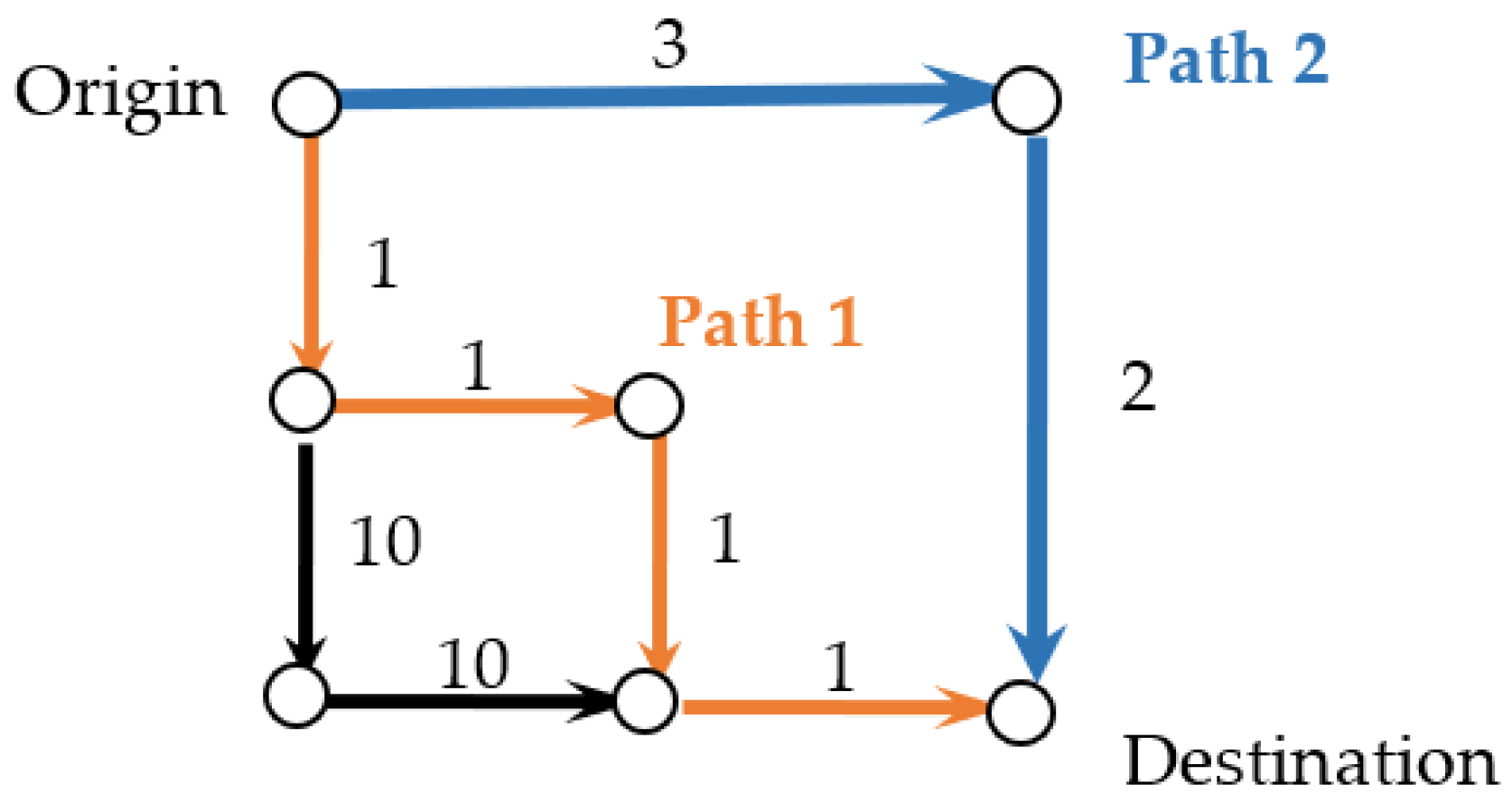
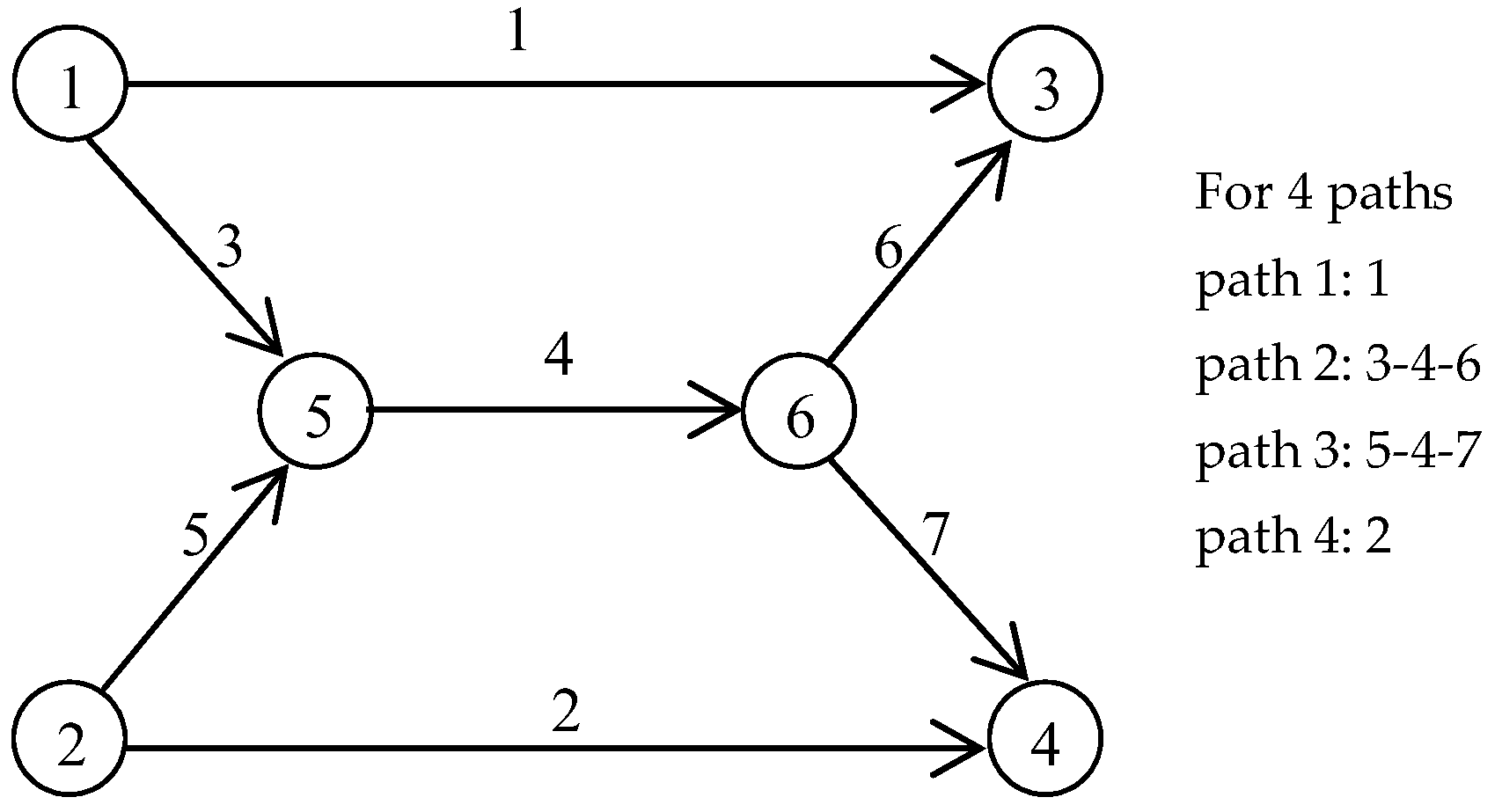
5.1. A Small Traffic Network
5.2. Analysis of Effective Travel Time
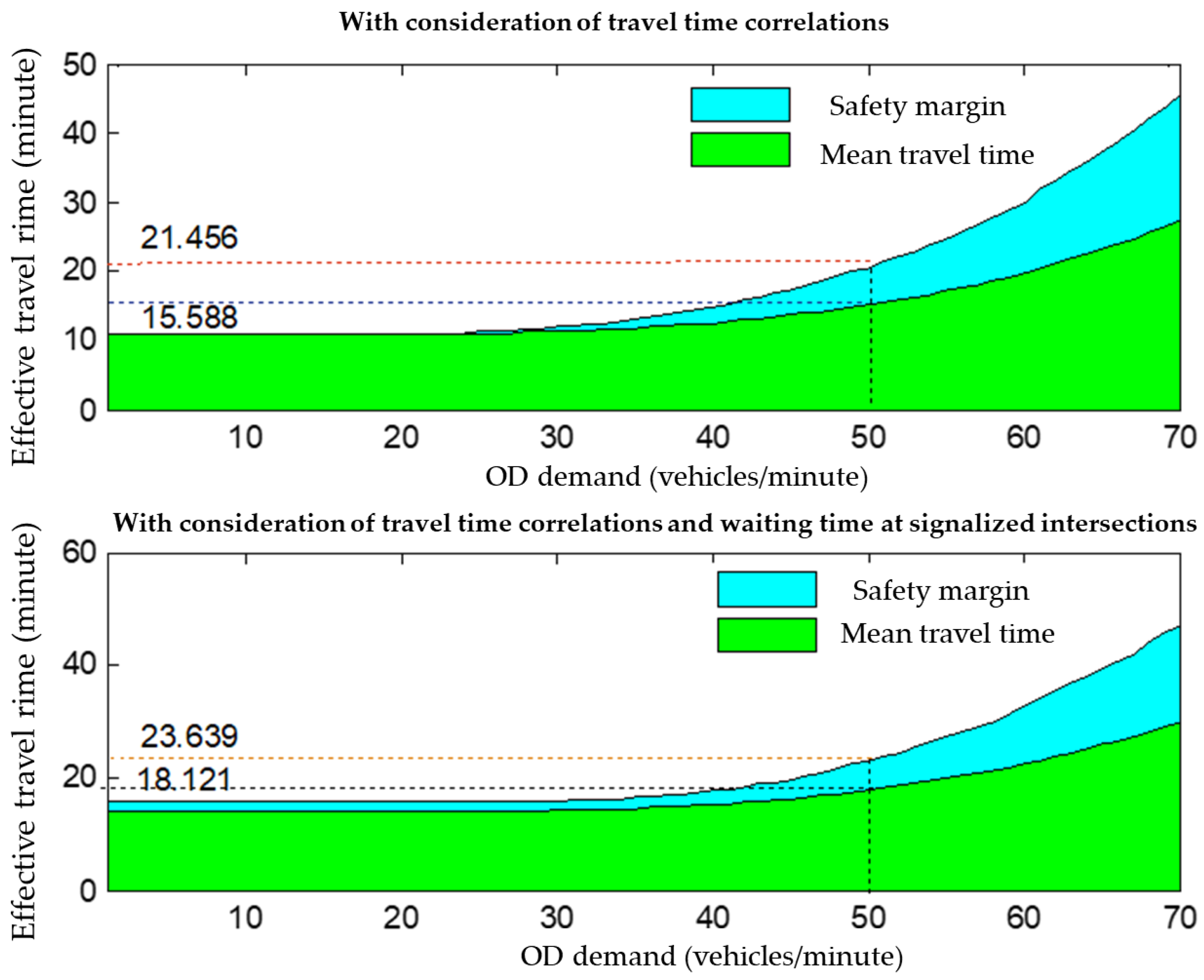
5.2.1. Comparisons between the Proposed Model and the Existing Models
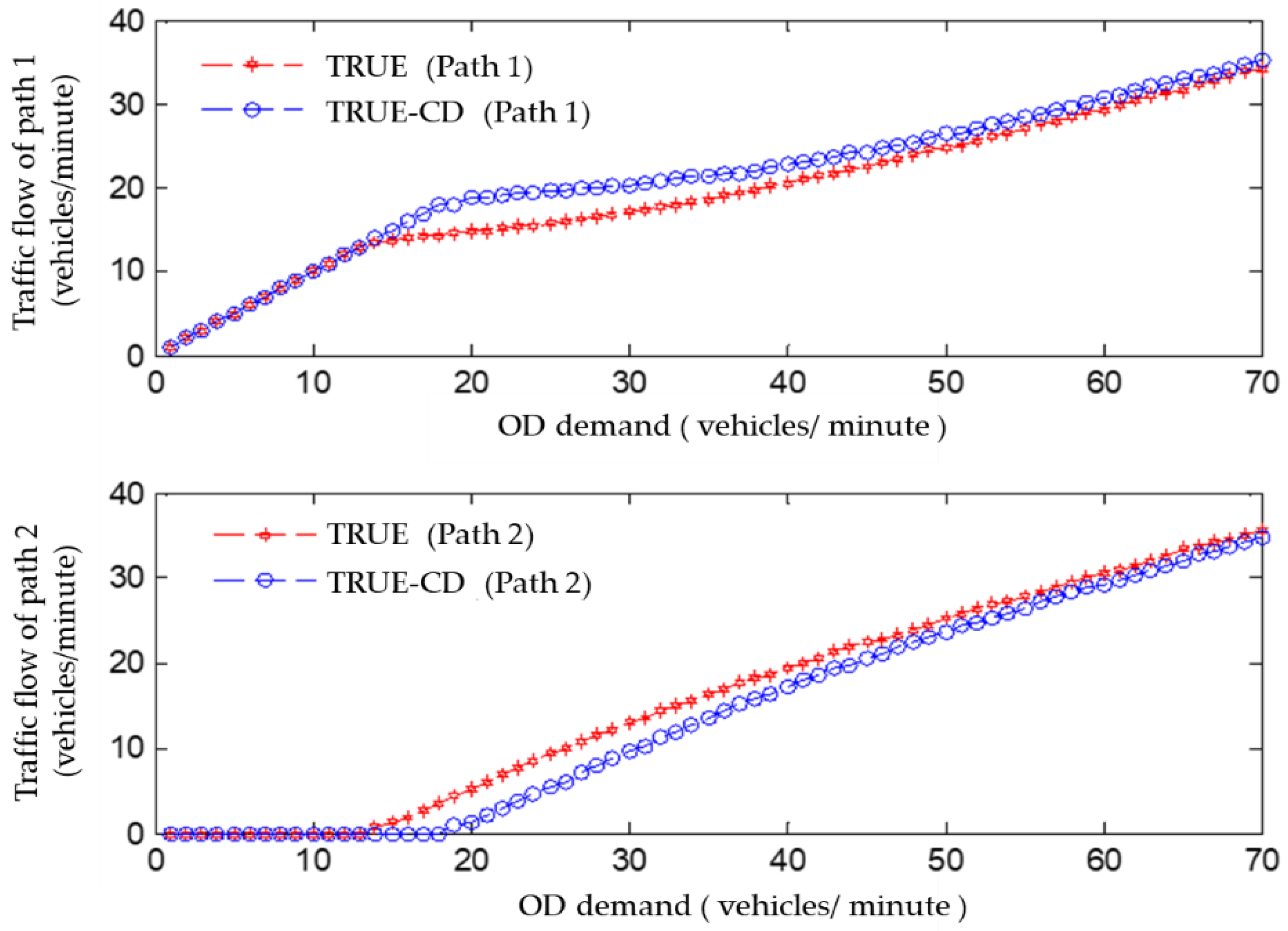
5.2.2. Comparison of Traffic Flow in TRUE and TRUE-CD Models
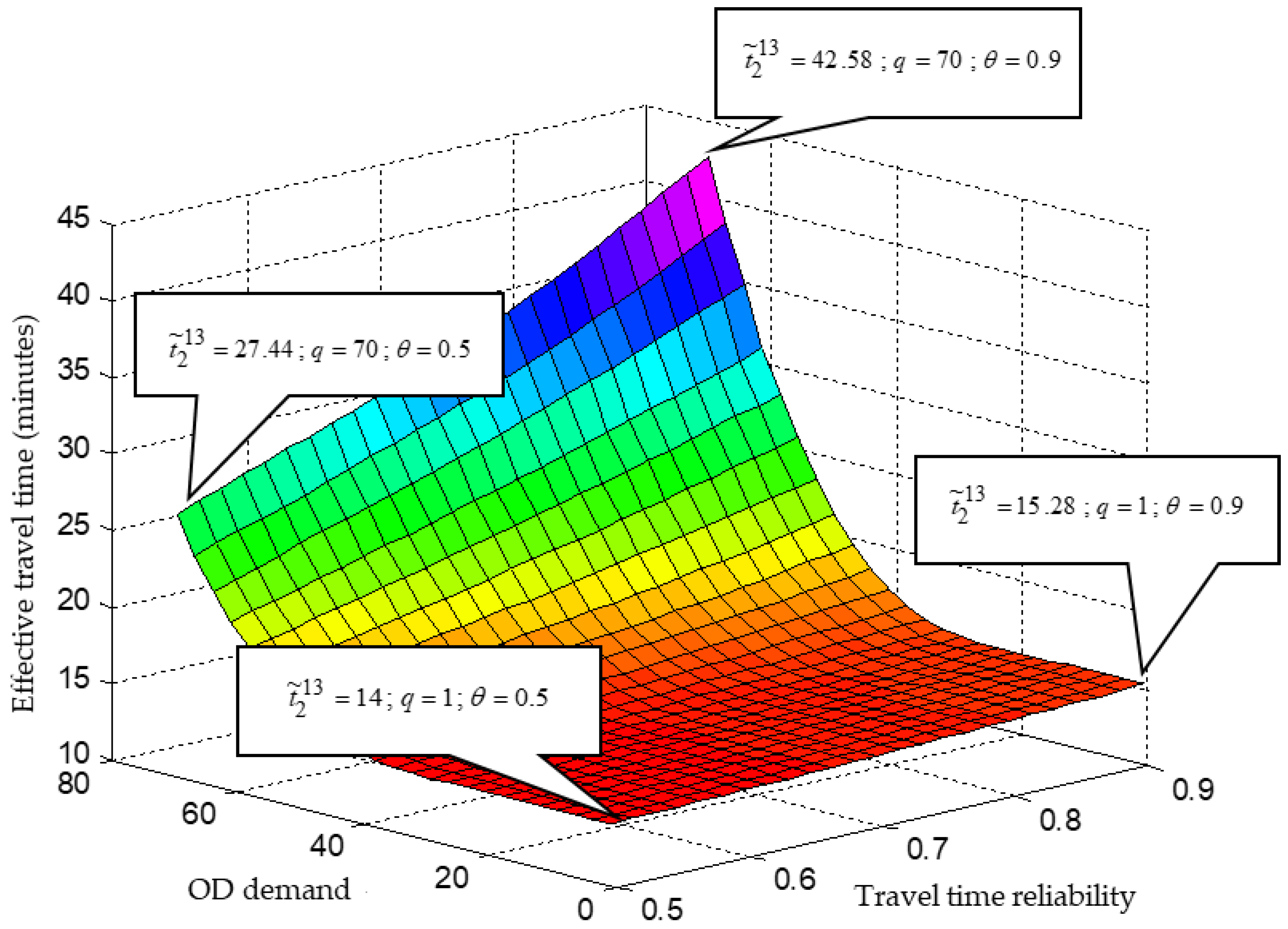
5.2.3. Effects of Different OD Demand and TTR on Effective Travel Time
5.3. A Medium-Sized Transportation Network
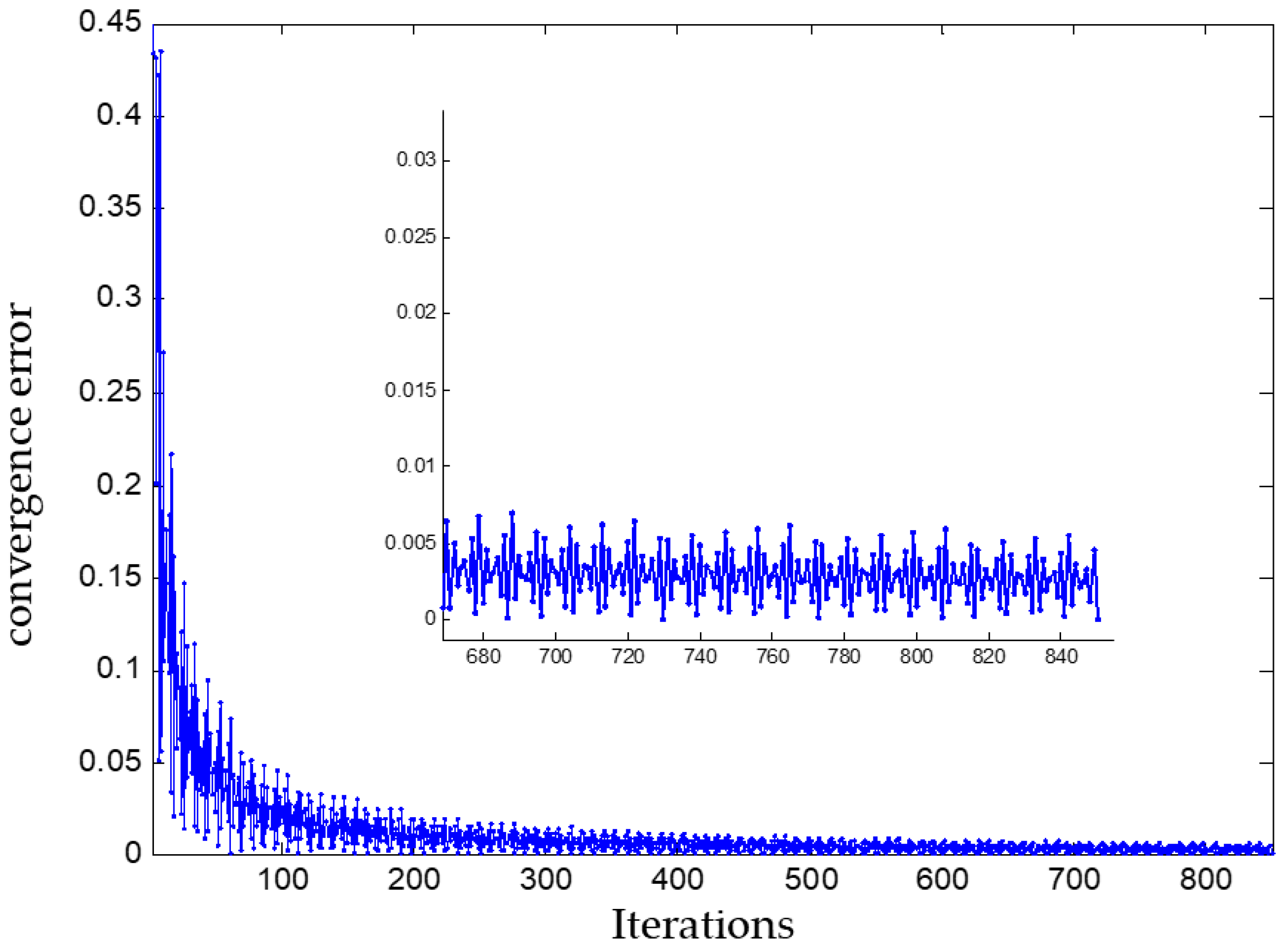
5.4. Algorithm Analysis
- (1)
- The first step of the algorithm in this paper is to input some basic parameters of the proposed model.
- (2)
- In the second step of the proposed algorithm, the shortest path algorithm (e.g., Dijkstra Algorithm) can be adopted to find the shortest path between each OD pair and put them into a path set under the condition of no traffic flow in transportation networks. The algorithm complexity of this step is .
- (3)
- The traffic flow of the OD pair is allocated to the set of paths obtained in the second step with the all-or-nothing criterion in the third step of the proposed algorithm.
- (4)
- (5)
- In the fifth and sixth steps, the MSA algorithm and Equations (36) and (37) are used to update the step size and iterative direction. According to previous studies [32], it can be found that the MSA algorithm is a forced convergence algorithm.
- (6)
- The stopping criterion is shown in the seventh step in order to determine when to stop the iteration of the proposed algorithm.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lo, H.K.; Tung, Y.K. Network with degradable links: Capacity analysis and design. Transp. Res. Part B 2003, 37, 345–363. [Google Scholar] [CrossRef]
- Lo, H.K.; Luo, X.W.; Siu, B.W.Y. Degradable transport network: Travel time budget of travelers with heterogeneous risk aversion. Transp. Res. Part B 2006, 40, 792–806. [Google Scholar] [CrossRef]
- Chen, A.; Yang, H.; Lo, H.K.; Tang, W.H. Capacity reliability of a road network: An assessment methodology and numerical results. Transp. Res. Part B 2002, 36, 225–252. [Google Scholar] [CrossRef]
- Asakura, Y.; Kashiwadani, M. Road network reliability caused by daily fluctuation of traffic flow. Eur. Transp. Highw. Plan. 1991, 19, 73–84. [Google Scholar]
- Clark, S.; Watling, D. Modeling network travel time reliability under stochastic demand. Transp. Res. Part B 2005, 39, 119–140. [Google Scholar] [CrossRef]
- Shao, H.; Lam, W.H.K.; Tam, M.L. A reliability-based stochastic traffic assignment model for network with multiple user classes under uncertainty in demand. Netw. Spat. Econ. 2006, 6, 173–204. [Google Scholar] [CrossRef]
- Zeng, W.L.; Miwa, T.; Wakita, Y.; Morikawa, T. Application of Lagrangian relaxation approach to -reliable path finding in stochastic networks with correlated link travel times. Transp. Res. Part C 2015, 56, 309–334. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Shen, Z.J.M.; Song, S.J. Lagrangian relaxation for the reliable shortest path problem with correlated link travel times. Transp. Res. Part B 2017, 104, 501–521. [Google Scholar] [CrossRef]
- Shen, L.; Shao, H.; Wu, T.; Lam, W.H.K.; Zhu, E.C. An energy-efficient reliable path finding algorithm for stochastic road networks with electric vehicles. Transp. Res. Part C 2019, 102, 450–473. [Google Scholar] [CrossRef]
- Shen, L.; Shao, H.; Wu, T.; Fainman, E.Z.; Lam, W.H.K. Finding the reliable shortest path with correlated link travel times in signalized traffic networks under uncertainty. Transp. Res. Part E 2020, 144, 102159. [Google Scholar] [CrossRef]
- Cantarella, G.E. A general fixed-point approach to multi-mode multi-user equilibrium assignment with elastic demand. Transp. Sci. 1997, 31, 107–128. [Google Scholar] [CrossRef]
- Xiong, Z.H.; Shao, C.F. Evaluation on the travel trait of road network under day-to-day stochastic demand-travel time reliability. J. Transp. Eng. Inf. 2006, 4, 40–44. (In Chinese) [Google Scholar]
- Kuang, A.W.; Huang, Z.X. On the Service Reliability in Stochastic Supply and Demand. Syst. Eng. 2007, 25, 25–30. (In Chinese) [Google Scholar]
- Cheng, L.; Li, Q.; Wang, J. Urban street network capacity reliability. J. Southeast Univ. 2004, 20, 235–239. [Google Scholar]
- Cantarella, G.E.; de Luca, S.; Cartenì, A. Stochastic equilibrium assignment with variable demand: Theoretical and implementation. Eur. J. Oper. Res. 2015, 241, 330–347. [Google Scholar] [CrossRef]
- Cantarella, G.E.; de Luca, S.; Di Gangi, M.; Di Pace, R. Approaches for solving the stochastic equilibrium assignment with variable demand: Internal vs. external solution algorithms. Optim. Methods Softw. 2015, 30, 338–364. [Google Scholar] [CrossRef]
- Chen, Q.; Pan, S.L. Direct formulation and algorithms for the probit-based stochastic user equilibrium traffic assignment problem. Transp. Plan. Technol. 2017, 40, 757–770. [Google Scholar] [CrossRef]
- Han, L.H.; Sun, H.J.; Wang, D.Z.W.; Zhu, C.J. A stochastic process traffic assignment model considering stochastic traffic demand. Transp. B Transp. Dyn. 2018, 6, 169–189. [Google Scholar] [CrossRef]
- Xu, J.X.; Guo, J.N.; Zhang, J. Research on traffic assignment model and algorithm based on cumulative prospect theory under uncertain factors. Transp. Res. Rec. 2021, 2675, 116–134. [Google Scholar] [CrossRef]
- Chen, A.; Zhou, Z. The alpha-reliable mean-excess traffic equilibrium model with stochastic travel times. Transp. Res. Part B 2010, 44, 493–513. [Google Scholar] [CrossRef]
- Wang, J.Y.T.; Ehrgott, M.; Chen, A. A bi-objective user equilibrium model of travel time reliability in a road network. Transp. Res. Part B 2014, 66, 4–15. [Google Scholar] [CrossRef]
- Shen, L.; Shao, H.; Li, C.J.; Sun, W.W.; Shao, F. Modeling stochastic overload delay in a reliability-based transit assignment model. IEEE Access 2019, 7, 3525–3533. [Google Scholar]
- Levin, M.W.; Duell, M.; Waller, S.T. Arrival time reliability in strategic user equilibrium. Netw. Spat. Econ. 2020, 20, 803–831. [Google Scholar] [CrossRef]
- Wang, S.; Lu, J.; Jiang, L.P. Time reliability of the maritime transportation networks for China’s crude oil imports. Sustainability 2020, 12, 198. [Google Scholar] [CrossRef]
- Jenelius, E.; Koutsopoulos, H.N. Travel time estimation for urban road networks using low frequency probe vehicle data. Transp. Res. Part B 2013, 53, 64–81. [Google Scholar] [CrossRef]
- Chen, B.Y.; Lam, W.H.K.; Li, Q.Q. Efficient solution algorithm for finding spatially dependent reliable shortest path in road networks. J. Adv. Transp. 2016, 50, 1413–1431. [Google Scholar] [CrossRef]
- Chen, A.; Subprasom, K.; Ji, Z.W. Mean-variance model for the build-operate-transfer scheme under demand uncertainty. Transp. Res. Rec. 2003, 1857, 93–101. [Google Scholar] [CrossRef]
- Srinivasan, K.K.; Prakash, A.A.; Seshadri, R. Finding most reliable paths on networks with correlated and shifted log-normal travel times. Transp. Res. Part B 2014, 66, 110–128. [Google Scholar] [CrossRef]
- Facchinei, F.; Pang, J.S. Finite-Dimensional Variational Inequalities and Complementarity Problems; Springer: New York, NY, USA, 2003. [Google Scholar]
- Dafermos, S. The general multimodal network equilibrium problem with elastic demand. Networks 1982, 12, 57–72. [Google Scholar] [CrossRef]
- Sheffii, Y. Urban Transportation Networks: Equilibrium Analysis with Mathematical Programming Models; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1985; pp. 18–104. [Google Scholar]
- Shao, H.; Lam, W.H.K.; Meng, Q.; Tam, M.L. Travel time reliability-based traffic assignment problem. J. Manag. Sci. China 2009, 12, 27–35. (In Chinese) [Google Scholar]
- Mao, X.H.; Wang, J.W.; Yuan, C.W.; Yu, W.; Gan, J.H. A dynamic traffic assignment model for the sustainability of pavement performance. Sustainability 2019, 11, 170. [Google Scholar] [CrossRef]

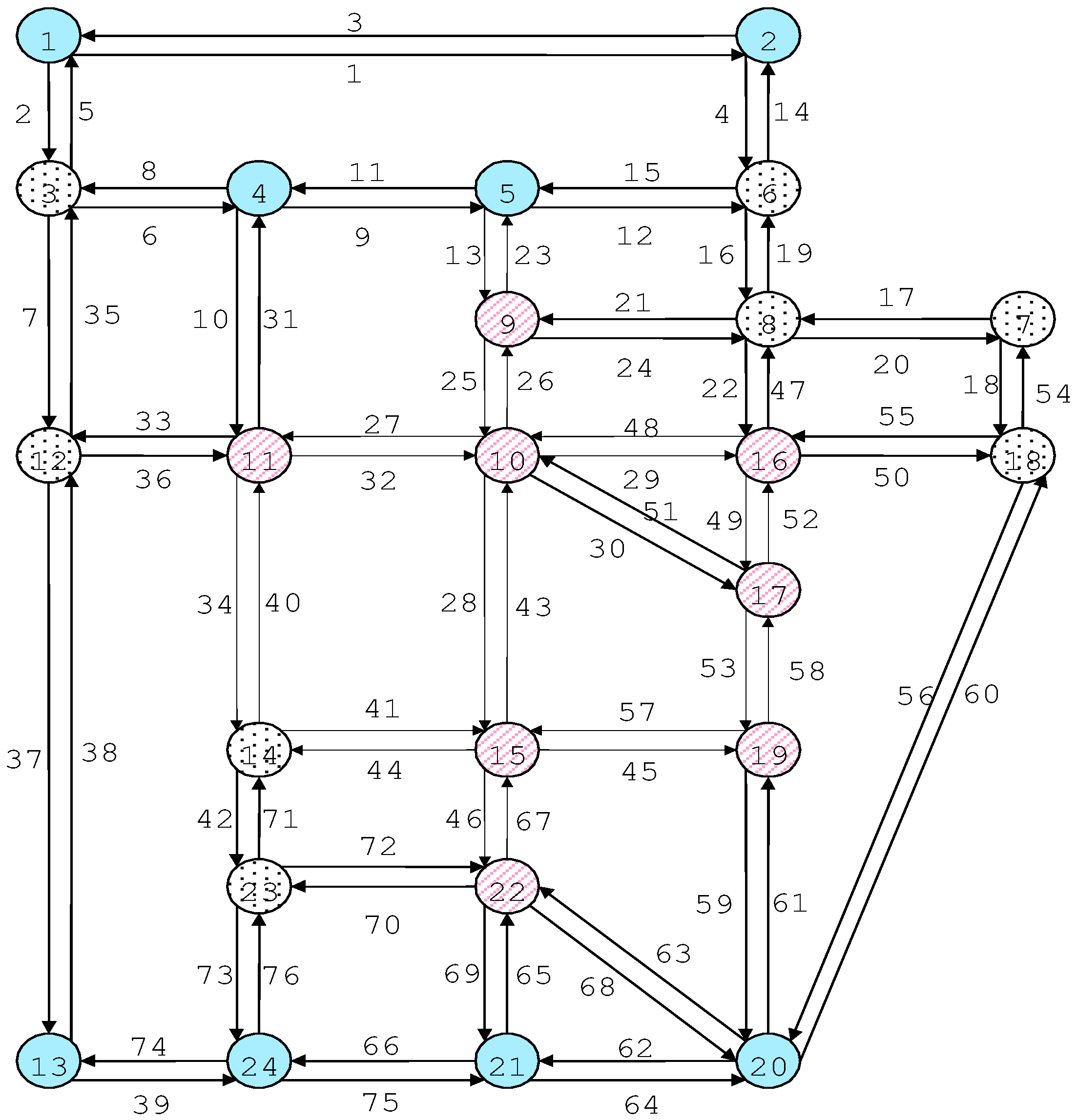
| Origin Nodes | Destination Nodes | Number of OD Pairs | |
|---|---|---|---|
| 15, 17, 19, 22 | 9, 10, 11, 16 | 16 | |
| 9, 10, 11, 16 | 15, 17, 19, 22 | 16 | |
| 6, 7, 8, 18 | 3, 12, 14, 23 | 16 | |
| 3, 12, 14, 23 | 6, 7, 8, 18 | 16 | |
| 13, 20, 21, 24 | 1, 2, 4, 5 | 16 | |
| 1, 2, 4, 5 | 13, 20, 21, 24 | 16 | |
| OD pair | Path | Path flow (vehicles/hour) | ETT (hour) |
| (8,3) | 21-25-27-31-8 | 167.4 | 0.747 |
| 19-14-3-2 | 132.6 | 0.747 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, L.; Wang, F.; Chen, Y.; Lv, X.; Wen, Z. A Reliability-Based Stochastic Traffic Assignment Model for Signalized Traffic Network with Consideration of Link Travel Time Correlations. Sustainability 2022, 14, 14520. https://doi.org/10.3390/su142114520
Shen L, Wang F, Chen Y, Lv X, Wen Z. A Reliability-Based Stochastic Traffic Assignment Model for Signalized Traffic Network with Consideration of Link Travel Time Correlations. Sustainability. 2022; 14(21):14520. https://doi.org/10.3390/su142114520
Chicago/Turabian StyleShen, Liang, Feiran Wang, Yueyuan Chen, Xinyi Lv, and Zongliang Wen. 2022. "A Reliability-Based Stochastic Traffic Assignment Model for Signalized Traffic Network with Consideration of Link Travel Time Correlations" Sustainability 14, no. 21: 14520. https://doi.org/10.3390/su142114520
APA StyleShen, L., Wang, F., Chen, Y., Lv, X., & Wen, Z. (2022). A Reliability-Based Stochastic Traffic Assignment Model for Signalized Traffic Network with Consideration of Link Travel Time Correlations. Sustainability, 14(21), 14520. https://doi.org/10.3390/su142114520