Spectrum Index for Estimating Ground Water Content Using Hyperspectral Information
Abstract
1. Introduction
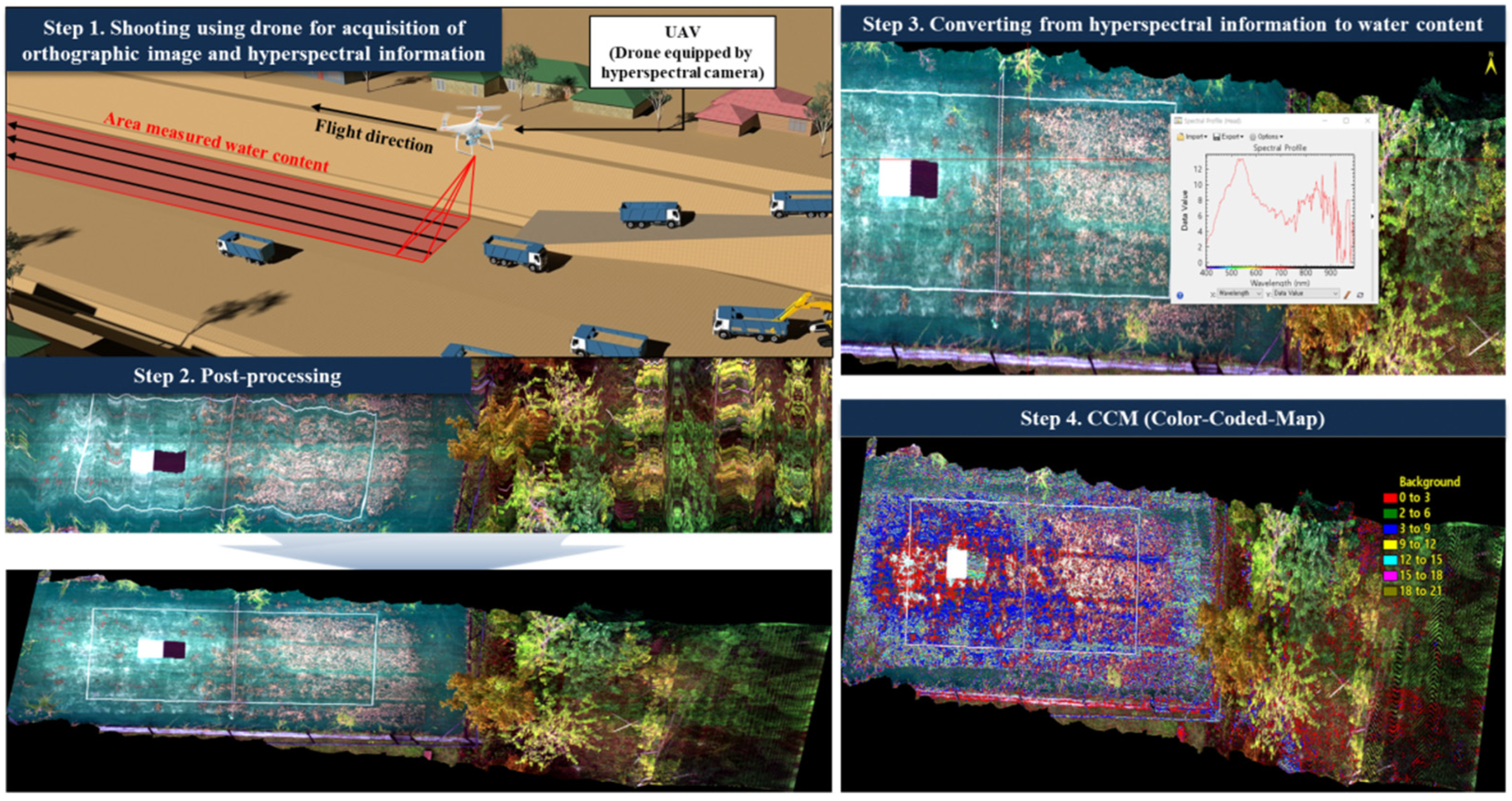
2. Methodology for Estimating Ground Water Content in Road Construction Site
3. Laboratory Tests for Obtaining Hyperspectral Information
3.1. System for Obtaining Hyperspectral Information
3.2. Laboratory Test of Soil Sample
3.2.1. Sieve Test
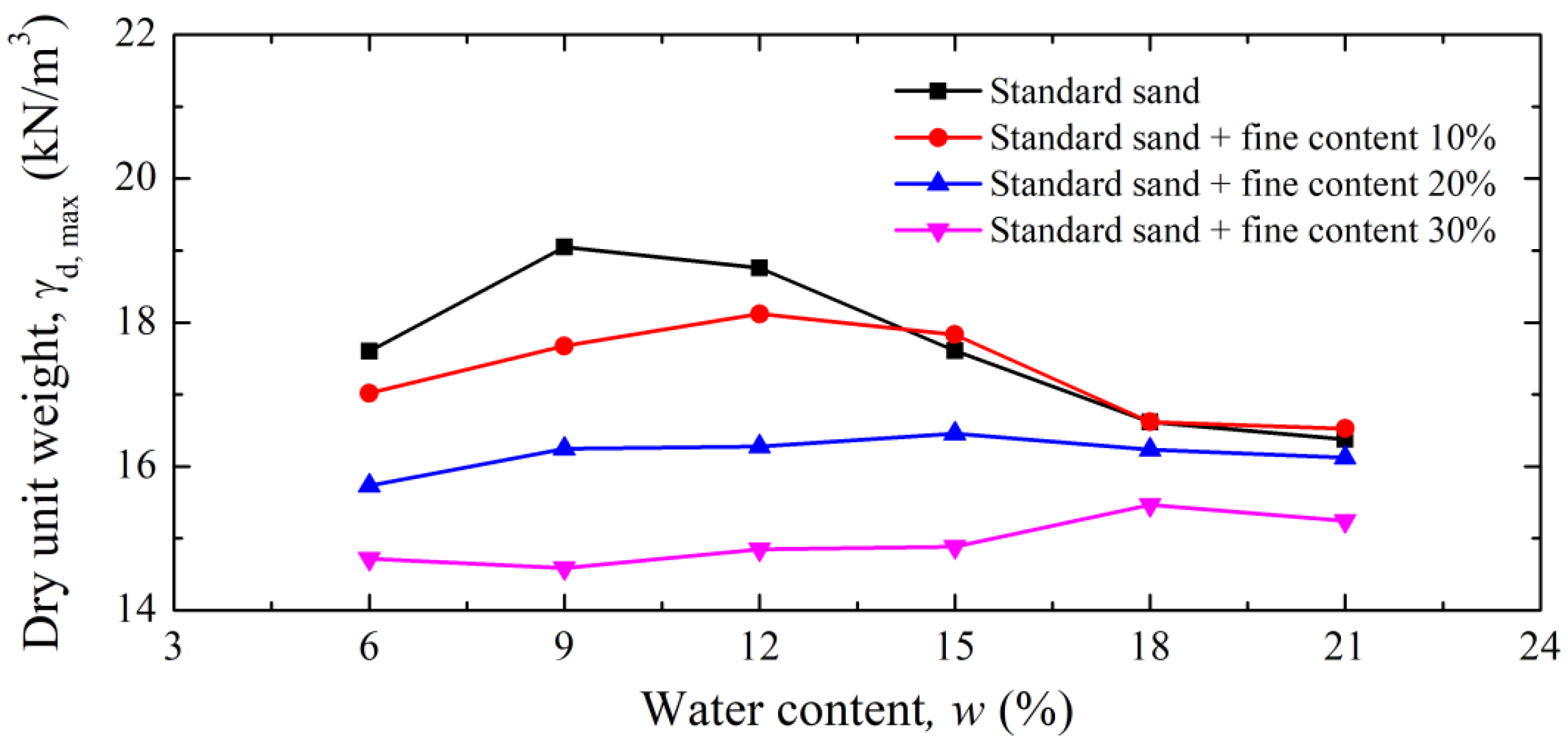
3.2.2. Standard Compaction Test
3.2.3. Composition of Specimens
3.3. Hyperspectral Information of Soil Sample
4. Estimation of the Spectrum Index for Water Content Prediction
4.1. Variability Analysis of Hyperspectral Information
4.1.1. Effects of Fine Contents
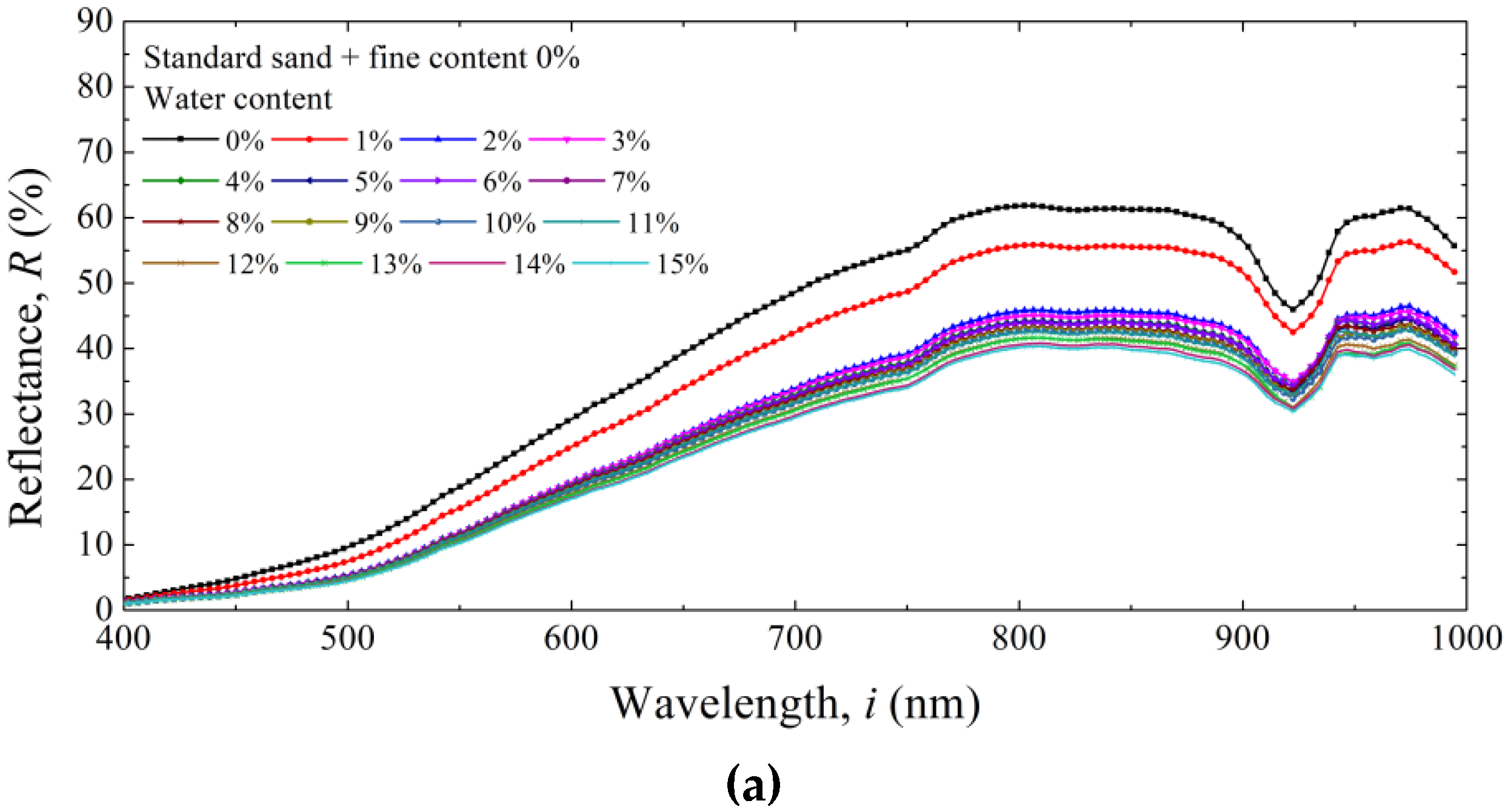
4.1.2. Effects of Water Contents
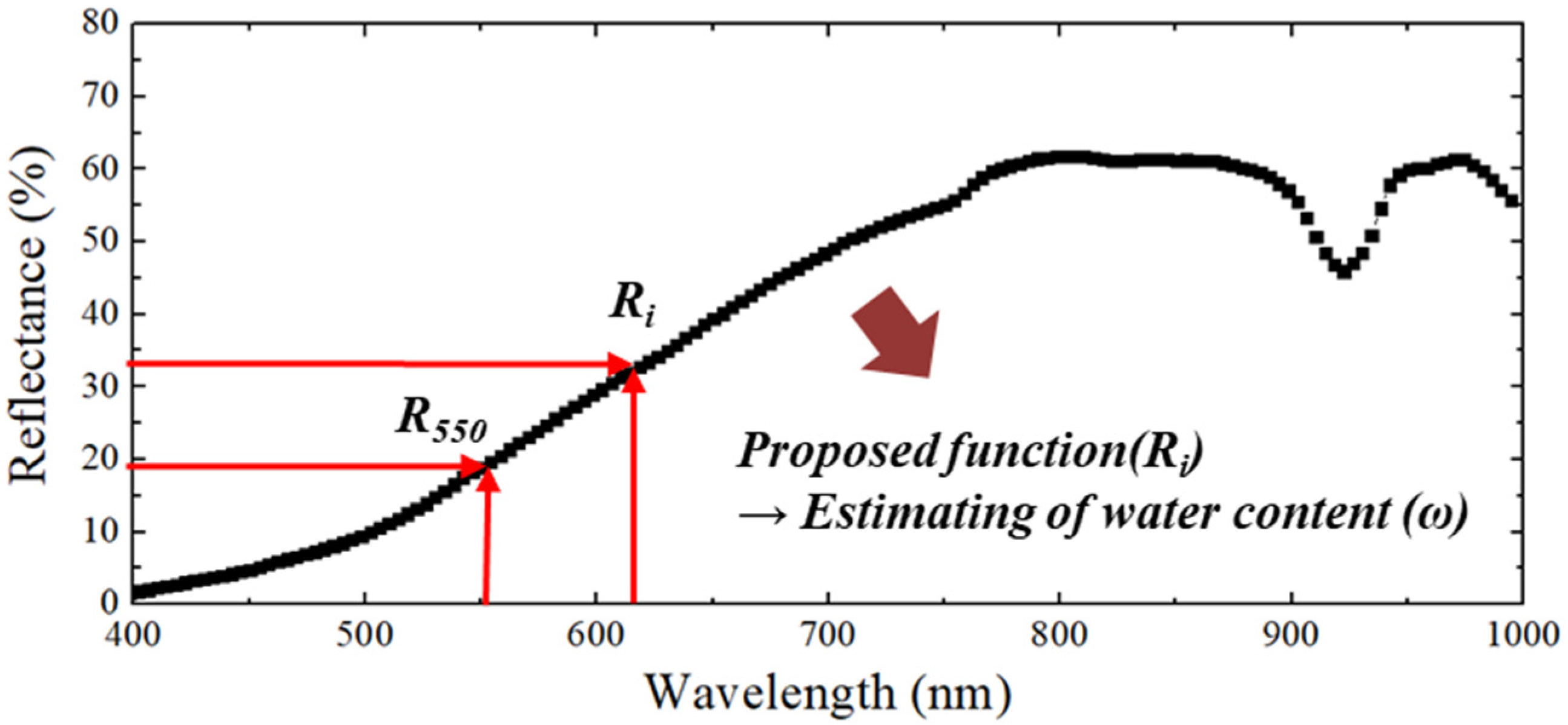
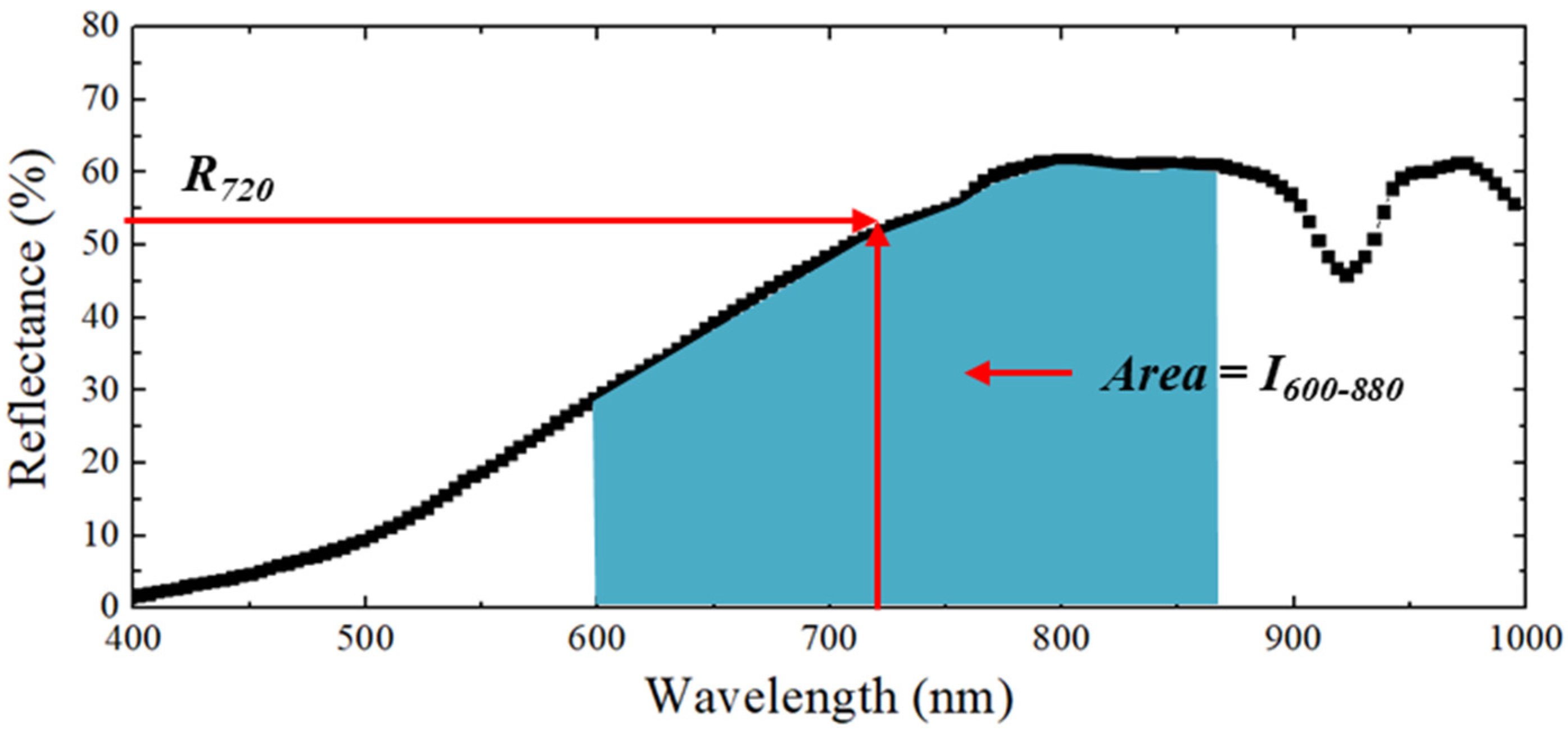
4.2. Spectrum Index Reflected by Selected Wavelength and Reflection
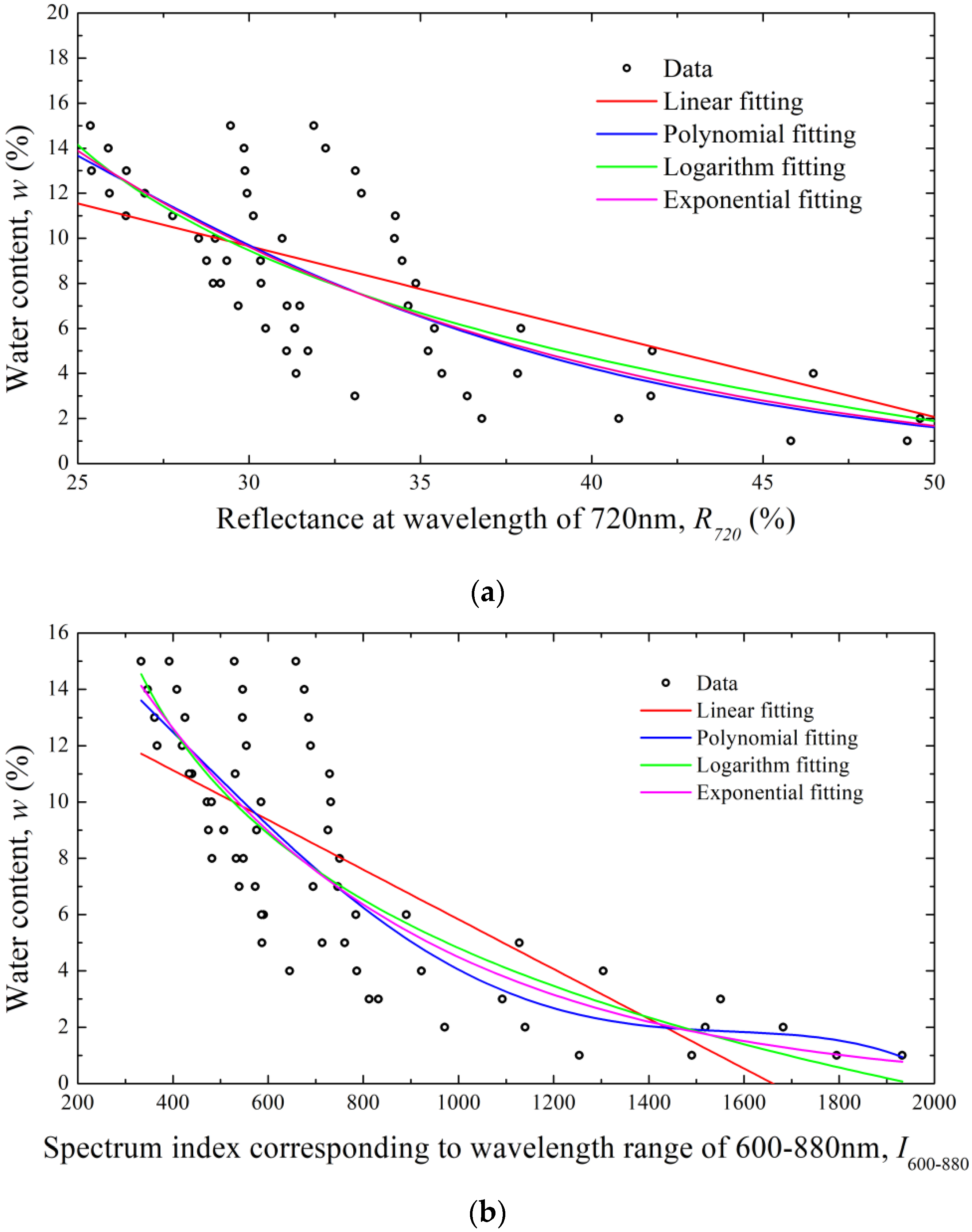
4.3. Equation for Predicting Water Content Using Spectrum Index
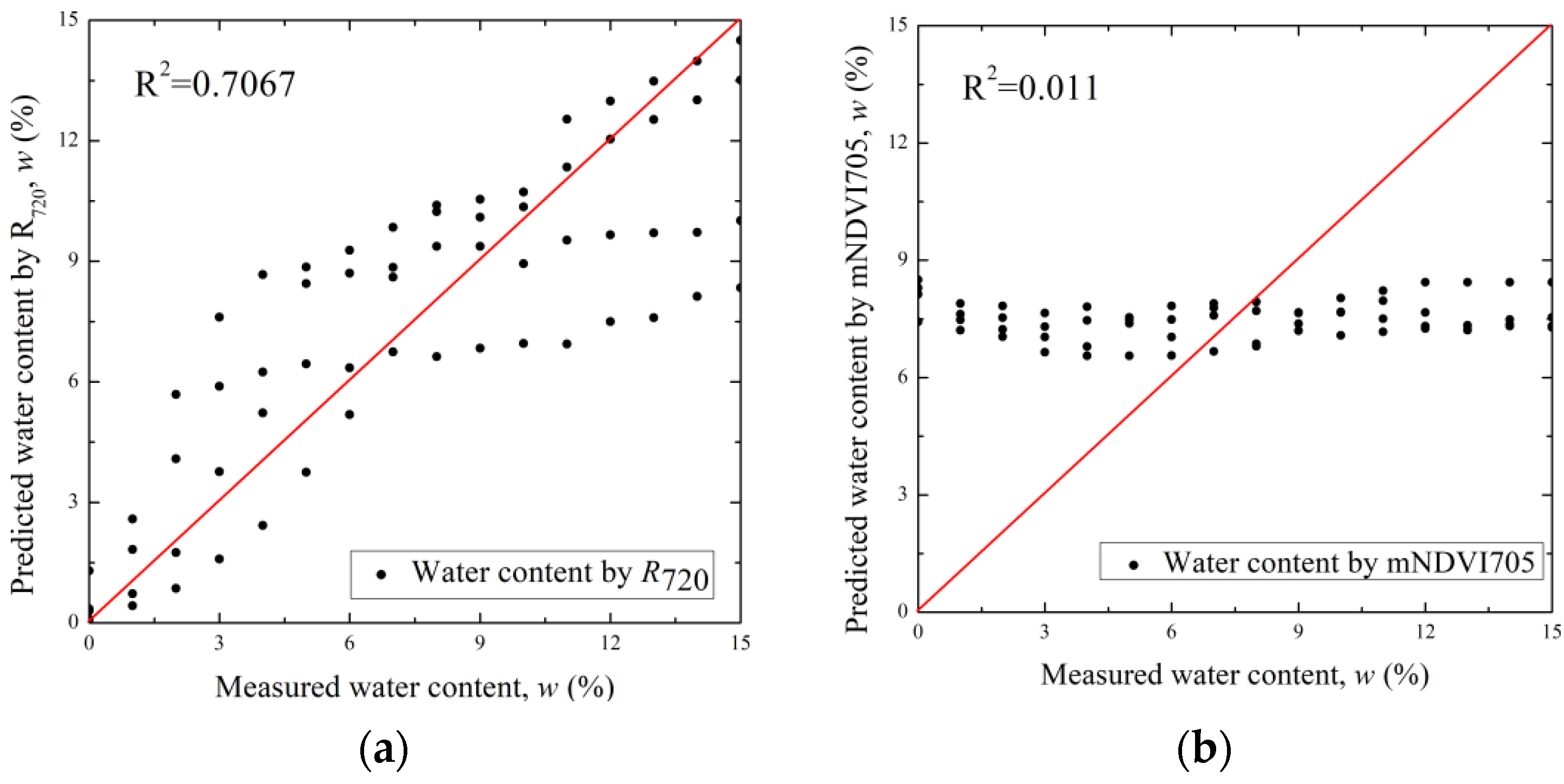
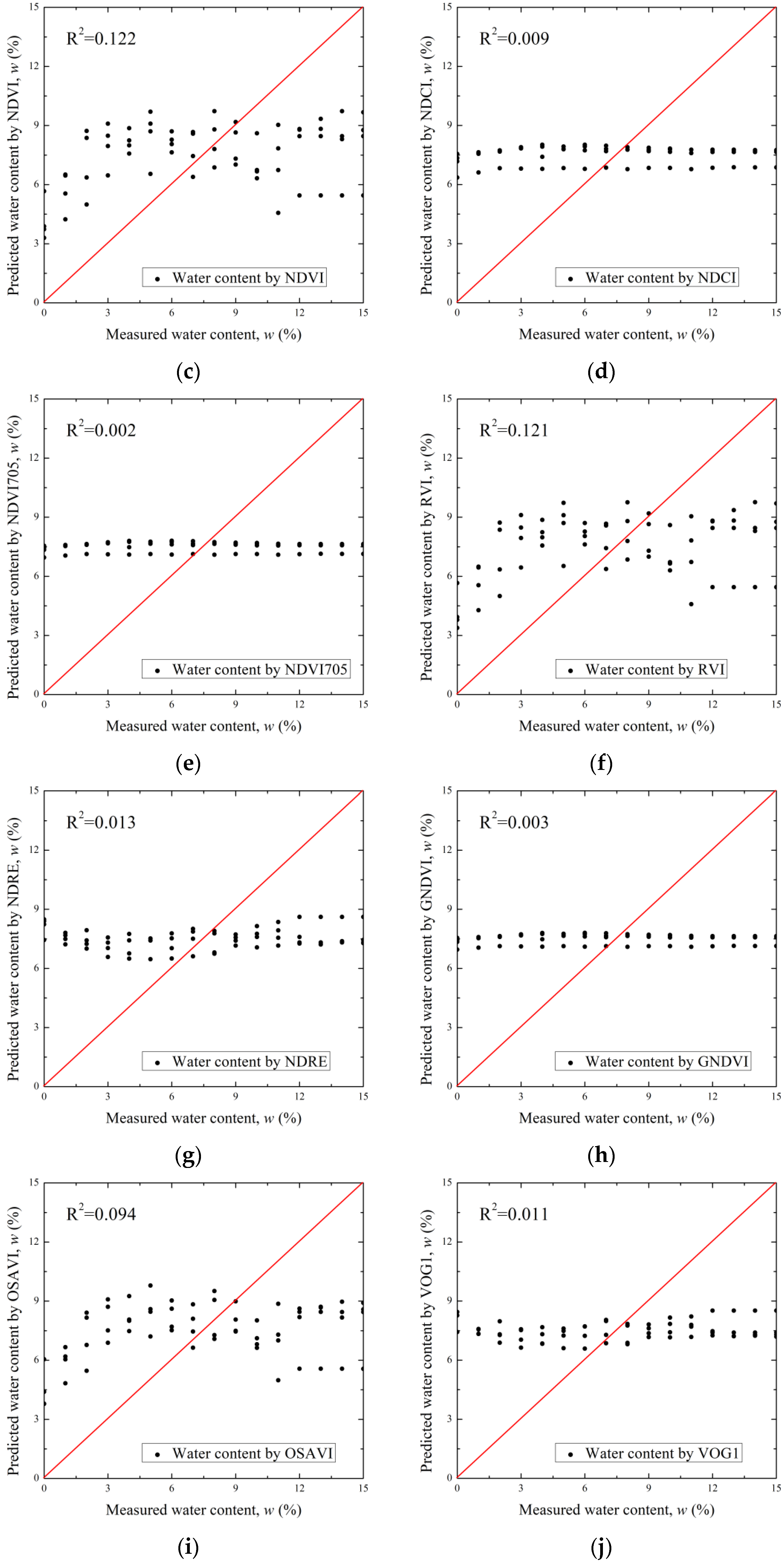
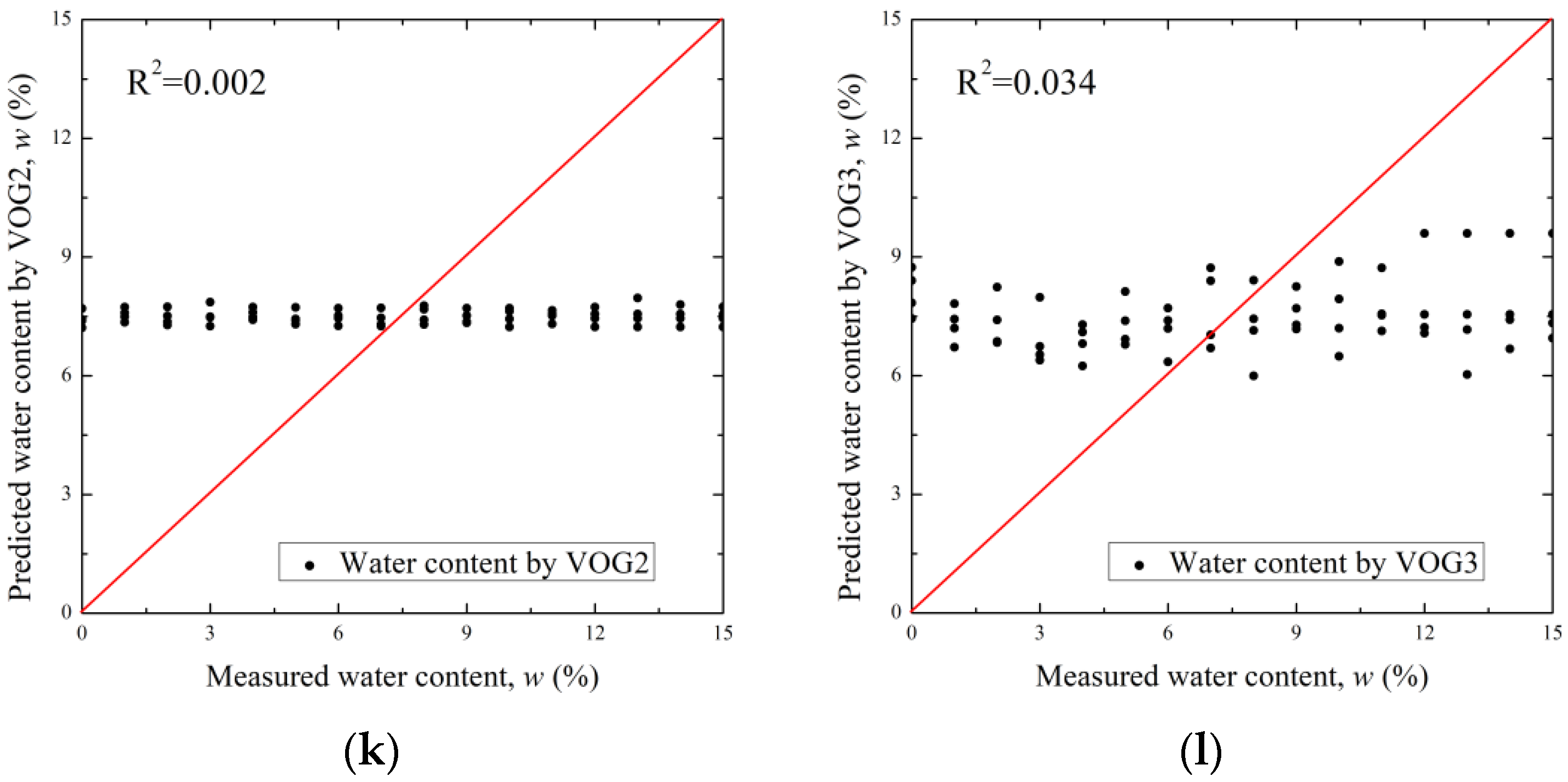
4.4. Comparison of the Literature with Proposed Spectrum Index Method
5. Conclusions
- In this study, sophisticated specimens were created by adding fine contents to standard sand, and hyperspectral information was obtained according to water content through precise laboratory tests. For hyperspectral information, a spectrum index was selected through various correlation analyses, and an equation to convert the spectrum index to water content was proposed.
- The suitable wavelength for calculating the spectrum index was 600–880 nm, as determined through variability analysis based on the water content and fine contents. The variability analysis results showed that no difference existed in the results of the equation for water content prediction even when a single wavelength within the range was selected. When the integral value of reflectance was used at 600–880 nm, R2 was rather low. This phenomenon was the result of the overlapping variability of wavelength and reflectance. Even when the R2 of the corresponding index was measured, it was not appropriate as it increased the time for calculating the spectrum index.
- The available equation for the prediction of the groundwater content is when the reflectance at a wavelength of 720 nm is applied to the exponential model. As a result of the linear regression analysis according to the measured and predicted water content, R2 was measured to be the highest, which means that it is most suitable for representing the water content in the ground. In terms of spectral range, 720 nm is deep red light.
- The correlation (R2: 0.009–0.122) when the existing spectrum index for water content prediction was substituted into the hyperspectral information obtained in this study was measured to be very low. Even when the existing equation was substituted into the hyperspectral information obtained by Ge et al. [26], the R2 ranged from 0.052 to 0.398, indicating that the reliability of the existing formula was low. Therefore, the R2 (0.7067) of our proposed equation for water content prediction according to R720 was large and reliable. This is because the existing method calculated the water content in a linear line through a simple linear regression analysis of the spectrum index.
- The disadvantage of this study is that the proposed equation was derived without going through an actual field test. Thus, in the field, errors may occur depending on actual variables, such as weather, temperature, humidity, and the skill level of the drone operator. Therefore, it is necessary to test the accuracy and reliability of the equation derived from this study in the field, and the equation must be modified through additional data acquisition.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Basu, D.; Misra, A.; Puppala, A.J. Sustainability and geotechnical engineering: Perspectives and review. Can. Geotech. J. 2015, 52, 96–113. [Google Scholar] [CrossRef]
- Brown, R.L. Building a Sustainable Society; W.W. Norton: New York, NY, USA, 1981. [Google Scholar]
- Brundtland, G.H. Our Common Future: Report of the World Commission on Environment and Development; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Socolow, R.; Andrews, C.; Berkhout, F.; Thomas, V. Industrial Ecology and Global Change; Cambridge University Press: Cambridge, UK, 1997; pp. 23–41. [Google Scholar]
- Kibert, C.J. Sustainable Construction; John Wiley and Sons Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Corriere, F.; Rizzo, A. Sustainability in road design: A methodological proposal for the drafting of guideline. Procedia-Soc. Behav. Sci. 2012, 53, 39–48. [Google Scholar] [CrossRef]
- Muench, S.T.; Anderson, J.; Bevan, T. Greenroads: A Sustainability Rating System for Roadways. Int. J. Pavement Res. Technol. 2010, 3, 270–279. [Google Scholar]
- Muench, S.T.; Anderson, J.L.; Hatfield, J.P.; Koester, J.R.; Söderlund, M.; Weiland, C. Greenroads Manual v1. 5; University of Washington: Washington, DC, USA, 2011. [Google Scholar]
- Jeon, D.H.; Cho, J.Y.; Jhun, J.P.; Ahn, J.H.; Jeong, S.; Jeong, S.Y.; Kumar, A.; Ryu, C.H.; Hwang, W.; Park, H.; et al. A lever-type piezoelectric energy harvester with deformation-guiding mechanism for electric vehicle charging station on smart road. Energy 2021, 218, 119540. [Google Scholar] [CrossRef]
- Kim, T.W.; Ryu, I.; Lee, H.; Jang, J.A. Dynamic Spatial Area Design for Transportation Management at Smart Road Lighting Platform System in Korea. In Proceedings of the 2021 International Conference on Information and Communication Technology Convergence (ICTC), Jeju, Korea, 20–22 October 2021. [Google Scholar]
- Ma, Y.; Luan, Y.C.; Zhang, W.G.; Zhang, Y.Q. Numerical simulation of intelligent compaction for subgrade construction. J. Cent. South Univ. 2020, 27, 2173–2184. [Google Scholar] [CrossRef]
- Ahmed, H.A. Electrical Resistivity Method for Water Content Characterization of Unsaturated Clay Soil. Doctoral Theses, Durham University, Durham, UK, 2014. [Google Scholar]
- Roodposhti, H.R.; Hafizi, M.K.; Kermani, M.R.S.; Nik, M.R.G. Electrical resistivity method for water content and compaction evaluation, a laboratory test on construction material. J. Appl. Geophys. 2019, 168, 49–58. [Google Scholar] [CrossRef]
- Abdullah, N.H.H.; Kuan, N.W.; Ibrahim, A.; Ismail, B.N.; Majid, M.R.A.; Ramli, R.; Mansor, N.S. Determination of soil water content using time domain reflectometer (TDR) for clayey soil. In Proceedings of the AIP Conference Proceedings, Maharashtra, India, 5–6 July 2018. [Google Scholar]
- Wen, M.M.; Liu, G.; Horton, R.; Noborio, K. An in situ probe-spacing-correction thermo-TDR sensor to measure soil water content accurately. Eur. J. Soil Sci. 2018, 69, 1030–1034. [Google Scholar] [CrossRef]
- Peng, W.; Lu, Y.; Xie, X.; Ren, T.; Horton, R. An improved thermo-TDR technique for monitoring soil thermal properties, water content, bulk density, and porosity. Vadose Zone J. 2019, 18, 1–9. [Google Scholar] [CrossRef]
- Ercoli, M.; Di Matteo, L.; Pauselli, C.; Mancinelli, P.; Frapiccini, S.; Talegalli, L.; Cannata, A. Integrated GPR and laboratory water content measures of sandy soils: From laboratory to field scale. Constr. Build. Mater. 2018, 159, 734–744. [Google Scholar] [CrossRef]
- Klotzsche, A.; Jonard, F.; Looms, M.C.; van der Kruk, J.; Huisman, J.A. Measuring soil water content with ground penetrating radar: A decade of progress. Vadose Zone J. 2018, 17, 1–9. [Google Scholar] [CrossRef]
- Zhou, L.; Yu, D.; Wang, Z.; Wang, X. Soil water content estimation using high-frequency ground penetrating radar. Water 2019, 11, 1036. [Google Scholar] [CrossRef]
- Eismann, M.T.; Stocker, A.D.; Nasrabadi, N.M. Automated hyperspectral cueing for civilian search and rescue. Proc. IEEE 2009, 97, 1031–1055. [Google Scholar] [CrossRef]
- Van Der Meer, F.D. Imaging Spectrometry-Basic Principles and Prospective Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Bassani, C.; Cavalli, R.M.; Cavalcante, F.; Cuomo, V.; Palombo, A.; Pascucci, S.; Pignatti, S. Deterioration status of asbestos-cement roofing sheets assessed by analyzing hyperspectral data. Remote Sens. Environ. 2007, 109, 361–378. [Google Scholar] [CrossRef]
- Smith, M.L.; Ollinger, S.V.; Martin, M.E.; Aber, J.D.; Hallett, R.A.; Goodale, C.L. Direct estimation of aboveground forest productivity through hyperspectral remote sensing of canopy nitrogen. Ecol. Appl. 2002, 12, 1286–1302. [Google Scholar] [CrossRef]
- Kokaly, R.F.; Asner, G.P.; Ollinger, S.V.; Martin, M.E.; Wessman, C.A. Characterizing canopy biochemistry from imaging spectroscopy and its application to ecosystem studies. Remote Sens. Environ. 2009, 113, S78–S91. [Google Scholar] [CrossRef]
- Zhang, F.; Zhou, G.S. Research progress on monitoring vegetation water content by using hyperspectral remote sensing. Chin. J. Plant Ecol. 2018, 42, 517. [Google Scholar]
- Zhang, F.; Zhou, G. Estimation of vegetation water content using hyperspectral vegetation indices: A comparison of crop water indicators in response to water stress treatments for summer maize. BMC Ecol. 2019, 19, 1–12. [Google Scholar] [CrossRef]
- Kovar, M.; Brestic, M.; Sytar, O.; Barek, V.; Hauptvogel, P.; Zivcak, M. Evaluation of hyperspectral reflectance parameters to assess the leaf water content in soybean. Water 2019, 11, 443. [Google Scholar] [CrossRef]
- Prošek, J.; Gdulová, K.; Barták, V.; Vojar, J.; Solský, M.; Rocchini, D.; Moudrý, V. Integration of hyperspectral and LiDAR data for mapping small water bodies. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102181. [Google Scholar] [CrossRef]
- Guo, Y.; Bi, Q.; Li, Y.; Du, C.; Huang, J.; Chen, W.; Shi, L.; Ji, G. Sparse Representing Denoising of Hyperspectral Data for Water Color Remote Sensing. Appl. Sci. 2022, 12, 7501. [Google Scholar] [CrossRef]
- Ge, X.; Wang, J.; Ding, J.; Cao, X.; Zhang, Z.; Liu, J.; Li, X. Combining UAV-based hyperspectral imagery and machine learning algorithms for soil moisture content monitoring. PeerJ 2019, 6926, 1–27. [Google Scholar] [CrossRef] [PubMed]
- Jain, S.K.; Singh, V.P. Water Resources Systems Planning and Management; Elsevier: Amsterdam, The Netherland, 2003. [Google Scholar]
- Lu, G.; Fei, B. Medical hyperspectral imaging: A review. J. Biomed. Opt. 2014, 19, 010901. [Google Scholar] [CrossRef] [PubMed]
- Angel, Y.; Turner, D.; Parkes, S.; Malbeteau, Y.; Lucieer, A.; McCabe, M.F. Automated georectification and mosaicking of UAV-based hyperspectral imagery from push-broom sensors. Remote Sens. 2020, 12, 34. [Google Scholar] [CrossRef]
- Jurado, J.M.; Pádua, L.; Hruška, J.; Feito, F.R.; Sousa, J.J. An Efficient Method for Generating UAV-Based Hyperspectral Mosaics Using Push-Broom Sensors. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6515–6531. [Google Scholar]
- Yi, L.; Chen, J.M.; Zhang, G.; Xu, X.; Ming, X.; Guo, W. Seamless Mosaicking of UAV-Based Push-Broom Hyperspectral Images for Environment Monitoring. Remote Sens. 2021, 13, 4720. [Google Scholar] [CrossRef]
- Ortega, S.; Guerra, R.; Diaz, M.; Fabelo, H.; López, S.; Callico, G.M.; Sarmiento, R. Hyperspectral push-broom microscope development and characterization. IEEE Access 2019, 7, 122473–122491. [Google Scholar] [CrossRef]
- ISO 679; Cement-Test Methods-Determination of Strength. International Organization for Standardization: Geneva, Switzerland, 2009.
- ASTM D422; Standard Test Method for Particle-Size Analysis of Soils. American Society for Testing of Materials: West Conshohocken, PA, USA, 2016.
- ASTM D2487; Standard Practice for Classification of Soils for Engineering Purposes (Unified Soil Classification System). American Society for Testing of Materials: West Conshohocken, PA, USA, 2017.
- ASTM D698; Standard Test Methods for Laboratory Compaction Characteristics of Soil Using Standard Effort (12,400 ft-lbf/ft3 (600 kN-m/m3)). American Society for Testing of Materials: West Conshohocken, PA, USA, 2017.
- Liang, L.; Di, L.; Zhang, L.; Deng, M.; Qin, Z.; Zhao, S.; Lin, H. Estimation of crop LAI using hyperspectral vegetation indices and a hybrid inversion method. Remote Sens. Environ. 2015, 165, 123–134. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Yao, X.; Wang, N.; Liu, Y.; Cheng, T.; Tian, Y.; Chen, Q.; Zhu, Y. Estimation of wheat LAI at middle to high levels using unmanned aerial vehicle narrowband multispectral imagery. Remote Sens. 2017, 9, 1304. [Google Scholar] [CrossRef]
- Vogelmann, J.E.; Rock, B.N.; Moss, D.M. Red edge spectral measurements from sugar maple leaves. Int. J. Remote Sens. 1993, 14, 1563–1575. [Google Scholar] [CrossRef]

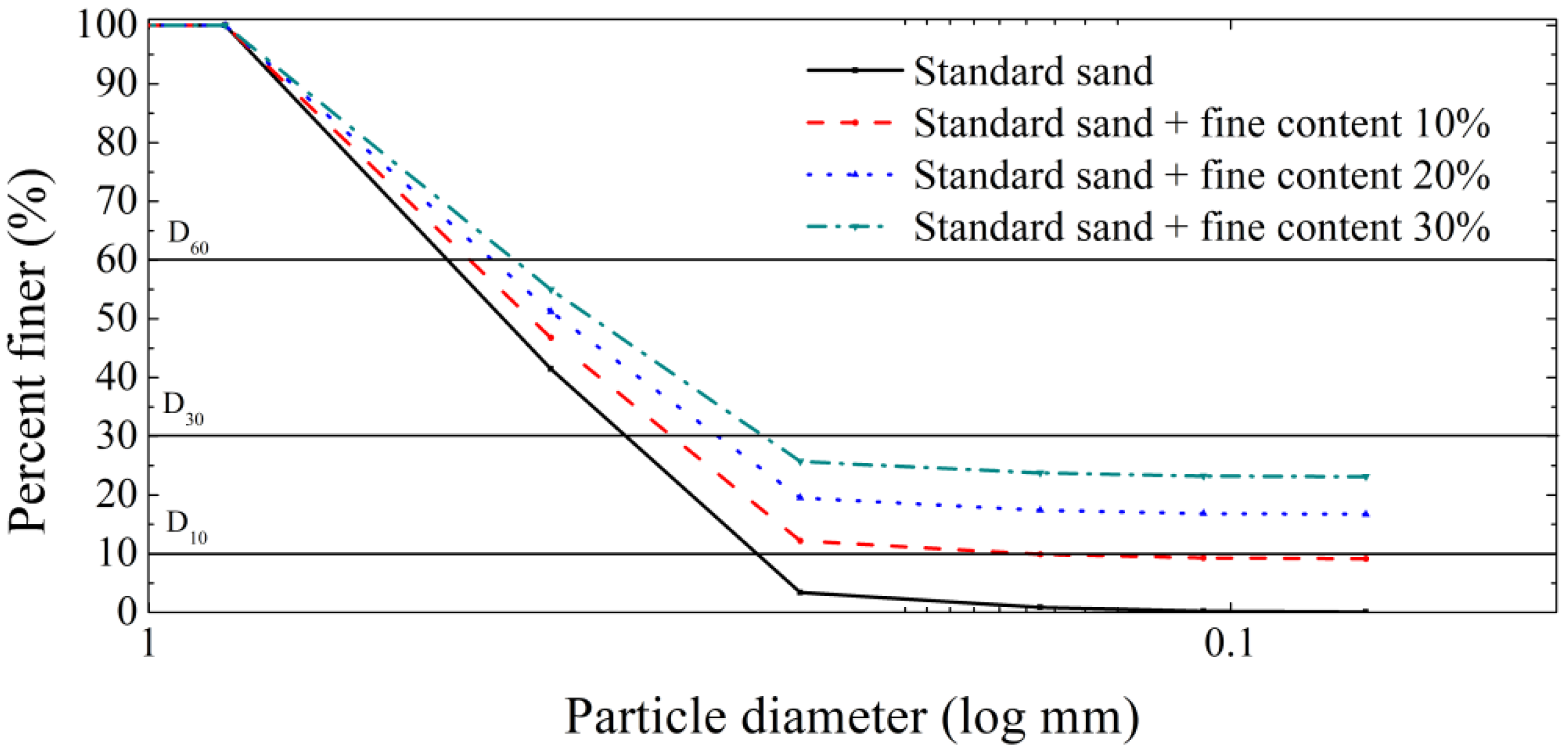






| Fine Content in Standard Sand (%) | D10 1 (mm) | D30 2 (mm) | D60 3 (mm) | Coefficient of Uniformity, Cu 4 | Coefficient of Curvature, Cc 5 | Percentage Passing No. 200 Sieve (%) | Soil Classification |
|---|---|---|---|---|---|---|---|
| 0 | 0.274 | 0.363 | 0.530 | 1.934 | 0.907 | 0.06 | SP |
| 10 | 0.150 | 0.329 | 0.505 | 3.367 | 1.429 | 9.15 | SP |
| 20 | - | 0.300 | 0.482 | - | - | 16.72 | SP |
| 30 | - | 0.272 | 0.461 | - | - | 23.13 | SP |
| Index | Fitting Model | Equation | R2 |
|---|---|---|---|
| R720 | Linear | 0.636 | |
| Polynomial | 0.687 | ||
| Logarithm | 0.695 | ||
| Exponential | 0.697 | ||
| I600–880 | Linear | 0.579 | |
| Polynomial | 0.637 | ||
| Logarithm | 0.643 | ||
| Exponential | 0.645 |
| Spectrum Index | Equation for Water Content Prediction | Ref. | |
|---|---|---|---|
| Sort | Equation | ||
| mNDVI705 | (R750 − R705)/(R740 + R705 + 2R445) | [41] | |
| NDVI | (R800 − R680)/(R800 + R680) | [42] | |
| NDCI | (R762 − R527)/(R762 + R527) | [41] | |
| NDVI705 | (R750 − R705)/(R750 + R705) | [43] | |
| RVI | R800/R680 | [43] | |
| NDRE | (R750 − R705)/(R750 + R705) | [44] | |
| GNDVI | (R750 − R550)/(R750 + R550) | [45] | |
| OSAVI | [(1 + 0.16) (R800 − R670)]/(R800 + R670 + 0.16) | [42] | |
| VOG1 | R740/R720 | [46] | |
| VOG2 | (R734 − R747)/(R715 − R726) | [46] | |
| VOG3 | (R734 − R747)/(R715 + R720) | [46] | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, K.; Kim, K.S.; Park, J.; Hong, G. Spectrum Index for Estimating Ground Water Content Using Hyperspectral Information. Sustainability 2022, 14, 14318. https://doi.org/10.3390/su142114318
Lee K, Kim KS, Park J, Hong G. Spectrum Index for Estimating Ground Water Content Using Hyperspectral Information. Sustainability. 2022; 14(21):14318. https://doi.org/10.3390/su142114318
Chicago/Turabian StyleLee, Kicheol, Ki Sung Kim, Jeongjun Park, and Gigwon Hong. 2022. "Spectrum Index for Estimating Ground Water Content Using Hyperspectral Information" Sustainability 14, no. 21: 14318. https://doi.org/10.3390/su142114318
APA StyleLee, K., Kim, K. S., Park, J., & Hong, G. (2022). Spectrum Index for Estimating Ground Water Content Using Hyperspectral Information. Sustainability, 14(21), 14318. https://doi.org/10.3390/su142114318








