Influence of Variable Speed Limit Control on Fuel and Electric Energy Consumption, and Exhaust Gas Emissions in Mixed Traffic Flows
Abstract
:1. Introduction
2. Related Work
3. Applied Methodology
3.1. Variable Speed Limit
3.2. Q-Learning Algorithm
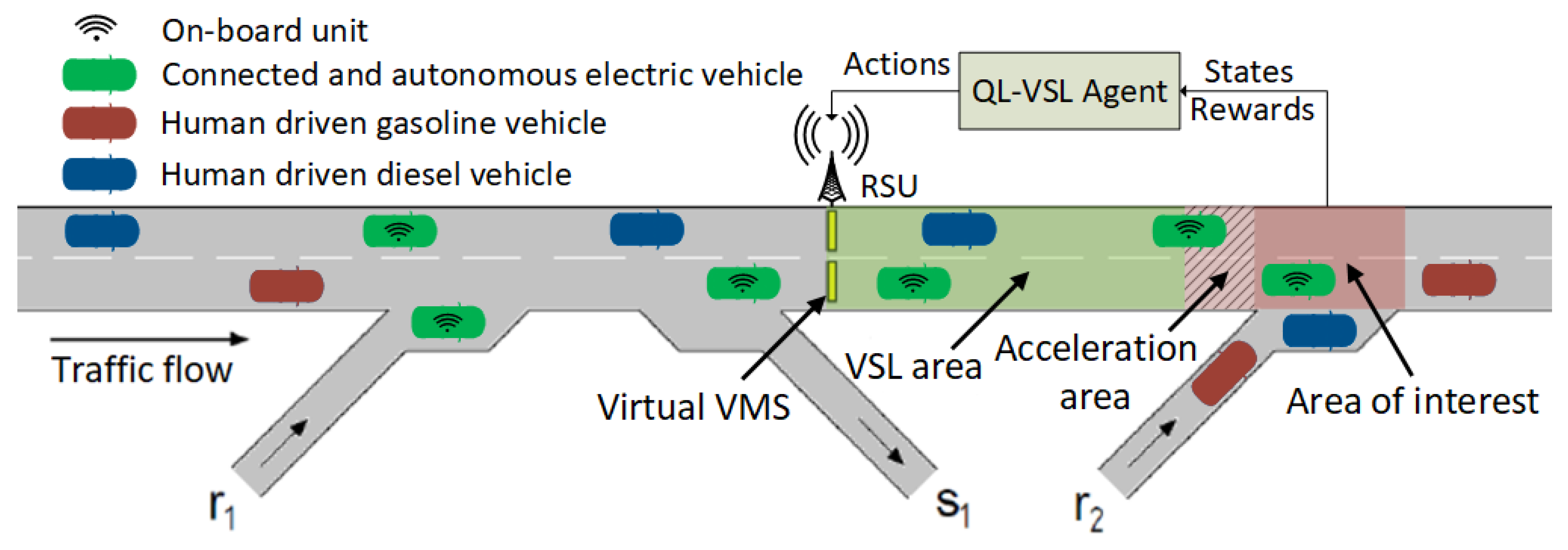
4. Modeling Q-Learning-Based Variable Speed Limit
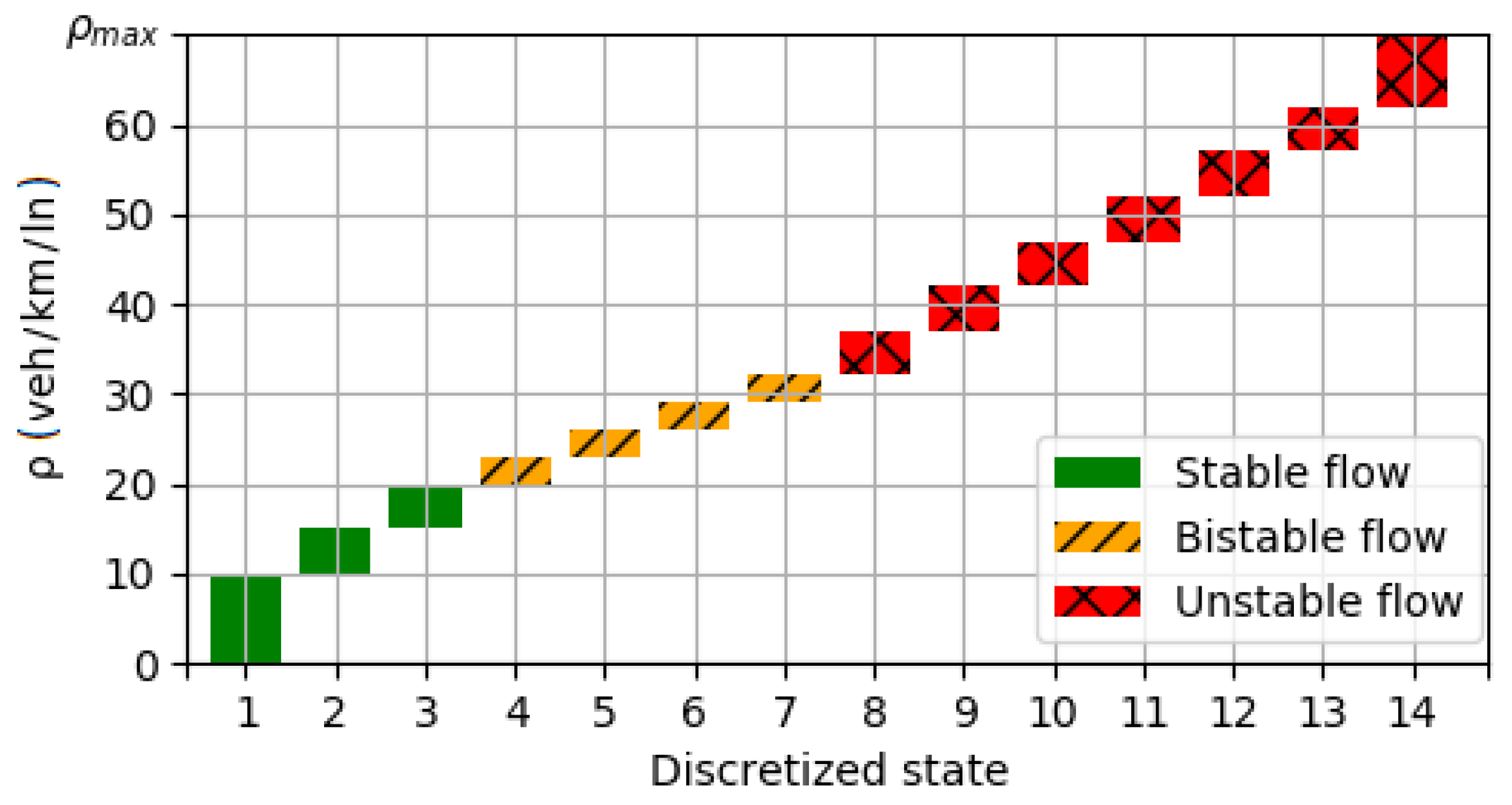
4.1. State–Action Space Description
4.2. Analyzed Reward Functions
4.2.1. Proportional Total Time Spent Reward
4.2.2. Proportional Total Energy Consumption Reward
5. Simulation Setup
5.1. Simulation Model
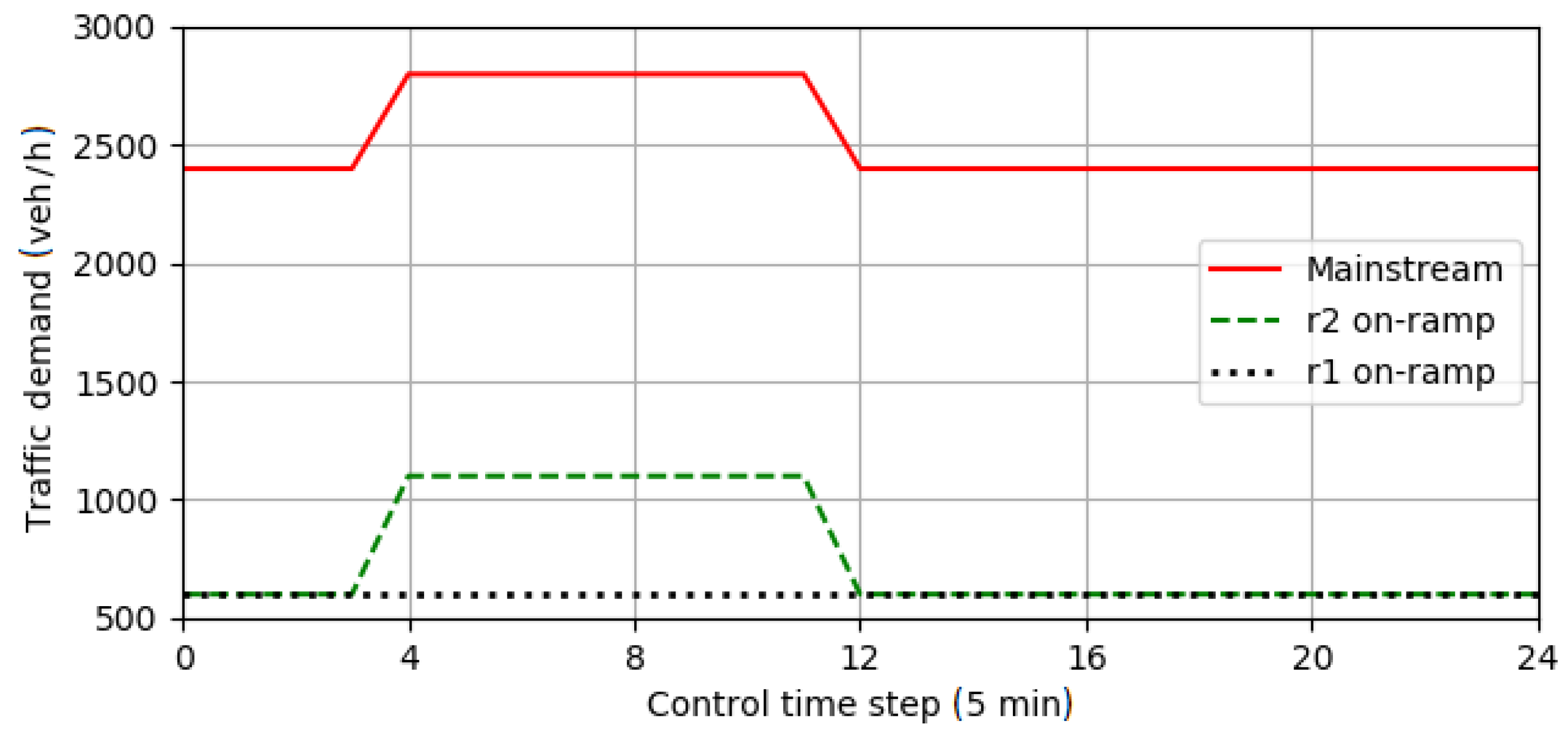
5.2. Traffic Scenarios
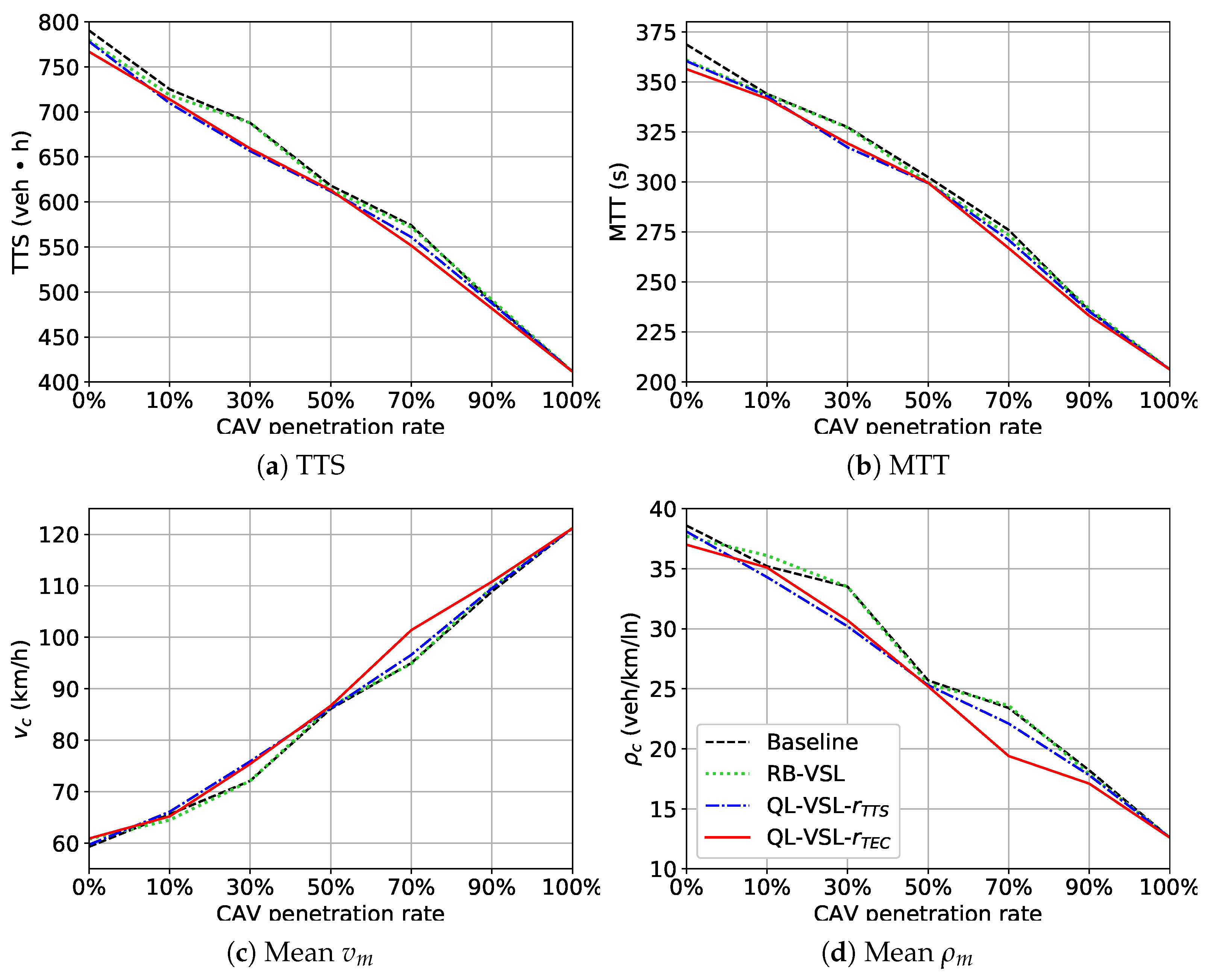
6. Results
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AV | Autonomous Vehicle |
| CAV | Connected Autonomous Vehicle |
| DQL | Deep Q-Learning |
| EEC | Electric Energy Consumption |
| FB | Full Bayes |
| FC | Fuel Consumption |
| HDV | Human-Driven Vehicle |
| I2V | Infrastructure-to-Vehicle |
| LoS | Level of Service |
| MDP | Markov Decision Process |
| MTT | Mean Travel Time |
| OBU | On-Board Unit |
| QL | Q-Learning |
| QL-VSL | Q-Learning Variable Speed Limit |
| RB-VSL | Rule-Based Variable Speed Limit |
| RL | Reinforcement Learning |
| RSU | Road Side Unit |
| SUMO | Simulation of Urban Mobility |
| TEC | Total Energy Consumption |
| TT | Travel Time |
| TTS | Total Time Spent |
| TTT | Total Travel Time |
| VMS | Variable Message Sign |
| VSL | Variable Speed Limit |
Appendix A
| Scenario (% CAVs) | rTTS TTS (veh·h) | rTEC TEC (MWh) | ||
|---|---|---|---|---|
| 0 | 759.5 | 49.565 | ||
| 10 | 727.7 | 45.482 | ||
| 30 | 678.9 | 37.742 | ||
| 0.7 | 50 | 608.7 | 29.984 | |
| 70 | 560.2 | 23.145 | ||
| 90 | 479.1 | 17.114 | ||
| 100 | 411.6 | 14.630 | ||
| 0 | 779 | 50.003 | ||
| 10 | 717.3 | 45.487 | ||
| 30 | 673.1 | 37.523 | ||
| 0.7 | 0.8 | 50 | 606.2 | 29.977 |
| 70 | 552.4 | 23.342 | ||
| 90 | 484.9 | 17.121 | ||
| 100 | 411.6 | 14.630 | ||
| 0 | 771.3 | 50.170 | ||
| 10 | 728.8 | 45.474 | ||
| 30 | 664.2 | 37.450 | ||
| 0.9 | 50 | 613.6 | 29.982 | |
| 70 | 552 | 23.223 | ||
| 90 | 487.3 | 17.108 | ||
| 100 | 411.6 | 14.630 | ||
| 0 | 778.1 | 49.561 | ||
| 10 | 722.5 | 45.671 | ||
| 30 | 682.8 | 37.301 | ||
| 0.7 | 50 | 611.1 | 29.945 | |
| 70 | 559.8 | 23.133 | ||
| 90 | 484.9 | 17.122 | ||
| 100 | 411.6 | 14.630 | ||
| 0 | 777.8 | 49.460 | ||
| 10 | 714.3 | 45.691 | ||
| 30 | 669.6 | 37.412 | ||
| 0.8 | 0.8 | 50 | 616.6 | 29.988 |
| 70 | 549.1 | 23.127 | ||
| 90 | 484.9 | 17.132 | ||
| 100 | 411.6 | 14.630 | ||
| 0 | 773.9 | 49.378 | ||
| 10 | 724.8 | 45.489 | ||
| 30 | 675.1 | 38.031 | ||
| 0.9 | 50 | 612.8 | 29.990 | |
| 70 | 559.5 | 23.122 | ||
| 90 | 485.8 | 17.108 | ||
| 100 | 411.6 | 14.630 | ||
| 0 | 771.3 | 50.074 | ||
| 10 | 723.6 | 45.479 | ||
| 30 | 671.5 | 37.428 | ||
| 0.7 | 50 | 613.5 | 29.985 | |
| 70 | 560.3 | 23.165 | ||
| 90 | 482.9 | 17.091 | ||
| 100 | 411.6 | 14.630 | ||
| 0 | 737 | 49.932 | ||
| 10 | 724.7 | 45.480 | ||
| 30 | 671.2 | 37.677 | ||
| 0.9 | 0.8 | 50 | 614.4 | 29.986 |
| 70 | 571.5 | 23.401 | ||
| 90 | 480.4 | 17.085 | ||
| 100 | 411.6 | 14.630 | ||
| 0 | 770.6 | 50.660 | ||
| 10 | 709.7 | 45.494 | ||
| 30 | 656.5 | 37.777 | ||
| 0.9 | 50 | 611.8 | 29.988 | |
| 70 | 560.9 | 23.119 | ||
| 90 | 487.5 | 17.104 | ||
| 100 | 411.6 | 14.630 |
References
- Grumert, E.; Tapani, A.; Ma, X. Characteristics of variable speed limit systems. Eur. Transp. Res. Rev. 2018, 10, 21. [Google Scholar] [CrossRef]
- Greenwood, I.D.; Dunn, R.C.; Raine, R.R. Estimating the Effects of Traffic Congestion on Fuel Consumption and Vehicle Emissions Based on Acceleration Noise. J. Transp. Eng. 2007, 133, 96–104. [Google Scholar] [CrossRef]
- Müller, E.; Carlson, R.; Kraus, W.; Papageorgiou, M. Microsimulation analysis of practical aspects of traffic control with variable speed limits. IEEE Trans. Intell. Transp. Syst. 2015, 16, 512–523. [Google Scholar] [CrossRef]
- Kušić, K.; Ivanjko, E.; Gregurić, M.; Miletić, M. An Overview of Reinforcement Learning Methods for Variable Speed Limit Control. Appl. Sci. 2020, 10, 4917. [Google Scholar] [CrossRef]
- Vrbanić, F.; Ivanjko, E.; Kušić, K.; Čakija, D. Variable Speed Limit and Ramp Metering for Mixed Traffic Flows: A Review and Open Questions. Appl. Sci. 2021, 11, 2574. [Google Scholar] [CrossRef]
- Kušić, K.; Ivanjko, E.; Gregurić, M. A Comparison of Different State Representations for Reinforcement Learning Based Variable Speed Limit Control. In Proceedings of the MED 2018–26th Mediterranean Conference on Control and Automation, Zadar, Croatia, 19–22 June 2018; pp. 266–271. [Google Scholar] [CrossRef]
- Vrbanić, F.; Ivanjko, E.; Mandžuka, S.; Miletić, M. Reinforcement Learning Based Variable Speed Limit Control for Mixed Traffic Flows. In Proceedings of the 2021 29th Mediterranean Conference on Control and Automation (MED), Puglia, Italy, 22–25 June 2021; pp. 560–565. [Google Scholar] [CrossRef]
- Van Brummelen, J.; O’Brien, M.; Gruyer, D.; Najjaran, H. Autonomous vehicle perception: The technology of today and tomorrow. Transp. Res. Part C Emerg. Technol. 2018, 89, 384–406. [Google Scholar] [CrossRef]
- Yu, J.J.Q.; Lam, A.Y.S.; Lu, Z. Double Auction-Based Pricing Mechanism for Autonomous Vehicle Public Transportation System. IEEE Trans. Intell. Veh. 2018, 3, 151–162. [Google Scholar] [CrossRef]
- Li, M.; Imou, K.; Wakabayashi, K.; Yokoyama, S. Review of research on agricultural vehicle autonomous guidance. Int. J. Agric. Biol. Eng. 2008, 2, 1–16. [Google Scholar] [CrossRef]
- Yu, J.J.Q.; Lam, A.Y.S. Autonomous Vehicle Logistic System: Joint Routing and Charging Strategy. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2175–2187. [Google Scholar] [CrossRef]
- Ayub, M.F.; Ghawash, F.; Shabbir, M.A.; Kamran, M.; Butt, F.A. Next Generation Security And Surveillance System Using Autonomous Vehicles. In Proceedings of the 2018 Ubiquitous Positioning, Indoor Navigation and Location-Based Services (UPINLBS), Wuhan, China, 22–23 March 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Croatian Bureau of Statistics. Transport and Communications-Registered Road Vehicles by Types, Age, Size of Engine and Type of Motor Energy. 2021. Available online: https://www.dzs.hr/Hrv/publication/FirstRelease/results.asp?pString=Transport%20i%20komunikacije&pSearchString=%Transport%20i%20komunikacije% (accessed on 15 October 2021).
- Khondaker, B.; Kattan, L. Variable speed limit: An overview. Transp. Lett. Int. J. Transp. Res. 2015, 7, 264–278. [Google Scholar] [CrossRef]
- Lu, X.Y.; Shladover, S. Review of Variable Speed Limits and Advisories. Transp. Res. Rec. J. Transp. Res. Board 2014, 2423, 15–23. [Google Scholar] [CrossRef]
- Gregurić, M.; Ivanjko, E.; Korent, N.; Kušić, K. Short Review of Approaches for Variable Speed Limit Control. In Proceedings of the International Scientific Conference on Science and Transport Development (ZIRP 2016), Zagreb, Croatia, 4 April 2016; pp. 41–52. [Google Scholar]
- Abdel-Aty, M.; Yu, R. State-of-practice of variable speed limit systems. In Proceedings of the 20th ITS World Congress, Tokyo, Japan, 14–18 October 2013. [Google Scholar]
- Tafti, M. An investigation on the approaches and methods used for variable speed limit control. In Proceedings of the 15th World Congress on Intelligent Transport Systems and ITS America’s 2008 Annual Meeting, New York, NY, USA, 16–20 November 2008; pp. 901–912. [Google Scholar]
- Walraven, E.; Spaan, M.T.; Bakker, B. Traffic flow optimization: A reinforcement learning approach. Eng. Appl. Artif. Intell. 2016, 52, 203–212. [Google Scholar] [CrossRef]
- Li, Z.; Xu, C.; Pu, Z.; Guo, Y.; Liu, P. Reinforcement Learning-Based Variable Speed Limits Control to Reduce Crash Risks near Traffic Oscillations on Freeways. IEEE Intell. Transp. Syst. Mag. 2020, 13, 64–70. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, J.; Xu, L.; Li, L.; Ran, B. A New Solution for Freeway Congestion: Cooperative Speed Limit Control Using Distributed Reinforcement Learning. IEEE Access 2019, 7, 41947–41957. [Google Scholar] [CrossRef]
- Kušić, K.; Ivanjko, E.; Vrbanić, F.; Gregurić, M.; Dusparic, I. Dynamic Variable Speed Limit Zones Allocation Using Distributed Multi-Agent Reinforcement Learning. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 3238–3245. [Google Scholar] [CrossRef]
- Li, Z.; Liu, P.; Xu, C.; Duan, H.; Wang, W. Reinforcement Learning-Based Variable Speed Limit Control Strategy to Reduce Traffic Congestion at Freeway Recurrent Bottlenecks. IEEE Trans. Intell. Transp. Syst. 2017, 18, 3204–3217. [Google Scholar] [CrossRef]
- Pu, Z.; Li, Z.; Jiang, Y.; Wang, Y. Full Bayesian Before-After Analysis of Safety Effects of Variable Speed Limit System. IEEE Trans. Intell. Transp. Syst. 2021, 22, 964–976. [Google Scholar] [CrossRef]
- Wu, Y.; Tan, H.; Qin, L.; Ran, B. Differential variable speed limits control for freeway recurrent bottlenecks via deep actor-critic algorithm. Transp. Res. Part C Emerg. Technol. 2020, 117, 102649. [Google Scholar] [CrossRef]
- Yu, M.; Fan, W. Optimal variable speed limit control in connected autonomous vehicle environment for relieving freeway congestion. J. Transp. Eng. Part A Syst. 2019, 145, 04019007. [Google Scholar] [CrossRef]
- Khondaker, B.; Kattan, L. Variable speed limit: A microscopic analysis in a connected vehicle environment. Transp. Res. Part C Emerg. Technol. 2015, 58, 146–159. [Google Scholar] [CrossRef] [Green Version]
- Grumert, E.; Ma, X.; Tapani, A. Analysis of a cooperative variable speed limit system using microscopic traffic simulation. Transp. Res. Part C Emerg. Technol. 2015, 52, 173–186. [Google Scholar] [CrossRef]
- Li, D.; Wagner, P. Impacts of gradual automated vehicle penetration on motorway operation: A comprehensive evaluation. Eur. Transp. Res. Rev. 2019, 11, 36. [Google Scholar] [CrossRef]
- Malikopoulos, A.; Hong, S.; Park, B.; Lee, J.; Ryu, S. Optimal Control for Speed Harmonization of Automated Vehicles. IEEE Trans. Intell. Transp. Syst. 2019, 20, 2405–2417. [Google Scholar] [CrossRef] [Green Version]
- Rongsheng, C.; Zhang, T.; Levin, M.W. Effects of Variable Speed Limit on Energy Consumption with Autonomous Vehicles on Urban Roads Using Modified Cell-Transmission Model. J. Transp. Eng. Part A Syst. 2020, 146, 04020049. [Google Scholar] [CrossRef]
- Hegyi, A.; Hoogendoorn, S.; Schreuder, M.; Stoelhorst, H.; Viti, F. Specialist: A dynamic speed limit control algorithm based on shock wave theory. In Proceedings of the 11th International IEEE Conference on Intelligent Transportation Systems (ITSC), Beijing, China, 12–15 October 2008; pp. 827–832. [Google Scholar] [CrossRef]
- Ma, J.; Li, X.; Zhou, F.; Hu, J.; Park, B. Parsimonious shooting heuristic for trajectory design of connected automated traffic part II: Computational issues and optimization. Transp. Res. Part B Methodol. 2017, 95, 421–441. [Google Scholar] [CrossRef] [Green Version]
- Miri, I.; Fotouhi, A.; Ewin, N. Electric vehicle energy consumption modelling and estimation—A case study. Int. J. Energy Res. 2021, 45, 501–520. [Google Scholar] [CrossRef]
- Xie, Y.; Li, Y.; Zhao, Z.; Dong, H.; Wang, S.; Liu, J.; Guan, J.; Duan, X. Microsimulation of electric vehicle energy consumption and driving range. Appl. Energy 2020, 267, 115081. [Google Scholar] [CrossRef]
- Luin, B.; Petelin, S.; Al-Mansour, F. Microsimulation of electric vehicle energy consumption. Energy 2019, 174, 24–32. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, F.; Ke, X.; Liu, Z.; Yuan, C. Predictive modeling of energy consumption and greenhouse gas emissions from autonomous electric vehicle operations. Appl. Energy 2019, 254, 113597. [Google Scholar] [CrossRef]
- Müller, E.; Carlson, R.; Kraus, W. Cooperative Mainstream Traffic Flow Control on Freeways. IFAC-PapersOnLine 2016, 49, 89–94. [Google Scholar] [CrossRef]
- Vinitsky, E.; Parvate, K.; Kreidieh, A.; Wu, C.; Bayen, A. Lagrangian Control through Deep-RL: Applications to Bottleneck Decongestion. In Proceedings of the 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 759–765. [Google Scholar] [CrossRef]
- Papageorgiou, M.; Kosmatopoulos, E.; Papamichail, I. Effects of Variable Speed Limits on Motorway Traffic Flow. Transp. Res. Rec. J. Transp. Res. Board 2008, 2047, 37–48. [Google Scholar] [CrossRef]
- Lee, C.; Hellinga, B.; Saccomanno, F. Evaluation of variable speed limits to improve traffic safety. Transp. Res. Part C Emerg. Technol. 2006, 14, 213–228. [Google Scholar] [CrossRef]
- Cremer, M. Der Verkehrsfluss auf Schnellstrassen: Modelle, Überwachung, Regelung; Springer: Berlin/Heidelberg, Germany, 1979. [Google Scholar]
- Carlson, R.C.; Papamichail, I.; Papageorgiou, M.; Messmer, A. Optimal Motorway Traffic Flow Control Involving Variable Speed Limits and Ramp Metering. Transp. Sci. 2010, 44, 238–253. [Google Scholar] [CrossRef]
- Ye, L.; Yamamoto, T. Evaluating the impact of connected and autonomous vehicles on traffic safety. Phys. A Stat. Mech. Its Appl. 2019, 526, 121009. [Google Scholar] [CrossRef]
- Olia, A.; Razavi, S.; Abdulhai, B.; Abdelgawad, H. Traffic capacity implications of automated vehicles mixed with regular vehicles. J. Intell. Transp. Syst. Technol. Plan. Oper. 2018, 22, 244–262. [Google Scholar] [CrossRef]
- Wang, Q.; Li, B.; Li, Z.; Li, L. Effect of connected automated driving on traffic capacity. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 633–637. [Google Scholar]
- Bellman, R. A Markovian Decision Process. J. Math. Mech. 1957, 6, 679–684. [Google Scholar] [CrossRef]
- Watkins, C.J.C.H.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Sutton, R.; Barto, A. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Universities and Colleges Climate Commitment for Scotland. UCCCfS Unit Converter. 2010. Available online: http://www.eauc.org.uk/file_uploads/ucccfs_unit_converter_v1_3_1.xlsx (accessed on 5 October 2021).
- Behrisch, M.; Bieker-Walz, L.; Erdmann, J.; Krajzewicz, D. SUMO—Simulation of Urban MObility: An Overview. In Proceedings of the Third International Conference on Advances in System Simulation, SIMUL 2011, Barcelona, Spain, 23–28 October 2011. [Google Scholar]
- Li, D.; Wagner, P. A novel approach for mixed manual/connected automated freeway traffic management. Sensors 2020, 20, 1757. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Volkswagen of America, Inc. Newspress Limited. World Premiere of the Fully Electric ID.3. 2019. Available online: https://media.vw.com/en-us/releases/1198 (accessed on 28 September 2021).
- Hausberger, S.; Krajzewicz, D. Extended Simulation Tool PHEM Coupled to SUMO with User Guide. 2014. Available online: https://web.archive.org/web/20190527152150/https://elib.dlr.de/98047/1/COLOMBO_D4.2_ExtendedPHEMSUMO_v1.7.pdf (accessed on 28 September 2021).
- Institute for Internal Combustion Engines and Thermodynamics. Passenger Car and Heavy Duty Emission Model. 2016. Available online: https://www.ivt.tugraz.at/assets/files/areas/em/PHEM_en.pdf (accessed on 28 September 2021).
- Elefteriadou, L.A. (Ed.) Highway Capacity Manual 6th Edition: A Guide for Multimodal Mobility Analysis; Transportation Research Board, The National Academies Press: Washington, DC, USA, 2016. [Google Scholar] [CrossRef]
- Tišljarić, L.; Carić, T.; Abramović, B.; Fratrović, T. Traffic State Estimation and Classification on Citywide Scale Using Speed Transition Matrices. Sustainability 2020, 12, 7278. [Google Scholar] [CrossRef]
- Hofman, T.; Dai, C. Energy efficiency analysis and comparison of transmission technologies for an electric vehicle. In Proceedings of the 2010 IEEE Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Nylund, N.O. Vehicle Energy Efficiencies. In Proceedings of the IEA EGRD Workshop Mobility: Technology Priorities and Strategic Urban Planning, Espoo, Finland, 22–23 May 2013. [Google Scholar]

| 0.7 | 0.8 | 0.9 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Scenario (% CAVs) | Control Strategy | TTS (veh·h) | MTT (s) | Mean vm (km/h) | Mean ρm (veh/km/ln) | TEC (MWh) | EEC (MWh) | FC (l) | CO2 (kg) | CO (kg) | NOx (kg) | PMx (kg) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Baseline | 790.4 | 368.7 | 59.3 | 38.6 | 50.64 | - | 4879.0 | 11,973.0 | 139.8 | 35.32 | 0.96 | |
| 0 | RB-VSL | 779.7 | 360.9 | 60.8 | 37.7 | 50.03 | - | 4819.9 | 11,828.9 | 139.4 | 35.13 | 0.95 |
| QL-VSL | 778.2 | 360.4 | 59.7 | 38.1 | 49.86 | - | 4803.0 | 11,786.1 | 138.7 | 34.93 | 0.95 | |
| Baseline | 725.2 | 344.0 | 65.6 | 35.2 | 46.03 | 1.35 | 4304.7 | 10,551.5 | 130.8 | 31.82 | 0.86 | |
| 10 | RB-VSL | 718.6 | 343.6 | 64.5 | 36.1 | 45.71 | 1.34 | 4274.7 | 10,478.8 | 130.7 | 31.69 | 0.85 |
| QL-VSL | 709.7 | 342.9 | 66.1 | 34.3 | 45.47 | 1.34 | 4252.0 | 10,422.1 | 130.4 | 31.57 | 0.85 | |
| Baseline | 687.8 | 327.4 | 72.1 | 33.5 | 38.32 | 4.04 | 3301.9 | 8087.0 | 105.8 | 24.80 | 0.67 | |
| 30 | RB-VSL | 687.8 | 327.1 | 72.1 | 33.5 | 38.07 | 4.02 | 3281.2 | 8035.3 | 104.5 | 24.49 | 0.66 |
| QL-VSL | 656.5 | 317.3 | 75.9 | 30.2 | 37.31 | 4.02 | 3207.4 | 7851.3 | 105.5 | 24.21 | 0.65 | |
| Baseline | 618.2 | 302.4 | 86.1 | 25.7 | 30.01 | 6.76 | 2239.8 | 5478.6 | 76.2 | 17.07 | 0.46 | |
| 50 | RB-VSL | 613.9 | 299.7 | 86.6 | 25.4 | 30.07 | 6.76 | 2246.0 | 5490.2 | 77.7 | 17.08 | 0.46 |
| QL-VSL | 611.8 | 299.4 | 86.2 | 25.3 | 30.00 | 6.78 | 2237.2 | 5468.6 | 77.5 | 16.98 | 0.46 | |
| Baseline | 574.0 | 276.0 | 95.0 | 23.4 | 23.36 | 9.67 | 1319.7 | 3224.1 | 46.7 | 10.09 | 0.27 | |
| 70 | RB-VSL | 571.9 | 273.5 | 94.9 | 23.6 | 23.35 | 9.75 | 1310.6 | 3200.8 | 47.1 | 10.00 | 0.27 |
| QL-VSL | 560.9 | 271.0 | 96.6 | 22.1 | 23.13 | 9.71 | 1292.7 | 3157.5 | 45.9 | 9.87 | 0.26 | |
| Baseline | 489.0 | 235.7 | 108.9 | 18.2 | 17.17 | 12.89 | 412.4 | 1006.8 | 14.9 | 3.14 | 0.08 | |
| 90 | RB-VSL | 491.2 | 236.6 | 109.7 | 17.9 | 17.13 | 12.87 | 410.8 | 1001.9 | 15.1 | 3.09 | 0.08 |
| QL-VSL | 487.5 | 235.2 | 109.5 | 17.8 | 17.16 | 12.93 | 407.8 | 993.9 | 15.3 | 3.06 | 0.08 | |
| Baseline | 411.6 | 206.3 | 121.2 | 12.6 | 14.63 | 14.63 | - | - | - | - | - | |
| 100 | RB-VSL | 411.6 | 206.3 | 121.2 | 12.6 | 14.63 | 14.63 | - | - | - | - | - |
| QL-VSL | 411.6 | 206.3 | 121.2 | 12.6 | 14.63 | 14.63 | - | - | - | - | - |
| Scenario (% CAVs) | Control Strategy | TTS (veh·h) | MTT (s) | Mean vm (km/h) | Mean ρm (veh/km/ln) | TEC (MWh) | EEC (MWh) | FC (l) | CO2 (kg) | CO (kg) | NOx (kg) | PMx (kg) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Baseline | 790.4 | 368.7 | 59.3 | 38.6 | 50.64 | - | 4879.0 | 11,973.0 | 139.8 | 35.32 | 0.96 | |
| 0 | RB-VSL | 779.7 | 360.9 | 60.8 | 37.7 | 50.03 | - | 4819.9 | 11,828.9 | 139.4 | 35.13 | 0.95 |
| QL-VSL | 766.8 | 356.4 | 60.9 | 37.0 | 49.56 | - | 4774.7 | 11,717.2 | 138.9 | 34.90 | 0.94 | |
| Baseline | 725.2 | 344.0 | 65.6 | 35.2 | 46.03 | 1.35 | 4304.7 | 10,551.5 | 130.8 | 31.82 | 0.86 | |
| 10 | RB-VSL | 718.6 | 343.6 | 64.5 | 36.1 | 45.71 | 1.34 | 4274.7 | 10,478.8 | 130.7 | 31.69 | 0.85 |
| QL-VSL | 714.0 | 341.7 | 65.2 | 35.1 | 45.67 | 1.33 | 4271.8 | 10,468.4 | 131.6 | 31.71 | 0.85 | |
| Baseline | 687.8 | 327.4 | 72.1 | 33.5 | 38.32 | 4.04 | 3301.9 | 8087.0 | 105.8 | 24.80 | 0.67 | |
| 30 | RB-VSL | 687.8 | 327.1 | 72.1 | 33.5 | 38.07 | 4.02 | 3281.2 | 8035.3 | 104.5 | 24.49 | 0.66 |
| QL-VSL | 659.3 | 319.3 | 75.4 | 30.7 | 37.30 | 4.04 | 3204.4 | 7858.2 | 105.7 | 24.16 | 0.65 | |
| Baseline | 618.2 | 302.4 | 86.1 | 25.7 | 30.01 | 6.76 | 2239.8 | 5478.6 | 76.2 | 17.07 | 0.46 | |
| 50 | RB-VSL | 613.9 | 299.7 | 86.6 | 25.4 | 30.07 | 6.76 | 2246.0 | 5490.2 | 77.7 | 17.08 | 0.46 |
| QL-VSL | 613.1 | 299.6 | 86.7 | 25.2 | 29.94 | 6.78 | 2232.1 | 5458.1 | 76.1 | 16.99 | 0.46 | |
| Baseline | 574.0 | 276.0 | 95.0 | 23.4 | 23.36 | 9.67 | 1319.7 | 3224.1 | 46.7 | 10.09 | 0.27 | |
| 70 | RB-VSL | 571.9 | 273.5 | 94.9 | 23.6 | 23.35 | 9.75 | 1310.6 | 3200.8 | 47.1 | 10.00 | 0.27 |
| QL-VSL | 551.5 | 266.9 | 101.4 | 19.4 | 23.13 | 9.75 | 1289.0 | 3146.7 | 46.8 | 9.87 | 0.26 | |
| Baseline | 489.0 | 235.7 | 108.9 | 18.2 | 17.17 | 12.89 | 412.4 | 1006.8 | 14.9 | 3.14 | 0.08 | |
| 90 | RB-VSL | 491.2 | 236.6 | 109.7 | 17.9 | 17.13 | 12.87 | 410.8 | 1001.9 | 15.1 | 3.09 | 0.08 |
| QL-VSL | 481.6 | 233.1 | 110.8 | 17.1 | 17.12 | 12.93 | 403.4 | 983.2 | 14.8 | 3.02 | 0.08 | |
| Baseline | 411.6 | 206.3 | 121.2 | 12.6 | 14.63 | 14.63 | - | - | - | - | - | |
| 100 | RB-VSL | 411.6 | 206.3 | 121.2 | 12.6 | 14.63 | 14.63 | - | - | - | - | - |
| QL-VSL | 411.6 | 206.3 | 121.2 | 12.6 | 14.63 | 14.63 | - | - | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vrbanić, F.; Miletić, M.; Tišljarić, L.; Ivanjko, E. Influence of Variable Speed Limit Control on Fuel and Electric Energy Consumption, and Exhaust Gas Emissions in Mixed Traffic Flows. Sustainability 2022, 14, 932. https://doi.org/10.3390/su14020932
Vrbanić F, Miletić M, Tišljarić L, Ivanjko E. Influence of Variable Speed Limit Control on Fuel and Electric Energy Consumption, and Exhaust Gas Emissions in Mixed Traffic Flows. Sustainability. 2022; 14(2):932. https://doi.org/10.3390/su14020932
Chicago/Turabian StyleVrbanić, Filip, Mladen Miletić, Leo Tišljarić, and Edouard Ivanjko. 2022. "Influence of Variable Speed Limit Control on Fuel and Electric Energy Consumption, and Exhaust Gas Emissions in Mixed Traffic Flows" Sustainability 14, no. 2: 932. https://doi.org/10.3390/su14020932
APA StyleVrbanić, F., Miletić, M., Tišljarić, L., & Ivanjko, E. (2022). Influence of Variable Speed Limit Control on Fuel and Electric Energy Consumption, and Exhaust Gas Emissions in Mixed Traffic Flows. Sustainability, 14(2), 932. https://doi.org/10.3390/su14020932







