A Metaheuristic-Based Micro-Grid Sizing Model with Integrated Arbitrage-Aware Multi-Day Battery Dispatching
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Literature Review
1.3. Knowledge Gaps
1.4. Novel Contributions
- Formulating a robust metaheuristic-based MG equipment capacity planning optimisation model tailored towards community-scale, 100%-renewable and -reliable energy projects.
- Developing an arbitrage-aware, dynamic, look-ahead, predictive dispatch strategy for the optimal scheduling of MGs—charging/discharging of energy storage systems and energy exchanges with the main power grid—over a moving 72-h dispatch horizon.
- Nesting the developed forward-looking operational planning problem—formulated to optimally respond to the dynamic nature of system conditions over a moving three-day period—within the proposed metaheuristic-based MG sizing model to jointly optimise the design and dispatch of MG systems.
1.5. Paper Organisation
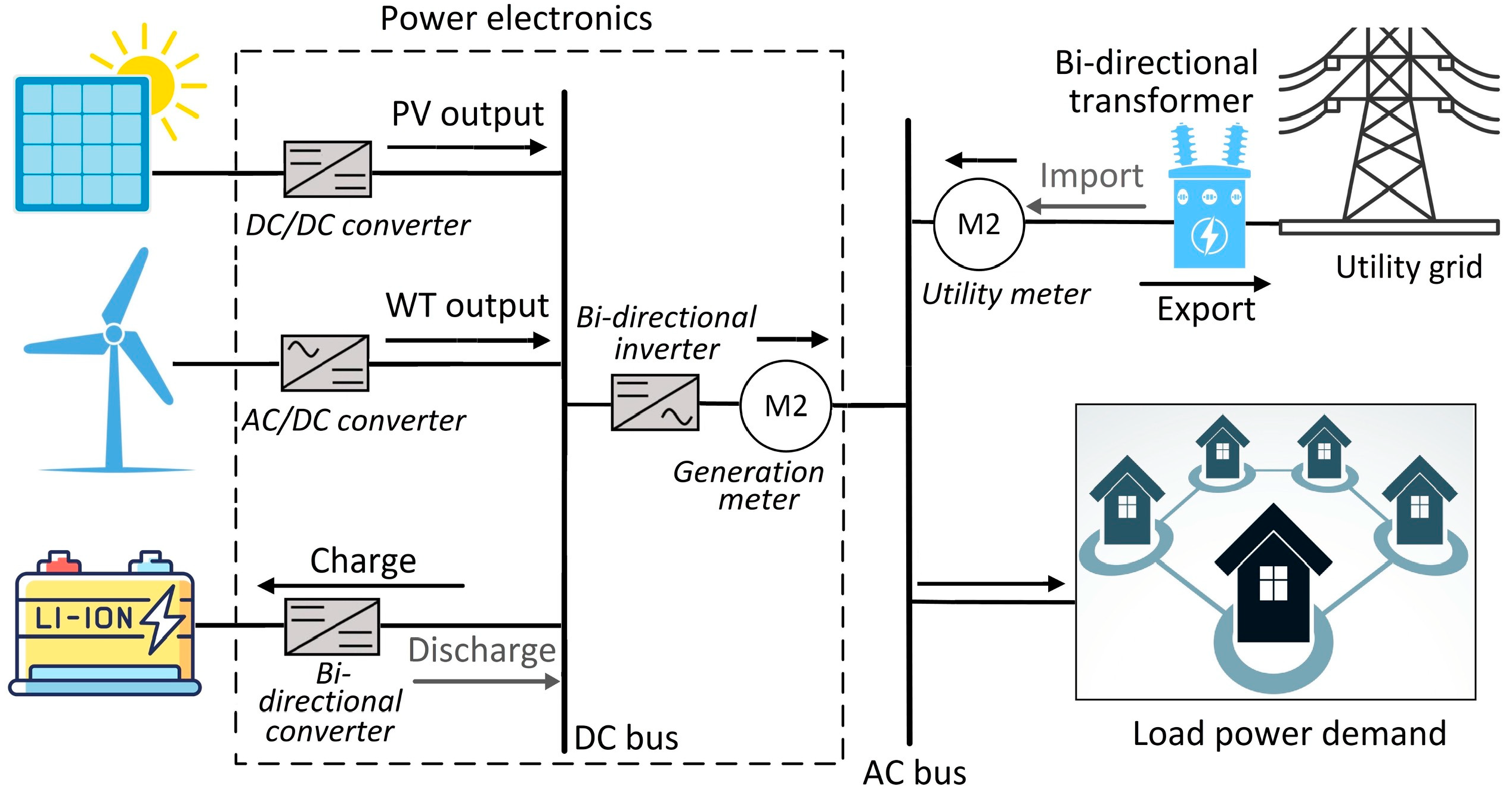
2. Test-Case Micro-Grid
2.1. Wind Turbines
2.2. PV Panels
2.3. Battery Storage
2.4. Inverter
3. Methodology
3.1. Targeted Arbitrage Opportunities
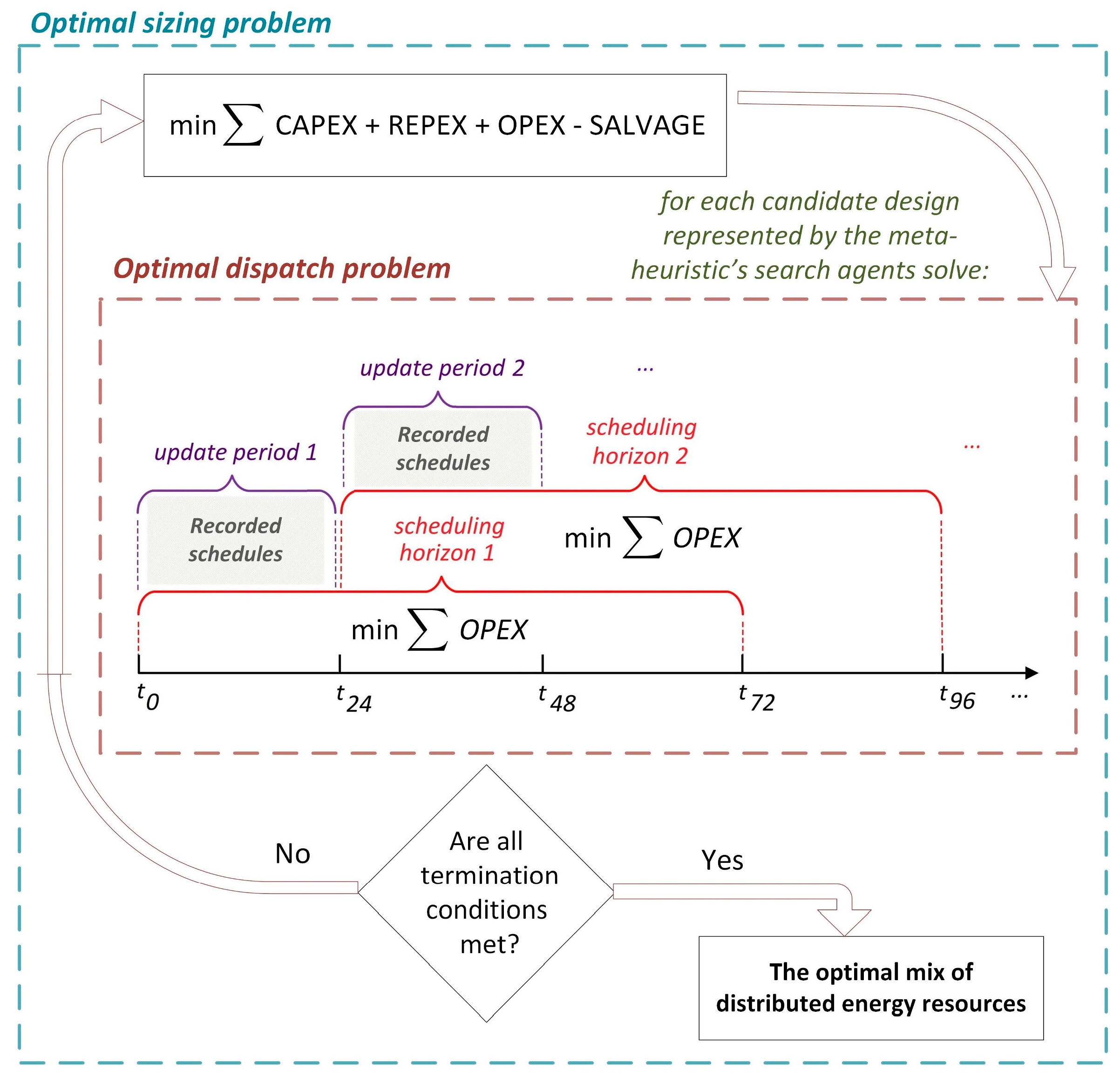
3.2. Optimal Capacity Planning Problem
Metaheuristic Optimisation Algorithm
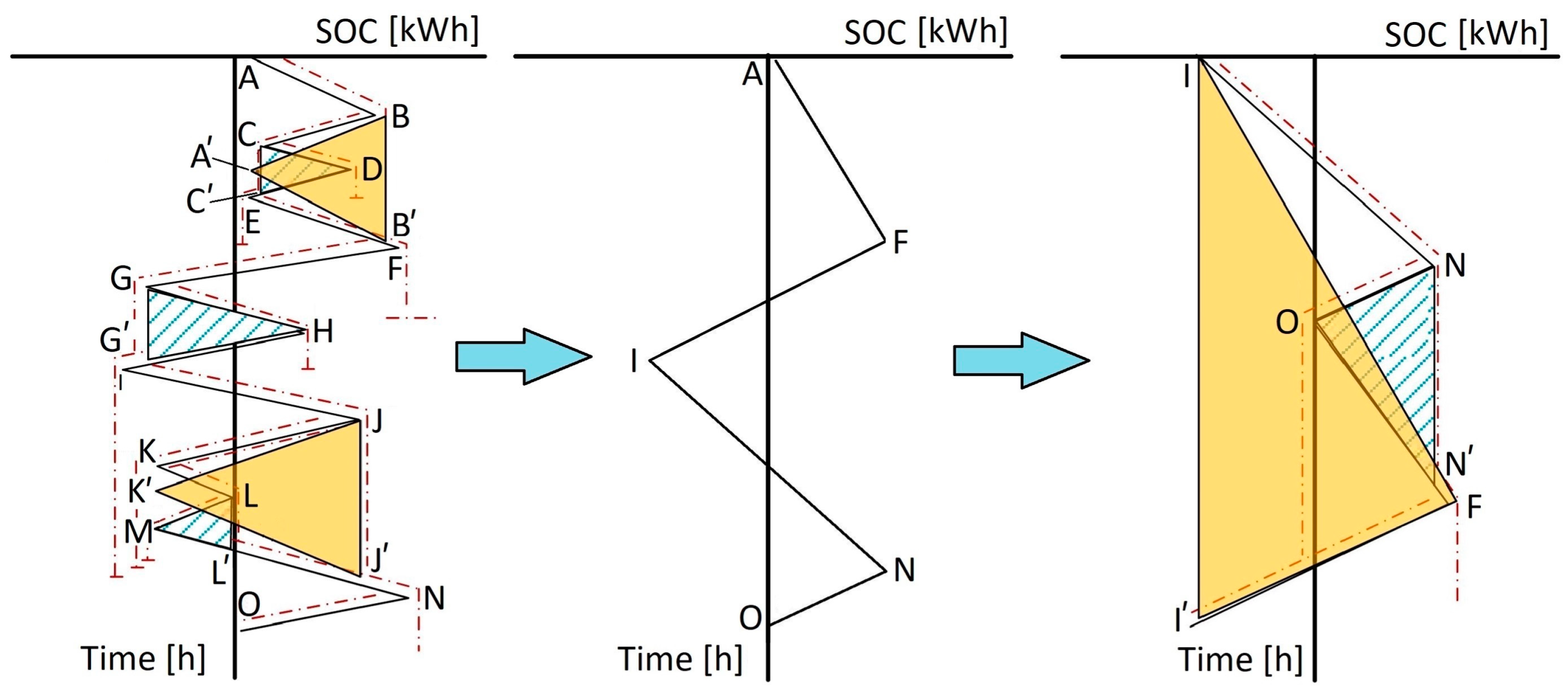
3.3. Multi-Day Energy Dispatch Scheduling Problem
3.4. Overview of the Overall Method
4. Case Study: Simulation Results and Discussion
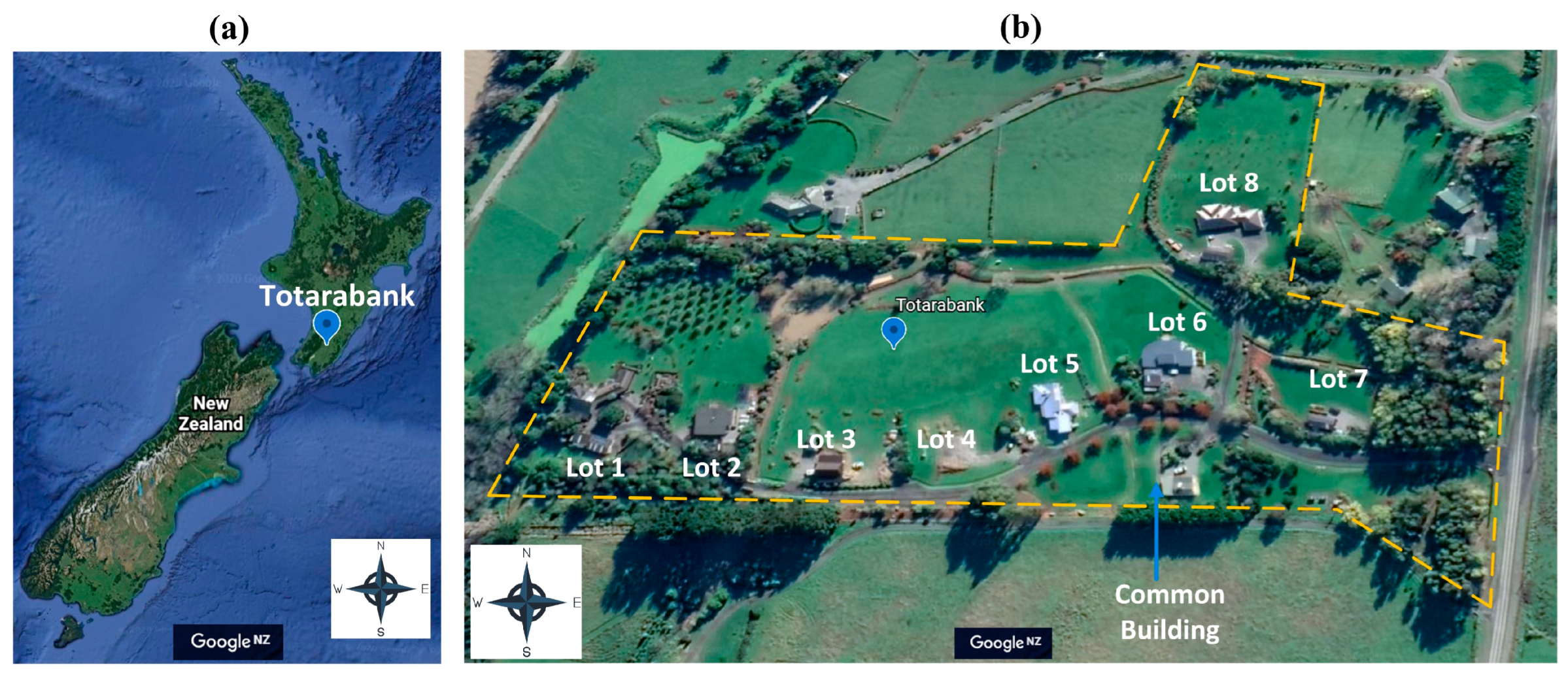
4.1. Input Data
4.2. Comparative Optimal MG Sizing Results
4.3. Economics of Daily Energy Arbitrage
Impact on the Optimal MG Sizing
4.4. Validation of the Equilibrium Optimiser
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Diab, A.A.Z.; El-Rifaie, A.M.; Zaky, M.M.; Tolba, M.A. Optimal Sizing of Stand-Alone Microgrids Based on Recent Metaheu-ristic Algorithms. Mathematics 2022, 10, 140. [Google Scholar] [CrossRef]
- Cardenas, G.A.R.; Khezri, R.; Mahmoudi, A.; Kahourzadeh, S. Optimal Planning of Remote Microgrids with Multi-Size Split-Diesel Generators. Sustainability 2022, 14, 2892. [Google Scholar] [CrossRef]
- Ding, X.; Guo, Q.; Qiannan, T.; Jermsittiparsert, K. Economic and environmental assessment of multi-energy microgrids under a hybrid optimization technique. Sustain. Cities Soc. 2020, 65, 102630. [Google Scholar] [CrossRef]
- Nikzad, M.; Samimi, A. Integration of designing price-based demand response models into a stochastic bi-level scheduling of multiple energy carrier microgrids considering energy storage systems. Appl. Energy 2020, 282, 116163. [Google Scholar] [CrossRef]
- Mohseni, S.; Brent, A.C.; Burmester, D. Off-Grid Multi-Carrier Microgrid Design Optimisation: The Case of Rakiura–Stewart Island, Aotearoa–New Zealand. Energies 2021, 14, 6522. [Google Scholar] [CrossRef]
- Sanjareh, M.B.; Nazari, M.H.; Gharehpetian, G.B.; Hosseinian, S.H. A novel approach for sizing thermal and electrical energy storage systems for energy management of islanded residential microgrid. Energy Build. 2021, 238, 110850. [Google Scholar] [CrossRef]
- Mohseni, S.; Brent, A.C.; Kelly, S.; Browne, W.N. Demand Response-Integrated Investment and Operational Planning of Re-newable and Sustainable Energy Systems Considering Forecast Uncertainties: A Systematic Review. Renew. Sustain. Energy Rev. 2022, 158, 112095. [Google Scholar] [CrossRef]
- Pimm, A.J.; Palczewski, J.; Morris, R.; Cockerill, T.T.; Taylor, P.G. Community energy storage: A case study in the UK using a linear programming method. Energy Convers. Manag. 2019, 205, 112388. [Google Scholar] [CrossRef]
- Lai, C.S.; Locatelli, G.; Pimm, A.; Wu, X.; Lai, L.L. A review on long-term electrical power system modeling with energy storage. J. Clean. Prod. 2020, 280, 124298. [Google Scholar] [CrossRef]
- Ersal, T.; Ahn, C.; Peters, D.L.; Whitefoot, J.W.; Mechtenberg, A.R.; Hiskens, I.A.; Peng, H.; Stefanopoulou, A.G.; Papalambros, P.Y.; Stein, J.L. Coupling Between Component Sizing and Regulation Capability in Microgrids. IEEE Trans. Smart Grid 2013, 4, 1576–1585. [Google Scholar] [CrossRef]
- Whitefoot, J.W.; Mechtenberg, A.R.; Peters, D.L.; Papalambros, P.Y. Optimal Component Sizing and Forward-Looking Dis-patch of an Electrical Microgrid for Energy Storage Planning. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Washington, DC, USA, 28–31 January 2011; Volume 54822, pp. 341–350. [Google Scholar]
- Li, B.; Roche, R.; Miraoui, A. Microgrid sizing with combined evolutionary algorithm and MILP unit commitment. Appl. Energy 2017, 188, 547–562. [Google Scholar] [CrossRef]
- Swaminathan, S.; Pavlak, G.S.; Freihaut, J. Sizing and dispatch of an islanded microgrid with energy flexible buildings. Appl. Energy 2020, 276, 115355. [Google Scholar] [CrossRef]
- Xiao, H.; Pei, W.; Dong, Z.; Kong, L. Bi-level planning for integrated energy systems incorporating demand response and energy storage under uncertain environments using novel metamodel. CSEE J. Power Energy Syst. 2018, 4, 155–167. [Google Scholar] [CrossRef]
- Chen, C.; Sun, H.; Shen, X.; Guo, Y.; Guo, Q.; Xia, T. Two-stage robust planning-operation co-optimization of energy hub considering precise energy storage economic model. Appl. Energy 2019, 252, 113372. [Google Scholar] [CrossRef]
- Subramanyam, V.; Jin, T.; Novoa, C. Sizing a renewable microgrid for flow shop manufacturing using climate analytics. J. Clean. Prod. 2019, 252, 119829. [Google Scholar] [CrossRef]
- Moretti, L.; Astolfi, M.; Vergara, C.; Macchi, E.; Pérez-Arriaga, J.I.; Manzolini, G. A Design and Dispatch Optimization Algo-rithm Based on Mixed Integer Linear Programming for Rural Electrification. Appl. Energy 2019, 233–234, 1104–1121. [Google Scholar] [CrossRef]
- Ishraque, F.; Shezan, S.A.; Ali, M.; Rashid, M. Optimization of load dispatch strategies for an islanded microgrid connected with renewable energy sources. Appl. Energy 2021, 292, 116879. [Google Scholar] [CrossRef]
- Moretti, L.; Polimeni, S.; Meraldi, L.; Raboni, P.; Leva, S.; Manzolini, G. Assessing the Impact of a Two-Layer Predictive Dis-patch Algorithm on Design and Operation of off-Grid Hybrid Microgrids. Renew. Energy 2019, 143, 1439–1453. [Google Scholar] [CrossRef]
- Goodall, G.; Hering, A.; Newman, A. Characterizing solutions in optimal microgrid procurement and dispatch strategies. Appl. Energy 2017, 201, 1–19. [Google Scholar] [CrossRef]
- Ogunmodede, O.; Anderson, K.; Cutler, D.; Newman, A. Optimizing design and dispatch of a renewable energy system. Appl. Energy 2021, 287, 116527. [Google Scholar] [CrossRef]
- Geng, S.; Vrakopoulou, M.; Hiskens, I.A. Chance-Constrained Optimal Capacity Design for a Renewable-Only Islanded Mi-crogrid. Electr. Power Syst. Res. 2020, 189, 106564. [Google Scholar] [CrossRef]
- Bustos, C.; Watts, D. Novel methodology for microgrids in isolated communities: Electricity cost-coverage trade-off with 3-stage technology mix, dispatch & configuration optimizations. Appl. Energy 2017, 195, 204–221. [Google Scholar] [CrossRef]
- Ren, F.; Lin, X.; Wei, Z.; Zhai, X.; Yang, J. A novel planning method for design and dispatch of hybrid energy systems. Appl. Energy 2022, 321, 119335. [Google Scholar] [CrossRef]
- Fares, D.; Fathi, M.; Mekhilef, S. Performance evaluation of metaheuristic techniques for optimal sizing of a stand-alone hybrid PV/wind/battery system. Appl. Energy 2021, 305, 117823. [Google Scholar] [CrossRef]
- Ramli, M.A.; Bouchekara, H.; Alghamdi, A.S. Optimal sizing of PV/wind/diesel hybrid microgrid system using multi-objective self-adaptive differential evolution algorithm. Renew. Energy 2018, 121, 400–411. [Google Scholar] [CrossRef]
- Ray, M.L.; Rogers, A.L.; McGowan, J.G. Analysis of Wind Shear Models and Trends in Different Terrains. Renewable Energy Research Laboratory. University of Massachusetts 2006. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.574.7468&rep=rep1&type=pdf (accessed on 6 October 2022).
- Bukar, A.L.; Tan, C.W.; Lau, K.Y. Optimal sizing of an autonomous photovoltaic/wind/battery/diesel generator microgrid using grasshopper optimization algorithm. Sol. Energy 2019, 188, 685–696. [Google Scholar] [CrossRef]
- Borhanazad, H.; Mekhilef, S.; Ganapathy, V.G.; Modiri-Delshad, M.; Mirtaheri, A. Optimization of micro-grid system using MOPSO. Renew. Energy 2014, 71, 295–306. [Google Scholar] [CrossRef]
- Chen, S.X.; Gooi, H.B.; Wang, M.Q. Sizing of Energy Storage for Microgrids. IEEE Trans. Smart Grid 2011, 3, 142–151. [Google Scholar] [CrossRef]
- Wu, F.-B.; Yang, B.; Ye, J.-L. (Eds.) Chapter 2—Technologies of Energy Storage Systems. In Grid-Scale Energy Storage Systems and Applications; Academic Press: Cambridge, MA, USA, 2019; pp. 17–56. ISBN 978-0-12-815292-8. [Google Scholar]
- Asian Development Bank (ADB). Handbook on Battery Energy Storage System. 2018. Available online: https://www.adb.org/sites/default/files/publication/479891/handbook-battery-energy-storage-system.pdf (accessed on 26 September 2022).
- Wang, Y.; Song, F.; Ma, Y.; Zhang, Y.; Yang, J.; Liu, Y.; Zhang, F.; Zhu, J. Research on capacity planning and optimization of regional integrated energy system based on hybrid energy storage system. Appl. Therm. Eng. 2020, 180, 115834. [Google Scholar] [CrossRef]
- Darras, C.; Sailler, S.; Thibault, C.; Muselli, M.; Poggi, P.; Hoguet, J.; Melscoet, S.; Pinton, E.; Grehant, S.; Gailly, F.; et al. Sizing of photovoltaic system coupled with hydrogen/oxygen storage based on the ORIENTE model. Int. J. Hydrogen Energy 2010, 35, 3322–3332. [Google Scholar] [CrossRef]
- Mohseni, S.; Brent, A.C. Economic Viability Assessment of Sustainable Hydrogen Production, Storage, and Utilisation Tech-nologies Integrated into on- and off-Grid Micro-Grids: A Performance Comparison of Different Meta-Heuristics. Int. J. Hydrogen Energy 2020, 45, 34412–34436. [Google Scholar] [CrossRef]
- Mohseni, S.; Brent, A.C.; Burmester, D.; Browne, W.N. Lévy-Flight Moth-Flame Optimisation Algorithm-Based Micro-Grid Equipment Sizing: An Integrated Investment and Operational Planning Approach. Energy AI 2021, 3, 100047. [Google Scholar] [CrossRef]
- Hakimi, S.M.; Moghaddas-Tafreshi, S.M. Optimal Sizing of a Stand-Alone Hybrid Power System via Particle Swarm Optimi-zation for Kahnouj Area in South-East of Iran. Renew Energy 2009, 34, 1855–1862. [Google Scholar] [CrossRef]
- Ehsan, A.; Yang, Q. Scenario-based investment planning of isolated multi-energy microgrids considering electricity, heating and cooling demand. Appl. Energy 2018, 235, 1277–1288. [Google Scholar] [CrossRef]
- Kerdphol, T.; Qudaih, Y.; Mitani, Y. Optimum battery energy storage system using PSO considering dynamic demand response for microgrids. Int. J. Electr. Power Energy Syst. 2016, 83, 58–66. [Google Scholar] [CrossRef]
- Lorestani, A.; Gharehpetian, G.; Nazari, M.H. Optimal sizing and techno-economic analysis of energy- and cost-efficient standalone multi-carrier microgrid. Energy 2019, 178, 751–764. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl. Based Syst. 2019, 191, 105190. [Google Scholar] [CrossRef]
- Totarabank–Sustainable Rural Living. Available online: https://totarabank.weebly.com/ (accessed on 26 August 2022).
- MATLAB; Version 9.5; The MathWorks Inc: Natick, MA, USA, 2018; R2018b.
- Anderson, B.; Eyers, D.; Ford, R.; Giraldo Ocampo, D.; Peniamina, R.; Stephenson, J.; Suomalainen, K.; Wilcocks, L.; Jack, M. New Zealand GREEN Grid Household Electricity Demand Study 2014–2018, 2018. [Data Collection]. Colchester, Essex: UK Data Service. Available online: https://reshare.ukdataservice.ac.uk/853334/ (accessed on 6 October 2022).
- National Institute of Water and Atmospheric Research (NIWA). New Zealand’s National Climate Database. Available online: https://cliflo.niwa.co.nz (accessed on 6 October 2022).
- Exchange Rates UK. US Dollar to New Zealand Dollar Spot Exchange Rates for 2021. Available online: https://www.exchangerates.org.uk/USD-NZD-spot-exchange-rates-history-2021.html (accessed on 6 September 2022).
- Canadian Solar Inc. CS6K-270|275|280P (2017). PV Module Product Datasheet V5.552_EN. Available online: https://www.collectiu-solar.cat/pdf/2-Panel-Canadian_Solar-Datasheet-CS6K.pdf (accessed on 26 August 2022).
- Fioriti, D.; Poli, D.; Duenas-Martinez, P.; Micangeli, A. Multiple Design Options for Sizing Off-Grid Microgrids: A Novel Sin-gle-Objective Approach to Support Multi-Criteria Decision Making. Sustain. Energy Grids Netw. 2022, 30, 100644. [Google Scholar] [CrossRef]
- Shin, J.; Lee, J.H.; Realff, M.J. Operational Planning and Optimal Sizing of Microgrid Considering Multi-Scale Wind Uncer-tainty. Appl. Energy 2017, 195, 616–633. [Google Scholar] [CrossRef]
- The X2000L Wind Turbine System. Available online: https://www.solazone.com.au/1kw-2kw-wind-turbines/ (accessed on 26 August 2022).
- Ju, L.; Tan, Q.; Zhao, R.; Gu, S.; Jiaoyang; Wang, W. Multi-objective electro-thermal coupling scheduling model for a hybrid energy system comprising wind power plant, conventional gas turbine, and regenerative electric boiler, considering uncertainty and demand response. J. Clean. Prod. 2019, 237, 117774. [Google Scholar] [CrossRef]
- CSIRO. GenCost 2019-20: Preliminary Results for Stakeholder Review. 2019. Available online: https://wa.aemo.com.au/-/media/Files/Electricity/NEM/Planning_and_Forecasting/Inputs-Assumptions-Methodologies/2019/CSIRO-GenCost2019-20_DraftforReview.pdf (accessed on 26 August 2022).
- RESU: Residential Energy Storage Unit for Photovoltaic Systems. Available online: https://www.solarelectricsupply.com/lg-chem-resu3-3-home-ess-energy-storage-battery-system (accessed on 26 August 2022).
- Sun, S.; Smith, B.; Wills, R.; Crossland, A. Effects of time resolution on finances and self-consumption when modeling domestic PV-battery systems. Energy Rep. 2020, 6, 157–165. [Google Scholar] [CrossRef]
- Leonics Co. Apollo GTP-500; 2018, P.LEN.BRO.INV.156 Rev. 12.00. Available online: http://www.leonics.com/product/renewable/inverter/dl/GTP-500-156.pdf (accessed on 26 August 2022).
- Mohseni, S.; Brent, A.C.; Burmester, D. A Demand Response-Centred Approach to the Long-Term Equipment Capacity Planning of Grid-Independent Micro-Grids Optimized by the Moth-Flame Optimization Algorithm. Energy Convers. Manag. 2019, 200, 112105. [Google Scholar] [CrossRef]
- Graham, P.; Hayward, J.; Foster, J.; Havas, L. GenCost 2020-21: Final Report; CSIRO: Newcastle, UK, 2021. [Google Scholar]
- Schmidt, O.; Melchior, S.; Hawkes, A.; Staffell, I. Projecting the Future Levelized Cost of Electricity Storage Technologies. Joule 2019, 3, 81–100. [Google Scholar] [CrossRef]
- Solar Power New Zealand. Solar Power Buy Back Rates New Zealand 2021. Available online: https://solar-power.co.nz/residential-solar-power-buy-back-rates-nz/ (accessed on 26 August 2022).
- Goldberg, D.E. Genetic Algorithms; Pearson Education India: Noida, India, 2013; ISBN 817758829X. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Settles, M.; Soule, T. Breeding Swarms: A GA/PSO Hybrid. In Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation, Washington, DC, USA, 25–29 June 2005; pp. 161–168. [Google Scholar]
- Yang, X.-S. Harmony Search as a Metaheuristic Algorithm. In Music-Inspired Harmony Search Algorithm; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–14. [Google Scholar]
- van Laarhoven, P.J.M.; Aarts, E.H.L. Simulated Annealing. In Simulated Annealing: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 1987; pp. 7–15. [Google Scholar]
- Karaboga, D. Artificial Bee Colony Algorithm. Scholarpedia 2010, 5, 6915. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant Colony Optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Mirjalili, S. The Ant Lion Optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]




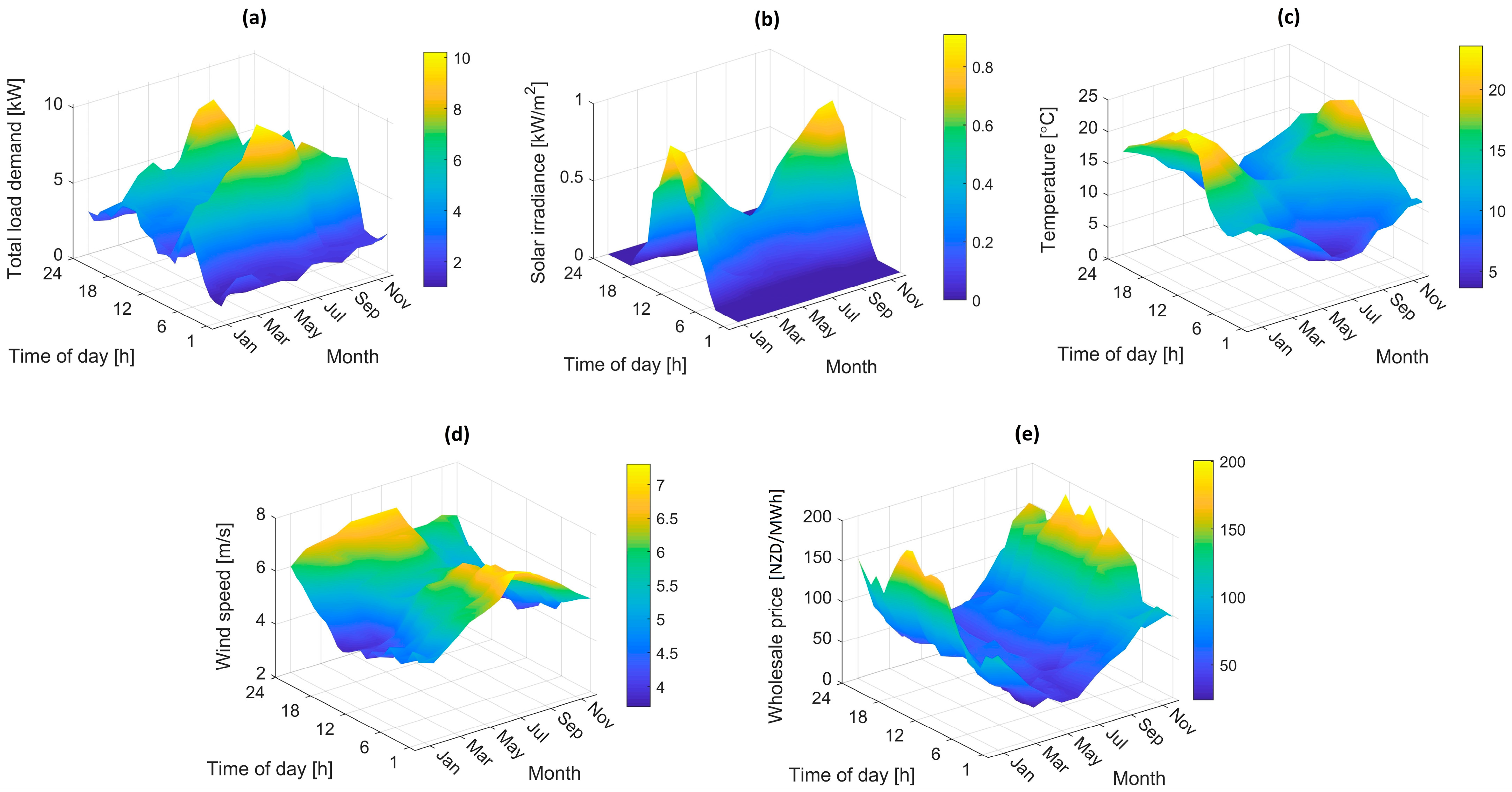

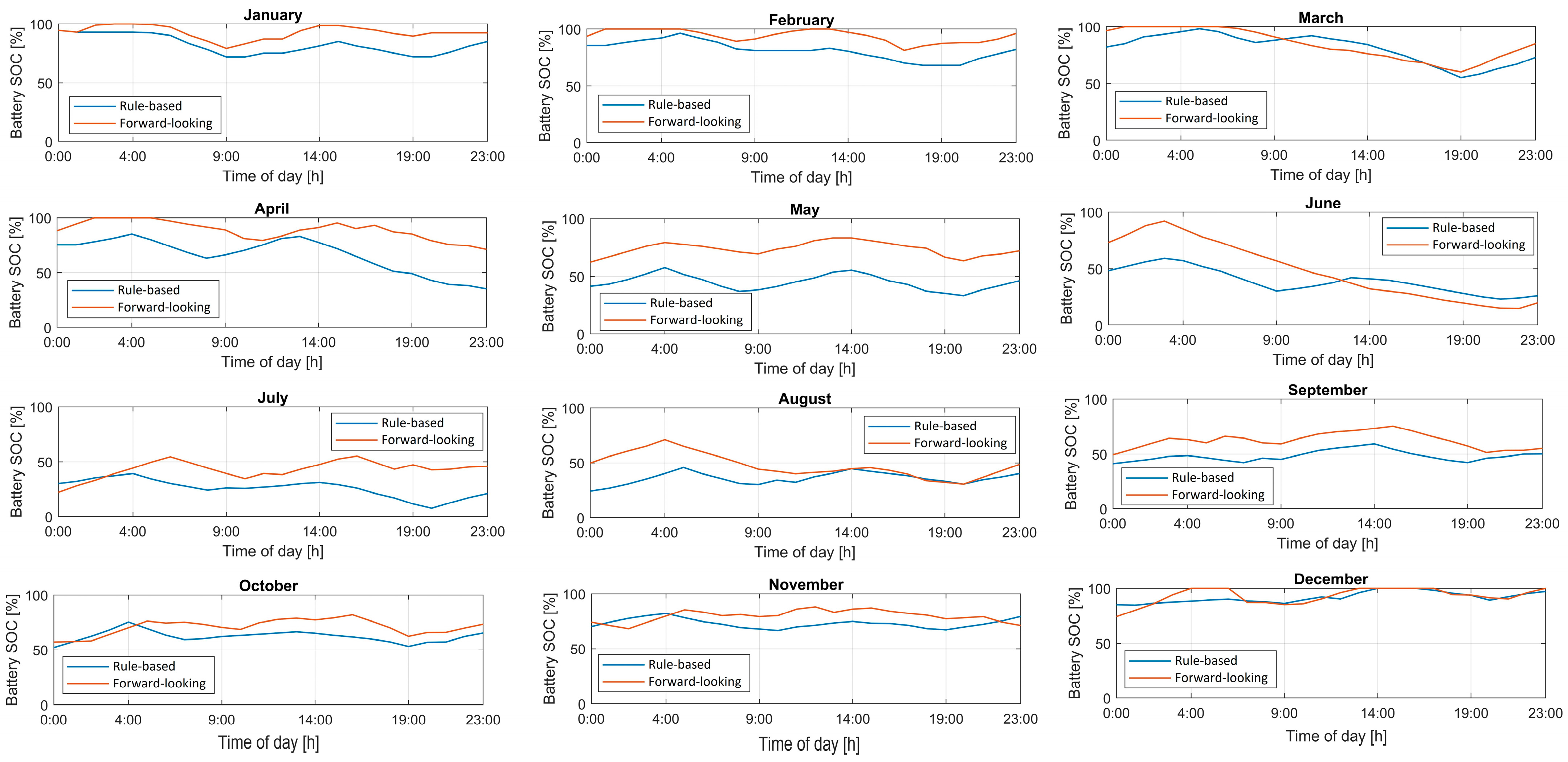
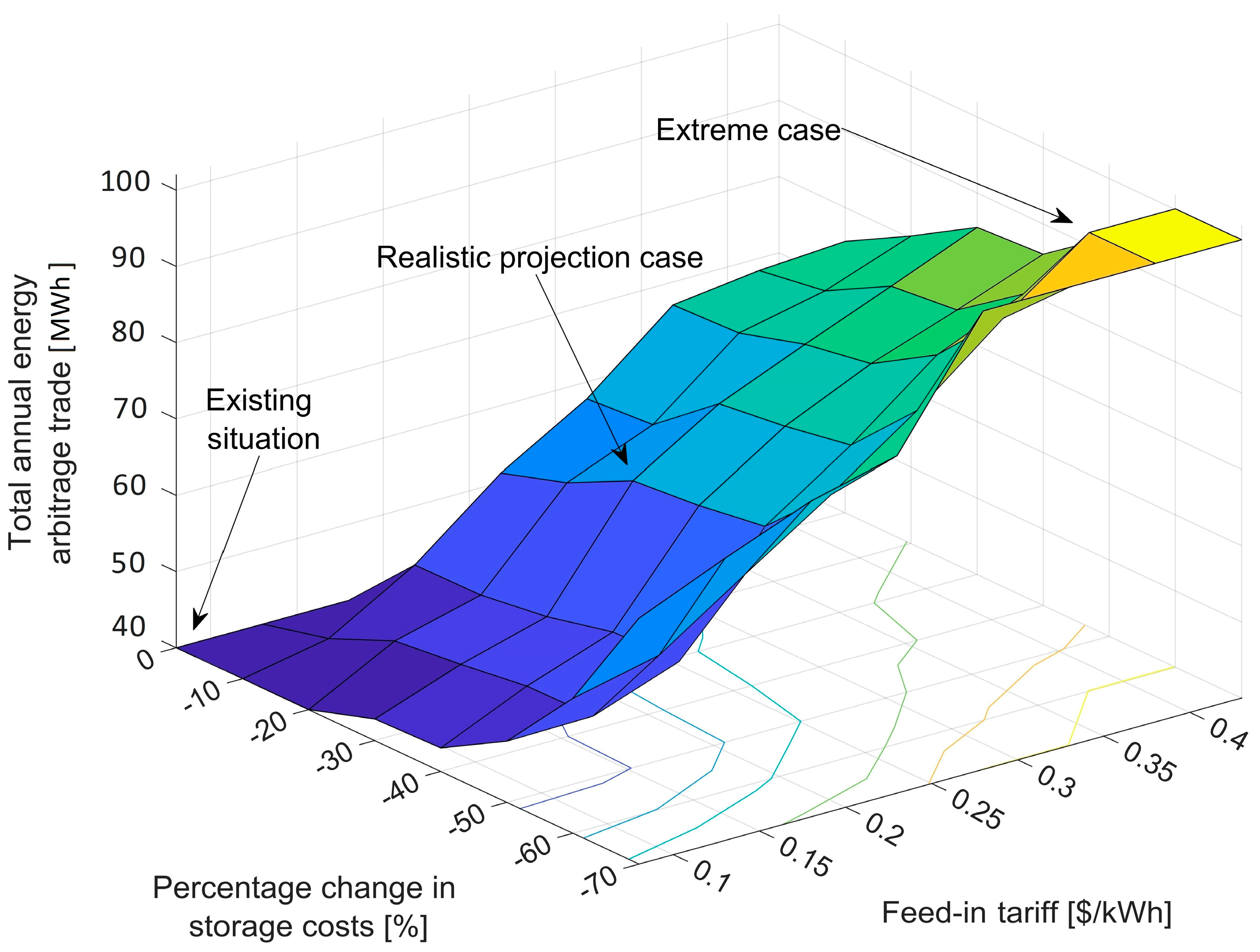
| Reference | Components | Real Input Data | Two-Stage Modelling | Arbitrage | Multi-Day Rolling Horizon | ||||
|---|---|---|---|---|---|---|---|---|---|
| Grid | PV | WT | BESS | Diesel | |||||
| [12] | × | ✓ | × | ✓ | × | × | ✓ | × | × |
| [13] | ✓ | ✓ | × | ✓ | × | ✓ | × | × | × |
| [14] | ✓ | ✓ | ✓ | ✓ | × | × | × | × | × |
| [15] | ✓ | ✓ | × | ✓ | ✓ | × | ✓ | × | × |
| [16] | ✓ | ✓ | ✓ | ✓ | × | × | × | × | × |
| [17] | × | ✓ | × | ✓ | ✓ | ✓ | ✓ | × | × |
| [18] | × | ✓ | ✓ | ✓ | ✓ | ✓ | × | × | × |
| [19] | × | ✓ | × | ✓ | × | ✓ | ✓ | × | × |
| [20] | × | ✓ | × | ✓ | ✓ | ✓ | × | × | × |
| [21] | × | ✓ | × | ✓ | × | ✓ | × | × | × |
| [22] | × | ✓ | ✓ | ✓ | × | × | × | × | × |
| [23] | × | ✓ | ✓ | ✓ | × | ✓ | × | × | × |
| [24] | ✓ | ✓ | × | ✓ | × | ✓ | × | × | × |
| [25] | × | ✓ | ✓ | ✓ | × | × | × | × | × |
| This study | ✓ | ✓ | ✓ | ✓ | × | ✓ | ✓ | ✓ | ✓ |
| Component | Capital Cost | Replacement Cost | Operation and Maintenance Cost | Lifetime | Efficiency | Source(s) |
|---|---|---|---|---|---|---|
| PV panel | NZD 1135/kW | NZD 915/kW | NZD 5/kW/year | 25 years | 17.11% | [5,47,48] |
| Wind turbine | NZD 1290/kW | NZD 1020/kW | NZD 191/kW/year | 25 years | N/A a | [49,50,51] |
| Battery pack b | NZD 1073/kWh | NZD 504/kWh | NZD 2.1/kWh/year | 15 years | 90% c | [52,53] |
| Hybrid inverter | NZD 533/kW | NZD 533/kW | NZD 1.3/kW/year | 15 years | 96% | [54,55] |
| Output | Dispatch Strategy | ||
|---|---|---|---|
| Multi-Day Scheduling | One-Day Scheduling | Cycle-Charging | |
| Total net present cost [NZD] | 55,175 | 60,244 | 69,466 |
| Levelised cost of energy [NZD/kWh] | 0.19 | 0.22 | 0.27 |
| Total discounted renewable energy generation [kWh] | 1,248,446 | 1,773,003 | 2,754,411 |
| Solar PV generator size [kW] | 8 | 10 | 16 |
| WT generator size [kW] | 11 | 17 | 20 |
| Li-ion battery storage size [kWh] | 31 | 19 | 12 |
| Multi-mode inverter size [kW] | 7 | 8 | 9 |
| TNPC of the components [NZD] | 99,581 | 86,383 | 84,610 |
| Total net energy purchased [kWh] | −249,471 | −175,170 | −302,882 |
| TNPC of the net electricity imports [NZD] | −44,406 | −26,139 | −15,144 |
| Total excess renewable energy curtailment [kWh] | 1509 | 11,738 | 19,121 |
| Battery bank autonomy a [h] | 11.2 | 7.1 | 4.5 |
| Output | Scenario | ||
|---|---|---|---|
| Existing Situation (Status Quo) a | Realistic Projection | Extreme-Case Projection | |
| Total net present cost [NZD] | 50,148 | 26,270 | 15,142 |
| Total net energy arbitrage trade profit [NZDm] | 0.09 | 0.11 | 0.13 |
| Optimal battery bank size [kWh] | 30 | 48 | 51 |
| Optimal multi-mode inverter size [kW] | 7 | 12 | 15 |
| Algorithm | Parameter Settings | Reference |
|---|---|---|
| GA | Mutation rate = 0.05, crossover probability = 0.1, mutation probability = 0.9 | [60] |
| PSO | Acceleration coefficients = 2, inertia weight = 0.7 | [61] |
| Hybrid GA-PSO | Mutation rate = 0.05, crossover probability = 0.1, mutation probability = 0.9, acceleration coefficients = 2, inertia weight = 0.7 | [62] |
| EO | Coefficients of the inertia weight equation = 2.0 | [41] |
| HS | Harmony memory accepting rate = 0.85 | [63] |
| SA | Initial acceptance probability = 0.4, cooling ratio = 0.95, size factor = 16, imbalance factor = 0.05 | [64] |
| ABC | Number of onlooker bees = 25, number of employed bees = 25 | [65] |
| ACO | Archive size = 50, locality of search = 0.1, convergence speed = 0.85 | [66] |
| ALO | Self-adaptive adjustment of a single control parameter | [67] |
| Algorithm | Optimised TNPC | Algorithm | Optimised TNPC |
|---|---|---|---|
| ABC | NZD 61,410 | HS | NZD 63,992 |
| ACO | NZD 64,739 | Hybrid GA-PSO | NZD 56,120 |
| ALO | NZD 63,005 | PSO | NZD 56,802 |
| EO | NZD 55,175 | SA | NZD 62,790 |
| GA | NZD 56,790 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohseni, S.; Brent, A.C. A Metaheuristic-Based Micro-Grid Sizing Model with Integrated Arbitrage-Aware Multi-Day Battery Dispatching. Sustainability 2022, 14, 12941. https://doi.org/10.3390/su141912941
Mohseni S, Brent AC. A Metaheuristic-Based Micro-Grid Sizing Model with Integrated Arbitrage-Aware Multi-Day Battery Dispatching. Sustainability. 2022; 14(19):12941. https://doi.org/10.3390/su141912941
Chicago/Turabian StyleMohseni, Soheil, and Alan C. Brent. 2022. "A Metaheuristic-Based Micro-Grid Sizing Model with Integrated Arbitrage-Aware Multi-Day Battery Dispatching" Sustainability 14, no. 19: 12941. https://doi.org/10.3390/su141912941
APA StyleMohseni, S., & Brent, A. C. (2022). A Metaheuristic-Based Micro-Grid Sizing Model with Integrated Arbitrage-Aware Multi-Day Battery Dispatching. Sustainability, 14(19), 12941. https://doi.org/10.3390/su141912941







