Computing Models to Predict the Compressive Strength of Engineered Cementitious Composites (ECC) at Various Mix Proportions
Abstract
1. Introduction
2. Literature Review
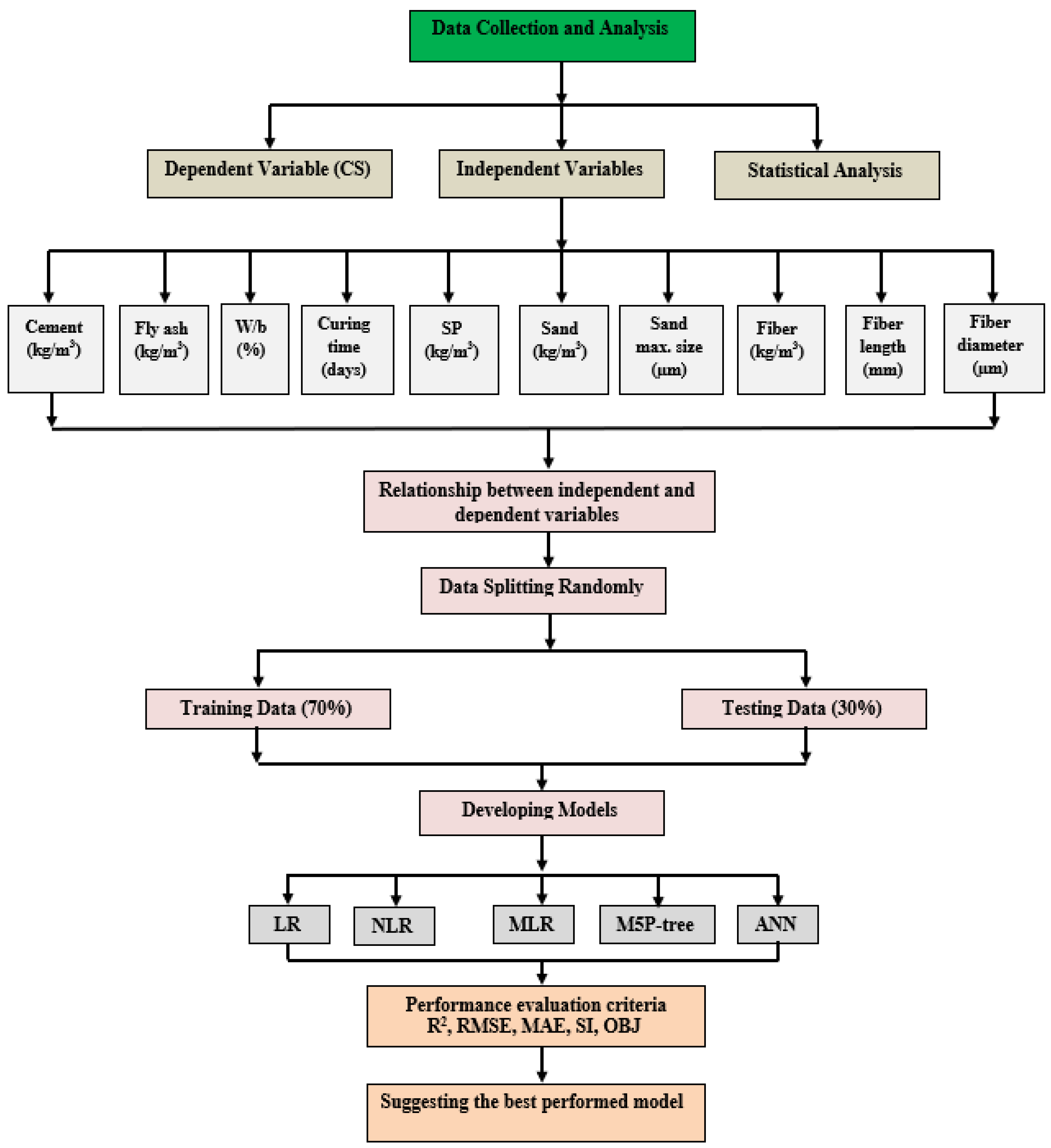
3. Methodology and Models
3.1. Data Collection
3.2. Modeling
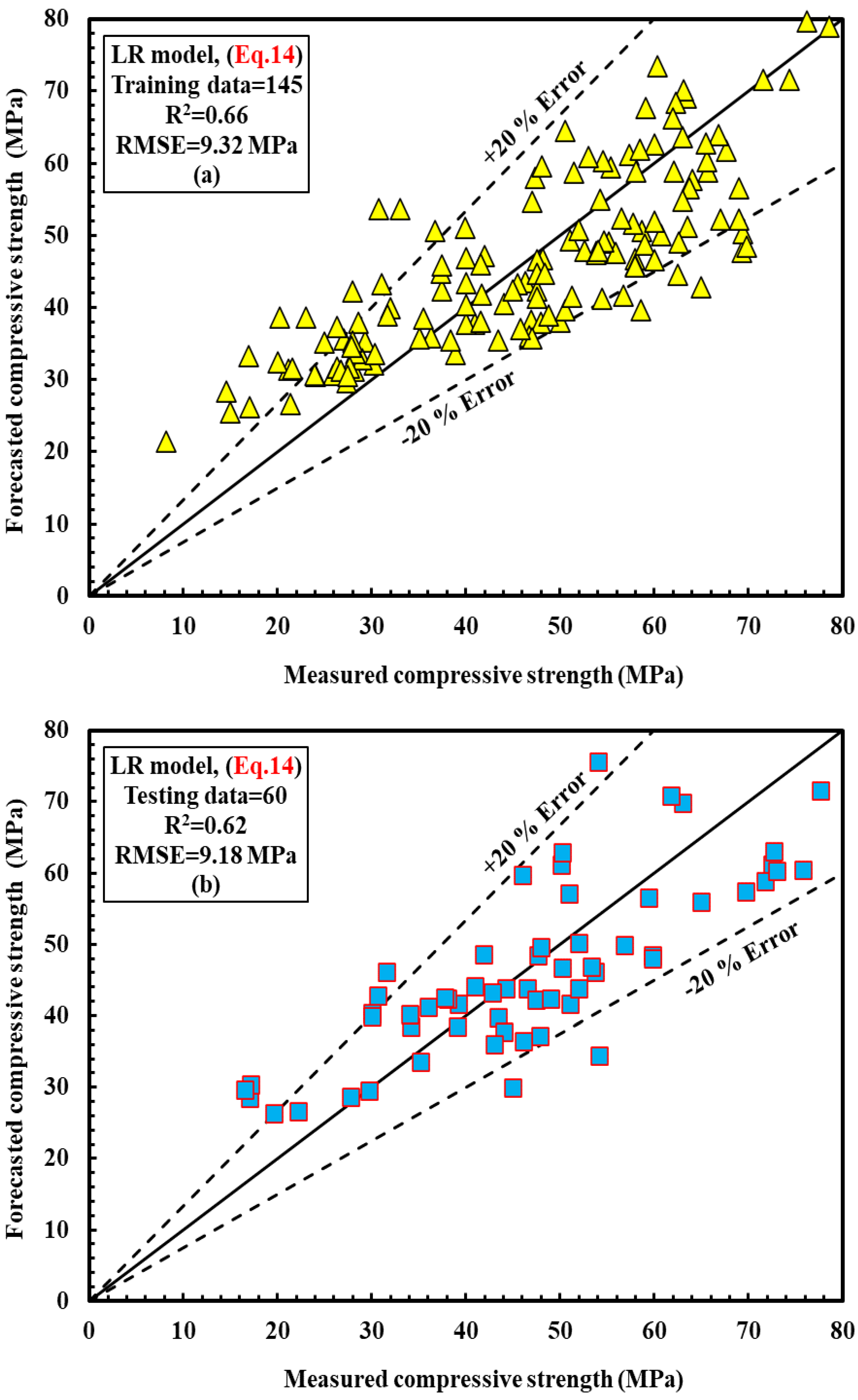
3.2.1. Linear Relationship Model (LR)
3.2.2. Nonlinear Model (NLR)
3.2.3. MLR Model
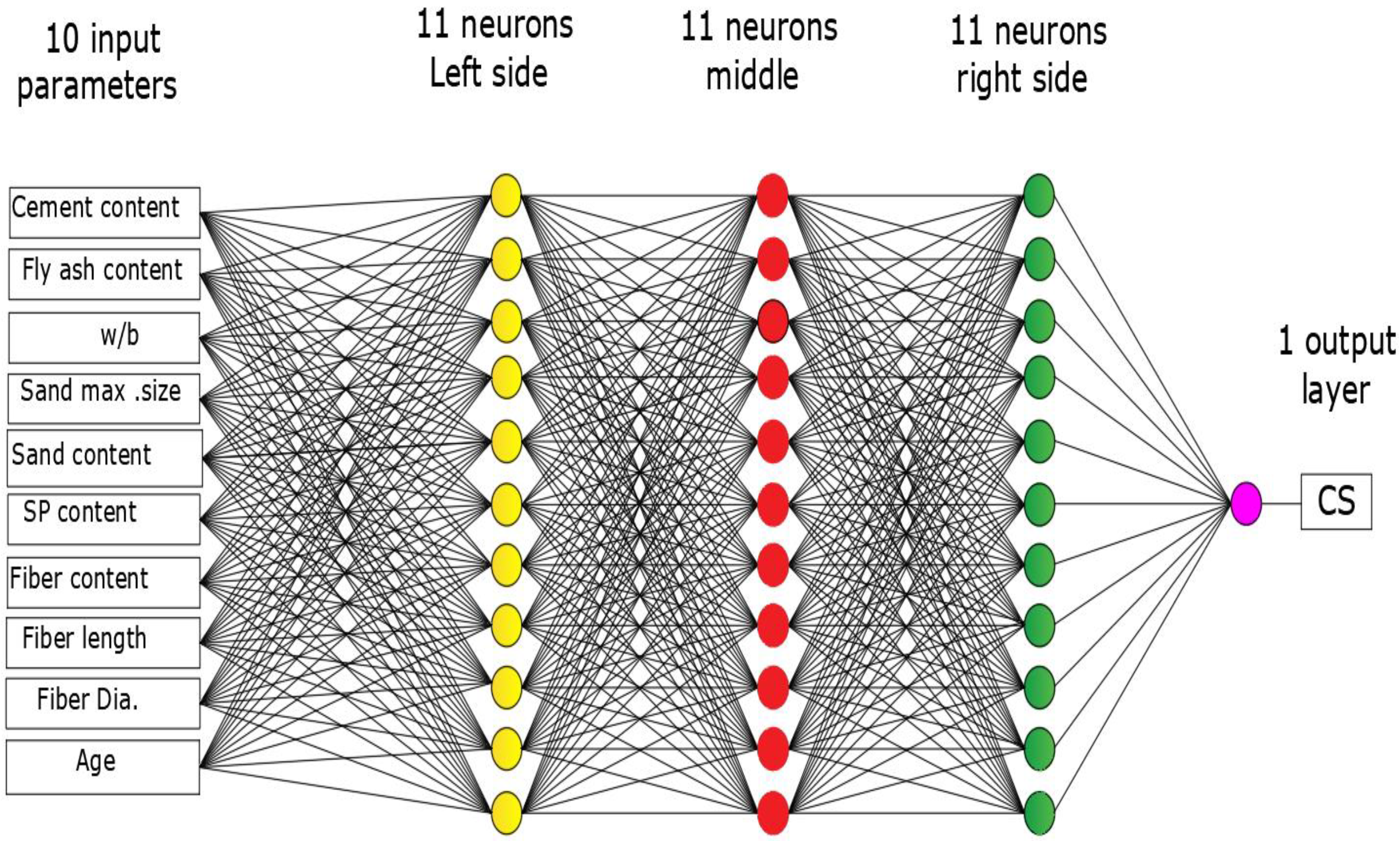
3.2.4. ANN Model
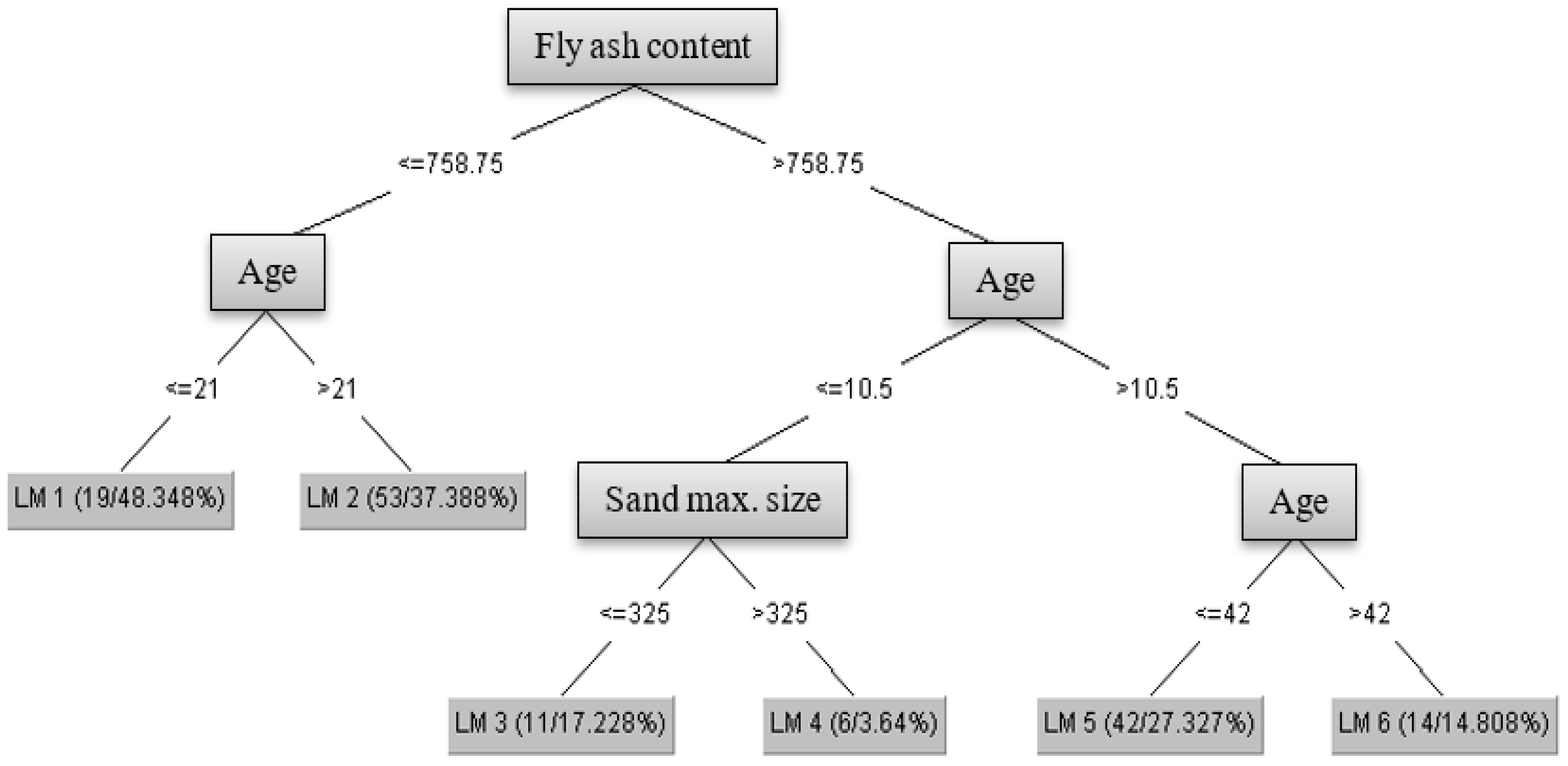
3.2.5. M5P-Tree Model (M5P)
3.3. Assessment Criteria for the Developed Models
4. Results and Discussion
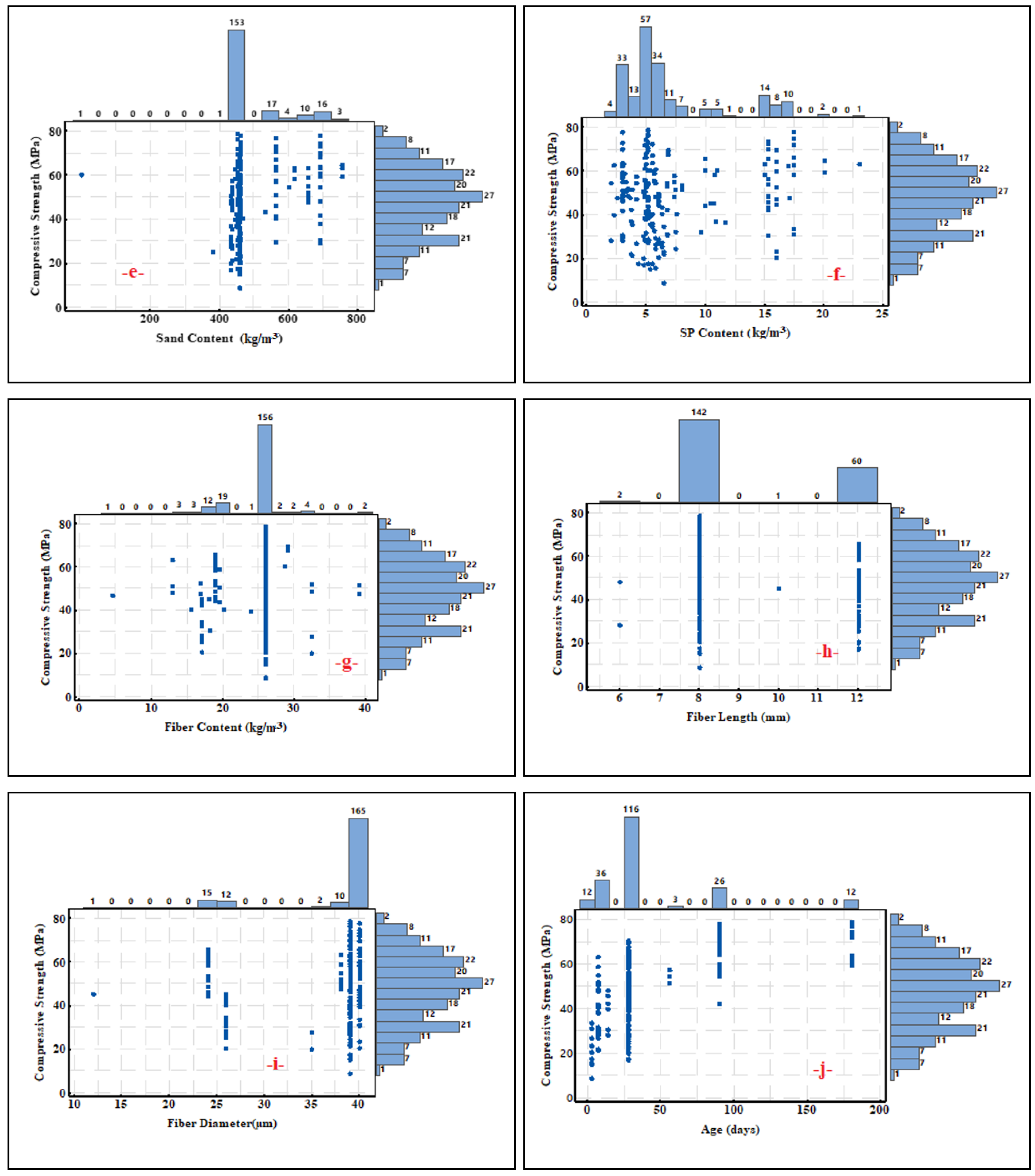
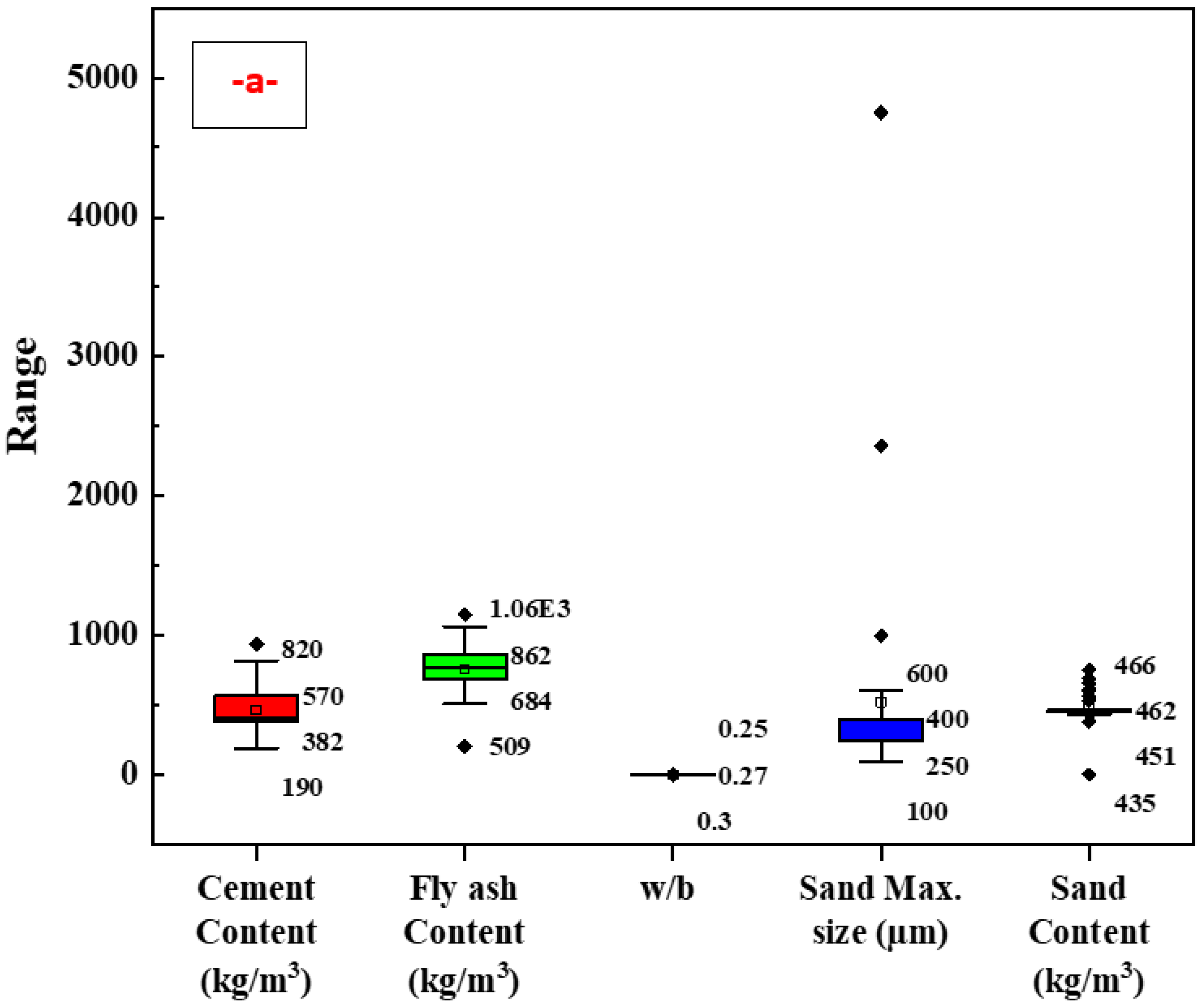
4.1. Statistical Analysis
4.2. Model Outputs
4.2.1. The LR Model
4.2.2. NLR Model
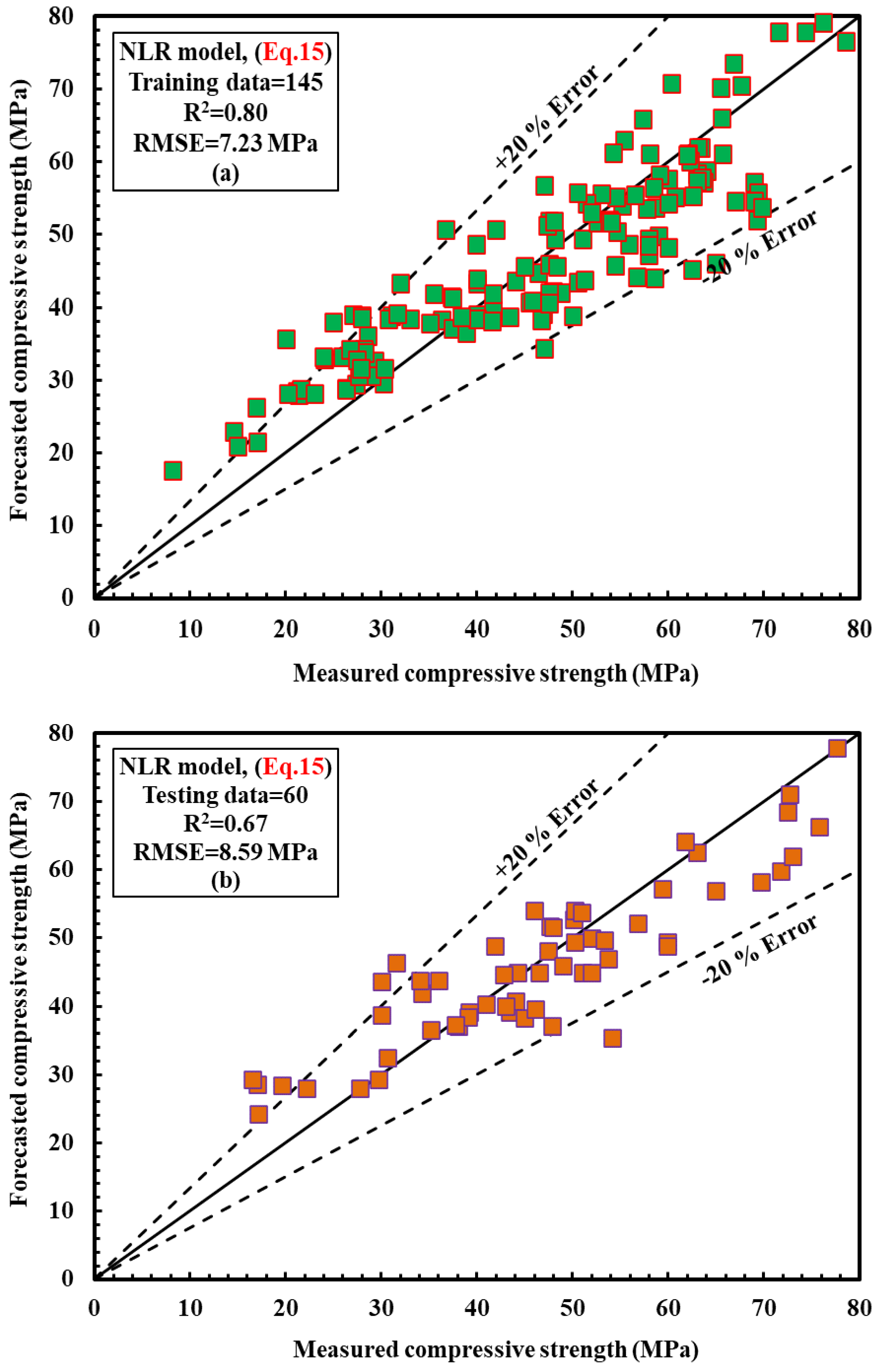
4.2.3. MLR Model
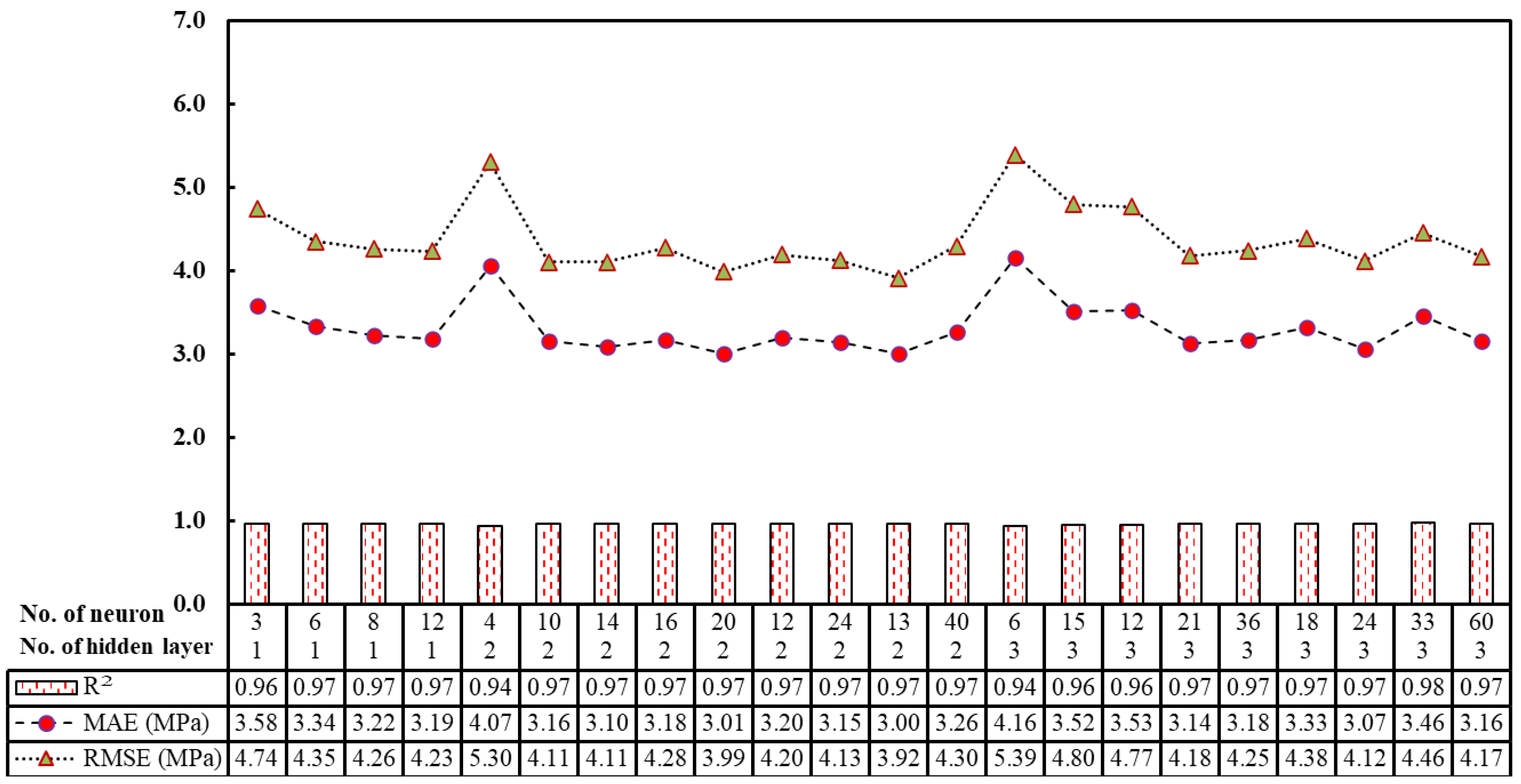
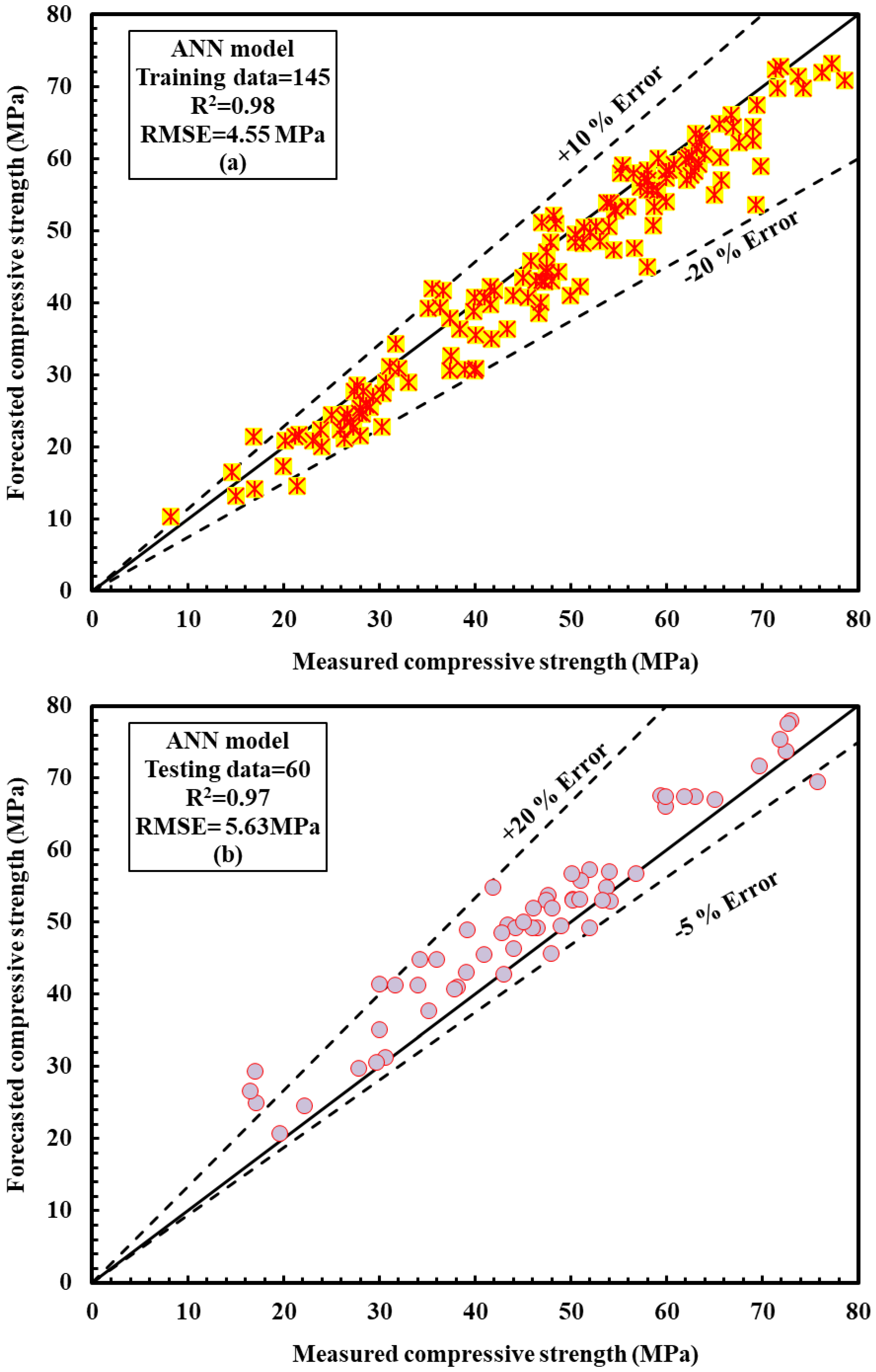
4.2.4. ANN Model
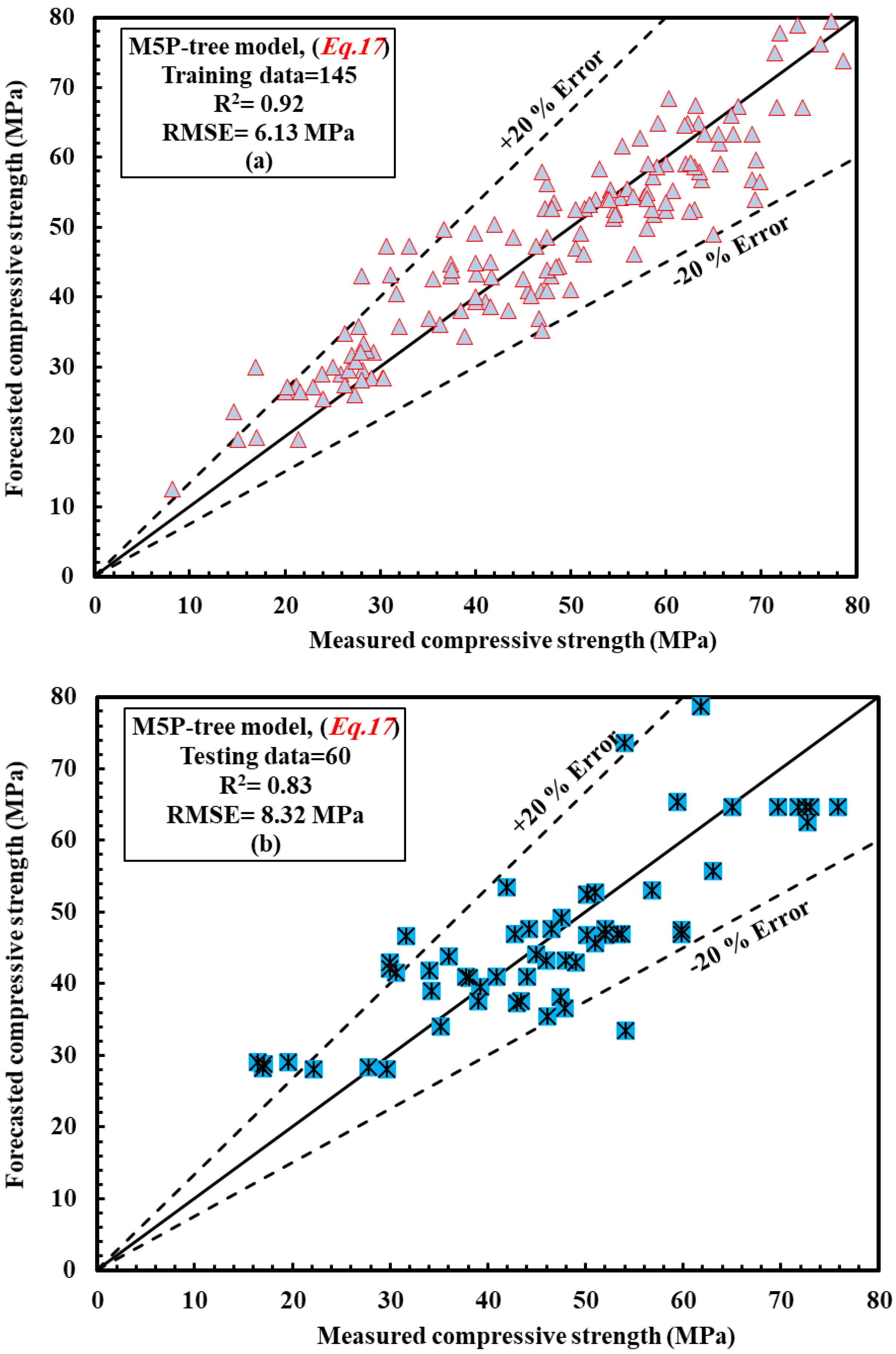
4.2.5. M5P Model
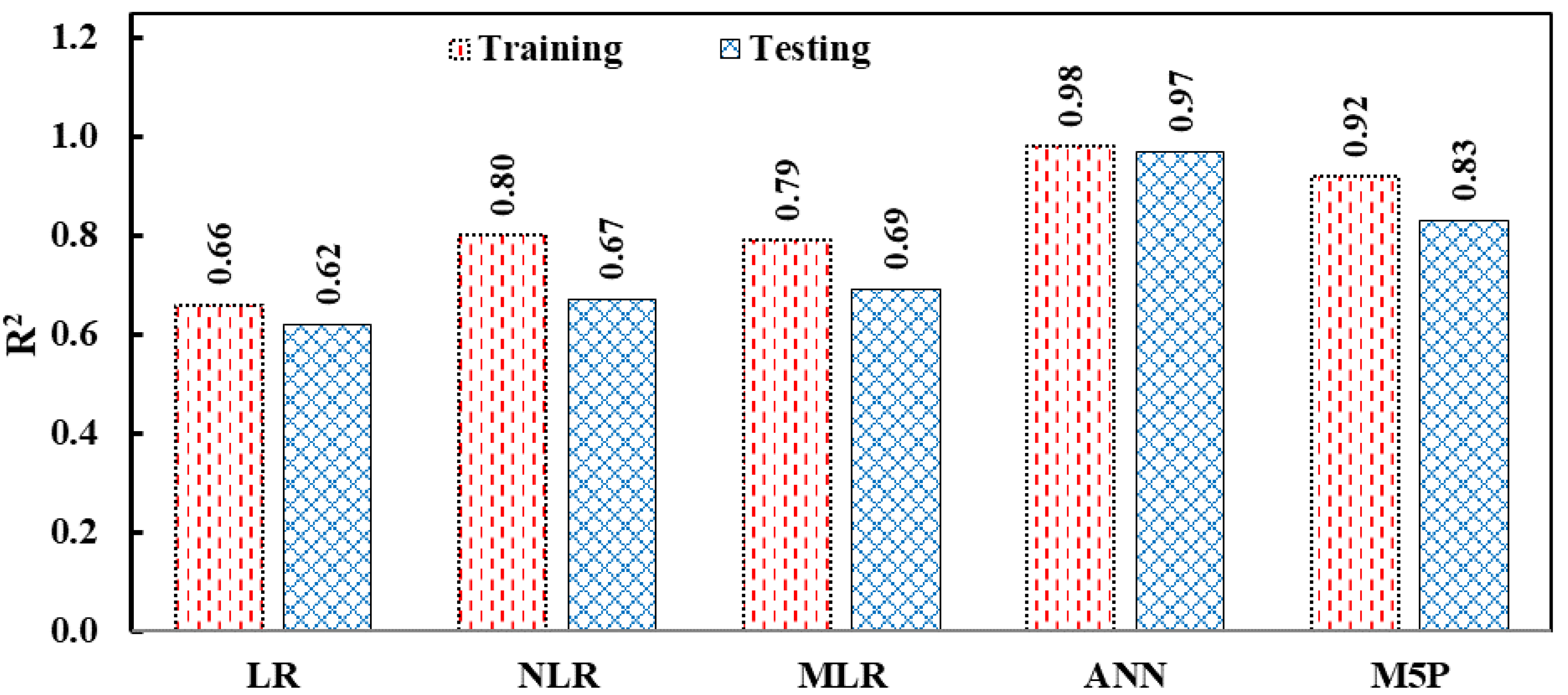
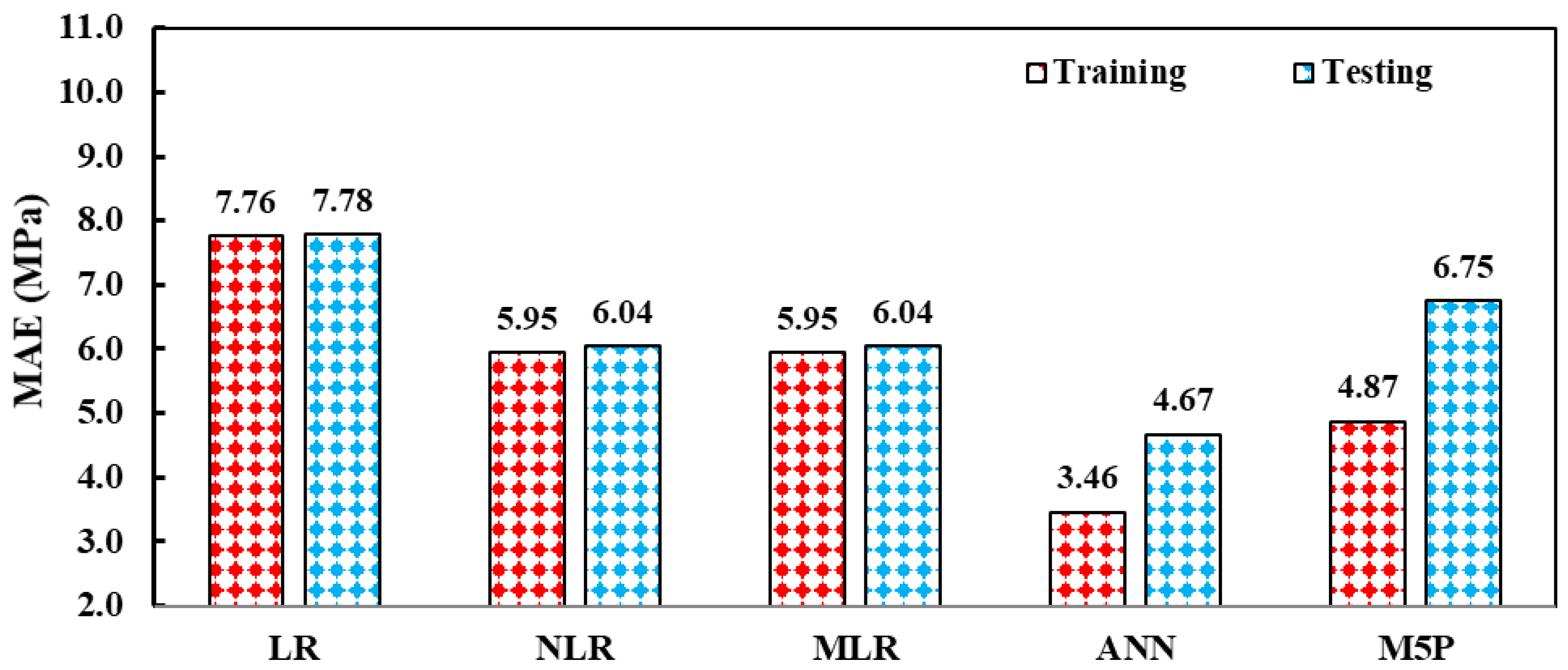
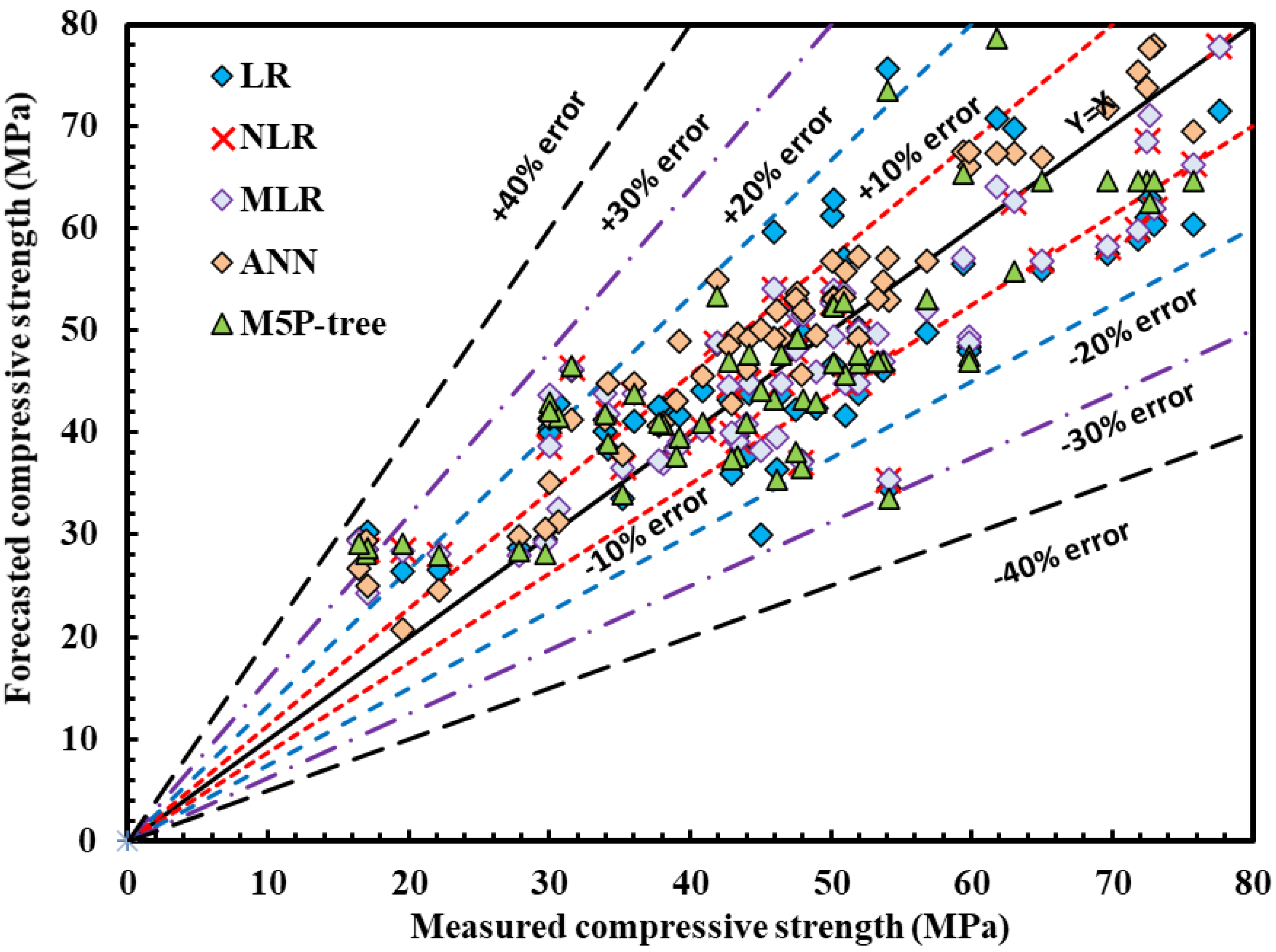
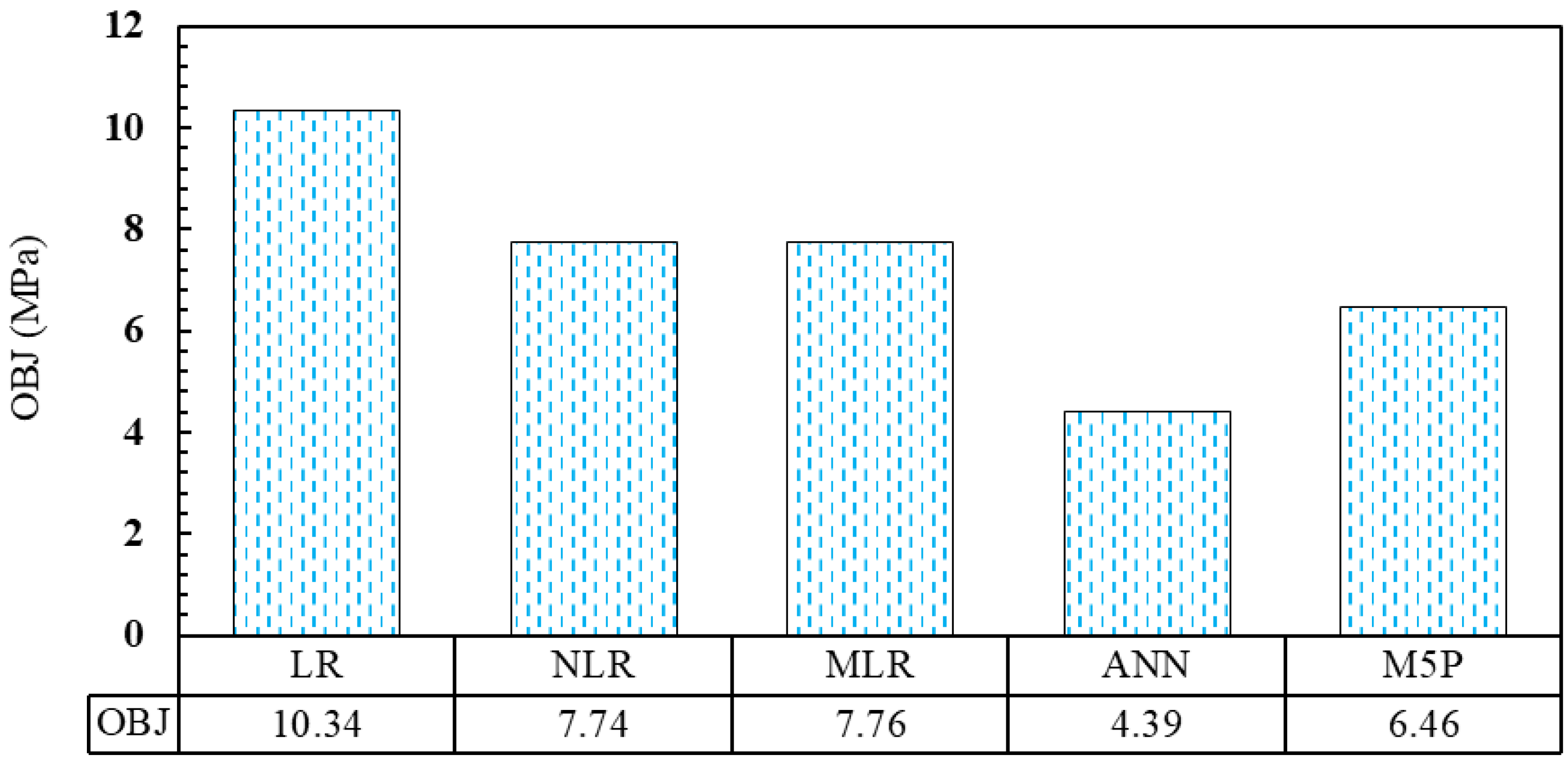
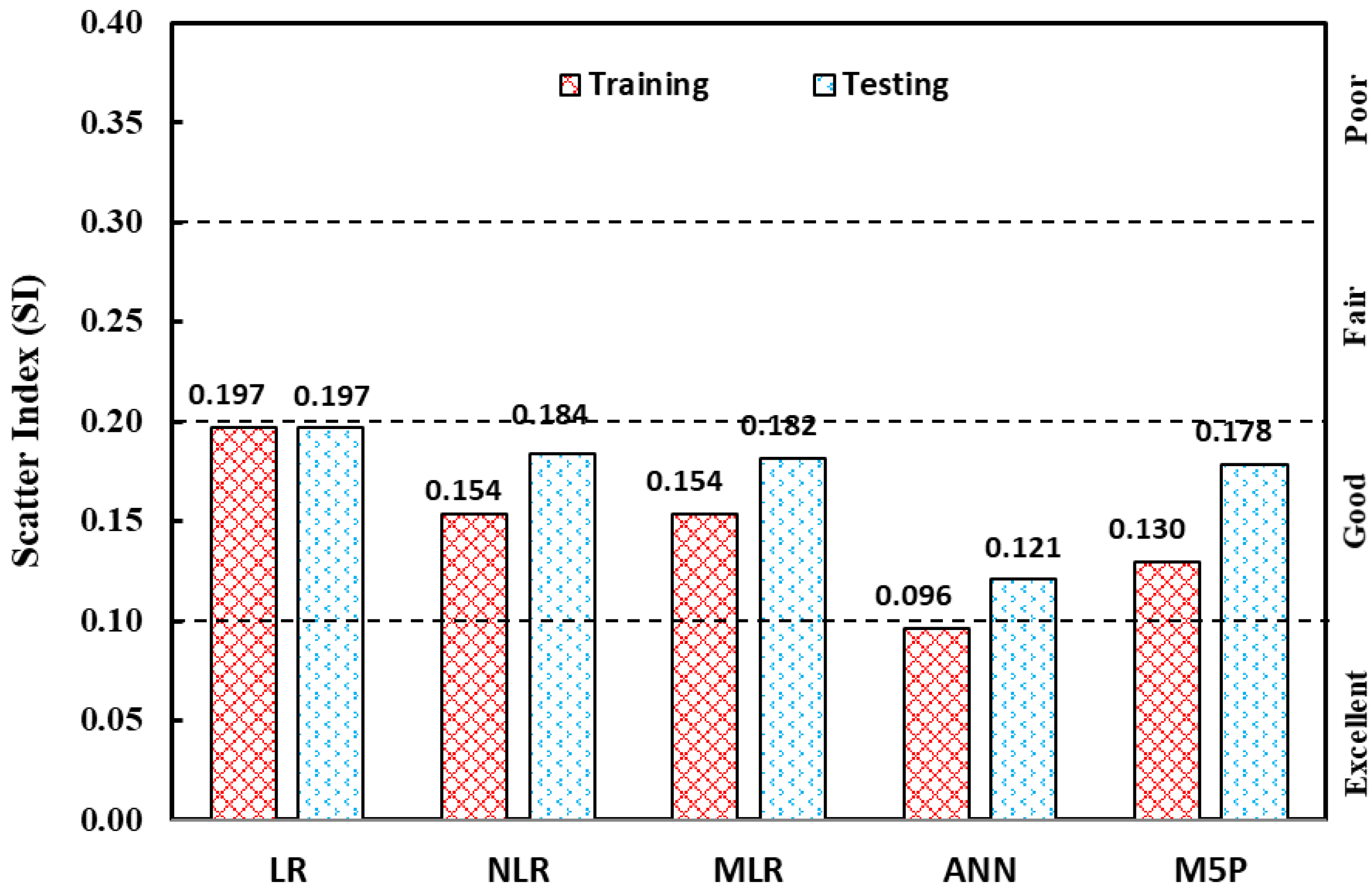
5. Model Comparisons
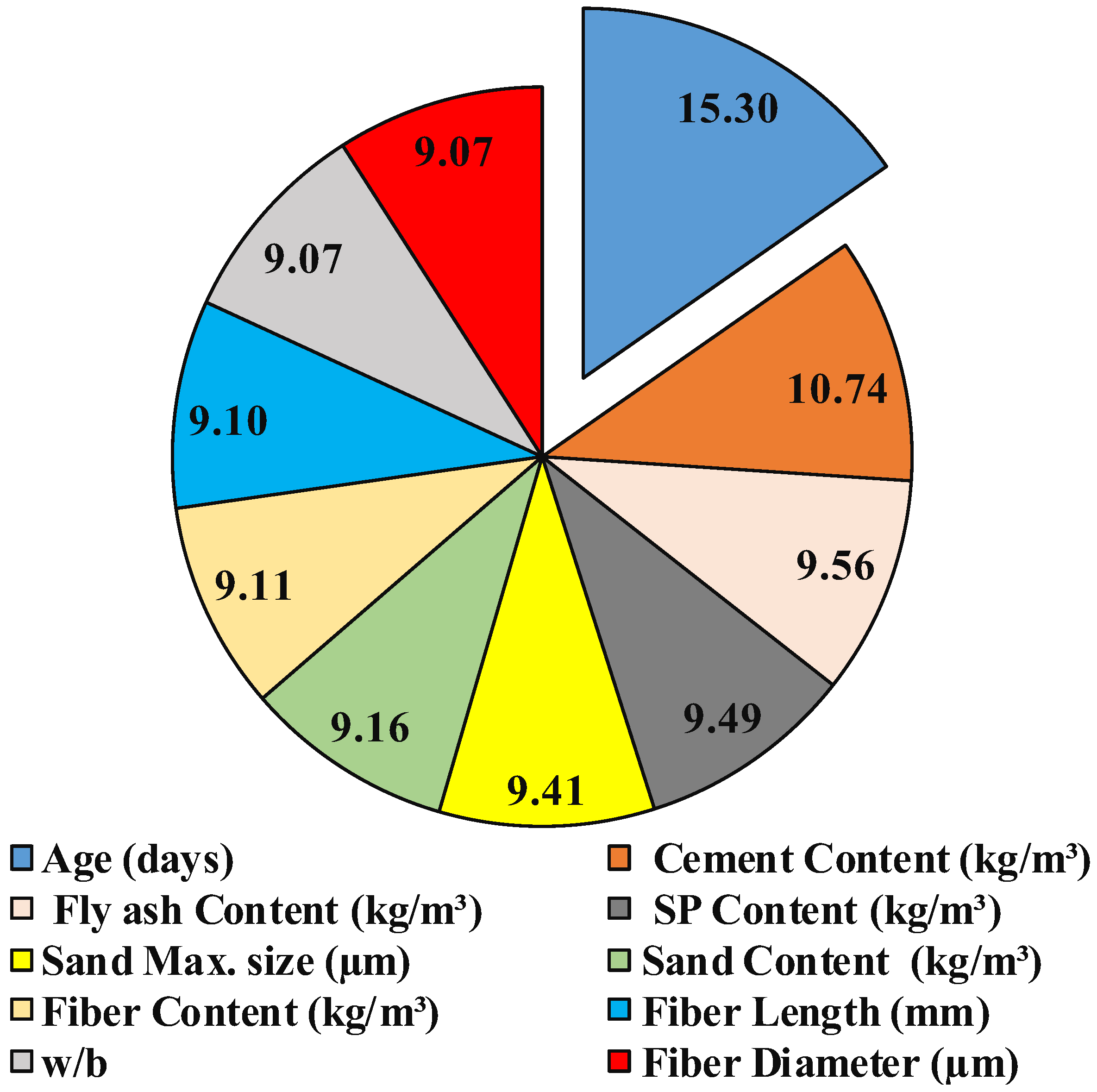
6. Sensitivity Analysis
7. Conclusions
- The average percentage of FA used in the manufacturing of ECC mixtures was 754.83 kg/m3. In addition, FA replacement with cement ranged from 201 to 1150 kg/m3. The findings from numerous experimental studies had a cure duration ranging from 3 to 180 days;
- Except the ANN model, the SI values for all models and stages were between 0.1 and 0.2, indicating that all models performed well. The SI values for the ANN model ranged from 0 to 0.1, indicating that it performed well;
- The ANN model’s OBJ value is 76 percent lower than the NLR and MLR models’, 135 percent lower than the LR model and 47 percent lower than the M5P model. This also demonstrates that the ANN model is more accurate and capable of estimating the CS of ECC mixtures, including FA, than the traditional approach;
- Overall, the data and analyses revealed that particular amounts of FA might be used successfully in ECC manufacturing. Furthermore, the models created in this work, particularly the ANN model, may be utilized to easily predict the mix proportions and CS of ECCs, lowering the number of experimental tests and trial batches in the laboratory.
Author Contributions
Funding
Conflicts of Interest
References
- Shah, S.P.; Swartz, S.E.; Ouyang, C. Fracture Mechanics of Concrete: Applications of Fracture Mechanics to Concrete, Rock and Other Quasi-Brittle Materials; John Wiley & Sons: Hoboken, NJ, USA, 1995. [Google Scholar]
- Li, V.C.C. Postcrack scaling relations for fiber reinforced cementitious composites. J. Mater. Civ. Eng. 1992, 4, 41–57. [Google Scholar] [CrossRef]
- Li, V.C.; Leung, C.K. Steady-state and multiple cracking of short random fiber composites. J. Eng. Mech. 1992, 118, 2246–2264. [Google Scholar] [CrossRef]
- Li, V.C.; Wu, H.C. Conditions for pseudo strain-hardening in fiber reinforced brittle matrix composites. Appl. Mech. Rev. 1992, 45, 390–398. [Google Scholar] [CrossRef]
- Li, V.C.; Wang, S.; Wu, C. Tensile strain-hardening behavior of polyvinyl alcohol engineered cementitious composite (PVA-ECC). Mater. J. 2001, 98, 483–492. [Google Scholar]
- Lim, Y.M.; Li, V.C. Durable repair of aged infrastructures using trapping mechanism of engineered cementitious composites. Cem. Concr. Compos. 1997, 19, 373–385. [Google Scholar] [CrossRef]
- Şahmaran, M.; Al-Emam, M.; Yıldırım, G.; Şimşek, Y.E.; Erdem, T.K.; Lachemi, M. High-early-strength ductile cementitious composites with characteristics of low early-age shrinkage for repair of infrastructures. Mater. Struct. 2015, 48, 1389–1403. [Google Scholar] [CrossRef]
- Maalej, M.; Quek, S.T.; Ahmed, S.F.U.; Zhang, J.; Lin, V.W.J.; Leong, K.S. Review of potential structural applications of hybrid fiber Engineered Cementitious Composites. Constr. Build. Mater. 2012, 36, 216–227. [Google Scholar] [CrossRef]
- Qudah, S.; Maalej, M. Application of Engineered Cementitious Composites (ECC) in interior beam–column connections for enhanced seismic resistance. Eng. Struct. 2014, 69, 235–245. [Google Scholar] [CrossRef]
- Pan, Z.; Wu, C.; Liu, J.; Wang, W.; Liu, J. Study on mechanical properties of cost-effective polyvinyl alcohol engineered cementitious composites (PVA-ECC). Constr. Build. Mater. 2015, 78, 397–404. [Google Scholar] [CrossRef]
- Yang, E.H.; Li, V.C. Strain-hardening fiber cement optimization and component tailoring by means of a micromechanical model. Constr. Build. Mater. 2010, 24, 130–139. [Google Scholar] [CrossRef]
- Madhavi, K.B.; Venugopal, M.; Rajesh, V.; Suresh, K. Experimental study on bendable concrete. Int. J. Eng. Res. Tech. 2016, 5, 501–550. [Google Scholar]
- Neville, A.M.; Brooks, J.J. Concrete Technology; Longman Scientific & Technical: London, UK, 1987; pp. 242–246. [Google Scholar]
- Neville, A.M. Properties of Concrete; Longman: London, UK, 1995. [Google Scholar]
- Yu, J.; Leung, C.K. Strength improvement of strain-hardening cementitious composites with ultrahigh-volume fly ash. J. Mater. Civ. Eng. 2017, 29, 05017003. [Google Scholar] [CrossRef]
- Kan, L.L.; Shi, R.X.; Zhu, J. Effect of fineness and calcium content of fly ash on the mechanical properties of Engineered Cementitious Composites (ECC). Constr. Build. Mater. 2019, 209, 476–484. [Google Scholar] [CrossRef]
- Yu, K.; Yu, J.; Lu, Z. Mechanical characteristics of ultra high performance strain hardening cementitious composites. In International Conference on Strain-Hardening Cement-Based Composites; Springer: Berlin/Heidelberg, Germany, 2017; pp. 230–237. [Google Scholar] [CrossRef]
- Faraj, R.H.; Mohammed, A.A.; Mohammed, A.; Omer, K.M.; Ahmed, H.U. Systematic multiscale models to predict the compressive strength of self-compacting concretes modified with nanosilica at different curing ages. Eng. Comput. 2021, 38, 2365–2388. [Google Scholar] [CrossRef]
- Aggarwal, S.; Bhargava, G.; Sihag, P. Prediction of Compressive Strength of SCC-Containing Metakaolin and Rice Husk Ash Using Machine Learning Algorithms. In Computational Technologies in Materials Science; CRC Press: Boca Raton, FL, USA, 2021; pp. 193–205. [Google Scholar]
- Gao, W.; Karbasi, M.; Derakhsh, A.M.; Jalili, A. Development of a novel soft-computing framework for the simulation aims: A case study. Eng. Comput. 2019, 35, 315–322. [Google Scholar] [CrossRef]
- Almohammed, F.; Sihag, P.; Sammen, S.S.; Ostrowski, K.A.; Singh, K.; Prasad, C.V.S.R.; Zajdel, P. Assessment of Soft Computing Techniques for the Prediction of Compressive Strength of Bacterial Concrete. Materials 2022, 15, 489. [Google Scholar] [CrossRef]
- Almasabha, G.; Alshboul, O.; Shehadeh, A.; Almuflih, A.S. Machine Learning Algorithm for Shear Strength Prediction of Short Links for Steel Buildings. Buildings 2022, 12, 775. [Google Scholar] [CrossRef]
- Alshboul, O.; Almasabha, G.; Shehadeh, A.; Al Hattamleh, O.; Almuflih, A.S. Optimization of the Structural Performance of Buried Reinforced Concrete Pipelines in Cohesionless Soils. Materials 2022, 15, 4051. [Google Scholar] [CrossRef]
- Kooh, M.R.R.; Thotagamuge, R.; Chau, Y.F.C.; Mahadi, A.H.; Lim, C.M. Machine learning approaches to predict adsorption capacity of Azolla pinnata in the removal of methylene blue. J. Taiwan Inst. Chem. Eng. 2022, 132, 104134. [Google Scholar] [CrossRef]
- Amlashi, A.T.; Abdollahi, S.M.; Goodarzi, S.; Ghanizadeh, A.R. Soft computing based formulations for slump, compressive strength, and elastic modulus of bentonite plastic concrete. J. Clean. Prod. 2019, 230, 1197–1216. [Google Scholar] [CrossRef]
- Feng, D.C.; Wang, W.J.; Mangalathu, S.; Hu, G.; Wu, T. Implementing ensemble learning methods to predict the shear strength of RC deep beams with/without web reinforcements. Eng. Struct. 2021, 235, 111979. [Google Scholar] [CrossRef]
- Bilir, T.; Gencel, O.; Topcu, I.B. Prediction of restrained shrinkage crack widths of slag mortar composites by Takagi and Sugeno ANFIS models. Neural Comput. Appl. 2016, 27, 2523–2536. [Google Scholar] [CrossRef]
- Behnood, A.; Daneshvar, D. A machine learning study of the dynamic modulus of asphalt concretes: An application of M5P model tree algorithm. Constr. Build. Mater. 2020, 262, 120544. [Google Scholar] [CrossRef]
- Ahmed, H.U.; Mohammed, A.S.; Mohammed, A.A.; Faraj, R.H. Systematic multiscale models to predict the compressive strength of fly ash-based geopolymer concrete at various mixture proportions and curing regimes. PLoS ONE 2021, 16, e0253006. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, H.U.; Mohammed, A.S.; Faraj, R.H.; Qaidi, S.M.; Mohammed, A.A. Compressive strength of geopolymer concrete modified with nano-silica: Experimental and modeling investigations. Case Stud. Constr. Mater. 2022, 16, e01036. [Google Scholar] [CrossRef]
- Alaloul, W.S.; Musarat, M.A.; Haruna, S.; Tayeh, B.A.; Norizan, M.N.B. Chemical attack on concrete containing a high volume of crumb rubber as a partial replacement for fine aggregate in engineered cementitious composite (ECC). Can. J. Civ. Eng. 2022, 49, 11–17. [Google Scholar] [CrossRef]
- Uddin, M.N.; Li, L.Z.; Ahmed, A.; Almajhali, K.Y.M. Prediction of PVA fiber effect in Engineered Composite cement (ECC) by Artificial neural Network (ANN). Mater. Today Proc. 2022, 65, 537–542. [Google Scholar] [CrossRef]
- Qadir, W.; Ghafor, K.; Mohammed, A. Characterizing and modeling the mechanical properties of the cement mortar modified with fly ash for various water-to-cement ratios and curing times. Adv. Civ. Eng. 2019, 2019, 7013908. [Google Scholar] [CrossRef]
- Da Costa, F.B.P.; Righi, D.P.; Graeff, A.G.; Da Silva Filho, L.C.P. Experimental study of some durability properties of ECC with a more environmentally sustainable rice husk ash and high tenacity polypropylene fibers. Constr. Build. Mater. 2019, 213, 505–513. [Google Scholar] [CrossRef]
- Felekoglu, B.; Tosun-Felekoglu, K.; Ranade, R.; Zhang, Q.; Li, V.C. Influence of matrix flowability, fiber mixing procedure, and curing conditions on the mechanical performance of HTPP-ECC. Compos. Part B Eng. 2014, 60, 359–370. [Google Scholar] [CrossRef]
- Sahmaran, M.; Yildirim, G.; Erdem, T.K. Self-healing capability of cementitious composites incorporating different supplementary cementitious materials. Cem. Concr. Compos. 2013, 35, 89–101. [Google Scholar] [CrossRef]
- Huang, X.; Ranade, R.; Ni, W.; Li, V.C. Development of green engineered cementitious composites using iron ore tailings as aggregates. Constr. Build. Mater. 2013, 44, 757–764. [Google Scholar] [CrossRef]
- Ma, H.; Qian, S.; Zhang, Z.; Lin, Z.; Li, V.C. Tailoring engineered cementitious composites with local ingredients. Constr. Build. Mater. 2015, 101, 584–595. [Google Scholar] [CrossRef]
- Meng, D.; Huang, T.; Zhang, Y.X.; Lee, C.K. Mechanical behaviour of a polyvinyl alcohol fibre reinforced engineered cementitious composite (PVA-ECC) using local ingredients. Constr. Build. Mater. 2017, 141, 259–270. [Google Scholar] [CrossRef]
- Soe, K.T.; Zhang, Y.X.; Zhang, L.C. Material properties of a new hybrid fibre-reinforced engineered cementitious composite. Constr. Build. Mater. 2013, 43, 399–407. [Google Scholar] [CrossRef]
- Yu, J.; Lin, J.; Zhang, Z.; Li, V.C. Mechanical performance of ECC with high-volume fly ash after sub-elevated temperatures. Constr. Build. Mater. 2015, 99, 82–89. [Google Scholar] [CrossRef]
- Zhang, Z.; Qian, S.; Ma, H. Investigating mechanical properties and self-healing behavior of micro-cracked ECC with different volume of fly ash. Constr. Build. Mater. 2014, 52, 17–23. [Google Scholar] [CrossRef]
- Yildirim, G.; Sahmaran, M.; Ahmed, H.U. Influence of hydrated lime addition on the self-healing capability of high-volume fly ash incorporated cementitious composites. J. Mater. Civ. Eng. 2015, 27, 04014187. [Google Scholar] [CrossRef]
- Abid, S.R.; Hilo, A.N.; Daek, Y.H.; Ayoob, N.S. Mechanical properties of ECC incorporating low-cost PVA fibers. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Bäch, Switzerland, 2020; Volume 897, pp. 78–84. [Google Scholar] [CrossRef]
- Li, L.Z.; Bai, Y.; Yu, K.Q.; Yu, J.T.; Lu, Z.D. Reinforced high-strength engineered cementitious composite (ECC) columns under eccentric compression: Experiment and theoretical model. Eng. Struct. 2019, 198, 109541. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Q.; Gu, C.; Su, H.; Li, V.C. Influence of micro-cracking on the permeability of engineered cementitious composites. Cem. Concr. Compos. 2016, 72, 104–113. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Q.; Li, V.; Su, H.; Gu, C. Durability study on engineered cementitious composites (ECC) under sulfate and chloride environment. Constr. Build. Mater. 2017, 133, 171–181. [Google Scholar] [CrossRef]
- Sahmaran, M.; Yücel, H.E.; Demirhan, S.; Arýk, M.T.; Li, V.C. Combined effect of aggregate and mineral admixtures on tensile ductility of engineered cementitious composites. ACI Mater. J. 2012, 109, 627. [Google Scholar]
- Said, S.H.; Razak, H.A.; Othman, I. Flexural behavior of engineered cementitious composite (ECC) slabs with polyvinyl alcohol fibers. Constr. Build. Mater. 2015, 75, 176–188. [Google Scholar] [CrossRef]
- Meng, D.; Lee, C.K.; Zhang, Y.X. Flexural and shear behaviours of plain and reinforced polyvinyl alcohol-engineered cementitious composite beams. Eng. Struct. 2017, 151, 261–272. [Google Scholar] [CrossRef]
- Lepech, M.D.; Li, V.C. Water permeability of engineered cementitious composites. Cem. Concr. Compos. 2009, 31, 744–753. [Google Scholar] [CrossRef]
- Qian, S.; Zhou, J.; De Rooij, M.R.; Schlangen, E.; Ye, G.; Van Breugel, K. Self-healing behavior of strain hardening cementitious composites incorporating local waste materials. Cem. Concr. Compos. 2009, 31, 613–621. [Google Scholar] [CrossRef]
- Qian, S.Z.; Zhou, J.; Schlangen, E. Influence of curing condition and precracking time on the self-healing behavior of engineered cementitious composites. Cem. Concr. Compos. 2010, 32, 686–693. [Google Scholar] [CrossRef]
- Şahmaran, M.; Li, V.C. Durability of mechanically loaded engineered cementitious composites under highly alkaline environments. Cem. Concr. Compos. 2008, 30, 72–81. [Google Scholar] [CrossRef]
- Şahmaran, M.; Li, V.C. Influence of microcracking on water absorption and sorptivity of ECC. Mater. Struct. 2009, 42, 593–603. [Google Scholar] [CrossRef]
- Şahmaran, M.; Li, V.C. De-icing salt scaling resistance of mechanically loaded engineered cementitious composites. Cem. Concr. Res. 2007, 37, 1035–1046. [Google Scholar] [CrossRef]
- Şahmaran, M.; Li, V.C. Durability properties of micro-cracked ECC containing high volumes fly ash. Cem. Concr. Res. 2009, 39, 1033–1043. [Google Scholar] [CrossRef]
- Sahmaran, M.; Li, M.; Li, V.C. Transport properties of engineered cementitious composites under chloride exposure. ACI Mater. J. 2007, 104, 604–611. [Google Scholar]
- Şahmaran, M.; Lachemi, M.; Hossain, K.M.; Li, V.C. Internal curing of engineered cementitious composites for prevention of early age autogenous shrinkage cracking. Cem. Concr. Res. 2009, 39, 893–901. [Google Scholar] [CrossRef]
- Şahmaran, M.; Özbay, E.; Yücel, H.E.; Lachemi, M.; Li, V.C. Frost resistance and microstructure of Engineered Cementitious Composites: Influence of fly ash and micro poly-vinyl-alcohol fiber. Cem. Concr. Compos. 2012, 34, 156–165. [Google Scholar] [CrossRef]
- Yang, E.H.; Yang, Y.; Li, V.C. Use of high volumes of fly ash to improve ECC mechanical properties and material greenness. ACI Mater. J. 2007, 104, 620. [Google Scholar]
- Yao, Y.; Zhu, Y.; Yang, Y. Incorporation superabsorbent polymer (SAP) particles as controlling pre-existing flaws to improve the performance of engineered cementitious composites (ECC). Constr. Build. Mater. 2012, 28, 139–145. [Google Scholar] [CrossRef]
- Gao, S.; Zhao, X.; Qiao, J.; Guo, Y.; Hu, G. Study on the bonding properties of Engineered Cementitious Composites (ECC) and existing concrete exposed to high temperature. Constr. Build. Mater. 2019, 196, 330–344. [Google Scholar] [CrossRef]
- Gencturk, B.; Hosseini, F. Evaluation of reinforced concrete and reinforced engineered cementitious composite (ECC) members and structures using small-scale testing. Can. J. Civ. Eng. 2015, 42, 164–177. [Google Scholar] [CrossRef]
- Guan, X.; Li, Y.; Liu, T.; Zhang, C.; Li, H.; Ou, J. An economical ultra-high ductile engineered cementitious composite with large amount of coarse river sand. Constr. Build. Mater. 2019, 201, 461–472. [Google Scholar] [CrossRef]
- Gulsan, M.E.; Mohammedameen, A.; Sahmaran, M.; Nis, A.; Alzeebaree, R.; Cevik, A. Effects of sulphuric acid on mechanical and durability properties of ECC confined by FRP fabrics. Adv. Concr. Constr. 2018, 6, 199. [Google Scholar] [CrossRef]
- Hu, S.; Cai, H.; Hong, R.; Li, M.; Yao, F. Performance test and microstructure of modified PVC aggregate-hybrid fiber reinforced engineering cementitious composite (ECC). Materials 2021, 14, 1856. [Google Scholar] [CrossRef]
- Zain, M.F.M.; Abd, S.M. Multiple regression model for compressive strength prediction of high: Performance concrete. J. Appl. Sci. 2009, 9, 155–160. [Google Scholar] [CrossRef]
- Demircan, E.; Harendra, S.; Vipulanandan, C. Artificial neural network and nonlinear models for gelling time and maximum curing temperature rise in polymer grouts. J. Mater. Civ. Eng. 2011, 23, 372–377. [Google Scholar] [CrossRef]
- Sarwar, W.; Ghafor, K.; Mohammed, A. Modeling the rheological properties with shear stress limit and compressive strength of ordinary Portland cement modified with polymers. J. Build. Pathol. Rehabil. 2019, 4, 25. [Google Scholar] [CrossRef]
- Ahmed, H.U.; Abdalla, A.A.; Mohammed, A.S.; Mohammed, A.A.; Mosavi, A. Statistical Methods for Modeling the Compressive Strength of Geopolymer Mortar. Materials 2022, 15, 1868. [Google Scholar] [CrossRef] [PubMed]
- Faraj, R.H.; Ahmed, H.U.; Rafiq, S.; Sor, N.H.; Ibrahim, D.F.; Qaidi, S.M. Performance of Self-Compacting Mortars Modified with Nanoparticles: A Systematic Review and Modeling. Clean. Mater. 2022, 4, 100086. [Google Scholar] [CrossRef]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software: An update. ACM SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Faraj, R.H.; Mohammed, A.A.; Omer, K.M.; Ahmed, H.U. Soft computing techniques to predict the compressive strength of green self-compacting concrete incorporating recycled plastic aggregates and industrial waste ashes. Clean. Technol. Environ. Policy 2022, 24, 2253–2281. [Google Scholar] [CrossRef]
- Ahmed, H.U.; Mohammed, A.S.; Mohammed, A.A. Multivariable models including artificial neural network and M5P-tree to forecast the stress at the failure of alkali-activated concrete at ambient curing condition and various mixture proportions. Neural Comput. Appl. 2022, 34, 17853–17876. [Google Scholar] [CrossRef]
- Ahmed, H.U.; Mohammed, A.A.; Mohammed, A. Soft computing models to predict the compressive strength of GGBS/FA-geopolymer concrete. PLoS ONE 2022, 17, e0265846. [Google Scholar] [CrossRef] [PubMed]
- Quinlan, J.R. Learning with continuous classes. In Proceedings of the 5th Australian Joint Conference on Artificial Intelligence, Hobart, Tasmania, 16–18 November 1992; Volume 92, pp. 343–348. [Google Scholar]
- Malerba, D.; Esposito, F.; Ceci, M.; Appice, A. Top-down induction of model trees with regression and splitting nodes. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 612–625. [Google Scholar] [CrossRef] [PubMed]
- Li, M.F.; Tang, X.P.; Wu, W.; Liu, H.B. General models for estimating daily global solar radiation for different solar radiation zones in mainland China. Energy Convers. Manag. 2013, 70, 139–148. [Google Scholar] [CrossRef]
- Ahmed, H.U.; Mohammed, A.S.; Mohammed, A.A. Proposing several model techniques including ANN and M5P-tree to predict the compressive strength of geopolymer concretes incorporated with nano-silica. Environ. Sci. Pollut. Res. 2022, 1–25. [Google Scholar] [CrossRef] [PubMed]






| Refer. | Cement Content (kg/m3) | Fly Ash Content (kg/m3) | w/b | Sand | SP Content (kg/m3) | Fiber | Age (Day) | CS (MPa) | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Max. Size (µm) | Content (kg/m3) | Content (kg/m3) | Length (mm) | Diameter(µm) | |||||||
| [24] | 313–570 | 684–940 | 0.28–0.32 | 300 | 380–532 | 2.5–10.4 | 17 | 12 | 26 | 28 | 20–45 |
| [34] | 412 | 1150 | 0.23 | 250 | 456 | 10.7 | 18 | 10 | 12 | 28 | 45 |
| [35] | 1009.16 | 0 | 0.35 | 300 | 757.53 | 7.05 | 17.9 | 10 | 12 | 28 | 45 |
| [36] | 222–375 | 825–978 | 0.26 | 200–425 | 432 | 4.8–5.04 | 26 | 12 | 39 | 28 | 27–50 |
| [37] | 471.6 | 754.5 | 0.27 | 300 | 444.1 | 10.8 | 26 | 8 | 39 | 28 | 58 |
| [38] | 240–545 | 654–960 | 0.25 | 250 | 432 | 4.8–10.9 | 26–32.5 | 12 | 39 | 28 | 19–32 |
| [39] | 570 | 684 | 0.3 | 300 | 0.36 | 5.7 | 28.6 | 12 | 39 | 28 | 59.86 |
| [40] | 570 | 684 | 0.56 | 250 | 456 | 6.84 | 29 | 8 | 39 | 7 | 13–69 |
| [41] | 232 | 1019 | 0.26 | 250 | 450 | 4.3 | 26 | 12 | 39 | 28 | 17 |
| [42] | 250–570 | 684–1000 | 0.25 | 250 | 450 | 7.5–17.1 | 26 | 8 | 39 | 28 | 24–47 |
| [43] | 570 | 684 | 0.27 | 400 | 455 | 5.1 | 26 | 8 | 39 | 28 | 53.8 |
| [44] | 570 | 684 | 0.27 | 250 | 455 | 4.9 | 26 | 6 | 39 | 7–28 | 28–48 |
| [45] | 936 | 201 | 0.32 | 250 | 601 | 4.2 | 26 | 8 | 39 | 56 | 54 |
| [46] | 393 | 865 | 0.25 | 250 | 457 | 5 | 26 | 12 | 39 | 28 | 41 |
| [47] | 393 | 865 | 0.25 | 250 | 457 | 5 | 26 | 12 | 39 | 28 | 40 |
| [48] | 392–570 | 684–862 | 0.27 | 400–1000 | 451–689 | 3–5.5 | 26 | 8 | 39 | 7–180 | 28–78 |
| [49] | 820 | 205 | 0.37 | 200 | 656 | 3.07–3.58 | 13–39 | 8–12 | 38 | 7 | 47–63 |
| [50] | 570 | 684 | 0.3 | 300 | 456 | 5.1 | 28.6 | 12 | 39 | 28 | 59.86 |
| [51] | 337–570 | 684–912 | 0.267 | 250 | 454 | 2.5–5 | 16.9 | 12 | 39 | 28 | 47–52 |
| [52] | 578 | 694 | 0.25 | 200 | 462 | 7.51 | 26 | 12 | 39 | 28 | 51 |
| [53,54] | 570 | 684 | 0.23 | 150 | 454 | 5.3 | 26 | 8 | 40 | 28 | 60 |
| [55,56] | 570 | 684 | 0.27 | 200 | 455 | 4.9 | 26 | 8 | 39 | 7–28 | 37–48 |
| [57,58] | 386–570 | 684–847 | 0.27 | 200 | 448–455 | 3.7–4.9 | 26 | 8 | 39 | 7–90 | 21–55 |
| [59] | 570 | 684 | 0.27 | 200 | 455 | 5.1 | 26 | 8 | 39 | 7–28 | 37.8–53 |
| [60,61] | 375–558 | 669–823 | 0.27 | 200 | 435–446 | 2–2.3 | 26 | 8 | 39 | 14–28 | 27–62 |
| [62] | 190–571 | 685–1063 | 0.25 | 250 | 456 | 5.1–6.8 | 26 | 8 | 39 | 3–28 | 8–54 |
| [63] | 382–636 | 636–890 | 0.25 | 250 | 462 | 16–17.4 | 26 | 8 | 40 | 3–90 | 17–77 |
| [64] | 583 | 699.9 | 0.25 | 100 | 465.7 | 7.6 | 20.1 | 12 | 40 | 28 | 39.9 |
| [65] | 418–570 | 684–836 | 0.19–0.25 | 600 | 456 | 5.7–7.41 | 26 | 8 | 40 | 28 | 54–58.6 |
| [66] | 404–502 | 605–753 | 0.24–0.3 | 212–4750 | 756 | 23 | 19 | 12 | 24 | 28 | 63 |
| [67] | 570 | 684 | 0.27 | 200 | 456 | 7.41 | 26 | 8 | 39 | 28–90 | 47.6–57 |
| [68] | 395 | 869 | 0.25 | 200 | 459 | 5.1 | 4.55–24 | 12 | 40 | 28 | 39–51 |
| Input Variables | Average | Median | St. Div. | Min. | Max. | Variance | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|
| Cement content (kg/m3) | 466.11 | 412 | 137.08 | 190 | 936 | 18,791.78 | 0.74 | 0.85 |
| Fly ash content (kg/m3) | 754.83 | 763.2 | 173.01 | 201 | 1150 | 29,932.73 | −1.45 | 3.27 |
| w/b | 0.27 | 0.27 | 0.04 | 0.19 | 0.56 | 0.00 | 4.21 | 24.82 |
| Sand max. size (µm) | 520.05 | 250 | 777.63 | 100 | 4750 | 604,707.45 | 4.31 | 19.88 |
| Sand content (kg/m3) | 494.64 | 456 | 92.70 | 380 | 756 | 8593.71 | 0.55 | 4.15 |
| SP content (kg/m3) | 7.18 | 5.26 | 4.65 | 2 | 23 | 21.60 | 1.38 | 0.72 |
| Fiber content (kg/m3) | 24.71 | 26 | 4.01 | 4.55 | 39 | 16.05 | −1.15 | 4.66 |
| Fiber length (mm) | 9.16 | 8 | 1.85 | 6 | 12 | 3.41 | 0.86 | −1.15 |
| Fiber diameter(µm) | 37.11 | 39 | 5.18 | 12 | 40 | 26.85 | −2.29 | 4.15 |
| Age (days) | 40.22 | 28 | 42.63 | 3 | 180 | 1817.72 | 2.17 | 4.30 |
| CS (MPa) | 47.00 | 47.6 | 15.78 | 8.2 | 78.56 | 249.15 | −0.15 | −0.74 |
| (LM) num: | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| α1 | +17.3699 | +33.6287 | +84.574 | +75.5592 | +126.5619 | +62.8256 |
| α2 | 0.0276 | 0.0103 | 0.0275 | 0.0316 | 0.0314 | 0.0519 |
| α3 | - | - | −0.048 | −0.0379 | −0.0664 | −0.0171 |
| α4 | +17.9526 | +30.3504 | −88.3962 | −88.3962 | −187.9927 | −108.9859 |
| α5 | +0.0012 | +0.0021 | +0.0059 | +0.0061 | +0.0113 | +0.0042 |
| α6 | +0.0064 | +0.0219 | - | - | +0.0228 | |
| α7 | +0.2525 | +0.4094 | +0.1043 | +0.1043 | −0.154 | +0.3398 |
| α8 | - | - | −0.2552 | −0.2552 | −0.4 | −0.115 |
| α9 | - | −1.2723 | - | - | - | - |
| α10 | - | - | - | - | - | |
| α11 | +0.0998 | +0.1302 | +0.1242 | +0.1242 | +0.1011 | +0.1453 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghafor, K.; Ahmed, H.U.; Faraj, R.H.; Mohammed, A.S.; Kurda, R.; Qadir, W.S.; Mahmood, W.; Abdalla, A.A. Computing Models to Predict the Compressive Strength of Engineered Cementitious Composites (ECC) at Various Mix Proportions. Sustainability 2022, 14, 12876. https://doi.org/10.3390/su141912876
Ghafor K, Ahmed HU, Faraj RH, Mohammed AS, Kurda R, Qadir WS, Mahmood W, Abdalla AA. Computing Models to Predict the Compressive Strength of Engineered Cementitious Composites (ECC) at Various Mix Proportions. Sustainability. 2022; 14(19):12876. https://doi.org/10.3390/su141912876
Chicago/Turabian StyleGhafor, Kawan, Hemn Unis Ahmed, Rabar H. Faraj, Ahmed Salih Mohammed, Rawaz Kurda, Warzer Sarwar Qadir, Wael Mahmood, and Aso A. Abdalla. 2022. "Computing Models to Predict the Compressive Strength of Engineered Cementitious Composites (ECC) at Various Mix Proportions" Sustainability 14, no. 19: 12876. https://doi.org/10.3390/su141912876
APA StyleGhafor, K., Ahmed, H. U., Faraj, R. H., Mohammed, A. S., Kurda, R., Qadir, W. S., Mahmood, W., & Abdalla, A. A. (2022). Computing Models to Predict the Compressive Strength of Engineered Cementitious Composites (ECC) at Various Mix Proportions. Sustainability, 14(19), 12876. https://doi.org/10.3390/su141912876











