Abstract
The purpose of this paper is to clarify the convergence pattern of China’s regional economies, explore the driving force of their coordinated development, and provide policy suggestions for coordinated and high-quality development. We used nighttime light data from 1992 to 2020 and combined an exploratory spatial data analytical method and a log-t test of a nonlinear time-varying factor model to identify the spatial convergence clubs of regional economic growth and the economic growth drivers of different clubs based on a spatial econometric model. We found that the eastern region is strong while the development of the central, western, and northeastern regions follows China’s long-term trend. Three high-level economic clubs (Shanghai, Jiangsu, and Zhejiang belong to Club 1; Shandong, Hebei, Anhui, Henan, and Liaoning belong to Club 2; Hainan, Fujian, and Guangdong belong to Club 3) have formed in the eastern coastal and central regions, while a low-level one (Inner Mongolia, Hubei, Chongqing, Qinghai, Guizhou, Sichuan, Guangxi, Yunnan, Xizang, Shaanxi, Gansu, Hunan, Ningxia, Xinjiang, Jiangxi, Heilongjiang, and Jilin) has formed in the central, western, and northeastern regions. Beijing, Tianjin, and Shanxi are not convergent. The coordinated development of these regions requires improving the levels of economic growth in the western and northeastern regions to give full play to the role of the Yangtze River Delta as a growth pole and its economic radiation capacity. An analysis of the influence mechanism and spatial spillover effects shows that industrial development and market vitality are the most important driving forces for economic growth. For the low-level club, service industry development, human capital, and resource consumption are also key factors for achieving sustained and stable economic growth.
1. Introduction
In recent years, changes in the global economic environment, COVID-19, and other unexpected factors have led China’s economic development to face three pressures: demand contractions, supply shocks, and weakening expectations. In December 2021, the Central Economic Work Conference put forward the economic development keynote of maintaining economic stability while making progress. At the national teleconference of May 2022 on stabilizing the economy, Premier Li Keqiang once again emphasized steady economic growth as the focus of the next stage. Considering the changes in the internal and external environments as well as the requirements for economic development, the effective implementation of regional policies and utilization of regional economic momentum has become one of the most effective ways to stabilize macroeconomic development. Defining development trends and mechanism of growth in regional economies can not only test the effects of regional policies and utilize the momentum of macroeconomic development but can also provide a prerequisite for the further formulation and implementation of regional policies.
The narrowing of regional differences and continuation of regional economic growth are the key objects of research on regional economics. The existing macroeconomic models mainly discuss these issues with respect to the convergence of economic growth [1]. Since the 1990s, China’s regional economy has mainly manifested as club convergence [2]. Researchers have discussed the convergent trend of the four major economic regions—eastern, central, western, and northeastern [3]—which basically conforms to the regional policy layout during this period. Since China has been faced with changes in the global trade structure and adjustments to the industrial divisions of labor since 2012, China’s regional policies have been moving towards a new path of coordinated development by strengthening regional cooperation and narrowing the economic gaps between the regions. In addition to emphasizing the coordinated development of the four major regions, it also focuses promoting regional development strategies, such as the “Coordinated development of the Beijing-Tianjin-Hebei Region” and the “Integration of the Yangtze River Delta” [4]. In 2018, a coordinated regional development strategy was implemented as a major national strategy. What is the convergent trend of China’s regional economic development arising from the new policy? Does this trend agree with the regional policy layout for the coordinated development of various sectors and economic zones? What are the mechanisms that drive the economic growth of different convergence trends?
To answer these questions and put forward feasible suggestions for promoting regional coordinated development and guaranteeing the stable economic growth of different regions, we used China’s provincial economic data in an exploratory spatial data analysis combined with a log-t test based on a nonlinear time-varying factor model to find spatial convergence clubs. Then, we explored the key driving forces of the economic growth of each club by using a spatial econometric model. We chose nighttime light (NTL) data from 1992 to 2020 as proxy variables for the regional economic levels because NTL is a unique surface landscape phenomenon, which has produced rich results for research on regional economic issues in China during recent years and has provided a reliable reference as a proxy of regional economic quality.
The remainder of this paper is arranged as follows. Section 2 reviews the literature on economic convergence and discusses the content, methods, and perspectives. Section 3 introduces the data and methods, including the correction and combination of NTL data, the identification method for spatial convergence clubs, and the data on the influencing factors. Section 4 discusses the results of the empirical test, including those of club convergence, and the analysis of the influencing factors. Section 5 presents the conclusion, discusses the results, and provides policy recommendations.
This work contributes to the literature in the following four ways. First, the combination of exploratory spatial data analysis and a log-t test based on a nonlinear time-varying factor model helps enrich the framework of spatial convergence identification. Second, the establishment of a spatial weight matrix with adjacency, distance, and economy can not only clarify the influences of different factors on regional spatial correlation but can also prove the stability of the convergence results of spatial clubs. Third, the identification of regional economic convergence patterns and the exploration of regional economic development momentum will help to promote better coordinated and higher quality development of China’s regions. Fourth, this study will broaden the source channels of economic growth substitution variables, which would be of great significance for exploring the characteristics and reliability of NTL data as economic indicators.
2. Literature Review
Regional economic growth not only depends on its own factor inputs but also the economic factors of adjacent spatial units. Recognition of the importance of spatial factors and the development of new theories in economic geography have led to the concept of spatial convergence clubs, which emphasizes the influences of adjacent spatial units on economic growth factors. Foreign studies have focused on the speed and steady-state levels of spatial convergence clubs within a country, and the regions above the country [5,6]. Domestic research has focused on spatial convergence tests based on a global scope [7]. The research perspective has gradually developed from the convergence of economic levels to the convergence of total factor productivity [8], economic growth quality [9], and green economics [10,11]. In addition, a large number of studies use NTL data as proxy variables for economic levels [12], thereby forming more objective and reliable conclusions as well as suggestions for the study of regional economic convergence, and also enriching empirical tests of regional economic coordination and high-quality development. More scholars have focused on testing the convergence of specific regions in China, e.g., the interactions among the eastern, central, and western regions, or between the coastal and inland regions. They have also focused on exploratory spatial data analysis and groupings of spatial correlation measures [13]. Some scholars have also discussed the club convergences of regional economies at different regional scopes. For example, Li et al. discussed the economic convergences of county-level regions [14], whereas Zhang et al. discussed those of prefecture-level cities [15]. Some studies have proved the significance of inter-regional spillover effects on economic convergence [1]. In addition to significant convergent trends, the spatial spillover effects within a region have different characteristics and convergence rates. In addition to the traditional indicators, such as technology, capital, and labor, scholars studying the influence mechanism of economic growth have begun to pay attention to the influences of regional policies and industrial structures on regional economic growth. China’s economic liberalization and marketization have accelerated its economic growth, so the influences of foreign direct investment (FDI) and other factors on the spatial convergences of regional economic growth have also become the focus of investigation [16].
On the whole, tests for spatial convergence clubs should first group regions and then test the convergence of each group. Two methods exist for grouping regions. The first method is the direct use of specific regional blocks as early groupings. However, this artificial standard limits possible convergences between regions and may lead to disconnections or deviations between China’s regional coordinated development and actual development trends. The second method is based on exploratory spatial data analysis, which uses spatial correlation measures. Regional combinations with four spatial correlation patterns are obtained by local Moran’s I indices. This grouping method has been widely used in recent studies [17,18]. The identification of economic convergence uses panel unit root tests, income distribution evolution, Markov chains, and σ convergence, but the most commonly used convergence test method is a spatial econometric model of the annual growth rates and levels of economic development in an initial year to evaluate the β convergence in a region by checking if the coefficients of the economic variables in the initial year are significantly negative [19,20]. However, because of the characteristics of China’s economy during the transition period, the multiple equilibrium growth of regional economies and the heterogeneity of convergence speeds, these methods have certain limitations. For example, β convergence ignores the stationarity of data [21], σ convergence cannot reflect the possible nonlinear convergence characteristics [22], the test power of random convergence is relatively weak [23], and Markov chain theory requires the stability of Markov processes [24].
As a convergence test, a log-t test based on a nonlinear time-varying factor model proposed by Phillips and Sul is more suitable for testing regional economic convergence in China. Phillips and Sul developed a model of convergence clubs by clustering cross-sectional individuals in a panel by testing for σ convergence [19]. Tian et al. [25], Zhang et al. [26], and Xiao et al. [26] adopted this method to identify convergences of economic growth among provincial-, municipal-, and county-level administrative units and to analyze the convergences and differences in regional economic growth. In general, this model is more suitable for testing regional economic convergence in China because of its applicability to convergence problems in transitional economies. Therefore, we firstly used exploratory spatial data analysis to find groups with spatial correlations and then we used a log-t test of a nonlinear time-varying factor model to identify the convergence of these groups as well as check if the convergent members of each group have both spatial correlation and temporal convergence to form a spatial convergence club.
3. Data and Methods
3.1. Club Identification and Influence Mechanism Exploration
In this study, exploratory spatial data analysis and a log-t test of a nonlinear time-varying factor model were combined to identify the spatial convergence of clubs; then, a spatial econometric model was used to find the influencing factors of a club’s economic growth. Spatial spillover effects depend not only on geographical location [27] but also on regional economic links. Therefore, an exploratory spatial data analysis based on the three spatial weight matrices of adjacency (w1), geographical distance (w2), and economic distance (w3) was conducted to explore the spatial correlations of regional economies. Where a spatial weight matrix is n*n symmetric, the value of element in w1 is defined as:
The value of in w2 is defined as , where represents the spatial distances between regions, and in w3 is defined as , where represents the economic level of a region.
For an early grouping of the spatial convergence club, the regions were categorized into four types according to local spatial correlations comprised of combinations of high- or low-level economic development with high- or low-level neighborhoods (HH, HL, LH, and LL).
For the test of club convergence, Phillips and Sul (2007) was used as a reference [19], in which a log-t test based on a nonlinear time-varying factor model was used to find the convergence members of a regional group:
where represents the time series of economic growth, is the common factor, and is the time-varying parameter containing the disturbance term, which expresses the change in individual heterogeneity over time. Firstly, the relative transfer coefficient, which is also called the relative transition path, is defined to eliminate the common factors among individuals so that only the time-varying characteristics of individual heterogeneity are retained:
Then, a semi-parametric model is constructed:
where is fixed and does not change with time, is the scale parameter of heterogeneity, is i.i.d. (0, 1), and is a slowly changing function that increases and diverges at infinity. is used in this paper and is the decay rate by regression in the following equation:
The null hypothesis of convergence is tested as follows:
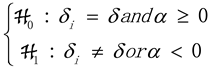
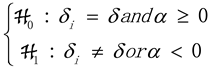
In Equation (4), , is the original length of the time series and represents the integer part of . A small part of in the time series needs to be discarded in the regression so that the test is focused on the trend of the later time series. , is the relative transition path in Equation (2) and , and are the least-squares estimation in H0. A one-way test is used for in the null hypothesis. At a significance level of 5%, if the statistic of is less than −1.65, the null hypothesis indicating convergence is rejected.
In the combination of the exploratory spatial data analysis with the log-t test, the convergence members of each group have both spatial correlation and temporal convergence, thus forming a spatial convergence club. To test the convergence mechanism of the economic growth of different clubs, we combined the spatial lag model (SLM), spatial error model (SEM), and spatial Durbin model (SDM), which are commonly used in empirical analyses [28] to test the spatial spillover effect mechanism and to select the appropriate model for estimation and analysis in accordance with the LM and LR test results.
3.2. Data Sets
3.2.1. NTL Data
The mean value of NTL in the 31 provincial-level regions of mainland China from 1992 to 2020 was used as the variable for the economic level. NTL consists of the global night luminescence remote sensing images (DMSP/OLS) from 1992 to 2013 captured by the operational line scanning sensor of the United States National Defense Meteorological Satellite Program. The new generation of noctilucent-sensor-visible near-infrared imaging radiation sensors (NPP/VIIRS), which was announced in 2012, is equipped with national polar-orbiting satellites to obtain NTL. This paper refers to [29] with regard to the constant target area method for the correction of light data combined with the 1:4 million vector topographic map of Chinese local administrative districts provided by the National Basic Geographic Information Center. The DMSP/OLS stable light data of 31 provincial-level administrative regions in China (excluding Hong Kong, Macao, and Taiwan) from 1992 to 2013 were subjected to mutual correction and saturation correction to obtain the DN value of each pixel after correction and then the mean value of the annual night lights in each region was extracted. Following [30], we transformed the monthly NPP/VIIRS data from 2012 to 2020 using an Albers projection coordinate system resampled to a 0.5 km spatial resolution by the nearest approach method and filtered out negative, maxima, and missing values to eliminate noise from light detection data associated with fires, gas flares, volcanoes, and background noise. Monthly data were averaged to synthesize annual data by using a raster calculator to extract regional light averages.
Because DMSP/OLS and NPP/VIIRS have obvious differences in resolution, digital features, and pixel value range, most studies on light data use only one type of data for analysis. With the progress of technical means in recent years, some studies [31] have integrated two kinds of data and used longer time series to realize comparability and continuity, thus bringing convenience to the application of NTL. Following Si Lijuan et al. (2021) [32], this study established a regression relationship based on the coincidence periods (2012 and 2013) of two types of NTL data and found that the quadratic term regression equation of the two types of NTL in 2012 was more significant:
where the goodness of fit was 0.984. This equation was used to convert the NPP/VIIRS data of 2012 into DMSP/OLS data. In accordance with the quantitative relationship between the NPP/VIIRS data from 2012 to 2020, the NPP/VIIRS data from 2013 to 2020 were converted into DMSP/OLS data and finally combined with the DMSP/OLS data from 1992 to 2013 to obtain the mean NTL data from 1992 to 2020.
3.2.2. Influencing Factor Data
Regional economic growth theory states that industrial structure, capital investment, labor force, and level of technological development are the main factors affecting economic development [33]. The neoclassical model emphasizes population growth, scientific and technological innovation, and other related indicators. The endogenous growth model emphasizes human capital and other indicators. Previous studies [34,35] that focused on the factors affecting the spatial convergence of regional economic growth have been used for reference and the characteristics of China’s economic development have been comprehensively considered in our study to examine the mechanism of regional club convergence along the seven dimensions of capital input, population growth, scientific and technological innovation, industrial structure, market vitality, economic liberalization, and resource consumption. Capital input is divided into physical and human types. Pursuing the objectives of our research and following the experiences of our predecessors [36,37,38], we adopted the total amount of fixed asset investment () as the indicator of physical capital investment and the number of employed people () as the indicator of human capital investment. Population growth is measured by annual population growth (), which is common in most studies. The index of scientific and technological innovation is measured by the number of invention patents granted (). The proportions of the output values of the secondary () and tertiary () industries in GDP are variables representing the industrial structure. Market vitality is measured by total retail sales of consumer goods (). The index of economic liberalization is measured by FDI (). Energy consumption is measured by power consumption (). All data have been taken from the China Statistical, Regional Statistical, and China Energy Statistical Yearbooks (1992–2020). The descriptive statistics of each variable are shown in Table 1.

Table 1.
Descriptive statistics of each variable.
4. Results
4.1. Spatial Correlation
4.1.1. Global Spatial Correlation
The global Moran’s I indices of the NTL for 31 regions are shown in Figure 1. The indices present overall upward trends. After neighboring, distance, and economic factors have been taken into account, the indices under the matrices are significant and indicate significant spatial correlations among the regions. In contrast, the index based on the adjacency weight matrix for 1992 to 2020 was the highest (0.579 to 0.667), followed by the geographical distance weight matrix (0.321 to 0.430), whereas the lowest (0.125 to 0.220) was based on the economic distance weight matrix, thus indicating that the economic correlations between geographically adjacent areas are the strongest and exceed the spatial correlation caused by distance and economic factors.
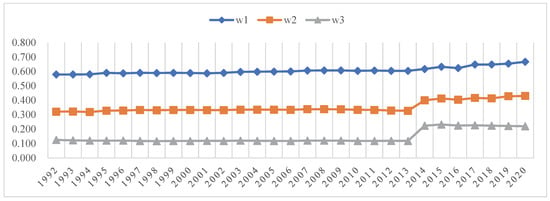
Figure 1.
Global Moran’s I indices of 31 regions based on different weight matrices from 1992–2020.
4.1.2. Local Spatial Correlations
We calculated the local Moran’s I indices of the NTL of the 31 regions for each year under different weight matrices and obtained Moran’s I scatter diagram, which depicted the HH, LH, LL, and HL types of regions in each year. Table 2 shows the partition results of the four types in 1992, 2006, and 2020 for each weight matrix. Most regions are in the HH and LL groups, which indicates positive correlations between regional economies. Although the regions belonging to all groups are different under different weight matrices, the regions belonging to the high (HH or HL group) and low (LH or LL group) levels of economic development are completely consistent. The beginning of the time series in 1992 had 16 high-level and 15 low-level regions, whereas the end of the time series in 2020 had 14 high-level and 17 low-level regions, thus reflecting the trend of regional economic changes in a few areas. There are two regions, Hubei and Jilin, that have transitioned from the high-level group to the low-level group, but this transition does not mean that the NTL in Hubei and Jilin have decreased; however, under the precondition that the NTL levels in all regions have increased, Hubei and Jilin have jumped to a relatively low-level group.

Table 2.
Results of local spatial autocorrelation groups under different weight matrices.
The geographic distribution of the high-level regions in Figure 2 shows that they had gradually shrunk from the eastern and the central regions to the eastern regions while the economic advantage of the northeastern region had gradually disappeared. At the beginning of the time series, the high-level regions included 10 eastern regions (Beijing, Tianjin, Hebei, Shandong, Jiangsu, Shanghai, Zhejiang, Fujian, Guangdong, and Hainan), 4 central regions (Shanxi, Henan, Anhui, and Hubei), and 2 northeastern regions (Jilin and Lining). In 2006, Hubei and Jilin became low-level and Liaoning remained the only high-level region among the three northeastern regions while Shaanxi developed into a high-level region. In 2020, Shaanxi returned to being a low-level region, thus forming a high-level regional group dominated by eastern coastal regions and a small number of central regions, whereas a low-level group was dominated by the central, western, and two northeastern regions. The economic growth of most regions showed positive spatial correlations from 1992 to 2020, with geographically adjacent high- and low-level regions being clustered and distributed, respectively. Therefore, spatial club convergences between both these regions are highly likely.
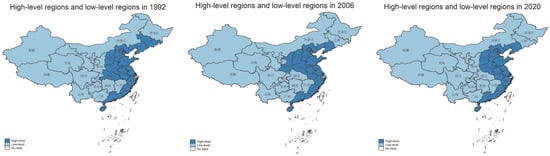
Figure 2.
Regional distributions of regions with high and low levels of economic development.
4.2. Space Club Identification
This study treated the high- and low-level regions as spatial groups to conduct a log-t test on their NTL of 2020 and identify the latest trend in the spatial convergence of their economies. In the high-level group, Beijing and Shanxi do not converge; the remaining 12 regions converge in two clubs of which the transition path is shown in Figure 3 (top). Four regions (Tianjin, Shanghai, Jiangsu, and Zhejiang) are in high-level Club 1 and eight regions (Hainan, Hebei, Fujian, Shandong, Anhui, Henan, Guangdong, and Liaoning) are in the high-level Club 2. However, in accordance with the requirement of geographical proximity for a spatial convergence club, Tianjin was excluded from high-level Club 1, which included only Shanghai, Zhejiang, and Jiangsu. High-level Club 2 was also divided into two clubs, which are Club 2 (Hebei, Shandong, Anhui, Henan, and Liaoning) and Club 3 (Hainan, Fujian, and Guangdong), respectively, in accordance with the clustering characteristics of geographical locations. For the low-growth areas belonging to the LL and LH groups, 17 regions (Hubei, Henan, Chongqing, Qinghai, Guangxi, Sichuan, Guizhou, Yunnan, Xizang, Shaanxi, Gansu, Inner Mongolia, Ningxia, Xinjiang, Jiangxi, Heilongjiang, and Jilin) converge in the same club of which the transition path is shown in Figure 3 (bottom). Finally, in accordance with the log-t test and spatial locations of the accumulation characteristics, the remaining 28 provincial-level regions, except Beijing, Shanxi and Tianjin, are divided into four spatial convergence clubs.
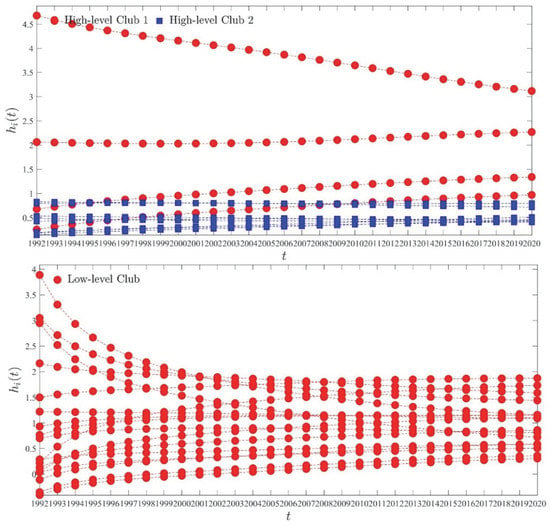
Figure 3.
Transition paths of (top) high- and (bottom) low-level economic spatial convergence clubs.
4.3. Influence Mechanism of Economic Growth of Clubs
4.3.1. Influential Factors of High-Level Economic Club
The three high-level clubs contain a total of 11 regions, whose influencing factors on the economy were tested. Moran’s I indices of the three weight matrices are 0.340, 0.196, and 0.334, respectively, which are significant at a 1% level and further prove a strong spatial correlation. The LM test results in Table 3 show that SEM should be selected under w1, whereas SLM should be selected under w2 and w3. SDM analysis was also used as a robustness test for comparison. Although the Hausman test’s results under some models were negative, we chose a fixed effect (FE) estimation model for two reasons. First, according to Lian Yujun, a Hausman test’s negative results can warrant the rejection of the null hypothesis [39], so FE should be used for estimation. Second, according to previous spatial econometric studies, each sample represents itself and all samples constitute the overall research object, which would not suit random sampling but FE would be more suitable. Therefore, we chose the time-individual double-FE estimation.

Table 3.
Empirical test of high-level economic space club.
For different weight matrices, the estimation results of the corresponding models are also shown in Table 3. (1) The influence factors in the weighting matrix, such as scientific and technological innovation, industrial proportion, social consumption, and power consumption, have stronger significance and consequently have positive influences on the level of economic growth, whereas the rate of population growth has negative influences. The absolute values of the coefficients of industry proportion and social consumption and power consumption are higher, which indicates that their influences are stronger. (2) The LR test values of SDM under each weight matrix are positive and all pass the significance test of 1%, so the null hypothesis can be rejected, i.e., the SDM cannot be simplified, which indicates that it could obtain more accurate estimation results. In addition, the log-likelihood value indicates that SDM would have a better data fitting effect under each weight matrix.
To explain more accurately the direct effect of each influencing factor on regional NTL growth and the spatial spillover effects between regions, we decomposed the spatial effect of SDM under the time-individual double-fixed effect through a partial differential method. The direct and indirect effects represent the influences of each explanatory variable in a region on the NTL of the region itself and the neighboring region, respectively. The total effect is the sum of both effects. Table 4 shows that: (1) Both fixed capital investment and rate of population growth have negative direct and indirect effects, which indicate that these two factors have negative effects on the economies of the local and neighboring regions. (2) The number of employed people has negative direct effects but no spatial spillover effects and the total effect was not significant. (3) Industrial proportion, social consumption, and power consumption have positive effects on local economic growth, indicating that these factors can have significant and important influences on promoting regional economic growth. However, their spatial spillovers are different. Industrial proportion has a negative coefficient under w1, w2, and w3, indicating that it has negative spatial spillover effects on the levels of economic development in adjacent regions with similar geographical distances and similar economies. Social consumption and power consumption have no spatial spillover effects. (4) FDI has positive spatial spillover effects on the levels of economic development in adjacent regions with similar geographical distances.

Table 4.
Direct, indirect, and total effects of SDM model of high-level economic spatial club.
For the direct effects, the coefficient of industry proportion is the largest, indicating that industrial development is the most important direct factor affecting regional economic growth. The second most important factors are social consumption and power consumption. Regardless of the weight matrix, these factors play significant roles in promoting regional economies. However, fixed capital investment, the number of employed people, and the rate of population growth are negatively affected. For the indirect effects, FDI under w1 and w2 are significantly positive, indicating that FDI has positive spatial spillover effects on the economic growth of the surrounding areas. A region’s fixed capital investment and industrial structure would have siphon effects that inhibit economic growth in the surrounding areas.
4.3.2. Influence Factors of Low-Level Economic Club
For the low-level economic club, Moran’s I indices under the three weight matrices were 0.538, 0.372, and 0.206 respectively, which were significant at a 1% level and indicated very significant positive correlations among the 17 low-level regions. The LM test results under different weight matrices are shown in Table 5. The results show that SLM should be selected under w1, w2, and w3. A spatial Durbin model was used as a robustness test for comparison. In accordance with the representativeness of the research objectives and the results of the Hausman test under different interaction effects, we chose the time-individual double-fixed effect model. For different weight matrices, the estimation results of the corresponding models show that: (1) In addition to fixed capital investment and population growth rate, the other factors are significant and the regression results under different weight matrices are consistent in the number of employees, industrial share, service share, social consumption, and power consumption, having positive effects on economic development, while patent authorization has negative effects on economic development. (2) The LR test and log-likelihood value show that SDM had a better fitting effect than SLM.

Table 5.
Empirical test of low-level economic space club.
The SDM under the time-individual double-fixed effect was decomposed into spatial effects through partial differentiation. Table 6 shows that: (1) The number of employees, industrial development, service industry development, social consumption, and power consumption can not only have positive effects on economic development but also can influence the surrounding areas by spatial spillover effects. The number of employees brings positive spillover effects to the economic growth of neighboring and similar distance areas but brings negative spillover effects to similar economies. Industrial development and service industry development brings positive spillover effects to the economic growth of neighboring regions with similar distances and similar economies. Social consumption brings negative spillover effects to similar economies. Power consumption brings positive spillover effects to neighboring areas but brings negative spillover effects to similar economies. (2) Scientific and technological innovation, as well as FDI, has negative effects on economic development. Scientific and technological innovation brings positive spillover effects to the economic growth of regions at similar distances areas but brings negative spillover effects to similar economies. FDI brings negative spillover effects to neighboring regions at similar distances.

Table 6.
Direct, indirect, and total effects of SDM model of low-level economic space club.
For the direct effects, the industrial development and service industry development are larger and more significant than those of the other factors, indicating that these two factors are important for promoting economic growth in low-level regions. Social consumption and power consumption are also important driving forces of economic growth. Both innovation and FDI are significantly negative, which is unexpected and indicates that innovation and economic liberalization in the low-level areas have not yet reflected the ability of economic promotion.
For the indirect effects, the development of industry and service industry has the strongest positive spatial spillover effects and shows that the optimization of industrial structure can bring radiation effects to low-level areas. The positive spillover effects of human capital are also strong for neighboring and nearby regions but it brings negative effects to economically comparable regions. Interestingly, scientific and technological innovation brings positive spatial spillover effect to regions with similar distances while bringing negative spatial spillover effects to economically comparable regions.
5. Conclusions
We examined the spatial convergence clubs of economic growth in 31 regions of mainland China. The results show that the level of economic development in each region has a significant spatial correlation. In both high- and low-level regions, spatial convergence clubs are formed. Three spatial convergence clubs were formed in the 11 high-level regions, which are mainly concentrated in the eastern coastal and central regions. The lower-level club consists of 17 regions, mainly in the central, western, and northeastern regions. Beijing, Tianjin, and Shanxi do not converge in any club. Among the four major regions, the eastern region still maintains the leading position. Except for Beijing and Tianjin, the remaining eight eastern regions are in the high-level club. As a bridge between the eastern and western regions, the central region is more closely connected with the western region. Except for Shanxi, Anhui, and Henan, the remaining three central regions are in the low-level club. All 12 western regions converge in the low-level club. The northeastern region became divided, as Liaoning’s level of economic development became higher than those of Heilongjiang and Jilin, so Liaoning subsequently joined the high-level club. The economic growth of Anhui is still behind that of the Yangtze River Delta economic zone. Hebei in the Beijing-Tianjin-Hebei economic zone is at a low level.
We constructed three weight matrices based on adjacency, distance, and economic factors; then, we analyzed the influencing factors for the economic growth of the different clubs by using spatial lag, error, and Durbin models. Industrial development was found to have the most important effects on the levels of economic development of both the high- and low-level clubs, indicating that industrialization has played a decisive role in economic development over the past 40 years. However, under new industrial divisions, patterns of competition, and the need for low-carbon development, regional development needs to break through the traditional mode of industrialization and take a new path of industrialization through technological innovation according to market demand [40]. Market vitality is also an important factor in the economic growth of a region. However, studies have shown that the diversification of consumer demand has led to mismatches with domestic supply, the lack of which hinders the upgrading of consumption, whose role in driving economic growth has lessened [41]. In the face of fierce international competition, increasing the added value of products, improving the supply capacity of the domestic market, expanding domestic demand, and promoting consumption upgrading through industrial and technological innovation are of great significance to realizing the long-term steady growth of regional economies.
The development of the service industry and power consumption are also significant for regional economic growth. Regardless of whether a region is high- or low-level, scientific and technological innovation cannot affect its economic growth but can produce only weak spatial spillover effects on a low-level region. Since the long-term innovation-driven effects are stronger than the short-term effects [42], the organic combination of innovation and related industries—for example, increasing the added value of products and services—can promote sustainable economic growth in backward regions, so as to achieve endogenous economic growth and form competitive advantages. Therefore, promoting independent innovation, improving the productivity of physical resources, optimizing and upgrading industrial structures, and transforming the modes of economic development in backward areas are important for their catching up with more developed areas.
Physical capital and human capital can have complicated spatial spillover effects on both the high- and low-level clubs. For limited physical and human capital, adjusting the proportions between developed and backward regions is the key to narrowing regional economic gaps. FDI in backward regions has yet to show its ability to promote economy. In fact, FDI in backward regions is far lower than in developed regions, which have absolute advantages when opening up more to the outside world. Therefore, the economic liberalization level of developed regions should be further deepened while positive policy guidance should be adopted for backward regions to reduce the barriers to FDI and improve the absorption capacity for new foreign technologies.
The results show that the eastern region is strong while the central, western, and northeastern regions are accelerating to catch up, which is the long-term trend of China’s regional economic development. Promoting economic zone construction requires economic growth in Hebei and Anhui to enhance the competitiveness of the Beijing-Tianjin-Hebei and Yangtze River Delta economic zones while encouraging regional integration. In addition to strengthening economic ties with the central and eastern regions, we should also focus on developing the Sichuan-Chongqing economic zone to exert the growth pole effect and drive the growth of the western region. We must strengthen the roles of Liaoning in driving northeast China, increasing regional connectivity, and promoting the revitalization of northeast China.
We propose the following suggestions to sustain the growth of high-level regions and encourage the rapid growth of low-level regions through the coordinated development of regional economies and stable development of the macroeconomy. First, when formulating regional policies, the government should pay attention to the spatial dependencies between regions and the heterogeneity of spatial spillover effects between regions and then formulate differentiated development strategies targeted at developed and underdeveloped regions. Second, the transformation of heavy industries into light and service industries has become a trend. To promote the economic growth of backward regions in addition to social consumption as the main focus, scientific and technological innovation that drives high-quality economic development is the key to implementing new development concepts and sustaining economic growth. Third, the transfer of labor-intensive industries from developed to backward regions is important for encouraging the flow of labor, breaking down barriers to population flow, and activating the resources and market potential of the backward regions. Fourth, increasing the economic liberalization of backward regions can be achieved by increasing the linkages among all the regions. Moreover, it is also important to participate in the global value chain while improving the quality and scope of investments by launching international enterprises in backward regions and overseas investments by launching domestic enterprises.
Regional economic convergence is a complex and long-term dynamic process. Academics have not yet provided a standard theoretical system, analytical framework, and test standard. Because of the selection of research methods and economic indicators, this study can be a resource for future studies of regional economic convergence. However, this study had the following limitations. First, the difference between NTL and traditional economic indicators has not been distinguished while the characteristics of NTL representing regional economies have been clarified. Second, the dynamic characteristics of regional economic convergence have not been explored, so the effects of dynamic changes in the influencing factors on regional dynamic convergence cannot be tested.
Author Contributions
Conceptualization: Y.W.; data curation: Q.X.; formal analysis: Q.X.; funding acquisition: Y.W.; methodology: Q.X.; software: Q.X.; original draft: Q.X. and Y.W.; revisions and proofing: Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partly supported by the Fundamental Research Funds for the Central Universities (Grant no. 222202224014).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://ngdc.noaa.gov/eog/download.html.
Conflicts of Interest
The authors declare that their research has been conducted in the absence of any commercial or financial relationship that could be construed as a potential conflict of interest.
References
- Wang, Q.; Liu, J.; Liu, D. The convergence characteristics and spatial spillover effect test of China’s provincial economic growth. World Econ. Pap. 2020, 3, 91–106. [Google Scholar]
- Pan, W. Regional economic difference and convergence in China. Soc. Sci. China 2010, 1, 72–84. [Google Scholar]
- Shen, K.; Ma, J. The characteristics of “Club Convergence” of China’s economic growth and Its causes. Econ. Res. J. 2002, 1, 33–39, 94–95. [Google Scholar]
- Li, L.; Liu, B. Prospects for Major Issues of China’s Regional Economy Development During the 14th Five-year Plan Period. J. Manag. World 2020, 36, 36–51. [Google Scholar]
- Iammarino, S.; Rodriguez-Pose, A.; Storper, M. Regional inequality in Europe: Evidence, theory and policy implications. J. Econ. Geogr. 2019, 19, 273–298. [Google Scholar] [CrossRef]
- Palomino, J.; Rodríguez, G. Peru’s Regional Growth and Convergence in 1979–2017: An Empirical Spatial Panel Data Analysis. Doc. Trab. Work. Pap. 2019. [Google Scholar] [CrossRef]
- Tian, L.; Wang, H.H.; Chen, Y.J. Spatial externalities in China regional economic growth. China Econ. Rev. 2010, 20, S20–S31. [Google Scholar] [CrossRef]
- Zhang, J.L.; He, L.; Chen, Y.J.; Cheng, L.D. Total factor productivity and convergence of China’s textile industry. Ind. Text. 2022, 73, 171–176. [Google Scholar]
- Kong, Q.X.; Li, R.R.; Ni, Y.; Peng, D. Does China’s green economic recovery generate a spatial convergence trend: An explanation using agglomeration effects and fiscal instruments. Econ. Chang. Restruct. 2022. [Google Scholar] [CrossRef]
- Zhu, Y.; Liang, D.; Liu, T. Can China’s underdeveloped regions catch up with green economy? A convergence analysis from the perspective of environmental total factor productivity. J. Clean. Prod. 2020, 255, 120216. [Google Scholar] [CrossRef]
- Li, Z.; Li, D.; Yang, W.; Qi, X. The spatial-temporal evolution and spatial convergence of ecological total factor productivity in China. Energy Environ. 2022, 33, 617–639. [Google Scholar] [CrossRef]
- Xiao, Q.L.; Wang, Y.; Zhou, W.X. Regional Economic Convergence in China: A Comparative Study of Nighttime Light and GDP. Front. Phys. 2021, 9, 525162. [Google Scholar] [CrossRef]
- Qin, C.; Ye, X.; Liu, Y. Spatial Club Convergence of Regional Economic Growth in Inland China. Sustainability 2017, 9, 1189. [Google Scholar] [CrossRef]
- Li, F.; Li, G.D.; Qin, W.S.; Qin, J.; Ma, H.T. Identifying Economic Growth Convergence Clubs and Their Influencing Factors in China. Sustainability 2018, 10, 2588. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, W.; Wang, X. Regional convergence clubs in China: Identification and conditioning factors. Ann. Reg. Sci. 2019, 62, 327–350. [Google Scholar] [CrossRef]
- Hao, R. Opening up, market reform, and convergence clubs in China. Asian Econ. J. 2008, 22, 133–160. [Google Scholar]
- Guo, Y.; Fan, B.; Long, J. Practical Evaluation of China’s Regional high-quality development and Its spatiotemporal Evolution Characteristics. J. Quant. Tech. Econ. 2020, 37, 118–132. [Google Scholar]
- Fang, L.; Nie, G.; Zhang, X.; Song, X.; Wang, Y. The Dynamic Evolution of Provincial Government Debt Development Level in China from 2009 to 2018. Econ. Geogr. 2021, 41, 23–29, 99. [Google Scholar]
- Zhou, D.; Zhong, S. Spatial Spillover and the Club Convergence of Financial Development: A case Study of the Yangtze River Delta. Manag. Rev. 2018, 30, 72–81. [Google Scholar]
- Furkova, A.; Chocholata, M. Spatial Econometric Modelling of Regional Club Convergence in the European Union. Ekon. Cas. 2016, 64, 367–386. [Google Scholar]
- Quah, D.T. Empirics for Growth and Distribution: Stratification, Polarization, and Convergence Clubs. J. Econ. Growth 1997, 2, 27–59. [Google Scholar] [CrossRef]
- Phillips, P.C.B.; Sul, D. Transition Modeling and Econometric Convergence Tests. Econometrica 2007, 75, 1771–1855. [Google Scholar] [CrossRef]
- Quah, D.T. Empirical Cross Section Dynamics in Economic Growth. Eur. Econ. Rev. 1993, 37, 426–434. [Google Scholar] [CrossRef]
- Bickenbach, F.; Bode, E. Markov or not Markov—This should be a question. In Proceedings of the 42nd Congress of the European Regional Science Association: “From Industry to Advanced Services—Perspectives of European Metropolitan Regions”, Dortmund, Germany, 27–31 August 2002. [Google Scholar]
- Tian, X.; Zhang, X.H.; Zhou, Y.H.; Yu, X.H. Regional income inequality in China revisited: A perspective from club convergence. Econ. Model. 2016, 56, 50–58. [Google Scholar] [CrossRef]
- Zhang, W.L.; Fu, J.B.; Ju, Q. A study on the model of economic growth convergence in developing regions: An empirical analysis from Henan Province, China. Empir. Econ. 2020, 59, 547–567. [Google Scholar] [CrossRef]
- Makeienko, M. Symbolic Analysis Applied to the Specification of Spatial Trends and Spatial Dependence. Entropy 2020, 22, 466. [Google Scholar] [CrossRef]
- Bai, J.; Li, S.; Wang, N.; Shi, J.; Li, X. Spatial Spillover Effect of New Energy Development on Economic Growth in Developing Areas of China-An Empirical Test Based on the Spatial Dubin Model. Sustainability 2020, 12, 3249. [Google Scholar] [CrossRef]
- Wu, J.S.; Peng, J.; Li, W.F. Intercalibration of DMSP-OLS Night-time Light Data by the Invariant Region Method. Int. J. Remote Sens. 2013, 34, 7356–7368. [Google Scholar] [CrossRef]
- Liu, H.; Wang, J.T.; Liu, H.B.; Chen, Y.Z.; Liu, X.H.; Guo, Y.L.; Huang, H. Identification of Relative Poverty Based on 2012–2020 NPP/VIIRS Night Light Data: In the Area Surrounding Beijing and Tianjin in China. Sustainability 2022, 14, 5559. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, B.; Yang, C. An extended time-series (2000–2018) of global NPP-VIIRS-like nighttime light data from a cross-sensor calibration. Earth Syst. Sci. Data 2020, 13, 889–906. [Google Scholar] [CrossRef]
- Si, L.J.; Wang, C.Q. Regional Economic Disparity, Dynamic Evolution and Convergence of Urban Agglometions in China: Research Based on Nighttime Light Data of Ten Urban Agglomeration. Shanghai J. Econ. 2021, 10, 38–52. [Google Scholar]
- Yan, T.; Zhang, X.; Chen, H.; Li, K. Evolution of Regional Differences in Urban Economic Development in China from 2001 to 2016. Econ. Geogr. 2019, 39, 11–20. [Google Scholar]
- Dai, M.; Mao, R. The Industrial Heterogeneity, the Industrial Structure, and the Provincial Growth Convergence in China. J. Manag. World 2015, 6, 34–46, 62, 187. [Google Scholar]
- Zou, W.; Zhou, H. Classification of Growth Clubs and Convergence Evidence from Panel Data in China. China World Econ. 2007, 15, 91–106. [Google Scholar] [CrossRef]
- Liu, S. Research on the Regional differences Decomposition and convergence Mechanism of economic quality in China. J. Quant. Tech. Econ. 2019, 36, 24–41. [Google Scholar]
- Ma, J.M.; Jia, H.Y. The Role of Foreign Direct Investment on Income Convergence in China after Early 1990s from a Spatial Econometric Perspective. Rev. Dev. Econ. 2015, 19, 829–842. [Google Scholar] [CrossRef]
- Zhao, J.; Fan, J. Empirical Research on the Inherent Relationship Between Economic Growth and Energy Consumption in China. Econ. Res. J. 2007, 8, 31–42. [Google Scholar]
- Lian, Y.; Wang, W.; Ye, R. The Efficiency of Hausman test statistics: A Monte Carlo Investigation. J. Appl. Stat. Manag. 2014, 33, 830–841. [Google Scholar]
- Shi, D. The Green Development and the New Stage of Industrialization: Progress in China and Comparison with Others. China Ind. Econ. 2018, 10, 5–18. [Google Scholar]
- Sun, Z.; Xu, X. Industrial Innovation and Consumption Upgrade: An Empirical Study Based on the Perspective of Supply-side Structural Reform. China Ind. Econ. 2018, 7, 98–116. [Google Scholar]
- Li, S.; Fu, Q.; Liu, K. Innovation-driven spatial spillover effect and regional economic convergence: Based on spatial measurement analysis. J. Ind. Eng. Eng. Manag. 2020, 34, 191–201. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).